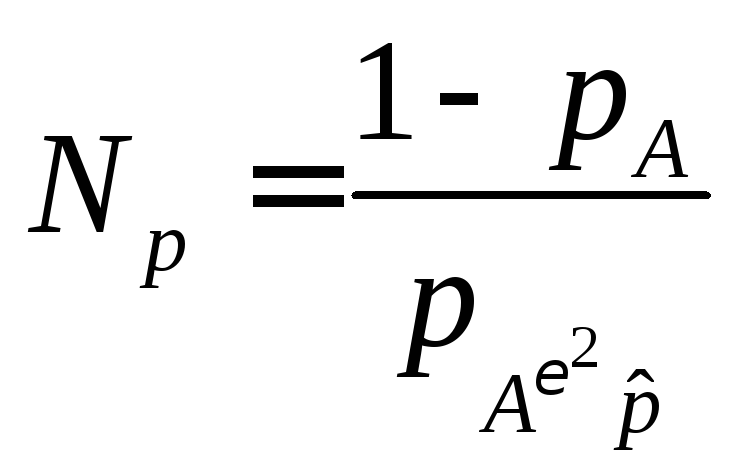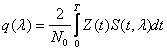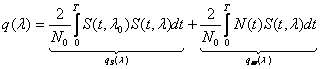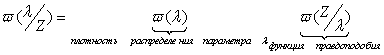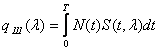Аномальные ошибки при оценке параметров сигналов

ГЛАВА 3.  Оценка неизвестных параметров сигнала

         Определим элементарный сеанс связи как совокупность следующих операций:

¨ выбор источником одного сообщения из множества возможных и отправление его получателю;

¨ преобразование посланного сигнала под действием помех в реализацию смеси, которая наблюдается получателем;

¨ принятие получателем по наблюдению реализации смеси решения о том, какое сообщение выбрал в данном случае источник, т.е. оценка сообщений. 

         Применение некоторого правила принятия решения (оценивания) – это установление соответствия между наблюдаемой получателем реализацией смеси и одной из возможных оценок.

         Функция двух переменных r(x_i, x_j^*), значение которой (в некотором масштабе) равно стоимости решения x_j^* при условии, что передавалось сообщение x_i , называется функцией потерь (риска, штрафа и т.д.) Если оценка ошибочна, т.е. при истинном передаваемом сообщении x_i принято решение  x_j^*≠ x_i , то неправильные действия получателя повлекут за собой некоторые потери r, которых бы не было, будь оценка безошибочной.

3.1. Байесовские оценки при различных функциях потерь

         Измерение координат и параметров сигналов является задачей статической в силу флюктуационной природы помех в смеси х(t) и в силу случайного (непредсказуемого) изменения параметров сигнала. Задачи оценки параметров сигнала и обнаружения сигнала имеют общую статистическую модель.

Рекомендуемые материалы

         Поскольку потери   r(x_i, x_j^*) в каждом элементарном сеансе случайны из-за случайности x_i, и x_j^* , построение критерия после задания функции потерь требует определения статистически устойчивого параметра, характеризующего качество системы на множестве сеансов. Чаще всего применяется подход, основанный на использовании математического ожидания потерь, при котором гарантируется минимум суммарных потерь. Математическое ожидание потерь:

                                                  (3.1)

называется средним риском, а система, минимизирующая средний риск (при условии, что функция потерь не зависит от правила решения), называется оптимальной байесовой системой.

                             (3.2)

где — совместное распределение вероятностей сообщения и оценки.

                                                                (3.3)

                                                                (3.4)

          Функцию p_z называют условным средним риском при данной реализации смеси, а р_х – условным средним риском при данном истинном сообщении. Условный средний риск при данном сообщении р_х может служить характеристикой качества системы, а условный средний риск при данной реализации смеси р_z используется для определения структуры оптимальной байесовой системы.

3.2. Неравенство Рао – Крамера

          Существует неравенство, с помощью которого можно определить нижнюю границу среднеквадратических ошибок при использовании любых оценок параметра. Предположим, что границы области действительной оси, где плотность распределения  отлична от нуля, не зависит от . Это условие выполняется, например, если на всей действительной оси и для х ≥ 0. Предположим, кроме того, что функция  дифференцируема по параметру .

          Введем новое обозначение

                                 (3.5)

чтобы подчеркнуть зависимость функции правдоподобия от неизвестного параметра .

          Неотрицательная величина

                        (3.6)

называется информацией по Фишеру о параметре , содержащейся в выборке х.

          Найдем искомую нижнюю границу дисперсии оценок (неравенство

Рао — Крамера)

                                       (3.7)

          Правая часть неравенства является также нижней границей среднеквадратических отклонений оценок от оцениваемого параметра.

          Для несмещенных оценок

                                                (3.8)

3.3. Оценки максимального правдоподобия, их свойства и связь с байесовскими

          Рассмотрим оценку векторного параметра , оптимальную по критерию максимального правдоподобия. Так как логарифм – монотонная функция, то экстремумы функций L_x() и ln L() достигаются при одинаковых аргументах . Поэтому критерий максимального правдоподобия можно представить в виде:

                                (3.9)

Функцию правдоподобия можно заменить статистикой отношения правдоподобия

                                           (3.10)

где  — фиксированный вектор.

Система уравнений максимального правдоподобия

                             (3.11)

          Оценку , удовлетворяющую системе уравнений, называют оценкой максимального правдоподобия векторного параметра   или совместной оценкой максимального правдоподобия компонента этого векторного параметра. Оценки максимального правдоподобия состоятельные и асимптотически совместно эффективные.

          Рассмотрим связь байесовых оценок с оценкой максимального правдоподобия на примере нормального распределения амплитуды сигнала.

          Байесовская оценка амплитуды а квазидетерминированного сигнала

                         (3.12)

где — оценка максимального правдоподобия,

— отношение дисперсии априорного распределения амплитуды к дисперсии ее оценки максимального правдоподобия.

          Из (3.11) следует, что байесовская оценка представляет среднее взвешенное двух величин: оценки максимального правдоподобия и априорного среднего а₀, причем отношение веса, приписываемого первой величине, к весу второй равно Ясно, что в рассматриваемом случае байесовская оценка распределенной по нормальному закону амплитуды сигнала, совпадает с оценкой максимальной апостериорной плотности

          Если отношение неограниченно возрастает, т.е. дисперсия оценки максимального правдоподобия много меньше дисперсии априорного распределения, то  ~, т.е. байесовская оценка приближается к оценке максимального правдоподобия. Если дисперсия априорного распределения много меньше дисперсии оценки максимального правдоподобия, то  ~, т.е. наблюдаемая реализация не влияет на оценку, которая принимается равной априорному среднему оцениваемого параметра.

3.4. Функционал отношения правдоподобия гауссовского процесса

          Оптимальный по любому из критериев качества аналоговый алгоритм проверки гипотезы Н₀ против альтернативы Н₁ предписывает сравнение с порогом логарифма функционала отношения правдоподобия. Поэтому для синтеза оптимального аналогового алгоритма обнаружения сигнала на фоне гауссовской помехи необходимо определить логарифм функционала отношения правдоподобия гауссовского случайного процесса с указанием ограничений, при которых этот функционал существует.

          Гипотеза Н₀ состоит в том, что наблюдаемая реализация принадлежит гауссовскому процессу с корреляционной функцией В(t,y) и средним значением s₀(t), а альтернатива Н₁ – в том, что реализация принадлежит гауссовскому процессу с той же корреляционной функцией и средним значением s₁(t). Для рассматриваемой здесь задачи обнаружения  s₀(t) ≡ 0 и s₁(t) ≡ s(t).

          Запишем логарифм отношения правдоподобия для дискретной выборки х=(х₁,…,х_n), полученной отбором на интервале (0,Т) через равные промежутки времени из реализации х(t) гауссовского случайного процесса

    (3.13)

где Х – вектор с компонентами s_1, s₀ – векторы с компонентами  — корреляционная матрица (положительно определенная) размером nxn.

Введем вектор V=K^-1(s₁-s₀).

Тогда s₁-s₀ = KV.

          После преобразований логарифм функционала отношения правдоподобия равен

                      (3.14)

где V(t) – решение интегрального уравнения:

                      (3.15)

тогда среднее значение логарифма функционала отношения правдоподобия при гипотезе и при альтернативе равен:

                                    (3.16)

где .

3.5. Оценка амплитуды детерминированного сигнала

          Рассмотрим оценку максимального правдоподобия неизвестной амплитуды а детерминированного сигнала as(t) на фоне аддитивной гауссовской помехи. Эта оценка является частным случаем оценки при m=1 и =a. Для рассматриваемого скалярного случая следует

                                          (3.17)

V(t) – решение линейного интегрального уравнения

                                       (3.18)

          Из анализа оценки максимального правдоподобия векторного параметра линейной модели сигнала следует, что оценка амплитуды сигнала несмещенная и эффективная, т.е.

   

          Доверительный интервал для неизвестной амплитуды сигнала может быть представлен неравенствами

                      (3.19)

где — процентная точка нормального распределения, определяемая по заданному коэффициенту доверия γ.

          Для реализации оптимального аналогового алгоритма оценивания амплитуды сигнала на фоне аддитивной гауссовской помехи необходимо вычислить нормированный корреляционный интеграл. Эту операцию можно осуществить при помощи аналогового коррелометра или физически реализуемого линейного фильтра с импульсной характеристикой

                                (3.20)

          Оптимальная оценка амплитуды получается в конце наблюдения на выходе фильтра, если только импульсная характеристика фильтра нормируется величиной s_T (или умножается на дисперсию оценки).

3.6. Оценки амплитуды и фазы гармонического сигнала

          Сигнал s(t;) – гармонический с известной частотой ω₀ и неизвестными амплитудой  а и фазой φ:

           (3.21)

                                                                          (3.22)

                                                         (3.23)

          Решая систему двух линейных относительно ₁ и ₂ уравнений, получаем оценки максимального правдоподобия этих параметров:

                            (3.24)

                              (3.25)

где

          Полагая ω₀Т = 2πk, где k – целое число, находим оценки максимального правдоподобия:

                                           (3.26)

                                           (3.27)

          Эти оценки максимального правдоподобия можно использовать для получения оценок амплитуды и фазы сигнала на фоне аддитивного белого гауссовского шума:

3.7. Совместная оценка частоты и фазы гармонического сигнала при аддитивном белом шуме

          Рассмотрим пример совместной оценки двух неэнергетических параметров – частоты ω и фазы φ гармонического сигнала, наблюдаемого в аддитивной смеси с белым шумом. Поскольку частота неизвестна, следует условиться, на какой момент времени приходится оценка фазы. Будем считать, что оценивается фаза, приходящаяся на середину интервала наблюдения, а наблюдение проводится, начиная с момента – Т/2 до момента Т/2.

          Уравнение, определяющее оценку частоты, запишется так:

          Приведенное уравнение не имеет аналитического решения, но можно показать, что оно имеет множество корней. Воспользуемся линеаризацией этой формулы, предположив, что известно опорное значение ω, близкое к искомому решению ω^* = ω + Δω^*, причем  Δω^*Т<< π/2. Тогда, считая,  что cos Δω^*(t₁ – t₂) ≈ 1 и sin Δω^*(t₁ – t₂) ≈ Δω^*(t₁ – t₂), получаем

                        (3.28)

          Если частота находится в диапазоне шириной Ω = ω_max — ω_min, то для определения опорного значения частоты ω_i требуется число каналов

                                                                 (3.29)

3.8. Понятие об аномальных ошибках измерения

          Ошибки системы, определяющей параметры радиосигнала, обычно принято делить на два вида: малые (нормальные) и большие (аномальные). Такое разделение ошибок имеет смысл потому, что каждый из видов удобнее оценивать различными критериями. При оценке аномальных ошибок величина среднеквадратической ошибки и максимальной ошибки чаще всего не важны, ибо само появление аномальной ошибки означает нарушение работы системы, невыполнение поставленной задачи. Аномальные ошибки наиболее удобно характеризовать вероятностью их появления, и при проектировании следует создавать условия, при которых эта вероятность пренебрежимо мала.

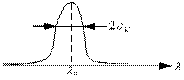
          Если речь идет о начальном этапе проектирования, когда система еще не определена и выбирается только радиосигнал, можно считать аномальными все ошибки, лежащие вне главного экстремума функции различия ε (Δх). Область нормальных ошибок обычно располагается симметрично около нуля на оси Δх (или около х_и на оси х). Обозначим соответствующие граничные точки х_н1 и х_н2 (рис. 3.1). Эти точки лежат внутри области априорной неопределенности, границы которой обозначены х_а1 и х_а2.

Рис. 3.1. К определению аномальных ошибок

          Допустим, что причиной является действие аддитивной помехи. Тогда, учитывая, что оценка параметра определяется наименьшим значением измеренной функцией различия, получаем достаточное условие отсутствия аномальных ошибок в виде

                                      (3.30)

          Это условие можно записать в виде

                          (3.31)

или, отбросив одинаковые члены в обеих частях неравенства, получим достаточное условие в виде

                                          (3.32)

причем это условие должно выполняться для всех х, лежащих вне области х_н1 – х_н2.

3.9. Понятие об оценке (фильтрации) меняющихся параметров сигналов

          Задача оценки сообщения сводится к задаче оценки совокупности параметров (при оценке в целом) или одного параметра (при фильтрации).

          Предположим, что на интервале наблюдения (0,Т) получена реализация х(t) аддитивной смеси сигнала ξ(t) и помехи η(t), которые представляют центрированные случайные процессы с известными корреляционными функциями В_ξ(u,υ)  и В_η(u,υ), причем и сигнал, и помеха необязательно гауссовские. Необходимо синтезировать оценку   стохастического сигнала по наблюдаемой реализации х(τ), 0≤ τ ≤ T.

          Определение оценки как функционала от х(τ) при t=T называется задачей фильтрации сигнала.

          Располагая реализацией аддитивной смеси сигнала и помехи, иногда необходимо определить также оценку некоторого стохастического сигнала , представляющего требуемую операцию над сигналом ξ(t). Это может быть линейная операция (сдвиг, однократные или многократные дифференцирование и интегрирование) или даже нелинейная.

3.10. Линейная и нелинейная фильтрация

          Линейная фильтрация. Рассмотрим задачу оптимальной линейной фильтрации сигнала на фоне аддитивной помехи, которая формируется следующим образом. В качестве оценки сигнала принимается линейный функционал

                            (3.33)

т.е. значение процесса на выходе линейного фильтра с импульсной характеристикой h(t,τ), когда на вход действует наблюдаемая реализация смеси сигнала с помехой. Необходимо в классе этих линейных фильтров определить фильтр, оптимальный по критерию минимума среднего квадрата ошибки оценивания

                            (3.34)

где

          Так как по предложению сигнал и помеха – центрированные случайные процессы, то средний квадрат ошибки совпадает с ее дисперсией. Поэтому критерий минимума среднего квадрата ошибки оценивания будем называть критерием минимума дисперсии ошибки. Для определения импульсной характеристики h^* (t,τ) такого оптимального фильтра достаточно располагать указанными априорными данными о сигнале и помехе.

          Если реализация х(τ) аддитивной смеси сигнала и помехи определена для всех действительных значений τ, тогда линейную оценку сигнала можно представить в виде

                                    (3.35)

Дисперсия ошибки оценивания

    (3.36)

         Из этой формулы видно, что дисперсия линейной оценки зависит только от корреляционных функций сигнала и помехи и не зависит от распределения вероятностей этих случайных процессов.

         Обозначим через h^* (t,τ) импульсную характеристику оптимального линейного фильтра, а через ε^*(t) ошибку оценивания сигнала при оптимальной линейной фильтрации. Тогда

 (3.37)

Это соотношение выражает так называемый принцип ортогонального проецирования, который является достаточным условием минимума дисперсии ошибок оценивания сигнала.

         Положительными свойствами линейных методов являются их простота по сравнению с нелинейными методами и для синтеза оптимального линейного фильтра требуются ограниченные статистические данные о сообщениях и смесях, что весьма важно с точки зрения практики.  

         Нелинейная фильтрация. Если отказаться от условия линейности алгоритма обработки наблюдаемой реализации, то в более широком классе допускаемых оценок можно получить оценки, которые по заданному критерию минимума среднего квадрата ошибки будут лучше линейных оценок. В общем случае оптимальной по критерию минимума среднего квадрата ошибки, оценкой сигнала  по наблюдаемой реализации х(τ) аддитивной смеси сигнала с помехой η(t), является условное среднее

                     (3.38)

         За исключением гауссовских процессов и η(t) вычисление нелинейного функционала встречает значительные трудности, связанные, прежде всего с определением апостериорной плотности вероятности. Один из подходов к решению задачи оптимальной нелинейной фильтрации состоит в ограничении класса исследуемых нелинейных процессов марковскими или их компонентами. При таком ограничении удается преодолеть трудности, связанные с вычислением апостериорной плотности оцениваемого процесса. После этого можно получить оценку по критерию минимума среднего квадрата ошибки. Мы рассмотрим другой подход, основанный на аппроксимации нелинейного функционала  рядом Вольтерра:

     (3.39)

         Если K_m≡0 для всех m>1, то получаем линейный функционал и K₁(u) можно трактовать как импульсную характеристику линейного фильтра. Добавление членов ряда при m>1 означает введение нелинейности. Совокупность функций K_m(u₁,…u_m), m=характеризует нелинейный фильтр n-го порядка. Ограничение  суммы ряда первыми n членами позволяет аппроксимировать функционал F[x(τ)] процессом на выходе фильтра n –го порядка при входной воздействии x(τ).

         Если n=2, то для формирования оценки использована простейшая нелинейная система – фильтр второго порядка. Задача состоит в том, чтобы определить характеристику K₂(u₁,u₂) нелинейности так, чтобы средний квадрат ошибки

                                     (3.40)

был минимальным.

         После преобразований получим минимальное значение дисперсии ошибки

 (3.41)

или

                    (3.42)

где

                          (3.43)

— минимальная дисперсия ошибки линейной оценки.

Таким образом, использование оптимального нелинейного корректирующего звена в фильтре второго порядка позволяет дополнительно уменьшить дисперсию ошибки на

            (3.44)

3.11. Фильтры Винера и Калмана

         Задача фильтрации (на фоне стационарного шума) сообщения, представляющего собой стационарный случайный процесс, при условии, что наблюдение длится бесконечно долго, называют обычно винеровской фильтрацией, а фильтры, структура которых находится при такой постановке задачи, называются винеровскими.

         Если и сигнал, и помеха стационарны, а фильтр представляет линейную систему с постоянными во  времени параметрами, то при t→∞ импульсная характеристика h^*(t) оптимального фильтра определяется решением интегрального уравнения

                   (3.45)

       При этом минимальное значение дисперсии ошибки

                                                                (3.46)

После преобразований следует

           (3.47)

                   Из этого условия находим передаточную функцию оптимального физически реализуемого фильтра

                           (3.48)

                   Обратным преобразованием Фурье из последней формулы находим импульсную характеристику h^*(t) оптимального физически реализуемого фильтра (решение уравнения Винера-Хопфа). Таким образом, определение оптимального физически реализуемого фильтра сводится к факторизации спектра аддитивной смеси сигнала и помехи, и разложению функции на сумму сопряженных функций. Указанная факторизация может быть всегда выполнена, если выполняется условие Винера-Пэли

                                    (3.49)

                   Фильтр Калмана. Если спектр сигнала представляет рациональную функцию переменной ω², то сигнал ξ(t) со спектром получаем на выходе формирующего фильтра, структура которого определяется дифференциальным уравнением первого порядка где — белый шум со спектральной интенсивностью S_0. Предположим, что помеха η(t) также представляет белый шум с интенсивностью N₀, причем  η(t) и  некоррелированы. Используя линейную оценку сигнала, получим

                        (3.50)

Бесплатная лекция: «4.16 Внешняя политика» также доступна.

где

                   Выражение (3.50) представляет собой оптимальный по критерию минимума дисперсии ошибки алгоритм фильтрации сигнала со спектром на фоне аддитивного белого шума. Соответствующая этому алгоритму структурная схема оптимального фильтра (фильтра Калмана) изображена на рис. 3.2, где, кроме того, показана структурная схема формирующего фильтра, на выходе которого получаем сигнал со спектром. Здесь осталась неизвестной функция k(t), которую называют коэффициентом усиления. Она равна

                                          (3.51)

т.е. коэффициент усиления полностью определяется минимальным значением дисперсии ошибки при линейной фильтрации сигнала.

Рис. 3.2. Схема фильтра Калмана

ОШИБКИ ИЗМЕРЕНИЯ ВРЕМЕННОГО ПОЛОЖЕНИЯ

ИМПУЛЬСНОГО СИГНАЛА

Цель работы

Изучение механизмов образования ошибок
измерения временного положения
радиоимпульсного сигнала и способов
обеспечения требуемой точности измерения

Общие сведения

В лабораторной работе, выполняемой на
ПЭВМ, изучаются ошибки измерения
временного положения импульсного
радиосигнала s(t),
поступающего на вход измерительного
приемника в смеси с белым шумомu_n(t):

,

Входное воздействие y(t)
наблюдается на интервале времениT,
обычно значительно большем, чем
длительность сигналаt₀.
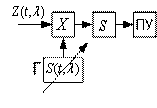
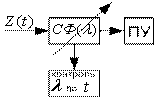
Оптимальный приемник (рисунок),
вырабатывающий оценку максимального
правдоподобия, состоит из фильтра СФ,
согласованного с сигналом, амплитудного
детектора АД и устройства, определяющего
координату абсолютного максимума
напряжения на выходе на интервале Т
[1].

Моделирование фильтрации и детектирования,
как правило, выполняют на основе метода
комплексной огибающей [2], поскольку
имитация сигналов на несущей (промежуточной)
частоте f₀потребовала
бы порядка 2f₀Tотсчетов сигнала равна П, то метод
огибающей позволяет уменьшить число
отсчетов до 2ПТ. Выигрыш в объеме
вычислений определяется отношениемf₀/П и достигает
десятков или даже сотен раз.

В работе имитируется сигнал без
внутриимпульсной модуляции с «колокольной»
(гауссовской) огибающей

Сигнал воспроизводится в пределах
,
следовательно параметримеет смысл его полной длительности.
Параметр,
входящий во второе из этих выражений,
является наиболее распространенным
определением длительности «колокольного»
импульса, определяемой по уровню

Если по этому же уровню определить и
ширину амплитудного спектра
этой огибающей, то оказывается.
Этим и объясняется общепринятость
такого определения.
Естественно параметрыисвязаны
между собой и их связь устанавливается,
как легко видеть, соотношением

Значение огибающей «на границах» сигнала

составляет всего 1% от максимального
значения S₀. При
таком достаточно полном воспроизведении
сигнала его параметры (эффективные
длительность и ширина спектра, энергия
и др.) могут вычисляться без учета
ограничения физической длительности.
Например, энергия может быть определена
по формуле

,

расширение пределов интегрирования в
которой до бесконечных существенно
упрощает результат. Аналогично можно
определить нормированную автокорреляционную
функцию сигнала

,

Откуда легко находится эффективная
ширина спектра

.

При имитации белого шума, имеющего, как
известно, бесконечную дисперсию,
дискретный эквивалент представляется
[3] последовательностью гауссовских
некоррелированных чисел с дисперсией
,
гдеN₀– спектральная
плотность мощности помехиu_n(t).

Обработка смеси сигнала с шумом приводит
к образованию на выходе АД напряжения,
подчиняющегося обобщенному распределению
Релея. Огибающая нормированной
корреляционной функции шума на выходе
СФ совпадает с корреляционной функцией
сигнала
,
что является следствием согласованной
фильтрации. С помощью приведенных выше
выражений, можно записать

.

Если, по аналогии с определением полной
длительности сигнала
,
пренебречь корреляцией значений шума,
когда,
то интервал корреляции.
При прохождении шума через детектор
происходит некоторое расширение его
спектра и, следовательно, уменьшение
интервала корреляции. Поэтому в качестве
оценки интервала корреляции шума на
выходе АД примем значение.

В работе изучаются ошибки измерения
временного положения сигнала (ИВПС)
трех видов:

– нормальные ошибки, вызванные действием
шума;

-аномальные ошибки;

-ошибки, обусловленные дискретизацией
сигнала.

Соответствующей манипуляцией параметров
модели значения отдельных составляющих
ошибки могут быть сделаны незначительными,
что позволяет изучать влияние оставшихся
компонентов.

Из трех перечисленных типов ошибок
здесь остановимся подробно на аномальных
в силу их особенной специфики, а также
определенной сложности регистрации в
эксперименте. Как известно [1], они
возникают при слабом сигнале, когда
выбросы шума на выходе АД (см.рисунок)
могут превысить значение смеси сигнала
с шумом. В этих случаях результат
измерения
t₀
существенно отличается отt_0,
что и оправдывает название
таких ошибок. Очевидно, что
– равномерно распределенная на
интервале (0,Т) случайная величина с
математическим ожиданием Т/2 и дисперсией
Т² /12.

(1)

Выражение (1) определяет условную
дисперсию ошибок- при условии, что
аномальное измерение состоялось.
Безусловная дисперсия ошибок с учетом
альтернативного результата определяется
формулой

(2)

В которой

(3)

— дисперсия нормальных измерений
(потенциальная точность);

—
отношение сигнал/шум (ОСШ);

— вероятность возникновения аномального
результата.

Для ее нахождения разобьем интервал Т
на М=ЕП_э/2,5 подынтервалов длиной,
приближено определяющей длительность
интервала корреляции выходного шума.
Последнее дает возможность рассматривать
отсчеты шума из различных подынтегралов
как независимые, что существенно
облегчает анализ аномальных измерений.

Введем локальную вероятность аномального
измерения
—
вероятность того, что при сравнении
напряжения смеси сигнала с шумом и
произвольного отсчета шума последний
окажется больше. При релеевских
распределениях этих отчетов нетрудно
получить формулу [1]:

Полную вероятность аномального измерения
в силу некоррелированности отчетов
шума, отстоящих на интервал 2,5/П_э ,
приближенного определим выражением

Представляя (1) и (3) в (2) и переходя к
относительной ошибке
,
получим

Величина
характеризует меру увеличения ошибок
(по отношению к нормальным), вызванного
аномальными измерениями. Непосредственное
измерение дисперсии(или нормированной дисперсии)
в эксперименте затруднено следующими
обстоятельствами.

Обычно интересуется зависимостью
(или)
от ОСШ.
Располагая этой зависимостью, можно
определить пороговое значение ОСШ, при
превышении которого обеспечивается
нормальный режим измерения. При уменьшениив процессе получения этой зависимости
вклад второго слагаемого в (2) возрастает
из-за увеличения
.Причем
при достаточно больших значениях(пропорционально, согласно)
величина этого вклад оказывается
доминирующей в (2) уже при весьма малых
значениях
.
Следовательно, среднее число экспериментов,
в которых наблюдаются аномальные
результаты , оказывается существенно
меньше общего числа экспериментовN.
Для получения статистических достоверных
результатов измерениятребуется, чтобы объем экспериментаоказывается непосильным даже для ПЭВМ
с высокой производительностью. Как
показывает более тонкий количественный
анализ, зависимости(или)
от,
при котором в эксперименте измеряется
зависимость
от,
а с ее помощью зависимостьотопределяется
расчетным путем по формуле (4).

При экспериментальном определении
вероятности аномального измерения
требуется классифицировать результат
обработки каждой реализации в приемнике,
как нормальной или аномальной, если

,
(5)

Что обусловлено следующими соображениями.
Полная длительность полезного сигнала
(“по нулям”) на входе СФ и АД (см. рисунок)
составляет
,
следовательно, его влияние на выходное
напряжение АД проявляется в пределах
этого временного интервала. Поэтому
появление оценкив пределах указанного промежутка не
относятся к числу аномальных результатов.
Следовательно, аномальными признаются
те оценки, которые отвечают условию
(5).

Известно. Что дисперсия статистического
измерения вероятности
определяется формулой

Откуда необходимый объем статистического
эксперимента

Где
—
относительная дисперсия измерения
вероятности.

Соседние файлы в папке Аномальные ош. + (методичка)

• #

  27.03.201514.28 Кб3RKEGA.COM
• #

  27.03.201534 б3rts.cmd

• #

  27.03.20157 б3TELEGR

• #

  27.03.20154.1 Кб3VGA.FNT

• #

  27.03.20151.02 Кб3Аномаль ошибки.lnk

• #

Журнал «Успехи современной радиоэлектроники» №5 за 2023 г.

Статья в номере:

Аномальные ошибки определения несущей частоты сигнала в широкополосных приемниках средств радиомониторинга. Часть 1. Выражения для оценки вероятностей возникновения аномальных ошибок

Тип статьи:
научная статья

DOI: https://doi.org/10.18127/j20700784-202305-02

УДК: 621.396.62

Авторы:

Аннотация:

Страницы: 20-34

Для цитирования

Подстригаев А.С., Смоляков А.В., Калинин Д.А. Аномальные ошибки определения несущей частоты сигнала в широкополосных приемниках средств радиомониторинга. Часть 1. Выражения для оценки вероятностей возникновения аномальных ошибок // Успехи современной радиоэлектроники. 2023. T. 77. № 5. С. 20–34. DOI: https://doi.org/10.18127/j20700784-202305-02

Список источников

Дата поступления: 27.03.2023

Одобрена после рецензирования: 13.04.2023

Принята к публикации: 28.04.2023

Применим закон распределения равновероятности:

              (4)

Подставляя (1) и (2) и (4) и вводя обозначения с фазой

Последовательная схема может быть
также реализована на основе СФ.

Нормальные
и аномальные ошибки.

Необходимо рассматривать

,
тогда

если ,
либо  соответствует , то 

Эта же задача стоит при
радиоизмерениях. И она может решаться при построении оптимального устройства, с
различными критериями.

Статистические
критерии оценки непрерывных параметров

сигнала.

Cуществуют
следующие критерии:

ü 
Критерий максимума функции правдоподобия.

ü 
максимальная апостериорная плотность распределения вероятности
параметра .

ü 
Критерий минимума средне квадратичной ошибки.

ü 
Критерий Баеса.

Распишем каждый критерий более
подробно.

Критерий максимального
правдоподобия.

 оценка
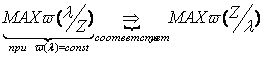
максимального правдоподобия.

Критерий максимальной
апостериорной вероятности.

Рассмотрим статистическую схему:

Оценивается значение
максимального параметра.

Критерий минимальной средне
квадратичной ошибки.

Ошибки, связанные с фиксацией , не выходящие за пределы
корреляционного пика называются нормальные ошибки (инстр. ошибки,
ошибки шума).

Шумовая составляющая:

Дисперсия:

Шумовая составляющая имеет вид , но её особенность, что
количество сигнальных выбросов тем больше, чем больше шумовой уровень.

При регистрации шумовой выброс
может быть принят за сигнальный выброс. Ошибка может составить , а нормальные ошибки не выходят за
корреляционные пределы. Вероятность появления аномальных ошибок характеризует
неправильность измерения вообще.

При проектировании задают
соотношение сигнал/шум, чтобы избежать аномальных ошибок.

А среднеквадратичная ошибка
параметра .

Расчёт среднеквадратической ошибки.

Рассмотрим формулу исходя из
геометрического происхождения сигнала.