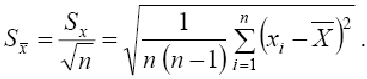Способы уменьшения случайных погрешностей.
1
Метод многократных измерений.
Тогда
2.
Метод комплексирования.
Проводят
измерения одной и той же величины при
следующих условиях:
А)
несколькими однотипными СИ одновременно
Б)
разнотипными
С)
различными методами( разными группами
экспериментаторов)
В
дальнейшем проводится объединение
результатов наблюдений по алгоритму
средневзвешенной оценки, более точным
наблюдениям больший вес. Объединение
может быть только для равноточных
результатов по систематической
погрешности.
3.
Метод косвенных измерений.
В
отдельных случаях позволяет уменьшить
случайную погрешность.
Средства измерений. Характеристики си для определения результатов измерений.
Средство
измерений –
это техническое средство (или комплекс),
предназначенное для измерений, имеющее
нормированные метрологические
характеристики, воспроизводящие и (или)
хранящие единицу физической величины,
размер которой принимается неизменным
(в пределах установленной погрешности)
в течение известного интервала времени
[24].
Данное определение раскрывает
метрологическую
сущность СИ,
заключающуюся
в умении хранить (или воспроизводить)
единицу ФВ
и
в неизменности размера хранимой единицы
во времени.
Первое обуславливает возможность
выполнения измерения, суть которого,
как известно, состоит в сравнении
измеряемой величины с ее единицей.
Второе принципиально необходимо,
поскольку при изменении размера хранимой
единицы ФВ с помощью данного СИ нельзя
получить результат с требуемой точностью.
Под метрологическими характеристиками
(MX)
понимают такие характеристики СИ,
которые позволяют судить об их пригодности
для измерений в известном диапазоне с
известной точностью. В отличие от СИ
приборы или вещества, не имеющие
нормированных MX,
называют индикаторами. СИ — это
техническая основа метрологического
обеспечения.
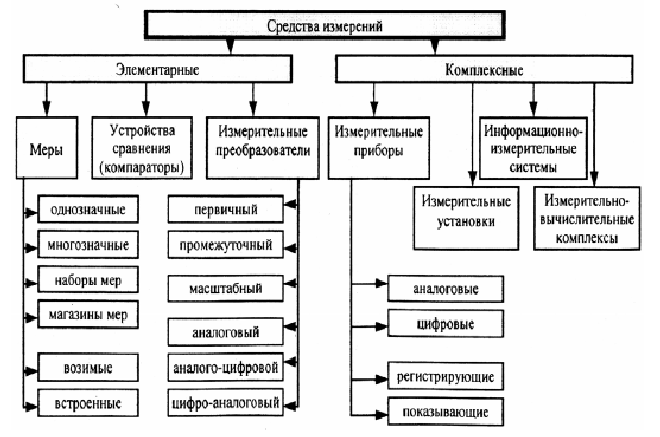
Классификация
средств измерений по их роли в процессе
измерения и
выполняемым
функциям
Эталон
–
средство измерений (или их комплекс),
предназначенное для воспроизведения
и (или) хранения единицы и передачи ее
размера нижестоящим по поверочной схеме
СИ и утвержденное в качестве эталона в
установленном порядке.
Меры
— это СИ, воспроизводящие или хранящие
физическую величину заданного размера.
Меры могут быть однозначными,
воспроизводящими одно значение физической
величины (гиря, калибр на заданный
размер, образцы твердости, шероховатости,
катушка сопротивления, нормальный
элемент, воспроизводящий значение
ЭДС), и
многозначными
— для воспроизведения плавно или
дискретно ряда значений одной и той же
физической величины (измерительный
конденсатор переменной емкости, набор
конечных мер, магазин емкостей,
индуктивности и сопротивления,
измерительные линейки).
Для
ряда областей измерений, и в первую
очередь для физико-химических измерений,
чрезвычайно перспективным средством
повышения эффективности поверочных
работ является применение стандартных
образцов (СО). Правила работы с СО
устанавливает ГОСТ 8.315—97. Согласно
этому документу,
стандартный
образец состава и свойств веществ и
материалов
— это средство измерений в виде вещества
(материала), состав или свойства которого
установлены аттестацией. Можно
дать и другое определение: стандартный
образец
— образец вещества (материала) с
установленными в результате метрологической
аттестации
значениями
одной или более величин, характеризующими
свойство или состав этого вещества
(материала).
Стандартные
образцы предназначены для обеспечения
единства и требуемой точности измерений
посредством:
•
градуировки,
метрологической аттестации и поверки
СИ;
•
метрологической
аттестации методик выполнения измерений;
•
контроля
показателей точности измерений;
•
измерения
ФВ, характеризующих состав или свойства
веществ материалов, методами сравнения.
По
своему назначению СО исполняют роль
мер, однако в отличие от «классических»
мер они имеют ряд особенностей. Например,
образцы состава воспроизводят значения
ФВ,
характеризующих
состав или свойства именно того материала
(вещества), из которого они изготовлены.
Стандартные образцы, как правило не
являются изделиями, они реализованы
обычно в виде части или порции однородного
вещества (материала), причем эта часть
является полноценным носителем
воспроизводимой единицы ФВ, а не ее
части Эта особенность образцов отражена
в требованиях к их однородности по
составу и свойствам. Однородность
материала, из которого сделан образец,
имеет принципиальное значение, в то
время как для меры такая характеристик
часто является второстепенной.
Измерительные
преобразователи
— СИ, предназначенные для выработки
сигнала измерительной информации в
форме, удобной для передачи, дальнейшего
преобразования, обработки и хранения,
но не доступной для непосредственного
восприятия наблюдателем. Это термопары,
измерительные трансформаторы,
усилители,
преобразователи давления. По месту,
занимаемому в измерительной цепи, они
делятся на первичные, промежуточные и
т. п. Конструктивно они выполняются либо
отдельными блоками, либо составной
частью СИ. Не следует отождествлять
измерительные преобразователи с
преобразовательными элементам. Последние
не имеют метрологических характеристик,
как, например, трансформатор тока или
напряжения.
Измерительный
прибор
— СИ, предназначенное для переработки
сигнала измерительной информации в
другие, доступные для непосредственного
восприятия наблюдателем формы. Различают
приборы прямого действия (амперметры,
вольтметры,
манометры)
и приборы сравнения (компараторы). По
способу отсчета измеряемой величины
СИ делятся на показывающие (аналоговые,
цифровые), регистрирующие (на
бумажную
или магнитную ленту) и т. п.
Измерительная
установка
— совокупность функционально объединенных
СИ и вспомогательных устройств,
расположенных в одном месте. Например,
поверочные установки, установки для
испытания электротехнических, магнитных
и других материалов. Измерительная
установка позволяет предусмотреть
определенный
метод
измерения и заранее оценить погрешность
измерения.
Измерительная
система
— это комплекс СИ и вспомогательных
устройств
с компонентами связи (проводные,
предназначенный
для выработки сигналов измерительной
информации в форме, удобной для
автоматической обработки, передачи
и/или
использования в автоматических системах
управления. В отличие от измерительных
установок, предусматривающих изменения
режима и условий функционирования,
измерительная система не воздействует
на режимы работы, а предназначена только
для сбора и/или хранения информации.
Частными случаями измерительной системы
являются информационно-вычислительный
комплекс (ИВК), информационно-измерительные
системы (ИИС). К последним можно отнести
системы автоматического контроля,
системы технического диагностирования,
системы распознавания образов, системы
для передачи неизмерительной информации.
При организации поверки рабочих СИ
используют различные эталоны и образцовые
СИ. СИ, как правило, работают совместно
с датчиками (измерительными
преобразователями), имеющими свои MX.
При
использовании средств измерений
принципиально важно знать степень
соответствия информации об измеряемой
величине, содержащейся в выходном
сигнале, ее истинному значению. С этой
целью для каждого СИ вводятся и нормируются
определенные метрологические
характеристики (МХ).
Метрологическими
называются
характеристики свойств СИ, оказывающие
влияние на результат измерения и его
погрешности. Характеристики, устанавливаемые
нормативными документами, называются
нормируемыми,
а определяемые экспериментально –
действительными.
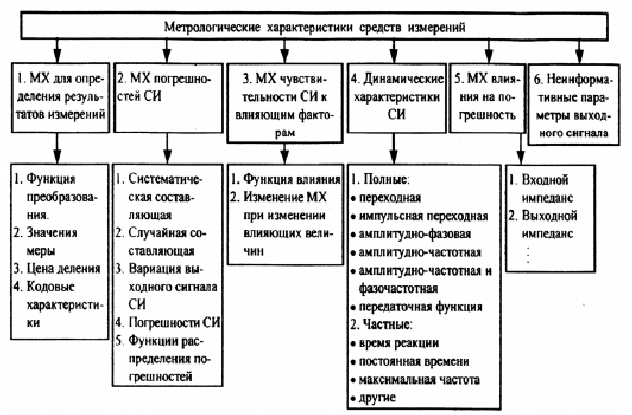
Номенклатура
метрологических характеристик средств
измерений
Неинформативным
называется параметр входного сигнала
СИ,
не связанный функционально с измеряемым
параметром. Например, частота переменного
тока при измерении его амплитуды.
Нормальные метрологические характеристики
(НМХ) устанавливаются документами. MX,
определенные документами, считаются
действительными. На практике наиболее
распространены следующие MX СИ.
Диапазон
измерений
— область значений измеряемой величины,
для которой нормированы допускаемые
пределы погрешности СИ (для преобразователей
— это диапазон преобразования):
Предел
измерения
— наибольшее или наименьшее значение
диапазона измерения. Для мер
— это номинальное значение воспроизводимой
величины.
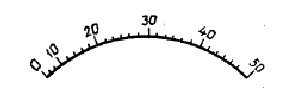
Рис
32 Неравномерная шкала СИ
Например,
у шкалы на рис. 32 начальный участок
(~20%) сжат, потому производить отсчеты
на нем неудобно. Тогда предел измерения
по шкале составляет 50 ед., а диапазон —
10…50 единиц.
Цена
деления шкалы
— разность значений величин,
соответствующих двум соседним
отметкам
шкалы. Приборы с равномерной шкалой
имеют постоянную цену деления, а с
неравномерной — переменную. В этом
случае нормируется минимальная цена
деления.
Чувствительность
— отношение изменения сигнала Δу на
выде СИ к вызвавшему это изменение
изменению Δх сигнала на входе
S=
Δу/Δх.
Например,
для стрелочного СИ — это отношение
перемещения dl
конца стрелки к вызвавшему его изменению
dx
измеряемой величины
S=
dl/dx.
Таким
образом, для неравномерных шкал величина
S=
var,
и степень неравномерности шкалы оценивают
через коэффициент
J=Smax/Smin
Для
равномерных шкал S
= Sср
= const
и Sср
= l/хN
где xN
— диапазон измерений.
Поскольку
х и у могут быть выражены в различных
единицах то величина S
имеет размерность [мм/А], [мм/В], [градус/В]и
т.д. Говоря о чувствительности, указывают
чувствительность тока, напряжения и т.
д. Иногда для оперирования безразмерными
единицами вводят понятие относительной
чувствительности
S0
= (Δy/y0)/(Δx/x0),
где
х0,
у0
— номинальные (или средние) величины.
Чувствительность нельзя отождествлять
с порогом чувствительности — наименьшим
значением измеряемой величины, вызывающим
заметное изменение показаний прибора.
Величину,
обратную чувствительности, называют
постоянной прибора С = 1/S.
Как
правило, выходным сигналом СИ является
отсчет (показание) в единицах величины.
В этом случае постоянная прибора С
равна цене деления. Поэтому для СИ с
неравномерной шкалой чувствительность
— величина переменная.
Вариация
(гистерезис)
— разность между показаниями СИ в данной
точке диапазона измерения при возрастании
и убывании измерений величины и неизменных
внешних условиях:
Н=
|хв
– xу|,
где
хв,
ху
— значения измерений образцовыми СИ
при возрастании и убывании величины
х. Следует иметь в виду, что, хотя вариация
показаний СИ вызывается случайными
факторами, сама она — не случайная
величина.
Зависимость
между выходным и входным сигналом СИ,
полученную экспериментально, называют
градуировочной характеристикой (или
статической характеристикой
преобразования), которая
может быть представлена аналитически,
графически или в виде таблицы.
Градуировочная характеристика может
изменяться под воздей ствием внешних
и внутренних причин. Например, при
быстром изменении тока подвижная часть
СИ, вследствие инерции, не успевает
«следить» за изменением тока.
Градуировочная характеристика в этом
случае должна выражаться дифференциальным
уравнением.
Характеристики
погрешности измерений в статике.
Статический
режим –
это такой режим работы СИ, при котором
изменением измеряемой величины за
время, требуемое для проведения одного
измерения, можно пренебречь. В динамическом
режиме такое
пренебрежение недопустимо, поскольку
указанное изменение превышает допустимую
погрешность.
Все
погрешности СИ в зависимости от внешних
условий делятся на основные и
дополнительные.
Основная
погрешность — это погрешность СИ при
нормальных условиях эксплуатации. Как
правило, нормальными условиями
эксплуатации являются: температура
293±5 К или 20±5 °С, относительная влажность
воздуха 65+15% при 20 °С, напряжение в сети
питания 220 В+10% с частотой 50 Гц±1%,
атмосферное давление от 97,4 до 104 кПа,
отсутствие электрических и магнитных
полей (наводок). В рабочих условиях,
зачастую отличающихся от нормальных
более широким диапазоном влияющих
величин, при необходимости нормируется
дополнительная погрешность СИ.
Классы
точности средств измерений
.
При технических измерениях, когда не
предусмотрено выделение случайных и
систематических составляющих, когда
не существенна динамическая погрешность
СИ, когда не учитываются влияющие
(дестабилизирующие) факторы и т.д., можно
пользоваться более грубым нормированием
— присвоением СИ определенного класса
точности по ГОСТ 8.401—80.
Класс
точности
–это обобщенная характеристика СИ,
выражаемая пределами допускаемых
значений его основной и дополнительной
погрешностей, а также другими
характеристиками,
влияющими на точность. Класс точности
не является непосредственной оценкой
точности измерений, выполняемых этим
СИ, поскольку погрешность зависит еще
от ряда факторов: метода измерений,
условий измерений и т.д. Класс точности
лишь позволяет судить о том, в каких
пределах находится погрешность СИ
данного типа. Общие положения деления
средств измерений по классу точности
устанавливает ГОСТ 8.401–80.года). Класс
точности СИ уже включает систематическую
и случайную погрешности. Однако он не
является непосредственной характеристикой
точности измерений, выполняемых с
помощью этих СИ, поскольку точность
измерения
зависит
и от метода измерения, взаимодействия
СИ с объектом, условий измерения и т.д.
В
связи с большим разнообразием как самих
СИ, так и их MX,
ГОСТ 8.401—80 устанавливает несколько
способов назначения классов точности.
При этом в основу заложены следующие
положения:
•
в
качестве норм служат пределы допускаемых
погрешностей, включающие систематические
и случайные составляющие;
•
основная
δосн
и все виды дополнительных погрешностей
δдоп
нормируются
порознь (см. п. 3.2).
Первое
положение свидетельствует о необходимости
разрабатывать СИ с учетом однократного
отсчета показаний по величине общей
погрешности. Второе положение направлено
на обеспечение максимальной однородности
однотипных СИ. .
Пределы
допускаемых основной и дополнительной
погрешностей выражают
в форме приведенных, относительных или
абсолютных
погрешностей.
Выбор формы представления зависит от
характера
изменения
погрешностей в пределах диапазона
измерений, а также от
условий
применения и назначения СИ.
Пределы
допускаемой абсолютной основной
погрешности
устанавливаются
по одной из формул: Δ
= ±а
или
Δ
= ±(а
+
bx),
где
х
–
значение
измеряемой величины или число делений,
отсчитанное по шкале;
а,
b
–
положительные числа, не зависящие от
х.
Первая формула описывает чисто аддитивную
погрешность (рис. 6.4, а), а вторая – сумму
аддитивной и мультипликативной (рис.
6.4, б) погрешностей (рис. 6.4, в). В технической
документации классы точности,
установленные
в виде абсолютных погрешностей,
обозначают, например, «Класс точности
М», а на приборе – буквой «М». Для
обозначения используются прописные
буквы латинского алфавита или римские
цифры, причём меньшие пределы погрешностей
должны соответствовать буквам, находящимся
ближе к началу алфавита, или меньшим
цифрам. Пределы допускаемой приведенной
основной погрешности определяются по
формуле γ
= Δ
/xN
=
± p
,
где xN
–
нормирующее значение, выраженное в тех
же единицах, что и Δ;
р
–
отвлеченное положительное число,
выбираемое из ряда значений:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;…..
.
Рис.
6.4. Аддитивная а), мультипликативная б)
и суммарная в)
погрешности
в абсолютной и относительной формах
Нормирующее
значение xN
устанавливается
равным большему из пределов измерений
(или модулей) для СИ с равномерной,
практически равномерной или степенной
шкалой и для измерительных преобразователей,
для которых нулевое значение выходного
сигнала
находится
на краю или вне диапазона измерений.
Для СИ, шкала которых имеет условный
нуль, xN
равно
модулю разности пределов измерений.
Для приборов с существенно неравномерной
шкалой xN
принимают
равным всей длине шкалы или ее части,
соответствующей диапазону измерении.
В этом случае пределы абсолютной
погрешности выражают, как и длину шкалы,
в единицах длины, а на средстве измерений
класс
точности
условно обозначают, например, в виде
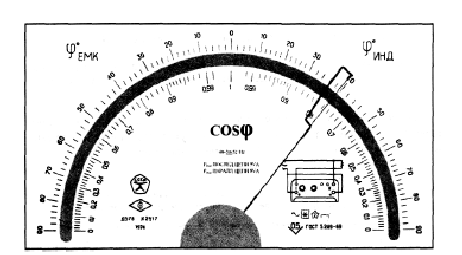
значка 0,5 , где 0,5 –значение числа р
Рис.
6.5.Лицевая панель фазометра класса
точности 0,5 с существенно
неравномерной
нижней шкалой
В
остальных рассмотренных случаях класс
точности обозначают конкретным числом
р,
например 1,5. Обозначение наносится на
циферблат,
щиток или корпус прибора (рис. 6.6).
Рис
6.6. Лицевая панель амперметра класса
точности 1,5
с
равномерной шкалой
В
случае если абсолютная погрешность
задается формулой ±(a
+
bx),
пределы допускаемой относительной
основной погрешности δ
= Δ
x
=
±[c
+
d(
|xk/
x|
−1)],
(6.2)
где
с,
d
–
отвлеченные положительные числа,
выбираемые из ряда:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;….
; xk
–
больший (по модулю) из пределов измерений.
При использовании формулы (6.2) класс
точности обозначается в виде «0,02/0,01»,
где числитель – конкретное значение
числа с,
знаменатель – числа d
(рис.
6.7).
Причем,
как правило, c>d.
Например, класс точности 0,02/0,01 означает,
что с = 0,02,
а
d=
0,01, т. е. приведенное значение относительной
погрешности к началу диапазона измерения
γн
= 0,02%, а к концу — γк=
0,01%.
В
обоснованных случаях пределы допускаемой
относительной основной погрешности
определяют по более сложным формулам
либо в виде графика или таблицы.
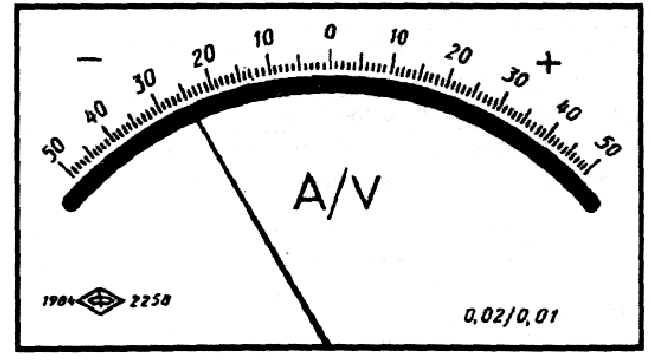
Рис.
6.7. Лицевая панель ампервольтметра
класса точности 0,02/0,01
с
равномерной шкалой
Пределы
допускаемой относительной основной
погрешности определяются по формуле
δ
= Δ /x
=
±q
,
если
Δ
= ±a
.
Значение
постоянного числа q
устанавливается
так же, как и значение числа p.
Класс точности на прибор обозначается
в виде
,
где 0,5 – конкретное значениеq
(рис.
6.8).
Так
обозначают классы точности мостов
переменного тока, счетчик0в электроэнергии,
делителей напряжения, измерительны
трансформаторов и др.
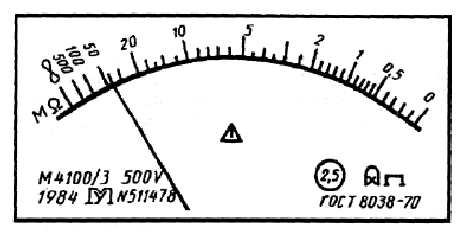
Рис
6.8. Лицевая панель мегаомметра класса
точности 2,5
с
неравномерной шкалой
В
стандартах и технических условиях на
СИ указывается минимальное значение
x0
, начиная с которого применим принятый
способ выражения пределов допускаемой
относительной погрешности. Отношение
xk/
x0
называется динамическим диапазоном
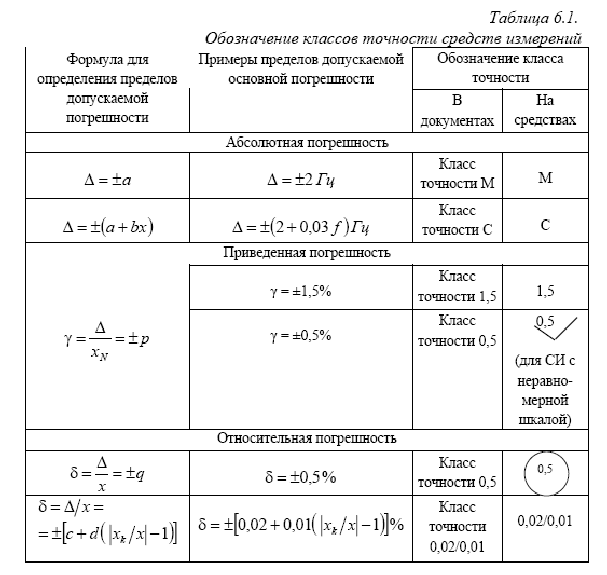
измерения. Правила построения и примеры
обозначения классов точности в
документации
и на средствах измерений приведены в
таблице 6.1.
Наиболее
широкое распространение (особенно для
аналоговых СИ) получило нормирование
класса точности по приведенной
погрешности:
γ=±Δ/xN100%
= ±A·10n.
xN
условное обозначение класса точности
в этом случае зависит от нормирующего
значения хN
т.
е. от шкалы СИ. Если xN
представляется в единицах измеряемой
величины, то класс точности обозначается
числом, совпадающим с пределом допускаемой
приведенной погрешности. Например,
класс 1,5 означает, что γ = 1,5%. Если xN
—
длина шкалы (например, у амперметров),
то класс 1.5 означает, что γ =1,5% длины
шкалы.
Не
всегда число, обозначающее класс
точности, показывает предел допускаемой
погрешности. В частности, у некоторых
однозначных мер электрических величин
оно характеризует нестабильность,
показывая, на сколько процентов значение
меры мо-
ет
изменяться в течение года.
Как уменьшить погрешность при проведении измерений: советы и рекомендации
При проведении измерений любой физической величины невозможно избежать определенной погрешности. Она может возникать из-за различных факторов, таких как неточность приборов, внешние условия, неопределенность измеряемых объектов и другие. Тем не менее, существуют различные способы, которые позволяют минимизировать погрешность при проведении измерений.
Определение типов погрешностей
На начальном этапе необходимо определить типы погрешностей, которые могут возникнуть при измерении.
Случайная погрешность
Самый распространенный вид погрешности, который возникает из-за случайных факторов, таких как температурные изменения, встряхивание прибора, дрожание руки и т.д.
Систематическая погрешность
Этот вид погрешности связан с инструментом измерения и возникает вследствие неправильной работы прибора, например, из-за его калибровки, неисправности датчика или возрастания пробега.
Советы по минимизации погрешности
После определения типов погрешностей можно перейти к поиску способов их уменьшения.
Обеспечение стабильных метеоусловий
Внешние условия играют важную роль в измерениях. По возможности следует проводить измерения при стабильных метеоусловиях, чтобы снизить влияние температурных, атмосферных и других факторов.
Правильная калибровка приборов
Систематическая погрешность связана с работой инструмента измерения. Поэтому, перед началом работы, необходимо убедиться, что прибор настроен на правильное измерение и калиброван.
Повышение верности приборов
Выбирая инструмент для измерения нужно уделить внимание уровню его верности. Чем выше точность устройства, тем меньше будет погрешность в измерениях.
Повторяемость измерений
При повторении измерений несколько раз можно снизить влияние случайных ошибок и получить более точные результаты.
Правильная техника измерения
Наконец, чтобы измерить физическую величину наиболее точно, необходимо использовать правильную технику измерения. Например:
- Для измерения длины следует использовать линейку с наименее возможными делениями и линиями.
- Для измерения массы следует использовать точные(электронные) весы.
- Для измерения напряжения и силы тока нужно выбирать подходящие приборы, соответствующие диапазонам величин.
Вывод
Погрешность — неизбежный фактор при проведении измерений. Однако, существует множество способов, которые помогают снизить ее влияние на результаты измерений. Качество измерений напрямую влияет на результаты в эксперименте, поэтому применение техники минимизации погрешностей должно стать обязательным при выполнении любых работ.
Статья рассмотрит определение, причины, типы и способы учета ошибок измерения, а также приведет примеры для лучшего понимания.
О чем статья
Введение
В теории вероятности существует понятие ошибки измерения, которое играет важную роль в оценке и предсказании случайных событий. Ошибка измерения возникает, когда результаты измерений отличаются от истинных значений. В данной лекции мы рассмотрим определение ошибки измерения, причины ее возникновения, типы ошибок и способы учета и уменьшения ошибок измерения. Также мы рассмотрим примеры ошибок измерения и их влияние на результаты исследований. Понимание ошибок измерения поможет нам более точно и надежно оценивать вероятности и принимать решения на основе статистических данных.
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Определение ошибки измерения
Ошибкой измерения называется расхождение между полученным результатом измерения и истинным значением величины, которую требуется измерить. Она возникает из-за неполноты или неточности используемых методов и средств измерения.
Ошибки измерения могут быть вызваны различными факторами, такими как:
- Неточность измерительных приборов и средств.
- Неправильная калибровка или настройка приборов.
- Влияние окружающей среды на измеряемую величину.
- Недостаточная квалификация оператора, осуществляющего измерение.
Ошибки измерения могут быть как систематическими, так и случайными. Систематические ошибки возникают вследствие постоянного смещения результатов измерений в одну сторону, например, из-за неправильной калибровки прибора. Случайные ошибки, в свою очередь, являются непредсказуемыми и могут возникать из-за различных факторов, таких как шумы в измерительной системе или неправильное чтение показаний прибора.
Для учета и уменьшения ошибок измерения используются различные методы, такие как повторные измерения, усреднение результатов, использование более точных приборов и т.д. Также важно проводить калибровку и проверку приборов регулярно, чтобы минимизировать возможные систематические ошибки.
Причины ошибок измерения
Ошибки измерения могут возникать по разным причинам. Рассмотрим некоторые из них:
Систематические ошибки
Систематические ошибки возникают из-за неправильной калибровки или неисправности измерительных приборов. Эти ошибки имеют постоянное значение и могут приводить к смещению результатов измерений в одну сторону. Например, если весы не откалиброваны правильно, то все измерения будут иметь постоянное смещение в большую или меньшую сторону.
Случайные ошибки
Случайные ошибки возникают из-за непредсказуемых факторов, таких как внешние воздействия, шумы в измерительной системе или неправильное чтение показаний прибора. Эти ошибки имеют случайное значение и могут приводить к разбросу результатов измерений. Например, при измерении температуры в помещении могут возникать случайные изменения из-за колебаний внешней температуры или воздушных потоков.
Человеческий фактор
Человеческий фактор также может быть причиной ошибок измерения. Неправильное обращение с приборами, неправильное чтение показаний, неправильное выполнение измерений – все это может привести к ошибкам. Например, неправильное установление шкалы на измерительном приборе или неправильное чтение показаний на цифровом дисплее.
Важно учитывать все эти причины ошибок измерения и принимать меры для их учета и уменьшения. Это поможет получить более точные и надежные результаты измерений.
Типы ошибок измерения
Ошибки измерения могут быть различными и классифицируются на несколько типов:
Систематические ошибки
Систематические ошибки возникают из-за постоянных и повторяющихся причин и приводят к постоянному смещению результатов измерений относительно истинного значения. Эти ошибки могут быть вызваны неправильной калибровкой прибора, несоответствием шкалы измерения или неправильным условиям эксперимента. Систематические ошибки могут быть учтены и скорректированы, если известна их природа и величина.
Случайные ошибки
Случайные ошибки возникают из-за случайных факторов, которые не могут быть полностью контролируемыми или предсказуемыми. Они могут быть вызваны флуктуациями внешних условий, неправильным чтением показаний прибора или неправильным обработкой данных. Случайные ошибки могут быть уменьшены путем повторения измерений и использования статистических методов для оценки их влияния.
Грубые ошибки
Грубые ошибки возникают из-за серьезных и очевидных ошибок в процессе измерения. Они могут быть вызваны неправильной установкой прибора, неправильным выбором метода измерения или неправильным обращением с образцом. Грубые ошибки обычно очевидны и могут быть легко обнаружены и исправлены.
Важно учитывать все эти типы ошибок измерения и принимать меры для их учета и уменьшения. Это поможет получить более точные и надежные результаты измерений.
Способы учета и уменьшения ошибок измерения
Ошибки измерения могут быть неизбежными, но существуют способы учета и уменьшения их влияния на результаты измерений. Вот некоторые из них:
Калибровка и контрольные измерения
Калибровка – это процесс сопоставления измеряемой величины с известным эталоном. Путем проведения контрольных измерений с использованием эталонов можно установить и скорректировать систематические ошибки измерения.
Использование повторных измерений
Повторные измерения позволяют учесть случайные ошибки и уменьшить их влияние на результаты. Чем больше повторных измерений проводится, тем более точные результаты можно получить путем усреднения значений.
Использование статистических методов
Статистические методы позволяют анализировать и оценивать ошибки измерения. Например, можно использовать методы регрессионного анализа для определения зависимостей между измеряемыми величинами и их ошибками.
Проверка и обслуживание измерительного оборудования
Регулярная проверка и обслуживание измерительного оборудования помогают обнаружить и исправить возможные неисправности, которые могут привести к ошибкам измерения.
Обучение и квалификация персонала
Обучение и квалификация персонала, работающего с измерительным оборудованием, играют важную роль в учете и уменьшении ошибок измерения. Правильное обращение с оборудованием и соблюдение методик измерения помогают минимизировать возможные ошибки.
Все эти способы помогают учесть и уменьшить ошибки измерения, что в свою очередь позволяет получить более точные и надежные результаты измерений.
Примеры ошибок измерения
Систематическая ошибка
Систематическая ошибка возникает, когда измерения смещены относительно истинного значения вследствие постоянного фактора или неправильной калибровки прибора. Например, если прибор для измерения длины имеет неправильно установленную шкалу, то все измерения будут смещены на одну и ту же величину.
Случайная ошибка
Случайная ошибка возникает вследствие непредсказуемых факторов, таких как шумы, вибрации, температурные изменения и т.д. Эта ошибка не имеет постоянного характера и может меняться при каждом измерении. Например, при измерении температуры в помещении с непостоянной температурой воздуха, каждое измерение может давать разные результаты.
Погрешность округления
Погрешность округления возникает при округлении чисел до определенного количества знаков после запятой. Например, если при измерении длины округлить результат до двух знаков после запятой, то возможна погрешность, так как истинное значение может быть ближе к следующему числу.
Погрешность параллакса
Погрешность параллакса возникает при измерении с помощью приборов, где наблюдатель не находится в одной плоскости с измеряемым объектом. Например, при измерении длины с помощью линейки, если наблюдатель не смотрит перпендикулярно к линейке, то измерение может быть неточным.
Погрешность прибора
Погрешность прибора возникает из-за неточности самого измерительного прибора. Каждый прибор имеет свою погрешность, которая указывается в его технических характеристиках. Например, если прибор для измерения массы имеет погрешность ±0.1 г, то результат измерения будет иметь погрешность в этом диапазоне.
Это лишь некоторые примеры ошибок измерения, которые могут возникать в различных ситуациях. Важно помнить, что ошибки измерения неизбежны, но с помощью правильных методов и техник их можно учесть и уменьшить, чтобы получить более точные результаты.
Таблица сравнения типов ошибок измерения
| Тип ошибки | Описание | Причины | Способы учета и уменьшения |
|---|---|---|---|
| Систематическая ошибка | Ошибка, которая возникает при измерении и всегда приводит к одному и тому же отклонению от истинного значения | Неправильная калибровка прибора, неправильная техника измерения | Повторное калибрование прибора, использование более точных методов измерения |
| Случайная ошибка | Ошибка, которая возникает при измерении и может приводить к различным отклонениям от истинного значения | Внешние факторы, такие как шум, вибрации, неправильное чтение прибора | Повторное измерение, усреднение результатов, использование статистических методов для оценки погрешности |
| Грубая ошибка | Очевидная ошибка, которая сильно отклоняется от истинного значения и может быть вызвана человеческим фактором или технической неисправностью | Неправильная установка прибора, неправильное чтение, неправильная обработка данных | Проверка и повторное измерение, исправление ошибки, обучение и обучение персонала |
Заключение
Ошибки измерения являются неизбежной частью любого измерительного процесса. Они могут возникать по разным причинам, таким как неточность приборов, неправильная калибровка или неправильное использование. Важно учитывать и уменьшать ошибки измерения, чтобы получить более точные результаты. Существуют различные способы учета и уменьшения ошибок, такие как повторные измерения, использование более точных приборов или применение математических методов коррекции. Понимание и учет ошибок измерения является важным навыком для всех, кто работает с данными и проводит измерения.
Способы уменьшения случайных погрешностей.
1
Метод многократных измерений.
Тогда
2.
Метод комплексирования.
Проводят
измерения одной и той же величины при
следующих условиях:
А)
несколькими однотипными СИ одновременно
Б)
разнотипными
С)
различными методами( разными группами
экспериментаторов)
В
дальнейшем проводится объединение
результатов наблюдений по алгоритму
средневзвешенной оценки, более точным
наблюдениям больший вес. Объединение
может быть только для равноточных
результатов по систематической
погрешности.
3.
Метод косвенных измерений.
В
отдельных случаях позволяет уменьшить
случайную погрешность.
Средства измерений. Характеристики си для определения результатов измерений.
Средство
измерений –
это техническое средство (или комплекс),
предназначенное для измерений, имеющее
нормированные метрологические
характеристики, воспроизводящие и (или)
хранящие единицу физической величины,
размер которой принимается неизменным
(в пределах установленной погрешности)
в течение известного интервала времени
[24].
Данное определение раскрывает
метрологическую
сущность СИ,
заключающуюся
в умении хранить (или воспроизводить)
единицу ФВ
и
в неизменности размера хранимой единицы
во времени.
Первое обуславливает возможность
выполнения измерения, суть которого,
как известно, состоит в сравнении
измеряемой величины с ее единицей.
Второе принципиально необходимо,
поскольку при изменении размера хранимой
единицы ФВ с помощью данного СИ нельзя
получить результат с требуемой точностью.
Под метрологическими характеристиками
(MX)
понимают такие характеристики СИ,
которые позволяют судить об их пригодности
для измерений в известном диапазоне с
известной точностью. В отличие от СИ
приборы или вещества, не имеющие
нормированных MX,
называют индикаторами. СИ — это
техническая основа метрологического
обеспечения.
Классификация
средств измерений по их роли в процессе
измерения и
выполняемым
функциям
Эталон
–
средство измерений (или их комплекс),
предназначенное для воспроизведения
и (или) хранения единицы и передачи ее
размера нижестоящим по поверочной схеме
СИ и утвержденное в качестве эталона в
установленном порядке.
Меры
— это СИ, воспроизводящие или хранящие
физическую величину заданного размера.
Меры могут быть однозначными,
воспроизводящими одно значение физической
величины (гиря, калибр на заданный
размер, образцы твердости, шероховатости,
катушка сопротивления, нормальный
элемент, воспроизводящий значение
ЭДС), и
многозначными
— для воспроизведения плавно или
дискретно ряда значений одной и той же
физической величины (измерительный
конденсатор переменной емкости, набор
конечных мер, магазин емкостей,
индуктивности и сопротивления,
измерительные линейки).
Для
ряда областей измерений, и в первую
очередь для физико-химических измерений,
чрезвычайно перспективным средством
повышения эффективности поверочных
работ является применение стандартных
образцов (СО). Правила работы с СО
устанавливает ГОСТ 8.315—97. Согласно
этому документу,
стандартный
образец состава и свойств веществ и
материалов
— это средство измерений в виде вещества
(материала), состав или свойства которого
установлены аттестацией. Можно
дать и другое определение: стандартный
образец
— образец вещества (материала) с
установленными в результате метрологической
аттестации
значениями
одной или более величин, характеризующими
свойство или состав этого вещества
(материала).
Стандартные
образцы предназначены для обеспечения
единства и требуемой точности измерений
посредством:
•
градуировки,
метрологической аттестации и поверки
СИ;
•
метрологической
аттестации методик выполнения измерений;
•
контроля
показателей точности измерений;
•
измерения
ФВ, характеризующих состав или свойства
веществ материалов, методами сравнения.
По
своему назначению СО исполняют роль
мер, однако в отличие от «классических»
мер они имеют ряд особенностей. Например,
образцы состава воспроизводят значения
ФВ,
характеризующих
состав или свойства именно того материала
(вещества), из которого они изготовлены.
Стандартные образцы, как правило не
являются изделиями, они реализованы
обычно в виде части или порции однородного
вещества (материала), причем эта часть
является полноценным носителем
воспроизводимой единицы ФВ, а не ее
части Эта особенность образцов отражена
в требованиях к их однородности по
составу и свойствам. Однородность
материала, из которого сделан образец,
имеет принципиальное значение, в то
время как для меры такая характеристик
часто является второстепенной.
Измерительные
преобразователи
— СИ, предназначенные для выработки
сигнала измерительной информации в
форме, удобной для передачи, дальнейшего
преобразования, обработки и хранения,
но не доступной для непосредственного
восприятия наблюдателем. Это термопары,
измерительные трансформаторы,
усилители,
преобразователи давления. По месту,
занимаемому в измерительной цепи, они
делятся на первичные, промежуточные и
т. п. Конструктивно они выполняются либо
отдельными блоками, либо составной
частью СИ. Не следует отождествлять
измерительные преобразователи с
преобразовательными элементам. Последние
не имеют метрологических характеристик,
как, например, трансформатор тока или
напряжения.
Измерительный
прибор
— СИ, предназначенное для переработки
сигнала измерительной информации в
другие, доступные для непосредственного
восприятия наблюдателем формы. Различают
приборы прямого действия (амперметры,
вольтметры,
манометры)
и приборы сравнения (компараторы). По
способу отсчета измеряемой величины
СИ делятся на показывающие (аналоговые,
цифровые), регистрирующие (на
бумажную
или магнитную ленту) и т. п.
Измерительная
установка
— совокупность функционально объединенных
СИ и вспомогательных устройств,
расположенных в одном месте. Например,
поверочные установки, установки для
испытания электротехнических, магнитных
и других материалов. Измерительная
установка позволяет предусмотреть
определенный
метод
измерения и заранее оценить погрешность
измерения.
Измерительная
система
— это комплекс СИ и вспомогательных
устройств
с компонентами связи (проводные,
предназначенный
для выработки сигналов измерительной
информации в форме, удобной для
автоматической обработки, передачи
и/или
использования в автоматических системах
управления. В отличие от измерительных
установок, предусматривающих изменения
режима и условий функционирования,
измерительная система не воздействует
на режимы работы, а предназначена только
для сбора и/или хранения информации.
Частными случаями измерительной системы
являются информационно-вычислительный
комплекс (ИВК), информационно-измерительные
системы (ИИС). К последним можно отнести
системы автоматического контроля,
системы технического диагностирования,
системы распознавания образов, системы
для передачи неизмерительной информации.
При организации поверки рабочих СИ
используют различные эталоны и образцовые
СИ. СИ, как правило, работают совместно
с датчиками (измерительными
преобразователями), имеющими свои MX.
При
использовании средств измерений
принципиально важно знать степень
соответствия информации об измеряемой
величине, содержащейся в выходном
сигнале, ее истинному значению. С этой
целью для каждого СИ вводятся и нормируются
определенные метрологические
характеристики (МХ).
Метрологическими
называются
характеристики свойств СИ, оказывающие
влияние на результат измерения и его
погрешности. Характеристики, устанавливаемые
нормативными документами, называются
нормируемыми,
а определяемые экспериментально –
действительными.
Номенклатура
метрологических характеристик средств
измерений
Неинформативным
называется параметр входного сигнала
СИ,
не связанный функционально с измеряемым
параметром. Например, частота переменного
тока при измерении его амплитуды.
Нормальные метрологические характеристики
(НМХ) устанавливаются документами. MX,
определенные документами, считаются
действительными. На практике наиболее
распространены следующие MX СИ.
Диапазон
измерений
— область значений измеряемой величины,
для которой нормированы допускаемые
пределы погрешности СИ (для преобразователей
— это диапазон преобразования):
Предел
измерения
— наибольшее или наименьшее значение
диапазона измерения. Для мер
— это номинальное значение воспроизводимой
величины.
Рис
32 Неравномерная шкала СИ
Например,
у шкалы на рис. 32 начальный участок
(~20%) сжат, потому производить отсчеты
на нем неудобно. Тогда предел измерения
по шкале составляет 50 ед., а диапазон —
10…50 единиц.
Цена
деления шкалы
— разность значений величин,
соответствующих двум соседним
отметкам
шкалы. Приборы с равномерной шкалой
имеют постоянную цену деления, а с
неравномерной — переменную. В этом
случае нормируется минимальная цена
деления.
Чувствительность
— отношение изменения сигнала Δу на
выде СИ к вызвавшему это изменение
изменению Δх сигнала на входе
S=
Δу/Δх.
Например,
для стрелочного СИ — это отношение
перемещения dl
конца стрелки к вызвавшему его изменению
dx
измеряемой величины
S=
dl/dx.
Таким
образом, для неравномерных шкал величина
S=
var,
и степень неравномерности шкалы оценивают
через коэффициент
J=Smax/Smin
Для
равномерных шкал S
= Sср
= const
и Sср
= l/хN
где xN
— диапазон измерений.
Поскольку
х и у могут быть выражены в различных
единицах то величина S
имеет размерность [мм/А], [мм/В], [градус/В]и
т.д. Говоря о чувствительности, указывают
чувствительность тока, напряжения и т.
д. Иногда для оперирования безразмерными
единицами вводят понятие относительной
чувствительности
S0
= (Δy/y0)/(Δx/x0),
где
х0,
у0
— номинальные (или средние) величины.
Чувствительность нельзя отождествлять
с порогом чувствительности — наименьшим
значением измеряемой величины, вызывающим
заметное изменение показаний прибора.
Величину,
обратную чувствительности, называют
постоянной прибора С = 1/S.
Как
правило, выходным сигналом СИ является
отсчет (показание) в единицах величины.
В этом случае постоянная прибора С
равна цене деления. Поэтому для СИ с
неравномерной шкалой чувствительность
— величина переменная.
Вариация
(гистерезис)
— разность между показаниями СИ в данной
точке диапазона измерения при возрастании
и убывании измерений величины и неизменных
внешних условиях:
Н=
|хв
– xу|,
где
хв,
ху
— значения измерений образцовыми СИ
при возрастании и убывании величины
х. Следует иметь в виду, что, хотя вариация
показаний СИ вызывается случайными
факторами, сама она — не случайная
величина.
Зависимость
между выходным и входным сигналом СИ,
полученную экспериментально, называют
градуировочной характеристикой (или
статической характеристикой
преобразования), которая
может быть представлена аналитически,
графически или в виде таблицы.
Градуировочная характеристика может
изменяться под воздей ствием внешних
и внутренних причин. Например, при
быстром изменении тока подвижная часть
СИ, вследствие инерции, не успевает
«следить» за изменением тока.
Градуировочная характеристика в этом
случае должна выражаться дифференциальным
уравнением.
Характеристики
погрешности измерений в статике.
Статический
режим –
это такой режим работы СИ, при котором
изменением измеряемой величины за
время, требуемое для проведения одного
измерения, можно пренебречь. В динамическом
режиме такое
пренебрежение недопустимо, поскольку
указанное изменение превышает допустимую
погрешность.
Все
погрешности СИ в зависимости от внешних
условий делятся на основные и
дополнительные.
Основная
погрешность — это погрешность СИ при
нормальных условиях эксплуатации. Как
правило, нормальными условиями
эксплуатации являются: температура
293±5 К или 20±5 °С, относительная влажность
воздуха 65+15% при 20 °С, напряжение в сети
питания 220 В+10% с частотой 50 Гц±1%,
атмосферное давление от 97,4 до 104 кПа,
отсутствие электрических и магнитных
полей (наводок). В рабочих условиях,
зачастую отличающихся от нормальных
более широким диапазоном влияющих
величин, при необходимости нормируется
дополнительная погрешность СИ.
Классы
точности средств измерений
.
При технических измерениях, когда не
предусмотрено выделение случайных и
систематических составляющих, когда
не существенна динамическая погрешность
СИ, когда не учитываются влияющие
(дестабилизирующие) факторы и т.д., можно
пользоваться более грубым нормированием
— присвоением СИ определенного класса
точности по ГОСТ 8.401—80.
Класс
точности
–это обобщенная характеристика СИ,
выражаемая пределами допускаемых
значений его основной и дополнительной
погрешностей, а также другими
характеристиками,
влияющими на точность. Класс точности
не является непосредственной оценкой
точности измерений, выполняемых этим
СИ, поскольку погрешность зависит еще
от ряда факторов: метода измерений,
условий измерений и т.д. Класс точности
лишь позволяет судить о том, в каких
пределах находится погрешность СИ
данного типа. Общие положения деления
средств измерений по классу точности
устанавливает ГОСТ 8.401–80.года). Класс
точности СИ уже включает систематическую
и случайную погрешности. Однако он не
является непосредственной характеристикой
точности измерений, выполняемых с
помощью этих СИ, поскольку точность
измерения
зависит
и от метода измерения, взаимодействия
СИ с объектом, условий измерения и т.д.
В
связи с большим разнообразием как самих
СИ, так и их MX,
ГОСТ 8.401—80 устанавливает несколько
способов назначения классов точности.
При этом в основу заложены следующие
положения:
•
в
качестве норм служат пределы допускаемых
погрешностей, включающие систематические
и случайные составляющие;
•
основная
δосн
и все виды дополнительных погрешностей
δдоп
нормируются
порознь (см. п. 3.2).
Первое
положение свидетельствует о необходимости
разрабатывать СИ с учетом однократного
отсчета показаний по величине общей
погрешности. Второе положение направлено
на обеспечение максимальной однородности
однотипных СИ. .
Пределы
допускаемых основной и дополнительной
погрешностей выражают
в форме приведенных, относительных или
абсолютных
погрешностей.
Выбор формы представления зависит от
характера
изменения
погрешностей в пределах диапазона
измерений, а также от
условий
применения и назначения СИ.
Пределы
допускаемой абсолютной основной
погрешности
устанавливаются
по одной из формул: Δ
= ±а
или
Δ
= ±(а
+
bx),
где
х
–
значение
измеряемой величины или число делений,
отсчитанное по шкале;
а,
b
–
положительные числа, не зависящие от
х.
Первая формула описывает чисто аддитивную
погрешность (рис. 6.4, а), а вторая – сумму
аддитивной и мультипликативной (рис.
6.4, б) погрешностей (рис. 6.4, в). В технической
документации классы точности,
установленные
в виде абсолютных погрешностей,
обозначают, например, «Класс точности
М», а на приборе – буквой «М». Для
обозначения используются прописные
буквы латинского алфавита или римские
цифры, причём меньшие пределы погрешностей
должны соответствовать буквам, находящимся
ближе к началу алфавита, или меньшим
цифрам. Пределы допускаемой приведенной
основной погрешности определяются по
формуле γ
= Δ
/xN
=
± p
,
где xN
–
нормирующее значение, выраженное в тех
же единицах, что и Δ;
р
–
отвлеченное положительное число,
выбираемое из ряда значений:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;…..
.
Рис.
6.4. Аддитивная а), мультипликативная б)
и суммарная в)
погрешности
в абсолютной и относительной формах
Нормирующее
значение xN
устанавливается
равным большему из пределов измерений
(или модулей) для СИ с равномерной,
практически равномерной или степенной
шкалой и для измерительных преобразователей,
для которых нулевое значение выходного
сигнала
находится
на краю или вне диапазона измерений.
Для СИ, шкала которых имеет условный
нуль, xN
равно
модулю разности пределов измерений.
Для приборов с существенно неравномерной
шкалой xN
принимают
равным всей длине шкалы или ее части,
соответствующей диапазону измерении.
В этом случае пределы абсолютной
погрешности выражают, как и длину шкалы,
в единицах длины, а на средстве измерений
класс
точности
условно обозначают, например, в виде
значка 0,5 , где 0,5 –значение числа р
Рис.
6.5.Лицевая панель фазометра класса
точности 0,5 с существенно
неравномерной
нижней шкалой
В
остальных рассмотренных случаях класс
точности обозначают конкретным числом
р,
например 1,5. Обозначение наносится на
циферблат,
щиток или корпус прибора (рис. 6.6).
Рис
6.6. Лицевая панель амперметра класса
точности 1,5
с
равномерной шкалой
В
случае если абсолютная погрешность
задается формулой ±(a
+
bx),
пределы допускаемой относительной
основной погрешности δ
= Δ
x
=
±[c
+
d(
|xk/
x|
−1)],
(6.2)
где
с,
d
–
отвлеченные положительные числа,
выбираемые из ряда:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;….
; xk
–
больший (по модулю) из пределов измерений.
При использовании формулы (6.2) класс
точности обозначается в виде «0,02/0,01»,
где числитель – конкретное значение
числа с,
знаменатель – числа d
(рис.
6.7).
Причем,
как правило, c>d.
Например, класс точности 0,02/0,01 означает,
что с = 0,02,
а
d=
0,01, т. е. приведенное значение относительной
погрешности к началу диапазона измерения
γн
= 0,02%, а к концу — γк=
0,01%.
В
обоснованных случаях пределы допускаемой
относительной основной погрешности
определяют по более сложным формулам
либо в виде графика или таблицы.
Рис.
6.7. Лицевая панель ампервольтметра
класса точности 0,02/0,01
с
равномерной шкалой
Пределы
допускаемой относительной основной
погрешности определяются по формуле
δ
= Δ /x
=
±q
,
если
Δ
= ±a
.
Значение
постоянного числа q
устанавливается
так же, как и значение числа p.
Класс точности на прибор обозначается
в виде
,
где 0,5 – конкретное значениеq
(рис.
6.8).
Так
обозначают классы точности мостов
переменного тока, счетчик0в электроэнергии,
делителей напряжения, измерительны
трансформаторов и др.
Рис
6.8. Лицевая панель мегаомметра класса
точности 2,5
с
неравномерной шкалой
В
стандартах и технических условиях на
СИ указывается минимальное значение
x0
, начиная с которого применим принятый
способ выражения пределов допускаемой
относительной погрешности. Отношение
xk/
x0
называется динамическим диапазоном
измерения. Правила построения и примеры
обозначения классов точности в
документации
и на средствах измерений приведены в
таблице 6.1.
Наиболее
широкое распространение (особенно для
аналоговых СИ) получило нормирование
класса точности по приведенной
погрешности:
γ=±Δ/xN100%
= ±A·10n.
xN
условное обозначение класса точности
в этом случае зависит от нормирующего
значения хN
т.
е. от шкалы СИ. Если xN
представляется в единицах измеряемой
величины, то класс точности обозначается
числом, совпадающим с пределом допускаемой
приведенной погрешности. Например,
класс 1,5 означает, что γ = 1,5%. Если xN
—
длина шкалы (например, у амперметров),
то класс 1.5 означает, что γ =1,5% длины
шкалы.
Не
всегда число, обозначающее класс
точности, показывает предел допускаемой
погрешности. В частности, у некоторых
однозначных мер электрических величин
оно характеризует нестабильность,
показывая, на сколько процентов значение
меры мо-
ет
изменяться в течение года.
Случайная погрешность и количество измерениий.
Для уменьшения случайной погрешности есть два пути: повышение точности измерений (уменьшение σх) и увеличение числа измерений n с целью использования соотношения (14). Считая, что все возможности совершенствования техники измерений использованы, рассмотрим второй путь. При этом отметим, что уменьшать случайную составляющую погрешности целесообразно лишь до тех пор, пока общая погрешность измерений не будет полностью определяться систематической составляющей Δс. Если систематическая погрешность определяется классом точности СИ Δси (или γси), то необходимо, чтобы доверительный интервал 
Обычно принимают от 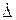
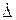
Для сравнения случайных погрешностей с различными законами распределения использование показателей, сводящих плотность распределения к одному или нескольким числам, обязательно. В качестве таких чисел и выступают СКО, доверительный интервал и доверительная вероятность.
Надежность самого СКО характеризуется величиной

Принято, что если σσ≤0,25σ, то оценка точности надежна. Это условие выполняется уже при n=8.
Наиболее вероятная погрешность Δв отдельного измерения определяется по формуле

Анализ этой формулы показывает, что с увеличением n величина Δв быстро уменьшается лишь до n=5 … 10. Следовательно, увеличение числа измерений на одном режиме свыше 5… 10 нецелесообразно, что совпадает с условием получения надежных значений σσ.
Число измерений можно выбрать по одной из формул:

где nот — число отбрасываемых экспериментальных результатов.
С учетом коэффициентов Стьюдента можно оценить относительную погрешность отдельного измерения как 

Определение систематических погрешностей.
Как правило, считают, что систематические погрешности могут быть обнаружены и исключены. Однако в реальных условиях полностью исключить систематическую составляющую погрешности невозможно. Всегда остаются какие-то не исключенные остатки, которые и нужно учитывать, чтобы оценить их границы. Это и будет систематическая погрешность измерения. То есть в принципе систематическая погрешность тоже случайна, и указание деление обусловлено лишь установившимися традициями обработки и представления результатов измерения.
Оставшаяся необнаруженной систематическая составляющая опаснее случайной: если случайная составляющая вызывает вариацию (разброс) результатов, то систематическая — устойчиво их искажает (смещает). В любом случае отсутствие или незначительность (с целью пренебрежения) систематической погрешности нужно доказать.
Действительно, если взять два ряда измерений одной и той же величины, то средние результаты этих рядов, как правило, будут различны. Это расхождение может быть определено случайной или систематической составляющей.
Методика выявления характера погрешности заключается в следующем:
1. Из двух рядов n1 и n2 независимых измерений находят средние арифметические х1, и х2.
2. Определяют значения
3. Вычисляют 
4. Вероятность того, что разность |x1-х2|>ε является случайной величиной, определяется равенством Р(|x1-х2|>ε)=1-Ptpn где tp=|x1-х2|/σ; n=n1+n2-2. Величина Р определяется по таблице Стьюдента.
Если полученная вероятность Р>0,95, то разность |x1-х2| носит систематический характер.
Пример.
Расчетные значения составили tp=3 и n=15. По таблице Стьюдента находим, что при
n-1=14 и tp=2,98≡3 величина Р=0,99. Тогда Р= 0,99 > 0,95, что свидетельствует о систематическом характере погрешности.
В отличие от случайной погрешности, выявленной в целом в, зависимости от ее источников, систематическая погрешность рассматривается по составляющим в зависимости от источников ее возникновения, причем различают методическую, инструментальную и субъективную составляющие погрешности.
Целесообразность разделения систематической погрешности на методическую и инструментальную составляющие определяется следующими моментами:
• для повышения точности измерений можно выделить лимитирующие факторы, а следовательно, принять решение об усовершенствовании методики или выборе более точных СИ;
• появляется возможность определить составляющую общей погрешности, увеличивающейся со временем или под влиянием внешних факторов, а следовательно, целенаправленно осуществлять периодические поверки и аттестации;
• инструментальная составляющая может быть оценена до разработки методики, а потенциальные точностные возможности выбранного метода определит только методическая составляющая.
То есть все виды составляющих погрешности нужно анализировать и выявлять в отдельности, а затем суммировать их в зависимости от характера, что является основной задачей при разработке и аттестации методик выполнения измерений.
В ряде случаев систематическая погрешность может быть исключена за счет устранения источников погрешности до начала измерений (профилактика погрешности), а в процессе измерений — путем внесения известных поправок в результаты измерений.
Профилактика погрешности — наиболее рациональный способ ее снижения и заключается в устранении влияния, например температуры (термостатированием и термоизоляцией), магнитных полей (магнитными экранами), вибраций и т. п. Сюда же относятся регулировка, ремонт и поверка СИ.
Исключение постоянных систематических погрешностей в процессе измерений осуществляют методом сравнения (замещения, противопоставления), компенсации по знаку (предусматривают два наблюдения, чтобы в результат каждого измерения систематическая погрешность входила с разным знаком), а исключение переменных и прогрессирующих — способами симметричных наблюдений или наблюдением четное число раз через полупериоды.
Способы уменьшения случайных погрешностей.
1
Метод многократных измерений.
Тогда
2.
Метод комплексирования.
Проводят
измерения одной и той же величины при
следующих условиях:
А)
несколькими однотипными СИ одновременно
Б)
разнотипными
С)
различными методами( разными группами
экспериментаторов)
В
дальнейшем проводится объединение
результатов наблюдений по алгоритму
средневзвешенной оценки, более точным
наблюдениям больший вес. Объединение
может быть только для равноточных
результатов по систематической
погрешности.
3.
Метод косвенных измерений.
В
отдельных случаях позволяет уменьшить
случайную погрешность.
Средства измерений. Характеристики си для определения результатов измерений.
Средство
измерений –
это техническое средство (или комплекс),
предназначенное для измерений, имеющее
нормированные метрологические
характеристики, воспроизводящие и (или)
хранящие единицу физической величины,
размер которой принимается неизменным
(в пределах установленной погрешности)
в течение известного интервала времени
[24].
Данное определение раскрывает
метрологическую
сущность СИ,
заключающуюся
в умении хранить (или воспроизводить)
единицу ФВ
и
в неизменности размера хранимой единицы
во времени.
Первое обуславливает возможность
выполнения измерения, суть которого,
как известно, состоит в сравнении
измеряемой величины с ее единицей.
Второе принципиально необходимо,
поскольку при изменении размера хранимой
единицы ФВ с помощью данного СИ нельзя
получить результат с требуемой точностью.
Под метрологическими характеристиками
(MX)
понимают такие характеристики СИ,
которые позволяют судить об их пригодности
для измерений в известном диапазоне с
известной точностью. В отличие от СИ
приборы или вещества, не имеющие
нормированных MX,
называют индикаторами. СИ — это
техническая основа метрологического
обеспечения.
Классификация
средств измерений по их роли в процессе
измерения и
выполняемым
функциям
Эталон
–
средство измерений (или их комплекс),
предназначенное для воспроизведения
и (или) хранения единицы и передачи ее
размера нижестоящим по поверочной схеме
СИ и утвержденное в качестве эталона в
установленном порядке.
Меры
— это СИ, воспроизводящие или хранящие
физическую величину заданного размера.
Меры могут быть однозначными,
воспроизводящими одно значение физической
величины (гиря, калибр на заданный
размер, образцы твердости, шероховатости,
катушка сопротивления, нормальный
элемент, воспроизводящий значение
ЭДС), и
многозначными
— для воспроизведения плавно или
дискретно ряда значений одной и той же
физической величины (измерительный
конденсатор переменной емкости, набор
конечных мер, магазин емкостей,
индуктивности и сопротивления,
измерительные линейки).
Для
ряда областей измерений, и в первую
очередь для физико-химических измерений,
чрезвычайно перспективным средством
повышения эффективности поверочных
работ является применение стандартных
образцов (СО). Правила работы с СО
устанавливает ГОСТ 8.315—97. Согласно
этому документу,
стандартный
образец состава и свойств веществ и
материалов
— это средство измерений в виде вещества
(материала), состав или свойства которого
установлены аттестацией. Можно
дать и другое определение: стандартный
образец
— образец вещества (материала) с
установленными в результате метрологической
аттестации
значениями
одной или более величин, характеризующими
свойство или состав этого вещества
(материала).
Стандартные
образцы предназначены для обеспечения
единства и требуемой точности измерений
посредством:
•
градуировки,
метрологической аттестации и поверки
СИ;
•
метрологической
аттестации методик выполнения измерений;
•
контроля
показателей точности измерений;
•
измерения
ФВ, характеризующих состав или свойства
веществ материалов, методами сравнения.
По
своему назначению СО исполняют роль
мер, однако в отличие от «классических»
мер они имеют ряд особенностей. Например,
образцы состава воспроизводят значения
ФВ,
характеризующих
состав или свойства именно того материала
(вещества), из которого они изготовлены.
Стандартные образцы, как правило не
являются изделиями, они реализованы
обычно в виде части или порции однородного
вещества (материала), причем эта часть
является полноценным носителем
воспроизводимой единицы ФВ, а не ее
части Эта особенность образцов отражена
в требованиях к их однородности по
составу и свойствам. Однородность
материала, из которого сделан образец,
имеет принципиальное значение, в то
время как для меры такая характеристик
часто является второстепенной.
Измерительные
преобразователи
— СИ, предназначенные для выработки
сигнала измерительной информации в
форме, удобной для передачи, дальнейшего
преобразования, обработки и хранения,
но не доступной для непосредственного
восприятия наблюдателем. Это термопары,
измерительные трансформаторы,
усилители,
преобразователи давления. По месту,
занимаемому в измерительной цепи, они
делятся на первичные, промежуточные и
т. п. Конструктивно они выполняются либо
отдельными блоками, либо составной
частью СИ. Не следует отождествлять
измерительные преобразователи с
преобразовательными элементам. Последние
не имеют метрологических характеристик,
как, например, трансформатор тока или
напряжения.
Измерительный
прибор
— СИ, предназначенное для переработки
сигнала измерительной информации в
другие, доступные для непосредственного
восприятия наблюдателем формы. Различают
приборы прямого действия (амперметры,
вольтметры,
манометры)
и приборы сравнения (компараторы). По
способу отсчета измеряемой величины
СИ делятся на показывающие (аналоговые,
цифровые), регистрирующие (на
бумажную
или магнитную ленту) и т. п.
Измерительная
установка
— совокупность функционально объединенных
СИ и вспомогательных устройств,
расположенных в одном месте. Например,
поверочные установки, установки для
испытания электротехнических, магнитных
и других материалов. Измерительная
установка позволяет предусмотреть
определенный
метод
измерения и заранее оценить погрешность
измерения.
Измерительная
система
— это комплекс СИ и вспомогательных
устройств
с компонентами связи (проводные,
предназначенный
для выработки сигналов измерительной
информации в форме, удобной для
автоматической обработки, передачи
и/или
использования в автоматических системах
управления. В отличие от измерительных
установок, предусматривающих изменения
режима и условий функционирования,
измерительная система не воздействует
на режимы работы, а предназначена только
для сбора и/или хранения информации.
Частными случаями измерительной системы
являются информационно-вычислительный
комплекс (ИВК), информационно-измерительные
системы (ИИС). К последним можно отнести
системы автоматического контроля,
системы технического диагностирования,
системы распознавания образов, системы
для передачи неизмерительной информации.
При организации поверки рабочих СИ
используют различные эталоны и образцовые
СИ. СИ, как правило, работают совместно
с датчиками (измерительными
преобразователями), имеющими свои MX.
При
использовании средств измерений
принципиально важно знать степень
соответствия информации об измеряемой
величине, содержащейся в выходном
сигнале, ее истинному значению. С этой
целью для каждого СИ вводятся и нормируются
определенные метрологические
характеристики (МХ).
Метрологическими
называются
характеристики свойств СИ, оказывающие
влияние на результат измерения и его
погрешности. Характеристики, устанавливаемые
нормативными документами, называются
нормируемыми,
а определяемые экспериментально –
действительными.
Номенклатура
метрологических характеристик средств
измерений
Неинформативным
называется параметр входного сигнала
СИ,
не связанный функционально с измеряемым
параметром. Например, частота переменного
тока при измерении его амплитуды.
Нормальные метрологические характеристики
(НМХ) устанавливаются документами. MX,
определенные документами, считаются
действительными. На практике наиболее
распространены следующие MX СИ.
Диапазон
измерений
— область значений измеряемой величины,
для которой нормированы допускаемые
пределы погрешности СИ (для преобразователей
— это диапазон преобразования):
Предел
измерения
— наибольшее или наименьшее значение
диапазона измерения. Для мер
— это номинальное значение воспроизводимой
величины.
Рис
32 Неравномерная шкала СИ
Например,
у шкалы на рис. 32 начальный участок
(~20%) сжат, потому производить отсчеты
на нем неудобно. Тогда предел измерения
по шкале составляет 50 ед., а диапазон —
10…50 единиц.
Цена
деления шкалы
— разность значений величин,
соответствующих двум соседним
отметкам
шкалы. Приборы с равномерной шкалой
имеют постоянную цену деления, а с
неравномерной — переменную. В этом
случае нормируется минимальная цена
деления.
Чувствительность
— отношение изменения сигнала Δу на
выде СИ к вызвавшему это изменение
изменению Δх сигнала на входе
S=
Δу/Δх.
Например,
для стрелочного СИ — это отношение
перемещения dl
конца стрелки к вызвавшему его изменению
dx
измеряемой величины
S=
dl/dx.
Таким
образом, для неравномерных шкал величина
S=
var,
и степень неравномерности шкалы оценивают
через коэффициент
J=Smax/Smin
Для
равномерных шкал S
= Sср
= const
и Sср
= l/хN
где xN
— диапазон измерений.
Поскольку
х и у могут быть выражены в различных
единицах то величина S
имеет размерность [мм/А], [мм/В], [градус/В]и
т.д. Говоря о чувствительности, указывают
чувствительность тока, напряжения и т.
д. Иногда для оперирования безразмерными
единицами вводят понятие относительной
чувствительности
S0
= (Δy/y0)/(Δx/x0),
где
х0,
у0
— номинальные (или средние) величины.
Чувствительность нельзя отождествлять
с порогом чувствительности — наименьшим
значением измеряемой величины, вызывающим
заметное изменение показаний прибора.
Величину,
обратную чувствительности, называют
постоянной прибора С = 1/S.
Как
правило, выходным сигналом СИ является
отсчет (показание) в единицах величины.
В этом случае постоянная прибора С
равна цене деления. Поэтому для СИ с
неравномерной шкалой чувствительность
— величина переменная.
Вариация
(гистерезис)
— разность между показаниями СИ в данной
точке диапазона измерения при возрастании
и убывании измерений величины и неизменных
внешних условиях:
Н=
|хв
– xу|,
где
хв,
ху
— значения измерений образцовыми СИ
при возрастании и убывании величины
х. Следует иметь в виду, что, хотя вариация
показаний СИ вызывается случайными
факторами, сама она — не случайная
величина.
Зависимость
между выходным и входным сигналом СИ,
полученную экспериментально, называют
градуировочной характеристикой (или
статической характеристикой
преобразования), которая
может быть представлена аналитически,
графически или в виде таблицы.
Градуировочная характеристика может
изменяться под воздей ствием внешних
и внутренних причин. Например, при
быстром изменении тока подвижная часть
СИ, вследствие инерции, не успевает
«следить» за изменением тока.
Градуировочная характеристика в этом
случае должна выражаться дифференциальным
уравнением.
Характеристики
погрешности измерений в статике.
Статический
режим –
это такой режим работы СИ, при котором
изменением измеряемой величины за
время, требуемое для проведения одного
измерения, можно пренебречь. В динамическом
режиме такое
пренебрежение недопустимо, поскольку
указанное изменение превышает допустимую
погрешность.
Все
погрешности СИ в зависимости от внешних
условий делятся на основные и
дополнительные.
Основная
погрешность — это погрешность СИ при
нормальных условиях эксплуатации. Как
правило, нормальными условиями
эксплуатации являются: температура
293±5 К или 20±5 °С, относительная влажность
воздуха 65+15% при 20 °С, напряжение в сети
питания 220 В+10% с частотой 50 Гц±1%,
атмосферное давление от 97,4 до 104 кПа,
отсутствие электрических и магнитных
полей (наводок). В рабочих условиях,
зачастую отличающихся от нормальных
более широким диапазоном влияющих
величин, при необходимости нормируется
дополнительная погрешность СИ.
Классы
точности средств измерений
.
При технических измерениях, когда не
предусмотрено выделение случайных и
систематических составляющих, когда
не существенна динамическая погрешность
СИ, когда не учитываются влияющие
(дестабилизирующие) факторы и т.д., можно
пользоваться более грубым нормированием
— присвоением СИ определенного класса
точности по ГОСТ 8.401—80.
Класс
точности
–это обобщенная характеристика СИ,
выражаемая пределами допускаемых
значений его основной и дополнительной
погрешностей, а также другими
характеристиками,
влияющими на точность. Класс точности
не является непосредственной оценкой
точности измерений, выполняемых этим
СИ, поскольку погрешность зависит еще
от ряда факторов: метода измерений,
условий измерений и т.д. Класс точности
лишь позволяет судить о том, в каких
пределах находится погрешность СИ
данного типа. Общие положения деления
средств измерений по классу точности
устанавливает ГОСТ 8.401–80.года). Класс
точности СИ уже включает систематическую
и случайную погрешности. Однако он не
является непосредственной характеристикой
точности измерений, выполняемых с
помощью этих СИ, поскольку точность
измерения
зависит
и от метода измерения, взаимодействия
СИ с объектом, условий измерения и т.д.
В
связи с большим разнообразием как самих
СИ, так и их MX,
ГОСТ 8.401—80 устанавливает несколько
способов назначения классов точности.
При этом в основу заложены следующие
положения:
•
в
качестве норм служат пределы допускаемых
погрешностей, включающие систематические
и случайные составляющие;
•
основная
δосн
и все виды дополнительных погрешностей
δдоп
нормируются
порознь (см. п. 3.2).
Первое
положение свидетельствует о необходимости
разрабатывать СИ с учетом однократного
отсчета показаний по величине общей
погрешности. Второе положение направлено
на обеспечение максимальной однородности
однотипных СИ. .
Пределы
допускаемых основной и дополнительной
погрешностей выражают
в форме приведенных, относительных или
абсолютных
погрешностей.
Выбор формы представления зависит от
характера
изменения
погрешностей в пределах диапазона
измерений, а также от
условий
применения и назначения СИ.
Пределы
допускаемой абсолютной основной
погрешности
устанавливаются
по одной из формул: Δ
= ±а
или
Δ
= ±(а
+
bx),
где
х
–
значение
измеряемой величины или число делений,
отсчитанное по шкале;
а,
b
–
положительные числа, не зависящие от
х.
Первая формула описывает чисто аддитивную
погрешность (рис. 6.4, а), а вторая – сумму
аддитивной и мультипликативной (рис.
6.4, б) погрешностей (рис. 6.4, в). В технической
документации классы точности,
установленные
в виде абсолютных погрешностей,
обозначают, например, «Класс точности
М», а на приборе – буквой «М». Для
обозначения используются прописные
буквы латинского алфавита или римские
цифры, причём меньшие пределы погрешностей
должны соответствовать буквам, находящимся
ближе к началу алфавита, или меньшим
цифрам. Пределы допускаемой приведенной
основной погрешности определяются по
формуле γ
= Δ
/xN
=
± p
,
где xN
–
нормирующее значение, выраженное в тех
же единицах, что и Δ;
р
–
отвлеченное положительное число,
выбираемое из ряда значений:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;…..
.
Рис.
6.4. Аддитивная а), мультипликативная б)
и суммарная в)
погрешности
в абсолютной и относительной формах
Нормирующее
значение xN
устанавливается
равным большему из пределов измерений
(или модулей) для СИ с равномерной,
практически равномерной или степенной
шкалой и для измерительных преобразователей,
для которых нулевое значение выходного
сигнала
находится
на краю или вне диапазона измерений.
Для СИ, шкала которых имеет условный
нуль, xN
равно
модулю разности пределов измерений.
Для приборов с существенно неравномерной
шкалой xN
принимают
равным всей длине шкалы или ее части,
соответствующей диапазону измерении.
В этом случае пределы абсолютной
погрешности выражают, как и длину шкалы,
в единицах длины, а на средстве измерений
класс
точности
условно обозначают, например, в виде
значка 0,5 , где 0,5 –значение числа р
Рис.
6.5.Лицевая панель фазометра класса
точности 0,5 с существенно
неравномерной
нижней шкалой
В
остальных рассмотренных случаях класс
точности обозначают конкретным числом
р,
например 1,5. Обозначение наносится на
циферблат,
щиток или корпус прибора (рис. 6.6).
Рис
6.6. Лицевая панель амперметра класса
точности 1,5
с
равномерной шкалой
В
случае если абсолютная погрешность
задается формулой ±(a
+
bx),
пределы допускаемой относительной
основной погрешности δ
= Δ
x
=
±[c
+
d(
|xk/
x|
−1)],
(6.2)
где
с,
d
–
отвлеченные положительные числа,
выбираемые из ряда:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;….
; xk
–
больший (по модулю) из пределов измерений.
При использовании формулы (6.2) класс
точности обозначается в виде «0,02/0,01»,
где числитель – конкретное значение
числа с,
знаменатель – числа d
(рис.
6.7).
Причем,
как правило, c>d.
Например, класс точности 0,02/0,01 означает,
что с = 0,02,
а
d=
0,01, т. е. приведенное значение относительной
погрешности к началу диапазона измерения
γн
= 0,02%, а к концу — γк=
0,01%.
В
обоснованных случаях пределы допускаемой
относительной основной погрешности
определяют по более сложным формулам
либо в виде графика или таблицы.
Рис.
6.7. Лицевая панель ампервольтметра
класса точности 0,02/0,01
с
равномерной шкалой
Пределы
допускаемой относительной основной
погрешности определяются по формуле
δ
= Δ /x
=
±q
,
если
Δ
= ±a
.
Значение
постоянного числа q
устанавливается
так же, как и значение числа p.
Класс точности на прибор обозначается
в виде
,
где 0,5 – конкретное значениеq
(рис.
6.8).
Так
обозначают классы точности мостов
переменного тока, счетчик0в электроэнергии,
делителей напряжения, измерительны
трансформаторов и др.
Рис
6.8. Лицевая панель мегаомметра класса
точности 2,5
с
неравномерной шкалой
В
стандартах и технических условиях на
СИ указывается минимальное значение
x0
, начиная с которого применим принятый
способ выражения пределов допускаемой
относительной погрешности. Отношение
xk/
x0
называется динамическим диапазоном
измерения. Правила построения и примеры
обозначения классов точности в
документации
и на средствах измерений приведены в
таблице 6.1.
Наиболее
широкое распространение (особенно для
аналоговых СИ) получило нормирование
класса точности по приведенной
погрешности:
γ=±Δ/xN100%
= ±A·10n.
xN
условное обозначение класса точности
в этом случае зависит от нормирующего
значения хN
т.
е. от шкалы СИ. Если xN
представляется в единицах измеряемой
величины, то класс точности обозначается
числом, совпадающим с пределом допускаемой
приведенной погрешности. Например,
класс 1,5 означает, что γ = 1,5%. Если xN
—
длина шкалы (например, у амперметров),
то класс 1.5 означает, что γ =1,5% длины
шкалы.
Не
всегда число, обозначающее класс
точности, показывает предел допускаемой
погрешности. В частности, у некоторых
однозначных мер электрических величин
оно характеризует нестабильность,
показывая, на сколько процентов значение
меры мо-
ет
изменяться в течение года.
При выборе прибора для тех или иных целей измерения необходимо внимательно рассмотреть и проанализировать ряд факторов и оптимизировать их по совокупности всех технических данных и характеристик.
Основные факторы, влияющие на выбор измерительного прибора следующие:
1. Возможность измерить исследуемый сигнал.
2. Тип параметра, который надо измерить.
3. Метод измерения (прямой, косвенный, совокупный, совместный и др.).
4. Продолжительность измерений.
5. Удобство прибора для проведения измерения (габаритные размеры, масса).
6. Нужная точность измерений.
7. Стоимость прибора.
8. Допускаемая погрешность измерений.
9. Климатические условия применения прибора.
10. Требования к форме фиксации результатов измерения (аналоговая, цифровая, аналого-цифровая и др.).
11. Предполагаемая форма использования прибора (автономно, в составе автоматизированной системы и др.).
При всяком измерении неизбежны обусловленные разно-образными причинами отклонения результата измерения от истинного значения измеряемой величины. Эти отклонения называют погрешностями измерений.
Погрешности измерений классифицируют по виду (абсолютная, относительная, случайная и др.), причинам возникновения, характеру проявления и др. Разумеется, что в процессе измерений необходимо учитывать все виды возникающих погрешностей и, поняв их причину, стремиться их уменьшить. Остановимся на методах уменьшения (исключения) систематических погрешностей измерения. Измерения проведены правильны, если систематические погрешности в их результатах близки к нулю.
Для определения и исключения систематических погрешностей используют методы: теоретического анализа, замещения, компенсации погрешности по знаку, статистический, различных измерений, образцовых сигналов, метод введения поправок и поправочных множителей.
Если исключить систематические погрешности не удается, то их уменьшают, устраняя причины их возникновения, регулируя средства измерения при поверке и перед началом измерения, применяя специальные методы измерения и др.
В состав современных измерительных приборов включают микропроцессоры, которые позволяют автоматически на-ходить значения систематической погрешности и исключать ее.
Метод теоретического анализа состоит в том, что систематическую погрешность можно рассчитать на основании известных характеристик используемых приборов или особенностей метода измерения, т. е. по формулам. Так, можно определить систематическую погрешность прибора, обусловленную собственным потреблением мощности, если известно его входное сопротивление и т. д.
Метод замещения заключается в том, что измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, измеряют ослабления аттенюатора с помощью образцового переменного аттенюатора.
Метод компенсации погрешности по знаку основан на том, что если источник погрешности имеет направленное действие (например, погрешности от влияния постоянных магнитных полей, термо-эдс и др.), то измерения проводят так, чтобы систематическая погрешность входила в результаты измерений дважды, но с противоположными знаками.
Статистический метод состоит в том, что для обработки результаты измерений разбивают на несколько независимых групп наблюдений. Разница между групповыми средними и групповыми дисперсиями (средними в группе) указывают на наличие систематической погрешности и позволяет вычислить ее.
Метод различных измерений позволяет обнаруживать систематические погрешности, источник которых неизвестен. Для этого величину измеряют несколькими различными методами, разными измерительными приборами, при различных условиях. В этом случае необходимо, чтобы используемые для измерений приборы имели примерно равные собственные погрешности.
Метод образцовых сигналов состоит в сравнении подаваемых на вход измерительного устройства сигналов: измеряемого и образцового такого же рода, что и измеряемый. Разность между ними определит систематическую погрешность.
Метод введения поправок и поправочных множителей. Поправкой называют значение величины, одноименной с измеряемой, прибавляемое к полученному при измерении значению с целью исключения систематической погрешности. Поправка численно равна абсолютной систематической погрешности, но имеет обратный знак. Поправки задаются в виде графиков, таблиц или формул.
Исключить систематическую погрешность измерения можно также путем умножения результатов измерения на поправочный множитель, который из-за малости систематических погрешностей обычно близок по значению к единице. Полагается, что поправки и поправочные множители предварительно определены при поверке средств измерений.
Снизить систематические погрешности можно термостатированием и термоизоляцией отдельных узлов или всего измерительного прибора, проведением измерений в термостатированных помещениях (для исключения температурной погрешности), применением экранов для защиты от влияния электромагнитных полей, использованием стабилизированных источников питания, амортизацией прибора, удалением его от источников возможного воздействия, от объектов измерений.
Уменьшению систематической погрешности прибора способствует регулировка средств измерения при поверке и перед началом измерения. Сюда входят проверка установки указателя прибора в нулевое положение, правильность положения самого прибора, его расположения относительно окружающих объектов и др.
Существенно уменьшает влияние систематической погрешности перевод ее в случайную. Так, если измерить некий параметр приборами несколько раз, а затем вычислить среднее арифметическое всех результатов, то значение погрешности существенно уменьшится.
Систематические погрешности при косвенных измерениях определяются по значениям систематических погрешностей непосредственно измеряемых независимых величин.
С уменьшением погрешности измерений повышается их точность. Точностью измерений называют их качество, отражающее близость полученного значения величины к ее истинному значению. Следует отметить, что для конкретных условий и целей измерения существует обычно некий рациональный уровень точности, который нецелесообразно превышать из-за усложнения процесса измерений и удорожания измерительных
приборов.
На практике для различных целей ежедневно и ежечасно выполняют большое количество измерений физических величин и, в частности, электротехнических. В интересах народного хозяйства страны необходимо, чтобы результаты этих измерений (имеются в виду измерения одинаковых величин), полученные в разное время и в различных местах с помощью измерительных средств, были бы равны или отличались на некоторое заданное значение.
Иными словами, должно существовать единство измерений.
Единство измерений — это состояние измерений, при котором их результаты выражены в узаконенных единицах, а погрешности известны с заданной вероятностью. Вопросами теории и практики обеспечения единства и необходимой точности измерений занимается метрология.
Метрология — наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. В методологическую основу метрологии — Государственную систему стандартов, обеспечивающую единство измерений— входит более 100 стандартов, регламентирующих: единицы физических величин; методы и средства передачи размеров единиц физических величин рабочим средствам измерений; номенклатуру и способы выражения погрешностей средств измерений; поверку используемых средств измерений для создания заданного уровня надежности метрологических характеристик; номенклатуру и способы представления результатов измерений.
В заключение отметим, что к систематическим погрешностям относятся: инструментальные, метода измерений, установки прибора, считывания.
Под инструментальной понимается погрешность применяемых средств измерений, вызванная несовершенством их изготовления.
Погрешности метода измерений связаны с ошибочностью или недостаточностью разработки теории метода измерений или с упрощениями, допущенными при проведении измерений.
Погрешность установки прибора может быть вызвана: неправильным выбором места измерения; влиянием неблагоприятных внешних условий (вибрации, температуры, влажности) ; удаленностью объекта измерения от приборов обработки измерительных сигналов; небрежной установкой прибора (например, не по отвесу или уровню).
Погрешности считывания, возникающие при не автоматизированных измерениях, объясняются индивидуальными особенностями наблюдателя.
Точность и продолжительность измерений при коррелированной погрешности
При использовании описанной в первой части статьи процедуры усреднения результатов измерений никак не учитывалось, за какое время выполняется серия измерений, поскольку предполагалось, что погрешность является некоррелированным (белым) шумом. Далее будут рассмотрены эффекты, которые возникают в реальных условиях, когда шум измерений является цветным. Попутно станет ясно, почему точные измерительные приборы работают медленно.
Измерительные каналы средств автоматизации обычно являются частью систем, компоненты которых распределены в пространстве и соединены между собой кабельными линиями. Поэтому на них воздействует весь спектр помех, имеющихся в конкретной электромагнитной обстановке. Основными компонентами случайной погрешности, вызванной помехами, являются белый шум, фликкер-шум (1/f-шум) и относительно узкополосные помехи от работающего электрооборудования, передатчиков и естественных источников электромагнитного излучения.
Пример одной реализации белого шума (некоррелированной погрешности измерений) показан на рис. 3 б (см. первую часть статьи в «СТА» 4/2009). Характерной его особенностью является то, что при изменении масштаба по оси времени внешний вид графика остаётся прежним, уменьшается только среднеквадратическое значение шума вследствие уменьшения ширины временного окна наблюдения.
В отличие от него, график реализации коррелированного шума изменяет свой внешний вид в зависимости от ширины окна наблюдения (см. рис. 3 а в первой части статьи). Коррелированный шум с заданной автокорреляционной функцией можно получить из белого, пропустив его через фильтр с заранее рассчитанной передаточной характеристикой.
Многократные измерения с усреднением всегда выполняются на конечном интервале времени Δt. Если случайная погрешность не коррелирована, то её математическое ожидание равно нулю и не зависит от величины интервала (Δt1, Δt2 на рис. 3 б) и момента начала измерения. Поэтому усреднение по формуле (3) может дать неограниченное уменьшение случайной составляющей погрешности измерений с ростом числа измерений.
Если же этот интервал усреднения Δt меньше времени корреляции (см. рис. 3 а), то на каждом отдельно взятом интервале усреднения Δt1 или Δt2 получим разные значения погрешности. В отличие от белого шума погрешность среднего арифметического при увеличении количества измерений будет стремиться к некоторому значению (xср1, xср2 на рис. 3 а), отличному от нуля. Поэтому формула (3) перестаёт быть справедливой.
Поскольку в реальных измерениях всегда присутствует, по крайней мере, фликкер-шум (это является фундаментальным законом природы), который делает шум измерений отличным от белого, то усреднение измерений не может снизить случайную составляющую погрешности до нуля. Кроме того, в цифровых средствах измерений всегда присутствует помеха с частотой тактового генератора, которая придаёт окраску белому шуму.
Предположим, что измерения выполняются в течение конечного промежутка времени T (то есть во временно́м окне шириной T) и за это время выполняется N измерений с равными интервалами τ = T/N между ними, после чего находится среднее значение xср (1). Предположим для простоты, что измеряемая величина равна нулю, то есть в результате измерений мы получаем только величину случайной погрешности, которую обозначим x(t).
Найдём среднеквадратическое отклонение погрешности xср. Для этого проведем множество измерений сериями по N, выполняя усреднение в пределах каждой серии. В результате получим множество значений xср.
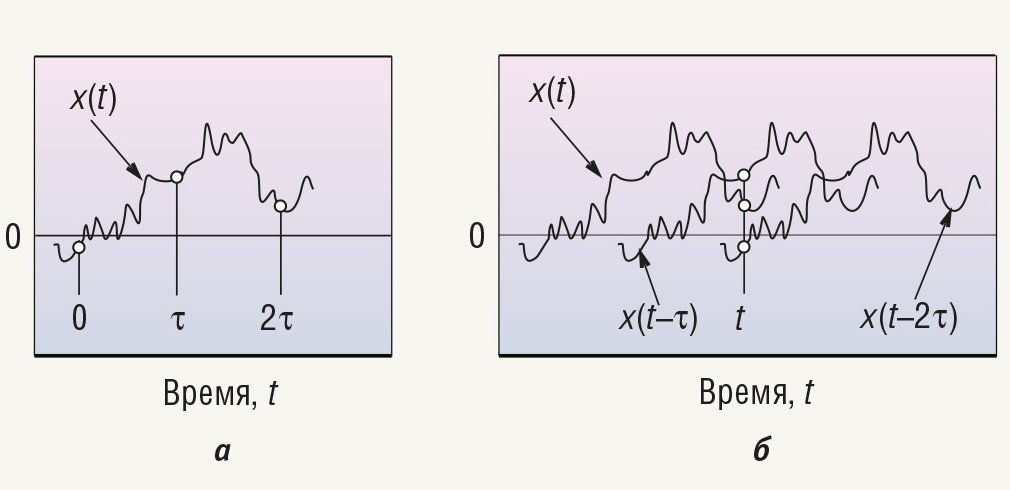
Измерения будем выполнять в моменты времени 0, τ, 2τ, … (рис. 4 а). Обратим внимание, что измерение в моменты времени 0, τ, 2τ, … эквивалентно измерению в один и тот же момент времени t (рис. 4 б), если использовать линии задержки, которые будут сдвигать реализацию случайного процесса на 0, τ, 2τ, … . Поэтому результат усреднения измерений, выполненных за время T = (N–1)τ, можно записать в виде:

где t — момент времени выполнения измерений.
Функцию xср(t) можно описать с помощью спектральной плотности мощности, для чего сначала найдём её Фурье-изображение:
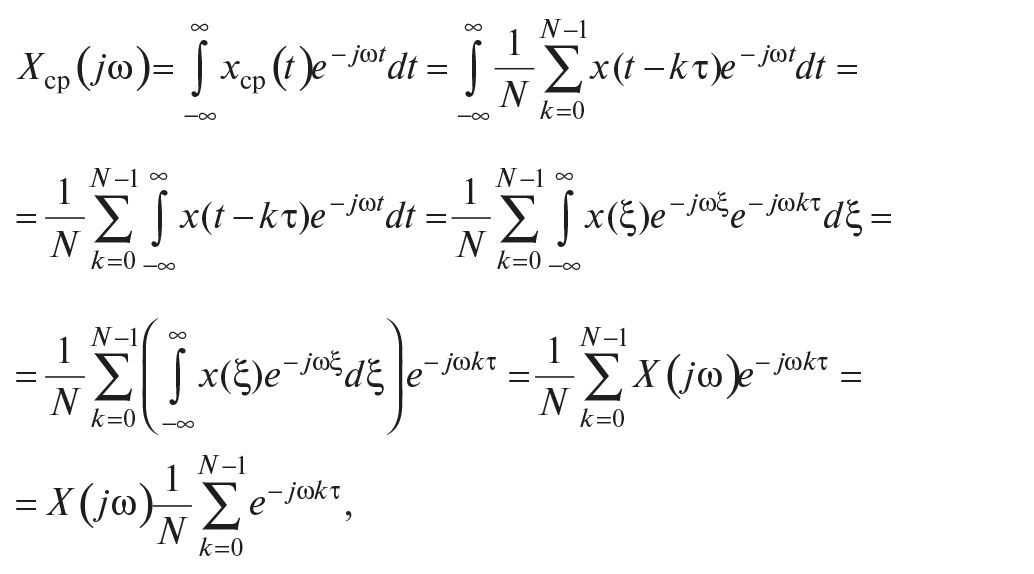
где сначала использована замена переменной t = ξ + kτ, затем введено обозначение
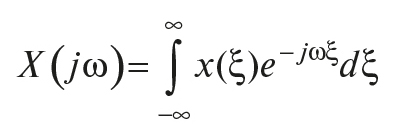
Фурье-изображения рассматриваемой случайной погрешности x(t).
Полученное выражение можно записать в виде:

где

Таким образом, процесс усреднения можно рассматривать как прохождение случайного процесса через усредняющий фильтр с передаточной характеристикой (9). Поскольку вследствие симметрии Фурье-изображений в (8) относительно оси ординат Xср(–jω) = W(–jω)X(–jω), то, умножая левую и правую часть этого выражения на соответствующие части из выражения (8), получим:
Xcp(jω)Xcp(−jω) =W(jω)W(−jω)X(jω)X(−jω),
откуда
|Xcp(jω)|2 = |W(jω)|2|X(jω)|2.
Пользуясь определением спектральной плотности мощности, из последнего выражения получим:
Scp(ω) = |W(jω)|2S(ω),
где S(ω) и Sср(ω) — спектральные плотности мощности случайной составляющей погрешности до процесса усреднения и после.
Рассмотрим передаточную функцию усредняющего фильтра (9). Используя формулу суммы членов геометрической прогрессии
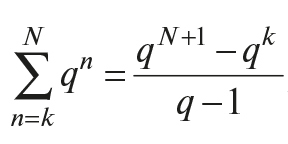
её можно записать в виде:
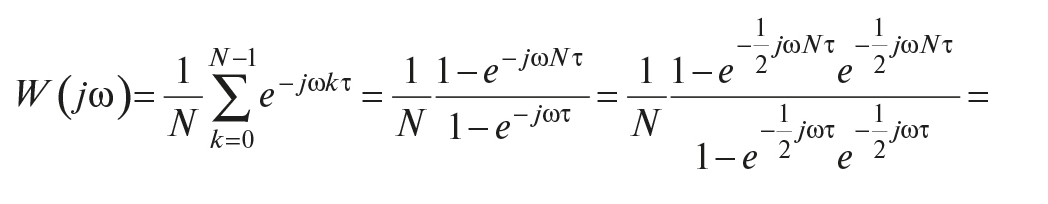
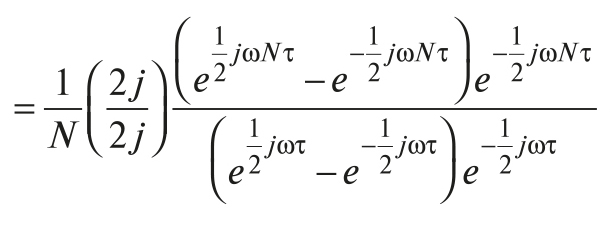
Пользуясь соотношением [exp(jx) – exp(–jx)]/2j = sin(x), окончательно получим:
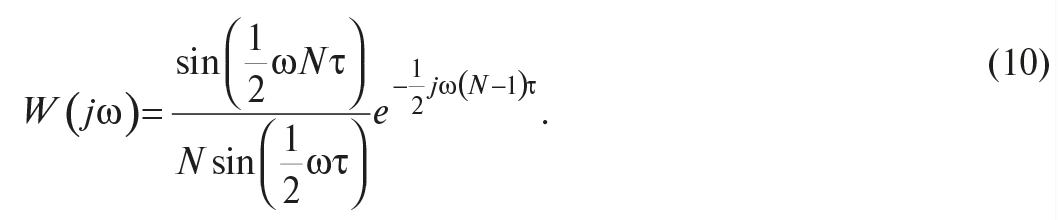
Выражение (10) является передаточной функцией цифрового sinc-фильтра [3] (список литературы в первой части статьи), то есть усреднение измерений, полученных в N точках, отстоящих друг от друга на τ, эквивалентно цифровой фильтрации в прямоугольном окне шириной Nτ. В результате фильтрации ослабляются спектральные составляющие погрешности измерений, расположенные выше граничной частоты фильтра.
Дисперсию погрешности измерений можно найти, интегрируя спектральную плотность мощности погрешности по всей полосе частот, от 0 до ∞:
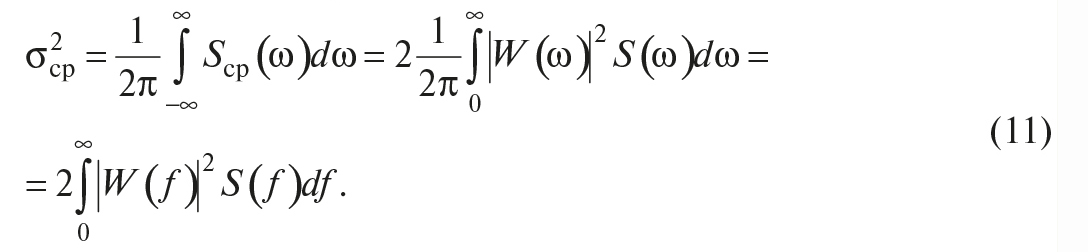
Это выражение справедливо для погрешности с любой спектральной плотностью. Предположим сначала, что погрешность является белым шумом, то есть S(ω)=S0=const. Тогда, подставляя (10) в (11), получим
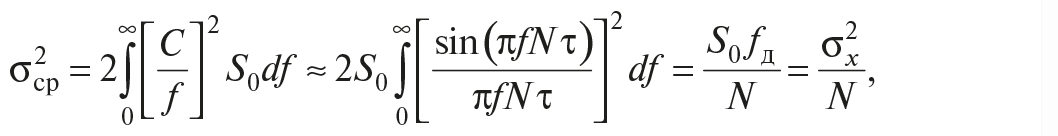
где fд = 1/τ — частота дискретизации (то есть измерений), откуда
σср=σх/√N
Это выражение совпадает с ранее полученным выражением (3), поскольку использовано предположение о преобладании белого шума. Таким образом, усреднение N однократных измерений, выполненных в N временных точках, отстоящих друг от друга на τ, при белом шуме уменьшает погрешность в √N раз.
В случае коррелированных измерений (цветного шума) необходимо использовать формулу (7). В неё входят коэффициенты корреляции rij, которые можно найти следующим образом. Предположим, что случайная составляющая погрешности измерений обусловлена смесью белого шума со спектральной плотностью S0 и фликкер-шума со спектральной плотностью , где c — константа, определяемая экспериментально (рис. 5).
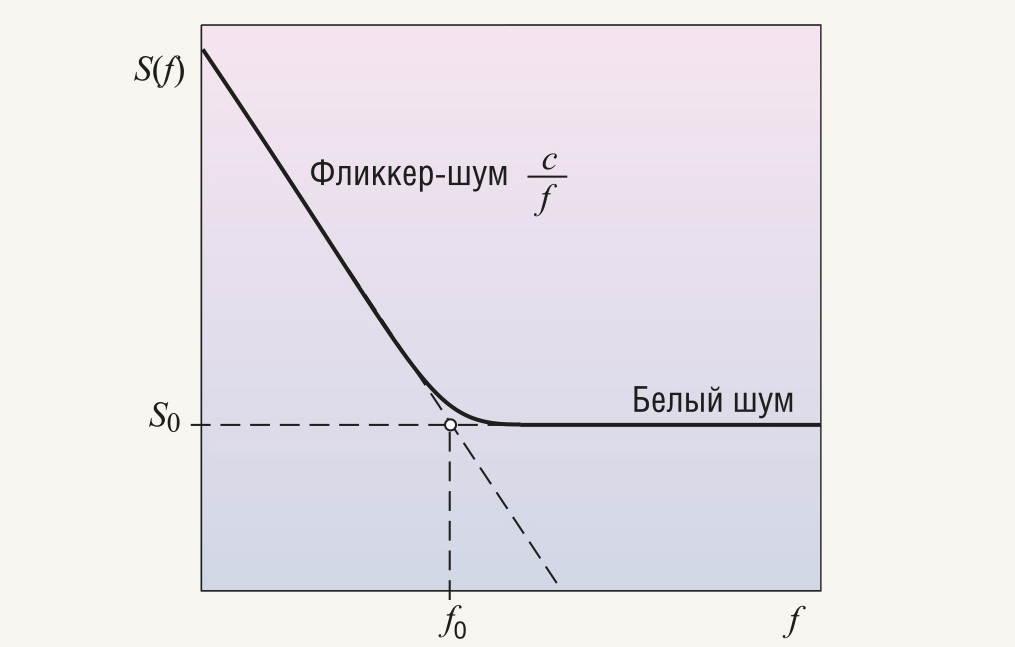
Тогда спектральную плотность мощности погрешности можно выразить как

Найдём частоту f0, на которой оба компонента шума одинаковы (рис. 5): S0=c/f0, откуда f0=c/S0.
При f → 0 спектральная плотность мощности (12) стремится к бесконечности, поэтому интеграл (11) для фликкер-шума расходится. Однако если учесть, что измерительные каналы систем автоматизации имеют режим автокалибровки, то низкочастотные компоненты фликкер-шума будут подавлены. Это позволяет выбрать ненулевую нижнюю границу спектра фликкер-шума, равную fн. Если калибровка в процессе эксплуатации прибора не выполняется, то величина fн будет определяться межповерочным интервалом средства измерений.
Для получения корреляционной матрицы сначала найдём функцию автокорреляции случайной погрешности Rx(τ), используя теорему Винера-Хинчина и преобразование Фурье:
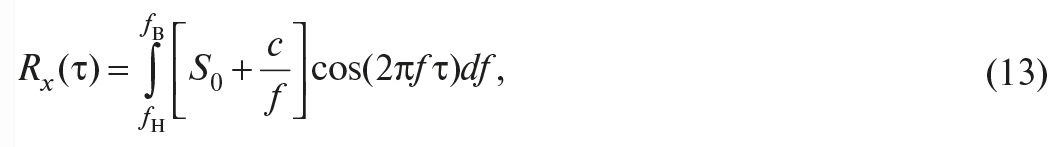
где τ — интервал времени между отдельными измерениями (сечениями случайного процесса). Здесь и далее мы используем односторонний энергетический спектр. Пределы интегрирования выбраны в предположении, что в реальных средствах измерений полоса частот погрешностей сверху ограничена верхней граничной частотой полосы пропускания измерительного канала fв, а снизу — межкалибровочным интервалом Tмк. Поэтому в спектре помехи не могут существовать компоненты с частотой ниже fн = 1/Tмк. Интегрируя (13) и используя дисперсию
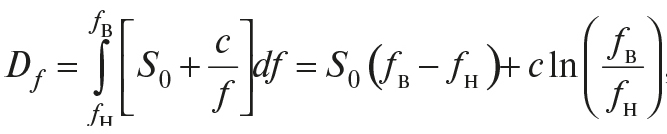
нормированную на Df автокорреляционную функцию можно записать в виде:
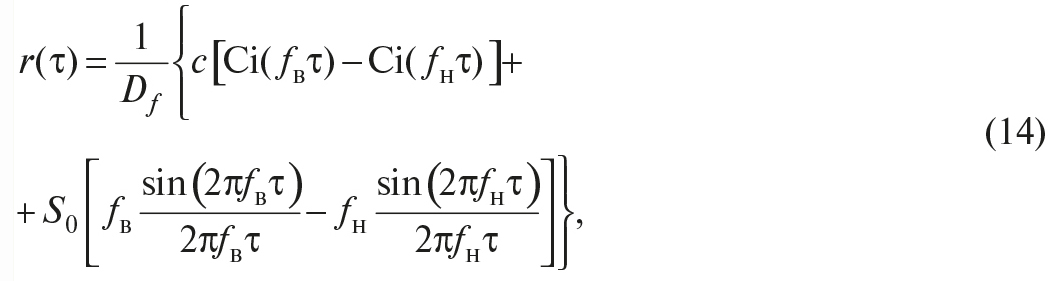
где Ci(·) — интегральный косинус,
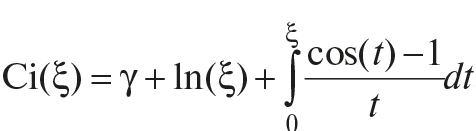
γ = 0,5772… — постоянная Эйлера.
Графики функции r(τ) при типичной для измерительных модулей систем промышленной автоматизации граничной частоте fв = 10 Гц [3], разных fн = 1/Tмк (то есть разных интервалах между калибровками Tмк) и при пересечении графиков с/f и S0 в точке S0 = 1 Гц показаны на рис. 6.
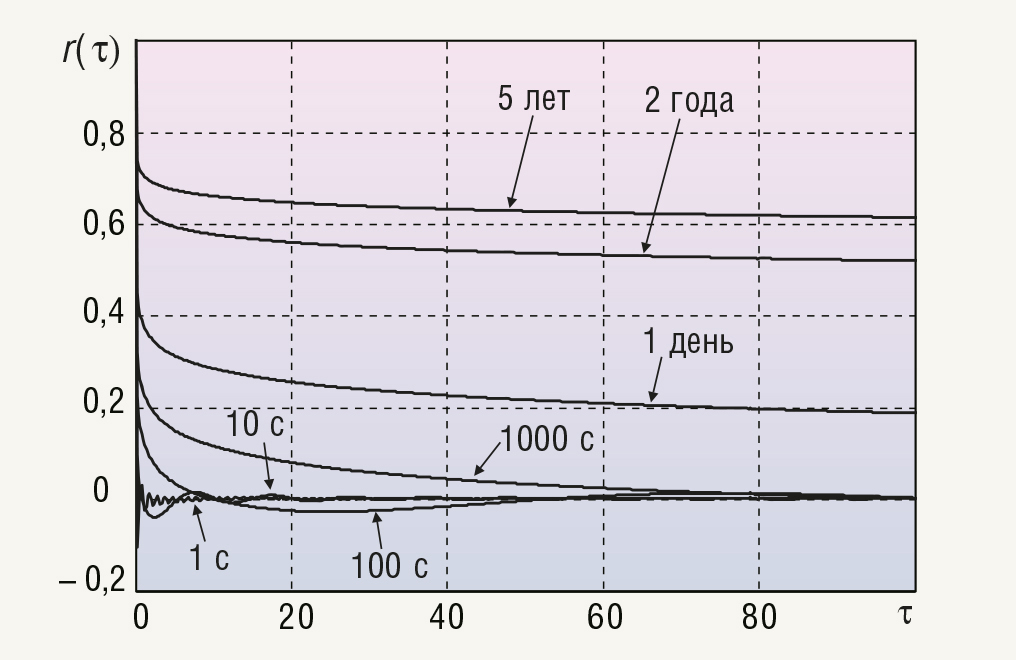
Как следует из рисунка, наиболее сильная корреляция между отдельными измерениями существует при измерениях с интервалом менее 10 с. При интервале между калибровками более 1 мин корреляция шумовой погрешности является относительно слабой; это характерно для приборов с автоматической калибровкой, которые калибруются, например, в момент включения или перед каждым измерением. Сильная корреляция погрешности (более 0,7) свойственна приборам, которые калибруются только во время периодической поверки (например, с интервалом 2 года и более).
Качественное объяснение приведённых графиков состоит в следующем. С увеличением интервала между калибровками растет доля спектральной плотности мощности погрешности, приходящаяся на низкочастотную часть энергетического спектра. Поэтому увеличивается вероятность того, что все измерения, сделанные за время, которое много меньше периода между калибровками, будут одинаково смещены в одну сторону.
Предположим, что усреднение по множеству значений случайной величины (погрешности измерений) в сечении случайного процесса можно заменить усреднением по времени (то есть случайный процесс является эргодическим). Тогда в качестве коэффициентов корреляции можно использовать значения автокорреляционной функции (14) в моменты измерений ti, tj, то есть rij = rf(τij), τij = ti – tj. Поскольку автокорреляционная функция зависит только от интервала между моментами измерений, то при одинаковых интервалах двойную сумму в (7) можно записать в виде:
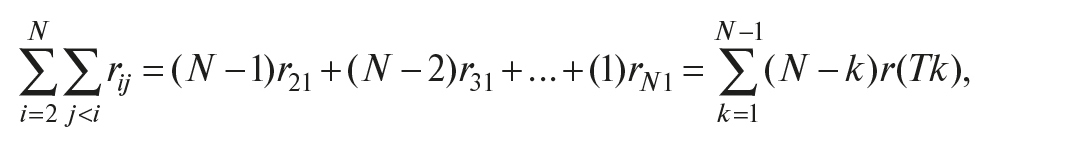
где k — порядковый номер измерения; T — интервал времени между соседними измерениями. Поэтому выражение (7) можно записать в виде:
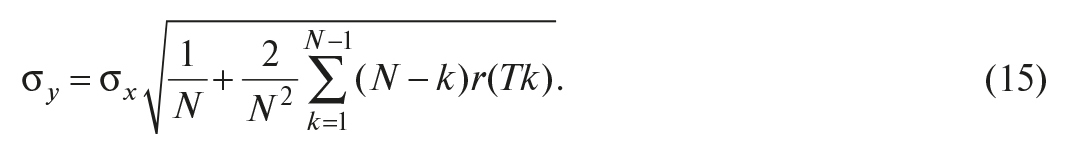
Для практических оценок эту формулу можно ещё более упростить. Как следует из рис. 6, при больших значениях автокорреляционной функции и малом количестве отсчётов можно принять r(τ) = r0 » const. Например, при интервале между измерениями 20 с и количестве измерений 10 коэффициент корреляции для верхней кривой на рис. 6 изменяется менее чем на 5%. Для этих случаев выражение (15) упрощается:

На рис. 7 показан график, построенный в соответствии с формулой (16).
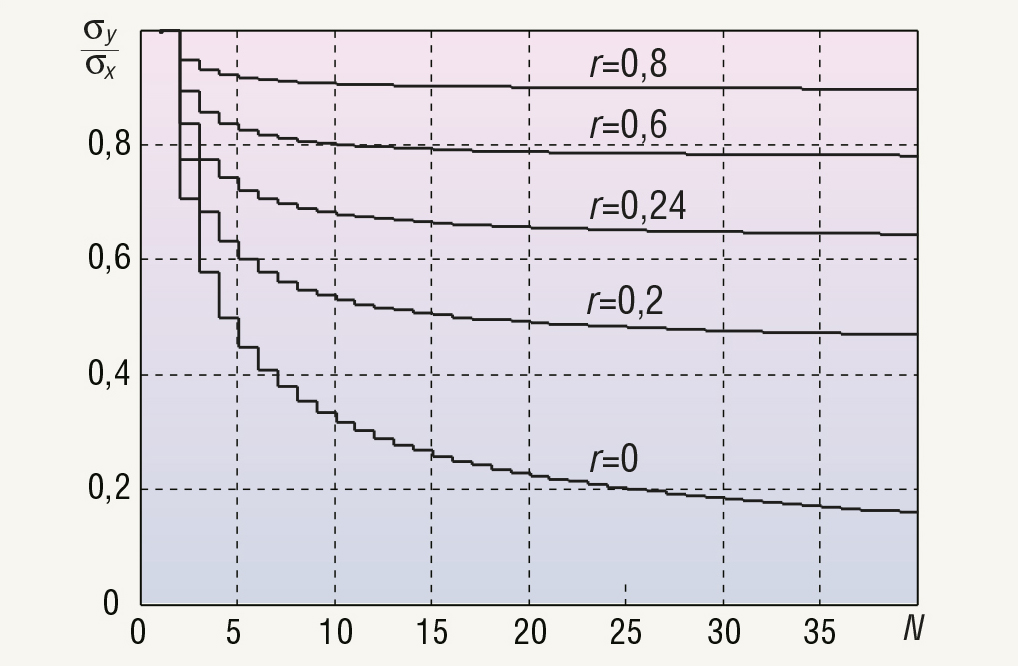
Погрешность при наличии узкополосных помех
Рассмотрим теперь влияние на погрешность измерений узкополосных помех из сети с частотой 50 Гц и от цифровой части средства измерений. Предположим, что среднеквадратическое отклонение помехи определяется её основной гармоникой:
e(t) = A cos(2πfst), (17)
где fs = 1/Ts, Ts — период колебания, A — амплитуда. Поскольку измерения выполняются в дискретные моменты времени с постоянным интервалом T, то величина погрешности измерений будет зависеть от соотношения Ts, T и количества измерений.
Рассмотрим сначала погрешность, вызванную помехой с частотой 50 Гц. Многократные измерения с периодом T эквивалентны дискретизации помехи в моменты измерений. Если период измерений стабилен, то помеха переносится в низкочастотную область благодаря алиасному (стробоскопическому) эффекту. Представим моменты измерений в виде:
tk = (MTs + δTs)k, (18)
где M = 1, 2, … — целое число, 0 < δ < 1 — доля периода, k ∈ [0,2,… N] — порядковый номер измерения. Тогда уравнение помехи (17) после дискретизации можно записать в виде:
e(t) = A cos(2πfs(MTs + δTs)k) = A cos(2πfsδTsk).
Здесь использована известная формула тригонометрии для косинуса суммы углов и соотношение cos(2πfsMT) = 1.
Количество измерений KT, приходящихся на период алиасной помехи, можно найти из соотношения 2πfsσTsKT = 2π, откуда KT = 1/σ. Интервал времени между измерениями, как следует из (18), равен T = MTs + σTs , поэтому период алиасных колебаний будет:

Таким образом, в результате измерений значений помехи со стабильным интервалом Ts её период увеличивается после дискретизации в (M + σ)/σ раз; во столько же раз падает частота.
Процесс усреднения результатов многократных измерений, выполненных с интервалом T, эквивалентен прохождению сигнала через дискретный sinc-фильтр [3]. Поэтому эффективность ослабления помехи будет зависеть от соотношения ширины окна усреднения (то есть полосы пропускания фильтра), частоты алиасной помехи fа = 1/Tа и частоты fа – 1/T, полученной вследствие размножения копий спектра алиасной помехи при её дискретизации.
Однако, как следует из (19), при σ → 0 (то есть когда на интервале измерений укладывается целое число периодов помехи) fа → 0 и частота помехи становится ниже граничной частоты усредняющего фильтра, а в пределе получаем постоянное смещение на уровень, величина которого зависит от случайной фазы помехи в момент измерений. Поэтому в общем случае ослабить помеху из сети 50 Гц с помощью усреднения невозможно. Теоретически такое ослабление было бы возможно только при искусственной синхронизации процесса измерений с сигналом помехи или при измерениях в некоррелированные случайные моменты времени.
Рассмотрим теперь случай, когда погрешность измерений вызвана высокочастотной помехой от цифровой части измерительной системы. Для неё Ts имеет порядок долей микросекунды. Разброс (нестабильность) меток времени в компьютере составляет десятые и сотые доли секунды, в ПЛК с операционной системой реального времени — десятки микросекунд [3]. Поэтому измерения помехи с частотой более 1 МГц (период менее 1 мкс) не могут быть периодическими. Величина помехи в момент измерения является случайной величиной и определяется законом распределения нестабильности тактирования pT(T) в компьютере или контроллере. К сожалению, корреляционная функция периода измерений с помощью компьютера или контроллера является неисследованной. Если предположить, что период измерений описывается моделью белого шума, то результат дискретизации помехи также будет белым шумом, который учитывается в погрешности измерений формулой (15).
Выводы
Из изложенного в данной статье можно сделать следующие выводы.
-
Увеличение точности путём усреднения результатов многократных измерений ограничено не только систематической составляющей погрешности, но и спектральным составом шума измерений. Фликкер-шум, спектральная плотность мощности которого растёт с понижением частоты, ограничивает возможность увеличения точности путём усреднения.
-
Наиболее практичным способом устранения погрешности, обусловленной фликкер-шумом, является периодическая автокалибровка средства измерений.
-
Погрешность усреднения в случае некоррелированной погрешности не зависит от ширины временного окна Nτ, а зависит только от количества отсчётов N.
-
Усреднение может применяться только при постоянном значении измеряемой величины. В противном случае нужно учитывать динамическую погрешность или уменьшать ширину окна усреднения.
-
Усреднение является разновидностью цифровой фильтрации методом «скользящего среднего», поэтому может быть использовано и при наличии шумов объекта измерений. Однако этой проблеме посвящена специальная литература.
-
Информация, необходимая для оценки функции автокорреляции, обычно отсутствует. Для её получения необходимо измерять спектральную плотность погрешности автоматизированными методами измерений [3], что является довольно трудоёмкой задачей. Поэтому предложенная методика оценки погрешности при коррелированном шуме может найти применение в редких случаях, когда целью является получение максимального количества информации, несмотря на трудозатраты на её получение. ●
Обновлено: 22.06.2023
Метрология — наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
· теоретическая (фундаментальная) — раздел метрологии, предметом которого является разработка фундаментальных основ метрологии.
· законодательная метрология — раздел метрологии, предметом которого является установление обязательных технических и юридических требований по применению единиц величин, эталонов, методов и средств измерений, направленных на обеспечение единства и требуемой точности измерений.
· практическая (прикладная) — раздел метрологии, предметом которого являются вопросы практического применения разработок metrology теоретической метрологии и положений законодательной метрологии.
Основные функции метрологии:
— создание общей теории измерений;
— образование единиц физических величин и систем единиц;
— разработка методов и средств измерений, методов определения точности, основ обеспечения единства и единообразия средств измерений;
— создание эталонов и образцовых средств, проверке мер и средств измерений.
Важнейшей задачей метрологии является обеспечение единства измерений,
Единство измерений—состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц, воспроизводимых первичными эталонами, а погрешности результатов измерений известны и с заданной вероятностью не выходят за установленные пределы.
Единство измерений достигается путем точного воспроизведения и хранения в специализированных организациях установленных единиц физических величин и передачи их размеров применяемым на практике СИ. Воспроизведение единицы физической величины осуществляется в результате операций по материализации единицы физической величины с помощью государственного эталона.
Передача размера единицы — приведение размера единицы физической величины, хранимой поверяемым средством измерений, к размеру единицы, воспроизводимой или хранимой эталоном, осуществляемое при их поверке (калибровке). Размер единицы передается от более точных средств измерений к менее точным.
Хранение единицы — совокупность операций, обеспечивающих неизменность во времени размера единицы, присущего данному средству измерений.
Определение измерения?
Измерение физической величины—совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.
Измерительная задача — задача определения значения физической величины путем ее измерения с требуемой точностью в заданных условиях измерений.
Объект измерения — тело (физическая система, процесс, явление и т.д.), которое характеризуется одной или несколькими измеряемыми физическими величинами.
§ Вал, у которого измеряют диаметр;
§ технологический процесс, во время которого измеряют температуру;
§ Положение корабля, координаты которого измеряют.
Область измерений — совокупность измерений физических величин, свойственных какой-либо области науки или техники и выделяющихся своей спецификой.
Примечание: Выделяют ряд областей измерений: механические, магнитные, акустические, измерения ионизирующих излучений и др.
Вид измерений — часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин.
Пример:В области акустических измерений могут быть выделены как виды измерений: измерения амплитуды, частоты, фазы, акустического давления и др.
Принцип измерений — физическое явление или эффект, положенное в основу измерений.
1. Применение явления термо-ЭДС для измерения температуры.
2. Применение явления упругости материала для измерения его твёрдости.
3. Применение эффекта Допплера для измерения скорости.
4. Использование силы тяжести при измерении массы взвешиванием.
Метод измерений — прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений.
Методика выполнения измерений (МВИ) — установленная совокупность операций и правил при измерении, выполнение которых обеспечивает получение результатов измерений с гарантированной точностью в соответствии с принятым методом.
Погрешности измерения и методы их уменьшения?
Точность результата измерений—одна изхарактеристик качества измерения, отражающая близость к нулю погрешности результата измерения.
Примечание: Точность измерений тем или иным средством измерений (СИ) определяется их погрешностью. Высокая точность измерений соответствует малым погрешностям как систематическим, так и случайным.
Погрешность результата измерений—отклонение результата измерения от истинного (действительного) значения измеряемой величины.
· Погрешность не следует путать с ошибкой измерений, связанной с субъективными обстоятельствами.
Абсолютная погрешность измерения—погрешность измерения, выраженная в единицах измеряемой величины.
Относительная погрешность измерения—погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.
Вагон массой 50000 кг измерен с абсолютной погрешностью ±50 кг, при этом относительная погрешность составляет: ±50/50000 = ±0,1%.
Примечание: Относительную погрешность в долях или процентах находят из отношений:
d = Dх/х, или d = Dх×100%/х,
где Dх — абсолютная погрешность измерений;
х — действительное или измеренное значение величины.
Систематическая погрешность — постоянная, или изменяющаяся по определенному закону при повторных измерениях одной и той же величины погрешность. Она может быть связана, например, с ошибкой в градуировке шкалы.
Постоянные погрешности—погрешности, которые длительное время сохраняют свое значение, например, в течение времени выполнения всего ряда измерений.
Периодические погрешности—погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.
Случайная погрешность измерения—составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.
В отличие от систематической ее нельзя исключить из результатов измерений, однако ее значение может быть уменьшено в результате специальных способов обработки результатов измерений, основанных на положениях теории вероятности и математической статистики.
Промах — погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Примечание: Иногда вместо термина «промах» применяют термин грубая погрешность измерений
Общим методом уменьшения погрешностей является конструктивно- технологический метод, основанный на выявлении и устранении причин и источников возникновения погрешностей.
Примерами использования такого метода являются: термостатирование прибора (для исключения температурной погрешности), применение экранов и фильтров (для уменьшения погрешностей от влияния электромагнитных полей, наводок и др.), рациональное расположение средств измерений по отношению друг к другу, к источнику влияющих воздействий и к объекту исследования (например, магнитоэлектрические приборы должны быть удалены друг от друга) и др.
Во многих случаях использование данного метода для достижения требуемой точности измерения встречает большие затруднения и может привести к резкому возрастанию стоимости средств измерений.
Более широкое применение получили методы структурной и (или) временной избыточности, т.е. на введении дополнительных средств измерений (измерительных преобразователей, приборов и др.) и (или) выполнении дополнительных измерений, результаты которых обрабатываются по определенному алгоритму.
1. использовать более точное измерительное устройство
2. пригласить более квалифицированного специалиста
3. если измерение не единоразовое, увеличить количество измерений (циклов)
а что именно измеряется то?
Ну, если речь идёт о стрелочных приборах, то:
1. Установить зеркало под стрелкой — это обеспечит гарантированно вертикальный взгляд на стрелку.
2. Вообще исключить человеческий фактор из измерений, пользуясь электронными приборами.
Эти сведения нехило устарели, но в большинстве наших вузов они всё еще актуальны.
Смотря что измерять. Для того, чтобы уменьшить погрешность измерения какой-то величины, необходим посмотреть КАКОЙ измеряемый параметр дает максимальный вклад в результат погрешности.
На этот вопрос отвечает наука — метрология.
А если по простому — взять более точный прибор.
Уменьшение систематической погрешности.
Систематическая погрешность проявляется в виде смещения Хизм относительно Х. Может быть учтена введением поправки.
При ∆с ≈ 0 – измерения правильные.
Способы уменьшения ∆с:
· повышение класса точности прибора;
· использование метода замещения;
· изменение знака выходной величины и др.
Уменьшение случайной погрешности.
Случайная погрешность проявляется в виде разброса значений Хизм относительно Х. Может быть оценена в виде доверительного интервала.
· повышение класса точности СИТ (при однократных измерениях);
· проведение многократных наблюдений при помощи приборов высокой чувствительности.
2.4 Классы точности
Класс точности – нормированная метрологическая характеристика средства измерения, определяемая пределами допускаемых погрешностей, а также другими свойствами, влияющими на точность.
1. Приборы с Δад >> Δмлт
Класс точности: . Пример обозначения: 1,0
Пример 1: Предел измерения амперметра 10 А, класс точности 0,5. Определить абсолютную и относительную погрешности измерения тока 5 А.
Приборы с Δад >> Δмлт и резко неравномерной шкалой (Хн = lполн).
Класс точности: . Пример обозначения:
Пример 2: Определить абсолютную погрешность измерения сопротивления резистора, если показание омметра 500 Ом, а на отметке измерения 1 мм шкалы соответствует 10 Ом. Класс точности омметра
2. Приборы с Δмлт >> Δад
Класс точности: . Пример обозначения:
Пример 3: Счетчик электрической энергии зарегистрировал расход энергии 200 кВт-час. Определить абсолютную погрешность измерения энергии, если класс точности счетчика .
3. Приборы с Δад ~ Δмлт
Класс точности: . Пример обозначения: 1,0/0,5 .
Пример 4 Предел измерения вольтметра 50 В, класс точности 0,5/0,2. Определить погрешность измерения напряжения 20 В.
Пример 5: Первый ваттметр имеет предел измерения Wн1 = 750 Bт и класс точности K1 = 0,5; второй ваттметр – соответственно Wн2 =1000 Bт и K2 = 0,5/0,1. Выбрать прибор, обеспечивающий меньшую погрешность измерения мощности 500 Вт.
Меньшую погрешность дает второй ваттметр.
Лекция 3ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
3.1 Показатели точности измерений
Результат измерения – числовое значение, приписываемое измеряемой величине, с указанием точности измерения.
Численные показатели точности:
· доверительный интервал (доверительные границы) погрешности ΔР;
· оценка СКО погрешности S.
Правила выражения показателей точности:
· численные показатели точности выражаются в единицах измеряемой величины;
· численные показатели точности должны содержать не более двух значащих цифр;
А.Крылов: «Всякая неверная цифра – ошибка, а всякая лишняя цифра – половина ошибки»;
· наименьшие разряды значения измеряемой величины и численных показателей точности должны быть одинаковыми.
3.2 Представление результатов измерений
Результат измерения:
Пример: U = 105,0 В, Δ0,95 = ± 1,5 B или U = 105,0 ± 1,5 B.
Уменьшение систематической погрешности.
Систематическая погрешность проявляется в виде смещения Хизм относительно Х. Может быть учтена введением поправки.
При ∆с ≈ 0 – измерения правильные.
Способы уменьшения ∆с:
· повышение класса точности прибора;
· использование метода замещения;
· изменение знака выходной величины и др.
Уменьшение случайной погрешности.
Случайная погрешность проявляется в виде разброса значений Хизм относительно Х. Может быть оценена в виде доверительного интервала.
· повышение класса точности СИТ (при однократных измерениях);
· проведение многократных наблюдений при помощи приборов высокой чувствительности.
2.4 Классы точности
Класс точности – нормированная метрологическая характеристика средства измерения, определяемая пределами допускаемых погрешностей, а также другими свойствами, влияющими на точность.
1. Приборы с Δад >> Δмлт
Класс точности: . Пример обозначения: 1,0
Пример 1: Предел измерения амперметра 10 А, класс точности 0,5. Определить абсолютную и относительную погрешности измерения тока 5 А.
Приборы с Δад >> Δмлт и резко неравномерной шкалой (Хн = lполн).
Класс точности: . Пример обозначения:
Пример 2: Определить абсолютную погрешность измерения сопротивления резистора, если показание омметра 500 Ом, а на отметке измерения 1 мм шкалы соответствует 10 Ом. Класс точности омметра
2. Приборы с Δмлт >> Δад
Класс точности: . Пример обозначения:
Пример 3: Счетчик электрической энергии зарегистрировал расход энергии 200 кВт-час. Определить абсолютную погрешность измерения энергии, если класс точности счетчика .
3. Приборы с Δад ~ Δмлт
Класс точности: . Пример обозначения: 1,0/0,5 .
Пример 4 Предел измерения вольтметра 50 В, класс точности 0,5/0,2. Определить погрешность измерения напряжения 20 В.
Пример 5: Первый ваттметр имеет предел измерения Wн1 = 750 Bт и класс точности K1 = 0,5; второй ваттметр – соответственно Wн2 =1000 Bт и K2 = 0,5/0,1. Выбрать прибор, обеспечивающий меньшую погрешность измерения мощности 500 Вт.
Меньшую погрешность дает второй ваттметр.
Лекция 3ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
3.1 Показатели точности измерений
Результат измерения – числовое значение, приписываемое измеряемой величине, с указанием точности измерения.
Численные показатели точности:
· доверительный интервал (доверительные границы) погрешности ΔР;
· оценка СКО погрешности S.
Правила выражения показателей точности:
· численные показатели точности выражаются в единицах измеряемой величины;
· численные показатели точности должны содержать не более двух значащих цифр;
А.Крылов: «Всякая неверная цифра – ошибка, а всякая лишняя цифра – половина ошибки»;
· наименьшие разряды значения измеряемой величины и численных показателей точности должны быть одинаковыми.
3.2 Представление результатов измерений
Результат измерения:
Пример: U = 105,0 В, Δ0,95 = ± 1,5 B или U = 105,0 ± 1,5 B.
Обычно выделяют три группы погрешностей: неустранимая погрешность; погрешность метода; вычислительная погрешность. Неустранимая погрешность порождается: а) неточностью входных данных в математическом описании задачи; б) несоответствия математической модели реальной задаче. Погрешность метода возникает из-за того, что используются приближенные методы. А погрешность вычислений возникает при вводе-выводе и при выполнении математических операций, а также при округлениях. Попробуем привести несколько практических приемов для уменьшения влияния вычислительной погрешности на результаты вычислений.
1. Сложение чисел необходимо проводить по мере их возрастания так как в машинной арифметике из-за погрешности округления существенен порядок выполнения операций.
2. В некоторых случаях имеет смысл выполнить предварительные преобразования вычисляемого выражения.
3. Необходимо исключать вычитание двух почти равных чисел, тем более когда такая разность находится в знаменателе выражения.
4. Если числа равны a и b почти равны, то вычитание этих чисел следует производить раньше, чем деление или умножение.
К примеру, следует отдать предпочтение выражению (a-b)/c, а не выражению a/c-b/c. Во-первых здесь меньше операций (смотри пункт 3 и 6), а во-вторых, после деления числа станут меньше и еще меньше будут отличаться друг от друга, что может привести к обращению разности в ноль.
5. При перемножении нескольких чисел надо сразу перемножать самое большое число и самое маленькое, так как умножение друг на друга нескольких маленьких чисел может привести к появлению машинного нуля.
6. Всегда следует стремиться к уменьшению числа арифметических операций. Это объясняется тем, что чем больше операций, тем больше суммирующие погрешности.
Читайте также:
- Слова о педагогическом коллективе школы
- Для чего нужна характеристика из школы
- Политическая символика как элемент политической культуры кратко
- Что такое ушу кратко
- Почему заселение территории россии происходило в основном на восток а не на запад кратко