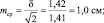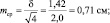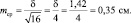Автор:
Laura McKinney
Дата создания:
7 Апрель 2021
Дата обновления:
17 Сентябрь 2023
Содержание
- Сравнительная таблица
- Определение стандартного отклонения
- Определение стандартной ошибки
- Ключевые различия между стандартным отклонением и стандартной ошибкой
- Вывод

Стандартная ошибка используется для измерения статистической точности оценки. Он в основном используется в процессе проверки гипотез и оценки интервала.
Это две важные концепции статистики, которые широко используются в области исследований. Разница между стандартным отклонением и стандартной ошибкой основана на различии между описанием данных и их выводом.
Сравнительная таблица
| Основа для сравнения | Стандартное отклонение | Стандартная ошибка |
|---|---|---|
| Имея в виду | Стандартное отклонение подразумевает меру отклонения набора значений от их среднего. | Стандартная ошибка означает меру статистической точности оценки. |
| Статистика | Описательный | Логический |
| Меры | Насколько наблюдения отличаются друг от друга. | Насколько точно среднее значение выборки соответствует истинному среднему значению генеральной совокупности. |
| Распределение | Распределение наблюдения относительно нормальной кривой. | Распределение оценки относительно нормальной кривой. |
| Формула | Корень квадратный из дисперсии | Стандартное отклонение, деленное на квадратный корень из размера выборки. |
| Увеличение размера выборки | Дает более конкретную меру стандартного отклонения. | Уменьшает стандартную ошибку. |
Определение стандартного отклонения
Стандартное отклонение — это мера разброса ряда или расстояния от стандарта. В 1893 году Карл Пирсон ввел понятие стандартного отклонения, которое, несомненно, является наиболее часто используемой мерой в научных исследованиях.
Это квадратный корень из среднего квадрата отклонений от их среднего значения. Другими словами, для данного набора данных стандартное отклонение — это среднеквадратичное отклонение от среднего арифметического. Для всего населения он обозначается греческой буквой «сигма (σ)», а для выборки — латинской буквой «s».
Стандартное отклонение — это мера, которая количественно определяет степень дисперсии набора наблюдений. Чем дальше точки данных от среднего значения, тем больше отклонение в наборе данных, что означает, что точки данных разбросаны по более широкому диапазону значений и наоборот.
Определение стандартной ошибки
Вы могли заметить, что разные выборки одинакового размера, взятые из одной и той же совокупности, дадут разные значения рассматриваемой статистики, т.е. выборочное среднее. Стандартная ошибка (SE) представляет собой стандартное отклонение различных значений выборочного среднего. Он используется для сравнения выборочных средних по совокупности.
Короче говоря, стандартная ошибка статистики — это не что иное, как стандартное отклонение ее выборочного распределения. Он играет большую роль в проверке статистических гипотез и интервальной оценке. Это дает представление о точности и достоверности сметы. Чем меньше стандартная ошибка, тем больше однородность теоретического распределения и наоборот.
- Формула: Стандартная ошибка для выборочного среднего = σ / √n
Где, σ — стандартное отклонение совокупности
Ключевые различия между стандартным отклонением и стандартной ошибкой
Приведенные ниже моменты существенны с точки зрения разницы между стандартным отклонением:
- Стандартное отклонение — это мера, которая оценивает степень вариации набора наблюдений. Стандартная ошибка измеряет точность оценки, т. Е. Является мерой изменчивости теоретического распределения статистики.
- Стандартное отклонение — это описательная статистика, тогда как стандартная ошибка — это выводимая статистика.
- Стандартное отклонение измеряет, насколько отдельные значения отличаются от среднего значения. Напротив, насколько близко среднее значение выборки к среднему значению генеральной совокупности.
- Стандартное отклонение — это распределение наблюдений относительно нормальной кривой. В отличие от этого, стандартная ошибка — это распределение оценки относительно нормальной кривой.
- Стандартное отклонение определяется как квадратный корень из дисперсии. И наоборот, стандартная ошибка описывается как стандартное отклонение, деленное на квадратный корень из размера выборки.
- Когда размер выборки увеличивается, это дает более конкретную меру стандартного отклонения. В отличие от стандартной ошибки, когда размер выборки увеличивается, стандартная ошибка имеет тенденцию к уменьшению.
Вывод
В целом стандартное отклонение считается одним из лучших показателей дисперсии, который измеряет отклонение значений от центрального значения. С другой стороны, стандартная ошибка в основном используется для проверки надежности и точности оценки, поэтому чем меньше ошибка, тем выше ее надежность и точность.
(note that I’m focusing on standard error of the mean, which I believe the questioner was as well, but you can generate a standard error for any sample statistic)
The standard error is related to the standard deviation but they are not the same thing and increasing sample size does not make them closer together. Rather, it makes them farther apart. The standard deviation of the sample becomes closer to the population standard deviation as sample size increases but not the standard error.
Sometimes the terminology around this is a bit thick to get through.
When you gather a sample and calculate the standard deviation of that sample, as the sample grows in size the estimate of the standard deviation gets more and more accurate. It seems from your question that was what you were thinking about. But also consider that the mean of the sample tends to be closer to the population mean on average. That’s critical for understanding the standard error.
The standard error is about what would happen if you got multiple samples of a given size. If you take a sample of 10 you can get some estimate of the mean. Then you take another sample of 10 and new mean estimate, and so on. The standard deviation of the means of those samples is the standard error. Given that you posed your question you can probably see now that if the N is high then the standard error is smaller because the means of samples will be less likely to deviate much from the true value.
To some that sounds kind of miraculous given that you’ve calculated this from one sample. So, what you could do is bootstrap a standard error through simulation to demonstrate the relationship. In R that would look like:
# the size of a sample
n <- 10
# set true mean and standard deviation values
m <- 50
s <- 100
# now generate lots and lots of samples with mean m and standard deviation s
# and get the means of those samples. Save them in y.
y <- replicate( 10000, mean( rnorm(n, m, s) ) )
# standard deviation of those means
sd(y)
# calcuation of theoretical standard error
s / sqrt(n)
You’ll find that those last two commands generate the same number (approximately). You can vary the n, m, and s values and they’ll always come out pretty close to each other.
(note that I’m focusing on standard error of the mean, which I believe the questioner was as well, but you can generate a standard error for any sample statistic)
The standard error is related to the standard deviation but they are not the same thing and increasing sample size does not make them closer together. Rather, it makes them farther apart. The standard deviation of the sample becomes closer to the population standard deviation as sample size increases but not the standard error.
Sometimes the terminology around this is a bit thick to get through.
When you gather a sample and calculate the standard deviation of that sample, as the sample grows in size the estimate of the standard deviation gets more and more accurate. It seems from your question that was what you were thinking about. But also consider that the mean of the sample tends to be closer to the population mean on average. That’s critical for understanding the standard error.
The standard error is about what would happen if you got multiple samples of a given size. If you take a sample of 10 you can get some estimate of the mean. Then you take another sample of 10 and new mean estimate, and so on. The standard deviation of the means of those samples is the standard error. Given that you posed your question you can probably see now that if the N is high then the standard error is smaller because the means of samples will be less likely to deviate much from the true value.
To some that sounds kind of miraculous given that you’ve calculated this from one sample. So, what you could do is bootstrap a standard error through simulation to demonstrate the relationship. In R that would look like:
# the size of a sample
n <- 10
# set true mean and standard deviation values
m <- 50
s <- 100
# now generate lots and lots of samples with mean m and standard deviation s
# and get the means of those samples. Save them in y.
y <- replicate( 10000, mean( rnorm(n, m, s) ) )
# standard deviation of those means
sd(y)
# calcuation of theoretical standard error
s / sqrt(n)
You’ll find that those last two commands generate the same number (approximately). You can vary the n, m, and s values and they’ll always come out pretty close to each other.
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
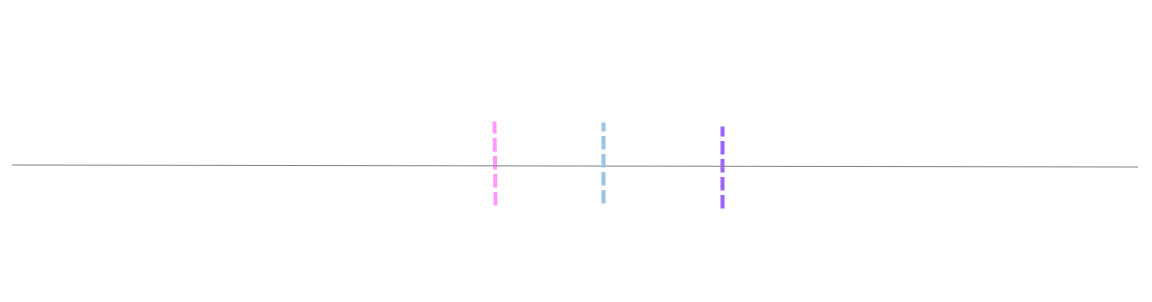
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
Чтобы
судить о том, насколько точно проведенные
измерения отражают состав генеральной
совокупности, необходимо вычислить
стандартную ошибку средней арифметической
выборочной совокупности.
Стандартная
ошибка средней арифметической
характеризует степень отклонения
выборочной средней арифметической от
средней арифметической генеральной
совокупности.
Стандартная
ошибка средней арифметической вычисляется
по формуле:
,
где
– стандартное отклонение результатов
измерений, n
– объем выборки.
Зачастую
мы имеем дело с одной случайной выборкой
и с одной полученной при ее обработке
выборочной средней. Задача заключается
в суждении о величине неизвестной
генеральной средней по полученной
неточной величине случайной выборочной
средней.
Вычислим
среднюю ошибку найденного выборочного
среднего значения роста:
195
см; σ = 8,8 см;
см.
2,8 см
составляют не максимальную, а среднюю
возможную ошибку среднего. Отдельные
выборочные средние могут отклоняться
от генеральной как больше, так и меньше,
чем на 2,8 см.
Каковы
же пределы возможных ошибок случайной
выборки, какова ее максимальная ошибка?
Величина максимальной ошибки зависит
от величины средней ошибки и вычисляется
по формуле
.
При
объеме выборки n
= 10:
.
Все
случайные выборочные средние, которые
могут быть получены в подобных опытах
(в том числе и фактически полученная
выборочная средняя
= 195 см), при своем варьировании около
неизвестного генерального среднего в
подавляющем количестве группируются
около него так, что лишь ничтожный
процент их отклоняется от генеральной
средней более, чем на величину максимальной
ошибки.
Другими
словами, генеральная средняя определяется
как
.
Эти пределы
колебаний значительно сужаются, если
средняя ошибка уменьшается благодаря
увеличению численности выборки.
Искомая
генеральная средняя лежит между
и
.
Таким образом, при высокой точности
выполнения эксперимента и достаточно
большом числе измерений можно определить
среднюю арифметическую бесконечно
большого числа экспериментов.
До сих
пор мы определяли максимальную ошибку
выборочной средней, исходя из того, что
все остальные показатели известны. Если
же мы хотим достичь определенной
точности, определенного приближения к
генеральной средней, в этом случае
встает вопрос о численности выборки (о
том, сколько измерений, опытов необходимо
провести).
Допустим, что
максимальная ошибка должна быть равна
5 см. Сколько человек надо обследовать
(измерить) в нашем случае?
.
Следовательно,
мы должны провести измерения роста у
36 баскетболистов высокого класса.
10. Достоверность различий
Следующим
важным вопросом практически для каждого
экспериментатора является умение
доказать достоверность различий между
двумя рядами признаков.
Проверку
достоверности различия двух рядов
измерений производят путем вычисления
критерия достоверности различия – t:
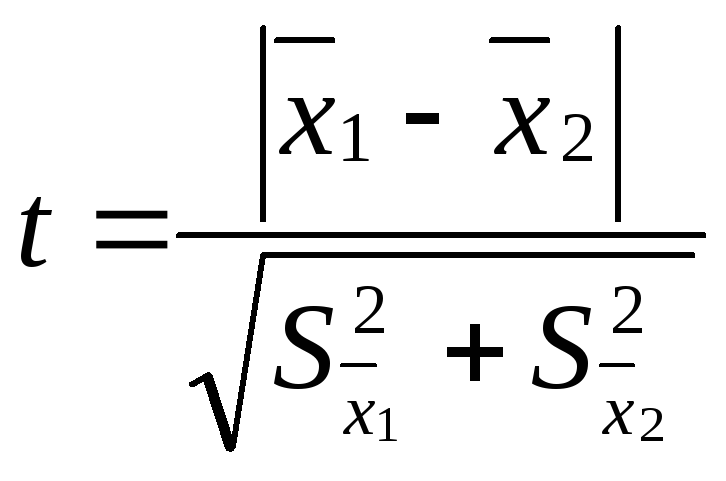
где
– средняя одной выборки;
– средняя другой выборки;
– средняя ошибка первой выборки;
– второй выборки. Если t < 2, то различие
между двумя выборками считается
недостоверным, если t
2, то различие между двумя выборками
достоверно на 95%.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка
Стандартная ошибка — это стандартное отклонение выборочного распределения статистики. Этот термин также может использоваться для оценки (хорошего предположения) этого стандартного отклонения, взятого из выборки всей группы.
Среднее значение некоторой части группы (называемой выборкой) является обычным способом оценки среднего значения для всей группы. Часто бывает слишком сложно или стоит слишком много денег, чтобы измерить всю группу. Но если измерить другую выборку, то ее среднее значение будет немного отличаться от первой выборки. Стандартная ошибка среднего — это способ узнать, насколько близка средняя по выборке к средней по всей группе. Это способ узнать, насколько вы можете быть уверены в среднем значении по выборке.
В реальных измерениях истинное значение стандартного отклонения среднего для всей группы обычно неизвестно. Поэтому термин стандартная ошибка часто используется для обозначения близкого к истинному значению для всей группы. Чем больше измерений в выборке, тем ближе к истинному значению для всей группы.
Для значения, отобранного с несмещенной нормально распределенной ошибкой, выше показана доля выборок, которые будут находиться в пределах 0, 1, 2 и 3 стандартных отклонений выше и ниже фактического значения.
Как найти стандартную ошибку среднего значения
Один из способов найти стандартную ошибку среднего — это множество выборок. Сначала находят среднее значение для каждой выборки. Затем находят среднее и стандартное отклонение этих средних по выборкам. Стандартное отклонение для всех средних по выборке и есть стандартная ошибка среднего. Это может быть большой объем работы. Иногда иметь большое количество образцов слишком сложно или стоит слишком много денег.
Другой способ найти стандартную ошибку среднего — использовать уравнение, для которого нужна только одна выборка. Стандартная ошибка среднего обычно оценивается по стандартному отклонению для выборки из всей группы (стандартное отклонение выборки), деленному на квадратный корень из размера выборки.
S E x ¯ = s n {displaystyle SE_{bar {x}} ={frac {s}{sqrt {n}}}}
где
s — стандартное отклонение выборки (т.е. выборочная оценка стандартного отклонения популяции), и
n — количество измерений в выборке.
Насколько большой должна быть выборка, чтобы оценка стандартной ошибки среднего была близка к фактической стандартной ошибке среднего для всей группы? В выборке должно быть не менее шести измерений. Тогда стандартная ошибка среднего для выборки будет находиться в пределах 5% от стандартной ошибки среднего, если бы измерялась вся группа.
Исправления для некоторых случаев
Существует еще одно уравнение, которое можно использовать, если количество измерений составляет 5% или более от всей группы:
Существуют специальные уравнения, которые необходимо использовать, если образец имеет менее 20 измерений.
Иногда выборка поступает из одного места, хотя вся группа может быть рассредоточена. Кроме того, иногда выборка может быть сделана за короткий промежуток времени, когда вся группа охватывает более длительный период. В этом случае числа в выборке не являются независимыми. Тогда используются специальные уравнения, чтобы попытаться исправить это.
Полезность
Практический результат: Можно быть более уверенным в среднем значении, если провести больше измерений в выборке. Тогда стандартная ошибка среднего значения будет меньше, поскольку стандартное отклонение делится на большее число. Однако, чтобы сделать неопределенность (стандартную ошибку среднего) среднего значения в два раза меньше, размер выборки (n) должен быть в четыре раза больше. Это происходит потому, что стандартное отклонение делится на квадратный корень из размера выборки. Чтобы сделать неопределенность на одну десятую больше, размер выборки (n) должен быть в сто раз больше!
Стандартные ошибки легко вычисляются и часто используются, потому что:
- Если известна стандартная ошибка нескольких отдельных величин, то во многих случаях можно легко рассчитать стандартную ошибку некоторой функции этих величин;
- Если вероятностное распределение значения известно, его можно использовать для расчета хорошего приближения к точному доверительному интервалу; и
- Если распределение вероятности неизвестно, для оценки доверительного интервала можно использовать другие уравнения
- Когда размер выборки становится очень большим, принцип центральной предельной теоремы показывает, что числа в выборке очень похожи на числа во всей группе (они имеют нормальное распределение).
Относительная стандартная ошибка
Относительная стандартная ошибка (RSE) — это стандартная ошибка, деленная на среднее значение. Это число меньше единицы. Умножение его на 100% дает его в процентах от среднего значения. Это помогает показать, является ли неопределенность важной или нет. Например, рассмотрим два исследования доходов домохозяйств, в результате которых среднее значение по выборке составляет $50 000. Если стандартная ошибка одного опроса составляет $10 000, а другого — $5 000, то относительные стандартные ошибки равны 20% и 10% соответственно. Опрос с меньшей относительной стандартной ошибкой лучше, потому что он имеет более точное измерение (неопределенность меньше).
На самом деле, люди, которым необходимо знать средние значения, часто решают, насколько мала должна быть неопределенность, прежде чем они решат использовать информацию. Например, Национальный центр статистики здравоохранения США не сообщает среднее значение, если относительная стандартная ошибка превышает 30%. NCHS также требует не менее 30 наблюдений для того, чтобы оценка была представлена в отчете. []
Пример
Например, в воде Мексиканского залива водится много красной рыбы. Чтобы узнать, сколько в среднем весит красноперка длиной 42 см, невозможно измерить всех красноперок длиной 42 см. Вместо этого можно измерить некоторых из них. Рыба, которую измеряют, называется образцом. В таблице показан вес двух образцов красноперки длиной 42 см. Средний (средний) вес первого образца составляет 0,741 кг. Средний (средний) вес второго образца — 0,735 кг, что немного отличается от первого образца. Каждое из этих средних значений немного отличается от среднего значения, которое было бы получено при измерении каждой красной рыбы длиной 42 см (что в любом случае невозможно).
Неопределенность среднего значения можно использовать для того, чтобы узнать, насколько близки средние значения выборок к среднему значению, которое было бы получено в результате измерения всей группы. Неопределенность среднего оценивается как стандартное отклонение для выборки, деленное на квадратный корень из числа выборок минус один. Из таблицы видно, что неопределенности в средних для двух выборок очень близки друг к другу. Кроме того, относительная неопределенность — это неопределенность среднего значения, деленная на среднее значение, умноженное на 100%. Относительная неопределенность в данном примере составляет 2,38% и 2,50% для двух образцов.
Зная неопределенность среднего, можно узнать, насколько близко выборочное среднее к среднему, которое было бы получено в результате измерения всей группы. Среднее по всей группе находится между а) средним по выборке плюс неопределенность в среднем и б) средним по выборке минус неопределенность в среднем. В данном примере средний вес всей красноперки длиной 42 см в Мексиканском заливе, как ожидается, составит 0,723-0,759 кг по первой выборке и 0,717-0,753 по второй выборке.
Пример красной рыбы (также известной как красный барабан, Sciaenops ocellatus), используемой в примере.
2.1. Стандартное отклонение среднего выборочного значения (ошибка среднего) и доверительный интервал
Результаты измерений обычно показывают с так называемой «средней статистической ошибкой средней величины» и для нашего случая (см. табл. 1.1) это будет запись: «высота сеянцев в опыте составила 5,0 ± 0,28 см». Словосочетание «средняя статистическая ошибка» обычно сокращают до названия «ошибка среднего» или просто «ошибка», обозначают буквой m и определяют по очень простой формуле. Для итогов упомянутой таблицы, где расчеты по 25 высотам дали значение δ = 1,42 см, эта ошибка составит:
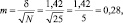
|
где δ – |
стандартное отклонение; |
|
N – |
число наблюдений или объем выборки, шт. |
Если объем выборки взять 100 шт., то ошибка снизится в 2 раза: 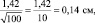
Рассмотрим эту «среднюю статистическую ошибку» (далее просто ошибка) подробно, так как именно в ней скрыто понимание того, что называют статистическим мышлением. Интуитивно мы понимаем, что малая выборка дает большую ошибку, т.е. неточное определение среднего значения. Последний термин настолько привычен, что мы даже не задумываемся о том, что его правильное и полное название «среднее выборочное значение», т.е. среднее, определяемое в некоторой выборке. И выборки могут быть очень разные по численности. Начнем с самых малых. Например, что произойдет с ошибкой, если объем выборки сократить до 2 измерений? Такие выборки бывают, например, в почвенных исследованиях, когда каждое измерение достается дорогой ценой. Для этого вернемся к рис. 1.1. На нем стандартное отклонение ±δ, которое отражает разброс значений вокруг среднего в левую и правую сторону в виде холма, наблюдается при объеме выборки 1 шт. В этом случае ошибка среднего выборочного значения будет равна стандартному отклонению: m = δ = 1,42. С увеличением N ошибка уменьшается:
при объеме выборки N = 2 ошибка будет
при объеме выборки N = 4 ошибка будет
при объеме выборки N = 16 ошибка будет
Важно понять, что ряд распределения частот этих выборочных средних будет постепенно как бы съеживаться и приближаться к центру, где находится так называемое «генеральное» среднее. Поясним, что в математике генеральное среднее значение называется математическим ожиданием и его обозначают буквой «М». Например, это может быть средняя высота, рассчитанная по всем измеренным в теплице сеянцам, или среднее число семян в 1 шишке у дерева после подсчета семян во всех собранных с дерева шишках (50, 100, 500 и т.д., т.е. весьма небольшая генеральная совокупность). Распределение частот значений выборочных средних, которых может быть множество, будет иметь форму такого же холма, как и распределение единичных значений на рис. 1.1. При этом, если выборка будет из 1 шт., то холм будет в точности таким же, но при выборках из 2 шт. его форма съежится в 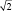
в 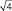
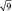
Для этих сокращающихся рядов распределения выборочных средних можно рассчитать свое, особое стандартное отклонение. Вероятно, чтобы не путать его со СТАНДОТКЛ, его стали называть по-другому, т.е. «средней статистической ошибкой средней величины». Чем больше по объему выборки, тем короче ряд распределения средних значений этих выборок с его «хвостами» в левую и правую сторону, и тем меньше величина этого особого стандартного отклонения. Закон распределения частот выборочных средних точно такой же, и имеет те же свойства: в пределах ±2m находится 95 % всех значений выборочных средних, в пределах ±3m – 99,5 %, а в пределах ±4m находится 100 % всех значений xср. Форма этого распределения меняется от пологой при малых выборках до очень крутой, вплоть до «схлопывания» в центре при выборках большого объема, когда ошибка среднего стремится к нулю.
Здесь следует пояснить, что, на наш взгляд, словосочетание «средняя статистическая ошибка средней величины», сокращаемое до «ошибки среднего значения» или просто до «ошибки», вводит нас в некоторое заблуждение, так как мы привыкли со школы, что ошибки надобно исправлять. Более правильным, вместо слов «ошибка среднего значения», будет использование слов «стандартное отклонение выборочных средних значений от генерального среднего». Не случайно математики выбрали для обозначения величины этого отклонения букву «m», а для обозначения генерального среднего (математического ожидания) – букву «М». Слова для объяснения этих сложных явлений могут быть разными, но и у математиков, и у биологов есть единодушие в понимании статистического смысла, лежащего за этими буквенными символами. Вообще, лучше было бы ввести некий иной термин вместо слов «ошибка» или «отклонение», так как они изначально имеют в нашем сознании иной смысл; на наш взгляд, более всего подходит слово «скачок» (чем сильнее отскакивает выборочное среднее от генерального среднего, тем реже оно встречается). Но так уж получилось, что не нашлось нейтрального (иностранного) слова, и слово «ошибка» традиционно используют, и мы также будем его использовать; важно понимать его иной, чем в обыденном употреблении, математический и статистический смысл.
Для самого точного определения средней высоты сеянцев нужно измерять все растения в питомнике, и тогда мы получим «генеральное среднее значение». Но так не делают, а измеряют несколько сотен растений в разных местах и этого бывает достаточно для определения среднего выборочного значения с приемлемой точностью. В нашем примере при 100 растениях ошибка его определения составит 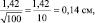
Вообще, точность опыта не самоцель; гораздо важнее сократить численность (объем) выборки до минимума. Представим себе, что средняя высота сеянцев xср = 5,0 см, а ее ±δ = 1,42 см, рассмотренные выше, получены при измерении 1000 растений потомства сосны, например, из Кунгура. Поделив ±δ на корень из 1000 получаем ошибку опыта m = ±0,045 см. Далее получаем точность опыта
Р = m/xср×100 = 0,045/5,0×100 = 0,9 %.
Точность получилась очень высокой. Но в питомнике есть потомства и из других мест и такой уровень точности совершенно не нужен, так как нужно узнать еще высоты сеянцев, например, из Очера, Осы, Добрянки и других районов. Если выборку из 1 тыс. растений снижать, то будет увеличиваться ошибка в определении средней высоты. И нужно найти приемлемую величину такой ошибки, которая позволит нам, тем не менее, уверенно утверждать, что это потомство растет быстрее, либо медленнее других. Причем происхождений может быть несколько сотен и минимизация выборок крайне важна, так как масштабы работ ограничены физическими возможностями бригады селекционеров. Следовательно, надо сокращать объем выборки. Как это сделать правильно?
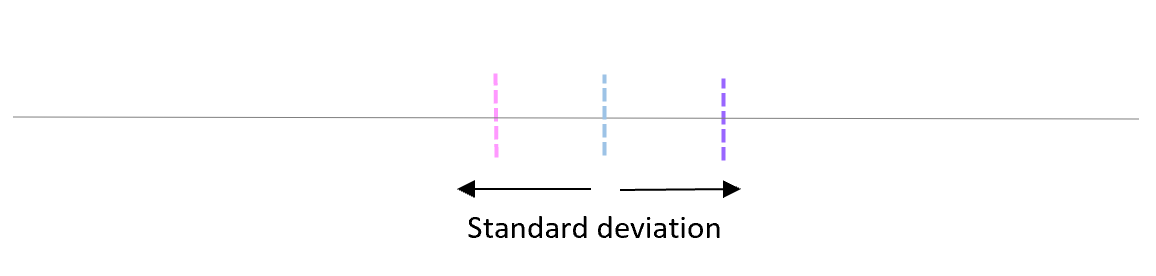
Рассмотрим два потомства. Первое – это упомянутые сеянцы происхождением из Кунгура (хср1), второе – сеянцы из Кизела с хср2 = 6,0 см и δ2 = ± 1,0 см (превышение высоты на 20 %). Надо это превышение доказать. При выборках из 100 растений ранее определенная ошибка m1 была равна 0,14 см, вторая ошибка m2 после расчетов по формуле (2.1) составит 0,1 см. По закону нормального распределения 99,5 % всех возможных значений этих средних хср1 и хср2 будут в пределах «плюс-минус три ошибки», что можно показать графически (рис. 2.1) или в виде формул:
хср1 ± 3m1 = 5,0 ± 3×0,14 = 5,0 ± 0,4 см
и
хср2 ± 3m2 = 6,0 ± 3×0,1 = 6,0 ± 0,3 см.
Возможные теоретические значения средних в генеральной совокупности не перекрывают друг друга, значит, различие достоверно. А если сократить выборки до 50 сеянцев? Тогда 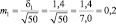
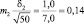
хср1 ± 3m1 = 5,0 ± 3×0,20 = 5,0 ± 0,6 см;
хср2 ± 3m2 = 6,0 ± 3×0,14 = 6,0 ± 0,3 см.
Рис. 2.1. Средние значения по выборкам из 100 растений и их тройные ошибки (пределы возможных значений выборочных средних в 99,5 % случаев)
Снова вынесем эти пределы на график (рис. 2.2).
Рис. 2.2. Средние значения при N = 50 растений и их тройные ошибки
Как видим, пределы сблизились и если еще сократить выборки, то они перекроются. Можно ли далее снижать объем выборки?
Можно, но здесь вступает в силу так называемое условие безошибочного прогноза. Мы это условие задали на уровне 99,5 % и для этого взяли ±3m для распределения ошибок. Но можно взять уровень пониже, с пределами ±2δ (уровень 95 %) и даже с пределами ±1,7δ (уровень 90 %).
При выборках из 25 штук сеянцев, получаем две ошибки: 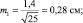
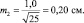
хср1 ± 2m1 = 5,0 ± 2×0,28 = 5,0 ± 0,56 см;
хср2 ± 2m2 = 6,0 ± 2×0,20 = 6,0 ± 0,40 см.
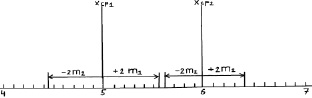
Выносим эти пределы опять на график (рис. 2.3).
Рис. 2.3. Средние значения при N = 25 растений и их двойные ошибки (пределы возможных значений средних в 95 % случаев)
Как видим, просвет все еще есть, и поэтому между возможными значениями средних высот сеянцев в других выборках из происхождений Кунгур и Кизел различия будут опять доказаны. Но уровень доказательства понизился до 95 %, и для 5 % оставшихся случаев нет гарантии, что различия будут иметь место при выборке из 25 растений. Их может и не быть, но эту вероятность в 5 % мы допускаем.
Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
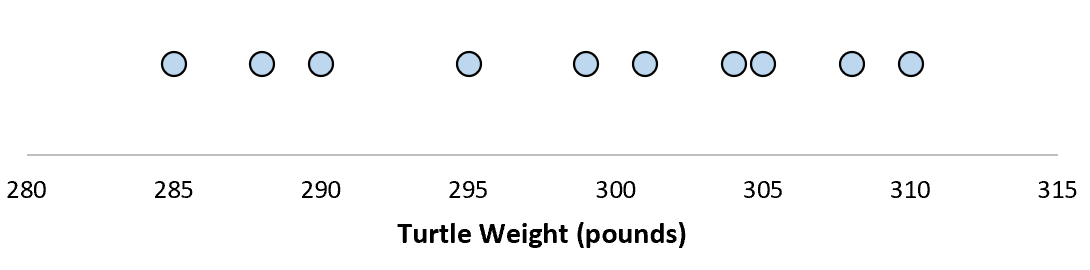
Предположим, мы измеряем вес 10 разных черепах.
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
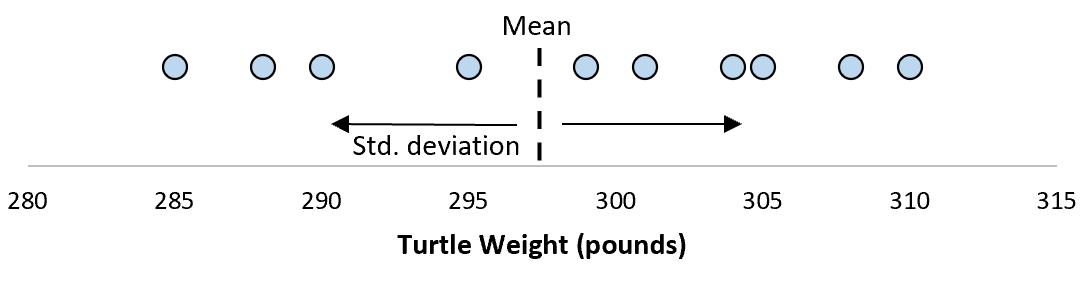
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
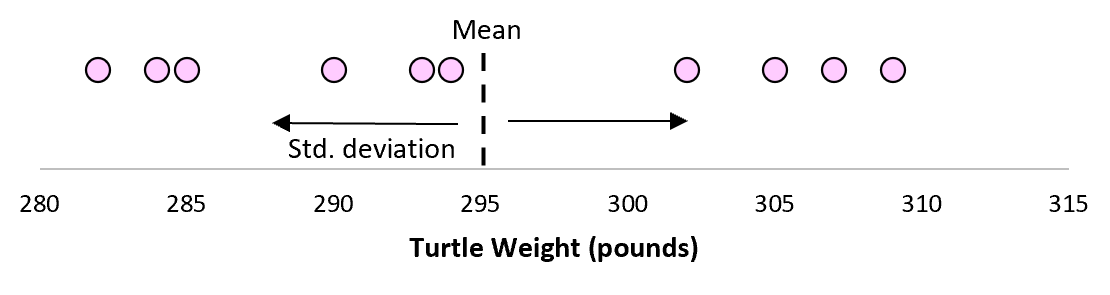
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
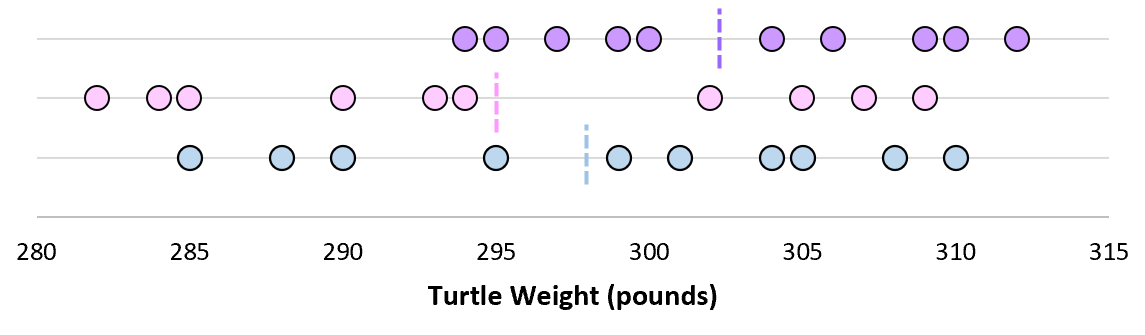
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
Стандартное отклонение этих средних значений известно как стандартная ошибка.
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.
What Is the Standard Error?
The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.
The standard error is a statistical term that measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population; this deviation is the standard error of the mean.
Key Takeaways
- The standard error (SE) is the approximate standard deviation of a statistical sample population.
- The standard error describes the variation between the calculated mean of the population and one which is considered known, or accepted as accurate.
- The more data points involved in the calculations of the mean, the smaller the standard error tends to be.
Standard Error
Understanding Standard Error
The term «standard error» is used to refer to the standard deviation of various sample statistics, such as the mean or median. For example, the «standard error of the mean» refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample will be of the overall population.
The relationship between the standard error and the standard deviation is such that, for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is also inversely proportional to the sample size; the larger the sample size, the smaller the standard error because the statistic will approach the actual value.
The standard error is considered part of inferential statistics. It represents the standard deviation of the mean within a dataset. This serves as a measure of variation for random variables, providing a measurement for the spread. The smaller the spread, the more accurate the dataset.
Standard error and standard deviation are measures of variability, while central tendency measures include mean, median, etc.
Formula and Calculation of Standard Error
Used in algorithmic trading, the standard error of an estimate can be calculated as the standard deviation divided by the square root of the sample size:
SE = σ / √n
where
- σ = the population standard deviation
- √n = the square root of the sample size
If the population standard deviation is not known, you can substitute the sample standard deviation, s, in the numerator to approximate the standard error.
Requirements for Standard Error
When a population is sampled, the mean, or average, is generally calculated. The standard error can include the variation between the calculated mean of the population and one which is considered known, or accepted as accurate. This helps compensate for any incidental inaccuracies related to the gathering of the sample.
In cases where multiple samples are collected, the mean of each sample may vary slightly from the others, creating a spread among the variables. This spread is most often measured as the standard error, accounting for the differences between the means across the datasets.
The more data points involved in the calculations of the mean, the smaller the standard error tends to be. When the standard error is small, the data is said to be more representative of the true mean. In cases where the standard error is large, the data may have some notable irregularities.
The standard deviation is a representation of the spread of each of the data points. The standard deviation is used to help determine the validity of the data based on the number of data points displayed at each level of standard deviation. Standard errors function more as a way to determine the accuracy of the sample or the accuracy of multiple samples by analyzing deviation within the means.
Standard Error vs. Standard Deviation
The standard error normalizes the standard deviation relative to the sample size used in an analysis. Standard deviation measures the amount of variance or dispersion of the data spread around the mean. The standard error can be thought of as the dispersion of the sample mean estimations around the true population mean. As the sample size becomes larger, the standard error will become smaller, indicating that the estimated sample mean value better approximates the population mean.
Example of Standard Error
Say that an analyst has looked at a random sample of 50 companies in the S&P 500 to understand the association between a stock’s P/E ratio and subsequent 12-month performance in the market. Assume that the resulting estimate is -0.20, indicating that for every 1.0 point in the P/E ratio, stocks return 0.2% poorer relative performance. In the sample of 50, the standard deviation was found to be 1.0.
The standard error is thus:
SE = 1.0/√50 = 1/7.07 = 0.141
Therefore, we would report the estimate as -0.20% ± 0.14, giving us a confidence interval of (-0.34 — -0.06). The true mean value of the association of the P/E on returns of the S&P 500 would therefore fall within that range with a high degree of probability.
Say now that we increase the sample of stocks to 100 and find that the estimate changes slightly from -0.20 to -0.25, and the standard deviation falls to 0.90. The new standard error would thus be:
SE = 0.90/√100 = 0.90/10 = 0.09.
The resulting confidence interval becomes -0.25 ± 0.09 = (-0.34 — -0.16), which is a tighter range of values.
What Is Meant by Standard Error?
Standard error is intuitively the standard deviation of the sampling distribution. In other words, it depicts how much disparity there is likely to be in a point estimate obtained from a sample relative to the true population mean.
What Is a Good Standard Error?
Standard error measures the amount of discrepancy that can be expected in a sample estimate compared to the true value in the population. Therefore, the smaller the standard error the better. In fact, a standard error of zero (or close to it) would indicate that the estimated value is exactly the true value.
How Do You Find the Standard Error?
The standard error takes the standard deviation and divides it by the square root of the sample size. Many statistical software packages automatically compute standard errors.
The Bottom Line
The standard error (SE) measures the dispersion of estimated values obtained from a sample around the true value to be found in the population. Statistical analysis and inference often involves drawing samples and running statistical tests to determine associations and correlations between variables. The standard error thus tells us with what degree of confidence we can expect the estimated value to approximate the population value.
Основные выводы:
-
Стандартная ошибка среднего указывает, насколько среднее значение генеральной совокупности может отличаться от среднего выборочного.
-
Вы можете уменьшить стандартную ошибку, увеличив размер выборки.
-
Стандартная ошибка среднего и стандартное отклонение являются мерами изменчивости, используемыми для обобщения наборов данных.
Если вы собираете данные для научных или статистических целей, стандартная ошибка среднего может помочь вам определить, насколько точно набор данных представляет фактическую совокупность. Проверка точности вашего образца подтверждает ваше клиническое исследование и помогает вам сделать правильные выводы.
В этой статье мы определяем стандартную ошибку среднего, объясняем, как она отличается от стандартного отклонения, и предлагаем формулу для ее расчета.
Какова стандартная ошибка среднего?
Стандартная ошибка среднего (SEM) используется для определения различий между более чем одной выборкой данных. Это помогает вам оценить, насколько хорошо ваши выборочные данные представляют всю совокупность, измеряя точность, с которой выборочные данные представляют совокупность, используя стандартное отклонение.
В статистике, среднеквадратичное отклонение является мерой того, насколько разбросаны числа. Иметь в виду относится к среднему числу. Стандартные функции ошибок используются для проверки точности выборки из нескольких выборок путем анализа отклонений в пределах средних значений.
Высокая стандартная ошибка показывает, что средние значения выборки широко разбросаны по среднему значению генеральной совокупности, поэтому ваша выборка может не точно представлять вашу генеральную совокупность. Низкая стандартная ошибка показывает, что средние значения выборки близко распределены вокруг среднего значения совокупности, что означает, что ваша выборка репрезентативна для вашей совокупности. Вы можете уменьшить стандартную ошибку, увеличив размер выборки.
Например, если вы измерите вес большой выборки мужчин, их вес может варьироваться от 125 до более чем 300 фунтов. Однако, если вы посмотрите на среднее значение выборочных данных, образцы будут различаться всего на несколько фунтов. Затем вы можете использовать стандартную ошибку среднего, чтобы определить, насколько вес отличается от среднего.
Связанный: Как рассчитать стандартную ошибку в Excel (с советами)
Стандартная ошибка среднего по сравнению со стандартным отклонением
Стандартная ошибка среднего и стандартное отклонение являются мерами изменчивости, используемыми для суммирования наборов данных.
Стандартная ошибка среднего значенияСтандартное отклонениеОценивает изменчивость в нескольких выборках генеральной совокупностиОписывает изменчивость в пределах одной выборкиВыводная статистика, которую можно оценитьОписательная статистика, которую можно рассчитатьИзмеряет, насколько вероятно, что среднее значение выборки будет отличаться от фактического среднего значения в популяции. выборка отличается от фактического среднего значенияСтандартная ошибка — это стандартное отклонение, деленное на квадратный корень размера выборкиСтандартное отклонение — это квадратный корень из дисперсии
Стандартная ошибка средней формулы
Формула для стандартной ошибки среднего выражается как:
SE = σ/√n
-
SE = стандартная ошибка выборки
-
σ = стандартное отклонение выборки
-
n = размер выборки
Обратите внимание, что σ — это греческая буква сигма, а √ — символ квадратного корня.
Формула стандартного отклонения выборки выражается следующим образом:
-
x̄ = среднее значение выборки, сначала найдите это значение
-
xᵢ = отдельные значения x
-
x = значение в наборе данных
-
n = количество точек данных
-
Σ — это сигма-обозначение для суммирования
Вот шаги, которые вы можете использовать для расчета стандартной ошибки среднего, используя выборку из пяти результатов теста SAT. Сначала рассчитайте стандартное отклонение, а затем подставьте это значение в формулу SEM.
1. Рассчитайте среднее
Сложите все образцы вместе и разделите общую сумму на количество образцов.
Пример: пять общих баллов SAT: 1000 + 1200 + 820 + 1300 + 680 = 5000.
Среднее (мк) = 5000 / 5 = 1000
2. Рассчитать отклонение от среднего
Рассчитайте отклонение каждого измерения от среднего, вычитая отдельные измерения из среднего.
Пример. Вычтите средний балл SAT, равный 1000, из каждого балла SAT.
хᵢ — мю
1000 — 1000 = 0
1200 — 1000 = 200
820 — 1000 = -180
1300 — 1000 = 300
680 — 1000 = -320
3. Возведите в квадрат каждое отклонение от среднего
Вычислите квадрат отклонения каждого измерения от среднего. Измерения, которые были отрицательными, после возведения в квадрат станут положительными.
Пример: Найдите квадратный корень отклонения каждой оценки от среднего.
(xᵢ — μ)²
0² = 0
200² = 40000
-180² = 32400
300² = 90000
-320² = 102400
4. Рассчитайте сумму квадратов отклонений
Определить сумму квадратов отклонений, сложив все числа из третьего шага.
Пример: 0 + 10 + 40000 + 32400 + 90000 + 102400 = 264810 = Σ
5. Разделите эту сумму на количество точек данных.
Возьмите сумму, которую вы подсчитали на четвертом шаге, и разделите ее на единицу меньше размера выборки. Используя приведенную выше формулу, это будет выглядеть как n-1.
Пример: 264810 / (5-1) = 66202,5
6. Вычислить квадратный корень, чтобы найти стандартное отклонение
Возьмите квадратный корень из числа, которое вы вычислили на пятом шаге. Это даст вам стандартное отклонение.
Пример: σ = √ 66202,5 = 257,298
7. Разделите стандартное отклонение на квадратный корень из размера выборки.
Используя стандартное отклонение, которое вы определили на шестом шаге, разделите это число на квадратный корень из размера выборки. Это позволит вам определить стандартную ошибку.
Пример: SE = σ/√n
SE = 257,298/√5
SE = 115,067
8. Рассчитайте стандартную ошибку среднего
Вычтите из среднего значения стандартную ошибку и запишите это число. Это стандартная ошибка ниже среднего. Затем добавьте стандартную ошибку к среднему значению и запишите число. Это стандартная ошибка выше среднего.
Пример:
SE ниже среднего: 1000 — 115,067 = 884,933
SE выше среднего: 1000 + 115,067 = 1115,067
Стандартная ошибка среднего может быть представлена следующим образом:
Средний балл SAT случайной выборки испытуемых составляет 1000 ± 115,067.
Пример СЭМ
Чтобы понять силу информации, которую вы можете получить из случайной выборки, используя стандартную ошибку среднего, рассмотрим следующий пример.
Вам дан вес при рождении 17 000 детей, рожденных в больницах Нью-Йорка. Средний вес при рождении составлял семь фунтов и три унции, а стандартное отклонение — один фунт три унции. Допустим, вы хотели узнать средний вес при рождении в этом районе, но получили веса только 30 случайных рождений по сравнению с общей численностью населения. Если бы эта выборка была взята только из всего населения, то вам лучше всего было бы предположить, что средний вес при рождении в выборке также будет равен семи фунтам и трем унциям.
Это предположение вряд ли будет точным, поскольку среднее значение выборки из 30 не будет таким точным, как среднее значение выборки из 17 000. Если бы вы продолжали брать случайные выборки из 30, вполне вероятно, что среднее значение каждой из них несколько изменилось бы.
Поскольку стандартное отклонение генеральной совокупности обычно неизвестно, вам необходимо оценить его, используя стандартное отклонение выборки. Чтобы сделать это с некоторой точностью, ваша выборка должна иметь нормальное распределение и состоять как минимум из 20 измерений. Хотя оценка может быть не совсем точной даже при большой выборке, ошибки в выборочной оценке стандартного отклонения генеральной совокупности будут уменьшены, если вы разделите его на квадратный корень из размера выборки.
Допустим, у вас есть шесть случайных выборок из 30 масс при рождении со стандартными отклонениями 1,3 фунта, 1,16 фунта, 1,14 фунта, 1,2 фунта, 1,25 фунта и 1,19 фунта, что на 0,098 фунта отличается от истинного значения стандартного отклонения населения. Эти шесть образцов приводят к оценкам стандартной ошибки, которые находятся в пределах 0,017 фунта от истинного значения. Ошибки стандартной ошибки средних оценок меньше, чем ошибки оценок стандартного отклонения, а значит, они более точные. Если бы размер выборки был больше 30, стандартная ошибка среднего была бы еще больше уменьшена.
Стандартная ошибка
Стандартная ошибка — это стандартное отклонение выборочного распределения статистики. Этот термин также может использоваться для оценки (хорошего предположения) этого стандартного отклонения, взятого из выборки всей группы.
Среднее значение некоторой части группы (называемой выборкой) является обычным способом оценки среднего значения для всей группы. Часто бывает слишком сложно или стоит слишком много денег, чтобы измерить всю группу. Но если измерить другую выборку, то ее среднее значение будет немного отличаться от первой выборки. Стандартная ошибка среднего — это способ узнать, насколько близка средняя по выборке к средней по всей группе. Это способ узнать, насколько вы можете быть уверены в среднем значении по выборке.
В реальных измерениях истинное значение стандартного отклонения среднего для всей группы обычно неизвестно. Поэтому термин стандартная ошибка часто используется для обозначения близкого к истинному значению для всей группы. Чем больше измерений в выборке, тем ближе к истинному значению для всей группы.
Для значения, отобранного с несмещенной нормально распределенной ошибкой, выше показана доля выборок, которые будут находиться в пределах 0, 1, 2 и 3 стандартных отклонений выше и ниже фактического значения.
Как найти стандартную ошибку среднего значения
Один из способов найти стандартную ошибку среднего — это множество выборок. Сначала находят среднее значение для каждой выборки. Затем находят среднее и стандартное отклонение этих средних по выборкам. Стандартное отклонение для всех средних по выборке и есть стандартная ошибка среднего. Это может быть большой объем работы. Иногда иметь большое количество образцов слишком сложно или стоит слишком много денег.
Другой способ найти стандартную ошибку среднего — использовать уравнение, для которого нужна только одна выборка. Стандартная ошибка среднего обычно оценивается по стандартному отклонению для выборки из всей группы (стандартное отклонение выборки), деленному на квадратный корень из размера выборки.
S E x ¯ = s n {displaystyle SE_{bar {x}} ={frac {s}{sqrt {n}}}}
где
s — стандартное отклонение выборки (т.е. выборочная оценка стандартного отклонения популяции), и
n — количество измерений в выборке.
Насколько большой должна быть выборка, чтобы оценка стандартной ошибки среднего была близка к фактической стандартной ошибке среднего для всей группы? В выборке должно быть не менее шести измерений. Тогда стандартная ошибка среднего для выборки будет находиться в пределах 5% от стандартной ошибки среднего, если бы измерялась вся группа.
Исправления для некоторых случаев
Существует еще одно уравнение, которое можно использовать, если количество измерений составляет 5% или более от всей группы:
Существуют специальные уравнения, которые необходимо использовать, если образец имеет менее 20 измерений.
Иногда выборка поступает из одного места, хотя вся группа может быть рассредоточена. Кроме того, иногда выборка может быть сделана за короткий промежуток времени, когда вся группа охватывает более длительный период. В этом случае числа в выборке не являются независимыми. Тогда используются специальные уравнения, чтобы попытаться исправить это.
Полезность
Практический результат: Можно быть более уверенным в среднем значении, если провести больше измерений в выборке. Тогда стандартная ошибка среднего значения будет меньше, поскольку стандартное отклонение делится на большее число. Однако, чтобы сделать неопределенность (стандартную ошибку среднего) среднего значения в два раза меньше, размер выборки (n) должен быть в четыре раза больше. Это происходит потому, что стандартное отклонение делится на квадратный корень из размера выборки. Чтобы сделать неопределенность на одну десятую больше, размер выборки (n) должен быть в сто раз больше!
Стандартные ошибки легко вычисляются и часто используются, потому что:
- Если известна стандартная ошибка нескольких отдельных величин, то во многих случаях можно легко рассчитать стандартную ошибку некоторой функции этих величин;
- Если вероятностное распределение значения известно, его можно использовать для расчета хорошего приближения к точному доверительному интервалу; и
- Если распределение вероятности неизвестно, для оценки доверительного интервала можно использовать другие уравнения
- Когда размер выборки становится очень большим, принцип центральной предельной теоремы показывает, что числа в выборке очень похожи на числа во всей группе (они имеют нормальное распределение).
Относительная стандартная ошибка
Относительная стандартная ошибка (RSE) — это стандартная ошибка, деленная на среднее значение. Это число меньше единицы. Умножение его на 100% дает его в процентах от среднего значения. Это помогает показать, является ли неопределенность важной или нет. Например, рассмотрим два исследования доходов домохозяйств, в результате которых среднее значение по выборке составляет $50 000. Если стандартная ошибка одного опроса составляет $10 000, а другого — $5 000, то относительные стандартные ошибки равны 20% и 10% соответственно. Опрос с меньшей относительной стандартной ошибкой лучше, потому что он имеет более точное измерение (неопределенность меньше).
На самом деле, люди, которым необходимо знать средние значения, часто решают, насколько мала должна быть неопределенность, прежде чем они решат использовать информацию. Например, Национальный центр статистики здравоохранения США не сообщает среднее значение, если относительная стандартная ошибка превышает 30%. NCHS также требует не менее 30 наблюдений для того, чтобы оценка была представлена в отчете. []
Пример
Например, в воде Мексиканского залива водится много красной рыбы. Чтобы узнать, сколько в среднем весит красноперка длиной 42 см, невозможно измерить всех красноперок длиной 42 см. Вместо этого можно измерить некоторых из них. Рыба, которую измеряют, называется образцом. В таблице показан вес двух образцов красноперки длиной 42 см. Средний (средний) вес первого образца составляет 0,741 кг. Средний (средний) вес второго образца — 0,735 кг, что немного отличается от первого образца. Каждое из этих средних значений немного отличается от среднего значения, которое было бы получено при измерении каждой красной рыбы длиной 42 см (что в любом случае невозможно).
Неопределенность среднего значения можно использовать для того, чтобы узнать, насколько близки средние значения выборок к среднему значению, которое было бы получено в результате измерения всей группы. Неопределенность среднего оценивается как стандартное отклонение для выборки, деленное на квадратный корень из числа выборок минус один. Из таблицы видно, что неопределенности в средних для двух выборок очень близки друг к другу. Кроме того, относительная неопределенность — это неопределенность среднего значения, деленная на среднее значение, умноженное на 100%. Относительная неопределенность в данном примере составляет 2,38% и 2,50% для двух образцов.
Зная неопределенность среднего, можно узнать, насколько близко выборочное среднее к среднему, которое было бы получено в результате измерения всей группы. Среднее по всей группе находится между а) средним по выборке плюс неопределенность в среднем и б) средним по выборке минус неопределенность в среднем. В данном примере средний вес всей красноперки длиной 42 см в Мексиканском заливе, как ожидается, составит 0,723-0,759 кг по первой выборке и 0,717-0,753 по второй выборке.
Пример красной рыбы (также известной как красный барабан, Sciaenops ocellatus), используемой в примере.
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.
В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .
Стандартная ошибка по сравнению с R-квадратом в регрессии
Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .
Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.
Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.
Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:
Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.
Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .
Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.
Преимущества использования стандартной ошибки
Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.
Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.
Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.
Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.
Дальнейшее чтение
Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?
Стандартная ошибка регрессии — это метрика, которая оценивает точность предсказания модели регрессии. Она измеряет расхождение между фактической и прогнозируемой зависимыми переменными. В более простых терминах, стандартная ошибка регрессии показывает, насколько точны прогнозы, сделанные с помощью модели регрессии.
Важным аспектом стандартной ошибки регрессии является ее влияние на результаты анализа данных. Например, если значение стандартной ошибки регрессии высоко, то это может указывать на то, что модель не способна точно предсказать зависимую переменную, что, в свою очередь, может привести к неверным выводам. Однако, если значение стандартной ошибки регрессии низко, то это свидетельствует о том, что модель способна точно прогнозировать зависимую переменную.
В данной статье мы рассмотрим, как стандартная ошибка регрессии влияет на результаты анализа данных и каким образом ее можно использовать для улучшения точности модели.
Содержание
- Стандартная ошибка регрессии
- Что такое стандартная ошибка регрессии?
- Какие факторы влияют на стандартную ошибку регрессии?
- Зачем важно знать стандартную ошибку регрессии?
- Как стандартная ошибка регрессии влияет на результаты анализа?
- Как уменьшить стандартную ошибку регрессии?
- Какой метод оценки стандартной ошибки регрессии является лучшим?
- Как использовать стандартную ошибку регрессии при принятии решений?
- Вопрос-ответ
- Что такое стандартная ошибка регрессии?
- Какая связь между стандартной ошибкой регрессии и точностью модели?
- Как стандартная ошибка регрессии влияет на результаты анализа?
- Что может вызвать увеличение стандартной ошибки регрессии?
Стандартная ошибка регрессии
Стандартная ошибка регрессии (standard error of regression) — это мера разброса оценок параметров регрессии вокруг их истинных значений. Она представляет собой скорректированное среднеквадратическое отклонение случайной ошибки в модели. Стандартная ошибка регрессии показывает, насколько точно можно оценить параметры регрессии и как отклонения от них могут влиять на точность прогнозов.
Стандартная ошибка регрессии играет важную роль в анализе результатов регрессионного анализа. Чем меньше ее значение, тем более точными и надежными будут оценки параметров модели. Если же значение стандартной ошибки регрессии высоко, то это говорит о том, что модель не объясняет все переменности и прогнозы могут быть неточными.
Чтобы уменьшить значение стандартной ошибки регрессии, необходимо увеличить размер выборки, улучшить качество данных, выбрать наиболее значимые переменные для моделирования и применять правильный функциональный вид модели.
- Плюсы стандартной ошибки регрессии:
- Позволяет определить точность оценок параметров регрессии;
- Помогает оценить прогнозируемую точность модели;
- Позволяет сравнить точность моделей с различными переменными и наборами параметров.
- Минусы стандартной ошибки регрессии:
- Не учитывает возможные нелинейные зависимости;
- Не показывает, насколько хорошо модель настраивается на данные;
- Не учитывает возможные проблемы с гетероскедастичностью или автокорреляцией ошибок.
Что такое стандартная ошибка регрессии?
Стандартная ошибка регрессии (Standard Error of the Estimate, SEE) – это показатель, который указывает на то, насколько точно прогнозы модели соответствуют реальным значениям.
Сущность понятия сводится к тому, что любая регрессионная линия, получаемая при нахождении модели линейной регрессии, не сможет проходить через все точки наблюдений. Из-за этого модель несет ошибку, которая описывается через стандартную ошибку.
Чем меньше значит стандартная ошибка регрессии, тем лучше модель и тем точнее регрессионные коэффициенты, генерируемые моделью, описывают зависимость между переменными. Чем выше – тем менее точно прогнозируются данные.
Выражение стандартной ошибки регрессии используют в статистических анализах и отчетах, для понимания уровня точности образующейся модели, а так же для сравнения точности нескольких моделей между собой.
Какие факторы влияют на стандартную ошибку регрессии?
Стандартная ошибка регрессии (standard error of the regression) — это мера рассеивания данных относительно линейной регрессии. Она показывает, насколько сильно значения зависимой переменной разбросаны относительно линейного уравнения модели.
Факторы, влияющие на стандартную ошибку регрессии включают:
- Размер выборки: чем больше выборка, тем меньше стандартная ошибка регрессии, поскольку увеличивается точность анализа. Однако, увеличение размера выборки не всегда приводит к уменьшению ошибки регрессии, особенно если данные содержат выбросы или ошибки.
- Случайность выборки: если выборка случайна, то вероятностный характер ошибки регрессии будет меньше, поскольку искажения в данных будут случайными. Однако, если выборка не случайна, то стандартная ошибка может быть завышена.
- Рассматриваемые переменные: количество и качество рассматриваемых переменных может существенно влиять на стандартную ошибку регрессии. Если переменные слабо коррелируют между собой, то ошибка регрессии будет меньше. Если же есть мультиколлинеарность, которая усиливает взаимосвязь между переменными, то ошибка регрессии может быть завышена.
- Функциональная форма модели: выбор функциональной формы модели может также влиять на ошибку регрессии. Некоторые функциональные формы могут работать лучше, чем другие, в зависимости от данных и характера модели.
Значение стандартной ошибки регрессии является важным индикатором для оценки точности модели и правильности применения регрессионного анализа. Чем меньше стандартная ошибка регресси, тем более точными будут значения коэффициентов регрессии и тем менее случайным будет коэффициент детерминации.
Зачем важно знать стандартную ошибку регрессии?
Стандартная ошибка регрессии (standard error of the regression) — это мера дисперсии ошибки в регрессионной модели. Она показывает, насколько сильно прогнозируемая переменная может отклоняться от своих реальных значений.
Понимание стандартной ошибки регрессии важно для оценки точности и достоверности модели. Если ошибка большая, то прогнозирование результата становится нестабильным и ненадежным. Высокая стандартная ошибка свидетельствует о том, что модель не может полностью объяснить изменения целевой переменной и, следовательно, нуждается в дополнительных изменениях.
Кроме того, стандартная ошибка регрессии помогает в процессе сравнения разных моделей. Если две модели имеют одинаковые значения коэффициентов, то выбирается та, у которой стандартная ошибка регрессии меньше. Значит, она более точно предсказывает значения целевой переменной.
Также стандартная ошибка регрессии может быть использована для проверки гипотезы о значимости коэффициентов регрессии. Если p-value значительно меньше уровня значимости, то можно сделать вывод, что коэффициент значим. Если же p-value больше уровня значимости, то коэффициент не является значимым и не будет учитываться в модели.
Итак, знание стандартной ошибки регрессии необходимо для оценки точности модели, выбора лучшей модели и проверки значимости коэффициентов регрессии. Кроме того, это важный инструмент статистического анализа данных, который может помочь принять правильные решения на основе полученных результатов.
Как стандартная ошибка регрессии влияет на результаты анализа?
Стандартная ошибка регрессии (standard error of the regression, SER) является очень важным показателем при анализе регрессионных данных. SER используется для измерения того, насколько точными могут быть оценки коэффициентов регрессии. Чем меньше SER, тем более точными будут оценки коэффициентов.
Однако, при увеличении SER увеличивается вероятность, что коэффициенты регрессии кажутся статистически не значимыми, тогда как на самом деле они имеют значение.
Использование стандартной ошибки регрессии при анализе регрессионных данных особенно важно при прогнозировании. Если SER слишком высок, то прогнозные значения могут быть не очень точными и не отражать реальную ситуацию.
Важно отметить, что для уменьшения SER нужно увеличивать объем выборки, что может быть довольно трудоемким. Кроме того, SER может быть снижен путем исключения выбросов и несущественных факторов. Однако, при этом необходимо осторожно подходить к выбору значимых факторов, чтобы не потерять важные данные.
В целом, SER — это очень важный инструмент при анализе регрессионных данных, который позволяет создавать более точные модели и прогнозы. Поэтому, необходимо уделять достаточно внимания серьезному подходу к его расчету и анализу при работе с регрессионными данными.
Как уменьшить стандартную ошибку регрессии?
Стандартная ошибка регрессии – это мера точности модели регрессии для прогнозирования зависимой переменной на основе независимых переменных. Чем меньше значение стандартной ошибки регрессии, тем выше точность модели. Есть несколько способов уменьшить стандартную ошибку регрессии.
1. Добавьте больше независимых переменных
Чем больше независимых переменных включено в модель, тем точнее будет прогнозирование значений зависимой переменной. Однако, необходимо учитывать, что включение лишних переменных может привести к переоснащению модели и тем самым ухудшить ее точность.
2. Отберите наиболее важные независимые переменные
Выбор качественных независимых переменных помогает увеличить точность модели и уменьшить стандартную ошибку регрессии. Важным этапом является корректный выбор переменных и анализ их статистической значимости.
3. Избегайте мультиколлинеарности
Мультиколлинеарность означает наличие сильной зависимости между двумя или более независимыми переменными. Она может привести к неверным результатам и увеличит стандартную ошибку регрессии. Чтобы избежать мультиколлинеарности необходимо провести анализ коэффициентов корреляции между парами переменных и исключить лишние переменные.
4. Увеличьте размер выборки
Увеличение размера выборки может уменьшить стандартную ошибку регрессии и увеличить точность модели. Однако, увеличение выборки сильно зависит от сложности и количества независимых переменных.
5. Проверьте модель на адекватность
Правильная спецификация модели, адекватность и качество данных, анализ выборки и корректный выбор независимых переменных являются ключевыми факторами, которые могут значительно повлиять на стандартную ошибку регрессии и точность прогнозирования модели. Поэтому всегда нужно тщательно проверять модель на адекватность.
Какой метод оценки стандартной ошибки регрессии является лучшим?
Оценка стандартной ошибки является важной частью анализа регрессии, так как она показывает, насколько точно коэффициенты регрессии оценены. Существует несколько методов оценки стандартной ошибки регрессии, в том числе:
- Стандартная ошибка МНК
- Стандартная ошибка Ньюи-Уэста
- Стандартная ошибка Уайта
Метод МНК является наиболее распространенным методом оценки стандартной ошибки регрессии. Этот метод основывается на минимизации суммы квадратов остатков. Недостатком этого метода является то, что он предполагает независимую и одинаково распределенную ошибку. Если эта предпосылка не выполняется, то оценки стандартной ошибки МНК могут быть неточными.
Метод Ньюи-Уэста и метод Уайта являются более универсальными методами оценки стандартной ошибки регрессии. Они учитывают различные виды гетероскедастичности и корреляции ошибок и могут давать более точные оценки стандартной ошибки, чем метод МНК. Однако они также могут быть более сложными в использовании и требуют больше вычислительных ресурсов.
В итоге, выбор метода оценки стандартной ошибки регрессии зависит от особенностей данных и задачи. Если данные удовлетворяют предпосылкам метода МНК, то этот метод может быть наиболее подходящим. Если данные не удовлетворяют этим предпосылкам, то методы Ньюи-Уэста или Уайта могут быть более подходящими.
Как использовать стандартную ошибку регрессии при принятии решений?
Стандартная ошибка регрессии — это мера точности модели регрессии. При ее использовании возможно определить, насколько доверительными являются результаты анализа. Чем меньше значение стандартной ошибки регрессии, тем выше точность модели.
Важно использовать стандартную ошибку регрессии вместе с другими показателями, такими как коэффициент детерминации R2 и коэффициент корреляции. Кроме того, стандартную ошибку регрессии необходимо рассматривать в контексте данных, на которых основывается модель.
При принятии решений на основе результатов анализа регрессии необходимо учитывать не только стандартную ошибку регрессии, но также и другие факторы, которые могут повлиять на результаты. Например, необходимо рассмотреть выбросы, эффект мультиколлинеарности и другие аномалии данных.
В целом, использование стандартной ошибки регрессии позволяет получить более точные результаты анализа, которые могут помочь в принятии решений в различных областях, таких как экономика, маркетинг, медицина и другие.
Вопрос-ответ
Что такое стандартная ошибка регрессии?
Стандартная ошибка регрессии (сокращенно SE) — это мера точности оценок коэффициентов регрессии. Она показывает, насколько сильно значения коэффициентов могут различаться в разных выборках данных при одном и том же размере выборки.
Какая связь между стандартной ошибкой регрессии и точностью модели?
Чем меньше стандартная ошибка регрессии, тем выше точность модели. Если SE мала, то прогнозируемые значения очень близки к истинным значениям, что означает, что модель дает точные прогнозы. Если же SE большая, то прогнозы будут менее точными.
Как стандартная ошибка регрессии влияет на результаты анализа?
Стандартная ошибка регрессии имеет прямое влияние на результаты анализа регрессии. Она применяется для определения того, насколько точны оценки коэффициентов регрессии и насколько значимы различия между наблюдением и прогнозируемым значением. Если SE высока, то прогнозы менее точны, а результаты анализа менее значимы.
Что может вызвать увеличение стандартной ошибки регрессии?
Увеличение стандартной ошибки регрессии может быть вызвано многими факторами, такими как малый размер выборки, наличие выбросов или ошибок в данных, неправильный выбор модели или нарушение предпосылок модели. Также ее увеличение может указывать на необъясненную переменную, которая влияет на прогнозируемую переменную.







.jpg)