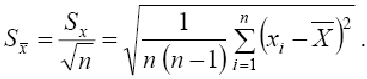Способы уменьшения случайных погрешностей.
1
Метод многократных измерений.
Тогда
2.
Метод комплексирования.
Проводят
измерения одной и той же величины при
следующих условиях:
А)
несколькими однотипными СИ одновременно
Б)
разнотипными
С)
различными методами( разными группами
экспериментаторов)
В
дальнейшем проводится объединение
результатов наблюдений по алгоритму
средневзвешенной оценки, более точным
наблюдениям больший вес. Объединение
может быть только для равноточных
результатов по систематической
погрешности.
3.
Метод косвенных измерений.
В
отдельных случаях позволяет уменьшить
случайную погрешность.
Средства измерений. Характеристики си для определения результатов измерений.
Средство
измерений –
это техническое средство (или комплекс),
предназначенное для измерений, имеющее
нормированные метрологические
характеристики, воспроизводящие и (или)
хранящие единицу физической величины,
размер которой принимается неизменным
(в пределах установленной погрешности)
в течение известного интервала времени
[24].
Данное определение раскрывает
метрологическую
сущность СИ,
заключающуюся
в умении хранить (или воспроизводить)
единицу ФВ
и
в неизменности размера хранимой единицы
во времени.
Первое обуславливает возможность
выполнения измерения, суть которого,
как известно, состоит в сравнении
измеряемой величины с ее единицей.
Второе принципиально необходимо,
поскольку при изменении размера хранимой
единицы ФВ с помощью данного СИ нельзя
получить результат с требуемой точностью.
Под метрологическими характеристиками
(MX)
понимают такие характеристики СИ,
которые позволяют судить об их пригодности
для измерений в известном диапазоне с
известной точностью. В отличие от СИ
приборы или вещества, не имеющие
нормированных MX,
называют индикаторами. СИ — это
техническая основа метрологического
обеспечения.
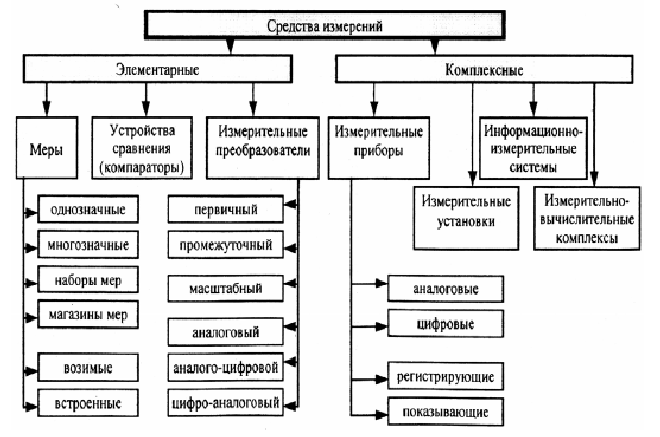
Классификация
средств измерений по их роли в процессе
измерения и
выполняемым
функциям
Эталон
–
средство измерений (или их комплекс),
предназначенное для воспроизведения
и (или) хранения единицы и передачи ее
размера нижестоящим по поверочной схеме
СИ и утвержденное в качестве эталона в
установленном порядке.
Меры
— это СИ, воспроизводящие или хранящие
физическую величину заданного размера.
Меры могут быть однозначными,
воспроизводящими одно значение физической
величины (гиря, калибр на заданный
размер, образцы твердости, шероховатости,
катушка сопротивления, нормальный
элемент, воспроизводящий значение
ЭДС), и
многозначными
— для воспроизведения плавно или
дискретно ряда значений одной и той же
физической величины (измерительный
конденсатор переменной емкости, набор
конечных мер, магазин емкостей,
индуктивности и сопротивления,
измерительные линейки).
Для
ряда областей измерений, и в первую
очередь для физико-химических измерений,
чрезвычайно перспективным средством
повышения эффективности поверочных
работ является применение стандартных
образцов (СО). Правила работы с СО
устанавливает ГОСТ 8.315—97. Согласно
этому документу,
стандартный
образец состава и свойств веществ и
материалов
— это средство измерений в виде вещества
(материала), состав или свойства которого
установлены аттестацией. Можно
дать и другое определение: стандартный
образец
— образец вещества (материала) с
установленными в результате метрологической
аттестации
значениями
одной или более величин, характеризующими
свойство или состав этого вещества
(материала).
Стандартные
образцы предназначены для обеспечения
единства и требуемой точности измерений
посредством:
•
градуировки,
метрологической аттестации и поверки
СИ;
•
метрологической
аттестации методик выполнения измерений;
•
контроля
показателей точности измерений;
•
измерения
ФВ, характеризующих состав или свойства
веществ материалов, методами сравнения.
По
своему назначению СО исполняют роль
мер, однако в отличие от «классических»
мер они имеют ряд особенностей. Например,
образцы состава воспроизводят значения
ФВ,
характеризующих
состав или свойства именно того материала
(вещества), из которого они изготовлены.
Стандартные образцы, как правило не
являются изделиями, они реализованы
обычно в виде части или порции однородного
вещества (материала), причем эта часть
является полноценным носителем
воспроизводимой единицы ФВ, а не ее
части Эта особенность образцов отражена
в требованиях к их однородности по
составу и свойствам. Однородность
материала, из которого сделан образец,
имеет принципиальное значение, в то
время как для меры такая характеристик
часто является второстепенной.
Измерительные
преобразователи
— СИ, предназначенные для выработки
сигнала измерительной информации в
форме, удобной для передачи, дальнейшего
преобразования, обработки и хранения,
но не доступной для непосредственного
восприятия наблюдателем. Это термопары,
измерительные трансформаторы,
усилители,
преобразователи давления. По месту,
занимаемому в измерительной цепи, они
делятся на первичные, промежуточные и
т. п. Конструктивно они выполняются либо
отдельными блоками, либо составной
частью СИ. Не следует отождествлять
измерительные преобразователи с
преобразовательными элементам. Последние
не имеют метрологических характеристик,
как, например, трансформатор тока или
напряжения.
Измерительный
прибор
— СИ, предназначенное для переработки
сигнала измерительной информации в
другие, доступные для непосредственного
восприятия наблюдателем формы. Различают
приборы прямого действия (амперметры,
вольтметры,
манометры)
и приборы сравнения (компараторы). По
способу отсчета измеряемой величины
СИ делятся на показывающие (аналоговые,
цифровые), регистрирующие (на
бумажную
или магнитную ленту) и т. п.
Измерительная
установка
— совокупность функционально объединенных
СИ и вспомогательных устройств,
расположенных в одном месте. Например,
поверочные установки, установки для
испытания электротехнических, магнитных
и других материалов. Измерительная
установка позволяет предусмотреть
определенный
метод
измерения и заранее оценить погрешность
измерения.
Измерительная
система
— это комплекс СИ и вспомогательных
устройств
с компонентами связи (проводные,
предназначенный
для выработки сигналов измерительной
информации в форме, удобной для
автоматической обработки, передачи
и/или
использования в автоматических системах
управления. В отличие от измерительных
установок, предусматривающих изменения
режима и условий функционирования,
измерительная система не воздействует
на режимы работы, а предназначена только
для сбора и/или хранения информации.
Частными случаями измерительной системы
являются информационно-вычислительный
комплекс (ИВК), информационно-измерительные
системы (ИИС). К последним можно отнести
системы автоматического контроля,
системы технического диагностирования,
системы распознавания образов, системы
для передачи неизмерительной информации.
При организации поверки рабочих СИ
используют различные эталоны и образцовые
СИ. СИ, как правило, работают совместно
с датчиками (измерительными
преобразователями), имеющими свои MX.
При
использовании средств измерений
принципиально важно знать степень
соответствия информации об измеряемой
величине, содержащейся в выходном
сигнале, ее истинному значению. С этой
целью для каждого СИ вводятся и нормируются
определенные метрологические
характеристики (МХ).
Метрологическими
называются
характеристики свойств СИ, оказывающие
влияние на результат измерения и его
погрешности. Характеристики, устанавливаемые
нормативными документами, называются
нормируемыми,
а определяемые экспериментально –
действительными.
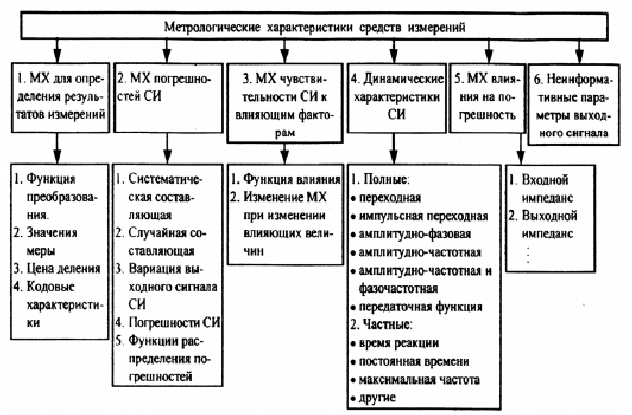
Номенклатура
метрологических характеристик средств
измерений
Неинформативным
называется параметр входного сигнала
СИ,
не связанный функционально с измеряемым
параметром. Например, частота переменного
тока при измерении его амплитуды.
Нормальные метрологические характеристики
(НМХ) устанавливаются документами. MX,
определенные документами, считаются
действительными. На практике наиболее
распространены следующие MX СИ.
Диапазон
измерений
— область значений измеряемой величины,
для которой нормированы допускаемые
пределы погрешности СИ (для преобразователей
— это диапазон преобразования):
Предел
измерения
— наибольшее или наименьшее значение
диапазона измерения. Для мер
— это номинальное значение воспроизводимой
величины.
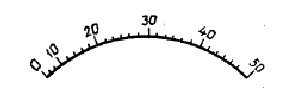
Рис
32 Неравномерная шкала СИ
Например,
у шкалы на рис. 32 начальный участок
(~20%) сжат, потому производить отсчеты
на нем неудобно. Тогда предел измерения
по шкале составляет 50 ед., а диапазон —
10…50 единиц.
Цена
деления шкалы
— разность значений величин,
соответствующих двум соседним
отметкам
шкалы. Приборы с равномерной шкалой
имеют постоянную цену деления, а с
неравномерной — переменную. В этом
случае нормируется минимальная цена
деления.
Чувствительность
— отношение изменения сигнала Δу на
выде СИ к вызвавшему это изменение
изменению Δх сигнала на входе
S=
Δу/Δх.
Например,
для стрелочного СИ — это отношение
перемещения dl
конца стрелки к вызвавшему его изменению
dx
измеряемой величины
S=
dl/dx.
Таким
образом, для неравномерных шкал величина
S=
var,
и степень неравномерности шкалы оценивают
через коэффициент
J=Smax/Smin
Для
равномерных шкал S
= Sср
= const
и Sср
= l/хN
где xN
— диапазон измерений.
Поскольку
х и у могут быть выражены в различных
единицах то величина S
имеет размерность [мм/А], [мм/В], [градус/В]и
т.д. Говоря о чувствительности, указывают
чувствительность тока, напряжения и т.
д. Иногда для оперирования безразмерными
единицами вводят понятие относительной
чувствительности
S0
= (Δy/y0)/(Δx/x0),
где
х0,
у0
— номинальные (или средние) величины.
Чувствительность нельзя отождествлять
с порогом чувствительности — наименьшим
значением измеряемой величины, вызывающим
заметное изменение показаний прибора.
Величину,
обратную чувствительности, называют
постоянной прибора С = 1/S.
Как
правило, выходным сигналом СИ является
отсчет (показание) в единицах величины.
В этом случае постоянная прибора С
равна цене деления. Поэтому для СИ с
неравномерной шкалой чувствительность
— величина переменная.
Вариация
(гистерезис)
— разность между показаниями СИ в данной
точке диапазона измерения при возрастании
и убывании измерений величины и неизменных
внешних условиях:
Н=
|хв
– xу|,
где
хв,
ху
— значения измерений образцовыми СИ
при возрастании и убывании величины
х. Следует иметь в виду, что, хотя вариация
показаний СИ вызывается случайными
факторами, сама она — не случайная
величина.
Зависимость
между выходным и входным сигналом СИ,
полученную экспериментально, называют
градуировочной характеристикой (или
статической характеристикой
преобразования), которая
может быть представлена аналитически,
графически или в виде таблицы.
Градуировочная характеристика может
изменяться под воздей ствием внешних
и внутренних причин. Например, при
быстром изменении тока подвижная часть
СИ, вследствие инерции, не успевает
«следить» за изменением тока.
Градуировочная характеристика в этом
случае должна выражаться дифференциальным
уравнением.
Характеристики
погрешности измерений в статике.
Статический
режим –
это такой режим работы СИ, при котором
изменением измеряемой величины за
время, требуемое для проведения одного
измерения, можно пренебречь. В динамическом
режиме такое
пренебрежение недопустимо, поскольку
указанное изменение превышает допустимую
погрешность.
Все
погрешности СИ в зависимости от внешних
условий делятся на основные и
дополнительные.
Основная
погрешность — это погрешность СИ при
нормальных условиях эксплуатации. Как
правило, нормальными условиями
эксплуатации являются: температура
293±5 К или 20±5 °С, относительная влажность
воздуха 65+15% при 20 °С, напряжение в сети
питания 220 В+10% с частотой 50 Гц±1%,
атмосферное давление от 97,4 до 104 кПа,
отсутствие электрических и магнитных
полей (наводок). В рабочих условиях,
зачастую отличающихся от нормальных
более широким диапазоном влияющих
величин, при необходимости нормируется
дополнительная погрешность СИ.
Классы
точности средств измерений
.
При технических измерениях, когда не
предусмотрено выделение случайных и
систематических составляющих, когда
не существенна динамическая погрешность
СИ, когда не учитываются влияющие
(дестабилизирующие) факторы и т.д., можно
пользоваться более грубым нормированием
— присвоением СИ определенного класса
точности по ГОСТ 8.401—80.
Класс
точности
–это обобщенная характеристика СИ,
выражаемая пределами допускаемых
значений его основной и дополнительной
погрешностей, а также другими
характеристиками,
влияющими на точность. Класс точности
не является непосредственной оценкой
точности измерений, выполняемых этим
СИ, поскольку погрешность зависит еще
от ряда факторов: метода измерений,
условий измерений и т.д. Класс точности
лишь позволяет судить о том, в каких
пределах находится погрешность СИ
данного типа. Общие положения деления
средств измерений по классу точности
устанавливает ГОСТ 8.401–80.года). Класс
точности СИ уже включает систематическую
и случайную погрешности. Однако он не
является непосредственной характеристикой
точности измерений, выполняемых с
помощью этих СИ, поскольку точность
измерения
зависит
и от метода измерения, взаимодействия
СИ с объектом, условий измерения и т.д.
В
связи с большим разнообразием как самих
СИ, так и их MX,
ГОСТ 8.401—80 устанавливает несколько
способов назначения классов точности.
При этом в основу заложены следующие
положения:
•
в
качестве норм служат пределы допускаемых
погрешностей, включающие систематические
и случайные составляющие;
•
основная
δосн
и все виды дополнительных погрешностей
δдоп
нормируются
порознь (см. п. 3.2).
Первое
положение свидетельствует о необходимости
разрабатывать СИ с учетом однократного
отсчета показаний по величине общей
погрешности. Второе положение направлено
на обеспечение максимальной однородности
однотипных СИ. .
Пределы
допускаемых основной и дополнительной
погрешностей выражают
в форме приведенных, относительных или
абсолютных
погрешностей.
Выбор формы представления зависит от
характера
изменения
погрешностей в пределах диапазона
измерений, а также от
условий
применения и назначения СИ.
Пределы
допускаемой абсолютной основной
погрешности
устанавливаются
по одной из формул: Δ
= ±а
или
Δ
= ±(а
+
bx),
где
х
–
значение
измеряемой величины или число делений,
отсчитанное по шкале;
а,
b
–
положительные числа, не зависящие от
х.
Первая формула описывает чисто аддитивную
погрешность (рис. 6.4, а), а вторая – сумму
аддитивной и мультипликативной (рис.
6.4, б) погрешностей (рис. 6.4, в). В технической
документации классы точности,
установленные
в виде абсолютных погрешностей,
обозначают, например, «Класс точности
М», а на приборе – буквой «М». Для
обозначения используются прописные
буквы латинского алфавита или римские
цифры, причём меньшие пределы погрешностей
должны соответствовать буквам, находящимся
ближе к началу алфавита, или меньшим
цифрам. Пределы допускаемой приведенной
основной погрешности определяются по
формуле γ
= Δ
/xN
=
± p
,
где xN
–
нормирующее значение, выраженное в тех
же единицах, что и Δ;
р
–
отвлеченное положительное число,
выбираемое из ряда значений:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;…..
.
Рис.
6.4. Аддитивная а), мультипликативная б)
и суммарная в)
погрешности
в абсолютной и относительной формах
Нормирующее
значение xN
устанавливается
равным большему из пределов измерений
(или модулей) для СИ с равномерной,
практически равномерной или степенной
шкалой и для измерительных преобразователей,
для которых нулевое значение выходного
сигнала
находится
на краю или вне диапазона измерений.
Для СИ, шкала которых имеет условный
нуль, xN
равно
модулю разности пределов измерений.
Для приборов с существенно неравномерной
шкалой xN
принимают
равным всей длине шкалы или ее части,
соответствующей диапазону измерении.
В этом случае пределы абсолютной
погрешности выражают, как и длину шкалы,
в единицах длины, а на средстве измерений
класс
точности
условно обозначают, например, в виде
значка 0,5 , где 0,5 –значение числа р
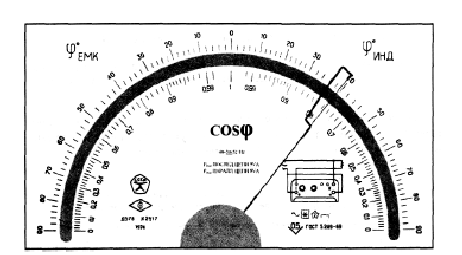
Рис.
6.5.Лицевая панель фазометра класса
точности 0,5 с существенно
неравномерной
нижней шкалой
В
остальных рассмотренных случаях класс
точности обозначают конкретным числом
р,
например 1,5. Обозначение наносится на
циферблат,
щиток или корпус прибора (рис. 6.6).
Рис
6.6. Лицевая панель амперметра класса
точности 1,5
с
равномерной шкалой
В
случае если абсолютная погрешность
задается формулой ±(a
+
bx),
пределы допускаемой относительной
основной погрешности δ
= Δ
x
=
±[c
+
d(
|xk/
x|
−1)],
(6.2)
где
с,
d
–
отвлеченные положительные числа,
выбираемые из ряда:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;….
; xk
–
больший (по модулю) из пределов измерений.
При использовании формулы (6.2) класс
точности обозначается в виде «0,02/0,01»,
где числитель – конкретное значение
числа с,
знаменатель – числа d
(рис.
6.7).
Причем,
как правило, c>d.
Например, класс точности 0,02/0,01 означает,
что с = 0,02,
а
d=
0,01, т. е. приведенное значение относительной
погрешности к началу диапазона измерения
γн
= 0,02%, а к концу — γк=
0,01%.
В
обоснованных случаях пределы допускаемой
относительной основной погрешности
определяют по более сложным формулам
либо в виде графика или таблицы.
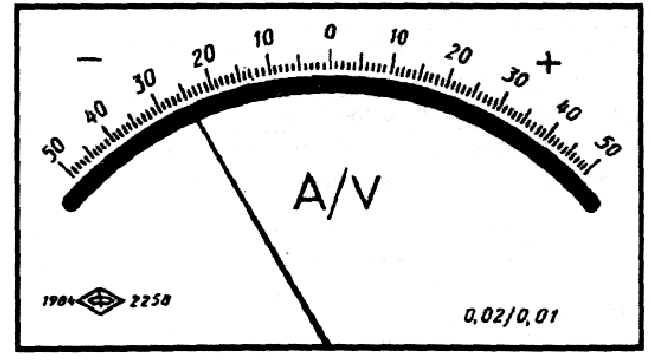
Рис.
6.7. Лицевая панель ампервольтметра
класса точности 0,02/0,01
с
равномерной шкалой
Пределы
допускаемой относительной основной
погрешности определяются по формуле
δ
= Δ /x
=
±q
,
если
Δ
= ±a
.
Значение
постоянного числа q
устанавливается
так же, как и значение числа p.
Класс точности на прибор обозначается
в виде
,
где 0,5 – конкретное значениеq
(рис.
6.8).
Так
обозначают классы точности мостов
переменного тока, счетчик0в электроэнергии,
делителей напряжения, измерительны
трансформаторов и др.
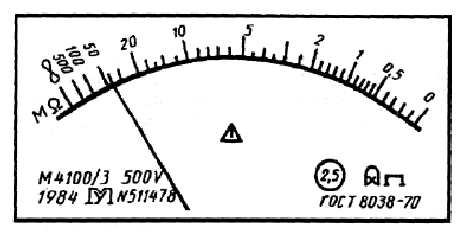
Рис
6.8. Лицевая панель мегаомметра класса
точности 2,5
с
неравномерной шкалой
В
стандартах и технических условиях на
СИ указывается минимальное значение
x0
, начиная с которого применим принятый
способ выражения пределов допускаемой
относительной погрешности. Отношение
xk/
x0
называется динамическим диапазоном
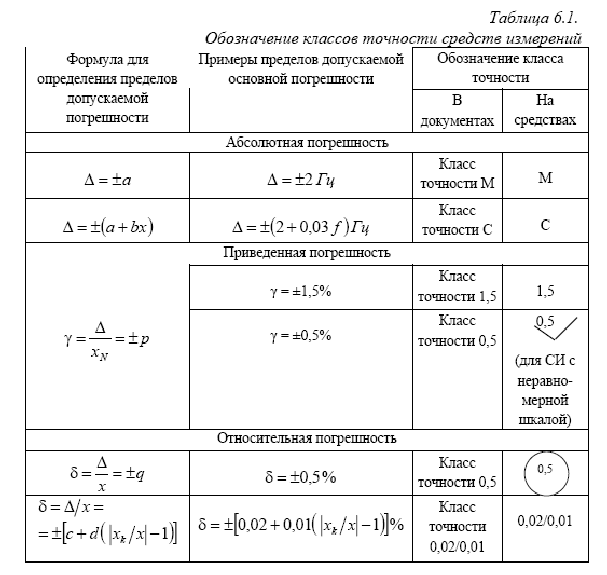
измерения. Правила построения и примеры
обозначения классов точности в
документации
и на средствах измерений приведены в
таблице 6.1.
Наиболее
широкое распространение (особенно для
аналоговых СИ) получило нормирование
класса точности по приведенной
погрешности:
γ=±Δ/xN100%
= ±A·10n.
xN
условное обозначение класса точности
в этом случае зависит от нормирующего
значения хN
т.
е. от шкалы СИ. Если xN
представляется в единицах измеряемой
величины, то класс точности обозначается
числом, совпадающим с пределом допускаемой
приведенной погрешности. Например,
класс 1,5 означает, что γ = 1,5%. Если xN
—
длина шкалы (например, у амперметров),
то класс 1.5 означает, что γ =1,5% длины
шкалы.
Не
всегда число, обозначающее класс
точности, показывает предел допускаемой
погрешности. В частности, у некоторых
однозначных мер электрических величин
оно характеризует нестабильность,
показывая, на сколько процентов значение
меры мо-
ет
изменяться в течение года.
Как уменьшить погрешность при проведении измерений: советы и рекомендации
При проведении измерений любой физической величины невозможно избежать определенной погрешности. Она может возникать из-за различных факторов, таких как неточность приборов, внешние условия, неопределенность измеряемых объектов и другие. Тем не менее, существуют различные способы, которые позволяют минимизировать погрешность при проведении измерений.
Определение типов погрешностей
На начальном этапе необходимо определить типы погрешностей, которые могут возникнуть при измерении.
Случайная погрешность
Самый распространенный вид погрешности, который возникает из-за случайных факторов, таких как температурные изменения, встряхивание прибора, дрожание руки и т.д.
Систематическая погрешность
Этот вид погрешности связан с инструментом измерения и возникает вследствие неправильной работы прибора, например, из-за его калибровки, неисправности датчика или возрастания пробега.
Советы по минимизации погрешности
После определения типов погрешностей можно перейти к поиску способов их уменьшения.
Обеспечение стабильных метеоусловий
Внешние условия играют важную роль в измерениях. По возможности следует проводить измерения при стабильных метеоусловиях, чтобы снизить влияние температурных, атмосферных и других факторов.
Правильная калибровка приборов
Систематическая погрешность связана с работой инструмента измерения. Поэтому, перед началом работы, необходимо убедиться, что прибор настроен на правильное измерение и калиброван.
Повышение верности приборов
Выбирая инструмент для измерения нужно уделить внимание уровню его верности. Чем выше точность устройства, тем меньше будет погрешность в измерениях.
Повторяемость измерений
При повторении измерений несколько раз можно снизить влияние случайных ошибок и получить более точные результаты.
Правильная техника измерения
Наконец, чтобы измерить физическую величину наиболее точно, необходимо использовать правильную технику измерения. Например:
- Для измерения длины следует использовать линейку с наименее возможными делениями и линиями.
- Для измерения массы следует использовать точные(электронные) весы.
- Для измерения напряжения и силы тока нужно выбирать подходящие приборы, соответствующие диапазонам величин.
Вывод
Погрешность — неизбежный фактор при проведении измерений. Однако, существует множество способов, которые помогают снизить ее влияние на результаты измерений. Качество измерений напрямую влияет на результаты в эксперименте, поэтому применение техники минимизации погрешностей должно стать обязательным при выполнении любых работ.
Способы уменьшения случайных погрешностей.
1
Метод многократных измерений.
Тогда
2.
Метод комплексирования.
Проводят
измерения одной и той же величины при
следующих условиях:
А)
несколькими однотипными СИ одновременно
Б)
разнотипными
С)
различными методами( разными группами
экспериментаторов)
В
дальнейшем проводится объединение
результатов наблюдений по алгоритму
средневзвешенной оценки, более точным
наблюдениям больший вес. Объединение
может быть только для равноточных
результатов по систематической
погрешности.
3.
Метод косвенных измерений.
В
отдельных случаях позволяет уменьшить
случайную погрешность.
Средства измерений. Характеристики си для определения результатов измерений.
Средство
измерений –
это техническое средство (или комплекс),
предназначенное для измерений, имеющее
нормированные метрологические
характеристики, воспроизводящие и (или)
хранящие единицу физической величины,
размер которой принимается неизменным
(в пределах установленной погрешности)
в течение известного интервала времени
[24].
Данное определение раскрывает
метрологическую
сущность СИ,
заключающуюся
в умении хранить (или воспроизводить)
единицу ФВ
и
в неизменности размера хранимой единицы
во времени.
Первое обуславливает возможность
выполнения измерения, суть которого,
как известно, состоит в сравнении
измеряемой величины с ее единицей.
Второе принципиально необходимо,
поскольку при изменении размера хранимой
единицы ФВ с помощью данного СИ нельзя
получить результат с требуемой точностью.
Под метрологическими характеристиками
(MX)
понимают такие характеристики СИ,
которые позволяют судить об их пригодности
для измерений в известном диапазоне с
известной точностью. В отличие от СИ
приборы или вещества, не имеющие
нормированных MX,
называют индикаторами. СИ — это
техническая основа метрологического
обеспечения.
Классификация
средств измерений по их роли в процессе
измерения и
выполняемым
функциям
Эталон
–
средство измерений (или их комплекс),
предназначенное для воспроизведения
и (или) хранения единицы и передачи ее
размера нижестоящим по поверочной схеме
СИ и утвержденное в качестве эталона в
установленном порядке.
Меры
— это СИ, воспроизводящие или хранящие
физическую величину заданного размера.
Меры могут быть однозначными,
воспроизводящими одно значение физической
величины (гиря, калибр на заданный
размер, образцы твердости, шероховатости,
катушка сопротивления, нормальный
элемент, воспроизводящий значение
ЭДС), и
многозначными
— для воспроизведения плавно или
дискретно ряда значений одной и той же
физической величины (измерительный
конденсатор переменной емкости, набор
конечных мер, магазин емкостей,
индуктивности и сопротивления,
измерительные линейки).
Для
ряда областей измерений, и в первую
очередь для физико-химических измерений,
чрезвычайно перспективным средством
повышения эффективности поверочных
работ является применение стандартных
образцов (СО). Правила работы с СО
устанавливает ГОСТ 8.315—97. Согласно
этому документу,
стандартный
образец состава и свойств веществ и
материалов
— это средство измерений в виде вещества
(материала), состав или свойства которого
установлены аттестацией. Можно
дать и другое определение: стандартный
образец
— образец вещества (материала) с
установленными в результате метрологической
аттестации
значениями
одной или более величин, характеризующими
свойство или состав этого вещества
(материала).
Стандартные
образцы предназначены для обеспечения
единства и требуемой точности измерений
посредством:
•
градуировки,
метрологической аттестации и поверки
СИ;
•
метрологической
аттестации методик выполнения измерений;
•
контроля
показателей точности измерений;
•
измерения
ФВ, характеризующих состав или свойства
веществ материалов, методами сравнения.
По
своему назначению СО исполняют роль
мер, однако в отличие от «классических»
мер они имеют ряд особенностей. Например,
образцы состава воспроизводят значения
ФВ,
характеризующих
состав или свойства именно того материала
(вещества), из которого они изготовлены.
Стандартные образцы, как правило не
являются изделиями, они реализованы
обычно в виде части или порции однородного
вещества (материала), причем эта часть
является полноценным носителем
воспроизводимой единицы ФВ, а не ее
части Эта особенность образцов отражена
в требованиях к их однородности по
составу и свойствам. Однородность
материала, из которого сделан образец,
имеет принципиальное значение, в то
время как для меры такая характеристик
часто является второстепенной.
Измерительные
преобразователи
— СИ, предназначенные для выработки
сигнала измерительной информации в
форме, удобной для передачи, дальнейшего
преобразования, обработки и хранения,
но не доступной для непосредственного
восприятия наблюдателем. Это термопары,
измерительные трансформаторы,
усилители,
преобразователи давления. По месту,
занимаемому в измерительной цепи, они
делятся на первичные, промежуточные и
т. п. Конструктивно они выполняются либо
отдельными блоками, либо составной
частью СИ. Не следует отождествлять
измерительные преобразователи с
преобразовательными элементам. Последние
не имеют метрологических характеристик,
как, например, трансформатор тока или
напряжения.
Измерительный
прибор
— СИ, предназначенное для переработки
сигнала измерительной информации в
другие, доступные для непосредственного
восприятия наблюдателем формы. Различают
приборы прямого действия (амперметры,
вольтметры,
манометры)
и приборы сравнения (компараторы). По
способу отсчета измеряемой величины
СИ делятся на показывающие (аналоговые,
цифровые), регистрирующие (на
бумажную
или магнитную ленту) и т. п.
Измерительная
установка
— совокупность функционально объединенных
СИ и вспомогательных устройств,
расположенных в одном месте. Например,
поверочные установки, установки для
испытания электротехнических, магнитных
и других материалов. Измерительная
установка позволяет предусмотреть
определенный
метод
измерения и заранее оценить погрешность
измерения.
Измерительная
система
— это комплекс СИ и вспомогательных
устройств
с компонентами связи (проводные,
предназначенный
для выработки сигналов измерительной
информации в форме, удобной для
автоматической обработки, передачи
и/или
использования в автоматических системах
управления. В отличие от измерительных
установок, предусматривающих изменения
режима и условий функционирования,
измерительная система не воздействует
на режимы работы, а предназначена только
для сбора и/или хранения информации.
Частными случаями измерительной системы
являются информационно-вычислительный
комплекс (ИВК), информационно-измерительные
системы (ИИС). К последним можно отнести
системы автоматического контроля,
системы технического диагностирования,
системы распознавания образов, системы
для передачи неизмерительной информации.
При организации поверки рабочих СИ
используют различные эталоны и образцовые
СИ. СИ, как правило, работают совместно
с датчиками (измерительными
преобразователями), имеющими свои MX.
При
использовании средств измерений
принципиально важно знать степень
соответствия информации об измеряемой
величине, содержащейся в выходном
сигнале, ее истинному значению. С этой
целью для каждого СИ вводятся и нормируются
определенные метрологические
характеристики (МХ).
Метрологическими
называются
характеристики свойств СИ, оказывающие
влияние на результат измерения и его
погрешности. Характеристики, устанавливаемые
нормативными документами, называются
нормируемыми,
а определяемые экспериментально –
действительными.
Номенклатура
метрологических характеристик средств
измерений
Неинформативным
называется параметр входного сигнала
СИ,
не связанный функционально с измеряемым
параметром. Например, частота переменного
тока при измерении его амплитуды.
Нормальные метрологические характеристики
(НМХ) устанавливаются документами. MX,
определенные документами, считаются
действительными. На практике наиболее
распространены следующие MX СИ.
Диапазон
измерений
— область значений измеряемой величины,
для которой нормированы допускаемые
пределы погрешности СИ (для преобразователей
— это диапазон преобразования):
Предел
измерения
— наибольшее или наименьшее значение
диапазона измерения. Для мер
— это номинальное значение воспроизводимой
величины.
Рис
32 Неравномерная шкала СИ
Например,
у шкалы на рис. 32 начальный участок
(~20%) сжат, потому производить отсчеты
на нем неудобно. Тогда предел измерения
по шкале составляет 50 ед., а диапазон —
10…50 единиц.
Цена
деления шкалы
— разность значений величин,
соответствующих двум соседним
отметкам
шкалы. Приборы с равномерной шкалой
имеют постоянную цену деления, а с
неравномерной — переменную. В этом
случае нормируется минимальная цена
деления.
Чувствительность
— отношение изменения сигнала Δу на
выде СИ к вызвавшему это изменение
изменению Δх сигнала на входе
S=
Δу/Δх.
Например,
для стрелочного СИ — это отношение
перемещения dl
конца стрелки к вызвавшему его изменению
dx
измеряемой величины
S=
dl/dx.
Таким
образом, для неравномерных шкал величина
S=
var,
и степень неравномерности шкалы оценивают
через коэффициент
J=Smax/Smin
Для
равномерных шкал S
= Sср
= const
и Sср
= l/хN
где xN
— диапазон измерений.
Поскольку
х и у могут быть выражены в различных
единицах то величина S
имеет размерность [мм/А], [мм/В], [градус/В]и
т.д. Говоря о чувствительности, указывают
чувствительность тока, напряжения и т.
д. Иногда для оперирования безразмерными
единицами вводят понятие относительной
чувствительности
S0
= (Δy/y0)/(Δx/x0),
где
х0,
у0
— номинальные (или средние) величины.
Чувствительность нельзя отождествлять
с порогом чувствительности — наименьшим
значением измеряемой величины, вызывающим
заметное изменение показаний прибора.
Величину,
обратную чувствительности, называют
постоянной прибора С = 1/S.
Как
правило, выходным сигналом СИ является
отсчет (показание) в единицах величины.
В этом случае постоянная прибора С
равна цене деления. Поэтому для СИ с
неравномерной шкалой чувствительность
— величина переменная.
Вариация
(гистерезис)
— разность между показаниями СИ в данной
точке диапазона измерения при возрастании
и убывании измерений величины и неизменных
внешних условиях:
Н=
|хв
– xу|,
где
хв,
ху
— значения измерений образцовыми СИ
при возрастании и убывании величины
х. Следует иметь в виду, что, хотя вариация
показаний СИ вызывается случайными
факторами, сама она — не случайная
величина.
Зависимость
между выходным и входным сигналом СИ,
полученную экспериментально, называют
градуировочной характеристикой (или
статической характеристикой
преобразования), которая
может быть представлена аналитически,
графически или в виде таблицы.
Градуировочная характеристика может
изменяться под воздей ствием внешних
и внутренних причин. Например, при
быстром изменении тока подвижная часть
СИ, вследствие инерции, не успевает
«следить» за изменением тока.
Градуировочная характеристика в этом
случае должна выражаться дифференциальным
уравнением.
Характеристики
погрешности измерений в статике.
Статический
режим –
это такой режим работы СИ, при котором
изменением измеряемой величины за
время, требуемое для проведения одного
измерения, можно пренебречь. В динамическом
режиме такое
пренебрежение недопустимо, поскольку
указанное изменение превышает допустимую
погрешность.
Все
погрешности СИ в зависимости от внешних
условий делятся на основные и
дополнительные.
Основная
погрешность — это погрешность СИ при
нормальных условиях эксплуатации. Как
правило, нормальными условиями
эксплуатации являются: температура
293±5 К или 20±5 °С, относительная влажность
воздуха 65+15% при 20 °С, напряжение в сети
питания 220 В+10% с частотой 50 Гц±1%,
атмосферное давление от 97,4 до 104 кПа,
отсутствие электрических и магнитных
полей (наводок). В рабочих условиях,
зачастую отличающихся от нормальных
более широким диапазоном влияющих
величин, при необходимости нормируется
дополнительная погрешность СИ.
Классы
точности средств измерений
.
При технических измерениях, когда не
предусмотрено выделение случайных и
систематических составляющих, когда
не существенна динамическая погрешность
СИ, когда не учитываются влияющие
(дестабилизирующие) факторы и т.д., можно
пользоваться более грубым нормированием
— присвоением СИ определенного класса
точности по ГОСТ 8.401—80.
Класс
точности
–это обобщенная характеристика СИ,
выражаемая пределами допускаемых
значений его основной и дополнительной
погрешностей, а также другими
характеристиками,
влияющими на точность. Класс точности
не является непосредственной оценкой
точности измерений, выполняемых этим
СИ, поскольку погрешность зависит еще
от ряда факторов: метода измерений,
условий измерений и т.д. Класс точности
лишь позволяет судить о том, в каких
пределах находится погрешность СИ
данного типа. Общие положения деления
средств измерений по классу точности
устанавливает ГОСТ 8.401–80.года). Класс
точности СИ уже включает систематическую
и случайную погрешности. Однако он не
является непосредственной характеристикой
точности измерений, выполняемых с
помощью этих СИ, поскольку точность
измерения
зависит
и от метода измерения, взаимодействия
СИ с объектом, условий измерения и т.д.
В
связи с большим разнообразием как самих
СИ, так и их MX,
ГОСТ 8.401—80 устанавливает несколько
способов назначения классов точности.
При этом в основу заложены следующие
положения:
•
в
качестве норм служат пределы допускаемых
погрешностей, включающие систематические
и случайные составляющие;
•
основная
δосн
и все виды дополнительных погрешностей
δдоп
нормируются
порознь (см. п. 3.2).
Первое
положение свидетельствует о необходимости
разрабатывать СИ с учетом однократного
отсчета показаний по величине общей
погрешности. Второе положение направлено
на обеспечение максимальной однородности
однотипных СИ. .
Пределы
допускаемых основной и дополнительной
погрешностей выражают
в форме приведенных, относительных или
абсолютных
погрешностей.
Выбор формы представления зависит от
характера
изменения
погрешностей в пределах диапазона
измерений, а также от
условий
применения и назначения СИ.
Пределы
допускаемой абсолютной основной
погрешности
устанавливаются
по одной из формул: Δ
= ±а
или
Δ
= ±(а
+
bx),
где
х
–
значение
измеряемой величины или число делений,
отсчитанное по шкале;
а,
b
–
положительные числа, не зависящие от
х.
Первая формула описывает чисто аддитивную
погрешность (рис. 6.4, а), а вторая – сумму
аддитивной и мультипликативной (рис.
6.4, б) погрешностей (рис. 6.4, в). В технической
документации классы точности,
установленные
в виде абсолютных погрешностей,
обозначают, например, «Класс точности
М», а на приборе – буквой «М». Для
обозначения используются прописные
буквы латинского алфавита или римские
цифры, причём меньшие пределы погрешностей
должны соответствовать буквам, находящимся
ближе к началу алфавита, или меньшим
цифрам. Пределы допускаемой приведенной
основной погрешности определяются по
формуле γ
= Δ
/xN
=
± p
,
где xN
–
нормирующее значение, выраженное в тех
же единицах, что и Δ;
р
–
отвлеченное положительное число,
выбираемое из ряда значений:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;…..
.
Рис.
6.4. Аддитивная а), мультипликативная б)
и суммарная в)
погрешности
в абсолютной и относительной формах
Нормирующее
значение xN
устанавливается
равным большему из пределов измерений
(или модулей) для СИ с равномерной,
практически равномерной или степенной
шкалой и для измерительных преобразователей,
для которых нулевое значение выходного
сигнала
находится
на краю или вне диапазона измерений.
Для СИ, шкала которых имеет условный
нуль, xN
равно
модулю разности пределов измерений.
Для приборов с существенно неравномерной
шкалой xN
принимают
равным всей длине шкалы или ее части,
соответствующей диапазону измерении.
В этом случае пределы абсолютной
погрешности выражают, как и длину шкалы,
в единицах длины, а на средстве измерений
класс
точности
условно обозначают, например, в виде
значка 0,5 , где 0,5 –значение числа р
Рис.
6.5.Лицевая панель фазометра класса
точности 0,5 с существенно
неравномерной
нижней шкалой
В
остальных рассмотренных случаях класс
точности обозначают конкретным числом
р,
например 1,5. Обозначение наносится на
циферблат,
щиток или корпус прибора (рис. 6.6).
Рис
6.6. Лицевая панель амперметра класса
точности 1,5
с
равномерной шкалой
В
случае если абсолютная погрешность
задается формулой ±(a
+
bx),
пределы допускаемой относительной
основной погрешности δ
= Δ
x
=
±[c
+
d(
|xk/
x|
−1)],
(6.2)
где
с,
d
–
отвлеченные положительные числа,
выбираемые из ряда:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;….
; xk
–
больший (по модулю) из пределов измерений.
При использовании формулы (6.2) класс
точности обозначается в виде «0,02/0,01»,
где числитель – конкретное значение
числа с,
знаменатель – числа d
(рис.
6.7).
Причем,
как правило, c>d.
Например, класс точности 0,02/0,01 означает,
что с = 0,02,
а
d=
0,01, т. е. приведенное значение относительной
погрешности к началу диапазона измерения
γн
= 0,02%, а к концу — γк=
0,01%.
В
обоснованных случаях пределы допускаемой
относительной основной погрешности
определяют по более сложным формулам
либо в виде графика или таблицы.
Рис.
6.7. Лицевая панель ампервольтметра
класса точности 0,02/0,01
с
равномерной шкалой
Пределы
допускаемой относительной основной
погрешности определяются по формуле
δ
= Δ /x
=
±q
,
если
Δ
= ±a
.
Значение
постоянного числа q
устанавливается
так же, как и значение числа p.
Класс точности на прибор обозначается
в виде
,
где 0,5 – конкретное значениеq
(рис.
6.8).
Так
обозначают классы точности мостов
переменного тока, счетчик0в электроэнергии,
делителей напряжения, измерительны
трансформаторов и др.
Рис
6.8. Лицевая панель мегаомметра класса
точности 2,5
с
неравномерной шкалой
В
стандартах и технических условиях на
СИ указывается минимальное значение
x0
, начиная с которого применим принятый
способ выражения пределов допускаемой
относительной погрешности. Отношение
xk/
x0
называется динамическим диапазоном
измерения. Правила построения и примеры
обозначения классов точности в
документации
и на средствах измерений приведены в
таблице 6.1.
Наиболее
широкое распространение (особенно для
аналоговых СИ) получило нормирование
класса точности по приведенной
погрешности:
γ=±Δ/xN100%
= ±A·10n.
xN
условное обозначение класса точности
в этом случае зависит от нормирующего
значения хN
т.
е. от шкалы СИ. Если xN
представляется в единицах измеряемой
величины, то класс точности обозначается
числом, совпадающим с пределом допускаемой
приведенной погрешности. Например,
класс 1,5 означает, что γ = 1,5%. Если xN
—
длина шкалы (например, у амперметров),
то класс 1.5 означает, что γ =1,5% длины
шкалы.
Не
всегда число, обозначающее класс
точности, показывает предел допускаемой
погрешности. В частности, у некоторых
однозначных мер электрических величин
оно характеризует нестабильность,
показывая, на сколько процентов значение
меры мо-
ет
изменяться в течение года.
Содержание
- Способы уменьшения случайных погрешностей.
- Случайные погрешности и способы их уменьшения
- Случайные погрешности измерений. Возникновение случайных погрешностей измерений и их свойства. Описание случайных погрешностей с помощью функции распределения. Доверительная вероятность и доверительный интервал. Способы уменьшения случайных погрешностей.
- Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Способы уменьшения случайных погрешностей.
1 Метод многократных измерений.
2. Метод комплексирования.
Проводят измерения одной и той же величины при следующих условиях:
А) несколькими однотипными СИ одновременно
С) различными методами( разными группами экспериментаторов)
В дальнейшем проводится объединение результатов наблюдений по алгоритму средневзвешенной оценки, более точным наблюдениям больший вес. Объединение может быть только для равноточных результатов по систематической погрешности.
3. Метод косвенных измерений.
В отдельных случаях позволяет уменьшить случайную погрешность.
Средства измерений. Характеристики СИ для определения результатов измерений.
Средство измерений – это техническое средство (или комплекс), предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящие и (или) хранящие единицу физической величины, размер которой принимается неизменным (в пределах установленной погрешности) в течение известного интервала времени [24]. Данное определение раскрывает метрологическую сущность СИ, заключающуюся в умении хранить (или воспроизводить) единицу ФВ
и в неизменности размера хранимой единицы во времени. Первое обуславливает возможность выполнения измерения, суть которого, как известно, состоит в сравнении измеряемой величины с ее единицей. Второе принципиально необходимо, поскольку при изменении размера хранимой единицы ФВ с помощью данного СИ нельзя получить результат с требуемой точностью. Под метрологическими характеристиками (MX) понимают такие характеристики СИ, которые позволяют судить об их пригодности для измерений в известном диапазоне с известной точностью. В отличие от СИ приборы или вещества, не имеющие нормированных MX, называют индикаторами. СИ — это техническая основа метрологического обеспечения.
Классификация средств измерений по их роли в процессе измерения и
Эталон – средство измерений (или их комплекс), предназначенное для воспроизведения и (или) хранения единицы и передачи ее размера нижестоящим по поверочной схеме СИ и утвержденное в качестве эталона в установленном порядке.
Меры — это СИ, воспроизводящие или хранящие физическую величину заданного размера. Меры могут быть однозначными, воспроизводящими одно значение физической величины (гиря, калибр на заданный размер, образцы твердости, шероховатости, катушка сопротивления, нормальный элемент, воспроизводящий значение ЭДС), и
многозначными — для воспроизведения плавно или дискретно ряда значений одной и той же физической величины (измерительный конденсатор переменной емкости, набор конечных мер, магазин емкостей, индуктивности и сопротивления, измерительные линейки).
Для ряда областей измерений, и в первую очередь для физико-химических измерений, чрезвычайно перспективным средством повышения эффективности поверочных работ является применение стандартных образцов (СО). Правила работы с СО устанавливает ГОСТ 8.315—97. Согласно этому документу,
стандартный образец состава и свойств веществ и материалов — это средство измерений в виде вещества (материала), состав или свойства которого установлены аттестацией. Можно дать и другое определение: стандартный образец — образец вещества (материала) с установленными в результате метрологической аттестации
значениями одной или более величин, характеризующими свойство или состав этого вещества (материала).
Стандартные образцы предназначены для обеспечения единства и требуемой точности измерений посредством:
• градуировки, метрологической аттестации и поверки СИ;
• метрологической аттестации методик выполнения измерений;
• контроля показателей точности измерений;
• измерения ФВ, характеризующих состав или свойства веществ материалов, методами сравнения.
По своему назначению СО исполняют роль мер, однако в отличие от «классических» мер они имеют ряд особенностей. Например, образцы состава воспроизводят значения ФВ,
характеризующих состав или свойства именно того материала (вещества), из которого они изготовлены. Стандартные образцы, как правило не являются изделиями, они реализованы обычно в виде части или порции однородного вещества (материала), причем эта часть является полноценным носителем воспроизводимой единицы ФВ, а не ее части Эта особенность образцов отражена в требованиях к их однородности по составу и свойствам. Однородность материала, из которого сделан образец, имеет принципиальное значение, в то время как для меры такая характеристик часто является второстепенной.
Измерительные преобразователи — СИ, предназначенные для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения, но не доступной для непосредственного восприятия наблюдателем. Это термопары, измерительные трансформаторы,
усилители, преобразователи давления. По месту, занимаемому в измерительной цепи, они делятся на первичные, промежуточные и т. п. Конструктивно они выполняются либо отдельными блоками, либо составной частью СИ. Не следует отождествлять измерительные преобразователи с преобразовательными элементам. Последние не имеют метрологических характеристик, как, например, трансформатор тока или напряжения.
Измерительный прибор — СИ, предназначенное для переработки сигнала измерительной информации в другие, доступные для непосредственного восприятия наблюдателем формы. Различают приборы прямого действия (амперметры, вольтметры,
манометры) и приборы сравнения (компараторы). По способу отсчета измеряемой величины СИ делятся на показывающие (аналоговые, цифровые), регистрирующие (на
бумажную или магнитную ленту) и т. п.
Измерительная установка — совокупность функционально объединенных СИ и вспомогательных устройств, расположенных в одном месте. Например, поверочные установки, установки для испытания электротехнических, магнитных и других материалов. Измерительная установка позволяет предусмотреть определенный
метод измерения и заранее оценить погрешность измерения.
Измерительная система — это комплекс СИ и вспомогательных
устройств с компонентами связи (проводные, предназначенный для выработки сигналов измерительной информации в форме, удобной для автоматической обработки, передачи
и/или использования в автоматических системах управления. В отличие от измерительных установок, предусматривающих изменения режима и условий функционирования, измерительная система не воздействует на режимы работы, а предназначена только для сбора и/или хранения информации. Частными случаями измерительной системы являются информационно-вычислительный комплекс (ИВК), информационно-измерительные системы (ИИС). К последним можно отнести системы автоматического контроля, системы технического диагностирования, системы распознавания образов, системы для передачи неизмерительной информации. При организации поверки рабочих СИ используют различные эталоны и образцовые СИ. СИ, как правило, работают совместно с датчиками (измерительными преобразователями), имеющими свои MX.
При использовании средств измерений принципиально важно знать степень соответствия информации об измеряемой величине, содержащейся в выходном сигнале, ее истинному значению. С этой целью для каждого СИ вводятся и нормируются определенные метрологические характеристики (МХ). Метрологическими называются характеристики свойств СИ, оказывающие влияние на результат измерения и его погрешности. Характеристики, устанавливаемые нормативными документами, называются нормируемыми, а определяемые экспериментально – действительными.
Номенклатура метрологических характеристик средств измерений
Неинформативным называется параметр входного сигнала СИ, не связанный функционально с измеряемым параметром. Например, частота переменного тока при измерении его амплитуды. Нормальные метрологические характеристики (НМХ) устанавливаются документами. MX, определенные документами, считаются действительными. На практике наиболее распространены следующие MX СИ.
Диапазон измерений — область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ (для преобразователей — это диапазон преобразования):
Предел измерения — наибольшее или наименьшее значение диапазона измерения. Для мер — это номинальное значение воспроизводимой величины.
Рис 32 Неравномерная шкала СИ
Например, у шкалы на рис. 32 начальный участок (
20%) сжат, потому производить отсчеты на нем неудобно. Тогда предел измерения по шкале составляет 50 ед., а диапазон — 10. 50 единиц.
Цена деления шкалы — разность значений величин, соответствующих двум соседним
отметкам шкалы. Приборы с равномерной шкалой имеют постоянную цену деления, а с неравномерной — переменную. В этом случае нормируется минимальная цена деления.
Чувствительность — отношение изменения сигнала Δу на выде СИ к вызвавшему это изменение изменению Δх сигнала на входе
Например, для стрелочного СИ — это отношение перемещения dl конца стрелки к вызвавшему его изменению dx измеряемой величины
Таким образом, для неравномерных шкал величина S= var, и степень неравномерности шкалы оценивают через коэффициент
Для равномерных шкал S = Sср = const и Sср = l/хN где xN — диапазон измерений.
Поскольку х и у могут быть выражены в различных единицах то величина S имеет размерность [мм/А], [мм/В], [градус/В]и т.д. Говоря о чувствительности, указывают чувствительность тока, напряжения и т. д. Иногда для оперирования безразмерными единицами вводят понятие относительной чувствительности
где х0, у0 — номинальные (или средние) величины. Чувствительность нельзя отождествлять с порогом чувствительности — наименьшим значением измеряемой величины, вызывающим заметное изменение показаний прибора. Величину, обратную чувствительности, называют постоянной прибора С = 1/S.
Как правило, выходным сигналом СИ является отсчет (показание) в единицах величины. В этом случае постоянная прибора С равна цене деления. Поэтому для СИ с неравномерной шкалой чувствительность — величина переменная.
Вариация (гистерезис) — разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измерений величины и неизменных внешних условиях:
где хв, ху — значения измерений образцовыми СИ при возрастании и убывании величины х. Следует иметь в виду, что, хотя вариация показаний СИ вызывается случайными факторами, сама она — не случайная величина.
Зависимость между выходным и входным сигналом СИ, полученную экспериментально, называют градуировочной характеристикой (или статической характеристикой преобразования),которая может быть представлена аналитически, графически или в виде таблицы. Градуировочная характеристика может изменяться под воздей ствием внешних и внутренних причин. Например, при быстром изменении тока подвижная часть СИ, вследствие инерции, не успевает «следить» за изменением тока. Градуировочная характеристика в этом случае должна выражаться дифференциальным уравнением.
Дата добавления: 2016-04-14 ; просмотров: 4118 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Случайные погрешности и способы их уменьшения
Случайные погрешности измерений. Возникновение случайных погрешностей измерений и их свойства. Описание случайных погрешностей с помощью функции распределения. Доверительная вероятность и доверительный интервал. Способы уменьшения случайных погрешностей.
| Рубрика | Производство и технологии |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 24.10.2017 |
| Размер файла | 561,2 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
1. Случайные погрешности измерений
1.1. Возникновение случайных погрешностей измерений
1.2. Свойства случайных погрешностей измерений
1.3. Описание случайных погрешностей с помощью функции распределения
1.4. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал
2. Способы уменьшения случайных погрешностей
2.1 Метод многократных измерений
2.2 Метод косвенных измерений
Начиная с производства строительных материалов и заканчивая возведением зданий и сооружений, в строительстве используются измерения различных видов.
Процесс измерения неизбежно сопровождается ошибками, которые вызываются несовершенством измерительных средств, нестабильностью условий проведения измерений, несовершенством самого метода и методики измерений и многими другими факторами.
Основная цель данного реферата — проанализировать и выявить наиболее точные способы уменьшения случайных погрешностей измерений. Для этой цели необходимо метрологическое обеспечение, т.е. установление и применение научных и организационных основ, технических средств, правил и норм, необходимых для достижения единства и требуемой точности измерений.
Техническими основами метрологического обеспечения являются: система государственных эталонов единиц физических величин, система передачи размеров единиц физических величин от эталона всем средствам измерений, система разработки, постановки на производство и выпуска рабочих средств измерений, система обязательных государственных испытаний средств измерений, система стандартных образцов состава свойств веществ и материалов.
В соответствии с данной целью определены следующие задачи: раскрыть понятие и классификацию погрешностей измерений; описать способы уменьшения случайных погрешностей.
Тема реферата «Случайные погрешности и способы их уменьшения» является актуальной, т.к. чем качественнее будет строительный материал (конструкция), тем он будет более конкурентноспособен на отечественном и мировом рынках. Определяющим условием выбора для потребителей в последнее время всё больше становится качество. Качеством продукции необходимо управлять, уметь количественно оценивать и анализировать его показатели, варьировать влияющими на него процессами.
1. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
1.1 Возникновения случайных погрешностей
Случайная погрешность — составляющая погрешности измерения, измеряющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера физической величины, проведенных с одинаковой тщательностью в одних и тех же условиях.
Факторы, определяющие возникновения случайных погрешностей, проявляются нерегулярно, в различных комбинациях и с интенсивностью, которую трудно предвидеть.
Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельности слабо влияет на результат измерения. По этой причине часто полагают распределение случайной погрешности «нормальным» (Центральная предельная теорема). «Нормальность» позволяет использовать в обработке данных весь арсенал математической статистики.
Однако априорная убежденность в «нормальности» на основании ЦПТ не согласуется с практикой — законы распределения ошибок измерений весьма разнообразны и, как правило, сильно отличаются от нормального.
Случайные погрешности могут быть связаны с:
· несовершенством приборов (трение в механических приборах и т. п.),
· тряской в городских условиях,
· несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления).
Основным документом для обеспечения качества измерений, обеспечения единства измерений является Федеральный закон от 26.06.2008 № 102-ФЗ (ред. от 13.07.2015) «Об обеспечении единства измерений». Глава 2. Требования к измерениям, единицам величин, эталонам единиц величин, стандартным образцам, средствам измерений. Статья 5.Требования к измерениям.
Допускает применение результатов измерений, выраженных в единицах величин только на территории Российской Федерации.
1.2 Свойства случайных погрешностей
Случайные погрешности характеризуются следующими свойствами.
1) При определенных условиях измерений случайные погрешности по абсолютной величине не могут превышать известного предела, называемого предельной погрешностью. Это свойство позволяет обнаруживать и исключать из результатов измерений грубые погрешности.
2) Положительные и отрицательные случайные погрешности примерно одинаково часто встречаются в ряду измерений, что помогает выявлению систематических погрешностей.
3) Чем больше абсолютная величина погрешности, тем реже она встречается в ряду измерений.
В соответствии с первым свойством случайных погрешностей для абсолютной величины случайной погрешности при данных условиях измерений существует допустимый предел, называемый предельной погрешностью. В строительных нормах предельная погрешность называется допускаемым отклонением.
Последнее свойство случайных погрешностей позволяет установить принцип получения из ряда измерений одной и той же величины результата, наиболее близкого к ее истинному значению, т. е. наиболее точного. Таким результатом является среднее арифметическое из п измеренных значений данной величины.
Для правильного использования результатов измерений необходимо знать, с какой точностью, т.е. с какой степенью близости к истинному значению измеряемой величины, они получены. Характеристикой точности отдельного измерения в теории погрешностей служит предложенная Гауссом средняя квадратическая погрешность.
1.3 Описание случайных погрешностей с помощью функции распределения
Интегральной функцией распределения F(x) называют функцию, значение которой для каждого x является вероятность появления значений (в i-м наблюдении), меньших x:
где Р — символ вероятности события, описание которого заключено в фигурных скобках.
Обычно график интегральной функции распределения результатов наблюдений представляет собой непрерывную неубывающую кривую, начинающуюся от нуля на отрицательной бесконечности и асимптотически приближающуюся к единице при увеличении аргумента до плюс бесконечности.
Если интегральная функция имеет точку перегиба при значении x, близком к истинному значению измеряемой величины, и принимает в этой точке значение, равное 0, 5, то говорят о симметричности распределения результатов.
Более наглядным является описание свойств результатов наблюдений, содержащих случайные погрешности, с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей:
Поскольку F(x = +) = 1, то , т.е. площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна единице. Вероятность попадания случайной величины х в заданный интервал ( равна площади, заключенной между абсциссами и :
При бесконечном увеличении числа наблюдений n>? и бесконечном уменьшении ширины интервалов ?l>0, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую f (x) (рис. 1), называемую кривой плотности распределения вероятностей случайной величины, а уравнение, описывающее ее, — дифференциальным законом распределения. Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде
Рис.1. Кривая плотности распределения вероятностей
Закон распределения дает полную информацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности.
Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал [- ?; + ?] равна единице, т.е. представляет собой достоверное событие.
Вероятность этого события называется функцией распределения случайной величины и обозначается F(x). Функцию распределения F(x) иногда называют также интегральной функцией распределения. В терминах интегральной функции распределения имеем
То есть вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала.
Рис. 2. Кривая плотности распределения вероятностей (дифференциальная функция распределения случайной величины).
1.4 Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал
случайный погрешность измерение интервал
Для количественной оценки случайных погрешностей и установления границ случайной погрешности результата измерения могут использоваться: предельная погрешность, интервальная оценка, числовые характеристики закона распределения. Выбор конкретной оценки определяется необходимой полнотой сведений о погрешности, назначением измерений и характером использования их результатов. Комплексы оценок показателей точности установлены стандартами.
Предельная погрешность ?m — погрешность, больше которой в данном измерительном эксперименте не может появиться. Теоретически, такая оценка погрешности правомерна только для распределений, границы которых четко выражены и существует такое значение ± ?m, которое ограничивает возможные значения случайных погрешностей с обеих сторон от центра распределения (например, равномерное).
На практике такая оценка есть указание наибольшей погрешности, которая может встретиться при многократных измерениях одной и той же величины.
Недостатком такой оценки является то, что она не содержит информации о характере закона распределения случайных погрешностей. При арифметическом суммировании предельных погрешностей получаемая сумма может значительно превышать действительные погрешности.
Более универсальными и информативными являются квантильные оценки. Площадь, заключенная под всей кривой плотности распределения погрешностей, отражает вероятность всех возможных значений погрешности и по условиям нормирования равна единице. Эту площадь можно разделить вертикальными линиями на части. Абсциссы таких линий называются квантилями.
Так, на рис. 3 ?x1, есть 25% -ная квантиль, так как площадь под кривой f (?x) слева от нее составляет 25% всей площади. Абсцисса ?x2 соответствует 75%-ной квантили. Между ?x1, и ?x2 заключено 50% всех возможных значений погрешности, а остальные лежат вне этого интервала.
Рис. 3 Квантильные оценки случайной величины
Квантильная оценка погрешности представляется интервалом от -?x(P) до +?x(P), на котором с заданной вероятностью С встречаются СЧ100% всех возможных значений случайной погрешности. Интервал с границами ± ?x(P) называется доверительным интервалом случайной погрешности, между границами которого с заданной доверительной вероятностью
где q — уровень значимости;
хН, хВ — нижняя и верхняя границы интервала, находится истинное значение оцениваемого параметра.
Принято границы доверительного интервала (доверительные границы) указывать симметричными относительно результата измерения. В метрологической практике используют главным образом квантильные оценки доверительного интервала. Под Р-процентным квантилем xP понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р %. Иначе говоря, квантиль — это значение случайной величины (погрешности) с заданной доверительной вероятностью Р.
Так как квантили, ограничивающие доверительный интервал по- грешности могут быть выбраны различными, то при оценивании случайной погрешности доверительными границами необходимо одновременно указывать значение принятой доверительной вероятности (например, ±0, 3 В при С = 0, 95).
Доверительные границы случайной погрешности ?x(P), соответствующие доверительной вероятности Р, находят по формуле
где t — коэффициент, зависящий от С и формы закона распределения.
Рис. 4. К понятию доверительных интервалов
На графике нормального распределения погрешностей (рис. 4) по оси абсцисс отложены интервалы с границами ±у, ±2у, ±3у, ±4у. Доверительные вероятности для этих интервалов приведены в табл. 1.
Таблица 1. Границы доверительных интервалов и соответствующие им доверительные вероятности
Источник
Измерения являются неотъемлемой частью нашей повседневной жизни и научной работы. Однако, часто возникает проблема случайной составляющей погрешности при измерениях, которая может вносить значительные искажения в полученные результаты.
Случайная составляющая погрешности обусловлена различными факторами, такими как неравномерность измеряемого объекта, ошибки при использовании измерительных приборов, внешнее воздействие и другие.
Для уменьшения случайной составляющей погрешности необходимо применять определенные методы и приемы. Во-первых, следует повысить качество используемых измерительных приборов. Чем точнее и более стабильны измерительные приборы, тем меньше погрешность измерений.
Во-вторых, важно проводить множественные измерения. Чем больше измерений мы производим, тем точнее будет полученный результат. Для этого можно использовать статистические методы обработки данных, такие как определение среднего значения, дисперсии и стандартного отклонения.
Содержание
- Определение оценки погрешности измерений
- Факторы случайной составляющей
- Техники уменьшения случайной погрешности
Определение оценки погрешности измерений
При проведении измерений невозможно избежать погрешностей, которые могут быть вызваны различными факторами. Однако, основная задача состоит в том, чтобы минимизировать случайную составляющую погрешности.
Для определения оценки погрешности измерений чаще всего используется статистический метод. Оценка погрешности измерения представляет собой числовую характеристику, которая показывает, насколько результат измерения может отличаться от точного значения величины. Она вычисляется как разность между полученным значением и известным эталонным значением.
Оценка погрешности может быть выражена в процентах или величинах, зависит от характера измеряемой величины и единиц ее измерения. Она позволяет оценить степень достоверности результатов измерений и выявить источники погрешностей для дальнейшего их устранения или уменьшения.
Для определения оценки погрешности применяются различные методы, такие как метод наименьших квадратов, метод наибольшего правдоподобия и др. В каждом случае выбор метода зависит от задачи и свойств измеряемой величины.
Оценка погрешности измерений играет важную роль в научных и технических областях, где требуется высокая точность и надежность измерений. Без правильного определения погрешности невозможно достичь точных результатов и сделать осмысленные выводы на основе измерений.
Поэтому, определение оценки погрешности измерений является неотъемлемой частью любого исследования или технического процесса, где требуются точные измерения. Оно позволяет учесть все возможные источники погрешностей и дать наиболее достоверные результаты.
Факторы случайной составляющей
1. Инструменты измерения. Качество и точность используемых инструментов непосредственно влияют на величину случайной составляющей погрешности. Некачественные или неоткалиброванные приборы могут значительно увеличить случайную погрешность.
2. Человеческий фактор. Ошибки, допущенные оператором при выполнении измерений, также могут привести к увеличению случайной составляющей погрешности. Недостаточная внимательность, неумение работать с измерительными приборами или неправильное использование методик измерений могут стать причиной значительных погрешностей.
3. Среда измерений. Условия, в которых проводятся измерения, также могут оказывать влияние на случайную погрешность. Это могут быть температурные колебания, вибрации, электромагнитные помехи и другие факторы, которые способны повлиять на точность измерения.
4. Случайные флуктуации. Кроме вышеперечисленных факторов, случайные флуктуации могут возникать из-за самой природы измеряемого параметра. Например, в некоторых случаях измеряемая величина может иметь случайный характер, что делает ее измерение более сложным и требующим дополнительных мер для снижения погрешности.
Для уменьшения случайной составляющей погрешности измерений необходимо проводить качественную калибровку и проверку инструментария, обучать операторов правильным методам измерений, создавать оптимальные условия для проведения измерений и использовать адекватные методики, основанные на характере измеряемого параметра.
Техники уменьшения случайной погрешности
При проведении измерений всегда существует некоторая случайная погрешность, вызванная различными факторами, такими как шумы, вибрации, механические колебания и др. Однако, существуют техники, которые позволяют уменьшить случайную погрешность и повысить точность измерений.
- Усреднение измерений: Одна из самых простых и эффективных методов уменьшения случайной погрешности. Путем проведения нескольких измерений одной и той же величины и нахождения их среднего значения, можно снизить влияние случайных факторов.
- Калибровка приборов: Тщательная настройка и калибровка приборов используется для минимизации систематической и случайной погрешностей. Проверка и корректировка показаний прибора с помощью эталонов помогает получить более точные измерения.
- Устранение внешних влияний: Для уменьшения случайной погрешности необходимо минимизировать воздействие внешних факторов. Это может включать использование экранирования от электромагнитных полей, установку приборов на устойчивые основания, устранение вибраций и шумов.
- Использование статистических методов: Применение статистических методов анализа данных может помочь определить степень случайности погрешности и учесть ее в расчетах. Такие методы могут включать использование стандартного отклонения, среднеквадратической ошибки и других показателей.
- Улучшение чувствительности приборов: Улучшение чувствительности приборов и датчиков помогает измерять более малые изменения величин. Это может быть достигнуто путем улучшения дизайна и материалов приборов, повышения частоты дискретизации, использования усилителей с малым уровнем шума и других технических решений.
Применение этих техник поможет уменьшить случайную погрешность и повысить точность измерений. Однако, необходимо учитывать, что некоторые методы могут быть применимы только в определенных ситуациях и требуют дополнительных затрат и усилий.
Содержание
- — Каким образом можно уменьшить погрешность измерений?
- — Каким образом можно существенно уменьшить случайные погрешности измерений можно ли совсем устранить случайные погрешности?
- — Как можно уменьшить случайную составляющую погрешности измерений?
- — Можно ли исключить из результатов измерений случайную погрешность?
- — Можно ли устранить прогрессирующие погрешности?
- — Как можно добиться повышения точности измерения?
- — Можно ли совсем устранить случайные погрешности?
- — Можно ли полностью исключить систематическую погрешность?
- — Как суммируются систематические погрешности?
- — Чему равна Случайная погрешность?
- — Что такое промах систематическая и случайная погрешность?
- — Как вычислить погрешность?
- — Как найти полную погрешность?
- — Как считается систематическая погрешность?
- — Какие погрешности относятся к неустранимым?
Их можно уменьшить путем изучения приборов, которыми пользуются при выполнении работ и введением соответствующих поправок в результат измерений. Случайные погрешности вызываются неточностями отсчетов, которую невольно может допустить всякий экспериментатор.
Каким образом можно уменьшить погрешность измерений?
Способы уменьшения ∆с:
- введение поправки: ∆п = –∆с;
- устранение причины;
- повышение класса точности прибора;
- использование метода замещения;
- изменение знака выходной величины и др.
Каким образом можно существенно уменьшить случайные погрешности измерений можно ли совсем устранить случайные погрешности?
В отличие от систематических случайные погрешности нельзя исключить из результатов измерений путем введения поправки, однако их можно существенно уменьшить путем увеличения числа наблюдений. … Они, как правило, возникают из-за ошибок или неправильных действий оператора или резких изменений условий проведения измерений.
Как можно уменьшить случайную составляющую погрешности измерений?
Во многих случаях влияние случайных погрешностей можно уменьшить путем выполнения многократных измерений с последующей статистической обработкой полученных результатов.
Можно ли исключить из результатов измерений случайную погрешность?
Случайные погрешно- сти служат причиной разброса результатов повторных измерений относительно истинного значения измеряемой величины. (хотя это может оказаться очень сложной задачей), то исключить случайные погрешности нельзя.
Можно ли устранить прогрессирующие погрешности?
Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. … В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений. По происхождению различают инструментальные и методические погрешности средств измерений.
Как можно добиться повышения точности измерения?
Повысить точность измерения можно, прибегая к следующим методам: • замене средств измерений более точными; • использованию более точной формулы измерений; • структурной информационной избыточности — тестовым методам; • функциональной информационной избыточности.
Можно ли совсем устранить случайные погрешности?
Случайной называют погрешность, изменяющуюся случайным образом при повторных измерениях одной и той же величины. … Случайные же погрешности полностью устранить невозможно. Значения их можно уменьшить, принимая меры для большей стабилизации тех факторов, которые оказывают влияние на данную погрешность.
Можно ли полностью исключить систематическую погрешность?
Если систематическую погрешность исключить, например, введением поправки, то случайные отклонения значений погрешности от значений поправки останутся не исключенными. … Внося в результат измерений поправку, взятую из аттестата, исключают из результата измерений систематическую погрешность шкалы.
Как суммируются систематические погрешности?
Систематические погрешности В наиболее типовом случае систематические составляющие основных погрешностей средств измерений суммируются геометрически, по формулам (4.30), (4.101), поскольку они являются случайными величинами. … Поэтому в формулах для расчета погрешностей она учитывается геометрически.
Чему равна Случайная погрешность?
Случайная погрешность — составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера величины с одинаковой тщательностью. В появлении этого вида погрешности не наблюдается какой-либо закономерности.
Что такое промах систематическая и случайная погрешность?
Систематические погрешности — такие погрешности, которые соот- ветствуют отклонению измеряемой величины от ее истинного значения все- гда в одну сторону — либо в сторону завышения, либо в сторону занижения. … При закономерных изменениях условий погрешность так- же меняется закономерно. Случайные погрешности.
Как вычислить погрешность?
Относительная погрешность измерения – это погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%.
Как найти полную погрешность?
7. Вычислить случайную абсолютную погрешность результата измерений: DAСЛ = tna×Sn. Здесь Dx, Dy, Dz — абсолютные погрешности приборов, измеряющих параметры x, y, z.
Как считается систематическая погрешность?
Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. … Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях.
Какие погрешности относятся к неустранимым?
Инструментальные (приборные, аппаратурные) погрешности – это погрешности применяемых средств измерения, связанные со схемными, конструктивными и техническими недостатками средств измерения, их состоянием в процессе эксплуатации. Приборные погрешности относятся к разряду неустранимых погрешностей.
Интересные материалы:
Как посмотреть сохраненные пароли в iCloud?
Как посмотреть сохраненные пароли в Internet Explorer?
Как посмотреть сохраненные пароли в opera?
Как посмотреть сохраненные пароли в опере 2019?
Как посмотреть сохраненные пароли в опере на андроид?
Как посмотреть сохраненные пароли в сафари?
Как посмотреть свой пароль Apple ID?
Как посмотреть в приложении вконтакте пароль?
Как поставить новый пароль на вай фай?
Как поставить пароль на dir 320?