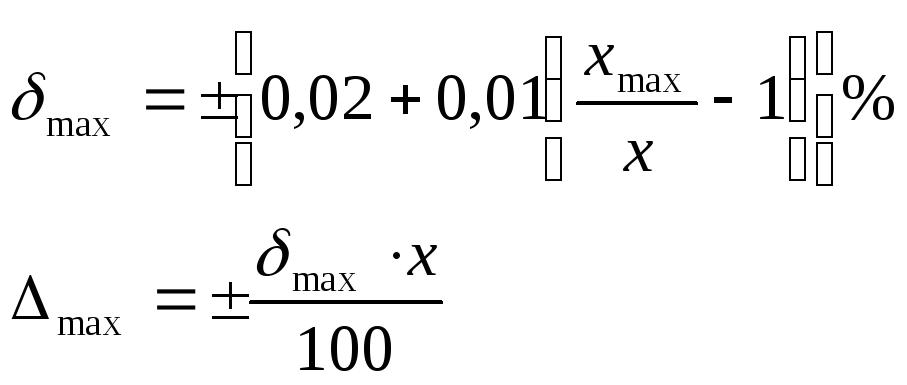Какая ошибка измерений считается допустимой

В.Д. Гвоздев. Допустимая погрешность измерений: выбор значения

(«Законодательная и прикладная метрология», 2013, №2)

Аннотация

Объектом анализа являются рекомендации по выбору допустимой погрешности измерений, содержащиеся в нормативных документах и публикациях по метрологии. Основное внимание уделено допусковому контролю качества. Подчеркивается, что концепция контроля точности линейных размеров, принятая в ГОСТ 24356, может быть причиной брака.

Ключевые слова: измерения, контроль, допустимая погрешность измерений, допускаемая погрешность измерений, допуск, оценка соответствия

Для обеспечения единства измерений необходимо, чтобы характеристики погрешности/неопределенности (далее погрешность — Δ) результата измерений не выходили за заданные (допустимые) границы. Методы определения характеристик точности результатов измерений – основная тема метрологии. Выбору значений допустимой погрешности уделяется немного внимания. Часто авторы книг ограничиваются указанием, что выбор допустимой (допускаемой) погрешности производится исходя из задач измерений. Связано это с тем, что в рамках метрологии обосновать выбор значения допустимой погрешности невозможно.

Однако оставить тему выбора допустимой погрешности без рассмотрения также нельзя, хотя бы потому, что при метрологической экспертизе проектов нормативных документов, конструкторской и технологической документации обязательно проверяют оптимальность требований к точности измерений.

Задача измерений – определение значения величины. Цели могут быть разные. Разделим их условно на две группы: 1 — получение информации о величине и 2 — контроль качества объектов.

В первом случае значения допустимой погрешности измерений обусловлены влиянием неопределенности результата измерений на последствия от принятия решения на его основе.

Например:

-если ставится задача повышения точности оценки какой-либо количественной характеристики по отношению к уже достигнутому уровню, допустимая погрешность измерения будет определяться разрядом последней цифры, надежность которой должна быть обеспечена;

-для научных и практических исследований, во многих случаях, допустимую погрешность измерений устанавливают из условия сопоставимости их результатов;

-в медицине точность измерений обусловливается взаимосвязью между изменением параметра и самочувствием пациента;

-в спорте выбор разрешающей способности средств измерений и погрешности измерений связаны с плотностью результатов спортсменов;

-при осуществлении торговых операций с продуктами, характеризуемыми массой или объемом, поставке электроэнергии, тепла, горючих и смазочных материалов и др. от значения допустимой погрешности измерений напрямую зависят экономические показатели поставщика и потребителя;

-при оценке характеристик точности технологических процессов, применении статистических методов контроля технологических процессов, статистическом приемочном контроле и входном контроле качества продукции исходят из критерия ничтожной погрешности измерения по отношению к технологическому допуску. Характеристики точности измерений принимают такими, чтобы среднеквадратическое отклонение (СКО) результата измерений было в 5…6 раз меньше СКО контролируемого параметра [1]. Если СКО контролируемого параметра неизвестно, руководствуются правилом: цена деления не должна превышать 1/6 значения допуска контролируемого параметра [2]. Погрешность измерения в этом случае рассматривают как составную часть погрешности изготовления.

При установлении требований к качеству объектов для значений показателей качества задают односторонние ограничения или двухсторонние ограничения (допуски), которые учитывают при выборе допустимой погрешности измерения. Определим место погрешности измерения при контроле показателя качества с двусторонним ограничением, то есть, когда задан допуск. Обратимся к положению, записанному в стандарте ГОСТ Р ИСО 10576-1-2006 [3]: «решение о соответствии требованиям может быть принято в том случае, если интервал неопределенности результатов измерений находится внутри области допустимых значений». Реализуя принципы оценки соответствия, установленные стандартом, изобразим области соответствия (контролируемый параметр А однозначно находится в заданных пределах) и несоответствия (контролируемый параметр А однозначно находится вне заданных пределов) на числовой оси (рис.).

Рис. Схема измерительного контроля качества отдельного объекта.

Область соответствия 1 определена условием А_min + Δ ≤ А ≤ А_max – Δ, области несоответствия 2 (области недопустимых значений) характеризуются неравенствами А ≤ А_min — Δ и A ≥ А_max + Δ. Интервалы А_min ± Δ и А_max ± Δ назовем областями неокончательного результата оценки соответствия 3. Если истинное значение измеряемой величины находится в области неокончательного результата оценки соответствия, то существует вероятность, что вследствие влияния погрешности измерений годное изделие может быть отнесено к бракованным (неправильно забракованное изделие), а бракованное изделие к годным (неправильно принятое изделие).

При известной функции распределения 4 погрешности измерений можно установить вероятности правильного и неверного решений о соответствии конкретного изделия. Применительно к ситуации, показанной на рисунке, если А^* истинное значение величины, то Р_г — вероятность признания изделия годным, а Р_б = 1- Р_г — вероятность забракования изделия. Если А^* измеренное значение, то Р_г — вероятность того, что изделие годное, а Р_б — вероятность, что оно бракованное. Достоверность такой информации не высока: сведения о законе распределения случайной погрешности измерений приблизительны или отсутствуют; неисключенные систематические погрешности, рассматриваемые при вычислении суммарной погрешности как случайные величины, в практических измерениях проявляют себя как систематические составляющие, значения и знаки которых неизвестны.

В стандарте [3] не приведены правила для ситуации, когда получен неокончательный результат оценки соответствия. В тоже время отмечается, что «применение двухэтапной процедуры вместо одноэтапной процедуры в общем случае приводит к уменьшению риска» принятия ошибочных решений. Двухэтапная процедура подразумевает повторное выполнение измерений, когда границы интервала неопределенности, рассчитанные после первого этапа, выходят за пределы поля допуска (т.е. результат измерений находится в области неокончательного результата оценки соответствия). Значение измеряемой величины и её неопределенность устанавливают как комбинацию результатов измерений двух этапов.

Для сближения границ области неокончательного результата оценки соответствия применимы меры по уменьшению погрешности измерений, рассмотренные в документе [4].

Границы области соответствия сужаются до нуля при допустимой погрешности измерения равной 0,5 допуска на изготовление и расширяются до границ поля допуска при отсутствии погрешности измерений. Отсюда следует вывод, что значение погрешности измерений при двухстороннем ограничении показателя качества должно быть менее половины значения допуска и чем оно меньше, тем лучше. Вывод согласуется с мнением авторов работ [5, 6] и это единственная общая рекомендация, которую целесообразно давать в рамках метрологии.

В нормативных документах и печатных изданиях по метрологии приводятся другие указания по выбору допустимой погрешности измерений, которые якобы позволяют «достичь необходимой точности изделий с наименьшими затратами труда и материальных средств» [7].

Наиболее известное соотношение [Δ] ≈ (0,2…0,35) ТА было предложено в работе [6] и закреплено в стандарте ГОСТ 8.051 «Погрешности, допускаемые при измерении линейных размеров до 500 мм». Авторы работы [6] честно указали, что «установление допустимых погрешностей измерения носит волевой характер».

Сходные между собой указания приведены в РМГ 63 [8] и ПМГ 92-2009 [9]: «если недостаточная точность измерений не может вызвать заметных потерь или других неблагоприятных последствий, пределы допускаемых значений, например, погрешности измерений могут составлять 0,2 — 0,3 границы симметричного допуска (для несимметричного допуска — размера поля допуска) на измеряемый параметр, а для параметров, не относящихся к наиболее важным, это соотношение может быть увеличено до 0,5» [9].

Те же документы содержат и иные рекомендации: «соотношения между погрешностью измерения и половиной допуска, удовлетворяющие «требованиям обеспечения эффективности измерений»: «для наиболее важных параметров» 0,2 … 0,7; «для параметров, не относящихся к наиболее важным» 0,3 … 1.

В книге [10] оптимальное соотношение между допустимой погрешностью измерения и допуском на изготовление, обосновано критерием ничтожной погрешности и равно [Δ]=0,15TA.

Интересная по замыслу книга [5] содержит такие выводы: «при выборе СИ и МВИ для контроля и измерения вспомогательных, некритичных для качества продукции параметров следует принимать К = Δ/(ТА/2) = 0,2…0,33, не прибегая к расчетам вероятностей ошибок контроля. При проведении научно-исследовательских работ выбирают К <0,2. При фактическом К< 0,1 расчеты вероятностей ошибок поверки не производят». В другом месте книги [5] , «наиболее простой способ установления допустимой погрешности измерения — принять ее значение в долях от допуска на изделие: [Δ]= С ∙ ТА. Если принять С = 0,1…0,35, то можно не определять ошибки контроля, так как в таком случае они являются априори малыми».

Особенностью перечисленных рекомендаций является то, что они не позволяют связать выбор значений допустимой погрешности измерений с конкретными последствиями от их использования. Обоснования по выбору коэффициентов опираются на абстрактные понятия «важный» и «неважный» параметры, «эффективность измерений», «заметные» потери и «малые» ошибки контроля, «неблагоприятные последствия», «симметричный», «несимметричный» и «односторонний» допуски (допуск это разность заданных предельных значений показателей качества, а разность не может быть симметричной или односторонней). Обращает на себя внимание противоречивость и существенное различие рекомендаций, приводимых не только в разных документах, но и в некоторых случаях в одном документе, а также широких разброс границ диапазонов коэффициентов, определяющих соотношение между допустимой погрешностью измерения и половиной допуска/допуском на изготовление.

Недостаточно внимательное и критичное отношение к таким рекомендациям, может привести к неправильным выводам, что их соблюдение является гарантией корректного решения конкретных измерительных задач. С другой стороны несоблюдение требований РМГ 63-2003 и ПМГ 92-2009 при выполнении метрологической экспертизы проектов нормативных документов или конструкторской и технологической документации может рассматриваться как нарушение метрологических норм и правил.

Рассмотрим конкретный пример контроля линейных размеров деталей. Принципы оценки соответствия для линейных размеров, прописанные в ГОСТ 25346-89 [11], отличаются от описанных в ГОСТ Р ИСО 10576-1-2006: деталь признается годной, если действительный (измеренный) размер находится между предельными размерами или равен одному из них. То есть границы области соответствия совпадают с границами допуска. Вследствие этого при использовании допустимых погрешностей, устанавливаемых по ГОСТ 8.051 (0,2…0,35 ТА), к числу годных, могут быть отнесены детали с истинными размерами, выходящими за заданные границы.

Поскольку вопрос точности актуален в первую очередь для размеров сопрягаемых поверхностей, была выполнена оценка влияния погрешности измерения на значение допуска посадки. Обычно при выборе посадок используют принцип полной взаимозаменяемости, согласно которому допуск посадки ТП равен сумме допусков отверстия TD и вала Td: ТП = TD + Td.

Получаемые при сборке значения зазоров и/или натягов в сопряжении можно оценить вероятностными границами. Предположим, что систематическая составляющая погрешности измерения отсутствует. С учетом погрешности/неопределенности измерений размахи рассеяния истинных значений размеров отверстий и валов, поступающих на сборку, составят ТD^* = TD + 2 ∙ Δ_D и Тd^* = Td +2 ∙ Δ_d . Представим взаимосвязь между погрешностью измерения и допуском в виде Δ = К ∙ Т. Запишем ТD^* = (1+2∙К)∙TD и Тd^* = (1+2∙К) ∙ Td. Найдем вероятностные значения допуска посадки: ТП_в = √( TD^*2 + Td^*2) = (1+2К) √( TD² + Td²)

Для стандартных рекомендуемых и предпочтительных посадок допуск отверстия равен допуску вала (тогда ТП = 2∙Td) или на один квалитет грубее (TD=1,6∙Td и ТП = 2,6∙Td). Для первого случая получим ТП_в1=(1+2∙К)∙1,41∙ Td, для второго — ТП_в2 = (1+2∙К) ∙ 1,89∙ Td.

Подставим значения К, принятые в ГОСТ 8.051 для сопрягаемых размеров, и вычислим вероятностные допуски посадки. Запишем, при К=0,2 — ТП_в1 = 1,97∙ Td, ТП_в2 =2,65 ∙ Td; при К=0,3 — ТП_в1 = 2,26 ∙ Td, ТП_в2 =3,03 ∙ Td.

Сравнивая ТП и ТП_в, отметим, что при К = 0,2, если центры группирования размеров отверстий и валов совпадают с серединами полей допусков, влияние погрешности измерения практически не отразится на качестве сборочной единицы (1,97<2 и 2,65≈2,6). При К=0,3 существует вероятность получения брака (2,26>2 и 3,03>2,6), что требует контроля качества соединения или сортировки деталей, поступающих на сборку. Эти же меры потребуются, если настроенность технологического процесса не совпадает с серединой поля допуска (что в той или иной мере всегда присутствует).

Отметим, что значение К=0,2 в ГОСТ 8.051 принято для квалитетов более десятого, для меньших квалитетов К>0,2.

Результаты анализа показывают, что значения допустимой погрешности измерений, рекомендуемые ГОСТ 8.051, завышены. Возникает вопрос: почему это обстоятельство не стало темой для обсуждения? Причин несколько. Укажем некоторые из них. 1. При выборе метода и средств измерений создают запас метрологической надежности. 2. Для универсальных средств измерений линейных размеров реальные погрешности их применения меньше значений, приведенных в РД 50-98 [7]. Вследствие 1 и 2 практическое соотношение между погрешностью измерения и допуском оказывается меньше установленного стандартом. 3. Дополнительный запас создается при выборе стандартной посадки, допуск которой, как правило, меньше функционального допуска посадки. 4. Технологию обработки детали выбирают так, чтобы технологический допуск был меньше конструкторского. 5. Вводят производственный допуск. 6. Вместо измерительного контроля используют контроль калибрами и т.д.

Все упомянутые выше рекомендации по установлению допустимой погрешности измерений укладываются в интервал (0…0,5) ТА. Это значит, что они справедливы. Но они и не безусловны и требуют проверки обоснованности и эффективности в каждом конкретном случае.

Возможные проблемы, связанные с применением ГОСТ 8.051, обусловлены не реализованными в нем соотношениями между допустимой погрешностью и допуском размера, а концепцией оценки соответствия, прописанной в ГОСТ 25346: «предельные размеры – два предельно допустимых размера элемента, между которыми должен находиться (или которым может быть равен) действительный размер». (Действительный размер – размер элемента, установленный измерением с допускаемой погрешностью). Это означает, что границы области соответствия совпадают с границами поля допуска и что детали, истинные значения размеров которых выходят за границы поля допуска, могут быть признаны годными «на законных основаниях». Для предупреждения этих событий в качестве одного из вариантов действий ГОСТ 8.051 предлагает конструкторам назначать предельные размеры детали смещенными относительно расчетных границ внутрь поля допуска на значение погрешности измерений. Внедрение указанного предложения может вызвать следующие неудобства. 1. Использование допустимых погрешностей, установленных ГОСТ 8.051, приведет к уменьшению конструкторского допуска по сравнению с расчетным допуском примерно в 2 раза и повышению требований к технологическому оборудованию. 2. Сведения о допустимой погрешности измерений, если она отличается от стандартной погрешности, необходимо будет указывать в конструкторской документации для каждого поля допуска. 3. При использовании для контроля деталей калибров придется задавать приемочные границы, исключающие погрешности измерений.

Общие требования к нормированию предельных значений, приведенные в ГОСТ Р ИСО 10576-1-2006, включают следующее положение: «устанавливаемые предельные значения не должны включать в себя (в явном или неявном виде) неопределенность/погрешность измерений». В свете сказанного в предыдущем абзаце, весьма разумное соображение.

Концепция оценки соответствия ГОСТ Р ИСО 10576-1-2006 более гибкая и позволяет производителю продукции самому принимать решения, связанные с обеспечением и контролем качества.

Для примера рассмотрим ситуацию, когда необходимо оценить годность вала, размер которого задан 40±0,195 мм (допуск размера Td = 390 мкм). В наличии (под рукой) имеется штангенциркуль с отсчетом 0,05 мм.

Из таблиц стандарта ГОСТ 8.051 найдем допустимую погрешность измерения [Δ]=80 мкм. Для штангенциркуля в РД 50-98 [7] для диапазона измерений свыше 30 мм до 50 мм указан предел погрешности измерений 100 мкм. Погрешность измерений штангенциркулем больше допустимой погрешности: штангенциркуль использовать нельзя. Концепция ГОСТ Р ИСО 10576-1-2006 позволяет нам это сделать. Ограничив область соответствия пределами 40±0,095 мм, оценку годности вала можно выполнить без риска отнесения к годным бракованных деталей.

В книгах по метрологии большое внимание уделяют возможности установления допустимой погрешности измерения исходя из заданной вероятности отнесения изделий к неправильно забракованным m и неправильно принятым n. На основе аппарата теории вероятностей авторы работ [6, 12] получили формулы и построили графики, устанавливающие зависимость значений m и n от соотношений между погрешностью измерений, параметрами технологического процесса и допуском на изготовление. Задав значения m и n при известной характеристике погрешности технологического процесса можно оценить требуемое значение допустимой погрешности измерения. Пример решения такой задачи приведен в книге [10].

Не ставя под сомнение корректность анализа и обоснованность полученных результатов и выводов, следует обратить внимание на применимость теоретических положений для практических целей.

Предложенные в книгах [6, 10, 12] графики относятся к ситуации, когда технологический допуск превышает допуск на изготовление. Такое на практике возможно, однако не соответствует принципам выбора способа изготовления, согласно которому технологический допуск должен быть меньше допуска на изготовление. В рекомендациях [14] в зависимости от значений коэффициента точности технологический процесс оценивают как точный, при K_т =6σ_тех/ТА≤0,75; удовлетворительный, при K_т = 0,76÷0,98 и неудовлетворительный, при K_т > 0,98 (σ_тех — СКО технологического процесса).

Задача измерений/контроля в первую очередь состоит в том, чтобы количество неправильно принятых изделий свести к нулю. При K_т < 0,98 и применении методов статистического контроля и регулирования технологических процессов она решается. При серийном и массовом производстве для контроля качества продукции в основном используют альтернативные методы контроля, а не средства измерений.

Средства измерений применяют при мелкосерийном, единичном производстве и ремонте, для оценки годности небольших партий или отдельных образцов продукции. Уменьшение количества неправильно принятых и неправильно забракованных изделий будет зависеть от значения погрешности измерений и от правильной организации контроля, например на принципах изложенных выше [3]. Целесообразность организации измерительного контроля на подобных принципах отмечена в работе [14]: «при разработке методик контроля должны использоваться только «индивидуальные» характеристики достоверности контроля отдельного параметра отдельного экземпляра изделия (или пробы продукции)».

Ограничения на значения показателей качества могут быть односторонними: только сверху или только снизу. Это не значит, что второе ограничение в принципе отсутствует. Например, для отгрузки сырой нефти требования к массовой доле серы могут быть заданы в виде: массовая доля серы должна быть не более 2 %. Вторая — нижняя граница реальна и объективна – 0%. В этом случае разность граничных значений можно рассматривать как допуск. Поскольку область соответствия при оценке качества будет начинаться с нуля, значение допустимой погрешности измерения выбираем из условия [Δ] < ТА. Другой пример, требование к продукту сформулировано в виде: массовая доля компонента А (предположим, жирность молока) должна быть не менее 3,2 %. Задана нижняя граница. Объективно существует и верхняя граница 100%. Однако связывать значение допустимой погрешности измерения с диапазоном 3,2…100% опрометчиво. Для удовлетворения заданных требований здесь уместен экономический подход к выбору метода и средств измерений в сочетании с введением приемочной границы (границы соответствия), смещенной на значение Δ в сторону увеличения.

Экономический подход к выбору метода и средств измерений описан в нескольких нормативных документах (например, [8, 9]). Идея заключается в следующем: «оптимальной (в экономическом отношении и для задач, не связанных с негативными социальными последствиями, например, такими, как причинение ущерба здоровью работников) считают точность измерений, при которой сумма потерь (добавим, или дополнительных затрат) от недостаточной точности результатов измерений и расходов на измерения будет минимальной».

Экономические расчеты – основной способ обоснования выбора допустимой погрешности измерений или метода и средств измерений при контроле качества объектов. Однако они могут быть применены только для конкретных, подробно описанных ситуаций.

Использование понятия «допустимая погрешность измерений» и её нормирование при контроле качества уместно только тогда, когда ограничительные границы на значение показателя качества установлены с учетом этой погрешности. Во всех остальных случаях (не только при контроле качества) предпочтительно применение термина «заданная погрешность», в предположении, что требуемые характеристики погрешности измерений устанавливаются вне сферы метрологии (например, в квалиметрии).

Список литературы

1. Управление качеством продукции» Справочник. — М.: Изд-во стандартов, 1985. – 464 с.

2. РД 50-605-86 Методические указания по применению стандартов на статистический приемочный контроль. – М.: Изд-во стандартов, 1986. 38 с.

3. ГОСТ Р ИСО 10576-1-2006 Статистические методы. Руководство по оценке соответствия установленным требованиям. Часть 1. Общие принципы. — М.: Стандартинформ, 2006. — 16 с.

4. РМГ 64-2003 ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Методы и способы повышения точности измерений. — М.: Изд-во стандартов, 2004.- 35 с.

5. Установление показателей качества продукции и технологических параметров и норм точности их измерения. / Под общ. ред. проф. А.А. Бегунова. – СПб.: ГОУВПО СПбГТУРП, 2008. – 85 с.

6. Марков Н.Н., Крайнер Г.Б., Сацердотов П.А. Погрешность и выбор средств при линейных измерениях. – М.: Машиностроение, 1967. – 392 с.

7. РД 50-98-86 Методические указания. Выбор универсальных средств измерений линейных размеров до 500 мм (По применению ГОСТ 8.051-81). – М.: Изд-во стандартов, 1987. — 105 с.

8. РМГ 63-2003 ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Метрологическая экспертиза технической документации. — М.: Изд-во стандартов, 2004. — 27 с.

9. ПМГ 92 – 2009 ГСИ. Метрологическая экспертиза проектов нормативных документов. — М.: Стандартинформ, 2011. — 9 с.

10. Артемьев Б.Г., Голубев С.М. Справочное пособие для работников метрологических служб. – М.: Изд-во стандартов, 1990. – 428 с.

11. ГОСТ 25346-89 Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений. — М.: Изд-во стандартов, 1992. — 23 с.

12. Фрумкин В.Д., Рубичев Н.А. Теория вероятностей и статистика в метрологии и измерительной технике. — М.: Машиностроение, 1987. — 168 с.

13. Р 50-601-19-91 Применение статистических методов регулирования технологических процессов. – М.: ВНИИС, 1997. 32 с.

14. Земельман М.А. Метрологические основы технических измерений. – М.: Изд-во стандартов, 1991. – 228 с.

Источник

From Wikipedia, the free encyclopedia

Probability densities of polls of different sizes, each color-coded to its 95% confidence interval (below), margin of error (left), and sample size (right). Each interval reflects the range within which one may have 95% confidence that the true percentage may be found, given a reported percentage of 50%. The margin of error is half the confidence interval (also, the radius of the interval). The larger the sample, the smaller the margin of error. Also, the further from 50% the reported percentage, the smaller the margin of error.

The margin of error is a statistic expressing the amount of random sampling error in the results of a survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a census of the entire population. The margin of error will be positive whenever a population is incompletely sampled and the outcome measure has positive variance, which is to say, whenever the measure varies.

The term margin of error is often used in non-survey contexts to indicate observational error in reporting measured quantities.

Concept[edit]

Consider a simple yes/no poll as a sample of respondents drawn from a population $N{\text{, }}(n\ll N)$ reporting the percentage of yes responses. We would like to know how close is to the true result of a survey of the entire population , without having to conduct one. If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), we would expect those subsequent results $p_{1},p_{2},\ldots$ to be normally distributed about $\overline {p}$ , the true but unknown percentage of the population. The margin of error describes the distance within which a specified percentage of these results is expected to vary from $\overline {p}$ .

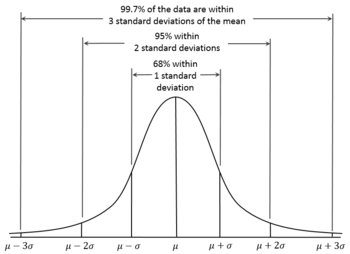
According to the 68-95-99.7 rule, we would expect that 95% of the results $p_{1},p_{2},\ldots$ will fall within about two standard deviations ( $\pm 2\sigma _{P}$ ) either side of the true mean $\overline {p}$ . This interval is called the confidence interval, and the radius (half the interval) is called the margin of error, corresponding to a 95% confidence level.

Generally, at a confidence level $\gamma$ , a sample sized of a population having expected standard deviation $\sigma$ has a margin of error

$MOE_{\gamma }=z_{\gamma }\times {\sqrt {\frac {\sigma ^{2}}{n}}}$

where $z_{\gamma }$ denotes the quantile (also, commonly, a z-score), and ${\sqrt {\frac {\sigma ^{2}}{n}}}$ is the standard error.

Standard deviation and standard error[edit]

We would expect the average of normally distributed values $p_{1},p_{2},\ldots$ to have a standard deviation which somehow varies with . The smaller , the wider the margin. This is called the standard error $\sigma _{\overline {p}}$ .

For the single result from our survey, we assume that $p={\overline {p}}$ , and that all subsequent results $p_{1},p_{2},\ldots$ together would have a variance $\sigma _{P}^{2}=P(1-P)$ .

${\text{Standard error}}=\sigma _{\overline {p}}\approx {\sqrt {\frac {\sigma _{P}^{2}}{n}}}\approx {\sqrt {\frac {p(1-p)}{n}}}$

Note that $p(1-p)$ corresponds to the variance of a Bernoulli distribution.

Maximum margin of error at different confidence levels[edit]

For a confidence level $\gamma$ , there is a corresponding confidence interval about the mean $\mu \pm z_{\gamma }\sigma$ , that is, the interval $[\mu -z_{\gamma }\sigma ,\mu +z_{\gamma }\sigma ]$ within which values of should fall with probability $\gamma$ . Precise values of $z_{\gamma }$ are given by the quantile function of the normal distribution (which the 68-95-99.7 rule approximates).

Note that $z_{\gamma }$ is undefined for $|\gamma |\geq 1$ , that is, $z_{1.00}$ is undefined, as is $z_{1.10}$ .

$\gamma$	$z_{\gamma }$		$\gamma$	$z_{\gamma }$
0.68	0.994457883210	0.999	3.290526731492
0.90	1.644853626951	0.9999	3.890591886413
0.95	1.959963984540	0.99999	4.417173413469
0.98	2.326347874041	0.999999	4.891638475699
0.99	2.575829303549	0.9999999	5.326723886384
0.995	2.807033768344	0.99999999	5.730728868236
0.997	2.967737925342	0.999999999	6.109410204869

Log-log graphs of $MOE_{\gamma }(0.5)$

vs sample size n and confidence level γ. The arrows show that the maximum margin error for a sample size of 1000 is ±3.1% at 95% confidence level, and ±4.1% at 99%.
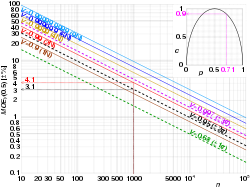
The inset parabola $\sigma _{p}^{2}=p-p^{2}$

illustrates the relationship between $\sigma _{p}^{2}$

at $p=0.71$

and $\sigma _{max}^{2}$

. In the example, MOE₉₅(0.71) ≈ 0.9 × ±3.1% ≈ ±2.8%.

Since $\max \sigma _{P}^{2}=\max P(1-P)=0.25$ at p=0.5 , we can arbitrarily set $p={\overline {p}}=0.5$ , calculate $\sigma _{P}$ , $\sigma _{\overline {p}}$ , and $z_{\gamma }\sigma _{\overline {p}}$ to obtain the maximum margin of error for at a given confidence level $\gamma$ and sample size , even before having actual results. With $p=0.5,n=1013$

$MOE_{95}(0.5)=z_{0.95}\sigma _{\overline {p}}\approx z_{0.95}{\sqrt {\frac {\sigma _{P}^{2}}{n}}}=1.96{\sqrt {\frac {.25}{n}}}=0.98/{\sqrt {n}}=\pm 3.1\%$

$MOE_{99}(0.5)=z_{0.99}\sigma _{\overline {p}}\approx z_{0.99}{\sqrt {\frac {\sigma _{P}^{2}}{n}}}=2.58{\sqrt {\frac {.25}{n}}}=1.29/{\sqrt {n}}=\pm 4.1\%$

Also, usefully, for any reported $MOE_{95}$

$MOE_{99}={\frac {z_{0.99}}{z_{0.95}}}MOE_{95}\approx 1.3\times MOE_{95}$

Specific margins of error[edit]

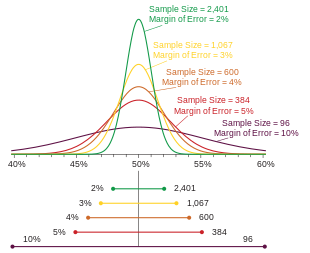
If a poll has multiple percentage results (for example, a poll measuring a single multiple-choice preference), the result closest to 50% will have the highest margin of error. Typically, it is this number that is reported as the margin of error for the entire poll. Imagine poll reports $p_{a},p_{b},p_{c}$ as $71\%,27\%,2\%,n=1013$

$MOE_{95}(P_{a})=z_{0.95}\sigma _{\overline {p_{a}}}\approx 1.96{\sqrt {\frac {p_{a}(1-p_{a})}{n}}}=0.89/{\sqrt {n}}=\pm 2.8\%$

(as in the figure above)

$MOE_{95}(P_{b})=z_{0.95}\sigma _{\overline {p_{b}}}\approx 1.96{\sqrt {\frac {p_{b}(1-p_{b})}{n}}}=0.87/{\sqrt {n}}=\pm 2.7\%$

$MOE_{95}(P_{c})=z_{0.95}\sigma _{\overline {p_{c}}}\approx 1.96{\sqrt {\frac {p_{c}(1-p_{c})}{n}}}=0.27/{\sqrt {n}}=\pm 0.8\%$

As a given percentage approaches the extremes of 0% or 100%, its margin of error approaches ±0%.

Comparing percentages[edit]

Imagine multiple-choice poll reports $p_{a},p_{b},p_{c}$ as $46\%,42\%,12\%,n=1013$ . As described above, the margin of error reported for the poll would typically be $MOE_{95}(P_{a})$ , as $p_{a}$ is closest to 50%. The popular notion of statistical tie or statistical dead heat, however, concerns itself not with the accuracy of the individual results, but with that of the ranking of the results. Which is in first?

If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), and report result $p_{w}=p_{a}-p_{b}$ , we could use the standard error of difference to understand how $p_{w_{1}},p_{w_{2}},p_{w_{3}},\ldots$ is expected to fall about ${\overline {p_{w}}}$ . For this, we need to apply the sum of variances to obtain a new variance, $\sigma _{P_{w}}^{2}$ ,

$\sigma _{P_{w}}^{2}=\sigma _{P_{a}-P_{b}}^{2}=\sigma _{P_{a}}^{2}+\sigma _{P_{b}}^{2}-2\sigma _{P_{a},P_{b}}=p_{a}(1-p_{a})+p_{b}(1-p_{b})+2p_{a}p_{b}$

where $\sigma _{P_{a},P_{b}}=-P_{a}P_{b}$ is the covariance of $P_{a}$ and $P_{b}$ .

Thus (after simplifying),

${\text{Standard error of difference}}=\sigma _{\overline {w}}\approx {\sqrt {\frac {\sigma _{P_{w}}^{2}}{n}}}={\sqrt {\frac {p_{a}+p_{b}-(p_{a}-p_{b})^{2}}{n}}}=0.029,P_{w}=P_{a}-P_{b}$

$MOE_{95}(P_{a})=z_{0.95}\sigma _{\overline {p_{a}}}\approx \pm {3.1\%}$

$MOE_{95}(P_{w})=z_{0.95}\sigma _{\overline {w}}\approx \pm {5.8\%}$

Note that this assumes that $P_{{c}}$ is close to constant, that is, respondents choosing either A or B would almost never chose C (making $P_{a}$ and $P_{b}$ close to perfectly negatively correlated). With three or more choices in closer contention, choosing a correct formula for $\sigma _{P_{w}}^{2}$ becomes more complicated.

Effect of finite population size[edit]

The formulae above for the margin of error assume that there is an infinitely large population and thus do not depend on the size of population , but only on the sample size . According to sampling theory, this assumption is reasonable when the sampling fraction is small. The margin of error for a particular sampling method is essentially the same regardless of whether the population of interest is the size of a school, city, state, or country, as long as the sampling fraction is small.

In cases where the sampling fraction is larger (in practice, greater than 5%), analysts might adjust the margin of error using a finite population correction to account for the added precision gained by sampling a much larger percentage of the population. FPC can be calculated using the formula^[1]

$\operatorname {FPC} ={\sqrt {\frac {N-n}{N-1}}}$

…and so, if poll were conducted over 24% of, say, an electorate of 300,000 voters,

$MOE_{95}(0.5)=z_{0.95}\sigma _{\overline {p}}\approx {\frac {0.98}{\sqrt {72,000}}}=\pm 0.4\%$

$MOE_{95_{FPC}}(0.5)=z_{0.95}\sigma _{\overline {p}}{\sqrt {\frac {N-n}{N-1}}}\approx {\frac {0.98}{\sqrt {72,000}}}{\sqrt {\frac {300,000-72,000}{300,000-1}}}=\pm 0.3\%$

Intuitively, for appropriately large ,

$\lim _{n\to 0}{\sqrt {\frac {N-n}{N-1}}}\approx 1$

$\lim _{n\to N}{\sqrt {\frac {N-n}{N-1}}}=0$

In the former case, is so small as to require no correction. In the latter case, the poll effectively becomes a census and sampling error becomes moot.

References[edit]

^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. Blackwell Publishing. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)

Sources[edit]

Sudman, Seymour and Bradburn, Norman (1982). Asking Questions: A Practical Guide to Questionnaire Design. San Francisco: Jossey Bass. ISBN 0-87589-546-8
Wonnacott, T.H.; R.J. Wonnacott (1990). Introductory Statistics (5th ed.). Wiley. ISBN 0-471-61518-8.

External links[edit]

«Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. «Margin of Error». MathWorld.

Источник

Источники
погрешностей (инструментальные и
методические погрешности, влияние
помех, субъективные ошибки). Номинальная
и реальная функция преобразования,
абсолютная и относительная погрешность
средства измерений, основная и
дополнительная погрешности. Пределы
допускаемых погрешностей, классы
точности средств измерений. Выявление
и уменьшение систематических погрешностей.
Оценка случайных погрешностей.
Доверительный интервал и доверительная
вероятность. Оценка погрешностей
косвенных измерений. Обработка результатов
измерений. [1:
с.23…35,40,41,53,54,56…61; 2:
с.22…53; 3:
с.48…91; 4:
с.21,22,35…52,63…71, 72…77,85…93].

II.1. Основные сведения и методические указания.

Одним из
основополагающих понятий Метрологии
является понятие погрешности измерений.

Погрешностью
измерения
называют отклонение измеренного

значения физической
величины от её истинного значения.

Погрешность
измерений, в общем случае, может быть
вызвана следующими причинами:

Несовершенством
принципа действия и недостаточным
качеством элементов используемого
средства измерения.
Несовершенством
метода измерений и влиянием используемого
средства измерения на саму измеряемую
величину, зависящим от способа
использования данного средства
измерения.
Субъективными
ошибками экспериментатора.

Так как истинное
значение измеряемой величины никогда
неизвестно (в противном случае отпадает
необходимость в проведении измерений),
то численное значение погрешности
измерений может быть найдено только
приближенно. Наиболее близким к истинному
значению измеряемой величины является
значение, которое может быть получено
при использовании эталонных средств
измерений (средств измерений наивысшей
точности). Это значение условились
называть действительным
значением измеряемой величины.
Действительное значение также является
неточным, однако, из-за малой погрешности
эталонных средств измерений, погрешностью
определения действительного значения
пренебрегают.

Классификация
погрешностей

По форме представления
различают понятия абсолютной погрешности
измерений и относительной погрешности
измерений.

Абсолютной
погрешностью
измерений называют разность между

измеренным и
действительным значениями измеряемой

величины:

где ∆ — абсолютная
погрешность,

–измеренное
значение,

–действительное
значение измеряемой величины.

Абсолютная
погрешность имеет размерность измеряемой
величины. Знак абсолютной погрешности
будет положительным, если измеренное
значение больше действительного, и
отрицательным в противном случае.

Относительной
погрешностью
называют отношение абсолютной

погрешности к
действительному значению измеряемой
величины:

где δ – относительная
погрешность.

Чаще всего
относительную погрешность определяют
приближенно в процентах от измеренного
значения:

Относительная
погрешность показывает, какую часть (в
%) от измеренного значения составляет
абсолютная погрешность. Относительная
погрешность позволяет нагляднее, чем
абсолютная погрешность, судить о точности
измеренного значения.

По источникам
происхождения погрешности подразделяют
на следующие виды:

— инструментальные
погрешности;

— методические
погрешности;

— субъективные
погрешности, допущенные экспериментатором
.

Инструментальными
называются погрешности, которые
принадлежат данному типу средств
измерения, могут быть определены при
их испытаниях и занесены в паспорт
средства измерения в виде пределов
допускаемых погрешностей.

Инструментальная
погрешность возникает из-за несовершенства
принципа действия и недостаточно
высокого качества элементов, применяемых
в конструкции средства измерений. По
этой причине реальная передаточная
характеристика каждого экземпляра
средства измерений в большей или меньшей
степени отличается от номинальной
(расчетной) передаточной характеристики.
Отличие реальной характеристики средства
измерений от номинальной (рис.1) определяет
величину инструментальной погрешности
средства измерений.

Рис.1. Иллюстрация
к определению понятия инструментальной

погрешности.

Здесь: 1 – номинальная
характеристика средства измерений;

2 – реальная
характеристика средства измерений.

Как видно из рис.1,
при изменении измеряемой величины,
инструментальная погрешность может
иметь различные значения (как положительные,
так и отрицательные).

При создании
средств измерений какой-либо физической
величины, к сожалению, не удается
полностью избавиться от реакции этого
средства измерений на изменение других
(не измеряемых) величин. Наряду с
чувствительностью средства измерения
к измеряемой величине, оно всегда
реагирует (хотя и существенно в меньшей
степени) на изменение условий эксплуатации.
По этой причине инструментальную
погрешность подразделяют на основную
погрешность и дополнительную
погрешности.

Основной
погрешностью
называют погрешность, имеющую место

в случае применения
средства измерений в нормальных условиях

эксплуатации.

Номенклатура
влияющих на средство измерений величин
и диапазоны их изменений определяются
разработчиками в качестве нормальных
условий для каждого типа средств
измерений. Нормальные условия эксплуатации
всегда указываются в техническом
паспорте средства измерений. Если
эксперимент выполняется в условиях,
отличных от нормальных для данного
средства измерений, его реальная
характеристика искажается сильнее, чем
в нормальных условиях. Погрешности,
которые при этом возникают, называют
дополнительными.

Дополнительной
погрешностью
называют погрешность средств

измерений, которая
возникает в условиях, отличающихся от

нормальных, но
входящих в допустимую рабочую область
условий

эксплуатации.

Рабочие условия
эксплуатации, так же как и нормальные,
в обязательном порядке приводятся в
техническом паспорте средств измерений.

Инструментальная
погрешность средств измерений
определенного типа не должна превышать
некоторого заданного значения – так
называемой предельно допустимой основной
погрешности средств измерений данного
типа. Фактическая основная погрешность
каждого конкретного экземпляра этого
типа является при этом случайной
величиной и может принимать различные
значения, иногда даже равные нулю, но в
любом случае инструментальная погрешность
не должна превышать заданного предельного
значения. Если это условие не выполняется,
средство измерений должно быть изъято
из обращения.

Методическими
называются погрешности, которые возникают
из-за неудачного выбора экспериментатором
средства измерения для решения
поставленной задачи. Они не могут быть
приписаны средству измерения и приведены
в его паспорте.

Методические
погрешности измерения зависят как от
характеристик применяемого средства
измерений, так и во многом от параметров
самого объекта измерения. Неудачно
выбранные средства измерений могут
исказить состояние объекта измерений.
При этом методическая составляющая
погрешности может оказаться существенно
больше инструментальной.

Субъективными
погрешностями
называют погрешности,

допускаемые
самим экспериментатором при проведении

измерений.

Этот тип погрешностей
связан обычно с невнимательностью
экспериментатора: применение прибора
без устранения смещения нуля, неправильное
определение цены деления шкалы, неточный
отсчет доли деления, ошибки в подключении
и т.п.

По характеру
проявления погрешности измерений
подразделяют на:

— систематические
погрешности;

— случайные
погрешности;

— промахи (грубые
ошибки).

Систематической
называют погрешность, которая при
повторных измерениях одной и той же
величины остается постоянной, или
изменяется закономерно.

Систематические
погрешности обусловлены как несовершенством
метода измерений и влиянием средства
измерений на измеряемый объект, так и
отклонением реальной передаточной
характеристики применяемого средства
измерений от номинальной характеристики.

Постоянные
систематические погрешности средств
измерений могут быть выявлены и численно
определены в результате сличения их
показаний с показаниями эталонных
средств измерений. Такие систематические
погрешности могут быть уменьшены
регулировкой приборов или введением
соответствующих поправок. Следует
заметить, что полностью исключить
систематические погрешности средств
измерений не удается, так как их реальные
передаточные характеристики изменяются
при изменении условий эксплуатации.
Кроме этого всегда имеют место так
называемые прогрессирующие погрешности
(возрастающие или убывающие), вызванные
старением элементов входящих в состав
средств измерений. Прогрессирующие
погрешности могут быть скорректированы
регулировкой или введением поправок
лишь на некоторое время.

Таким образом,
даже после регулировки или введения
поправок, всегда имеет место так
называемая неисключенная систематическая
погрешность результата измерений.

Случайной
называют погрешность, которая при
повторных измерениях одной и той же
величины принимает различные значения.

Случайные погрешности
обусловлены хаотичным характером
изменений физических величин (помех),
влияющих на передаточную характеристику
средства измерений, суммированием помех
с измеряемой величиной, а также наличием
собственных шумов средства измерений.
При создании средств измерений
предусматриваются специальные меры
защиты от помех: экранирование входных
цепей, использование фильтров, применение
стабилизированных источников питающего
напряжения и т.д. Это позволяет уменьшить
величину случайных погрешностей при
проведении измерений. Как правило, при
повторных измерениях одной и той же
величины результаты измерений либо
совпадают, либо отличаются на одну, две
единицы младшего разряда. В такой
ситуации случайной погрешностью
пренебрегают и оценивают только величину
неисключенной систематической
погрешности.

Наиболее сильно
случайные погрешности проявляются при
измерении малых значений физических
величин. Для повышения точности в таких
случаях производятся многократные
измерения с последующей статистической
обработкой результатов методами теории
вероятности и математической статистики.

Промахами
называют грубые погрешности, существенно
превышающие ожидаемые погрешности при
данных условиях проведения измерений.

Промахи большей
частью возникают из-за субъективных
ошибок экспериментатора или из-за сбоев
в работе средства измерений при резких
изменениях условий эксплуатации (броски
или провалы сетевого напряжения, грозовые
разряды и т.п.) Обычно промахи легко
выявляются при повторных измерениях и
исключаются из рассмотрения.

Оценка погрешностей
косвенных измерений.

При косвенных
измерениях результат измерений
определяется по функциоральной
зависимости от результатов прямых
измерений. Поэтому погрешность косвенных
измерений определяется как полный
дифференциал этой функции от величин,
измеряемых с помощью прямых измерений.

;

Где:
—
предельные абсолютные погрешности
результатов прямых

измерений;

—
предельная абсолютная погрешность
результата косвенного

измерения;

—
соответствующие предельные относительные
погрешности.

—
функциональная связь между искомой
измеряемой величиной и

величинами,
подвергающимися прямым измерениям.

Статистическая
обработка результатов измерений

Из-за влияния на
средство измерений помех различного
происхождения (изменение температуры
окружающей среды, электромагнитных
полей, вибраций, изменения частоты и
амплитуды сетевого напряжения, изменения
атмосферного давления, влажности и
т.д.), а также из-за наличия собственных
шумов элементов, входящих в состав
измерительных приборов, результаты
повторных измерений одной и той же
физической величины (особенно ее малых
значений) будут в большей или меньшей
степени отличаться друг от друга. В этом
случае результат измерений является
случайной величиной, которая характеризуется
наиболее вероятным значением и разбросом
(рассеянием) результатов повторных
измерений вблизи наиболее вероятного
значения. Если при повторных измерениях
одной и той же величины результаты
измерений не отличаются друг от друга,
то это означает, что разрешающая
способность отсчетного устройства не
позволяет обнаружить это явление. В
этом случае случайная составляющая
погрешности измерений является
несущественной и ею можно пренебречь.
При этом неисключенную систематическую
погрешность результата измерений
оценивают по величине пределов допускаемых
погрешностей применяемых средств
измерений. Если же при повторных
измерениях одной и той же величины
наблюдается разброс показаний, то это
означает, что наряду с большей или
меньшей неисключенной систематической
погрешностью, имеет место и случайная
погрешность, принимающая при повторных
измерениях различные значения.

Для определения
наиболее вероятного значения измеряемой
величины при наличии случайных
погрешностей и для оценки погрешности,
с которой определено это наиболее
вероятное значение, применяется
статистическая обработка результатов
измерений. Статистическая обработка
результатов серии измерений при
проведении экспериментов позволяет
решить следующие задачи.

Более точно
определить результат измерения путем
усреднения отдельных наблюдений.
Оценить область
неопределенности уточненного результата
измерений.

Основной смысл
усреднения результатов измерений
заключается в том, что найденная
усредненная оценка имеет меньшую
случайную погрешность, чем отдельные
результаты, по которым эта усредненная
оценка определяется. Следовательно
усреднение не устраняет полностью
случайного характера усредненного
результата, а лишь уменьшает ширину
полосы его неопределенности.

Таким образом, при
статистической обработке, прежде всего,
определяют наиболее вероятное значение
измеряемой величины путем вычисления
среднего арифметического всех отсчетов:

где: x_i
– результат i
– го измерения;

n
– число проведенных измерений в данной
серии измерений.

После этого
оценивают отклонение результатов
отдельных измерений x_i
от этой оценки среднего значения
;.

Затем находят
оценку среднеквадратического отклонения
наблюдений, характеризующую степень
рассеяния результатов отдельных
наблюдений вблизи,
по формуле:

Точность оценки
наиболее вероятного значения измеряемой
величины
зависит от числа наблюдений.
Нетрудно убедиться в том, что результаты
нескольких оценокпо одному и тому же числуотдельных измерений будут отличаться.
Таким образом, сама оценкатакже является случайной величиной. В
связи с этим вычисляется оценка
среднеквадратического отклонения
результата измерения,
которую обозначают.
Эта оценка характеризует степень
разброса значенийпо отношению к истинному значению
результата, т.е. характеризует точность
результата, полученного усреднением
результата многократных измерений.
Следовательно, поможет быть оценена систематическая
составляющая результата серии измерений.
Для различныхона определяется по формуле:

Следовательно,
точность результата многократных
измерений увеличивается с ростом числа
последних.

Однако в большинстве
практических случаев нам важно определить
не просто степень рассеивания значения
погрешности при проведении серии
измерений (т.е. величину
),
а оценить вероятность возникновения
погрешности измерения, не превышающую
допустимую, т.е. не выходящую за пределы
некоторого заданного интервала разброса
получаемых погрешностей.

Доверительным
интервалом
называют
интервал, который с заданной вероятностью,
называемой
доверительной вероятностью
накрывает истинное значение измеряемой
величины.

При определении
доверительных интервалов необходимо,
прежде всего, учитывать, что закон
распределения погрешностей, получаемых
при проведении многократных измерений,
при числе измерений в серии меньше 30,
описывается не нормальным законом
распределения, а так называемым законом
распределения Стьюдента. И, в этих
случаях, величину доверительного
интервала обычно оценивают по формуле:

где
— так называемый коэффициент Стьюдента.

В табл.4.1 приведены
значения коэффициентов Стьюдента
в зависимости от заданной доверительной
вероятности и числа проведенных
наблюдений.
При выполнении измерений обычно задаются
доверительной вероятностью 0,95 или 0,99.

Таблица 4.1

Значения
коэффициентов Стьюдента
.

n
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99

2	1,00	1,38	1,96	3,08	6,31	12,71	31,82	63,66
3	0,82	1,06	1,34	1,89	2,92	4,30	6,97	9,93
4	0,77	0,98	1,25	1,64	2,35	3,18	4,54	5,84
5	0,74	0,94	1,19	1,53	2,13	2,78	3,75	4,60
6	0,73	0,92	1,16	1,48	2,02	2,62	3,37	4,03
7	0,72	0,91	1,13	1,44	1,94	2,45	3,14	3,71
8	0,71	0,90	1,12	1,42	1,90	2,37	3,00	3,50
9	0,71	0,89	1,11	1,40	1,86	2,31	2,90	3,36
10	0,70	0,88	1,10	1,38	1,83	2,26	2,82	3,25
16	0,69	0,87	1,07	1,34	1,75	2,13	2,60	2,95
25	0,69	0,86	1,06	1,32	1,71	2,06	2,49	2,80

При изучении
материалов данного раздела следует
хорошо уяснить, что погрешности
результатов измерений и погрешности
средств измерений – не идентичные
понятия. Погрешность средства измерения
это его свойство, характеристика, для
описания которого используют ряд правил,
закрепленных в стандартах и нормативных
документах. Это та доля погрешности
измерения, которая определяется только
самим средством измерения. Погрешность
же измерений (результата измерений) –
это число, которое характеризует границы
неопределенности значения измеряемой
величины. В нее, кроме погрешности
средства измерений, могут входить
составляющие погрешности, порожденные
применяемым методом измерения
(методические погрешности), действием
влияющих (неизмеряемых) величин,
погрешность отсчета и др.

Нормирование
погрешностей средств измерения.

Точность СИ
определяется предельно-допустимыми
погрешностями, которые могут быть
получены при его использовании.

Нормированием
погрешностей средств измерений называют

процедуру
назначения допустимых границ основной
и

дополнительных
погрешностей, а также выбор формы
указания

этих границ
в нормативно-технической документации.

Пределы допускаемой
основной и дополнительных погрешностей
определяются разработчиками для каждого
типа средств измерений на стадии
подготовки производства. В зависимости
от назначения средства измерений и
характера изменения погрешности в
пределах диапазона измерений нормируется
для средств измерений различного типа
либо предельно-допустимое значение
основной абсолютной погрешности, либо
предельно-допустимое значение основной
приведенной погрешности, либо
предельно-допустимое значение основной
относительной погрешности.

Для каждого типа
средств измерений характер изменения
погрешности в пределах диапазона
измерений зависит от принципа действия
этого средства измерений и может быть
самым разнообразным. Однако, как показала
практика, среди этого многообразия
часто удается выделить три типовых
случая, предопределяющих выбор формы
представления пределов допускаемой
погрешности. Типовые варианты отклонения
реальных передаточных характеристик
средств измерений от номинальной
характеристики и соответствующие им
графики изменения предельных значений
абсолютной и относительной погрешностей
в зависимости от измеряемой величины
приведены на рис 2.

Если реальная
передаточная характеристика средства
измерений смещена по отношению к
номинальной (1-й график на рис.2а),
абсолютная погрешность, возникающая
при этом, (1-й график на рис.2б), не зависит
от измеряемой величины.

Составляющую
погрешности средства измерений, не
зависящую от измеряемой величины,
называют аддитивной
погрешностью.

Если угол наклона
реальной передаточной характеристики
средства измерений отличается от
номинального (2-й график на рис. 2а), то
абсолютная погрешность будет линейно
зависеть от измеряемой величины (2-й
график на рис. 2б).

Составляющую
погрешности средства измерений, линейно
зависящую от измеряемой величины,
называют мультипликативной
погрешностью.

Если реальная
передаточная характеристика средства
измерений смещена по отношению к
номинальной и угол ее наклона отличается
от номинального (3-й график на рис. 2а),
то в этом случае имеет место как
аддитивная, так и мультипликативная
погрешность.

Аддитивная
погрешность возникает из-за неточной
установки нулевого значения перед
началом измерений, ухода нуля в процессе
измерений, из-за наличия трений в опорах
измерительного механизма, из-за наличия
термо-эдс в контактных соединениях и
т.д.

Мультипликативная
погрешность возникает при изменении
коэффициентов усиления или ослабления
входных сигналов (например, при изменении
температуры окружающей среды, или
вследствие старения элементов), из-за
изменения значений, воспроизводимых
мерами, встроенными в измерительные
приборы, из-за изменений жесткости
пружин, создающих противодействующий
момент в электромеханических приборах
и т.д.

Ширина полосы
неопределенности значений абсолютной
(рис.2б) и относительной (рис.2в) погрешностей
характеризует разброс и изменение в
процессе эксплуатации индивидуальных
характеристик множества находящихся
в обращении средств измерений определенного
типа.

А) Нормирование
пределов допускаемой основной погрешности
для

средств
измерений с преобладающей аддитивной
погрешностью.

Для средств
измерений с преобладающей аддитивной
погрешностью (1-й график на рис.2) удобно
нормировать одним числом предельно-допустимое
значение абсолютной погрешности (∆_max=
±а). В этом случае фактическая абсолютная
погрешность ∆ каждого экземпляра
средства измерений данного типа на
различных участках шкалы может иметь
различные значения, но не должна превышать
предельно-допустимой величины (∆ ≤
±а). В многопредельных измерительных
приборах с преобладающей аддитивной
погрешностью для каждого предела
измерений пришлось бы указывать свое
значение предельно допустимой абсолютной
погрешности. К сожалению, как видно из
1-го графика на рис.2в, нормировать одним
числом предел допускаемой относительной
погрешности в различных точках шкалы
не представляется возможным. По этой
причине для средств измерений с
преобладающей аддитивной погрешностью
часто нормируют одним числом значение
так называемой основной приведенной
относительной
погрешности

где X_N
– нормирующее значение.

Таким способом,
например, нормируются погрешности
большинства электромеханических и
электронных приборов со стрелочными
индикаторами. В качестве нормирующего
значения X_N
обычно используется предел измерений
(X_N
= X_max),
удвоенное значение предела измерений
(если нулевая отметка находится в
середине шкалы), или длина шкалы (для
приборов с неравномерной шкалой). Если
X_N= X_max,
то значение приведенной погрешности γ
равно пределу допускаемой относительной
погрешности средства измерений в точке,
соответствующей пределу измерений. По
заданному значению предела допускаемой
основной приведенной погрешности легко
определить предел допускаемой основной
абсолютной погрешности для каждого
предела измерений многопредельного
прибора:.

После этого для
любой отметки шкалы X
может быть произведена оценка
предельно-допустимой основной
относительной погрешности:

Б) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с преобладающей мультипликативной

погрешностью.

Как видно из рис.2
(2-й график), для средств измерений с
преобладающей мультипликативной
погрешностью, одним числом удобно
нормировать предел допускаемой основной
относительной погрешности (рис.2в) δ_max=
± b∙100%.
В этом случае, фактическая относительная
погрешность каждого экземпляра средства
измерений данного типа на различных
участках шкалы может иметь различные
значения, но не должна превышать предельно
допустимой величины (δ ≤ ± b∙100%).
По заданному значению предельно
допустимой относительной погрешности
δ_max
для любой точки шкалы может быть
произведена оценка предельно-допустимой
абсолютной погрешности:

К числу средств
измерений с преобладающей мультипликативной
погрешностью относится большинство
многозначных мер, счетчики электрической
энергии, счетчики воды, расходомеры и
др. Следует отметить, что для реальных
средств измерений с преобладающей
мультипликативной погрешностью не
удается полностью устранить аддитивную
погрешность. По этой причине в технической
документации всегда указывается
наименьшее значение измеряемой величины,
для которого предел допускаемой основной
относительной погрешности ещё не
превышает заданного значения δ_max.
Ниже этого наименьшего значения
измеряемой величины погрешность
измерений не нормируется и является
неопределенной.

В) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с соизмеримой аддитивной и мультипликативной

погрешностью.

Если аддитивная
и мультипликативная составляющая
погрешности средства измерений соизмеримы
(3-й график на рис.2), то задание
предельно-допустимой погрешности одним
числом не представляется возможным. В
этом случае либо нормируется предел
допускаемой абсолютной основной
погрешности (указываются предельно-допустимые
значения a
и b),
либо (чаще всего) нормируется предел
допускаемой относительной основной
погрешности. В последнем случае численные
значения предельно-допустимых
относительных погрешностей в различных
точках шкалы оцениваются по формуле:

где X_max
– предел измерений;

X
— измеренное значение;

d
=

— значение приведенной к пределу измерений

аддитивной
составляющей основной погрешности;

с =
— значение результирующей относительной

основной
погрешности в точке, соответствующей
пределу

измерений.

Рассмотренным
выше способом (указанием численных
значений c
и d)
нормируются, в частности, предельно-допустимые
значения относительной основной
погрешности цифровых измерительных
приборов. В этом случае относительные
погрешности каждого экземпляра средств
измерений определенного типа не должны
превышать установленных для этого типа
средств измерений значений
предельно-допустимой погрешности:

При этом абсолютная
основная погрешность определяется по
формуле

Г)
Нормирование дополнительных погрешностей.

Наиболее часто
пределы допускаемых дополнительных
погрешностей указывают в технической
документации либо одним значением для
всей рабочей области величины, влияющей
на точность средства измерений (иногда
несколькими значениями для поддиапазонов
рабочей области влияющей величины),
либо отношением предела допускаемой
дополнительной погрешности к интервалу
значений влияющей величины. Пределы
допускаемых дополнительных погрешностей
указываются на каждой , влияющей на
точность средства измерений величине.
При этом, как правило, значения
дополнительных погрешностей устанавливают
в виде дольного или кратного значения
предела допускаемой основной погрешности.
Например, в документации может быть
указано, что при температуре окружающей
среды за пределами нормальной области
температур, предел допускаемой
дополнительной погрешности, возникающей
по этой причине, не должен превышать
0,2% на 10^оС.

Классы
точности средств измерений.

Исторически по
точности средства измерений подразделяют
на классы. Иногда их называют классами
точности, иногда классами допуска,
иногда просто классами.

Класс точности
средства измерений
– это его характеристика, отражающая
точностные возможности средств измерений
данного типа.

Допускается
буквенное или числовое обозначение
классов точности. Средствам измерений,
предназначенным для измерения двух и
более физических величин, допускается
присваивать различные классы точности
для каждой измеряемой величины. Средствам
измерений с двумя или более переключаемыми
диапазонами измерений также допускается
присваивать два или более класса
точности.

Если нормируется
предел допускаемой абсолютной основной
погрешности, или в различных поддиапазонах
измерений установлены разные значения
пределов допускаемой относительной
основной погрешности, то , как правило,
применяется буквенное обозначение
классов. Так, например платиновые
термометры сопротивления изготовляют
с классом допуска А
или классом
допуска В.
При этом для
класса А
установлен
предел допускаемой абсолютной основной
погрешности
,
а для классаВ
—
,
где– температура измеряемой среды.

Если для средств
измерений того или иного типа нормируется
одно значение предельно-допустимой
приведенной основной погрешности, или
одно значение предельно-допустимой
относительной основной погрешности,
или указываются значения c
и d,
то для обозначения классов точности
используются десятичные числа. В
соответствии с ГОСТом 8.401-80 для обозначения
классов точности допускается применение
следующих чисел:

1∙10ⁿ;
1,5∙10ⁿ;
2∙10ⁿ;
2,5∙10ⁿ;
4∙10ⁿ;
5∙10ⁿ;
6∙10ⁿ,
где n
= 0, -1, -2, и т.д.

Для средств
измерений с преобладающей аддитивной
погрешностью численное значение класса
точности выбирается из указанного ряда
равным предельно-допустимому значению
приведенной основной погрешности,
выраженной в процентах. Для средств
измерений с преобладающей мультипликативной
погрешностью численное значение класса
точности соответствует пределу
допускаемой относительной основной
погрешности также выраженной в процентах.
Для средств измерений с соизмеримыми
аддитивными и мультипликативными
погрешностями числа с
и d
также
выбираются из указанного выше ряда. При
этом класс точности средства измерений
обозначается двумя числами, разделенными
косой чертой, например, 0,05/0,02. В этом
случае с
= 0,05%; d
= 0,02%. Примеры
обозначений классов точности в
документации и на средствах измерений,
а также расчетные формулы для оценки
пределов допускаемой основной погрешности
приведены в Таблице 1.

Правила округления
и записи результата измерений.

Нормирование
пределов допускаемых погрешностей
средств измерений производится указанием
значения погрешностей с одной или двумя
значащими цифрами. По этой причине при
расчете значений погрешностей измерений
также должны быть оставлены только
первые одна или две значащие цифры. Для
округления используются следующие
правила:

Погрешность
результата измерения указывается двумя
значащими цифрами, если первая из них
не более 2, и одной цифрой, если первая
из них 3 и более.
Показание прибора
округляется до того же десятичного
разряда, которым заканчивается
округленное значение абсолютной
погрешности.
Округление
производится в окончательном ответе,
промежуточные вычисления выполняют с
одной – двумя избыточными цифрами.

Пример 1:

— показание прибора
— 5,361 В;

— вычисленное
значение абсолютной погрешности — ±
0,264 В;

— округленное
значение абсолютной погрешности — ±
0,26 В;

— результат измерения
— (5,36 ± 0,26) В.

Таблица
1

Примеры обозначения
классов точности средств измерений и
расчетные

формулы для оценки
пределов допускаемой основной погрешности.

Форма

представления

нормируемой

основной

погрешности

Примеры обозначения

класса
точности

Расчетные формулы для

оценки пределов

допускаемой основной

погрешности

Примечания

документации

На

средствах

измерений

Нормируется

предел допускаемой

абсолютной

основной
погрешности

Варианты:

— класс B;

— класс допуска В;

— класс
точностиВ.

или

Значения a иb

приводятся в

документации

на средство

измерений.

Нормируется

предел допускаемой

приведенной

основной
погрешности

Варианты:

— класс точности 1,5

2,5

— не обозначается.

1,5

гдепредел
измерений.

Для приборов

с равномерной

шкалой и нулевой

отметкой в

начале шкалы

Варианты:

— класс точности 2,5;

— не обозначается

—
предел допускаемой абсолютной
погрешности в мм.

— длина всей шкалы.

Для приборов с

неравномерной

шкалой. Длина шкалы

указывается в

документации.

Нормируется

предел допускаемой

относительной

основной
погрешности

Класс точности
0,5.

0,5

Для средств измерений

с преобладающей

мультипликативной

погрешностью.

Варианты:

— класс точности

0,02/0,01;

-не обозначается.

0,02/0,01

Для средств измерений

с соизмеримыми

аддитивной и

мультипликативной

погрешностью

Пример 2:

— показание прибора
– 35,67 мА;

— вычисленное
значение абсолютной погрешности — ±
0,541 мА;

— округленное
значение абсолютной погрешности — ± 0,5
мА;

— результат измерений
– (35,7 ± 0,5) мА.

Пример 3:

— вычисленное
значение относительной погрешности –
± 1,268 %;

— округленное
значение относительной погрешности –
± 1,3 %.

Пример 4:

— вычисленное
значение относительной погрешности —
± 0,367 %;

— округленное
значение относительной погрешности —
± 0,4 %.

II.2.
Вопросы для самопроверки

Чем вызываются
погрешности измерений?
Перечислите
разновидности погрешностей, возникающих
в процессе измерений?
Какая разница
между абсолютной, относительной и
приведенной погрешностями измерения
и в чем смысл их введения?
Чем отличается
основная погрешность измерения от
дополнительной?
Чем отличается
методическая погрешность измерения
от инструментальной?
Чем отличается
систематическая погрешность измерения
от случайной?
Что понимается
под аддитивной и мультипликативной
оставляющими погрешности?
В каких случаях
целесообразно использовать статистическую
обработку результатов измерений?
Какие статистические
характеристики обработки наиболее
часто используются на практике?
Как оценивается
неисключенная систематическая
погрешность при статистической обработке
результатов измерений?

11. Что характеризует
величина среднеквадратического
отклонения ?

12. В чем заключается
суть понятий «доверительной вероятности»
и «доверительного интервала», используемых
при статистической обработке результатов
измерений?

13. В чем заключается
разность понятий «погрешность измерения»
и

«погрешность
средства измерения»?

В.Д. Гвоздев. Допустимая погрешность измерений: выбор значения

(«Законодательная и прикладная метрология», 2013, №2)

Аннотация

Например:

Рис. Схема измерительного контроля качества отдельного объекта.

Отметим, что значение К=0,2 в ГОСТ 8.051 принято для квалитетов более десятого, для меньших квалитетов К>0,2.

Список литературы

1. Управление качеством продукции» Справочник. — М.: Изд-во стандартов, 1985. – 464 с.

9. ПМГ 92 – 2009 ГСИ. Метрологическая экспертиза проектов нормативных документов. — М.: Стандартинформ, 2011. — 9 с.

13. Р 50-601-19-91 Применение статистических методов регулирования технологических процессов. – М.: ВНИИС, 1997. 32 с.

14. Земельман М.А. Метрологические основы технических измерений. – М.: Изд-во стандартов, 1991. – 228 с.

II.1. Основные сведения и методические указания.

Одним из
основополагающих понятий Метрологии
является понятие погрешности измерений.

Погрешностью
измерения
называют отклонение измеренного

значения физической
величины от её истинного значения.

Погрешность
измерений, в общем случае, может быть
вызвана следующими причинами:

Несовершенством
принципа действия и недостаточным
качеством элементов используемого
средства измерения.
Несовершенством
метода измерений и влиянием используемого
средства измерения на саму измеряемую
величину, зависящим от способа
использования данного средства
измерения.
Субъективными
ошибками экспериментатора.

Классификация
погрешностей

По форме представления
различают понятия абсолютной погрешности
измерений и относительной погрешности
измерений.

Абсолютной
погрешностью
измерений называют разность между

измеренным и
действительным значениями измеряемой

величины:

где ∆ — абсолютная
погрешность,

–измеренное
значение,

–действительное
значение измеряемой величины.

Относительной
погрешностью
называют отношение абсолютной

погрешности к
действительному значению измеряемой
величины:

где δ – относительная
погрешность.

Чаще всего
относительную погрешность определяют
приближенно в процентах от измеренного
значения:

По источникам
происхождения погрешности подразделяют
на следующие виды:

— инструментальные
погрешности;

— методические
погрешности;

— субъективные
погрешности, допущенные экспериментатором
.

Рис.1. Иллюстрация
к определению понятия инструментальной

погрешности.

Здесь: 1 – номинальная
характеристика средства измерений;

2 – реальная
характеристика средства измерений.

Основной
погрешностью
называют погрешность, имеющую место

в случае применения
средства измерений в нормальных условиях

эксплуатации.

Дополнительной
погрешностью
называют погрешность средств

измерений, которая
возникает в условиях, отличающихся от

нормальных, но
входящих в допустимую рабочую область
условий

эксплуатации.

Субъективными
погрешностями
называют погрешности,

допускаемые
самим экспериментатором при проведении

измерений.

По характеру
проявления погрешности измерений
подразделяют на:

— систематические
погрешности;

— случайные
погрешности;

— промахи (грубые
ошибки).

Оценка погрешностей
косвенных измерений.

;

Где:
—
предельные абсолютные погрешности
результатов прямых

измерений;

—
предельная абсолютная погрешность
результата косвенного

измерения;

—
соответствующие предельные относительные
погрешности.

—
функциональная связь между искомой
измеряемой величиной и

величинами,
подвергающимися прямым измерениям.

Статистическая
обработка результатов измерений

Более точно
определить результат измерения путем
усреднения отдельных наблюдений.
Оценить область
неопределенности уточненного результата
измерений.

где: x_i
– результат i
– го измерения;

n
– число проведенных измерений в данной
серии измерений.

После этого
оценивают отклонение результатов
отдельных измерений x_i
от этой оценки среднего значения
;.

Следовательно,
точность результата многократных
измерений увеличивается с ростом числа
последних.

где
— так называемый коэффициент Стьюдента.

Таблица 4.1

Значения
коэффициентов Стьюдента
.

n
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99

2	1,00	1,38	1,96	3,08	6,31	12,71	31,82	63,66
3	0,82	1,06	1,34	1,89	2,92	4,30	6,97	9,93
4	0,77	0,98	1,25	1,64	2,35	3,18	4,54	5,84
5	0,74	0,94	1,19	1,53	2,13	2,78	3,75	4,60
6	0,73	0,92	1,16	1,48	2,02	2,62	3,37	4,03
7	0,72	0,91	1,13	1,44	1,94	2,45	3,14	3,71
8	0,71	0,90	1,12	1,42	1,90	2,37	3,00	3,50
9	0,71	0,89	1,11	1,40	1,86	2,31	2,90	3,36
10	0,70	0,88	1,10	1,38	1,83	2,26	2,82	3,25
16	0,69	0,87	1,07	1,34	1,75	2,13	2,60	2,95
25	0,69	0,86	1,06	1,32	1,71	2,06	2,49	2,80

Нормирование
погрешностей средств измерения.

Нормированием
погрешностей средств измерений называют

процедуру
назначения допустимых границ основной
и

дополнительных
погрешностей, а также выбор формы
указания

этих границ
в нормативно-технической документации.

А) Нормирование
пределов допускаемой основной погрешности
для

средств
измерений с преобладающей аддитивной
погрешностью.

где X_N
– нормирующее значение.

Б) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с преобладающей мультипликативной

погрешностью.

В) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с соизмеримой аддитивной и мультипликативной

погрешностью.

где X_max
– предел измерений;

X
— измеренное значение;

d
=

— значение приведенной к пределу измерений

аддитивной
составляющей основной погрешности;

с =
— значение результирующей относительной

основной
погрешности в точке, соответствующей
пределу

измерений.

При этом абсолютная
основная погрешность определяется по
формуле

Г)
Нормирование дополнительных погрешностей.

Классы
точности средств измерений.

1∙10ⁿ;
1,5∙10ⁿ;
2∙10ⁿ;
2,5∙10ⁿ;
4∙10ⁿ;
5∙10ⁿ;
6∙10ⁿ,
где n
= 0, -1, -2, и т.д.

Правила округления
и записи результата измерений.

Погрешность
результата измерения указывается двумя
значащими цифрами, если первая из них
не более 2, и одной цифрой, если первая
из них 3 и более.
Показание прибора
округляется до того же десятичного
разряда, которым заканчивается
округленное значение абсолютной
погрешности.
Округление
производится в окончательном ответе,
промежуточные вычисления выполняют с
одной – двумя избыточными цифрами.

Пример 1:

— показание прибора
— 5,361 В;

— вычисленное
значение абсолютной погрешности — ±
0,264 В;

— округленное
значение абсолютной погрешности — ±
0,26 В;

— результат измерения
— (5,36 ± 0,26) В.

Таблица
1

Примеры обозначения
классов точности средств измерений и
расчетные

формулы для оценки
пределов допускаемой основной погрешности.

Форма

представления

нормируемой

основной

погрешности

Примеры обозначения

класса
точности

Расчетные формулы для

оценки пределов

допускаемой основной

погрешности

Примечания

документации

На

средствах

измерений

Нормируется

предел допускаемой

абсолютной

основной
погрешности

Варианты:

— класс B;

— класс допуска В;

— класс
точностиВ.

или

Значения a иb

приводятся в

документации

на средство

измерений.

Нормируется

предел допускаемой

приведенной

основной
погрешности

Варианты:

— класс точности 1,5

2,5

— не обозначается.

1,5

гдепредел
измерений.

Для приборов

с равномерной

шкалой и нулевой

отметкой в

начале шкалы

Варианты:

— класс точности 2,5;

— не обозначается

—
предел допускаемой абсолютной
погрешности в мм.

— длина всей шкалы.

Для приборов с

неравномерной

шкалой. Длина шкалы

указывается в

документации.

Нормируется

предел допускаемой

относительной

основной
погрешности

Класс точности
0,5.

0,5

Для средств измерений

с преобладающей

мультипликативной

погрешностью.

Варианты:

— класс точности

0,02/0,01;

-не обозначается.

0,02/0,01

Для средств измерений

с соизмеримыми

аддитивной и

мультипликативной

погрешностью

Пример 2:

— показание прибора
– 35,67 мА;

— вычисленное
значение абсолютной погрешности — ±
0,541 мА;

— округленное
значение абсолютной погрешности — ± 0,5
мА;

— результат измерений
– (35,7 ± 0,5) мА.

Пример 3:

— вычисленное
значение относительной погрешности –
± 1,268 %;

— округленное
значение относительной погрешности –
± 1,3 %.

Пример 4:

— вычисленное
значение относительной погрешности —
± 0,367 %;

— округленное
значение относительной погрешности —
± 0,4 %.

II.2.
Вопросы для самопроверки

Чем вызываются
погрешности измерений?
Перечислите
разновидности погрешностей, возникающих
в процессе измерений?
Какая разница
между абсолютной, относительной и
приведенной погрешностями измерения
и в чем смысл их введения?
Чем отличается
основная погрешность измерения от
дополнительной?
Чем отличается
методическая погрешность измерения
от инструментальной?
Чем отличается
систематическая погрешность измерения
от случайной?
Что понимается
под аддитивной и мультипликативной
оставляющими погрешности?
В каких случаях
целесообразно использовать статистическую
обработку результатов измерений?
Какие статистические
характеристики обработки наиболее
часто используются на практике?
Как оценивается
неисключенная систематическая
погрешность при статистической обработке
результатов измерений?

11. Что характеризует
величина среднеквадратического
отклонения ?

13. В чем заключается
разность понятий «погрешность измерения»
и

«погрешность
средства измерения»?

Статья обновлена 10.07.2022

Что такое погрешность измерения

Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.

Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.

Математическая погрешность: формула для каждого типа

Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?

Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.

Формулы погрешностей вычисляются следующим образом.

Абсолютная погрешность измерений: формула

Формула дает разницу между измеренным и реальным значением.

Формула абсолютной погрешности

Относительная погрешность: формула

Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.

Формула относительной погрешности

Приведенная погрешность: формула

Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Формула приведенной погрешности

Классификация оценочной погрешности

Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.

Классификация оценочной погрешности

Что такое случайная погрешность

Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.

Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.

Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.

Что такое систематическая погрешность

Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.

В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.

Погрешность выборки

Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.

Погрешность структуры

Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.

Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.

Погрешность аудитории

Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.

Погрешность отбора

Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.

Как минимизировать погрешность выборки

Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам.
Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию.
Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.

Погрешность измерения

Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.

К погрешностям измерения приводят следующие виды ошибок.

Ошибка цели

Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.

Предвзятость ответов

Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.

Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.

Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.

Предвзятость интервьюера

Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.

Ошибка обработки

Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.

Ошибка ввода

Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.

Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.

Как минимизировать погрешность измерения

Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью.
Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка.
Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования.
Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.

Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.

Источник

II.1. Основные сведения и методические указания.

Одним из
основополагающих понятий Метрологии
является понятие погрешности измерений.

Погрешностью
измерения
называют отклонение измеренного

значения физической
величины от её истинного значения.

Погрешность
измерений, в общем случае, может быть
вызвана следующими причинами:

Несовершенством
принципа действия и недостаточным
качеством элементов используемого
средства измерения.
Несовершенством
метода измерений и влиянием используемого
средства измерения на саму измеряемую
величину, зависящим от способа
использования данного средства
измерения.
Субъективными
ошибками экспериментатора.

Классификация
погрешностей

По форме представления
различают понятия абсолютной погрешности
измерений и относительной погрешности
измерений.

Абсолютной
погрешностью
измерений называют разность между

измеренным и
действительным значениями измеряемой

величины:

где ∆ — абсолютная
погрешность,

–измеренное
значение,

–действительное
значение измеряемой величины.

Относительной
погрешностью
называют отношение абсолютной

погрешности к
действительному значению измеряемой
величины:

где δ – относительная
погрешность.

Чаще всего
относительную погрешность определяют
приближенно в процентах от измеренного
значения:

По источникам
происхождения погрешности подразделяют
на следующие виды:

— инструментальные
погрешности;

— методические
погрешности;

— субъективные
погрешности, допущенные экспериментатором
.

Рис.1. Иллюстрация
к определению понятия инструментальной

погрешности.

Здесь: 1 – номинальная
характеристика средства измерений;

2 – реальная
характеристика средства измерений.

Основной
погрешностью
называют погрешность, имеющую место

в случае применения
средства измерений в нормальных условиях

эксплуатации.

Дополнительной
погрешностью
называют погрешность средств

измерений, которая
возникает в условиях, отличающихся от

нормальных, но
входящих в допустимую рабочую область
условий

эксплуатации.

Субъективными
погрешностями
называют погрешности,

допускаемые
самим экспериментатором при проведении

измерений.

По характеру
проявления погрешности измерений
подразделяют на:

— систематические
погрешности;

— случайные
погрешности;

— промахи (грубые
ошибки).

Оценка погрешностей
косвенных измерений.

;

Где:
—
предельные абсолютные погрешности
результатов прямых

измерений;

—
предельная абсолютная погрешность
результата косвенного

измерения;

—
соответствующие предельные относительные
погрешности.

—
функциональная связь между искомой
измеряемой величиной и

величинами,
подвергающимися прямым измерениям.

Статистическая
обработка результатов измерений

Более точно
определить результат измерения путем
усреднения отдельных наблюдений.
Оценить область
неопределенности уточненного результата
измерений.

где: x_i
– результат i
– го измерения;

n
– число проведенных измерений в данной
серии измерений.

После этого
оценивают отклонение результатов
отдельных измерений x_i
от этой оценки среднего значения
;.

Следовательно,
точность результата многократных
измерений увеличивается с ростом числа
последних.

где
— так называемый коэффициент Стьюдента.

Таблица 4.1

Значения
коэффициентов Стьюдента
.

n
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99

2	1,00	1,38	1,96	3,08	6,31	12,71	31,82	63,66
3	0,82	1,06	1,34	1,89	2,92	4,30	6,97	9,93
4	0,77	0,98	1,25	1,64	2,35	3,18	4,54	5,84
5	0,74	0,94	1,19	1,53	2,13	2,78	3,75	4,60
6	0,73	0,92	1,16	1,48	2,02	2,62	3,37	4,03
7	0,72	0,91	1,13	1,44	1,94	2,45	3,14	3,71
8	0,71	0,90	1,12	1,42	1,90	2,37	3,00	3,50
9	0,71	0,89	1,11	1,40	1,86	2,31	2,90	3,36
10	0,70	0,88	1,10	1,38	1,83	2,26	2,82	3,25
16	0,69	0,87	1,07	1,34	1,75	2,13	2,60	2,95
25	0,69	0,86	1,06	1,32	1,71	2,06	2,49	2,80

Нормирование
погрешностей средств измерения.

Нормированием
погрешностей средств измерений называют

процедуру
назначения допустимых границ основной
и

дополнительных
погрешностей, а также выбор формы
указания

этих границ
в нормативно-технической документации.

А) Нормирование
пределов допускаемой основной погрешности
для

средств
измерений с преобладающей аддитивной
погрешностью.

где X_N
– нормирующее значение.

Б) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с преобладающей мультипликативной

погрешностью.

В) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с соизмеримой аддитивной и мультипликативной

погрешностью.

где X_max
– предел измерений;

X
— измеренное значение;

d
=

— значение приведенной к пределу измерений

аддитивной
составляющей основной погрешности;

с =
— значение результирующей относительной

основной
погрешности в точке, соответствующей
пределу

измерений.

При этом абсолютная
основная погрешность определяется по
формуле

Г)
Нормирование дополнительных погрешностей.

Классы
точности средств измерений.

1∙10ⁿ;
1,5∙10ⁿ;
2∙10ⁿ;
2,5∙10ⁿ;
4∙10ⁿ;
5∙10ⁿ;
6∙10ⁿ,
где n
= 0, -1, -2, и т.д.

Правила округления
и записи результата измерений.

Погрешность
результата измерения указывается двумя
значащими цифрами, если первая из них
не более 2, и одной цифрой, если первая
из них 3 и более.
Показание прибора
округляется до того же десятичного
разряда, которым заканчивается
округленное значение абсолютной
погрешности.
Округление
производится в окончательном ответе,
промежуточные вычисления выполняют с
одной – двумя избыточными цифрами.

Пример 1:

— показание прибора
— 5,361 В;

— вычисленное
значение абсолютной погрешности — ±
0,264 В;

— округленное
значение абсолютной погрешности — ±
0,26 В;

— результат измерения
— (5,36 ± 0,26) В.

Таблица
1

Примеры обозначения
классов точности средств измерений и
расчетные

формулы для оценки
пределов допускаемой основной погрешности.

Форма

представления

нормируемой

основной

погрешности

Примеры обозначения

класса
точности

Расчетные формулы для

оценки пределов

допускаемой основной

погрешности

Примечания

документации

На

средствах

измерений

Нормируется

предел допускаемой

абсолютной

основной
погрешности

Варианты:

— класс B;

— класс допуска В;

— класс
точностиВ.

или

Значения a иb

приводятся в

документации

на средство

измерений.

Нормируется

предел допускаемой

приведенной

основной
погрешности

Варианты:

— класс точности 1,5

2,5

— не обозначается.

1,5

гдепредел
измерений.

Для приборов

с равномерной

шкалой и нулевой

отметкой в

начале шкалы

Варианты:

— класс точности 2,5;

— не обозначается

—
предел допускаемой абсолютной
погрешности в мм.

— длина всей шкалы.

Для приборов с

неравномерной

шкалой. Длина шкалы

указывается в

документации.

Нормируется

предел допускаемой

относительной

основной
погрешности

Класс точности
0,5.

0,5

Для средств измерений

с преобладающей

мультипликативной

погрешностью.

Варианты:

— класс точности

0,02/0,01;

-не обозначается.

0,02/0,01

Для средств измерений

с соизмеримыми

аддитивной и

мультипликативной

погрешностью

Пример 2:

— показание прибора
– 35,67 мА;

— вычисленное
значение абсолютной погрешности — ±
0,541 мА;

— округленное
значение абсолютной погрешности — ± 0,5
мА;

— результат измерений
– (35,7 ± 0,5) мА.

Пример 3:

— вычисленное
значение относительной погрешности –
± 1,268 %;

— округленное
значение относительной погрешности –
± 1,3 %.

Пример 4:

— вычисленное
значение относительной погрешности —
± 0,367 %;

— округленное
значение относительной погрешности —
± 0,4 %.

II.2.
Вопросы для самопроверки

Чем вызываются
погрешности измерений?
Перечислите
разновидности погрешностей, возникающих
в процессе измерений?
Какая разница
между абсолютной, относительной и
приведенной погрешностями измерения
и в чем смысл их введения?
Чем отличается
основная погрешность измерения от
дополнительной?
Чем отличается
методическая погрешность измерения
от инструментальной?
Чем отличается
систематическая погрешность измерения
от случайной?
Что понимается
под аддитивной и мультипликативной
оставляющими погрешности?
В каких случаях
целесообразно использовать статистическую
обработку результатов измерений?
Какие статистические
характеристики обработки наиболее
часто используются на практике?
Как оценивается
неисключенная систематическая
погрешность при статистической обработке
результатов измерений?

11. Что характеризует
величина среднеквадратического
отклонения ?

13. В чем заключается
разность понятий «погрешность измерения»
и

«погрешность
средства измерения»?

Источник

Выбор того или иного средства измерения для целей приемочного контроля требует обязательной оценки влияния погрешности измерения на результаты контроля. ГОСТ 8.051—73 ограничивает допустимую погрешность измерения 32% от стандартного поля допуска изделия для 2—7-го квалитетов ИСО, 25% — для 8-го квалитета и 20% — для более грубых квалитетов. Это предопределяет возможность больших переходов действительных размеров изделий за границу поля допуска, чем при контроле калибрами, и стимулирует изготовителя [c.635]

Однако в общем случае расчет по (2.28) и (2.29) дает завышенные результаты. Для более обоснованной оценки погрешности результата измерения у формально используют тот же подход, что и при многократных измерениях, при этом средние квадратические погрешности результатов измерения независимых переменных заменяют абсолютными погрешностями (например, приборными). Предельную допустимую погрешность Ау находят по формуле [c.80]

Поэтому для оценки максимально допустимой погрешности косвенных измерений часто используют выражение [c.9]

Принимая обычный для измерений 2—6-кратный запас точности, получим, что допустимая погрешность профильной оценки высоты неровностей [c.85]

Несмотря на то, что область изменения нормально распределенной величины лежит в интервале от —оо до +оо, а большинство реальных величин имеют конечный верхний или нижний предел (иногда и оба), это не мешает использовать нормальное распределение для описания таких случайных величин, у которых среднее отстоит от предела на большое число (более 3—4) квадратических отклонений. Сказанное позволяет считать, что в практике оценки погрешности измерений нормальное распределение должно встречаться, по крайней мере, не реже остальных типов распределения. Учитывая, что многие типы распределений, кривые плотности которых мало отличаются от нормальной, часто допустимо аппроксимировать последней, следует сделать вывод о превалирующем значении нормального распределения в исследованиях, связанных с оценкой погрешности измерений. Ошибка, вследствие неверно принятого допущения о нормальности распределения, будет различной в каждом конкретном случае. Многие статистические методы, разработанные при этом допущении, остаются справедливыми в случае умеренных отклонений от распределения нормального типа. В то же время, если допущение о нормальности распределения ошибочно используется для определения доли попаданий случайной величины выше или ниже некоторого значения, лежащего в области 27 419 [c.419]

Если Ао удовлетворяет неравенству Ао>До , то (3.17)—это вероятность необнаруженного брака, то есть вероятность признать, что погрешность удовлетворяет своей норме в то время, как в действительности она норме не удовлетворяет. Обозначим эту вероятность Р(Ао)1,а»). Наибольшее значение вероятность необнаруженного брака Р(Ло.)л7 принимает при погрешности Ао, выходящей за предел допустимого значения, но возможно более близко к нему, в пределе можно принять при Ао = Ао,. При этом Р(Лй)ьам =0,5. Никаким повышением точности измерений, то есть уменьшением основания функции /(Л ), эту вероятность уменьшить нельзя. Следовательно, вероятность необнаруженного брака л 1Л няется, в зависимости от истинного значения контролируемой погрешности, от нуля до 0,5 (если при контроле оценка контролируемой погрешности сравнивается с пределом Аз.,, ее допустимых значений). [c.155]

Для оценки условий измерения температуры газов экранированными ПТ с отсосом газа служит номограмма (рис. 6.14), которая позволяет выбрать скорости отсасываемого газа, при которых погрешность измерения не будет превышать допустимого значения, а также соответствующий вид защиты ПТ от лучеиспускания. [c.168]

Для исключения возможных недоразумений и конфликтов на производстве при оценке качества изделий по размерам в ГОСТ 7713—62 действительный размер изделия определяется как размер, полученный в результате измерения с допустимой погрешностью. Поэтому знание при измерениях пределов возможных погрешностей позволяет определить достоверность результатов измерений. [c.63]

Существуют два метода оценки погрешностей измерительной системы. В первом методе производится оценка пределов погрешностей измерительной системы по пределам допускаемых основных и дополнительных погрешностей средств измерений, входящих в систему, определяемым их классом точности, т. е. фактически производится оценка погрешности сверху, определяется максимальное значение погрешности системы. Эта допустимая погрешность измерительной системы оценивается как корень квадратный из суммы квадратов пределов допустимых значений погрешностей [4] [c.14]

Одним из важных вопросов, касающихся измерительной аппаратуры дефектоскопов, является достаточность получаемой информации для оценки параметров дефектов сплошности с заданной точностью при имеющейся погрешности измерений. Разработана методика, позволяющая определить количество информации, получаемой внутритрубным дефектоскопом, и оценить максимально допустимую точность определения параметров дефекта сплошности. Это позволяет не только реально оценивать границы возможностей данного типа дефектоскопа в лабораторных условиях, но и выявлять «узкие» места в измерительной аппаратуре. Постановка обоснованных требований к качеству измерений приводит к значительной экономии средств при разработке дефектоскопической аппаратуры. Например, в вопросе применения других типов датчиков магнитного поля оказалось, что в определенных условиях они не дают дополнительной информации и лишь дублируют сигналы с имеющихся преобразователей поля, что позволило отказаться от применения такого технического решения. [c.228]

Основная трудность здесь заключается в том, что интегрирование в формулах должно производиться по всей области, где п—1) и у, отличны от нуля, тогда как реальные измерения проводятся в весьма ограниченном спектральном интервале, обычно не включающем, например, мощные полосы поглощения в дальнем ультрафиолете (Я,<2000 А). Поэтому основная проблема здесь заключается в разумной экстраполяции данных за пределы, в которых проведены измерения, в том интервале частот, где отражение существенно зависит от частоты, и в корректном учете возникающих отсюда погрешностей и внесении соответствующих поправок. Весьма важно при этом иметь хотя бы качественное представление об общем виде спектра или грубо приближенные измерения поглощения в широком интервале. В литературе рассмотрены процедуры экстраполяции, оценка погрешностей и допустимости экстраполяции, методы подбора оптимальных пределов интегрирования [178— 180], а также возможности выбора дискретных опорных точек [181]. По-видимому, в ряде случаев можно практически добиться точности 0,5—1%. Наиболее приемлема, видимо, экстраполяция, использующая определенные предположения об асимптотическом поведении коэффициента отражения (см. [182, а также 183]). [c.290]

Точечные оценки недостаточно полно характеризует результаты измерений из-за их естественного рассеяния. В каждой конкретной серии измерений значение оценки в той или иной степени отличается от полученных ранее и от истинного значения параметра. Поэтому необходимо знание величины погрешности, с которой оценен параметр, или, как говорят, получить интервальную оценку параметра. Ее обычно характеризуют доверительным интервалом для заданной вероятности у попадания предлагаемой оценки в этот интервал. Величину у выбирают, исходя из допустимой вероятности а того, что истинное значение измеряемой величины окажется вне указанного интервала. [c.222]

Так, для рассмотренного выше примера погрешность измерения размера штангенциркулем составит Д = 62,30 — 62,25 = 0,05 мм, если за истинный рамер взять действительный размер, полученный измерением микрометром, и А = 62,3 — 62,254 = 0,046 мм, если действительный размер будет получен измерением на вертикальном длинномере. Ошибка в определении погрешности измерения в первом случае по сравнению со вторым составит 0,004 мм, т. е. 8%.Экспериментатор обычно легко решает вопрос о том, что достаточна ли точность определения погрешности измерения для поставленной цели эксперимента. В большинстве случаев 10%-ная погрешность в оценке самой погрешности считается вполне допустимой. Погрешность измерения указанного размера микрометром составит Л = 62,250 — 62,254 = —0,004 мм при сравнении с действительным значением, определенным на длиномере. [c.36]

При назначении допусков часто исходят из табличных значений возможных зазоров или натягов в соединении, которые могут получиться при сочетании предельных размеров сопрягаемых компонентов. В этих случаях об—наруживаются противоречия, одним из разительных примеров которых может явиться тугая посадка, превращающаяся в подвижную посадку при сочетании наибольшего предельного размера отверстия с наименьшим предельным размером вала. Практическая оценка таких противоречий возможна только путём применения основных принципов теории вероятностей в области взаимозаменяемости. Этот метод, базирующийся на определении параметров рассеивания размеров сопрягаемых компонентов и на учёте вероятности различных значений зазоров и натягов, щироко применяется при разрешении всех вопросов, относящихся к взаимозаменяемости. С помощью этого же метода разрешается вопрос о допустимой погрешности отдельных звеньев механизма в зависимости от заданной, предельной погрешности всего механизма, о вероятностях различных значений зазоров и натягов в соединении, о вероятностях случаев нарушения взаимозаменяемости в зависимости от увеличения допусков отдельных компонентов, о вероятностях получения брака при выбранном технологическом процессе, о влиянии погрешностей измерений на отклонения размеров контролируемых объектов и т. д. [c.2]

Погрешностью измерения называют обычно алгебраическую разность между значением, полученцьш при измерении, и действительным (истинным) значением измеряемой величины. Погрешности устройств информации могут быть выражены в абсолютных, относительных (по отношению к измеряемой величине) единицах, а также в форме приведенной погрешности. Последней называют отношение абсолютной погрешности к нормирующему значению — обычно к разности между верхним и нижним пределами измерения устройства информации. Критерием оценки качества устройства информации служит допускаемая (допустимая) погрешность, соответствующая в большинстве случаев доверительной вероятности в 95% и более (см. теорию вероятностен)- [c.210]

Стенды для испытания агрегатов и Деталей на усталостнук) прочность должны обеспечивать достаточную точность измерения задаваемой нагрузки согласно ГОСТ 2860—65 погрешность не должна превышать 3% заданного напряжения, а следовательно, и нагрузки. Такая высокая точность измерения необходима потому, что число циклов нагружения до разрушения детали связано с нагрузкой Qj, вызывающей это разрушение, степенной зависимостью = onst. Таким образом, небольшая ошибка в регистрации нагрузки при последовательном испытании нескольких деталей может привести к большом.у разбросу результатов по числу циклов, что затрудняет количественную оценку долговечности детали. Чтобы выдержать заданную точность при измерении нагрузки, надо применять приборы с допустимой погрешностью до 1,5%. [c.159]

Все это позволяет подойти к контролю таких МХ несколько упрошенно, без использования показателей достоверности контроля. Контроль заключается по-прежнему в оценивании МХ и сравнении полученной оценки с нормой. Но результат контроля может считаться заслуживающим доверия, если погрешность оценивания МХ не превышает наибольшего допустимого значения, которое может быть установлено разработчиком средств измерений вне связи с показателями достоверности контроля. Следовательно, методики контроля МХ второй группы могут разрабатываться на основе только заданной наибольшей допустимой погрешности оценивания при контроле. Сложившаяся практика контроля МХ второй группы полностью соответствует данной схеме, и нет оснований считать ее неудовлетворительной. [c.150]

При оценке скорости коррозии методом измерения содержания водорода в паре используются водородомеры различных конструкций. До поступления в датчик водороломера анализируемая проба должна быть сконденсирована и охлаждена до температуры 20 2 С. Прибор позволяет измерять содержание молекулярного водорода от о до 20 мкг/кг с погрешностью 5%. Допустимый объем отбираемой пробы составляет 30 5 л/ч. Датчик представляет собой устройство, в котором смонтированы газовая система, измерительная ячейка, электролизеры, преобразователь сигнала в унифицированный сигнал, а также источник питания. Пробоотборный тракт из нержавеющей стали должен быть полностью герметичным. Измерительная ячейка изготовляется из коррозионно-стойких и газонепроницаемых материалов. Водомеры устанавливаются на входе, выходе из котла и по тракту котла. [c.21]

Интервал времени, у которого началом отсчета является пуск после планово-предупредительного ремонта, а окончанием — наработка, при которой вероятность безотказной работы достигает 0,85 при относительной погрешности, не превышающей 5%, можно считать ресурсом между смежными планово-предупредительн1ши ремонтами. Из этого не следует, что при P[t) 0,8 0,05 нужна замена тех однотипных деталей, часть из которых повредилась и явилась причиной отказа. При этом во избежание перебраковки должна быть проведена тщательная диагностика. Ресурс, определенный статистико-вероятностным методом, не является предельным. Предельный ресурс определяется на основании прямых измерений, выполняющихся с помощью различных измерительных инструментов и приборов. Возможно несколько подходов к оценке предельного состояния. Однако план решения этой задачи при всех подходах однозначен. На первом этапе определяются даты проведения диагностики, связанной с признаками старения. Это могут быть длительные наработки времени, близкие к назначенному сроку службы котлов остаточная деформация, близкая к предельно допустимой или превышающая ее появление отдулин, свищей и других аномалий, присущих либо длительным наработкам, либо резко отрицательным событиям (упус-кам воды, резким выбегам температуры выше 480 С, пускам с нарушением условий нормального разогрева деталей, превышениям давления выше допустимых по НТД значений, пропариваниям, видимым растрескиваниям металла и др.). [c.170]

Свойства средств измерений (СИ) определяются их метрологическими и эксплуатационными характеристиками (см. гл. VI, раздел 2). Первые позволяют установить связь между показаниями (выходным сигналом) средства измерений и измеряемой зеличиной и содержат исходные данные для вычисления оценки погрешности результата измерений. Вторые определяют область применения средства измерений как диапазоны допустимых значений измеряемой величины и влияющих величин, в том числе изменений неинформативных параметров входного сигнала. [c.301]

Перечисленные особенности операций оценивания (то есть фактически, измерения) МХ средств измерений важны с точки зрения установления требований к этим операциям. Итак, оценивание МХ — это есть ее измерение, то есть экспериментальное получение значения конкретной МХ отдельного экземпляра средства измерений в определенной точке его диапазона измерений. Оценки МХ— это результаты оценивания (измерения), сопровождающиеся погрешностями оценивания (измерения), отражающими степень близости оценок к истинным значениям оцениваемых МХ. Отсюда вытекает основное метрологическое требование к методикам оценивания МХ (как к любым МВИ) характеристика погрешностн оценивания, то есть погрешности любого результата оценивания (оценки), полученного по данной методике в заданных условиях, не должна превышать наперед заданного наибольшего допустимого значения. Характеристики погрешности оценивания могут быть характеристиками погрешностей прямых измерений или характеристиками погрешностей косвенных измерений. [c.142]

Ао = Ао + Ак, определяются функциями /(«Ак ), построенными вокруг истинных значений коитролируемых погрешностей, т. е. вокруг точек I, 2 и 5. Из рис. 3.1 ясно, что при двух значениях контролируемой погрешности — в точках 1 и 2 — контроль будет безошибочным. В точке 1 результат контроля всегда будет положительным, и погрешность Ао в этой точке действительно соответствует норме. В точке 2 результат контроля всегда будет отрицательным, и погрешность Ао в этой точке действительно превышает наибольшее допустимое значение Ао/, Лишь в точке 3, лежащей за пределом допустимых значений, но близко к нему, оценка ногрешности может и.меть значение, меньшее доп -хтимого предела. Это значит, что при истинном значении погрешности, соответствующем точке 3, то есть при погрешности, выходящей за допустимые пределы, опенка погрешности может показать, что средство измерений в данной точке диапазона измерений исправно. При этом имеет. место необнаруженный брак, вероятность его не равна нулю. Что касается точки 2 на рис. 3.1, то при истинном значении погрешности, соответствующем этой точке, вероятность необнаруженного брака равна нулю. Дальнейшее изложение задачи о достоверности контроля погрешности основано на [71]. [c.154]

РСД — числовые значения физических констант или свойств материатов и веществ, полученные на основе оценки погрешности результатов их определения (измерений, испытаний, расчетов), аттестованные и утвержденные ВНИЦСМВ. Допустимое значение погрешности РСД должно удовлетворять за-дача.м, для решения которых рекомендуются данные с учетом требований государственной системы обеспечения единства измерений. [c.61]

Свободная энергия образования. В табл. 3.11 и на рис. 3.16 приведены значения S.F, полученные в разных работах для U , U g и U2 3. В приведенных значениях наблюдается значительное расхождение, превышающее в отдельных интервалах температур допустимые пределы. В случае юпределения AF из измерений давления пара по третьему закону термодинамики при 2000° К погрешность в общем случае достигает 13 кдж/моль. Ошибки в оценках энтропии повышают погрешность в оценке энтальпии до 20 кдж/моль. При использовании второго закона термодинамики погрешность определения свободной энергии образования связана главным образом с ошибками измерения температуры она увеличивается по мере сужения исследуемой области температур. Практически погрешность может составлять 20—40 кдж/моль [116]. Расчетные уравнения Кубашевского и Эванса 161] и значения, согласованные на Венском симпозиуме по термодинамике 17], базирующиеся не на очень точных калориметрических данных, также не могут быть признаны правильными. [c.187]

Источник

Concept[edit]

Standard deviation and standard error[edit]

Maximum margin of error at different confidence levels[edit]

Specific margins of error[edit]

Comparing percentages[edit]

Effect of finite population size[edit]

See also[edit]

References[edit]

Sources[edit]

External links[edit]

II.1. Основные сведения и методические указания.

II.1. Основные сведения и методические указания.

Что такое погрешность измерения

Математическая погрешность: формула для каждого типа

Абсолютная погрешность измерений: формула

Относительная погрешность: формула

Приведенная погрешность: формула

Классификация оценочной погрешности

Что такое случайная погрешность

Что такое систематическая погрешность

Погрешность выборки

Как минимизировать погрешность выборки

Погрешность измерения

Как минимизировать погрешность измерения

II.1. Основные сведения и методические указания.

Интересное по теме: