About Error Function Calculator
The Error Function Calculator is used to calculate the error function of a given number.
Error Function
In mathematics, the error function is a special function (non-elementary) of sigmoid shape, which occurs in probability, statistics and partial differential equations. It is also called the Gauss error function or probability integral.
The error function is defined as:
Error Function Table
The following is the error function and complementary error function table that shows the values of erf(x) and erfc(x) for x ranging from 0 to 3.5 with an increment of 0.01.
| x | erf(x) | erfc(x) |
|---|---|---|
| 0.0 | 0.0 | 1.0 |
| 0.01 | 0.011283416 | 0.988716584 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.03 | 0.033841222 | 0.966158778 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.05 | 0.056371978 | 0.943628022 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.07 | 0.07885772 | 0.92114228 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.09 | 0.101280594 | 0.898719406 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.11 | 0.123622896 | 0.876377104 |
| 0.12 | 0.134758352 | 0.865241648 |
| 0.13 | 0.145867115 | 0.854132885 |
| 0.14 | 0.156947033 | 0.843052967 |
| 0.15 | 0.167995971 | 0.832004029 |
| 0.16 | 0.179011813 | 0.820988187 |
| 0.17 | 0.189992461 | 0.810007539 |
| 0.18 | 0.200935839 | 0.799064161 |
| 0.19 | 0.211839892 | 0.788160108 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.21 | 0.233521923 | 0.766478077 |
| 0.22 | 0.244295912 | 0.755704088 |
| 0.23 | 0.2550226 | 0.7449774 |
| 0.24 | 0.265700059 | 0.734299941 |
| 0.25 | 0.27632639 | 0.72367361 |
| 0.26 | 0.286899723 | 0.713100277 |
| 0.27 | 0.297418219 | 0.702581781 |
| 0.28 | 0.307880068 | 0.692119932 |
| 0.29 | 0.318283496 | 0.681716504 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.31 | 0.33890815 | 0.66109185 |
| 0.32 | 0.349125995 | 0.650874005 |
| 0.33 | 0.359278655 | 0.640721345 |
| 0.34 | 0.369364529 | 0.630635471 |
| 0.35 | 0.379382054 | 0.620617946 |
| 0.36 | 0.389329701 | 0.610670299 |
| 0.37 | 0.399205984 | 0.600794016 |
| 0.38 | 0.409009453 | 0.590990547 |
| 0.39 | 0.4187387 | 0.5812613 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.41 | 0.43796909 | 0.56203091 |
| 0.42 | 0.447467618 | 0.552532382 |
| 0.43 | 0.456886695 | 0.543113305 |
| 0.44 | 0.466225115 | 0.533774885 |
| 0.45 | 0.47548172 | 0.52451828 |
| 0.46 | 0.48465539 | 0.51534461 |
| 0.47 | 0.493745051 | 0.506254949 |
| 0.48 | 0.502749671 | 0.497250329 |
| 0.49 | 0.511668261 | 0.488331739 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.51 | 0.52924362 | 0.47075638 |
| 0.52 | 0.53789863 | 0.46210137 |
| 0.53 | 0.546464097 | 0.453535903 |
| 0.54 | 0.55493925 | 0.44506075 |
| 0.55 | 0.563323366 | 0.436676634 |
| 0.56 | 0.571615764 | 0.428384236 |
| 0.57 | 0.579815806 | 0.420184194 |
| 0.58 | 0.5879229 | 0.4120771 |
| 0.59 | 0.595936497 | 0.404063503 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.61 | 0.611681219 | 0.388318781 |
| 0.62 | 0.619411462 | 0.380588538 |
| 0.63 | 0.627046443 | 0.372953557 |
| 0.64 | 0.634585829 | 0.365414171 |
| 0.65 | 0.642029327 | 0.357970673 |
| 0.66 | 0.649376688 | 0.350623312 |
| 0.67 | 0.656627702 | 0.343372298 |
| 0.68 | 0.663782203 | 0.336217797 |
| 0.69 | 0.670840062 | 0.329159938 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.71 | 0.68466555 | 0.31533445 |
| 0.72 | 0.691433123 | 0.308566877 |
| 0.73 | 0.698103943 | 0.301896057 |
| 0.74 | 0.704678078 | 0.295321922 |
| 0.75 | 0.711155634 | 0.288844366 |
| 0.76 | 0.717536753 | 0.282463247 |
| 0.77 | 0.723821614 | 0.276178386 |
| 0.78 | 0.730010431 | 0.269989569 |
| 0.79 | 0.736103454 | 0.263896546 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.81 | 0.748003281 | 0.251996719 |
| 0.82 | 0.753810751 | 0.246189249 |
| 0.83 | 0.759523757 | 0.240476243 |
| 0.84 | 0.765142711 | 0.234857289 |
| 0.85 | 0.770668058 | 0.229331942 |
| 0.86 | 0.776100268 | 0.223899732 |
| 0.87 | 0.781439845 | 0.218560155 |
| 0.88 | 0.786687319 | 0.213312681 |
| 0.89 | 0.791843247 | 0.208156753 |
| 0.9 | 0.796908212 | 0.203091788 |
| 0.91 | 0.801882826 | 0.198117174 |
| 0.92 | 0.806767722 | 0.193232278 |
| 0.93 | 0.811563559 | 0.188436441 |
| 0.94 | 0.816271019 | 0.183728981 |
| 0.95 | 0.820890807 | 0.179109193 |
| 0.96 | 0.82542365 | 0.17457635 |
| 0.97 | 0.829870293 | 0.170129707 |
| 0.98 | 0.834231504 | 0.165768496 |
| 0.99 | 0.83850807 | 0.16149193 |
| 1.0 | 0.842700793 | 0.157299207 |
| 1.01 | 0.846810496 | 0.153189504 |
| 1.02 | 0.850838018 | 0.149161982 |
| 1.03 | 0.854784211 | 0.145215789 |
| 1.04 | 0.858649947 | 0.141350053 |
| 1.05 | 0.862436106 | 0.137563894 |
| 1.06 | 0.866143587 | 0.133856413 |
| 1.07 | 0.869773297 | 0.130226703 |
| 1.08 | 0.873326158 | 0.126673842 |
| 1.09 | 0.876803102 | 0.123196898 |
| 1.1 | 0.88020507 | 0.11979493 |
| 1.11 | 0.883533012 | 0.116466988 |
| 1.12 | 0.88678789 | 0.11321211 |
| 1.13 | 0.88997067 | 0.11002933 |
| 1.14 | 0.893082328 | 0.106917672 |
| 1.15 | 0.896123843 | 0.103876157 |
| 1.16 | 0.899096203 | 0.100903797 |
| 1.17 | 0.902000399 | 0.097999601 |
| 1.18 | 0.904837427 | 0.095162573 |
| 1.19 | 0.907608286 | 0.092391714 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.21 | 0.912955508 | 0.087044492 |
| 1.22 | 0.915533881 | 0.084466119 |
| 1.23 | 0.918050104 | 0.081949896 |
| 1.24 | 0.920505184 | 0.079494816 |
| 1.25 | 0.922900128 | 0.077099872 |
| 1.26 | 0.925235942 | 0.074764058 |
| 1.27 | 0.927513629 | 0.072486371 |
| 1.28 | 0.929734193 | 0.070265807 |
| 1.29 | 0.931898633 | 0.068101367 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.31 | 0.936063123 | 0.063936877 |
| 1.32 | 0.938065155 | 0.061934845 |
| 1.33 | 0.940015026 | 0.059984974 |
| 1.34 | 0.941913715 | 0.058086285 |
| 1.35 | 0.943762196 | 0.056237804 |
| 1.36 | 0.945561437 | 0.054438563 |
| 1.37 | 0.947312398 | 0.052687602 |
| 1.38 | 0.949016035 | 0.050983965 |
| 1.39 | 0.950673296 | 0.049326704 |
| 1.4 | 0.95228512 | 0.04771488 |
| 1.41 | 0.953852439 | 0.046147561 |
| 1.42 | 0.955376179 | 0.044623821 |
| 1.43 | 0.956857253 | 0.043142747 |
| 1.44 | 0.95829657 | 0.04170343 |
| 1.45 | 0.959695026 | 0.040304974 |
| 1.46 | 0.96105351 | 0.03894649 |
| 1.47 | 0.9623729 | 0.0376271 |
| 1.48 | 0.963654065 | 0.036345935 |
| 1.49 | 0.964897865 | 0.035102135 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.51 | 0.967276748 | 0.032723252 |
| 1.52 | 0.968413497 | 0.031586503 |
| 1.53 | 0.969516209 | 0.030483791 |
| 1.54 | 0.97058569 | 0.02941431 |
| 1.55 | 0.971622733 | 0.028377267 |
| 1.56 | 0.972628122 | 0.027371878 |
| 1.57 | 0.973602627 | 0.026397373 |
| 1.58 | 0.974547009 | 0.025452991 |
| 1.59 | 0.975462016 | 0.024537984 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.61 | 0.977206837 | 0.022793163 |
| 1.62 | 0.978038088 | 0.021961912 |
| 1.63 | 0.97884284 | 0.02115716 |
| 1.64 | 0.97962178 | 0.02037822 |
| 1.65 | 0.980375585 | 0.019624415 |
| 1.66 | 0.981104921 | 0.018895079 |
| 1.67 | 0.981810442 | 0.018189558 |
| 1.68 | 0.982492787 | 0.017507213 |
| 1.69 | 0.983152587 | 0.016847413 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.71 | 0.984407008 | 0.015592992 |
| 1.72 | 0.985002827 | 0.014997173 |
| 1.73 | 0.9855785 | 0.0144215 |
| 1.74 | 0.986134595 | 0.013865405 |
| 1.75 | 0.986671671 | 0.013328329 |
| 1.76 | 0.987190275 | 0.012809725 |
| 1.77 | 0.987690942 | 0.012309058 |
| 1.78 | 0.988174196 | 0.011825804 |
| 1.79 | 0.988640549 | 0.011359451 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.81 | 0.989524545 | 0.010475455 |
| 1.82 | 0.989943156 | 0.010056844 |
| 1.83 | 0.990346805 | 0.009653195 |
| 1.84 | 0.990735948 | 0.009264052 |
| 1.85 | 0.99111103 | 0.00888897 |
| 1.86 | 0.991472488 | 0.008527512 |
| 1.87 | 0.991820748 | 0.008179252 |
| 1.88 | 0.992156223 | 0.007843777 |
| 1.89 | 0.992479318 | 0.007520682 |
| 1.9 | 0.992790429 | 0.007209571 |
| 1.91 | 0.99308994 | 0.00691006 |
| 1.92 | 0.993378225 | 0.006621775 |
| 1.93 | 0.99365565 | 0.00634435 |
| 1.94 | 0.993922571 | 0.006077429 |
| 1.95 | 0.994179334 | 0.005820666 |
| 1.96 | 0.994426275 | 0.005573725 |
| 1.97 | 0.994663725 | 0.005336275 |
| 1.98 | 0.994892 | 0.005108 |
| 1.99 | 0.995111413 | 0.004888587 |
| 2.0 | 0.995322265 | 0.004677735 |
| 2.01 | 0.995524849 | 0.004475151 |
| 2.02 | 0.995719451 | 0.004280549 |
| 2.03 | 0.995906348 | 0.004093652 |
| 2.04 | 0.99608581 | 0.00391419 |
| 2.05 | 0.996258096 | 0.003741904 |
| 2.06 | 0.996423462 | 0.003576538 |
| 2.07 | 0.996582153 | 0.003417847 |
| 2.08 | 0.996734409 | 0.003265591 |
| 2.09 | 0.996880461 | 0.003119539 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.11 | 0.997154845 | 0.002845155 |
| 2.12 | 0.997283607 | 0.002716393 |
| 2.13 | 0.997407023 | 0.002592977 |
| 2.14 | 0.997525293 | 0.002474707 |
| 2.15 | 0.997638607 | 0.002361393 |
| 2.16 | 0.997747152 | 0.002252848 |
| 2.17 | 0.997851108 | 0.002148892 |
| 2.18 | 0.997950649 | 0.002049351 |
| 2.19 | 0.998045943 | 0.001954057 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.21 | 0.998224438 | 0.001775562 |
| 2.22 | 0.998307948 | 0.001692052 |
| 2.23 | 0.998387832 | 0.001612168 |
| 2.24 | 0.998464231 | 0.001535769 |
| 2.25 | 0.998537283 | 0.001462717 |
| 2.26 | 0.998607121 | 0.001392879 |
| 2.27 | 0.998673872 | 0.001326128 |
| 2.28 | 0.998737661 | 0.001262339 |
| 2.29 | 0.998798606 | 0.001201394 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.31 | 0.998912423 | 0.001087577 |
| 2.32 | 0.998965513 | 0.001034487 |
| 2.33 | 0.999016195 | 0.000983805 |
| 2.34 | 0.99906457 | 0.00093543 |
| 2.35 | 0.999110733 | 0.000889267 |
| 2.36 | 0.999154777 | 0.000845223 |
| 2.37 | 0.99919679 | 0.00080321 |
| 2.38 | 0.999236858 | 0.000763142 |
| 2.39 | 0.999275064 | 0.000724936 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.41 | 0.999346202 | 0.000653798 |
| 2.42 | 0.999379283 | 0.000620717 |
| 2.43 | 0.999410802 | 0.000589198 |
| 2.44 | 0.999440826 | 0.000559174 |
| 2.45 | 0.99946942 | 0.00053058 |
| 2.46 | 0.999496646 | 0.000503354 |
| 2.47 | 0.999522566 | 0.000477434 |
| 2.48 | 0.999547236 | 0.000452764 |
| 2.49 | 0.999570712 | 0.000429288 |
| 2.5 | 0.999593048 | 0.000406952 |
| 2.51 | 0.999614295 | 0.000385705 |
| 2.52 | 0.999634501 | 0.000365499 |
| 2.53 | 0.999653714 | 0.000346286 |
| 2.54 | 0.999671979 | 0.000328021 |
| 2.55 | 0.99968934 | 0.00031066 |
| 2.56 | 0.999705837 | 0.000294163 |
| 2.57 | 0.999721511 | 0.000278489 |
| 2.58 | 0.9997364 | 0.0002636 |
| 2.59 | 0.999750539 | 0.000249461 |
| 2.6 | 0.999763966 | 0.000236034 |
| 2.61 | 0.999776711 | 0.000223289 |
| 2.62 | 0.999788809 | 0.000211191 |
| 2.63 | 0.999800289 | 0.000199711 |
| 2.64 | 0.999811181 | 0.000188819 |
| 2.65 | 0.999821512 | 0.000178488 |
| 2.66 | 0.999831311 | 0.000168689 |
| 2.67 | 0.999840601 | 0.000159399 |
| 2.68 | 0.999849409 | 0.000150591 |
| 2.69 | 0.999857757 | 0.000142243 |
| 2.7 | 0.999865667 | 0.000134333 |
| 2.71 | 0.999873162 | 0.000126838 |
| 2.72 | 0.999880261 | 0.000119739 |
| 2.73 | 0.999886985 | 0.000113015 |
| 2.74 | 0.999893351 | 0.000106649 |
| 2.75 | 0.999899378 | 0.000100622 |
| 2.76 | 0.999905082 | 9.4918e-05 |
| 2.77 | 0.99991048 | 8.952e-05 |
| 2.78 | 0.999915587 | 8.4413e-05 |
| 2.79 | 0.999920418 | 7.9582e-05 |
| 2.8 | 0.999924987 | 7.5013e-05 |
| 2.81 | 0.999929307 | 7.0693e-05 |
| 2.82 | 0.99993339 | 6.661e-05 |
| 2.83 | 0.99993725 | 6.275e-05 |
| 2.84 | 0.999940898 | 5.9102e-05 |
| 2.85 | 0.999944344 | 5.5656e-05 |
| 2.86 | 0.999947599 | 5.2401e-05 |
| 2.87 | 0.999950673 | 4.9327e-05 |
| 2.88 | 0.999953576 | 4.6424e-05 |
| 2.89 | 0.999956316 | 4.3684e-05 |
| 2.9 | 0.999958902 | 4.1098e-05 |
| 2.91 | 0.999961343 | 3.8657e-05 |
| 2.92 | 0.999963645 | 3.6355e-05 |
| 2.93 | 0.999965817 | 3.4183e-05 |
| 2.94 | 0.999967866 | 3.2134e-05 |
| 2.95 | 0.999969797 | 3.0203e-05 |
| 2.96 | 0.999971618 | 2.8382e-05 |
| 2.97 | 0.999973334 | 2.6666e-05 |
| 2.98 | 0.999974951 | 2.5049e-05 |
| 2.99 | 0.999976474 | 2.3526e-05 |
| 3.0 | 0.99997791 | 2.209e-05 |
| 3.01 | 0.999979261 | 2.0739e-05 |
| 3.02 | 0.999980534 | 1.9466e-05 |
| 3.03 | 0.999981732 | 1.8268e-05 |
| 3.04 | 0.999982859 | 1.7141e-05 |
| 3.05 | 0.99998392 | 1.608e-05 |
| 3.06 | 0.999984918 | 1.5082e-05 |
| 3.07 | 0.999985857 | 1.4143e-05 |
| 3.08 | 0.99998674 | 1.326e-05 |
| 3.09 | 0.999987571 | 1.2429e-05 |
| 3.1 | 0.999988351 | 1.1649e-05 |
| 3.11 | 0.999989085 | 1.0915e-05 |
| 3.12 | 0.999989774 | 1.0226e-05 |
| 3.13 | 0.999990422 | 9.578e-06 |
| 3.14 | 0.99999103 | 8.97e-06 |
| 3.15 | 0.999991602 | 8.398e-06 |
| 3.16 | 0.999992138 | 7.862e-06 |
| 3.17 | 0.999992642 | 7.358e-06 |
| 3.18 | 0.999993115 | 6.885e-06 |
| 3.19 | 0.999993558 | 6.442e-06 |
| 3.2 | 0.999993974 | 6.026e-06 |
| 3.21 | 0.999994365 | 5.635e-06 |
| 3.22 | 0.999994731 | 5.269e-06 |
| 3.23 | 0.999995074 | 4.926e-06 |
| 3.24 | 0.999995396 | 4.604e-06 |
| 3.25 | 0.999995697 | 4.303e-06 |
| 3.26 | 0.99999598 | 4.02e-06 |
| 3.27 | 0.999996245 | 3.755e-06 |
| 3.28 | 0.999996493 | 3.507e-06 |
| 3.29 | 0.999996725 | 3.275e-06 |
| 3.3 | 0.999996942 | 3.058e-06 |
| 3.31 | 0.999997146 | 2.854e-06 |
| 3.32 | 0.999997336 | 2.664e-06 |
| 3.33 | 0.999997515 | 2.485e-06 |
| 3.34 | 0.999997681 | 2.319e-06 |
| 3.35 | 0.999997838 | 2.162e-06 |
| 3.36 | 0.999997983 | 2.017e-06 |
| 3.37 | 0.99999812 | 1.88e-06 |
| 3.38 | 0.999998247 | 1.753e-06 |
| 3.39 | 0.999998367 | 1.633e-06 |
| 3.4 | 0.999998478 | 1.522e-06 |
| 3.41 | 0.999998582 | 1.418e-06 |
| 3.42 | 0.999998679 | 1.321e-06 |
| 3.43 | 0.99999877 | 1.23e-06 |
| 3.44 | 0.999998855 | 1.145e-06 |
| 3.45 | 0.999998934 | 1.066e-06 |
| 3.46 | 0.999999008 | 9.92e-07 |
| 3.47 | 0.999999077 | 9.23e-07 |
| 3.48 | 0.999999141 | 8.59e-07 |
| 3.49 | 0.999999201 | 7.99e-07 |
| 3.5 | 0.999999257 | 7.43e-07 |
See also:
-
Complementary Error Function Calculator
-
Beta Function Calculator
-
Gamma Function Calculator
-
Standard Error Calculator (High Precision)
-
Percentage Error Calculator
-
Proportion Calculator
Frequently Used Miniwebtools:
-
Random Name Picker
-
High-Precision Summation (Sum) Calculator
-
Percent Off Calculator
-
Small Text Generator ⁽ᶜᵒᵖʸ ⁿ ᵖᵃˢᵗᵉ⁾
-
Amortization Calculator
-
Sort Number
-
Ovulation Calendar
-
Average Calculator (High Precision)
-
Cat Years to Human Years Calculator
-
MAC Address Generator
-
ERA Calculator
-
Cm to Feet and Inches Converter
-
Feet and Inches to Cm Converter
-
PVIF Calculator (High Precision)
-
Half Life Calculator
-
Roman Numerals Converter
-
Slugging Percentage Calculator
-
First n Digits of Pi
-
Mean Absolute Deviation Calculator
-
KPa to Psi Converter
-
Cube Root Calculator
-
Psi to KPa Converter
-
Area of a Trapezoid Calculator
-
Surface Area of a Rectangular Prism Calculator (High Precision)
-
Ellipse Circumference Calculator
-
Day of Year Calendar
-
Feet to Meters Converter
-
Hex Calculator
-
Surface Area of a Cone Calculator (High Precision)
-
Random Quote Generator
-
Fixed Asset Turnover Calculator
-
Equivalent Fractions Calculator
-
Error Function Calculator
-
Antilog Calculator
-
Coefficient of Variation Calculator
-
PPM to Percent Converter
-
Sum of Squares Calculator
-
Golden Rectangle Calculator
-
Salary Conversion Calculator
-
Area of a Parallelogram Calculator
-
Leap Years List
-
Midrange Calculator
-
Prime Factor Calculator
-
Batting Average Calculator
-
Doubling Time Calculator
-
10 Minutes
-
Bitwise Calculator
-
Word to Phone Number Converter
-
Cube Numbers List
-
Acid Test Ratio Calculator
-
Total Asset Turnover Calculator
-
Area of A Sector Calculator
-
Line Counter
-
Volume of a Rectangular Prism Calculator (High Precision)
-
Surface Area of Sphere Calculator (High Precision)
-
Sum of Positive Integers Calculator
-
Relative Standard Deviation Calculator (High Precision)
-
On Base Percentage Calculator
-
Log Base 2 Calculator
-
Binary to Gray Code Converter
-
Log Base 10 Calculator
-
Square Numbers List
-
Phone Number Extractor
-
Gray Code to Binary Converter
-
Present Value of Annuity Calculator
-
PVIFA Calculator (High Precision)
-
Binary Calculator
-
Percent to PPM Converter
-
Remove Spaces
Use this ERF calculator to easily calculate the Gauss error function erf(x) for any real-valued x and the inverse error function erf-1(y), y ∈ [-1, 1]. It can also output their complementary functions erfc(x) and erfc-1(y). High-precision calculation up to 25 significant digits. A table of x values and corresponding values of erf and erfc is included as reference.
Quick navigation:
- Using the error function calculator
- What is an error function?
- Error function formula
- Complementary error function
- Inverse error function
- Error function table
- Example application
Using the error function calculator
The erf calculator can be used to compute the error function of any number on the real line. The output also contains the complementary error function for the same number as well as a function plot showing where erf(x) lies relative to other possible function values. erf(x) returns a result between zero and one for any real value of x.
In inverse error function mode the output contains the inverse of erf and its complement. The input y needs to be a real number between minus one and one (y ∈ [-1, 1]).
What is an error function?
In mathematics and statistics, the error function a.k.a. the Gauss error function or just erf, is a complex function of a complex variable defined as [1,2]:
Aside from applied mathematics where it is used to solve differential equations and in physics in solutions of the heat equation in the case where boundary conditions are given by the Heaviside step function, it also sees use in statistics where the inverse error function is used in the calculation of critical values, p-values, confidence intervals which are all related to statistical hypothesis testing and estimation.
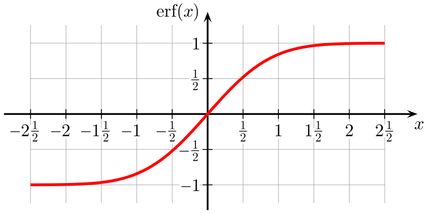
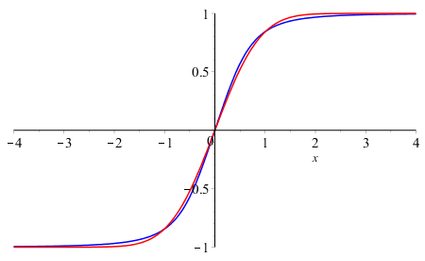
The function plot illustrates its sigmoid shape:
Since e-t2 is an even function and erf(-x) = -erf(x), the error function is an odd function.
Error function formula
To calculate erf(x) one performs an integration from minus infinity to x of the equation e-t2. The formula can therefore be expressed by the following integral equation:
The equation has no closed-form solution and various approximations are in use. In this calculator we use a polynomial approximation with a maximal error of 1.2 × 107 for any real argument as per reference [3].
Complementary error function
The equation for the complementary error function is given by:
Its solution is a simple subtraction from one. It sees application in physics problems.
Inverse error function
The inverse error function, denoted erf-1(y) takes as input the result of y = erf(x), and produces the corresponding x value. While a true inverse function would be multivalued and thus would not have a unique solution, for values of y between −1 and 1 there is a unique real number solution to the equation:
The solution can easily be found by various root-finding methods.
Error function table
An erf table contains tabulated values of real numbers and their corresponding error function values.
Table of commonly used numbers:
| x | erf(x) | erfc(x) |
|---|---|---|
| 0.000 | 0.000000 | 1.000000 |
| 0.01 | 0.011283 | 0.988717 |
| 0.02 | 0.022565 | 0.977435 |
| 0.05 | 0.056372 | 0.943628 |
| 0.10 | 0.112463 | 0.887537 |
| 0.20 | 0.222703 | 0.777297 |
| 0.30 | 0.328627 | 0.671373 |
| 0.40 | 0.428392 | 0.571608 |
| 0.50 | 0.520500 | 0.479500 |
| 0.60 | 0.603856 | 0.396144 |
| 0.70 | 0.677801 | 0.322199 |
| 0.80 | 0.742101 | 0.257899 |
| 0.90 | 0.796908 | 0.203092 |
| 1.00 | 0.842701 | 0.157299 |
| 1.10 | 0.880205 | 0.119795 |
| 1.20 | 0.910314 | 0.089686 |
| 1.30 | 0.934008 | 0.065992 |
| 1.40 | 0.952285 | 0.047715 |
| 1.50 | 0.966105 | 0.033895 |
| 1.60 | 0.976348 | 0.023652 |
| 1.70 | 0.983790 | 0.016210 |
| 1.80 | 0.989091 | 0.010909 |
| 1.90 | 0.992790 | 0.007210 |
| 2.00 | 0.995322 | 0.004678 |
| 2.25 | 0.998537 | 0.001463 |
| 2.50 | 0.999593 | 0.000407 |
| 2.75 | 0.999899 | 0.000101 |
| 3.00 | 0.999978 | 0.000022 |
| 3.50 | 0.999999 | 0.000001 |
| 4.00 | 1.000000 | 0.000000 |
Example application
The inverse error function can be used to compute the quantile function (inverse distribution function) of a normal distribution. For example, if we want to find the cut-off for the top decile of a normal distribution with mean μ = 0 and standard deviation σ = 3, we would use the equation:
F-1(0.9) = μ + σ · √2 · erf-1(2 · p — 1)
Knowing that the top decile represents the top 10 percent, we need to find the cut-off at 90%, or 0.9. Replacing the known values we get:
F-1(0.9) = 0 + 3 · √2 · erf-1(2 · 0.9 — 1) = 3 · √2 · erf-1(0.8)
Using a square root calculator we find √2 equals 1.4142 and using this calculator we find erf-1(0.8) = 0.9062. Replacing once again we find the solution:
F-1(0.9) = 3 · 1.4142 · 0.9062 = 3.8446 which is accurate to four significant digits, same as the accuracy of all numbers used in obtaining the result.
References
1 Glaisher, J.W.L. (1871) «On a class of definite integrals» London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 4 42(277): 294–302. DOI 10.1080/14786447108640568
2 Glaisher, J.W.L. (1871) «On a class of definite integrals. Part II.» London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 4 42(279): 421–426. DOI 10.1080/14786447108640600
3 «Numerical Recipes in Fortran 77: The Art of Scientific Computing» (1992), page 214, Cambridge University Press ISBN 0-521-43064-X
Created by Anna Szczepanek, PhD
Reviewed by
Dominik Czernia, PhD and Jack Bowater
Last updated:
Jun 05, 2023
Welcome to the error function calculator! It helps you compute the values of the four function from the erf family:
- Error function itself;
- Complementary error function;
- Inverse error function; and
- Inverse complementary error function.
If you are not sure what the Gaussian error function actually is, don’t worry! If you scroll down, you will find all the necessary definitions and plots, as well as a short explanation of why the error function matters. As a bonus, we will show you how to (approximately) calculate erf by hand! Finally, at the very bottom of the page, you can find the error function table.
What is the error function?
The error function (often abbreviated to erf, also known as the Gaussian error function) is a special function that we encounter in applied mathematics and mathematical physics, e.g., in solutions to the heat equation.
For a real number x, the erf function is defined as
erf(x)=2π∫0xexp(−t2)dt\small
\textrm{erf}(x) = \frac 2{\sqrt{\pi}}\int_0^x\operatorname{exp}(-t^2)\textrm{d}t
In the plot below, we see that erf is an odd sigmoid function.
In statistics and probability theory, the error function has the following interpretation: for a random variable Z that follows the normal distribution with mean 0 and variance 0.5, the probability that Z falls in the interval [−x, x] is equal to erf(x), where we assume that x is non-negative. As a consequence, the error function is involved in many different calculations, in particular those you can encounter in the following Omni tools:
- p-value calculator;
- Confidence intervals calculator; and
- Critical values calculator.
Complementary error function
The complementary error function, most often denoted by erfc, is defined as one minus the error function. That is, we have
erfc(x)=1−erf(x)\textrm{erfc}(x) = 1 — \textrm{erf}(x)
which we can also write as
erfc(x)=2π∫x∞exp(−t2)dt\small
\textrm{erfc}(x) = \frac 2{\sqrt{\pi}}\int_x^\infty\operatorname{exp}(-t^2)\textrm{d}t
In statistics, the complementary error function erfc(x), where we assume that x is non-negative, describes the probability that a random variable Z following the Gaussian normal distribution with mean 0 and variance 0.5 falls outside the interval [−x, x].
Inverse error function
As we can see from the plot of the error function, if −1 < x < 1, then there exists a unique real number denoted erf-1(x), such that:
erf(erf−1(x))=x.\textrm{erf}(\textrm{erf}^{-1}(x)) =x.
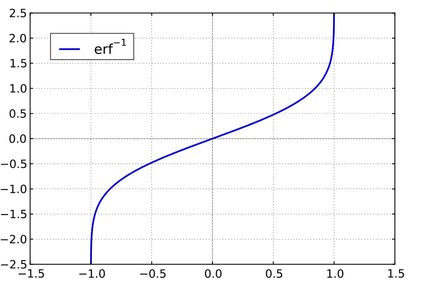
In this way we obtain the inverse error function. Below you can see its plot:
Finally, there is the inverse complementary error function erfc-1, which we define as
erfc−1(x)=erf−1(1−x).\textrm{erfc}^{-1}(x) = \textrm{erf}^{-1}(1-x).
How to calculate erf using this error function calculator?
As the error function is a non-elementary function (as are the other three functions we defined above with the help of erf), it’s not easy to find their values for a given argument x. Fortunately, Omni’s erf calculator is here to help!
-
In the
modefield, choose which of the four functions from the erf family you want to calculate. -
Enter the value of the argument at which you want the function evaluated.
-
Our error function calculator returns the answer immediately. Enjoy!
How to calculate erf by hand?
What if one day you need to determine the Gaussian error function without a dedicated calculator at hand? Your situation isn’t hopeless. There are several good ways of approximating erf. Let us mention two of them.
- The error function has the following Taylor (Maclaurin) series:
erf(x)=2π∑n=0∞(−1)nx2n+1(2n+1)n!=2π(x−x33+x510−x742+…)\footnotesize
\begin{align*}
\textrm{erf}(x) & = \frac 2{\sqrt{\pi}}\sum_{n=0}^\infty \frac{(-1)^n x^{2n+1}}{(2n+1)n!}\\
& = \frac 2{\sqrt{\pi}}\left(\!x \!-\! \frac{x^3}{3} \!+\! \frac{x^5}{10} \!-\! \frac{x^7}{42} \!+\! \ldots \! \right)
\end{align*}
It holds for all real arguments x. In practical applications, you need to compute a partial sum of this series, i.e., the sum of several initial terms. The more, the better the approximation.
- It turns out that a suitably transformed cyclometric (inverse trigonometric) function,
arctan, can serve as a quite good approximation of the error function:
erf(x)≈2πarctan(2x(1+x4))\small
\textrm{erf}(x) \approx \frac 2{{\pi}}\operatorname{arctan}(2x(1+x^4))
The plot below shows these two functions so that you can see how good the approximation is.
Error function table
Since erf is a special function and cannot be easily calculated without a dedicated calculator, there’s been a long tradition of tabulating its values. In case you ever need such a table, we give it below. It covers the arguments between 0 and 3. For negative arguments you need to utilize the fact that erf is an odd function, i.e., that erf(-x) = -erf(x).
|
x |
erf(x) |
erfc(x) |
|---|---|---|
|
0 |
0 |
1 |
|
0.01 |
0.011283416 |
0.988716584 |
|
0.02 |
0.022564575 |
0.977435425 |
|
0.03 |
0.033841222 |
0.966158778 |
|
0.04 |
0.045111106 |
0.954888894 |
|
0.05 |
0.056371978 |
0.943628022 |
|
0.06 |
0.067621594 |
0.932378406 |
|
0.07 |
0.07885772 |
0.92114228 |
|
0.08 |
0.090078126 |
0.909921874 |
|
0.09 |
0.101280594 |
0.898719406 |
|
0.1 |
0.112462916 |
0.887537084 |
|
0.2 |
0.222702589 |
0.777297411 |
|
0.3 |
0.328626759 |
0.671373241 |
|
0.4 |
0.428392355 |
0.571607645 |
|
0.5 |
0.520499878 |
0.479500122 |
|
0.6 |
0.603856091 |
0.396143909 |
|
0.7 |
0.677801194 |
0.322198806 |
|
0.8 |
0.742100965 |
0.257899035 |
|
0.9 |
0.796908212 |
0.203091788 |
|
1 |
0.842700793 |
0.157299207 |
|
1.1 |
0.88020507 |
0.11979493 |
|
1.2 |
0.910313978 |
0.089686022 |
|
1.3 |
0.934007945 |
0.065992055 |
|
1.4 |
0.95228512 |
0.04771488 |
|
1.5 |
0.966105146 |
0.033894854 |
|
1.6 |
0.976348383 |
0.023651617 |
|
1.7 |
0.983790459 |
0.016209541 |
|
1.8 |
0.989090502 |
0.010909498 |
|
1.9 |
0.992790429 |
0.007209571 |
|
2 |
0.995322265 |
0.004677735 |
|
2.5 |
0.999593048 |
0.000406952 |
|
3 |
0.99997791 |
0.00002209 |
|
3.5 |
0.999999257 |
0.000000743 |
Absolute value equationAbsolute value inequalitiesAdding and subtracting polynomials… 37 more
Description
Complementary error function. ERFC(x) returns the error function integrated between x and infinity.
$$\operatorname{erfc}(x) = \frac{2}{\sqrt{\pi}} \int_x^{\infty} e^{-t^2}\,\mathrm dt $$
The argument x can be a real number or a matrix. When it is a matrix, the function returns a matrix with the same dimensions and with the ERFC function applied to all elements.
ERFC(x)=1-ERF(x)
Calculator
ERFC( )
Graph
| Function: | ERFC() | |
|---|---|---|
| X-axis | Y-axis | |
| Minimum: | ||
| Maximum: | ||
Related functions
- ERF error function
- List of Engineering functions
Функция ошибок
| Аргумент функции ошибок erf(x) |
| Функция ошибок |
| Дополнительная функция ошибок |
Функция ошибок, она же функция Лапласа, он же интеграл вероятности — все это одна и та же сущность, которая выражается функцией
и используется в статистике и теории вероятностей.
Функция неэлементарная, то есть её нельзя представить в виде элементарных (тригонометрических и алгебраических) функций.
Для расчета в нашем калькуляторе, мы используем связь с неполной гамма функцией
Кроме этого мы сможем здесь же вычислить, дополнительную функцию ошибок, обозначаемую 

В приницпе это все, что можно сказать о ней.
Калькулятор высчитывает результат как в вещественном так и комплексном поле.
Замечание: Функция прекрасно работает на всем поле комплексных чисел при условии если аргумент ( фаза) меньше 180 градусов. Это связано с особенностью вычисления этой функции, неполной гамма функции, интегральной показательной функцией через непрерывные дроби.
Отсюда следует вывод, что при отрицательных вещественных аргументах, функция будет выдавать неверные решения. Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.
Несколько примеров:

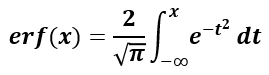

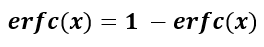

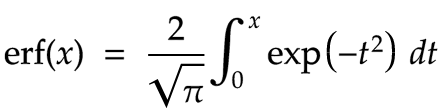


}{{\sqrt%20%20\pi%20}}})
