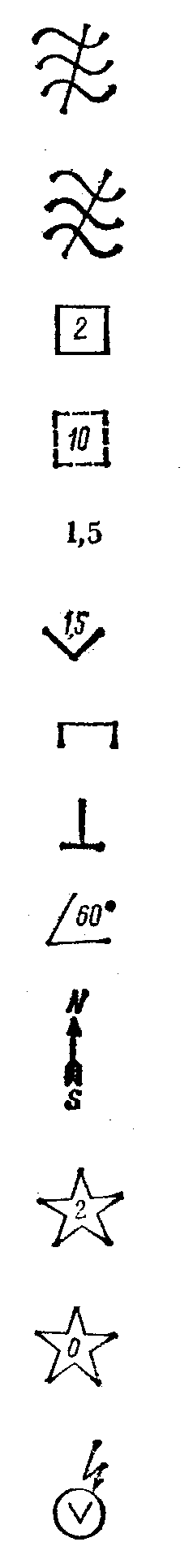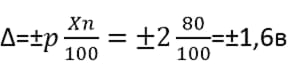Точность измерения
характеризуется его возможными
погрешностями. Эти погрешности при
каждом конкретном измерении не должны
превышать некоторого определенного
значения. В зависимости от способа
числового выражения различают погрешности
абсолютные и относительные, а применительно
к показывающим приборам — еще и
приведенные.
Абсолютная
погрешность ∆А
— это разность между измеренным Лиз
и действительным А
значениями
измеряемой величины:
∆А
= Аиз-А.
Например,
амперметр показывает Аиз
= 9
А, а действительное значение тока А =
8,9 А, следовательно, ∆А
=0,1 А.
Чтобы определить
действительное значение величины, нужно
к измеренному значению прибавить
поправку — абсолютную погрешность,
взятую с обратным знаком.
Точность
измерения оценивается обычно не
абсолютной, а относительной
погрешностью —
выраженным в процентах отношением
абсолютной погрешности к действительному
значению измеряемой . величины:
γо
= (∆А/А)·100%
а так
как разница между А
и
Aиз
обычно относительно мала, то практически
в большинстве случаев можно считать,
что у
=
= (∆A/Aиз)·100
%
Для
приведенного примера измерения тока
относительная погрешность у0=
(0,1/9)·100 % = 1,11 %.
О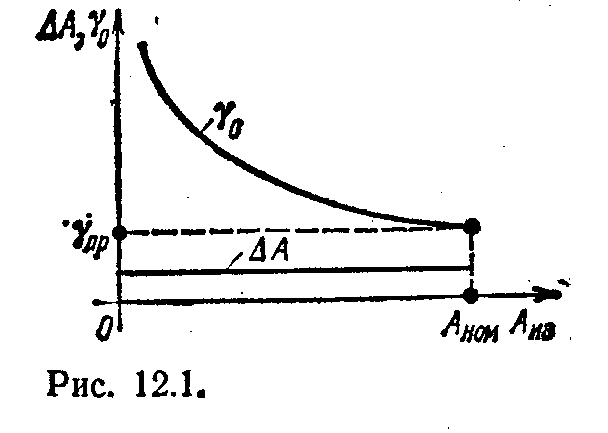
оценивать по относительной погрешности
точность самых распространенных
показывающих приборов со стрелочным
указателем неудобно. Дело в том, что
абсолютная погрешность ∆А у них имеет
обычно один и тот же порядок вдоль всей
шкалы. При постоянной абсолютной
погрешности ∆А с уменьшением измеряемой
величины Аиз
быстро растет относительная погрешность
(рис. 12.1). Поэтому рекомендуется выбирать
пределы измерения показывающего прибора
так, чтобы отсчитывать показания в
пределах второй половины шкалы, ближе
к ее концу.
Для
оценки точности самих показывающих
измерительных приборов служит их
приведенная
погрешность. Так
называется выраженное в процентах
отношение абсолютной погрешности
показания ∆А к А
ном —
номинальному значению, соответствующему
наибольшему показанию прибора:
упр
= (А/Аном)·100о/0.
(12.1)
Если
в рассмотренном примере предел измерения
амперметра A
ном
= 10 А, то приведенная погрешность упр
= (0,1/10)-100
% = 1 %
Погрешности
прибора обусловливаются недостатками
самого прибора и внешними влияниями.
Приведенная погрешность, зависящая
лишь от самого прибора, называется
основной
погрешностью. Нормальные
рабочие условия — это температура
окружающей среды 20 °С (или та, которая
обозначена на шкале прибора), нормальное
рабочее положение прибора (указанное
условным знаком на его шкале), отсутствие
вблизи прибора ферромагнитных масс и
внешних магнитных полей (кроме земного)
и прочие нормальные условия (номинальные:
напряжение, частота тока, синусоидальная
форма кривой тока и т. д.).
Допускаемая
основная погрешность электроизмерительного
прибора определяет его класс точности.
Обозначением класса точности служит
допускаемая основная погрешность
приборов, принадлежащих к этому классу:
0,05; 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Принадлежность
прибора к определенному классу указывает,
что основная погрешность прибора на
всех делениях шкалы не превышает
значения, определяемого классом точности
этого прибора (например, у прибора класса
1 допускаемая основная погрешность 1
%). Отклонение внешних условий от
нормальных вызывает дополнительные
погрешности.
В
зависимости от чувствительности к
внешним магнитным или электрическим
полям электроизмерительные приборы
делятся на две категории: I
— приборы менее чувствительные и II
— приборы
более чувствительные.
Для правильного
применения электроизмерительного
прибора важны его технические особенности.
Эти особенности указываются на шкале
прибора условными обозначениями,
приведенными в табл. 12.1. 12.4. ПОТРЕБЛЕНИЕ
ЭНЕРГИИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫМИ ПРИБОРАМИ
Включение
измерительного прибора в исследуемую
электрическую цепь неизбежно в некоторой
степени изменяет ее режим работы. Это
изменение вызывается по существу тем,
что работающий прибор потребляет
некоторую энергию. Поэтому при исследовании
объектов малой мощности могут существенно
исказиться результаты. Желательно,
чтобы собственное потребление энергии
измерительным прибором было возможно
меньше.
Простейшим примером
влияния собственного потребления
энергии измерительными приборами на
результаты, измерения может служить
измерение сопротивления резистора (при
постоянном токе) при помощи вольтметра
и амперметра с вычислением по закону
Ома. Для такого измерения возможны две
схемы включения приборов (рис. 12.2), причем
в обоих случаях для точного измерения
сопротивления резистора необходимо
учесть влияние собственного потребления
энергии приборами.
Таблица 12.1.
Условные обозначения на шкалах
электроизмерительных приборов
Прибор трехфазного
тока для неравномерной нагрузки фаз
Прибор трехфазного
тока с двухэлементным измерительным
механизмом
Защита от внешних
магнитных полей, например 2 мТл
Защита от внешних
электрических полей, например 10 кВ/м
Класс точности
при нормировании погрешности в процентах
от диапазона измерения, например 1,5
То же при нормировании
погрешности в процентах от длины шкалы,
например 1,5
Горизонтальное
положение шкалы
Вертикальное
положение шкалы
Наклонное положение
шкалы под определенным углом к горизонту,
например 60°
Направление
ориентировки прибора в земном магнитном
поле
Измерительная
цепь изолирована от корпуса и испытана
напряжением, например 2 кВ
Прибор испытанию
прочности изоляции не подлежит
Осторожно!
Прочность изоляции измерительной цепи
по отношению к корпусу не соответствует
нормам (знак выполняется красного цвета)
В схеме
рис. 12.2, а
амперметр
измеряет ток / в резисторе с сопротивлением
г, а вольтметр измеряет напряжение U’
=
U
+ rАI,
где
rА
—
сопротивление амперметра, т. е. напряжение,
равное сумме напряжения U
на
резисторе и напряжения между выводами
амперметра. Следовательно, на основании
закона Ома определяется сумма сопротивлений
резистора и амперметра:
U’/I
= r’
= r+rA
Действительное
значение сопротивления резистора
r
= r'(1-rA/r’).
Очевидно, что
ошибка измерения будет тем меньше, чем
меньше сопротивление амперметра.
При
измерении по схеме рис. 12.2, б
вольтметр
присоединен непосредственно к выводам
резистора и показывает напряжение U
на резисторе, а амперметр измеряет сумму
токов в резисторе и в цепи вольтметра:
I’
= I
+ Iv
Таким
образом, в этом случае на основании
показаний приборов определяется
проводимость
где
rv
—
сопротивление вольтметра.
Чтобы определить
проводимость объекта измерения —
резистора, нужно из найденной проводимости
вычесть проводимость вольтметра:
т. е.
Чем
больше сопротивление вольтметра rv,
тем
меньше поправка к результатам измерения.
При измерении
мощности ваттметром также неизбежно
влияние
е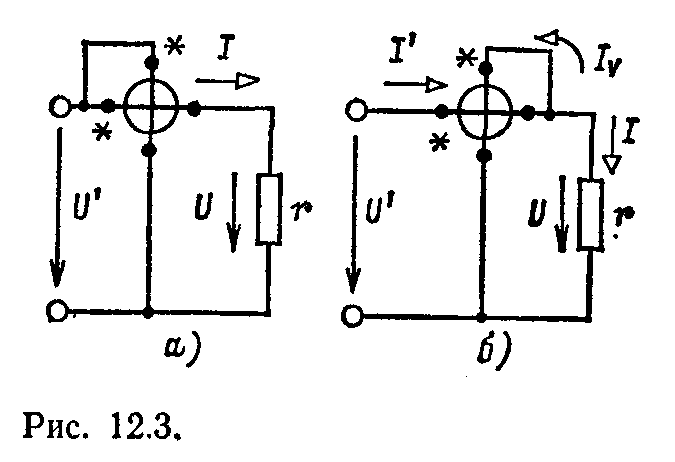
собственного потребления энергии на
результаты измерения. Две основные
схемы такого измерения (рис. 12.3)
соответствуют двум вышеприведенным
схемам измерения сопротивления: в первом
случае погрешность вызвана сопротивлением
цепи тока ваттметраrА,
во
втором случае — собственным потреблением
энергии цепи напряжения ваттметра.
В схеме
рис. 12.3, а
ваттметр
измеряет кроме мощности Р
в
сопротивлении нагрузки еще и мощность
потерь в сопротивлении собственной
цепи тока, т. е.
Риз
= Р + rАI2
Если мощность
измеряется по схеме рис. 12.3, б, то ваттметр
измеряет кроме мощности в сопротивлении
нагрузки еще и мощность потерь в своей
цепи напряжения, т. е.
Pиз
= P
+ gvU2
При переменном
токе учет поправок осложняется тем, что
сопротивления цепей переменного
тока — величины комплексные.
Чем меньше мощности
контролируемых цепей, тем существеннее
влияние собственного потребления
энергии измерительными приборами на
результаты измерений. В частности, эти
влияния обычно значительны в цепях
управления автоматики и в цепях
электронных устройств.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание материала
- Класс точности
- Класс точности
- Что такое класс точности прибора?
- Виды маркирования
- Пределы
- Вопрос выбора
- ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- Как определить класс точности электроизмерительного прибора, формулы расчета
- Нормирование
- Для чего используются
- Измерение
- Защита
- Разновидности амперметров
- Как определить класс точности манометра
- Какие классы точности бывают, как обозначаются
- Определение погрешности
Класс точности
Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.
Вовремя выяснить ошибки измерительного средства помогут нормированные величины погрешностей. Под этим определением стоит понимать предельные, для измерительного средства показатели. Они могут быть разными по величине и зависеть от разных условий, но пренебрегать ими не стоит ни в коем случае, ведь это может привести к серьезной ошибке в дальнейшем. Нормированные значения должны быть меньше чем покажет прибор. Границы допустимых величин ошибок и необходимые коэффициенты вносятся в паспорт каждого замеряющего размеры устройства. Узнать подробные значения нормирования для любого прибора можно воспользовавшись соответствующим ГОСТом.
Класс точности
Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.
Вовремя выяснить ошибки измерительного средства помогут нормированные величины погрешностей. Под этим определением стоит понимать предельные, для измерительного средства показатели. Они могут быть разными по величине и зависеть от разных условий, но пренебрегать ими не стоит ни в коем случае, ведь это может привести к серьезной ошибке в дальнейшем. Нормированные значения должны быть меньше чем покажет прибор. Границы допустимых величин ошибок и необходимые коэффициенты вносятся в паспорт каждого замеряющего размеры устройства. Узнать подробные значения нормирования для любого прибора можно воспользовавшись соответствующим ГОСТом.
Что такое класс точности прибора?
Класс точности – это характеристика прибора, которая определяется границами допускаемых основной и дополнительной погрешностей, а также другими свойствами, предусмотренными стандартами на данный вид изделия, которые оказывают влияние на точность. Этот параметр присутствует в технических характеристиках многих приборов, которые имеют эталонные выходные параметры, будь то электронные или механические измерительные устройства. Класс точности является основной характеристикой измерительной техники: весов, мультиметров, осциллографов, КИПовского оборудования и прочего. Чем выше это значение у прибора, тем больше стоит такое устройство, это связано со сложностью производства таких изделий.
Нормированная погрешность
Класс точности приборов измерений характеризует свойства таких изделий по отношению к точности, но при этом не является показателем точности этих измерений, выполненных при помощи данного устройства. С целью преждевременного выявления погрешности прибора, которую данное средство внесет в измеряемый результат, используют нормированные значения погрешностей. Значение этого параметра у каждого технического приспособления одной группы является индивидуальным, оно имеет отличные друг от друга случайные и систематические составляющие, но такая погрешность любого измерительного прибора одного класса не должна превышать установленное нормированное значение. Границы главной погрешности и коэффициента влияния заносятся в паспорт любого измерительного прибора. Все основные методы нормирования допустимых погрешностей и обозначения класса измеряющих устройств установлены ГОСТом, например, класс точности весов предусмотрен ГОСТом 24104-2001, который вступил в силу 01.07.2002.
Виды маркирования
Класс точности любого измерительного прибора маркируется на шкале устройства в виде числа. Это значение указывает нормированную величину погрешности, выраженную в процентном отношении. Если класс точности на шкале прибора обведен кружком, например 2,5, то это значит, что величина погрешности чувствительности устройства составляет 2,5 процента. По такому принципу нормируют погрешность масштабных преобразователей (измерительных шунтов, делителей напряжения, измерителей трансформаторов напряжения и тока и т. п.). Если значение класса точности на шкале прибора не подчеркнуто, например 0,7, это значит, что устройство нормируется погрешностью нуля равным 0,7. Эти приборы при любых з начениях Х имеют абсолютную погрешность нуля, равную константе. В случае степенной или равномерной отметки класса точности на шкале устройства принимается верхний предел измерения. В том случае, когда нулевая отметка расположена по центру шкалы, то это значение принимается равным протяженности измеряемого диапазона. При этом будет неправильным считать, что амперметр с классом точности 0,7 обеспечит во всем измеряемом диапазоне погрешность результата 0,7%. В таком случае относительная погрешность будет равна классу точности только на последнем значении шкалы. На приборах с неравномерной шкалой (омметры) класс точности маркируют в долях от длины шкалы, его обозначают ниже значения знака «угол». В случае если класс точности указан в дробном виде (например, 0,03/0,02), это значит, что погрешность в конце измеряемого диапазона составит 0,03, а в начале 0,01. Такими приборами являются постоянные потенциометры, цифровые вольтметры и другие высокоточные измерительные приборы.
Виды маркирования
Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.
Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.
Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.
Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.
Пределы
Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.
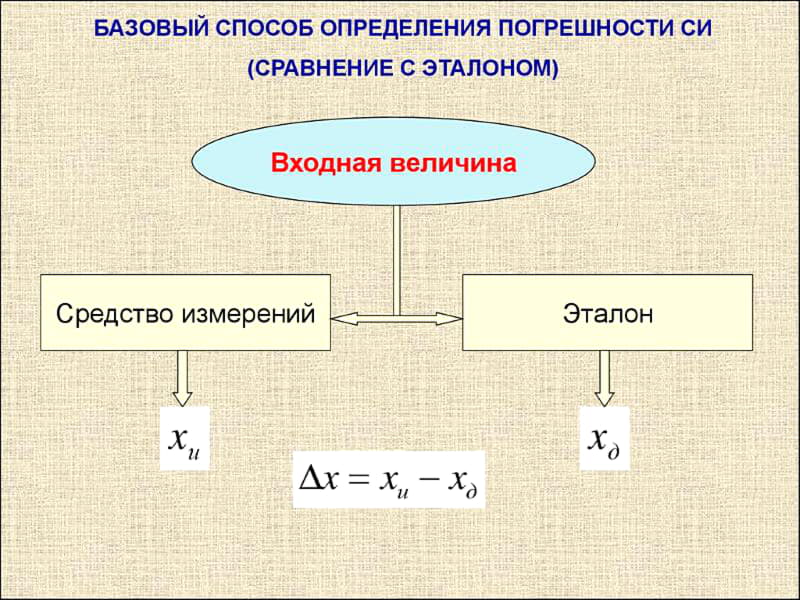
Базовый способ определения погрешности
При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.
Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.
Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.
Класс точности 2,5
Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.
Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.
Дополнительная случается в результате изменений величин, которые каким-либо образом влияют на измерения (например температура или влажность). Выход за установленные пределы можно выявить, если сложить все дополнительные погрешности.
Случайные ошибки имеют непредсказуемые значения в результате того, что факторы, оказывающие на них влияние постоянно меняются во времени. Для их учета пользуются теорией вероятности из высшей математики и ведут записи происходивших раньше случаев.
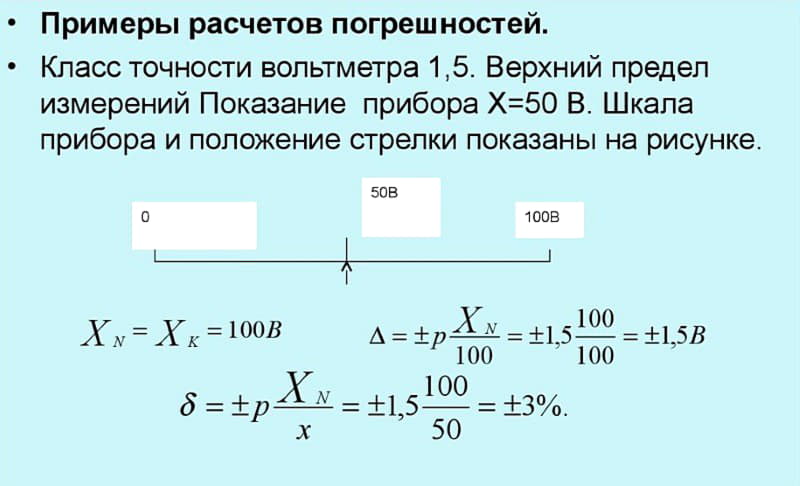
Пример расчета погрешности
Статистическая измерительного средства учитывается при измерении какой-либо константы или же редко подверженной изменениям величины.
Динамическая учитывается при замерах величин, которые часто меняют свои значения за небольшой отрезок времени.
Вопрос выбора
Для установки электросчётчика в частном доме или квартире подойдут модели, которые имеют класс не менее 2.
Кроме этого, отправляясь за электрическим счётчиком в магазин, следует точно знать следующие характеристики:
- Фазность электрической сети. Если электрическая сеть, которая подведена к счётчику, является однофазной, то устройство должно быть также для однофазной сети. Трёхфазный электросчётчик также можно установить для подсчёта использования электроэнергии, но такие устройства, как правило, имеют более высокую стоимость. Когда счётчик устанавливается для измерения трёхфазного тока, то на нём обязательно указывается соответствующая надпись. Для подсчёта трёхфазного тока однофазные приборы не используются.
- Нагрузка, при которой будет эксплуатироваться данное устройство. В зависимости от максимальной нагрузки, которая будет подключена к устройству подсчёта электроэнергии, выбирается модель, на корпусе которой обозначается такой показатель. Для стандартной нагрузки, которая используется в частном доме, применяются модели электросчётчиков рассчитанных на максимальный ток – 60 А. Если планируется подключать мощные отопительные электрические котлы, то электросчётчик выбирается с показателем не менее – 100 А.
- Если поставщик электроэнергии может продавать электроэнергию по 2 тарифам, то тарифность счётчика также учитывается при покупке. Значительно экономить на оплате электричества позволяет двухтарифные устройства. При использовании электроэнергии в ночное время такой счётчик будет регистрировать расход отдельно. Если поставщик электроэнергии позволяет производить такую оплату, то установка многотарифного счётчика позволит использовать электричество более рационально.
- Способ крепления. Позволяет установить прибор в уже имеющийся короб, или на место прибора который был установлен ранее.
ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ Измеренная прибором величина всегда отличается от истинного значения на некоторое число, называемое погрешностью прибора. Погрешности измерительных приборов определяют поверкой, т. е. сравнением показаний поверяемого прибора с показаниями более точного, образцового прибора при измерении ими одной и той же величины. Значение измеряемой величины, определенное по образцовому прибору, принято считать действительным. Однако действительное значение отличается от истинного на погрешность, присущую данному образцовому прибору. Различают абсолютную, относительную и приведенную погрешности измерения.
Как определить класс точности электроизмерительного прибора, формулы расчета
Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.
Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12
Находим относительную погрешность:
Y= 100×0,025/12=0,208 или 2,08%
(вывод: класс точности – 2,5).
Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:
Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12
Предел абсолютной допустимой погрешности:
Относительная погрешность одного деления:
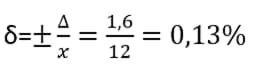
Нормирование
Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й
Нормирование осуществляется по:
- абсолютной;
- относительной;
- приведенной.
Формулы расчета абсолютной погрешности по ГОСТ 8.401
Каждый прибор из конкретной группы приспособлений для замера размеров имеет определенное значение неточностей. Оно может незначительно отличаться от установленного нормированного показателя, но не превышать общие показатели. Каждый такой агрегат имеет паспорт, в который записываются минимальные и максимальные величины ошибок, а также коэффициенты, оказывающие влияние в определенных ситуациях.
Скачать ГОСТ 8.401-80
Все способы нормирования СИ и обозначения их классов точности устанавливаются в соответствующих ГОСТах.
Для чего используются
Разнообразные виды измерительных трансформаторов встречаются как в небольших приборах размером со спичечный коробок, так и в крупных энергетических установках. Их основное назначение – понижать первичные токи и напряжения до значений, необходимых для измерительных устройств, защитных реле и автоматики. Применение понижающих катушек обеспечивает защиту цепи низшего и высшего ранга, поскольку они разделены между собой.
Понижающие средства разделяют по признакам эксплуатации и предназначены для:
- измерений. Они передают вторичный ток на приборы;
- защиты токовых цепей;
- применения в лабораториях. Такие понижающие средства имеют высокую классность точности;
- повторного конвертирования, они относятся к промежуточным инструментам.
Измерение
Измерительный трансформатор необходим для понижения высокого тока основного напряжения и передачу его на измерительные устройства. Для подключения стандартных приборов к высоковольтной сети потребовались бы громоздкие установки. Реализовывать инструменты таких размеров экономически не выгодно и не целесообразно.
Использование понижающих трансформаторов позволяет применять обычные устройства измерения в обычном режиме, что расширяет спектр их применения. Благодаря снижению напряжения, они не требуют дополнительных модификаций. Трансформатор отделяет высоковольтное напряжение сети от питающего напряжения приборов, обеспечивая безопасность из использования. От их классности зависит точность учета электрической энергии.
Защита
Кроме питания измерительных приборов понижающие трансформаторы подают напряжение на системы защиты и автоматической блокировки. Поскольку в сетевой электросети происходят перепады и скачки напряжения, которое губительно для высокоточного оборудования цепи.
В энергетических установках оборудование делится на силовое и вторичное, которое контролирует процессы первичной схемы подключения устройств. Высоковольтная аппаратура располагается на открытых площадках или устройствах. Вторичное оборудование находится на релейных планках внутри распределительных шкафов.
Промежуточным элементом передачи информации между силовыми агрегатами и средствами измерения, управления, контроля и защиты являются понижающие или измерительные трансформаторы. Они разделяют первичную и вторичную цепь от пагубного воздействия силовых агрегатов на чувствительные измерительные приборы, а также защищают обслуживающий персонал от повреждений.
Разновидности амперметров
Они могут быть электромеханическими или аналоговыми, цифровыми или электронными. Базовый набор, как правило, состоит из детектора, передающего устройства и индикатора, самописца или запоминающего устройства.
Аналоговые устройства — самые старые из используемых инструментов. Хотя они надежны для статических и стабильных измерений, они не подходят для динамических и переходных условий. Кроме того, они довольно громоздкие и имеют ограничения из-за использования стрелочной индикации.
Электронные инструменты реагируют быстрее и способны мгновенно обнаруживать динамические изменения тока в сети. Примером является цифровой мультиметр, который способен измерить значения тока в динамическом или переходном режиме за секунды.
Как определить класс точности манометра
Манометр — измерительный прибор, который позволяет установить значение избыточного давления, действующего в трубопроводе или в рабочих частях различных видов оборудования. Такие приборы широко применяются в системах отопления, водоснабжения, газоснабжения, других инженерных сетях коммунального и промышленного назначения. В зависимости от условий эксплуатации измерителя существуют определенные ограничения по допустимому пределу его погрешности. Поэтому важно знать, как определить класс точности манометра.
Какие классы точности бывают, как обозначаются
Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже
Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.
Приборы, способные выполнять множество различных замеров, могут быть одновременно более двух классов.
Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.
- 0,1, 0,2 – считается самым высоким классом
- 0,5, 1 – чаще применяется для устройств средней ценовой категории, например, бытовых
- 1,5, 2,5 – используется для приборов измерения с низкой точностью или индикаторов, аналоговых датчиков
Примечание. На корпусе высокоточных измерителей, класс может не наносится. Обозначение таких устройств как правило выполняется особыми знаками.
Определение погрешности
Владельцев измерительных приборов интересует, прежде всего, величина максимальной погрешности, характерной для манометра. Она зависит не только от класса точности, но и от диапазона измерений. Таким образом, чтобы получить значение погрешности, нужно произвести некоторые вычисления. Например, для манометра с диапазоном измерений, равным 6 МПа, и классом точности 1,5 погрешность будет рассчитываться по формуле 6*1,5/100=0,09 МПа.
Необходимо отметить, что таким способом можно посчитать только основную погрешность. Ее величина определяется идеальными условиями эксплуатации. На нее оказывают влияние только конструктивные характеристики, а также особенности сборки прибора, например, точность градуировки делений на шкале, сила трения в измерительном механизме. Однако эта величина может отличаться от фактической, поскольку существует также дополнительная погрешность, определяемая условиями, в которых эксплуатируется манометр. На нее может влиять вибрация трубопровода или оборудования, температура, уровень влажности и другие параметры.
Также точность измерения давления зависит от еще одной характеристики манометра — величины его вариации, которую определяют в ходе поверки. Это максимальная разница показаний измерителя, выявленная по результатам нескольких измерений. Величина вариации в значительной мере зависит от конструкции манометра, а именно от способа уравновешивания, которое может быть жидкостным (давлением столба жидкости) или механическим (пружиной). Механические манометры имеют более выраженную вариацию, что часто обусловлено дополнительным трением при плохой смазке или износе деталей, потере упругости пружины и другими факторами.
Источник:
Теги
Класс точности
Класс точности – это основная метрологическая характеристика прибора, определяющая допустимые значения основных и дополнительных погрешностей, влияющих на точность измерения.
Погрешность может нормироваться, в частности, по отношению к:
- результату измерения (по относительной погрешности), в этом случае, по ГОСТ 8.401-80 (взамен ГОСТ 13600-68), цифровое обозначение класса точности (в процентах) заключается в кружок.
- длине (верхнему пределу) шкалы прибора (по приведенной погрешности)
Для стрелочных приборов принято указывать класс точности, записываемый в виде числа, например, 1,5 или 2,5. Это число даёт максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Например, для манометра ДМ 93-100-1-М, работающего в диапазоне измерений 0-10 кгс/см2, класс точности 1,0 определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,1 кгс/см2. Относительная погрешность результата зависит от значения измеряемого давления, становясь недопустимо высокой для малых давлений. Конкретно в данном случае это означает, что таким манометром не следует пытаться измерить давление, меняющееся в диапазоне 0,01..0,2 кгс/см2, точного результата не получить.
Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, за погрешность прибора всегда принимают половину цены его наименьшего деления. Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.
У манометров, которые мы предлагаем, на цифеблатах нанесена круговая шкала в соответствии с ГОСТ 2405-88. Пределы допускаемой приведённой основной погрешности выражены в процентах от дипапзона измерений: ±0,15%; ±0,25%; ±0,4%; ±0,6%; ±1%; ±1,5%; ±2,5%; ±4%. Класс точности выбирается из ряда 0,15; 0,25; 0,4; 0,6; 1; 1,5; 2,5; 4, в соответствии с пределами допускаемой приведённой основной погрешности.
Класс точности у обычных технических показывающих манометров с диаметром шкалы 40; 50 мм, как правило, 2,5 или 4. У манометров с диаметром шкалы 60 (63) мм 1,5; 2,5 или 4. У манометров со шкалами 100 и 150 (160) мм класс точности 1,5 или, под заказ, 1. Классы точности 0,4; 0,6 характерны для манометров точных измерений, а 0,15; 0,25 – для манометров образцовых.
Исходя из вышеизложенного, можно ответить на вопрос «какой класс точности выше, 1 или 1,5?», что выше класс точности 1.