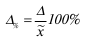Классификация ошибок выборочного наблюдения

Между
признаками выборочной совокупности и
признаками генеральной совокупности,
как правило, существует некоторое
расхождение, которое называется ошибкой
статистического наблюдения. При массовом
наблюдении ошибки неизбежны, но возникают
они в результате действия различных
причин. Величина возможной ошибки
выборочного признака происходит из-за
ошибок регистрации и ошибок
репрезентативности. Ошибки регистрации,
или технические ошибки, связаны с
недостаточной квалификацией наблюдателей,
неточностью подсчетов, несовершенством
приборов и т. п.

Под
ошибкой
репрезентативности
(представительства) понимают расхождение
между выборочной характеристикой и
предполагаемой характеристикой
генеральной совокупности. Ошибки
репрезентативности бывают случайными
и систематическими. Систематические
ошибки связаны с нарушением установленных
правил отбора. Случайные
ошибки объясняются недостаточно
равномерным представлением в выборочной
совокупности различных категорий
единиц генеральной совокупности.

В
результате первой причины выборка
легко может оказаться смещенной, так
как при отборе каждой единицы допускается
ошибка, всегда направленная в одну и
ту же сторону. Эта ошибка получила
название ошибки
смещения.
Ее размер может превышать величину
случайной ошибки. Особенность ошибки
смещения состоит в том, что, являясь
постоянной частью ошибки репрезентативности,
она увеличивается с увеличением объема
выборки. Случайная же ошибка с увеличением
объема выборки уменьшается. Кроме того,
величину случайной ошибки можно
определить, тогда как размер ошибки
смещения практически определить очень
сложно, а иногда и невозможно, поэтому
важно знать причины, вызывающие ошибку
смещения, и предусмотреть мероприятия
по ее устранению.

Ошибки
смещения бывают преднамеренные и
непреднамеренные. Причиной возникновения
преднамеренной
ошибки
является тенденциозный подход к выбору
единиц из генеральной совокупности.
Чтобы не допустить появление такой
ошибки, необходимо соблюдать принцип
случайности отбора единиц.

Непреднамеренные
ошибки
могут возникать на стадии подготовки
выборочного наблюдения, формирования
выборочной совокупности и анализа ее
данных. Чтобы не допустить появление
таких ошибок, необходима хорошая основа
выборки, т. е. та генеральная
совокупность, из которой предполагается
производить отбор, например список
единиц отбора. Основа выборки должна
быть достоверной, полной и соответствовать
цели исследования, а единицы отбора и
их характеристики должны соответствовать
действительному их состоянию на момент
подготовки выборочного наблюдения.
Нередки случаи, когда в отношении
некоторых единиц, попавших в выборку,
трудно собрать сведения из-за их
отсутствия на момент наблюдения,
нежелания дать сведения и т. п. В
таких случаях эти единицы приходится
заменять другими. Необходимо следить,
чтобы замена осуществлялась равноценными
единицами.

Случайная
ошибка
выборки возникает в результате случайных
различий между единицами, попавшими в
выборку, и единицами генеральной
совокупности, т. е. она связана со
случайным отбором. Теоретическим
обоснованием появления случайных
ошибок выборки является теория
вероятностей и ее предельные теоремы.

Сущность
предельных
теорем
состоит в том, что в массовых явлениях
совокупное влияние различных случайных
причин на формирование закономерностей
и обобщающих характеристик будет сколь
угодно малой величиной или практически
не зависит от случая. Так как случайная
ошибка выборки возникает в результате
случайных различий между единицами
выборочной и генеральной совокупностей,
то при достаточно большом объеме выборки
она будет сколь угодно мала.

Предельные
теоремы теории вероятностей позволяют
определять размер случайных ошибок
выборки. Различают среднюю (стандартную)
и предельную ошибку выборки. Под средней
(стандартной) ошибкой
выборки понимают такое расхождение
между средней выборочной и генеральной
совокупностями (~ —), которое не превышает
±.
Предельной
ошибкой
выборки принято считать максимально
возможное расхождение (~ —), т. е.
максимум ошибки при заданной вероятности
ее появления.

В
математической теории выборочного
метода сравниваются средние характеристики
признаков выборочной и генеральной
совокупностей и доказывается, что с
увеличением объема выборки вероятность
появления больших ошибок и пределы
максимально возможной ошибки уменьшаются.
Чем больше обследуется единиц, тем
меньше будет величина расхождений
выборочных и генеральных характеристик.
На основании теоремы, доказанной П.Л.
Чебышевым, величину стандартной ошибки
простой случайной выборки при достаточно
большом объеме выборки (n)
можно определить по формуле

– стандартная
ошибка.

Из
этой формулы средней (стандартной)
ошибки простой случайной выборки видно,
что величина зависит от изменчивости
признака в генеральной совокупности
(чем больше вариация признака, тем
больше ошибка выборки) и от объема
выборки n
(чем больше обследуется единиц, тем
меньше будет величина расхождений
выборочных и генеральных характеристик).

Академик
A.M. Ляпунов доказал, что вероятность
появления случайной ошибки выборки
при достаточно большом ее объеме
подчиняется закону нормального
распределения. Эта вероятность
определяется по формуле

В
математической статистике употребляют
коэффициент доверия t, значения функции
F(t)
табулированы при разных его значениях,
при этом получают соответствующие
уровни доверительной вероятности
(табл. 6.1).

Таблица
6.1

Коэффициент
доверия t и соответствующие уровни
доверительной вероятности

Коэффициент
доверия позволяет вычислить предельную
ошибку выборки,

т. е.
предельная ошибка выборки равна
t-кратному числу средних ошибок выборки.

Таким
образом, величина предельной ошибки
выборки может быть установлена с
определенной вероятностью. Как видно
из последней графы табл. 6.1, вероятность
появления ошибки равной или большей
утроенной средней ошибки выборки,
т. е. 

крайне
мала и равна 0,003(1–0,997). Такие маловероятные
события считаются практически
невозможными, а потому величину

можно
принять за предел возможной ошибки
выборки.

Выборочное
наблюдение дает возможность определить
среднюю арифметическую выборочной
совокупности и величину предельной
ошибки этой средней, которая показывает
(с определенной вероятностью), насколько
выборочная величина может отличаться
от генеральной средней в большую или
меньшую сторону. Тогда величина
генеральной средней будет представлена
интервальной оценкой, для которой
нижняя граница будет равна

Интервал,
в который с данной степенью вероятности
будет заключена неизвестная величина
оцениваемого параметра, называют
доверительным,
а вероятность Р
– доверительной вероятностью.
Чаще всего доверительную вероятность
принимают равной 0,95 или 0,99, тогда
коэффициент доверия t
равен соответственно 1,96 и 2,58. Это
означает, что доверительный интервал
с заданной вероятностью заключает в
себе генеральную среднюю.

Наряду
с абсолютной величиной предельной
ошибки выборки рассчитывается и
относительная
ошибка
выборки, которая определяется как
процентное отношение предельной ошибки
выборки к соответствующей характеристике
выборочной совокупности:

Чем
больше величина предельной ошибки
выборки, тем больше величина доверительного
интервала и тем, следовательно, ниже
точность оценки. Средняя (стандартная)
ошибка выборки зависит от объема выборки
и степени вариации признака в генеральной
совокупности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #

  12.04.2015613.89 Кб24pr.doc

• #
• #
• #
• #

1. Выборочное наблюдение

10:21:25 PM
1

2. Определение выборочного наблюдения

• Выборочное наблюдение — это способ несплошного
статистического наблюдения, при котором обследуются
не все единицы изучаемой (генеральной) совокупности,
а лишь часть ее (выборка), отобранная по
определенным правилам и обеспечивающая получение
данных, характеризующих совокупность в целом.
Причины применения:
Экономия
Невозможность проведения сплошного исследования
10:21:25 PM
2

3.

Вся изучаемая совокупность называется генеральной
совокупностью
Часть генеральной совокупности, которая подвергается
обследованию – называется выборочной совокупностью
(выборкой).
Для того, чтобы выборочная совокупность давала объективные
результаты, она должна быть репрезентативной (каждая
единица генеральной совокупности должна иметь равную
возможность попасть в выборку).
Некоторые единицы могут попадать в выборку дважды, трижды или
даже большее число раз. Такой отбор в выборку называется
повторным.
При бесповторном отборе попавшая в выборку единица
подвергается обследованию и в дальнейшей процедуре отбора не
участвует.
Теоретической
основой выборки являются теоремы
закона больших
10:21:25 PM
3
чисел (Чебышева, Ляпунова, Бернулли и др.)

4. Классификация ошибок выборочного наблюдения

Ошибки выборочного наблюдения
Ошибки регистрации
Систематические
Случайные
Ошибки репрезентативности
Систематические
Случайные
• Ошибки регистрации являются следствием неправильного установления
значения наблюдаемого признака или неправильной записи.
• Ошибки репрезентативности обусловлены тем, что выборочная совокупность
не может по всем параметрам в точности воспроизвести генеральную
совокупность.
• Систематические ошибки репрезентативности связаны с нарушением
принципов формирования выборочной совокупности.
• Случайные ошибки репрезентативности обусловлены действием случайных
10:21:25 PM
4
факторов, не содержащих каких-либо элементов системности

5.

В 1936 г. в США проводился опрос, проведенный «Литэрари Дайджест»
(«Литературное обозрение») относительно исхода президентских выборов.
Кандидатами на этих выборах были Ф. Д. Рузвельт и А. М. Ландон. Редакция
журнала организовала план выборки следующим образом. В выборку попали
более двух миллионов американцев, выбранных при помощи случайного
отбора из списков, имеющихся в телефонных книгах. По всей стране
попавшим в выборку лицам были разосланы открытки с просьбой назвать
фамилию будущего президента. Затратив огромную сумму на рассылку, сбор и
обработку полученных открыток, журнал информировал общественность, что
на предстоящих выборах президентом США с большим перевесом будет
избран А. М. Ландон. Результаты выборов опровергли этот прогноз.
В то же время социологи Д. Гэллап и Э. Роупер правильно предсказали победу
Ф. Д. Рузвельта, основываясь только на четырех тысячах анкет.
Ошибочный прогноз относительно возможного президента объясняется
неправильным планом выборки, который не обеспечил полного отражения в
ней всей генеральной совокупности: в телефонных книгах, которые
использовались для организации выборки, были представлены лишь наиболее
обеспеченные слои американского населения. Поскольку обеспеченные слои
американцев составляли меньшую часть генеральной совокупности, то
распространение мнения этой части населения на всю страну в целом
оказалось
10:21:25 PM ошибочным.
5

6. Задачи выборочного метода

Определение доверительного интервала, в котором
находится характеристика генеральной
совокупности
Определение минимального объема выборки
Определение доверительной вероятности того, что
разность между характеристиками выборочной и
генеральной совокупностей не превзойдет наперед
заданного числа
10:21:25 PM
6

7.

Основные обозначения:
N– объем генеральной совокупности (количество единиц
генеральной совокупности);
n – объем выборочной совокупности (количество единиц
выборочной совокупности);
x — генеральная средняя (средняя величина, которая имеет место в
генеральной совокупности);
~x — выборочная среднее;
М – численность единиц генеральной совокупности
определенным вариантом (численность городского населения,
число нерентабельных предприятий и т.д.);
m — численность единиц выборочной совокупности определенным
вариантом;
Р – генеральная доля, т.е. доля единиц, обладающих
определенным вариантом (доля городского населения, доля
нерентабельных предприятий), определяется как M/N;
w – выборочная доля, т.е. доля единиц, обладающих
определенным вариантом, определяется как m/n;
μ — средняя ошибка выборки;
Δ — предельная ошибка выборки
10:21:25 PM
7

8. Теорема П.Л. Чебышева

• При достаточно большом числе независимых наблюдений можно
с вероятностью, близкой к единице (т.е. почти с достоверностью),
утверждать, что отклонение выборочной средней от генеральной
будет сколько угодно малым.
• В теореме доказано, что величина предельной ошибки Δ не
должна превышать tμ, где t — число, связанное с вероятностью
через таблицу закона нормального распределения.
• В свою очередь, величина μ, выражающая среднее
квадратическое отклонение выборочной средней от генеральной
средней, зависит от колеблемости признака в генеральной
совокупности σ и числа отобранных единиц n. Эта величина
называется средней ошибкой выборки и выражается формулой:
2
n
10:21:25 PM
μ зависит также и от способа производства выборки.
8

9. Теорема А.М. Ляпунова

Вероятность предельной ошибки при достаточно большом объеме
выборки подчиняется закону нормального распределения
P t
t2
e 2 dt
1
2 t
t
F( t )
• Значения этого интеграла для различных значений коэффициента
доверия t приводятся в специальных математических таблицах. В
частности, при t = 1, Р = 0,683; t = 2, Р = 0,954; t = 3, Р = 0,997;
это может быть прочитано так: в 68,3% случаев ошибка
репрезентативности не выйдет за пределы ± μ.
• Зная выборочную среднюю величину признака ( ~x ) и предельную
ошибку выборки Δ, можно определить границы (пределы), в
которых заключена генеральная средняя: ~x ~x x ~x ~x
~x x ~
x
или
. Зная выборочную долю признака (w) , можно
определить
доля (р):
w p генеральная
w границы,
p w в которых заключена
10:21:25 PM
w
w
w9

10.

Из теорем Чебышева, Ляпунова и закона больших чисел
следует:
Хотя каждая выборочная средняя отличается от
генеральной, среднее значение по ним равно
генеральной:
~
x
n
10:21:25 PM
x
10

11. Условия проведения выборки

Выборка будет представлять всю совокупность с
приемлемой точностью при выполнении двух условий.
Во-первых, она должна быть достаточно многочисленной,
чтобы в ней могли проявиться закономерности,
существующие в генеральной совокупности.
Во-вторых, элементы выборки должны быть отобраны
объективно, независимо от воли исследователя, чтобы
каждый из них имел одинаковые шансы быть
отобранным или чтобы эти шансы были известны
исследователю.
10:21:25 PM
11

12. Способы отбора

• По виду различают индивидуальный, групповой и
комбинированный отбор. При индивидуальном отборе в
выборочную совокупность отбираются отдельные единицы
генеральной совокупности, при групповом отборе – группы
единиц, а комбинированный отбор предполагает сочетание
группового и индивидуального отбора.
• Способ отбора определяет конкретный механизм или процедуру
выборки единиц из генеральной совокупности. В практике
выборочных обследований наибольшее распространение
получили следующие выборки:
• собственно-случайная;
• механическая;
• типическая (стратифицированная);
• серийная;
10:21:25 PM
12
• комбинированная.

13. 1. Простая случайная выборка

при которой n объектов случайно извлекаются из генеральной
совокупности N объектов (например с помощью таблицы или
датчика случайных чисел), причем каждая из возможных
выборок имеют равную вероятность. Такие выборки называются
собственно-случайными.
Случайная выборка — основа всех других способов отбора.
Случайная выборка осуществляется методом жеребьевки: все
единицы совокупности нумеруются, номера записываются на
карточки, а потом отбираются.
На практике осуществляется с помощью таблиц случайных чисел.
10:21:25 PM
13

14. Формулы предельных ошибок выборки

• Если отбор единиц из генеральной совокупности произведен
бесповторным способом, то в формулы средней ошибки выборки
вносится поправка: 1 n
N
Наименование ошибки
Способ отбора
повторный
бесповторный
Средняя ошибка :
для средней
2
n
для доли
w(1 w )
n
2
n
1
n
N
w(1 w )
n
1
n
N
Предельная ошибка :
для средней
для10:21:25
долиPM
2
~x t
n
p t
w(1 w )
n
~x t
14
p
t
2
n
n
1
N
w(1 w )
n
1
n
N

15.

Пример. Для определения среднего срока службы изделий было
обследовано 250 изделий. При этом средний срок службы был
установлен на уровне 41,9 месяца. Среднее квадратическое
отклонение равно 6,2 месяцам.
С вероятностью 0,9973 определить, в каких пределах
находится средний срок службы всех изделий.
Р=0,9973, t=3 (из таблицы интеграла вероятностей закона
нормального распределения).
2
6, 2
~x 3
1,2мес
250
41,9 1,2 x 41,9 1,2
40,7мес x 43,1мес
Определить вероятность того,
что предельная ошибка
среднего срока службы
не превысит 1 месяц.
10:21:25 PM
t
~x
2
n
p 0,9892
1
2
6, 2
250
15
2,55

16. .

Пример. Определение минимального объема выборки
Сколько следует прохронометрировать операций, чтобы с
. вероятностью 0,9973 можно было бы утверждать, что разность
между средней продолжительностью операций в выборочной и
генеральной совокупности не превысит 1 секунды, если по
результатам предыдущего испытания установлено, что средняя
продолжительность операции равна 30 секундам, а среднее
квадратическое отклонение равно 7 секундам?
n ?
1
2
2
2
2
t
3 7
n 2
441
2
x
1
Ответ: нужно прохронометрировать не менее 441 операции.
10:21:25 PM
16

17. 2. Механическая (систематическая) выборка

применяется в случаях, когда генеральная совокупность какимлибо образом упорядочена, т.е. имеется определенная
последовательность в расположении единиц (табельные номера
работников, списки избирателей, телефонные номера
респондентов, номера домов и квартир и т. п.).
• Для проведения механической выборки устанавливается
пропорция отбора, которая определяется соотнесением объемов
выборочной и генеральной совокупностей. Отбор единиц
осуществляется в соответствии с установленной пропорцией
через равные интервалы. Например, при пропорции 1 : 50
(2%-ная выборка) отбирается каждая 50-я единица, при пропорции
1 : 20 (5 %-ная выборка) — каждая 20-я единица и т. д.
• Для определения средней ошибки механической выборки
используется формула средней ошибки при собственнослучайном
бесповторном отборе.
10:21:25 PM
17

18. 3. Типическая (стратифицированная) выборка

заключается в том, что генеральная совокупность объема N
подразделяется на части совокупности или слои (страты)
объема N1, N2, … , Nr, так что N1 + N2 + … + Nr = N.
Страты — однородные объекты с точки зрения статистических
характеристик. Например:
сельское
население
городское
из каждой типической группы отбирается
некоторое количество единиц.
Отбор может быть как пропорциональным
объёму типических групп, так и
непропорциональным
10:21:26 PM
18

19. Объем типической выборки

При отборе, пропорциональном объему типических групп,
число наблюдений по каждой группе определяется по
формуле:
Ni
ni n
N
ni -объем выборки из i-й типической группы.
n-общий объем выборки.
Ni-объем i -й типической группы в генеральной
совокупности.
N-объем генеральной совокупности.
10:21:26 PM
19

20. 4. Серийная выборка

• Приемы серийного отбора используются для
формирования серийных или гнездовых выборок. Они
удобны в том случае, если необходимо обследовать сразу
«блок» или серию объектов (например, партию товара,
продукцию определенной серии или предприятия
территориально-административной единицы).
• Вся совокупность делится на серии, после чего
механическим или собственно случайным способом
отбирается некоторое количество серий. Все единицы
совокупности, входящие в отобранные серии,
подвергаются сплошному контролю.
10:21:26 PM
20

21. Объем выборки

Число наблюдений n, образующих выборку, называется объемом
выборки. Если объем выборки n достаточно велик (n ),
выборка считается большой, в противном случае она называется
выборкой ограниченного объема.
Выборка считается малой, если при измерении одномерной
случайной величины X объем выборки не превышает 30 (n <= 30),
а при измерении одновременно нескольких (k) признаков в
многомерном пространстве отношение n к k не превышает 10
(n/k < 10).
Если мы работаем с обычной выборкой, то используется таблица
«Интеграла вероятностей закона нормального распределения».
В случае малой выборки необходимо пользоваться таблицей
«Распределение Стьюдента», при этом число степеней свободы :
K=n-1
10:21:26 PM
21

22. Определение необходимого объема выборки .

• Для определения необходимой численности выборки
исследователь должен задать уровень точности выборочной
совокупности с определенной вероятностью. В частности,
необходимая численность случайной повторной выборки
определяется по формуле:
t2 2
n
2
2
• которая вытекает из формулы предельной ошибки: t
n
• Эта формула показывает, что с увеличением предполагаемой
ошибки выборки значительно уменьшается необходимый объем
выборки. Так, увеличение допустимой ошибки выборки в 2 раза
уменьшает необходимый ее объем в 4 раза. Необходимая
численность выборки прямо пропорциональна дисперсии 2
признака и величине t 2 .
10:21:26 PM
22

23.

Вид выборочного
наблюдения
Повторный отбор
Бесповторный отбор
Собственно-случайная выборка, механическая выборка:
а) при определении
2
2
2
2
~x N
t
~x
t
среднего размера
n 2
n
2
~x N t 2 2~x
признака
~x
б) при определении доли
признака
10:21:26 PM
t 2 w (1 w )
n
2w
t 2 w(1 w ) N
n 2
w N t 2 w(1 w )
23

24.

Пример. В городе 2000 семей. Предполагается провести
выборочное обследование методом случайной бесповторной
выборки для нахождения среднего размера семьи.
Определить необходимую численность выборки
при условии, что с вероятностью 0,954 ошибка
выборки не превысит 1 человека при среднем
квадратическом отклонении 3 человека.
Решение
t2 2 N
4 9 2000
n
36
2
2
2
2000 1 4 9
N x t
Т.е. необходимо обследовать не менее 36 семей.
10:21:26 PM
24