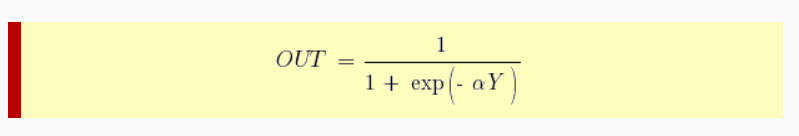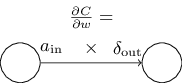Метод обратного распространения ошибки (англ. backpropagation)— метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. А.И. Галушкиным[1], а также независимо и одновременно Полом Дж. Вербосом[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом[3] и независимо и одновременно С.И. Барцевым и В.А. Охониным (Красноярская группа)[4].. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.
Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределённые системы, и т. п.[5]
Для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. Метод является модификацией классического метода градиентного спуска.
Содержание
- 1 Сигмоидальные функции активации
- 2 Функция оценки работы сети
- 3 Описание алгоритма
- 4 Алгоритм
- 5 Математическая интерпретация обучения нейронной сети
- 6 Недостатки алгоритма
- 6.1 Паралич сети
- 6.2 Локальные минимумы
- 6.3 Размер шага
- 7 Литература
- 8 Ссылки
- 9 Примечания
Сигмоидальные функции активации[править | править вики-текст]
Наиболее часто в качестве функций активации используются следующие виды сигмоид:
Функция Ферми (экспоненциальная сигмоида):
Рациональная сигмоида (
Гиперболический тангенс:
,
где s — выход сумматора нейрона, 
Менее всего, сравнительно с другими сигмоидами, процессорного времени требует расчет рациональной сигмоиды. Для вычисления гиперболического тангенса требуется больше всего тактов работы процессора. Если же сравнивать с пороговыми функциями активации, то сигмоиды рассчитываются очень медленно. Если после суммирования в пороговой функции сразу можно начинать сравнение с определенной величиной (порогом), то в случае сигмоидальной функции активации нужно рассчитать сигмоид (затратить время в лучшем случае на три операции: взятие модуля, сложение и деление), и только потом сравнивать с пороговой величиной (например, нулём). Если считать, что все простейшие операции рассчитываются процессором за примерно одинаковое время, то работа сигмоидальной функции активации после произведённого суммирования (которое займёт одинаковое время) будет медленнее пороговой функции активации как 1:4.
Функция оценки работы сети[править | править вики-текст]
В тех случаях, когда удается оценить работу сети, обучение нейронных сетей можно представить как задачу оптимизации. Оценить — означает указать количественно, хорошо или плохо сеть решает поставленные ей задачи. Для этого строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) — от всех её параметров. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:
,
где 
Метод наименьших квадратов далеко не всегда является лучшим выбором оценки. Тщательное конструирование функции оценки позволяет на порядок повысить эффективность обучения сети, а также получать дополнительную информацию — «уровень уверенности» сети в даваемом ответе[6].
Описание алгоритма[править | править вики-текст]
Архитектура многослойного перцептрона
Алгоритм обратного распространения ошибки применяется для многослойного перцептрона. У сети есть множество входов 




Как модифицировать веса? Мы будем реализовывать стохастический градиентный спуск, то есть будем подправлять веса после каждого обучающего примера и, таким образом, «двигаться» в многомерном пространстве весов. Чтобы «добраться» до минимума ошибки, нам нужно «двигаться» в сторону, противоположную градиенту, то есть, на основании каждой группы правильных ответов, добавлять к каждому весу
,
где 
Производная считается следующим образом. Пусть сначала 


Аналогично, 

где 
Если же j-й узел — не на последнем уровне, то у него есть выходы; обозначим их через Children(j). В этом случае
,
и
.
Ну а 



- для узла последнего уровня
- для внутреннего узла сети
- для всех узлов
, где 

Получающийся алгоритм представлен ниже. На вход алгоритму, кроме указанных параметров, нужно также подавать в каком-нибудь формате структуру сети. На практике очень хорошие результаты показывают сети достаточно простой структуры, состоящие из двух уровней нейронов — скрытого уровня (hidden units) и нейронов-выходов (output units); каждый вход сети соединен со всеми скрытыми нейронами, а результат работы каждого скрытого нейрона подается на вход каждому из нейронов-выходов. В таком случае достаточно подавать на вход количество нейронов скрытого уровня.
Алгоритм[править | править вики-текст]
Алгоритм: BackPropagation
- Инициализировать
маленькими случайными значениями,
- Повторить NUMBER_OF_STEPS раз:
- Для всех d от 1 до m:
- Подать
на вход сети и подсчитать выходы
каждого узла.
- Для всех
.
- Для каждого уровня l, начиная с предпоследнего:
- Для каждого узла j уровня l вычислить
.
- Для каждого ребра сети {i, j}
.
.
- Выдать значения
.
где 
Математическая интерпретация обучения нейронной сети[править | править вики-текст]
На каждой итерации алгоритма обратного распространения весовые коэффициенты нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации.
Обучение нейронной сети характеризуется четырьмя специфическими ограничениями, выделяющими обучение нейросетей из общих задач оптимизации: астрономическое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач, необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. В остальном проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы («как правило») связана с тем, что на самом деле нам неизвестны и никогда не будут известны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки. Минимизация оценки — сложная проблема: параметров астрономически много (для стандартных примеров, реализуемых на РС — от 100 до 1000000), адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов.
Недостатки алгоритма[править | править вики-текст]
Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Паралич сети[править | править вики-текст]
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.
Локальные минимумы[править | править вики-текст]
Обратное распространение использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Основную трудность при обучении нейронных сетей составляют как раз методы выхода из локальных минимумов: каждый раз выходя из локального минимума снова ищется следующий локальный минимум тем же методом обратного распространения ошибки до тех пор, пока найти из него выход уже не удаётся.
Размер шага[править | править вики-текст]
Внимательный разбор доказательства сходимости[3] показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведёт к бесконечному времени обучения. Размер шага должен браться конечным. Если размер шага фиксирован и очень мал, то сходимость слишком медленная, если же он фиксирован и слишком велик, то может возникнуть паралич или постоянная неустойчивость. Эффективно увеличивать шаг до тех пор, пока не прекратится улучшение оценки в данном направлении антиградиента и уменьшать, если такого улучшения не происходит. П. Д. Вассерман[7] описал адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения. В книге А. Н. Горбаня[8] предложена разветвлённая технология оптимизации обучения.
Следует также отметить возможность переобучения сети, что является скорее результатом ошибочного проектирования её топологии. При слишком большом количестве нейронов теряется свойство сети обобщать информацию. Весь набор образов, предоставленных к обучению, будет выучен сетью, но любые другие образы, даже очень похожие, могут быть классифицированы неверно.
Литература[править | править вики-текст]
- Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика. — М.: «Мир», 1992.
- Хайкин С. Нейронные сети: Полный курс. Пер. с англ. Н. Н. Куссуль, А. Ю. Шелестова. 2-е изд., испр. — М.: Издательский дом Вильямс, 2008, 1103 с.
Ссылки[править | править вики-текст]
- Копосов А. И., Щербаков И. Б., Кисленко Н. А., Кисленко О. П., Варивода Ю. В. и др. Отчет по научно-исследовательской работе «Создание аналитического обзора информационных источников по применению нейронных сетей для задач газовой технологии». — М.: ВНИИГАЗ, 1995.
- Книги по нейроинформатике на сайте NeuroSchool.
- Терехов С. А., Лекции по теории и приложениям искусственных нейронных сетей.
- Миркес Е. М., Нейроинформатика: Учеб. пособие для студентов с программами для выполнения лабораторных работ. Красноярск: ИПЦ КГТУ, 2002, 347 с. Рис. 58, табл. 59, библиогр. 379 наименований. ISBN 5-7636-0477-6
- Принцип обучения многослойной нейронной сети с помощью алгоритма обратного распространения
- Алгоритм обратного распространения ошибки с регуляризацией на C#
Примечания[править | править вики-текст]
- ↑ Галушкин А. И. Синтез многослойных систем распознавания образов. — М.: «Энергия», 1974.
- ↑ Werbos P. J., Beyond regression: New tools for prediction and analysis in the behavioral sciences. Ph.D. thesis, Harvard University, Cambridge, MA, 1974.
- ↑ 1 2 Rumelhart D.E., Hinton G.E., Williams R.J., Learning Internal Representations by Error Propagation. In: Parallel Distributed Processing, vol. 1, pp. 318—362. Cambridge, MA, MIT Press. 1986.
- ↑ Барцев С. И., Охонин В. А. Адаптивные сети обработки информации. Красноярск : Ин-т физики СО АН СССР, 1986. Препринт N 59Б. — 20 с.
- ↑ Барцев С. И., Гилев С. Е., Охонин В. А., Принцип двойственности в организации адаптивных сетей обработки информации, В кн.: Динамика химических и биологических систем. — Новосибирск: Наука, 1989. — С. 6-55.
- ↑ Миркес Е. М., Нейрокомпьютер. Проект стандарта. — Новосибирск: Наука, Сибирская издательская фирма РАН, 1999. — 337 с. ISBN 5-02-031409-9 Другие копии онлайн: [1].
- ↑ Wasserman P. D. Experiments in translating Chinese characters using backpropagation. Proceedings of the Thirty-Third IEEE Computer Society International Conference. — Washington: D. C.: Computer Society Press of the IEEE, 1988.
- ↑ Горбань А. Н. Обучение нейронных сетей. — М.: СП ПараГраф, 1990.
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(\ldots (g_1(x)) \ldots))$, то $\frac{\partial f}{\partial x} = \frac{\partial g_m}{\partial g_{m-1}}\frac{\partial g_{m-1}}{\partial g_{m-2}}\ldots \frac{\partial g_2}{\partial g_1}\frac{\partial g_1}{\partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $\frac{\partial g_m}{\partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(\ldots g_1(w_0)\ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(\ldots g_1(w_0)\ldots))\cdot g’_{m-1}(g_{m-2}(\ldots g_1(w_0)\ldots))\cdot\ldots \cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),\ldots,g_{m-1}(\ldots g_1(w_0)\ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(\ldots g_1(w_0)\ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(\ldots g_1(w_0)\ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
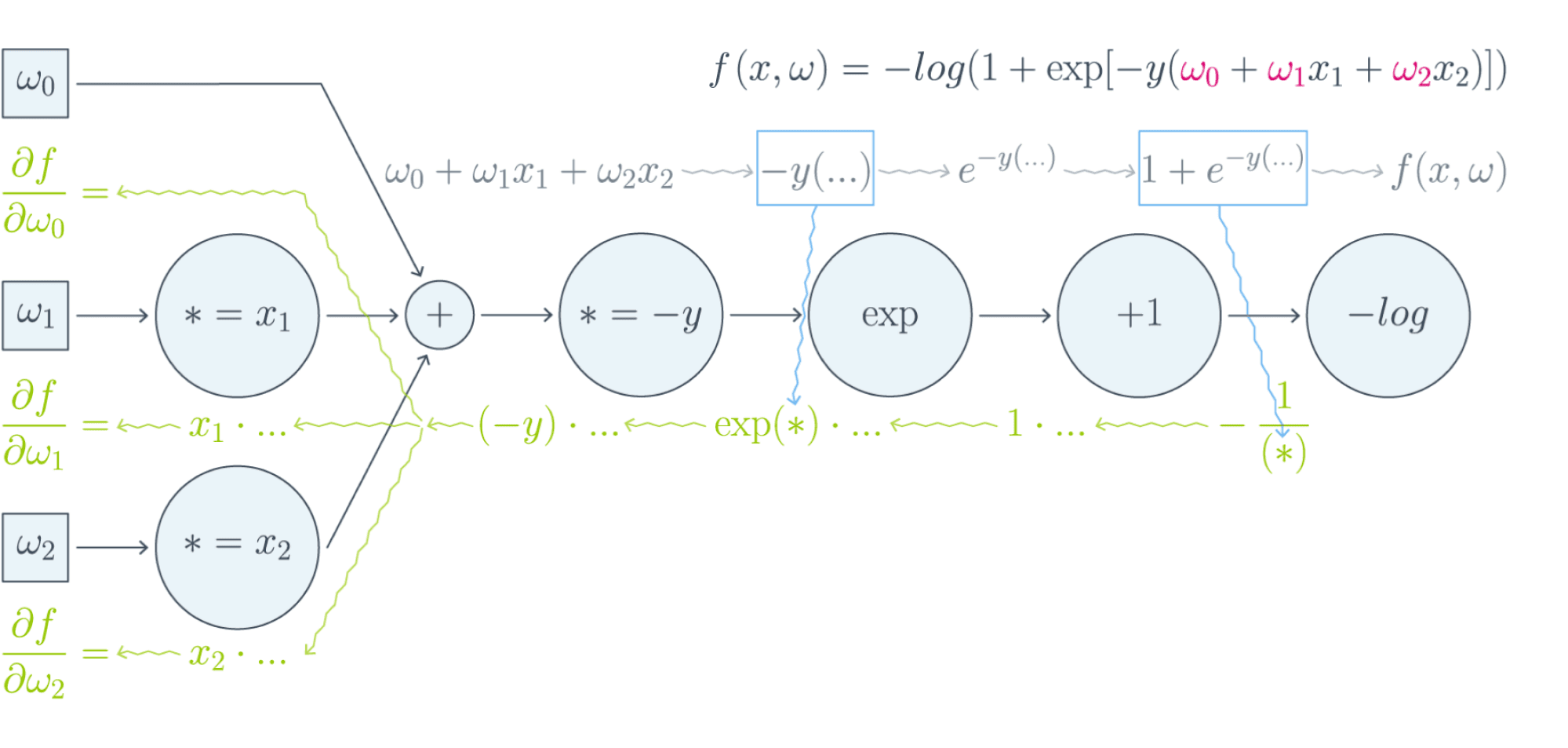
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$\frac{\partial f}{\partial w_0} = (-y)\cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}\cdot\frac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$\frac{\partial f}{\partial w_1} = x_1\cdot(-y)\cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}\cdot\frac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$\frac{\partial f}{\partial w_2} = x_2\cdot(-y)\cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}\cdot\frac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $N\times M$ и $N\times K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $\frac{\partial\mathcal{L}}{\partial X^{r+1}_{ij}}$ функции потерь $\mathcal{L}$, тогда
$$\frac{\partial\mathcal{L}}{\partial X^{r}_{st}} = \sum_{i,j}\frac{\partial f^{r+1}_{ij}}{\partial X^{r}_{st}}\frac{\partial\mathcal{L}}{\partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $\frac{\partial\mathcal{L}}{\partial X_{ij}^{r+1}}$ и $\frac{\partial\mathcal{L}}{\partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $\frac{\partial f_{ij}^{r+1}}{\partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $\frac{\partial f^{r+1}}{\partial X^{r}}$ рассматривать не как вычисляемые объекты $\frac{\partial f_{ij}^{r+1}}{\partial X_{st}^{r}}$, а как преобразования, которые превращают $\frac{\partial\mathcal{L}}{\partial X_{ij}^{r+1}}$ в $\frac{\partial\mathcal{L}}{\partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx,\ A\in Mat_{n}{\mathbb{R}}\text{ — матрица размера }n\times n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$\left[D_{x_0} (\color{#5002A7}{u} \circ \color{#4CB9C0}{v}) \right](h) = \color{#5002A7}{\left[D_{v(x_0)} u \right]} \left( \color{#4CB9C0}{\left[D_{x_0} v\right]} (h)\right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$\left[D_{x_0} f \right] (x-x_0) = \langle\nabla_{x_0} f, x-x_0\rangle.$$
С другой стороны,
$$\left[D_{h(x_0)} g \right] \left(\left[D_{x_0}h \right] (x-x_0)\right) = \langle\nabla_{h_{x_0}} g, \left[D_{x_0} h\right] (x-x_0)\rangle = \langle\left[D_{x_0} h\right]^* \nabla_{h(x_0)} g, x-x_0\rangle.$$
То есть $\color{#FFC100}{\nabla_{x_0} f} = \color{#348FEA}{\left[D_{x_0} h \right]}^* \color{#FFC100}{\nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $\nabla_{h(x_0)} g$.
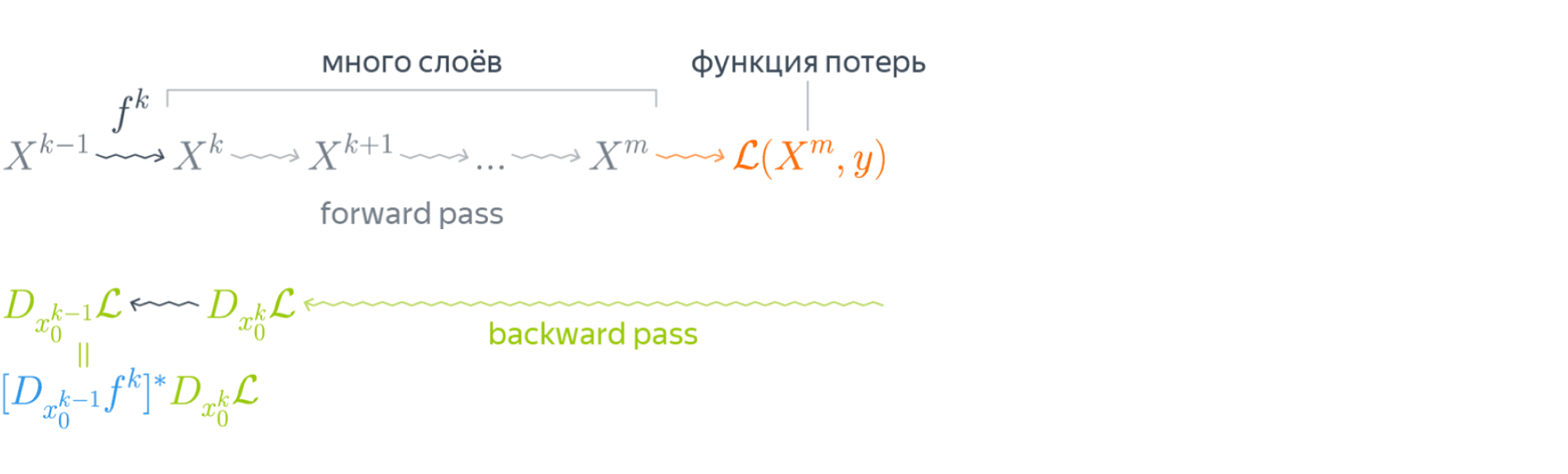
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$v\begin{pmatrix}
x_1 \\
\vdots\\
x_N
\end{pmatrix}
= \begin{pmatrix}
v(x_1)\\
\vdots\\
v(x_N)
\end{pmatrix}$$Тогда, как мы знаем,
$$\left[D_{x_0} f\right] (h) = \langle\nabla_{x_0} f, h\rangle = \left[\nabla_{x_0} f\right]^T h.$$
Следовательно,
$$
\left[D_{v(x_0)} u\right] \left( \left[ D_{x_0} v\right] (h)\right) = \left[\nabla_{v(x_0)} u\right]^T \left(v'(x_0) \odot h\right) =\\
$$$$
= \sum\limits_i \left[\nabla_{v(x_0)} u\right]_i v'(x_{0i})h_i
= \langle\left[\nabla_{v(x_0)} u\right] \odot v'(x_0), h\rangle.
,$$где $\odot$ означает поэлементное перемножение. Окончательно получаем
$$\color{#348FEA}{\nabla_{x_0} f = \left[\nabla_{v(x_0)}u\right] \odot v'(x_0) = v'(x_0) \odot \left[\nabla_{v(x_0)} u\right]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $\frac{\partial f}{\partial x_i} = \sum_j\big(\frac{\partial z_j}{\partial x_i}\big)\cdot\big(\frac{\partial h}{\partial z_j}\big)$. В этом случае матрица $\big(\frac{\partial z_j}{\partial x_i}\big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $\big(\frac{\partial z_j}{\partial x_i}\big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$\left[D_{X_0} f \right] (X-X_0) = \text{tr}, \left(\left[\nabla_{X_0} f\right]^T (X-X_0)\right).$$
Тогда
$$
\left[ D_{X_0W} g \right] \left(\left[D_{X_0} \left( \ast W\right)\right] (H)\right) =
\left[ D_{X_0W} g \right] \left(HW\right)=\\
$$ $$
= \text{tr}\, \left( \left[\nabla_{X_0W} g \right]^T \cdot (H) W \right) =\\
$$ $$
=
\text{tr} \, \left(W \left[\nabla_{X_0W} (g) \right]^T \cdot (H)\right) = \text{tr} \, \left( \left[\left[\nabla_{X_0W} g\right] W^T\right]^T (H)\right)
$$Здесь через $\ast W$ мы обозначили отображение $Y \hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
\text{tr} , (A B C) = \text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$\color{#348FEA}{\nabla_{X_0} f = \left[\nabla_{X_0W} (g) \right] \cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
\left[D_{W_0} f \right] (H) = \text{tr} , \left( \left[\nabla_{W_0} f \right]^T (H)\right)
$$Тогда
$$
\left[D_{XW_0} g \right] \left( \left[D_{W_0} \left(X \ast\right) \right] (H)\right) = \left[D_{XW_0} g \right] \left( XH \right) = \
$$ $$
= \text{tr} , \left( \left[\nabla_{XW_0} g \right]^T \cdot X (H)\right) =
\text{tr}, \left(\left[X^T \left[\nabla_{XW_0} g \right] \right]^T (H)\right)
$$Здесь через $X \ast$ обозначено отображение $Y \hookrightarrow XY$. Значит,
$$\color{#348FEA}{\nabla_{X_0} f = X^T \cdot \left[\nabla_{XW_0} (g)\right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $N\times K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = \left(\frac{e^{x_1}}{\sum_te^{x_t}},\ldots,\frac{e^{x_K}}{\sum_te^{x_t}}\right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $\frac{\partial s_l}{\partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = \frac{e^{x_l}} {\sum_te^{x_t}}$. Нетрудно проверить, что
$$\frac{\partial s_l}{\partial x_j} = \begin{cases}
s_j(1 — s_j),\ & j = l,\
-s_ls_j,\ & j\ne l
\end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$\frac{\partial s_{rl}}{\partial x_{ij}} = \begin{cases}
s_{ij}(1 — s_{ij}),\ & r=i, j = l,\
-s_{il}s_{ij},\ & r = i, j\ne l,\
0,\ & r\ne i
\end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $\nabla_{rl} = \nabla g = \frac{\partial\mathcal{L}}{\partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$\frac{\partial\mathcal{L}}{\partial x_{ij}} = \sum_{r,l}\frac{\partial s_{rl}}{\partial x_{ij}} \nabla_{rl}$$
Так как $\frac{\partial s_{rl}}{\partial x_{ij}} = 0$ при $r\ne i$, мы можем убрать суммирование по $r$:
$$\ldots = \sum_{l}\frac{\partial s_{il}}{\partial x_{ij}} \nabla_{il} = -s_{i1}s_{ij}\nabla_{i1} — \ldots + s_{ij}(1 — s_{ij})\nabla_{ij}-\ldots — s_{iK}s_{ij}\nabla_{iK} =$$
$$= -s_{ij}\sum_t s_{it}\nabla_{it} + s_{ij}\nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$\begin{multline*}
\color{#348FEA}{\nabla_{X_0}f =}\\
\color{#348FEA}{= -softmax(X_0) \odot \text{sum}\left(
softmax(X_0)\odot\nabla_{softmax(X_0)}g, \text{ axis = 1}
\right) +}\\
\color{#348FEA}{softmax(X_0)\odot \nabla_{softmax(X_0)}g}
\end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, \ldots, X^m = \widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
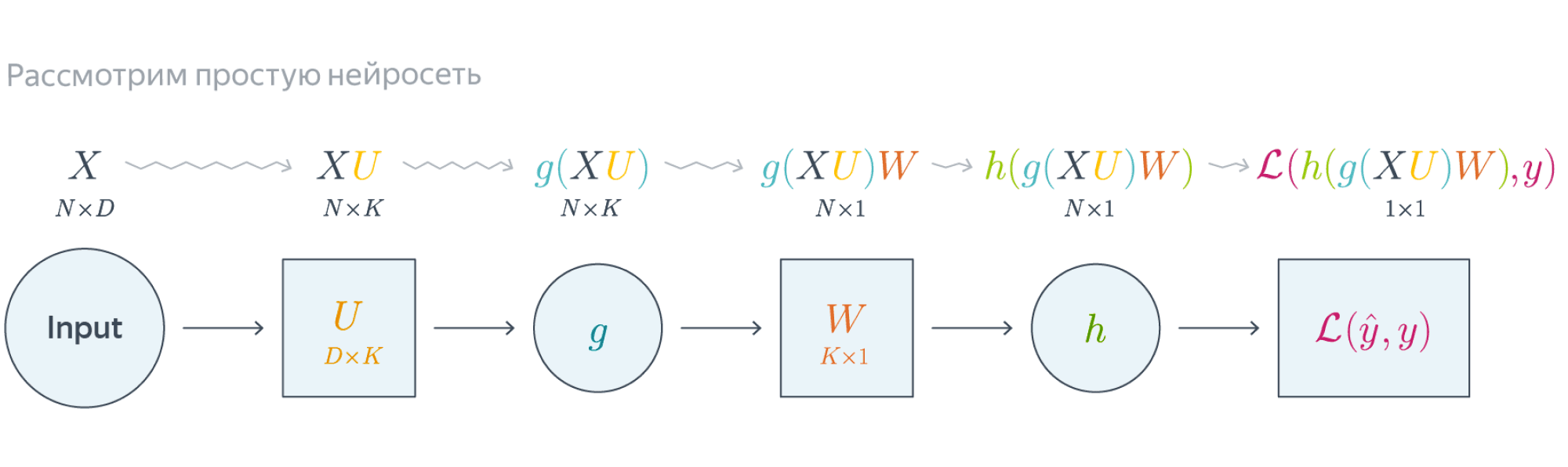
$$\nabla_{W_0}\mathcal{L} = \nabla_{W_0}{\left({\vphantom{\frac12}\mathcal{L}\circ h\circ\left[W\mapsto g(XU_0)W\right]}\right)}=$$
$$=g(XU_0)^T\nabla_{g(XU_0)W_0}(\mathcal{L}\circ h) = \underbrace{g(XU_0)^T}_{k\times N}\cdot
\left[\vphantom{\frac12}\underbrace{h’\left(\vphantom{\int_0^1}g(XU_0)W_0\right)}_{N\times 1}\odot
\underbrace{\nabla_{h\left(\vphantom{\int_0^1}g(XU_0)W_0\right)}\mathcal{L}}_{N\times 1}\right]$$
Итого матрица $k\times 1$, как и $W_0$
$$\nabla_{U_0}\mathcal{L} = \nabla_{U_0}\left(\vphantom{\frac12}
\mathcal{L}\circ h\circ\left[Y\mapsto YW_0\right]\circ g\circ\left[ U\mapsto XU\right]
\right)=$$
$$=X^T\cdot\nabla_{XU^0}\left(\vphantom{\frac12}\mathcal{L}\circ h\circ [Y\mapsto YW_0]\circ g\right) =$$
$$=X^T\cdot\left(\vphantom{\frac12}g'(XU_0)\odot
\nabla_{g(XU_0)}\left[\vphantom{\in_0^1}\mathcal{L}\circ h\circ[Y\mapsto YW_0\right]
\right)$$
$$=\ldots = \underset{D\times N}{X^T}\cdot\left(\vphantom{\frac12}
\underbrace{g'(XU_0)}_{N\times K}\odot
\underbrace{\left[\vphantom{\int_0^1}\left(
\underbrace{h’\left(\vphantom{\int_0^1}g(XU_0)W_0\right)}_{N\times1}\odot\underbrace{\nabla_{h(\vphantom{\int_0^1}g\left(XU_0\right)W_0)}\mathcal{L}}_{N\times 1}
\right)\cdot \underbrace{W^T}_{1\times K}\right]}_{N\times K}
\right)$$
Итого $D\times K$, как и $U_0$
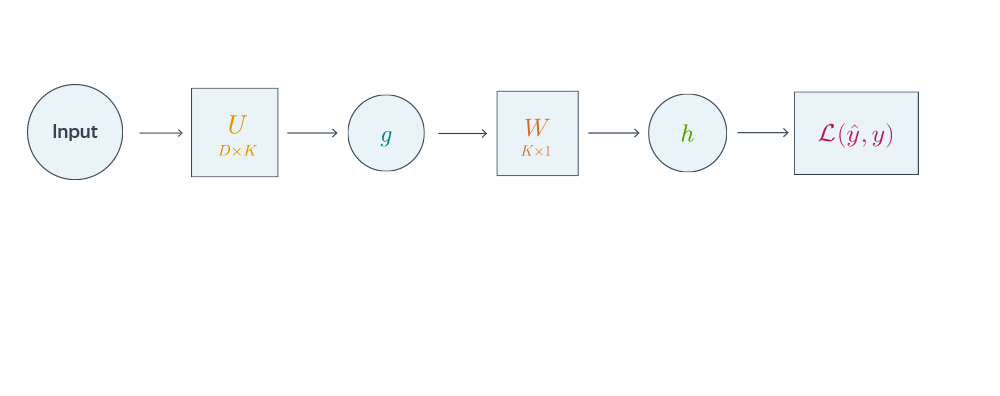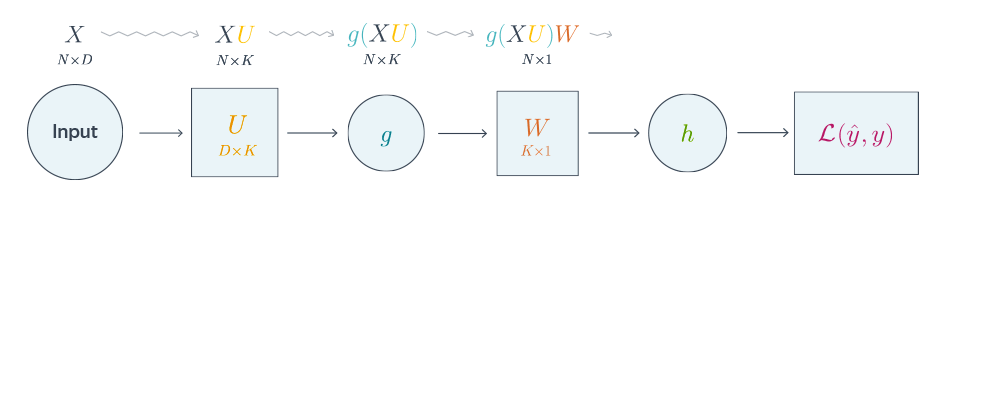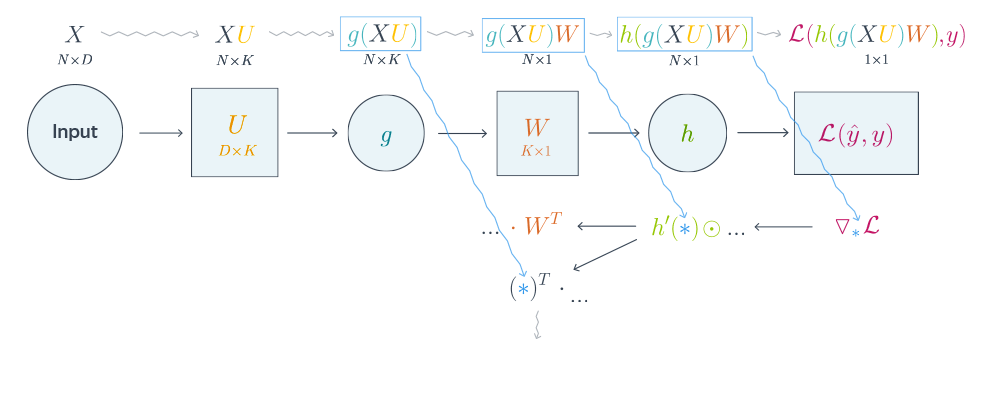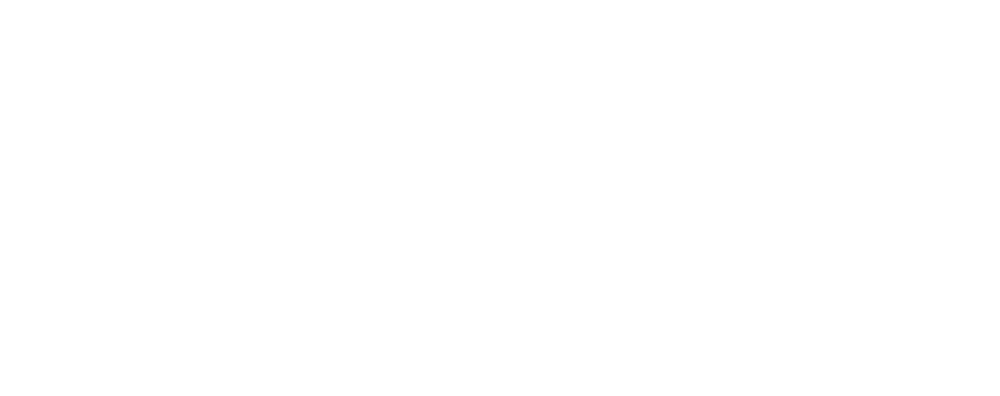
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = \sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
\widehat{y} = \sigma(X^1 W^2) = \sigma\Big(\big(\sigma(X^0 W^1 )\big) W^2 \Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = \sigma(X^0 W^1_0)$, $X^3 = \sigma(X^0 W^1_0) W^2_0$, $X^4 = \sigma(\sigma(X^0 W^1_0) W^2_0) = \widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = \mathcal{L}(y, \widehat{y}) = y \log(\widehat{y}) + (1-y) \log(1-\widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $\mathcal{L}$ по предсказаниям имеет вид
$$
\nabla_{\widehat{y}}l = \frac{y}{\widehat{y}} — \frac{1 — y}{1 — \widehat{y}} = \frac{y — \widehat{y}}{\widehat{y} (1 — \widehat{y})},
$$где, напомним, $ \widehat{y} = \sigma(X^3) = \sigma\Big(\big(\sigma(X^0 W^1_0 )\big) W^2_0 \Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $\sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $\sigma$, в которую подставлено предыдущее промежуточное представление:
$$
\nabla_{X^3}l = \sigma'(X^3)\odot\nabla_{\widehat{y}}l = \sigma(X^3)\left( 1 — \sigma(X^3) \right) \odot \frac{y — \widehat{y}}{\widehat{y} (1 — \widehat{y})} =
$$$$
= \sigma(X^3)\left( 1 — \sigma(X^3) \right) \odot \frac{y — \sigma(X^3)}{\sigma(X^3) (1 — \sigma(X^3))} =
y — \sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
\color{blue}{\nabla_{W^2_0}l} = (X^2)^T\cdot \nabla_{X^3}l = (X^2)^T\cdot(y — \sigma(X^3)) =
$$$$
= \color{blue}{\left( \sigma(X^0W^1_0) \right)^T \cdot (y — \sigma(\sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
\nabla_{X^2}l = \nabla_{X^3}l\cdot (W^2_0)^T = (y — \sigma(X^3))\cdot (W^2_0)^T =
$$$$
= (y — \sigma(X^2W_0^2))\cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $\sigma$.
$$
\nabla_{X^1}l = \sigma'(X^1)\odot\nabla_{X^2}l = \sigma(X^1)\left( 1 — \sigma(X^1) \right) \odot \left( (y — \sigma(X^2W_0^2))\cdot (W^2_0)^T \right) =
$$$$
= \sigma(X^1)\left( 1 — \sigma(X^1) \right) \odot\left( (y — \sigma(\sigma(X^1)W_0^2))\cdot (W^2_0)^T \right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
\color{blue}{\nabla_{W^1_0}l} = (X^0)^T\cdot \nabla_{X^1}l = (X^0)^T\cdot \big( \sigma(X^1) \left( 1 — \sigma(X^1) \right) \odot (y — \sigma(\sigma(X^1)W_0^2))\cdot (W^2_0)^T\big) =
$$$$
= \color{blue}{(X^0)^T\cdot\big(\sigma(X^0W^1_0)\left( 1 — \sigma(X^0W^1_0) \right) \odot (y — \sigma(\sigma(X^0W^1_0)W_0^2))\cdot (W^2_0)^T\big) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}\mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $\nabla_{X^k_0}\mathcal{L}$ в $\nabla_{X^{k-1}_0}\mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $\nabla_{W^k_0}\mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.
Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.
Общее описание алгоритма обратного распространения ошибки
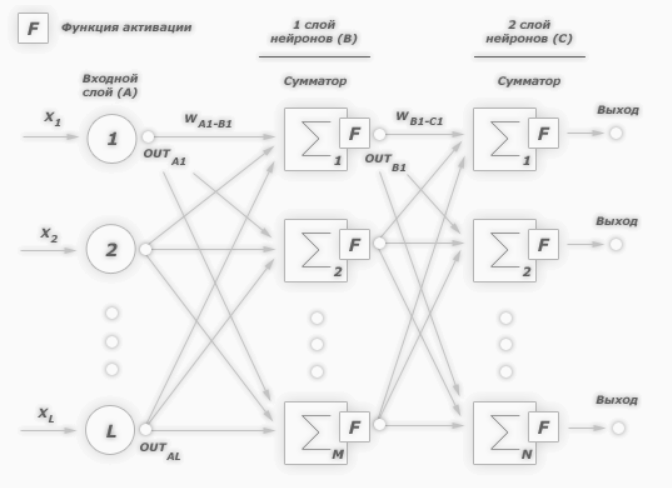
К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:
В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:
Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.
Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция. Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления. Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.
Цель обучения сети
Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.
Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.
При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.
Пошаговая реализация метода обратного распространения ошибки
Необходимо выполнить следующие действия:
1. Инициализировать синаптические веса случайными маленькими значениями.
2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор.
3. Выполнить вычисление выходных значений нейронной сети.
4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки.
6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.
Виды обучения сети по методу обратного распространения
Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).
Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.
Преимущества и недостатки метода
К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы:
• неопределенно долгий процесс обучения;
• вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»;
• алгоритм уязвим к попаданию в локальные минимумы функции ошибки.
Значение метода обратного распространения
Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.
Источники:
— «Алгоритм обратного распространения ошибки»;
— «Back propagation algorithm».
Впервые метод обратного распространения ошибки был описан в 1974 г. А. И. Галушкиным[1], а также независимо и одновременно Полом Дж. Вербосом[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом[3] и независимо и одновременно С.И. Барцевым и В.А. Охониным (Красноярская группа)[4]. Метод представляет собой итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного персептрона и получения желаемого выхода. Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. Метод является модификацией классического метода градиентного спуска.
Упрощенная модель
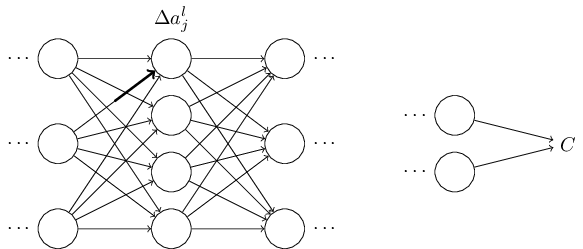
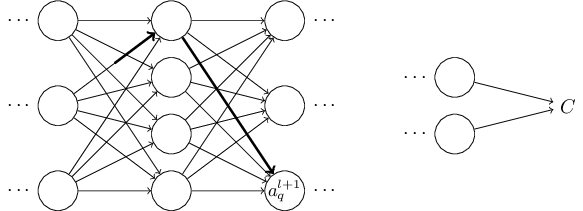
В основе обратного распространения лежит выражение для частной производной функции стоимости C относительно любого веса w (или смещения b ) в нейронной сети. Выражение говорит нам, как быстро меняется стоимость, когда мы меняем веса и смещения.
Для примера, будем рассматривать 4-слойную нейронную сеть, которая состоит из 4 нейронов для входного слоя, 4 нейронов для скрытых слоев и 1 нейрона для выходного слоя
Значения для скрытых нейронов (зеленый цвет), определяется по следующим формулам:
где z(2) — взвешенные входные данные и a(2) — активация для слоя 2. Аналогичная формула и для слоя 3. Активация a вычисляется с использованием функции активации, которая является нелинейной и дифференцируемой ( сигмоидальная, RELU, tanh). Далее для простоты представления переменных и их расчета используется матрица.
W¹ — это весовая матрица формы (n, m), где n — количество выходных нейронов (нейронов в следующем слое), а m — количество входных нейронов (нейронов в предыдущем слое). Для нас n = 2 и m = 4 .Первое число индекса веса обозначает индекс нейрона в следующем слое (Hidden2), а второй индекс нейрона в предыдущем слое (входной слой).
x — входной вектор матрицы (m, 1), где m — количество входных нейронов, в нашем случае m = 4.
b¹ — вектор смещения матрицы (n, 1), где n — число нейронов в текущем слое, в нашем случае n = 2 .
Таким образом уравнение для z(2) выглядит следующим образом:
И последнее уравнение для выходного слоя, который дает нам результат в виде предикативного значения. В нашем примере он представлен в виде одного нейрона, окрашенного в синий цвет.
Прямое распространение
Первоначально вычисляются значения переменных для прохода от входного слоя до выходного слоя.
Последним шагом в прямом проходе является оценка прогнозируемых выходных данных s относительно ожидаемого выходного значения y. Выразим функцию потерь C следующим образом:
Для оценки функции потерь обычно используют MSE (средняя квадратическая ошибка).
Получив значении C, модель определяет как нужно настроить ее параметры, чтобы приблизиться к ожидаемому результату y. Это происходит с использованием алгоритма обратного распространения.
Обратное распространение
Алгоритм обратного распространения основан на общих линейных алгебраических операциях — таких как сложение векторов, умножение вектора на матрицу и так далее. Обратное распространение направлено на минимизацию функции стоимости путем корректировки весов и смещений сети. Уровень корректировки определяется градиентами функции стоимости по отношению к этим параметрам. Для чего нужно определять градиенты ?
Сначала определимся с понятием градиента.
Градиент функции C (x_1, x_2,…, x_m) в точке x называется вектор частных производных C по x.
Производная функции C измеряет чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента x (входного значения) . Другими словами, производная говорит нам о том в каком направлении движется функция C.
Градиент показывает, насколько необходимо изменить параметр x (в положительном или отрицательном направлении), чтобы минимизировать функцию C.
Вычисление этих градиентов происходит с использованием техники, называемой цепным правилом.
Для одного веса градиент вычисляется по формуле:
Аналогичный набор уравнений может быть применен bjl.
Общую часть в обоих уравнениях называют «локальным градиентом»
Градиенты позволяют оптимизировать параметры модели:
Начальные значения w и b выбираются случайным образом или же, например, инициализатором Ксавье.
w и b — матричные представления весов и смещений. ε- скорость обучения . Производная C по w или b может быть рассчитана с использованием частных производных C по каждому весу или смещению. Завершаются вычисления после минимизации функции затрат.
Чтобы не усложнять процедуру вычислений, покажем на примере вычисления одного веса как работает обратное распространение. Вычислим значение градиента C относительно одного веса (w_22) ² .
Вес (w_22) ² соединяет (a_2) ² и (z_2) ² , поэтому для вычисления градиента необходимо применить правило цепочки из (z_2) ³ и (a_2) ³:
Общая модель
Обратное распространение основано на четырех фундаментальных уравнениях.
Первое уравнение определяет ошибку в выходном слое:
Первый член, δС/δajL, измеряет скорость изменения функции стоимости в зависимости от активации выхода jth. Второй член σ'(zjL) измеряет, насколько быстро активируется функция в зависимости от веса соответствующего входа.
Второе уравнение показывает ошибку в конкретном слое в зависимости от следующего слоя.
где первый член представляет собой вес транспонированной весовой матрицы для слоя l+1. Когда мы применяем матрицу транспонирования веса, wl+1, интуитивно это представляется как перемещение ошибки назад по сети. Комбинируя последовательно уравнение 1 и 2 мы можем вычислить ошибку для любого слоя сети.
Третье уравнение определяет скорость изменения стоимости относительно любого смещения в сети.
Четвертое уравнение вычисляет скорость изменения стоимости относительно любого веса в сети.
где первый множитель является активацией входа нейрона слоя k, а второй — δ, является ошибкой выхода нейрона слоя j , которые связаны весом w. Графически это можно изобразить так:
Следствием последнего уравнения является то, что когда активация ain мала, градиентный член ∂C/∂w также будет стремиться быть небольшим. В этом случае мы будем говорить, что вес учится медленно , а это означает, что он не сильно меняется во время градиентного спуска.
Функция σ становится очень плоской, когда σ(ziL) составляет приблизительно 0 или 1, поскольку она представляет собой сигмоиду. Отсюда вывод заключается в том, что вес в последнем слое будет учиться медленно, если выходной нейрон имеет низкую активацию (0) или высокую активацию ( ≈1 ). В этом случае принято говорить, что выходной нейрон насыщен и, как следствие, вес перестал учиться (или учится медленно). Аналогичные замечания справедливы и для смещений выходного нейрона.
В заключении хотелось бы провести аналогию с биологическими объектами. Обратное распространение в искусственных нейронных сетях перекликается с функционированием биологических нейронов, которые реагируют на такой активатор, как дофамин, служит важной частью «системы вознаграждения» мозга, поскольку вызывает чувство удовольствия (или удовлетворения), чем влияет на процессы мотивации и обучения.
Источники
- http://neuralnetworksanddeeplearning.com/chap2.html
- https://towardsdatascience.com/understanding-backpropagation-algorithm-7bb3aa2f95fd
- https://brilliant.org/wiki/backpropagation/
- https://skymind.ai/wiki/backpropagation
В прошлой главе мы видели, как нейросети могут самостоятельно обучаться весам и смещениям с использованием алгоритма градиентного спуска. Однако в нашем объяснении имелся пробел: мы не обсуждали подсчёт градиента функции стоимости. А это приличный пробел! В этой главе я расскажу быстрый алгоритм для вычисления подобных градиентов, известный, как обратное распространение.
Впервые алгоритм обратного распространения придумали в 1970-х, но его важность не была до конца осознана вплоть до знаменитой работы 1986 года, которую написали Дэвид Румельхарт, Джоффри Хинтон и Рональд Уильямс. В работе описано несколько нейросетей, в которых обратное распространение работает гораздо быстрее, чем в более ранних подходах к обучению, из-за чего с тех пор можно было использовать нейросеть для решения ранее неразрешимых проблем. Сегодня алгоритм обратного распространения – рабочая лошадка обучения нейросети.
Эта глава содержит больше математики, чем все остальные в книге. Если вам не особенно по нраву математика, у вас может возникнуть искушение пропустить эту главу и просто относиться к обратному распространению, как к чёрному ящику, подробности работы которого вы готовы игнорировать. Зачем тратить время на их изучение?
Причина, конечно, в понимании. В основе обратного распространения лежит выражение частной производной ∂C / ∂w функции стоимости C по весу w (или смещению b) сети. Выражение показывает, насколько быстро меняется стоимость при изменении весов и смещений. И хотя это выражение довольно сложное, у него есть своя красота, ведь у каждого его элемента есть естественная и интуитивная интерпретация. Поэтому обратное распространение – не просто быстрый алгоритм для обучения. Он даёт нам подробное понимание того, как изменение весов и смещений меняет всё поведение сети. А это стоит того, чтобы изучить подробности.
Учитывая всё это, если вы хотите просто пролистать эту главу или перепрыгнуть к следующей, ничего страшного. Я написал остальную книгу так, чтобы она была понятной, даже если считать обратное распространение чёрным ящиком. Конечно, позднее в книге будут моменты, с которых я делаю отсылки к результатам этой главы. Но в тот момент вам должны быть понятны основные заключения, даже если вы не отслеживали все рассуждения.
Для разогрева: быстрый матричный подход вычисления выходных данных нейросети
Перед обсуждением обратного распространения, давайте разогреемся быстрым матричным алгоритмом для вычисления выходных данных нейросети. Мы вообще-то уже встречались с этим алгоритмом к концу предыдущей главы, но я описал его быстро, поэтому его стоит заново рассмотреть подробнее. В частности, это будет хороший способ приспособиться к записи, используемой в обратном распространении, но в знакомом контексте.
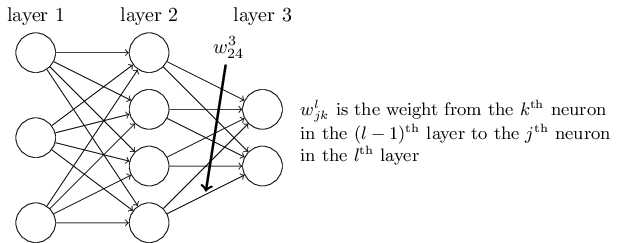
Начнём с записи, позволяющей нам недвусмысленно обозначать веса в сети. Мы будем использовать wljk для обозначения веса связи нейрона №k в слое №(l-1) с нейроном №j в слое №l. Так, к примеру, на диаграмме ниже показан вес связи четвёртого нейрона второго слоя со вторым нейроном третьего слоя:
Сначала такая запись кажется неуклюжей, и требует некоторых усилий на привыкание. Однако вскоре она покажется вам простой и естественной. Одна её особенность – порядок индексов j и k. Вы могли бы решить, что разумнее было бы использовать j для обозначения входного нейрона, а k – для выходного, а не наоборот, как у нас. Причину такой особенности я объясню ниже.
Сходные обозначения мы будем использовать для смещений и активаций сети. В частности, blj будет обозначать смещение нейрона №j в слое №l. alj будет обозначать активацию нейрона №j в слое №l. На следующей диаграмме показаны примеры использования этой записи:
С такой записью активация alj нейрона №j в слое №l связана с активацией в слое №(l-1) следующим уравнением (сравните с уравнением (4) и его обсуждением в прошлой главе):
где сумма идёт по всем нейронам k в слое (l-1). Чтобы перезаписать это выражение в матричном виде, мы определим матрицу весов wl для каждого слоя l. Элементы матрицы весов – это просто веса, соединённые со слоем №l, то есть, элемент в строке №j и столбце №k будет wljk. Сходным образом для каждого слоя l мы определяем вектор смещения bl. Вы, наверное, догадались, как это работает – компонентами вектора смещения будут просто значения blj, по одному компоненту для каждого нейрона в слое №l. И, наконец, мы определим вектор активации al, компонентами которого будут активации alj.
Последним ингредиентом, необходимым для того, чтобы перезаписать (23), будет матричная форма векторизации функции σ. С векторизацией мы вскользь столкнулись в прошлой главе – идея в том, что мы хотим применить функцию σ к каждому элементу вектора v. Мы используем очевидную запись σ(v) для обозначения поэлементного применения функции. То есть, компонентами σ(v) будут просто σ(v)j = σ(vj). Для примера, если у нас есть функция f(x) = x2, то векторизованная форма f даёт нам
то есть, векторизованная f просто возводит в квадрат каждый элемент вектора.
Учитывая все эти формы записи, уравнение (23) можно переписать в красивой и компактной векторизованной форме:
Такое выражение позволяет нам более глобально взглянуть на связь активаций одного слоя с активациями предыдущего: мы просто применяем матрицу весов к активациям, добавляем вектор смещения и потом применяем сигмоиду. Кстати, именно эта запись и требует использования записи wljk. Если бы мы использовали индекс j для обозначения входного нейрона, а k для выходного, нам пришлось бы заменить матрицу весов в уравнении (25) на транспонированную. Это небольшое, но раздражающее изменение, и мы бы потеряли простоту заявления (и размышления) о «применении матрицы весов к активациям». Такой глобальный подход проще и лаконичнее (и использует меньше индексов!), чем понейронный. Это просто способ избежать индексного ада, не теряя точности обозначения происходящего. Также это выражение полезно на практике, поскольку большинство матричных библиотек предлагают быстрые способы перемножения матриц, сложения векторов и векторизации. Код в прошлой главе непосредственно пользовался этим выражением для вычисления поведения сети.
Используя уравнение (25) для вычисления al, мы вычисляем промежуточное значение zl ≡ wlal−1+bl. Эта величина оказывается достаточно полезной для именования: мы называем zl взвешенным входом нейронов слоя №l. Позднее мы активно будем использовать этот взвешенный вход. Уравнение (25) иногда записывают через взвешенный вход, как al = σ(zl). Стоит также отметить, что у zl есть компоненты , то есть, zlj — это всего лишь взвешенный вход функции активации нейрона j в слое l.
Два необходимых предположения по поводу функции стоимости
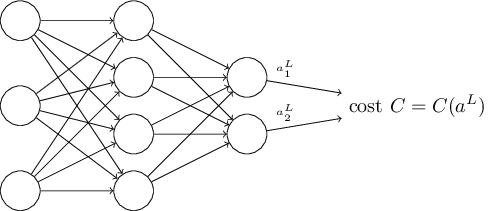
Цель обратного распространения – вычислить частные производные ∂C/∂w и ∂C/∂b функции стоимости C для каждого веса w и смещения b сети. Чтобы обратное распространение сработало, нам необходимо сделать два главных предположения по поводу формы функции стоимости. Однако перед этим полезно будет представлять себе пример функции стоимости. Мы используем квадратичную функцию из прошлой главы (уравнение (6)). В записи из предыдущего раздела она будет иметь вид
где: n – общее количество обучающих примеров; сумма идёт по всем примерам x; y=y(x) – необходимые выходные данные; L обозначает количество слоёв в сети; aL = aL (x) – вектор выхода активаций сети, когда на входе x.
Ладно, так какие нам нужны предположения касательно функции стоимости С, чтобы применять обратное распространение? Первое – функцию стоимости можно записать как среднее C = 1/n ∑x Cx функций стоимости Cx для отдельных обучающих примеров x. Это выполняется в случае квадратичной функции стоимости, где стоимость одного обучающего примера Cx = 1/2 ||y − aL||2. Это предположение будет верным и для всех остальных функций стоимости, которые встретятся нам в книге.
Это предположение нужно нам потому, что на самом деле обратное распространение позволяет нам вычислять частные производные ∂C/∂w и ∂C/∂b, усредняя по обучающим примерам. Приняв это предположение, мы предположим, что обучающий пример x фиксирован, и перестанем указывать индекс x, записывая стоимость Cx как C. Потом мы вернём x, но пока что лучше его просто подразумевать.
Второе предположение касательно функции стоимости – её можно записать как функцию выхода нейросети:
К примеру, квадратичная функция стоимости удовлетворяет этому требованию, поскольку квадратичную стоимость одного обучающего примера x можно записать, как
что и будет функцией выходных активаций. Конечно, эта функция стоимости также зависит от желаемого выхода y, и вы можете удивиться, почему мы не рассматриваем C как функцию ещё и от y. Однако вспомним, что входной обучающий пример x фиксирован, поэтому выход y тоже фиксирован. В частности, его мы не можем изменить, меняя веса и смещения, то есть, это не то, что выучивает нейросеть. Поэтому имеет смысл считать C функцией от только выходных активаций aL, а y – просто параметром, помогающим её определять.
Произведение Адамара s⊙t
Алгоритм обратного распространения основан на обычных операциях линейной алгебры – сложении векторов, умножении вектора на матрицу, и т.д. Однако одна из операций используется менее часто. Допустим, s и t – два вектора одной размерности. Тогда через s⊙t мы обозначим поэлементное перемножение двух векторов. Тогда компоненты s⊙t будут просто (s⊙t)j = sjtj. Например:
Такое поэлементное произведение иногда называют произведением Адамара или произведением Шура. Мы будем называть его произведением Адамара. Хорошие библиотеки для работы с матрицами обычно имеют быструю реализацию произведения Адамара, и это бывает удобно при реализации обратного распространения.
Четыре фундаментальных уравнения в основе обратного распространения
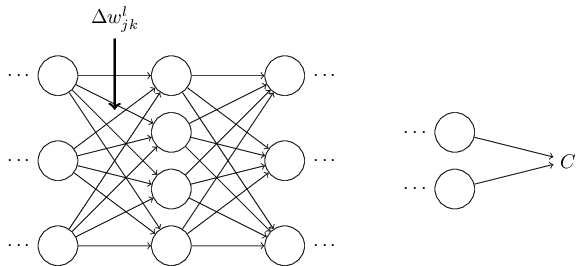
Обратное распространение связано с пониманием того, как изменение весов и смещений сети меняет функцию стоимости. По сути, это означает подсчёт частных производных ∂C/∂wljk и ∂C/∂blj. Но для их вычисления сначала мы вычисляем промежуточное значение δlj, которую мы называем ошибкой в нейроне №j в слое №l. Обратное распространение даст нам процедуру для вычисления ошибки δlj, а потом свяжет δlj с ∂C/∂wljk и ∂C/∂blj.
Чтобы понять, как определяется ошибка, представьте, что в нашей нейросети завёлся демон:
Он сидит на нейроне №j в слое №l. При поступлении входных данных демон нарушает работу нейрона. Он добавляет небольшое изменение Δzlj к взвешенному входу нейрона, и вместо того, чтобы выдавать σ(zlj), нейрон выдаст σ(zlj + Δzlj). Это изменение распространится и через следующие слои сети, что в итоге изменит общую стоимость на (∂C/∂zlj) * Δzlj.
Но наш демон хороший, и он пытается помочь вам улучшить стоимость, то есть, найти Δzlj, уменьшающее стоимость. Допустим, значение ∂C/∂zlj велико (положительное или отрицательное). Тогда демон может серьёзно уменьшить стоимость, выбрав Δzlj со знаком, противоположным ∂C/∂zlj. А если же ∂C/∂zlj близко к нулю, тогда демон не может сильно улучшить стоимость, меняя взвешенный вход zlj. Так что, с точки зрения демона, нейрон уже близок к оптимуму (это, конечно, верно только для малых Δzlj. Допустим, таковы ограничения действий демона). Поэтому в эвристическом смысле ∂C/∂zlj является мерой ошибки нейрона.
Под мотивацией от этой истории определим ошибку δlj нейрона j в слое l, как
По обычному нашему соглашению мы используем δl для обозначения вектора ошибок, связанного со слоем l. Обратное распространение даст нам способ подсчитать δl для любого слоя, а потом соотнести эти ошибки с теми величинами, которые нас реально интересуют, ∂C/∂wljk и ∂C/∂blj.
Вас может интересовать, почему демон меняет взвешенный вход zlj. Ведь было бы естественнее представить, что демон изменяет выходную активацию alj, чтобы мы использовали ∂C/∂alj в качестве меры ошибки. На самом деле, если сделать так, то всё получается очень похожим на то, что мы будем обсуждать дальше. Однако в этом случае представление обратного распространения будет алгебраически чуть более сложным. Поэтому мы остановимся на варианте δlj = ∂C/∂zlj в качестве меры ошибки.
В задачах классификации термин «ошибка» иногда означает количество неправильных классификаций. К примеру, если нейросеть правильно классифицирует 96,0% цифр, то ошибка будет равна 4,0%. Очевидно, это совсем не то, что мы имеем в виду под векторами δ. Но на практике обычно можно без труда понять, какое значение имеется в виду.
План атаки: обратное распространение основано на четырёх фундаментальных уравнениях. Совместно они дают нам способ вычислить как ошибку δl, так и градиент функции стоимости. Я привожу их ниже. Не нужно ожидать их мгновенного освоения. Вы будете разочарованы. Уравнения обратного распространения настолько глубоки, что для хорошего их понимания требуется ощутимое время и терпение, и постепенное углубление в вопрос. Хорошие новости в том, что это терпение окупится сторицей. Поэтому в данном разделе наши рассуждения только начинаются, помогая вам идти по пути глубокого понимания уравнений.
Вот схема того, как мы будем углубляться в эти уравнения позже: я дам их краткое доказательство, помогающее объяснить, почему они верны; мы перепишем их в алгоритмической форме в виде псевдокода, и увидим, как реализовать его в реальном коде на python; в последней части главы мы выработаем интуитивное представление о значении уравнений обратного распространения, и о том, как их можно найти с нуля. Мы будем периодически возвращаться к четырём фундаментальным уравнениям, и чем глубже вы будете их понимать, тем более комфортными, и возможно, красивыми и естественными они будут вам казаться.
Уравнение ошибки выходного слоя, δL: компоненты δL считаются, как
Очень естественное выражение. Первый член справа, ∂C / ∂aLj, измеряет, насколько быстро стоимость меняется как функция выходной активации №j. Если, к примеру, C не особенно зависит от конкретного выходного нейрона j, тогда δLj будет малым, как и ожидается. Второй член справа, σ'(zLj), измеряет, насколько быстро функция активации σ меняется в zLj.
Заметьте, что всё в (BP1) легко подсчитать. В частности, мы вычисляем zLj при подсчёте поведения сети, и на вычисление σ'(zLj) уйдёт незначительно больше ресурсов. Конечно, точная форма ∂C / ∂aLj зависит от формы функции стоимость. Однако, если функция стоимости известна, то не должно быть проблем с вычислением ∂C / ∂aLj. К примеру, если мы используем квадратичную функцию стоимости, тогда C = 1/2 ∑j (yj − aLj)2, поэтому ∂C / ∂aLj = (aLj − yj), что легко подсчитать.
Уравнение (BP1) – это покомпонентное выражение δL. Оно совершенно нормальное, но не записано в матричной форме, которая нужна нам для обратного распространения. Однако, его легко переписать в матричной форме, как
Здесь ∇a C определяется, как вектор, чьими компонентами будут частные производные ∂C / ∂aLj. Его можно представлять, как выражение скорости изменения C по отношению к выходным активациям. Легко видеть, что уравнения (BP1a) и (BP1) эквивалентны, поэтому далее мы будем использовать (BP1) для отсылки к любому из них. К примеру, в случае с квадратичной стоимостью, у нас будет ∇a C = (aL — y), поэтому полной матричной формой (BP1) будет
Всё в этом выражении имеет удобную векторную форму, и его легко вычислить при помощи такой библиотеки, как, например, Numpy.
Выражение ошибки δl через ошибку в следующем слое, δl+1: в частности,
где (wl+1)T — транспонирование весовой матрицы wl+1 для слоя №(l+1). Уравнение кажется сложным, но каждый его элемент легко интерпретировать. Допустим, мы знаем ошибку δl+1 для слоя (l+1). Транспонирование весовой матрицы, (wl+1)T, можно представить себе, как перемещение ошибки назад по сети, что даёт нам некую меру ошибки на выходе слоя №l. Затем мы считаем произведение Адамара ⊙σ'(zl). Это продвигает ошибку назад через функцию активации в слое l, давая нам значение ошибки δl во взвешенном входе для слоя l.
Комбинируя (BP2) с (BP1), мы можем подсчитать ошибку δl для любого слоя сети. Мы начинаем с использования (BP1) для подсчёта δL, затем применяем уравнение (BP2) для подсчёта δL-1, затем снова для подсчёта δL-2, и так далее, до упора по сети в обратную сторону.
Уравнение скорости изменения стоимости по отношению к любому смещению в сети: в частности:
То есть, ошибка δlj точно равна скорости изменения ∂C / ∂blj. Это превосходно, поскольку (BP1) и (BP2) уже рассказали нам, как подсчитывать δlj. Мы можем перезаписать (BP3) короче, как
где δ оценивается для того же нейрона, что и смещение b.
Уравнение для скорости изменения стоимости по отношению к любому весу в сети: в частности:
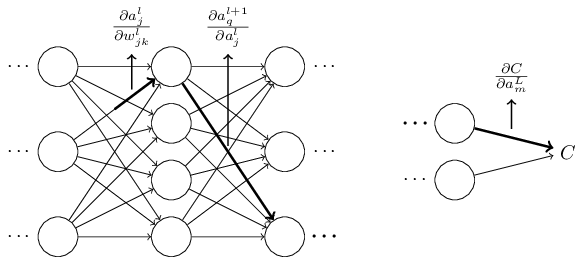
Отсюда мы узнаём, как подсчитать частную производную ∂C/∂wljk через значения δl и al-1, способ расчёта которых нам уже известен. Это уравнение можно переписать в менее загруженной индексами форме:
где ain — активация нейронного входа для веса w, а δout — ошибка нейронного выхода от веса w. Если подробнее посмотреть на вес w и два соединённых им нейрона, то можно будет нарисовать это так:
Приятное следствие уравнения (32) в том, что когда активация ain мала, ain ≈ 0, член градиента ∂C/∂w тоже стремится к нулю. В таком случае мы говорим, что вес обучается медленно, то есть, не сильно меняется во время градиентного спуска. Иначе говоря, одним из следствий (BP4) будет то, что весовой выход нейронов с низкой активацией обучается медленно.
Из (BP1)-(BP4) можно почерпнуть и другие идеи. Начнём с выходного слоя. Рассмотрим член σ'(zLj) в (BP1). Вспомним из графика сигмоиды из прошлой главы, что она становится плоской, когда σ(zLj) приближается к 0 или 1. В данных случаях σ'(zLj) ≈ 0. Поэтому вес в последнем слое будет обучаться медленно, если активация выходного нейрона мала (≈ 0) или велика (≈ 1). В таком случае обычно говорят, что выходной нейрон насыщен, и в итоге вес перестал обучаться (или обучается медленно). Те же замечания справедливы и для смещений выходного нейрона.
Сходные идеи можно получить и касательно более ранних слоёв. В частности, рассмотрим член σ'(zl) в (BP2). Это значит, что δlj, скорее всего, будет малой при приближении нейрона к насыщению. А это, в свою очередь, означает, что любые веса на входе насыщенного нейрона будут обучаться медленно (правда, это не сработает, если у wl+1Tδl+1 будут достаточно большие элементы, компенсирующие небольшое значение σ'(zLj)).
Подытожим: мы узнали, что вес будет обучаться медленно, если либо активация входного нейрона мала, либо выходной нейрон насыщен, то есть его активация мала или велика.
В этом нет ничего особенно удивительного. И всё же, эти наблюдения помогают улучшить наше представление о том, что происходит при обучении сети. Более того, мы можем подойти к этим рассуждениям с обратной стороны. Четыре фундаментальных уравнения справедливы для любой функции активации, а не только для стандартной сигмоиды (поскольку, как мы увидим далее, в доказательствах не используются свойства сигмоиды). Поэтому эти уравнения можно использовать для разработки функций активации с определёнными нужными свойствами обучения. Для примера, допустим, мы выбрали функцию активации σ, непохожую на сигмоиду, такую, что σ’ всегда положительна и не приближается к нулю. Это предотвратить замедление обучения, происходящее при насыщении обычных сигмоидных нейронов. Позднее в книге мы увидим примеры, где функция активации меняется подобным образом. Учитывая уравнения (BP1)-(BP4), мы можем объяснить, зачем нужны такие модификации, и как они могут повлиять на ситуацию.
Итог: уравнения обратного распространения
Задачи
- Альтернативная запись уравнений обратного распространения. Я записал уравнения обратного распространения с использованием произведения Адамара. Это может сбить с толку людей, не привыкших к этому произведению. Есть и другой подход, на основе обычного перемножения матриц, который может оказаться поучительным для некоторых читателей. Покажите, что (BP1) можно переписать, как
где Σ'(zL) – квадратная матрица, у которой по диагонали расположены значения σ'(zLj), а другие элементы равны 0. Учтите, что эта матрица взаимодействует с ∇a C через обычное перемножение матриц.
Покажите, что (BP2) можно переписать, как
Комбинируя предыдущие задачи, покажите, что:
Для читателей, привычных к матричному перемножению, это уравнение будет легче понять, чем (BP1) и (BP2). Я концентрируюсь на (BP1) и (BP2) потому, что этот подход оказывается быстрее реализовать численно. [здесь Σ — это не сумма (∑), а заглавная σ (сигма) / прим. перев.]
Доказательство четырёх фундаментальных уравнений (необязательный раздел)
Теперь докажем четыре фундаментальных уравнения (BP1)-(BP4). Все они являются следствиями цепного правила (правила дифференцирования сложной функции) из анализа функций многих переменных. Если вы хорошо знакомы с цепным правилом, настоятельно рекомендую попробовать посчитать производные самостоятельно перед тем, как продолжить чтение.
Начнём с уравнения (BP1), которое даёт нам выражение для выходной ошибки δL. Чтобы доказать его, вспомним, что, по определению:
Применяя цепное правило, перепишем частные производные через частные производные по выходным активациям:
где суммирование идёт по всем нейронам k в выходном слое. Конечно, выходная активация aLk нейрона №k зависит только от взвешенного входа zLj для нейрона №j, когда k=j. Поэтому ∂aLk / ∂zLj исчезает, когда k ≠ j. В итоге мы упрощаем предыдущее уравнение до
Вспомнив, что aLj = σ(zLj), мы можем переписать второй член справа, как σ'(zLj), и уравнение превращается в
то есть, в (BP1) в покомпонентном виде.
Затем докажем (BP2), дающее уравнение для ошибки δl через ошибку в следующем слое δl+1. Для этого нам надо переписать δlj = ∂C / ∂zlj через δl+1k = ∂C / ∂zl+1k. Это можно сделать при помощи цепного правила:
где в последней строчке мы поменяли местами два члена справа, и подставили определение δl+1k. Чтобы вычислить первый член на последней строчке, отметим, что
Продифференцировав, получим
Подставив это в (42), получим
То есть, (BP2) в покомпонентной записи.
Остаётся доказать (BP3) и (BP4). Они тоже следуют из цепного правила, примерно таким же методом, как и два предыдущих. Оставлю их вам в качестве упражнения.
Упражнение
- Докажите (BP3) и (BP4).
Вот и всё доказательство четырёх фундаментальных уравнений обратного распространения. Оно может показаться сложным. Но на самом деле это просто результат аккуратного применения цепного правила. Говоря менее лаконично, обратное распространение можно представить себе, как способ подсчёта градиента функции стоимости через систематическое применение цепного правила из анализа функций многих переменных. И это реально всё, что представляет собой обратное распространение – остальное просто детали.
Алгоритм обратного распространения
Уравнения обратного распространения дают нам метод подсчёта градиента функции стоимости. Давайте запишем это явно в виде алгоритма:
- Вход x: назначить соответствующую активацию a1 для входного слоя.
- Прямое распространение: для каждого l = 2,3,…,L вычислить zl = wlal−1+bl и al = σ(zl).
- Выходная ошибка δL: вычислить вектор δL = ∇a C ⊙ σ'(zL).
- Обратное распространение ошибки: для каждого l = L−1,L−2,…,2 вычислить δl = ((wl+1)Tδl+1) ⊙ σ'(zl).
- Выход: градиент функции стоимости задаётся
и
.
Посмотрев на алгоритм, вы поймёте, почему он называется обратное распространение. Мы вычисляем векторы ошибки δl задом наперёд, начиная с последнего слоя. Может показаться странным, что мы идём по сети назад. Но если подумать о доказательстве обратного распространения, то обратное движение является следствием того, что стоимость – это функция выхода сети. Чтобы понять, как меняется стоимость в зависимости от ранних весов и смещений, нам нужно раз за разом применять цепное правило, идя назад через слои, чтобы получить полезные выражения.
Упражнения
- Обратное распространение с одним изменённым нейроном. Допустим, мы изменили один нейрон в сети с прямым распространением так, чтобы его выход был f(∑j wjxj+b), где f – некая функция, не похожая на сигмоиду. Как нам поменять алгоритм обратного распространения в данном случае?
- Обратное распространение с линейными нейронами. Допустим, мы заменим обычную нелинейную сигмоиду на σ(z) = z по всей сети. Перепишите алгоритм обратного распространения для данного случая.
Как я уже пояснял ранее, алгоритм обратного распространения вычисляет градиент функции стоимости для одного обучающего примера, C = Cx. На практике часто комбинируют обратное распространение с алгоритмом обучения, например, со стохастическим градиентным спуском, когда мы подсчитываем градиент для многих обучающих примеров. В частности, при заданном мини-пакете m обучающих примеров, следующий алгоритм применяет градиентный спуск на основе этого мини-пакета:
- Вход: набор обучающих примеров.
- Для каждого обучающего примера x назначить соответствующую входную активацию ax,1 и выполнить следующие шаги:
- Прямое распространение для каждого l=2,3,…,L вычислить zx,l = wlax,l−1+bl и ax,l = σ(zx,l).
- Выходная ошибка δx,L: вычислить вектор δx,L = ∇a Cx ⋅ σ'(zx,L).
- Обратное распространение ошибки: для каждого l=L−1,L−2,…,2 вычислить δx,l = ((wl+1)Tδx,l+1) ⋅ σ'(zx,l).
- Градиентный спуск: для каждого l=L,L−1,…,2 обновить веса согласно правилу
, и смещения согласно правилу
.
Конечно, для реализации стохастического градиентного спуска на практике также понадобится внешний цикл, генерирующий мини-пакеты обучающих примеров, и внешний цикл, проходящий по нескольким эпохам обучения. Для простоты я их опустил.
Код для обратного распространения
Поняв абстрактную сторону обратного распространения, теперь мы можем понять код, использованный в предыдущей главе, реализующий обратное распространение. Вспомним из той главы, что код содержался в методах update_mini_batch и backprop класс Network. Код этих методов – прямой перевод описанного выше алгоритма. В частности, метод update_mini_batch обновляет веса и смещения сети, подсчитывая градиент для текущего mini_batch обучающих примеров:
class Network(object):
...
def update_mini_batch(self, mini_batch, eta):
"""Обновить веса и смещения сети, применяя градиентный спуск с использованием обратного распространения к одному мини-пакету. mini_batch – это список кортежей (x, y), а eta – скорость обучения."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]Большую часть работы делают строки delta_nabla_b, delta_nabla_w = self.backprop(x, y), использующие метод backprop для подсчёта частных производных ∂Cx/∂blj и ∂Cx/∂wljk. Метод backprop почти повторяет алгоритм предыдущего раздела. Есть одно небольшое отличие – мы используем немного другой подход к индексированию слоёв. Это сделано для того, чтобы воспользоваться особенностью python, отрицательными индексами массива, позволяющими отсчитывать элементы назад, с конца. l[-3] будет третьим элементом с конца массива l. Код backprop приведён ниже, вместе со вспомогательными функциями, используемыми для подсчёта сигмоиды, её производной и производной функции стоимости. С ними код получается законченным и понятным. Если что-то неясно, обратитесь к первому описанию кода с полным листингом.
class Network(object):
...
def backprop(self, x, y):
"""Вернуть кортеж ``(nabla_b, nabla_w)``, представляющий градиент для функции стоимости C_x. ``nabla_b`` и ``nabla_w`` - послойные списки массивов numpy, похожие на ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# прямой проход
activation = x
activations = [x] # список для послойного хранения активаций
zs = [] # список для послойного хранения z-векторов
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# обратный проход
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
"""Переменная l в цикле ниже используется не так, как описано во второй главе книги. l = 1 означает последний слой нейронов, l = 2 – предпоследний, и так далее. Мы пользуемся преимуществом того, что в python можно использовать отрицательные индексы в массивах."""
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
...
def cost_derivative(self, output_activations, y):
"""Вернуть вектор частных производных (чп C_x / чп a) для выходных активаций."""
return (output_activations-y)
def sigmoid(z):
"""Сигмоида."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Производная сигмоиды."""
return sigmoid(z)*(1-sigmoid(z))Задача
- Полностью основанный на матрицах подход к обратному распространению на мини-пакете. Наша реализация стохастического градиентного спуска использует цикл по обучающим примерам из мини-пакета. Алгоритм обратного распространения можно поменять так, чтобы он вычислял градиенты для всех обучающих примерах мини-пакета одновременно. Вместо того, чтобы начинать с одного вектора x, мы можем начать с матрицы X=[x1x2…xm], чьими столбцами будут векторы мини-пакета. Прямое распространение идёт через произведение весовых матриц, добавление подходящей матрицы для смещений и повсеместного применения сигмоиды. Обратное распространение идёт по той же схеме. Напишите псевдокод для такого подхода для алгоритма обратного распространения. Измените network.py так, чтобы он использовал этот матричный подход. Преимуществом такого подхода будет использование всех преимуществ современных библиотек для линейной алгебры. В итоге он может работать быстрее цикла по мини-пакеты (к примеру, на моём компьютере программа ускоряется примерно в 2 раза на задачах классификации MNIST). На практике все серьёзные библиотеки для обратного распространения используют такой полноматричный подход или какой-то его вариант.
В каком смысле обратное распространение является быстрым алгоритмом?
В каком смысле обратное распространение является быстрым алгоритмом? Для ответа на этот вопрос рассмотрим ещё один подход к вычислению градиента. Представьте себе ранние дни исследований нейросетей. Возможно, это 1950-е или 1960-е годы, и вы – первый человек в мире, придумавший использовать для обучения градиентный спуск! Но чтобы это сработало, вам нужно подсчитать градиент функции стоимости. Вы вспоминаете алгебру и решаете посмотреть, можно ли использовать цепное правило для вычисления градиента. Немного поигравшись, вы видите, что алгебра кажется сложной, и вы разочаровываетесь. Вы пытаетесь найти другой подход. Вы решаете считать стоимость функцией только весов C=C(w) (к смещениям вернёмся чуть позже). Вы нумеруете веса w1, w2,… и хотите вычислить ∂C/∂wj для веса wj. Очевидный способ – использовать приближение
Где ε > 0 – небольшое положительное число, а ej — единичный вектор направления j. Иначе говоря, мы можем приблизительно оценить ∂C/∂wj, вычислив стоимость C для двух немного различных значений wj, а потом применить уравнение (46). Та же идея позволит нам подсчитать частные производные ∂C/∂b по смещениям.
Подход выглядит многообещающим. Концептуально простой, легко реализуемый, использует только несколько строк кода. Он выглядит гораздо более многообещающим, чем идея использования цепного правила для подсчёта градиента!
К сожалении, хотя такой подход выглядит многообещающим, при его реализации в коде оказывается, что работает он крайне медленно. Чтобы понять, почему, представьте, что у нас в сети миллион весов. Тогда для каждого веса wj нам нужно вычислить C(w + εej), чтобы подсчитать ∂C/∂wj. А это значит, что для вычисления градиента нам нужно вычислить функцию стоимости миллион раз, что потребует миллион прямых проходов по сети (на каждый обучающий пример). А ещё нам надо подсчитать C(w), так что получается миллион и один проход по сети.
Хитрость обратного распространения в том, что она позволяет нам одновременно вычислять все частные производные ∂C/∂wj, используя только один прямой проход по сети, за которым следует один обратный проход. Грубо говоря, вычислительная стоимость обратного прохода примерно такая же, как у прямого.
Поэтому общая стоимость обратного распространения примерно такая же, как у двух прямых проходов по сети. Сравните это с миллионом и одним прямым проходом, необходимым для реализации метода (46)! Так что, хотя обратное распространение внешне выглядит более сложным подходом, в реальности он куда как более быстрый.
Впервые это ускорение сполна оценили в 1986, и это резко расширило диапазон задач, решаемых с помощью нейросетей. В свою очередь, это привело к увеличению количества людей, использующих нейросети. Конечно, обратное распространение – не панацея. Даже в конце 1980-х люди уже натолкнулись на её ограничения, особенно при попытках использовать обратное распространение для обучения глубоких нейросетей, то есть сетей со множеством скрытых слоёв. Позже мы увидим, как современные компьютеры и новые хитрые идеи позволяют использовать обратное распространение для обучения таких глубоких нейросетей.
Обратное распространение: в общем и целом
Как я уже объяснил, обратное распространение являет нам две загадки. Первая, что на самом деле делает алгоритм? Мы выработали схему обратного распространения ошибки от выходных данных. Можно ли углубиться дальше, получить более интуитивное представление о происходящем во время всех этих перемножений векторов и матриц? Вторая загадка – как вообще кто-то мог обнаружить обратное распространение? Одно дело, следовать шагам алгоритма или доказательству его работы. Но это не значит, что вы так хорошо поняли задачу, что могли изобрести этот алгоритм. Есть ли разумная цепочка рассуждений, способная привести нас к открытию алгоритма обратного распространения? В этом разделе я освещу обе загадки.
Чтобы улучшить понимание работы алгоритма, представим, что мы провели небольшое изменение Δwljk некоего веса wljk:
Это изменение веса приведёт к изменению выходной активации соответствующего нейрона:
Это приведёт к изменению всех активаций следующего слоя:
Эти изменения приведут к изменениям следующего слоя, и так далее, вплоть до последнего, а потом к изменениям функции стоимости:
Изменение ΔC связано с изменением Δwljk уравнением
Из этого следует, что вероятным подходом к вычислению ∂C/∂wljk будет тщательное отслеживание распространения небольшого изменения wljk, приводящего к небольшому изменению в C. Если мы сможем это сделать, тщательно выражая по пути всё в величинах, которые легко вычислить, то мы сможем вычислить и ∂C/∂wljk.
Давайте попробуем. Изменение Δwljk вызывает небольшое изменение Δalj в активации нейрона j в слое l. Это изменение задаётся
Изменение активации Δalj приводит к изменениям во всех активациях следующего слоя, (l+1). Мы сконцентрируемся только на одной из этих изменённых активаций, допустим, al+1q,
Это приведёт к следующим изменениям:
Подставляя уравнение (48), получаем:
Конечно, изменение Δal+1q изменит и активации в следующем слое. Мы даже можем представить путь по всей сети от wljk до C, где каждое изменение активации приводит к изменению следующей активации, и, наконец, к изменению стоимости на выходе. Если путь проходит через активации alj, al+1q,…,aL−1n, aLm, тогда итоговое выражение будет
То есть, мы выбираем член вида ∂a/∂a для каждого следуюшего проходимого нами нейрона, а также для члена ∂C / ∂aLm в конце. Это представление изменений в C из-за изменений в активациях по данному конкретному пути сквозь сеть. Конечно, существует много путей, по которым изменение в wljk может пройти и повлиять на стоимость, а мы рассматривали только один из них. Чтобы подсчитать общее изменение C разумно предположить, что мы должны просуммировать все возможные пути от веса до конечной стоимости:
где мы просуммировали все возможные выборы для промежуточных нейронов по пути. Сравнивая это с (47), мы видим, что:
Уравнение (53) выглядит сложно. Однако у него есть приятная интуитивная интерпретация. Мы подсчитываем изменение C по отношению к весам сети. Оно говорит нам, что каждое ребро между двумя нейронами сети связано с фактором отношения, являющимся только лишь частной производной активации одного нейрона по отношению к активации другого нейрона. У ребра от первого веса до первого нейрона фактор отношения равен ∂alj / ∂wljk. Коэффициент отношения для пути – это просто произведение коэффициентов по всему пути. А общий коэффициент изменения ∂C / ∂wljk является суммой коэффициентов по всем путям от начального веса до конечной стоимости. Эта процедура показана далее, для одного пути:
Пока что мы давали эвристический аргумент, способ представить происходящее при изменении весов сети. Позвольте мне обрисовать дальнейший вариант мышления на эту тему для развития данного аргумента. Во-первых, можно вывести точные выражение для всех отдельных частных производных в уравнении (53). Это легко сделать с использованием несложной алгебры. После этого можно попробовать понять, как записать все суммы по индексам в виде произведений матриц. Это оказывается утомительной задачей, требующей терпения, но не чем-то экстраординарным. После всего этого и максимального упрощения вы увидите, что получился ровно тот же самый алгоритм обратного распространения! Поэтому алгоритм обратного распространения можно представлять себе, как способ вычисления суммы коэффициентов по всем путям. Или, если переформулировать, алгоритм обратного распространения – хитроумный способ отслеживания небольших изменений весов (и смещений), когда они распространяются по сети, достигают выхода и влияют на стоимость.
Здесь я не буду делать всего этого. Это дело малопривлекательное, требующее тщательной проработки деталей. Если вы готовы к такому, вам может понравиться этим заниматься. Если нет, то надеюсь, что подобные размышления дадут вам некоторые идеи по поводу целей обратного распространения.
Что насчёт другой загадки – как вообще можно было открыть обратное распространение? На самом деле, если вы последуете по обрисованному мною пути, вы получите доказательство обратного распространения. К несчастью, доказательство будет длиннее и сложнее чем то, что я описал ранее. Так как же было открыто то короткое (но ещё более загадочное) доказательство? Если записать все детали длинного доказательства, вам сразу бросятся в глаза несколько очевидных упрощений. Вы применяете упрощения, получаете более простое доказательство, записываете его. А затем вам опять на глаза попадаются несколько очевидных упрощений. И вы повторяете процесс. После нескольких повторений получится то доказательство, что мы видели ранее – короткое, но немного непонятное, поскольку из него удалены все путеводные вехи! Я, конечно, предлагаю вам поверить мне на слово, однако никакой загадки происхождения приведённого доказательства на самом деле нет. Просто много тяжёлой работы по упрощению доказательства, описанного мною в этом разделе.
Однако в этом процессе есть один хитроумный трюк. В уравнении (53) промежуточные переменные – это активации, типа al+1q. Хитрость в том, чтобы перейти к использованию взвешенных входов, типа zl+1q, в качестве промежуточных переменных. Если не пользоваться этим, и продолжать использовать активации, полученное доказательство будет немногим более сложным, чем данное ранее в этой главе.



 ,
, ,
,

 ,
,




 ,
, .
.




 маленькими случайными значениями,
маленькими случайными значениями, 
 на вход сети и подсчитать выходы
на вход сети и подсчитать выходы 
 .
. .
. .
. .
. .
.