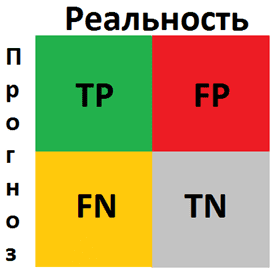
Матрица ошибок confusion matrix

Матрица ошибок – это метрика производительности классифицирующей модели Машинного обучения (ML).

Когда мы получаем данные, то после очистки и предварительной обработки, первым делом передаем их в модель и, конечно же, получаем результат в виде вероятностей. Но как мы можем измерить эффективность нашей модели? Именно здесь матрица ошибок и оказывается в центре внимания.

Матрица ошибок – это показатель успешности классификации, где классов два или более. Это таблица с 4 различными комбинациями сочетаний прогнозируемых и фактических значений.

Давайте рассмотрим значения ячеек (истинно позитивные, ошибочно позитивные, ошибочно негативные, истинно негативные) с помощью «беременной» аналогии.

Истинно позитивное предсказание (True Positive, сокр. TP)
Вы предсказали положительный результат, и женщина действительно беременна.

Истинно отрицательное предсказание (True Negative, TN)
Вы предсказали отрицательный результат, и мужчина действительно не беременен.

Ошибочно положительное предсказание (ошибка типа I, False Positive, FN)
Вы предсказали положительный результат (мужчина беременен), но на самом деле это не так.

Ошибочно отрицательное предсказание (ошибка типа II, False Negative, FN)
Вы предсказали, что женщина не беременна, но на самом деле она беременна.

Давайте разберемся в матрице ошибок с помощью арифметики.

Пример. Мы располагаем датасетом пациентов, у которых диагностируют рак. Зная верный диагноз (столбец целевой переменной «Y на самом деле»), хотим усовершенствовать диагностику с помощью модели Машинного обучения. Модель получила тренировочные данные, и на тестовой части, состоящей из 7 записей (в реальных задачах, конечно, больше) и изображенной ниже, мы оцениваем, насколько хорошо прошло обучение.

Модель сделала свои предсказания для каждого пациента и записала вероятности от 0 до 1 в столбец «Предсказанный Y». Мы округляем эти числа, приводя их к нулю или единице, с помощью порога, равного 0,6 (ниже этого значения – ноль, пациент здоров). Результаты округления попадают в столбец «Предсказанная вероятность»: например, для первой записи модель указала 0,5, что соответствует нулю. В последнем столбце мы анализируем, угадала ли модель.

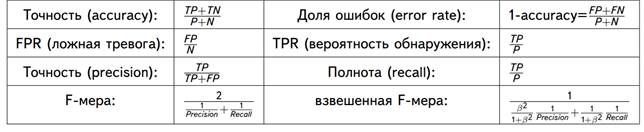
Теперь, используя простейшие формулы, мы рассчитаем Отзыв (Recall), точность результата измерений (Precision), точность измерений (Accuracy), и наконец поймем разницу между этими метриками.

Отзыв

Из всех положительных значений, которые мы предсказали правильно, сколько на самом деле положительных? Подсчитаем, сколько единиц в столбце «Y на самом деле» (4), это и есть сумма TP + FN. Теперь определим с помощью «Предсказанной вероятности», сколько из них диагностировано верно (2), это и будет TP.

$$Отзыв = \frac{TP}{TP + FN} = \frac{2}{2 + 2} = \frac{1}{2}$$

Точность результата измерений (Precision)

В этом уравнении из неизвестных только FP. Ошибочно диагностированных как больных здесь только одна запись.

$$Точность\spaceрезультата\spaceизмерений = \frac{TP}{TP + FP} = \frac{2}{2 + 1} = \frac{2}{3}$$

Точность измерений (Accuracy)

Последнее значение, которое предстоит экстраполировать из таблицы – TN. Правильно диагностированных моделью здоровых людей здесь 2.

$$Точность\spaceизмерений = \frac{TP + TN}{Всего\spaceзначений} = \frac{2 + 2}{7} = \frac{4}{7}$$

F-мера точности теста

Эти метрики полезны, когда помогают вычислить F-меру – конечный показатель эффективности модели.

$$F-мера = \frac{2 * Отзыв * Точность\spaceизмерений}{Отзыв + Точность\spaceизмерений} = \frac{2 * \frac{1}{2} * \frac{2}{3}}{\frac{1}{2} + \frac{2}{3}} = 0,56$$

Наша скромная модель угадывает лишь 56% процентов диагнозов, и такой результат, как правило, считают промежуточным и работают над улучшением точности модели.

SkLearn

С помощью замечательной библиотеки Scikit-learn мы можем мгновенно определить множество метрик, и матрица ошибок – не исключение.

from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
confusion_matrix(y_true, y_pred)

Выводом будет ряд, состоящий из трех списков:

array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

Значения диагонали сверху вниз слева направо [2, 0, 2] – это число верно  предсказанных значений.

Фото: @opeleye

From Wikipedia, the free encyclopedia

Terminology and derivations
from a confusion matrix

condition positive (P) the number of real positive cases in the data condition negative (N) the number of real negative cases in the data true positive (TP) A test result that correctly indicates the presence of a condition or characteristic true negative (TN) A test result that correctly indicates the absence of a condition or characteristic false positive (FP), Type I error A test result which wrongly indicates that a particular condition or attribute is present false negative (FN), Type II error A test result which wrongly indicates that a particular condition or attribute is absent sensitivity, recall, hit rate, or true positive rate (TPR) specificity, selectivity or true negative rate (TNR) precision or positive predictive value (PPV) negative predictive value (NPV) miss rate or false negative rate (FNR) fall-out or false positive rate (FPR) false discovery rate (FDR) false omission rate (FOR) Positive likelihood ratio (LR+) Negative likelihood ratio (LR-) prevalence threshold (PT) threat score (TS) or critical success index (CSI) Prevalence accuracy (ACC) balanced accuracy (BA) F1 score is the harmonic mean of precision and sensitivity: phi coefficient (φ or rφ) or Matthews correlation coefficient (MCC) Fowlkes–Mallows index (FM) informedness or bookmaker informedness (BM) markedness (MK) or deltaP (Δp) Diagnostic odds ratio (DOR) Sources: Fawcett (2006),[1] Piryonesi and El-Diraby (2020),[2] Powers (2011),[3] Ting (2011),[4] CAWCR,[5] D. Chicco & G. Jurman (2020, 2021, 2023),[6][7][8] Tharwat (2018).[9] Balayla (2020)[10]

In the field of machine learning and specifically the problem of statistical classification, a confusion matrix, also known as error matrix,^[11] is a specific table layout that allows visualization of the performance of an algorithm, typically a supervised learning one; in unsupervised learning it is usually called a matching matrix.

Each row of the matrix represents the instances in an actual class while each column represents the instances in a predicted class, or vice versa – both variants are found in the literature.^[12] The name stems from the fact that it makes it easy to see whether the system is confusing two classes (i.e. commonly mislabeling one as another).

It is a special kind of contingency table, with two dimensions («actual» and «predicted»), and identical sets of «classes» in both dimensions (each combination of dimension and class is a variable in the contingency table).

Example[edit]

Given a sample of 12 individuals, 8 that have been diagnosed with cancer and 4 that are cancer-free, where individuals with cancer belong to class 1 (positive) and non-cancer individuals belong to class 0 (negative), we can display that data as follows:

Individual Number	1	2	3	4	5	6	7	8	9	10	11	12
Actual Classification	1	1	1	1	1	1	1	1	0	0	0	0

Assume that we have a classifier that distinguishes between individuals with and without cancer in some way, we can take the 12 individuals and run them through the classifier. The classifier then makes 9 accurate predictions and misses 3: 2 individuals with cancer wrongly predicted as being cancer-free (sample 1 and 2), and 1 person without cancer that is wrongly predicted to have cancer (sample 9).

Individual Number	1	2	3	4	5	6	7	8	9	10	11	12
Actual Classification	1	1	1	1	1	1	1	1	0	0	0	0
Predicted Classification	0	0	1	1	1	1	1	1	1	0	0	0

Notice, that if we compare the actual classification set to the predicted classification set, there are 4 different outcomes that could result in any particular column. One, if the actual classification is positive and the predicted classification is positive (1,1), this is called a true positive result because the positive sample was correctly identified by the classifier. Two, if the actual classification is positive and the predicted classification is negative (1,0), this is called a false negative result because the positive sample is incorrectly identified by the classifier as being negative. Third, if the actual classification is negative and the predicted classification is positive (0,1), this is called a false positive result because the negative sample is incorrectly identified by the classifier as being positive. Fourth, if the actual classification is negative and the predicted classification is negative (0,0), this is called a true negative result because the negative sample gets correctly identified by the classifier.

We can then perform the comparison between actual and predicted classifications and add this information to the table, making correct results appear in green so they are more easily identifiable.

Individual Number	1	2	3	4	5	6	7	8	9	10	11	12
Actual Classification	1	1	1	1	1	1	1	1	0	0	0	0
Predicted Classification	0	0	1	1	1	1	1	1	1	0	0	0
Result	FN	FN	TP	TP	TP	TP	TP	TP	FP	TN	TN	TN

The template for any binary confusion matrix uses the four kinds of results discussed above (true positives, false negatives, false positives, and true negatives) along with the positive and negative classifications. The four outcomes can be formulated in a 2×2 confusion matrix, as follows:

		Predicted condition
Total population = P + N	Positive (PP)	Negative (PN)
Actual condition	Positive (P)	True positive (TP)	False negative (FN)
Negative (N)	False positive (FP)	True negative (TN)
Sources: [13][14][15][16][17][18][19][20]

The color convention of the three data tables above were picked to match this confusion matrix, in order to easily differentiate the data.

Now, we can simply total up each type of result, substitute into the template, and create a confusion matrix that will concisely summarize the results of testing the classifier:

		Predicted condition
Total 8 + 4 = 12	Cancer 7	Non-cancer 5
Actual condition	Cancer 8	6	2
Non-cancer 4	1	3

In this confusion matrix, of the 8 samples with cancer, the system judged that 2 were cancer-free, and of the 4 samples without cancer, it predicted that 1 did have cancer. All correct predictions are located in the diagonal of the table (highlighted in green), so it is easy to visually inspect the table for prediction errors, as values outside the diagonal will represent them. By summing up the 2 rows of the confusion matrix, one can also deduce the total number of positive (P) and negative (N) samples in the original dataset, i.e. and .

Table of confusion[edit]

In predictive analytics, a table of confusion (sometimes also called a confusion matrix) is a table with two rows and two columns that reports the number of true positives, false negatives, false positives, and true negatives. This allows more detailed analysis than simply observing the proportion of correct classifications (accuracy). Accuracy will yield misleading results if the data set is unbalanced; that is, when the numbers of observations in different classes vary greatly.

For example, if there were 95 cancer samples and only 5 non-cancer samples in the data, a particular classifier might classify all the observations as having cancer. The overall accuracy would be 95%, but in more detail the classifier would have a 100% recognition rate (sensitivity) for the cancer class but a 0% recognition rate for the non-cancer class. F1 score is even more unreliable in such cases, and here would yield over 97.4%, whereas informedness removes such bias and yields 0 as the probability of an informed decision for any form of guessing (here always guessing cancer).

According to Davide Chicco and Giuseppe Jurman, the most informative metric to evaluate a confusion matrix is the Matthews correlation coefficient (MCC).^[21]

Other metrics can be included in a confusion matrix, each of them having their significance and use.

		Predicted condition	Sources: [22][23][24][25][26][27][28][29][30] view talk edit
Total population = P + N	Positive (PP)	Negative (PN)	Informedness, bookmaker informedness (BM) = TPR + TNR − 1	Prevalence threshold (PT) =
Actual condition	Positive (P)	True positive (TP), hit	False negative (FN), type II error, miss, underestimation	True positive rate (TPR), recall, sensitivity (SEN), probability of detection, hit rate, power = TP/P = 1 − FNR	False negative rate (FNR), miss rate = FN/P = 1 − TPR
Negative (N)	False positive (FP), type I error, false alarm, overestimation	True negative (TN), correct rejection	False positive rate (FPR), probability of false alarm, fall-out = FP/N = 1 − TNR	True negative rate (TNR), specificity (SPC), selectivity = TN/N = 1 − FPR
	Prevalence = P/P + N	Positive predictive value (PPV), precision = TP/PP = 1 − FDR	False omission rate (FOR) = FN/PN = 1 − NPV	Positive likelihood ratio (LR+) = TPR/FPR	Negative likelihood ratio (LR−) = FNR/TNR
Accuracy (ACC) = TP + TN/P + N	False discovery rate (FDR) = FP/PP = 1 − PPV	Negative predictive value (NPV) = TN/PN = 1 − FOR	Markedness (MK), deltaP (Δp) = PPV + NPV − 1	Diagnostic odds ratio (DOR) = LR+/LR−
Balanced accuracy (BA) = TPR + TNR/2	F1 score = 2 PPV × TPR/PPV + TPR = 2 TP/2 TP + FP + FN	Fowlkes–Mallows index (FM) =	Matthews correlation coefficient (MCC) =	Threat score (TS), critical success index (CSI), Jaccard index = TP/TP + FN + FP

Confusion matrices with more than two categories[edit]

Confusion matrix is not limited to binary classification and can be used in multi-class classifiers as well.^[31] The confusion matrices discussed above have only two conditions: positive and negative. For example, the table below summarizes communication of a whistled language between two speakers, zero values omitted for clarity.^[32]

Perceived vowel Vowel produced	i	e	a	o	u
i	15		1
e	1		1
a			79	5
o			4	15	3
u				2	2

See also[edit]

• Positive and negative predictive values

References[edit]

Мы уже рассказывали, как машинное обучение применяется для прогнозирования будущих событий в финансовом секторе, нефтегазовой промышленности, логистике, HR-менеджменте, девелопменте, страховании, муниципальном управлении, маркетинге, ритейле и других отраслях экономики. Сегодня рассмотрим еще несколько практических примеров такого приложения Machine Learning и в этом контексте разберем одно из ключевых понятий Data Science по оценке моделей. Читайте в нашей статье, что такое матрица ошибок (confusion matrix) и как она помогает измерить эффективность используемых ML-алгоритмов и других инструментов бизнес-аналитики, оценив потенциальные убытки и выгоды от возможных сценариев будущего в задаче прогнозирования спроса.

От ритейла до банка: 5 примеров применения Big Data и Machine Learning в задачах прогнозирования спроса и предложения

Вообще сегодня задача прогнозирования спроса стала довольно обыденным приложением методов Machine Learning (ML) в реальном бизнесе. В частности, в декабре 2019 года сервис объявлений «Юла» ускорил публикацию объявлений по продаже товаров с помощью функции их распознавания по фотографии. Помимо собственно распознавания того, что сфотографировано, нейросетевые модели предлагают пользователю уточнить характеристики продукта и оценивают его стоимость в среднем по рынку. При этом пользователю выдается прогноз, насколько быстро он продаст товар при различных ценах [1].

Другой пример, московский сервис приготовления и доставки еды навынос «Кухня на районе» с помощью нейросетей и ежедневной статистики продаж рассчитывает, сколько продуктов нужно привезти на каждую точку, чтобы минимизировать количество остатков. Анализируя данные по проданным позициям в разных локациях, нейросеть из 3 500 вариантов отбирает сотню блюд, которые будут максимально востребованы, чтобы готовить именно их на районных кухнях в течение следующей недели [2].

Подобным образом, на основе постоянного анализа продаж, машинное обучение позволяет эффективно решить задачу ценообразования, установив наиболее оптимальную стоимость на отдельные продукты и целые товарные категории. Например, именно это было сделано в отечественном интернет-магазине детских игрушек Babadu.ru, когда методы Machine Learning помогли разработать несколько маркетинговых стратегий, наиболее выгодных для ритейлера [3]. Аналогично строятся ML-модели эластичного спроса в другом российском гиганте интернет-торговли, Ozon.ru. Разработанный алгоритм анализирует значения более 150 признаков в истории продаж, чтобы на выходе предоставить точный прогноз по будущим заказам. При этом в модели заложена функция минимизации денежных потерь на покупку и хранение лишних товаров на складе или отток клиента (Churn Rate) из-за отсутствия нужного продукта [4].

Похожая задача прогнозирования спроса актуальна и для банков, которые стремятся оптимизировать процессы работы с наличными деньгами в своих банкоматах. Финансовые корпорации хотят, с одной стороны, чтобы средства не лежали в банкоматах «без дела»: гораздо выгоднее, например, разместить их на краткосрочном депозите. Но, клиенты будут недовольны, когда столкнутся с отказом из-за недостаточного количества денег в банкомате. Это грозит репутационными потерями, поэтому банк стремится решить данную проблему с помощью точного предсказания спроса на наличность в каждой точке расположения банкоматов. При этом нужно учитывать, что спрос на наличные зависит от множества параметров: макроэкономические факторы, политические новости, социальные события, расположение банкомата, прогноз погоды, время года, день недели и т.д. Чтобы предсказать завтрашнюю потребность в наличных для конкретного банкомата, Сбербанк, например, с 2016 года использует адаптивные алгоритмы машинного обучения вместе с классическими методами анализа временных рядов. Такие модели обеспечивают динамическое перестроение всех анализируемых параметров, предоставляя на выходе эффективный план оптимального распределения и перемещения наличных между банкоматами [5].

Что такое матрица ошибок и зачем она нужна: пример расчета стоимости ошибки прогнозирования

Поскольку в бизнесе поиск баланса между спросом и предложением напрямую конвертируется в деньги, возникает вопрос, насколько выгодно применение методов Machine Learning для решения этой задачи. С целью сопоставления предсказаний и реальности в Data Science используется матрица ошибок (confusion matrix) – таблица с 4 различными комбинациями прогнозируемых и фактических значений. Прогнозируемые значения описываются как положительные и отрицательные, а фактические – как истинные и ложные [6]. Вообще матрица ошибок используется для оценки точности моделей в задачах классификации. Но прогнозирование и распознавание образов можно рассматривать как частный случай этой проблемы, поэтому confusion matrix актуальна и для измерения точности предсказаний. Важно, что матрица ошибок позволяет оценить эффективность прогноза не только в качественном, но и в количественном выражении, т.е. измерить стоимость ошибки в деньгах. Например, каковы будут расходы на удержание пользователя, если машинное обучение предсказало, что он перестанет приносить компании пользу [7]? Аналогичный вопрос по предсказанию оттока (Churn Rate) актуален и в HR-сфере для удержания ключевых сотрудников, мотивация которых снижается. Впрочем, матрица ошибок может использоваться не только в рамках применения Machine Learning. По сути, этот метод оценки стоимости прогноза является универсальным аналитическим инструментом.

Прогноз	Реальность
+	—
+	True Positive (истинно-положительное решение): прогноз совпал с реальностью, результат положительный произошел, как и было предсказано ML-моделью	False Positive (ложноположительное решение): ошибка 1-го рода, ML-модель предсказала положительный результат, а на самом деле он отрицательный
—	False Negative (ложноотрицательное решение): ошибка 2-го рода – ML-модель предсказала отрицательный результат, но на самом деле он положительный	True Negative (истинно-отрицательное решение): результат отрицательный, ML-прогноз совпал с реальностью

С математической точки зрения оценить точность ML-модели можно с помощью следующих метрик [8]:

• Точность – сколько всего результатов было предсказано верно;
• Доля ошибок;
• Полнота – сколько истинных результатов было предсказано верно;
• F-мера, которая позволяет сравнить 2 модели, одновременно оценив полноту и точность. Здесь используется среднее гармоническое вместо среднего арифметического, сглаживая расчеты за счет исключения экстремальных значений.

В количественном выражении это будет выглядеть так:

• P – число истинных результатов, P = TP + FN;
• N – число ложных результатов, N = TN + FP.

Рассмотрим матрицу ошибок на практическом примере для задачи прогнозирования спроса на скоропортящуюся продукцию, которая должна быть продана конечному пользователю в течение суток. Например, букеты цветов, продающиеся по цене k рублей при закупочной стоимости в p рублей. Предположим, с помощью Machine Learning было предложена 2 варианта:

• Положительный прогноз (+), что по цене k будут полностью раскуплены все цветы в количестве n букетов.
• Отрицательный прогноз (+), что по цене k будут полностью раскуплены не все цветы, останется m не проданных букетов.

Соответственно, матрица ошибок для этого случая будет выглядеть следующим образом:

Прогноз	Реальность
Проданы все букеты цветов	Остались не проданные m букетов
+: Проданы все n букетов по k рублей c ценой закупки p	True Positive: прогноз совпал с реальностью, все закупленные n букетов проданы Выручка = n*k Затраты = n*p Прибыль = n*(k-p) Стоимость ошибки = 0	False Positive: ошибка 1-го рода, ML-модель предсказала, что будет n продаж, а на самом деле их было (n-m), осталось m не проданных букетов, которые пропали и не вернули затраты на их покупку Выручка = (n-m)*k Затраты = n*p Прибыль = n*(k-p) – m*k Стоимость ошибки = m*p
—: Остались не проданные m букетов c ценой закупки p	False Negative: ошибка 2-го рода – ML-модель предсказала, что n букетов не будет продано, поэтому закупили (n-m) букетов, но спрос был на n букетов. Эффект недополученной прибыли Выручка = (n-m)*k Затраты = (n-m)*p Прибыль = (n-m)*(k-p) Стоимость ошибки = m*k	True Negative: ML-прогноз совпал с реальностью, было раскуплено (n-m) букетов по цене k, сколько и было изначально закуплено по цене p Выручка = (n-m)*k Затраты = (n-m)*p Прибыль = (n-m)*(k-p) Стоимость ошибки = 0

Таким образом, с помощью confusion matrix можно измерить эффективность прогноза в денежном выражении, что весьма актуально для практического бизнес-приложения Machine Learning. Впрочем, отметим еще раз, что данный метод предварительной оценки будущих сценариев можно использовать и вне сферы Data Science, оценивая риски и перспективы в рамках классического бизнес-анализа.

Другие практические вопросы системного и бизнес-анализа рассматриваются в рамках нашей Школы прикладного бизнес-анализа. А особенности практического применения больших данных и машинного обучения разбираются на наших образовательных курсах в лицензированном учебном центре обучения и повышения квалификации ИТ-специалистов (менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data) в Москве:

• Аналитика больших данных для руководителей
• Машинное обучение на Python

Источники

1. https://www.the-village.ru/village/city/news-city/371179-tseny
2. https://www.the-village.ru/village/business/businessmen/371631-kuhnya-na-rayone
3. https://chernobrovov.ru/articles/kak-mashinnoe-obuchenie-pomogaet-pravilno-ustanavlivat-pravilnye-ceny.html
4. https://habr.com/ru/company/ozontech/blog/431950/
5. http://futurebanking.ru/post/3213
6. https://hranalytic.ru/kak-ponyat-matrica-nesootvetstvij-confusion-matrix/
7. https://chernobrovov.ru/articles/kak-izmerit-effektivnost-machine-learning-schitaem-metriki-i-dengi-na-primere-prognozirovaniya-ottoka-polzovatelej.html
8. http://www.machinelearning.ru/wiki/images/archive/5/54/20151001162720!Kitov-ML-05-Model_evaluation.pdf

Уровень сложности
Простой

Время на прочтение
7 мин

Количество просмотров 2.3K

Матрица Несоответствий довольно широко освещённый термин в науке о данных, про него без труда можно найти публикации в сети. В данной статье дано как само описание и принципы построения Матрицы Несоответствий (другие названия — Confusion matrix или Матрица Ошибок), так и основанные на этом понятии принципы работы различных метрик в задачах классификации в Машинном обучении. Несмотря на то, что само понятие Confusion Matrix является довольно простым в объяснении, начинающим Data Scientist-специалистам бывает порой нелегко разобраться в отношениях True Positive (TP), False Positive (FP), True Negative (TN), False Negative (FN) — кирпичиками, составляющими данную матрицу. Цель этой статьи познакомить читателя с альтернативным представлением Матрицы Ошибок. Данный способ, по мнению автора, является наиболее наивным методом восприятия самой Матрицы Несоответствий, что в свою очередь позволит легко ориентироваться в выводах, основанных на комбинации ее элементов, глубже понять проблему дисбаланса классов в задачах классификации.

План данной статьи:

• приведем ряд сокращений с пояснениями, которые будут использоваться в статье;

• повторим классическое описание Матрицы Ошибок и ее основных составляющих;

• представим альтернативный способ запоминания Матрицы Несоответствий, в основе которого лежит графическое отношение комбинации ее элементов;

• разберем понятия Precision, Recall, TPR, FPR;

• рассмотрим понятия ROC-AUC, F1-меры метрик задач классификации;  

• рассмотрим проблему дисбаланса классов в задачах классификации.

Сокращения, термины-синонимы, используемые в статье:

• Confusion Matrix — Матрица Несоответствий, Матрица Ошибок

• ML — Машинное обучение

• Модель  (в данной статье) — алгоритм  классификации

• TP — истинно-положительные объекты ( True Positive )

• FP — ложно-положительные объекты ( False Pasitive )

• TN — истинно-отрицательные объекты ( True Negative )

• FN — ложно-отрицательные объекты ( False Negative )

• TPR — True Positive Rate

• FPR — False Positive Rate

• ROC — Receiver Operating Characteristic curve

• AUC — Area Under Curve

Автор предполагает, что читатель знаком с задачей классификации объектов в Машинном обучении, и поэтому в статье данный вопрос будет затронут поверхностно. Для простоты разберем бинарную классификацию, где истинные метки объектов принадлежат пространству.

Дадим пояснения:

0 — объекты относятся к нулевому классу,

1 — объекты относятся к классу 1.

Алгоритм машинного обучения выдает свой прогноз по этим меткам

здесь 0 — метки объектов, которые алгоритм классифицирует как объекты класса 0, и 1 — метки объектов, которые алгоритм считает за объекты класса 1.

Приведем модельный пример: допустим, у нас есть альбом с фотографиями животных и людей. Все фото, где присутствуют животные, пометим как объекты класса 1, а где их нет, как объекты класса 0.  Сформулируем задачу: написать, алгоритм, способный понять, присутствует ли изображение животного на снимке или отсутствует. Сложность ситуации в том, что созданный классификатор не знает истинное значение, какой объект к какому классу принадлежит в реальности, и поэтому может ошибаться в своих ответах.

Для описания комбинаций, которые могут получаться при сопоставлении ответов алгоритма и истинных меток объекта в Машинном обучении, используются следующие понятия:

• TP — истинно-положительные объекты ( True Positive) — объект представляет собой класс 1 и алгоритм его идентифицирует как класс 1

• FP — ложно-положительные объекты ( False Positive) — объект представляет собой класс 0, алгоритм его идентифицирует как класс 1 (ошибается)

• TN — истинно-отрицательные объекты ( True Negative) — объект представляет собой класс 0 и алгоритм его идентифицирует как класс 0

• FN — ложно-отрицательные объекты ( False Negative) — объект представляет собой класс 1, алгоритм его идентифицирует как класс 0.

Данные элементы являются составными частями Матрицы Несоответствий, построенной в координатах истинные ответы и ответы классификатора.

Для оценки качества работы алгоритма в Машинном обучении применяются различные метрики, часть которых основана на применении отношений комбинаций элементов Матрицы Несоответствий.

Так, например, понятия , и

используются в таких метриках, как F1-мера, Accuracy, Balanced Accuracy, Precision-Recall

curve и др. В метрике ROC-AUC применяется , и

При этом ни Precision, Recall, ни FPR, TPR не являются самостоятельными мерами оценки качества работы алгоритма, а используются в соответствующих метриках в различных парных комбинациях.

Значительное количества метрик, формул, плюс проблема дисбаланса классов (непропорциональное отношение количества объектов класса 0 к классу 1) — все это во время работы с данными предполагает постоянное обращение к классическому представлению Матрицы Несоответствий. В этой статье для более легкого интуитивного усвоения описанных понятий предлагается отойти от «сухого» табличного формата, попытаться понять изложенную информацию через ее визуализацию.

Для этого представим, что мы пришли в тир пострелять по мишени.

Здесь следует напомнить, что все многообразие мира бинарная классификация делит на объекты, принадлежащие классу 1 и классу 0.  Это и будет наша мишень. Изобразим это на рисунке.

Возвращаясь к нашей задаче поиска животных на фотоснимках в альбоме, объекты класса 1 — это те фотографии, на которых имеются изображения животных, объекты класса 0 — снимки, которые их не содержат в реальности.

Теперь разберемся с понятием Precision. В переводе с английский этот термин обозначает “точность”, в Машинном Обучении под Precision подразумевается насколько наш алгоритм способен правильно классифицировать класс 1 из всех объектов, которые он распознал как единички или доля тех фотографий, где есть на самом деле животные из всего объема фотографий, в которых алгоритм указал, что на них имеется целевое изображение. На данном этапе предлагаю не заучивать данное объяснение, тем более что мы интуитивно выведем его сами на примере.

Возвращаемся в импровизированный тир, тогда “точность” — это будет выстрел нашего алгоритма, который пытается найти объекты класса 1, стреляя в центр мишени.

Все объекты, заключенные в контуре круга, для нашего алгоритма будут иметь метку 1, то есть интерпретированы как фотографии с животными. При этом мы видим, что алгоритм может ошибаться, так как в центр мишени вошли как фотографии с животными (объекты класса 1), так и изображения без животных (класса 0). Область, где наш алгоритм справился со своей задачей и правильно угадал класс 1, будет соответствовать True Positive (истинно положительные ответы, животные есть на снимках на самом деле), а где ошибся False Positive (ложно положительные ответы, здесь классификатор предполагает, что на фото животные есть, но на самом деле их нет).

Зона, где наш объект правильно идентифицирует объекты класса 0 и не ошибается на них, соответствует понятию True Negative — истинно негативные объекты, то есть те фотографии, где животных в реальности нет, и алгоритм с этим согласен. На рисунке 05 данный участок отмечен как TN. 

Соответственно, одна непромаркерованная область будет соответствовать как по смыслу, так и по методу исключения понятию False Negative или FN (ложно отрицательные, то есть наш алгоритм не смог эти объекты правильно классифицировать как объекты класса 1, например, спящую собаку в углу какого-то снимка распознал как камень или что-либо другое).

Теперь дополним наш рисунок новой информацией и сравним с табличной формой Матрицы Ошибок.

Объекты, отвечающие за расчет Precision (точность), сконцентрированы внутри центрального контура. Глядя на картинку, попробуйте сами сформулировать термин Precision.

Сравните с правильным ответом: Precision — доля объектов, предсказанных алгоритмом как класс 1 и являющиеся на самом деле классом 1. В нашей задаче по определению есть ли животное на фото, это будет звучать как доля фотографий, где алгоритм распознал наличие животного, и оно на самом деле там присутствует.

Термин Recall имеет тоже довольно простую интерпретацию: способность нашего алгоритма определять класс 1.

В применении к нашей задаче поиска определенных фотографий термин Полнота или Recall будет трактоваться как способность нашего алгоритма находить фото с животным из всех снимков, которые в реальности их содержат.

Настало время дать оценку насколько хорошо работает модель Машинного обучения. Для этого используют различные метрики, особенность их состоит в том, что такие метрики, как F1-мера, Accuracy, Balanced Accuracy, применяют различные комбинации разобранных нами методов Precision и Recall. Как эти понятия взаимодействуют между собой, очень хорошо можно понять через визуальное представление Матрицы Ошибок.  

Разберем это на примере F1-мера, которая является частным случаем среднегармонической F-меры:

F1-мера является довольно стабильной метрикой при равном балансе классов (в примере с фотографиями животных, когда количество снимков, где присутствуют животные, примерно равно количеству снимков без животных). На практике большинство задач имеют перекос в балансе классов. Посмотрим, что будет происходит с описанными понятиями в этом случае.

Как видно из рисунка выше, Recall пропорционально изменяется вместе с балансом классов, в то время как Precision сильно меняет значения. Для нивелирования перекоса предполагается использование некоторого β коэффициента — это и будет среднегармоническая F-мера. Хотя в отличие от нашего примера, в Машинном обучении при дисбалансе классов принято более редкий класс обозначать через 1, а наибольший через 0, но это не меняет идеи того, что изменения F-меры обусловлены нестабильным в таком случае параметром Precision. Подбор  β коэффициента напрямую влияет на качество оценки работы модели. Обоснование и поиск данного коэффициента выходит за рамки данной статьи.

Среднегармоническая F-мера

Теперь рассмотрим метрику ROC-AUC (Area Under Curve). Данная оценка работы алгоритма классификации рассчитывается как площадь под ROC кривой, которая строится в координатах TPR и FPR.  Указанная метрика более устойчива к дисбалансу классов ввиду того, что в отличие от F1-меры здесь задействованы все элементы матрицы. Отметим, что термин TPR (True Positive Rate) равен рассмотренному ранее Recall.

Из рисунка понятно причина стабильности метрики ROC-AUC при дисбалансе классов: при увеличении, например, количества объектов класса 0 все элементы входящие в FPR будут также пропорционально увеличиваться, а элементы, составляющие TPR наоборот уменьшаться. Но при этом итоговое значение FPR и TPR будут примерно соотноситься к тем значениям, когда дисбаланса класса нет. 

Из рисунка понятно причина стабильности метрики ROC-AUC при дисбалансе классов: при увеличении, например, количества объектов класса 0 все элементы входящие в FPR будут также пропорционально увеличиваться, а элементы, составляющие TPR наоборот уменьшаться. Но при этом итоговое значение FPR и TPR будут примерно соотноситься к тем значениям, когда дисбаланса класса нет. 

Заключение

В машинном обучении в задачах классификации для оценки насколько хорошо работает построенная модель и сравнения ее с другими алгоритмами применяются специальные агрегированные метрики. Для наилучшего освоения основ применения данных метрик специалисту по данным необходимо хорошо понимать концепцию их описания в терминах ошибок классификации — Матрице Ошибок или Матрице Несоответствий. В данной статье, предложен способ визуализировать Confusion Matrix в более легкий формат для восприятия в сравнении с классическим табличным видом. Через это представление рассмотрены часть метрик классификации и их элементов, разобрано поведение этих метрик при сбалансированных выборках и дисбалансе классов.