Меры изменчивости
Меры центральной
тенденции говорят о концентрации группы
значений на числовой шкале. Каждая мера
дает такое значение, которое
«представляет» в каком-то смысле все
оценки группы. В этом случае пренебрегают
различиями, существующими между
отдельными значениями. Для измерения
вариации оценок внутри группы требуются
другие описательные статистики.
Всякая научная
деятельность связана с понятием
изменчивости. Когда есть много
необъяснимых причин вариабельности,
прогнозы не будут очень точными. Зато,
когда объяснения причинразличий
людей и вещей представлены в виде
некоторой модели, неопределенность
можно уменьшить, а часть вариации
устранить.
Например, если бы
было совсем неизвестно, почему люди
различаются между собой по умственному
развитию, то попытка прогнозировать
интеллект наталкивалась бы на большую
неопределенность; некоторые люди
выглядели бы «смышлеными», а другие –
«глупыми», и никто не знал бы, почему.
Однако если известно, что наследственность
и окружающая среда оказывают
количественное влияние на IQ,
то информация о происхождении ребенка
и его воспитании в раннем детстве
позволила бы дать более точный прогноз
его умственного развития в зрелости.
Другими словами, вариабельность IQ у лиц
со сходной наследственностью и окружающей
средой меньше, чем у людей вообще.
4.1 Размах
Размах(иногда эту величину называют разбросом
выборки) измеряет на числовой шкале
расстояние, в пределах которого изменяются
оценки, и обозначается буквойR.
Это самый простой показатель, который
можно получить для выборки, – разность
между максимальным и минимальным
значениями вариационного ряда, т.е.
(4.1)
Понятно, что чем
сильнее варьирует измеряемый признак,
тем больше величина R,
и наоборот.
Однако может
случиться так, что у двух выборочных
рядов и средние, и размах совпадают,
однако характер варьирования этих рядов
будет различный. Для того чтобы более
четко представлять характер варьирования
выборок, следует обратиться к их
распределениям.
4.2 Дисперсия и стандартное отклонение
Значения отклонений,
то есть значения вида
,
несут информацию о вариации выборочной
совокупности значений. Совокупность с
большой неоднородностью будет иметь
несколько больших отклонений. Каковы
были бы отклонения, если бы все значения
и совокупности равнялись 8? Среднее было
бы 8, следовательно, каждое отклонение
было бы 8 – 8 = 0. В предельно однородной
совокупности, которая в принципе
достижима, все отклонения равны нулю.
Некоторая комбинация отклонений могла
бы быть полезной мерой вариации.
Если бы нам
требовалось просуммировать все
отклонения, то характеризовала ли бы
эта сумма вариацию исходных данных?
Нет, поскольку эта сумма всегда точно
равна нулю:
.
Для обхода этого
факта мы можем возвести в квадрат каждое
отклонение и найти сумму квадратов.
Следовательно, для данной совокупности
мера вида
будет большой,
когда данные неоднородны, и малой для
однородных. Чтобы избавиться от знаков,
мы могли бы обойтись без квадратов
отклонений; мы могли бы просто рассматривать
эти отклонения как положительные (взятые
по их абсолютной величине). Это привело
бы к другой мере вариации, называемой
средним отклонением.
Величина суммы
квадратов зависит также от того, сколько
имеется данных Чем больше п,тем
больше сумма. Если хотят сравнить
изменчивость двух совокупностей, которые
отличаются по объему, то возникает
ограничение. Оно снимается после деления
суммы наn-1 и называетсявыборочной дисперсией:

(4.2)
где – выборочная дисперсия;
xi– значение признака;
–выборочная
средняя;
n
– объем выборки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Меры разброса (изменчивости) применяются в психологии для численного выражения величины межиндивидуальной вариации признака и показывают, насколько хорошо данные значения представляют данную совокупность.
Минимальное и максимальное
Минимальное (Xmin) — это наименьшее значение измерения (переменной) в выборке.
Максимальное (Xmax) — это самое большое значение измерения (переменной) в выборке.
Сами по себе эти меры не очень информативны. Особенно если величина распределяется по нормальному закону. Но если мы измеряем какое-то конкретное свойство на примере узкой выборки (например, агрессивность людей, страдающих каким-то заболеванием), то минимальное и максимальное значения могут дать возможность качественно описать эту выборку и лучше понимать особенности ее представителей.
Размах
Размах — разность между наибольшим и наименьшим значениями результатов наблюдений, является одной из самых простых мер изменчивости набора числовых значений. Дает информацию о ширине интервала, в котором сосредоточен весь набор числовых данных, геометрически — ширина отрезка, в котором располагаются все значения.
\( R = X_{max} — X_{min} \)
Простота расчета, наглядность и интуитивная понятность этой характеристики рассеяния значений является очевидным преимуществом перед такими мерами рассеяния как дисперсия и среднее квадратическое отклонение (стандартное отклонение). Существенным недостатком размаха является то, что он не содержит информацию о характере распределения результатов в интервале рассеяния и не устойчив к выбросам, в определенной степени ограничивает его использование.
Пример: допустим у нас есть выборка значений {3,4,5,6,7} где максимальное значение 7, а минимальное 3, получим:
\( R = 7 — 3 = 4 \)
Минимальное, максимальное и размах измерений свойства у представителей двух независимых выборок (например, мужчин и женщин), представленные в виде графика, позволяют визуально определить наличие различий в проявлении изучаемого свойства. А значит предположить влияние признака (в нашем примере –это пол испытуемых) на выраженность свойства.
Межквартильный размах
В статистике для анализа выборки часто прибегают к более стабильному к выбросам показателю вариации – межквартильному размаху (IQR). Квартиль (Q) – это то значение, которое делит отсортированные (ранжированные) данные на части, кратные одной четверти, или 25%, что равносильно 25-му процентлю или квантилю 0.25. Так, 1-й квартиль (Q1) – это значение, ниже которого находится 25% выборки. 2-й квартиль (Q2) делит выборку данных пополам и равен медиане, ну и 3-й квартиль (Q3) это значение выше которого находится 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями.
\( IQR = Q3 -Q1 \)
У данного показателя есть одно неоспоримое преимущество: он является робастным.
Пример: допустим у нас есть выборка отсортированных значений {0,1,3,4,5,6,7,100}. Первым делом определяем медиану по которую выборку разделим на две равные части. Медиана у нас 4.5, получаем две выборки {0,1,3,4} и {5,6,7,100}. Теперь для полученых выборок определим медиану. Для первой это будет 2 и это значение будет соответствовать первому квартилю (Q1). Для второй выборки это будет 6.5 и соответствовать третьему квартилю (Q3). Тогда:
\( IQR = 6.5 — 2 = 4.5 \)
Дисперсия
Один из способов измерения рассеяния данных заключается в том, чтобы определить степень отклонения каждого наблюдения от выборочного среднего. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений.
Однако мы не можем использовать среднее этих отклонений как меру рассеяния, потому что положительные отклонения компенсируют отрицательные отклонения, их сумма равна нулю. Чтобы решить эту проблему, мы возводим в квадрат каждое отклонение и находим среднее возведенных в квадрат отклонений.
\( D = \sigma^{2}=\frac{\sum_{i=1}^n(X_{i}- \bar{X})^{2}}{n-1} \)
Дисперсия является одним из параметров нормального закона распределения. Чем больше дисперсия, тем более пологими являются «склоны» распределения и длиннее его «хвосты».
Чем выше дисперсия показателей измеряемого свойства (коэффициентов регрессии, значений переменных и т.д.), тем менее устойчивой она будет. Высокая дисперсия исходных данных позволяет предположить высокую значимость в них случайной компоненты, возможном наличии шума, выбросов и аномальных значений.
Пример: допустим у нас есть выборка значений {3,4,5,6,7} первым делом расчитываем выборочное среднее:
\( \bar{X}=\frac{3+4+5+6+7}{5}=\frac{25}{5}=5 \)
Теперь приступим к расчету дисперсии
\( D=\frac{(3-5)^{2}+(4-5)^{2}+(5-5)^{2}+(6-5)^{2}+(7-5)^{2}}{5-1} = \frac{4+1+0+1+4}{4} = 2.5 \)
К сожалению, не существует никаких ориентиров, чтобы интерпретировать величину дисперсии. Тем более, что на ее величину будет влиять размер шкалы измерения. Однако, расчет дисперсии нам необходим для определения следующих статистик.
Стандартное отклонение
Это наиболее распространенный показатель в статистике и теории вероятности, оценивающий среднеквадратичное отклонение случайной величины относительно ее математического ожидания на основе несмещенной оценки ее дисперсии. Измеряется в единицах измерения самой случайной величины.
\( \sigma=\sqrt{D}=\sqrt{\frac{\sum_{i=1}^n(X_{i}- \bar{X})^{2}}{n-1}} \)
Если перейти на «человеческий» язык, то стандартное отклонение — это показатель того, насколько резво какой-либо показатель меняется со временем или у разных людей. Т.е. чем больше этот показатель, тем сильнее изменчивость ряда значений.
Стандартное отклонение используют для анализа наборов значений. Иногда два набора с одинаковым средним значением могут оказаться совершенно разными по разбросу величин.
Пример: расчитывать стандартное отклонение достаточное легко после того как расчитали дисперсию. Допустим у нас есть все та же выборка {3,4,5,6,7}, для нее мы уже расчитали дисперсию и она равна 2.5, тогда
\( \sigma=\sqrt{2.5} = 1.58113883 \)
Синонимы:
- среднее квадратическое отклонение
- среднеквадратичное отклонение
- среднеквадратическое отклонение
- квадратичное отклонение
- стандартный разброс
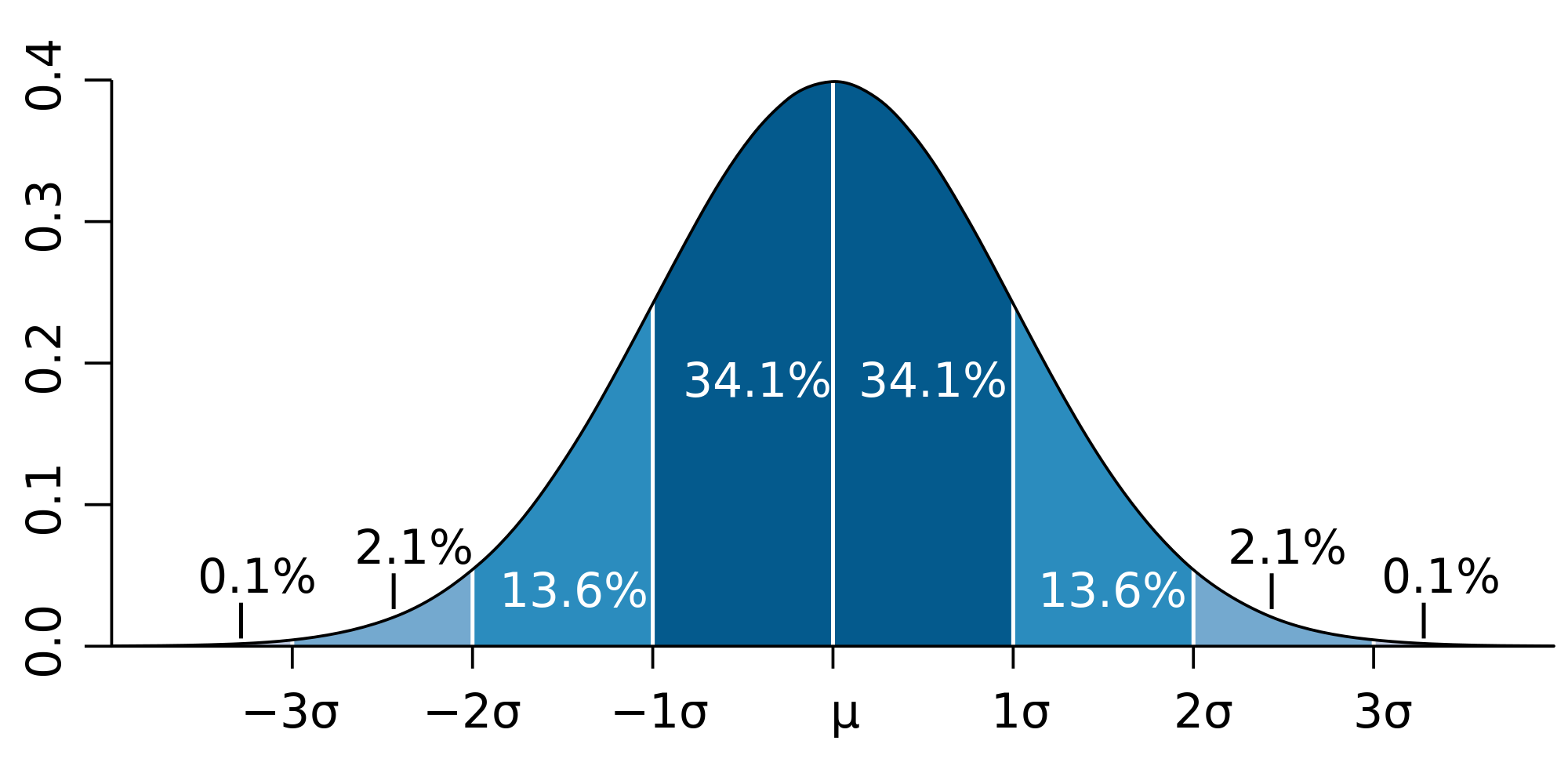
Для психологии расчет стандартного отклонения необходим для определения нормативных интервалов выраженности свойства. Для этого используется «правило трех сигм».
Это правило утверждает, что вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три среднеквадратических отклонения, практически равна нулю. Правило справедливо только для случайных величин, распределенных по нормальному закону, поэтому часто используется в современной психометрике.
Как показано на рисунке интервал [-3σ;-1σ] – это значения, соответствующие низкому уровню выраженности свойства, интервал[-1σ;1σ] – среднему уровню, а интервал [1σ;3σ] – высокому.
Пример:
Мы измеряем беглость мышления по шкале от 0 до 12. Для применения правила нам нужно высчитать среднее выборочное и стандартное отклонение.
Допустим, мы определили, что среднее М = 7, а стандартное отклонение σ = 1,5.
Далее, как показано на рисунке, нам нужно трижды отнять стандартное отклонение от среднего (получим: -1σ = 5,5; -2σ = 4, -3σ = 2,5), и трижды прибавить (1σ = 8,5; 2σ = 10, 3σ = 11,5).
Таким образом получим интервал низких значений [2,5; 5,5]; интервал средних значений [5,5; 8,5]; интервал высоких значений [8,5; 11,5].
Коэффициент вариации
Коэффициент вариации — это величина, используемая в статистике, равная отношению стандартного отклонения случайной величины к ее математическому ожиданию (среднему выборочному). Он применяется для сравнения вариативности одного и того же признака в нескольких совокупностях с различным средним арифметическим. Т.к. коэффициент вариации величина относительная, то обычно она выржаеться в процентах.
\( CV = \frac{\sigma}{\bar{X}}\cdot100 \)
В статистике принято, что:
- если коэффициент вариации меньше 10%, то степень рассеивания данных считается незначительной;
- если от 10% до 20% — средней;
- больше 20% и меньше или равно 33% — значительной.
Если значение коэффициента вариации не превышает 33%, то совокупность считается однородной, а если больше 33%, то — неоднородной.
Пример: берем ранее используемый ряд данных {3,4,5,6,7}, для него у нас посчитано уже и стандартное отклонение и выборочное среднее, получим:
\( CV = \frac{1.58113883}{5}\cdot100 = 31.6227766 \)
Исходя из получившегося результата можем утверждать, что степень рассеивания данных значительная, а сама выборка однородная. Если бы мы изучали какое-то свойство, это бы означало, что оно стабильно закрепилось у представителей выборки на уровне, соответствующем среднему выборочному. А значит мы можем смело утверждать, что изучаемое свойство характерно для представителей нашей выборки.
Меры изменчивости
Меры центральной
тенденции говорят о концентрации группы
значений на числовой шкале. Каждая мера
дает такое значение, которое
«представляет» в каком-то смысле все
оценки группы. В этом случае пренебрегают
различиями, существующими между
отдельными значениями. Для измерения
вариации оценок внутри группы требуются
другие описательные статистики.
Всякая научная
деятельность связана с понятием
изменчивости. Когда есть много
необъяснимых причин вариабельности,
прогнозы не будут очень точными. Зато,
когда объяснения причинразличий
людей и вещей представлены в виде
некоторой модели, неопределенность
можно уменьшить, а часть вариации
устранить.
Например, если бы
было совсем неизвестно, почему люди
различаются между собой по умственному
развитию, то попытка прогнозировать
интеллект наталкивалась бы на большую
неопределенность; некоторые люди
выглядели бы «смышлеными», а другие –
«глупыми», и никто не знал бы, почему.
Однако если известно, что наследственность
и окружающая среда оказывают
количественное влияние на IQ,
то информация о происхождении ребенка
и его воспитании в раннем детстве
позволила бы дать более точный прогноз
его умственного развития в зрелости.
Другими словами, вариабельность IQ у лиц
со сходной наследственностью и окружающей
средой меньше, чем у людей вообще.
4.1 Размах
Размах(иногда эту величину называют разбросом
выборки) измеряет на числовой шкале
расстояние, в пределах которого изменяются
оценки, и обозначается буквойR.
Это самый простой показатель, который
можно получить для выборки, – разность
между максимальным и минимальным
значениями вариационного ряда, т.е.
(4.1)
Понятно, что чем
сильнее варьирует измеряемый признак,
тем больше величина R,
и наоборот.
Однако может
случиться так, что у двух выборочных
рядов и средние, и размах совпадают,
однако характер варьирования этих рядов
будет различный. Для того чтобы более
четко представлять характер варьирования
выборок, следует обратиться к их
распределениям.
4.2 Дисперсия и стандартное отклонение
Значения отклонений,
то есть значения вида
,
несут информацию о вариации выборочной
совокупности значений. Совокупность с
большой неоднородностью будет иметь
несколько больших отклонений. Каковы
были бы отклонения, если бы все значения
и совокупности равнялись 8? Среднее было
бы 8, следовательно, каждое отклонение
было бы 8 – 8 = 0. В предельно однородной
совокупности, которая в принципе
достижима, все отклонения равны нулю.
Некоторая комбинация отклонений могла
бы быть полезной мерой вариации.
Если бы нам
требовалось просуммировать все
отклонения, то характеризовала ли бы
эта сумма вариацию исходных данных?
Нет, поскольку эта сумма всегда точно
равна нулю:
.
Для обхода этого
факта мы можем возвести в квадрат каждое
отклонение и найти сумму квадратов.
Следовательно, для данной совокупности
мера вида
будет большой,
когда данные неоднородны, и малой для
однородных. Чтобы избавиться от знаков,
мы могли бы обойтись без квадратов
отклонений; мы могли бы просто рассматривать
эти отклонения как положительные (взятые
по их абсолютной величине). Это привело
бы к другой мере вариации, называемой
средним отклонением.
Величина суммы
квадратов зависит также от того, сколько
имеется данных Чем больше п,тем
больше сумма. Если хотят сравнить
изменчивость двух совокупностей, которые
отличаются по объему, то возникает
ограничение. Оно снимается после деления
суммы наn-1 и называетсявыборочной дисперсией:

(4.2)
где – выборочная дисперсия;
xi– значение признака;
–выборочная
средняя;
n
– объем выборки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Меры разброса (изменчивости) применяются в психологии для численного выражения величины межиндивидуальной вариации признака и показывают, насколько хорошо данные значения представляют данную совокупность.
Минимальное и максимальное
Минимальное (Xmin) — это наименьшее значение измерения (переменной) в выборке.
Максимальное (Xmax) — это самое большое значение измерения (переменной) в выборке.
Сами по себе эти меры не очень информативны. Особенно если величина распределяется по нормальному закону. Но если мы измеряем какое-то конкретное свойство на примере узкой выборки (например, агрессивность людей, страдающих каким-то заболеванием), то минимальное и максимальное значения могут дать возможность качественно описать эту выборку и лучше понимать особенности ее представителей.
Размах
Размах — разность между наибольшим и наименьшим значениями результатов наблюдений, является одной из самых простых мер изменчивости набора числовых значений. Дает информацию о ширине интервала, в котором сосредоточен весь набор числовых данных, геометрически — ширина отрезка, в котором располагаются все значения.
( R = X_{max} — X_{min} )
Простота расчета, наглядность и интуитивная понятность этой характеристики рассеяния значений является очевидным преимуществом перед такими мерами рассеяния как дисперсия и среднее квадратическое отклонение (стандартное отклонение). Существенным недостатком размаха является то, что он не содержит информацию о характере распределения результатов в интервале рассеяния и не устойчив к выбросам, в определенной степени ограничивает его использование.
Пример: допустим у нас есть выборка значений {3,4,5,6,7} где максимальное значение 7, а минимальное 3, получим:
( R = 7 — 3 = 4 )
Минимальное, максимальное и размах измерений свойства у представителей двух независимых выборок (например, мужчин и женщин), представленные в виде графика, позволяют визуально определить наличие различий в проявлении изучаемого свойства. А значит предположить влияние признака (в нашем примере –это пол испытуемых) на выраженность свойства.
Межквартильный размах
В статистике для анализа выборки часто прибегают к более стабильному к выбросам показателю вариации – межквартильному размаху (IQR). Квартиль (Q) – это то значение, которое делит отсортированные (ранжированные) данные на части, кратные одной четверти, или 25%, что равносильно 25-му процентлю или квантилю 0.25. Так, 1-й квартиль (Q1) – это значение, ниже которого находится 25% выборки. 2-й квартиль (Q2) делит выборку данных пополам и равен медиане, ну и 3-й квартиль (Q3) это значение выше которого находится 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями.
( IQR = Q3 -Q1 )
У данного показателя есть одно неоспоримое преимущество: он является робастным.
Пример: допустим у нас есть выборка отсортированных значений {0,1,3,4,5,6,7,100}. Первым делом определяем медиану по которую выборку разделим на две равные части. Медиана у нас 4.5, получаем две выборки {0,1,3,4} и {5,6,7,100}. Теперь для полученых выборок определим медиану. Для первой это будет 2 и это значение будет соответствовать первому квартилю (Q1). Для второй выборки это будет 6.5 и соответствовать третьему квартилю (Q3). Тогда:
( IQR = 6.5 — 2 = 4.5 )
Дисперсия
Один из способов измерения рассеяния данных заключается в том, чтобы определить степень отклонения каждого наблюдения от выборочного среднего. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений.
Однако мы не можем использовать среднее этих отклонений как меру рассеяния, потому что положительные отклонения компенсируют отрицательные отклонения, их сумма равна нулю. Чтобы решить эту проблему, мы возводим в квадрат каждое отклонение и находим среднее возведенных в квадрат отклонений.
( D = sigma^{2}=frac{sum_{i=1}^n(X_{i}- bar{X})^{2}}{n-1} )
Дисперсия является одним из параметров нормального закона распределения. Чем больше дисперсия, тем более пологими являются «склоны» распределения и длиннее его «хвосты».
Чем выше дисперсия показателей измеряемого свойства (коэффициентов регрессии, значений переменных и т.д.), тем менее устойчивой она будет. Высокая дисперсия исходных данных позволяет предположить высокую значимость в них случайной компоненты, возможном наличии шума, выбросов и аномальных значений.
Пример: допустим у нас есть выборка значений {3,4,5,6,7} первым делом расчитываем выборочное среднее:
( bar{X}=frac{3+4+5+6+7}{5}=frac{25}{5}=5 )
Теперь приступим к расчету дисперсии
( D=frac{(3-5)^{2}+(4-5)^{2}+(5-5)^{2}+(6-5)^{2}+(7-5)^{2}}{5-1} = frac{4+1+0+1+4}{4} = 2.5 )
К сожалению, не существует никаких ориентиров, чтобы интерпретировать величину дисперсии. Тем более, что на ее величину будет влиять размер шкалы измерения. Однако, расчет дисперсии нам необходим для определения следующих статистик.
Стандартное отклонение
Это наиболее распространенный показатель в статистике и теории вероятности, оценивающий среднеквадратичное отклонение случайной величины относительно ее математического ожидания на основе несмещенной оценки ее дисперсии. Измеряется в единицах измерения самой случайной величины.
( sigma=sqrt{D}=sqrt{frac{sum_{i=1}^n(X_{i}- bar{X})^{2}}{n-1}} )
Если перейти на «человеческий» язык, то стандартное отклонение — это показатель того, насколько резво какой-либо показатель меняется со временем или у разных людей. Т.е. чем больше этот показатель, тем сильнее изменчивость ряда значений.
Стандартное отклонение используют для анализа наборов значений. Иногда два набора с одинаковым средним значением могут оказаться совершенно разными по разбросу величин.
Пример: расчитывать стандартное отклонение достаточное легко после того как расчитали дисперсию. Допустим у нас есть все та же выборка {3,4,5,6,7}, для нее мы уже расчитали дисперсию и она равна 2.5, тогда
( sigma=sqrt{2.5} = 1.58113883 )
Синонимы:
- среднее квадратическое отклонение
- среднеквадратичное отклонение
- среднеквадратическое отклонение
- квадратичное отклонение
- стандартный разброс
Для психологии расчет стандартного отклонения необходим для определения нормативных интервалов выраженности свойства. Для этого используется «правило трех сигм».
Это правило утверждает, что вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три среднеквадратических отклонения, практически равна нулю. Правило справедливо только для случайных величин, распределенных по нормальному закону, поэтому часто используется в современной психометрике.
Как показано на рисунке интервал [-3σ;-1σ] – это значения, соответствующие низкому уровню выраженности свойства, интервал[-1σ;1σ] – среднему уровню, а интервал [1σ;3σ] – высокому.
Пример:
Мы измеряем беглость мышления по шкале от 0 до 12. Для применения правила нам нужно высчитать среднее выборочное и стандартное отклонение.
Допустим, мы определили, что среднее М = 7, а стандартное отклонение σ = 1,5.
Далее, как показано на рисунке, нам нужно трижды отнять стандартное отклонение от среднего (получим: -1σ = 5,5; -2σ = 4, -3σ = 2,5), и трижды прибавить (1σ = 8,5; 2σ = 10, 3σ = 11,5).
Таким образом получим интервал низких значений [2,5; 5,5]; интервал средних значений [5,5; 8,5]; интервал высоких значений [8,5; 11,5].
Коэффициент вариации
Коэффициент вариации — это величина, используемая в статистике, равная отношению стандартного отклонения случайной величины к ее математическому ожиданию (среднему выборочному). Он применяется для сравнения вариативности одного и того же признака в нескольких совокупностях с различным средним арифметическим. Т.к. коэффициент вариации величина относительная, то обычно она выржаеться в процентах.
( CV = frac{sigma}{bar{X}}cdot100 )
В статистике принято, что:
- если коэффициент вариации меньше 10%, то степень рассеивания данных считается незначительной;
- если от 10% до 20% — средней;
- больше 20% и меньше или равно 33% — значительной.
Если значение коэффициента вариации не превышает 33%, то совокупность считается однородной, а если больше 33%, то — неоднородной.
Пример: берем ранее используемый ряд данных {3,4,5,6,7}, для него у нас посчитано уже и стандартное отклонение и выборочное среднее, получим:
( CV = frac{1.58113883}{5}cdot100 = 31.6227766 )
Исходя из получившегося результата можем утверждать, что степень рассеивания данных значительная, а сама выборка однородная. Если бы мы изучали какое-то свойство, это бы означало, что оно стабильно закрепилось у представителей выборки на уровне, соответствующем среднему выборочному. А значит мы можем смело утверждать, что изучаемое свойство характерно для представителей нашей выборки.
Слайд 1ГРАФИКИ
И ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Cтат. методы в психологии
(Радчикова Н.П.)

Слайд 4Описательная статистика
Методы и способы, используемые для «суммирования», организации и
«уменьшения» большого количества наблюдений (статистических опытов).

Слайд 5Описательная статистика
Частотные распределения и графики
Меры центральной тенденции
Меры изменчивости
Меры положения
Меры формы
…

Слайд 6Группировка данных
Предположим, мы спрашивали студентов, насколько их провал на экзамене зависел
от причин, которые они никак не могли контролировать.
Ответы даются по шкале от 1 до 7
(1 — совсем не зависел, 7 — полностью зависел)
Гипотетические данные опроса 25 студентов:
3,5,6,5,2,3,6,4,6,7,6,4,5,5,1,2,5,4,4,5,5,7,3,3,4

Слайд 7Группировка данных
Гипотетические данные опроса 25 студентов:
3,5,6,5,2,3,6,4,6,7,6,4,5,5,1,2,5,4,4,5,5,7,3,3,4
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7

Слайд 8Группировка данных
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7

Слайд 10Группировка данных
Столбчатая диаграмма
Слайд 14Группировка данных
А если значений много?
40, 48, 11, 16, 52, 64, 21,
33, 39, 69, 45, 8,35, 22, 57, 74, 13, 25, 47, 27, 38, 43, 15, 33, 66, 52, 47, 37, 0, 24, 43, 61, 35, 29, 52, 40, ….

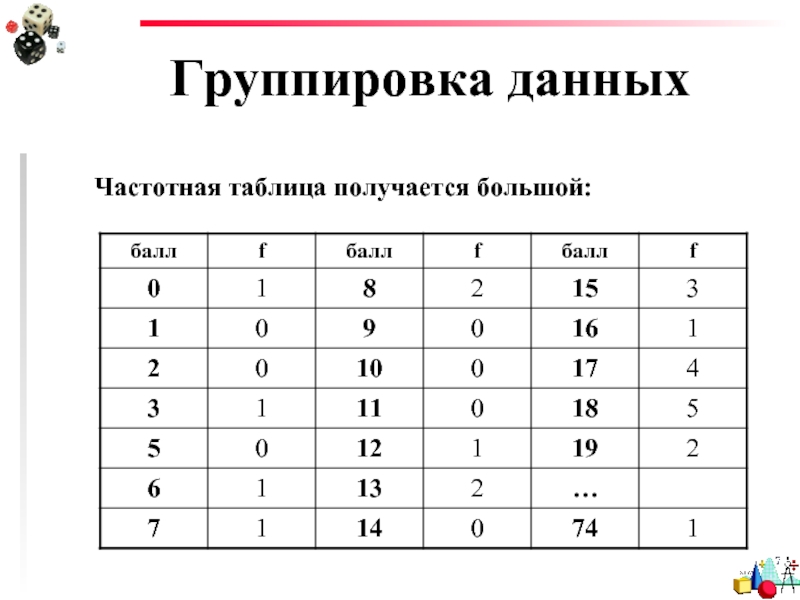
Слайд 15Группировка данных
Частотная таблица получается большой:
Слайд 16Группировка данных
Тогда стоит сгруппировать значения переменной в интервалы
1. Найти разницу между
наибольшим и наименьшим значением
и прибавить к ней 1
(74-0)+1=75
2. Разделить ответ на число выбранных интервалов и округлить до ближайшего нечетного числа
i=75/10=7.5 ≈ 7
3. К самому маленькому значению переменной прибавить i-1
0+i-1=0+7-1=6
Первый интервал будет от 0 до 6
4. Следующий интервал начинается с числа, которое следует за наибольшим значением предыдущего интервала
7+i-1=7+7-1=13
Второй интервал будет от 7 до 13

Слайд 21Использование графиков
Lie factor – отношение разницы в размере элементов графика к
разнице величин, которые они представляют
Наиболее информативные («честные») графики имеют Lie factor =1

Слайд 23Использование графиков
Следует избегать соединения изменений в оформлении графика с изменениями в
данных

Слайд 25Использование графиков
Еще одна проблема – многомерные изменения, т.е. изменения сразу по
нескольким размерностям, например, по высоте и ширине.
Если масштабирование ведется сразу по двум измерениям, площадь изменяется пропорционально квадрату изменений!

Слайд 29
Основные понятия
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
Генеральной
совокупностью называют совокупность объектов, из которых производится выборка.

Слайд 30
Основные понятия
Параметры – это меры описания, полученные при сплошном описании (описании
генеральной совокупности).
Статистики (или оценки параметров) – это те же меры, но полученные при выборочном наблюдении (т.е. параметры описывают генеральную совокупность, а статистики – ее выборку).

Слайд 31Генеральная и выборочная совокупности
Генеральная совокупность
Выборка
Параметр
Статистика
Слайд 32Выборки
Выборки бывают разные!
Классификация Л.Мюллера и К. Шусслера
По критерию методов отбора выборки
бывают
1) Не случайные
2) Случайные (вероятностные, пробабилистские)

Слайд 33Выборки
Классификация Л.Мюллера и К. Шусслера
1) Не случайные – не имеют теоретико-вероятностного
обоснования и, следовательно, не соответствуют критерию репрезентативности, т.е. статистики не могут выступать оценками генеральной совокупности

Слайд 34Выборки
Классификация Л.Мюллера и К. Шусслера
1) Не случайные
1.1) Бессистемная выборка
1.2) Доступная выборка
1.3)
Целенаправленная выборка

Слайд 35Выборки
Классификация Л.Мюллера и К. Шусслера
1.1) Бессистемная выборка
Отбор любых случайно
встретившихся прохожих, согласившихся принять участие в исследовании.
Может использоваться только для самого первого ознакомления с проблемной ситуацией

Слайд 36Выборки
Классификация Л.Мюллера и К. Шусслера
1.2) Доступная выборка
Формируется из числа
лиц, которые по субъективным и объективным факторам могут быть включены в число респондентов, т.е. доступны физически.
Используется для накопления данных о латентных или аномальных явлениях

Слайд 37Выборки
Классификация Л.Мюллера и К. Шусслера
1.3) Целенаправленная выборка
Преднамеренный отбор определенной
категории респондентов, которые по оценке исследователя в наибольшей степени информированы по проблеме или заинтересованы в ее изучении
Используется в экспертных опросах, лабораторных исследованиях и социальных экспериментах

Слайд 38Выборки
Классификация Л.Мюллера и К. Шусслера
2) Случайные
2.1) Простая случайная
2.2) Серийная
2.3) Систематическая (интервальная)
2.4)
Стратифицированная
2.5) Комбинированная

Слайд 39Выборки
Классификация Л.Мюллера и К. Шусслера
2.1) Простая случайная – формируется путем случайного
отбора единиц наблюдения из однородной генеральной совокупности (жребий, таблицы случайных чисел, компьютерное моделирование)
.

Слайд 40Выборки
Классификация Л.Мюллера и К. Шусслера
2.2) Серийная – единицами отбора являются статистические
серии (таксоны, гнезда) – территориальные общности, коллективы, семьи и т.д. Серии выбираются по методике простой случайной выборки

Слайд 41Выборки
Классификация Л.Мюллера и К. Шусслера
2.3) Систематическая (интервальная) – отбор единиц производится
через один и тот же интервал, при этом начало отсчета определяется случайным образом

Слайд 42Выборки
Классификация Л.Мюллера и К. Шусслера
2.4) Стратифицированная выборка на основе предварительного выделения
в генеральной совокупности однородных частей, типических групп (страт). В каждой страте производится случайный отбор единиц наблюдения, как правило, пропорционально их доле в генеральной совокупности.

Слайд 43Выборки
Классификация Л.Мюллера и К. Шусслера
2.5) Комбинированная – выборка, в которой используются
различные способы отбора.
Например: Гнездовая выборка – по два предприятия из типичных групп (сильных, средних и слабых). Далее отбор респондентов осуществляется интервальным методом.

Слайд 45
Меры центральной тенденции
Среднее арифметическое (М или х)
Медиана Me или
срединное значение
Мода Md (наиболее вероятное значение)

Слайд 46
Меры центральной тенденции
Среднее арифметическое
M=(x1+…+xN)/N
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7
М=(1+2+2+3+3+….+6+7+7)/25=4,4

Слайд 47
Меры центральной тенденции
Медиана Me
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7
прибавляем 1 к числу значений (размеру выборки)
и делим на 2. Затем определяет значение, которое соответствует вычисленной позиции в последовательности значений.
(25+1)/2=13

Слайд 48
Меры центральной тенденции
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7
А что же делать, когда у нас четное число
значений? В этом случае медиана — это значение, которое приходится как раз посередине двух срединных значений. (24+1)/2=12,5
значит, значение медианы будет между 12-й и 13-й позицией

Слайд 49
Меры центральной тенденции
Мода
Мd=5
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7

Слайд 50
Доверительный интервал
Доверительный интервал
(95% confidence limits of mean)
для среднего представляет интервал
значений вокруг оценки, где с данным уровнем доверия находится «истинное» (неизвестное) среднее генеральной совокупности.

Слайд 51
Доверительный интервал
Если среднее выборки равно 23, а нижняя и верхняя границы
доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее генеральной совокупности.

Слайд 52
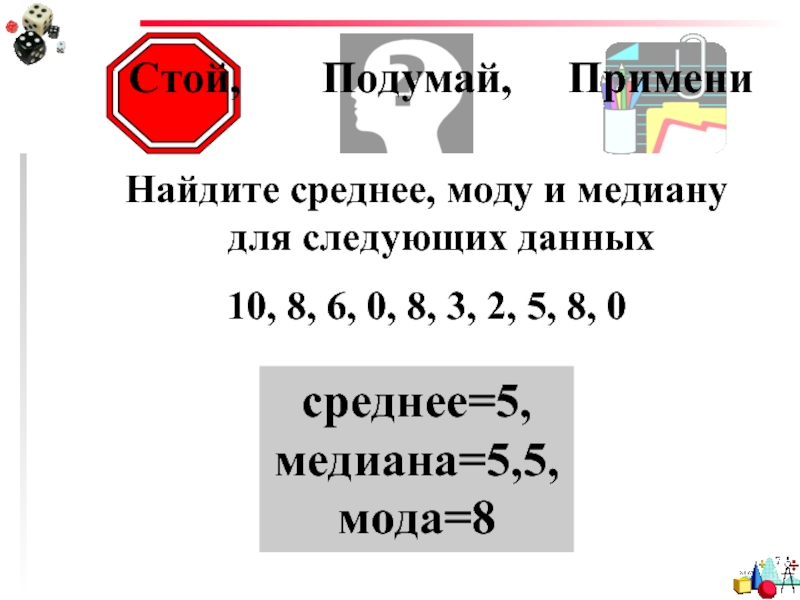
Стой, Подумай, Примени
Найдите среднее, моду
и медиану для следующих данных
10, 8, 6, 0, 8, 3, 2, 5, 8, 0
среднее=5, медиана=5,5, мода=8
Слайд 53
Стой, Подумай, Примени
Среди мужчин, приговоренных
к пожизненному заключению, только 10 % подвергаются повторному наказанию.
Среди тех, кого осудили на срок до 6 месяцев, повторно судимых (и опять приговоренных) 60 %. Следовательно, более длительное тюремное заключение более эффективно

Слайд 54
Стой, Подумай, Примени
Смертность американских солдат
во время войны в Персидском заливе была 9 человек на 1000. В это же время смертность гражданских лиц, например в Нью-Йорке была 16 человек на 1000. Следовательно, во время войны действующая армия − самое безопасное место.

Слайд 55
Стой, Подумай, Примени
Знаете ли вы
что….
Большинство людей из Великобритании имеют больше ног, чем человек в среднем?
Это поистине очевидно. Среди 57 млн. жителей Великобритании около 5 000 имеют одну ногу. Следовательно, среднее количество ног будет
((5000*1)+(56995000*2))/ 57000000= 1.999123
Так как большинство имеют две ноги…

Слайд 56Меры изменчивости
Размах
Дисперсия
Стандартное (среднеквадратичное) отклонение
Стандартная ошибка

Слайд 57Меры изменчивости
Средний вес команды = 95 кг
Слайд 58Меры изменчивости
Средний вес команды тоже = 95 кг

Слайд 59Меры изменчивости
Размах R = Xmax- Xmin
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7
R = Xmax– Xmin=7-1=6

Слайд 61Меры изменчивости
Пример. Вычислить дисперсию для следующей выборки:
5, 6, 3, 8, 5,
9
Вычисляем среднее арифметическое: = (5+6+3+8+5+9)/6=6

Слайд 62Меры изменчивости
Подставляем в формулу:

Слайд 63Меры изменчивости
Другая формула для дисперсии:

Слайд 64Меры изменчивости
Стандартное отклонение

Слайд 65Меры изменчивости
Стандартная ошибка среднего значения — это стандартное отклонение, деленное на
квадратный корень из объема выборки.

Слайд 66Меры изменчивости
Стандартная ошибка среднего значения — это стандартное отклонение, деленное на
квадратный корень из объема выборки.
Гляньте-ка! СЕКС!
И прямо тут, в формуле!
Слайд 67Меры изменчивости
В диапазоне удвоенной стандартной ошибки по обе стороны от среднего
значения с вероятностью примерно 95% находится среднее значение генеральной совокупности.

Слайд 68
Стой, Подумай, Примени
Найдите размах и
дисперсию для следующих данных
10, 8, 6, 0, 8, 3, 2, 5, 8, 0
размах=10, дисперсия=12,8889

Слайд 69
Меры положения
Квантили — структурные характеристики вариационного ряда, отсекающие в пределах ряда
определенную часть его членов.
К ним относятся квартили, децили и перцентили (центили).

Слайд 70
Меры положения
Квантиль – это точка на числовой оси, на которой откладываются
результаты наблюдений. Эта точка делит всю совокупность наблюдений на части (группы) с определенными пропорциями между ними.

Слайд 71
Процентили
Перцентили (центили, процентили) отделяют от совокупности по 0,01 части (делят совокупность
на 100 равных частей), их 99.

Слайд 72
Процентили
В 1985 году примерно 24,7 миллионов людей в Соединенных Штатах были
в возрасте 65 лет и старше
Таня набрала 41 балл по тесту по математике в этом году

Слайд 73
Процентили
В 1985 году примерно 24,7 миллионов людей в Соединенных Штатах были
в возрасте 65 лет и старше
89% населения США находится в возрасте не старше 65 лет
89 – это и есть процентиль для 65-летних

Слайд 74
Процентили
Процентиль какого-либо значения, таким образом, представляет собой процент случаев, которые имеют
то же самое или меньшее значение
Сказать «возрасту 65 лет соответствует 89 процентиль» — это сказать, что
«89% населения США находится в возрасте 65 лет и меньше»

Слайд 75
Процентили
Таня набрала 41 балл по тесту по математике в этом году,
и это соответствует 62 процентилю.
62% белорусских абитуриентов сдали так же, как Таня или еще хуже,
и только 38% были лучше ее.

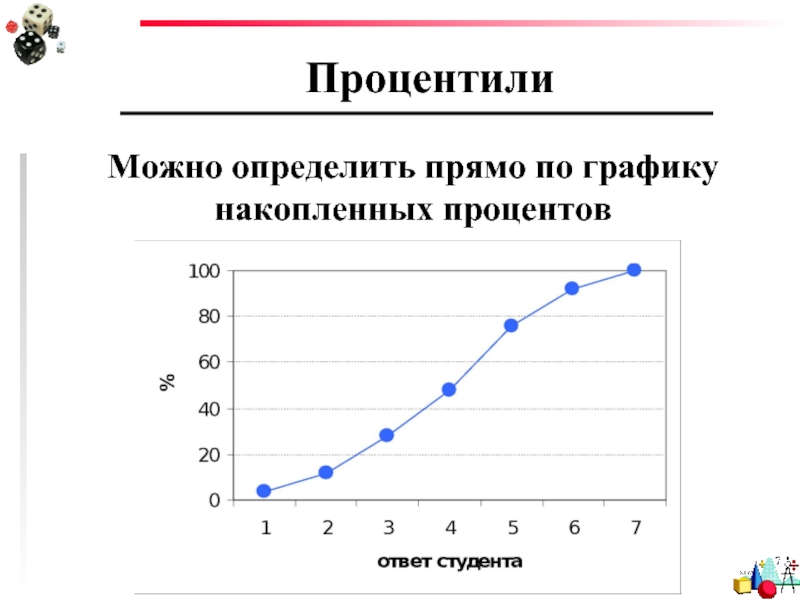
Слайд 76Процентили
Можно определить прямо по графику накопленных процентов
Слайд 77Процентили
Какой процентиль соответствует ответу 4?
Какой процент студентов считает, что результат провала
на экзамене скорее зависел от них, чем от причин, которые они не могли контролировать?

Слайд 78Процентили
Какой процентиль соответствует ответу 4?
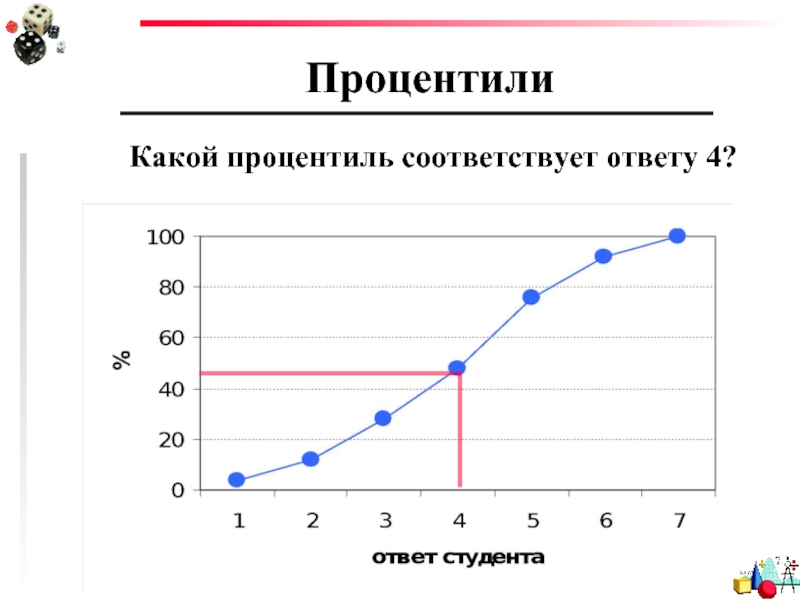
Слайд 79
Процентили
Можно определить по формуле
Процентиль=(накопленная частота/N)*100

Слайд 80
Процентили
Seiden, R.H. (1966) “Campus Tragedy: A Story of Students Suicide” Journal
of Abnormal Psychology, 71, 389-399
Правда ли, что сессионная пара – необычайно стрессовая ситуация для студента, которая приводит даже к самоубийствам?

Слайд 82
Процентили
Процентиль всегда выражает положение значения по отношению к какой-либо выборке:
Таня набрала такое количество баллов по тесту по математике, которое соответствует 93 процентилю.
Она сдавала математику с 8-классниками обычной школы
Она сдавала математику с 11-классниками математической школы

Слайд 83
Меры положения
Квартили — значения, которые делят две половины выборки (разбитые медианой)
еще раз пополам.
Таким образом, медиана и квартили делят диапазон значений переменной на четыре равные части.

Слайд 84
Меры положения
Верхний квартиль (Q3) делит пополам верхнюю часть выборки (значения переменной
больше медианы).
Нижний квартиль (Q1) делит пополам нижнюю часть выборки (значения переменной меньше медианы).
Внутриквартильный (квартильный) размах = Q3-Q1

Слайд 85
Меры положения
Нижний квартиль часто обозначают символом 25%, это означает, что 25%
значений переменной меньше нижнего квартиля.
Верхний квартиль часто обозначают символом 75%, это означает, что 75% значений переменной меньше верхнего квартиля.

Слайд 86
Меры положения
Квинтили делят значения наблюдений на 5 частей, их 4 (К1,
К2, К3, К4).
Децили делят совокупность на 10 частей, их 9 (D1, …, D9).

Слайд 89
Меры формы
Асимметрия является мерой несимметричности распределения. Если этот коэффициент значительно отличается
от 0, распределение является асимметричным
А=

Слайд 90
Меры формы
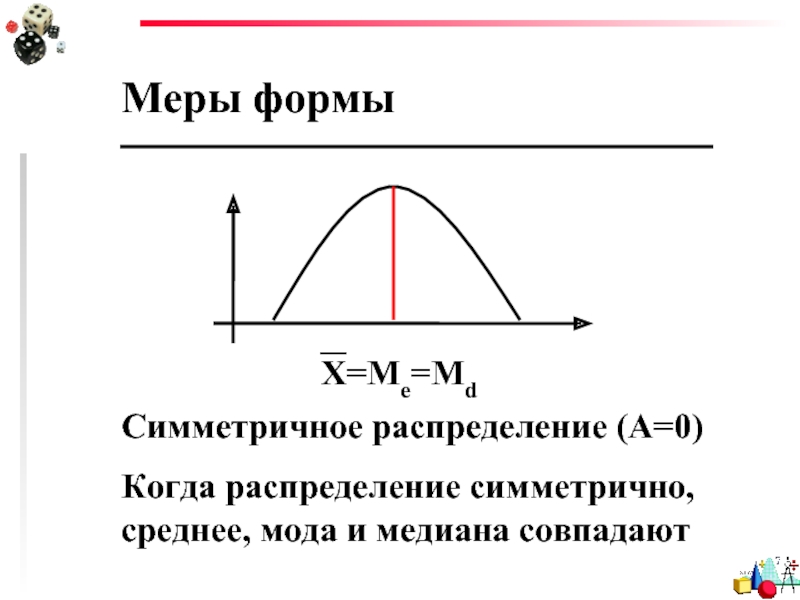
Симметричное распределение (А=0)
Когда распределение симметрично, среднее, мода и медиана совпадают
Слайд 91
Меры формы
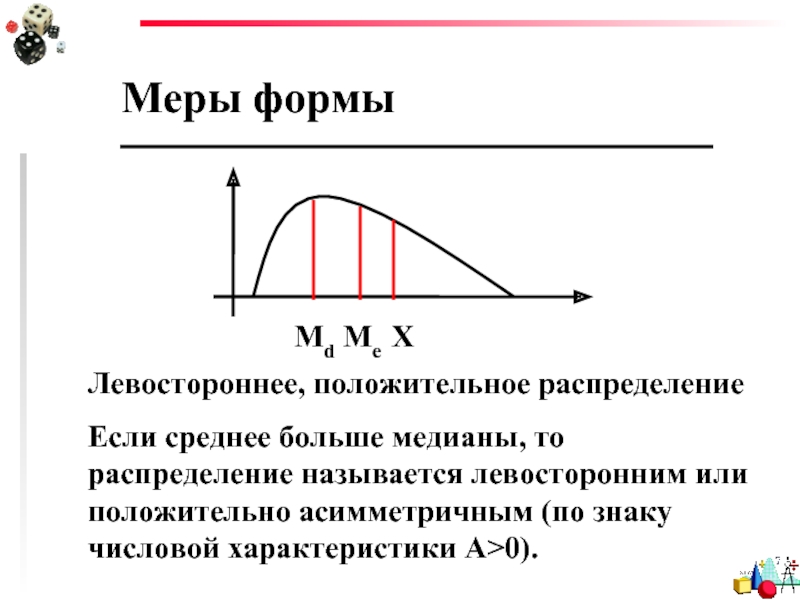
Левостороннее, положительное распределение
Если среднее больше медианы, то распределение называется
левосторонним или положительно асимметричным (по знаку числовой характеристики А>0).
Md Ме Х
Слайд 92
Меры формы
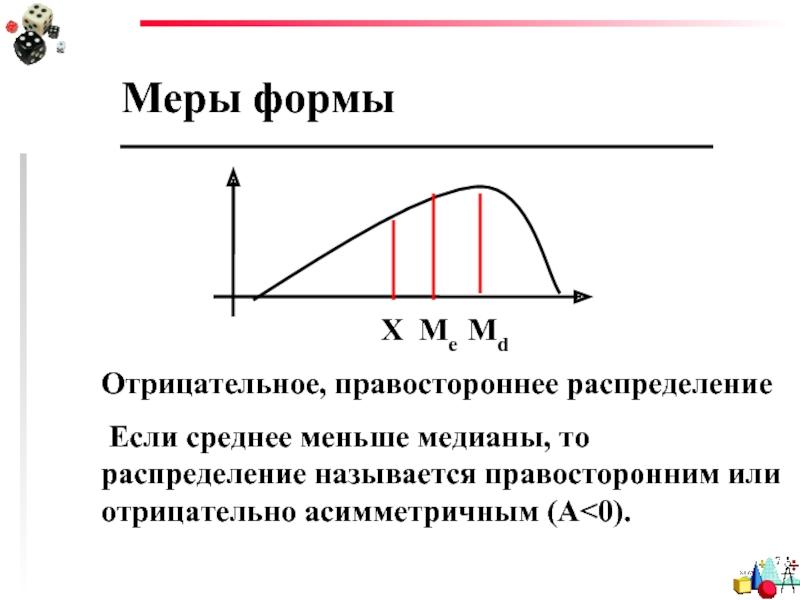
Отрицательное, правостороннее распределение
Если среднее меньше медианы, то распределение
называется правосторонним или отрицательно асимметричным (A<0).
Х Ме Md
Слайд 93
Меры формы
Эксцесс измеряет остроту пика распределения
Е=

Слайд 96
Нормальное распределение
Нормальное распределение:
f(x)=(1/σ√2π)exp{(x-m)2/2σ2}
cреднее значение m
дисперсия σ2
асимметрия А = 0
эксцесс Е =
3
Стандартное нормальное распределение имеет нулевое среднее и единичную дисперсию

Слайд 97
Нормальное распределение
Форма, которую надо запомнить!

Слайд 99
Нормальное распределение
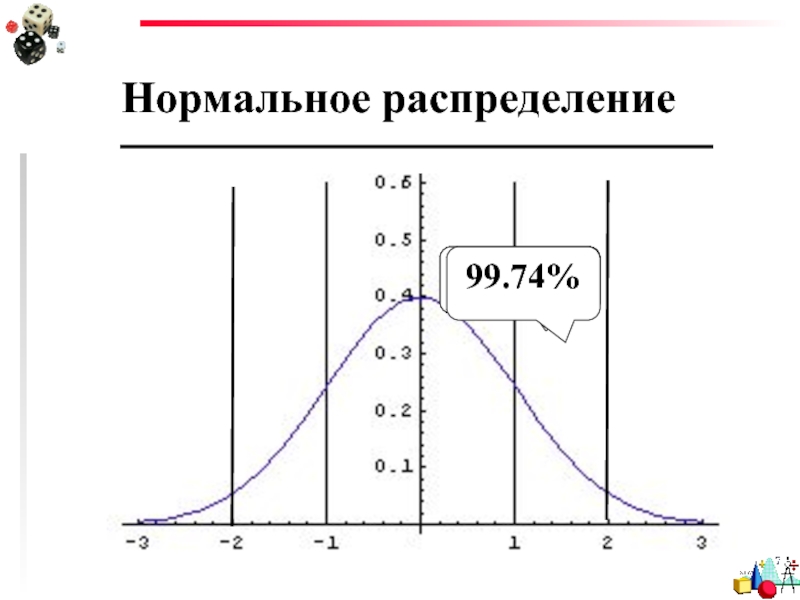
68.26%
95.44%
99.74%
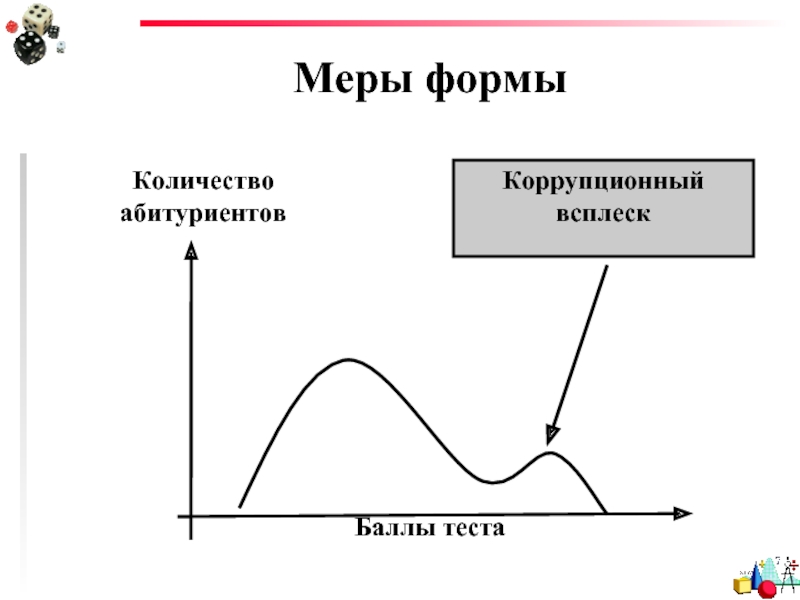
Слайд 100Меры формы
Коррупционный
всплеск
Баллы теста
Количество абитуриентов
Слайд 101
Нормальное распределение
Нормальная кривая человеческих достижений:
2 года – не писать в штаны
10
лет – иметь много друзей и много тусоваться
20 лет – иметь сексуальные отношения
30 лет – много зарабатывать и иметь крутую тачку
50 лет – много зарабатывать и иметь крутую тачку
60 лет – иметь сексуальные отношения
70 лет – иметь много друзей и много тусоваться
78 лет – не писать в штаны

Слайд 103
Какую меру выбрать?
Медиана используется когда
1) распределение асимметрично
2) есть опасность перекоса
из-за экстремальных значений. Медиана не чувствительна к экстремальным значениям, в то время как среднее очень чувствительно.
3)медиану можно вычислять для данных шкалы порядка и выше.

Слайд 104
Что мы должны знать?
Как строить частотные таблицы и графики
Меры центральной тенденции
Меры
изменчивости
2) Меры положения
3) Меры формы
4) Свойства нормального распределения

Слайд 105Полезная литература:
К следующей лекции прочитать:
Clay Helberg: Pitfalls of Data Analysis
(or How
to Avoid Lies and Damned Lies)
Barnett A. How Numbers can trick you// Technology Review, October 1994 (на русском)
(есть в эл.виде в папке
«Дополнительная литература»)

Введение в описательную статистику
Перевод
Ссылка на автора
Описательный статистический анализ помогает вам понять ваши данные и является очень важной частью машинного обучения. Это связано с тем, что машинное обучение сводится к прогнозированию. С другой стороны, статистика сводится к тому, чтобы делать выводы из данных, что является необходимым начальным шагом. В этом посте вы узнаете о наиболее важных описательных статистических концепциях. Они помогут вам лучше понять, что ваши данные пытаются вам сказать, что приведет к общей лучшей модели машинного обучения и понимания.
Оглавление:
- Введение
- Нормальное распределение
- Центральная тенденция (средняя, мода, медиана)
- Меры изменчивости (диапазон, межквартильный диапазон)
- Дисперсия и стандартное отклонение
- модальность
- перекос
- эксцесс
- Резюме
Введение
Выполнение описательного статистического анализа вашего набора данных абсолютно необходимо. Многие люди пропускают эту часть и поэтому теряют много ценной информации о своих данных, что часто приводит к неправильным выводам. Потратьте время и тщательно запустите описательную статистику и убедитесь, что данные соответствуют требованиям для дальнейшего анализа.
Но, прежде всего, мы должны рассмотреть статистику:
Статистика — это раздел математики, который занимается сбором, интерпретацией, организацией и интерпретацией данных.
В статистике есть две основные категории:
1. Описательная статистика:В «Описательной статистике» вы описываете, представляете, обобщаете и систематизируете свои данные (совокупность) с помощью численных расчетов, графиков или таблиц.
2. Логическая статистика:Логическая статистика создается более сложными математическими вычислениями и позволяет нам выявлять тенденции и делать предположения и прогнозы о населении на основе изучения выборки, взятой из нее.
Нормальное распределение
Нормальное распределение является одним из наиболее важных понятий в статистике, поскольку почти все статистические тесты требуют нормально распределенных данных. Это в основном описывает, как выглядят большие выборки данных при их построении. Его иногда называют «кривой колокола» или «кривой Гаусса».
Инференциальная статистика и расчет вероятностей требуют нормального распределения. По сути, это означает, что если ваши данные обычно не распространяются, вам нужно быть очень осторожным, какие статистические тесты вы применяете к ним, поскольку они могут привести к неправильным выводам.
Нормальное распределение дается, если ваши данные симметричны, имеют форму колокола, центрированы и унимодальны.
В идеальном нормальном распределении каждая сторона является точным зеркалом другой. Это должно выглядеть как распределение на картинке ниже:
Вы можете видеть на картинке, что распределение имеет форму колокола, что просто означает, что оно не сильно пиковое. Унимодал означает, что есть только один пик.
Главная тенденция
В статистике мы имеем дело со средним, модой и медианой. Их также называют «центральной тенденцией». Это всего лишь три вида «средних» и, безусловно, самые популярные.
Среднее значение просто среднееи считается наиболее надежным показателем центральной тенденции делать предположения о населении из одной выборки. Центральная тенденция определяет склонность значений ваших данных группироваться вокруг их среднего значения, режима или медианы. Среднее значение рассчитывается как сумма всех значений, деленная на количество значений.
Режим — это значение или категория, которые чаще всего встречаются в данных.Поэтому в наборе данных нет режима, если число не повторяется или если ни одна категория не совпадает. Возможно, в наборе данных имеется более одного режима, но об этом я расскажу в разделе «Модальность» ниже.
Режим также является единственным показателем центральной тенденции, который можно использовать для категориальных переменных, поскольку вы не можете вычислить, например, среднее значение для переменной «пол». Вы просто сообщаете категориальные переменные в виде чисел и процентов.
Медиана — это «среднее» значение или средняя точка в ваших данныхи также называется «50-й процентиль». Обратите внимание, что на медиану гораздо меньше влияют выбросы и перекос данных, чем на среднее. Я объясню это на примере: представьте, что у вас есть набор призов на жилье, который колеблется в основном от 100 000 до 300 000 долларов, но содержит несколько домов стоимостью более 3 миллионов долларов. Эти дорогие дома будут сильно влиять, а значит, так как это сумма всех значений, деленная на количество значений. Медиана не будет сильно затронута этими выбросами, поскольку это только «среднее» значение всех точек данных. Поэтому медиана — это гораздо более подходящая статистика, чтобы сообщать о ваших данных.
При нормальном распределении все эти показатели попадают в одну среднюю точку. Это означает, что среднее, мода и медиана все равны
Меры изменчивости
Наиболее популярными показателями изменчивости являются диапазон, межквартильный диапазон (IQR), дисперсия и стандартное отклонение. Они используются для измерения количества разброса или изменчивости в ваших данных.
Диапазон описывает разницу между самой большой и самой маленькой точками в ваших данных.
Межквартильный диапазон (IQR) является мерой статистического разброса между верхним (75-м) и нижним (25-м) квартилями.
В то время как диапазон измеряет, где находятся начало и конец вашей точки данных, межквартильный диапазон является мерой того, где лежит большинство значений.
Разницу между стандартным отклонением и дисперсией часто трудно понять новичкам, но я подробно объясню это ниже.
Дисперсия и стандартное отклонение
Стандартное отклонение и дисперсия также измеряют, как диапазон и IQR, насколько разбросаны наши данные (например, дисперсия). Поэтому они оба получены из среднего значения.
Дисперсия вычисляется путем нахождения разницы между каждой точкой данных и среднего значения, возводя их в квадрат, суммируя и затем беря среднее из этих чисел.
Квадраты используются во время расчета, потому что они взвешивают выбросы в большей степени, чем точки, близкие к среднему. Это препятствует тому, чтобы различия выше среднего нейтрализовали различия ниже среднего.
Проблема с дисперсией состоит в том, что из-за возведения в квадрат она не находится в той же единице измерения, что и исходные данные.
Допустим, вы имеете дело с набором данных, который содержит значения в сантиметрах. Ваша разница будет в сантиметрах в квадрате и, следовательно, не лучшее измерение.
Вот почему стандартное отклонение используется чаще, потому что оно находится в исходной единице. Это просто квадратный корень дисперсии, и поэтому он возвращается к исходной единице измерения.
Давайте рассмотрим пример, который иллюстрирует разницу между дисперсией и стандартным отклонением:
Представьте себе набор данных, который содержит значения в сантиметрах от 1 до 15, что дает среднее значение 8. Возведение в квадрат разницы между каждой точкой данных и средним значением и усреднение квадратов дает дисперсию 18,67 (квадратные сантиметры), тогда как стандартное отклонение составляет 4,3 сантиметра.
Когда у вас низкое стандартное отклонение, ваши точки данных, как правило, близки к среднему. Высокое стандартное отклонение означает, что ваши данные распределены в широком диапазоне.
Стандартное отклонение лучше всего использовать, когда данные являются одномодальными. При нормальном распределении примерно 34% точек данных лежат между средним и одним стандартным отклонением выше или ниже среднего. Поскольку нормальное распределение является симметричным, 68% точек данных находятся между одним стандартным отклонением выше и одним стандартным отклонением ниже среднего. Приблизительно 95% находятся между двумя стандартными отклонениями ниже среднего и двумя стандартными отклонениями выше среднего. И примерно 99,7% находятся между тремя стандартными отклонениями выше и тремя стандартными отклонениями ниже среднего.
Картинка ниже прекрасно это иллюстрирует.
С помощью так называемой «Z-Score» вы можете проверить, сколько стандартных отклонений ниже (или выше) среднего значения, лежит конкретная точка данных. С пандами вы можете просто использовать Функция std (), Чтобы лучше понять концепцию нормального распределения, теперь мы обсудим понятия модальности, симметрии и пика.
модальность
Модальность распределения определяется количеством пиков, которые оно содержит.В большинстве дистрибутивов есть только один пик, но возможно, что вы встретите дистрибутивы с двумя или более пиками.
На рисунке ниже показаны наглядные примеры трех типов модальности:
Унимодальный означает, что у распределения есть только один пик, что означает, что у него есть только один часто встречающийся счет, сгруппированный сверху. Бимодальное распределение имеет два часто встречающихся значения (два пика), а мультимодальное имеет два или несколько часто встречающихся значений.
перекос
Асимметрия — это измерение симметрии распределения.
Поэтому он описывает, насколько распределение отличается от нормального распределения, либо слева, либо справа. Значение асимметрии может быть положительным, отрицательным или нулевым. Обратите внимание, что идеальное нормальное распределение будет иметь нулевую асимметрию, потому что среднее значение равно медиане.
Ниже вы можете увидеть иллюстрацию различных типов асимметрии:
Мы говорим о перекосе позитива, если данные сложены влево, который оставляет хвост, указывающий направо.
Отрицательный перекос происходит, если данные накапливаются вправо, который оставляет хвост, указывающий налево. Обратите внимание, что положительные перекосы встречаются чаще, чем отрицательные.
Хорошим измерением асимметрии распределения является коэффициент асимметрии Пирсона, который обеспечивает быструю оценку симметрии распределений. Чтобы вычислить асимметрию в пандах, вы можете просто использовать Функция «skew ()»
эксцесс
Куртоз измеряет, является ли ваш набор данных «тяжелым» или «легким» по сравнению с обычным распределением. Наборы данных с высоким эксцессом имеют тяжелые хвосты и больше выбросов, а наборы данных с низким эксцессом имеют тенденцию иметь легкие хвосты и меньше выбросов. Обратите внимание, что гистограмма — это эффективный способ показать как асимметрию, так и эксцесс в наборе данных, потому что вы можете легко определить, если что-то не так с вашими данными. График вероятности также является отличным инструментом, потому что нормальное распределение будет следовать по прямой линии.
Вы можете увидеть оба набора данных с положительным перекосом на изображении ниже:
Хороший способ математически измерить эксцесс распределения — это эксцентричное измерение эксцесса.
Теперь мы обсудим три наиболее распространенных типа куртоза.
Нормальное распределение называетсяmesokurticи имеет эксцесс или около нуля.platykurticРаспределение имеет отрицательный эксцесс и хвосты очень тонкие по сравнению с нормальным распределением.Leptokurticраспределения имеют эксцесс, превышающий 3, а жирные хвосты означают, что распределение дает более экстремальные значения и что оно имеет относительно небольшое стандартное отклонение.
Если вы уже поняли, что распределение искажено, вам не нужно рассчитывать его эксцесс, поскольку распределение уже не является нормальным. В пандах вы можете просмотреть эксцесс, просто позвонив Функция «kurtosis ()»,
Резюме
Этот пост дал вам хорошее введение в описательную статистику. Вы узнали, как выглядит нормальное распределение и почему оно важно. Кроме того, вы получили знания о трех различных типах средних (среднее, модальное и медианное), также называемых центральной тенденцией. После этого вы узнали о диапазоне, межквартильном диапазоне, дисперсии и стандартном отклонении. Затем мы обсудили три типа модальности, и вы можете описать, насколько распределение отличается от нормального распределения с точки зрения асимметрии. Наконец, вы узнали о распределениях лептокуртов, мезокуртов и платикуртов.
Этот пост изначально был опубликован в моем блоге (https://machinelearning-blog.com).
Содержание
Показать
Что такое статистика?
Статистика – это наука, методология и инструментальный аппарат, который занимается сбором, систематизацией, анализом, интерпретацией и представлением данных, а также извлечением информации из этих данных для принятия обоснованных выводов и принятия решений. Она изучает различные явления и явления массового характера, а также применяет статистические методы и модели для изучения взаимосвязей, закономерностей и изменений в данных.
Статистика играет важную роль в различных областях и дисциплинах, таких как экономика, социология, бизнес, медицина, государственное управление и многие другие. Она помогает исследователям, ученым и принимающим решениям понять и описать структуру, характеристики и вариабельность данных, а также выявить закономерности и тренды, скрытые в этих данных.
Основная задача статистики состоит в том, чтобы преобразовать сырые данные в информацию, которая может быть понята и использована для принятия решений. Для этого статистика использует различные методы, включая описательную статистику, вероятность, математическую статистику и эконометрику. Описательная статистика позволяет описать и представить данные с помощью показателей, таких как среднее значение, медиана, мода, дисперсия и стандартное отклонение. Вероятность изучает вероятностные модели и методы, которые позволяют измерить степень возможности наступления событий. Математическая статистика предоставляет инструменты для формулирования и проверки статистических гипотез и оценки параметров популяции на основе выборочных данных. Эконометрика применяет статистические методы для изучения экономических явлений и моделирования экономических отношений.
В этой статье мы рассмотрим основные понятия и принципы статистики.
Основные понятия
Генеральная совокупность
Генеральная совокупность – это полный набор всех элементов, которые исследуются в рамках конкретного исследования или анализа. Она представляет собой все возможные единицы или объекты, о которых хотим сделать выводы или получить информацию.
Пример:
Допустим, у вас есть исследование о предпочтений потребителей кофе среди покупателей данного напитка. Генеральная совокупность в этом случае будет представлять собой все возможные потребители, которые покупают кофе. Это включает всех людей, независимо от их возраста, пола, страны проживания и других факторов.
Популяция
Популяция – это группа или совокупность всех элементов или единиц, которые исследуются или на которые делаются выводы в рамках конкретного исследования или анализа.
Главное отличие между популяцией и генеральной совокупностью заключается в их области применения. Генеральная совокупность охватывает все возможные случаи или объекты, в то время как популяция представляет собой конкретную группу или сегмент генеральной совокупности, выбранный для исследования или анализа. Популяция является более узким понятием, отражающим фокус исследования на конкретных характеристиках или особенностях интересующей группы.
Пример:
Примером популяции в статистике может быть группа всех покупателей кофе определенного бренда. Допустим, вы хотите изучить предпочтения и покупательские привычки людей, которые приобретают кофе определенного бренда “ABC Coffee”.
Выборка
Выборка – это подмножество элементов, выбранных из популяции для анализа или исследования. Это означает, что вместо изучения всех элементов или единиц популяции, исследователи выбирают определенное количество элементов, которые являются представительными для всей группы.
Выборка обычно осуществляется из-за ограничений в ресурсах, времени и доступности данных. Использование выборки позволяет сократить затраты и время, необходимые для проведения исследования, при условии, что выборка является представительной и достаточно большой.
Важно отметить, что качество выборки влияет на достоверность и обобщаемость результатов. Чем более представительная выборка, тем более точные и надежные будут выводы, сделанные на основе этой выборки. Для достижения представительности выборки, исследователи могут использовать различные методы выборки, такие как случайная выборка, стратифицированная выборка или кластерная выборка.
Использование выборки в статистике позволяет сделать выводы о популяции, основываясь на анализе и исследовании только небольшой части данных. Однако, важно помнить, что результаты, полученные на основе выборки, могут иметь статистическую погрешность, и поэтому необходимо применять соответствующие методы статистического анализа для оценки степени уверенности в выводах.
Пример:
Исследователь хочет узнать, какое количество людей пьет кофе каждый день, он может провести опрос среди некоторой группы людей, выбранных случайным образом из общей популяции. Эта группа людей, которую исследователь выбрал для опроса, будет представлять собой выборку для его исследования. Результаты опроса будут использованы для оценки среднего количества кофе, которое потребляет в день вся популяция.
Дисперсия
Дисперсия – это мера разброса или изменчивости значений в выборке или генеральной совокупности. Она показывает, насколько значения распределены вокруг среднего значения.
Дисперсия позволяет оценить степень изменчивости данных. Большая дисперсия указывает на большой разброс значений относительно среднего, что свидетельствует о большой вариабельности данных. Маленькая дисперсия, наоборот, указывает на меньший разброс значений и более сгруппированные данные вокруг среднего.
Дисперсия широко используется в статистическом анализе для изучения и сравнения различных наборов данных. Она позволяет оценить степень разброса данных и сравнивать вариации между разными группами или условиями.
Пример:
Допустим, у вас есть данные о количестве кофе, которое люди выпивают за неделю. Ваша выборка состоит из следующих значений:$$[3, 4, 2, 5, 3]$$Шаг 1: Вычисление среднего значения. Сначала вычислим среднее значение, сложив все значения и разделив их на общее количество значений:$${3 + 4 + 2 + 5 + 3\over 5} = {17 \over 5} = 3.4$$Шаг 2: Вычисление отклонений от среднего. Теперь вычислим отклонение каждого значения от среднего. Для этого вычитаем среднее значение из каждого значения:$$3-3.4 = -0.4$$ $$4-3.4 = 0.6 $$ $$2- 3.4 = -1.4 $$ $$5- 3.4 = 1.6 $$ $$3- 3.4 = -0.4$$Шаг 3: Возведение отклонений в квадрат. Теперь возведем каждое отклонение в квадрат:$$(-0.4)^2 = 0.16$$ $$ (0.6)^2 = 0.36$$ $$ (-1.4)^2 = 1.96$$ $$ (1.6)^2 = 2.56 $$ $$(-0.4)^2 = 0.16$$Шаг 4: Вычисление суммы квадратов отклонений. Сложим все квадраты отклонений:
$$0.16 + 0.36 + 1.96 + 2.56 + 0.16 = 4.2$$Шаг 5: Вычисление дисперсии. Наконец, разделим сумму квадратов отклонений на общее количество значений:
$${4.2 \over5} = 0.84$$Таким образом, дисперсия кофе, основанная на данной выборке, составляет 0.84.
Стандартное отклонение
Стандартное отклонение — это мера разброса или изменчивости данных вокруг их среднего значения. Оно показывает, насколько значения в выборке различаются от среднего значения и помогает оценить степень разброса данных.
Стандартное отклонение позволяет оценить, насколько значения в выборке различаются от среднего значения. Чем больше стандартное отклонение, тем больший разброс или изменчивость имеют данные.
Стандартное отклонение вычисляется путем извлечения квадратного корня из дисперсии.
Пример:
При известной дисперсии для количества потребляемого кофе, мы можем рассчитать стандартное отклонение следующим образом: вычисляем квадратный корень из 0.84$$ {\sqrt 0.84} = 0.91651513899$$Результат будет примерно равен 0.917.
Коэффициент вариации
Коэффициент вариации – это относительная мера изменчивости или разброса данных в статистике. Он используется для сравнения степени изменчивости между разными наборами данных, учитывая их отличия в средних значениях.
Коэффициент вариации рассчитывается путем деления стандартного отклонения на среднее значение и умножения результата на 100, чтобы получить процентное значение. Формула для расчета коэффициента вариации выглядит следующим образом: $$CV = {Стандартное \ отклонение \over Среднее \ значение} \times 100\%$$Чем выше значение коэффициента вариации, тем больше разброс данных и тем выше степень их изменчивости относительно среднего значения. В то же время, низкое значение коэффициента вариации указывает на более однородные данные с небольшим разбросом.
Пример:
Предположим, у нас есть данные о потреблении кофе для двух различных групп людей: группа A и группа B. Рассчитаем коэффициент вариации для каждой группы, чтобы оценить их степень изменчивости относительно среднего значения.
Группа A:
– Среднее значение потребления кофе: 4 чашки в день
– Стандартное отклонение: 1 чашка в день $${1\over 4}\times100=25\% $$Группа B:
– Среднее значение потребления кофе: 2.5 чашки в день
– Стандартное отклонение: 0.5 чашка в день $${0.5\over 2.5}\times100=20\% $$Итак, у нас есть коэффициенты вариации для группы A и группы B. Эти значения показывают, что группа A имеет большую степень изменчивости в потреблении кофе (25%), чем группа B (20%). То есть, в группе A наблюдается больший разброс в потреблении кофе по сравнению с группой B, относительно их средних значений.
Корреляция
Корреляция – это статистическая мера, которая показывает взаимосвязь или степень связи между двумя переменными. Она измеряет направление и силу связи между двумя наборами данных. Корреляция может быть положительной, если две переменные движутся в одном направлении (т.е. при росте одной переменной, растет и другая), или отрицательной, если две переменные движутся в противоположных направлениях (т.е. при росте одной переменной, убывает другая).
Коэффициент корреляции, измеряемый в диапазоне от -1 до +1, предоставляет числовую оценку степени корреляции. Значение близкое к +1 указывает на сильную положительную корреляцию, близкую к -1 – на сильную отрицательную корреляцию, а значение близкое к 0 – на отсутствие или слабую корреляцию между переменными.
Корреляция является важным инструментом в статистике и используется для изучения взаимосвязей между различными явлениями или переменными, такими как связь между доходом и образованием, между температурой и продажами и т.д.
Пример:
Пример статистической корреляции с потреблением кофе может быть следующим: предположим, у нас есть набор данных о потреблении кофе и уровне энергии людей в течение дня. Мы хотим выяснить, есть ли связь между количеством выпитого кофе и уровнем энергии.
После сбора данных и проведения статистического анализа, мы можем получить коэффициент корреляции между этими двумя переменными. Пусть коэффициент корреляции составляет +0,75. Это положительное значение говорит о существовании сильной положительной корреляции между потреблением кофе и уровнем энергии. То есть, люди, потребляющие больше кофе, склонны иметь более высокий уровень энергии.
Обратно, если коэффициент корреляции составил -0,60, это говорит о существовании сильной отрицательной корреляции. Это может означать, что люди, употребляющие меньше кофе, имеют более высокий уровень энергии, чем те, кто потребляет больше кофе.
В обоих случаях статистическая корреляция позволяет нам оценить связь между потреблением кофе и уровнем энергии, помогая нам понять, как эти две переменные взаимодействуют друг с другом.
Регрессия
Регрессия – это статистический метод, который используется для изучения связи между зависимой переменной (отклик) и одной или несколькими независимыми переменными (предикторами). Регрессия, в отличие от корреляции, строит математическую модель, которая описывает зависимость между независимыми и зависимой, что позволяет предсказывать значения зависимой переменной на основе значений независимых переменных.
Цель регрессионного анализа состоит в построении математической модели, которая описывает отношение между переменными и позволяет предсказывать значения зависимой переменной при заданных значениях независимых переменных.
Наиболее распространенным методом регрессии является линейная регрессия, где модель строится в виде линейной функции, связывающей зависимую и независимые переменные. Однако существуют и другие методы регрессии, такие как полиномиальная регрессия, логистическая регрессия, регрессия с использованием деревьев решений и другие, которые могут учитывать более сложные взаимосвязи между переменными.
Пример:
Представим, что вы подчиняетесь зависимость между количеством продаж кофе в день и температурой на улице. Вы собрали данные за неделю и установили следующую корреляцию:
– При температуре 10 градусов – было продано 50 чашек кофе
– При температуре 15 градусов – было продано 70 чашек кофе
– При температуре 20 градусов – было продано 90 чашек кофе
– При температуре 25 градусов – было продано 110 чашек кофе
Тогда можно построить линейную регрессию, чтобы описать эту зависимость:
$$количество \ продаж = 30 + 2 \times температура$$ Это означает, что каждые 5 градусов температурного изменения увеличивают прошлую продажу на 10 кофейных чашек. Таким образом, предполагается, что при температуре 30 градусов, можно продать около 130 чашек кофе.
Однако, стоит помнить, что продажи кофе могут зависеть не только от температуры. Например, на количество продаж может влиять время дня, день недели, местоположение и другие факторы. Поэтому, регрессию всегда нужно применять с осторожностью и анализировать все возможные влияния и факторы.
Основные принципы
Случайность
Случайность в статистике означает использование случайных выборок и случайных процессов для сбора и анализа данных. Принцип случайности заключается в том, что выборка или экспериментальные условия должны быть устроены таким образом, чтобы каждый элемент или событие в генеральной совокупности имел равные шансы быть выбранным или произойти.
Использование случайности позволяет получить репрезентативные и объективные данные, уменьшая возможность систематических ошибок и искажений в выводах. Случайный подход также позволяет учитывать разнообразие и неопределенность в данных и устанавливать статистические выводы на основе вероятностных распределений.
Представительность
Представительность (или репрезентативность) в статистике относится к тому, насколько выборка или данные являются достоверным отражением генеральной совокупности или явления, которое изучается. Принцип представительности подразумевает, что выборка должна быть такой, чтобы каждый элемент или единица из генеральной совокупности имела равные шансы попасть в выборку.
Для достижения представительности выборки необходимо учесть различные факторы, такие как разнообразие, размер, географическое распределение и другие характеристики генеральной совокупности. Чтобы выборка была представительной, она должна быть сбалансированной и отражать разнообразие характеристик генеральной совокупности, таких как возраст, пол, географическое распределение и т.д.
Принцип представительности важен для обеспечения достоверности и обобщаемости статистических результатов. Если выборка не является представительной, то статистические выводы могут быть смещенными и не могут быть обобщены на генеральную совокупность или на другие ситуации. Поэтому важно стремиться к созданию представительной выборки при проведении статистического исследования.
Вариативность
Вариативность (или изменчивость) в статистике относится к степени разброса или изменения значений в наборе данных или генеральной совокупности. Принцип вариативности подразумевает, что данные могут различаться по своим значениям, и это разнообразие представляет собой важную характеристику, которую необходимо изучать и анализировать.
Вариативность может быть измерена различными статистическими показателями, такими как размах, дисперсия, стандартное отклонение и коэффициент вариации. Они позволяют оценить степень разброса или изменчивости данных внутри выборки или генеральной совокупности.
Принцип вариативности важен в статистике, поскольку он помогает понять, насколько данные различаются и какие факторы могут влиять на эту вариативность. Изучение вариативности позволяет выявлять закономерности, проводить сравнительные анализы, выявлять выбросы и тенденции, а также принимать решения на основе статистического анализа данных.
Измерение и понимание вариативности помогает статистикам и исследователям получать более полное представление о данных и их распределении, а также понимать, насколько достоверны и репрезентативны статистические выводы.
Независимость
Независимость в статистике относится к отсутствию связи или взаимосвязи между двумя или более переменными. Когда переменные являются независимыми, изменение одной переменной не влияет на значения другой переменной.
Независимость является важным предположением во многих статистических методах и моделях. Если переменные являются зависимыми, то статистические выводы и анализ могут быть неверными или искаженными.
Принцип независимости важен при выборе и использовании статистических методов. Например, при применении тестов на сравнение средних значений, предполагается, что выборки независимы. Если выборки зависимы, то необходимо использовать специальные методы, такие как парные тесты или методы для анализа зависимых данных.
Независимость также важна при проведении регрессионного анализа, где предполагается, что независимые переменные не связаны между собой и не влияют друг на друга. Независимость переменных позволяет оценить отдельные эффекты каждой переменной на зависимую переменную.
Проверка независимости переменных является важным этапом в статистическом анализе данных. Для этого используются различные методы, включая корреляционный анализ, анализ регрессии, а также проверка статистических гипотез и использование соответствующих тестов.
Нормальность
Нормальность в статистике относится к распределению данных, которое следует нормальному распределению или распределению Гаусса. Нормальное распределение является симметричным вокруг среднего значения и характеризуется своими параметрами, такими как среднее и стандартное отклонение.
Нормальность данных имеет важное значение, так как многие статистические методы и тесты предполагают или работают наилучшим образом с нормально распределенными данными. Некоторые из этих методов включают тесты на сравнение средних значений, анализ дисперсии, регрессионный анализ и многие другие.
Проверка нормальности данных может быть выполнена различными способами. Один из наиболее распространенных способов – это визуальная проверка с помощью построения гистограммы или графика плотности распределения, которые позволяют оценить, насколько данные соответствуют нормальному распределению. Также используются статистические тесты, такие как тест Шапиро-Уилка или Колмогорова-Смирнова, чтобы проверить статистическую значимость отклонения данных от нормальности.
В случае, если данные не соответствуют нормальному распределению, могут быть применены альтернативные статистические методы или трансформация данных, чтобы сделать их более нормально распределенными.
Эффективность
В статистике, эффективность относится к мере точности и надежности статистических оценок или методов анализа данных. Она оценивает, насколько хорошо статистический метод или процедура способны извлекать полезную информацию из данных или делать достоверные выводы.
Эффективность измеряется с помощью различных показателей, таких как средняя квадратическая ошибка, которая представляет собой среднее значение квадратов отклонений между оценками и истинными значениями параметров. Чем меньше значение среднеквадратической ошибки, тем более эффективным является статистический метод или оценка.
Эффективность также может быть измерена с помощью других критериев, таких как смещение оценок, доверительные интервалы, статистические тесты и другие. Важно отметить, что эффективность статистического метода зависит от предполагаемой модели данных и соответствующих предположений.
Цель статистической эффективности состоит в том, чтобы получить наиболее точные и надежные оценки параметров или сделать наиболее информативные выводы на основе доступных данных. Эффективные методы позволяют более эффективно использовать информацию, содержащуюся в данных, и достичь более точных статистических выводов.
Сопоставимость
В статистике, сопоставимость (comparability) относится к возможности сравнивать и анализировать данные, которые собраны или получены из разных источников или в различных условиях. Она обеспечивает основу для объективных и надежных сравнений между группами, временными периодами или другими сущностями, которые изучаются в статистическом анализе.
Сопоставимость данных является важным аспектом статистического исследования, поскольку она позволяет сделать выводы на основе сравнений между различными группами или наблюдениями. Она требует, чтобы данные были собраны и измерены с использованием одинаковых или сопоставимых методов, шкал измерения и условий сбора данных.
Для обеспечения сопоставимости данных, статистики обращают особое внимание на стандартизацию процедур сбора данных, использование единых определений и понятий, а также контроль за возможными искажениями или систематическими ошибками, которые могут повлиять на сравнительный анализ.
Например, при сравнении доходов между разными странами, чтобы сделать данные сопоставимыми, необходимо использовать одну и ту же валюту, учитывать различия в ценах и уровне жизни, а также применять единые методы сбора информации о доходах.
Обеспечение сопоставимости данных важно для получения достоверных и объективных выводов и обеспечивает основу для принятия рациональных решений на основе статистического анализа.
Доверительность
В статистике, доверительность (confidence) относится к степени уверенности, с которой мы можем делать выводы на основе выборочных данных. Она описывает вероятность того, что интервал или оценка, полученные из выборки, содержат истинное значение параметра генеральной совокупности.
Доверительность обычно выражается в виде доверительного интервала или доверительного уровня, который определяет диапазон значений, внутри которого с определенной вероятностью находится истинное значение параметра. Например, доверительный интервал может быть сформулирован как “С вероятностью 95% истинное значение параметра лежит в интервале от 20 до 30”.
Доверительность основана на статистических методах, которые учитывают случайность выборки и изменчивость данных. Чем больше выборка и меньше изменчивость данных, тем выше доверительность оценки.
Например, если мы проводим опрос среди 1000 случайно выбранных людей и получаем результат, что 60% из них поддерживают определенную политическую партию, мы можем сказать, что с определенной доверительностью (например, 95%) доля поддерживающих эту партию в генеральной совокупности будет лежать в некотором интервале, например, от 55% до 65%.
Доверительность является важным понятием в статистике, поскольку позволяет оценивать достоверность результатов и делать статистически обоснованные выводы на основе выборочных данных.
Вероятностный подход
Вероятностный подход в статистике основан на применении теории вероятностей для анализа данных и принятия статистических выводов. Он предполагает, что данные являются результатом случайных явлений и могут быть описаны с использованием вероятностных моделей.
Основные принципы вероятностного подхода в статистике включают:
- Вероятностные модели: Данные рассматриваются как реализации случайных переменных, которые подчиняются вероятностным законам. Вероятностные модели могут быть заданы различными распределениями, такими как нормальное распределение, биномиальное распределение и т.д.
- Вероятностные оценки: Статистические параметры, такие как среднее значение, дисперсия, корреляция и др., оцениваются с использованием вероятностных методов. Например, среднее значение выборки может использоваться для оценки среднего значения в генеральной совокупности.
- Вероятностные выводы: На основе вероятностных моделей и оценок можно делать статистические выводы. Например, можно определить вероятность того, что различие между двумя выборками является случайным или статистически значимым.
- Доверительные интервалы: Вероятностный подход также позволяет строить доверительные интервалы, которые указывают наличие неопределенности в оценке параметров. Доверительный интервал показывает диапазон значений, в котором с определенной вероятностью содержится истинное значение параметра.
Вероятностный подход является основополагающим в статистике и обеспечивает строгое математическое обоснование для статистических методов и выводов. Он позволяет изучать случайность данных, измерять неопределенность и принимать статистически обоснованные решения на основе вероятностных моделей.
1. План лекции 4 «Меры изменчивости »
1. Лимиты
2. Размах
3. Квантили
4. Размах от 90-го до 10-го процентиля
5. Полу-междуквартильный размах
6. Дисперсия
7. Свойства дисперсии
8. Стандартное отклонение
9. Среднее отклонение
10. Коэффициент вариации
11. Стандартизированные данные
12. Асимметрия
13. Эксцесс
30.03.2017
Управление в социальных и
экономических системах
1
2. Вариабельность данных
Меры центральной тенденции говорят нам о
концентрации данных на числовой оси. Каждая
такая мера в каком-то смысле наилучшим
образом «представляет» данные.
Меры центральной тенденции игнорируют
различия между данными.
Для измерения вариабельности данных
требуются другие описательные статистики.
30.03.2017
Управление в социальных и
экономических системах
2
3. Зачем нужны меры вариабельности данных?
Научная работа связана с понятием
вариабельности данных. Если есть много
необъяснимых причин вариабельности, прогнозы
будут неточными. Задача науки найти причины
вариабельности данных и тем самым увеличить
точность прогноза.
Например установлено, что наследственность и
окружающая среда влияют на IQ ребенка. Поэтому
информация о родителях ребенка и его воспитании
позволяет более точно прогнозировать его умственное
развитие в зрелости. Без такой информации прогноз
будет менее точным.
30.03.2017
Управление в социальных и
экономических системах
3
4. Наиболее часто используемые меры вариабельности данных
1. Лимиты
2. Размах
3. Квантили
4. Дисперсия
5. Стандартная ошибка
6. Среднее отклонение
7. Коэффициент вариации
30.03.2017
Управление в социальных и
экономических системах
4
5. Лимиты
Это самая простая мера изменчивости.
Определяется минимальное (Xmin) и
максимальное значение (Xmax) массива данных.
Между этими статистиками находятся все
данные массива.
Несмотря на свою простоту эта мера
используется редко, потому что экстремальные
значения сильно подвержены ошибкам.
Поэтому трудно определить влияние факторов
на вариабельность данных.
30.03.2017
Управление в социальных и
экономических системах
5
6. Размах
Определяет расстояние на числовой оси, в пределах
которого варьируются данные. R=Xmax-Xmin.
Исключающий размах – это разность
максимального и минимального значений.
Включающий размах – это разность между
естественной верхней границей интервала,
содержащего максимальное значение и естественной
нижней границей интервала, содержащего
минимальное значение.
Например рост 5 мальчиков равен 150, 155, 157, 165
и 168. Исключающий размах равен 168-150=18,
включающий размах равен 168,5 – 149,5=19.
30.03.2017
Управление в социальных и
экономических системах
6
7. Квантили
Это характеристики вариационного ряда, которые
отсекают определенную его часть. Наиболее часто
используются квартили, децили и процентили.
Квартиль – это статистика, отсекающая ¼ часть ряда.
Три квартиля Q1, Q2 и Q3 делят ряд на четыре,
равные по объемы части (кварты).
Дециль (Di) – это статистика, отсекающая 1/10 часть
ряда. Девять децилей делят ряд на 10 равных частей.
Процентиль (Pi) — это статистика, отсекающая 1/100
часть ряда. Девяносто девять процентилей делят ряд
на 100 равных частей.
30.03.2017
Управление в социальных и
экономических системах
7
8. Зачем нужны квантили?
Квантили, как и медиана, — это важные
характеристики вариационного ряда, особенно
для асимметричных распределений. Часто
квантили используются для установления
границ тех или иных нормативов.
Размах от 90-ого до 10-ого процентиля
является более стабильной мерой, чем размах.
Полу-междуквартильный размах Q3-Q1
содержит 50% наблюдений вариационного
ряда.
30.03.2017
Управление в социальных и
экономических системах
8
9. Дисперсия
При вычислении всех предыдущих мер
вариабельности не учитывалось каждое
отдельное значение массива данных.
Отклонения наблюдений от мер
центральной тенденции несут информацию о
вариабельности данных. Чем больше
отклонения, тем больше вариабельность.
Однако
n
_
yi y. 0
i 1
30.03.2017
Управление в социальных и
экономических системах
9
10. Формула для вычисления дисперсии
xi
n
1
i 1
2
2
sx
xi
n 1 i 1
n
n
30.03.2017
Управление в социальных и
экономических системах
2
10
11. Свойства дисперсии
1. Прибавление константы с к каждому
значению не влияет на дисперсию (а на
среднее?)
2. Умножение каждого значения на
константу с увеличивает дисперсию в с2 раз.
3. Дисперсия объединенной совокупности
зависит как от дисперсий, так и от средних
объединяемых групп
_
_
_
_
2
(
n
1)
s
(
n
1)
s
n
(
x
x
)
n
(
x
x
)
.
a
..
.
b
..
a
b
a
b
s2
na nb 1
2
a
30.03.2017
2
b
Управление в социальных и
экономических системах
2
11
12. Задача 3. Вычислить средние и дисперсии совокупностей:
А (3, 3, 3, 3) и В (7,7,7,7)
_
_
xa
xa
x a b
s
s
2
a b
_
2
a
30.03.2017
2
a
s
Управление в социальных и
экономических системах
12
13. Стандартное отклонение
Эта мера тесно связана с дисперсией. Стандартное
отклонение – это положительный корень из дисперсии.
s s2
Стандартное отклонение измеряется в тех же единицах,
что и исходные данные. Например, как интерпретировать
кг2 или л2?
Полезность этой меры еще и в том, что для многих
распределений мы знаем, какая доля наблюдений
находится внутри одного, двух, трех и более стандартных
отклонений. Поэтому эта мера используется наиболее
часто.
30.03.2017
Управление в социальных и
экономических системах
13
14. Среднее отклонение
Формула имеет вид
N
x x
i 1
i
.
/N
Несмотря на легкость вычисления и простоту
интерпретации эта мера используется редко. Это
объясняется тем, что эта мера неудобна для
аналитический преобразований (например необходимо
брать производную для поиска минимума функции).
Эта формула неудобна также для вычисления
стандартизированных отклонений.
30.03.2017
Управление в социальных и
экономических системах
14
15. Коэффициент вариации
Формула для вычисления имеет вид
_
v s x.
Эта мера позволяет сравнивать вариабельность
признаков имеющих разные единицы измерения.
Эта мера часто используется в биологии и других
науках, где измеряемые признаки отличны от
нуля.
30.03.2017
Управление в социальных и
экономических системах
15
16. Стандартизированные данные
Формула для вычисления имеет вид
_
xi x .
zi
sx
Таким образом любое множество данных на
основе вычисленных среднего и стандартного
отклонения можно преобразовать в
стандартизированное множество с нулевым
средним и единичной дисперсией. Это удобно для
проверки различных статистических гипотез.
30.03.2017
Управление в социальных и
экономических системах
16
17. Задача 4. Вычислить средние и дисперсии двух массивов
x1
10
15
20
25
30
35
40
45
50 x1.
x2
10
28
28
30
30
30
32
32
50 x2.
(x1-x.)
(x2-x.)
(x1-x.)2
(x2-x.)2
30.03.2017
Управление в социальных и
экономических системах
17
18. Задача. Вычислить дисперсию тестового балла
№
xi
п.п.
1
6
4
7
10
7
2
2
3
4
5
6
Сумм
а
S
2
30.03.2017
36
N
x
i 1
i
xi x.
0
38
0
-2
1
4
1
-4
x.
N 1
xi x.
2
38
5
S
Управление в социальных и
экономических системах
2
0
4
1
16
1
16
S2
7,6 2,76
18
19. Рекомендуемая литература
1. Гмурман В.Е. Теория вероятностей и
математическая статистика. – М.: Высшая школа, 2004,
479 с.
2. Гмурман В.Е. Руководство к решению задач по
теории вероятностей и математической статистике. –
М.: Высшая школа, 2004, 400 с.
3. Гласс Дж., Стэнли Дж. Статистические методы
в педагогике и психологии. Пер. с англ. – М.:
Издательство «Прогресс», 1976. -496 с.
4. Маслак А.А. Основы планирования и анализа
сравнительного эксперимента в педагогике и
психологии. – Курск: РОСИ, 1998. – 167 с.
30.03.2017
Управление в социальных и
экономических системах
19