Рассмотрим задачу
многомерной глобальной условной
оптимизации
, (1)
где множество
допустимых значений
(2)
определяется, как
ограничениями типа неравенств, так и
ограничениями типа равенств.
Метод Монте-Карло
относится к классу прямых методов
случайного поиска.
Схема метода
Монте-Карло
-
Задаем общее
количество испытаний N. -
С помощью какого-либо
программного генератора случайных
чисел генерируем n
компонент вектора
,
вычисляем величинуи полагаем
,
.
-
Аналогично п. 2
генерируем случайную точку
и вычисляем соответствующее значение
критерия оптимальности.
-
Выполняем следующие
присваивания:
-
Если
,
то полагаеми переходим на п. 3. Иначе — принимаем
в качестве приближенного решения задачи
и заканчиваем вычисления●
Отметим, что в
простейшем случае точки
генерируются равномерно распределенными
в областиD.
Для областей, имеющих сложную топологию,
эта может представлять собой достаточно
сложную задачу. Обычно с этой целью
используют точки, равномерно распределенные
в гиперкубе, описанном вокруг области
D.
С целью сокращения вычислительных
затрат и при наличии априорной информации
о положении точки глобального минимума,
целесообразно использовать законы
распределения, в которых вероятность
генерации точки в окрестности
предполагаемого глобального минимума
выше, чем вне этой окрестности.
Для локализации
с помощью метода Монте-Карло глобального
минимума с высокой вероятностью и
точностью, требуется очень большое
количество испытаний N.
Поэтому метод Монте-Карло обычно
комбинируют с каким-либо методом
локальной оптимизации.
Комбинация метода
Монте-Карло с методом локальной
оптимизации (метод
мультистарта)
-
Задаем общее
количество исходных случайных точек
N
и полагаем
.
-
С помощью какого-либо
программного генератора случайных
чисел генерируем координаты точки
.
-
Исходя из точки
,
каким-либо методом многомерной локальной
условной оптимизации находим локальный
минимумфункции
в окрестности точки
и вычисляем
.
Полагаем.
-
По рассмотренной
схеме генерируем координаты точки
.
-
Выполняем действия,
указанные в п. 3 – находим величины
,
.
Полагаем
-
Если
,
то полагаеми переходим к п. 4. Иначе – заканчиваем
вычисления●
13
Соседние файлы в папке Все вместе
- #
- #
- #
- #
- #
- #
- #
- #
Аннотация: Цель работы: Изучить и практически освоить метод Монте-Карло на примерах расчета площадей плоских фигур, объемов пространственных тел, а также вычисления кратных интегралов. Среда программирования — MATLAB.
Теоретическая часть
Сущность метода Монте-Карло состоит в следующем: требуется найти значение 


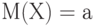
Практически же поступают следующим образом: производят 


и принимают 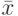
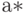

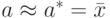
Поскольку метод Монте-Карло требует произведения большого числа испытаний, его часто называют методом статистических испытаний.
1. Оценка погрешности метода Монте-Карло
Как отмечалось, для получения оценки математического ожидания случайной величины 



При этом возможны следующие случаи оценки числа испытаний:
-
Случайная величина
распределена нормально и ее среднее квадратическое отклонение (стандартное отклонение)
известно. В этом случае с заданной вероятностью
верхняя граница ошибки определяется по формуле
(
4.1)где:
— число испытаний (разыгранных значений случайной величины
);
— значение аргумента функции Лапласа
или интеграла вероятности, при котором она равна половине заданной вероятности;
— известное среднее квадратическое отклонение.
Из формулы (4.1) может быть найдено число испытаний. Один из вариантов интеграла вероятностей (функции Лапласа) имеет вид [6]
(
4.2)Значения
табулированы и приведены в большинстве учебников по теории вероятностей и математической статистике.
В зарубежной литературе большое распространение получила так называемая функция ошибок (
)
:
(
4.3)Связь между функцией ошибок (4.3) и интегралом вероятностей (4.2) выражается в виде
(
4.4) -
Случайная величина
распределена нормально, причем ее среднее квадратическое отклонение неизвестно. В этом случае с заданной вероятностью
верхняя граница ошибки вычисляется по формуле
(
4.5)где:
— число испытаний;
— «исправленное» среднее квадратическое отклонение;
находят по специальным таблицам, например, приведенной в [6].
Из формулы (4.5) может быть найдено число испытаний для определения верхней границы ошибки.
-
Случайная величина
распределена по закону, отличному от нормального. В этом случае при достаточно большом числе испытаний (
), с вероятностью, приближенно равной
(заданной вероятностью), верхняя граница ошибки может быть вычислена по формуле (4.1), если среднее квадратическое отклонение случайной величины известно; если же оно неизвестно, то можно подставить в формулу (4.1) его оценку — «исправленное» среднее квадратическое отклонение — либо воспользоваться формулой (4.5). При этом чем больше число испытаний, тем меньше различие между результатами, которые дают обе формулы.
2. Вычисление кратных интегралов методом Монте-Карло
В случае когда, например, определенный интеграл не может быть вычислен в квадратурах, либо прибегают к численным методам интегрирования, либо расчет ведется с помощью метода Монте-Карло. Применение метода Монте-Карло становится оправданным при кратности интеграла больше трех. В данной лабораторной работе мы используем метод Монте-Карло для расчета интегралов с кратностью не более трех. Это позволит более ясно представить технику применения метода.
Сначала рассмотрим вычисление простого определенного интеграла
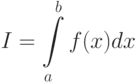 |
( 4.6) |
где 
Введем под знак интеграла постоянный множитель (равный единице):
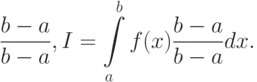 |
( 4.7) |
Вынесем из-под интеграла числитель дроби, получим
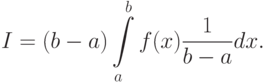 |
( 4.8) |
Как известно, если случайная величина 

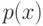
Кроме того, если известно распределение случайной величины 

![M[x]](https://intuit.ru/sites/default/files/tex_cache/b34133f00814d1d8749df12a4aaef591.png)
Соответственно, математическое ожидание от функции случайной величины будет определяться следующим образом:
![M[f(x)]=\int\limits_{a}^{b}f(x)\frac{1}{b-a}dx.](https://intuit.ru/sites/default/files/tex_cache/42149a4cde11c98da0e505e2279d7980.png) |
( 4.9) |
Сопоставляя (4.8) и (4.9), приходим к выводу, что определенный интеграл может быть рассчитан по формуле
![I=(b-a)M[f(x)].](https://intuit.ru/sites/default/files/tex_cache/6a755a2e5019e4067dd39dccfab13a63.png) |
( 4.10) |
Несмещенной оценкой математического ожидания случайной величины, как известно, является ее среднее арифметическое. Поэтому математическое ожидание можем приближенно найти по формуле
![M[f(x)]\approx \frac{1}{n}\sum\limits_{i=1}^{n}f(x_i).](https://intuit.ru/sites/default/files/tex_cache/1e2f3c404db3d6b0d0a520572ddefc3e.png) |
( 4.11) |
С учетом (4.11) получаем выражение для приближенного расчета определенного интеграла
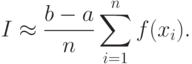 |
( 4.12) |
Чем больше число испытаний 
Рассмотрим общий подход вычисления 
Пусть задан 
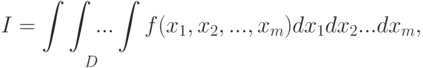 |
( 4.13) |
где подынтегральная функция 
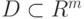
Погрузим область интегрирования 

![D^* = [a_1, b_1]\times[a_2, b_2]\times ... [a_m, b_m],](https://intuit.ru/sites/default/files/tex_cache/23a20b84ad54eb95a594f5c785f6284a.png) |
( 4.14) |
имеющий меру
 |
( 4.15) |
Определим в промежутке (4.15) функцию
 |
( 4.16) |
Тогда в соответствии с (4.13) и (4.16) получим
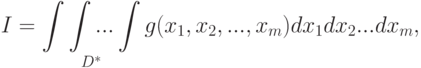 |
( 4.17) |
Введем в рассмотрение 

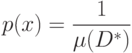 |
( 4.18) |
Функция плотности равномерного распределения есть величина постоянная, поэтому введем ее под знак интеграла (4.17) следующим образом:
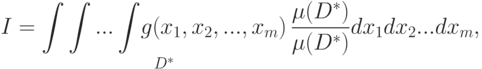 |
( 4.19) |
Вынесем числитель дроби за знак интеграла, т. е.
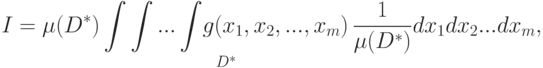 |
( 4.20) |
В (4.20) 


![I=\mu (D^{*})M[g(x)],](https://intuit.ru/sites/default/files/tex_cache/cf20ace0be47f575d3035d97a4879769.png) |
( 4.21) |
где 
В свою очередь математическое ожидание может быть оценено с помощью арифметического среднего. Тогда приближенное значение 
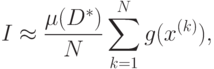 |
( 4.22) |
где 


Чтобы смоделировать выборку 


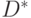



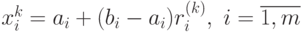
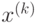
Таким образом, техника применения метода Монте-Карло здесь будет заключаться в определении области 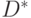

Расчет площадей и объемов можно рассматривать как частный случай вычисления кратных интегралов. Например, вычисление объема тел с помощью трехкратного интеграла сводится к взятию интеграла по области при подынтегральной функции, тождественно равной единице.
Метод Монте-Карло и его точность
Время на прочтение
5 мин
Количество просмотров 222K
Под метдом Монте-Карло понимается численный метод решения
математических задач при помощи моделирования случайных величин. Представление об истории метода и простейшие примеры его применения можно найти в Википедии.
В самом методе нет ничего сложного. Именно эта простота объясняет популярность данного метода.
Метод имеет две основных особенности. Первая — простая структура вычислительного алгоритма. Вторая — ошибка вычислений, как правило, пропорциональна
, где
— некоторая постоянная, а
— число испытаний. Ясно, что добиться высокой точности на таком пути невозможно. Поэтому обычно говорят, что метод Монте-Карло особенно эффективен при решении тех задач, в которых результат нужен с небольшой точностью.
Однако одну и ту же задачу можно решать различными вариантами метода Монте-Карло, которым отвечают различные значения . Во многих задачах удается значительно увеличить точность, выбрав способ расчета, которому соответствует значительно меньшее значение
.
Общая схема метода
Допустим, что нам требуется вычислить какую-то неизвестную величину m. Попытаемся придумать такую случайную величину , чтобы
. Пусть при этом
.
Рассмотрим независимых случайных величин
(реализаций), распределения которых совпадают с распределением
. Если
достаточно велико, то согласно центральной предельной теореме распределение суммы
будет приблизительно нормальным с параметрами
,
.
На основе Центральной предельной теоремы (или если хотите предельной теоремы Муавра-Лапласа) не трудно получить соотношение:
где — функция распределения стандартного нормального распределения.
Это — чрезвычайно важное для метода Монте-Карло соотношение. Оно дает и метод расчета , и оценку погрешности.
В самом деле, найдем значений случайной величины
. Из указанного соотношения видно, что среднее арифметическое этих значений будет приближенно равно
. С вероятностью близкой к
ошибка такого приближения не превосходит величины
. Очевидно, эта ошибка стремится к нулю с ростом
.
В зависимости от целей последнее соотношение используется по разному:
- Если взять k=3, то получим так называемое «правило
»:
- Если требуется конкретный уровень надежности вычислений
,
Точность вычислений
Как видно из приведенных выше соотношений, точность вычислений зависит от параметра и величины
– среднеквадратичного отклонения случайной величины
.
В этом пункте хотелось бы указать важность именно второго параметра . Лучше всего это показать на примере. Рассмотрим вычисление определенного интеграла.
Вычисление определенного интеграла эквивалентно вычислению площадей, что дает интуитивно понятный алгоритм вычисления интеграла (см. статью в Википедии). Я рассмотрю более эффективный метод (частный случай формулы для которого, впрочем, тоже есть в статье из Википедии). Однако не все знают, что вместо равномерно распределенной случайной величины в этом методе можно использовать практически любую случайную величину, заданную на том же интервале.
Итак, требуется вычислить определенный интеграл:
Выберем произвольную случайную величину с плотностью распределения
, определенной на интервале
. И рассмотрим случайную величину
.
Математическое ожидание последней случайной величины равно:
Таким образом, получаем:
Последнее соотношение означает, что если выбрать значений
, то при достаточно большом
:
.
Таким образом, для вычисления интеграла, можно использовать практически любую случайную величину . Но дисперсия
, а вместе с ней и оценка точности, зависит от того какую случайную величину
взять для проведения расчетов.
Можно показать, что будет иметь минимальное значение, когда
пропорционально |g(x)|. Выбрать такое значение
в общем случае очень сложно (сложность эквивалентна сложности решаемой задачи), но руководствоваться этим соображением стоит, т.е. выбирать распределение вероятностей по форме схожее с модулем интегрируемой функции.
Численный пример
Теория, конечно, дело хорошее, но давайте рассмотрим численный пример: ;
;
.
Вычислим значение интеграла с применением двух различных случайных величин.
В первом случае будем использовать равномерно распределенную случайную величину на [a,b], т.е. .
Во втором случае возьмем случайную величину с линейной плотностью на [a,b], т.е. .
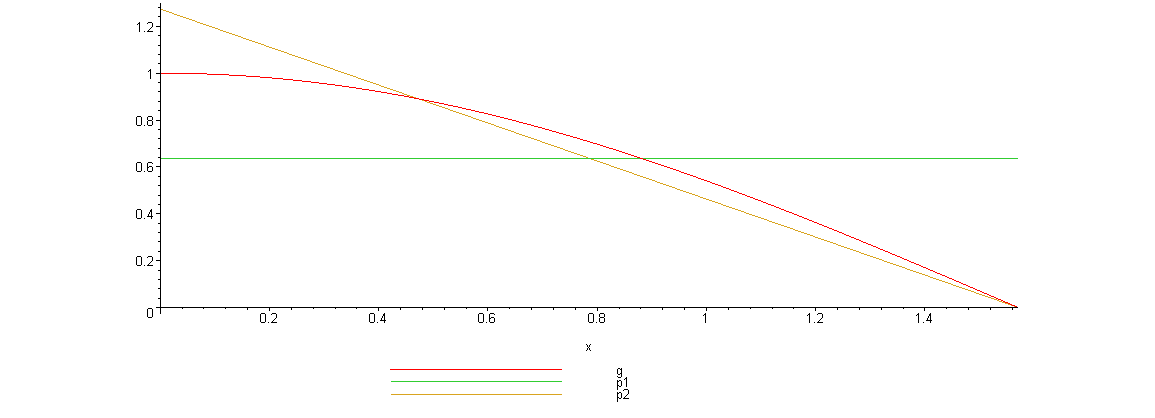
Вот график, указанных функций
Нетрудно видеть, что линейная плотность лучше соответствует функции .
Код программы модельного примера в математическом пакете Maple
restart;
with(Statistics):
with(plots):
#исходные функции
g:=x->cos(x):
a:=0:
b:=Pi/2:
N:=10000:
#плотности распределений
p1:=x->piecewise(x>=a and x<b,1/(b-a)):
p2:=x->piecewise(x>=a and x<b,4/Pi-8*x/Pi^2):
#графики
plot([g(x),p1(x),p2(x)],x=a..b, legend=[g,p1,p2]);
#Точное значение интеграла
I_ab:=int(g(x),x=0..b);
#функция метода Монте-Карло для вычисления приближенного вычисления интеграла
#не стоит ее использовать при реальных расчетах
INT:=proc(g,p,N)
local xi;
xi:=Sample(RandomVariable(Distribution(PDF = p)),N);
evalf(add(g(xi[i])/p(xi[i]),i=1..N)/N);
end proc:
#Приближенное значение интеграла
I_p1:=INT(g,p1,N);#c равномерной плотностью
I_p2:=INT(g,p2,N);#c линейной плотностью
#Абсолютная погрешность
Delta1:=abs(I_p1-I_ab);#c равномерной плотностью
Delta2:=abs(I_p2-I_ab);#c линейной плотностью
#Относительные погрешности в процентах
delta1:=Delta1/I_ab*100;#c равномерной плотностью
delta2:=Delta2/I_ab*100;#c линейной плотностью
#Вычисление дисперсий
Dzeta1:=evalf(int(g(x)^2/p1(x),x=a..b)-1);
Dzeta2:=evalf(int(g(x)^2/p2(x),x=a..b)-1);
#Оценка погрешности в первом случае
3*sqrt(Dzeta1)/sqrt(N);
#Оценка погрешности во втором случае
3*sqrt(Dzeta2)/sqrt(N);
Файл с данной программой можно взять тут
Точное значение интеграла легко вычислить аналитически, оно равно 1.
Результаты одного моделирования при :
Для равномерно распределенной случайной величины: .
Для случайной величины с линейной плотностью распределения: .
В первом случае относительная погрешность более 21%, а во втором 2.35%. Точность в первом случае равна 0.459, а во втором – 0.123.
Думаю, данный модельный пример показывает важность выбора случайной величины в методе Монте-Карло. Выбрав, правильную случайную величину, можно получить более высокую точность вычислений, при меньшем числе итераций.
Конечно, так не вычисляют одномерные интегралы, для этого есть более точные квадратурные формулы. Но ситуация меняется при переходе к многомерным интегралам, т.к. квадратурные формулы становятся громоздкими и сложными, а метод Монте-Карло применяется лишь с небольшими изменениями.
Количество итераций и генераторы случайных чисел
Не трудно видеть, что точность вычислений зависит от количества случайных величин включенных в сумму. Причем, для увеличения точности вычислений в 10 раз нужно увеличить
в 100 раз.
При решении некоторых задач для получения приемлемой точности оценки требуется брать очень большое число . А учитывая, что метод зачастую работает очень быстро, то реализовать последнее при современных вычислительных возможностях совсем не сложно. И возникает соблазн просто увеличить число
.
Если в качестве источника случайности используется некоторое физическое явление (физический датчик случайных чисел), то все работает отлично.
Часто для вычислений по методу Монте-Карло применяют датчики псевдослучайных чисел. Главная особенность таких генераторов – наличие некоторого периода.
Метод Монте-Карло можно использовать при значениях не превышающих (лучше много меньших) период вашего генератора псевдослучайных чисел. Последний факт вытекает из условия независимости случайных величин, используемых при моделировании.
При проведении больших расчетов нужно убедиться, что свойства генератора случайных чисел позволяют вам провести эти расчеты. В стандартных генераторах случайных чисел (в большинстве языков программирования) период чаще всего не превосходит 2 в степени разрядности операционной системы, а то и еще меньше. При использовании таких генераторов нужно быть чрезвычайно осторожным. Лучше изучить рекомендации Д.Кнута, и построить свой генератор, имеющий наперед известный и достаточно большой период.
Литература
Популярные лекции по математике 1968. Выпуск 46. Соболь И.М. Метод Монте-Карло. М.: Наука, 1968. — 64 с.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Содержание
|
Введение |
3 |
|
1 Понятие «неопределенность измерений» и методы ее оценивания |
5 |
|
5 |
|
19 |
|
22 |
|
24 |
|
32 |
|
32 |
|
2.1.1 Возникновение метода Монте-Карло и его общая характеристика |
32 |
|
2.1.2 Применение метода Монте-Карлодля оценивания неопределенности измерений |
33 |
|
2.1.3 Оценка входной величины |
34 |
|
2.1.4 Оценка выходной величины |
35 |
|
2.1.5 Интервал охвата для выходной величины |
36 |
|
2.1.6 Адаптивная реализация метода Монте-Карло |
37 |
|
2.1.7 Преимущества и недостатки метода Монте-Карло |
39 |
|
42 |
|
45 |
|
Заключение |
54 |
|
Список использованных источников |
55 |
Введение
При обработке результатов измерений, получаемых при международных сличениях эталонов, испытаниях, калибровке или поверке средств измерений для зарубежных стран, при исследованиях первичных национальных эталонов, в качестве характеристики качества измерений используют неопределенность измерений. В связи с этим задача обеспечения международного единства в подходе к представлению и оцениванию неопределенности результата измерений является актуальной.
Существует несколько методов оценивания неопределенности измерений. Одним из них является метод Монте-Карло, который используется как метод трансформирования распределений на основе моделирования случайных выборок из этих распределений. Этот метод может быть применен к любым моделям, имеющим единственную выходную величину, в которых входные величины характеризуются любыми заданными функциями распределения вероятностей.
В большинстве случаях оценивания неопределенности измерений метод Монте-Карло используется, когда:
— вклад разных составляющих неопределенности существенно неодинаков;
— распределение выходной величины не является нормальным или масштабированным смещенным t — распределением;
— модель достаточно сложная;
— плотности распределения вероятностей входных величин асимметричны;
— оценка выходной величины и соответствующая стандартная неопределенность имеют приблизительно равные значения.
Цель данной работы состоит в изучении методов оценивания неопределенности измерений и применении метода Монте-Карло для оценивания неопределенности измерений.
Задачи работы:
— изучение различий между понятиями «погрешность измерений» и «неопределенность измерений»,
— изучение методов оценивания неопределенности измерений и оценивания неопределенности методом Монте-Карло,
— сравнение результатов оценки неопределенности измерений методом Монте-Карло и расчетным методом, изложенным в ИСО/МЭК «Руководство по выражению неопределенности измерений (GUM)».
Автор аттестационной работы выражает глубокую благодарность руководителю – старшему преподавателю кафедры МСК ПГУ Сибринину Борису Петровичу за проявленное внимание и участие в решении проблем, которые возникали в процессе выполнения аттестационной работы.
1 ПОНЯТИЕ «НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЙ» И МЕТОДЫ ЕЕ ОЦЕНИВАНИЯ
1.1 Понятие «неопределенность измерений» и его связь с термином «погрешность измерений»
Считается, что термин «неопределенность» пришел на замену термину «погрешность». Однако, это не так. Термин «погрешность» остается существовать, и он входит в международный метрологический словарь VIM [12].
В 1993 г. был выпущен документ ИСО/МЭК «Руководство по выражению неопределенности измерений (GUM)» [15], в котором было введено понятие «неопределенность измерений».
В Руководстве большое внимание уделяется различию терминов «погрешность» и «неопределенность». Утверждается, что они не синонимы и представляют собой совершенно различные понятия. По определению авторов Руководства, погрешность измерения – отклонение результата измерения от истинного значения измерения. Поскольку истинное значение не может быть определено, то и погрешность, как идеализированное понятие не может быть известна точно. Поэтому, авторы постарались во — первых, по возможности отказаться, от использования при изложении понятий «погрешность» и «истинное значение измеряемой величины» в пользу понятий «неопределенность» и «оцененное значение измеряемой величины», во — вторых, переход от деления погрешностей по природе их проявления на «случайные» и «систематические» к другому делению – по способу оценивания неопределенностей измерений (по типу А – методами математической статистики и по типу В – другими методами).
Основным понятием, используемым в Руководстве, является понятие «неопределенность измерения». В разделе II дается два определения этого понятия:
— «в своем самом широком смысле «неопределенность измерения» означает сомнение относительно достоверности результата измерения»;
— «неопределенность измерения есть параметр, связанный с результатом измерения, который характеризует дисперсию значений, которые могли быть обоснованно приписаны измеряемой величине».
Обратимся к формулам, описывающим термины «неопределенность измерения» и «погрешность измерения».
При определении погрешности измерения, обозначаемой Δ, исходной является хорошо известная всем формула:
Δ= хизм — хист (1),
где хизми хист ‑ результат измерения и истинное значение измеряемой величины, соответственно.
Но по причине невозможности экспериментального определения истинногозначения измеряемой величины с философской точки зрения, вслед за формулой(1) пишется похожая, но вместе с тем принципиально другая формула:
Δхизм– хдейст (2)
где хдейст — действительное значение измеряемой величины, которое должно быть достаточно близким к истинному значению.
Вопрос о том, насколько близким – один из наиболее трудных вопросов втеории погрешностей измерений.
Следует заметить, что в формуле (2) вместо знака строгого равенства появляется знак приближенного равенства «». С этого момента мы вынуждены рассматривать погрешность измерений (Δ), как сугубо неопределенную величину, для которой можно получать лишь более или менее приемлемые (по точности) оценки.
Основным количественным выражением неопределенности измерений является стандартная неопределенность.
В Руководстве не оперируют формулами вида (1) и (2), а измеряемая величина Y определяется как функция
Y = ƒ(X1, X2, …, XN), (3)
где X1, X2, …, XN – входные величины (непосредственно измеряемые или другие величины, влияющие на результат измерения);
N– число этих величин;
ƒ – вид функциональной зависимости.
Оценка измеряемой величины y вычисляется как функция оценок входных величин x1, x2, …, xN после внесения поправок на все известные источники, имеющие систематический характер:
y = f (x1, x2, …, xN) (4)
Затем вычисляются стандартные неопределенности входных величин u(xi) (i=1, 2,…, N).
Различают два типа вычисления стандартной неопределенности:
— вычисление по типу А – как среднеквадратическое (стандартное) отклонение закона распределения результата измерения с классической частотной интерпретацией;
— вычисление по типуВ – с использованием других способов.
Исходными данными для оценки стандартной неопределенности по типу А являются результаты многократных измерений: xi, ( i=1, 2,…, n)
В большинстве случаев наилучшей оценкой ожидаемого значения μx величины x, изменяющийся случайным образом, для которой получены n независимых наблюдений xi при одинаковых условиях измерения, является среднее арифметическое или среднее значение из nнаблюдений:
Экспериментальная дисперсия наблюдений, которая оценивает дисперсию σ2 распределения вероятностей x, определяется по формуле
Эта оценка дисперсии выборки и ее положительный квадратный корень sназываемый экспериментальным стандартным отклонением, характеризует изменчивость наблюдаемых значений xi или, точнее, их дисперсию относительно среднего значения . Наилучшая оценка σ2() дисперсии среднего значения определяется как:
(6).
Экспериментальная дисперсия среднего и экспериментальное стандартное отклонение среднего значения s(x), равное положительному квадратному корню из , количественно определяют, насколько хорошо оценивает математическое ожидание μx величины x. Таким образом, для входной величины Xi, определенной из nнезависимых наблюдений, стандартная неопределенность u(xi) ее оценки xi= есть u(xi) c , вычисленным согласно уравнению (5), т.е.
Исходными данными для оценки неопределенности по типу В являются:
— данные предшествовавших измерений величин, входящих в уравнение измерения;
— сведения о виде распределения вероятностей;
— данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;
— неопределенности констант и справочных данных;
— данные поверки, калибровки, сведения изготовителя о приборе и др.
Неопределенности этих данных обычно представляются в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания об измеряемой величине базируется на постулате равномерного закона распределения в указанных (нижней и верхней) границах (a—, a+). При этом стандартная неопределенность, оцененная по типуВ, равна:
Для симметричных границ (±a):
u = uB.
В случае других законов распределения формулы для вычисления стандартной неопределенности по типу В будут иными.
На практике часто входные величины получаются из одновременных наблюдений двух и более взаимосвязанных величин, т.е., они коррелированны и эти корреляции должны приниматься во внимание при вычислении стандартных неопределенностей измеряемых величин.
Суммарная стандартная неопределенность uс(y) – стандартная неопределенность результата измерений, полученного через значения других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других величин, взвешенными в соответствии с тем, как результат измерений изменяется при изменении этих величин [2]. Суммарная дисперсия рассчитывается по формуле
и характеризует разброс значений, которые могут быть, с достаточным основанием, приписаны измеряемой величине Y.
В случае некоррелированных оценок (x1, x2, …, xN) суммарная стандартная неопределенность вычисляется по формуле
В случае коррелированных оценок x1 , x2 , …, xNuc(y) вычисляется по формуле
где ;
‑ коэффициент корреляции, который является мерой относительной взаимной зависимости двух случайных величин, равной отношению их ковариаций к положительному квадратному корню из произведений их дисперсий. Таким образом, коэффициент корреляции будет равен
Следует отметить, что коэффициент корреляции является числом в диапазоне
-1 ≤ ≤ +1.
Расширенная неопределенность, как величина, определяющая интервал вокруг результата измерения, в пределах которого можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли быть приписаны измеряемой величине, определяется по формуле
U =k×uc(y), (12)
где k – коэффициент охвата – числовой коэффициент, используемый как множитель суммарной стандартной неопределенности для получения расширенной неопределенности.
Коэффициент охвата определяют по формуле:
k = t(νэфф),
где t(νэфф)– коэффициент Стьюдента при числе эффективных степеней свободы νэфф.
Значение νэфф находят по формуле Велча-Статтертвейта:
где νi= n-1 – число степеней свободы для оценивания неопределенности по типу А,
n– число результатов измерений;
νi = ∞ для оценивания по типу В.
Значение коэффициента охвата k выбирается для заданного уровня доверия. В идеале хотелось бы иметь возможность выбрать значение коэффициента охвата k, которое обеспечивало бы интервал
Y = y ± U = y±k×uc(y),
соответствующий выбранному уровню доверия, такому как 0,95 или 0,99. Равным образом, для заданного значения k хотелось бы иметь возможность четко указать уровень доверия, связанный с этим интервалом. Однако это нелегко осуществить на практике, поскольку требуется полное знание закона распределения вероятностей, характеризуемого результатом измерения y и его суммарной стандартной неопределенностью uc(y). Во многих практических случаях при вычислении неопределенностей измерений делают предположение о нормальности закона распределения возможных значений измеряемой величины и полагают: k =2 при уровне доверия p≈ 0,95 или k =3 при уровне доверия p≈ 0,99[1].
Для корректного расчета суммарной стандартной (и расширенной) неопределенности измерений необходимо представлять, из каких составляющих она складывается.
Составляющие неопределенности (погрешности) измерений рассмотрены в [6] и включают:
а) Методические составляющие:
1) составляющие, обусловленные неадекватностью выбранной модели объекта измерений его свойствам;
2) составляющие, обусловленные отклонением от номинальных значений параметров функции, связывающей измеряемую величину с величиной на входе средства измерений;
3) составляющие, обусловленные квантованием по уровню (при использовании средств измерений с аналого-цифровым преобразованием);
4) составляющие, обусловленные вычислительными алгоритмами;
б) Инструментальные составляющие:
1) основная погрешность средства измерений;
2) дополнительные погрешности средства измерений;
3) составляющая, обусловленная вариацией (гистерезисом) средства измерений;
4) составляющая, обусловленная взаимодействием средства измерений с объектом измерений;
5) динамическая составляющая, обусловленная инерционностью средства измерений;
6) составляющие, связанные с отбором и приготовлением проб веществ.
в) Составляющие, обусловленные действиями оператора (субъективные составляющие):
1) составляющие, обусловленные неточностью отсчетов результатов измерений (искажения температурного поля, механические воздействия и т.п.);
2) составляющие, обусловленные воздействием оператора на объект и средства измерений (искажения температурного поля, механические воздействия и т.п.).
Результаты сопоставления количественных оценок погрешности измерений и неопределенности измерений представлены в таблице 1.
Сравнение способов оценки расширенной неопределенности и доверительных границ суммарной погрешности показывает, что:
— для большинства случаев получаемые оценки отличаются незначительно;
— различие проявляется лишь в крайних случаях, когда одна из составляющих (систематическая или случайная, оцененная по типу А или В) существенно превышает другую.
Таблица 1 – Сопоставление количественных оценок погрешности измерений и неопределенности измерений
|
Погрешность измерения |
Неопределенность измерения |
|
СКО, характеризующее случайную погрешность где |
Стандартная неопределенность, оцененная по типу А где |
|
СКО, характеризующее неисключенную систематическую погрешность где k=1,1 при P=0,95 и k=1,4при P=0,99 n>4 |
Стандартная неопределенность, оцененная по типу В В случае неизвестного закона распределения вероятностей наибо-лее распространенный способ формализации неполного знания об измеряемой величине базируется на постулате вероятностного закона распределения (обычно равномерно-го) в указанных (нижней и верхней) границах (а+, а—). При этом стандартная неопределенность, оцененная по типу В, равна uB= Для симметричных границ неисключенных систематических погрешностей (±а) uB= |
|
СКО, характеризующее суммарную погрешность |
Суммарная неопределенность |
Окончание таблицы 1
|
Погрешность измерения |
Неопределенность измерения |
|
Доверительные границы погрешности Упрощенный вариант где t – квантиль распределения Стьюдента |
Расширенная неопределенность UР=kuc, где k – коэффициент охвата (k ≈2 на уровне доверия P=0,95; k ≈3при уровне доверия P=0,99) |
|
Интерпретация результата Интервал (-ΔР; + ΔР) с вероятностью содержит погрешность измерений, что равносильно тому, что интервал (y-ΔР;y + ΔР)содержит истинное значение измеряемой величины |
Интерпретация результата Интервал (y-UР; y + UР) содержит большую долю (Р) распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине |
|
Примечание 1. Полная формула для вычисления доверительных границ погрешности 2. Полный вариант выбора коэффициента охвата k=tP(vэфф), где эффективное количество степеней свободы Значение коэффициента охвата выбирается из специальных таблиц в зависимости от уровня доверия и эффективного количества степеней свободы. |
Указанные границы (отложенные от результата измерения) накрывают истинное значение измеряемой величины с заданной доверительной вероятностью (частотная интерпретация вероятности). В то же время расширенная неопределенность (аналогичный интервал) трактуется в Руководстве как интервал, содержащий заданную долю распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине (субъективная интерпретация вероятности) [4].
Различие между традиционным подходом, использующим понятие «погрешность измерения», и подходом, изложенным в Руководстве, сводится к различию систем координат, относительно которых рассматривают значение измеряемой величины и результат измерений. При рассмотрении погрешности измерений начало системы координат совмещают со значением измеряемой величины, наблюдая рассеяние результата измерений; при рассмотрении неопределенности измерений – с результатом измерений, что и создает эффект рассеяния единственного значения измеряемой величины. Поскольку конкретному результату измерений соответствует совокупность возможных значений измеряемой величины, каждое из которых удовлетворяет условию: сумма возможного значения измеряемой величины и соответствующей ему реализации погрешности измерений должна быть равна результату измерений, закон распределения вероятностей возможных значений измеряемой величины определяется законом распределения вероятностей погрешности измерений.
Если характеристики погрешности измерений – это параметр центрированной случайной величины, представляющей собой разность между результатом измерений и значением измеряемой величины, то неопределенность измерений в соответствии с Руководством может быть определена как параметр центрированной случайной величины, представляющей собой разность между возможным значением измеряемой величины и результатом измерений, т.е. величины, совпадающей по модулю с погрешностью измерений, но противоположной ей по знаку. Закон распределения этой случайной величины представляет собой зеркальное отражение закона распределения вероятностей погрешности измерений.
Поскольку характеристики погрешности и неопределенность измерений определяются на основе второго центрального момента, нечувствительного к знаку случайной величины, количественно характеристики погрешности измерений и соответствующие виды неопределенности измерений совпадают [6].
На рисунке 1 изображена плотность вероятностей φ(aP), характеризующая распределение результата измерений aP, которую можно одновременно рассматривать и как плотность вероятностей φ(ΔИ) абсолютной погрешности измерений ΔИ, если перенести начало координат в точку, соответствующую истинному значению измеряемой величины Аист.
Рисунок 1 ‑ Плотность вероятностей φ(aP), характеризующая
распределение результата измерений aP
Представим наблюдателя, который всякий раз будет располагаться в точке числовой оси, соответствующей очередной реализации Аpi результата измерений, и наделим его способностью наблюдать на числовой оси истинное значение измеряемой величины Аист. В точке Ap1 он будет видеть Аист слева, в точке Ap2 ‑ справа, в точке Ap3 ‑ близко от себя, в точке Ap4 ‑ далеко. Он будет наблюдать Аист как случайную величину, закон распределения которой определяется законом распределения погрешности измерений.
Для более четкого понимания поместим наблюдателя в своего рода «инерциальную» систему координат, жестко привязанную к результату измерений, в которой наблюдатель остается «неподвижным». Чтобы подчеркнуть, что размер рассматриваемой измеряемой величины неизменен (фиксирован), наделим наблюдателя способностью видеть истинное значение измеряемой величины вместе с числовой осью истинных значений, которая в системе координат наблюдателя будет занимать, как это мы выяснили из рисунка 1, случайное положение. Тогда рисунок 1 трансформируется в рисунок 2, где Аистi – «реализации» истинного значения измеряемой величины в системе координат наблюдателя.
Набрав необходимую статистику, наблюдатель обнаружит, что наблюдаемый им закон распределения φ(aист) истинного значения измеряемой величины aист представляет собой зеркальное отражение закона распределения результата измерений или, с точностью до математического ожидания – закона распределения погрешности измерений.
Для симметричных законов распределения свойство «зеркальности» не имеет значения. Иллюстрация «зеркальности» для несимметричного закона распределения приведена на рисунке 3 [8].
Рисунок 2 ‑ Плотность вероятностей φ(aист), характеризующая
распределение результата измерений aист
Рисунок 3 ‑ Несимметричный закон распределения
1.2 Требования к точности измерений и описание методик измерений
Требования к точности измерений в методиках измерений приводят путем задания показателей точности и ссылки на документы, в которых эти значения установлены.
При описании требований к выражению погрешности и неопределенности измерений, выполненных с использованиемтеории шкал, применяют положения рекомендаций по межгосударственной стандартизации РМГ 83-2007 «ГСИ. Шкалы измерений. Термины и определения» с учетом особенностей конкретных шкал измерений.
Методы и средства измерений выбирают в соответствии с документами, относящимися к выбору методов и средств измерений данного вида, а при отсутствии таких документов – в соответствии с общими рекомендациями по метрологии МИ 1967-89 «ГСИ. Выбор методов и средств измерений при разработке методик выполнения измерений. Общие положения».
Если методика измерений предназначена для использования всфере государственного регулирования обеспечения единства измерений, то применяемые средства измерений и стандартные образцы должны быть утвержденных типов, внесенные в Государственный реестр СИ (стандартных образцов), поверенные, с не истекшим межповерочным интервалом; испытательное оборудование должно быть аттестовано.
Требования к точности измерений устанавливают с учетом всех составляющих погрешности (методической, инструментальной, вносимой оператором, возникающей при отборе и приготовлении пробы и др.).
Если полученное значение погрешности измерений выходит за заданные пределы, то погрешность измерений может быть уменьшена в соответствии с рекомендациями по межгосударственной стандартизации РМГ62-2003 «ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Оценивание погрешности измерений при ограниченной исходной информации».
Показатели точности измерений должны соответствовать исходным данным на разработку методики измерений.
Планирование экспериментов по оценке характеристик погрешности методик измерений состава и свойств веществ и материалов и выбор способов экспериментальной оценки этих характеристик проводят в соответствии с ГОСТ Р ИСО 5725-1 ‑ ГОСТ Р ИСО 5725-6, неопределенности ‑ в соответствии с руководством ЕВРАХИМ/СИТАК «Количественное описание неопределенности в аналитических измерениях».
В документе, регламентирующем методику измерений, указывают [5]:
— наименование методики измерений;
— назначение методики измерений;
— область применения;
— условия выполнения измерений;
— метод (методы) измерений;
— допускаемую и (или) приписанную неопределенность измерений или норму погрешности и (или) приписанные характеристики погрешности измерений;
— применяемые средства измерений, стандартные образцы, их метрологические характеристики и сведения об утверждении ихтипов;
— операции при подготовке к выполнению измерений, в том числе по отбору проб;
— операции при выполнении измерений;
— операции обработки результатов измерений;
— требования к оформлению результатов измерений;
— процедуры и периодичность контроля точности получаемых результатов измерений;
— требования к квалификации операторов;
— требования к обеспечению безопасности выполняемых работ;
— требования к обеспечению экологической безопасности;
— другие требования и операции (при необходимости).
1.3 Основные этапы расчета погрешности и неопределенности измерений
Порядок расчета неопределенности измерений сводится к следующим этапам:
а) составление уравнения измерения, характеризующего измерительный процесс;
б) определение источников неопределенности для каждой входной величины, составление перечня источников и соответствующих им составляющих неопределенности измерений;
в) исследование возможности оценивания каждого источника по типу А или по типу В;
г) определение предполагаемого закона распределения для неопределенностей типа В;
д) расчет стандартных неопределенностей и составление бюджета (таблица) стандартных неопределенностей. (Составление бюджета неопределенности это всегда процесс творческий. Количество компонентов – источников неопределенности – может быть разное, в зависимости, прежде всего, от необходимого уровня точности измерения. Обычно для рабочих средств измерения в бюджет включают значительно меньше компонентов, чем в случае прецизионных средств измерений);
е) расчет суммарной и расширенной неопределенности измерения.
Этапы расчета погрешности измерений:
а) составление уравнения измерения, характеризующего измерительный процесс;
б) определение источников погрешности измерений для каждой входной величины, составление перечня источников и соответствующих им составляющих погрешности измерений;
в) формирование исходных данных для расчета погрешности;
г) количественная оценка составляющих погрешности, приведенных к одной и той же точке измерительной схемы;
д) объединение (суммирование) составляющих погрешности измерений, получение результирующей (суммарной) характеристики качества измерений [6].
1.4 Методы оценивания неопределенности измерений
Существует несколько методов оценивания неопределенности измерений, такие как метод, изложенный в ИСО/МЭК «Руководство по выражению неопределенности измерений (GUM)»; экспериментальный метод; метод Монте-Карло (подробнее данный метод рассмотрим в п. 2) и другие.
Процедура оценивания неопределенности измерений по GUM состоит из следующих этапов:
а) Выражают связь между измеряемой величиной Y и входными величинами Xi, от которых она зависит, в виде функциональной зависимости . Функция f должна содержать все величины, включая поправки и поправочные коэффициенты, которые могут существенно повлиять на неопределенность результата измерения;
б) Получают оценку xiвходной величины Xiлибо на основе статистического анализа ряда наблюдений, либо другими способами (к ним относятся величины, связанные с аттестованными эталонами, стандартными образцами веществ или материалов, и величины, значения которых указаны в справочниках);
в) Оценивают стандартную неопределенность u(xi) каждой входной оценки xi. При оценивании стандартной неопределенности по типу А используют формулу (7), по типу В – формулу (8).
г) Если среди входных величин есть коррелированные между собой, то оценивают их ковариации согласно формуле (11);
д) Рассчитывают результат измерения, т.е. находят оценку измеряемой величины у по функциональной зависимости f, используя в качестве аргументов Xi оценки xi, полученный на этапе б;
е) Определяют суммарную стандартную неопределенность uс(y) результата измерения у по стандартным неопределенностям и ковариациям входных оценок по формулам (9) и (10);
ж) Если требуется знать расширенную неопределенность U для определения интервала от у-U до у+U, в пределах которого, предположительно, находится большая часть распределения значений, которые можно с достаточным основанием приписать измеряемой величине Y, то суммарную стандартную неопределенность uс(y) умножают на коэффициент охвата k, обычно принимающий значения в диапазоне от 2 до 3, чтобы получить значение U по формуле (12);
и) Представляют результат измерения у вместе с его суммарной стандартной неопределенностью uс(y)или расширенной неопределенностью U.
Если мерой неопределенности результата измерения является суммарная стандартная неопределенность uс(y), то при представлении результата измерения необходимо:
— дать подробное определение измеряемой величины Y,
— привести оценку у измеряемой величины Y и суммарной стандартной неопределенности uс(y) с указанием единиц измерений,
— при необходимости указать относительную суммарную стандартную неопределенность uс(y)/|y|, у≠0.
Если мерой неопределенности результата измерения является расширенная неопределенность U, то при представлении результата измерения необходимо:
— дать подробное определение измеряемой величины Y,
— указать результат измерения в виде Y=yU с указанием единиц измерений для у и U,
— при необходимости указать относительную расширенную неопределенность U/|y|, у≠0,
— указать использованное для получения расширенной неопределенности значение k,
— указать приблизительный уровень доверия для интервала yU и пояснить, как он был определен.
Схематично последовательность оценивания неопределенности измерений по GUM представлена на рисунке 4 [2].
Рисунок 4 — Схема последовательности вычисления неопределенности
измерений
Экспериментальный метод оценивания неопределенности разделяется на два подхода:
а) использование данных внутрилабораторных исследований по разработке и оценки пригодности метода;
б) использование данных межлабораторных исследований.
Внутрилабораторные исследования, проводимые при разработке и оценки пригодности метода, сводятся к определению характеристик эффективности (прецизионность, правильность, нелинейность, порог чувствительности, повторяемость). При оценивании неопределенности на основе полученных при этом данных используют:
— наиболее достоверную из имеющихся оценок общей прецизионности;
— наиболее достоверную имеющуюся оценку правильности и неопределенности (смещение нужно для введения поправки, неопределенность для оценки неопределенности);
— оценки любых неопределенностей, связанные с теми факторами, которые недостаточно полно отражены в установленных характеристиках эффективности.
Оценка прецизионности должна охватывать, по возможности, длительный период времени и учитывать естественное варьирование всех факторов, влияющих на результат. Эта оценка может представлять собой:
— стандартное отклонение результатов для типичной пробы, проанализированной, насколько возможно, разными аналитиками и на разных приборах в течение определенного периода времени;
— стандартное отклонение, полученное по результатам повторных определений, выполненных на каждой из нескольких проб в разное время;
— оценки дисперсии для каждого из влияющих факторов, получаемых с применением планов многофакторного эксперимента методами дисперсионного анализа.
Прецизионность – степень близости друг к другу результатов испытаний в одной лаборатории, полученных в конкретных регламентированных условиях.
Существует два случая прецизионности: повторяемость и воспроизводимость.
Прецизионность в условиях повторяемости:
— одна и та же методика,
— идентичные пробы,
— одинаковые условия,
— параллельные измерения (одновременно).
Прецизионнность в условиях воспроизводимости:
— одна и та же методика,
— разные условия (разные аналитики, партии реактивов одного типа, наборы мерной посуды, экземпляры средств измерений одного типа, лаборатории),
— разное время.
Количественными оценками прецизионности являются:
а) стандартное отклонение повторяемости – СКО результатов испытаний в одной лаборатории, полученных по методике в условиях повторяемости:
где — выборочное СКО результатов единичного анализа, полученных вi-ой лаборатории, которое определяется по формуле:
На основе расчета значений в m-ом образце проверяют гипотезу о равенстве генеральных дисперсий, используя критерий Кохрена:
б) предел повторяемости – допускаемое для принятой вероятности 95 % абсолютное расхождение между наибольшими наименьшим из n результатов испытаний в одной лаборатории, полученных в условиях повторяемости:
для P=0,95.
в) стандартное отклонение воспроизводимости – СКО результатов анализа, полученных в условиях воспроизводимости:
где Xm – среднее арифметическое результатов анализа, полученных в L лабораториях, которое определяется по формуле:
г) предел воспроизводимости — допускаемое для принятой вероятности 95% абсолютное расхождение между наибольшими наименьшим из n результатов единичного анализа, полученных в условиях воспроизводимости:
где коэффициент k=1,2;…; 2,0, учитывающий условия проведения эксперимента, для P=0,95 .
Для того чтобы оценить показатель правильности методики измерений необходимо:
а) Рассчитать оценку математического ожидания систематической погрешности методики анализа:
где — среднее значение результатов анализа; ‑ аттестованное значение m-го образца.
б) Проверить значимость вычисленных значений по критерию Стьюдента, вычисляя
где ‑ погрешность аттестованного значения m-го образца.
Значение определяется по формуле
Если условие выполняется, то Θпринимается равным нулю. Если условие не выполняется, то вводят дополнительное условие:
|Θ| ≤ ξσRm,
где ξ = 0,5; …; 1, в зависимости от условий, средств измерений и характеристик объекта анализа.
Стандартная неопределенность с использованием показателей правильности и прецизионности вычисляется согласно ISO 21748:2010 «Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений».
Основная модель [9]:
где m – общее среднее;
В – лабораторная составляющая систематического сдвига в условиях повторяемости с нулевым средним значением и стандартным отклонением σL;
е – случайная погрешность лаборатории, распределенная нормально с нулевым средним значением и стандартным отклонением σW.
Исходя из этого выражения, неопределенность y будет равна:
где — оценка межлабораторного стандартного отклонения, равная значению ;
u(e) – оценка стандартного отклонения повторяемости, равная значению Sr, которое определяется по формуле
Так как – оценка дисперсии воспроизводимости, то
Если в модель включаются данные правильности, то она принимает следующий вид:
где ‑ опорное значение;
δ – систематический сдвиг метода.
Отсюда:
где — неопределенность, соответствующая сертифицированному значению , используемому для оценки правильности при совместном исследовании метода;
— оценка стандартного отклонения смещения, причем
где L – количество лабораторий;
n – количество повторений в каждой лаборатории.
Если y=f(x1, x2, … , xm)и существуют отклонения от номинальных значений xi, не учитываемые в процессе совместного исследования, то объединенная модель будет иметь следующий вид:
где — коэффициент чувствительности, определяемый по формуле
Неопределенность результата измерений в этом случае будет равна:
2 АНАЛИЗ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ МЕТОДОМ МОНТЕ-КАРЛО И СРАВНЕНИЕС МЕТОДОМ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ GUM
2.1 Метод Монте-Карло
2.1.1 Возникновение метода Монте-Карло и его общая характеристика
В 1930-х годах Энрико Ферми (Италия), а затем и Джон фон Нейман и Станислав Улам в 1940-х в Лос-Аламосе (США) предположили, что связь между стохастическими (случайными) процессами и дифференциальными уравнениями можно использовать «в обратную сторону». Они предложили воспользоваться стохастическим подходом для аппроксимации многомерных интегралов в уравнениях переноса, возникших в связи с задачей движения нейтрона в изотропной среде.
Идея была развита Станиславом Уламом, который раскладывал пасьянс и заинтересовался вопросом: «Какова вероятность того, что пасьянс сложится?» Вместо того, что бы использовать обычные комбинации, он предположил, что можно поставить эксперимент множество раз и оценить вероятность, подсчитав число удачных попыток.
Годом рождения метода Монте-Карло является 1949 год, когда была опубликована статья Николаса Метрополиса и Станислава Улама «Метод Монте-Карло». Название метода происходит от названия города в княжестве Монако, широко известного своими многочисленными казино, ведь именно рулетка является одним из самых известных генераторов случайных чисел. Станислав Улам пишет в своей автобиографии «Приключения математика», что название было предложено Николасом Метрополисом в честь его дяди, который был азартным игроком.
При расчете неопределенности измерений метод Монте-Карло (ММК) используется как метод трансформирования распределений на основе моделирования случайных выборок из этих распределений [3].
Этот метод может быть применен к любым моделям, имеющим единственную выходную величину, в которых входные величины характеризуются любыми заданными функциями распределения вероятностей.
Поскольку ММК требует проведения большого числа испытаний, его часто называют методом статистических испытаний.
В большинстве случаях оценивания неопределенности измерений ММК используется, когда:
— вклад разных составляющих неопределенности существенно неодинаков;
— распределение выходной величины не является нормальным или масштабированным смещенным t — распределением;
— трудно найти частные производные от функции измерения, как того требует закон трансформирования неопределенностей;
— модель достаточно сложная;
— плотности распределения вероятностей входных величин асимметричны;
— оценка выходной величины и соответствующая стандартная неопределенность имеют приблизительно равные значения.
2.1.2 Применение метода Монте-Карло
Для применения ММК необходимо выбрать число испытаний М, то есть число наблюдений выходных значений модели. Это число может быть выбрано до проведения испытаний, но тогда будет исключена возможность управления точностью результатов, полученных с помощью данного метода. Причиной является то, что число испытаний, необходимое для получения результата вычисления с заданной точностью, зависит от формы плотности распределения вероятностей выходной величины и от заданного значения вероятности охвата. Кроме того, метод вычисления является стохастическим по своей природе, поскольку зависит от случайной выборки.
Реализация метода Монте-Карло представлена на рисунке 5.
Рисунок 5 — Реализация ММК
2.1.3 Оценка входной величины
Необходимо выбирать M ‑ количество оцениваний модели, которое необходимо произвести. Лучше всего выбирать достаточно большие значение М (например, превышающие в 104 раз) по сравнению с 1/(1-p). Тогда можно ожидать, что функция распределения G обеспечит приемлемое дискретное представление GY(η) (функции распределения для Y) вблизи границ 100 p %-ного интервала охвата для Y.
Для применения метода формируют М векторов xr,r=1,…, M в соответствии с плотностями распределения вероятностей gXi(ξi) для Nвходных величин Xi или, если это необходимо, из совместной плотности распределения gX (о).
Модель оценивается для каждого из М извлечений из функции плотности вероятности (ФПВ) для N входных величин. Конкретнее, необходимо обозначить M извлечений через x1, …, xM, где r-е значение xr состоит из случайных значений x1,r, …, xN,r, а xi,r ‑ случайное значение из ФПВ для Xi. Тогда значения модели можно представить в виде:
yr = f(xr), r = 1, …, M.
Дискретное представление G функции распределения GY(η) для выходной величины Y может быть получено следующим образом:
а) необходимо рассортировать значения модели yr, r = 1, …, M, полученные по ММК, в неубывающем порядке. Обозначить рассортированные значения модели как y(r), r = 1, …, M;
б) если необходимо, создать возмущения для любых дублирующих значений модели y(r) так, чтобы конечный полный набор y(r), r = 1, …, M, формировал строго возрастающую последовательность;
в) полученная последовательность y(r), r = 1, …, M определяет G.
Если выходная величина Y будет рассматриваться как входная величина при оценивании неопределенности другого измерения, то выборку из ее распределения легко получить случайным (равновероятным) выбором значений из y(r), r = 1, …, M.
Последовательность y(r) (или yr) может быть скомпонована в гистограмму (при подходящей ширине ячеек) и представлять собой частотное распределение, которое, при условии, что оно нормировано, чтобы иметь единичную площадь, обеспечивает приближение к ФПВ gY(η) для Y. Вычисления характеристик распределения обычно проводятся не в терминах этой гистограммы, разрешение которой зависит от выбора ширины ячеек, а в терминах G. Тем не менее, гистограмма может быть полезна для понимания природы ФПВ, например степени ее асимметрии.
В ряде случаев полезна аппроксимация GY(η) непрерывной функцией.
2.1.4 Оценка выходной величины
В качестве оценки выходной величины Y используется выборочное среднее:
а в качестве оценки ее стандартной неопределенности u(y) – выборочное стандартное отклонение
При некоторых особых обстоятельствах, когда одной из входных величин приписано t-распределение с числом степеней свободы менее трех, математическое ожидание и стандартное отклонение Y, описываемой ФПВ gY(η), могут не существовать. Формулы (14) и (15) могут не обеспечить получение содержательных результатов. Однако интервал охвата для Y может быть сформирован, т. к. G имеет смысл и может быть определена.
2.1.5 Интервал охвата для выходной величины
Пусть q = pM, если pM ‑ целое число. В противном случае в качестве q можно выбрать целую часть (pM+1/2). Тогда [ylow, yhigh] ‑ это100p % интервал охвата для Y, где для любого r из ряда r = 1, …, (M – q),ylow= y(r) и yhigh= y(r+q). Вероятностно симметричный 100p % интервал охвата можно получить, взявr = (M − q)/2, если (M − q)/2 — целое число, r=int[(M− q + 1)/2] ‑ в противном случае.
Для нахождения наименьшего 100p % интервала охвата задается определение r* ,чтобы, что для r = 1, …, M – q выполнялось неравенство:
y(r*+ q) – y(r*) ≤ y(r+q) – y(r).
Из-за стохастичности в ММК некоторые из протяженностей этихM-q интервалов могут быть короче, чем они будут в среднем, а некоторые ‑ длиннее. Таким образом, при выборе такой наименьшей протяженности (аппроксимация) к наикратчайшему 100p % интервалу охвата имеет тенденцию быть, по крайней мере, меньше, чем при вычислении из GY(η), приводя к тому, что типичная вероятность охвата меньше, чем 100p %. Однако для больших М этим отличием можно пренебречь.
2.1.6 Адаптивная реализация метода Монте-Карло
Суть адаптивной процедуры состоит в последовательном увеличении числа испытаний до тех пор, пока полученные числовые оценки статистических характеристик не станут установившимися. Численный результат считается установившимся, если соответствующее ему удвоенное стандартное отклонение станет меньше заданной точности вычисления стандартной неопределенности u(y) [3].
Пусть ndig ‑ число десятичных знаков, рассматриваемых как значащие в числовом представлении величины z. Предел погрешности вычисления δ, в таком случае, определяется следующим образом:
а) выражают значениеz в виде c*10l, где с ‑ это целое от ndig десятичных знаков, а l ‑ целое число;
б) δ определяют по формуле:
δ (15)
Практический подход, включающий проведение последовательных применений ММК заключается в следующем:
а) необходимо задать ndig;
б) задают M = max(J, 104), где J ‑ наименьшее целое, которое больше или равно 100/(1 — p);
в) задают h = 1 (счетчик итераций ММК);
г) проводят M испытаний методом Монте-Карло;
д) используют M полученных на выходе модели значений y1, …, yM, для вычислений h-й оценки y(h)величины Y, ее стандартной неопределенности u[y(h)], левой и правой границ 100p % интервала охвата;
е) еслиh = 1, то увеличивают h на единицу и возвращаются к шагу г);
ж) вычисляют выборочное стандартное отклонение sy, связанное со средним оценок y(1), …, y(h) величины Y, задающееся как:
и) аналогичным образом вычисляют выборочное стандартное отклонение для средних значений оценок u(y),,;
к) используют далее все hM доступные значения модели для вычисления u(y);
л) определяют предел погрешности δ, связанной с u(y);
м) если хотя бы одно из значений 2sy, 2su(y),или превышает δ, необходимо увеличить h на единицу и вернуться к шагу г);
н) если возврата к этапу г) не произошло, и значения всех вычисляемых значений можно считать установившимися, то на основе hM полученных значений выходной величины вычисляют y, u(y) и 100p% интервал охвата.
Обычно на этапе а) выбирается ndig=1 или ndig=2.
На этапе ж) y может рассматриваться как реализация случайной величины со стандартным отклонением sy.
В ситуациях, где интервал охвата не требуется, проверка стабилизации вычислений на этапе м) может быть основана вместо этого только на 2sy и 2su(y).
Альтернативный неадаптивный подход для симметричного интервала охвата при вероятности 95 %, основанный на использовании статистик биноминального распределения, состоит в следующем. Выбирают М = 105 или М= 106. Формируется интервал [y(r), y(s)], где для М = 105, r= 2420 и s=97581, а для М = 106, r= 24747 и s= 975254. Этот интервал ‑ 95 % статистический интервал охвата при уровне доверия 0,99, т. е. вероятность охвата будет не менее 95 % в, как минимум, 99 % применений ММК. Средняя вероятность охвата такого интервала будет (s− r)/(M + 1), что превышает 95 % на величину, которая становится меньше при возрастании M, а именно, 95,16 % для М = 105 и 95,05 % для М = 106.
Эти результаты могут быть распространены на другие значения вероятности охвата (и другие значения M).
В результате применения адаптивной процедуры должны быть определены:
а) оценка y величины Y,
б) соответствующая стандартная неопределенность u(y);
в) границы ylow и yhigh интервала охвата для Y, соответствующего заданной вероятности охвата.
При этом каждая из этих четырех величин должна удовлетворять требуемой числовой точности.
При применении данной процедуры следует учитывать, что из-за своей стохастической природе процедура не может безусловно гарантировать выполнение требования к точности вычислений.
2.1.7 Преимущества и недостатки метода Монте-Карло
Проанализируем недостатки и преимущества численного метода вычисления неопределенности на основе метода Монте-Карло.
Преимущества:
а) возможна оценка любых статистических характеристик результата измерения Y, а не только стандартного отклонения;
б) возможность поэтапного оценивания неопределенности, когда выход одной модели служит входом другой модели (допускается любое количество таких этапов);
в) применимость для любых типов математических моделей результатов измерений, как линейных, так и нелинейных (не нужно определять необходимое количество членов ряда Тейлора для аппроксимации функции f);
г) неопределенность входных величин может быть сколь угодно велика;
д) нет необходимости знать или делать предположения о виде закона распределения выходной величины Y математической модели результата измерения;
е) не нужно делать никаких допущений о симметричности законов распределения, как входных величин, так и выходной, либо приводить входные величины к симметрично распределенным;
ж) нет необходимости оценивать коэффициенты чувствительности (частные производные первого порядка);
и) нет необходимости вычислять число эффективных степеней свободы по формуле Велча-Статерсвейта;
к) вычислительная сложность определяется числом М реализаций входных величин и временем вычисления функции f.
Недостатки:
а) необходимо иметь эффективные генераторы псевдослучайных чисел с длинным периодом;
б) сложные модели могут требовать много вычислительного времени для М реализаций;
в) коэффициенты чувствительности математической модели не могут быть получены;
г) математическая модель должна быть численно стабильной в связи с оцениванием не только в окрестности приписанного значения, но и на всех интервалах всех распределений входных величин [7].
Анализ недостатков:
а) любые современные математические программные пакеты содержат в себе ГПСЧ с длинным периодом (>> 106);
б) это не критично при расчете на ПЭВМ с помощью математических программных пакетов и, особенно, с использованием специализированного ПО, например, «Неопределенность 1.5» (демо-версия программы доступна на сайте http://www.novikov.biz.ua);
в) для работы алгоритма ММК не требуется знания коэффициентов чувствительности модели;
г) данный недостаток можно рассматривать, только если сама математическая модель измерения оценивалась численно.
2.2 Сравнение метода оценивания неопределенности GUM и метода Монте-Карло
Для целей сравнения оценивания неопределенности GUM и ММК полезно сделать обзор соображений GUM, касающихся оценивания неопределенностей по типу А и по типу В. Для оценивания по типу А GUM предоставляет руководство для получения наилучшей оценки величины и соответствующей стандартной неопределенности из среднего и связанного с ним стандартного отклонения набора показаний величины, полученных независимо.
Для оценивания по типу В используются априорные знания, касающиеся величины, чтобы охарактеризовать ее с помощью функции плотности вероятности (ФПВ), из которой определяется наилучшая оценка величины и стандартная неопределенность, связанная с этой оценкой. GUM утверждает, что оба типа оценивания базируются на распределениях вероятностей и что оба подхода используют общепризнанные трактовки вероятностей.
GUM рассматривает ФПВ как фундамент оценивания неопределенности: в контексте закона распространения неопределенности он ясно ссылается на входные и выходную величины как описываемые или характеризуемые распределениями вероятностей.
Метод оценивания неопределенности GUM не определяет явно ФПВ для выходной величины. Однако на распределение вероятностей, используемое этим методом для определения характеристик выходной величины, иногда ссылаются как на «предусмотренное» или «следующее из» метода оценивания неопределенности GUM.
Так как метод оценивания неопределенности GUM явно использует только наилучшие оценки xi и связанные с ними стандартные неопределенности (а также ковариации и степени свободы, где это необходимо), он ограничен в информации, которую может предоставить о ФПВ для Y. По-существу, он ограничен предоставлением оценки y для Y и соответствующей стандартной неопределенности u(y), связанной с y, а также, возможно, связанных с ними (эффективных) степеней свободы.
Значения y и u(y) будут обоснованны для модели, которая линейна по X. Любая другая информация об Y, например интервалы охвата, получается с помощью дополнительных предположений о том, к примеру, что распределение для Y нормальное или масштабированное и сдвинутое t-распределение.
Некоторые преимущества ММК таковы:
a) уменьшение аналитических работ, требуемых для усложненных или нелинейных моделей, (так как частные производные первого или более высоких порядков, необходимые для представления коэффициентов чувствительности в законе распространения неопределенности, не требуются);
б) улучшенная, в общем случае, оценка Y для нелинейных моделей;
в) улучшенная стандартная неопределенность, связанная с оценкой Y для нелинейных моделей, особенно когда Xi приписываются не гауссовские (например, асимметричные) ФПВ, без необходимости получать производные более высоких порядков;
г) предоставление интервала охвата, соответствующего оговоренной вероятности охвата, когда ФПВ для Y не может быть адекватно аппроксимирована нормальным распределением или масштабированным и сдвинутым t-распределением, т. е. когда центральная предельная теорема неприменима. Такая неадекватная аппроксимация может возникнуть, когда ФПВ, приписанная доминирующей Xi, не является распределением Гаусса или масштабированным и сдвинутым t-распределением, модель не линейна или ошибка аппроксимации, возникающая при использовании формулы Велча-Саттертвейта для эффективных степеней свободы, не является пренебрежимо малой;
д) при определении интервала охвата не требуется нахождение значения коэффициента охвата.
Проанализировав свойства ММК и метода оценивания неопределенности GUM, можно прийти к выводу, что описанный метод Монте-Карло является практической альтернативой методу оценивания неопределенности GUM.
ММК имеет преимущества, когда:
а) линеаризация модели измеряемой величины не обеспечивает адекватного представления;
б) функция плотности вероятностей для выходной величины заметно отклоняется от распределения Гаусса или масштабированного и сдвинутого t-распределения, например, из-за явной асимметрии.
В случае a) оценка выходной величины и соответствующей стандартной неопределенности, полученные при оценивании неопределенности GUM, могут оказаться ненадежными.
В случае б) результатом могут стать нереалистичные интервалы охвата (обобщение «расширенной неопределенности» в оценивании неопределенности GUM).
3 КОЛИЧЕСТВЕННОЕ СРАВНЕНИЕ РЕЗУЛЬТАТОВ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ МЕТОДАМИ GUM И МОНТЕ-КАРЛО
Для количественного сравнения результатов оценивания неопределенности измерений методами GUM и Монте-Карло оценим неопределенность измерения объемного расхода природного газа в трубопроводе в рабочих условиях.
Объемный расход определяется по формуле из ГОСТ 8.586.1-2005(п. 5.1):
где d – диаметр отверстия сужающего устройства, м;
KШ – поправочный коэффициент, учитывающий шероховатость внутренней поверхности трубопровода;
KП – поправочный коэффициент, учитывающий притупление входной кромки диафрагмы;
С – коэффициент истечения;
Е – коэффициент скорости входа;
‑ коэффициент расширения среды;
‑ плотность среды, кг/м3;
Δp – перепад давления на диафрагме, Па.
Для упрощения расчетов предположим, что природный газ состоит исключительно из метана (т.е. примеси отсутствуют) и примем =0,668 кг/м3; KШ=1; KП=1; С =0,6050; Е=1,1426; =0,9964 (для следующих условий: t=20 oС; p=101,3 кПа).
Пусть , тогда .
Так как A=0,6619 (м3/кг)1/2, .
Рассчитаем неопределенность измерения методом GUM.
Базовый алгоритм оценивания неопределенности:
а) записываем модельное уравнение
б) входные величины равны:
x1 = (0,0800±0,0002) м,
x2 = (16,00±0,32)*103 Па;
в) вычисляем оценку результата измерения:
y=0,7578 м3/с;
г) вычисляем стандартные неопределенности входных величин:
— вычисление стандартной неопределенности по типу В проводим для симметричных границ по формуле
— вычисление вкладов неопределенности входных величин u(xi) и неопределенности измеряемой величины:
u(yi) =ciu(xi),
где сi – коэффициент чувствительности.
Коэффициенты чувствительности сi находят как частные производные выходной величины y по каждой из входной величин xi:
Коэффициенты чувствительности будут равны:
Вклад неопределенности измерения диаметра в неопределенность объемного расхода будет равен:
Вклад неопределенности измерения перепада давления в неопределенность объемного расхода будет равен:
3) Определяем суммарную стандартную неопределенность. Так как величины некоррелированы, то суммарная стандартная неопределенность рассчитывается по формуле:
4) Рассчитываем расширенную неопределенность по формуле:
где k – коэффициент охвата (в данном случае k=2).
е) Записываем результат измерения
Рассчитаем неопределенность измерения объемного расхода природного газа методом Монте-Карло.
а) Генерируем 2 массива случайных чисел (для входных величин d и Δp) объемом M=, подчиняющихся равномерным законам распределения с помощью программы STATGRAPHICS Plus v 5.0.
Фрагменты массивов полученных данных представлены на рисунках 6.1 и 6.2 (d– Col_1, Δp ‑Col_2).
Рисунок 6.1 – Массивы входных данных
Рисунок 6.2 – Массивы входных величин
б) Получаем массив оценки выходной величины qv (на рисунке 7 – Col_3). Сортировка массива по возрастанию и построение гистограммы выполнены в той же программе.
Рисунок 7 ‑ Массив оценки выходной величины qv
Гистограмма распределения выходной величины представлена на рисунке 8.
Рисунок 8 – Гистограмма распределения выходной величины
в) Вычисляем оценки параметров полученного распределения:
— математическое ожидание :
-
суммарная стандартная неопределенность:
-
расширенная неопределенность:
-
коэффициент охвата:
k=0,0182/0,0049=3,7.
г) Записываем результат измерения:
Сравним результаты измерения, полученные методами GUM и Монте-Карло:
Числовые значения результата измерений, полученные обоими методами, одинаковы. Значения расширенной неопределенности измерений отличаются существенно, причем значение, полученное по ММК, в 1,8 раза больше, чем по GUM, за счет того, что закон распределения результата измерений явно отличен от нормального (см. рисунок 8). Расчет по ММК требует больше времени (в основном, за счет большой продолжительности сортировки массива результатов измерений), но может выполняться менее квалифицированным персоналом, так как не требуется находить частные производные модели результата измерений.
Сформулируем основные преимущества оценивания неопределенности измерений методом Монте-Карло:
-
возможна оценка любых статистических характеристик результата измерения Y, а не только стандартного отклонения;
-
возможность поэтапного оценивания неопределенности, когда выход одной модели служит входом другой модели (допускается любое количество таких этапов);
-
применимость для любых типов математических моделей результатов измерений, как линейных, так и нелинейных (не нужно определять необходимое количество членов ряда Тейлора для аппроксимации функции f);
-
неопределенность входных величин может быть сколь угодно велика;
-
нет необходимости знать или делать предположения о виде закона распределения выходной величины Y математической модели результата измерения;
-
не нужно делать никаких допущений о симметричности законов распределения как входных величин, так и выходной, либо приводить входные величины к симметрично распределенным;
-
нет необходимости оценивать коэффициенты чувствительности (частные производные первого порядка);
-
нет необходимости вычислять число эффективных степеней свободы по формуле Велча-Саттертвейта;
-
вычислительная сложность определяется числом М реализаций входных величин и временем вычисления функции f с последующей сортировкой массива данных.
Проанализировав метод Монте-Карло и метод оценивания неопределенности GUM, можно прийти к выводу, что описанный метод Монте-Карло является практической альтернативой методу оценивания неопределенности GUM, во многих случаях более прост в применении и обеспечивает высокую достоверность оценивания неопределенности измерений.
Заключение
Результатом данной аттестационной работы стало выяснение различий между понятиями «погрешность измерений» и «неопределенность измерений», сравнение результатов оценки неопределенности измерений методом Монте-Карло и расчетным методом, изложенным в ИСО/МЭК «Руководство по выражению неопределенности измерений (GUM)».
В ходе сравнения результатов оценивания неопределенности измерений методом Монте-Карло и методом, изложенным в ИСО/МЭК «Руководство по выражению неопределенности измерений (GUM)», был сделан вывод о том, что метод Монте-Карло является практической альтернативой методу оценивания неопределенности GUM, во многих случаях более прост в применении и обеспечивает высокую достоверность оценивания неопределенности измерений.
Список использованных источников
-
Захаров И. П. Теория неопределенности в измерениях. / И. П. Захаров, В. Д. Кукуш. ‑ Харьков: Консум, 2002. ‑ 256 с.
-
РМГ 43-2001 ГСИ. Применение «Руководства по выражению неопределенности измерений».
-
ГОСТ Р54500.3.1 – 2011/Руководство ИСО/МЭК 98-3:2008 «Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения. Дополнение 1. Трансформирование распределений с использованием метода Монте-Карло».
-
Артемьев Б.Г. Метрология и метрологическое обеспечение. М.: Стандартинформ, 2010.‑568 с.
-
ГОСТ Р 8.563- 2009. ГСИ. Методики (методы) измерений
-
ПМГ 96-2009.ГСИ. Результаты и характеристики качества измерений. Формы представления.
-
Новиков В.В. Численные методы в вычислении неопределенности. / В. В. Новиков // Системи обробки інформації. – Харків, 2008. Вип.4 (71). С.126-128.
-
Кузнецов В. П. Сопоставительный анализ погрешности и неопределенности измерений./ Кузнецов В. П.//Измерительная техника. ‑ 2003. ‑ №8. С. 18.
-
ISO 21748:2010 «Руководство по использованию оценок повторяемости, воспроизводимости и достоверности при оценивании погрешностей измерений».
-
Новиков В.В. Вычисление расширенной неопределенности / В. В. Новиков // Системи обробки інформації. – Харків, 2007, Вип.6 (64). С.73-77.
-
Захаров И. П. Неопределенность измерений для чайников и … начальников: учеб. пособ. /И.П. Захаров, ‑ Харьков, 2013, ‑ 36 с.
-
Международный словарь по метрологии. Основные и общие понятия и соответствующие термины: пер. с англ. и фр. / Всерос. науч.-исслед. ин-т метрологии им. Д. И. Менделеева, Белорус. гос. ин-т метрологии. Изд. 2-е, испр. ‑ СПб.: НПО «Профессионал», 2010. ‑ 82 с.
-
РМГ 29-99 ГСИ. Метрология. Основные термины и определения.
-
Novikov V.V. Numerical methods for uncertainty of measurements’ results calculation. // Конференція молодих учених із сучасних проблем механіки і математики імені академіка Я.С. Підстригача. Тези доповідей. – Львів, 2009. С. 147-148.
-
ГОСТ Р 54500.3-2011 Неопределенность. Ч. 3. Руководство по выражению неопределенности измерения.
61
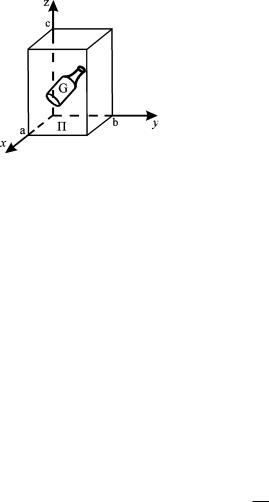
|
108 |
|||||||
|
Возьмем |
прямоугольный |
параллелепипед |
, |
||||
|
содержащий область |
G . Объем параллелепипеда П |
||||||
|
известен и равен V a b c . Разыграем координаты N |
|||||||
|
случайных точек, равномерно распределенных в |
|||||||
|
области , и обозначим через |
NG количество точек, |
||||||
|
попавших в |
область |
G. При |
большом |
N |
будет |
||
|
Рис. 9.1 |
приближенно выполняться соотношение |
||||||
|
NG / N VG /V , |
|||||||
|
из которого найдем |
|||||||
|
VG V NG / N . |
(9.2) |
||||||
|
В нашем примере случайная величина |
|||||||
|
V |
, G, |
||||||
|
G, |
|||||||
|
0, |
|||||||
а среднее арифметическое равно
|
1 |
N |
G |
|
|
i |
V (NG / N ) . |
||
|
N |
|||
|
i 1 |
(9.3)
При решении задач ММК необходимо генерировать случайные величины равномерно распределенные в интервале [0; 1].
,
Монте-Карло
Оценка точности результатов, полученных методом Монте-Карло, основана на центральной предельной теореме теории вероятностей, из которой следует, что
|
при большом объеме выборки N относительная частота события |
A |
сходится по |
вероятности к вероятности события pA , а среднее арифметическое выборочных данных сходится по вероятности к их математическому ожиданию. Используя ММК, можно провести большое число независимых опытов и с заданной точностью найти оценки искомых величин. При расчетах ММК возникает вопрос оценки точности полученных результатов. Ответ на этот вопрос можно получить на основе центральной предельной теоремы, из которой следует, что при
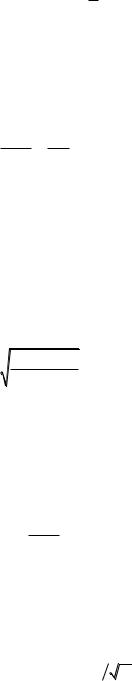
109
большом объеме выборки плотность вероятности выборочного среднего приближается к нормальному распределению.
Пусть производится большое число N независимых опытов, в каждом из
которых событие
A
появляется с вероятностью
. Введем СВ
|
1, |
если |
A, |
|
X |
если |
A, |
|
0, |
||
|
Оценка вероятности p |
A |
события |
A |
определяется формулой |
|||||||||||||||
|
N |
|||||||||||||||||||
|
x |
|||||||||||||||||||
|
i |
N |
||||||||||||||||||
|
p |
i 1 |
A |
, |
(9.4) |
|||||||||||||||
|
A |
|||||||||||||||||||
|
N |
N |
||||||||||||||||||
|
где N A число опытов, в которых появилось событие |
A |
. Отношение |
NA / N |
||||||||||||||||
|
определяет относительную частоту события |
A |
. Распределение |
p |
A |
при большом |
||||||||||||||
|
значении N близко к нормальному с математическим ожиданием |
m ( p |
A |
) p |
A |
и |
||||||||||||||
|
1 |
среднеквадратическим отклонением
Если СВ вид
X
является непрерывной, то оценка математического ожидания имеет
|
N |
||||
|
i |
||||
|
x |
||||
|
mx |
i 1 |
, |
(9.6) |
|
|
N |
||||
где xi выборочные данные. Оценка (1.8) при большом значении N является приближенно нормальной СВ со средним M mx M X и
среднеквадратическим отклонением
.
Рассмотрим два примера по определению точности результатов расчетов, полученных ММК.

|
110 |
||||
|
Пример 1. Проведено N независимых опытов, в каждом из которых событие |
A |
|||
|
появляется с некоторой неизвестной нам вероятностью p . В результате этих |
||||
|
ˆ |
||||
|
опытов получена оценка pA по формуле (3.4). Найти вероятность P pA pA |
||||
|
ˆ |
||||
|
того, что pA отличается от вероятности pA не больше чем на заданную |
||||
|
величину 0 . Так как оценка |
p |
A |
– при большом N нормальная СВ с |
|
|
математическим ожиданием pA |
и среднеквадратическим отклонением (3.5), то |
|||
|
искомая вероятность равна |
|
P pA pA |
N |
||||||||
|
2 |
. |
||||||||
|
p |
(1 |
p |
) |
||||||
|
A |
A |
||||||||
Здесь
(9.7)
|
функция Лапласа. Как пользоваться формулой (3.7), если вероятность |
pA |
нам |
|
неизвестна и мы ее находим? В выражение (3.7) pA нужно заменить на |
p A . |
Задавая достаточно большую величину вероятности, например, равную 0,95,
|
0,98, можно найти необходимое значение |
N для достижения заданной |
||||||||
|
точности. |
|||||||||
|
Пример 2. Проведено N независимых опытов, в каждом из которых |
|||||||||
|
наблюдается значение СВ |
X |
. Вычисляется оценка среднего значения mx |
по |
||||||
|
формуле (3.6). Найти вероятность P mx mx того, что оценка mx |
|||||||||
|
отклоняется от математического ожидания mx |
не больше чем на заданную |
||||||||
|
величину 0 . Как и в предыдущем примере |
|||||||||
|
P mx mx |
2 |
N |
, |
(9.9) |
|||||
|
2 |
x |
||||||||
|
(mx ) |
|||||||||
|
где x – среднеквадратичное отклонение СВ |
X. Если величина x неизвестна, |
то вместо нее можно использовать соответствующую оценку
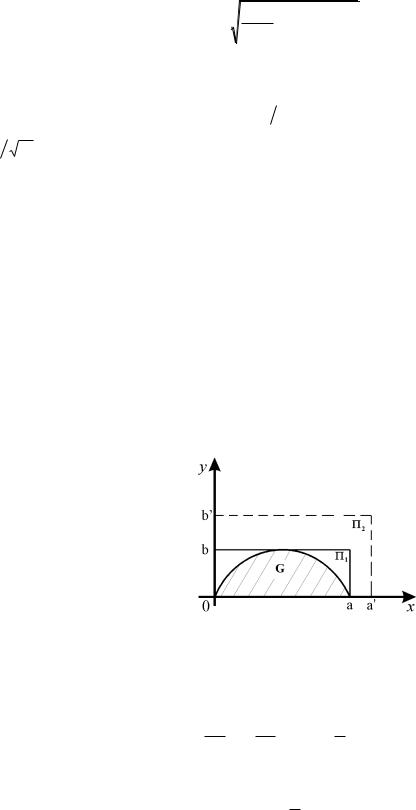
111
|
1 |
N |
2 |
|||||
|
x |
xi mx |
. |
(9.10) |
||||
|
N 1 |
|||||||
|
i1 |
|||||||
|
Обычно на практике точность характеризуют величиной относительной |
|||||||
|
среднеквадратической ошибки x |
mx , которая уменьшается с ростом |
N |
как |
||||
|
1 |
N . |
9.3.Лабораторное задание
1.Разработать алгоритм вычисления площади заданной фигуры методом
Монте-Карло и написать для него программу в пакете Mathcad. Определить величину относительной средне-квадратичной ошибки вычисленной оценки для
|
различных прямоугольных областей |
, содержащих заданную фигуру |
|
G (см. рис. 9.2). Найти точное значение площади заданной фигуры и сравнить |
|
|
полученные результаты. |
Рис. 9.2
Фигура задана следующей кривой
|
y(x) |
2b |
x |
4b |
x |
x |
a |
. |
||||
|
a |
a |
2 |
|||||||||
|
2 |
|||||||||||
|
a |
2 |
||||||||||
|
Площадь фигуры равна S |
y(x)dx |
ab . |
|||||||||
|
3 |
|||||||||||
|
0 |
|||||||||||
|
Значения параметров a, a и b,b |
приведены в таблице 9.1. |
(9.11)
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
варианта |

a b a b
|
112 |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
5 |
4 |
3 |
2 |
1 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
9 |
8 |
7 |
|
3 |
3 |
5 |
5 |
7 |
7 |
6 |
6 |
4 |
4 |
|
5 |
5 |
6 |
8 |
8 |
10 |
10 |
10 |
10 |
10 |
2. Разработать алгоритм вычисления объёма заданной фигуры методом МонтеКарло и написать для него для него программу в пакете Mathcad. Определить величину относительной средне-квадратичной ошибки вычисленной оценки для различных прямоугольных областей , содержащих заданную фигуру
G (см. рис. 1.3). Найти точное значение объема заданной фигуры и сравнить полученные результаты.
Фигура представляет собой прямоугольный параллелепипед с размерами a b h , срезанный сверху параболоидом вращения
|
x |
2 |
y |
2 |
|
|
y(x, y) h |
2 |
p |
. |
|
Вершина параболоида совпадает с центром верхнего основания.
(9.12)
Объём фигуры равен
|
a / 2 |
b / 2 |
||
|
V |
z(x, y)dxdy abh |
||
|
a / 2 b / 2 |
.
Значения параметров
p, h
,
a,b
и
a ,b , h
приведены в таблице 9.2.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
варианта |
|
1 |
1,5 |
2 |
2,5 |
3 |
4 |
0,5 |
0,1 |
1 |
2 |
|
10 |
12 |
15 |
18 |
11 |
13 |
8 |
9 |
6 |
7 |
|
1 |
2 |
3 |
4 |
5 |
5 |
2 |
1 |
2 |
1 |
|
4 |
5 |
5 |
6 |
5 |
6 |
1 |
0,5 |
2 |
5 |
|
2 |
3 |
4 |
5 |
6 |
6 |
3 |
2 |
3 |
2 |

b h
|
113 |
|||||||||
|
5 |
6 |
6 |
7 |
6 |
7 |
2 |
1 |
3 |
6 |
|
11 |
13 |
16 |
20 |
12 |
15 |
10 |
10 |
7 |
8 |
Указания. Для вычисления объема VG (площади SG ) заданной геометрической фигуры G необходимо разыграть координаты N случайных точек с равномерным распределением в прямоугольной области . Тогда оценки
величины объема (площади ˆ ) можно вычислить по формулам:
V G SG
где
NG
– число точек,
|
V G a b h N |
G |
/ |
|
SG a b N |
G |
/ N |
попавших в область G .
N,
,
Если в математическом пакете отсутствует равномерный датчик случайных
|
чисел из интервала [ p; q], то значение СВ |
z с равномерной плотностью |
|
вероятности в заданном интервале [ p; q] можно получить с помощью линейного |
|
|
преобразования |
|
z p x (q p) , |
(9.13) |
||
|
где |
x |
обозначает СВ с равномерной плотностью вероятности в интервале [0; |
1]. Величину относительной среднеквадратической погрешности оценок объема
|
V G (площади S G ) можно вычислить по формуле: |
||||
|
N NG |
. |
|||
|
NNG |
Контрольные вопросы
1. Что можно сказать о точности результатов, полученных методом численного моделирования, и как они зависят от объема выборки?

|
114 |
|
|
2. Определите величину интервала , |
в котором находится найденная оценка |
площади (объема) заданной фигуры с вероятностью 0,9. Значения функции Лапласа приведены в таблице 9.3.
|
1 |
x |
t |
2 |
||||||
|
Таблица 9.3. Значения функции Лапласа (x) |
e |
2 |
dt |
[2] |
|||||
|
2 |
|||||||||
|
0 |
|||||||||
x
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
(x)
0,0000
0,0040
0,0080
0,0120
0,0160
0,0199
0,0239
0,0279
0,0319
0,0359
0,0398
0,0438
0,0478
0,0517
0,0557
O,O596
0,0636
0,0675
0,0714
0,0753
x
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
(x)
0,1217
0,1255
0,1293
0,1331
0,1368
0,1406
0,1443
0,1480
0,1517
0,1554
0,1591
0,1628
0,1664
0,1700
0,1736
0,1772
0,1808
0,1844
0,1879
0,1915
x
0,62
0,63
0,64
0,65
0,66
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,80
0,81
(x)
0,2324
0,2357
0,2389
0,2422
0,2454
0,2486
0,2517
0,2549
0,2580
0,2611
0,2642
0,2673
0,2703
0,2734
0,2764
0,2794
0,2823
0,2852
0,2881
0,2910
x
0,93
0,94
0,95
0,96
0,97
0,98
0,99
1,00
1,01
1 02
1 04
1,04
1,05
1,06
1,07
1,08
1,09
1,10
1,11
1,12
(x)
0,3238
0,3264
0,3289
0,3315
0,3340
0,3365
0,3389
0,3413
0 3438
0,3461
0 3485
0,3508
0,3531
0,3554
0,3577
0,3599
0,3621
0,3643
0,3665
0,3686

|
115 |
||||||||||||||
|
0,20 |
0,51 |
0,1950 |
0,82 |
0,2939 |
1,13 |
0,3708 |
||||||||
|
0,0793 |
||||||||||||||
|
0,21 |
0,0832 |
0,52 |
0,1985 |
0,83 |
0,2967 |
1,14 |
0,3729 |
|||||||
|
0,22 |
0,0871 |
0,53 |
0,2019 |
0,84 |
0,2995 |
1,15 |
0,3749 |
|||||||
|
0,23 |
0,0910 |
0,54 |
0,2054 |
0,85 |
0,3023 |
1,16 |
0,3770 |
|||||||
|
0,24 |
0,0948 |
0,55 |
0,2088 |
0,86 |
0,3051 |
1 17 |
0,3790 |
|||||||
|
0,25 |
0,0987 |
0,56 |
0,2123 |
0,87 |
0,3078 |
1,18 |
0,3810 |
|||||||
|
0,26 |
0,1026 |
0,57 |
0,2157 |
0,88 |
0,3106 |
1,19 |
0,3830 |
|||||||
|
0,27 |
0,1064 |
0,58 |
0,2190 |
0,89 |
0,3133 |
1,20 |
0,3849 |
|||||||
|
0,28 |
0,1103 |
0,59 |
0,2224 |
0,90 |
0,3159 |
1,21 |
0,3869 |
|||||||
|
0,29 |
0,1141 |
0,60 |
0,2257 |
0,91 |
0,3186 |
1,22 |
0,3883 |
|||||||
|
0,30 |
0,1179 |
0,61 |
0,2291 |
0,92 |
0,3212 |
1,23 |
0,3907 |
|||||||
Продолжение приложения
|
x |
(x) |
x |
|
|
1,24 |
1,58 |
||
|
0,3925 |
|||
|
1,25 |
0,3944 |
1,59 |
|
|
1,26 |
0,3962 |
1,60 |
|
|
1 27 |
0,3980 |
1,61 |
|
|
1,28 |
0,3997 |
1,62 |
|
|
1,29 |
0,4015 |
1,63 |
|
|
1,30 |
0,4032 |
1,64 |
|
|
1,31 |
0,4049 |
1,65 |
|
|
1,32 |
0,4066 |
1,66 |
|
|
1,33 |
0,4082 |
1,67 |
|
|
1,34 |
0 4099 |
1,68 |
|
|
1,35 |
0,4115 |
1,69 |
|
(x)
0,4429
0,4441
0,4452
0,4463
0,4474
0,4484
0,4495
0,4505
0,4515
0,4525
0,4535
0,4545
x
1,92
1,93
1,94
1,95
1,96
1,97
1,98
1,99
2,00
2,02
2,04
2,06
(x)
0,4726
0,4732
0,4738
0,4744
0,4750
0,4756
0,4761
0,4767
0,4772
0,4783
0,4793
0,4803
x
2,52
2,54
2,56
2,58
2,60
2,62
2,64
2,66
2,68
2,70
2,72
2,74
(x)
0,4941
0,4945
0,4948
0,4951
0,4953
0,4956
0,4959
0,4961
0,4963
0,4965
0,4967
0,4969
|
116 |
||||||||||||||
|
1,36 |
1,70 |
0,4554 |
2,08 |
0,4812 |
2,76 |
0,4971 |
||||||||
|
0,4131 |
||||||||||||||
|
1,37 |
0,4147 |
1,71 |
0,4564 |
2,10 |
0,4821 |
2,78 |
0,4973 |
|||||||
|
1,38 |
0,4162 |
1,72 |
0,4573 |
2,12 |
0,4830 |
2,80 |
0,4974 |
|||||||
|
1,39 |
0,4177 |
1,73 |
0,4582 |
2,14 |
0,4838 |
2,82 |
0,4976 |
|||||||
|
1,40 |
0,4192 |
1,74 |
0,4591 |
2,16 |
0,4846 |
2,84 |
0,4977 |
|||||||
|
1,41 |
0,4207 |
1,75 |
0,4599 |
2,18 |
0,4854 |
2,86 |
0,4979 |
|||||||
|
1,42 |
0,4222 |
1,76 |
0,4608 |
2,20 |
0,4861 |
2,88 |
0,4980 |
|||||||
|
1,43 |
0,4236 |
1,77 |
0,4616 |
2,22 |
0,4868 |
2,90 |
0,4981 |
|||||||
|
1,44 |
0,4251 |
1,78 |
0,4625 |
2,24 |
0,4875 |
2,92 |
0,4982 |
|||||||
|
1,45 |
0,4265 |
1,79 |
0,4633 |
2,26 |
0,4881 |
2,94 |
0,4984 |
|||||||
|
1,46 |
0,4279 |
1,80 |
0,4641 |
2,28 |
0,4887 |
2,96 |
0,4985 |
|||||||
|
1,47 |
0,4292 |
1,81 |
0,4649 |
2,30 |
0,4893 |
2,98 |
0,4986 |
|||||||
|
1,48 |
0,4306 |
1,82 |
0,4656 |
2,32 |
0,4898 |
3,00 |
0,49865 |
|||||||
|
1,49 |
0,4319 |
1,83 |
0,4664 |
2,34 |
0,4904 |
3,20 |
0,49931 |
|||||||
|
1,50 |
0,4332 |
1,84 |
0,4671 |
2,36 |
0,4909 |
3,40 |
0,49966 |
|||||||
|
1,51 |
0,4345 |
1,85 |
0,4678 |
2,38 |
0,4913 |
3,60 |
0,499841 |
|||||||
|
1,52 |
0,4357 |
1,86 |
0,4686 |
2,40 |
0,4918 |
3,80 |
0,499928 |
|||||||
|
1,53 |
0,4370 |
1,87 |
0,4693 |
2,42 |
0,4922 |
4,00 |
0,499968 |
|||||||
|
1,54 |
0,4382 |
1,88 |
0,4699 |
2,44 |
0,4927 |
4,50 |
0,499997 |
|||||||
|
1,55 |
0,4394 |
1,89 |
0,4706 |
2,46 |
0,4931 |
5,00 |
0,499997 |
|||||||
|
1,56 |
0,4406 |
1,90 |
0,4713 |
2,48 |
0,4934 |
|||||||||
|
1,57 |
0,4418 |
1,91 |
0,4719 |
2,50 |
0,4938 |
|||||||||




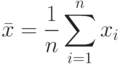
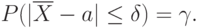
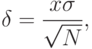
 — число испытаний (разыгранных значений случайной величины
— число испытаний (разыгранных значений случайной величины  — значение аргумента функции Лапласа
— значение аргумента функции Лапласа 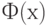 или интеграла вероятности, при котором она равна половине заданной вероятности;
или интеграла вероятности, при котором она равна половине заданной вероятности; — известное среднее квадратическое отклонение.
— известное среднее квадратическое отклонение.
 )
) 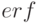 :
: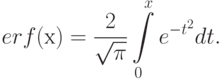

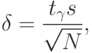
 — «исправленное» среднее квадратическое отклонение;
— «исправленное» среднее квадратическое отклонение;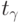 находят по специальным таблицам, например, приведенной в [6].
находят по специальным таблицам, например, приведенной в [6]. ), с вероятностью, приближенно равной
), с вероятностью, приближенно равной 
![M[x]=\int\limits_{a}^{b}x\frac{1}{b-a}dx.](https://intuit.ru/sites/default/files/tex_cache/ab07d5a2a1952a4ee11260438dcb63e6.png)