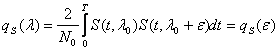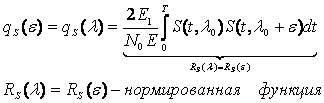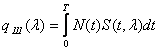In statistics and signal processing, a minimum mean square error (MMSE) estimator is an estimation method which minimizes the mean square error (MSE), which is a common measure of estimator quality, of the fitted values of a dependent variable. In the Bayesian setting, the term MMSE more specifically refers to estimation with quadratic loss function. In such case, the MMSE estimator is given by the posterior mean of the parameter to be estimated. Since the posterior mean is cumbersome to calculate, the form of the MMSE estimator is usually constrained to be within a certain class of functions. Linear MMSE estimators are a popular choice since they are easy to use, easy to calculate, and very versatile. It has given rise to many popular estimators such as the Wiener–Kolmogorov filter and Kalman filter.
Motivation[edit]
The term MMSE more specifically refers to estimation in a Bayesian setting with quadratic cost function. The basic idea behind the Bayesian approach to estimation stems from practical situations where we often have some prior information about the parameter to be estimated. For instance, we may have prior information about the range that the parameter can assume; or we may have an old estimate of the parameter that we want to modify when a new observation is made available; or the statistics of an actual random signal such as speech. This is in contrast to the non-Bayesian approach like minimum-variance unbiased estimator (MVUE) where absolutely nothing is assumed to be known about the parameter in advance and which does not account for such situations. In the Bayesian approach, such prior information is captured by the prior probability density function of the parameters; and based directly on Bayes theorem, it allows us to make better posterior estimates as more observations become available. Thus unlike non-Bayesian approach where parameters of interest are assumed to be deterministic, but unknown constants, the Bayesian estimator seeks to estimate a parameter that is itself a random variable. Furthermore, Bayesian estimation can also deal with situations where the sequence of observations are not necessarily independent. Thus Bayesian estimation provides yet another alternative to the MVUE. This is useful when the MVUE does not exist or cannot be found.
Definition[edit]
Let 







where the expectation 




The MMSE estimator is then defined as the estimator achieving minimal MSE:
Properties[edit]
- When the means and variances are finite, the MMSE estimator is uniquely defined[1] and is given by:
-
- In other words, the MMSE estimator is the conditional expectation of
given the known observed value of the measurements. Also, since
is the posterior mean, the error covariance matrix
is equal to the posterior covariance
matrix,
.
- The MMSE estimator is unbiased (under the regularity assumptions mentioned above):
- The MMSE estimator is asymptotically unbiased and it converges in distribution to the normal distribution:
-
- where
is the Fisher information of
. Thus, the MMSE estimator is asymptotically efficient.
-
- for all
in closed, linear subspace
of the measurements. For random vectors, since the MSE for estimation of a random vector is the sum of the MSEs of the coordinates, finding the MMSE estimator of a random vector decomposes into finding the MMSE estimators of the coordinates of X separately:
- for all i and j. More succinctly put, the cross-correlation between the minimum estimation error
and the estimator
should be zero,
Linear MMSE estimator[edit]
In many cases, it is not possible to determine the analytical expression of the MMSE estimator. Two basic numerical approaches to obtain the MMSE estimate depends on either finding the conditional expectation 
One possibility is to abandon the full optimality requirements and seek a technique minimizing the MSE within a particular class of estimators, such as the class of linear estimators. Thus, we postulate that the conditional expectation of 







One advantage of such linear MMSE estimator is that it is not necessary to explicitly calculate the posterior probability density function of 




The expression for optimal 

where 






Thus, the expression for linear MMSE estimator, its mean, and its auto-covariance is given by
where the 


Lastly, the error covariance and minimum mean square error achievable by such estimator is
Univariate case[edit]
For the special case when both 

where 


The above two equations allows us to interpret the correlation coefficient either as normalized slope of linear regression
or as square root of the ratio of two variances
.
When 








Computation[edit]
Standard method like Gauss elimination can be used to solve the matrix equation for 




Linear MMSE estimator for linear observation process[edit]
Let us further model the underlying process of observation as a linear process: 




Thus the expression for the linear MMSE estimator matrix 
Putting everything into the expression for 
Lastly, the error covariance is
The significant difference between the estimation problem treated above and those of least squares and Gauss–Markov estimate is that the number of observations m, (i.e. the dimension of 






Alternative form[edit]
An alternative form of expression can be obtained by using the matrix identity
which can be established by post-multiplying by 

and
Since 



In this form the above expression can be easily compared with weighed least square and Gauss–Markov estimate. In particular, when 







Sequential linear MMSE estimation[edit]
In many real-time applications, observational data is not available in a single batch. Instead the observations are made in a sequence. One possible approach is to use the sequential observations to update an old estimate as additional data becomes available, leading to finer estimates. One crucial difference between batch estimation and sequential estimation is that sequential estimation requires an additional Markov assumption.
In the Bayesian framework, such recursive estimation is easily facilitated using Bayes’ rule. Given 


The 





This is the Markov assumption.
The MMSE estimate 


Thus, the prior density for k-th time step is the posterior density of (k-1)-th time step. This structure allows us to formulate a recursive approach to estimation.
In the context of linear MMSE estimator, the formula for the estimate will have the same form as before: 




For the prior density 
,
and its covariance matrix is given by the previous error covariance matrix,
as per by the properties of MMSE estimators and the stationarity assumption.
Similarly, for the linear observation process, the mean of the likelihood 

.
The difference between the predicted value of 



![{\displaystyle \mathrm {E} [{\tilde {y}}_{k}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7333e06de208be900c7d618273db57bf678fb1f)

Hence, in the estimate update formula, we should replace 








Thus, we have the new estimate as new observation 
and the new error covariance as
From the point of view of linear algebra, for sequential estimation, if we have an estimate 

The repeated use of the above two equations as more observations become available lead to recursive estimation techniques. The expressions can be more compactly written as
The matrix 
The repetition of these three steps as more data becomes available leads to an iterative estimation algorithm. The generalization of this idea to non-stationary cases gives rise to the Kalman filter. The three update steps outlined above indeed form the update step of the Kalman filter.
Special case: scalar observations[edit]
As an important special case, an easy to use recursive expression can be derived when at each k-th time instant the underlying linear observation process yields a scalar such that 





where 

The 
Here, no matrix inversion is required. Also, the gain factor, 



Alternative approaches: This important special case has also given rise to many other iterative methods (or adaptive filters), such as the least mean squares filter and recursive least squares filter, that directly solves the original MSE optimization problem using stochastic gradient descents. However, since the estimation error 


where 

[edit]
In many practical applications, the observation noise is uncorrelated. That is, 



where 












Examples[edit]
Example 1[edit]
We shall take a linear prediction problem as an example. Let a linear combination of observed scalar random variables 



![{\displaystyle z=[z_{1},z_{2},z_{3},z_{4}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45cb1f9123fdf786074088616e42dfbcc1359d07)
then our task is to find the coefficients 

In terms of the terminology developed in the previous sections, for this problem we have the observation vector ![{\displaystyle y=[z_{1},z_{2},z_{3}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fdeb8eb600c7a066561d28e2b3f32fb5b1572b9)
![W=[w_{1},w_{2},w_{3}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd8e9343b228a9044dbb8208e9ceeb31270b04c1)


The cross correlation matrix 
We now solve the equation 

So we have 

as the optimal coefficients for 
mean square error then gives ![{\displaystyle \left\Vert e\right\Vert _{\min }^{2}=\operatorname {E} [z_{4}z_{4}]-WC_{YX}=15-WC_{YX}=.2857}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44558ab7a0b5ead1b9571853096d800773b38877)


Example 2[edit]
Consider a vector 



![1=[1,1,\ldots ,1]^{T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43fec89f837a5e8d53869fb49ec95a9e56a788f0)

![[-x_{0},x_{0}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e79873ca5ddfd5d6b0168f6373b33c8bc3756c69)


![[-x_{0},x_{0}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e79873ca5ddfd5d6b0168f6373b33c8bc3756c69)








Thus, the linear MMSE estimator is given by
We can simplify the expression by using the alternative form for 
where for ![y=[y_{1},y_{2},\ldots ,y_{N}]^{T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8317c7045e5b1318cec0c4ee89727a02cdeecafc)

Similarly, the variance of the estimator is
Thus the MMSE of this linear estimator is
For very large 
while the variance will be unaffected by data 
However, the estimator is suboptimal since it is constrained to be linear. Had the random variable 

Example 3[edit]
Consider a variation of the above example: Two candidates are standing for an election. Let the fraction of votes that a candidate will receive on an election day be ![x\in [0,1].](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c44eb6b4643a03d3c166df0e61c4925b6d4d4f0)


![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)








As with previous example, we have
Here, both the 


where the weights are given by
Here, since the denominator term is constant, the poll with lower error is given higher weight in order to predict the election outcome. Lastly, the variance of 
which makes 

In general, if we have 



Example 4[edit]
Suppose that a musician is playing an instrument and that the sound is received by two microphones, each of them located at two different places. Let the attenuation of sound due to distance at each microphone be 







We can model the sound received by each microphone as
Here both the 
where the i-th weight is given as
See also[edit]
- Bayesian estimator
- Mean squared error
- Least squares
- Minimum-variance unbiased estimator (MVUE)
- Orthogonality principle
- Wiener filter
- Kalman filter
- Linear prediction
- Zero-forcing equalizer
Notes[edit]
- ^ «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 9 May 2017.
- ^ Moon and Stirling.
Further reading[edit]
- Johnson, D. «Minimum Mean Squared Error Estimators». Connexions. Archived from Minimum Mean Squared Error Estimators the original on 25 July 2008. Retrieved 8 January 2013.
- Jaynes, E.T. (2003). Probability Theory: The Logic of Science. Cambridge University Press. ISBN 978-0521592710.
- Bibby, J.; Toutenburg, H. (1977). Prediction and Improved Estimation in Linear Models. Wiley. ISBN 9780471016564.
- Lehmann, E. L.; Casella, G. (1998). «Chapter 4». Theory of Point Estimation (2nd ed.). Springer. ISBN 0-387-98502-6.
- Kay, S. M. (1993). Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice Hall. pp. 344–350. ISBN 0-13-042268-1.
- Luenberger, D.G. (1969). «Chapter 4, Least-squares estimation». Optimization by Vector Space Methods (1st ed.). Wiley. ISBN 978-0471181170.
- Moon, T.K.; Stirling, W.C. (2000). Mathematical Methods and Algorithms for Signal Processing (1st ed.). Prentice Hall. ISBN 978-0201361865.
- Van Trees, H. L. (1968). Detection, Estimation, and Modulation Theory, Part I. New York: Wiley. ISBN 0-471-09517-6.
- Haykin, S.O. (2013). Adaptive Filter Theory (5th ed.). Prentice Hall. ISBN 978-0132671453.
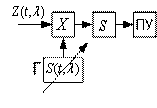
Во время синтеза
системы может оказаться ситуация, при
которой два сигнала: сигнал управления
и сигналы возмущения, оба имеют случайный
характер. В таком случае принципиальная
задача синтеза системы: определить
параметры системы, доставляющие минимум
средней квадратической ошибки, значение
которой определяется с помощью следующего
выражения:
Можно
обеспечить этот минимум двумя путями:
-
осуществить
параметрический синтез, то-есть,
определить параметры системы, без
изменения её структуры, доставляющие
минимум
-
определить
структуру и параметры системы,
обеспечивающие минимум
(структурно-параметрический синтез).
Параметрический
синтез
осуществляется в следующей
последовательности.
1.Определение
корреляционной функции полезного
сигнала и сигнала возмущения по
практическим экспериментальным данным.
Затем делаем прямое преобразование
Фурье корреляционных функций и приходим
к спектральным плотностям:
Учитывая, что
— функция четная и что
,
получаем
2.
Рассчитываем передаточные функции
системы с обратной связью для ошибки ,
вызванной случайным сигналом управления
и возмущающим воздействием
3. Используя
соответствующие выражения, рассчитываем
спектральную плотность общей ошибки
4. Определяем
дисперсию ошибки по выражению
Парсеваля как
функцию параметров системы
где
,
,
— коэффициенты и постоянные времени
элементов системы.
5. Определяем
числовые значения параметров, решая
систему уравнений
6. Подставляя
числовые значения параметров, определенных
в п.5, в выражение
,
получаем
и
среднеквадратичную ошибку
Если
где
— допустимая ошибка,
означает, что
задача решена. Если неравенство не
выполняется, необходимо приниматься
за структурно-параметрический синтез
системы.
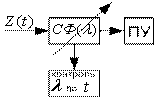
Структурно-параметрический
синтез выполняется
на базе метода оптимальной фильтрации
Винера. Презентация
метода
делается
на
рис.11.7.
Здесь:
канал I
– осуществляет желаемую передачу
входного сигнала
по
следующему выражению:
Второй канал II
– передача, осуществляемая оптимальной
системой
,
в присутствии
В связи с этим ошибка системы
должна удовлетворять критерию
Можно рассматривать
систему
как оптимальный фильтр сигнала
.
Прежде, чем решать
предложенную задачу, рассмотрим
зависимость между корреляционными
функциями сигналов на входе и на выходе
Запишем выражение взаимной корреляционной
функции:
.
Используя выражение
,
приходим к следующей форме :
Или изменяя
последовательность интегрирования,
имеем
.
Полученное выражение
называется уравнением Винера- Хопфа.
Используя
прямое преобразование Фурье, приходим
к замечательному выражению
.
Заметим, что
полученное выражение позволяет определить
частотный образ системы
по реализациям сигналов на входе и на
выходе (результаты пассивного
эксперимента), то-есть, без активного
вмешательства в исследуемый процесс:
.
Определим дисперсию
ошибки, учитывая
:
.
Норберт Винер
доказал , что условием необходимым и
достаточным минимумаявляется
то, что функция веса
должна
быть решением уравнения Винера-Хопфа:
.
Имеем тогда,
Но частотные
характеристики, определенные по этому
выражению
в большинстве практических случаях
имеют нереализуемые свойства, так как
система с
будет неустойчивой.
В этой связи для
отыскания оптимальной функции
,
удовлетворяющей условиям устойчивости,
применяют разложение
на комплексные множители:
Из этого
следует, что
.
Н Винер доказал,
что можно определить оптимальную
передаточную функцию следующим образом:
где
;
Exemple
определения
.
Пусть спектральная
плотность управляющего сигнала
а у помехи типа белого шума
Причем, известно, что
не коррелированны. Необходимо найти
следящей системы.
Решение
Для следящей системы
Поэтому
Учитывая, что
,
можно написать:
принято в рассмотрение
здесь, что
как для сигналов, которые не коррелированны.
Подставляя известные выражения
спектральной плотности, полученные
выше, получаем в нашем случае:
Разложим последнее
выражение на сопряженные множители:
Вычисляем
в соответствии с ранее написанными
выражениями:
Разложив функцию
под знаком интеграла на простые дроби,
получаем
Для вычисления
необходимо взять прямое преобразование
Фурье
которое, в свою очередь, результат
обратного преобразования Фурье выражения,
стоящего в квадратных скобках.
Следовательно,
будет равен этому выражению в квадратных
скобках. Исходя из условий реализуемости
,
отбрасываем слагаемые подынтегральной
функции , имеющей корни в правой
полуплоскости. Тогда
.
Искомая передаточная
функция примет вид
или
,
где
Таким образом,
оптимальный фильтр в данном случае
представляет собой апериодическое
звено первого порядка.
В
заключение заметим, что решение задачи
оптимальной фильтрации может быть также
произведено с помощью фильтра Калмана.
В этом методе предполагается, что на
вход системы поступает аддитивная смесь
управляющего воздействияи
случайного процесса Маркова и помеха
,
представляющая собой гауссовский
«белый» шум. Сигналы
и
не коррелированны. Физически
реализуемый
линейный оператор замкнутой системы,
при котором процесс
на выходе системы является оптимальным
по критерию
минимума
среднеквадратической ошибки, находится
по специально разработанному алгоритму.
Этот алгоритм достаточно громоздок и,
в частности, связан с решением
дифференциального уравнения
Риккатти, для чего,
как правило, требуется применять
численные
методы с использованием
компьютерных технологий. В конечном
итоге, алгоритм
Калмана дает тот же результат, что и
алгоритм
Винера, но в отличие
от последнего, позволяет синтезировать
оптимальные фильтры не только для
установившегося, но и для переходного
режимов, при случайных нестационарных
входных воздействиях.
189
Соседние файлы в папке Лекции по ТАУ-11-мин
- #
- #
- #
- #
- #
- #
Диагностика систем машинного обучения
178 мин на чтение
(210.95 символов)
Что такое метрики эффективности?
Для того, чтобы эффективно проводить обучение моделей необходимо иметь способ оценки, насколько хорошо та или иная модель выполняет свою работу — предсказывает значение целевой переменной. Кажется, мы уже что-то подобное изучали. У каждой модели есть функция ошибки, которая показывает, на сколько модель соответствует эмпирическим значениям. Однако, использование функции ошибки не очень удобно для оценки именно “качества” уже построенных моделей. Ведь эта функция специально создается для единственной цели — организации процесса обучения. Поэтому для оценки уже построенных моделей используется не функция ошибки, а так называемые метрики эффективности — специальные функции, которые показывают, насколько эффективна уже готовая, обученная модель.
Метрики эффективности на первый взгляд очень похожи на функции ошибки, ведь у них одна цель — отличать хорошие модели от плохих. Но делают они это по-разному, по-разному и применяются. К метрикам эффективности предъявляются совершенно другие требования, нежели к функциям ошибки. Поэтому давайте рассмотрим, для чего нужны и те и другие.
Функция ошибки нужна в первую очередь для формализации процесса обучения модели. То есть для того, чтобы подбирать параметры модели именно такими, чтобы модель как можно больше соответствовала реальным данным в обучающей выборке. Да, значение этой функции можно использовать как некоторую оценку качества модели уже после того, как она обучена, но это не удобно.
Функция ошибки нужна, чтобы формализовать отклонения предсказанных моделью значений от реальных. Например, в методе линейной регрессии функция ошибки (среднеквадратическое отклонение) используется для метода градиентного спуска. Поэтому функция ошибки обязательно должна быть везде дифференцируемой, мы это отдельно отмечали, когда говорили про метод градиентного спуска. Это требование — дифференцируемость — нужно исключительно для метода оптимизации, то есть для обучения модели.
Зато функция, которая используется для оценки качества модели совершенно не должна быть аналитической и гладкой. Ведь мы не будем вычислять ее производную, мы только вычислим ее один раз для того, чтобы понять, насколько хорошая модель получилась. Так что не любую метрику эффективности вообще физически возможно использовать как функцию ошибки — метод обучения может просто не сработать.
Кроме того, функция ошибки должна быть вычислительно простой, ведь ее придется считать много раз в процессе обучения — тысячи или миллионы раз. Это еще одно требование, которое совершенно необязательно для метрики эффективности. Она как раз может считаться довольно сложно, ведь вычислять ее приходится всего несколько раз.
Зато метрика эффективности должна быть понятной и интерпретируемой, в отличие от функции ошибки. Раньше мы подчеркивали, что само абсолютное значение функции ошибки ничего не показывает. Важно лишь, снижается ли оно в процессе обучения. И разные значения функции ошибки имеет смысл сравнивать только на одних и тех же данных. Что значит, если значение функции ошибки модели равно 35 000? Да ничего, только то, что эта модель хуже, чем та, у которой ошибка 32 000.
Для того, чтобы значение было более понятно, метрики эффективности зачастую выражаются в каких-то определенных единицах измерения — чеще всего в натуральных или в процентах. Натуральные единицы — это единицы измерения целевой переменной. Допустим, целевая переменная выражается в рублях. То есть, мы предсказываем некоторую стоимость. В таком случае будет вполне понятно, если качество этой модели мы тоже выразим в рублях. Например, так: модель в среднем ошибается на 500 рублей. И сразу становится ясно, насколько эта модель применима на практике.
Еще одно важное отличие. Как мы сказали, требования к функции ошибки определяются алгоритмом оптимизации. Который, в свою очередь зависит от типа модели. У линейной регрессии будет один алгоритм (и одна функция ошибки), а у, например, решающего дерева — другой алгоритм и совершенно другая функция ошибки. Это в частности значит, что функцию ошибки невозможно применять для сравнения нескольких разных моделей, обученных на одной и той же задаче.
И вот для этого как раз и нужны метрики эффективности. Они не зависят от типа модели, а выбираются исходя из задачи и тех вопросов, ответы на которые мы хотим получить. Например, в одной задаче качество модели лучше измерять через среднеквадратическую логарифмическую ошибку, а в другой — через медианную ошибку. Как раз в этой главе мы посмотрим на примеры разных метрик эффективности, на их особенности и сферы применения.
Кстати, это еще означает, что в каждой конкретной задаче вы можете применять сразу несколько метрик эффективности, для более глубокого понимания работы модели. Зачастую так и поступают, ведь одна метрика не может дать полной информации о сильных и слабых сторонах модели. Тут исследователи ничем не ограничены. А вот функция ошибки обязательно должна быть только одна, ведь нельзя одновременно находить минимум сразу нескольких разных функций (на самом деле можно, но многокритериальная оптимизация — это гораздо сложнее и не используется для обучения моделей).
| Функция ошибки | Метрика эффективности |
|---|---|
| Используется для организации процесса обучения | Используется для оценки качества полученной модели |
| Используется для нахождения оптимума | Используется для сравнения моделей между собой |
| Должна быть быстро вычислимой | Должна быть понятной |
| Должна конструироваться исходя их типа модели | Должна выбираться исходя из задачи |
| Может быть только одна | Может быть несколько |
Еще раз определим, эффективность — это свойство модели машинного обучения давать предсказания значения целевой переменной, как можно ближе к реальным данным. Это самая главная характеристика модели. Но надо помнить, что исходя из задачи и ее условий, к моделям могут предъявляться и другие требования, как сказали бы в программной инженерии — нефункциональные. Типичный пример — скорость работы. Иногда маленький выигрыш в эффективности не стоит того, что модель стала работать в десять раз меньше. Другой пример — интерпретируемость модели. В некоторых областях важно не только сделать точное предсказание, но и иметь возможность обосновать его, провести анализ, выработать рекомендации по улучшению ситуации и так далее. Все эти нефункциональные требования — скорость обучения, скорость предсказания, надежность, робастность, федеративность, интерпретируемость — выходят за рамки данного пособия. Здесь мы сконцентрируемся на измерении именно эффективности модели.
Обратите внимание, что мы старательно избегаем употребления слова “точность” при описании качества работы модели. Хотя казалось бы, оно подходит как нельзя лучше. Дело в том, что “точностью” называют одну из метрик эффективности моделей классификации. Поэтому мы не хотим внести путаницу в термины.
Как мы говорили, метрики эффективности не зависят от самого типа модели. Для их вычисления обычно используется два вектора — вектор эмпирических значений целевой переменной (то есть тех, которые даны в датасете) и вектор теоретических значений (то есть тех, которые выдала модель). Естественно, эти вектора должны быть сопоставимы — на соответствующих местах должны быть значения целевой переменной, соответствующие одном у и тому же объекту. И, конечно, у них должна быть одинаковая длина. То есть метрика зависит от самих предсказаний, но не от модели, которая их выдала. Причем, большинство метрик устроены симметрично — если поменять местами эти два вектора, результат не изменится.
При рассмотрении метрик надо помнить следующее — чем выше эффективность модели, тем лучше. Но некоторые метрики устроены как измерение ошибки модели. В таком случае, конечно, тем ниже, тем лучше. Так что эффективность и ошибка модели — это по сути противоположные понятия. Так сложилось, что метрики регрессии чаще устроены именно как ошибки, а метрики классификации — как метрики именно эффективности. При использовании конкретной метрики на это надо обращать внимание.
Выводы:
- Метрики эффективности — это способ показать, насколько точно модель отражает реальный мир.
- Метрики эффективность должны выбираться исходя из задачи, которую решает модель.
- Функция ошибки и метрика эффективности — это разные вещи, к ним предъявляются разные требования.
- В задаче можно (и, зачастую, нужно) применять несколько метрик эффективности.
- Наряду с метриками эффективности есть и другие характеристики моделей — скорость обучения, скорость работы, надежность, робастность, интерпретируемость.
- Метрики эффективности вычисляются как правило из двух векторов — предсказанных (теоретических) значений целевой переменной и эмпирических (реальных) значений.
- Обычно метрики устроены таким образом, что чем выше значение, тем модель лучше.
Метрики эффективности для регрессии
Как мы говорили в предыдущей главе, метрики зависят от конкретной задачи. А все задачи обучения с учителем разделяются на регрессию и классификацию. Совершенно естественно, что метрики для регрессии и для классификации будут разными.
Метрики эффективности для регрессии оценивают отклонение (расстояние) между предсказанными значениями и реальными. Кажется, что это очевидно, но метрики эффективности классификации устроены по-другому. Предполагается, что чем меньше каждое конкретное отклонение, тем лучше. Разница между разными метриками в том, как учитывать индивидуальные отклонения в общей метрике и в том, как агрегировать ряд значений в один интегральный показатель.
Все метрики эффективности моделей регрессии покажутся вам знакомыми, если вы изучали математическую статистику, ведь именно статистические методы легли в основу измерения эффективности моделей машинного обучения. Причем, метрики эффективности — это лишь самые простые статистические показатели, которые можно использовать для анализа качества модели. При желании можно и нужно задействовать более мощные статистические методы исследования данных. Например, можно проанализировать вид распределения отклонений, и сделать из этого вывод о необходимость корректировки моделей. Но в 99% случаев можно обойтись простым вычислением одной или двух рассматриваемых ниже метрик.
Так как метрики эффективности позволяют интерпретировать оценку качества модели, они зачастую неявно сравнивают данную модель с некоторой тривиальной. Тривиальна модель — это очень простая, даже примитивная модель, которая выдает предсказания оценки целевой переменной абсолютно без оглядки на эффективность и вообще соответствие реальным данным. Тривиальной моделью может выступать, например, предсказание для любого объекта среднего значения целевой переменной из обучающей выборки. Такие тривиальные модели нужны, чтобы оценить, насколько данная модель лучше или хуже них.
Естественно, мы хотим получить модель, которая лучше тривиальной. Причем, у нас есть некоторый идеал — модель, которая никогда не ошибается, то есть чьи предсказания всегда совпадают с реальными значениями. Поэтому реальная модель может быть лучше тривиальной только до этого предела. У такой идеальной модели, говорят, 100% эффективность или нулевая ошибка.
Но надо помнить, что в задачах регрессии модель предсказывает непрерывное значение. Это значит, что величина отклонения может быть неограниченно большой. Так что не бывает нижнего предела качества модели. Модель регрессии может быть бесконечно далекой от идеала, бесконечно хуже даже тривиальной модели. Поэтому ошибки моделей регрессии не ограничиваются сверху (или, что то же самое, эффективность моделей регрессии не ограничивается снизу).
Поэтому в задачах регрессии
Выводы:
- Метрики эффективности для регрессий обычно анализируют отклонения предсказанных значений от реальных.
- Большинство метрик пришло в машинное обучение из математической статистики.
- Результаты работы модели можно исследовать более продвинутыми статистическими методами.
- Обычно метрики сравнивают данную модель с тривиальной — моделью, которая всегда предсказывает среднее реальное значение целевой переменной.
- Модель могут быть точны на 100%, но плохи они могут быть без ограничений.
Коэффициент детерминации (r-квадрат)
Те, кто раньше хотя бы немного изучал математическую статистику, без труда узнают первую метрику эффективности моделей регрессии. Это так называемый коэффициент детерминации. Это доля дисперсии (вариации) целевой переменной, объясненная данной моделью. Данная метрика вычисляется по такой формуле:
[R^2(y, hat{y}) = 1 — frac
{sum_{i=1}^n (y_i — hat{y_i})^2}
{sum_{i=1}^n (y_i — bar{y_i})^2}]
где
$y$ — вектор эмпирических (истинных) значений целевой переменной,
$hat{y}$ — вектор теоретических (предсказанных) значений целевой переменной,
$y_i$ — эмпирическое значение целевой переменной для $i$-го объекта,
$hat{y_i}$ — теоретическое значение целевой переменной для $i$-го объекта,
$bar{y_i}$ — среднее из эмпирических значений целевой переменной для $i$-го объекта.
Если модель всегда предсказывает идеально (то есть ее предсказания всегда совпадают с реальностью, другими словами, теоретические значения — с эмпирическими), то числитель дроби в формуле будет равен 0, а значит, вся метрика будет равна 1. Если же мы рассмотрим тривиальную модель, которая всегда предсказывает среднее значение, то числитель будет равен знаменателю, дробь будет равна 1, а метрика — 0. Если модель хуже идеальной, но лучше тривиальной, то метрика будет в диапазоне от 0 до 1, причем чем ближе к 1 — тем лучше.
Если же модель предсказывает такие значения, что отклонения их от теоретических получаются больше, чем от среднего значения, то числитель будет больше знаменателя, а значит, что метрика будет принимать отрицательные значения. Запомните, что отрицательные значения коэффициента детерминации означают, что модель хуже, чем тривиальная.
В целом эта метрика показывает силу линейной связи между двумя случайными величинами. В нашем случае этими величинами выступают теоретические и эмпирические значения целевой переменной (то есть предсказанные и реальные). Если модель дает точные предсказания, то будет наблюдаться сильная связь (зависимость) между теоретическим значением и реальным, то есть высокая детерминация, близкая к 1. Если эе модель дает случайные предсказания, никак не связанные с реальными значениями, то связь будет отсутствовать.
Причем так как нас интересует, насколько значения совпадают, нам достаточно использовать именно линейную связь. Ведь когда мы оцениваем связь, например, одного из факторов в целевой переменной, то связь может быть нелинейной, и линейный коэффициент детерминации ее не покажет, то есть пропустит. Но в данному случае это не важно, так как наличие нелинейной связи означает, что предсказанные значения все-таки отклоняются от реальных. Такую линейную связь можно увидеть на графике, если построить диаграмму рассеяния между теоретическими и эмпирическими значениями, вот так:
1
2
3
4
5
6
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X, Y)
Y_ = reg.predict(X)
plt.scatter(Y, Y_)
plt.plot(Y, Y)
Здесь мы еще строим прямую $y = y$. Она нужна только для удобства. Вот как может выглядеть этот график:
Здесь мы видим, что точки немного отклоняются от центральной линии, но в целом ей следуют. Такая картина характерна для высокого коэффициента детерминации. А вот как может выглядеть менее точная модель:
И в целом, чем точки ближе к центральной линии, тем лучше модель и тем ближе коэффициент детерминации к 1.
В англоязычной литература эта метрика называется $R^2$, так как в определенных случаях она равна квадрату коэффициента корреляции. Пусть это название не вводит вас в заблуждение. Некоторые думаю, что раз метрика в квадрате, то она не может быть отрицательной. Это лишь условное название.
Пару слов об использовании метрик эффективности в библиотеке sklearn. Именно коэффициент детерминации чаще всего используется как метрика по умолчанию, которую можно посмотреть при помощи метода score() у модели регрессии. Обратите внимание, что этот метод принимает на вход саму обучающую выборку. Это сделано для единообразия с методами наподобие fit().
Но более универсально будет использовать эту метрику независимо от модели. Все метрики эффективности собраны в отдельный пакет metrics. Данная метрика называется r2_score. Обратите внимание, что при использовании этой функции ей надо передавать два вектора целевой переменной — сначала эмпирический, а вторым аргументом — теоретический.
1
2
3
4
5
6
7
8
from sklearn.metrics import r2_score
def r2(y, y_):
return 1 - ((y - y_)**2).sum() / ((y - y.mean())**2).sum()
print(reg.score(X, Y))
print(r2_score(Y, Y_))
print(r2(Y, Y_))
В данном коде мы еще реализовали самостоятельный расчет данной метрики, чтобы пояснить применение формулы выше. Можете самостоятельно убедиться, что три этих вызова напечатают одинаковые значения.
Коэффициент детерминации, или $R^2$ — это одна из немногих метрик эффективности для моделей регрессии, значение которой чем больше, тем лучше. Почти все остальные измеряют именно ошибку, что мы и увидим ниже. Еще это одна из немногих несимметричных метрик. Ведь если в формуле поменять теоретические и эмпирические значения, ее смысл и значение могут поменяться. Поэтому при использовании этой метрики нужно обязательно следить за порядком передачи аргументов.
При использовании этой метрики есть один небольшой подводный камень. Так как в знаменатели у этой формулы стоит вариация реального значения целевой переменной, важно следить, чтобы эта вариация присутствовала. Ведь если реальное значение целевой переменной будет одинаковым для всех объектов выборки, то вариация этой переменной будет равна 0. А значит, метрика будет не определена. Причем это единственная причина, почему эта метрика может быть неопределена. Надо понимать, что отсутствие вариации целевой переменной ставит под сомнение вообще целесообразность машинного обучения и моделирования в целом. Ведь что нам предсказывать если $y$ всегда один и тот же? С другой стороны, такая ситуация может случиться, например, при случайном разбиении выборки на обучающую и тестовую. Но об этом мы поговорим дальше.
Выводы:
- Коэффициент детерминации показывает силу связи между двумя случайными величинами.
- Если модель всегда предсказывает точно, метрика равна 1. Для тривиальной модели — 0.
- Значение метрики может быть отрицательно, если модель предсказывает хуже, чем тривиальная.
- Это одна из немногих несимметричных метрик эффективности.
- Эта метрика не определена, если $y=const$. Надо следить, чтобы в выборке присутствовали разные значения целевой переменной.
Средняя абсолютная ошибка (MAE)
Коэффициент детерминации — не единственная возможная характеристика эффективности моделей регрессии. Иногда полезно оценить отклонения предсказаний от истинных значений более явно. Как раз для этого служат сразу несколько метрик ошибок моделей регрессии. Самая простая из них — средняя абсолютная ошибка (mean absolute error, MAE). Она вычисляется по формуле:
[MAE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} |y_i — hat{y_i}|]
Данная метрика действительно очень проста: это средняя величина разницы между предсказанными и реальными значениями целевой переменной. Причем эта разница берется по модулю, чтобы компенсировать возможные отрицательные отклонения. Мы уже рассматривали похожую функцию, когда говорили о конструировании функции ошибки для градиентного спуска. Но тогда мы отмели использование абсолютного значения, так как эта функция не везде дифференцируема. Но вот для метрики эффективности такого требования нет и MAE вполне можно использовать.
Если модель предсказывает идеально, то, естественно, все отклонения равны 0 и MAE в целом равна нулю. Но эта метрика не учитывает явно сравнение с тривиальной моделью — она просто тем хуже, чем больше. Ниже нуля она быть, конечно, не может.
Данная метрика выражается в натуральных единицах и имеет очень простой и понятный смысл — средняя ошибка модели. Степень применимости модели в таком случае можно очень просто понять исходя из предметной области. Например, наша модель ошибается в среднем на 500 рублей. Хорошо это или плохо? Зависит от размерности исходных данных. Если мы предсказываем цены на недвижимость — то модель прекрасно справляется с задачей. Если же мы моделируем цены на спички — то такая модель скорее всего очень неэффективна.
Использование данной метрики в пакете sklearn очень похоже на любую другую метрику, меняется только название:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
Выводы:
- MAE показывает среднее абсолютное отклонение предсказанных значений от реальных.
- Чем выше значение MAE, тем модель хуже. У идеальной модели $MAE=0$
- MAE очень легко интерпретировать — на сколько в среднем ошибается модель.
Средний квадрат ошибки (MSE)
Средний квадрат ошибки (mean squared error, MSE) очень похож на предыдущую метрику, но вместо абсолютного значения (модуля) используется квадрат:
[MSE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2]
Граничные случаи у этой метрики такие же, как у предыдущей — 0 у идеальной модели, а в остальном — чем больше, тем хуже. MSE у тривиальной модели будет равна дисперсии целевой переменной. Но это не то, чтобы очень полезно на практике.
Эта метрика используется во многих моделях регрессии как функция ошибки. Но вот как метрику эффективности ее применяют довольно редко. Дело в ее интерпретируемости. Ведь она измеряется в квадратах натуральной величины. А какой физический смысл имеют, например, рубли в квадрате? На самом деле никакого. Поэтому несмотря на то, что математически MAE и MSE в общем-то эквивалентны, первая более проста и понятна, и используется гораздо чаще.
Единственное существенное отличие данной метрики от предыдущей состоит в том, что она чуть больший “вес” в общей ошибке придает большим значениям отклонений. То есть чем больше значение отклонения, тем сильнее оно будет вкладываться в значение MSE. Это иногда бывает полезно, когда исходя из задачи стоит штрафовать сильные отклонения предсказанных значений от реальных. Но с другой стороны это свойство делает эту метрику чувствительной к аномалиям.
Пример расчета метрики MSE:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred, squared=False)
0.612...
Выводы:
- MAE показывает средний квадрат отклонений предсказанных значений от реальных.
- Чем выше значение MSE, тем модель хуже. У идеальной модели $MSE=0$
- MSE больше учитывает сильные отклонения, но хуже интерпретируется, чем MAE.
Среднеквадратичная ошибка (RMSE)
Если главная проблема метрики MSE в том, что она измеряется в квадратах натуральных величин, что что будет, если мы возьмем от нее квадратный корень? Тогда мы получим среднеквадратичную ошибку (root mean squared error, RMSE):
[RMSE(y, _hat{y}) = sqrt{frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2}]
Использование данной метрики достаточно привычно при статистическом анализе данных. Однако, для интерпретации результатов машинного обучения она имеет те же недостатки, что и MSE. Главный из них — чувствительность к аномалиям. Поэтому при интерпретации эффективности моделей регрессии чаще рекомендуется применять метрику MAE.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
Выводы:
- RMSE — это по сути корень из MSE. Выражается в тех же единицах, что и целевая переменная.
- Чаще применяется при статистическом анализа данных.
- Данная метрика очень чувствительна к аномалиям и выбросам.
Среднеквадратичная логарифмическая ошибка (MSLE)
Еще одна довольно редкая метрика — среднеквадратическая логарифмическая ошибка (mean squared logarithmic error, MSLE). Она очень похожа на MSE, но квадрат вычисляется не от самих отклонений, а от разницы логарифмов (про то, зачем там +1 поговорим позднее):
[MSLE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (
ln(1 + y_i) — ln(1 + hat{y_i})
)^2]
Данная материка имеет специфическую, но довольно полезную сферу применения. Она применяется в тех случаях, когда значения целевой переменной простираются на несколько порядков величины. Например, если мы анализируем доходы физических лиц, они могут измеряться от тысяч до сотен миллионов. Понятно, что при использовании более привычных метрик, таких как MSE, RMSE и даже MAE, отклонения в больших значениях, даже небольшие относительно, будут полностью доминировать над отклонениями в малых значениях.
Это приведет к тому, что оценка моделей в подобных задачах классическими метриками будет давать преимущество моделям, которые более точны в одной части выборки, но почти не будут учитывать ошибки в других частях выборки. Это может привести к несправедливой оценке моделей. А вот использование логарифма поможет сгладить это противоречие.
Чаще всего, величины с таким больших размахом, что имеет смысл использовать логарифмическую ошибку, возникают в тех задачах, которые моделируют некоторые естественные процессы, характеризующиеся экспоненциальным ростом. Например, моделирование популяций, эпидемий, финансов. Такие процессы часто порождают величины, распределенные по экспоненциальному закону. А они чаще всего имеют область значений от нуля до плюс бесконечности, то есть иногда могут обращаться в ноль.
Проблема в том, что логарифм от нуля не определен. Именно поэтому в формуле данной метрики присутствует +1. Это искусственный способ избежать неопределенности. Конечно, если вы имеете дело с величиной, которая может принимать значение -1, то у вас опять будут проблемы. Но на практике такие особые распределения не встречаются почти никогда.
Использование данной метрике в коде полностью аналогично другим:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.039...
Выводы:
- MSLE это среднее отклонение логарифмов реальных и предсказанных данных.
- Так же, идеальная модель имеет $MSLE = 0$.
- Данная метрика используется, когда целевая переменная простирается на несколько порядков величины.
- Еще эта метрика может быть полезна, если моделируется процесс в экспоненциальным ростом.
Среднее процентное отклонение (MAPE)
Все метрики, которые мы рассматривали до этого рассчитывали абсолютную величину отклонения. Но ведь отклонение в 5 единиц при истинном значении 5 и при значении в 100 — разные вещи. В первом случае мы имеем ошибку в 100%, а во втором — только в 5%. Очевидно, что первый и второй случай должны по-разному учитываться в ошибке. Для этого придумана средняя абсолютная процентная ошибка (mean absolute percentage error, MAPE). В ней каждое отклонение оценивается в процентах от истинного значения целевой переменной:
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, |y_i|)}]
Эта метрика имеет одно критическое преимущество над остальными — с ее помощью можно сравнивать эффективность моделей на разных обучающих выборках. Ведь если мы возьмем классические метрики (например, MAE), то размер отклонений будет очевидно зависеть от самих данных. А в двух разных выборках и средняя величина скорее всего будет разная. Поэтому метрики MAE, MSE, RMSE, MSLE не сопоставимы при сравнении предсказаний, сделанных на разных выборках.
А вот по метрике MAPE можно сравнивать разные модели, которые были обучены на разных данных. Это очень полезно, например, в научных публикациях, где метрика MAPE (и ее вариации) практически обязательны для описания эффективности моделей регрессии.Ведь если одна модель ошибается в среднем на 3,9%, а другая — на 3,5%, очевидно, что вторая более точна. А вот если оперировать той же MAE, так сказать нельзя. Ведь если одна модель ошибается в среднем на 500 рублей, а вторая — на 490, очевидно ли, что вторая лучше? Может, она даже хуже, просто в исходных данных величина целевой переменной во втором случае была чуть меньше.
При этом у метрики MAPE есть пара недостатков. Во-первых, она не определена, если истинное значение целевой переменной равно 0. Именно для преодоления этого в знаменателе формулы этой метрики присутствует $max(epsilon, |y_i|)$. $epsilon$ — это некоторое очень маленькое значение. Оно нужно только для того, чтобы избежать деления на ноль. Это, конечно, настоящий математический костыль, но позволяет без опаски применять эту метрику на практике.
Во-вторых, данная метрика дает преимущество более низким предсказаниям. Ведь если предсказание ниже, чем реальное значение, процентное отклонение может быть от 0% до 100%. В это же время если предсказание выше реального, то верхней границы нет, предсказание может быть больше и на 200%, и на 1000%.
В-третьих, эта метрика несимметрична. Ведь в этой формуле $y$ и $hat{y}$ не взаимозаменяемы. Это не большая проблема и может быть исправлена использованием симметричного варианта этой метрики, который называется SMAPE (symmetric mean absolute percentage error):
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, (|hat{y_i}|, |y_i|) / 2)}]
В русскоязычной литературе данная метрика часто называется относительной ошибкой, так как она учитывает отклонение относительно целевого значения. В английском названии метрики она называется абсолютной. Тут нет никакого противоречия, так как “абсолютный” здесь значит просто взятие по модулю.
С точки зрения использования в коде, все полностью аналогично:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_percentage_error
>>> y_true = [1, 10, 1e6]
>>> y_pred = [0.9, 15, 1.2e6]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.2666...
Выводы:
- Идея этой метрики — это чувствительность к относительным отклонениям.
- Данная модель выражается в процентах и имеет хорошую интерпретируемость.
- Идеальная модель имеет $MAPE = 0$. Верхний предел — не ограничен.
- Данная метрика отдает предпочтение предсказанию меньших значений.
Абсолютная медианная ошибка
Практически во всех ранее рассмотренных метриках используется среднее арифметическое для агрегации частных отклонений в общую величину ошибки. Иногда это может быть не очень уместно, если в выборке присутствует очень неравномерное распределение по целевой переменной. В таких случаях может быть целесообразно использование медианной ошибки:
[MedAE(y, _hat{y}) = frac{1}{n} median_{i=0}^{n-1}
|y_i — hat{y_i}|]
Эта метрика полностью аналогична MAE за одним исключением: вместо среднего арифметического подсчитывается медианное значение. Медиана — это такое значение в выборке, больше которого и меньше которого примерно половина объектов выборки (с точностью до одного объекта).
Эта метрика чаще всего применяется при анализе демографических и экономических данных. Ее особенность в том, что она не так чувствительна к выбросам и аномальным значениям, ведь они практически не влияют на медианное значение выборки, что делает эту метрику более надежной и робастной, чем абсолютная ошибка.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
Выводы:
- Медианная абсолютная ошибка похожа на среднюю абсолютную, но более устойчива к аномалиям.
- Применяется в задачах, когда известно, что в данных присутствуют выбросы, аномальные , непоказательные значения.
- Эта метрика более робастная, нежели MAE.
Максимальная ошибка
Еще одна достаточно экзотическая, но очень простая метрика эффективности регрессии — максимальная ошибка:
[ME(y, _hat{y}) = max_{i=0}^{n-1}
|y_i — hat{y_i}|]
Как следует из названия, это просто величина максимального абсолютного отклонения предсказанных значений от теоретических. Особенность этой метрики в том, что она вообще не характеризует распределение отклонений в целом. Поэтому она практически никогда не применяется самостоятельно, в качестве единственной метрики.
Эта метрика именно вспомогательная. В сочетании с другими метриками, она может дополнительно охарактеризовать, насколько сильно модель может ошибаться в самом худшем случае. Опять же, в зависимости от задачи, это может быть важно. В некоторых задачах модель, которая в среднем ошибается пусть чуть больше, но при этом не допускает очень больших “промахов”, может быть предпочтительнее, чем более точная модель в среднем, но у которой встречаются сильные отклонения.
Применение этой метрики та же просто, как и других:
1
2
3
4
5
>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [9, 2, 7, 1]
>>> max_error(y_true, y_pred)
6
Выводы:
- Максимальная ошибка показывает наихудший случай предсказания модели.
- В некоторых задачах важно, чтобы модель не ошибалась сильно, а небольшие отклонения не критичны.
- Зачастую эта метрика используется как вспомогательная совместно с другими.
Метрики эффективности для классификации
Приступим к рассмотрению метрик эффективности, которые применяются для оценки моделей классификации. Для начала ответим на вопрос, почему для них нельзя использовать те метрики, которые мы уже рассмотрели в предыдущей части? Дело в том, что метрики эффективности регрессии так или иначе оценивают расстояние от предсказанного значения до реального. Это подразумевает, что в значениях целевой переменной существует определенный порядок. Формально говоря, предполагается, что целевая переменная измеряется по относительной шкале. Это значит, что разница между значениями имеет какой-то смысл. Например, если мы ошиблись в предполагаемой цене товара на 10 рублей, это лучше, чем ошибка на 20 рублей. Причем, можно сказать, что это в два раза лучше.
Но вот целевые переменные, которые существуют в задачах классификации обычно не обладают таким свойством. Да, метки классов часто обозначают числами (класс 0, класс 1, класс 5 и так далее). И мы используем эти числа в качестве значения переменных в программе. Но это ничего не значит. Представим объект, принадлежащий 0 классу, что бы этот класс не значил. Допустим, мы предсказали 1 класс. Было бы хуже, если бы мы предсказали 2 класс. Можно ли сказать, что во втором случае модель ошиблась в два раза сильнее? В общем случае, нельзя. Что в первом, что во втором случае модель просто ошиблась. Имеет значение только разница между правильным предсказанием и неправильным. Отклонение в задачах классификации не играет роли.
Поэтому метрики эффективности для классификации оценивают количество правильно и неправильно классифицированных (иногда еще говорят, распознанных) объектов. При этом разные метрики, как мы увидим, концентрируются на разных соотношениях этих количеств, особенно в случае, когда классов больше двух, то есть имеет место задача множественной классификации.
Причем метрики эффективности классификации тоже нельзя применять для оценки регрессионных моделей. Дело в том, что в задачах регрессии почти никогда не встречается полное совпадение предсказанного и реального значения. Так как мы работам с непрерывным континуумом значений, вероятность такого совпадения равна, буквально, нулю. Поэтому по метрикам для классификации практически любая регрессионная модель будет иметь нулевую эффективность, даже очень хорошая и точная модель. Именно потому, что для метрик классификации даже самая небольшая ошибка уже считается как промах.
Как мы говорили ранее,для оценки конкретной модели можно использовать несколько метрик одновременно. Это хорошая практика для задач регрессии, но для классификации — это практически необходимость. Дело в том, что метрики классификации гораздо легче “обмануть” с помощью тривиальных моделей, особенно в случае несбалансированных классов (об этом мы поговорим чуть позже). Тривиальной моделью в задачах классификации может выступать модель, которая предсказывает случайный класс (такая используется чаще всего), либо которая предсказывает всегда какой-то определенный класс.
Надо обратить внимание, что по многим метрикам, ожидаемая эффективность моделей классификации сильно зависит от количества классов в задаче. Чем больше классов, тем на меньшую эффективность в среднем можно рассчитывать.Поэтому метрики эффективности классификации не позволяют сопоставить задачи, состоящие из разного количества классов. Это следует помнить при анализе моделей. Если точность бинарной классификации составляет 50%, это значит, что модель работает не лучше случайного угадывания. Но в модели множественной классификации из, допустим, 10 000 классов, точность 50% — это существенно лучше случайного гадания.
Еще обратим внимание, что некоторые метрики учитывают только само предсказание, в то время, как другие — степень уверенности модели в предсказании. Вообще, все модели классификации разделяются на логические и метрические. Логические методы классификации выдают конкретное значение класса, без дополнительной информации. Типичные примеры — дерево решений, метод ближайших соседей. Метрические же методы выдают степень уверенности (принадлежности) объекта к одному или, чаще, ко всем классам. Так, например, работает метод логистической регрессии в сочетании с алгоритмом “один против всех”. Так вот, в зависимости, от того, какую модель классификации вы используете, вам могут быть доступны разные метрики. Те метрики, которые оценивают эффективность классификации в зависимости от выбранной величины порога не могут работать с логическими методами. Поэтому, например, нет смысла строить PR-кривую для метода ближайших соседей. Остальные метрики, которые не используют порог, могут работать с любыми методами классификации.
Выводы:
- Метрики эффективности классификации подсчитывают количество правильно распознанных объектов.
- В задачах классификации почти всегда надо применять несколько метрик одновременно.
- Тривиальной моделью в задачах классификации считается та, которая предсказывает случайный класс, либо самый популярный класс.
- Качество бинарной классификации при прочих равных почти всегда будет сильно выше, чем для множественной.
- Вообще, чем больше в задаче классов, тем ниже ожидаемые значения эффективности.
- Некоторые метрики работают с метрическими методами, другие — со всеми.
Доля правильных ответов (accuracy)
Если попробовать самостоятельно придумать способ оценить качество модели классификации, ничего не зная о существующих метриках, скорее всего получится именно метрика точности (accuracy). Это самая простая и естественная метрика эффективности классификации. Она подсчитывается как количество объектов в выборке, которые были классифицированы правильно (то есть, для которых теоретическое и эмпирическое значение метки класса — целевой переменной — совпадает), разделенное на общее количество объектов выборки. Вот формула для вычисления точности классификации:
[acc(y, hat{y}) = frac{1}{n} sum_{i=0}^{n} 1(hat{y_i} = y_i)]
В этой формуле используется так называемая индикаторная функция $1()$. Эта функция равна 1 тогда, когда ее аргумент — истинное выражение, и 0 — если ложное. В данном случае она равна единице для всех объектов, у которых предсказанное значение равно реальному ($hat{y_i} = y_i$). Суммируя по всем объектам мы получим количество объектов, классифицированных верно. Перед суммой стоит множитель $frac{1}{n}$, где $n$ — количество объектов в выборке. То есть в итоге мы получаем долю правильных ответов исследуемой модели.
Значение данной метрики может быть выражено в долях единицы, либо в процентах, домножив значение на 100%. Чем выше значение accuracy, тем лучше модель классифицирует выборку, то есть тем лучше ответы модели соответствуют значениям целевой переменной, присутствующим в выборке. Если модель всегда дает правильные предсказания, то ее accuracy будет равн 1 (или 100%). Худшая модель, которая всегда предсказывает неверно будет иметь accuracy, равную нулю, причем это нижняя граница, хуже быть не может.
В дальнейшем, для обозначения названий метрик эффективности я буду использовать именно английские названия — accuracy, precision, recall. У каждого из этих слов есть перевод на русский, но так случилось, что в русскоязычных терминах существует путаница. Дело в том, что и accuracy и precision чаще всего переводятся словом “точность”. А это разные метрики, имеющие разный смысл и разные формулы. Accuracy еще называют “правильность”, precision — “прецизионность”. Причем у последнего термина есть несколько другое значение в метрологии. Поэтому, пока будем обозначать эти метрики изначальными названиями.
А вот accuracy тривиальной модели будет как раз зависеть от количества классов. Если мы имеем дело с бинарной классификацией, то модель будет ошибаться примерно в половине случаев. То есть ее accuracy будет 0,5. В общем же случае, если есть $m$ классов, то тривиальная модель, которая предсказывает случайный класс будет иметь accuracy в среднем около $frac{1}{m}$.
Но это в случае, если в выборке объекты разных классов встречаются примерно поровну. В реальности же часто встречаются несбалансированные выборки, в которых распределение объектов по классам очень неравномерно. Например, может быть такое, что объектов одного класса в десять раз больше, чем другого. В таком случае, accuracy тривиальной модели может быть как выше, так и ниже $1/m$. Вообще, метрика accuracy очень чувствительна к соотношению классов в выборке. И именно поэтому мы рассматриваем другие способы оценки качества моделей классификации.
Использование метрики accuracy в библиотеке sklearn ничем принципиальным не отличается от использования других численных метрик эффективности:
1
2
3
4
5
6
>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
В данном примере в задаче 4 класса (0, 1, 2, 3) и столько же объектов, по одному на каждый класс. Модель правильно классифицировала первый и третий объект, то есть половину. Поэтому ее accuracy составляет 0,5 или 50%.
Выводы:
- Точность (accuracy) — самая простая метрика качества классификации, доля правильных ответов.
- Может быть выражена в процентах и в долях единицы.
- Идеальная модель дает точность 1.0, тривиальная — 0.5, самая худшая — 0.0.
- Тривиальная модель в множественной сбалансированной задаче классификации дает точность 1/m.
- Метрика точности очень чувствительная к несбалансированности классов.
Метрики классификации для неравных классов (precision, recall, F1)
Как мы говорили ранее, метрика accuracy может быть чувствительна к несбалансированности классов. Рассмотрим типичный пример — диагностика заболевания. Допустим, в случайной выборке людей заболевание встречается один раз на 100 человек. То есть в выборке у нас может быть всего 1% объектов, принадлежащих положительному классу и 99% — отрицательному, то есть почти в 100 раз больше. Какая accuracy будет у абсолютно тривиальной модели, которая всегда предсказывает отрицательный класс? Такая модель будет права в 99% случаев и ошибаться только в 1%. То есть иметь accuracy 0,99. Естественно, ценность такой модели минимальна, несмотря на высокий показатель метрики. Поэтому в случае с сильно несбалансированными классами метрика accuracy не то, чтобы неверна, она непоказательна, то есть не дает хорошего представления о качественных характеристиках модели.
Для более полного описания модели используется ряд других метрик. Для того, чтобы понять, как они устроены и что показывают нужно разобраться с понятием ошибок первого и второго рода. Пока будем рассматривать случай бинарной классификации, а о том, как эти метрики обобщаются на множественные задачи, поговорим позднее. Итак, у нас есть задача бинарной классификации, объекты положительного и отрицательного класса. Идеальным примером для этого будет все та же медицинская диагностика.
По отношению к модели бинарной классификации все объекты выборки можно разделить на четыре непересекающихся множества. Истинноположительные (true positive, TP) — это те объекты, которые отнесены моделью к положительному классу и действительно ему принадлежат. Истинноотрицательные (true negative, TN) — соответственно те, которые правильно распознаны моделью как принадлежащие отрицательному классу. Ложноположительные объекты (FP, false positive) — это те, которые модель распознала как положительные, хотя на самом деле они отрицательные. В математической статистике такая ситуация называется ошибкой первого рода. И, наконец, ложноотрицательные значения (false negative, FN) — это те, которые ошибочно отнесены моделью к отрицательному классу, хотя на самом деле они принадлежат положительному.
В примере с медицинско диагностикой, ложноположительные объекты или ошибки первого рода — это здоровые пациенты, которых при диагностике ошибочно назвали больными. Ложноотрицательные, или ошибки второго рода, — это больные пациенты, которых диагностическая модель “пропустила”, ошибочно приняв за здоровых. Очевидно, что в этой задаче, как и во многих других, ошибки первого и второго рода не равнозначны. В медицинской диагностике, например, гораздо важнее распознать всех здоровых пациентов, то есть не допустить ложноотрицательных объектов или ошибок второго рода. Ошибки же первого рода, или ложноположительные предсказания, тоже нежелательны, но значительно меньше, чем ложноотрицательные.
Так вот, метрика accuracy учитывает и те и другие ошибки одинаково, абсолютно симметрично. В терминах наших четырех классов она может выражаться такой формулой:
[A = frac{TP + TN}{TP + TN + FP + FN}]
Обратите внимание, что если в модели переименовать положительный класс в отрицательный и наоборот, то это никак не повлияет на accuracy. Так вот, в зависимости от решаемой задачи, нам может быть необходимо воспользоваться другими метриками. Вообще, их существует большое количество, но на практике чаще других применяются метрики precision и recall.
Precision (чаще переводится как “точность”, “прецизионность”) — это доля объектов, плавильно распознанных как положительные из всех, распознанных как положительные. Считается этот показатель по следующей формуле: $P = frac{TP}{TP + FP}$. Как можно видеть, precision будет равен 1, если модель не делает ошибок первого рода, то есть не дает ложноположительных предсказаний. Причем ошибки второго рода (ложноотрицательные) вообще не влияют на величину precision, так как эта метрика рассматривает только объекты, отнесенные моделью к положительным.
Precision характеризует способность модели отличать положительный класс от отрицательного, не делать ложноположительных предсказаний. Ведь если мы будем всегда предсказывать отрицательный класс, precision будет не определен. А вот если модель будет всегда предсказывать положительный класс, то precision будет равен доли объектов этого класса в выборке. В нашем примере с медицинской диагностикой, модель, всех пациентов записывающая в больные даст precision всего 0,01.
Метрика recall (обычно переводится как “полнота” или “правильность”) — это доля положительных объектов выборки, распознанных моделью. То есть это отношение все тех же истинноположительных объектов к числу всех положительных объектов выборки: $R = frac{TP}{TP + FN}$. Recall будет равен 1 только в том случае, если модель не делает ошибок второго рода, то есть не дает ложноотрицательных предсказаний. А вот ошибки первого рода (ложноположительные) не влияют на эту метрику, так как она рассматривает только объекты, которые на самом деле принадлежат положительному классу.
Recall характеризует способность модели обнаруживать все объекты положительного класса. Если мы будем всегда предсказывать отрицательный класс, то данная метрика будет равна 0, а если всегда положительный — то 1. Метрика Recall еще называется полнотой, так как она характеризует полноту распознавания положительного класса моделью.
В примере с медицинской диагностикой нам гораздо важнее, как мы говорили, не делать ложноотрицательных предсказаний. Поэтому метрика recall будет для нас важнее, чем precision и даже accuracy. Однако, как видно из примеров, каждый из этих метрик легко можно максимизировать довольно тривиальной моделью. Если мы будет ориентироваться на recall, то наилучшей моделью будет считаться та, которая всегда предсказывает положительный класс. Если только на precision — то “выиграет” модель, которая всегда предсказывает наоборот, положительный. А если брать в расчет только accuracy, то при сильно несбалансированных классах модель, предсказывающая самый популярный класс. Поэтому эти метрики нелья использовать по отдельности, только сразу как минимум две из них.
Так как метрики precision и recall почти всегда используются совместно, часто возникает ситуация, когда есть две модели, у одной из которых выше precision, а у второй — recall. Возникает вопрос, как выбрать лучшую? Для такого случая можно посчитать среднее значение. Но для этих метрик больше подойдет среднее не арифметическое, а гармоническое, ведь оно равно 0, если хотя бы одно число равно 0. Эта метрика называется $F_1$:
[F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN}]
Эта метрика полезна, если нужно одно число, которое в себе объединяет и precision и recall. Но эта формула подразумевает, что нам одинаково важны и то и другое. А как мы заметили раньше, часто одна из этих метрик важнее. Поэтому иногда используют обобщение метрики $F_1$, так называемое семейство F-метрик:
[F_{beta} = (1 + beta^2) frac{P R}{beta^2 P + R}]
Эта метрика имеет параметр $beta > 0$, который определяет, во сколько раз recall важнее precision. Если этот параметр больше единицы, то метрика будет полагать recall более важным. А если меньше — то важнее будет precision. Если же $beta = 1$, то мы получим уже известную нам метрику $F_1$. Все метрики из F-семейства измеряются от 0 до 1, причем чем значение больше, тем модель лучше.
1
2
3
4
5
6
7
8
9
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...
Выводы:
- Если классы в задаче не сбалансированы, то метрика точности не дает полного представления о качестве работы моделей.
- Для бинарной классификации подсчитывается количество истинно положительных, истинно отрицательных, ложно положительных и ложно отрицательных объектов.
- Precision — доля истинно положительных объектов во всех, распознанных как положительные.
- Precision характеризует способность модели не помечать положительные объекты как отрицательные (не делать ложно положительных прогнозов).
- Recall — для истинно положительных объектов во всех положительных.
- Recall характеризует способность модели выявлять все положительные объекты (не делать ложно отрицательных прогнозов).
- F1 — среднее гармоническое между этими двумя метриками. F1 — это частный случай. Вообще, семейство F-метрик — это взвешенное среднее гармоническое.
- Часто используют все вместе для более полной характеристики модели.
Матрица классификации
Матрица классификации — это не метрика сама по себе, но очень удобный способ “заглянуть” внутрь модели и посмотреть, насколько хорошо она классифицирует какую-то выборку объектов. Особенно удобна эта матрица в задачах множественной классификации, когда из-за большого количества классов численные метрики не всегда наглядно показывают, какие объекты к каким классам относятся.
С использованием библиотеки sklearn матрица классификации может быть сформирована всего одной строчкой кода:
1
2
3
4
5
6
7
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
В этой матрице по строкам располагаются истинные значения целевой переменной, то есть действительные значения классов. По столбцам же отмечены предсказанные классы. В самой матрице на пересечении строки и столбца отмечается число объектов, которые принадлежат данному действительному классу, но моделью были распознаны как объекты данного предсказанного класса.
Естественно, элементы, располагающиеся на главной диагонали, показывают объекты, которые были правильно распознаны моделью. Элементы же вне этой диагонали — это ошибки классификации. Поэтому чем лучше модель, тем выше должны быть значения по диагонали и тем меньше — вне ее. В идеале все элементы вне главной диагонали должны быть нулевыми.
Но гораздо удобнее представлять ее в графическом виде:
В таком виде матрица представляется в виде тепловой карты, в которой чем выше значение, тем насыщеннее оттенок цвета. Это позволяет при первом взгляде на матрицу понять, как часто она ошибается и в каких именно классах. В отличие от простых численных метрик, матрица классификации может дать информацию о паттернах распространенных ошибок, которые допускает данная модель.
Практически любое аномальное или тривиальное поведение модели будет иметь отражение в матрице классификации. Например, если модель чаще чем нужно предсказывает один класс, это сразу подсветит отдельный столбец в ней. Если же модель путает два класса, то есть не различает объекты этих классов, то в матрице будут подсвечены четыре элемента, располагающиеся в углах прямоугольника. Еще одно распространенное поведение модель — когда она распознает объекты одного класса, как объекты другого — подсветит один элемент вне главной диагонали.
Эта матрица очень наглядно показывает, как часто и в каких конкретно классах ошибается модель. Поэтому анализ этой матрицы может дать ценную информацию о путях увеличения эффективности моделей. Например, можно провести анализ ошибок на основе показаний данной матрицы — проанализировать объекты, на которых модель чаще всего ошибается. Может, будет выявлена какая-то закономерность, либо общая характеристика. Добавление информации о таких параметрах объектов к матрице атрибутов обычно очень сильно улучшает эффективность моделей.
Выводы:
- Матрица классификации, или матрица ошибок представляет собой количество объектов по двум осям — истинный класс и предсказанный класс.
- Обычно, истинный класс располагается по строкам, а предсказанный — по столбцам.
- Для идеальной модели матрица должна содержать ненулевые элементы только на главной диагонали.
- Матрица позволяет наглядно представить результаты классификации и увидеть, в каких случаях модель делает ошибки.
- Матрица незаменима при анализе ошибок, когда исследуется, какие объекты были неправильно классифицированы.
Метрики множественной классификации
Все метрики, о которых мы говорили выше рассчитываются в случае бинарной классификации, так как определяются через понятия ложноположительных, ложноотрицательных прогнозов. Но на практике чаще встречаются задачи множественной классификации. В них не определяется один положительный и один отрицательный класс, поэтому все рассуждения о precision и recall, казалось бы, не имеют смысла.
На самом деле, все рассмотренные метрики прекрасно обобщаются на случай множественных классов. Рассмотрим простой пример. У нас есть три класса — 0, 1 и 2. Есть пять объектов, каждый их которых принадлежит одному их этих трех классов. Истинные значения целевой переменной такие: $y = lbrace 0, 1, 2, 2, 0 rbrace$. Имеется модель, которая предсказывает классы этих объектов, соответственно так: $hat{y} = lbrace 0, 0, 2, 1, 0 rbrace$. Давайте рассчитаем известные нам метрики качества классификации.
С метрикой accuracy все просто. Модель правильно предсказала класс в трех случаях из пяти — первом, третьем и пятом. А в двух случаях — ошиблась. Поэтому метрика рассчитывается так: $A = 3 / 5 = 0.6$. То есть точность модели — 60%.
А вот precision и recall рассчитываются более сложно. В моделях множественной классификации эти метрики могут быть рассчитаны отдельно по каждому классу. Подход в этом случае очень похож на алгоритм “один против всех” — для каждого класса он предполагается положительным, а все остальные классы — отрицательными. Давайте рассчитаем эти метрики на нашем примере.
Возьмем нулевой класс. Его обозначим за 1, а все остальные — за 0. Тогда вектора эмпирических и теоретических значений целевой пременной станут выглядеть так:
$y = lbrace 1, 0, 0, 0, 1 rbrace$,
$hat{y} = lbrace 1, 1, 0, 0, 1 rbrace$.
Тогда $P = frac{TP}{TP + FP} = frac{2}{3} approx 0.67$, ведь у нас получается 2 истинноположительных предсказания (первый и пятый объекты) и одно ложноположительное (второй). $R = frac{TP}{TP + FN} = frac{2}{2} = 1$, ведь в модели нет ложноотрицательных прогнозов.
$F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN} = frac{2 cdot 2}{2 cdot 2 + 1 + 0} = frac{4}{5} = 0.8$.
Аналогично рассчитываются метрики и по остальным классам. Например, для первого класса вектора целевой переменной будут такими:
$y = lbrace 0, 1, 0, 0, 0 rbrace$,
$hat{y} = lbrace 0, 0, 0, 1, 0 rbrace$. Обратите внимание, что в данном случае получается, что модель ни разу не угадала. Такое тоже бывает, и в таком случае, метрики будут нулевые. Для третьего класса попробуйте рассчитать метрики самостоятельно, а чуть ниже можно увидеть правильный ответ.
Конечно, при использовании библиотечный функций не придется рассчитывать все эти метрики вручную. В библиотеке sklearn для этого есть очень удобная функция — classification_report, отчет о классификации, которая как раз вычисляет все необходимые метрики и представляет результат в виде наглядной таблицы. Вот как будет выглядеть рассмотренный нами пример:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Здесь мы видим несколько строк, соответствующих классам в нашей задаче. По каждому классу рассчитаны метрики precision, recall и $F_1$. Последний столбец называется support — это количество объектов данного класса в используемой выборке. Это тоже важный показатель, так как чем меньше объектов какого-то класса, тем хуже он обычно распознается.
Ниже приведены интегральные, то есть общие метрики эффективности модели. Это три последние строки таблицы. В первую очередь это accuracy — она всегда рассчитывается один раз. Обратите внимание, что в столбце support здесь везде стоит 5 — это общее число объектов выборки. Ниже приведены средние значения по метрикам precision, recall и $F_1$. Почему же строк две? Дело в том, что усреднять эти метрики можно по-разному.
Во-первых, можно взять обычное среднее арифметическое из метрик всех классов. Это называется macro average. Это самый простой способ, но у него есть одна проблема. Почему метрики очень малочисленных классов должны давать тот же вклад в итоговый результат, что и метрики очень многочисленных? Можно усреднить метрики используя в качестве весов долю каждого класса в выборке. Такое усреднение называется weighted average. Обратите внимание, что при усреднении метрика $F_1$ может получиться не между precision и recall.
Отчет о классификации — очень полезная функция, использование которой практически обязательно при анализе эффективности моделей классификации. Особенно для задач множественной классификации. Эта таблица может дать важную информацию о том, какие классы распознаются моделью лучше, какие — хуже, как это связано в численностью классов в выборке. Анализ этой таблицы может навести на необходимость определенных действий по повышению эффективности модели. Например, можно понять, какие данные полезно будет добавить в модель.
Выводы:
- Метрики для каждого класса рассчитываются, полагая данный класс положительным, а все остальные — отрицательными.
- Каждую метрику можно усреднить арифметически или взвешенно по классам. Весами выступают объемы классов.
- В модуле sklearn реализовано несколько алгоритмов усреднения они выбираются исходя их задачи.
- В случае средневзвешенного, F1-метрика может получиться не между P и R.
- Отчет о классификации содержит всю необходимую информацию в стандартной форме.
- Отчет показывает метрики для каждого класса, а так же объем каждого класса.
- Также отчет показывает средние и средневзвешенные метрики для всей модели.
- Отчет о классификации — обязательный элемент представления результатов моделирования.
- По отчету можно понять сбалансированность задачи, какие классы определяются лучше, какие — хуже.
PR-AUC
При рассмотрении разных моделей классификации мы упоминали о том, что они подразделяются на метрические и логические методы. Логические методы (дерево решений, k ближайших соседей) выдают конкретную метку класса,без какой-либо дополнительной информации. Метрические методы (логистическая регрессия, перцептрон, SVM) выдают принадлежность данного объекта к разным классам, присутствующим в задаче. При рассмотрении модели логистической регрессии мы говорили, что предсказывается положительный класс, если значение логистической функции больше 0,5.
Но это пороговое значение можно поменять. Что будет, если мы измени его на 0,6? Тогда мы для некоторых объектовы выборки изменим предсказание с положительного класса на отрицательный. То есть без изменения модели можно менять ее предсказания. Это значит, что изменятся и метрики модели, то есть ее эффективность.
Чем больше мы установим порог, тем чаще будем предсказывать отрицательный класс. Это значит, что в среднем, у модели будет меньше ложноположительных предсказаний, но может стать больше ложноотрицательных. Значит, у модели может увеличится precision, то упадет recall. В крайнем случае, если мы возьмем порог равный 1, мы всегда будем предсказывать отрицательный класс. Тогда у модели будет $P = 1, R = 0$. Если же, наоборот, возьмем в качестве порога 0, то мы всегда будем предсказывать отрицательный класс, а значит у модели будет $P = 0, R = 1$, так как она не будет давать ложноположительных прогнозов, но будут встречаться ложноотрицательные.
Это означает, что эффективность моделей метрической классификации зависит не только от того, как модель соотносится с данными, но и от значения порога. Из этого следует, кстати, что было бы не совсем правильно вообще сравнивать метрики двух разных моделей между собой. Ведь значение этих метрик будет зависеть не только от самих моделей, но и от порогов, которые они используют. Может, первая модель будет лучше, если немного изменить ее пороговое значение? Может, одна из метрик второй модели станет выше, если изменить ее порог.
Это все сильно затрудняет анализ метрических моделей классификации. Для сравнения разных моделей необходим способ “убрать” влияние порога, сравнить модели вне зависимости от его значения. И такой способ есть. Достаточно просто взять все возможные значения порога, посчитать метрики в каждом из них и затем усреднить. Для этого служит PR-кривая или кривая “precision-recall”:
Каждая точка на этом графике представляет собой значение precision и recall для конкретного значения порога. Для построения этого графика выбирают все возможные значение порога и отмечают на графике. Давайте рассмотрим простой пример из 10 точек. Истинные значения классов этих точек равны, соответственно, $y = lbrace 0, 0, 0, 0, 0, 1, 1, 1, 1, 1 rbrace$. Модель (сейчас совершенно неважно, какая) выдает следующие предсказания для этих объектов: $h(x) = lbrace 0.1, 0.2, 0.3, 0.45, 0.6, 0.4, 0.55, 0.7, 0.8, 0.9 rbrace$. Заметим, что модель немного ошибается для средних объектов, то есть она не будет достигать стопроцентной точности. Построим таблицу, в которой переберем некоторые значения порога и вычислим, к какому классу будет относиться объект при каждом значении порога:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,3 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,45 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0,4 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,55 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0,8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0,9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Можно сразу заметить, что чем выше порог, тем чаще предсказывается отрицательный класс. В крайних случаях модель всегда предсказывает либо положительный класс (при малых значениях порога), либо отрицательный (при больших).
Далее, для каждого значения порога рассчитаем количество истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных предсказаний. На основе этих данных легко рассчитать и метрики precision и recall. Запишем это в таблицу:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TP | 5 | 5 | 5 | 5 | 5 | 4 | 3 | 3 | 2 | 1 | 0 | |
| TN | 0 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 5 | 5 | 5 | |
| FP | 5 | 5 | 4 | 3 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | |
| FN | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 3 | 4 | 5 | |
| P | 0,50 | 0,50 | 0,56 | 0,63 | 0,71 | 0,80 | 0,75 | 1,00 | 1,00 | 1,00 | 1,00 | |
| R | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 |
При самом низком значении порога модель всегда предсказывает отрицательный класс, метрика recall равна 1, а метрика precision равна доли отрицательного класса в выборке. Причем ниже этого значения precision уже не опускается. Можно заметить, что в целом при повышении порога precision повышается, а recall понижается. В другом крайнем случае, когда порог равен 1, модель всегда предсказывает отрицательный класс, метрика recall равна 0, а precision — 1 (на самом деле эта метрика не определена, но считается равной именно 1, так как ее значение стремится к этому при повышении порога). За счет чего это происходит?
При повышении порога может произойти один из трех случаев. Первый заключается в том, что данное изменение может не влияет ни на одно предсказание. Так происходит, например, при повышении порога с 0,1 до 0,15. Оценка ни одного объекта не попадает в данный диапазон, поэтому ни одно предсказание не меняется. И, соответственно, не изменится ни одна метрика.
Если же повышение порога все-таки затрагивает один или несколько объектов, то изменение предсказания может произойти только с положительного на отрицательное. Допустим, для простоты, что повышение порога затрагивает только один объект. То есть мы изменяем предсказание по одному объекту с 1 на 0. Второй случай заключается в том, что это изменение правильное. То есть объект в действительности принадлежит отрицательному классу. Так происходит, например, при изменении порога с 0,15 до 0,2. В данном случае первый объект из ложноположительного стал истинно отрицательным. Такое изменение не влияет на recall, но повышает precision.
Третий случай заключается в том, что изменение предсказаные было неверным. То есть объект из истинно положительного стал ложноотрицательным. Это происходит, например, при изменении порога с 0,4 до 0,5 — в данном случае шестой объект становится классифицированным ошибочно. Уменьшение количества истинно положительных объектов снижает обе метрики — и precision и recall.
Таким образом можно заключить, что recall при повышении порога может оставаться неизменным или снижаться, а precision может как повышаться, так и понижаться, но в среднем будет повышаться за счет уменьшения доли ложноположительных предсказаний. Если изобразить рассмотренный пример на графике можно получить такую кривую:
PR-кривая не всегда монотонна, обе метрики могут изменяться как однонаправленно, так и разнонаправленно при изменении порогового значения. Но главный смысл этой кривой не в этом. При таком анализе очень просто обобщить эффективность модели вне зависимости от значения порога. Для этого нужно всего лишь найти площадь под графиком этой кривой. Эта метрика называется PR-AUC (area under the curve) или average precision (AP). Чем она выше, тем качественнее модель.
Давайте порассуждаем, ка будет вести себя идеальная модель. Крайние случаи, когда порога равны 0 и 1, значения метрик будут такими же, как и всегда. Но вот при любом другом значении порога модель будет классифицировать все объекты правильно. И обе метрики у нее будут равны 1. Таким образом, PR-кривая выродится в два отрезка, один из которых проходит из точки (0, 1) в точку (1, 1). и площадь под графиком будет равна 1. У самой худшей же модели метрики будут равны 0, так как она всегда будет предсказывать неверно. И площадь тоже будет равна 0.
У случайной модели, как можно догадаться, площадь под графиком будет равна 0,5. Поэтому метрика PR-AUC может использоваться для сравнения разных моделей метрической классификации вне зависимости от значения порога. Также эта метрика показывает соотношение данной модели и случайной. Если PR-AUC модели меньше 0,5, значит она хуже предсказывает класс, чем простое угадывание.
Выводы:
- Кривая precision-recall используется для методов метрической классификации, которые выдают вероятность принадлежности объекта данному классу.
- Дискретная классификации производится при помощи порогового значения.
- Чем больше порог, тем больше объектов модель будет относить к отрицательному классу.
- Повышение порога в среднем увеличивает precision модели, но понижает recall.
- PR-кривая используется чтобы выбрать оптимальное значение порога.
- PR-кривая нужна для того, чтобы сравнивать и оценивать модели вне зависимости от выбранного уровня порога.
- PR-AUC — площадь под PR-кривой, у лучшей модели — 1.0, у тривиальной — 0.5, у худшей — 0.0.
ROC_AUC
Помимо кривой PR есть еще один довольно популярный метод оценки эффективности метрических моделей классификации. Он использует тот же подход, что и PR-кривая, но немного другие координаты. ROC-кривая (receiver operating characteristic) — это график показывающий соотношение доли истинно положительных предсказаний и ложноположительных предсказаний в модели метрической классификации для разных значений порога.
В этой кривой используются два новых термина — доля истинно положительных и доля ложноположительных предсказаний. Доля истинно положительных предсказаний (TPR, true positive rate), как можно догадаться, это отношение количества объектов выборки, правильно распознанных как положительные, ко всем положительным объектам. Другими словами, это всего лишь иное название метрики recall.
А вот доля ложноположительных предсказаний (FPR, false positive rate) считается как отношение количества отрицательных объектов, неправильно распознанных как положительные, в общем количестве отрицательных объектов выборки:
[TPR = frac{TP}{TP + FN} = R \
FRP = frac{FP}{TN + FP} = 1 — S]
Обратите внимание, что FPR — мера ошибки модели. То есть, чем больше — тем хуже. У идеальной модели $FRP=0$, а у наихудшей — $FPR=1$. Для иллюстрации давайте рассчитаем эти метрики для нашего примера, который мы использовали выше (для дополнительной информации еще приведена метрика accuracy для каждого значения порога):
| y | h(x) | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TPR | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 | |
| FPR | 1,00 | 0,80 | 0,60 | 0,40 | 0,20 | 0,20 | 0,00 | 0,00 | 0,00 | 0,00 | |
| A | 0,50 | 0,60 | 0,70 | 0,80 | 0,80 | 0,70 | 0,80 | 0,70 | 0,60 | 0,50 |
Можно заметить, что при увеличении порога обе эти метрики увеличиваются, начиная со значения 1 до нуля. Причем, движения этих двух показателей всегда однонаправленно. Давайте опять же разберемся, почему так. Если увеличение порога приводит к правильному изменению классификации, то есть изменению ложноположительного значения на истинно отрицательное, то это уменьшит FRP, но не затронет TRP. Если же изменение будет неверным, то есть истинно положительное значение поменялось на ложноотрицательное, это однозначно уменьшит TPR, при этом FRP либо уменьшится так же, либо останется неименным.
В итоге, кривая получается монотонной, причем она всегда проходит через центр координат и через точку (1, 1). В нашем примере кривая будет выглядеть так:
Более сложные данные могут выглядеть с большим количеством деталей, но общая форма и монотонность сохраняются:
Также, как и с кривой PR, важное значение имеет площадь под графиком. Эта метрика называется ROC-AUC и является одной из самых популярных метрик качества метрических моделей классификации. Ее главное преимущество перед другими метриками состоит в том, что она позволяет объективно сопоставить уровень качества разных моделей классификации, решающих одну и ту же задачу, но обученных на разных данных. Это приводит к частому использованию ROC-AUC, например, в научной литературе для представления результатов моделирования.
Существует множество споров, какая диагностическая кривая более адекватно измеряет качество классификации — ROC или PR. Считается, что PR-кривая больше ориентирована на задачи, в которых присутствует дисбаланс классов. Это задачи в которых объектов одного класса значительно больше чем другого, классы имеют разное толкование и, как следствие, ошибки первого и второго рода не равнозначны. Зачастую это модели бинарной классификации. ROC же дает более адекватную картину в задачах, где классов примерно поровну в выборке. Но для полного анализа модели все равно рекомендуется использовать оба метода.
В случае с множественной классификацией построение диагностических кривых происходит отдельно по каждому классу. Так же, как и при расчете метрик precision и recall, каждый класс поочередно полагается положительным, а остальные — отрицательными. Каждая такая частная кривая показывает качество распознавания конкретного класса. Поэтому кривые могут выглядеть примерно так:
На данном графике мы видим PR-кривую модели множественной классификации из 3 классов. Кроме отдельных значений precision и recall в каждой точке рассчитываются и усредненные значения. Так формируется кривая средних значений. Интегральная метрика качества модели классификации считается как площадь под кривой средних значений. Алгоритм построения ROC-кривой полностью аналогичен.
Выводы:
- ROC-кривая показывает качество бинарной классификации при разных значениях порога.
- В отличие от PR-кривой, ROC-кривая монотонна.
- Площадь под графиком ROC-кривой, ROC_AUC — одна из основных метрик качества классификационных моделей.
- ROC_AUC можно использовать для сравнения качества разных моделей, обученных на разных данных.
- ROC чаще используют для сбалансированных и множественных задач, PR — для несбалансированных.
- Кривые для множественной классификации строятся отдельно для каждого класса.
- Метрика AUC считается по кривой средних значений.
Топ k классов
Все метрики, которые мы обсуждали выше оперируют точным совпадением предсказанного класса с истинным. В некоторых особых задачах может быть полезно немного смягчить это условие. Как мы говорили, метрические методы классификации выдают больше информации — степень принадлежности объекта выборки каждому классу. Обычно, мы выбираем из них тот класс, который имеет наибольшую принадлежность. Но можно выбрать не один класс, а несколько. Таким образом можно рассматривать не единственный вариант класса для конкретного объекта, а 3, 5, 10 и так далее.
Другими словами можно говорить о том, находится ли истинный класс объекта среди 3, 5 или 10 классов, которые выбрала для него модель. Количество классов, которые мы рассматриваем, можно брать любым. В данной метрике оно обозначается k. Таким образом, можно построить метрику, которая оценивает долю объектов выборки, для которых истинный класс находится среди k лучших предсказаний модели:
[tka(y, hat{f}) = frac{1}{n} sum_{i=0}^{n-1}
sum_{j=1}^{k} 1(hat{f_{ij}} = y_i)]
где $hat{f_{ij}}$ — это j-й в порядке убывания уверенности модели класс i-го объекта.
Рассмотрим такой пример. Пусть у нас есть задача классификации из 3 классов. Мы оцениваем 4 объекта, которые имеют на самом деле такие классы:
$y = lbrace 0, 1, 2, 2 rbrace$.
1
2
3
>>> import numpy as np
>>> from sklearn.metrics import top_k_accuracy_score
>>> y_true = np.array([0, 1, 2, 2])
Модель предсказывает следующие вероятности для каждого объекта:
1
2
3
4
>>> y_score = np.array([[0.5, 0.2, 0.2],
... [0.4, 0.3, 0.2],
... [0.2, 0.4, 0.3],
... [0.7, 0.2, 0.1]])
То есть для первого объекта она выбирает первый класс, но немного предполагает и второй. А вот, например, последний, четвертый объект она уверенно относит тоже к первому классу. Давайте посчитаем метрику топ-2 для этой модели. Для этого для каждого объекта рассмотрим, какие 2 класса модель называет наиболее вероятными. Для первого — это 0 и 1, для второго — также 0 и 1, причем модель отдает предпочтение 0 классу, хотя на самом деле объект относится к 1 классу. Для третьего — уже 2 и 2 класс, причем класс 1 кажется модели более вероятным, для четвертого — так же наиболее вероятными модели кажутся 0 и 1 класс.
Если бы мы говорили об обычной accuracy, то для такой модели она была бы равна 0,25. Ведь только для первого объекта модель дала правильное предсказание наиболее вероятного класса. Но по метрике топ-2, для целых трех объектов истинный класс находится среди двух наиболее вероятных. Модель полностью ошибается только в последнем случае. Так что эта метрика равна 0,75. Это же подтверждают и автоматические расчеты:
1
2
>>> top_k_accuracy_score(y_true, y_score, k=2)
0.75
Как мы говорили, количество классов k можно взять любым. В частном случае $k=1$ эта метрика превращается в классическую accuracy. Чем больше возьмем k, тем выше будет значение данной метрики, но слабее условие. Так что брать очень большие k нет никакого смысла. В другом крайнем случае, когда k равно количеству классов, метрика будет равна 1 для любой модели.
Эта метрика имеет не очень много практического смысла. Ведь при прикладном применении моделей машинного обучения важен все-таки итоговый результат классификации. И если модель ошиблась, то модель ошиблась. Но эта метрика может пролить свет на внутреннее устройство модели, показать, насколько сильно она ошибается. Ведь одно дело, если модель иногда называет правильный ответ может и не наиболее вероятным, но в топ, скажем, 3. Совсем другое дело, если модель не находит правильный ответ и среди топ-10. Так что эта метрика может использоваться для диагностики моделей классификации и для поиска путей их совершенствования. Еще она бывает полезна, если две модели имеют равные значения метрики accuracy, но нужно понять, какая их них адекватнее имеющимся данным.
Такие проблемы часто возникают в задачах, где классов очень много. Например, в распознавании объектов на изображениях количество объектов может быть несколько тысяч. А в задачах обработки текста количество классов может определяться количеством слов в языке — сотни тысяч и миллионы (если учитывать разные формы слов). Естественно, что эффективность моделей классификации в таких задачах, измеренная обычными способами будет очень низкой. А данная метрика позволяет эффективно сравнивать и оценивать такие модели.
Выводы:
- Эта метрика — обобщение точности для случая, когда модель выдает вероятности отнесения к каждому классу.
- Вычисляется как доля объектов, для которых правильный класс попадает в список k лучших предсказанных классов.
- Чем больше k, тем выше метрика, но бесполезнее результат.
- Эта метрика часто применяется в задачах с большим количеством классов.
- Применимость этой метрики сильно зависит от характера задачи.
Проблема пере- и недообучения
Проблема Bias/Variance
При решении задачи методами машинного обучения всегда встает задача выбора вида модели. Как мы обсуждали в предыдущих главах, существует большое количество классов модели — достаточно вспомнить линейные модели, метод опорных векторов, перцептрон и другие. Каждая их этих моделей, будучи обученной на одном и том же наборе данных может давать разные результаты. Важно понимать, что мы не говорим о степени подстройки модели к данным. Даже если обучение прошло до конца, найдены оптимальные значения параметров, все равно модели могут и, скорее всего, будут различаться.
Причем многие классы моделей представляют собой не одно, а целое множество семейств функций. Например, та же логарифмическая регрессия — это не одна функция, а бесконечное количество — квадратичные, кубические, четвертой степени и так далее. Множество функций или моделей, имеющих единую форму, но различающуюся значениями параметров составляет так называемое параметрическое семейство функций. Так, все возможные линейные функции — это одно параметрическое семейство, все возможные квадратические — другое, а, например, множество всех возможных однослойных перцептронов с 5 нейронами во входном, 3 нейронами в скрытом и одном нейроне в выходном слое — третье семейство.
Таким образом можно говорить, что перед аналитиком стоит задача выбора параметрического семейства модели, которую он будет обучать на имеющихся данных. Причем разные семейства дадут модели разного уровня качества после обучения. К сожалению, очень сложно заранее предугадать, какое семейство моделей после завершения обучения даст наилучшее качество предсказания по данной выборке.
Что является главным фактором выбора этого семейства? Как показывает практика, самое существенное влияние на эффективность оказывает уровень сложности модели. Любое параметрическое семейство моделей имеет определенное количество степеней свободы, которое определяет то, насколько сложное и изменчивое поведение может демонстрировать получившаяся функция.
Сложность модели можно определять разными способами, но в контексте нашего рассуждения сложность однозначно ассоциируется с количеством параметров в модели. Чем больше параметров, тем больше у модели степеней свободы, возможности изменять свое поведение при разных значениях входных признаков. Конечно, это не означает полной эквивалентности разных типов моделей с одинаковым количеством параметров. Например, никто не говорит, что модель, скажем, регрессии по методу опорных векторов эквивалентна модели нейронной сети с тем же самым количеством весов. Главное, что модели со сходным уровнем сложности демонстрируют сходное поведение по отношению к конкретному набору данных.
Влияние уровня сложности на поведение модели относительно данных наиболее наглядно можно проследить на примере модели полиномиальной модели. Степень полинома — это очень показательная характеристика уровня сложности модели. Давайте рассмотрим три модели регрессии — линейную (которую можно рассматривать как полином первой степени), полином второй и восьмой степени. Мы обучили эти модели на одном и том же датасете и вот что получилось:
Следует отдельно заметить, что в каждом из представленных случаев модель обучалась до конца, то есть до схождения метода численной оптимизации параметров. То есть для каждой модели на графике представлены оптимальные значения параметров. Гладя на эти три графика и то, как эти линии ложатся в имеющиеся точки, можно заметить некоторое противоречие. Естественно предположить, что модель, изображенная на втором графике показывает наилучшее описание точек данных. Но по любой метрике качества третья модель будет показывать более высокий результат.
Человек, глядя на график третьей модели, сразу сделает вывод, что она “слишком” хорошо подстроилась под имеющиеся данные. Сравните это поведение с первым графиком, который демонстрирует самую низкую эффективность на имеющихся данных. Можно проследить, как именно сложность модели влияет на ее применимость. Если модель слишком простая, то она может не выявить имеющиеся сложные зависимости между признаками и целевой переменной. Говорят, что у простых моделей низкая вариативность (variance). Слишком же сложная модель имеет слишком высокую вариативность, что тоже не очень хорошо.
Те же самые рассуждения можно применить и к моделям классификации. Можно взглянуть на форму границы принятия решения для трех моделей разного уровня сложности, обученных на одних и тех же данных:
В данном случае мы видим ту же картину — слишком простая модель не может распознать сложную форму зависимости между факторами и целевой переменной. Такая ситуация называется недообучение. Обратите внимание, что недообучение не говорит о том, что модель не обучилась не до конца. Просто недостаток сложности, вариативности модели не дает ни одной возможной функции их этого параметрического семейства хорошо описывать данные.
Слишком сложные модели избыточно подстраиваются под малейшие выбросы в данных. Это увеличивает значение метрик эффективности, но снижает пригодность модели на практике, так как очевидно, что модель будет делать большие ошибки на новых данных из той же выборки. Такая ситуация называется переобучением. Переобучение — это очень коварная проблема моделей машинного обучения, ведь на “бумаге” все метрики показывают отличный результат.
Конечно, в общем случае не получится так наглядно увидеть то, как модель подстраивается под данные. Ведь в случае, когда данные имеют большую размерность, строить графики в проекции не даст представления об общей картине. Поэтому ситуацию пере- и недообучения довольно сложно обнаружить. Для этого нужно проводить отдельную диагностику.
Это происходит потому, что в практически любой выборке данных конкретное положение точек, их совместное распределение определяется как существенной зависимостью между признаками и целевой переменной, так и случайными отклонениями. Эти случайные отклонения, выбросы, аномалии не позволяют сделать однозначный вывод, что модель, которая лучше описывает имеющиеся данные, является лучшей в глобальном смысле.
Выводы:
- Прежде чем обучать модель, нужно выбрать ее вид (параметрическое семейство функций).
- Разные модели при своих оптимальных параметрах будут давать разный результат.
- Чем сложнее и вариативнее модель, тем больше у нее параметров.
- Простые модели быстрые, но им недостает вариативности, изменчивости, у них высокое смещение (bias).
- Сложные модели могут описывать больше зависимостей, но вычислительно более трудоемкие и имеют большую дисперсию (variance).
- Слишком вариативные (сложные) модели алгоритм может подстраиваться под случайный шум в данных — переобучение.
- Слишком смещенные (простые) модели алгоритм может пропустить связь признака и целевой переменной — недообучение.
- Не всегда модель, которая лучше подстраивается под данные (имеет более высокие метрики эффективности) лучше.
Обобщающая способность модели, тестовый набор
Как было показано выше, не всякая модель, которая показывает высокую эффективность на тех данных, на которых она обучалась, полезна на практике. Нужно всегда помнить, что модели машинного обучения строят не для того, чтобы точно описывать объекты из обучающего набора. На то он и обучающий набор, что мы уже знаем правильные ответы. Цель моделирования — создать модель, которая на примере этих данных формализует некоторые внутренние зависимости в данных для того, чтобы адекватно описывать новые объекты, которые модель не учитывала при обучении.
Полезность модели машинного обучения определяется именно способность описывать новые данные. Это называется обобщающей способностью модели. И как мы показали в предыдущей главе, эффективность модели на тех данных, на которых она обучается, не дает адекватного понимания этой самой обобщающей способности модели. Вместе с тем, обобщающая способность — это главный показатель качества модели машинного обучения и у нас должен быть способ ее измерять.
Конечно, мы не можем измерить эффективность модели на тех данных, которых у нас нет. Поэтому для того, чтобы иметь адекватное представление об уровне качества модели применяется следующий трюк: до начала обучения весь имеющийся датасет разбивают на две части. Первая часть носит название обучающая выборка (training set) и используется для подбора оптимальных параметров модели, то есть для ее обучения. Вторая часть — тестовый набор (test set) — используется только для оценки эффективности модели.
Такая эффективность, измеренная на “новых” данных — объектах, которые модель не видела при своем обучении — дает более объективную оценку обобщающей силы модели, то есть эффективности, которую модель будет показывать на неизвестных данных. В машинном обучении часто действует такое правило — никогда не оценивать эффективность модели на тех данных, на которых она обучалась. Не то, чтобы этого нельзя делать категорически (и в следующих главах мы это часто будем применять), просто нужно осознавать, что эффективность модели на обучающей выборки всегда будет завышенной, ведь модель подстроилась именно к этим данным, включая все их случайные колебания.
Надо помнить, что все рассуждения и выводы в этой и последующих главах носят чисто вероятностный характер. Так что в конкретном случае, тестовая эффективность вполне может оказаться даже выше, чем эффективность на обучающей выборке. Когда мы говорим о наборах данных и случайных процессах, все возможно. Но смысл в том, что распределение оценки эффективности модели, измеренное на обучающих данных имеет значимо более высокое математическое ожидание, чем “истинная” эффективность этой модели.
Для практического применения этого приема надо ответить на два вопроса: как делить выборку и сколько данных оставлять на тестовый датасет. Что касается способа деления, здесь чуть проще — практически всегда делят случайным образом. Случайное разбиение выгодно тем, что у каждого объекта датасета равная вероятность оказаться в обучающей или в тестовой выборке. Причем, эта вероятность независима для всех объектов выборки. Это делает все случайные ошибки выборки нормально распределенными, то есть их математическое ожидание равно нулю. Об этом мы еще поговорим в следующей главе.
Алгоритм случайного разбиения, который используется чаще всего лежит в основе встроенной функции sklearn train_test_split(), которая как раз и разбивает выборку на две части в соответствии с заданной пропорцией. Так как этот алгоритм использует генератор случайных чисел, он будет давать разные результаты при разных запусках. То есть вы можете запустить один и тот же код два раза, и он покажет разные результаты. То есть модели будут обучаться на немного разных данных, а значит и метрики могут немного “плавать”.
Если по каким-то причинам вам важно обеспечить идентичную работу алгоритма при разных запусках, то для этого используют специальный аргумент random_state. Они присутствует в разных функциях sklearn, использующих случайность. Значение этого аргумента используется для инициализации встроенного генератора случайных чисел. После инициализации определенным числом он будет генерировать определенную последовательность случайных (точнее псевдослучайных) чисел. Это значит, что все случайные процессы будут протекать полностью идентично. Если изменить значение random_state, последовательность уже будет другой и результаты будут отличаться. Этот параметр нужен для обеспечения воспроизводимости результатов выполнения кода.
Но этот способ не работает в случае со специальными наборами данных. Например с временными рядами. Ведь при разбиении выборки важно, чтобы сами объекты в тестовой выборке были независимы от объектов обучающей. В случае, если мы анализируем какое-то неупорядоченное множество объектов, это почти всегда выполняется. Но для временных рядов это не так. Объекты более позднего времени могут зависеть от предыдущих объектов. Так цена актива за текущий период однозначно зависит от цены актива за предыдущий. Поэтому нельзя допустить, чтобы в обучающей выборке оказались объекты более ранние, чем в обучающей. Поэтому такие временные ряды делят строго хронологически — в тестовую выборку попадает определенное количество последних по времени объектов. Но анализ временных рядов сам по себе довольно специфичен как статистическая дисциплина, и как раздел машинного обучения.
Что касается пропорции деления, то, опять же, как правило, выборку разделяют в соотношении 80/20. То есть если в исходном датасете, например, 1000 объектов, то случайно выбранные 800 из них образуют обучающую выборку, а оставшиеся 200 — тестовую. Но это соотношение “по умолчанию” в общем-то ничем не обосновано. Его можно изменять в любую сторону исходя из обстоятельств. Но для этого надо понимать, как вообще формируется эта пропорция и что на нее влияет.
Что будет, если на тестовую выборку оставить слишком много данных, скажем, 50% всего датасета? Очевидно, у нас останется мало данных для обучения. То есть модель будет обучена на всего лишь небольшой части объектов, которых может не хватить для того, чтобы модель “распознала” зависимости в данных. Вообще, чем больше данных для обучения, тем в целом лучше, так как на маленьком объеме большую роль играют те самые случайные колебания. Поэтому модель может переобучаться. И чем меньше данных, тем переобученнее и “случайнее” будет получившаяся модель. И это не проблема модели, это именно проблема нехватки данных. А чем больше точек данных, тем больше все эти случайные колебания будут усредняться и это сильно повысит качество обученной модели.
А что будет, если наоборот, слишком мало данных оставить на тестовую выборку? Скажем, всего 1% от имеющихся данных. Мы же сказали, что чем больше данных для обучения, тем лучше. Значит, но обучающую выборку надо оставить как можно большую часть датасета? Не совсем так. Да, обучение модели пройдет более полно. Но вот оценка ее эффективности будет не такой надежной. Ведь такие же случайные колебания будут присутствовать и в тестовой выборке. И если мы оценим эффективность модели на слишком маленьком количестве точек, случайные колебания этой оценки будут слишком большими. Другими словами мы получим оценку, в которой будет сильно не уверены. Истинная оценка эффективности может быть как сильно больше, так и сильно меньше получившегося уровня. То есть даже если модель обучается хорошо, мы этого никогда не узнаем с точностью.
То есть пропорция деления выборки на обучающуюся и тестовую является следствием компромисса между полнотой обучения и надежность оценки эффективности. Соотношение 80/20 является хорошим балансом — не сильно много, но и не сильно мало. Но это оптимально для среднего размера датасетов. Если у вас очень мало данных, то его можно немного увеличить в пользу тестовой выборки. Если же данных слишком много — то в пользу обучающей. Кроме того, при использовании кросс-валидации размер тестовой выборки тоже можно уменьшить.Но на практике очень редько используются соотношения больше, чем 70/30 или меньше чем 90/10 — такое значения уже считаются экстремальными.
Выводы:
- Цель разработки моделей машинного обучения — не описывать обучающий набор, а на его примере описывать другие объекты реального мира.
- Главное качество модели — описывать объекты, которых она не видела при обучении — обобщающая способность.
- Для того, чтобы оценить обобщающую способность модели нужно вычислить метрики эффективности на новых данных.
- Для этого исходный датасет разбивают на обучающую и тестовую выборки. Делить можно в любой пропорции, обычно 80-20.
- Чаще всего выборку делят случайным образом, но временные ряды — только в хронологической последовательности.
- Обучающая выборки используется для подбора параметров модели (обучения), а тестовая — для оценки ее эффективности.
- Никогда не оценивайте эффективность модели на тех же данных, на которых она училась — оценка получится слишком оптимистичная.
Кросс-валидация
Как мы говорили ранее, маленькая тестовая выборка проблемна тем, что большое влияние на результат оценки эффективности модели имеют случайные отклонения. Это становится меньше заметно при росте объема выборки, но полностью проблема не исчезает. Эта проблема состоит в том, что каждый раз разбивая датасет на две выборки, мы вносим случайные ошибки выборки. Эта случайная ошибка обоснована тем, что две получившиеся подвыборки наверняка будут демонстрировать немного разное распределение. Даже если взять простой пример. Возьмем группу людей и разделим ее случайным образом на две половины. В каждой половине посчитаем какую-нибудь статистику, например, средний рост. Будут ли в двух группах выборочные средние точно совпадать? Наверняка нет. Обосновано ли чем-то существенным такое различие? Тоже нет, это случайные отклонения, которые возникают при выборке объектов из какого-то множества.
Поэтому разбиение выборки на тестовую и обучающую вносит такие случайные колебания, из-за которых мы не можем быть полностью уверены в получившейся оценке эффективности модели. Допустим, мы получили тестовую эффективность 95% (непример, измеренную по метрике accuracy, но вообще это не важно). Можем ли мы быть уверены, что это абсолютно точный уровень эффективности? Нет, ведь как любая выборочная оценка, то есть статистика, рассчитанная на определенной выборке метрика эффективности представляет собой случайную величину с некоторым распределением. А у этого распределения есть математическое ожидание и дисперсия. Как мы говорили в предыдущей главе, случайное разделение выборки на тестовую и обучающую приводит к тому, что распределение этой величины имеет математическое ожидание, совпадающее с истинным уровнем эффективности модели. Но это именно математическое ожидание. И у этой случайной величины есть какая-то ненулевая дисперсия. Это значит, что при каждом измерении, выборочная оценка может отклоняться от матожидания, то есть быть произвольно больше или меньше.
Есть ли способ уменьшить эту дисперсию, то есть неопределенность при измерении эффективности модели? Да, очень простой. Нужно всего лишь повторить измерение несколько раз, а затем усреднить полученные значения. Так как математическое ожидание случайных отклонений всегда предполагается равным нулю, чем больше независимых оценок эффективности мы получим, тем ближе среднее этих оценок будет к математическом ожиданию распределения, то есть к истинному значению эффективности.
Проблема в том, что эти измерения должны быть независимы, то есть производиться на разных данных. Но кратное увеличение тестовой выборки имеет существенные недостатки — соответствующее уменьшение обучающей выборки. Поэтому так никогда не делают. Гораздо лучше повторить случайное разбиение датасета на обучающую и тестовую выборки еще раз и измерить метрику эффективности на другой тестовой выборки из того же изначального датасета.
К сожалению, это означает, что и обучающая выборка будет другая. То есть нам необходимо будет повторить обучение. Но зато после обучения мы получим новую, независимую оценку эффективности модели. Если мы повторим этот процесс несколько раз, мы сможем усреднить эти значения и получить гораздо более точную оценку эффективности модели.
Имейте в виду, что все, что мы говорим в этой части применимо к любой метрике эффективности или метрике ошибки модели. Чаще всего, на практике измеряют метрики accuracy для моделей классификации и $R^2$ для регрессии. Но вы можете использовать эти методики для оценки любых метрик качества моделей машинного обучения. Напомним, что они должны выбираться исходя из задачи.
Конечно, можно реализовать это случайное разбиение руками и повторить процедуру оценивания несколько раз, но на практике используют готовую схему, которая называется кросс-валидация или перекрестная проверка. Она заключается в том, что датасет заранее делят на несколько равных частей случайным образом. Затем каждая из этих частей выступает как тестовый набор, а остальные вместе взятые — как обучающий:
На схеме части датасета изображены для наглядности непрерывными блоками, но на самом деле это именно случайные разбиения. Так что они буду в датасете “вперемешку”. Количество блоков, на которые делится выборка задает количество проходов или оценок. Это количество называется k. Обычно его берут равным 5 или трем. Это называется, 5-fold cross-validation. То есть на первом проходе блоки 1,2,3 и 4 в совокупность составляют обучающую выборку. Модель обучается на них, а затем ее эффективность измеряется на блоке 5. Во втором проходе та же модель заново обучается на данных их блоков 1,2,3 и 5, и ее эффективность измеряется на блоке 4. И таким образом мы получаем 5 независимых оценок эффективности модели. Они могут различаться из-за тех самых случайных оценок выборки. Но если посчитать их среднее, оно будет значительно ближе к истинному значению эффективности. Поэтому что статистика.
Количество проходов k еще определяет то, сколько раз будет повторяться обучение модели. Чем больше выбрать k, тем более надежными будут оценки, но вся процедура займет больше машинного времени. Это особенно актуально для моделей, которые сами по себе обучаются долго — например, глубокие нейронные сети. Надо помнить, что использование кросс-валидации сильно замедляет процесс обучения. Если же выбрать k слишком маленьким, то не будет главного эффекта кросс-валидации — усреднения индивидуальных оценок эффективности. Кроме того, чем больше k, тем меньшая часть выборки будет отводиться на тестовый набор. Поэтому k не стоит брать больше, скажем, 10, даже если у вас достаточно вычислительных мощностей.
Кросс-валидация никак не влияет на эффективность модели. Многие думают, что валидированные модели получаются более эффективными. Это не так, просто использование перекрестной проверки позволяет более точно и надежно измерить уже имеющуюся эффективность данной модели. И уж тем более кросс-валидация не может ускорить процесс обучения, совсем наоборот. Но несмотря на это, использование кросс-валидации с k равным 5 или, в крайнем случае, 3, совершенно обязательно в любом серьезном проекте по машинному обучению, ведь оценки, полученные без использования этой методики совершенно ненадежны.
В библиотеке sklearn, естественно, кросс-валидация реализована в виде готовых функций. Поэтому ее применение очень просто. В примере ниже используется кросс-валидация с количеством проходов по умолчанию для получения робастных оценок заранее выбранных метрик (precision и recall):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro','recall_macro']
>>> clf =
svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores =
cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time',
'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
Такой код просто оценивает значение метрик. Но обратите внимание, что он возвращает не просто одно значение метрики, но целый вектор. Это именно те индивидуальные оценки. Из них очень легко получить средние и выборочную дисперсию. Эта выборочная дисперсия как раз и показывает степень уверенности в данной оценке — чем она ниже, тем уверенность больше, как доверенный интервал в статистике. Кроме такого явного использования кросс-валидации для оценки метрик, она зачастую встроена в большое количество функций, которые используют ее неявно. О некоторых таких функциях, осуществляющих оптимизацию гиперпараметров модели, пойдет речь чуть позже.
Выводы:
- Разбиение выборки на обучающую и тестовую может внести случайные ошибки.
- Нужно повторить разбиение несколько раз, посчитать метрики и усреднить.
- Кросс-валидация разбивает выборку на $k$ блоков, каждый из которых используется по очереди как тестовый.
- Сколько задать $k$, столько и будет проходов. Обычно берут 3 или 5.
- Чем больше $k$ тем надежнее оценка, но дольше ее получение, так как модель каждый раз заново обучается.
- Использование кросс-валидации обязательно для получения робастных оценок.
- В библиотеке sklearn кросс-валидация (CV) встроена во многие функции.
Кривые обучения
Как мы говорили раньше, не следует ориентироваться на эффективность модели, измеренную на обучающей выборке, ведь она получается слишком оптимистичной. Но эта обучающая эффективность все равно может дать интересную информацию о работе модели. А именно с ее помощью можно оценить, переобучается модель или недообучается. В этой главе мы расскажем об одном из самых наглядных способов диагностики моделей машинного обучения — кривых обучения.
Построение кривых обучения может быть проведено после разделения датасета на обучающую и тестовую выборки. Происходит это следующим образом. Тестовый набор фиксируется и каждый раз используется один и тот же. Из обучающего набора же сначала берут малую часть, скажем 10% от общего количества точек в нем. Обучают модель на этой малой части, а затем измеряют ее эффективность на этой части и на постоянной тестовой выборке. Первая оценка называется обучающая эффективность (training score), а вторая — тестовая эффективность (test score). Затем повторяют процесс с чуть большей частью обучающей выборки, например, 20%, затем еще с большей и так, пока мы не дойдем до полной обучающей выборки.
На каждом этапе мы измеряем обучающую эффективность (измеренную именно на той части данных, на которых модель училась, не на полной обучающей выборке) и тестовую эффективность. Таким образом мы получаем зависимость эффективности модели от размера обучающей выборки. Эти данные можно построить на графике. Это график и называется кривой обучения (learning curve). Такой график может выглядеть, например, так:
В данном случае, на графике мы видим всего пять точек на каждой кривой. Верхняя кривая показывает обучающую эффективность, нижняя — тестовую. Значит, мы использовали всего пять делений обучающей выборки на подвыборки разного размера. Это размер как раз и отложен на горизонтальной оси. Сколько таких разбиений брать? Если взять слишком мало, то не будет понятна форма графика, а именно она нам важна для диагностики. Если же взять слишком много — то построение кривой обучения займет много времени, так как каждая точка на графике — это заново обученная модель.
Давайте объясним форму этого графика. Слева, когда обучающая выборка мала, обучающая эффективность довольно высока. Это вполне понятно, ведь чем меньше данных, тем проще модели к ним подстроиться. Помните, что через любые две точки можно провести линию (то есть линейную регрессию)? Это, конечно, крайний случай, но в общем, чем меньше обучающая выборка, тем большую эффективность одной и той же модели (параметрического семейства функций) можно на ней ожидать. А вот тестовая эффективность довольно маленькая. Это тоже понятно. Ведь на маленькой выборке модель не смогла обнаружить зависимости в данных так, чтобы эффективно предсказывать значение целевой переменной в новых данных. То есть она подстроилась под конкретные точки без какой-либо обобщающей способности.
Сперва отметим, что обычно кривые обучения демонстрируют некоторые общие тенденции. Например, при малых объемах обучающей выборки, обучающая эффективность модели может быть очень большой. Ведь чем меньше данных, тем проще подобрать параметры любой, пусть даже простой модели, так, чтобы эта модель ошибалась меньше. В самом предельном случае, вспомните, что через любые две точки можно провести прямую. Это значит, что линейная регрессия, обученная на двух точках, всегда будет давать нулевую ошибку или полную, 100%-ю эффективность. То же можно сказать и про квадратичную функцию, обученную на трех точках. Но и в целом, чем меньше данных, тем меньше можно ожидать суммарную ошибку любого рассматриваемого класса моделей на этих данных.
Тестовая же эффективность модели, обученной на малом объеме выборки, скорее всего будет очень невысокой. Это тоже естественно. Ведь модель видела всего малую часть примеров и не может подстроиться под какие-то глобальные зависимости в данных. Поэтому в левой части кривых обучения почти всегда будет большой зазор.
При повышении объема обучающей выборки обучающая же эффективность будет падать. Это связано в тем, что чем больше данных, тем больше пространства для ошибки для конкретной модели. Поэтому чем больше точек описывает модель, тем хуже она это делает в среднем. Это неизбежно и не страшно. Важно то, что тестовая эффективность наоборот, растет. Это происходит потому, что чем больше данных, тем больше вероятность того, что модель подстроится под существенные связи между признаками и целевой переменной, и таким образом, повысит обобщающую способность, свою предсказательную силу.
В итоге, кривая обучения показывает, как изменяется эффективность модели по сравнению к конкретному набору данных. В частности, именно с помощью кривых обучения можно предположить пере- и недообучение модели, что является главной целью диагностики моделей машинного обучения. Например, взглянув на график кривой обучения, приведенный выше, можно ответить на вопрос, хватает ли модели данных для обучения. Для этого можно спросить, улучшится ли тестовая эффективность модели, если добавить в датасет больше точек. Для этого можно мысленно продолжить кривую обучения вправо.
При построении кривых обучения обращайте внимание на деления вертикальной оси. Если вы строите графики с использованием библиотечных инструментов, то они автоматически масштабируются по осям. Имейте в виду, что одна и та же кривая обучения может выглядеть при разном масштабе совершенно по-разному. А навык сопоставления разных кривых очень важен при диагностике моделей. Лучше всего вручную задавать масштаб вертикальной оси и использовать один и тот же для всех графиков в одной задаче.
Обратите внимание, что на графике помимо самих кривых обучения присутствуют еще какие-то полосы. Что они значат? Дело в том, что при построении кривых обучения очень часто применяется кросс-валидация, о которой мы говорили в предыдущей главе. Ведь разбиение выборки на тестовую и обучающую вносит случайные ошибки. Поэтому для построения на кривых обучения более надежных оценок всех измеряемых оценок эффективности процесс повторяют несколько раз и усредняют полученные оценки. Каждая точка на графике — это не просто оценка эффективности, это среднее из всех кросс-валидированных оценок. Именно поэтому, кстати, в легенде нижняя линяя называется не test score, а cross-validation score. А ширина полосы вокруг точки определяется величиной дисперсии этих оценок. Чем шире полоса, тем больше разброс оценки на разных проходах кросс-валидации и тем меньше мы уверены в значении этой оценки. При построении кривых обучения эта неопределенность почти всегда выше при малых объемах обучающей выборки (слева на графике) и меньше — справа.
Выводы:
- Кривая обучения — это зависимость эффективности модели от размера обучающей выборки.
- Для построения кривых обучения модель обучают много раз, каждый раз с другим размером обучающей выборки (от одного элемента до всех, что есть).
- При малых объемах обучающая эффективность будет очень большой, а тестовая — очень маленькой.
- При увеличении объема обучающей выборки они будут сходиться, но обычно тестовая эффективность всегда ниже обучающей.
- Кривые обучения позволяют увидеть, как быстро модель учится, хватает ли ей данных, а также обнаруживать пере- и недообучение.
- Кривые обучения часто используют кросс-валидацию.
Обнаружение пере- и недообучения
Как мы говорили, построение кривых обучения — это исключительно диагностическая процедура. Именно они позволяют нам предполагать, к чему более склонна модель, обученная на конкретном наборе данных — к переобучению или к недообучению. Это важно, так как подходы у повышению эффективности в этих двух случаях будут совершенно противоположными. Давайте предположим, как будут вести себя на кривых обучения переобученные и недообученные модели.
Что будет, если модель слишком проста для имеющихся данных? При увеличении количества объектов в обучающей выборке, эффективность, измеренная на ней же будет вначале заметно падать по причинам, описанным выше. Но постепенно она будет выходить на плато и больше не будет уменьшаться. Это связано с тем, что начиная с какого-то объема выборки в ней будут превалировать нелинейные зависимости, слишком сложные для данной модели. С ростом объема обучающей выборки неизбежно растет тестовая эффективность, но так как модель слишком проста и не может ухватить этих сложных зависимостей в данных, то ее тестовая эффективность не будет повышаться сильно. Причем при достаточном объеме обучающей выборки тестовая и обучающая эффективности будут достаточно близкими. Другими словами, простые модели одинаково работают как на старых, так и на новых данных, но одинаково плохо.
А что будет происходить со слишком сложной моделью для существующих данных? Ее показатели в левой части графика будут аналогичны — высокая обучающая и низкая тестовая эффективности. Причины все те же. Но вот с ростом объема обучающей выборки, разрыв между этими двумя показателями не будет сокращаться так сильно. Модель, обученная на полном датасете покажет высокую эффективность на обучающей выборке, но гораздо более низкую — на тестовой. Это же практически определение переобучения — низкая ошибка, но отсутствие обобщающей способности. Это происходит, как мы уже обсуждали, за счет того, что слишком сложная модель имеет достаточный запас вариативности, чтобы подстроиться под случайные отклонения в данных.
Таким образом, недообученные и переобученные модели демонстрируют совершенно разное поведение на кривых обучения. А значит, недообучение и переобучения можно выявить, проанализировав поведение модели на графике. Типичное переобучение характеризуется большим разрывом между тестовой и обучающей эффективность. Признак типичного недообучения — низкая эффективность как на тестовой, так и на обучающей выборке. Но на практике, конечно, диагностика моделей машинного обучения не такая простая.
На данном графике представлены абстрактные картины, наиболее характерные для недообучения, переобучения, и ситуации, когда сложность модели оптимальна — мы назовем ее качественное обучение. Именно анализируя схожесть кривой обучения исследуемой модели с этими “идеальными” случаями, можно сделать обоснованный вывод о наличии недо- или переобучения модели.
Как вы могли заметить, мы нигде не говорим о четких критериях. Недо- и переобученность моделей — это вообще относительные понятия. И кривые обучения измеряют их только косвенно. Поэтому диагностика не сводится к оценке какой-либо метрики или статистики. Нам нужно оценить общую форму графика кривых обучения, что не является точной наукой. Возникает множество вопросов. Например, мы говорили, что большой зазор между тестовой и обучающей эффективностью — это признак переобучения. Но какой зазор считать большим? Это вопрос интерпретации. Точно так же, что считать низким уровнем эффективности? 50%? Может, 75%? Вообще это очень зависит от самой задачи. В некоторых задачах 80% accuracy — это выдающийся результат, а в других — даже 99% считается недостаточной точностью.
Поэтому рассматривая один график кривой обучения очень сложно понять, особенно без опыта анализа моделей машинного обучения, на что мы смотрим — на слишком простую недообученную модель, или на слишком сложную — переобученную. Вообще, строго говоря, большой зазор между эффективностями модели указывает на присутствующую в модели вариативность (variance), а низкий,не 100%-й уровень обучающей эффективности — на наличие в модели смещения (bias). А любые модели в той или иной степени обладают этими характеристиками. Вопрос в их соотношении друг к другу и к конкретному набору данных.
Чтобы облегчить задачу диагностики модели очень часто эффективность данной модели рассматривают не абстрактно, а сравнивают с аналогами. Практически всегда выбор моделей осуществляется от простого к сложному — сначала строят очень простые модели. Их тестовая эффективность может задать некоторых базовый уровень, планку, по сравнению к которой уже можно готовить об улучшении эффективности у данной, более сложной модели, насколько это улучшение существенно и так далее. Кроме того, строя кривые обучения нескольких моделей можно получить сравнительное представление о том, как эти модели соотносятся между собой, какие из них более недообученные, какие — наоборот.
Ситуация еще очень осложняется тем, что на практике вы никогда не получите таких красивых и однозначных кривых обучения, как в учебнике. Положение точек на кривых обучения зависит, в том числе и от тех самых случайных отклонений в данных, которые так портят нам жизнь. Поэтому в реальности графики могут произвольно искривляться, быть немонотонными. Тестовая эффективность вообще может быть выше обучающей. Что это начит для диагностики? Да в общем-то, ничего, это лишь свидетельствует об особом характере имеющихся данных. И, естественно, чем меньше данных, тем более явно проявляются эти случайности и тем менее показательными будут графики.
Достаточно сильно от этих случайных колебаний помогает применение кросс-валидации. Так как усреднение случайности — это и есть цель перекрестной проверки, она может быть полезна и для “сглаживания” кривых обучения. Еще надо помнить, что во многих библиотеках по умолчанию кривые обучения строятся на основе всего нескольких точек, то есть всего пяти-десяти вариантов размера обучающей выборки. Если такой график не дает достаточной информации, можно попробовать построить кривую по большему количеству точек. Но при этом и случайные колебания тоже могут проявиться сильнее.
Вообще, все факторы, которые улучшают “читаемость” кривых обучения, одновременно сильно замедляют их построение — кросс-валидация, использование большей выборки, построение большего количества точек. Помните, что это приводит к кратному увеличению количества циклов обучения модели.
Как мы говорили, поведение модели в целом не зависит от выбранной метрики, которую вы используете для построения кривых обучения. Поэтому зачастую используют не метрики эффективности, а метрики ошибок. Поэтому графики кривых обучения выглядят “перевернутыми” — тестовая ошибка больше, чем обучающая и так далее. Следует помнить, что все сказанное выше остается справедливым в этом случае, только следует помнить, где у модели высокая эффективность и малая ошибка.
На этом графике вы видите тоже идеальные случаи, но выраженные в терминах величины ошибки, а не эффективности. Можно проследить те же тенденции, но как бы “отраженные” по вертикальной оси.
Как мы говорили, реальные наборы данных, имеющие случайные колебания, ненадежные зависимости, случайные ошибки выборки могут существенно искажать кривые обучения. Рассмотри пример, приближенный к реальности. Возьмем датасет, содержащий рукописные цифры и обучим на нем классификатор по методу опорных векторов с гауссовым ядром. Для примера возьмем значение параметра “гамма”, который задает масштабирование функции расстояния в ядре, равным 0,008. Построив кривые обучения для этой модели мы получаем следующий график:
Данный график, несмотря на свою сложную форму достаточно легко интерпретируется. Мы видим, что обучающая эффективность равна 1 при любых объемах обучающей выборки. То есть модель разделяет классы полностью идеально. Но вот тестовая эффективность всегда остается гораздо ниже. И хотя она растет при увеличении объема обучающей выборки, все равно, даже при использовании полного набора данных, остается большой разрыв между тестовой и обучающей эффективностями модели. Налицо явное и типичное переобучение.
Теперь давайте уменьшим параметр “гамма” в четыре раза. В методе опорных векторов это может ограничить вариативность модели. Получаем следующий график кривых обучения:
Видно, что общее поведение модели значительно улучшилось. Обратите внимание на масштаб вертикальной оси. На первом графике мы говорили о разнице между тестовой и обучающей эффективностью в примерно 0,3. На этом же графике разница сократилась до примерно 0,025 — больше, чем в 10 раз. Это говорит о том, что модель очень сильно увеличила свою обобщающую способность. Давайте теперь уменьшим параметр еще в сто раз и посмотрим на кривую обучения:
Поведение модели явно не улучшилось. Хотя, итоговая эффективность тоже получается достаточно высокой (около 0,9), она все равно значительно меньше, чем в предыдущем случае. Другими словами, дальнейшее сокращение “гаммы” не пошло модели на пользу. Низкая тестовая эффективность и небольшая разница между тестовой и обучающей эффективностью — типичные признаки недообучения.
Обратите внимание, что интерпретация графика кривых обучения и, соответственно, диагностика модели, приобретает гораздо больше смысла к контексте сравнения нескольких моделей. Третья модель дает относительно неплохой результат с тестовой эффективностью в 0,9. Эту модель вполне можно признать валидной и качественно обученной, если бы мы не знали, что мы можем достичь точности в 0,975 (вторая модель).
Для сравнения рассмотрим результаты анализа еще одной модели на тех же самых данных — наивного байесовского классификатора с гауссовым распределением:
Хотя график сильно отличается от любого из трех предыдущих, самое главное, на что следует обратить внимание — низкое значение обучающей эффективности на полном наборе данных. Это показывает, что даже если мы продолжим добавлять данные в обучающую выборку, максимум, на который мы можем рассчитывать — это что тестовая эффективность приблизится к обучающей, которая все равно недостаточная (в данном примере меньше 0,9). Это свидетельствует о недообученности модели.
Как мы говорили, недообучение и переобучение — это условные понятия, которые называют распространенные ситуации при использовании моделей машинного обучения. Недообучение — это когда у модели низкая вариация и высокое смещение. Переобучение — это наоборот, когда низкое смещение и высокая вариация. На самом деле эти свойства в моделях присутствуют всегда. Более тщательный анализ может сделать вывод, что последняя модель имеет как высокую вариацию (что выражается в сильной разнице между эффективностями), так и высокое смещение (об этом говорит низкое значение обучающей эффективности).
Выводы:
- При недообучении тестовая и обучающая эффективности будут достаточно близкими, но недостаточными.
- При переобучении тестовая и обучающая эффективности будут сильно различаться — тестовая будет значительно ниже.
- Пере- и недообучение — это относительные понятия.
- Более простые модели склонны к недообучению, более сложные — к переобучению.
- Диагностика пере- и недообучения очень важна, так как для повышения эффективности предпринимаются противоположные меры.
- Для построения можно использовать функцию ошибки, метрику эффективности или метрику ошибки, важна только динамика этих показателей.
- Диагностика моделей машинного обучения — это не точная наука, здесь нужно принимать в расчет и задачу, и выбор признаков и многие другие факторы.
Методы повышения эффективности моделей
Регуляризация
Как мы говорили, диагностика моделей нужна для поиска путей повышения ее эффективности. И мы выяснили, что пере- и недообучение моделей напрямую связаны с уровнем сложности моделей. Можно рассмотреть гипотетический график, на котором показан уровень ошибок моделей на конкретном наборе данных в зависимости от уровня сложности этой модели. Пока мы не сталкивались с тем, как можно плавно менять уровень сложности модели в рамках одного параметрического класса. Но представим, что речь идет о полиномиальной модели, а по горизонтали отложена степень этого полинома.
Если модель слишком проста, то уровень тестовых и обучающих ошибок будет высок и достаточно близок друг к другу. Мы говорили об этом (правда другими словами, в терминах эффективности) в предыдущей главе. По мере увеличения сложности разрыв между этими уровнями ошибок будет в среднем увеличиваться. Это происходит за счет более глубокой подстройки модели именно к обучающей выборке. Причем уровень ошибок на обучающей выборке будет в среднем падать за счет повышения вариативности модели. Но уровень ошибок не может опуститься ниже нуля. Поэтому либо с какого-то момента он стабилизируется, либо будет асимптотически приближаться к 0. А это значит, что уровень тестовой ошибки неизбежно рано или поздно начнет повышаться с ростом сложности модели. Таким образом, у уровня тестовой ошибки есть некоторое оптимальное значение.
Другими словами, для любого конкретного датасета существует некоторый оптимальный уровень сложности модели, который дает наименьшую ошибку на тестовой выборке. Модели, имеющие более низкую сложность будут недообучаться, а более высокую — переобучаться. Поэтому существует задача нахождения этого оптимального уровня сложности. К сожалению, это не получится сделать методом обучения, или любой другой численной оптимизации, так как изменение уровня сложности модели требует запуска ее обучения заново. Мы не можем непрерывно менять уровень сложности, как какой-то дополнительный параметр модели.
Изучив несколько видов моделей обучения с учителем легко сделать вывод, что сложность модели — это некоторое “встроенное” свойство, которое определяется видом самой модели, то есть параметрическим классом функций, которые аппроксимируются этой моделью. Некоторые модели просто сложнее чем другие. Например, многослойный перцептрон гораздо сложнее линейной регрессии, а глубокое дерево решений сложнее более мелкого.
Выше мы определяли уровень сложности модели через количество ее параметров. Но стоит сказать, что численное значение этих параметров тоже имеет значение. Рассмотрим для примера две модели — линейную ($y = b_0 + b_1 x$) и квадратичную ($y = b_0 + b_1 x + b_2 x^2$). Очевидно, вторая модель сложнее, так как у нее больше параметров. Квадратичная функция имеет больше степеней свободы и демонстрирует нелинейное поведение — рост функции на разных участках может сильно отличаться.
Но что, если параметр $b_2$ у квадратичной модели будет очень маленьким, скажем, $b_2 = 0.0001$. Если у нас есть функция, например, $y = -8 + 15 x + 0.0001 x^2$, то взглянув на ее график мы не отличим ее от линейной. Да, формально она будет относиться к классу квадратичных функций, но на практике она будет почти прямой линией. Рост функции на разных участках будет отличаться, но очень незначительно. Тем более, что нас интересует поведение функции не на всей числовой прямой а в окрестностях имеющихся точек данных. Если на этом участке функция ведет себя как линейная, то для прикладной задачи она и эквивалентна линейной.
То есть чем ближе параметр $b_2$ к нулю, тем эффективно ближе квадратичная модель к линейной. Так можно сказать про любой параметр любой модели обучения с учителем. Только в более сложных моделях связь между конкретным параметром и уровнем сложности не так очевидна, так в случае с полиномиальными функциями. Но в любом случае, чем меньше в модели параметров, существенно отклоняющихся от нуля, тем она проще. Причем, это обычно не распространяется на свободный коэффициент $b_0$, у него особая роль — его значение смещает все предсказания модели (поэтому он часто называется параметром смещения). Его отличие от нуля несущественно. На этом эффекте основан один очень полезный и распространенный на практике математический прием, который позволяет гибко и очень удобно управлять сложностью параметрических моделей машинного обучения. Этот прием называется регуляризация.
Допустим, у нас есть набор данных и мы не знаем, модель какого вида подойдет к нему лучше — линейная или квадратичная. При прочих равных, квадратичная модель всегда даст меньшую величину ошибки и поэтому будет предпочтительнее. Но мы уже видели, что малая ошибка — не всегда показатель качества модели. Если обычная функция ошибки, основанная на суммарном отклонении значений данных от модели (которую мы рассматривали до этого), не дает адекватной оценки качества модели, может стоит ее как-нибудь изменить?
Функция ошибки — это по сути система штрафов. Каждый раз, когда модель ошибается, к значению ошибки прибавляется величина, пропорциональная отклонению. Это — штраф за ошибку модели. Но может быть, мы можем штрафовать что-нибудь еще? Например, уровень сложности модели. Представьте, что мы добавляем к ошибке некоторые штрафы за высокие значения параметров модели. Тогда алгоритм обучения, который минимизирует именно функцию ошибки будет не так сильно отдавать сложным переобученным моделям. Небольшие ошибки модели могут быть скомпенсированы тем, что модель становится более простой.
Причем эти штрафы очень легко выражаются математически. Если штраф за ошибки модели — это некоторое математическое выражение, основанное на отклонениях предсказанных значений от эмпирических, то штрафы за сложность модели — это выражение, основанное на отклонениях параметров самой модели от нуля. Существует несколько конкретных реализаций регуляризации и о них мы поговорим чуть далее. Кстати, регуляризация обычно не затрагивает свободный коэффициент. Причины этого мы только что обсуждали — он не влияет на сложность модели.
В этом и состоит идея регуляризации — модификация функции ошибки таким образом, чтобы штрафовать сложные модели в пользу более простых. Да, достаточно странно складывать отклонения целевой переменной (которые могут быть выражены в натуральных единицах) и безразмерные параметры модели. Это может выглядеть, как сложение метров с красным. Регуляризация — это именно математический трюк. У нее нет физического значения, какой-то внятной интерпретации в терминах предметной области.Это лишь способ отдавать предпочтение моделям с низкими значениями параметров, ведь такие модели ведут себя как более простые и поэтому менее склонны к переобучению.
Можно заметить, что регуляризация — это способ искусственно понизить сложность модели. То есть при использовании регуляризации берут модель более сложную, которая в “чистом” виде будет явно переобучаться на имеющихся данных. Но за счет этих дополнительных штрафов, ее сложность принижают. Причем, самое удобное в регуляризации то, что она параметрическая. То есть соотношением “силы” штрафа за ошибки и штрафа за сложность легко управлять, введя множитель — так называемый параметр регуляризации. Чем он больше, тем сильнее штрафуются сложные модели, то есть даже большие ошибки модели могут быть скомпенсированы небольшим понижением сложности. Таким образом, возвращаясь к графику в начале главы, именно параметр регуляризации может быть отложен на нем по горизонтали.
Регуляризация настолько удобна и универсальна, что большинство библиотечных реализаций тех моделей, которые мы проходили раньше, уже реализуют встроенную регуляризацию. Причем это относится равно как к моделям классификации, так и к моделям регрессии, это прием не зависит от типа задачи обучения с учителем. За счет способности уменьшить сложность любой модели регуляризация является одним их основных способов борьбы с переобучением.
Обратите внимание, что мы в основном говорим именно о борьбе с переобучением. Борьба с недообучением в основном сводится к использованию более сложной модели. В настоящее время разработаны настолько сложные модели, что узким местом современного машинного обучения становятся вычислительные мощности и доступность данных.
Выводы:
- Регуляризация — это способ искусственно ограничить вариативность моделей.
- При использовании регуляризации можно применять более сложные модели и снижать склонность к переобучению.
- Регуляризация модифицирует функцию ошибки модели, добавляя в нее штрафы за повышение сложности.
- Основная идея регуляризации — отдавать предпочтение низким значениям параметров в модели.
- Регуляризация обычно не затрагивает свободный коэффициент $b_0$.
- Регуляризация обычно параметрическая, можно управлять ее степенью.
Ridge
Зачастую переобучение модели, которое является следствием большого количества параметров в модели, появляется потому, что в наборе данных присутствует много “лишних” атрибутов. Количество параметров любой модели обучения с учителем зависит от количества признаков в данных. Для борьбы с этим явлением используется регуляризация. Как мы говорили, регуляризация “штрафует” отклонения параметров модели (за исключением свободного) от нуля. Совершенно естественно формализовать это отклонение так же, как и в самой функции ошибки — как сумму квадратов этих значений. Такая модель называется гребневой регрессией (ridge regression). В ней функция ошибки принимает такой вид:
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} b_j^2]
Как мы можем видеть, что функция ошибки аналогична обычной модели регрессии, но имеет одно дополнительное слагаемое — регуляризационный член. Это сумма квадратов значений параметров модели (начиная с первого). Эта сумма умножается на специальный параметр — параметр регуляризации $lambda$. Он как раз отвечает за “силу” регуляризации модели. В передельном случае, когда $lambda = 0$, мы имеем обычную нерегуляризованную регрессию. Чем больше этот параметр, тем сравнительно больший вклад в ошибку дают отклонения параметров модели. То есть, чем больше этот параметр, тем более простые модели мы будем получать после обучения, при достижении минимума этой функции. Естественно, параметр регуляризации не может быть отрицательным, так как в таком случае мы наоборот, будем отдавать предпочтение более сложным моделям. А сложность, как и ошибка могут возрастать неограниченно.
Но если мы модифицируем функцию ошибки, то это влечет изменение и метода градиентного спуска. На самом деле он меняется незначительно. Вспомним, что градиентный спуск основан на вычислении частной производной функции ошибки по параметрам модели. Если взять свободный параметр, то вообще ничего не меняется, так как регуляризационный член от него не зависит:
[frac{partial}{partial b_0} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_0} h_b(x_i)]
Если же рассматривать другие параметры модели, то в выражение производной добавится всего одно небольшое слагаемое:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i) + 2 lambda b_i]
Это слагаемое $2 lambda b_i$ как раз и будет учитывать значения параметров при выполнении шагов градиентного спуска в регуляризованной модели регрессии. В остальном метод обучения никак не меняется. Если мы рассматриваем линейную модель, то получается почти знакомое нам по предыдущим главам выражение:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot x_i + 2 lambda b_i]
Как мы уже говорили, этот прием может быть применен как к задачам классификации, так и к задачам регрессии. Но применяя регуляризованные модели на практике стоит быть внимательнее. Дело в том, что в некоторых моделях (например, в методе опорных векторов) регуляризация задается чуть иначе:
[J(vec{b}) = С frac{1}{m} sum_{i=1}^{m} cost(h_b(x_i) , y^{(i)}) + sum_{j=1}^{n} b_j^2]
Где $C$ — это тоже параметр регуляризации. Обратили внимание, что этот множитель стоит перед другим слагаемым — самой функцией ошибки? Численно, это эквивалентно предыдущей формализации, если полагать, что $C = frac{1}{lambda}$. Но стоит помнить, что в такой форме чем больше $C$, тем меньше регуляризации присутствует в модели.
Гребневую регрессию еще называют регрессией по L2-норме (L2 означает норма Лагранжа второго порядка) или регуляризацией Тихонова. Простыми словами это означает, что мы считаем сумму квадратов параметров.Гребневая регрессия полезна тем, что она может помочь повысить эффективность модели, если в данных присутствует большое количество мультиколлинеарных факторов, то есть атрибутов, которые очень сильно зависят друг от друга. Вообще, мультиколлинеарность в статистике — это в принципе не очень хорошее явление. В машинном обучении она опасна тем, что оптимальные параметры модели становятся гораздо менее устойчивыми, а значит обучение будет не очень надежным. Ну и вдобавок, большое количество признаков, как мы уже говорили, увеличивает количество параметров и порядок сложности модели, что приводит к переобучению. На практике мультиколлинеарные признаки можно обнаруживать и удалять из датасета руками, но гребневая регрессия может это делать автоматически.
Рассмотрим работу гребневой регрессии на примере. Для лучшего понимания того, как регуляризация влияет на получаемую модель, мы возьмем одни и те же данные и построим одну и ту же модель классификации с L2 регуляризацией, но с разными значениями параметра регуляризации. В качестве базовой модели мы используем полином пятой степени. Для начала классификация без регуляризации ($lambda=0$):
Мы видим достаточно сложную границу принятия решения и высокую точность модели — на этих данных эта модель показывает 0,91 accuracy. Давайте возьмем $lambda=2$:
За счет использования регуляризации точность модели немного снизилась и составила 0,89. Граница принятия решения тоже стала более гладкой и простой.
Обратите внимание, что расположение границы принятия решения полностью изменилось по сравнению с первой моделью. Ведь параметр регуляризации — это не то же самое, что и обычный параметр модели, коэффициент в функции. Один и тот же алгоритм, обученный с разными значениями параметра регуляризации даст две совершенно разные модели, не имеющие ничего общего. Поэтому нельзя, например, плавно менять параметр регуляризации и смотреть, как изменится граница принятия решения. И физического смысла параметр регуляризации никакого не несет. Это лишь численная переменная в алгоритме обучения, которая влияет на то, какая модель из определенного параметрического класса будет считаться оптимальной для данной задаче. В дальнейшем такие “сложные” параметры мы будем называть гиперпараметрами.
Увеличим регуляризацию еще больше и получим такую модель:
Точность снизилась еще больше — до 0,85. Очевидно, что точность регуляризованных моделей будет меньше, так как функция ошибки может “променять” точность на упрощение модели. Но в метриках эффективности сложность модели не учитывается, поэтому они падают. Ну и граница принятия решения тоже становится все более плоской.
Рассмотрим влияние регуляризации на модель регрессии. Для этого также возьмем один и тот же набор данных и будем строить на нем разные модели. Также будем использовать полиномиальные признаки пятой степени. Но на этот раз обратим внимание и на сами коэффициенты модели. Для начала посмотрим на модель практически без регуляризации ($lambda=0.1$):
Эта модель имеет точность 0,714 (по метрике r-квадрат) и следующие коэффициенты — 0, -2.84, -4.49, 8.03, -2.92, 0.34. Как видно, все полиномиальные признаки имеют влияние на модель, коэффициенты при них отличаются от нуля существенн. Теперь добавим регуляризацию ($lambda=1$):
Точность модели немного упала — до 0,712. Теперь взглянем на коэффициенты: 0, -2.51, -0.97, 4.48, -1.76, 0.22. Заметно, что все они сильно уменьшились (в абсолютном выражении), особенно третий и четвертый. Это как раз и есть влияние регуляризации — она стремится держать коэффициенты как можно более близкими к нулю, даже за счет понижения точности. А параметр регуляризации — это своего рода “обменный курс” между коэффициентами и точностью. Давайте поднимем его еще сильнее (до $lambda=100$):
Точность модели понизилась более существенно — до 0,698. А вот ее коэффициенты: 0, 0.13, 0.37, 0.49, -0.04, 0.01. По мере увеличения регуляризации ни один из коэффициентов не удалялся от нуля. А некоторые вплотную к нему приблизились. При этом заметим, что ни один коэффициент не стал нулем — гребневая регрессия даже с запредельным уровнем регуляризации стремится оставить в модели все имеющиеся признаки.
Выводы:
- $lambda > 0$ — параметр регуляризации.
- Чем он больше, тем сильнее штрафуются сложные модели.
- Этот прием может применяться как к классификации, так и к регрессии.
- Ridge еще называют регуляризацией по L2-норме. Она же — гребневая регрессия.
- Такая регуляризация делает параметры более робастными к мультиколлинеарности признаков.
Lasso
У гребневой регрессии есть один недостаток, проявляющий себя при работе с данным, в которых есть много “лишних” признаков — она всегда включает в модель все признаки. Но параметры у них могут быть близки к нулю, что затрудняет интерпретацию модели и не сокращает размерность задачи. На практике в данных могут присутствовать не просто мультиколлинеарные атрибуты, но и такие, которые имеют очень маленькое влияние на целевую переменную или не имеют его вообще. Включать их в модель не имеет никакого смысла.
Для решения этой проблемы существует так называемая лассо-регрессия. Она по своей формализации очень похожа на гребневую, но чуть по-другому учитывает значения параметров модели:
[J(vec{b}) = sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} mid b_j mid]
В данном случае говорят о регуляризации по L1-норме. За счет того, что функция абсолютного значения, которая используется здесь не везде дифференцируема, для обучения такой модели используется специальный метод координатного спуска (coordinate descent), а не градиентного. Но рассмотрение всех вариантов алгоритмов обучения выходит за рамки данного пособия. В остальном же использование лассо на практике абсолютно идентично другим моделям обучения с учителем.
Из-за своей специфической формализации, модель лассо стремиться обратить в ноль как можно больше параметров модели. Это значит, что если какой-то признак не оказывает сильного влияния на целевую переменную, то модель с L1-регуляризацией с большой долей вероятности “занулит” этот признак. Это бывает очень полезно в задачах, где в данных присутствует больше количество ненужной информации. Такие задачи еще часто называют разреженными. К ним часто относятся, например, задачи анализа текстов.
В таких задачах регрессия по методу лассо может использоваться для отбора признаков. Часто эта модель потом вообще не используется, а на оставшихся признаках строится какая-то другая модель обучения с учителем. Так лассо-регрессия может играть вспомогательную роль. Регрессию лассо поэтому часто называют методом понижения размерности — после ее применения в модели остаются (ненулевыми) только те признаки, которые действительно влияют на значение целевой переменной. Хотя это не совсем то, что называют понижением размерности в задачах обучения без учителя.
Также как и любая регуляризация, лассо управляет компромиссом между bias и variance модели за счет введения параметра регуляризации. Он имеет точно такой же смысл, как и в гребневой регрессии — чем он больше численно, тем более простые модели будет предпочитать этот алгоритм. Можно построить график зависимость обучающей и тестовой эффективностей модели от значения параметра регуляризации:
Здесь мы видим, что при малых значениях этого параметра наблюдается большая разница между эффективностями. ПО мере увеличения значения параметра регуляризации сложность, а следовательно и обучающая эффективность модели падают, а разница между ними сокращается. Тестовая же эффективность поначалу растет, но начиная в определенного значения параметра регуляризации (в районе $10^{-1}$) снова начинает снижаться. В левой части этого графика мы наблюдаем ситуацию переобучения, а в правой — недообучения. А примерно $10^{-1}$ — это оптимальное значение параметра регуляризации, при котором получается наиболее качественная модель линейной регрессии.
Давайте построим регрессию по методу лассо на тех же данных, на которых строили в предыдущей главе гребневую регрессию. На этот раз ограничимся одной моделью со средним уровнем регуляризации ($lambda=1$):
Обратим внимание на коэффициенты модели: 0, 0, 0, 0.55, 0, 0. Даже при таком небольшом значении параметра регуляризации модель оставила только один признак — признак третьей степени (что мы и видим на графике — это кубическая парабола, только масштабированная по вертикали). В этом и проявляется действие алгоритма лассо — он стремится как можно больше коэффициентов обратить в ноль.
Lasso, кстати, расшифровывается как least absolute shrinkage and selection operator, оператор наименьшего абсолютного сокращения и выбора.
В данном примере можно сделать вывод, что среди полиномиальных признаков только признак третьей степени оказывал сколь-нибудь существенное влияние на целевую переменную. Таким образом, регрессия по методу лассо работает как алгоритм отбора признаков. В дальнейшем можно используя только этот один признак строить и другие модели машинного обучения на данной задаче, или просто ввести его в датасет, таким образом лассо станет основой для инжиниринга признаков.
Выводы:
- Lasso еще называют регуляризацией по L1-норме.
- Lasso заставляет модель использовать меньше ненулевых коэффициентов.
- Фактически, эта регуляризация уменьшает количество признаков, от которых зависит модель.
- Может использоваться для отбора признаков.
- Полезна в задачах с разреженной матрицей признаков.
Elastic net
После прочтения двух предыдущих разделов может появиться вопрос: какой метод регуляризации лучше? Как всегда не существует универсального ответа. Это целиком зависит от данных. С разреженностью признаков лучше справляется лассо, а с мультиколлинеарностью — гребневая модель. Как всегда, когда есть два подхода, каждый со своими преимуществами, есть способ их скомбинировать. Рассмотрим модель, которая обычно называется elastic net или “эластичная сеть”:
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 +
lambda_1 sum_{j=1}^{n} | b_j | + lambda_2 sum_{j=1}^{n} b_j^2]
Как мы видим, функция ошибки такой модели комбинирует подходы гребневой и лассо-регрессии. То есть включает в себя регуляризацию и по L1 и по L2 нормам. Поэтому в этой модели присутствует целых два параметра регуляризации, причем они независимы друг от друга и задают не только соотношение регуляризации того или иного типа и классической функции ошибки, но и соотношение силы двух типов регуляризации между собой.
А между тем мы еще не говорили о том, как подбирать оптимальные значение параметров регуляризации. А ведь это достаточно серьезная проблема. Их не подберешь обычным методом обучения — это не просто параметры модели. Чуть позже мы назовем их гиперпараметрами. Но подбирать их можно только непосредственной проверкой, то есть подбором в классическом смысле. И это достаточно трудоемкий процесс, так как надо проверить потенциально бесконечное количество значений, причем еще хорошо бы использовать кросс-валидацию для надежности результатов.
А как быть с двумя гиперпараметрами. Обычно их значения подбираются “наивным” способом, в два прохода. Сначала находится оптимальный параметр $lambda_2$ для гребневой регрессии, а потом он фиксируется и подбирается наилучший параметр $lambda_1$ для лассо. Понятно, что они могут зависеть еще и друг от друга. И чуть позже мы изучим более вычислительно емкий, но правильный способ искать оптимальные значения гиперпараметров.
Давайте построим регрессию методом эластичной сети по уже известным нам данным из двух предыдущих глав. В данном случае используем $lambda_1 = lambda_2 = 10$:
Коэффициенты у модели следующие: 0, 0, 0, 0, 0.202, -0.016. Очень заметно совместное влияние двух регуляризаций. L1 выбирает только самые значимые признаки, оставляя у других коэффициенты равными нулю, а L2 еще приближает к нулю оставшиеся коэффициенты. В результате получается очень компактная модель, которая имеет только очень обоснованные коэффициенты.
Конечно, приведенные в данных главах модели не являются обязательно лучшими или оптимальными для решения данной задачи регрессии. Их цель — проиллюстрировать работу алгоритмов и для этого зачастую приходилось на максимум “выкручивать” регуляризацию. В реальности надо искать оптимальный уровень регуляризации, но об этом речь пойдет в следующих главах.
Выводы:
- По сути, это комбинация регуляризации по L1 и L2 нормам.
- Имеет два параметра, которые определяют соотношение соответствующих норм.
- Комбинирует достоинства предыдущих двух методов.
- Недостаток в необходимости задавать сразу два параметра регуляризации.
Методы борьбы с недообучением
В этой главе мы говорим о диагностике моделей машинного обучения в контексте диагностики недо- и переобучения. И мы много говорили о том, как обнаружить эти состояния модели. Так что же делать, если мы обнаружили, что наша модель недообучается. Сейчас поговорим о типичных путях повышения эффективности моделей. И начнем с более простого случая — недообучения.
В первую очередь напомним себе, что такое недообучение. Это ситуация, когда модель демонстрирует слишком большой bias по отношению к имеющимся данным. Модели не хватает вариативности, чтобы “ухватить” зависимости между признаками и целевой переменной. С точки зрения модели, их вообще нет. Простыми словами можно сказать, что модель слишком проста, примитивна для решения поставленной задачи. При этом может быть такое, что имеющиеся данные действительно не содержат необходимой информации, позволяющей надежно предсказать значение целевой переменной.
Поэтому при недообучении первое о чем нужно подумать: есть ли в датасете информация (признак или комбинация признаков), которые бы определяли значение целевой переменной. Если таких нет, то неважно, сколько точек данных, примеров мы соберем, модель всегда будет недообучаться. Неважно, насколько сложную модель мы будем использовать, она покажет случайных шум. Наиболее эффективный способ борьбы с недообучением — инжиниринг признаков. Необходимо ввести в модель признаки (или атрибуты, неважно, важно чтобы была нужная информация), которые позволят модели предсказать значение целевой переменной.
Помните, как мы решали задачу с полиномиальными признаками, как они превращали нерешаемую задачу классификации в линейно разделимую? Так может произойти в любой задаче. Может, одного свойства объекта нам и не хватает, чтобы превратить случайный перемешанный набор точек в многомерном пространстве в четкую и очевидную зависимость.
К сожалению, нет универсального алгоритма инжиниринга признаков. Это всегда творческая деятельность, которая требует, причем, глубокого знания предметной области. Иногда нужно просто вернуться на этап сбора данных и найти (или сгенерировать) больше информации. Иногда помогает вдумчивое и осмысленное преобразование имеющихся атрибутов. Главный вопрос, который надо себе задать: что в реальности влияет на целевую переменную? Затем собирать как можно больше информации об этом, добавлять ее в модель в виде признаков и надеяться, что это повысит эффективность моделей.
Если такой возможности нет, то очевидно, имеет смысл уменьшить степень регуляризации модели. Конечно, этот способ подходит только, если вы используете регуляризованные модели. Но как мы уже обсуждали выше, очень многие модели используют регуляризацию автоматически. А если она применяется, то можно легко манипулировать ее степенью. Понижение регуляризации приведет к тому, что после обучения мы получим более сложную и вариативную модель, что может исправить ситуацию с недообучением.
Другой очевидный способ — использование более сложных моделей в целом. Имеется в виду смена класса моделей. Если недообучается, например, модель линейной регрессии, стоит попробовать дерево решений. Если недообучилась логистическая — попробуйте многослойный перцептрон. Хотя, регуляризация обычно работает более эффективно, чем использование более сложной модели, она ограничена рамками одного параметрического класса функций.
Возможно стоит попытаться повторить обучение или увеличить количество итераций обучения. Возможна ситуация, когда существующего количества итераций недостаточно для схождения метода обучения к локальному минимуму функции ошибки. Это опять же может происходить вследствие того, что задача слишком сложна. В особо сложных случаях можно использовать предобученные модели. Это так называемое трансферное обучение — когда используют уже обученную модель на каком-то одном наборе данных для решения подобной задачи на другом датасете. Например, существуют так называемые глубокие языковые модели — огромные нейросети с миллиардами параметров, которые обучаются на гигантских корпусах текстов. Они используются для разнообразных задач текстовой аналитики. Конечно, каждый раз нецелесообразно обучать такую огромную модель с нуля — можно воспользоваться уже обученной и дообучить ее (или обучить, например, только последний слой нейронной сети) под собственную задачу. Трансферное обучение — отдельная и очень интересная дисциплина машинного обучения, но ее подробное рассмотрение выходит за рамки этого пособия.
Отдельно стоит сказать, что не поможет при недообучении. Вам вряд ли поможет увеличение объема выборки. Многие думают, что собрать больше данных — это универсальный рецепт эффективности. Это тоже не так. Хотя, большая по объему выборка особенно и не помешает, то есть не уменьшит эффективность модели, она увеличит вычислительную емкость. Другими словами, модель будет обучаться значительно дольше, но без видимого положительного эффекта по эффективности.
Обратите внимание, что мы здесь всегда имеем в виду эффективность, измеренную на тестовой выборке. А еще лучше — с использованием кросс-валидации. Эффективность на обучающей выборке нужна только для диагностики и анализа моделей.
Стоит помнить, что машинное обучение — это всегда итеративный процесс. Построив первую модель нужно ее исследовать и пытаться улучшить, увеличить эффективность. При этом возможно стоит попробовать множество разных видов моделей и способов обработки данных.
Выводы:
- Ввести в модель новые данные об объектах (атрибуты).
- Уменьшение степени регуляризации модели.
- Введение полиномиальных и других суррогатных признаков.
- В целом, инжиниринг признаков.
- Использование более сложных моделей.
- Увеличение количества итераций.
- Трансферное обучение.
Методы борьбы с переобучением
Переобучение на практике более частая и более коварная проблема потому, что несложно взять для решение конкретной задачи более сложную модель. Гораздо труднее заставить ее работать хорошо на новых данных. Проблему переобучения обнаружить сложнее и потому, что при этой ситуации модель работает вроде бы хорошо — дает низкую ошибку на данных. Но на других точках модель почему-то начинает ошибаться гораздо сильнее.
Опять же вспомним, что суть ситуации переобучения состоит в том, что модель оказывается слишком сложной для имеющихся данных и зависимостей в них. Поэтому вместо общих тенденций модель начинает обращать внимание на конкретное расположение точек в обучающей выборке, на случайные флуктуации, которые не несут смысловой нагрузки и не будут повторяться в новых данных.
Чем меньше данных присутствует в обучающей выборке, тем больше в них “шума” по отношению к полезному “сигналу” — информации о случайных колебаниях значений признаков по сравнению с информацией о тенденциях и реальных зависимостях. Поэтому неудивительно, что на малых объемах данных при прочих равных модели склонны к переобучению. Взгляните на график выше — даже человеку неочевидно, что точки выборки образуют линейную тенденцию — их просто слишком мало, чтобы показать эту тенденцию.
Самый действенный способ борьбы с переобучением — собрать больше обучающих примеров.
Если мы добавим больше точек, принадлежащих тому же распределению, мы неизбежно более четко увидим имеющуюся тенденцию. Все дело в том, что основное свойство случайных колебаний — их математическое ожидание равно нулю. То есть значение показателя может под воздействием неизвестных или неучтенных факторов отклоняться от “правильного” значения как в сторону увеличения, так и в сторону уменьшения. Причем вероятность этого примерно равна. И если мы рассматриваем одну точку данных, то сложно сказать, чем обосновано ее конкретное значение — существенными факторами или случайностью. Но если рассмотреть большое множество точек, можно увидеть, что они группируются вокруг некоторого среднего.
Другими словами, при увеличении количества точек обучающей выборки все случайные колебания будут усредняться — на каждое положительное отклонение найдется примерно равное отрицательное. А тенденция же будет, наоборот, усиливаться. В итоге и человеку и модели будет значительно легче эту тенденцию “ухватить”. Посмотрите, например, что будет, если к выборке, изображенной на рисунке выше добавить еще в 10 раз больше точек из того же распределения:
Теперь довольно очевидно, что на лицо линейная тенденция. И даже более сложная полиномиальная функция работает гораздо более эффективно на этих данных. Именно так добавление данных борется с переобучением моделей.
Причем необходимое количество данных зависит от вида тенденции и величины случайных отклонений. Чем более сложная, нелинейная тенденция в данных существует, чем тоньше зависимость целевой переменной от значения атрибутов, тем больше данных нужно для адекватной работы моделей. И чем больше по величине случайные отклонения, чем “сильнее” они размывают эту тенденцию, тем больше данных понадобится. Поэтому не существует какого-то оптимального объема данных, все зависит от конкретной задачи.
Как мы видели на примерах ранее, переобучение зачастую возникает вследствие того, что в модели присутствует большое количество параметров за счет большого количества лишних признаков в датасете. Именно для борьбы с этим используется регуляризация и в целом отбор признаков. Незначимые атрибуты лучше убирать из данных еще на этапе предварительного анализа и очистки данных. Чем меньше в данных будет лишних признаков, тем более четко и ясно будет прослеживаться та самая заветная тенденция.
Однако следует помнить, что регуляризация на практике работает лучше, чем ручное удаление признаков, так как подбор коэффициентов модели происходит автоматически. При этом регуляризация имеет свои недостатки — необходимость подбора параметра регуляризации. Поэтому стоит комбинировать эти способы — если какие-то признаки явно не влияют на целевую переменную — их стоит убрать при обработке данных, а если есть сомнения — то лучше оставить на усмотрение регуляризации.
Кроме того, следует помнить, что в других классах моделей могут применяться и иные способы управления сложностью модели, которые эффективно в чем-то похожи на регуляризацию. Например, в деревьях решений — это ограничение глубины дерева. Мы уже говорили об этом: чем больше слоев в дереве, тем сложнее получается модель. В нейронных сетях для подобного же используются Dropout-слои. Подробно мы не сможем рассказать про все эти способы, тем более что они специфичны для разных классов моделей. Но на практике они применяются примерно также, как и обычная регуляризация.
Как мы видим на втором графике даже после добавления большого количества точек более простая модель все равно описывает выборку лучше, так как полиномиальная модель имеет не очень понятные “хвосты” на концах распределения. Поэтому при обнаружении переобучения стоит задуматься об использовании более простого параметрического класса функций. Этот способ работает лучше в совокупности с увеличением объема выборки. Вообще, комбинация нескольких способов может быть более эффективной, чем применение только одного.
В глубоком обучении есть эмпирическое правило, которое гласит, что количество параметров модели должно быть в 2-3 раза меньше, чем количество примеров в обучающей выборке. Это ни в коем случае не универсальное правило и не гарантия от переобучения. Помните, вся зависит от задачи. Но можно помнить об этом ориентире. Если количество параметров больше, чем рекомендует это правило, вы практически точно получите переобученную модель.
Кроме того, не стоит забывать о ложных корреляциях в данных, которые тоже могут стать причиной переобучения. Хотя, ложные зависимости данных в силу их ограниченности — это явление несколько другой природы, на практике оно проявляет себя точно как переобучение — снижает обобщающую способность модели. Для устранения ложных корреляций необходимо хорошо разбираться в предметной области или привлекать для анализа данных экспертов.
Еще устраняют или сильно снижают переобучение так называемые ансамблевые модели, особенно основанные на методе бустинга. Ансамблевые модели это отдельная большая тема, которую мы не сможем рассмотреть в этой главе, про них можно написать отдельную книгу. Но если вкратце, ансамбль — это набор моделей, обученных на одном и том же наборе данных. Метод бустинга заключается в том, что каждая следующая модель в ансамбле исправляет или компенсирует ошибки предыдущей. В итоге мы получаем такую метамодель, которая может работать более эффективно, чем каждая модель ансамбля по отдельности.
Еще один способ избежать переобучения моделей — ранняя остановка обучения. Раньше мы говорили, что процесс обучения всегда продолжается до полной сходимости, то есть до нахождения оптимальных значений параметров по заданной функции ошибки. Но это не всегда так. В процессе обучения можно контролировать ту самую тестовую эффективность и остановить обучение тогда, когда она начнет падать. Этот способ часто применяется в обучении нейронных сетей, так как оно начинается с малых случайных значений весов (параметров) сети. Поэтому само обучение, то есть подбор весов, немного имеет эффект повышения значения коэффициентов, который противоположен регуляризации, то есть повышение степени сложности модели. Поэтому ранняя остановка обучения эффективно похожа на введение регуляризации в модель. Важно остановить обучение именно в тот момент, когда сложность модели начнет превышать оптимальное значение, после которого начинается переобучение. Это простой, но не очень универсальный способ.
Каждый способ борьбы с переобучением (впрочем как и с недообучением) имеет свои достоинства и недостатки. Не существует универсального алгоритма действий. Поэтому всегда надо исходить из поставленной задачи, а также руководствоваться всеми факторами: характер модели, нефункциональные требования, особенности набора данных, возможность собрать больше точек или атрибутов. При возможности стоит попробовать несколько разных способов увеличения эффективности моделей.
Выводы:
- Ввести в модель данные о новых объектах, использовать выборку большего объема.
- Убрать признаки из модели, использовать отбор признаков, устранить ложные корреляции.
- Увеличить степень регуляризации модели.
- Использовать более простые модели.
- Регуляризация обычно работает лучше уменьшения количества параметров.
- Можно использовать ансамблевые модели.
- Ранняя остановка обучения.
Анализ ошибок
Рассматривая алгоритмические и математические способы повышения эффективности работы моделей машинного обучения не стоит забывать и о самом простом, но в тоже время одном из самых эффективных — ручном анализе ошибок модели. После обучения модели, если она не достигает желаемого уровня эффективности стоит просто обратить внимание на те объекты, на которых она делает ошибки. Этот подход называется анализ ошибок и может дать достаточно неожиданную информацию о модели, данных и самой задаче.
В отдельных случаях анализ ошибок приводит к выводу, что модель работает хорошо. Например, очень известна задача по распознаванию рукописных цифр по картинке. Даже относительно простые модели справляются с ней очень хорошо, но могут не достигать стопроцентной эффективности. Вот пример картинки, которую простая модель может классифицировать неправильно:
Свидетельствует ли эта ошибка о том, что модель обучилась неправильно? Скорее нет, это свидетельствует о низком разрешении картинок и наличии некоторых двусмысленных объектов в обучающей выборке. Такую рукописную цифру и человек бы не распознал.
Кроме того, в данных могут присутствовать просто ошибки. Особенно это касается датасетов, размеченных вручную. Человек мог просто опечататься или ошибиться и в наборе данных появился объект с неправильным значением целевой переменной. На практике все случается и именно ручной анализ ошибок может выявить такую ситуацию.
Ручная проверка индивидуальных объектов, на которых модель работает неправильно часто подсказывает, какие общие характеристики имеют такие объекты или чем они отличаются от остальной выборки. Поняв эти особенности можно найти способы модифицировать признаки таким образом, чтобы лучше учитывать эти особенности. Например, анализируя модель распознавания человека по лицу можно придти к выводу о том, что такая модель значительно чаще ошибается на лицах с растительностью или на людях в очках. Это вполне объяснимо с логической точки зрения. Так что же делать в таком случае? Можно просто собрать больше точек данных, лиц с растительностью или очками. Это не только просто повысит эффективность модели, но и сделает ее более устойчивой к подобным особенностям в принципе.
При проведении анализа ошибок следует ориентироваться на ошибки, которые модель делает именно в тестовой выборке. В задачах классификации в первую очередь следует проанализировать ошибки в тех классах, в которых модель делает больше всего ошибок. Это очень заметно в отчете о классификации и в марице классификации. Обычно бывает, что модель постоянно относит объекты одного класса к какому-то другому. А в задачах регрессии очень логично обратить внимание на объекты, на которых модель ошибается сильнее всего в численном выражении.
Выводы:
- Анализ ошибок — это ручная проверка объектов, на которых модель делает ошибки.
- Анализ характеристик таких объектов может подсказать направление инжиниринга признаков.
- Можно сравнить эти объекты с остальной выборкой. Может, это аномалии.
- В задачах регрессии в первую очередь обращать внимание на объекты с самым высоким отклонением.
Выбор модели
При решении конкретной задачи машинного обучения нельзя сказать заранее, какой вид модели будет наиболее эффективен. Разные типы моделей могут давать кардинально разный результат и показывать очень разную эффективность на одних и тех же данных. В одних задачах хорошо себя показывают линейные модели, а в других они совершенно непригодны. Какие-то данные прекрасно моделируются деревом решений, а другой набор данных лучше всего описывается методом ближайших соседей. Другими словами, на практике стоит проблема выбора модели для решения имеющейся задачи. И здесь имеются некоторые неочевидные нюансы, про которые и поговорим в этой главе.
Проблему выбора модели чаще всего решают перебором — нужно попробовать разные типы моделей и выбрать те, которые показывают наибольшую эффективность. При этом стоит учитывать те ограничения и характерные черты разных моделей, которые мы обсуждали в предыдущей главе. Особенно это касается нефункциональных требований к информационной системе. Всегда следует помнить, что модели машинного обучения часто создаются не только для научного и исследовательского интереса, но и для работы в реальных программных системах. И к этим системам могут предъявляться специфические требования. Например, по скорости работы, по объему используемой памяти. К работе самих алгоритмов тоже могут существовать особые требования, например, по интерпретируемости.
Характер данных тоже может подсказать, какие модели будут эффективны с большей вероятностью. Еще до начала моделирования, по результатам предварительного анализа данных, или по истории решения подобных задач можно прикинуть порядок сложности решаемой проблемы. Например, известно, что задача генерации осмысленного текста на естественном языке относится к разряду очень сложных. Такую задачу скорее всего не решить простыми линейными классификаторами. Здесь понадобится тяжелая артиллерия — глубокие нейронные сети. В глубоком обучении есть специализированные модели, которые “заточены” на анализ определенного типа информации. Например сверточные сети хорошо работают с графическими изображениями, а рекуррентные — с последовательностями. За исключением этого аналитику приходится в выборе типа моделей полагаться на свою интуицию, сравнение как можно большего количества моделей.
Если решается известная задача, то обязательно надо проводить анализ литературы и прошлой истории решения подобных проблем. Во многих известных задачах есть известные алгоритмы, которые решают задачу лучше всего. Они часто известны под названием state-of-the-art. В таких задачах целесообразно использовать именно их как базу сравнения. Если у вас получилось создать модель, которая превзошла state-of-the-art — это уже огромный успех и несомненный повод опубликовать свое исследование. Для более последовательного сравнения разных моделей, которые решают одну и ту же или сходные задачи существуют специальные модельные датасеты — наборы данных, которые служат эталоном, по которым сравнивают разные модели и подходы к решению задачи.
Если же никакой информации о предпочтительных видах моделей у исследователя нет, то самым естественным первым шагом будет построение самых простых моделей. Здесь имеются в виду простые как по классу сложности, так и по вычислительным затратам. Логичным выбором будет использование линейной или логистической регрессии (в зависимости от поставленной задачи) и дерева решения (иногда используют его ансамблевый вариант — случайный лес). Эти модели хороши тем, что довольно быстро работают, даже на относительно больших массивах данных. Кроме того, их результаты интерпретируемы — внутреннее устройство этих моделей можно проанализировать вручную и сделать какие-то значимые выводы о данных.
В любом случае, результат работы таких простых моделей дает нам оценку начального уровня эффективности модели, с которым можно сравнивать качество более сложных моделей, если придется такие строить. База сравнения — это очень полезная вещь в машинном обучении, особенно если вы решаете новую задачу, по которой нет научной литературы и не с чем сравнивать (либо известную задачу, но на принципиально других данных). Эта базовая эффективность станет нижним порогом для других моделей. То есть будет очевидно, что если более сложная модель показывает уровень качества ниже, чем такая базовая, то это совершенно неудовлетворительный результат.
После построения базовой модели обязательно надо провести диагностику для поиска путей повышения ее эффективности. Про это мы подробно говорили в предыдущих главах. Здесь первоочередная задача — детектировать пере- или недообучение. Стоит сказать, что такой анализ целесообразно проводить только в том случае, если эффективность базовой модели является неудовлетворительной. Довольно часто на практике бывает так, что даже самая простая модель уже достигает желаемого уровня точности. Ведь в прикладной области иногда не нужно стремиться к максимальной точности, достаточно достигнуть какого-то заранее определенного уровня.
Часто при начале моделирования строят большое количество самых разных моделей на одних и тех же данных для определения наиболее потенциальных. Можно определить пул из 15 — 20 различных алгоритмов машинного обучения и их вариаций, построить их на одинаковых данных и сравнить их эффективность. Например, для задачи классификации такой пул может выглядеть, например так:
- Логистическая регрессия
- Полиномиальная регрессия 3 степени
- Полиномиальная регрессия 7 степени
- Классификатор на опорных векторах без ядра
- Классификатор на опорных векторах с гауссовым ядром
- Классификатор на опорных векторах с сигмоидальным ядром
- Наивный байесовский классификатор
- Однослойный перцептрон
- Многослойный перцептрон с 1 скрытым слоем с количеством нейронов, равным количеству признаков
- Многослойный перцептрон с 3 слоями, на каждом из которых количество нейронов уменьшается вдвое
- Дерево решений
- Случайный лес
- К ближайших соседей
- Пассивно-агрессивный классификатор
- Классификатор на гауссовых процессах
- Экстремально рандомизированные деревья
- AdaBoost
- Градиентный бустинг
- XGBoost
- CatBoost
По сути это все модели, реализованные в sklearn за исключением моделей специального назначения (типа пассивно-агрессивного классификатора), плюс несколько сторонних моделей, реализованных в других библиотеках. Такой пул даст неплохой охват разных типов моделей. На практике после оценки эффективности модели всего несколько из этого списка показывают относительно неплохую эффективность, остальные же сильно отстают. Такой поиск перебором помогает определить один-два класса моделей, на которых можно сосредоточиться более подробно в своем анализе, а остальные — без сожаления отбросить. Кроме того такой способ даст более полную картину базового уровня сложности задачи и эффективности простых моделей.
Как мы понимаем, такой перебор может занимать достаточно много времени, особенно при большом объеме данных. Некоторые модели их списка могут обучаться на порядки дольше остальных. Если поиск занимает слишком большое время, можно взять для перебора не весь датасет а случайную часть, например, 10% (для этого можно использовать тот же_train_test_split_). По результатам анализа можно отобрать 5-6 наиболее перспективных моделей и повторить обучение на более полном наборе данных. Часто это сильно быстрее, чем обучать все на всем.
Вообще, выбор модели в машинном обучении, как и многие другие задачи — творческий и непредсказуемый процесс. В нем надо руководствоваться многими факторами — требованиями к моделям, интуицией, анализом данных, результатами диагностики. При этом приходится повторять одни и те же действия по многу раз. Конечно, существуют попытки автоматизировать эту задачу. Существуют специальные библиотеки (типа auto-sklearn), которые производят некоторые операции алгоритмически. Эта сфера в машинном обучении называется AutoML — автоматизированное построение и поиск моделей. Но на сегодняшний день эти алгоритмы пока недалеко ушли от примитивного перебора. И следует помнить, что применение этих подходов по-прежнему на порядки увеличивает время, необходимое на подбор и обучение модели.
Выводы:
- Очень сложно сказать априори какой класс моделей будет работать лучше на конкретных данных.
- Следует учитывать нефункциональные требования к задаче.
- Обычно начинают с самых простых моделей — они быстро считаются и дают базовый уровень эффективности.
- В исследовательских задачах модели сравниваются со state-of-the-art.
- По результатам диагностики простых моделей принимают решение о дальнейших действиях.
- Можно провести поиск по разным классам моделей для определения самых перспективных.
- Выбор модели — это творческий и исследовательский процесс.
- Есть подходы автоматизации выбора модели (AutoML), но они пока несовершенны.
Гиперпараметры модели
Усложняет задачу выбора модели тот факт, что у многих типов моделей существуют разные вариации, особые параметры. Например, при использовании полиномиальной регрессии мы должны указать степень полинома. При этом полиномиальные модели с разной степенью — это по сути дела разные классы. Поэтому в списке выше некоторые модели повторяются несколько раз, но с разными значениями этих “параметров”. В кавычках потому, что они ведут себя не как обычные параметры модели. Оптимальные значения обычных параметров мы подбираем в процессе обучения, в этом он, собственно, и заключается. Оптимальную степень полинома не подберешь в процессе градиентного спуска — если посередине алгоритма ее поменять, то мы окажемся о совершенно другом семействе функций, что нарушит связность алгоритма.
Эти особенные значения называются гиперпараметрами моделей. Гиперпараметры не подбираются при обучении — они задаются при определении модели и должны оставаться неизменными до схождения алгоритма обучения. Если мы хотим изменить значение гиперпараметра, мы должны заново запустить процесс обучения. В этом их основное отличие от параметров модели. Схожесть же в том, что гиперпараметры — это тоже численные значения, которые влияют на работу модели. Более конкретно они влияют на то, какая конкретная модель из всего класса моделей получится в результате обучения. То есть их действие более косвенное.
На самом деле мы знаем уже много примеров гиперпараметров — практически в каждом типе модели они есть. В методе k ближайших соседей то самое k, количество соседей, которое алгоритм учитывает, тоже является гиперпараметром. В дереве решений максимальная глубина дерева — тоже гиперпараметр. В моделях, использующих регуляризацию, коэффициент этой самой регуляризации (или два коэффициента, как в эластичной сети) — тоже является гиперпараметром. Вообще, у каждой модели может быть довольно много гиперпараметров. В библиотеке sklearn значения гиперпараметров задаются при создании объекта модели. Раньше мы использовали конструктор по умолчанию, но стоит посмотреть в документации, какие аргументы принимает конструктор того или иного объекта модели — некоторые их этих аргументов и есть гиперпараметры.
Рассмотрим, например, конструктор объекта KNeighborsClassifier. Он принимает семь необязательных аргументов:
- n_neighbors — количество ближайших соседей (то самое k);
- weights — метод взвешивания соседей по расстоянию (чтобы более близкие соседи влияли на значение больше чем далекие), причем по умолчанию используется метод без весов, то есть отсутствие взвешивания;
- algorithm — алгоритм вычисления матрицы ближайших соседей (кроме брут-форса есть более оптимизированные на некоторых данных способы);
- leaf_size — размер ячейки для одного из алгоритмов вычисления матрицы (для других алгоритмов этот аргумент бесполезен);
- metric — метрика вычисления расстояния (по умолчанию используется метрика Минковского);
- p — степень метрики (метрика Минковского использует это значение, при $p=2$ получается обычное Евклидово расстояние);
- n_jobs — количество потоков, которые используются для параллельных вычислений для ускорения работы алгоритма;
Итого из 7 аргументов конструктора 4 являются гиперпараметрами (n_neighbors, weights, metric, p). И это алгоритм ближайших соседей, который считается одним из самых простых. В других видах моделей гиперпараметров еще больше. Конкретный набор гиперпараметров зависит от деталей программной реализации самой модели, поэтому для определения, какие гиперпараметры существуют у данной модели необходимо обратиться к документации соответствующего класса. При этом все аргументы конструктора имеют значения по умолчанию. То есть даже если вы не задаете их значения, они все равно присутствуют в модели. Для гиперпараметров это важно — они всегда имеют какое-то значение. Модель нельзя не является строго определенной, если у хотя бы одного используемого гиперпараметра не определено значение.
При этом обратите внимание, что не все аргументы конструктора являются гиперпараметрами. Например, для рассмотренного выше класса, аргумент algorithm не влияет на то, какая конкретная модель получится в результате обучения. Да, алгоритм расчета матрицы может оказать влияние на скорость подсчета, но результат расчета или обучения модели от него на зависит. Поэтому этот аргумент нельзя считать гиперпараметром.
Рассматривая различные гиперпараметры можно заметить, что они бывают категориальные и численные. Например, вид метрики в методе ближайших соседей — это категориальный гиперпараметр. Он может принимать одно из конечного множества заранее известных значений. При разных значениях в модели используются разные формулы расчета расстояний между точками. А вот, для примера, параметр регуляризации — это численный гиперпараметр. Он может принимать любые значения больше нуля. Поэтому в отличие от обычных параметров моделей, которые бывают только численные, гиперпараметры могут быть категориальные.
Очевидно, что при разных значениях гиперпараметров будут получаться различные оптимальные модели, которые покажут разный уровень эффективности. Поэтому стоит задача нахождения оптимальных значений гиперпараметров. Но мы не можем подбирать их в процессе обучения. Задав до начала обучения значения всех гиперпараметров модели, мы не можем менять их. Поэтому мы можем только говорить о нахождении оптимальной модели при определенных значениях гиперпараметров.
Обычные параметры модели мы можем подбирать в процессе обучения потому, что сами модели сконструированы таким образом, чтобы существовал математический способ оптимизировать набор их значений. Этот способ может быть аналитический (как метод нормальный уравнений, который используется в самых простых случаях линейной регрессии), численный (как метод градиентного спуска) или алгоритмический (как методы построения оптимальных деревьев решений). Но в случае с гиперпараметрами таких алгоритмов в общем случае не существует. То есть мы не имеем представления о виде зависимости эффективности получающейся оптимальной модели от значения гиперпараметров — в общем случае она слишком сложная, неочевидная, может быть имеющая разрывы, в общем ведет себя полностью непредсказуемо. В каких-то частных случаях мы можем предполагать гладкость и выпуклость такой зависимости. Например, мы рассуждали о наличии оптимального значения параметра регуляризации. Это значит, что этот гиперпараметр всегда имеет один глобальный оптимум. Но в других случаях мы не можем утверждать даже этого наверняка.
Поэтому единственный применимый на практике способ нахождения оптимальных значений гиперпараметров — перебор. То есть нам нужно построить несколько моделей одного класса с разными значениями гиперпараметров и сравнить их эффективность на тестовой выборке. Конечно это подразумевает многократное повторение процесса обучения модели. Поэтому оптимизация гиперпараметров — это очень вычислительно емкий процесс. Это, наверное, самая вычислительно трудная и тяжелая часть машинного обучения. И конечно на практике невозможно проверить все возможные комбинации значений гиперпараметров. Для организации поиска существуют две главные стратегии, о которых мы поговорим в следующих главах.
Может быть вы обратили внимание на то, что в предыдущей главе мы похожим образом описывали процесс выбора наилучшей модели. Это не совпадение. Давайте рассмотрим степень полинома в полиномиальных моделях. Можно считать, что, например, квадратичная и кубические функции — это два разных параметрических класса моделей (у которых просто используются похожие алгоритмы обучения). А можно считать степень полинома гиперпараметром, тогда эти две модели будут считаться одним классом. Или, например, метод опорных векторов с разными ядерными функциями, что это — разные модели или просто разные значения гиперпараметра? В многослойном перцептроне можно рассматривать количество скрытых слоев тоже как особый гиперпараметр.
Формально, модели считаются разными, если у них разный набор обычных параметров. Но на практике различие между двумя моделями можно представить как гиперпараметр. Доводя это рассуждение до предела можно сказать, что сам вид модели тоже можно рассматривать как такой особый категориальный гиперпарамер. Важно, что как разные значения гиперпараметров приводят к различным моделям после обучения, так и разные классы моделей тоже порождают разные модели в результате. Поэтому задача оптимизации гиперпараметров и задача выбора модели — это принципиально одна и та же проблема. Именно поэтому мы начали говорить о гиперпараметрах моделей именно в этой главе. Методологические подходы к решению этих двух задач одинаковы.
Выводы:
- Гиперпараметр модели — это численное значение, которое влияет на работу модели, но не подбирается в процессе обучения.
- Гиперпараметры модели нужно задавать до начала обучения.
- Если значение гиперпараметра изменилось, то обучение надо начинать заново.
- Примеры гиперпараметров — k в kNN, параметр регуляризации, степень полиномиальной регрессии, глубина дерева решения.
- У каждой модели множество гиперпараметров, которые можно посмотреть в документации.
- Гиперпараметры бывают дискретные и непрерывные.
- Оптимизация гиперпараметров осуществляется перебором.
- Оптимизация гиперпараметров и задача выбора модели — одно и то же.
Поиск по сетке
В предыдущей главе мы говорили, что единственный применимый на практике способ нахождения оптимальных значений гиперпараметров модели — полный перебор. Однако, есть две трудности в организации такого процесса. Во-первых, если у модели несколько гиперпараметров, то их оптимум надо искать в совокупности. Не получится сначала оптимизировать один из них, а потом следующий. Дело в том, что значения гиперпараметров могут сложным способом взаимодействовать в модели и оптимальное значение по одному из них может измениться при изменении значения другого.
Например, в уже рассмотренной модели ближайших соседей. Допустим, мы нашли, что наилучшая модель получается при рассмотрении 10 соседей (при всех остальных гиперпараметрах имеющих значения по умолчанию). Теперь мы хотим понять наилучший алгоритм взвешивания соседей и начинаем изменять его. Но оптимальное количество соседей мы нашли для метода взвешивания по умолчанию (в данном примере — без взвешивания). А если мы будем строить взвешенные модели, то оптимальное количество соседей может быть совершенно другим. Поэтому два этих гиперпараметра надо изменять вместе — то есть проверять все комбинации значений количества соседей и алгоритмов взвешивания. И так для всех гиперпараметров модели.
Конечно, это означает огромный рост количества циклов обучения модели, так как для проверки каждой комбинации значений нужно заново проводить обучение до сходимости. Поэтому на практике бывает возможно проверить только определенное количество значений. И это вторая проблема оптимизации гиперпараметров: невозможно проверить все возможные комбинации значений. А значит, невозможно найти абсолютно оптимальные значения гиперпараметров модели. Тем более, что у всех моделей присутствуют и численные гиперпараметры, у которых может быть бесконечное количество значений. Типичный пример — праметр регуляризации — только по нему одному нельзя проверить все возможные значения.
Все это заставляет искать метод, который позволяет максимизировать вероятность нахождения более-менее оптимальной модели в условиях ограниченных ресурсов. И один из популярных методов — поиск по сетке. Его идея довольно проста. Для начала рассмотрим один непрерывный гиперпараметр. Допустим, область его допустимых значений лежит в некотором диапазоне. И где-то внутри этого диапазона есть оптимальное значение. Вряд ли мы найдем его точно, но мы можем приблизиться к нему, насколько это возможно. Для этого разделим диапазон на некоторое количество равных интервалов и проверим значения гиперпараметра на концах этих интервалов. То есть если мы проверяем диапазон, например, от 0 до 100, то мы можем поделить его на, допустим, 10 равных интервалов и проверить 11 разных значений — 0, 10, 20 и так далее. Или можно поделить на 2 интервала и проверить всего три разных значения — 0, 50 и 100.
Если добавить сюда еще один численный гиперпараметр, то по второму можно провести точно такое же разбиение. Причем здесь может быть совершенно другое количество проверяемых значений. Теперь мы должны проверить все комбинации значений первого параметра и второго. То есть если у нас 10 значений первого параметра и, допустим, 5 значений второго, то всего получается 50 комбинаций. Заметьте, как быстро растет количество комбинаций при росте количества гиперпараметров. Поиск по сетке демонстрирует экспоненциальный рост сложности — это очень неэффективный алгоритм.
Как сюда вписываются категориальные гиперпараметры? Очень просто, мы всего лишь должны определить список значений, которые будем проверять. А дальше работает та же логика — составляются все возможные комбинации значений и на каждой их них обучается модель. Заметьте, что если для какого-то параметра мы будем проверять только одно значение, это не добавит сложности. Поэтому можно проверять не все гиперпараметры, а только часть — по остальным будут использоваться значения по умолчанию.
Но что делать, если гиперпараметр измеряется по полуоткрытой шкале? Например тот же параметр регуляризации имеет область допустимых значений от нуля до плюс бесконечности. Как делить такой диапазон? В таком случае чаще всего применяют логарифмическую шкалу. Поэтому в качестве опорных значений берут, например, 0.01, 0.1, 1, 10, 100 и так далее. Такое разбиение более равномерно покрывает все возможные значения. Тем более, что для таких параметров решающее значение имеет именно порядок величины, использование для них логарифмической шкалы очень логично.
Ту же самую логику можно применить и для построения, например, диагностических кривых. Например, при построении графика зависимости между уровнем регуляризации и точностью модели. Не пытайтесь воспользоваться равномерным диапазоном значений. Для таких параметров разница между, например, уровнем 3 и 4 не так существенна, как между 0.1 и 0.01. Возьмите за правило — если переменная измеряется на полуоткрытом диапазоне и покрывает несколько порядков величины — ее надо рассматривать на логарифмической шкале.
Очевидно, что чем больше значений мы проверяем, тем больше вероятность получить модель, близкую к оптимальной — мы проходим более частой сеткой. Но чем подробнее наш поиск, тем больше времени он занимает. Так что количество проверяемых значений это результат компромисса между доступными вычислительными ресурсами и желанием получить более оптимальные значения, то есть модель с наибольшей эффективностью. Для хоть какого-то ускорения работы поиска его часто проводят только на части обучающей выборки, особенно если она очень большая.
Логика поиска по сетке уже реализована в библиотеке sklearn в соответствующих методах. Чтобы ими воспользоваться нужно определить перебираемые гиперпараметры и их значения. Для этого используют вспомогательный словарь. Рассмотрим для примера метод опорных векторов. Допустим, мы хотим проверить две разных функции ядра и несколько значений параметра регуляризации. Для этого создадим такой словарь:
1
2
3
4
tuned_parameters = {
"kernel": ["rbf"], ["linear"]
"C": [1, 10, 100, 1000]
}
Такой словарь называется пространство поиска. Здесь важно, чтобы ключи в этом словаре совпадали с названиями соответствующих аргументов конструктора модели. Иначе метод не сработает. После этого можно создать объект поиска по сетке. Ему передается сам объект модели и созданный словарь значений гиперпараметров:
1
2
3
4
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
grid_search = GridSearchCV(SVC(), tuned_parameters).fit(X_train, y_train)
Обратите внимание, что у данного объекта есть метод fit(), как у любого объекта модели. В этом опять проявляется единообразие библиотеки sklearn в построении интерфейсов. Здесь обучение будет проходить много раз, используя каждую комбинацию значений гиперпараметров. После завершения обучения в этом объекте будут доступны ссылка на лучшую модель, лучший набор значений гиперпараметров, максимально достигнутая эффективность и еще много внутренней информации (все результаты всех обучений в том числе). Например лучшую модель можно получить вот так (причем по умолчанию, она будет уже обучена на переданных в поиск данных):
1
best_model = grid_search.best_estimator_
Обратите внимание, что в названии этого метода есть CV. Это означает, что он внутри себя использует кросс-валидацию. По умолчанию используется пятипроходная кросс-валидация, но это можно изменить специальным аргументом (cv). Поэтому давайте посчитаем, сколько раз будет проходить обучение в данном примере? Мы проверяем два значения функции ядра и четыре значения параметра регуляризации. Итого получается 8 комбинаций, причем каждая их них обучается пять раз из-за кросс-валидации, то есть всего данный код запустит обучение 40 раз. Таким образом, если модель обучается за полторы минуты, то подбор гиперпараметров займет ровно час. А мы даже не рассматривали все гиперпараметры модели. Оптимизация гиперпараметров — очень вычислительно сложный и долгий процесс.
Несмотря на то, что кросс-валидация кратно увеличивает время поиска, ее все равно крайне желательно использовать. Ведь значения метрик, измеренные без нее могут существенно отклоняться от истинных. Так что мы можем получить не оптимальные значения гиперпараметров. Да. обучение пройдет быстрее, но результат будет гораздо менее надежным. Гораздо лучше использовать перекрестную проверку, а сэкономить время, например, используя только часть обучающей выборки.
Также можно вручную задать метрики, которые используются для оценки моделей. По умолчанию используется оценка модели, встроенная в сам объект модели через метод score, то есть точность (accuracy) для классификации и коэффициент детерминации (r-квадрат) для регрессии. Метод поиска по сетке подбирает модель, которая показывает наилучшее значение именно этой метрики. Но в разных задачах для нас могут быть важны разные метрики. Поэтому часто необходимо указать, что выбирать модель стоит по другой метрике. Для этого у метода поиска по сетке есть аргумент scoring, которому можно передать одну или несколько метрик в массиве, по которым и будет проводиться поиск:
1
2
3
scores = ["precision", "recall"]
grid_search = GridSearchCV(SVC(), tuned_parameters,
scoring=scores).fit(X_train, y_train)
Зачем может понадобится указывать сразу несколько метрик? Это может быть полезно, если два алгоритма показывают одинаковый результат по одной метрике, но разную эффективность по другой. Например, две модели (или два разных набора значений гиперпараметров, что сейчас для нас одно и то же) показывают precision 0.92, но у первой recall составляет 0.85, а у второй — 0.7. В таком случае если мы укажем только precision как критерий оптимизации, то алгоритм может назвать лучшей любую из этих моделей, в зависимости от того, какая попадется позже. А если мы указываем две метрики, то при равенстве первой из них будет учитываться вторая. То есть поиск точно назовет лучшей первую модель. При этом решающее значение будет все-таки иметь первая метрика.
А что делать, если нужно значения одних гиперпараметров зависят от других? Например, в методе опорных векторов с гауссовым ядром есть гиперпараметр gamma, который влияет на параметры ядерной функции. Его тоже можно оптимизировать. Проблема в том, что для метода опорных векторов без ядра этого гиперпараметра не существует. Поэтому мы не можем просто написать:
1
2
3
4
5
tuned_parameters = {
"kernel": ["rbf", "linear"],
"gamma": [1e-3, 1e-4],
"C": [1, 10, 100, 1000]
}
Это приведет к ошибке, когда метод поиска по сетке попытается составить все комбинации значений гиперпараметров. Именно в таких случаях можно задавать несколько разных комбинаций гиперпараметров:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
tuned_parameters = [
{"kernel": ["rbf"],
"gamma": [1e-3, 1e-4],
"C": [1, 10, 100, 1000]},
{"kernel": ["linear"],
"C": [1, 10, 100, 1000]},
]
scores = ["precision", "recall"]
grid_search = GridSearchCV(SVC(), tuned_parameters,
scoring=scores).fit(X_train, y_train)
В данном примере мы определяем разные наборы гиперпараметров для разных значений ядерной функции. То есть получается такой условный набор. Сколько же в итоге комбинаций проверит этот код? Для гауссовой функции — восемь, для линейного ядра — четыре. Итого получается 12 комбинаций.
Как вы могли заметить, экспоненциальный рост сложности поиска по сетке существенно ограничивает количество комбинаций, которые мы можем проверить за разумное время. Если мы хотим перебрать, например, всего шесть гиперпараметров по десять значений в каждом, это нам даст миллион возможных комбинаций. Даже если одна модель обучается всего секунду, такой поиск займет 11 дней. И это без использования кросс-валидации. Для того, чтобы хоть как-то уменьшить количество проверяемых комбинаций можно использовать иерархический подход: сначала пройтись по пространству возможных значений крупной сеткой, а потом по окрестностях оптимальных значений более мелкой. Либо можно использовать более сложные стратегии поиска, например двоичный поиск (HalvingGridSearchCV).
Выводы:
- Поиск по сетке — полный перебор всех комбинаций значений гиперпараметров для поиска оптимальных значений.
- Для его организации надо задать список гиперпараметров и их конкретных значений.
- Непрерывные гиперпараметры надо дискретизировать.
- Для непрерывных гиперпараметров часто используется логарифмическая шкала.
- Поиск по сетке имеет экспоненциальную сложность.
- Чем больше параметров и значений задать, тем лучше получится модель, но дольше поиск.
- Можно задать критерии поиска — целевые метрики.
- Рекомендуется использовать кросс-валидацию.
Случайный поиск
Хуже всего поиск по сетке работает с непрерывными гиперпараметрами. Мало того, что невозможно проверить все возможные их значения, интересующие нас значения еще очень часто неравномерно распределены по числовой оси. Метод случайного поиска реализует совсем другую стратегию проверки разных комбинаций. Поиск по сетке просто проверяет все возможные комбинации по порядку. Это дает гарантированный результат (то есть мы всегда найдем наилучшую комбинацию из представленных), но работает очень долго.
Случайный поиск, как следует из названия, проверяет разные комбинации значений гиперпараметров в случайном порядке. Для его организации мы также должны сначала задать, какие гиперпараметры мы будем проверять, и какие их значения нас интересуют. Но на каждой итерации поиска данный алгоритм будет просто случайно выбирать значение каждого гиперпараметра из приведенного списка. Казалось бы, что эта стратегия строго хуже полного перебора, так как она теперь вообще ничего не гарантирует. Но у нее есть несколько особенностей, из-за которых на практике к ней стоит присмотреться.
Самое главное отличие случайного поиска от поиска по сетке состоит в том, мы можем не просто явно перечислять возможные значения каждого гиперпараметра. Мы можем задать вид его распределения. Давайте рассмотрим такой код:
1
2
3
4
5
6
7
8
clf = SGDClassifier(loss="hinge", penalty="elasticnet", fit_intercept=True)
param_dist = {
"average": [True, False],
"l1_ratio": stats.uniform(0, 1),
"alpha": loguniform(1e-2, 1e0),
}
Здесь мы задаем пространство поиска из трех параметров. Значения первого мы будем выбирать их списка. Именно так мы задавали значения в поиске по сетке. Значения второго будем генерировать случайно из равномерного распределения от 0 до 1. То есть каждую новую итерацию для второго гиперпараметра будет просто браться новое случайное число от 0 до 1. А значения третьего параметра будем генерировать из логравномерного. Это распределение очень подходит для таких гиперпараметров, как, например, параметр регуляризации, для которых значим именно порядок величины. Таких параметров достаточно много. Они обычно измеряются от 0 до бесконечности, а “среднее значение” у них — 1. То есть “равномерное” распределение таких параметров, например — 0.01, 0.1, 1, 10, 100 и так далее.
Так как на каждой итерации мы заново генерируем случайно все значения параметров, мы можем это делать произвольное количество раз. То есть мы можем задать явно количество итераций поиска, не оглядываясь на число используемых гиперпараметров и количество их потенциальных значений. Вот как запускается случайный поиск:
1
2
3
4
n_iter_search = 15
random_search = RandomizedSearchCV(
clf, param_distributions=param_dist, n_iter=n_iter_search
).fit(X, y)
Здесь мы явно указываем, что хотим произвести 15 случайных генераций значений гиперпараметров. То есть такой код будет искать наилучшую модель среди 15, значения гиперпараметров которых сгенерированы по заданному описанию случайно. Это даст нам 75 циклов обучения моделей (не забывайте про кросс-валидацию). С теми же значениями мы могли бы задать 5, 10 или 100 итераций.
Естественно, что чем больше итераций мы пройдем, тем более оптимальную модель мы найдем (скорее всего). Также как и в поиске по сетке, чем “мельче” сетка, чем больше комбинаций мы проверим, тем больше вероятность, что мы найдем хорошую (то есть более эффективную) модель. Различие лишь в том, что в случайном поиске количество итераций не фиксировано, а может задаваться произвольно.
Кстати, это означает, что мы можем добавлять в поиск новые гиперпараметры без опасений экспоненциального роста вычислительной сложности. Можно добавить еще один гиперпараметр и оставить количество итераций прежним. В таком случае поиск станет более разреженным. Или можно увеличить количество проходов вдвое, втрое или насколько позволяют вычислительные мощности. Случайный поиск позволяет ориентироваться именно на имеющиеся мощности и желаемое время поиска, а не на количество гиперпараметров. Он в каком-то смысле даже более предсказуемый, чем поиск по сетке, ведь он будет идти именно столько времени, сколько вы ему отвели.
Еще одно существенной отличие случайного поиска в том, что он именно случаен. То есть запустив два раза поиск с теми же самыми исходными данными, совершенно не факт, что мы получим одинаковый результат. Так как значения генерируются случайно, скорее всего, наоборот, мы получим, разные значения. Особенно, если количество итераций сильно меньше, чем потенциальное пространство поиска. И получаемые лучшие модели могут очень сильно отличаться. Чем больше итераций проводить, тем вероятнее, что модели будут более схожи. Но об этой особенности случайного поиска нужно помнить: он не гарантирует результат. Даже можно получить модель, которая хуже, чем “дефолтная” (со значениями гиперпараметров по умолчанию). Хотя на практике почти всегда случайный поиск находит более эффективный набор параметров.
Если необходимо обеспечить воспроизводимость результатов случайного поиска, то есть, чтобы при последующих запусках генерировались одни и те же значения, то можно использовать аргумент random_state, также, как и в train_test_split(). Этот параметр устанавливает значение инициализации генератора случайных чисел и он генерирует одну и ту же последовательность. Это бывает полено в демонстрационных и учебных целях.
В многих технических моментах, разные алгоритмы оптимизации гиперпараметров имеют общие черты. Так же, как и в поиске по сетке можно задавать другие метрики поиска, можно запускать поиск параллельно в многопоточном режиме, можно задавать свой алгоритм кросс-валидации и использовать другие возможности библиотеки, описанные в документации. Отдельно заметим, что использование кросс-валидации в случайном поиске не менее актуально, чем с поиске по сетке и в любых других алгоритмах оптимизации гиперпараметров.
Выводы:
- Случайный поиск позволяет задать распределение гиперпараметра, в котором будет вестись поиск.
- Случайный поиск генерирует набор значений гиперпараметров из указанных распределений.
- Можно задать количество итераций поиска независимо от количества гиперпараметров.
- Добавление параметров не влияет на продолжительность поиска.
- Результат не гарантируется. Воспроизводимость можно настроить.
- Также рекомендуется использовать кросс-валидацию.
Сравнение эффективности моделей (валидационный набор)
При сравнении эффективности нескольких моделей, либо при оптимизации гиперпараметров модели возникает еще одна незаметная, но значимая проблема. Когда мы сравниваем несколько моделей по какой-то метрике эффективности, мы выбираем среди них наилучшую. Допустим, у нас есть три модели, которые показали значение метрики, например, accuracy 0.91, 0.93 и 0.95. Эти метрики были измерены методом кросс-валидации, но есть в их надежности можно не сомневаться. Соответственно, мы делаем вывод, что третья модель лучше всего описывает данные и поэтому именно ее мы будем использовать. Неожиданный вопрос: а какая у этой модели будет эффективность на новых данных? Казалось бы, очевидно, 0.95, ведь это валидированная оценка качества этой модели. Но не все так просто.
Дело в том, что мы специально выбрали эту модель за ее высокое значение точности. А в этом значении, как мы знаем, всегда какую-то долю составляют случайные составляющие, даже при использовании кросс-валидации. Получается, что полученная оценка 0.95 может быть слишком оптимистичной. Здесь работает та же логика, что и с оптимизацией обычных параметров. Так как мы специально подбираем значения параметров под данные обучающей выборки, модель под них подстраивается и на новых данных может показывать чуть худшую эффективность. Также и при оптимизации гиперпараметров модель немного подстраивается именно под используемую выборку (и обучающую и тестовую вместе).
Поэтому при выборе модели для итоговой оценки ее эффективности опять нужно использовать новые данные, которые мы не использовали ни при обучении модели, ни при оптимизации гиперпараметров. Причем, так как оптимизация гиперпараметров и выбор модели — по сути одно и то же, точно такое же рассуждение можно применить и к нашему примеру выше. Можно думать об этом так: когда мы выбираем модель, дающую наилучший показатель эффективности, мы выбираем модель, лучше приспособленную под этот показатель эффективности. Получается, что как только мы выбрали лучшую модель по значению какой-то метрики, само это значение становится ненадежным и его надо заново измерить на новых данных. Это очень неочевидный момент и даже многие серьезные исследователи пропускают его в крупных научных публикациях.
Приведем еще одно объяснение этого феномена. Как мы сказали, при любом измерении возникают некоторые случайные факторы, которые обусловлены как минимум ограниченностью имеющихся данных, случайными ошибками выборки, недостаточностью признаков датасета для детерминированного предсказания целевой переменной, и вообще неучтенными факторами. Поэтому мы не можем быть уверенны ни в каком измерении на 100%, втом числе в оценке значения метрик эффективности. Если мы получили, ка в примере выше, 0.95, то “в реальности” модель может иметь эффективность как чуть выше, так и чуть ниже. То есть измеренное значение может иметь отрицательный или положительный случайный компонент.
Так как математическое ожидание случайной ошибки равно нулю, то в разных измерениях эти случайные компоненты встречаются как и положительные, так и отрицательные с равной вероятностью. Но, когда мы выбираем наилучшую модель, то с большей вероятностью выберем такую, в значении оценки качества которой этот самый случайный компонент именно положительный, то есть работает на рост этой оценки. Поэтому после выбора оптимальной модели мы получаем в среднем оптимистическую, то есть завышенную оценку ее качества.
Единственный способ оценить более близкое к реальному значению ее эффективности — измерить его на новом, еще не использованном наборе данных. Причем может получиться парадоксальная ситуация. В примере выше мы выбрали модель с эффективностью 95%. Но когда мы измерили ту же метрику, но на новых данных, модель показала, скажем всего 92%. Получается, что эта “самая лучшая” модель показала эффективность ниже, чем другая. Значит ли это, что мы выбрали неправильно? Нет, так как в оценке каждой из трех моделей сидит этот случайный, неизвестный нам компонент.
Такая схема выбора модели, как любое вероятностное рассуждение, не дает гарантированного результата, но обеспечивает наилучшую стратегию в среднем. То есть пользуясь таким способом мы чаще будем получать оптимальные модели и более надежные оценки их точности. Поэтому использование третьего набора данных для оценки эффективности при сравнении нескольких моделей является обязательной частью хорошей методики проведения машинного обучения.
При использовании этой методики все имеющиеся данные разделяют на три непересекающиеся части. Первая — обучающий набор — используется для подбора параметров модели (или моделей). Вторая — ее в таком случае чаще всего называют валидационным набором — используется для оценки эффективности разных моделей, их сравнения и выбора наилучшей, а также для оптимизации гиперпараметров. А третья — тестовый набор — используется только для итоговой оценки эффективности наилучшей модели. Обратите внимание, что тестовый набор используется только один раз.
Но как мы говорили, на практике всегда необходимо использовать кросс-валидацию. Перекрестная проверка по сути разбивает выборку на обучающий и валидационный наборы. Поэтому при начале машинного обучения исходный датасет разбивают всего на две части. Меньшая становится тестовым набором, она понадобится только на последнем этапе. Поэтому эти данные еще часто называют отложенным набором (holdout set). Оставшиеся данные (которые часто называют обучающей выборкой, что вносит определенную путаницу в термины) используют для кросс-валидированного выбора моделей.
Надо сказать, что вся эта сложная схема нужна только для наиболее точного и надежного выбора наилучшей модели и оценки ее эффективности, в которой мы можем быть максимально уверенными. То есть в итоге мы получаем модель (то есть параметрический класс функций, с определенными значениями гиперпараметров), про которую знаем с уверенностью, что она во-первых, лучше всех других моделей решает конкретную задачу, и, во-вторых, будет показывать на новых данных вот такую эффективность. После этого мы можем взять эту модель и обучить на всех имеющихся данных для запуска в реальную эксплуатацию. То есть не нужно использовать разбиение выборки для реального применения моделей машинного обучения, скажем, в пользовательских приложениях. Если мы уже выбрали наилучшую модель, для максимальной эффективности стоит использовать для обучения все данные, которые имеются в наличии.
Выводы:
- При сравнении нескольких моделей между собой возникает проблема оптимистичной оценки эффективности.
- Поэтому для исследования выбранной модели нужно использовать третью часть выборки.
- Это также надо использовать при оптимизации гиперпараметров.
- Во многих случаях использование кросс-валидации автоматически разбивает выборку.
- На практике после выбора модели и оценки ее эффективности ее обучают на всех имеющихся данных для реального использования.
Критерий — минимум — среднеквадратичная ошибка
Cтраница 1
Критерий минимума среднеквадратичной ошибки используется для решения более сложных задач по сравнению с задачей определения оптимальных параметров при известной структуре системы.
[1]
Идея приближения по критерию минимума среднеквадратичной ошибки, как уже указывалось, не единственна.
[2]
Тх корректирующего устройства по критерию минимума среднеквадратичной ошибки, если полезный сигнал и помеха независимы и приложены к одной точке системы.
[3]
Первое из этих условий удовлетворялось и при синтезе по критерию минимума среднеквадратичной ошибки.
[4]
Адекватность полученной модели и необходимость ее коррекции оценивают чаще всего по критерию минимума среднеквадратичной ошибки. Этот метод наиболее целесообразен.
[5]
Причем объем вычислений может быть значительно уменьшен за счет незначительного ухудшения качества, фильтрации по критерию минимума среднеквадратичной ошибки.
[6]
В большинстве практически встречающихся случаев представляется возможным, хотя бы в первом приближении, рассматривать процессы изменения технологических величин или других производственных показателей как стационарные случайные функции с нормальным распределением. Поэтому обычно критерий минимума среднеквадратичной ошибки является наиболее приемлемым в качестве критерия наилучшего предсказания в большинстве рассматриваемых задач управления.
[7]
Кроме того, по критерию минимума среднеквадратичной ошибки определяются оптимальная структура и передаточная функция замкнутой системы, обеспечивающие минимальную величину погрешности.
[8]
Анализ и синтез нелинейных систем с неизвестной структурой предлагается проводить с помощью многопеременных прямоугольных функций. Практически реализуемый алгоритм с применением этих функций получен на основе критерия минимума среднеквадратичной ошибки. Алгоритм применим при входных стационарных сигналах с произвольной плотностью распределения вероятностей.
[9]
Задача заключается в оценке значений, к-рые реализация рассматриваемого процесса ( или нек-рых его параметров, таких, как ср. Здесь в большинстве случаев определяется инвариантный во времени линейный реализуемый фильтр, оптимизирующий оценку по критерию минимума среднеквадратичной ошибки. Возможны и часто желательны др. критерии, но указанный критерий отличается математич. Для решения задач такого рода часто применяется теория Винера — Колмогорова. В этой теории предполагается, что сигнал S ( t) характеризуется только статистич. Мешающий шум N ( t) представляет также чисто случайный процесс, комбинируется с сигналом аддитивно и может быть с ним связан статистически. Далее предполагается, что накопление и обработка данных совершаются только над прошлым процессов на входе, к-рые считаются стационарными в широком смысле и имеющими положительно определенные ковариант-ные ф-ции. Кроме того, в большинстве случаев реализуются оптимальные линейные фильтры, к-рые не только реализуемы, но также и инвариантны во времени. При этих условиях импульсная переходная ф-ция линейного фильтра определяется из интегр.
[10]
Задача заключается в оценке значений, к-рые реализация рассматриваемого процесса ( или нек-рых его параметров, таких, как ср. Здесь в большинство случаев определяется инвариантный во времени линейный реализуемый фильтр, оптимизирующий оценку по критерию минимума среднеквадратичной ошибки. Возможны и часто желательны др. критерии, но указанный критерий отличается математич. Для решения задач такого рода часто применяется теория Винера — Колмогорова. В этой теории предполагается, что сигнал S ( t) характеризуется только статпстич. Мешающий шум N ( t) представляет также чисто случайный процесс, комбинируется с сигналом аддитивно и может быть с ним связан статистически. Далее предполагается, что накопление и обработка данных совершаются только над прошлым процессов па входе, к-рые считаются стационарными в широком смысле и имеющими положительно определенные ковариант-ные ф-ции. Кроме того, в большинстве случаев реализуются оптимальные линейные фильтры, к-рые не только реализуемы, но также и инвариантны во времени. При этих условиях импульсная переходная ф-ция линейного фильтра определяется из интегр.
[11]
После определения среднеквадратичной ошибки необходимо обеспечить минимальное значение ее. Наиболее просто задача решается путем минимизации среднеквадратичной ошибки по тому или иному параметру системы при заданных воздействиях. В качестве параметров, которые желательно сделать оптимальными на основе критерия минимума среднеквадратичной ошибки, могут рассматриваться различные постоянные, имеющие большое значение для определения динамических свойств системы.
[12]
Страницы:
1
Анализ систем на основе критерия минимума среднеквадратичной ошибки [c.189]
Если ковариационные функции процессов Х( ) и У(/) известны точно, то можно воспользоваться винеровским критерием минимума среднеквадратичной ошибки Этот критерий утверждает, что функция /г(и) должна быть выбрана так, чтобы минимизировать среднеквадратичную ошибку шумовой компоненты, т е [c.190]
Синтез следящих систем. Одно из первых инженерных применений анализа на основе критерия минимума среднеквадратичной ошибки было сделано при синтезировании следящих систем для зенитных орудий и в радиолокационных следящих системах [5] Например, от радиолокационной следящей системы требуется, чтобы она следила за самолетом несмотря на возмущения отра- [c.189]
Другое применение критерий минимума среднеквадратичной ошибки находит в задаче об идентификации системы В этом случае в распоряжении имеются входной сигнал и соответствующий ему выходной сигнал от некоторой системы, требуется вывести линейное приближение к этой системе для дальнейшего его использования при управлении или моделировании Предположим, например, что система представляет собой черный ящик (рис 5 7). Если вход является реализацией случайного процесса Х 1), то выход можно рассматривать как реализацию случайного процесса У(0< где [c.190]
Оптимальное в любом смысле корреляционное окно, например (7 2 3), будет зависеть от неизвестного спектра Гхх(/). Этот недостаток свойствен не только спектральному анализу Вообще говоря, справедливо правило, согласно которому наилучший план действий должен опираться на некоторые представления об истинном положении вещей Следовательно, очень валено проводить четкое различие между планированием спектрального анализа до сбора данных и самим анализом данных, после того как они собраны Мы хотели бы использовать критерии минимума среднеквадратичной ошибки или какой-нибудь аналогичный критерий до проведения спектрального анализа, чтобы решить, например, какой длины нужно взять запись Но после того как данные собраны, могло бы оказаться, что наши представления относительно Гхх (/) были абсолютно неправильны [c.26]
Если плотность вероятности ге ([х у) симметрична относительно среднего значения гпг [х у и унимодальна (т. е. монотонно невозрастающая функция [х — /П] [х у ), то байесовская оценка (5.18) совпадает с оценкой по критерию максимума апостериорной плотности вероятности. В этом случае функция С (х) не должна быть обязательно выпуклой, а лишь монотонно неубывающей функцией х (см. приложение С). Так как нормальная плотность вероятности унимодальна, то всегда, когда плотность вероятности ге ([х I у) нормальна, оценка по максимуму апостериорной плотности вероятности совпадает с широким классом байесовских оценок, который включает оценки по минимуму среднеквадратичной ошибки (или минимуму дисперсии). [c.158]

достаточно простом выражении для дисперсии это может быть определено непосредственным дифференцированием и приравниванием нулю частных производных.
В более сложных случаях приходится искать минимум дисперсии путем числового задания интересующих параметров и построения соответствующих графиков.
Другая постановка задачи при расчете по критерию минимума среднеквадратичной ошибки заключается в том, что ставится вопрос о нахождении оптимальной структуры и значений параметров автоматической системы, при которых обеспечивается получение теоретического минимума среднеквадратичной ошибки при заданных вероятностных характеристиках полезного сигнала и помехи. Эта задача будет решена, если найти, например, передаточную функцию
замкнутой системы 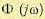
Задача относится к категории вариационных задач. Приведем здесь некоторые результаты ее решения [120] для случая, когда полезный сигнал g (t) и помеха f (I) представляют собой центрированные стационарные случайные процессы, приложенные на входе системы. Перед системой ставится задача преобразовывать входной сигнал g (t) так, чтобы на ее выходе воспроизводилась величина h (t), связанная с g (t) некоторой формулой преобразования
тде Н (р) — преобразующий оператор.
Так, например, при 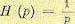
сглаживанием помехи (обычная следящая система при наличии помех), при 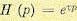
На основании изложенного ошибку системы можно представить в виде
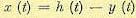
Выходная величина системы регулирования
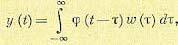
где 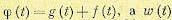
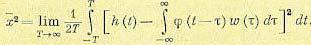
Задача заключается в том, чтобы найти частотную передаточную функцию замкнутой системы, связанную с весовой функцией преобразованием Фурье
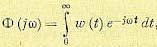
таким образом, чтобы минимизировать значение 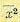
Раскроем в выражении (11.132) скобки и изменим порядок интегрирования:

Так как в реальных системах 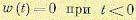
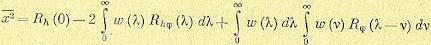
Из последнего выражения видно, что оптимальная весовая функция, соответствующая минимуму среднего квадрата ошибки, определяется только видом корреляционных функций полезного сигнала и помехи.
Можно показать [120], что необходимое и достаточное условие минимизации выражения (11.139), которое должно быть наложено на весовую функцию, заключается в том, чтобы она была решением интегрального уравнения Винера — Хопфа
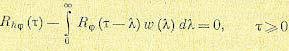
Оптимальная передаточная функция (11.133), соответствующая оптимальной весовой функции, являющейся решением уравнения (11.140), может быть представлена в виде

где
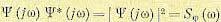
Вчастном случае, когда преобразующий оператор Н(р) = 1, т. е в так называемом случае оптимального сглаживания, имеем
Вэтом случае решение (11.141) может быть представлено в более простом виде:
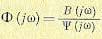
Числитель этого выражения определяется следующим образом. Рассмотрим следующее выражение:
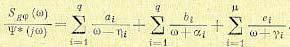
Здесь 
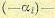
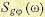
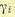
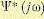
(11.145)

При реализации в системе оптимальной передаточной функции получится теоретический минимум среднего квадрата ошибки. Этот минимум определяется выражением или, в другом виде,
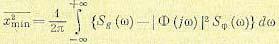
или, в другом виде,
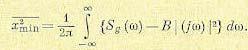
Рассмотрим иллюстративный пример. Предположим, что полезному сигналу и помехе на входе системы регулирования соответствуют спектральные плотности:
причем корреляция между ними отсутствует и 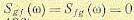
Отсюда знаменатель искомой передаточной функции (11.143)
Отбросив первый член в скобках, соответствующий полюсу в нижней полуплоскости, находим числитель искомой передаточной функции (11.143):
Нахождение оптимальной передаточной функции еще не означает, что реальная автоматическая система может быть выполнена оптимальной, так как реализация ее может быть сопряжена с большими трудностями. Оптимальную передаточную функцию, за исключением простейших случаев, следует считать идеальной функцией, к которой по возможности надо стремиться при выполнении реальной автоматической системы. Теория оптимальных систем излагается в работах [26, 108, 120, 121].
ГЛАВА 12. МЕТОДЫ СИНТЕЗА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
§ 12.1. Общие соображения
Под синтезом системы автоматического регулирования понимается направленный расчет, имеющий конечной целью отыскание рациональной структуры системы и установление оптимальных величин параметров ее отдельных звеньев. По отношению к основе синтеза в настоящее время имеются разные точки зрения.
Синтез можно трактовать как пример вариационной задачи и рассматривать такое построение системы автоматического регулирования, при котором для данных условий работы (управляющие и возмущающие воздействия, помехи, ограничения по времени работы и т. п.) обеспечивается теоретический минимум ошибки.
Синтез также можно трактовать как инженерную задачу, сводящуюся к такому построению системы автоматического регулирования, при котором обеспечивается выполнение технических требований к ней. Подразумевается, что из.многих возможных решений Инженер, проектирующий систему, будет выбирать те, которые являются оптимальными с точки зрения существующих конкретных условий и требований к габаритам, весу, простоте, надежности и т. п.
Иногда в понятие инженерного синтеза вкладывается еще более узкий смысл и рассматривается синтез, имеющий целью определение вида и параметров корректирующих средств, которые необходимо добавить к некоторой неизменяемой части системы регулирования (объект с регулятором), чтобы обеспечить требуемые динамические качества.
При инженерном синтезе системы автоматического регулирования необходимо обеспечить, во-первых, требуемую точность и, во-вторых, приемлемый характер переходных процессов.
Решение первой задачи в большинстве случаев сводится к определению требуемого общего коэффициента усиления системы и, в случае необходимости,— вида корректирующих средств, повышающих точность системы (регулирование по управляющему и возмущающему воздействиям, изодром-ные механизмы и т. п.). Эта задача может решаться при помощи определения ошибок в типовых режимах на основе тех критериев точности, которые были изложены в главе 8. Решение этой задачи, как правило, не сопряжено с трудностями принципиального или вычислительного характера, так как критерии точности достаточно просты для их практического использования. В сложных случаях можно прибегать к помощи моделирования. Решение оказывается сравнительно простым вследствие необходимости установления значений относительно небольшого числа параметров. В простейшем случае необходимо найти только общий коэффициент усиления системы.
Решение второй задачи — обеспечение приемлемых переходных процессов — оказывается почти всегда более трудным вследствие большого числа варьируемых параметров и многозначности решения задачи демпфирования системы. Поэтому существующие инженерные методы часто ограничиваются решением только второй задачи, так как их авторы считают, что обеспечение требуемой точности может быть достаточно просто сделано на основании использования существующих критериев точности и совершенствования их практически не требуется.
В настоящее время для целей синтеза систем автоматического регулирования широко используются электронные и электромеханические вычислительные машины, позволяющие производить полное или частичное моделирование проектируемой системы. При таком моделировании становится возможным наиболее полно исследовать влияние различных факторов нелинейности, зависимость параметров от времени и т. п.
Однако моделирование на вычислительных машинах не может заменить расчетных методов проектирования, которые во многих случаях позволяют исследовать вопрос в общем виде и среди многих решений найти оптимальное. Поэтому, несмотря на развитие и распространение машинных методов синтеза, теория должна располагать собственными методами, которые дополняли бы моделирование и являлись бы теоретической базой при отыскании оптимального решения.
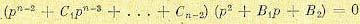
§ 12.2. Корневой метод
Наиболее простой корневой метод разработан Т. Н. Соколовым [117]. Сущность его сводится к следующему. [В соответствии с изложенным в § 12.1 рассматривается только задача
.получения приемлемых динамических качеств при заданном значении общего коэффициента усиления, т. е. последнего члена характеристического уравнения.]
Пусть имеется характеристическое уравнение системы

С точки зрения скорейшего затухания переходного процесса важно, чтобы вещественные части всех корней характеристического уравнения были наибольшими. Сумма вещественных частей всех корней численно равна первому коэффициенту характеристического уравнения (12.1). Поэтому при заданной величине этого коэффициента наивыгоднейшие результаты получаются при равенстве вещественных частей всех корней/ Однако расчеты и исследования построенных систем показывают, что стремление удовлетворить поставленному требованию приводит к совершенно нереальным конструктивным характеристикам отдельных звеньев. Эти расчеты и исследования показывают, что из общего числа корней характеристического уравнения всегда можно выделить два или три корня с меньшей по абсолютному значению вещественной частью, которые и определяют ход основного процесса. Остальные же корни характеризуют быстро затухающие составляющие, оказывающие влияние только на начальной стадии переходного процесса.
Примем, что основной характер переходного процесса определяется двумя корнями. Тогда уравнение (12.1) удобно представить в виде
(12.2)
Второй сомножитель (12.2) и будет определять основной характер процесса.
Для уменьшения погрешностей проектируемой системы важно, чтобы коэффициент В2 в основном множителе имел возможно большую величину. Однако чрезмерное увеличение В2 приводит к колебательному характеру переходного процесса.
Оптимальное соотношение между коэффициентами B1 и В2 определяется из условия получения затухания за один период 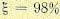

где 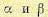

Множитель 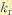
Из (12.3) можно также получить требуемое соотношение между мнимой и вещественной частями корня (колебательность):
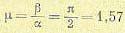
В ряде случаев для описания основного переходного процесса оказывается более целесообразным воспользоваться уравнением третьей степени

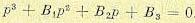
Это уравнение можно представить в виде
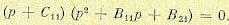
Между коэффициентами уравнений (12.6) и (12.7) имеют место соотношения:
Положим, что во втором множителе (12.7) по-прежнему
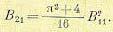
Поэтому корни характеристического уравнения (12.6) и (12.7) равны: 
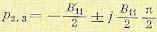
Так как вещественная часть корней должна быть возможно большей, то целесообразно задать
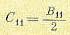
и, следовательно,
Подставив полученные значения в формулы разложения, находим зависимость между коэффициентами основного уравнения. Если В1 задано, то
Эти соотношения должны реализоваться при проектировании системы регулирования. Корни основного уравнения
Выбор уравнения для описания основной составляющей переходного процесса зависит от структурной схемы проектируемой системы.
Рассмотрим теперь связь между основной и дополнительной составляющими переходного процесса для заданного затухания ξ (8.40). Для этой цели полезно представить характеристическое уравнение (12.1) в таком виде:

где 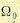
Записанное в такой форме уравнение третьей степени принимает вид
Разлагая его на множители, находим
Соотношения для коэффициентов:
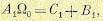

Введем коэффициент а и положим
откуда
Таким образом, безразмерные коэффициенты А1 и A2 являются функциями критерия переходного процесса &ш зависящего от. желаемой степени затухания и коэффициента разложения а, определяющего соотношение постоянных времени затухания отдельных составляющих.
Следовательно, обе составляющие переходного процесса затухают с одинаковой скоростью. Аналогичным образом можно получить выражения для коэффициентов
характеристического уравнения четвертой, пятой и более высоких степеней [117].
Синтез системы регулирования начинается с того, что для выбранной структурной схемы и введенных корректирующих средств находится характеристическое уравнение. Затем варьируются параметры основного канала регулирования и корректирующих средств таким образом, чтобы получить требуемые значения коэффициентов характеристического уравнения
(12.1) или (12.20).
Этот метод оказывается достаточно эффективным в случае сравнительно невысокой степени характеристического уравнения (n=2-4). В более сложных случаях обеспечить требуемые значения коэффициентов характеристического уравнения оказывается затруднительно, так как некоторые параметры системы и корректирующих средств могут влиять сразу на несколько коэффициентов характеристического уравнения.
Недостатком этого метода является также то, что необходимо задаваться видом корректирующих средств. Поэтому получаемое решение будет во многом зависеть от опытности проектанта.
§ 12.3. Метод корневых годографов
Качество системы регулирования с точки зрения быстродействия и запаса устойчивости может характеризоваться расположением корней числителя и знаменателя передаточной функции замкнутой системы, т. е. расположением нулей и полюсов передаточной функции (§ 8.6).
Зная эти корни, можно изобразить их расположение на комплексной плоскости корней. При расчете регулируемой системы целесообразно проследить, как меняется общая картина расположения корней при изменении отдельных параметров, например общего коэффициента усиления, постоянных времени корректирующих цепей и т. п., с целью установления оптимальных значений этих параметров.
При плавном изменении значения какого-либо параметра корни будут перемещаться на плоскости корней, прочерчивая некоторую кривую, которую будем называть корневым
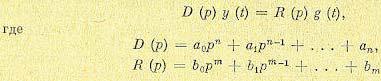
годографом или траекторией корней. Построив траектории всех корней, можно выбрать такое значение варьируемого параметра, которое соответствует наилучшему расположению корней.
Первый способ построения траекторий корней заключается в следующем. Пусть имеется дифференциальное уравнение замкнутой системы, записанное для регулируемой величины при наличии задающего воздействия (5.3):
Это уравнение записано здесь для случая равенства нулю возмущающих воздействий. Оно может быть записано также для любого возмущающего-воздействия. Это не изменит его формы и не отразится на дальнейших рассуждениях.
Передаточная функция замкнутой системы
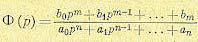
Полюсы передаточной функции, т. е. корни знаменателя, обозначим через 
ее нули (корни числителя) —через 
Коэффициенты числителя и знаменателя (12.29) определенным образом выражены через параметры регулируемого объекта, регулятора и корректирующих устройств. Если нужно
выбрать величину какого-либо параметра 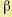
значения для всех остальных параметров, а для искомого параметра 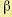
числовые значения 
Если нужно выбрать два или несколько параметров регулируемой системы, то такого рода вычисления нужно проделать несколько раз, меняя каждый раз один из параметров при заданных значениях всех остальных.
Вычисление корней при этом можно производить любым численным методом, возможно более простым, так как ввиду приближенности корневой оценки здесь не требуется большой точности вычислений. В настоящее время имеются электрические устройства, позволяющие строить на экране траектории корней непосредственно по заданным коэффициентам уравнения.
Из простых численных методов определения корней можно рекомендовать, например, метод последовательных делений [98].
Другой способ построения траекторий корней, разработанный Ивэнсом и Э. Г. Удерманом [128], в отличие от первого, пригодного для выбора любого параметра системы, специально приспособлен для выбора общего коэффициента усиления передаточной функции разомкнутой системы (5.10), которую запишем следующим образом:
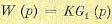
Здесь К = Кr — общий коэффициент усиления разомкнутой системы, имеющий размерность сек-r, где r — степень астатизма; G1 (р) — операторная часть передаточной функции разомкнутой системы.
Характеристическое уравнение системы может быть записано в виде
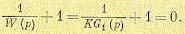
Обозначим полюсы и нули передаточной функции разомкнутой системы соответственно через 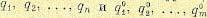

Каждый сомножитель в выражении (12.32) можно изобразить в виде вектора на комплексной плоскости (рис. 12.1), где р — текущая точка. Обозначим длину (модуль) каждого
вектора в знаменателе (12.32) через 

(аргумент) для знаменателя обозначим 

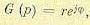
где
Траектории корней (рис. 12.1) строятся таким образом, чтобы они удовлетворяли условию (12.38). После этого по формуле (12.34) для каждой
конкретной комбинации корней можно вычислить А и величину r, а затем по формуле (12.37) — общий коэффициент усиления К.
Для упрощения построения траекторий корней используются следующие свойства. 1.При К = 0 корни характеристического уравнения замкнутой системы совпадают с
полюсами передаточной функции разомкнутой системы W (р) или G (р), так как согласно (12.31) при К = 0 имеем 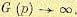
2. При 
как при 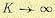
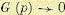
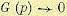

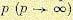
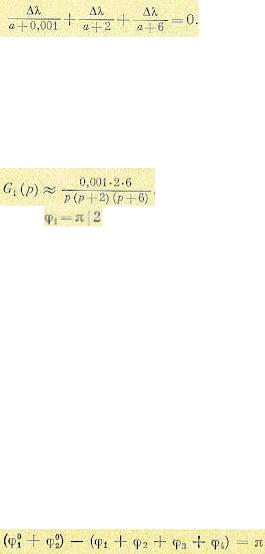
откуда аргумент комплексного числа 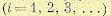
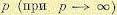
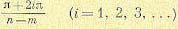
3.На вещественной оси траектории корней представляют собой отрезки прямой, соединяющие нули и полюсы функции G (р), расположенные на этой оси. Началом траекторий на вещественной оси служит нуль, расположенный правее всех остальных.
4.Если траектория отклоняется от вещественной оси, то положение точки р = а, в которой траектория отходит от этой оси, можно оценить из того условия, что при малом отклонении 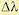
Так, например, пусть имеется функция
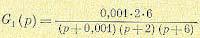
При К = 0 траектории исходят из точек (—0,001), (—2) и (—6), лежащих на вещественной
оси. Отрезки траекторий лежат между точками (—0,001) ж (—2) и между (—6) и 
Решение этого квадратного уравнения дает 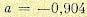
5. Положение точки, в которой траектория пересекает мнимую ось при переходе в правую полуплоскость комплексной переменной р, часто можно оценить, пренебрегая влиянием малого по абсолютной величине полюса функции G (р).
Рассмотрим в качестве примера опять функцию (12.42). При значительных по модулю величинах комплексной переменной р эту функцию можно с хорошей точностью аппроксимировать функцией
Тогда (рис. 12.2) и, следовательно, условие (12.38) сводится к равенству
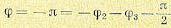
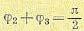
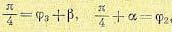
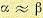
6. Направление касательной к траектории при выходе ее из какого-либо полюса или при подходе к какому-либо нулю нетрудно определить путем вычисления угла между этой касательной в данном полюсе или нуле и вещественной осью. При таком вычислении используется зависимость (12.38) для аргументов всех нулей и полюсов, расположенных по условию в левой полуплоскости комплексной переменной р.
На рис. 12.3 изображены траектории корней передаточной функции G (р), имеющей два нуля и два полюса на вещественной оси и одну пару комплексных сопряженных полюсов. При
достаточно малом удалении точки р от полюса q4 углы 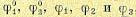
остальным нулям и полюсам, останутся неизменными. Таким образом, в силу (12.38) угол 
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Применим закон распределения равновероятности:
(4)
Подставляя (1) и (2) и (4) и вводя обозначения с фазой
Последовательная схема может быть
также реализована на основе СФ.
Нормальные
и аномальные ошибки.
Необходимо рассматривать
,
тогда
если ,
либо соответствует
, то
Эта же задача стоит при
радиоизмерениях. И она может решаться при построении оптимального устройства, с
различными критериями.
Статистические
критерии оценки непрерывных параметров
сигнала.
Cуществуют
следующие критерии:
ü
Критерий максимума функции правдоподобия.
ü
максимальная апостериорная плотность распределения вероятности
параметра .
ü
Критерий минимума средне квадратичной ошибки.
ü
Критерий Баеса.
Распишем каждый критерий более
подробно.
Критерий максимального
правдоподобия.
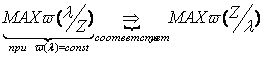
максимального правдоподобия.
Критерий максимальной
апостериорной вероятности.
Рассмотрим статистическую схему:
Оценивается значение
максимального параметра.
Критерий минимальной средне
квадратичной ошибки.
Ошибки, связанные с фиксацией , не выходящие за пределы
корреляционного пика называются нормальные ошибки (инстр. ошибки,
ошибки шума).
Шумовая составляющая:
Дисперсия:
Шумовая составляющая имеет вид , но её особенность, что
количество сигнальных выбросов тем больше, чем больше шумовой уровень.
При регистрации шумовой выброс
может быть принят за сигнальный выброс. Ошибка может составить , а нормальные ошибки не выходят за
корреляционные пределы. Вероятность появления аномальных ошибок характеризует
неправильность измерения вообще.
При проектировании задают
соотношение сигнал/шум, чтобы избежать аномальных ошибок.
А среднеквадратичная ошибка
параметра .
Расчёт среднеквадратической ошибки.
Рассмотрим формулу исходя из
геометрического происхождения сигнала.










































![{\displaystyle {\bar {x}}_{k}=\mathrm {E} [x_{k}|y_{1},\ldots ,y_{k-1}]=\mathrm {E} [x_{k-1}|y_{1},\ldots ,y_{k-1}]={\hat {x}}_{k-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/831099b32c20d3fd925ced1a7bdb9246af3b2cbf)

















![{\displaystyle \operatorname {cov} (Z)=\operatorname {E} [zz^{T}]=\left[{\begin{array}{cccc}1&2&3&4\\2&5&8&9\\3&8&6&10\\4&9&10&15\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90889a9de7192d317decb8381ca25cda49892b5c)
![{\displaystyle C_{Y}=\left[{\begin{array}{ccc}E[z_{1},z_{1}]&E[z_{2},z_{1}]&E[z_{3},z_{1}]\\E[z_{1},z_{2}]&E[z_{2},z_{2}]&E[z_{3},z_{2}]\\E[z_{1},z_{3}]&E[z_{2},z_{3}]&E[z_{3},z_{3}]\end{array}}\right]=\left[{\begin{array}{ccc}1&2&3\\2&5&8\\3&8&6\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50c0831c4af6cc131c13cd4da73e21ee08aac40c)
![{\displaystyle C_{YX}=\left[{\begin{array}{c}E[z_{4},z_{1}]\\E[z_{4},z_{2}]\\E[z_{4},z_{3}]\end{array}}\right]=\left[{\begin{array}{c}4\\9\\10\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0b4e00619f85de1c0967817d68b6b154557af03)
![{\displaystyle C_{Y}^{-1}C_{YX}=\left[{\begin{array}{ccc}4.85&-1.71&-0.142\\-1.71&0.428&0.2857\\-0.142&0.2857&-0.1429\end{array}}\right]\left[{\begin{array}{c}4\\9\\10\end{array}}\right]=\left[{\begin{array}{c}2.57\\-0.142\\0.5714\end{array}}\right]=W^{T}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f29d9505d5f630feae8a4566c23bae8dd82fd5d)















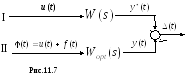
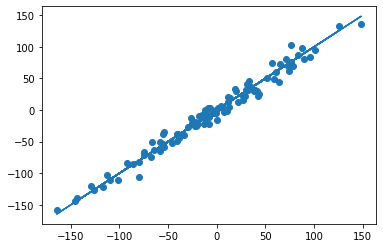
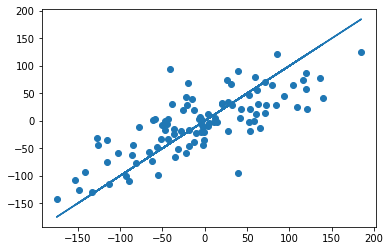
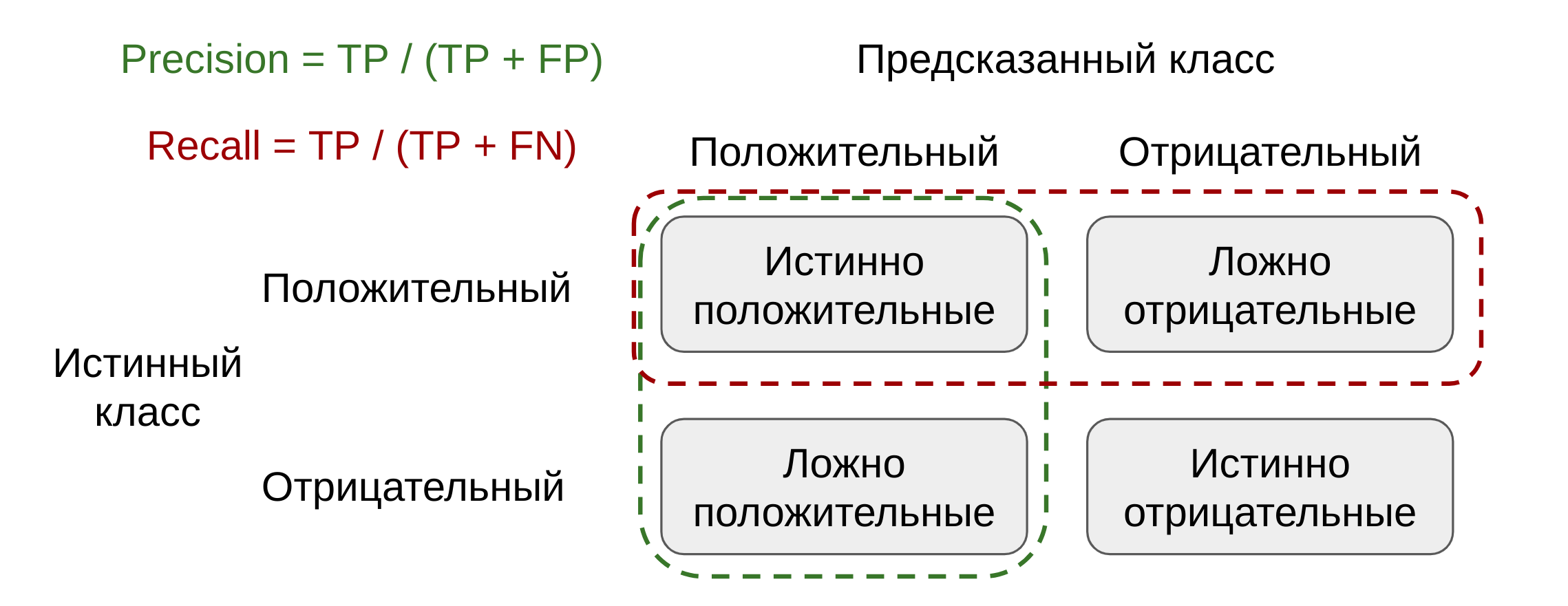
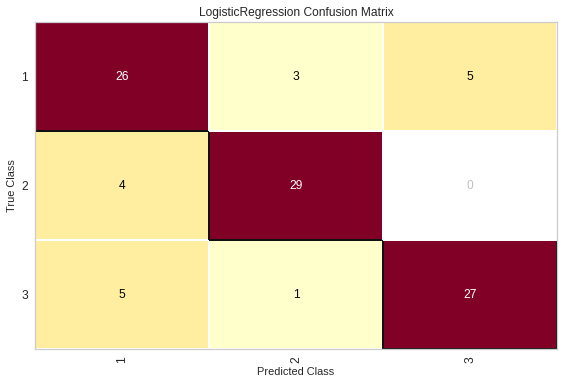
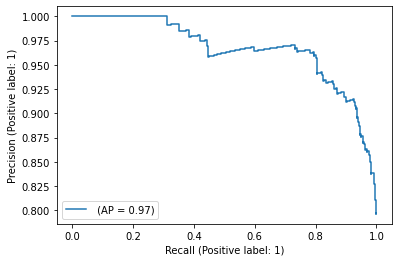
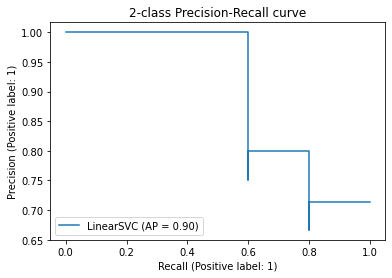
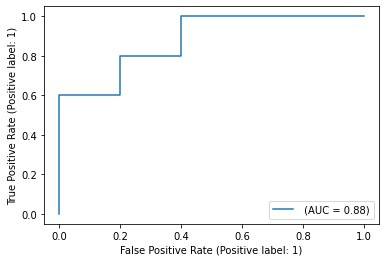
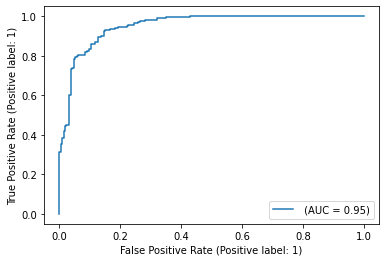
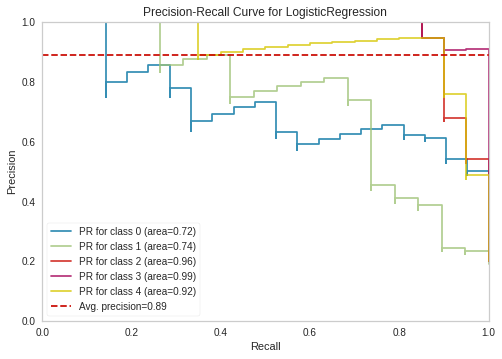
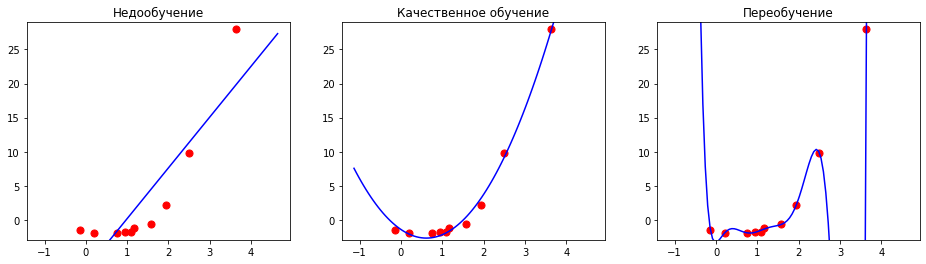
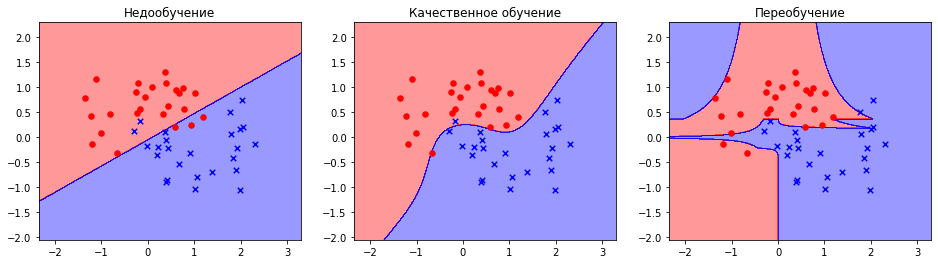
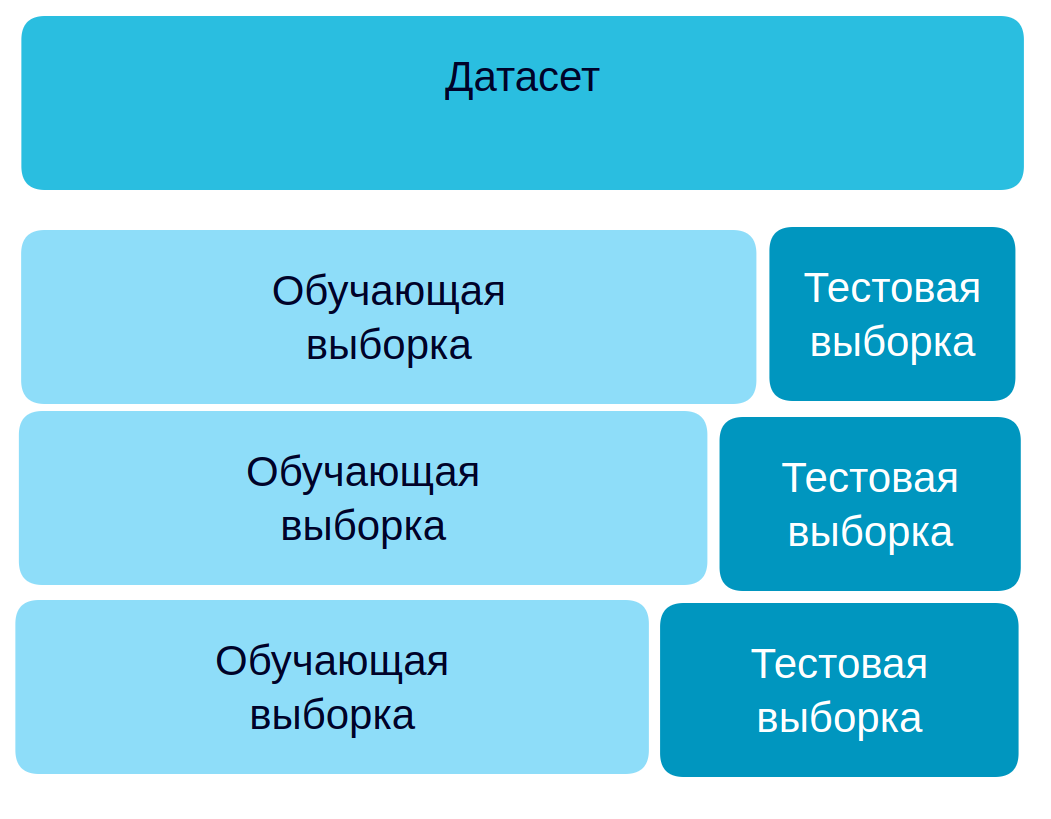
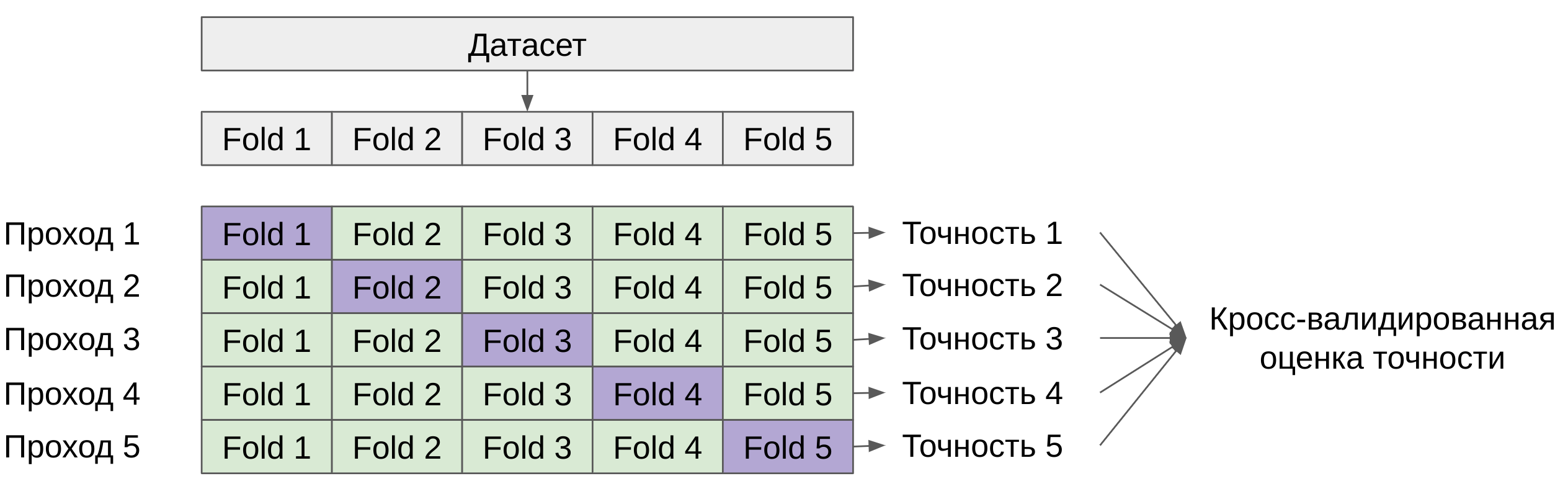
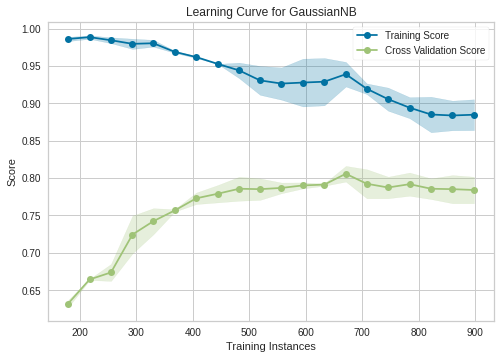
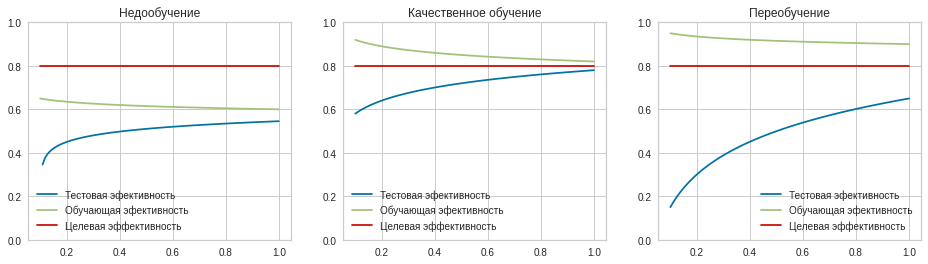
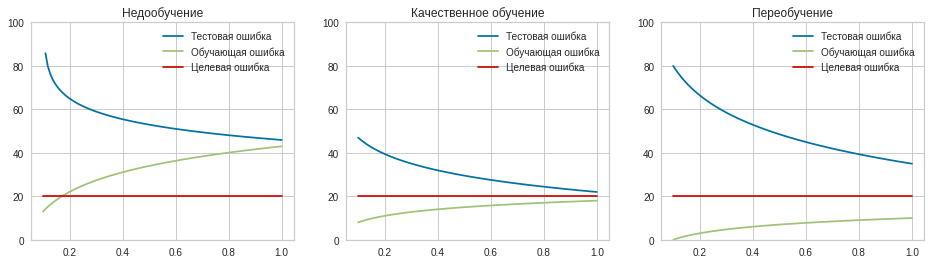
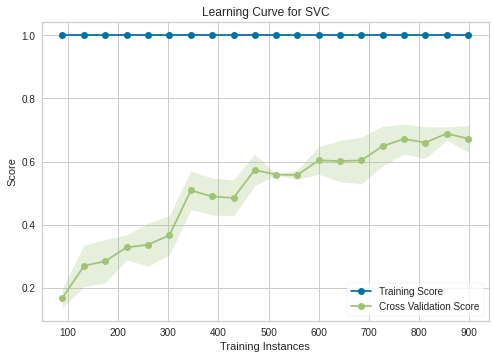
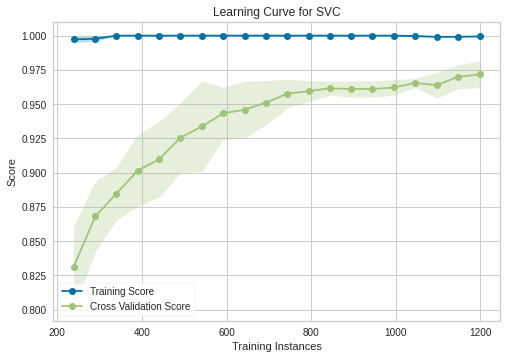
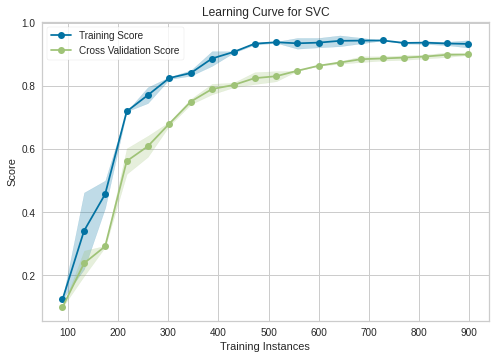
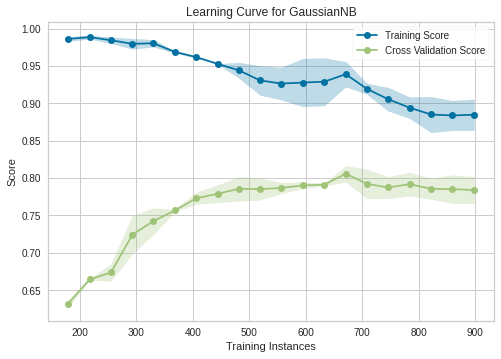
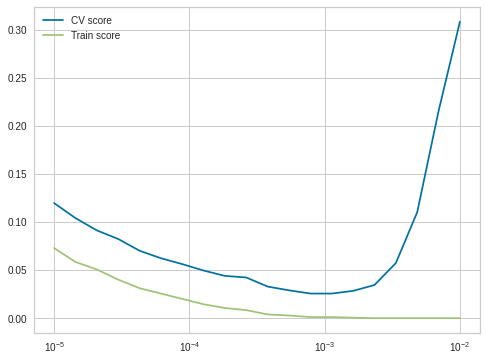
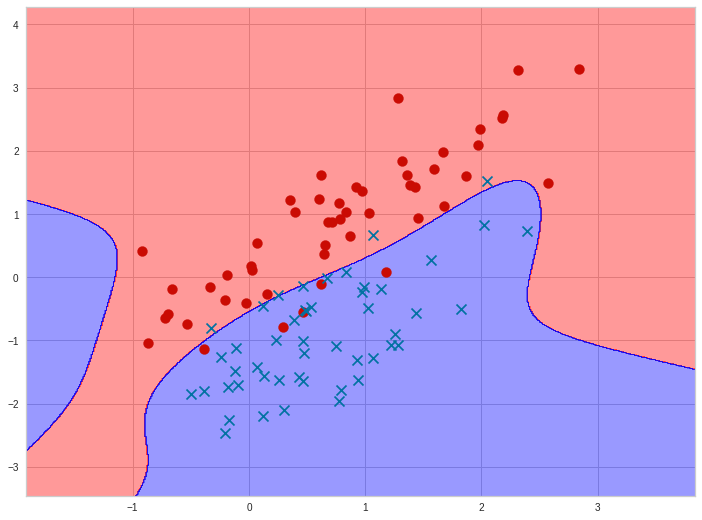
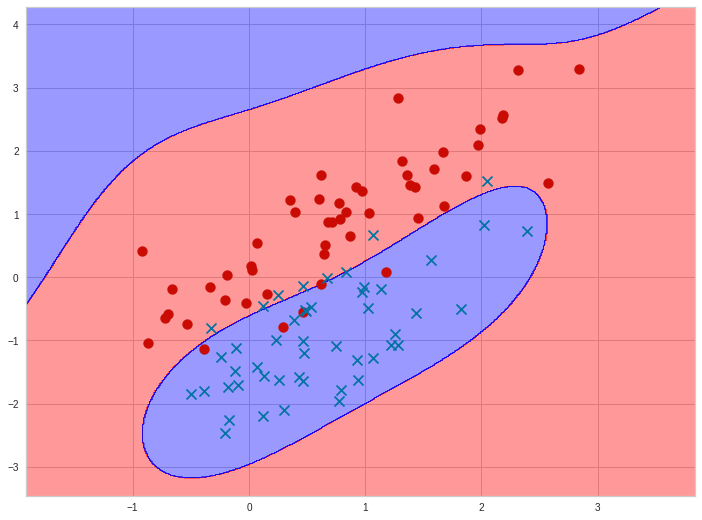
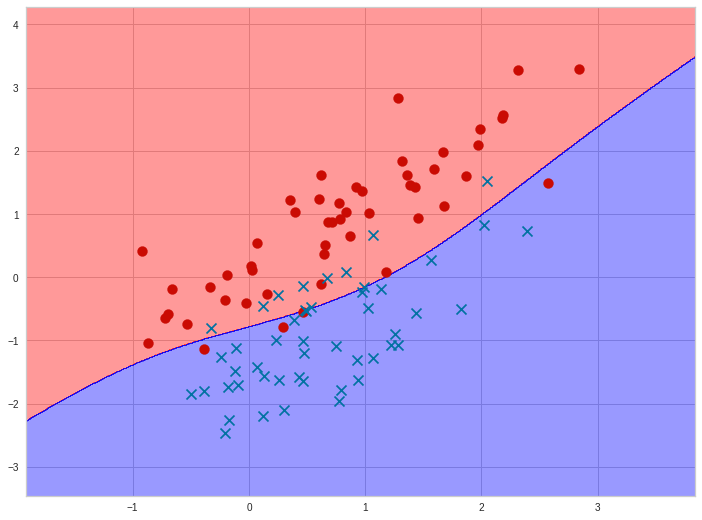
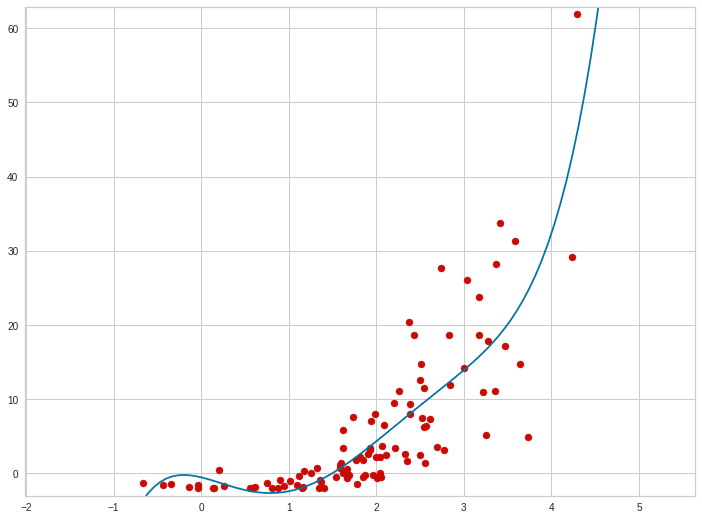
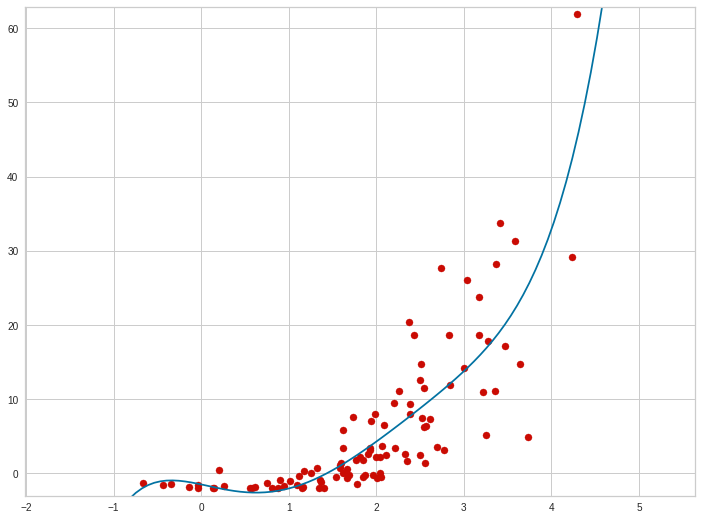
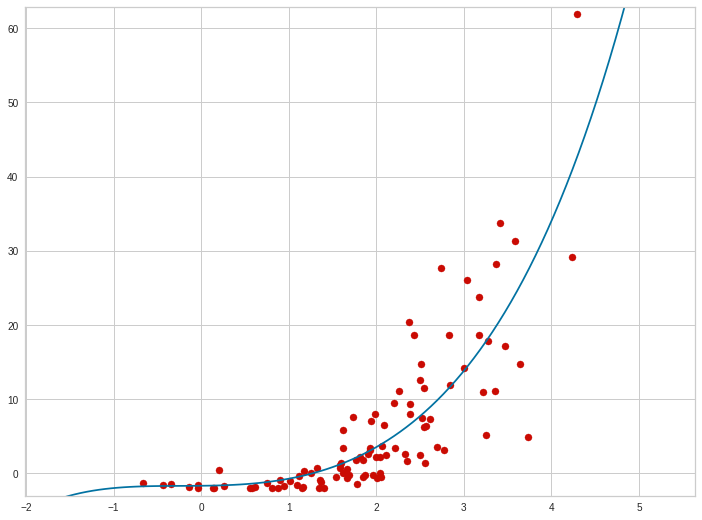
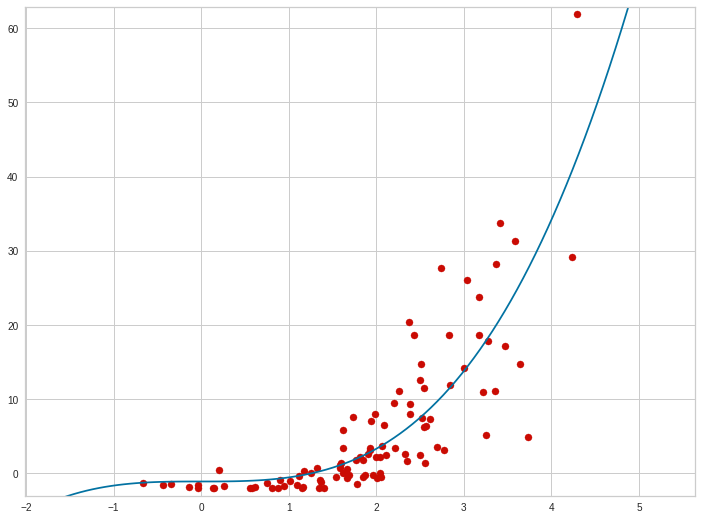
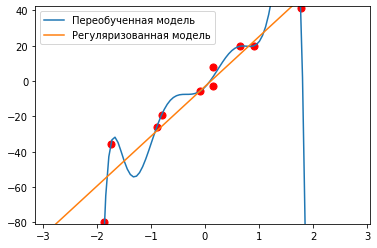
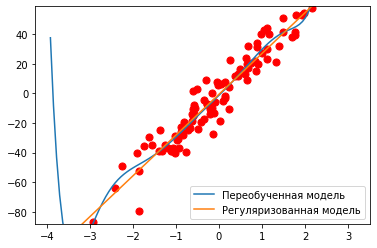
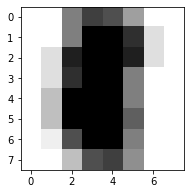
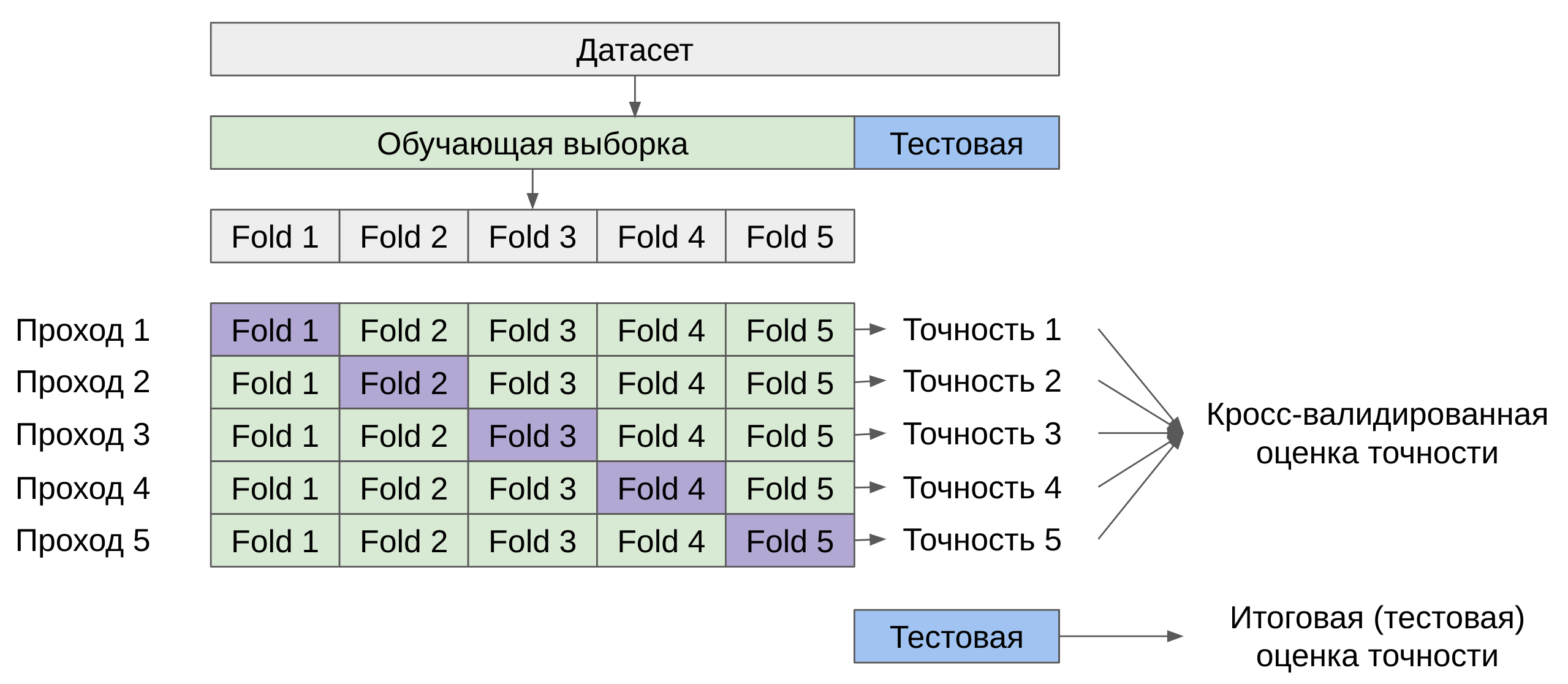
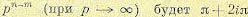



![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)