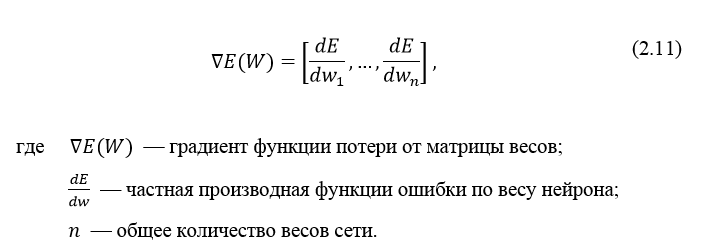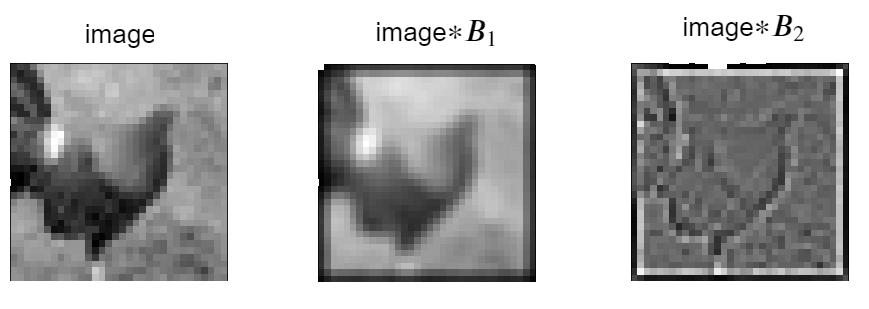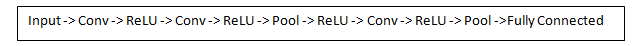Метод обратного распространения ошибки для сверточной сети

Время на прочтение
5 мин

Количество просмотров 83K

В первой части были рассмотрены: структура, топология, функции активации и обучающее множество. В этой части попробую объяснить как происходит обучение сверточной нейронной сети.

Обучение сверточной нейронной сети

На начальном этапе нейронная сеть является необученной (ненастроенной). В общем смысле под обучением понимают последовательное предъявление образа на вход нейросети, из обучающего набора, затем полученный ответ сравнивается с желаемым выходом, в нашем случае это 1 – образ представляет лицо, минус 1 – образ представляет фон (не лицо), полученная разница между ожидаемым ответом и полученным является результат функции ошибки (дельта ошибки). Затем эту дельту ошибки необходимо распространить на все связанные нейроны сети.

Таким образом обучение нейронной сети сводится к минимизации функции ошибки, путем корректировки весовых коэффициентов синаптических связей между нейронами. Под функцией ошибки понимается разность между полученным ответом и желаемым. Например, на вход был подан образ лица, предположим, что выход нейросети был 0.73, а желаемый результат 1 (т.к. образ лица), получим, что ошибка сети является разницей, то есть 0.27. Затем веса выходного слоя нейронов корректируются в соответствии с ошибкой. Для нейронов выходного слоя известны их фактические и желаемые значения выходов. Поэтому настройка весов связей для таких нейронов является относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Долгое время не было известно алгоритма распространения ошибки по скрытым слоям.

Алгоритм обратного распространения ошибки

Для обучения описанной нейронной сети был использован алгоритм обратного распространения ошибки (backpropagation). Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом. Метод был предложен в 1986 г. Румельхартом, Макклеландом и Вильямсом. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Данный алгоритм является первым и основным практически применимым для обучения многослойных нейронных сетей.

Для выходного слоя корректировка весов интуитивна понятна, но для скрытых слоев долгое время не было известно алгоритма. Веса скрытого нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.

Основные соотношения метода обратного распространения ошибки получены при следующих обозначениях:

Величина ошибки определяется по формуле 2.8 среднеквадратичная ошибка:

Неактивированное состояние каждого нейрона j для образа p записывается в виде взвешенной суммы по формуле 2.9:

Выход каждого нейрона j является значением активационной функции

, которая переводит нейрон в активированное состояние. В качестве функции активации может использоваться любая непрерывно дифференцируемая монотонная функция. Активированное состояние нейрона вычисляется по формуле 2.10:

В качестве метода минимизации ошибки используется метод градиентного спуска, суть этого метода сводится к поиску минимума (или максимума) функции за счет движения вдоль вектора градиента. Для поиска минимума движение должно быть осуществляться в направлении антиградиента. Метод градиентного спуска в соответствии с рисунком 2.7.

Градиент функции потери представляет из себя вектор частных производных, вычисляющийся по формуле 2.11:

Производную функции ошибки по конкретному образу можно записать по правилу цепочки, формула 2.12:

Ошибка нейрона обычно записывается в виде символа δ (дельта). Для выходного слоя ошибка определена в явном виде, если взять производную от формулы 2.8, то получим t минус y, то есть разницу между желаемым и полученным выходом. Но как рассчитать ошибку для скрытых слоев? Для решения этой задачи, как раз и был придуман алгоритм обратного распространения ошибки. Суть его заключается в последовательном вычислении ошибок скрытых слоев с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.

Ошибка δ для скрытого слоя рассчитывается по формуле 2.13:

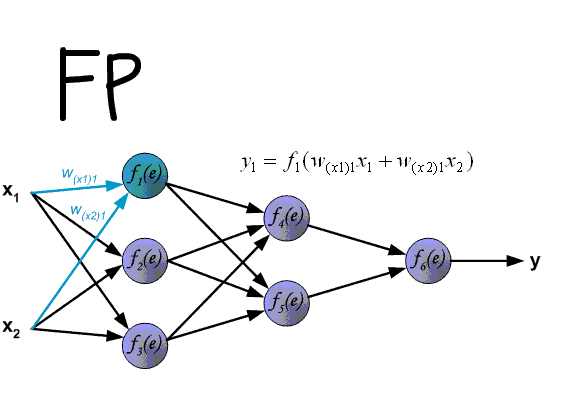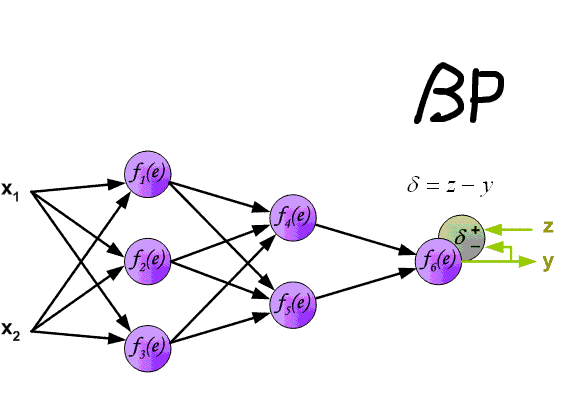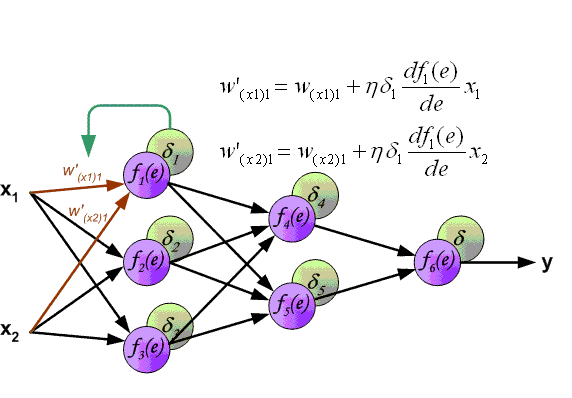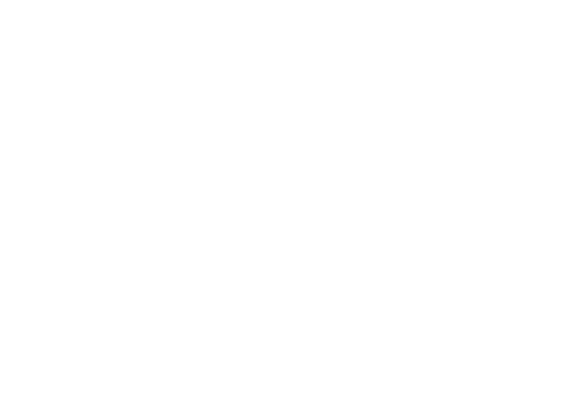
Алгоритм распространения ошибки сводится к следующим этапам:

• прямое распространение сигнала по сети, вычисления состояния нейронов;
• вычисление значения ошибки δ для выходного слоя;
• обратное распространение: последовательно от конца к началу для всех скрытых слоев вычисляем δ по формуле 2.13;
• обновление весов сети на вычисленную ранее δ ошибки.

Алгоритм обратного распространения ошибки в многослойном персептроне продемонстрирован ниже:

До этого момента были рассмотрены случаи распространения ошибки по слоям персептрона, то есть по выходному и скрытому, но помимо них, в сверточной нейросети имеются подвыборочный и сверточный.

Расчет ошибки на подвыборочном слое

Расчет ошибки на подвыборочном слое представляется в нескольких вариантах. Первый случай, когда подвыборочный слой находится перед полносвязным, тогда он имеет нейроны и связи такого же типа, как в полносвязном слое, соответственно вычисление δ ошибки ничем не отличается от вычисления δ скрытого слоя. Второй случай, когда подвыборочный слой находится перед сверточным, вычисление δ происходит путем обратной свертки. Для понимания обратно свертки, необходимо сперва понять обычную свертку и то, что скользящее окно по карте признаков (во время прямого распространения сигнала) можно интерпретировать, как обычный скрытый слой со связями между нейронами, но главное отличие — это то, что эти связи разделяемы, то есть одна связь с конкретным значением веса может быть у нескольких пар нейронов, а не только одной. Интерпретация операции свертки в привычном многослойном виде в соответствии с рисунком 2.8.

Рисунок 2.8 — Интерпретация операции свертки в многослойный вид, где связи с одинаковым цветом имеют один и тот же вес. Синим цветом обозначена подвыборочная карта, разноцветным – синаптическое ядро, оранжевым – получившаяся свертка

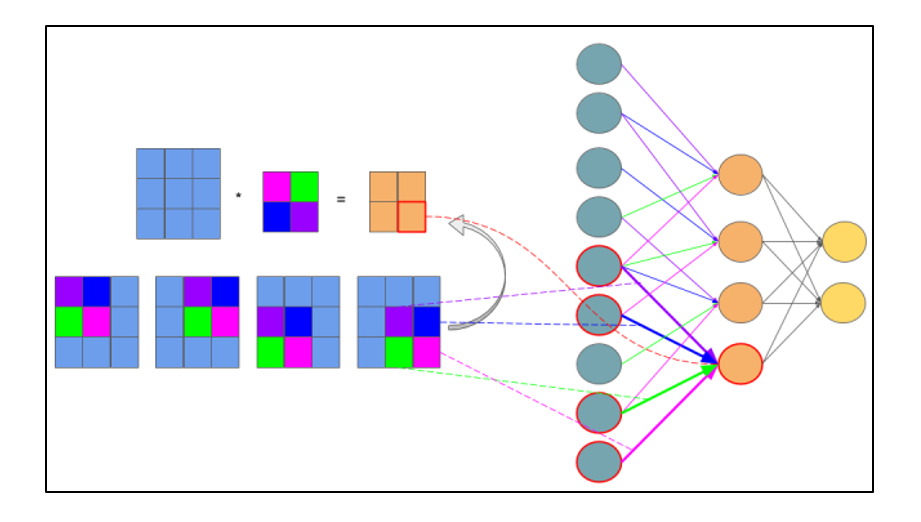
Теперь, когда операция свертки представлена в привычном многослойном виде, можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети. Соответственно имея вычисленные ранее дельты сверточного слоя можно вычислить дельты подвыборочного, в соответствии с рисунком 2.9.

Рисунок 2.9 — Вычисление δ подвыборочного слоя за счет δ сверточного слоя и ядра

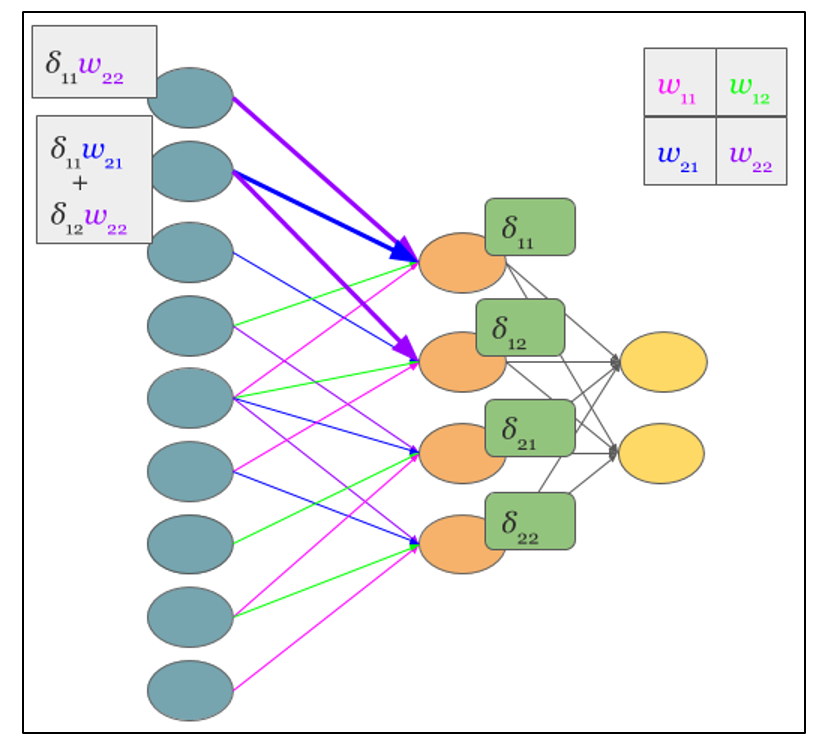
Обратная свертка – это тот же самый способ вычисления дельт, только немного хитрым способом, заключающийся в повороте ядра на 180 градусов и скользящем процессе сканирования сверточной карты дельт с измененными краевыми эффектами. Простыми словами, нам необходимо взять ядро сверточной карты (следующего за подвыборочным слоем) повернуть его на 180 градусов и сделать обычную свертку по вычисленным ранее дельтам сверточной карты, но так чтобы окно сканирования выходило за пределы карты. Результат операции обратной свертки в соответствии с рисунком 2.10, цикл прохода обратной свертки в соответствии с рисунком 2.11.

Рисунок 2.10 — Результат операции обратной свертки

Рисунок 2.11 — Повернутое ядро на 180 градусов сканирует сверточную карту

Расчет ошибки на сверточном слое

Обычно впередиидущий слой после сверточного это подвыборочный, соответственно наша задача вычислить дельты текущего слоя (сверточного) за счет знаний о дельтах подвыборочного слоя. На самом деле дельта ошибка не вычисляется, а копируется. При прямом распространении сигнала нейроны подвыборочного слоя формировались за счет неперекрывающегося окна сканирования по сверточному слою, в процессе которого выбирались нейроны с максимальным значением, при обратном распространении, мы возвращаем дельту ошибки тому ранее выбранному максимальному нейрону, остальные же получают нулевую дельту ошибки.

Заключение

Представив операцию свертки в привычном многослойном виде (рисунок 2.8), можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети.

Источники

Алгоритм обратного распространения ошибки для сверточной нейронной сети

Обратное распространение ошибки в сверточных слоях
раз и два

Обратное распространение ошибки в персептроне

Еще можно почитать в РГБ диссертацию Макаренко: АЛГОРИТМЫ И ПРОГРАММНАЯ СИСТЕМА КЛАССИФИКАЦИИ

В этой главе мы на примере задачи распознавания изображений познакомимся со свёрточными нейронными сетями, уже ставшими стандартом в области. Для начала мы разберёмся, с какого рода данными придётся работать, затем попробуем решить задачу «в лоб» при помощи знакомых вам полносвязных сетей и поймём, чем это чревато, после чего рассмотрим свёртки и попробуем выработать нужную интуицию.

Формат данных

Картинки в большинстве случаев представляют собой упорядоченный набор пикселей, где каждый пиксель – это вектор из трех «каналов» (интенсивность красного, интенсивность зелёного, интенсивность синего).

Каждая интенсивность характеризуется числом от 0 до 1, но для привычных нам изображений этот интервал равномерно дискретизирован, чтобы уместиться в 8 бит (от 0 до 255), для экономии памяти. При этом (0, 0, 0), нулевая интенсивность, соответствует чёрному цвету, а (255, 255, 255), максимальная интенсивность, – белому.

Когда мы наблюдаем изображение на мониторе компьютера, мы видим эти пиксели «уложенными» в строки одинаковой длины (человек не сможет воспринять картинку, вытянутую в один вектор). Длину каждой такой строки называют шириной W картинки, а количество строк – высотой H. Резюмирую, мы можем рассматривать картинку, как тензор HxWx3, состоящий из чисел uint8.

Существует множество разных форматов хранения картинок: вместо трех интенсивностей мы можем использовать триплет (оттенок,насыщенность,интенсивность), а сами картинки хранить, например, как тензор CxHxW.

MLP

Наверное, самый простой способ построить нейронную сеть для решения задачи классификации на наших данных – это «развернуть» нашу картинку в вектор, а затем использовать обычную многослойную сеть с кросс-энтропией в качестве лосса.

Однако, такой подход имеет несколько недостатков:

1. Количество параметров. В первом слое у нас получается HxWxCxCout параметров, где Cout – это количество нейронов в первом слое. Если поставить Cout слишком маленьким, мы рискуем потерять много важной информации, особенно, если рассматривать картинки размером, например, 1920×1080. Если же выставить Cout большим, рискуем получить слишком много параметров (а это только первый слой), а с этим и все вытекающие проблемы (переобучение, сложность оптимизации).

2. Структура данных никак не учитывается. Что здесь имеется в виду под «структурой»? Попробуем объяснить на примере. Для этого рассмотрим картинку щеночка:

   

   Если мы сдвинем картинку на несколько пикселей, то мы все еще будем уверены в том, что это щенок:

   

   Точно также мы останемся неизменны в своем мнении, если картинку отмасштабировать:

   

   или повернуть/развернуть:

   
   

Получается, что нейронная сеть должна «сама» понять, что ее ответ должен быть инвариантен к описанным преобразованиям. Но, обычно, это достигается за счет увеличения количества нейронов в скрытых слоях (как мы можем помнить из universal approximation theorem), что и так для нас является головной болью из-за первого пункта.

С частью этих проблем нам поможет новый «строительный блок» – свёртка. О ней в следующем разделе.

Свёртки

Мотивация

Строгое определение свёртки мы дадим ниже, а вначале разберёмся в мотивации.

Давайте попробуем решить хотя бы проблему инвариантности к сдвигу. Щенок может быть где угодно на картинке, и мы не можем наверняка сказать, в какой части изображения наша модель «лучше всего» научилась видеть щенков. Поэтому для надёжного предсказания будет логично посдвигать картинку на все возможные смещения (пустоты заполним нулями):

Затем для каждого смещения мы предскажем вероятность наличия щенка на картинке. Получившиеся предсказания можно уже агрегировать как удобно: среднее, максимум и тп.

Давайте взглянем на эту операцию под другим углом. Рассмотрим картинку, размером в 3 раза превышающую оригинальную, в центре которой находится наше изображение щеночка:

Возьмём окно размером с исходную картинку, и будем его сдвигать на все возможные смещения внутри нового изображения:

Легко видеть, что получается то же самое, как если бы мы картинку сдвигали относительно окна.

Представим себе самую простую модель, основанную на данном принципе – что-то вроде ансамбля линейных. Каждую из сдвинутых картинок вытянем в вектор и скалярно умножим на вектор весов (для простоты один и тот же для всех сдвигов) – получим линейный оператор, для которого есть специальное имя – свёртка, и это один из важнейших компонент в свёрточных нейронных сетях. Веса свёртки, упорядоченные в тензор (в нашем случае размерности HxWx3), составляют её ядро. Область картинки, которая обрабатывается в текущий момент, обычно называется окном свёртки. Обратите внимание, что обычно такие свёртки называются двумерными – так как окно свёртки пробегает по двум измерениям картинки (при этом все цветовые каналы участвуют в вычислениях). Следующая картинка поможет разобраться (внимание: на ней нет изображения весов оператора):

Каждый «кубик» на картинке – это число. Большой черный тензор слева – это изображение щеночка $X$. Фиолетовым на нем выделено окно, из которого мы достаем все пиксели и разворачиваем в вектор (аналогично операции flatten в numpy) $v$. Далее этот вектор умножается на вектор весов класса «щенок» $w_1$, и получается число $k_1$ – логит интересующего класса. Добавив остальные классы, получим матрицу весов $W$ – прямо как в мультиномиальной логистической регрессии. Эту операцию мы повторяем для каждого возможного сдвига окна свёртки.

Результаты домножения удобно бывает скомпоновать в двумерную табличку, которую при желании можно трактовать, как некоторую новую картинку (в серых тонах, потому что канал уже только один). Воспользуемся этим, чтобы получше осознать, что происходит в ходе свёртки.

Вопрос на подумать. Какой геометрический смысл имеет свёртка с ядром

$$B_1 = \frac19\begin{pmatrix}1 & 1 & 1\\ 1 & 1 & 1\\ 1 & 1 & 1\end{pmatrix}?$$

А с ядром

$$B_2 = \begin{pmatrix}-1 & -1 & -1\\ -1 & 8 & -1\\ -1 & -1 & -1\end{pmatrix}?$$

Подумайте самостоятельно, прежде чем смотреть ответ.Первая свёртка усредняет каждый пиксель с соседними; таким образом, изображение размывается. Смысл второй можно грубо описать так: пиксели из однородных участков изображения слабеют, тогда как контрастные точки, напротив, усиливаются. Можно сказать, что такая свёртка выделяет границы. Проиллюстрируем работу этих ядер на примере небольшого изображения в серых тонах:

В донейросетевую эпоху различные свёртки играли существенную роль в обработке изображений, и сейчас мы видим, почему.

Вопрос на подумать. На краях картинок из ответа к предыдущему вопросу заметны тёмные рамки. Что это такое? Откуда они берутся?

Подумайте самостоятельно, прежде чем смотреть ответ.Их появление связано с особенностями обработки свёртками краёв изображения. Вообще, есть несколько стратегий борьбы с краями. Например:

• Дополнить изображение по краям нулями. Когда мы будем рассматривать окна свёртки с центрами в крайних пикселях, они будут захватывать эти нули. Такая свёртка будет превращать изображение размером HxWx3 в изображение размером HxW, без уменьшения размера. Но так как нули соответствуют чёрному цвету, это будет вносить определённые изменения в крайние пиксели результата. Именно благодаря этому у картинок из предыдущего вопроса на подумать по краям появились тёмные рамки.
• Разрешить только такие окна, которые целиком лежат внутри изображения. Это будет приводить к падению размера. Например, для окна размером 5x5 картинка размером HxWx3 превратится в картинку размером (H-2)x(W-2).

Решив проблему обеспечения устойчивости к сдвигу картинки и имея на руках наш огромный свёрточный фильтр, давайте попробуем теперь справиться с первой проблемой – количество параметров. Самое простое, что можно придумать, – это уменьшить размер окна с HxW до, допустим, kxk (обычно нечётное и $k \in [3,11])$. В этом случае получается радикальное снижение количества параметров и сложности вычислений.

К сожалению, с таким подходом возникает новая проблема: предсказание для какого-то окна никак не учитывает контекст вокруг него. Получается, мы можем получить разумные предсказания только в случае, если распознаваемый объект обладает признаками, которые «помещаются» в окно свёртки (например, лого автомобиля при классификации марок машин), либо объекты заметно отличаются по своей текстуре (шерсть кошки vs кирпич, например). На картинке ниже сделана попытка изобразить проблему:

Область картинки, на которую «смотрит» наша нейронная сеть, назвается receptive field – и про него приходится часто думать в задачах компьютерного зрения. Давайте и мы подумаем, как его можно было бы увеличить, не увеличивая размер ядра. Вспомним, что в нашей нейронке сейчас есть только один слой, сразу предсказывающий класс. Выглядит так, что мы можем применить уже знакомую технику стекинга слоев: пусть на первой стадии мы делаем $C_1$ разных свёрток с фильтрам размером kxk. Результаты каждой свёртки можно упорядочить в виде новой «картинки», а из этих «картинок» сложить трёхмерный тензор. Получаем так называемую карту признаков размером HxWxC_1. Применим к ней поэлементно нелинейность и воспользуемся K новыми свёртками для получения предсказаний для каждого пикселя. На таком шаге получается, что наш receptive field для финальных нейронов вырос от kxk до (2k-1)x(2k-1) (пояснение на картинке). Повторяя такую операцию, мы можем добиться, чтобы наши финальные нейроны уже могли «видеть» почти всю нужную информацию для хорошего предикта. Более того, у нас возникает меньшее количество параметров и падает сложность вычислений в сравнении с использованием одной большой полносвязной сети.

Как это схематично выглядит:

Промежуточный тензор $L_1$, полученный при помощи $C_1$ свёрток, можно себе представить, как новую картинку, у которой уже $C_1$ каналов.

На следующей картинке можно отследить, как меняется receptive field в зависимости от глубины:

На картинке схематично изображен «плоский» двумерный тензор (количество каналов = 1), к которому последовательно применили три свёртки 3×3. В каждом случае рассматривается пиксель в центре. Каждый соответствующий тензор помечен, как $L_i$. Если рассматривать первую свёртку ($X\to L_1$), то размер receptive field равен размеру е окна = 3. Рассмотрим вторую свёртку $L_1 \to L_2$. В ее вычислении участвуют пиксели из квадрата 3х3, причём каждый из них, в свою очередь, был получен при помощи предыдущей свёртки $X \to L_1$. Получается, что receptive field композиции свёрток $X\to L_1\to L_2$ – это объединение receptive fields свёртки $X\to L_1$ по всем пикселям из окна свёртки $L_1\to L_2$, образуя новый, размером 5×5. Аналогичные рассуждения можно повторить и для всех последующих свёрток.

Ещё один способ увеличить receptive field – это использовать dilated convolution, в которых окно свёртки (то есть те пиксели картинки, на которые умножается ядро) не обязано быть цельным, а может идти с некоторым шагом (вообще говоря, даже разным по осям H и W). Проиллюстрируем, как будет выглядеть окно для обычной свёртки и для свёртки с шагом dilation=2:

Если установить параметр dilation=(1,1), получится обычная свёртка.

Итак, свёртки помогли нам решить сразу две проблемы: устойчивости к сдвигу и минимизации числа параметров. Теперь давайте попробуем определить оператор более формально.

Формальное определение свёртки

Вопрос на подумать. Пусть у нас есть тензор размером HxWxC_{in}, к которому одновременно применяется $C_{out}$ свёрток, размер окна каждой равен kxk. Посчитайте количество обучаемых параметров. Как изменится формула, если к свёртке добавить смещение (bias)? Во сколько раз изменится количество параметров, если увеличить размер окна в 2 раза? А если увеличить количество каналов $C_{in}$ и $C_{out}$ в два раза? А если увеличить размер входного тензора в 2 раза по высоте и ширине?

Вопрос на подумать. Оцените количество операций сложений-умножений для предыдущего упражнения. Как оно поменяется, если увеличить в два раза размер окна? Количество каналов? Размер входного тензора?

Вопрос на подумать. Пусть последовательно применяется $N$ свёрток $k \times k$. Посчитайте размер receptive field для последнего оператора.

Свёртки не только для изображений

Нетрудно видеть, что аналоги двумерной свёртки можно определить и для тензоров другой размерности, в любой ситуации, когда для нас актуально поддерживать устойчивость модели к сдвигам данных. Например, это актуально для работы с текстами. Обычно текст разбивается на последовательные токены (например, на слова или какие-то subword units), и каждому из этих токенов ставится в соответствие вектор (более подробно об этом вы можете почитать в главе про работу с текстами или в разделе про вложения слов учебника по NLP Лены Войта).

Представим теперь, что мы хотим определить, является ли этот текст позитивно или негативно окрашенным. Мы можем предположить, что эмоциональная окраска локальна и может проявляться на любом участке текста, и тогда нам нужна модель, которая может «посмотреть» отдельно на каждый последовательный фрагмент текста некоторой длины. И здесь тоже может сработать свёртка:

Существуют свёртки и для тензоров более высокой размерности, например, для видео (где прибавляется ещё координата «время»).

Инвариантность не только к сдвигам?

А что делать с остальными проблемами: поворот, отражение, масштабирование? К сожалению, на момент написания главы, автору не было известно об успешном опыте решения этих проблем в архитектуре сети. При этом оказывается, что приведенного оператора уже достаточно, чтобы нейронная сеть могла хорошо обобщать на невиданные ранее картинки (лишь бы свёрток было больше и сеть глубже).

В качестве потенциально интересного – но пока не проявившего себя на практике – направления исследований можно упомянуть капсульные нейросети. Кроме того, вам может быть интересно познакомиться с геометрическим глубинным обучением(в качестве короткого введения рекомендуем посмотреть вот этот keynote с ICLR 2021), которое ставит своей целью исследование общих принципов, связывающих устойчивость к различным преобразованием и современные нейросетевые архитектуры (авторы сравнивают свои идеи с эрлангенской программой Феликса Кляйна – отсюда название).

Свёрточный слой и обратное распространение ошибки

Поговорим о том, как через свёрточный слой протекают градиенты. Нам нужно будет научиться градиент по выходу превращать в градиент по входу и в градиент по весам из ядра.

Начнём с иллюстрации для одномерной свёртки с одним входным каналом, ядром длины $3$ с дополнением по бокам нулями. Заметим, что её можно представить в виде матричного умножения:

$$(x_1,\ldots,x_d) \ast (w_{-1},w_0,w_1) = $$

$$= (0,x_1,\ldots,x_d,0) \cdot\begin{pmatrix}
w_{-1} & & & & \\
w_0 & w_{-1} & & & \\
w_1 & w_0 & w_{-1} & & \\
& w_1 & w_0 & \ddots & \\
& & w_1 & \ddots & w_{-1} \\
& & & \ddots & w_0 \\
& & & & w_1 \\
\end{pmatrix} = $$

$$= (x_1,\ldots,x_d) \cdot\begin{pmatrix}
w_0 & w_{-1} & & & & & \\
w_1 & w_0 & w_{-1} & & & & \\
& w_1 & w_0 & w_{-1} & && \\
& & w_1 & w_0 & \ddots & & \\
& & & w_1 & \ddots & w_{-1} & \\
& & & & \ddots & w_0 & w_{-1} \\
& & & & & w_1 & w_0 \\
\end{pmatrix} = $$

Обозначим последнюю матрицу через $\widehat{W}$, а ядро свёртки через $W$. Что происходит с градиентом при переходе через матричное умножение, мы уже отлично знаем. Градиент по весам равен

$$\nabla_{X_0}\mathcal{L} = \nabla_{X_0\ast W}\mathcal{L}\cdot\widehat{W}^T$$

Разберёмся, что из себя представляет умножение на $\widehat{W}^T$ справа. Эта матрица имеет вид

$$\begin{pmatrix}
w_0 & w_1 & & & & & \\
w_{-1} & w_0 & w_1 & & & & \\
& w_{-1} & w_0 & w_1 & && \\
& & w_{-1} & w_0 & \ddots & & \\
& & & w_{-1} & \ddots & w_1 & \\
& & & & \ddots & w_0 & w_1 \\
& & & & & w_{-1} & w_0 \\
\end{pmatrix}$$

Она тоже соответствует свёртке, только:

• с симметричным исходному ядром $(w_1, w_0, w_{-1})$;
• с дополнением вектора $\nabla_{X_0\ast W}$ нулями (это как раз соответствует неполным столбцам: можно считать, что «выходящие» за границы матрицы и отсутствующие в ней элементы умножаются на нули).

Вопрос на подумать. Поменяется ли что-нибудь, если исходный вектор не дополнять нулями?

Общий случай

Рассмотрим теперь двумерную свёртку, для простоты нечётного размера и без свободного члена

$$(X\ast W)_{ijc} = \sum_{p=1}^{c_{\text{in}}}\sum_{k_1 = -k}^k\sum_{k_2=-k}^kW^{c}_{k+1+k_1, k+1+k_2, p}X_{i + k_1, j + k_1, p}$$

1. Продифференцируем по $X_{stl}$:

$$\frac{\partial\mathcal{L}}{\partial X_{stl}} = \sum_{i, j, c}\frac{\partial (X\ast W)_{ijc}}{\partial X_{stl}}\cdot\frac{\partial\mathcal{L}}{\partial(X\ast W)_{ijc}}$$

Разберёмся с производной $\frac{\partial (X\ast W)_{ijc}}{\partial X_{stl}}$. Во всей большой сумме из определения свёртки для $(X\ast W)_{ijc}$ элемент $X_{stl}$ может встретиться в позициях $X_{i+k_1, j+k_2, l}$ при $i + k_1 = s$, $j + k_2 = t$ и всевозможных $c$, причём это возможно лишь если $k_1 = s — i\in\{-k,\ldots,k\}$, $k_2 = t — j\in\{-k,\ldots,k\}$ (для всех остальных $(X\ast W)_{ijc}$ производная по $X_{stl}$ нулевая). Соответствующий коэффициент при $X_{stl}$ будет равен $W_{k + 1 + k_1, k + 1 + k_2, c}$. Таким образом, производная будет иметь вид:

$$\frac{\partial\mathcal{L}}{\partial X_{stl}} = \sum_{c=1}^{c_{\text{out}}}\sum_{k_1=-k}^k\sum_{k_2=-k}^kW_{k + 1 + k_1, k + 1 + k_2, c}\cdot\frac{\partial\mathcal{L}}{\partial(X\ast W)_{s — k_1, t — k_2, c}}$$

Легко заметить, что это тоже свёртка, но поскольку индексы $k_1, k_2$ в $W$ и в $\frac{\partial\mathcal{L}}{\partial(X\ast W)}$ стоят с разными знаками, получаем, что

$$\color{blue}{\nabla_{X}\mathcal{L} = W\text{[::-1,::-1,:]}\ast\nabla_{X\ast W}\mathcal{L}}$$

1. Продифференцируем по $W^q_{ab}$:

$$\frac{\partial\mathcal{L}}{\partial W^q_{ab}} = \sum_{i, j, c}\frac{\partial (X\ast W)_{ijc}}{\partial W^q_{ab}}\cdot\frac{\partial\mathcal{L}}{\partial(X\ast W)_{ijc}}$$

В формуле для $(X\ast W)_{ijc}$ элемент $W^q_{ab}$ может встретиться в позициях $W^q_{k + 1 + k_1, k + 1 + k_2}$, для $k + 1 + k_1 = a$, $k + 1 + k_2 = b$, с коэффициентами $X_{i + k_1, j + k_2, p}$ (для любых $p$). Значит, производная будет иметь вид:

$$\frac{\partial\mathcal{L}}{\partial W^q_{ab}} = \sum_{p=1}^{c_{\text{in}}}\sum_{i=1}^H\sum_{j=1}^WX_{a — k — 1, b — k — 1, p}\cdot\frac{\partial\mathcal{L}}{\partial(X\ast W)_{a — k — 1, b — k — 1, q}}$$

В этой формуле тоже нетрудно узнать свёртку:

$$\color{blue}{\nabla_{W}\mathcal{L} = X\ast\nabla_{X\ast W}\mathcal{L}}$$

Вопрос на подумать. Если всё-таки есть свободные члены, как будет выглядить градиент по $b_c$?

Остальные важные блоки свёрточных нейронных сетей

Наигравшись с нашими мысленными экспериментами, давайте обратимся к опыту инженеров и исследователей, который копился с 2012 года (alexnet), чтобы разобраться с тем, как эффективней всего строить картиночные нейронки. Здесь будут перечислены самые важные, по мнению автора, на момент написания главы блоки.

Max pool

Каждая из $C$ свёрток очередного свёрточного слоя – это новая карта признаков для нашего изображения, и нам, конечно, хотелось бы, чтобы таких карт было побольше: ведь это позволит нам выучивать больше новых закономерностей. Но для картинок в высоком разрешении это может быть затруднительно: слишком уж много будет параметров. Выходом оказалось использование следующей эвристики: сначала сделаем несколько свёрток с $C_1$ каналами, а затем как-нибудь уменьшим нашу карту признаков в 2 раза и одновременно увеличим количество свёрток во столько же. Посчитаем, как в таком случае изменится число параметров: было $H \times W \times K \times K \times C_1 \times C_1$, стало $(H/2) \times (W/2) \times K \times K \times (C_1 \times 2) \times (C_1 \times 2) = H \times W \times K \times K \times C_1 \times C_1$, то есть, ничего не изменилось, а количество фильтров удвоилось, что приводит к выучиванию более сложных зависимостей.

Осталось разобраться, как именно можно понижать разрешение картинки. Тривиальный способ – взять все пиксели с нечетными индексами. Такой подход будет работать, но, как может подсказать здравый смысл, выкидывать пиксели = терять информацию, а этого не хотелось бы делать. Здесь есть много вариантов: например, брать среднее/максимум по обучаемым весам в окне 2x2, которое идет по карте признаков с шагом 2. Экспериментально выяснилось, что максимум – хороший выбор, и, в большинстве архитектур, используют именно его. Обратите внимание, что максимум берется для каждого канала независимо.

Еще одно преимущество – увеличение receptive field. Получается, что он увеличивается в 2 раза:

Операция понижения разрешения со взятием максимума в окне называется max pooling, а со взятием среднего – average pooling.

Вопрос на подумать. Как будет преобразовываться градиент во время error backpropagation для maxpool с окном и шагом 2×2? А для average pool?

Кстати, ещё одним способом уменьшать размер карт признаков по ходу применения свёрточной сети является использование strided convolution, в которых ядро свёртки сдвигается на каждом шаге на некоторое большее единицы число пикселей (возможно, разное для осей H и W; обычная свёртка получается, если установить параметр stride=(1,1)).

Global average pool

Как свёрточные слои, так и пулинг превращают картинку в «стопку» карт признаков. Но если мы решаем задачу классификации или регрессии, то в итоге нам надо получить число (или вектор логитов, если речь про многоклассовую классификацию). Один из способов добиться этого – воспользоваться тем, что свёртка без дополнения нулями и пулинг уменьшают размер карты признаков, и в итоге при должном терпении и верном расчёте мы можем получить тензор 1x1xC (финальные, общие признаки изображения), к которому уже можно применить один или несколько полносвязных слоёв. Или же можно, не дождавшись, пока пространственные измерения схлопнутся, «растянуть» всё в один вектор и после этого применить полносвязные слои (именно так, как мы не хотели делать, не правда ли?). Примерно так и происходило в старых архитектурах (alexnet, vgg).

Вопрос на подумать. Попробуйте соорудить конструкцию из свёточных слоёв и слоёв пулинга, превращающую изображение размера 128x128x3 в тензор размера 1x1xC.

Но у такого подхода есть как минимум один существенный недостаток: для каждого размера входящего изображения нам придётся делать новую сетку.

Позднее было предложено следующее: после скольких-то свёрточных слоёв мы будем брать среднее вдоль пространственных осей нашего последнего тензора и усреднять их активации, а уже после этого строить MLP. Это и есть Global Average Pooling. У такого подхода есть несколько преимуществ:

1. Радикально меньше параметров
2. Теперь мы можем применять нейронку к картинку любого размера
3. Мы сохраняем «магию» инвариантности предсказаний к сдвигам

Residual connection

Оказывается, что, если мы будем бесконтрольно стекать наши свёртки, то, несмотря на использование relu и batch normalization, градиенты все равно будут затухать, и на первых слоях будут почти нулевыми. Интересное решение предлагают авторы архитектуры resnet: давайте будем «прокидывать» признаки на предыдущем слое мимо свёрток на следующем:

Таким образом получается, что градиент доплывет даже до самых первых слоев, что существенно ускоряет сходимость и качество полученной модели. Вопрос: почему именно сумма? Может, лучше конкатенировать? Авторы densenet именно такой подход и предлагают (с оговорками), получая результаты лучше, чем у resnet. Однако, такой подход получается вычислительно сложным и редко используется на практике.

Регуляризация

Несмотря на наши ухищрения со свёртками, в современных нейронных сетях параметров все равно оказывается больше, чем количество картинок. Поэтому часто оказывается важным использовать различные комбинации регуляризваторов, которых уже стало слишком много, чтобы все опысывать в этой главе, так что мы рассмотрим лишь несколько наиболее важных.

Классические

Почти все регуляризаторы, которые использовались в классической машинке и полносвязных сетях, применимы и здесь: l1/l2, dropout и так далее.

Вопрос на подумать. Насколько разумно использовать dropout в свёрточных слоях? Как можно модифицировать метод, чтобы он стал «более подходящим»?

Аугментации

Это один из самых мощных инструментов при работе с картинками. Помогает, даже если картинок несколько тысяч, а нейронная сеть с миллионами параметров. Мы уже выяснили, что смещение\поворот\прочее не меняют (при разумных параметрах) факта наличия на картинке того или иного объекта. На самом деле, есть огромное множество операций, сохраняющих это свойство:

1. сдвиги, повороты и отражения;
2. добавление случайного гауссового шума;
3. вырезание случайно части картинки (cutout);
4. перспективные преобразования;
5. случайное изменение оттенка\насыщщености\яркости для всей картинки;
6. и многое другое.

Пример хорошой библиотеки с аугментациями: Albumentations.

Label smoothing

Часто оказывается, что нейронная сеть делает «слишком уверенные предсказания»: 0.9999 или 0.00001. Это становится головной болью, если в нашей разметке есть шум – тогда градиенты на таких объектах могут сильно портить сходимость. Исследователи пришли к интересной идее: давайте предсказывать не one-hot метку, а ее сглаженный вариант. Итак, пусть у нас есть $K$ классов:

$$y_{ohot}=(0, 0, \dots, 1, \dots, 0)$$

$$y_{ls}=\left(\frac{\varepsilon}{k-1},\frac{\varepsilon}{k-1}, \dots, 1-\varepsilon,\frac{\varepsilon}{k-1}, \dots, \frac{\varepsilon}{k-1}\right)$$

$$\sum_i y^i_{ohot}=\sum_i y^i_{ls}=1$$

Обычно берут $\varepsilon=0.1$. Тем самым модель штрафуется за слишком уверенные предсказания, а шумные лейблы уже не вносят такого большого вклада в градиент.

Mixup

Самый интересный вариант. А что будет, если мы сделаем выпуклую комбинацию двух картинок и их лейблов:

где $\alpha$ обычно семплируется из какого-нибудь Бета распределения. Оказывается, что такой подход заставляет модель выучивать в каком-то смысле более устойчивые предсказания, так как мы форсируем некую линейность в отображении из пространства картинок в пространство лейблов. На практике часто оказывается, что это дает значимое улучшение в качестве модели.

Итого

Мы разобрались, что для картинок эффективно использовать свёрточные фильтры в качестве основных операторов. Выяснили, какие основные блоки есть почти в каждой картиночной нейронной сети и зачем они там нужны. Разобрались, какие методы регуляризаторы сейчас самые популярные и какая за ними идея.

Знаковые архитектуры в мире свёрточных нейронных сетей для задачи классификации изображений

Дисклеймер: это мнение одного автора. Приведённые в этом разделе вехи связаны преимущественно с архитектурами моделей, а не способом их оптимизации.

Здесь перечислены знаковые архитектуры, заметно повлиявшие на мир свёрточных нейронных сетей в задаче классификации картинок (и не только). К каждой архитектуре указана ссылка на оригинальную статью, а также комментарий автора главы с указанием ключевых нововведений. Значение метрики error rate на одном из влиятельных датасетов imagenet указано для финального ансамбля из нейросетей, если не указано иное.

Зачем это полезно изучить (вместе с чтением статей)? Основных причин две:

1. Общее развитие. Полезно понимать, откуда взялись и чем мотивированы те или иные компоненты.
2. Этот вопрос задают на собеседовании, когда не знают, что еще спросить

lenet (1998)

Ссылка на статью

7 слоев

Первая свёрточная нейронная сеть, показавшая SOTA (State Of The Art) результаты на задаче классификации изображений цифр MNIST. В архитектуре впервые успешно использовались свёрточные слои с ядром 5x5. В качестве активации использовался tanh, а вместо max pool в тот момент использовался average.

alexnet (2012)

Ссылка на статью

11 слоев

Первая CNN (Convolutional Neural Network), взявшая победу на конкурсе imagenet. Автор предложил использовать ReLU вместо сигмоид (чтобы градиенты не затухали) и популяризовал max-pool вместо average. Что самое важное, обучение модели было перенесено на несколько GPU, что позволило обучать достаточно большую модель за относительное небольшое время (6 дней на двух видеокартах того времени). Также автор обратил внимание, что глубина нейросети важна, так как убирание хотя бы одного слоя стабильно ухудшало качество на несколько процентов.

network in network (2013)

Ссылка на статью

В статье не привели интересных SOTA результатов, но зато ввели два очень популярных впоследствии модуля. Первый – это GAP (Global Average Pooling), который стоит после последнего свёрточного слоя и усредняет все активации вдоль пространственных осей. Второй – стекинг 1x1 свёрток поверх 3x3, что эквивалентно тому, что вместо линейной свёртки используется полносвязный слой.

vgg (2014)

Ссылка на статью

19 слоев

Авторы предложили декомпозировать большие свёртки (5x5, 7x7 и выше) на последовательное выполнение свёрток 3x3 с нелинейностями между ними. Впоследствии, за нечастым исключением, свёртки 3x3 стали стандартом в индустрии (вместе со свёртками 1x1).

googleLeNet aka Inception (2014)

Ссылка на статью

22 слоя

Ввели inception слой, просуществовавший довольно продолжительное время. Сейчас сам слой уже не используется, но идея лежащая в его основе, эксплуатируется. Идея следующая: будем параллельно применять свёртки с разным пространственными размерами ядер, чтобы можно было одновременно обрабатывать как low, так и high level признаки. Еще полезной для сообщества оказалась идея с dimensionality reduction: перед тяжелой операцией поставим свёртку 1×1, чтобы уменьшить количество каналов и кратно ускорить вычисление.

batch normalization (2015)

Ссылка на статью

Авторы внедрили вездесущую batch normalization, которая стабилизирует сходимость, позволяя увеличить шаг оптимизатора и скорость сходимости. Применив идею к архитектуре inception, они превзошли человека на imagenet.

kaiming weight initialization (2015)

Ссылка на статью

В статье предложили использовать инициализацию весов, берущую во внимание особенность активации ReLU (в предыдущих работах предполагалось, что $Var[x] = \mathbb{E}[x^2]$, что, очевидно, нарушается для $\hat{x} = max(0, x)$). Применение этой и других «свистелок:: на VGG19 позволило существенно уменьшить ошибку на imagenet.

ResNet (2015)

Ссылка на статью

152 слоя

Архитектура, до сих пор (на момент написания – вторая половина 2021 года) являющаяся бейзлайном и отправной точкой во многих задачах. Основная идея – использование skip connections, что позволило градиенту протекать вплоть до первых слоев. Благодаря этому эффекту получилось успешно обучать очень глубокие нейронные сети, например, с 1202 слоями (впрочем, результаты на таких моделях менее впечатляющие, чем на 152 слойной). После этой статьи также стали повсеместно использоваться GAP и уменьшение размерности свёртками 1x1.

MobileNet (2017)

Ссылка на статью

Очень популярная модель для быстрого инференса (на мобильных устройствах или gpu). По качеству хоть и немного проигрывает «монстрам», но в индустрии, оказывается, зачастую этого достаточно (особенно если брать последние варианты модели). Основная деталь – это использование depthwise convolutions: параллельный стекинг свёрток 3x3x1x1 – то есть таких, в которых вычисление для каждого $с_{\text{out}}$ канала просходит только на основе признаков одного $c_{\text{in}}$ канала. Чтобы скомбинировать фичи между каналами, используется классическая 1x1 свёртка.

EfficientNet (2019)

Ссылка на статью

Одна из первых моделей, полученных при помощи NAS (Neural Architecture Search), которая взяла SOTA на imagenet. После этого, модели, где компоненты подбирались вручную, уже почти не показывали лучших результатов на классических задачах.

Бонус: не классификацией единой

Свёрточными нейронными сетями можно решать большой спектр задач, например:

1. Сегментация. Если убрать в конце слои GlobalAveragePool или flatten, то можно делать предсказания для каждого пикселя в отдельности (подумайте, что делать, если в сети есть maxpool) – получаем сегментацию картинки. Проблема – долгая и дорогая разметка.
2. Детекция. Часто намного дешевле получить разметку объектов обрамляющими прямоугольниками. Здесь уже можно для каждого пикселя предсказывать размеры прямоугольника, который обрамляет объект, к которому принадлежит пиксель. Проблемы – нужен этап агрегации прямоугольников + много неоднозначностей во время разметки + много эверистик на всех этапах + данных нужно больше.
3. Понимание видео. Добавляем в тензор новый канал – временной, считаем четырехмерные свёртки – и получаем распознавание сцен на видео.
4. Metric learning. Часто мы не можем собрать все интересующие нас классы, например, в задаче идентификации человека по лицу (или товара на полке). В этом случае используют такой трюк: научим модель в некотором смысле (обычно по косиносному расстоянию) разделять эмбеддинги существующих классов (уникальных людей). Если на руках была репрезентативная выборка, то модель, скорее всего (а обычно – всегда), выучит генерировать дискриминативные эмбеддинги, которые уже позволят различать между собой ранее невиданные лица.
5. и многое другое.

Обратное распространение в сверточном слое

  Перевод

  Ссылка на автора

Введение

мотивация

Цель этого поста — подробно описать, как работает обратное распространение градиента в сверточном слое нейронной сети. Обычно выход этого слоя будет входом выбранной функции активации (reluнапример). Мы делаем предположение, что нам дан градиентdyобратно от этой функции активации. Поскольку я не смог найти в Интернете полное, подробное и «простое» объяснение того, как это работает. Я решил сделать математику, пытаясь понять шаг за шагом, как она работает на простых примерах, прежде чем обобщать. Перед дальнейшим чтением вы должны быть знакомы с нейронными сетями, и особенно с прямым проходом, обратным распространением градиента в вычислительном графе и базовой линейной алгеброй с тензорами.

нотации

*будет относиться к свертке 2 тензоров в случае нейронной сети (входxи фильтрw).

• когдаxа такжеwэто матрицы:
• еслиxа такжеwиметь одинаковую форму,x*wбудет скаляр, равный сумме по результатам поэлементного умножения между массивами.
• еслиwменьшеx, мы получим карту активацииyгде каждое значение является предопределенной операцией свертки подобласти x с размерами w. Этот субрегион, активируемый фильтром, скользит по всему входному массивуx,
• еслиxа такжеwимеют более двух измерений, мы рассматриваем последние 3 для свертки и последние 2 для выделенной области скольжения (мы просто добавляем одну глубину к нашей матрице)

Обозначения и переменные такие же, как те, которые используются в Отличный Стэнфордский курс на сверточных нейронных сетях для визуального распознавания и особенно те из задание 2, Подробности о сверточном слое и прямом проходе будут найдены в этом видео и пример наивной реализации прямого прохода после,

Цель

Наша цель — выяснить, как градиент распространяется назад в сверточном слое. Прямой проход определяется так:

Вход состоит из N точек данных, каждая из которых имеет каналы C, высоту H и ширину W. Мы сворачиваем каждый вход с F различными фильтрами, где каждый фильтр охватывает все каналы C и имеет высоту HH и ширину WW.

Входные данные:

• x: входные данные формы (N, C, H, W)
• w: фильтр весов формы (F, C, HH, WW)
• b: уклоны формы (F,)
• conv_param: словарь со следующими ключами:
• ‘Шага’: количество пикселей между смежными рецептивными полями в горизонтальном и вертикальном направлениях.
• ‘Pad’: количество пикселей, которые будут использоваться для ввода нуля ввода.

Во время заполнения нули «pad» должны располагаться симметрично (т.е. одинаково с обеих сторон) вдоль осей высоты и ширины входа.

Возвращает кортеж из:

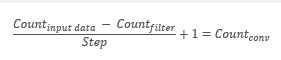
• out: Выходные данные формы (N, F, H ’, W’), где H ’и W’, определяются как

H ’= 1 + (H + 2 * pad — HH) / шаг

W ’= 1 + (W + 2 * pad — WW) / шаг

• кеш: (x, w, b, conv_param)

Прямой проход

Общий случай (упрощенно с N = 1, C = 1, F = 1)

N = 1 один вход, C = 1 один канал, F = 1 один фильтр.

х: В × Ш
х = х с дополнением
w: HH × WW
смещение b: скаляр
y: H ′ × W ′
шаг с

Особый случай: шаг = 1, пад = 0 и без смещения.

обратное распространение

Мы знаем:

Мы хотим вычислитьдх,с.в.а такжедецибел, частные производные нашего стоимостного функционала L. Предположим, что градиент этой функции был обратно распространен до y.

Тривиальный случай: вход x является вектором (1 измерение)

Мы ищем интуицию того, как это работает на легкой установке, и позже мы попытаемся обобщить.

вход

Выход

Прямой проход — свертка с одним фильтром w, шагом = 1, заполнением = 0

обратное распространение

Мы знаем градиент нашей функции стоимости L относительно y:

Это можно записать с помощью якобианской нотации:

DY и Y имеют одинаковую форму:

Мы ищем

децибел

Используя правило цепочки и формулу прямого прохода (1), мы можем написать:

с.в.

Мы можем заметить, что dw является сверткой входа x с фильтром dy. Давайте посмотрим, действительно ли это все еще действует с дополнительным измерением.

дх

Еще раз, у нас есть свертка. На этот раз немного сложнее. Мы должны рассмотреть вход dy с 0-отступом размера 1, свернутый с «инвертированным» фильтром w, как (вес2,вес1)

Следующим шагом будет посмотреть, как это работает на маленьких матрицах.

Ввод x представляет собой матрицу (2 измерения)

вход

Выход

Еще раз, мы выберем самый простой случай: шаг = 1 и без заполнения Форма у будет (3,3)

Перевал

Мы будем иметь:

Написано с подписками:

обратное распространение

Мы знаем:

децибел

Использование соглашения Эйнштейна для смягчения формул (когда переменная индекса появляется дважды в умножении, это подразумевает суммирование этого члена по всем значениям индекса)

Суммирование по i и j. И у нас есть:

с.в.

Мы ищем

Используя формулу (4) имеем:

Все условия

Кроме (К,Lзнак равном,N), где это 1, случай, встречающийся только один раз в двойной сумме. Следовательно:

Используя формулу (3), мы теперь имеем:

Если мы сравним это уравнение с формулой (1), дающей результат свертки, мы можем различить аналогичную схему, где dy — фильтр, применяемый к входу x.

дх

Используя правило цепочки, как мы это делали для (5), мы имеем:

На этот раз мы ищем

Используя уравнение (4):

Теперь у нас есть:

В нашем примере наборы диапазонов для индексов:

Когда мы установимКзнак равном—я+1 мы выйдем за установленные границы м—я+ 1) ∈ [-1,4]

Чтобы сохранить уверенность в формуле выше, мы решили расширить определение матрицывессо значениями 0, как только индексы выйдут за пределы указанного диапазона.

Еще раз в двойной сумме, у нас только одна частная производная от х равна 1. Итак:

гдевесэто наш 0-расширенный начальный фильтр, таким образом:

Позволяет визуализировать его по нескольким выбранным значениям для индексов.

Используя ∗ обозначение для свертки, имеем:

КакдуОстанемся прежними, мы будем только смотреть на значения индексов w. Длядх22, диапазон для w: 3-я, 3-J

Теперь у нас есть свертка между матрицей dy и w, определяемая как:

Еще один случай, чтобы увидеть, что происходит.дх43, ш: 4-я, 3-J

Последнийдх44

Мы видим всплывающий «инвертированный фильтр» w ’. На этот раз у нас есть свертка между входомдус 0-отступной границей размера 1 и фильтром w, скользящим с шагом 1.

Краткое изложение обратных уравнений

Принимая во внимание глубины

Все становится немного сложнее, когда мы пытаемся принять во внимание глубину (C каналов для входа x, и F различных фильтров для w)

Входы:

• х: форма (C, H, W)
• w: форма весов фильтра (F, C, HH, WW)
• б: форма (F,)

Выходы:

• y: форма (F, H ’, W’)

Математические формулы видят появление многих индексов, что затрудняет их чтение. Формула прямого прохода в нашем примере будет:

децибел

Расчет дб остается простым, так как каждыйb_fсвязано с картой активацииy_f:

с.в.

Используя формулу прямого прохода, так как двойная сумма не использует индексы dy, мы можем написать:

Алгоритм

Теперь, когда у нас есть интуиция того, как это работает, мы решили не писать весь набор уравнений (что может быть довольно утомительно), но мы будем использовать то, что было закодировано для прямого прохода, и, играя с измерениями, попытаемся закодировать Backprop для каждого градиента. К счастью, мы можем вычислить числовое значение градиента, чтобы проверить нашу реализацию. Эта реализация действительна только для шага = 1, вещь становится немного более сложной с отчетливым шагом, и необходим другой подход. Может быть, для другого поста!

Градиентная числовая проверка

Testing conv_backward_naive function
dx error:  7.489787768926947e-09
dw error:  1.381022780971562e-10
db error:  1.1299800330640326e-10

Почти 0 каждый раз, кажется, все в порядке!

Ссылки

• Этот пост в моем блоге с уравнениями mathjax:)
• Стэнфордский курс по сверточным нейронным сетям для визуального распознавания
• Стэнфордское задание CNN 2
• Сверточная нейронная сеть, прямой проход
• Слой свертки: Наивная реализация прямого прохода,
• Обратное распространение в сверточных нейронных сетях
• Cet Article En Français

Комментарии могут улучшить этот пост, не стесняйтесь связаться со мной!

Содержание

• Введение
• 1. Отличительные особенности сверточных нейронных сетей
• 1.1. Сверточный слой
• 1.2. Подвыборочный слой
• 2. Принципы обучения нейронов сверточных слоев
• 3. Построение сверточной нейронной сети
• 3.1. Базовый класс нейронов
• 3.1.1. Прямой проход
• 3.1.2. Расчет градиента ошибки
• 3.2. Элемент подвыборочного слоя
• 3.2.1. Прямой проход
• 3.2.2. Расчет градиента ошибки
• 3.3. Элемент сверточного слоя
• 3.4. Создание класса сверточной нейронной сети
• 3.4.1. Конструктор класса сверточной нейронной сети
• 3.4.2. Метод прямого прохода сверточной нейронной сети
• 3.4.3. Метод обратного прохода сверточной нейронной сети
• 4. Тестирование
• Заключение
• Ссылки
• Программы, используемые в статье

Введение

Продолжая тему нейронных сетей, предлагаю рассмотреть принципы работы и построения сверточных нейронных сетей (Convolutional Neural Network). Данный вид нейронных сетей широко применяется в задачах распознования объектов на фото и видеоизображениях. Считается, что сверточные нейронные сети устойчивы к изменению масштаба, смене ракурса и прочим пространственным искажениям изображения. Их архитектура позволяет одинаково успешно находить объекты в любом месте сцены. Применительно к трейдингу, с использованием сверточных нейронных сетей хочу улучшить детектирование торговых паттернов на ценовом графике.

1. Отличительные особенности сверточных нейронных сетей

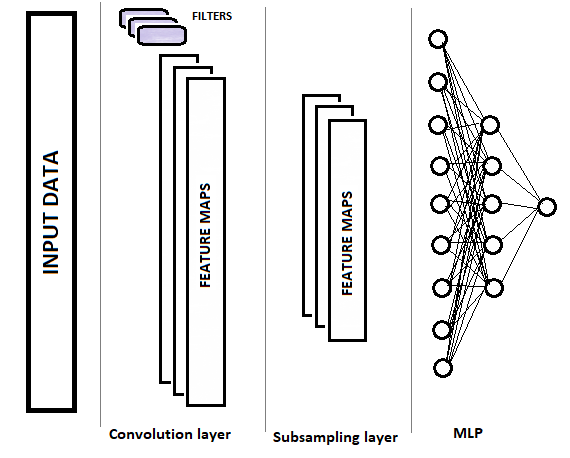
В сверточных сетях, по сравнению с полносвязным перцептроном, добавляются 2 новых вида слоев: сверточный(фильтр) и подвыборочный (субдискретизирующий). Чередуясь, указанные слои призваны выделить основные компоненты и отсеять шумы в исходных данных с параллельным понижением размерности (объема) данных, которые в последующем передаются на вход полносвязного перцептрона для принятия решения. Графически структура сверточной нейронной сети представлена на рисунке ниже. В зависимости от решаемых задач допускается последовательное использование нескольких групп из чередующихся сверточного и подвыборочного слоев.

1.1. Сверточный слой

За распознавание объектов в массиве исходных данных отвечает сверточный слой (Convolution layer). В данном слое осуществляются последовательные операции математической свертки исходных данных с небольшим шаблоном (фильтром), выступающими в качестве ядра свертки.

Свёртка — операция в функциональном анализе, которая при применении к двум функциям f и g возвращает третью функцию, соответствующую взаимокорреляционной функции f(x) и g(-x). Операцию свёртки можно интерпретировать как «схожесть» одной функции с отражённой и сдвинутой копией другой.(Wikipedia)

Иными словами, сверточный слой осуществляет поиск шаблонного элемента во всей исходной выборке. При этом на каждой итерации шаблон сдвигается по массиву исходных данных с заданным шагом, который может быть от «1» до размера шаблона. Если величина шага смещения меньше размера шаблона, то такая свертка называется с перекрытием.

В результате операции свертки получаем массив признаков, показывающих «схожесть» исходных данных с искомым шаблоном на каждой итерации. Для нормализации данных используются функции активации. Размер полученного массива будет меньше массива исходных данных, количество таких массивов равно количеству шаблонов (фильтров).

Немаловажен для нас и тот факт, что сами шаблоны не задаются при проектировании нейронной сети, а подбираются в процессе обучения.

1.2. Подвыборочный слой

Следующий, подвыборочный слой используется для снижения размерности массива признаков и фильтрации шумов. Применение данной итерации обусловлено предположением, что наличие сходства исходных данных с шаблоном первично, а точные координаты признака в массиве исходных данных не столь важны. Это позволяет решать проблему масштабирования, т.к. допускает некую вариативность расстояния между искомыми объектами.

На данном этапе происходит уплотнение данных путем сохранения максимального или среднего значения в пределах заданного «окна». Таким образом, сохраняется только одно значение для каждого «окна» данных. Операции осуществляются итерационно со смещением окна на заданный шаг при каждой новой итерации. Уплотнение данных выполняется отдельно для каждого массива признаков.

Довольно часто применяются подвыборочные слои с окном и шагом равным 2, что позволяет вдвое снизить размерность массива признаков. Но в практике допускается и использование большего размера окна, а также итерации уплотнения могут осуществляться как с перекрытием (величина шага меньше размера окна), так и без.

На выходе подвыборочного слоя получаем массивы признаков меньшей размерности. 

В зависимости от сложности решаемых задач, после подвыборочного слоя возможно использование еще одну или несколько групп из сверточного и подвыборочного слоя. Принципы их построения и функциональность соответствуют описанным выше. В общем же случае, после одной или нескольких групп свертка + уплотнения массивы полученных признаков по всем фильтрам собираются в единый вектор и подаются на вход многослойного перцептрона для принятия решения нейронной сетью (о построение многослойного перцептрона рассказано в первой части данного цикла статей).

2. Принципы обучения нейронов сверточных слоев

Обучение сверточных нейронных сетей отсуществляется уже известным из предыдущих публикаций методом обратного распространения ошибки. Данный метод относится к методам обучения с учителем и заключается в спуске градиента ошибки от выходного слоя нейронов, через скрытые слои к входному слою нейронов с корректировкой весовых коэффициентов в сторону антиградиента.

Об обучении многослойного перцептрона я уже рассказывал в первой статье этого цикла, поэтому не буду останавливаться. Рассмотрим обучение нейронов подвыборочного и сверточного слоев.

В подвыборочном слое градиент ошибки считается для каждого элемента в массиве признаков по аналогии с градиентами нейронов полносвязного перцепртрона. Алгоритм передачи градиента на предыдущий слой зависит от применяемой операции уплотнения. Если берется только максимальное значение, то и весь градиент передается на нейрон с максимальным значением (для остальных элементов в пределах окна уплотнения устанавливается нулевой градиент). Если же используется операция усреднения в пределах окна, то и градиент равномерно распределяется на все элементы в пределах окна.

Т.к. в операции уплотнения не используются весовые коэффициенты, то и в процессе обучения ничто не корректируется.

Немного сложнее происходят вычисления при обучении нейронов сверточного слоя. Градиент ошибки рассчитывается для каждого элемента массива признаков и спускается к соответствующим нейронам предыдущего слоя. В основе процесса обучения сверточного слоя лежат операции свертки и обратной свертки.

Для передачи градиента ошибки от подвыборочного слоя к сверточному, сначала дополняются края массива градиентов ошибок, полученных от подвыборочного слоя, нулевыми элементами и затем производится свертка полученного массива с ядром свертки, развернутым на 180°. На выходе получаем массив градиентов ошибок размером равным массиву входных данных, в котором индексы градиентов будут соответствовать индексу корреспондирующего нейрона, предшествующего сверточному слою.

Для получения дельт весовых коэффициентов осуществляется свертка матрицы входных значений с матрицей градиентов ошибок данного слоя, развернутой на 180°. На выходе получим массив дельт с размером равным ядру свертки. Полученные дельты нужно скорректировать на производную функции активации сверточного слоя и коэффициент обучения. После чего, весовые коэффициенты ядра свертки изменяются на величину скорректированных дельт.

Наверное, звучит довольно сложно для понимания. Попробуем прояснить данные моменты при подробном рассмотрении кода.

3. Построение сверточной нейронной сети

Как уже было сказана выше, сверточная нейронная сеть будет состоять из 3-х типов нейронных слоев (сверточный, подвыборочный и полносвязный) с отличительными классами нейронов и различными функциями для прямого и обратного прохода. В тоже время, нам нужно объединить все нейроны в единую сеть и организовать вызов именно того метода обработки данных, который соответствует обрабатываемому нейрону. На мой взгляд, наиболее простой способ организовать данный процесс с помощью функционала наследования классов и виртуализации функций.

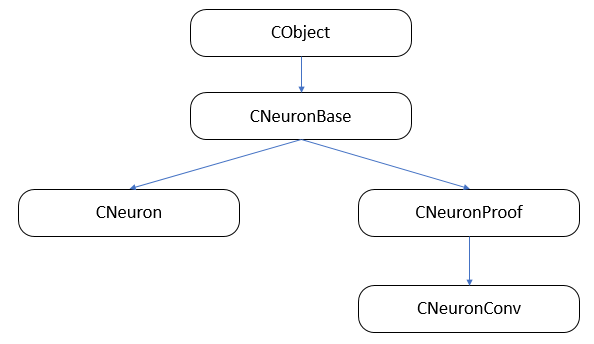
Вначале построим структуру наследования классов.

3.1. Базовый класс нейронов.

В первой статье мы создали класс слоя CLayer наследником класса CArrayObj, который является классом динамического массива для хранения ссылок на объекты класса CObject. Следовательно, все нейроны у нас должны унаследоваться от данного класса. На базе класса CObject создадим базовый класс CNeuronBase. В теле класса объявим общие для всех типов нейронов переменные и создадим шаблоны основных методов. Все методы класса объявлены виртуальными для возможности последующего переопределения. 

class CNeuronBase    :  public CObject
  {
protected:
   double            eta;
   double            alpha;
   double            outputVal;
   uint              m_myIndex;
   double            gradient;
   CArrayCon        *Connections;

   virtual bool      feedForward(CLayer *prevLayer)               {  return false;     }
   virtual bool      calcHiddenGradients( CLayer *&nextLayer)     {  return false;     }
   virtual bool      updateInputWeights(CLayer *&prevLayer)       {  return false;     }
   virtual double    activationFunction(double x)                 {  return 1.0;       }
   virtual double    activationFunctionDerivative(double x)       {  return 1.0;       }
   virtual CLayer    *getOutputLayer(void)                        {  return NULL;      }
public:
                     CNeuronBase(void);
                    ~CNeuronBase(void);
   virtual bool      Init(uint numOutputs, uint myIndex);

   virtual void      setOutputVal(double val)                     {  outputVal=val;    }
   virtual double    getOutputVal()                               {  return outputVal; }
   virtual void      setGradient(double val)                      {  gradient=val;     }
   virtual double    getGradient()                                {  return gradient;  }

   virtual bool      feedForward(CObject *&SourceObject);
   virtual bool      calcHiddenGradients( CObject *&TargetObject);
   virtual bool      updateInputWeights(CObject *&SourceObject);

   virtual bool      Save( int const file_handle);
   virtual bool      Load( int const file_handle)                  {  return(Connections.Load(file_handle)); }

   virtual int       Type(void)        const                       {  return defNeuronBase;                  }
  };

Названия переменных и методов соответствуют описанным ранее. Предлагаю рассмотреть методы feedForward(CObject *&SourceObject), сalcHiddenGradients(CObject *&TargetObject) и updateInputWeights(CObject *&SourceObject), так как в указанных методах осуществляется диспетчеризация по работе с полносвязными и сверточными слоями.

3.1.1. Прямой проход.

Метод feedForward(CObject *&SourceObject) вызывается при прямом проходе для вычисления результирующего значения нейрона. При прямом проходе в полносвязных слоях каждый нейрон берет значения всех нейронов предыдущего слоя и, соответственно, на вход должен получить весь предыдущий слой. В сверточных и подвыборочных слоях на вход нейрона подается только часть данных, относящаяся к данному фильтру. В рассматриваемом методе выбор алгоритма осуществляется на основании типа класса, полученного в параметрах.

В начале проверяем действительность ссылки на объект, полученной в параметрах метода.

bool CNeuronBase::feedForward(CObject *&SourceObject)
  {
   bool result=false;

   if(CheckPointer(SourceObject)==POINTER_INVALID)
      return result;

Так как внутри оператора выбора нельзя объявлять экземпляры классов, подготовим шаблоны заранее.

   CLayer *temp_l;
   CNeuronProof *temp_n;

Далее в операторе выбора проверим тип полученного в параметрах объекта. Если мы получили ссылку на слой нейронов, то предыдущий слой является полносвязным и, следовательно, вызовем метод для работы с полносвязными слоями (подробно описано в первой статье). Если же мы имеем дело с нейроном сверточного или подвыборочного слоя, то сначала мы получим слой выходных нейронов данного фильтра и затем воспользуемся методом обработки полносвязного слоя, передав ему в параметрах слой нейронов текущего фильтра с сохранением результата отработки в переменную result (подробнее о строении нейронов сверточного и подвыборочного слоев будет рассказано ниже). После отработки выходим из метода с передачей результата работы.

   switch(SourceObject.Type())
     {
      case defLayer:
        temp_l=SourceObject;
        result=feedForward(temp_l);
        break;
      case defNeuronConv:
      case defNeuronProof:
        temp_n=SourceObject;
        result=feedForward(temp_n.getOutputLayer());
        break;
     }

   return result;
  }

3.1.2. Расчет градиента ошибки.

По аналогии с прямым проходом создан диспетчер для вызова функции расчета градиента ошибки на скрытых слоях нейронной сети сalcHiddenGradients(CObject *&TargetObject). Структура построения и логика метода аналогична описанному выше. Сначала проверяем действительность полученной ссылки. Затем объявляем переменные для хранения ссылок на соответствующие объекты. И в функции выбора по типу полученного объекта выбираем нужный метод. Отличия начинаются если в параметрах передана ссылка на элемент сверточного или подвыборочного слоя. Расчет градиента ошибки через такие нейроны отличается и распространяется не на все нейроны предыдущего слоя, а только в пределах окна выборки. Поэтому, расчет градиента перенесен в эти нейроны в метод calcInputGradients. При этом есть отличия в методах для расчета по слою или для конкретного нейрона. Следовательно, требуемый метод вызывается в зависимости от типа объекта из которого вызывается.  

bool CNeuronBase::calcHiddenGradients(CObject *&TargetObject)
  {
   bool result=false;

   if(CheckPointer(TargetObject)==POINTER_INVALID)
      return result;

   CLayer *temp_l;
   CNeuronProof *temp_n;
   switch(TargetObject.Type())
     {
      case defLayer:
        temp_l=TargetObject;
        result=calcHiddenGradients(temp_l);
        break;
      case defNeuronConv:
      case defNeuronProof:
        switch(Type())
          {
           case defNeuron:
             temp_n=TargetObject;
             result=temp_n.calcInputGradients(GetPointer(this),m_myIndex);
             break;
           default:
             temp_n=GetPointer(this);
             temp_l=temp_n.getOutputLayer();
             temp_n=TargetObject;
             result=temp_n.calcInputGradients(temp_l);
             break;
          }
        break;
     }

   return result;
  }

Диспетчер updateInputWeights(CObject *&SourceObject) для обновления весовых коэффициентов построен по принципам описанным выше. С подробным кодом метода можно ознакомиться во вложении.

3.2. Элемент подвыборочного слоя.

Основным кирпичиком подвыборочного слоя выступает класс CNeuronProof, который наследуется от ранее описанного базового класса CNeuronBase. При проработке архитектуры было принято решение о создании в подвыборочном слое одного экземпляра такого класса на каждый фильтр. В связи с этим вводятся дополнительные переменные iWindow и iStep для хранения размера окна уплотнения и шага сдвига, соответственно. Также добавляем внутренний слой нейронов для хранения массивов признаков, градиентов ошибок и, при необходимости, весовых коэффициентов для передачи признаков в полносвязный перцептрон. И добавим метод для получения ссылки на внутренний слой нейронов по запросу. 

class CNeuronProof : public CNeuronBase
  {
protected:
   CLayer            *OutputLayer;
   int               iWindow;
   int               iStep;
   
   virtual bool      feedForward(CLayer *prevLayer);
   virtual bool      calcHiddenGradients( CLayer *&nextLayer);
   
public:
                     CNeuronProof(void){};
                    ~CNeuronProof(void);
   virtual bool      Init(uint numOutputs,uint myIndex,int window, int step, int output_count);

   virtual CLayer   *getOutputLayer(void)  { return OutputLayer;  }
   virtual bool      calcInputGradients( CLayer *prevLayer) ;
   virtual bool      calcInputGradients( CNeuronBase *prevNeuron, uint index) ;
   
   virtual bool      Save( int const file_handle)                         { return(CNeuronBase::Save(file_handle) && OutputLayer.Save(file_handle));   }
   virtual bool      Load( int const file_handle)                         { return(CNeuronBase::Load(file_handle) && OutputLayer.Load(file_handle));   }
   virtual int       Type(void)   const   {  return defNeuronProof;   }
  };

Не забываем переопределить логику работы для объявленных в базовом классе виртуальных функций.

3.2.1. Прямой проход.

Метод feedForward предназначен для отсеивания шумов и понижения размерности массива признаков. В описываемом решении для уплотнения данных используется функция арифметического среднего. Рассмотрим детальнее код метода. Вначале метода проверим актуальность полученной ссылки на предыдущий слой нейронов.

bool CNeuronProof::feedForward(CLayer *prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID)
      return false;

Затем организуем цикл по перебору всех нейронов полученного в параметрах слоя с заданным шагом.

   int total=prevLayer.Total()-iWindow+1;
   CNeuron *temp;
   for(int i=0;(i<=total && result);i+=iStep)
     {

В теле цикла создадим вложенный цикл для подсчета суммы выходных значений нейронов предыдущего слоя в пределах заданного окна уплотнения.

      double sum=0;
      for(int j=0;j<iWindow;j++)
        {
         temp=prevLayer.At(i+j);
         if(CheckPointer(temp)==POINTER_INVALID)
            continue;
         sum+=temp.getOutputVal();
        }

После подсчета суммы обратимся к соответствующему нейрону внутреннего слоя хранения результирующих данных и запишем в его результирующее значение отношение полученной суммы к размеру окна, что и составит среднее арифметическое для текущего окна уплотнения.

      temp=OutputLayer.At(i/iStep);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      temp.setOutputVal(sum/iWindow);
     }

   return true;
  }

По завершении перебора всех нейронов завершаем работу метода.

3.2.2. Расчет градиента ошибки.

Для расчета градиента ошибки в данном классе создана два метода: calcHiddenGradients и calcInputGradients. Первый собирает данные о градиентах ошибки последующего слоя и считает градиент для элементов текущего слоя. Второй на основе данных полученных в первом методе распределяет ошибку по элементам предыдущего слоя.

В начале метода calcHiddenGradients, как обычно, проверим действительность полученной в параметрах ссылки. Дополнительно проверим состояния внутреннего слоя нейронов.

bool CNeuronProof::calcHiddenGradients( CLayer *&nextLayer)
  {
   if(CheckPointer(nextLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID || OutputLayer.Total()<=0)
      return false;

Далее в цикле переберем все нейроны внутреннего слоя и вызовем метод по подсчету градиента ошибки.

   gradient=0;
   int total=OutputLayer.Total();
   CNeuron *temp;
   for(int i=0;i<total;i++)
     {
      temp=OutputLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      temp.setGradient(temp.sumDOW(nextLayer));
     }

   return true;
  }

Хочу обратить внимание, что данный метод правильно отрабатывает, если далее следует полносвязный слой нейронов. Если далее следует сверточный или подвыборочный слой необходимо использовать метод calcInputGradients нейрона последующего слоя.

В параметрах метод calcInputGradients получает ссылку на предыдущий слой. И мы сразу, в начале метода, проверяем действительность данной ссылки состояние внутреннего слоя нейронов.

bool CNeuronProof::calcInputGradients(CLayer *prevLayer) 
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID)
      return false;

Затем проверяем тип первого элемента полученного в параметрах слоя. В случае, если полученная ссылка указывает на подвыборочный или сверточный слой, то запросим ссылку на внутренний слой нейронов, соответствующего фильтра.

   if(prevLayer.At(0).Type()!=defNeuron)
     {
      CNeuronProof *temp=prevLayer.At(m_myIndex);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      prevLayer=temp.getOutputLayer();
      if(CheckPointer(prevLayer)==POINTER_INVALID)
         return false;
     }

Далее организуем цикл по перебору всех нейронов предыдущего слоя с обязательной проверкой действительность ссылки на обрабатываемый нейрон.

   CNeuronBase *prevNeuron, *outputNeuron;
   int total=prevLayer.Total();
   for(int i=0;i<total;i++)
     {
      prevNeuron=prevLayer.At(i);
      if(CheckPointer(prevNeuron)==POINTER_INVALID)
         continue;

Определим на какие нейроны внутреннего слоя влияет обрабатываемый нейрон.

      double prev_gradient=0;
      int start=i-iWindow+iStep;
      start=(start-start%iStep)/iStep;
      double stop=(i-i%iStep)/iStep+1;

В цикле посчитаем градиент ошибки для обрабатываемого нейрона и сохраним полученный результат. После перебора всех нейронов предыдущего слоя завершаем работу метода.

      for(int out=(int)fmax(0,start);out<(int)fmin(OutputLayer.Total(),stop);out++)
        {
         outputNeuron=OutputLayer.At(out);
         if(CheckPointer(outputNeuron)==POINTER_INVALID)
            continue;
         prev_gradient+=outputNeuron.getGradient()/iWindow;
        }
      prevNeuron.setGradient(prev_gradient);
     }

   return true;
  }

Аналогичным образом построен метод с аналогичным названием для подсчета градиента отдельного нейрона. Отличие заключается в исключении внешнего цикла по перебору нейронов. Вместо него идет обращение по порядковому номеру нейрона.

Так как в подвыборочном слое не используются весовые коэффициенты, то и метод их обновления можно опустить. Или, как вариант, для сохранения унификации структуры классов нейронов можно создать пустой метод, который при вызове будет возвращать значение true. 

С полным кодом всех методов и функций можно ознакомиться во вложении.

3.3. Элемент сверточного слоя.

Для построения сверточного слоя будем использовать объекты класса CNeuronConv, которые будут наследоваться от класса CNeuronProof. В качестве функции активации для данного типа нейронов я выбрал параметрическую ReLU. Данная функция более легкая для расчета, по сравнению с гиперболическим тангенсом, используемым в нейронах полносвязного перцептрона. Для ее расчета введем дополнительную переменную param.

class CNeuronConv  :  public CNeuronProof
  {
protected:
   double            param;   
   virtual bool      feedForward(CLayer *prevLayer);
   virtual bool      calcHiddenGradients(CLayer *&nextLayer);
   virtual double    activationFunction(double x);
   virtual bool      updateInputWeights(CLayer *&prevLayer);
public:
                     CNeuronConv() :   param(0.01) { };
                    ~CNeuronConv(void)             { };

   virtual bool      calcInputGradients(CLayer *prevLayer) ;
   virtual bool      calcInputGradients(CNeuronBase *prevNeuron, uint index) ;
   virtual double    activationFunctionDerivative(double x);
   virtual int       Type(void)   const   {  return defNeuronConv;   }
  };

Методы прямого и обратного прохода построены по алгоритмам аналогичным класса  CNeuron Proof. Отличия заключаются только в использовании функции активации и весовых коэффициентов. Поэтому не вижу причин для их детального рассмотрения. Разберем метод корректировки весовых коэффициентов updateInputWeights.

В параметрах метод получает ссылку на предшествующий слой нейронов и мы сразу проверяем действительность полученной ссылки и состояние внутреннего слоя.

bool CNeuronConv::updateInputWeights(CLayer *&prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID)
      return false;

Далее, создаем цикл по перебору всех весовых коэффициентов и, разумеется, после получения ссылки на объект очередной связи проверяем ее действительность.

   CConnection *con;
   for(int n=0; n<iWindow && !IsStopped(); n++)
     {
      con=Connections.At(n);
      if(CheckPointer(con)==POINTER_INVALID)
         continue;

После этого считаем свертку массива входных данных с массивом градиентов ошибок внутреннего слоя, развернутого на 180°. Для этого организовываем цикл по перебору всех элементов внутреннего слоя и умножению на элементы массива входных данных по схеме:

• первый элемент массива входных данных (со сдвигом на количество шагов равных порядковому номеру весового коэффициента) на последний элемент массива градиента ошибок.
• второй элемент массива входных данных (со сдвигом на количество шагов равных порядковому номеру весового коэффициента) на предпоследний элемент массива градиента ошибок.
• и т.д. до элемент с индексом равным количеству элементов в массиве внутреннего слоя со сдвигом на количество шагов равных порядковому номеру весового коэффициента умножается на первый элемент массива градиента ошибок.

Полученные произведения суммируем.

      double delta=0;
      int total_i=OutputLayer.Total();
      CNeuron *prev, *out;
      for(int i=0;i<total_i;i++)
        {
         prev=prevLayer.At(n*iStep+i);
         out=OutputLayer.At(total_i-i-1);
         if(CheckPointer(prev)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID)
            continue;
         delta+=prev.getOutputVal()*out.getGradient();
        }

Рассчитанная сумма произведений и является базой для корректировки весовых коэффициентов. Корректируем весовые коэффициенты с учетом заданной скорости обучения.

      con.weight+=con.deltaWeight=(delta!=0 ? eta*delta : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0);
     }

   return true;  
  }

После корректировки всех весовых коэффициентов выходим из метода.

Класс CNeuron подробно описан в первой статье данного цикла и практически не изменился, поэтому разрешите не останавливаться на нем в этой статье.

3.4. Создание класса сверточной нейронной сети.

Теперь, когда созданы все кирпичики можно приступать к строительству дома — создадим класс сверточной нейронной сети, который объединит все типы нейронов в четкую структуру и организует работу нашей нейронной сети. Первый вопрос, который возникает при создании данного класса — это как мы будем задавать требуемую структуру сети. В полносвязный перцептрон мы передавали массив элементов в котором указывали количество нейронов в каждом слое. Сейчас же нам нужно больше информации для генерации нужного слоя сети. Создадим небольшой класс CLayerDescription для описания построения слоя. Данный класс не содержит никаких методов (кроме конструктора и деструктора), а включает только переменные для указания типа нейронов в слое, количество таких нейронов, размер окна и шага для нейронов сверточного и подвыборочного слоев. В параметрах же конструктора класса сверточной нейронной сети мы будем передавать ссылку на массив классов с описанием слоев.

class CLayerDescription    :  public CObject
  {
public:
                     CLayerDescription(void);
                    ~CLayerDescription(void){};

   int               type;
   int               count;
   int               window;
   int               step;
  };



CLayerDescription::CLayerDescription(void)   :  type(defNeuron),
                                                count(0),
                                                window(1),
                                                step(1)
  {}

Рассмотрим структуру класса сверточной нейронной сети CNetConvolution. Данный класс содержит:

• layers — массив слоев;
• recentAverageError  — текущая ошибка сети;
• recentAverageSmoothingFactor  — фактор усреднения ошибки;
• CNetConvolution  — конструктор класса;
• ~CNetConvolution  — деструктор класса;
• feedForward  — метод прямого прохода;
• backProp  — метод обратного прохода;
• getResults  — метод для получения результатов последнего прямого прохода;
• getRecentAverageError  — метод для получения текущей ошибки сети;
• Save и Load  — методы для сохранения и загрузки ранее созданной и обученной сети.

class CNetConvolution
  {
public:
                     CNetConvolution(CArrayObj *Description);
                    ~CNetConvolution(void)                     {  delete layers; }
   bool              feedForward( CArrayDouble *inputVals);
   void              backProp( CArrayDouble *targetVals);
   void              getResults(CArrayDouble *&resultVals) ;
   double            getRecentAverageError()                   { return recentAverageError; }
   bool              Save( string file_name, double error, double undefine, double forecast, datetime time, bool common=true);
   bool              Load( string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true);
   
   static double     recentAverageSmoothingFactor;
   virtual int       Type(void)   const   {  return defNetConv;   }

private:
   CArrayLayer       *layers;
   double            recentAverageError;
  };

Наименование методов и алгоритмы построения аналогичны описанным ранее для полносвязного перцептрона в первой статье данного цикла. Остановимся только на основных методах класса.

3.4.1. Конструктор класса сверточной нейронной сети.

Рассмотрим конструктор класса. В параметрах конструктор получает ссылку на массив описаний слоев для построения сети. Соответственно, проверяем действительность полученной ссылки, определяем количество слоев для построения и создаем новый экземпляр массива слоев. 

CNetConvolution::CNetConvolution(CArrayObj *Description)
  {
   if(CheckPointer(Description)==POINTER_INVALID)
      return;

   int total=Description.Total();
   if(total<=0)
      return;

   layers=new CArrayLayer();
   if(CheckPointer(layers)==POINTER_INVALID)
      return;

Далее объявляем внутренние переменные.

   CLayer *temp;
   CLayerDescription *desc=NULL, *next=NULL, *prev=NULL;
   CNeuronBase *neuron=NULL;
   CNeuronProof *neuron_p=NULL;
   int output_count=0;
   int temp_count=0;

На этом подготовительный этап закончен и приступаем непосредственно к цикличности генерации слое нейронной сети. В начале цикла считываем информацию о текущем и последующем слоях.

   for(int i=0;i<total;i++)
     {
      prev=desc;
      desc=Description.At(i);
      if((i+1)<total)
        {
         next=Description.At(i+1);
         if(CheckPointer(next)==POINTER_INVALID)
            return;
        }
      else
         next=NULL;

Подсчитаем количество выходных связей для слоя и создадим новый экземпляр класса нейронного слоя. Обратите внимание, что количество связей на выходе слоя указываем только перед полносвязным слоем, в противном случае указываем нулевое значение. Это связано с тем, что сверточные нейроны сами хранят входные весовые коэффициенты, а подвыборочный слой их вообще не использует.

      int outputs=(next==NULL || next.type!=defNeuron ? 0 : next.count);
      temp=new CLayer(outputs);

Далее в цикле идет генерация нейронов с разделением алгоритма по типу нейронов в создаваемом слое. Для полносвязных слоев осуществляется создание нового экземпляра нейрона и его инициализация. Обратите внимание, что для полносвязных слоев создается на один нейрон больше, чем указано в описании. Данный нейрон будет использоваться в качестве байесовского смещения.

      for(int n=0;n<(desc.count+(i>0 && desc.type==defNeuron ? 1 : 0));n++)
        {
         switch(desc.type)
           {
            case defNeuron:
              neuron=new CNeuron();
              if(CheckPointer(neuron)==POINTER_INVALID)
                {
                 delete temp;
                 delete layers;
                 return;
                }
              neuron.Init(outputs,n);
              break;

Для сверточного слоя создадим новый экземпляр нейрона. Посчитаем количество выходных элементов на основании информации о предыдущем слое и инициализируем только-что созданный нейрон.

            case defNeuronConv:
              neuron_p=new CNeuronConv();
              if(CheckPointer(neuron_p)==POINTER_INVALID)
                {
                 delete temp;
                 delete layers;
                 return;
                }
              if(CheckPointer(prev)!=POINTER_INVALID)
                {
                 if(prev.type==defNeuron)
                   {
                    temp_count=(int)((prev.count-desc.window)%desc.step);
                    output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                   }
                 else
                    if(n==0)
                      {
                       temp_count=(int)((output_count-desc.window)%desc.step);
                       output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                      }
                }
              if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count))
                 neuron=neuron_p;
              break;

Аналогичный алгоритм применяется для нейронов подвыборочного слоя.

            case defNeuronProof:
              neuron_p=new CNeuronProof();
              if(CheckPointer(neuron_p)==POINTER_INVALID)
                {
                 delete temp;
                 delete layers;
                 return;
                }
              if(CheckPointer(prev)!=POINTER_INVALID)
                {
                 if(prev.type==defNeuron)
                   {
                    temp_count=(int)((prev.count-desc.window)%desc.step);
                    output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                   }
                 else
                    if(n==0)
                      {
                       temp_count=(int)((output_count-desc.window)%desc.step);
                       output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                      }
                }
              if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count))
                 neuron=neuron_p;
              break;
           }

После объявления и инициализации нейрона добавляем его в нейронный слой.

         if(!temp.Add(neuron))
           {
            delete temp;
            delete layers;
            return;
           }
         neuron=NULL;
        }

По завершению цикла генерации нейронов очередного слоя добавляем слой в хранилище. После генерации всех слоев выходим из метода.

      if(!layers.Add(temp))
        {
         delete temp;
         delete layers;
         return;
        }
     }

   return;
  }

3.4.2. Метод прямого прохода сверточной нейронной сети.

Вся работа нейронной сети организована в методе прямого прохода feedForward. В параметрах данный метод получает исходные данные для анализа (в нашем случае это информация с ценового графика и используемых индикаторов). Первым делом проверяем действительность полученной ссылки на массив данных и состояние инициализации нейронной сети.

bool CNetConvolution::feedForward(CArrayDouble *inputVals)
  {
   if(CheckPointer(layers)==POINTER_INVALID || CheckPointer(inputVals)==POINTER_INVALID || layers.Total()<=1)
      return false;

Затем объявляем вспомогательные переменные и переносим полученные внешние данные на входной слой нейронной сети.

   CLayer *previous=NULL;
   CLayer *current=layers.At(0);
   int total=MathMin(current.Total(),inputVals.Total());
   CNeuronBase *neuron=NULL;
   for(int i=0;i<total;i++)
     {
      neuron=current.At(i);
      if(CheckPointer(neuron)==POINTER_INVALID)
         return false;
      neuron.setOutputVal(inputVals.At(i));
     }

После загрузки исходных данных в нейронную сеть запускаем цикл последовательно перебора нейронных слоев от входа нейронной сети к ее выходу.

   CObject *temp=NULL;
   for(int l=1;l<layers.Total();l++)
     {
      previous=current;
      current=layers.At(l);
      if(CheckPointer(current)==POINTER_INVALID)
         return false;

Внутри запущенного цикла для каждого слоя запускаем вложенный цикл по перебору всех нейронов слоя с пересчетом их значений. Обратите внимание, что для полносвязных нейронных слоев не пересчитывается значение на последнем нейроне. Как уже говорилось выше, он используется в качестве байесовского смещения, и мы будем использовать только его весовой коэффициент.

      total=current.Total();
      if(current.At(0).Type()==defNeuron)
         total--;

      for(int n=0;n<total;n++)
        {
         neuron=current.At(n);
         if(CheckPointer(neuron)==POINTER_INVALID)
            return false;

Далее выбор метода зависит от типа нейронов предыдущего слоя. Для полносвязных слоев вызовем метод прямого распространения с указанием в параметрах ссылки на предыдущий слой.

         if(previous.At(0).Type()==defNeuron)
           {
            temp=previous;
            if(!neuron.feedForward(temp))
               return false;
            continue;
           }

Если ранее был сверточный или подвыборочный слой, то посмотрим на тип пересчитываемого нейрона. Для нейрона полносвязного слоя соберем внутренние слои всех нейронов предыдущего слоя в единый слой и затем вызовем метод прямого распространения текущего нейрона с указанием в параметрах ссылки на суммарный слой нейронов. 

         if(neuron.Type()==defNeuron)
           {
            if(n==0)
              {
               CLayer *temp_l=new CLayer(total);
               if(CheckPointer(temp_l)==POINTER_INVALID)
                  return false;
               CNeuronProof *proof=NULL;
               for(int p=0;p<previous.Total();p++)
                 {
                  proof=previous.At(p);
                  if(CheckPointer(proof)==POINTER_INVALID)
                     return false;
                  temp_l.AddArray(proof.getOutputLayer());
                 }
               temp=temp_l;
              }
            if(!neuron.feedForward(temp))
               return false;
            if(n==total-1)
              {
               CLayer *temp_l=temp;
               temp_l.FreeMode(false);
               temp_l.Shutdown();
               delete temp_l;
              }
            continue;
           }

По завершении цикла перебора всех нейронов такого слоя нужно удалить объект суммарного нейрона. При этом нам нужно удалить объект слоя без удаления объектов нейронов, содержащихся в данном слое, т. к. эти же объекты и далее будут использоваться в наших сверточных и подвыборочных слоях. Для этого установим флаг m_free_mode в состояние false и только потом удалим объект.

Если же перед нами элемент сверточного или подвыборочного слоя, то вызовем метод прямого распространения с передачей в параметрах ссылки на предыдущий элемент соответствующего фильтра.

         temp=previous.At(n);
         if(CheckPointer(temp)==POINTER_INVALID)
            return false;
         if(!neuron.feedForward(temp))
            return false;
        }
     }

   return true;
  }

После перебора всех нейронов и слоев выходим из метода.

3.4.3. Метод обратного прохода сверточной нейронной сети.

Обучение нейронной сети осуществляется в методе обратного прохода backProp. В нем реализован метод обратного распространения ошибки от выходного слоя нейронной сети к ее входам. Следовательно, в параметрах данный метод получает фактические данные.

В начале метода проверяем действительность ссылки на объект эталонных значений.

void CNetConvolution::backProp(CArrayDouble *targetVals)
  {
   if(CheckPointer(targetVals)==POINTER_INVALID)
      return;

Затем, посчитаем среднеквадратичную ошибку на выходе прямого прохода нейронной сети от фактических данных и рассчитаем градиенты ошибки нейронов выходного слоя.

   CLayer *outputLayer=layers.At(layers.Total()-1);
   if(CheckPointer(outputLayer)==POINTER_INVALID)
      return;

   double error=0.0;
   int total=outputLayer.Total()-1;
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron=outputLayer.At(n);
      double target=targetVals.At(n);
      double delta=(target>1 ? 1 : target<-1 ? -1 : target)-neuron.getOutputVal();
      error+=delta*delta;
      neuron.calcOutputGradients(targetVals.At(n));
     }
   error/= total;
   error = sqrt(error);

   recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor;

 Следующим шагом организуем цикл с перебором всех слоев нейронной сети в обратном порядке, в котором запустим вложенный цикл с перебором всех нейронов соответствующего слоя для пересчета градиентов ошибок нейронов в скрытых слоях.

   CNeuronBase *neuron=NULL;
   CObject *temp=NULL;
   for(int layerNum=layers.Total()-2; layerNum>0; layerNum--)
     {
      CLayer *hiddenLayer=layers.At(layerNum);
      CLayer *nextLayer=layers.At(layerNum+1);
      total=hiddenLayer.Total();
      for(int n=0; n<total && !IsStopped(); ++n)
        {

Как и при прямом проходе, выбор нужного метода обновления градиентов ошибок осуществляется на основании анализа типов текущего нейрона и нейронов последующего слоя. Если далее следует полносвязный слой нейронов, то вызываем метод calcHiddenGradients анализируемого нейрона с передачей в параметрах ссылки на объект последующего слоя нейронной сети.

         neuron=hiddenLayer.At(n);
         if(nextLayer.At(0).Type()==defNeuron)
           {
            temp=nextLayer;
            neuron.calcHiddenGradients(temp);
            continue;
           }

Если же далее следует сверточный или подвыборочный слой, то в таком случае проверяем тип текущего нейрона. Для полносвязного нейрона организуем цикл по перебору всех фильтров последующего слоя с запуском пересчета градиента ошибки по каждому фильтру для данного нейрона и суммируем полученные градиенты. В случае, когда текущий слой также является сверточный или подвыборочный, определим градиент ошибки по соответствующему фильтру.

         if(neuron.Type()==defNeuron)
           {
            double g=0;
            for(int i=0;i<nextLayer.Total();i++)
              {
               temp=nextLayer.At(i);
               neuron.calcHiddenGradients(temp);
               g+=neuron.getGradient();
              }
            neuron.setGradient(g);
            continue;
           }
         temp=nextLayer.At(n);
         neuron.calcHiddenGradients(temp);
        }
     }

После обновления всех градиентов запустим аналогичные циклы с той же логикой разветвления для обновления весовых коэффициентов нейронов. После обновления весов выходим из метода.

   for(int layerNum=layers.Total()-1; layerNum>0; layerNum--)
     {
      CLayer *layer=layers.At(layerNum);
      CLayer *prevLayer=layers.At(layerNum-1);
      total=layer.Total()-(layer.At(0).Type()==defNeuron ? 1 : 0);
      int n_conv=0;
      for(int n=0; n<total && !IsStopped(); n++)
        {
         neuron=layer.At(n);
         if(CheckPointer(neuron)==POINTER_INVALID)
            return;
         if(neuron.Type()==defNeuronProof)
            continue;
         switch(prevLayer.At(0).Type())
           {
            case defNeuron:
              temp=prevLayer;
              neuron.updateInputWeights(temp);
              break;
            case defNeuronConv:
            case defNeuronProof:
              if(neuron.Type()==defNeuron)
                {
                 for(n_conv=0;n_conv<prevLayer.Total();n_conv++)
                   {
                    temp=prevLayer.At(n_conv);
                    neuron.updateInputWeights(temp);
                   }
                }
              else
                {
                 temp=prevLayer.At(n);
                 neuron.updateInputWeights(temp);
                }
              break;
            default:
              temp=NULL;
              break;
           }
        }   
     }
  }

С полным кодом всех методов и классов можно ознакомиться во вложении. 

4. Тестирование

Для проверки работы сверточной нейронной сети был взят советник классификации из второй статьи данного цикла. Напомню, перед нейронной сетью стоит задача предсказания фрактала на текущей свече. Для этого на вход нейронной сети подается информация о формациях N последних свечей и данные 4-х осцилляторов за тот же период.

В сверточном слое нашей новой нейронной сети мы создадим 4 фильтра, которые будут искать паттерны в совокупности данных о формации свечи и показаниях осцилляторов на анализируемой свече. Окно и шаг фильтров будут соответствовать количеству данных на описание одной свечи. Иными словами, мы сравним всю информацию о каждой свече с неким паттерном и вернем значение сходимости. Такой подход позволит нам при необходимости дополнять исходные данные новой информацией о свечах (включение дополнительных индикаторов для анализа и т. д.) без существенной потери производительности.

В подвыборочном слое мы уменьшим размер массива признаков и сгладим результаты путем усреднения данных.

В самом советнике потребовались минимальные изменения. Это изменение класса нейронной сети при объявлении переменных и создании экземпляра.

CNetConvolution     *Net;

Также изменения были внесены в части задании структуры нейронной сети в функции OnInit. Для тестирования была использована сеть с одним сверточным и одним подвыборочным слоем и 4-мя фильтрами в каждом. Структура полносвязных слоев осталась без изменений (сделано намеренно для оценки влияния сверточных слоев на работу всей сети). 

   Net=new CNetConvolution(NULL);
   ResetLastError();
   if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false))
     {
      printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError());
      CArrayObj *Topology=new CArrayObj();
      if(CheckPointer(Topology)==POINTER_INVALID)
         return INIT_FAILED;

      CLayerDescription *desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=(int)HistoryBars*12;
      desc.type=defNeuron;
      if(!Topology.Add(desc))
         return INIT_FAILED;

      int filters=4;
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=filters;
      desc.type=defNeuronConv;
      desc.window=12;
      desc.step=12;
      if(!Topology.Add(desc))
         return INIT_FAILED;

      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=filters;
      desc.type=defNeuronProof;
      desc.window=3;
      desc.step=2;
      if(!Topology.Add(desc))
         return INIT_FAILED;

      int n=1000;
      bool result=true;
      for(int i=0;(i<4 && result);i++)
        {
         desc=new CLayerDescription();
         if(CheckPointer(desc)==POINTER_INVALID)
            return INIT_FAILED;
         desc.count=n;
         desc.type=defNeuron;
         result=(Topology.Add(desc) && result);
         n=(int)MathMax(n*0.3,20);
        }
      if(!result)
        {
         delete Topology;
         return INIT_FAILED;
        }

      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=3;
      desc.type=defNeuron;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      delete Net;
      Net=new CNetConvolution(Topology);
      delete Topology;
      if(CheckPointer(Net)==POINTER_INVALID)
         return INIT_FAILED;
      dError=-1;
      dUndefine=0;
      dForecast=0;
      dtStudied=0;
     }

В остальном код советника остался без изменений.

Тестирование проводилось на паре EURUSD период H1. В одном терминале на разных графиках одного инструмента одновременно было запущено 2 советника: со сверточной и полносвязной нейронной сетью. Параметры полносвязных слоев сверточной нейронной сети аналогичны полносвязной сети второго советника, т. е. к ранее построенной сети мы только добавили сверточный и подвыборочный слои.

Тестирование показала небольшой прирост производительности в сверточной нейронной сети. Несмотря на добавление двух слоев, по результатам 24 эпох среднее время обучения одной эпохи сверточной нейронной сети составило 2 часа 4 минуты, а полносвязной сети 2 часа 10 минут.

 

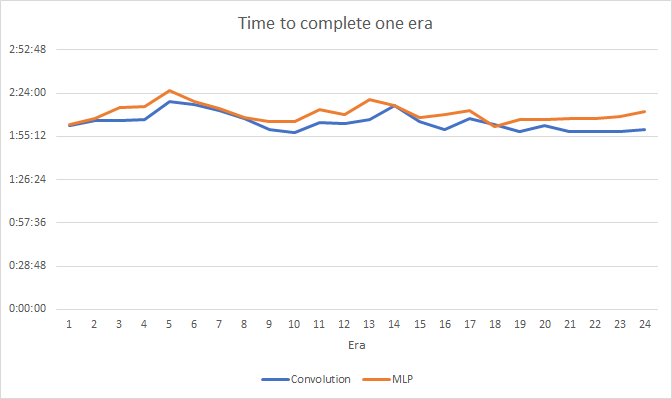
При этом сверточная нейронная сеть показывает немногим лучшие результаты по погрешности предсказания и «попадании в цель».

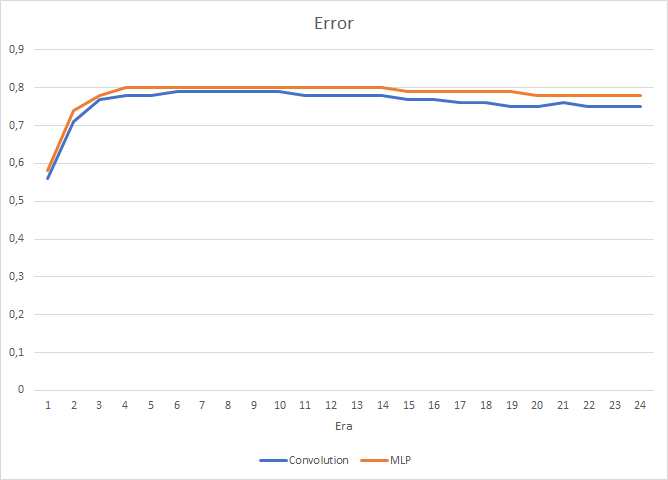
Визуально можно заметить, что на графике сверточной нейронной сети сигналы появляются реже, но ближе к цели.

Заключение

В данной статье мы рассмотрели возможность использование сверточных нейронных сетей на финансовых рынках. И тестирование показывает, что их использование позволяет улучшить результаты работы полносвязной нейронной сети. В частности, это может быть связано с предварительной обработкой данных, подаваемых на вход полносвязного перцептрона. В сверточном и подвыборочном слоях осуществляется фильтрация данных от шума, что позволяет повысить качество исходных данных и, как результат, качество работы нейронной сети. А снижение размерности помогает уменьшить количество связей перцептрона с исходными данными, что дает прирост в производительности.

Ссылки

1. Нейросети — это просто
2. Нейросети — это просто (Часть 2): обучение и тестирование сети

Программы, используемые в статье

#	Имя	Тип	Описание
1	Fractal.mq5	Советник	Советник с нейронной сетью регрессии (1 нейрон в выходном слое)
2	Fractal_2.mq5	Советник	Советник с нейронной сетью классификации (3 нейрона в выходном слое)
3	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети (перцептрона)
4	Fractal_conv.mq5	Советник	Советник со сверточной нейронной сетью классификации (3 нейрона в выходном слое)

Введение

Оригинал на английском здесь.

Свёрточные нейронные сети (СНС). Звучит как странное сочетание биологии и математики с примесью информатики, но как бы оно не звучало, эти сети — одни из самых влиятельных инноваций в области компьютерного зрения. Впервые нейронные сети привлекли всеобщее внимание в 2012 году, когда Алекс Крижевски благодаря им выиграл конкурс ImageNet (грубо говоря, это ежегодная олимпиада по машинному зрению), снизив рекорд ошибок классификации с 26% до 15%, что тогда стало прорывом. Сегодня глубинное обучения лежит в основе услуг многих компаний: Facebook использует нейронные сети для алгоритмов автоматического проставления тегов, Google — для поиска среди фотографий пользователя, Amazon — для генерации рекомендаций товаров, Pinterest — для персонализации домашней страницы пользователя, а Instagram — для поисковой инфраструктуры.

Но классический, и, возможно, самый популярный вариант использования сетей это обработка изображений. Давайте посмотрим, как СНС используются для классификации изображений.

Задача

Задача классификации изображений — это приём начального изображения и вывод его класса (кошка, собака и т.д.) или группы вероятных классов, которая лучше всего характеризует изображение. Для людей это один из первых навыков, который они начинают осваивать с рождения.

Мы овладеваем им естественно, без усилий, став взрослыми. Даже не думая, мы можем быстро и легко распознать пространство, которое нас окружает, вместе с объектами. Когда мы видим изображение или просто смотрим на происходящее вокруг, чаще всего мы можем сразу охарактеризовать место действия, дать каждому объекту ярлык, и все это происходит бессознательно, незаметно для разума. Эти навыки быстрого распознавания шаблонов, обобщения уже полученных знаний, и адаптации к различной запечатлённой на фото обстановке не доступны нашим электронным приятелям.

Вводы и выводы

Когда компьютер видит изображение (принимает данные на вход), он видит массив пикселей. В зависимости от разрешения и размера изображения, например, размер массива может быть 32х32х3 (где 3 — это значения каналов RGB). Чтобы было понятней, давайте представим, у нас есть цветное изображение в формате JPG, и его размер 480х480. Соответствующий массив будет 480х480х3. Каждому из этих чисел присваивается значение от 0 до 255, которое описывает интенсивность пикселя в этой точке. Эти цифры, оставаясь бессмысленными для нас, когда мы определяем что на изображении, являются единственными вводными данными, доступными компьютеру.  Идея в том, что вы даете компьютеру эту матрицу, а он выводит числа, которые описывают вероятность класса изображения (.80 для кошки, .15 для собаки, .05 для птицы и т.д.).

Чего мы хотим от компьютера

Теперь, когда мы определили задачу, ввод и вывод, давайте думать о том, как подбираться к решению. Мы хотим, чтобы компьютер мог различать все данные ему изображения и распознавать уникальные особенности, которые делают собаку собакой, а кошку кошкой. У нас и этот процесс происходит подсознательно. Когда мы смотрим на изображение собаки, мы можем отнести его к конкретному классу, если у изображения есть характерные особенности, которые можно идентифицировать, такие как лапы или четыре ноги. Аналогичным образом компьютер может выполнять классификацию изображений через поиск характеристик базового уровня, например границ и искривлений, а затем с помощью построения более абстрактных концепций через группы свёрточных слоев. Это общее описание того, что делают СНС. Теперь перейдём к специфике.

Биологические связи

В начале немного истории. Когда вы впервые услышали термин сверточные нейронные сети, возможно подумали о чем-то связанном с нейронауками или биологией, и отчасти были правы. В каком-то смысле. СНС — это действительно прототип зрительной коры мозга. Зрительная кора имеет небольшие участки клеток, которые чувствительны к конкретным областям поля зрения. Эту идею детально рассмотрели с помощью потрясающего эксперимента Хьюбел и Визель в 1962 году (видео), в котором показали, что отдельные мозговые нервные клетки реагировали (или активировались) только при визуальном восприятии границ определенной ориентации. Например, некоторые нейроны активировались, когда воспринимали вертикальные границы, а некоторые — горизонтальные или диагональные. Хьюбел и Визель выяснили, что все эти нейроны сосредоточены в виде стержневой архитектуры и вместе формируют визуальное восприятие. Эту идею специализированных компонентов внутри системы, которые решают конкретные задачи (как клетки зрительной коры, которые ищут специфические характеристики) и используют машины, и эта идея — основа СНС.

Структура

Вернёмся к специфике. Что конкретно делают СНС? Берётся изображение, пропускается через серию свёрточных, нелинейных слоев, слоев объединения и полносвязных слоёв, и генерируется вывод. Как мы уже говорили, выводом может быть класс или вероятность классов, которые лучше всего описывают изображение. Сложный момент — понимание того, что делает каждый из этих слоев. Так что давайте перейдем к самому важному.

Первый cлой — математическая часть

Первый слой в СНС всегда свёрточный. Вы же помните, какой ввод у этого свёрточного слоя? Как уже говорилось ранее, вводное изображение — это матрица 32 х 32 х 3 с пиксельными значениями. Легче всего понять, что такое свёрточный слой, если представить его в виде фонарика, который светит на верхнюю левую часть изображения. Допустим свет, который излучает этот фонарик, покрывает площадь 5 х 5. А теперь давайте представим, что фонарик движется по всем областям вводного изображения. В терминах компьютерного обучения этот фонарик называется фильтром (иногда нейроном или ядром), а области, на которые он светит, называются рецептивным полем (полем восприятия). То есть наш фильтр — это матрица (такую матрицу ещё называют матрицей весов или матрицей параметров). Заметьте, что глубина у фильтра должна быть такой же, как и глубина вводного изображения (тогда есть гарантия математической верности), и размеры этого фильтра — 5 х 5 х 3. Теперь давайте за пример возьмем позицию, в которой находится фильтр.  Пусть это будет левый верхний угол. Поскольку фильтр производит свёртку, то есть передвигается по вводному изображению, он умножает значения фильтра на исходные значения пикселей изображения ( поэлементное умножение). Все эти умножения суммируются (всего 75 умножений). И в итоге получается одно число. Помните, оно просто символизирует нахождение фильтра в верхнем левом углу изображения. Теперь повторим этот процесс в каждой позиции. (Следующий шаг — перемещение фильтра вправо на единицу, затем еще на единицу вправо и так далее). Каждая уникальная позиция введённого изображения производит число. После прохождения фильтра по всем позициям получается матрица 28 х 28 х 1, которую называют функцией активации или картой признаков. Матрица 28 х 28 получается потому, что есть 784 различных позиции, которые могут пройти через фильтр 5 х 5 изображения 32 х 32. Эти 784 числа преобразуются в матрицу 28 х 28.

(Небольшая ремарка: некоторые изображения, в том числе то, что вы видите выше, взяты из потрясающей книги «Нейронные сети и глубинное обучение» Майкла Нильсена («Neural Networks и Deep Learning«, by Michael Nielsen). Настоятельно рекомендую).

Допустим, теперь мы используем два 5 х 5 х 3 фильтра вместо одного. Тогда выходным значением будет 28 х 28 х 2.

Первый слой

Давайте поговорим о том, что эта свертка на самом деле делает на высоком уровне. Каждый фильтр можно рассматривать как идентификатор свойства. Когда я говорю свойство, я имею в виду прямые границы, простые цвета и кривые. Подумайте о самых простых характеристиках, которые имеют все изображения в общем. Скажем, наш первый фильтр 7 х 7 х 3, и он будет детектором кривых. (Сейчас давайте игнорировать тот факт, что у фильтра глубина 3, и рассмотрим только верхний слой фильтра и изображения, для простоты). У фильтра пиксельная структура, в которой численные значения выше вдоль области, определяющей форму кривой (помните, фильтры, о которых мы говорим, это просто числа!).

Вернемся к математической визуализации. Когда у нас в левом верхнем углу вводного изображения есть фильтр, он производит умножение значений фильтра на значения пикселей этой области. Давайте рассмотрим пример изображения, которому мы хотим присвоить класс, и установим фильтр в верхнем левом углу.

Помните, всё что нам нужно, это умножить значения фильтра на исходные значения пикселей изображения.

По сути, если на вводном изображении есть форма, в общих чертах похожая на кривую, которую представляет этот фильтр, и все умноженные значения суммируются, то результатом будет большое значение! Теперь давайте посмотрим, что произойдёт, когда мы переместим фильтр.

Значение намного ниже! Это потому, что в новой области изображения нет ничего, что фильтр определения кривой мог засечь. Помните, что вывод этого свёрточного слоя — карта свойств. В самом простом случае, при наличии одного фильтра свертки (и если этот фильтр — детектор кривой), карта свойств покажет области, в которых больше вероятности наличия кривых. В этом примере в левом верхнем углу значение нашей 28 х 28 х 1 карты свойств будет 6600. Это высокое значение показывает, что, возможно, что-то похожее на кривую присутствует на изображении, и такая вероятность активировала фильтр. В правом верхнем углу значение у карты свойств будет 0, потому что на картинке не было ничего, что могло активировать фильтр (проще говоря, в этой области не было кривой). Помните, что это только для одного фильтра. Это фильтр, который обнаруживает линии с изгибом наружу. Могут быть другие фильтры для линий, изогнутых внутрь или просто прямых. Чем больше фильтров, тем больше глубина карты свойств, и тем больше информации мы имеем о вводной картинке.

Ремарка: Фильтр, о котором я рассказал в этом разделе, упрощён для упрощения математики свёртывания. На рисунке ниже видны примеры фактических визуализаций фильтров первого свёрточного слоя обученной сети. Но идея здесь та же. Фильтры на первом слое сворачиваются вокруг вводного изображения и «активируются» (или производят большие значения), когда специфическая черта, которую они ищут, есть во вводном изображении.

(Заметка: изображения выше — из Стэнфордского курса 231N, который преподают Андрей Карпатый и Джастин Джонсон (Andrej Karpathy and Justin Johnson). Рекомендую тем, кто хочет лучше изучить СНС).

Идём глубже по сети

Сегодня в традиционной сверточной нейронной сетевой архитектуре существуют и другие слои, которые перемежаются со свёрточными. Я очень рекомендую тем, кто интересуется темой, почитать об этих слоях, чтобы понять их функциональность и эффекты. Классическая архитектура СНС будет выглядеть так:

Последний слой, хоть и находится в конце, один из важных — мы перейдём к нему позже. Давайте подытожим то, в чём мы уже разобрались. Мы говорили о том, что умеют определять фильтры первого свёрточного слоя. Они обнаруживают свойства базового уровня, такие как границы и кривые. Как можно себе представить, чтобы предположить какой тип объекта изображён на картинке, нам нужна сеть, способная распознавать свойства более высокого уровня, как например руки, лапы или уши. Так что давайте подумаем, как выглядит выходной результат сети после первого свёрточного слоя. Его размер 28 х 28 х 3 (при условии, что мы используем три фильтра 5 х 5 х 3).  Когда картинка проходит через один свёрточный слой, выход первого слоя становится вводным значением 2-го слоя. Теперь это немного сложнее визуализировать. Когда мы говорили о первом слое, вводом были только данные исходного изображения. Но когда мы перешли ко 2-му слою, вводным значением для него стала одна или несколько карт свойств — результат обработки предыдущим слоем. Каждый набор вводных данных описывает позиции, где на исходном изображении встречаются определенные базовые признаки.

Теперь, когда вы применяете набор фильтров поверх этого (пропускаете картинку через второй свёрточный слой), на выходе будут активированы фильтры, которые представляют свойства более высокого уровня. Типами этих свойств могут быть полукольца (комбинация прямой границы с изгибом) или квадратов (сочетание нескольких прямых ребер). Чем больше свёрточных слоёв проходит изображение и чем дальше оно движется по сети, тем более сложные характеристики выводятся в картах активации. В конце сети могут быть фильтры, которые активируются при наличии рукописного текста на изображении, при наличии розовых объектов и т.д. Если вы хотите узнать больше о фильтрах в свёрточных сетях, Мэтт Зейлер и Роб Фергюс написали отличную научно-исследовательскую работу на эту тему. Ещё на ютубе есть видео Джейсона Йосински c отличным визуальным представлением этих процессов.

Еще один интересный момент. Когда вы двигаетесь вглубь сети, фильтры работают со все большим полем восприятия, а значит, они в состоянии обрабатывать информацию с большей площади первоначального изображения (простыми словами, они лучше приспособляются к обработке большей области пиксельного пространства).

Полносвязные слои

Теперь, когда мы можем обнаружить высокоуровневые свойства, самое крутое — это прикрепление полносвязного слоя в конце сети. Этот слой берёт вводные данные и выводит N-пространственный вектор, где N — число классов, из которых программа выбирает нужный. Например, если вы хотите программу по распознаванию цифр, у N будет значение 10, потому что цифр 10. Каждое число в этом N-пространственном векторе представляет собой вероятность конкретного класса. Например, если результирующий вектор для программы распознавания цифр это [0 0,1 0,1 0,75 0 0 0 0 0,05], значит существует 10% вероятность, что на изображении «1», 10% вероятность, что на изображение «2», 75% вероятность — «3», и 5% вероятность — «9» (конечно, есть и другие способы представить вывод).

Способ, с помощью которого работает полносвязный слой — это обращение к выходу предыдущего слоя (который, как мы помним, должен выводить высокоуровневые карты свойств) и определение свойств, которые больше связаны с определенным классом. Например, если программа предсказывает, что на каком-то изображении собака, у карт свойств, которые отражают высокоуровневые характеристики, такие как лапы или 4 ноги, должны быть высокие значения. Точно так же, если программа распознаёт, что на изображении птица — у неё будут высокие значения в картах свойств, представленных высокоуровневыми характеристиками вроде крыльев или клюва. Полносвязный слой смотрит на то, что функции высокого уровня сильно связаны с определенным классом и имеют определенные веса, так что, когда вы вычисляете произведения весов с предыдущим слоем, то получаете правильные вероятности для различных классов.

Обучение (или «Что заставляет эту штуку работать»)

Это один из аспектов нейронных сетей, о котором я специально до сих пор не упоминал. Вероятно, это самая важная часть. Возможно, у вас появилось множество вопросов. Откуда фильтры первого свёрточного слоя знают, что нужно искать границы и кривые? Откуда полносвязный слой знает, что ищет карта свойств? Откуда фильтры каждого слоя знают, какие хранить значения? Способ, которым компьютер способен корректировать значения фильтра (или весов) — это обучающий процесс, который называют методом обратного распространения ошибки.

Перед тем, как перейти к объяснению этого метода, поговорим о том, что нейронной сети нужно для работы. Когда мы рождаемся, наши головы пусты. Мы не понимаем как распознать кошку, собаку или птицу. Ситуация с СНС похожа: до момента построения сети, веса или значения фильтра случайны. Фильтры не умеют искать границы и кривые. Фильтры верхних слоёв не умеют искать лапы и клювы. Когда мы становимся старше, родители и учителя показывают нам разные картинки и изображения и присваивают им соответствующие ярлыки. Та же идея показа картинки и присваивания ярлыка используется в обучающем процессе, который проходит СНС. Давайте представим, что у нас есть набор обучающих картинок, в котором тысячи изображений собак, кошек и птиц. У каждого изображения есть ярлык с названием животного.

Метод обратного распространения ошибки можно разделить на 4 отдельных блока: прямое распространение, функцию потери, обратное распространение и обновление веса. Во время прямого распространения, берётся тренировочное изображение — как помните, это матрица 32 х 32 х 3 — и пропускается через всю сеть. В первом обучающем примере, так как все веса или значения фильтра были инициализированы случайным образом, выходным значением будет что-то вроде [.1 .1 .1 .1 .1 .1 .1 .1 .1 .1], то есть такое значение, которое не даст предпочтения какому-то определённому числу. Сеть с такими весами не может найти свойства базового уровня и не может обоснованно определить класс изображения. Это ведёт к функции потери. Помните, то, что мы используем сейчас — это обучающие данные. У таких данных есть и изображение и ярлык. Допустим, первое обучающее изображение — это цифра 3. Ярлыком изображения будет [0 0 0 1 0 0 0 0 0 0]. Функция потери может быть выражена по-разному, но часто используется СКО (среднеквадратическая ошибка), это 1/2 умножить на (реальность — предсказание) в квадрате.

Примем это значение за переменную L. Как вы догадываетесь, потеря будет очень высокой для первых двух обучающих изображений. Теперь давайте подумаем об этом интуитивно. Мы хотим добиться того, чтобы спрогнозированный ярлык (вывод свёрточного слоя) был таким же, как ярлык обучающего изображения (это значит, что сеть сделала верное предположение). Чтобы такого добиться, нам нужно свести к минимуму количество потерь, которое у нас есть. Визуализируя это как задачу оптимизации из математического анализа, нам нужно выяснить, какие входы (веса, в нашем случае) самым непосредственным образом способствовали потерям (или ошибкам) сети.

(Один из способов визуализировать идею минимизации потери — это трёхмерный график, где веса нейронной сети (очевидно их больше, чем 2, но тут пример упрощен) это независимые переменные, а зависимая переменная — это потеря. Задача минимизации потерь — отрегулировать веса так, чтобы снизить потерю. Визуально нам нужно приблизиться к самой нижней точке чашеподобного объекта. Чтобы добиться этого, нужно найти производную потери (в рамках нарисованного графика — рассчитать угловой коэффициент в каждом направлении) с учётом весов).

Это математический эквивалент dL/dW, где W — веса определенного слоя. Теперь нам нужно выполнить обратное распространение через сеть, которое определяет, какие веса оказали большее влияние на потери, и найти способы, как их настроить, чтобы уменьшить потери. После того, как мы вычислим производную, перейдём к последнему этапу — обновлению весов. Возьмём все фильтровые веса и обновим их так, чтобы они менялись в направлении градиента.

Скорость обучения — это параметр, который выбирается программистом. Высокая скорость обучения означает, что в обновлениях веса делались более крупные шаги, поэтому образцу может потребоваться меньше времени, чтобы набрать оптимальный набор весов. Но слишком высокая скорость обучения может привести к очень крупным и недостаточно точным скачкам, которые помешают достижению оптимальных показателей.

Процесс прямого распространения, функцию потери, обратное распространение и обновление весов, обычно называют одним периодом дискретизации (или epoch — эпохой). Программа будет повторять этот процесс фиксированное количество периодов для каждого тренировочного изображения. После того, как обновление параметров завершится на последнем тренировочном образце, сеть в теории должна быть достаточно хорошо обучена и веса слоёв настроены правильно.

Тестирование

Наконец, чтобы увидеть, работает ли СНС, мы берём другой набор изображений и ярлыков и пропускаем изображения через сеть. Сравниваем выходы с реальностью и смотрим, работает ли наша сеть.

Как компании используют СНС

Данные, данные, данные. Компании, у которых тонны этого шестибуквенного магического добра, имеют закономерное преимущество перед остальными конкурентами. Чем больше тренировочных данных, которые можно скормить сети, тем больше можно создать обучающих итераций, больше обновлений весов и перед уходом в продакшн, получить лучше обученную сеть. Facebook (и Instagram) могут использовать все фотографии миллиарда пользователей, которые у них сегодня есть, Pinterest — информацию из 50 миллиардов пинов, Google — данные поиска, а Amazon — данные о миллионах продуктов, которые ежедневно покупаются. И теперь вы знаете какое волшебство они используют в своих целях.

Источник
Вторая часть (на английском)