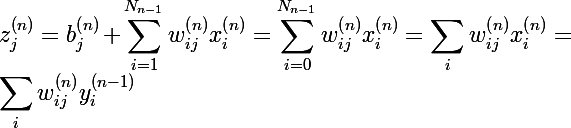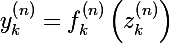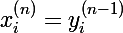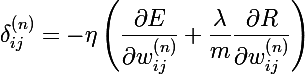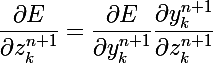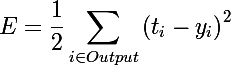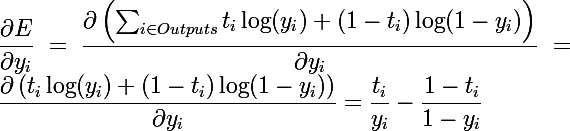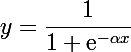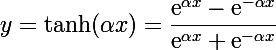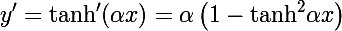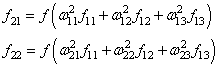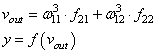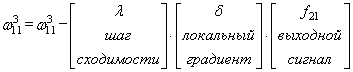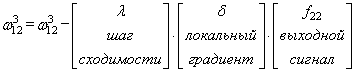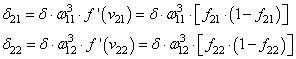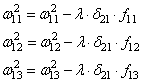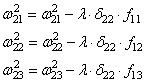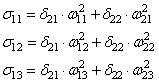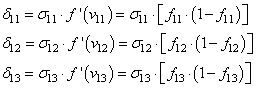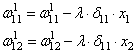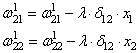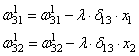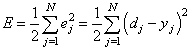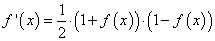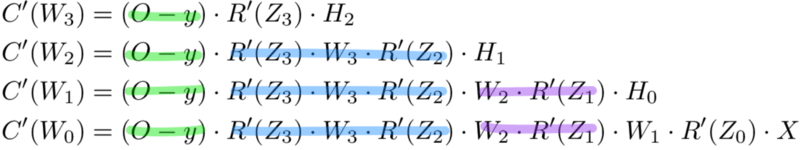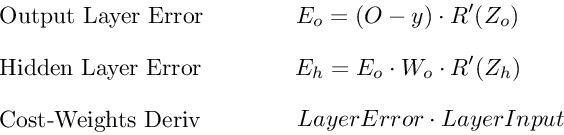Время на прочтение
14 мин
Количество просмотров 84K
Привет. Я хочу продолжить тему реализации методов машинного обучения на c#, и в этой статье я расскажу про алгоритм обратного распространения ошибки для обучения нейронной сети прямого распространения, а также приведу его реализацию на языке C#. Особенность данной реализации в том, что реализация алгоритма абстрагирована от реализаций целевой функции (той, которую нейросеть пытается минимизировать) и функции активации нейронов. В итоге получится некий конструктор, с помощью которого можно поиграться с различными параметрами сети и алгоритма обучения, посмотреть и сравнить результат. Предполагается, что вы уже знакомы с тем, что такое искусственная нейросеть (если нет, то настоятельно рекомендую для начала изучить википедию или одну из подобных статей). Интересно? Лезем под кат.
Обозначения
Для начала рассмотрим обозначения, которые я буду использовать в статье, а за одно вспомним основные понятия, я не буду приводить картинок с нейронами и слоями, этого всего полно в википедии и здесь, на хабре. Итак, сразу в бой, индуцированное локальное поле нейрона (или просто сумматор) выглядит следующим образом:
Функция активации нейрона, или передаточная функция от значения сумматора:
- у каждого нейрона сети может быть своя функция активации
- для всех слоев кроме первого, входным вектором будет являться выходной вектор предыдущего слоя, так что
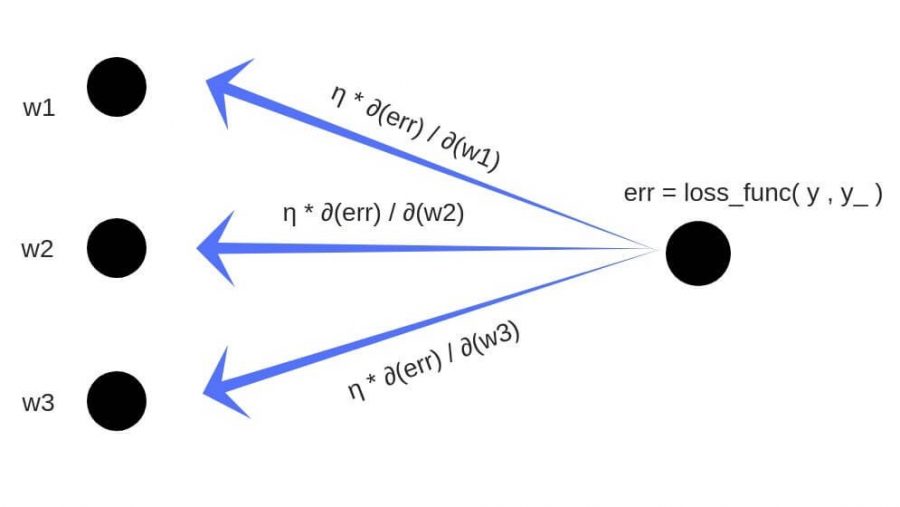
От нейрона перейдем к самой сети. Нейросеть — это модель, она обладает параметрами, и задача алгоритма обучения заключается в подборе таких параметров сети, чтобы минимизоровать значение функции ошибки. Функцию ошибки будем обозначать через E. Параметрами модели являются веса нейронов: 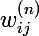
Греческой эта 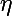
Изменение веса обозначим через дельта:
- направление градиента показывает нам в сторону роста значения функции, но нам для минимизации необходимо двигаться в обратном направлении
Таким образом, новый вес нейрона выглядит следующим образом:
Стоит упомянуть, что к изменению веса еще можно (или, скорее, нужно) добавить регуляризацию. Функция регуляризации R — это функция от параметров модели, в нашем случае это веса нейронов. Таким образом, новая функция ошибки выглядит как E + R, а формула изменения веса преобразуется в следующую:
- лямбда — гиперпараметр обучения, коэффициент регуляризации (похож на скорость обучения)
- m — размер обучающей выборки
Вообще говоря, реализацию регуляризации тоже можно абстрагировать от алгоритма обучения, но я пока этого делать не буду, поскольку текущая реализация алгоритма обучения и так не самая быстрая, поскольку в противному случае на каждой эпохе обучения (прогон всех обучающих примеров) придется в одном цикле считать аккумулированную ошибку, а в другом — регуляризацию.Еще одна причина заключается в том, что существует не так много видов регуляризации (я, например, знаю только L1 и L2), которые применяются при обучении нейросетей. В данной реализации я буду использовать L2 норму, и она будет неотъемлемой частью алгоритма обучения.
Алгоритм обратного распространения ошибки
Для начала остановимся на режимах обучения. Изменять веса можно несколькими способами:
- либо после каждого обучающего примера (обучение в реальном режиме времени, online обучение, batchSize = 1)
- либо накопить изменения для всей обучающей выборки, а затем изменить все веса (full-batch, batchSize = trainingSet.Length)
- либо после прогона некоторого количества обучающих примеров (mini-batch, batchSize = any_number < trainingSet.Length)
Рассмотрим ситуацию с онлайн-обучением, так будет проще. Итак, на вход сети пришел импульс 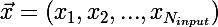
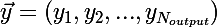
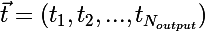
Рассмотрим частную производную функции ошибки E:
Дальнейшее рассуждение разделяется на две ветки: для последнего слоя и для остальных слоев.
Выходной слой
Для выходного слоя все просто, для коррекции ошибки нам достаточно вычислить производную целевой функции по одному из весов и вычислить значение дельты. Учтем, что целевая функция полностью зависит только от выходного значения нейрона, или значения функции активации, а сама функция активации зависит только от сумматора
Тут видно, что для вычисления ошибки выходного слоя нужно вычислить значение частных производных в точках, независимо от того, какая у нас целевая функция или же функция активации нейрона.
Любой скрытый слой
Но если слой не выходной, то нам нужно аккумулировать значения ошибок всех последующих слоев.
PS: я заметил, что в верхних индексах забыл ставить скобки, чтобы обозначить, что это не степень, а индекс слоя; учтите это, пока степеней нигде не было.
Что же мы имеем:
- вычисление производной некой функции активации — это как раз то что нужно
- вычисление частной производной целевой функции по значению сумматора следующего слоя; тут тоже все просто, мы ведь находимся не на последнем слое, и вычисление изменений весов ведем от последнего к первому, так что это значение уже вычислено на предыдущем шаге
- в случае, если следующий слой последний, то мы вычислим это значение для текущего слоя, и таким образом распространим решение на всю сеть
Реализация
Функция ошибки
С формулами покончили, давайте перейдем к реализации, и начнем с понятия функции ошибки. У меня это представлено в виде метрики (по сути, это так и есть). Метод CalculatePartialDerivaitveByV2Index вычисляет значение частной производной функции для входных векторов по индексу переменное из v2.
public interface IMetrics<T>
{
double Calculate(T[] v1, T[] v2);
/// <summary>
/// Calculate value of partial derivative by v2[v2Index]
/// </summary>
T CalculatePartialDerivaitveByV2Index(T[] v1, T[] v2, int v2Index);
}
Таким образом, мы можем вычислить значение частной производной функции ошибки для последнего слоя по реальному выходу сети 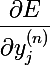
Для примера давайте напишем несколько реализаций.
Минимизация половины квадрата Евклидова расстояния
А производная будет выглядеть следующим образом:
internal class HalfSquaredEuclidianDistance : IMetrics<T>
{
public override double Calculate(double[] v1, double[] v2)
{
double d = 0;
for (int i = 0; i < v1.Length; i++)
{
d += (v1[i] - v2[i]) * (v1[i] - v2[i]);
}
return 0.5 * d;
}
public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index)
{
return v2[v2Index] - v1[v2Index];
}
}
Минимизация логарифмического правдоподобия
internal class Loglikelihood : IMetrics<double>
{
public override double Calculate(double[] v1, double[] v2)
{
double d = 0;
for (int i = 0; i < v1.Length; i++)
{
d += v1[i]*Math.Log(v2[i]) + (1 - v1[i])*Math.Log(1 - v2[i]);
}
return -d;
}
public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index)
{
return -(v1[v2Index]/v2[v2Index] - (1 - v1[v2Index])/(1 - v2[v2Index]));
}
}
Здесь главное не забыть, что логарифмическое правдоподобие вычисляется со знаком минус в начале, и производная тоже будет с минусом. Я не заостряю внимания на проверках или избегания случаев деления на ноль, или логарифма от нуля.
Функция активации нейрона
Аналогичным способом опишем функцию активации нейрона.
public interface IFunction
{
double Compute(double x);
double ComputeFirstDerivative(double x);
}
И примеры.
Сигмоид
internal class SigmoidFunction : IFunction
{
private double _alpha = 1;
internal SigmoidFunction(double alpha)
{
_alpha = alpha;
}
public double Compute(double x)
{
double r = (1 / (1 + Math.Exp(-1 * _alpha * x)));
//return r == 1f ? 0.9999999f : r;
return r;
}
public double ComputeFirstDerivative(double x)
{
return _alpha * this.Compute(x) * (1 - this.Compute(x));
}
}
Гиперболический тангенс
internal class HyperbolicTangensFunction : IFunction
{
private double _alpha = 1;
internal HyperbolicTangensFunction(double alpha)
{
_alpha = alpha;
}
public double Compute(double x)
{
return (Math.Tanh(_alpha * x));
}
public double ComputeFirstDerivative(double x)
{
double t = Math.Tanh(_alpha*x);
return _alpha*(1 - t*t);
}
}
Нейрон, слой и сеть
В данном разделе рассмотрим представление основных элементов сети, реализацию их я приводить не буду, т.к. она очевидно. Алгоритм будет приведен для полносвязной «слоеной» сети, так что и реализацию сети нужно будет делать соответствующую.
Итак, нейрон выглядит следующим образом.
public interface INeuron
{
/// <summary>
/// Weights of the neuron
/// </summary>
double[] Weights { get; }
/// <summary>
/// Offset/bias of neuron (default is 0)
/// </summary>
double Bias { get; set; }
/// <summary>
/// Compute NET of the neuron by input vector
/// </summary>
/// <param name="inputVector">Input vector (must be the same dimension as was set in SetDimension)</param>
/// <returns>NET of neuron</returns>
double NET(double[] inputVector);
/// <summary>
/// Compute state of neuron
/// </summary>
/// <param name="inputVector">Input vector (must be the same dimension as was set in SetDimension)</param>
/// <returns>State of neuron</returns>
double Activate(double[] inputVector);
/// <summary>
/// Last calculated state in Activate
/// </summary>
double LastState { get; set; }
/// <summary>
/// Last calculated NET in NET
/// </summary>
double LastNET { get; set; }
IList<INeuron> Childs { get; }
IList<INeuron> Parents { get; }
IFunction ActivationFunction { get; set; }
double dEdz { get; set; }
}
Т.к. мы рассматриваем полносвязную «слоеную» сеть, то Childs и Parents можно не имплементировать, но если делать общий алгоритм, то придется. Рассмотрим поля, которые особо важны для алгоритма обучения:
- LastNET — сумматор нейрона, тут хранится последнее вычисленное значение
- LastState — выход нейрона, тут хранится последнее вычисленное значение
- dEdz — это то самое dE/dz нейрона, что упоминается выше, и вычисляется в зависимости от того на каком слое находится текущий нейрон; частная производная функции ошибки по сумматору нейрона
Слой сети выглядит проще:
public interface ILayer
{
/// <summary>
/// Compute output of the layer
/// </summary>
/// <param name="inputVector">Input vector</param>
/// <returns>Output vector</returns>
double[] Compute(double[] inputVector);
/// <summary>
/// Get last output of the layer
/// </summary>
double[] LastOutput { get; }
/// <summary>
/// Get neurons of the layer
/// </summary>
INeuron[] Neurons { get; }
/// <summary>
/// Get input dimension of neurons
/// </summary>
int InputDimension { get; }
}
И представление сети:
public interface INeuralNetwork
{
/// <summary>
/// Compute output vector by input vector
/// </summary>
/// <param name="inputVector">Input vector (double[])</param>
/// <returns>Output vector (double[])</returns>
double[] ComputeOutput(double[] inputVector);
Stream Save();
/// <summary>
/// Train network with given inputs and outputs
/// </summary>
/// <param name="inputs">Set of input vectors</param>
/// <param name="outputs">Set if output vectors</param>
void Train(IList<DataItem<double>> data);
}
Но мы рассматриваем многослойную нейросеть, так что будет использоваться особое представление:
public interface IMultilayerNeuralNetwork : INeuralNetwork
{
/// <summary>
/// Get array of layers of network
/// </summary>
ILayer[] Layers { get; }
}
Алгоритм обучения
Алгоритм обучения будет реализован через паттерн стратегия:
public interface ILearningStrategy<T>
{
/// <summary>
/// Train neural network
/// </summary>
/// <param name="network">Neural network for training</param>
/// <param name="inputs">Set of input vectors</param>
/// <param name="outputs">Set of output vectors</param>
void Train(T network, IList<DataItem<double>> data);
}
Для более наглядного понимания приведу типичную функцию Train любой нейросети в контексте данной реализации:
public void Train(IList<DataItem<double>> data)
{
_learningStrategy.Train(this, data);
}
Формат входных данных
Я использую следующий формат входных данных:
public class DataItem<T>
{
private T[] _input = null;
private T[] _output = null;
public DataItem()
{
}
public DataItem(T[] input, T[] output)
{
_input = input;
_output = output;
}
public T[] Input
{
get { return _input; }
set { _input = value; }
}
public T[] Output
{
get { return _output; }
set { _output = value; }
}
}
Как видно из кода в предыдущих частях, нейросеть работает с
DataItem.Параметры алгоритма обучения
Данным классом описываются параметры алгоритма обучения, я думаю названия полей говорят сами за себя (и комментарии), так что не буду дублировать текстом:
public class LearningAlgorithmConfig
{
public double LearningRate { get; set; }
/// <summary>
/// Size of the butch. -1 means fullbutch size.
/// </summary>
public int BatchSize { get; set; }
public double RegularizationFactor { get; set; }
public int MaxEpoches { get; set; }
/// <summary>
/// If cumulative error for all training examples is less then MinError, then algorithm stops
/// </summary>
public double MinError { get; set; }
/// <summary>
/// If cumulative error change for all training examples is less then MinErrorChange, then algorithm stops
/// </summary>
public double MinErrorChange { get; set; }
/// <summary>
/// Function to minimize
/// </summary>
public IMetrics<double> ErrorFunction { get; set; }
}
Алгоритм
Ну и наконец, показав весь контекст, можно перейти к собственно реализации алгоритма обучения нейросети
internal class BackpropagationFCNLearningAlgorithm : ILearningStrategy, функция public void Train(IMultilayerNeuralNetwork network, IList<DataItem> data).
Для начала подготавливаем некоторые переменные (общие для всех эпох обучения) для работы алгоритма:
if (_config.BatchSize < 1 || _config.BatchSize > data.Count)
{
_config.BatchSize = data.Count;
}
double currentError = Single.MaxValue;
double lastError = 0;
int epochNumber = 0;
Logger.Instance.Log("Start learning...");
Затем запустится основной цикл работы алгоритма, в котором происходит прямой и обратный прогон всего массива данных, один прогон называется эпохой:
do
{
//...
} while (epochNumber < _config.MaxEpoches &&
currentError > _config.MinError &&
Math.Abs(currentError - lastError) > _config.MinErrorChange);
Заходим в цикл, и перед тем как пройтись по всем примерам, инициализируем вспомогательные переменные важные только для текущей эпохи. В случае, если batch не полный, то перемешиваем данные.
lastError = currentError;
DateTime dtStart = DateTime.Now;
//preparation for epoche
int[] trainingIndices = new int[data.Count];
for (int i = 0; i < data.Count; i++)
{
trainingIndices[i] = i;
}
if (_config.BatchSize > 0)
{
trainingIndices = Shuffle(trainingIndices);
}
Далее наступает процесс обработки данных, в зависимости от размера пачки, и изменение весов, это выглядит так:
//process data set
int currentIndex = 0;
do
{
#region initialize accumulated error for batch, for weights and biases
double[][][] nablaWeights = new double[network.Layers.Length][][];
double[][] nablaBiases = new double[network.Layers.Length][];
for (int i = 0; i < network.Layers.Length; i++)
{
nablaBiases[i] = new double[network.Layers[i].Neurons.Length];
nablaWeights[i] = new double[network.Layers[i].Neurons.Length][];
for (int j = 0; j < network.Layers[i].Neurons.Length; j++)
{
nablaBiases[i][j] = 0;
nablaWeights[i][j] = new double[network.Layers[i].Neurons[j].Weights.Length];
for (int k = 0; k < network.Layers[i].Neurons[j].Weights.Length; k++)
{
nablaWeights[i][j][k] = 0;
}
}
}
#endregion
//process one batch
for (int inBatchIndex = currentIndex; inBatchIndex < currentIndex + _config.BatchSize && inBatchIndex < data.Count; inBatchIndex++)
{
//forward pass
double[] realOutput = network.ComputeOutput(data[trainingIndices[inBatchIndex]].Input);
//backward pass, error propagation
//last layer
//.......................................ОБРАБОТКА ПОСЛЕДНЕГО СЛОЯ
//hidden layers
//.......................................ОБРАБОТКА СКРЫТЫХ СЛОЕВ
}
//update weights and bias
for (int layerIndex = 0; layerIndex < network.Layers.Length; layerIndex++)
{
for (int neuronIndex = 0; neuronIndex < network.Layers[layerIndex].Neurons.Length; neuronIndex++)
{
network.Layers[layerIndex].Neurons[neuronIndex].Bias -= nablaBiases[layerIndex][neuronIndex];
for (int weightIndex = 0; weightIndex < network.Layers[layerIndex].Neurons[neuronIndex].Weights.Length; weightIndex++)
{
network.Layers[layerIndex].Neurons[neuronIndex].Weights[weightIndex] -=
nablaWeights[layerIndex][neuronIndex][weightIndex];
}
}
}
currentIndex += _config.BatchSize;
} while (currentIndex < data.Count);
Рассмотрим обработку последнего слоя:
- инициализировали "наблЫ", там мы храним аккумулированное значение градиента для пачки входных данных (при онлайн обучении, там окажется просто градиент по одному примеру)
- пробегаемся по всем нейронам последнего слоя
- вычисляем dE/dz
- а затем вычисляем значение градиента для весов и смещения
//last layer
for (int j = 0; j < network.Layers[network.Layers.Length - 1].Neurons.Length; j++)
{
network.Layers[network.Layers.Length - 1].Neurons[j].dEdz =
_config.ErrorFunction.CalculatePartialDerivaitveByV2Index(data[inBatchIndex].Output,
realOutput, j) *
network.Layers[network.Layers.Length - 1].Neurons[j].ActivationFunction.
ComputeFirstDerivative(network.Layers[network.Layers.Length - 1].Neurons[j].LastNET);
nablaBiases[network.Layers.Length - 1][j] += _config.LearningRate *
network.Layers[network.Layers.Length - 1].Neurons[j].dEdz;
for (int i = 0; i < network.Layers[network.Layers.Length - 1].Neurons[j].Weights.Length; i++)
{
nablaWeights[network.Layers.Length - 1][j][i] +=
_config.LearningRate*(network.Layers[network.Layers.Length - 1].Neurons[j].dEdz*
(network.Layers.Length > 1 ?
network.Layers[network.Layers.Length - 1 - 1].Neurons[i].LastState :
data[inBatchIndex].Input[i])
+
_config.RegularizationFactor *
network.Layers[network.Layers.Length - 1].Neurons[j].Weights[i]
/ data.Count);
}
}
Очень похоже на последний слой выглядит обработка всех скрытых слоев сети:
- пробегаемся по всем скрытым слоям
- инициализировали "наблЫ", там мы храним аккумулированное значение градиента для пачки входных данных (при онлайн обучении, там окажется просто градиент по одному примеру)
- пробегаемся по всем нейронам последнего слоя
- вычисляем dE/dz, но уже для этого мы используем значения вычисленные, на слое старше текущего
- а затем вычисляем значение градиента для весов и смещения
//hidden layers
for (int hiddenLayerIndex = network.Layers.Length - 2; hiddenLayerIndex >= 0; hiddenLayerIndex--)
{
for (int j = 0; j < network.Layers[hiddenLayerIndex].Neurons.Length; j++)
{
network.Layers[hiddenLayerIndex].Neurons[j].dEdz = 0;
for (int k = 0; k < network.Layers[hiddenLayerIndex + 1].Neurons.Length; k++)
{
network.Layers[hiddenLayerIndex].Neurons[j].dEdz +=
network.Layers[hiddenLayerIndex + 1].Neurons[k].Weights[j]*
network.Layers[hiddenLayerIndex + 1].Neurons[k].dEdz;
}
network.Layers[hiddenLayerIndex].Neurons[j].dEdz *=
network.Layers[hiddenLayerIndex].Neurons[j].ActivationFunction.
ComputeFirstDerivative(
network.Layers[hiddenLayerIndex].Neurons[j].LastNET
);
nablaBiases[hiddenLayerIndex][j] += _config.LearningRate*
network.Layers[hiddenLayerIndex].Neurons[j].dEdz;
for (int i = 0; i < network.Layers[hiddenLayerIndex].Neurons[j].Weights.Length; i++)
{
nablaWeights[hiddenLayerIndex][j][i] += _config.LearningRate * (
network.Layers[hiddenLayerIndex].Neurons[j].dEdz *
(hiddenLayerIndex > 0 ? network.Layers[hiddenLayerIndex - 1].Neurons[i].LastState : data[inBatchIndex].Input[i])
+
_config.RegularizationFactor * network.Layers[hiddenLayerIndex].Neurons[j].Weights[i] / data.Count
);
}
}
}
Тут основной код заканчивается, и остается сделать пару штрихов в виде вычисления средней ошибки сети на массиве данных (с учетом регуляризации), и логирование:
//recalculating error on all data
//real error
currentError = 0;
for (int i = 0; i < data.Count; i++)
{
double[] realOutput = network.ComputeOutput(data[i].Input);
currentError += _config.ErrorFunction.Calculate(data[i].Output, realOutput);
}
currentError *= 1d/data.Count;
//regularization term
if (Math.Abs(_config.RegularizationFactor - 0d) > Double.Epsilon)
{
double reg = 0;
for (int layerIndex = 0; layerIndex < network.Layers.Length; layerIndex++)
{
for (int neuronIndex = 0; neuronIndex < network.Layers[layerIndex].Neurons.Length; neuronIndex++)
{
for (int weightIndex = 0; weightIndex < network.Layers[layerIndex].Neurons[neuronIndex].Weights.Length; weightIndex++)
{
reg += network.Layers[layerIndex].Neurons[neuronIndex].Weights[weightIndex] *
network.Layers[layerIndex].Neurons[neuronIndex].Weights[weightIndex];
}
}
}
currentError += _config.RegularizationFactor * reg / (2 * data.Count);
}
epochNumber++;
Logger.Instance.Log("Eposh #" + epochNumber.ToString() +
" finished; current error is " + currentError.ToString() +
"; it takes: " +
(DateTime.Now - dtStart).Duration().ToString());
Этот блок находится прямиком перед выходом из основного цикла, продублирую код для наглядности:
} while (epochNumber < _config.MaxEpoches &&
currentError > _config.MinError &&
Math.Abs(currentError - lastError) > _config.MinErrorChange);
Итог
Собственно все. От себя хочу вот что добавить, данный текст я привел примерно в том виде, в каком я его хотел бы видеть, когда первый раз читал про алгоритм обратного распространения. Обычно в литературе авторы заранее говорят что будет использоваться такая то функция ошибки и активации нейрона. И в процессе вывода формул с частными производными они вставляют эти производные в вывод, и в итоге получается примерно так же, как, например, в википедии, где рассматривается алгоритм для минимизации квадрата Евклидова расстояния.
Вот формула для последнего слоя:
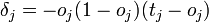
и для остальных:

Конечно, если вы очень умны, то вам не составит труда понять что тут от какого дифференциала, но я смог понять это только когда взял в руки ручку и бумагу, и написал весь вывод. Потом то же самое сделал для другой функции ошибки и только потом обобщил и осознал -)
Перевод
Ссылка на автора
Алгоритм обратного распространения — это классическая искусственная нейронная сеть с прямой связью.
Эта техника до сих пор используется для тренировки большого глубокое обучение сетей.
В этом руководстве вы узнаете, как реализовать алгоритм обратного распространения с нуля с помощью Python.
После завершения этого урока вы узнаете:
- Как переадресовать входные данные для вычисления выходных данных.
- Как распространять ошибки и обучать сеть.
- Как применить алгоритм обратного распространения к реальной задаче прогнозного моделирования.
Давайте начнем.
- Обновление ноябрь 2016: Исправлена ошибка в функции activ (). Спасибо Алекс!
- Обновление январь / 2017: Изменено вычисление fold_size в cross_validation_split (), чтобы оно всегда было целым числом. Исправляет проблемы с Python 3.
- Обновление январь / 2017: Обновлена небольшая ошибка в update_weights (). Спасибо, Томаш!
- Обновление апрель / 2018: Добавлена прямая ссылка на набор данных CSV.
- Обновление Авг / 2018: Протестировано и обновлено для работы с Python 3.6.
Описание
В этом разделе дается краткое введение в алгоритм обратного распространения и набор данных семян пшеницы, которые мы будем использовать в этом руководстве.
Алгоритм обратного распространения
Алгоритм обратного распространения — это контролируемый метод обучения для многослойных сетей прямой связи из области искусственных нейронных сетей.
Прямые нейронные сети вдохновлены обработкой информации одной или нескольких нейронных клеток, называемых нейронами. Нейрон принимает входные сигналы через свои дендриты, которые передают электрический сигнал в тело клетки. Аксон передает сигнал в синапсы, которые являются связями аксона клетки с дендритами другой клетки.
Принцип обратного распространения заключается в моделировании заданной функции путем изменения внутренних весовых коэффициентов входных сигналов для получения ожидаемого выходного сигнала. Система обучается с использованием метода контролируемого обучения, где ошибка между выходными данными системы и известным ожидаемым выходным значением представляется системе и используется для изменения ее внутреннего состояния.
Технически алгоритм обратного распространения — это метод обучения весов в многослойной нейронной сети с прямой связью. Как таковой, он требует, чтобы сетевая структура была определена из одного или нескольких уровней, где один уровень полностью связан со следующим уровнем. Стандартная сетевая структура — это один входной слой, один скрытый слой и один выходной слой.
Обратное распространение можно использовать как для задач классификации, так и для задач регрессии, но в этом руководстве мы сосредоточимся на классификации.
В задачах классификации наилучшие результаты достигаются, когда сеть имеет один нейрон в выходном слое для каждого значения класса. Например, проблема 2-классовой или двоичной классификации со значениями классов A и B. Эти ожидаемые результаты должны быть преобразованы в двоичные векторы с одним столбцом для каждого значения класса. Например, [1, 0] и [0, 1] для A и B соответственно. Это называется горячим кодированием.
Набор данных семян пшеницы
Набор данных семян включает в себя прогнозирование видов с учетом измерений семян из разных сортов пшеницы.
Есть 201 записей и 7 числовых входных переменных. Это проблема классификации с 3 выходными классами. Шкала для каждого числового входного значения варьируется, поэтому может потребоваться некоторая нормализация данных для использования с алгоритмами, которые взвешивают входные данные, такие как алгоритм обратного распространения.
Ниже приведен образец первых 5 строк набора данных.
15.26,14.84,0.871,5.763,3.312,2.221,5.22,1
14.88,14.57,0.8811,5.554,3.333,1.018,4.956,1
14.29,14.09,0.905,5.291,3.337,2.699,4.825,1
13.84,13.94,0.8955,5.324,3.379,2.259,4.805,1
16.14,14.99,0.9034,5.658,3.562,1.355,5.175,1При использовании алгоритма нулевого правила, который прогнозирует наиболее распространенное значение класса, базовая точность задачи составляет 28,095%.
Вы можете узнать больше и загрузить набор данных семян из UCI Хранилище Машинного Обучения,
Загрузите набор данных seed и поместите его в текущий рабочий каталог с именем файлаseeds_dataset.csv,
Набор данных представлен в формате табуляции, поэтому его необходимо преобразовать в CSV с помощью текстового редактора или программы для работы с электронными таблицами.
Обновите, загрузите набор данных в формате CSV напрямую:
- Скачать набор данных семян пшеницы
Руководство
Этот урок разбит на 6 частей:
- Инициализировать сеть.
- Вперед Распространять.
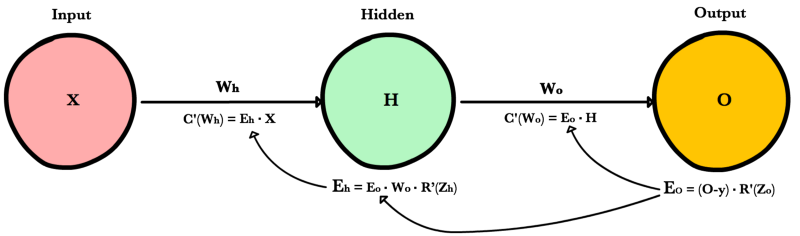
- Ошибка обратного распространения.
- Сеть поездов.
- Предсказать.
- Пример набора данных семян.
Эти шаги обеспечат основу, необходимую для реализации алгоритма обратного распространения с нуля и применения его к собственным задачам прогнозного моделирования.
1. Инициализировать сеть
Давайте начнем с чего-то простого, создания новой сети, готовой к обучению.
Каждый нейрон имеет набор весов, которые необходимо поддерживать. Один вес для каждого входного соединения и дополнительный вес для смещения. Нам нужно будет хранить дополнительные свойства для нейрона во время обучения, поэтому мы будем использовать словарь для представления каждого нейрона и сохранять свойства по именам, таким как ‘веса‘Для весов.
Сеть организована в слои. Входной слой на самом деле просто строка из нашего набора обучающих данных Первый настоящий слой — это скрытый слой. Затем следует выходной слой, который имеет один нейрон для каждого значения класса.
Мы организуем слои как массивы словарей и будем рассматривать всю сеть как массив слоев.
Хорошей практикой является инициализация весов сети небольшими случайными числами. В этом случае мы будем использовать случайные числа в диапазоне от 0 до 1.
Ниже приведена функция с именемinitialize_network ()это создает новую нейронную сеть, готовую к обучению. Он принимает три параметра: количество входов, количество нейронов в скрытом слое и количество выходов.
Вы можете видеть, что для скрытого слоя мы создаемn_hiddenнейроны и каждый нейрон в скрытом слое имеетn_inputs + 1веса, один для каждого входного столбца в наборе данных и дополнительный для смещения.
Вы также можете видеть, что выходной слой, который подключается к скрытому слою, имеетn_outputsнейроны, каждый сn_hidden + 1веса. Это означает, что каждый нейрон в выходном слое соединяется (имеет вес) с каждым нейроном в скрытом слое.
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return networkДавайте проверим эту функцию. Ниже приведен полный пример, который создает небольшую сеть.
from random import seed
from random import random
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
seed(1)
network = initialize_network(2, 1, 2)
for layer in network:
print(layer)Запустив пример, вы можете увидеть, что код распечатывает каждый слой по одному. Вы можете видеть, что скрытый слой имеет один нейрон с 2 входными весами плюс смещение. Выходной слой имеет 2 нейрона, каждый с 1 весом плюс смещение.
[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}]
[{'weights': [0.2550690257394217, 0.49543508709194095]}, {'weights': [0.4494910647887381, 0.651592972722763]}]Теперь, когда мы знаем, как создать и инициализировать сеть, давайте посмотрим, как мы можем использовать ее для вычисления результата.
2. Вперед Распространение
Мы можем вычислить выход из нейронной сети, распространяя входной сигнал через каждый уровень, пока выходной уровень не выведет свои значения.
Мы называем это продвижением вперед.
Это метод, который нам понадобится для генерации прогнозов во время обучения, который необходимо будет исправить, и это метод, который нам понадобится после обучения сети для прогнозирования новых данных.
Мы можем разбить распространение вперед на три части:
- Активация нейронов.
- Передача нейронов.
- Вперед Распространение.
2.1. Активация нейронов
Первым шагом является вычисление активации одного нейрона с учетом входных данных.
Входными данными может быть строка из нашего обучающего набора данных, как в случае со скрытым слоем. Это также могут быть выходы от каждого нейрона в скрытом слое, в случае выходного слоя.
Активация нейрона рассчитывается как взвешенная сумма входов. Очень похоже на линейную регрессию.
activation = sum(weight_i * input_i) + biasкудавесвес сети,входявляется входом,яэто индекс веса или ввода исмещениеэто специальный вес, который не имеет входных данных для умножения (или вы можете думать, что входные данные всегда равны 1,0).
Ниже приведена реализация этого в функции с именемактивировать (), Вы можете видеть, что функция предполагает, что смещение является последним весом в списке весов. Это помогает здесь и позже сделать код легче для чтения.
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activationТеперь давайте посмотрим, как использовать активацию нейронов.
2.2. Нейрон Трансфер
Как только нейрон активирован, нам нужно перенести активацию, чтобы увидеть, что на самом деле представляет собой выход нейрона.
Различные передаточные функции могут быть использованы. Традиционно использовать функция активации сигмовидной кишки, но вы также можете использовать танх (тангенс гиперболический) функция для передачи выходов. Совсем недавно передаточная функция выпрямителя был популярен в крупных сетях глубокого обучения.
Функция активации сигмоида выглядит как S-образная форма, ее также называют логистической функцией. Он может принимать любое входное значение и производить число от 0 до 1 на S-кривой. Это также функция, из которой мы можем легко рассчитать производную (наклон), которая понадобится нам позже при ошибке обратного распространения.
Мы можем передать функцию активации с помощью функции сигмоида следующим образом:
output = 1 / (1 + e^(-activation))кудаеявляется основанием натуральных логарифмов (Номер Эйлера).
Ниже приведена функция с именемперечислить()который реализует сигмовидное уравнение.
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))Теперь, когда у нас есть кусочки, давайте посмотрим, как они используются.
2,3. Прямое распространение
Вперед, распространение входных данных просто.
Мы работаем через каждый слой нашей сети, вычисляя выходы для каждого нейрона. Все выходы из одного слоя становятся входами для нейронов на следующем слое.
Ниже приведена функция с именемforward_propagate ()это реализует прямое распространение для ряда данных из нашего набора данных с нашей нейронной сетью.
Вы можете видеть, что выходное значение нейрона хранится в нейроне с именем ‘выход«. Вы также можете увидеть, что мы собираем выходные данные для слоя в массиве с именемnew_inputsэто становится массивомвходныеи используется в качестве входных данных для следующего слоя.
Функция возвращает выходные данные из последнего слоя, также называемого выходным слоем.
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputsДавайте соединим все эти части и протестируем прямое распространение нашей сети.
Мы определяем нашу сеть, встроенную одним скрытым нейроном, который ожидает 2 входных значения, и выходной слой с двумя нейронами.
from math import exp
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# test forward propagation
network = [[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}],
[{'weights': [0.2550690257394217, 0.49543508709194095]}, {'weights': [0.4494910647887381, 0.651592972722763]}]]
row = [1, 0, None]
output = forward_propagate(network, row)
print(output)Выполнение примера распространяет входной шаблон [1, 0] и выдает выходное значение, которое печатается. Поскольку выходной слой имеет два нейрона, мы получаем список из двух чисел в качестве вывода.
Фактические выходные значения на данный момент просто бессмыслица, но затем мы начнем изучать, как сделать веса в нейронах более полезными.
[0.6629970129852887, 0.7253160725279748]3. Ошибка обратного распространения
Алгоритм обратного распространения назван по способу обучения весов.
Ошибка рассчитывается между ожидаемыми выходами и выходами, передаваемыми по сети. Эти ошибки затем распространяются в обратном направлении через сеть от выходного уровня к скрытому слою, назначая вину за ошибку и обновляя веса по мере их появления.
Математика для ошибки обратного распространения коренится в исчислении, но мы останемся на высоком уровне в этом разделе и сосредоточимся на том, что рассчитывается и как, а не почему расчеты принимают эту конкретную форму.
Эта часть разбита на две части.
- Передача Производная.
- Ошибка обратного распространения.
3.1. Производная передача
Учитывая выходное значение от нейрона, нам нужно вычислить его наклон.
Мы используем передаточную функцию сигмоида, производную которой можно рассчитать следующим образом:
derivative = output * (1.0 - output)Ниже приведена функция с именемtransfer_derivative ()который реализует это уравнение.
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)Теперь посмотрим, как это можно использовать.
3.2. Ошибка обратного распространения
Первым шагом является вычисление ошибки для каждого выходного нейрона, это даст нам наш сигнал ошибки (вход) для распространения в обратном направлении по сети.
Ошибка для данного нейрона может быть рассчитана следующим образом:
error = (expected - output) * transfer_derivative(output)кудаожидаемыйявляется ожидаемым выходным значением для нейрона,выходэто выходное значение для нейрона иtransfer_derivative ()вычисляет наклон выходного значения нейрона, как показано выше.
Этот расчет ошибки используется для нейронов в выходном слое. Ожидаемое значение — это само значение класса. В скрытом слое все немного сложнее.
Сигнал ошибки для нейрона в скрытом слое рассчитывается как взвешенная ошибка каждого нейрона в выходном слое. Подумайте об ошибке, связанной с перемещением весов выходного слоя к нейронам в скрытом слое.
Обратно распространяющийся сигнал ошибки накапливается и затем используется для определения ошибки для нейрона в скрытом слое следующим образом:
error = (weight_k * error_j) * transfer_derivative(output)кудаerror_jэто сигнал ошибки отJй нейрон в выходном слое,weight_kэто вес, который соединяетКТретий нейрон к текущему нейрону и выход — это выход для текущего нейрона.
Ниже приведена функция с именемbackward_propagate_error ()который реализует эту процедуру.
Вы можете видеть, что сигнал ошибки, рассчитанный для каждого нейрона, хранится с именем «delta». Вы можете видеть, что слои сети перебираются в обратном порядке, начиная с выхода и работая в обратном направлении. Это гарантирует, что нейроны в выходном слое сначала рассчитывают значения «дельта», которые нейроны в скрытом слое могут использовать в последующей итерации. Я выбрал имя «дельта», чтобы отразить изменение, которое ошибка вносит в нейрон (например, дельта веса).
Вы можете видеть, что сигнал ошибки для нейронов в скрытом слое накапливается от нейронов в выходном слое, где скрыт номер нейронаJтакже индекс веса нейрона в выходном слоенейрон [грузики ‘] [J],
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])Давайте соберем все части вместе и посмотрим, как это работает.
Мы определяем фиксированную нейронную сеть с выходными значениями и распространяем ожидаемый выходной шаблон. Полный пример приведен ниже.
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# test backpropagation of error
network = [[{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}],
[{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095]}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763]}]]
expected = [0, 1]
backward_propagate_error(network, expected)
for layer in network:
print(layer)При выполнении примера печатается сеть после обратного распространения ошибки. Вы можете видеть, что значения ошибок рассчитываются и сохраняются в нейронах для выходного слоя и скрытого слоя.
[{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614], 'delta': -0.0005348048046610517}]
[{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095], 'delta': -0.14619064683582808}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763], 'delta': 0.0771723774346327}]Теперь давайте использовать обратное распространение ошибки для обучения сети.
4. Сеть поездов
Сеть обучается с использованием стохастического градиентного спуска.
Это включает в себя несколько итераций представления обучающего набора данных в сеть и для каждой строки данных, передавая входные данные, распространяя ошибку в обратном направлении и обновляя веса сети.
Эта часть разбита на две части:
- Обновление весов.
- Сеть поездов.
4.1. Обновление весов
Как только ошибки рассчитаны для каждого нейрона в сети с помощью метода обратного распространения, описанного выше, их можно использовать для обновления весов.
Веса сети обновляются следующим образом:
weight = weight + learning_rate * error * inputкудавесзаданный вес,learning_rateэто параметр, который вы должны указать,ошибкаошибка, рассчитанная по процедуре обратного распространения для нейрона ивходэто входное значение, вызвавшее ошибку
Та же процедура может использоваться для обновления веса смещения, за исключением того, что нет входного термина или входное значение является фиксированным значением 1,0.
Скорость обучения определяет, насколько изменить вес, чтобы исправить ошибку. Например, значение 0,1 обновит вес на 10% от суммы, которую он мог бы обновить. Предпочтительными являются малые скорости обучения, которые вызывают более медленное обучение в течение большого количества итераций обучения. Это увеличивает вероятность того, что сеть найдет хороший набор весов на всех уровнях, а не самый быстрый набор весов, которые минимизируют ошибку (так называемая преждевременная сходимость).
Ниже приведена функция с именемupdate_weights ()который обновляет весовые коэффициенты для сети с учетом входной строки данных, скорости обучения и предполагает, что прямое и обратное распространение уже выполнено.
Помните, что вход для выходного слоя представляет собой набор выходов из скрытого слоя.
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] += l_rate * neuron['delta']Теперь мы знаем, как обновить вес сети, давайте посмотрим, как мы можем сделать это многократно.
4.2. Сеть поездов
Как уже упоминалось, сеть обновляется с использованием стохастического градиентного спуска.
Это включает в себя первый цикл для фиксированного числа эпох и в каждой эпохе обновление сети для каждой строки в наборе обучающих данных.
Поскольку обновления производятся для каждого шаблона обучения, этот тип обучения называется онлайн-обучением. Если ошибки были накоплены за период до обновления весов, это называется периодическим обучением или пакетным градиентным спуском.
Ниже приведена функция, которая реализует обучение уже инициализированной нейронной сети с заданным набором обучающих данных, скоростью обучения, фиксированным числом эпох и ожидаемым количеством выходных значений.
Ожидаемое количество выходных значений используется для преобразования значений класса в обучающих данных в одно горячее кодирование. Это двоичный вектор с одним столбцом для каждого значения класса, чтобы соответствовать выходу сети. Это необходимо для расчета ошибки для выходного слоя.
Вы также можете видеть, что ошибка квадрата суммы между ожидаемым выходом и выходом сети накапливается каждую эпоху и печатается. Это полезно для отслеживания того, насколько сеть изучает и совершенствует каждую эпоху.
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
sum_error = 0
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))])
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))Теперь у нас есть все для обучения сети. Мы можем собрать пример, который включает в себя все, что мы видели до сих пор, включая инициализацию сети и обучение сети на небольшом наборе данных.
Ниже приведен небольшой надуманный набор данных, который мы можем использовать для тестирования нашей нейронной сети.
X1 X2 Y
2.7810836 2.550537003 0
1.465489372 2.362125076 0
3.396561688 4.400293529 0
1.38807019 1.850220317 0
3.06407232 3.005305973 0
7.627531214 2.759262235 1
5.332441248 2.088626775 1
6.922596716 1.77106367 1
8.675418651 -0.242068655 1
7.673756466 3.508563011 1Ниже приведен полный пример. Мы будем использовать 2 нейрона в скрытом слое. Это проблема двоичной классификации (2 класса), поэтому в выходном слое будет два нейрона. Сеть будет обучаться в течение 20 эпох со скоростью обучения 0,5, что является высоким показателем, потому что мы готовим так мало итераций.
from math import exp
from random import seed
from random import random
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] += l_rate * neuron['delta']
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
sum_error = 0
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))])
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))
# Test training backprop algorithm
seed(1)
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
n_inputs = len(dataset[0]) - 1
n_outputs = len(set([row[-1] for row in dataset]))
network = initialize_network(n_inputs, 2, n_outputs)
train_network(network, dataset, 0.5, 20, n_outputs)
for layer in network:
print(layer)При запуске примера сначала выводится ошибка квадрата суммы в каждую эпоху обучения. Мы можем видеть тенденцию уменьшения этой ошибки с каждой эпохой.
После обучения распечатывается сеть с отображением изученных весов. Также все еще в сети находятся выходные и дельта-значения, которые можно игнорировать. Мы могли бы обновить нашу функцию обучения, чтобы удалить эти данные, если мы хотим.
>epoch=0, lrate=0.500, error=6.350
>epoch=1, lrate=0.500, error=5.531
>epoch=2, lrate=0.500, error=5.221
>epoch=3, lrate=0.500, error=4.951
>epoch=4, lrate=0.500, error=4.519
>epoch=5, lrate=0.500, error=4.173
>epoch=6, lrate=0.500, error=3.835
>epoch=7, lrate=0.500, error=3.506
>epoch=8, lrate=0.500, error=3.192
>epoch=9, lrate=0.500, error=2.898
>epoch=10, lrate=0.500, error=2.626
>epoch=11, lrate=0.500, error=2.377
>epoch=12, lrate=0.500, error=2.153
>epoch=13, lrate=0.500, error=1.953
>epoch=14, lrate=0.500, error=1.774
>epoch=15, lrate=0.500, error=1.614
>epoch=16, lrate=0.500, error=1.472
>epoch=17, lrate=0.500, error=1.346
>epoch=18, lrate=0.500, error=1.233
>epoch=19, lrate=0.500, error=1.132
[{'weights': [-1.4688375095432327, 1.850887325439514, 1.0858178629550297], 'output': 0.029980305604426185, 'delta': -0.0059546604162323625}, {'weights': [0.37711098142462157, -0.0625909894552989, 0.2765123702642716], 'output': 0.9456229000211323, 'delta': 0.0026279652850863837}]
[{'weights': [2.515394649397849, -0.3391927502445985, -0.9671565426390275], 'output': 0.23648794202357587, 'delta': -0.04270059278364587}, {'weights': [-2.5584149848484263, 1.0036422106209202, 0.42383086467582715], 'output': 0.7790535202438367, 'delta': 0.03803132596437354}]Как только сеть обучена, мы должны использовать ее для прогнозирования.
5. Предсказать
Делать прогнозы с помощью обученной нейронной сети достаточно просто.
Мы уже видели, как распространять входной шаблон для получения выходного сигнала. Это все, что нам нужно сделать, чтобы сделать прогноз. Мы можем непосредственно использовать выходные значения как вероятность того, что шаблон принадлежит каждому выходному классу.
Возможно, было бы более полезно превратить этот вывод в четкое предсказание класса. Мы можем сделать это, выбрав значение класса с большей вероятностью. Это также называется функция arg max,
Ниже приведена функция с именемпредсказать, ()который реализует эту процедуру. Возвращает индекс в выходных данных сети, который имеет наибольшую вероятность. Предполагается, что значения класса были преобразованы в целые числа, начиная с 0.
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))Мы можем соединить это с нашим кодом выше для входного распространения и с нашим небольшим надуманным набором данных, чтобы проверить предсказания с уже обученной сетью. Пример жестко кодирует сеть, обученную на предыдущем шаге.
Полный пример приведен ниже.
from math import exp
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))
# Test making predictions with the network
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
network = [[{'weights': [-1.482313569067226, 1.8308790073202204, 1.078381922048799]}, {'weights': [0.23244990332399884, 0.3621998343835864, 0.40289821191094327]}],
[{'weights': [2.5001872433501404, 0.7887233511355132, -1.1026649757805829]}, {'weights': [-2.429350576245497, 0.8357651039198697, 1.0699217181280656]}]]
for row in dataset:
prediction = predict(network, row)
print('Expected=%d, Got=%d' % (row[-1], prediction))При выполнении примера выводится ожидаемый результат для каждой записи в наборе обучающих данных, за которым следует четкое предсказание, сделанное сетью.
Это показывает, что сеть достигает 100% точности в этом небольшом наборе данных.
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1Теперь мы готовы применить наш алгоритм обратного распространения к реальному набору данных.
6. Набор данных семян пшеницы
В этом разделе применяется алгоритм обратного распространения к набору данных семян пшеницы.
Первым шагом является загрузка набора данных и преобразование загруженных данных в числа, которые мы можем использовать в нашей нейронной сети. Для этого мы будем использовать вспомогательную функциюload_csv ()загрузить файл,str_column_to_float ()преобразовать строковые числа в числа с плавающей запятой иstr_column_to_int ()преобразовать столбец класса в целочисленные значения.
Входные значения различаются по масштабу и должны быть нормализованы в диапазоне от 0 до 1. Обычно рекомендуется нормализовать входные значения в диапазоне выбранной передаточной функции, в данном случае сигмоидальной функции, которая выводит значения в диапазоне от 0 до 1. .dataset_minmax ()а такжеnormalize_dataset ()вспомогательные функции были использованы для нормализации входных значений.
Мы оценим алгоритм с использованием k-кратной перекрестной проверки с 5-кратным увеличением. Это означает, что 201/5 = 40,2 или 40 записей будут в каждом сгибе. Мы будем использовать вспомогательные функцииevaluate_algorithm ()оценить алгоритм с перекрестной проверкой иaccuracy_metric ()рассчитать точность прогнозов.
Новая функция с именемback_propagation ()был разработан для управления приложением алгоритма Backpropagation, сначала инициализируя сеть, обучая ее на наборе обучающих данных, а затем используя обученную сеть, чтобы делать прогнозы на тестовом наборе данных.
Полный пример приведен ниже.
# Backprop on the Seeds Dataset
from random import seed
from random import randrange
from random import random
from csv import reader
from math import exp
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, 'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Find the min and max values for each column
def dataset_minmax(dataset):
minmax = list()
stats = [[min(column), max(column)] for column in zip(*dataset)]
return stats
# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
for row in dataset:
for i in range(len(row)-1):
row[i] = (row[i] - minmax[i][0]) / (minmax[i][1] - minmax[i][0])
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = int(len(dataset) / n_folds)
for i in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# Calculate accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set, [])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[-1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] += l_rate * neuron['delta']
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))
# Backpropagation Algorithm With Stochastic Gradient Descent
def back_propagation(train, test, l_rate, n_epoch, n_hidden):
n_inputs = len(train[0]) - 1
n_outputs = len(set([row[-1] for row in train]))
network = initialize_network(n_inputs, n_hidden, n_outputs)
train_network(network, train, l_rate, n_epoch, n_outputs)
predictions = list()
for row in test:
prediction = predict(network, row)
predictions.append(prediction)
return(predictions)
# Test Backprop on Seeds dataset
seed(1)
# load and prepare data
filename = 'seeds_dataset.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])-1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])-1)
# normalize input variables
minmax = dataset_minmax(dataset)
normalize_dataset(dataset, minmax)
# evaluate algorithm
n_folds = 5
l_rate = 0.3
n_epoch = 500
n_hidden = 5
scores = evaluate_algorithm(dataset, back_propagation, n_folds, l_rate, n_epoch, n_hidden)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))Была построена сеть с 5 нейронами в скрытом слое и 3 нейронами в выходном слое. Сеть была подготовлена для 500 эпох с темпом обучения 0,3. Эти параметры были найдены с небольшой пробой и ошибкой, но вы можете сделать это намного лучше.
При выполнении примера выводится средняя точность классификации для каждого сгиба, а также средняя производительность по всем сгибам.
Вы можете видеть, что обратное распространение и выбранная конфигурация достигли средней точности классификации около 93%, что значительно лучше, чем алгоритм нулевого правила, который немного лучше, чем точность 28%.
Scores: [92.85714285714286, 92.85714285714286, 97.61904761904762, 92.85714285714286, 90.47619047619048]
Mean Accuracy: 93.333%расширения
В этом разделе перечислены расширения к учебнику, которые вы можете изучить.
- Параметры алгоритма настройки, Попробуйте большие или меньшие сети, обученные дольше или короче. Посмотрите, сможете ли вы улучшить производительность набора данных seed.
- Дополнительные методы, Поэкспериментируйте с различными методами инициализации веса (такими как небольшие случайные числа) и различными передаточными функциями (такими как tanh).
- Больше слоев, Добавьте поддержку для большего количества скрытых слоев, обученных так же, как один скрытый слой, используемый в этом руководстве.
- регрессия, Измените сеть так, чтобы в выходном слое был только один нейрон, и чтобы было предсказано реальное значение. Выберите регрессионный набор данных для практики. Линейная передаточная функция может использоваться для нейронов в выходном слое, или выходные значения выбранного набора данных могут быть масштабированы до значений между 0 и 1.
- Пакетный градиентный спуск, Измените процедуру обучения с онлайн на пакетный градиентный спуск и обновляйте веса только в конце каждой эпохи.
Вы пробовали какие-либо из этих расширений?
Поделитесь своим опытом в комментариях ниже.
Обзор
В этом руководстве вы узнали, как реализовать алгоритм обратного распространения с нуля.
В частности, вы узнали:
- Как переслать распространение входа для расчета выхода сети.
- Как обратно распространять ошибки и обновлять вес сети.
- Как применить алгоритм обратного распространения к реальному набору данных.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
На предыдущих
занятиях мы с вами рассматривали НС с выбранными весами, либо устанавливали их,
исходя из определенных математических соображений. Это можно сделать, когда
сеть относительно небольшая. Но при увеличении числа нейронов и связей, ручной
подбор становится попросту невозможным и возникает задача нахождения весовых
коэффициентов связей НС. Этот процесс и называют обучением нейронной сети.
Один из
распространенных подходов к обучению заключается в последовательном
предъявлении НС векторов наблюдений и последующей корректировки весовых
коэффициентов так, чтобы выходное значение совпадало с требуемым:
Это называется обучение
с учителем, так как для каждого вектора мы знаем нужный ответ и именно его
требуем от нашей НС.
Теперь, главный
вопрос: как построить алгоритм, который бы наилучшим образом находил весовые
коэффициенты. Наилучший – это значит, максимально быстро и с максимально
близкими выходными значениями для требуемых откликов. В общем случае эта задача
не решена. Нет универсального алгоритма обучения. Поэтому, лучшее, что мы можем
сделать – это выбрать тот алгоритм, который хорошо себя зарекомендовал в
прошлом. Основной «рабочей лошадкой» здесь является алгоритм back propagation (обратного
распространения ошибки), который, в свою очередь, базируется на алгоритме градиентного
спуска.
Сначала, я думал
рассказать о нем со всеми математическими выкладками, но потом решил этого не
делать, а просто показать принцип работы и рассмотреть реализацию конкретного
примера на Python.
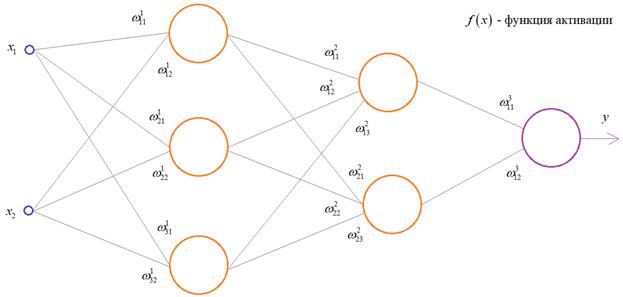
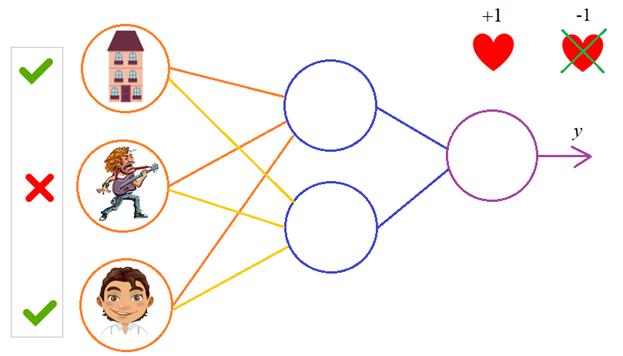
Чтобы все лучше
понять, предположим, что у нас имеется вот такая полносвязная НС прямого
распространения с весами связей, выбранными произвольным образом в диапазоне от
[-0.5; 0,5]. Здесь верхний индекс показывает принадлежность к тому или иному слою
сети. Также, каждый нейрон имеет некоторую активационную функцию :
На первом шаге
делается прямой проход по сети. Мы пропускаем вектор наблюдения через
эту сеть, и запоминаем все выходные значения нейронов скрытых слоев:
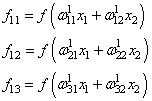
и последнее
выходное значение y:
Далее, мы знаем
требуемый отклик d для текущего вектора ,
значит для него можно вычислить ошибку работы НС. Она будет равна:
На данный момент
все должно быть понятно. Мы на первом занятии подробно рассматривали процесс
распространения сигнала по НС. И вы это уже хорошо себе представляете. А вот
дальше начинается самое главное – корректировка весов. Для этого делается
обратный проход по НС: от последнего слоя – к первому.
Итак, у нас есть
ошибка e и некая функция
активации нейронов .
Первое, что нам нужно – это вычислить локальный градиент для выходного нейрона.
Это делается по формуле:
Этот момент
требует пояснения. Смотрите, ранее используемая пороговая функция:
нам уже не
подходит, т.к. она не дифференцируема на всем диапазоне значений x. Вместо этого
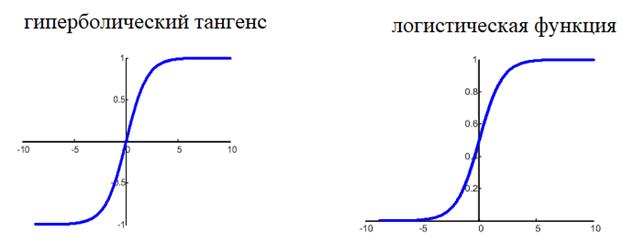
для сетей с небольшим числом слоев, часто применяют или гиперболический
тангенс:
или логистическую
функцию:
Фактически, они
отличаются только тем, что первая дает выходной интервал [-1; 1], а вторая – [0;
1]. И мы уже берем ту, которая нас больше устраивает в данной конкретной
ситуации. Например, выберем логистическую функцию.
Ее производная
функции по аргументу x дает очень простое выражение:
Именно его мы и
запишем в нашу формулу вычисления локального градиента:
Но, так как
то локальный
градиент последнего нейрона, равен:
Отлично, это
сделали. Теперь у нас есть все, чтобы выполнить коррекцию весов. Начнем со
связи ,
формула будет такой:
Для второй связи
все то же самое, только входной сигнал берется от второго нейрона:
Здесь у вас
может возникнуть вопрос: что такое параметр λ и где его брать? Он
подбирается самостоятельно, вручную самим разработчиком. В самом простом случае
можно попробовать следующие значения:
(Мы подробно о
нем говорили на занятии по алгоритму градиентного спуска):
Итак, мы с вами
скорректировали связи последнего слоя. Если вам все это понятно, значит, вы уже
практически поняли весь алгоритм обучения, потому что дальше действуем подобным
образом. Переходим к нейрону следующего с конца слоя и для его входящих связей
повторим ту же саму процедуру. Но для этого, нужно знать значение его
локального градиента. Определяется он просто. Локальный градиент последнего
нейрона взвешивается весами входящих в него связей. Полученные значения на
каждом нейроне умножаются на производную функции активации, взятую в точках
входной суммы:
А дальше
действуем по такой же самой схеме, корректируем входные связи по той же
формуле:
И для второго
нейрона:
Осталось
скорректировать веса первого слоя. Снова вычисляем локальные градиенты для
нейронов первого слоя, но так как каждый из них имеет два выхода, то сначала
вычисляем сумму от каждого выхода:
А затем,
значения локальных градиентов на нейронах первого скрытого слоя:
Ну и осталось
выполнить коррекцию весов первого слоя все по той же формуле:
В результате, мы
выполнили одну итерацию алгоритма обучения НС. На следующей итерации мы должны
взять другой входной вектор из нашего обучающего множества. Лучше всего это
сделать случайным образом, чтобы не формировались возможные ложные
закономерности в последовательности данных при обучении НС. Повторяя много раз
этот процесс, весовые связи будут все точнее описывать обучающую выборку.
Отлично, процесс
обучения в целом мы рассмотрели. Но какой критерий качества минимизировался
алгоритмом градиентного спуска? В действительности, мы стремились получить
минимум суммы квадратов ошибок для обучающей выборки:
То есть, с
помощью алгоритма градиентного спуска веса корректируются так, чтобы
минимизировать этот критерий качества работы НС. Позже мы еще увидим, что на
практике используется не только такой, но и другие критерии.
Вот так, в целом
выглядит идея работы алгоритма обучения по методу обратного распространения
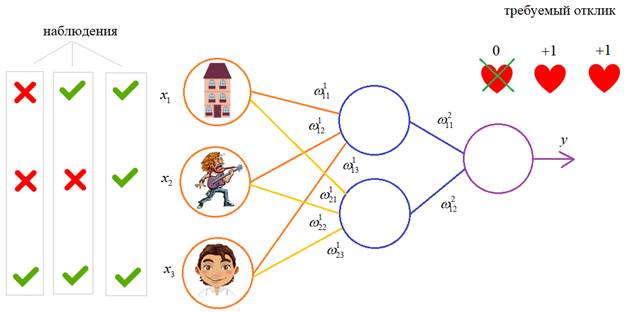
ошибки. Давайте теперь в качестве примера обучим следующую НС:
В качестве
обучающего множества выберем все возможные варианты (здесь 1 – это да, -1 – это
нет):
|
Вектор |
Требуемый |
|
[-1, -1, -1] |
-1 |
|
[-1, -1, |
1 |
|
[-1, 1, -1] |
-1 |
|
[-1, 1, 1] |
1 |
|
[1, -1, -1] |
-1 |
|
[1, -1, 1] |
1 |
|
[1, 1, -1] |
-1 |
|
[1, 1, 1] |
-1 |
На каждой
итерации работы алгоритма, мы будем подавать случайно выбранный вектор и
корректировать веса, чтобы приблизиться к значению требуемого отклика.
В качестве
активационной функции выберем гиперболический тангенс:
со значением
производной:
Программа на Python будет такой:
lesson 3. Back propagation.py
Ну, конечно, это
довольно простой, примитивный пример, частный случай, когда мы можем обучить НС
так, чтобы она вообще не выдавала никаких ошибок. Часто, в задачах обучения встречаются
варианты, когда мы этого сделать не можем и, конечно, какой-то процент ошибок
всегда остается. И наша задача сделать так, чтобы этих ошибок было как можно
меньше. Но более подробно как происходит обучение, какие нюансы существуют, как
создавать обучающую выборку, как ее проверять и так далее, мы об этом подробнее
будем говорить уже на следующем занятии.
Видео по теме
Практическая работа №1: Реализация метода обратного распространения ошибки для двухслойной полностью связанной нейронной сети
Задача
Требуется вывести расчетные формулы и спроектировать программную реализацию метода обратного распространения ошибки для двухслойной полносвязной нейронной сети. Обучение и тестирование сети происходит на наборе данных MNIST, функция активации скрытого слоя – relu, функция активации выходного слоя – softmax, функция ошибки – кросс-энтропия.
Математическая модель
Модель нейрона описывается следующими уравнениями:
где – входной сигнал,
– синаптический вес сигнала
,
– функция активации,
– смещение
Прямой ход
Для получения предсказания сети, производится прямой ход: для каждого нейрона последовательно, от начальных слоёв к конечным, вычисляется линейная активация входных сигналов, к ней применяется функция активации, после чего этот сигнал передаётся на следующий слой. В случае данной архитектуры:
где – выход скрытого слоя,
– функция активации скрытого слоя (relu),
– вход сети,
– выход сети,
– функция активации выходного слоя (softmax),
Метод обратного распространения ошибки
Метод обратного распространения ошибки определяет стратегию выбора весов сети 𝑤 с использованием градиентных методов оптимизации.
Схема обратного распространения ошибки состоит из следующих этапов:
-
Прямой проход по нейронной сети. На данном этапе вычисляются значения выходных сигналов каждого слоя, а так же производные их функций активации.
-
Вычисление значений целевой функции и её производной.
Целевая функция – кросс-энтропия, вычисляется как
где
– ожидаемый выход (метки)
Производную целевой функции по весам можно вывести следующим образом:
По весам второго слоя:
из условия
получаем
По весам первого слоя
-
Обратный проход нейронной сети и корректировка весов
-
Повторение этапов 1-3 до выполнения условия останова
Описание программной реализации
Network.py
Содержит реализацию нейронной сети
Класс NN содержит данные и методы для работы с сетью
Поля класса NN:
_input_size – размер входного слоя
_hidden_size – размер скрытого слоя
_output_size – размер выходного слоя
_w1, _b1 – массивы для хранения весов и смещений первого слоя
_w2, _b2 – массивы для хранения весов и смещений второго слоя
Методы класса NN:
_forward(input) – прямой проход сети. Возвращает выходной сигнал первого и второго слоя
_calculate_dE(input, label, output1, output2) – вычисление градиента функции ошибки. Возвращает градиент функции по весам и биасам первого и второго слоёв
_backprop(learning_rate, size, dEb1, dEb2) – корректировка весов сети при помощи посчитанных градиентов
init_weights() – инициализация весов нормальным распределением с дисперсией 1/10
fit(input, label, validate_data = None, batch_size = 100, learning_rate = 0.1, epochs = 100) – пакетное обучение сети на epochs эпохах, скоростью обучения learning_rate, размером пакета batch_size. Выводит точность и значение целевой функции на каждой эпохе
predict(input) – получение предсказания сети
utils.py:
Содержит вспомогательные функции.
relu(X) – функция relu
reluD(X) – производная функции relu
calcilate_E(predict, label) – подсчёт функции ошибки на основании предсказания сети и верной разметки
calculate_acc(prediction ,label) – посчёт точности на основании предсказания сети и верной разметки
main.py
Обучает сеть из класса NN на MNIST с параметрами из аргументов запуска. Измеряет время обучения.
Аргументы:
-
—hidden – количество нейронов в скрытом слое
-
—epochs – количество эпох обучения
-
—lr – скорость обучения
-
—batch – размер пакета
Как вызывать:
python main.py --hidden 30 --epochs 20 --lr 0,1 --batch 100
(в примере указаны параметры по умолчанию)
Эксперименты
Размер скрытого слоя: 30, эпох: 20, скорость обучения: 0,1, размер пакета: 100
train accuracy: 0.9729 train error: 0.0913
validate accuracy: 0.9613 validate error: 0.1238
Time: 28.309726 seconds
Размер скрытого слоя: 10, эпох: 20, скорость обучения: 0,1, размер пакета: 100
train accuracy: 0.9469 train error: 0.1805
validate accuracy: 0.9404 validate error: 0.2013
Time: 18.23942 seconds
Размер скрытого слоя: 10, эпох: 20, скорость обучения: 0,1, размер пакета: 100
train accuracy: 0.9874 train error: 0.0467
validate accuracy: 0.9721 validate error: 0.0878
Time: 58.233283 seconds
Размер скрытого слоя: 30, эпох: 50, скорость обучения: 0,1, размер пакета: 100
train accuracy: 0.9875 train error: 0.0418
validate accuracy: 0.9678 validate error: 0.1216
Time: 70.004101 seconds
Размер скрытого слоя: 30, эпох: 20, скорость обучения: 0,5, размер пакета: 100
train accuracy: 0.9766 train error: 0.0732
validate accuracy: 0.9622 validate error: 0.1614
Time: 26.213141 seconds
Размер скрытого слоя: 30, эпох: 30, скорость обучения: 0,05, размер пакета: 100
train accuracy: 0.971 train error: 0.0998
validate accuracy: 0.9625 validate error: 0.1225
Time: 40.577051 seconds
Размер скрытого слоя: 30, эпох: 20, скорость обучения: 0,1, размер пакета: 10
train accuracy: 0.9724 train error: 0.0928
validate accuracy: 0.9533 validate error: 0.2423
Time: 65.179444 seconds
Размер скрытого слоя: 30, эпох: 20, скорость обучения: 0,1, размер пакета: 1000
train accuracy: 0.9268 train error: 0.2588
validate accuracy: 0.9264 validate error: 0.2576
Time: 25.455479 seconds
Обратное распространение ошибки — это способ обучения нейронной сети. Цели обратного распространения просты: отрегулировать каждый вес пропорционально тому, насколько он способствует общей ошибке. Если мы будем итеративно уменьшать ошибку каждого веса, в конце концов у нас будет ряд весов, которые дают хорошие прогнозы.
Обновление правила цепочки
Прямое распространение можно рассматривать как длинный ряд вложенных уравнений. Если вы так думаете о прямом распространении, то обратное распространение — это просто приложение правила цепочки (дифференцирования сложной функции) для поиска производных потерь по любой переменной во вложенном уравнении. С учётом функции прямого распространения:
f(x)=A(B(C(x)))
A, B, и C — функции активации на различных слоях. Пользуясь правилом цепочки, мы легко вычисляем производную f(x) по x:
f′(x)=f′(A)⋅A′(B)⋅B′(C)⋅C′(x)
Что насчёт производной относительно B? Чтобы найти производную по B, вы можете сделать вид, что B (C(x)) является константой, заменить ее переменной-заполнителем B, и продолжить поиск производной по B стандартно.
f′(B)=f′(A)⋅A′(B)
Этот простой метод распространяется на любую переменную внутри функции, и позволяет нам в точности определить влияние каждой переменной на общий результат.
Применение правила цепочки
Давайте используем правило цепочки для вычисления производной потерь по любому весу в сети. Правило цепочки поможет нам определить, какой вклад каждый вес вносит в нашу общую ошибку и направление обновления каждого веса, чтобы уменьшить ошибку. Вот уравнения, которые нужны, чтобы сделать прогноз и рассчитать общую ошибку или потерю:
Учитывая сеть, состоящую из одного нейрона, общая потеря нейросети может быть рассчитана как:
Cost=C(R(Z(XW)))
Используя правило цепочки, мы легко можем найти производную потери относительно веса W.
C′(W)=C′(R)⋅R′(Z)⋅Z′(W)=(y^−y)⋅R′(Z)⋅X
Теперь, когда у нас есть уравнение для вычисления производной потери по любому весу, давайте обратимся к примеру с нейронной сетью:
Какова производная от потери по Wo?
C′(WO)=C′(y^)⋅y^′(ZO)⋅Z′O(WO)=(y^−y)⋅R′(ZO)⋅H
А что насчет Wh? Чтобы узнать это, мы просто продолжаем возвращаться в нашу функцию, рекурсивно применяя правило цепочки, пока не доберемся до функции, которая имеет элемент Wh.
C′(Wh)=C′(y^)⋅O′(Zo)⋅Z′o(H)⋅H′(Zh)⋅Z′h(Wh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)⋅X
И просто забавы ради, что, если в нашей сети было бы 10 скрытых слоев. Что такое производная потери для первого веса w1?
C(w1)=(dC/dy^)⋅(dy^/dZ11)⋅(dZ11/dH10)⋅(dH10/dZ10)⋅(dZ10/dH9)⋅(dH9/dZ9)⋅(dZ9/dH8)⋅(dH8/dZ8)⋅(dZ8/dH7)⋅(dH7/dZ7)⋅(dZ7/dH6)⋅(dH6/dZ6)⋅(dZ6/dH5)⋅(dH5/dZ5)⋅(dZ5/dH4)⋅(dH4/dZ4)⋅(dZ4/dH3)⋅(dH3/dZ3)⋅(dZ3/dH2)⋅(dH2/dZ2)⋅(dZ2/dH1)⋅(dH1/dZ1)⋅(dZ1/dW1)
Заметили закономерность? Количество вычислений, необходимых для расчёта производных потерь, увеличивается по мере углубления нашей сети. Также обратите внимание на избыточность в наших расчетах производных. Производная потерь каждого слоя добавляет два новых элемента к элементам, которые уже были вычислены слоями над ним. Что, если бы был какой-то способ сохранить нашу работу и избежать этих повторяющихся вычислений?
Сохранение работы с мемоизацией
Мемоизация — это термин в информатике, имеющий простое значение: не пересчитывать одно и то же снова и снова. В мемоизации мы сохраняем ранее вычисленные результаты, чтобы избежать пересчета одной и той же функции. Это удобно для ускорения рекурсивных функций, одной из которых является обратное распространение. Обратите внимание на закономерность в уравнениях производных приведённых ниже.
Каждый из этих слоев пересчитывает одни и те же производные! Вместо того, чтобы выписывать длинные уравнения производных для каждого веса, можно использовать мемоизацию, чтобы сохранить нашу работу, так как мы возвращаем ошибку через сеть. Для этого мы определяем 3 уравнения (ниже), которые вместе выражают в краткой форме все вычисления, необходимые для обратного распространения. Математика та же, но уравнения дают хорошее сокращение, которое мы можем использовать, чтобы отслеживать те вычисления, которые мы уже выполнили, и сохранять нашу работу по мере продвижения назад по сети.
Для начала мы вычисляем ошибку выходного слоя и передаем результат на скрытый слой перед ним. После вычисления ошибки скрытого слоя мы передаем ее значение обратно на предыдущий скрытый слой. И так далее и тому подобное. Возвращаясь назад по сети, мы применяем 3-ю формулу на каждом слое, чтобы вычислить производную потерь по весам этого слоя. Эта производная говорит нам, в каком направлении регулировать наши веса, чтобы уменьшить общие потери.
Примечание: термин ошибка слоя относится к производной потерь по входу в слой. Он отвечает на вопрос: как изменяется выход функции потерь при изменении входа в этот слой?
Ошибка выходного слоя
Для расчета ошибки выходного слоя необходимо найти производную потерь по входу выходному слою, Zo. Это отвечает на вопрос: как веса последнего слоя влияют на общую ошибку в сети? Тогда производная такова:
C′(Zo)=(y^−y)⋅R′(Zo)
Чтобы упростить запись, практикующие МО обычно заменяют последовательность (y^−y)∗R'(Zo) термином Eo. Итак, наша формула для ошибки выходного слоя равна:
Eo=(y^−y)⋅R′(Zo)
Ошибка скрытого слоя
Для вычисления ошибки скрытого слоя нужно найти производную потерь по входу скрытого слоя, Zh.
C′(Zh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)
Далее мы можем поменять местами элемент Eo выше, чтобы избежать дублирования и создать новое упрощенное уравнение для ошибки скрытого слоя:
Eh=Eo⋅Wo⋅R′(Zh)
Эта формула лежит в основе обратного распространения. Мы вычисляем ошибку текущего слоя и передаем взвешенную ошибку обратно на предыдущий слой, продолжая процесс, пока не достигнем нашего первого скрытого слоя. Попутно мы обновляем веса, используя производную потерь по каждому весу.
Производная потерь по любому весу
Вернемся к нашей формуле для производной потерь по весу выходного слоя Wo.
C′(WO)=(y^−y)⋅R′(ZO)⋅H
Мы знаем, что можем заменить первую часть уравнением для ошибки выходного слоя Eh. H представляет собой активацию скрытого слоя.
C′(Wo)=Eo⋅H
Таким образом, чтобы найти производную потерь по любому весу в нашей сети, мы просто умножаем ошибку соответствующего слоя на его вход (выход предыдущего слоя).
C′(w)=CurrentLayerError⋅CurrentLayerInput
Примечание: вход относится к активации с предыдущего слоя, а не к взвешенному входу, Z.
Подводя итог
Вот последние 3 уравнения, которые вместе образуют основу обратного распространения.
Вот процесс, визуализированный с использованием нашего примера нейронной сети выше:
Обратное распространение: пример кода
def relu_prime(z): if z > 0: return 1 return 0 def cost(yHat, y): return 0.5 * (yHat - y)**2 def cost_prime(yHat, y): return yHat - y def backprop(x, y, Wh, Wo, lr): yHat = feed_forward(x, Wh, Wo) # Layer Error Eo = (yHat - y) * relu_prime(Zo) Eh = Eo * Wo * relu_prime(Zh) # Cost derivative for weights dWo = Eo * H dWh = Eh * x # Update weights Wh -= lr * dWh Wo -= lr * dWo