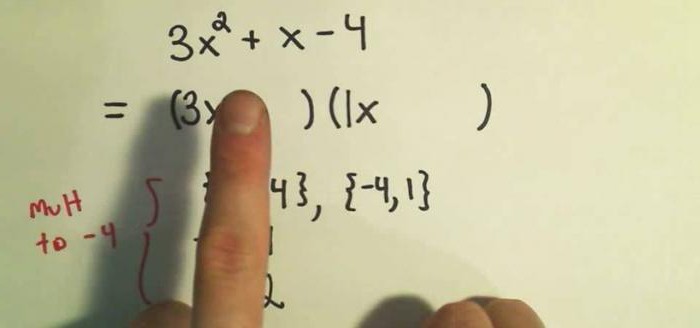Метод проб и ошибок
Метод
проб и ошибок (в просторечии также: метод
(научного) тыка)
— является врождённым методом мышления
человека. Также этот метод называют методом
перебора вариантов.
В 1898
году описан Э.
Торндайком как
форма научения,
основанная на закреплении случайно
совершённых двигательных и
мыслительных актов,
за счет которых была решена значимая
для животного задача.
Считается,
что для метода проб и ошибок выполняется
правило — «первое
пришедшее в голову решение —
слабое». Объясняют
этот феномен тем, что человек старается
поскорее освободиться от неприятной
неопределённости и делает то, что пришло
в голову первым.
МПиО —
аббревиатура, обозначающая метод проб
и ошибок. Часто встречается в текстах,
так или иначе связанных с Теорией
решения изобретательских задач.
В ТРИЗ метод проб и ошибок рассматривается
как эталон неэффективности. Для оценки
какого-либо другого эвристического
метода его сравнивают с МПиО. Так как
МПиО — это метод перебора вариантов,
то можно количественно определить число
вариантов при использовании МПиО и
сравнить с ним какой-либо другой
эвристический метод. Такое математическое
исследование предполагает, что количество
необходимых вариантов обратно
пропорционально эффективности метода
и прямо пропорционально времени
нахождения решения при его использовании.
Однако точные количественные и
статистические исследования проводятся
редко. В ТРИЗ ограничиваются приблизительной
количественной оценкой эффективности
по уровням изобретательских задач (Ю.
П. Саламатов).
Синектика
Синектика (англ. Synectics) —
методика исследования, основанная на
социально-психологической мотивации
коллективной интеллектуальной
деятельности, предложенная В. Дж.
Гордоном. Является развитием и
усовершенствованиемметода
мозгового штурма.
Д. Гордон разработал этот метод решения
проблем, когда руководил группой
исследования изобретений для Артура
Д. Литтла.
При
синектическом штурме допустима критика,
которая позволяет развивать и видоизменять
высказанные идеи. Этот штурм ведет
постоянная группа. Её члены постепенно
привыкают к совместной работе, перестают
бояться критики, не обижаются, когда
кто-то отвергает их предложения.
В
методе применены четыре вида аналогий —
прямая, символическая, фантастическая,
личная.
Виды
аналогий:
-
При прямой
аналогии рассматриваемый
объект сравнивается с более или менее
похожим аналогичным объектом в природе
или технике. Например, для усовершенствования
процесса окраски мебели применение
прямой аналогии состоит в том, чтобы
рассмотреть, как окрашены минералы,
цветы, птицы и т. п. или как окрашивают
бумагу, киноплёнки и т. п. -
Символическая
аналогия требует
в парадоксальной форме сформулировать
фразу, буквально в двух словах отражающую
суть явления. Например, при решении
задачи, связанной с мрамором, найдено
словосочетание «радужное постоянство»,
так как отшлифованный мрамор (кроме
белого) — весь в ярких узорах,
напоминающих радугу, но все эти узоры
постоянны. -
При фантастической
аналогии необходимо
представить фантастические средства
или персонажи, выполняющие то, что
требуется по условиям задачи. Например,
хотелось бы, чтобы дорога существовала
там, где её касаются колёса автомобиля. -
Личная
аналогия (эмпатия)
позволяет представить себя тем предметом
или частью предмета, о котором идёт
речь в задаче. В примере с окраской
мебели можно вообразить себя белой
вороной, которая хочет окраситься. Или,
если совершенствуется зубчатая передача,
то представить себя шестерней, которая
крутится вокруг своей оси, подставляя
бока соседней шестерне. Нужно в буквальном
смысле входить «в образ» этой шестерни,
чтобы на себе почувствовать всё, что
достаётся ей, и какие она испытывает
неудобства или перегрузки. Что даёт
такое перевоплощение? Оно значительно
уменьшает инерцию
мышления и
позволяет рассматривать задачу с новой
точки зрения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
21.03.2016431.83 Кб173op.pdf
1. Метод проб и ошибок
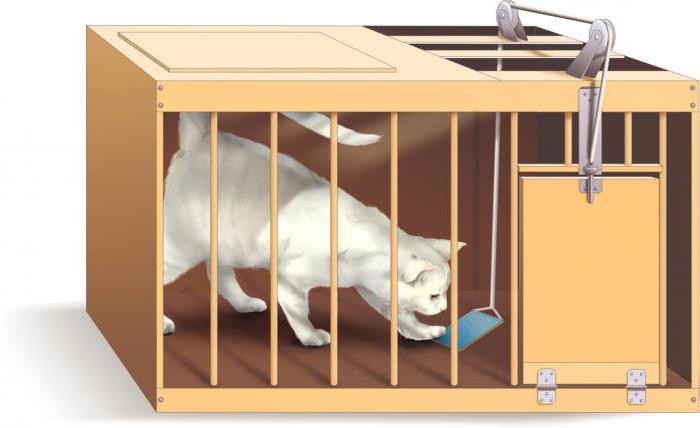
Метод проб и ошибок (МПИО — (англ. trial—and—rror learning) известен человечеству с незапамятных времен. Это форма научения, детально описанная в докторской диссертации Э. Торндайка (1898). Э. Торндайк придавал доминирующее значение навыку, который, согласно его взглядам,обра-зуется путем закрепления случайных двигательных и мыслительных актов, приводящих к дос-тижению необходимых для живого существа результатов. Так, кошка, посаженная в так называ-емую проблемную клетку и лишенная пищи, начинает метаться по клетке, находит выход, вы-ходит на свободу и получает пищу. При повторении опытов время, затрачиваемое животным на то, чтобы выйти из клетки, постепенно, хотя и с большими колебаниями, уменьшается. В ко-нце концов животное открывает клетку сразу, что может быть воспринято наблюдателем, не видевшим предшествующих опытов, как «догадка» животного.
Критики МПИО отмечали, что хаотические и нецелесообразные движения во время научения наблюдаются главным образом в ситуациях, когда проблема неадекватна уровню развития об-следуемого (как животного, так и человека),чрезмерно трудна. При решении адекватной проблемы испытуемый прежде всего пытается применить прошлый опыт с учетом того нового, что со-держится в проблеме. Тем не менее в процессе формирования новых форм поведения возникает экспериментальный поиск с последующей проверкой, предполагающей применение МПИО в ограниченных пределах.
Метод проб и ошибок.
Рассмотрение методов мы, конечно, начнем с метода проб и ошибок. Этот метод еще называют методом перебора вариантов. В шутку говорят: «Перебор вариантов еще не самое худшее, хуже, когда предлагается всего один вариант!» Для примера решим задачу. Анаграммами «дорогвон» и «невежа» зашифрованы названия двух известных городов. Что это за города? Проследите, что вы начали делать? Наверняка начали перебирать слоги и буквы. Это и есть МПиО. (Ответ: Новгород и Женева.)
Мышление методом проб и ошибок зарождается в раннем детстве, когда ребенок начинает познавать мир: трогает руками, пробует, смотрит, слушает — накапливает образы и понятия, ищет связи между своими действиями и результатами этих действий. Затем, накопив некоторый опыт (на своих ошибках и победах) и знания, ребенок постепенно переходит от наглядно-действенного и наглядно-образного мышления к более сложным видам: абстрактно-понятийному и логическому. Тогда полнее начинает работать «здравый смысл» — толковый, рассудительный, трезвый, «взрослый».
Здравый смысл — это наша логичность, умение анализировать. Здравому смыслу, мышлению по аналогии и по ассоциации посвящены специальные разделы книги.
Есть задачи, которые иначе как перебором вариантов не решить.
Например, такая: дано пять стаканов с бесцветной жидкостью, внешне совершенно одинаковых. Известно, что сливание двух каких-то жидкостей дает смесь красного цвета. Как найти эту пару жидкостей? Придется переливать наугад. В этой задаче нет творчества. Единственное, что можно сделать, это исключить повторные сливания: пронумеровав стаканы, определим общее число переливаний без повторов по формуле сочетаний (в данном случае из пяти по два находим, что число таких сочетаний равно десяти) и составим таблицу сочетаний. Может быть, конечно, повезет и понадобится менее десяти переливаний.
Или такая простенькая задачка: приведите примеры, когда количество букв в названии числа равно самому числу. Начали перебирать: один, два, ТРИ! — (годится), четыре… Найдите и другие совпадения.
Решите старинную задачу.
Представьте, что вам дали два кувшина сложной формы емкостью 9 л и 4 л и попросили из большой бочки отлить 6 л дорогого вина, не больше и не меньше. Других сосудов нет. А теперь последите за своим мышлением! Что вы начали делать? По всей вероятности, вы начали мысленно наполнять и переливать из кувшина в кувшин вино — это тоже МПиО. Получить 6 л, вылив в 9-литровый кувшин 4 л и еще 2 л, наполнив 4-литровый кувшин до половины, нельзя по условию задачи — кувшины сложной формы.
Если не решили методом пробных переливаний, воспользуемся здравым смыслом. Он говорит, что самый простой способ получить 6 л — это слить 3 л из наполненного 9-литрового кувшина. Но куда? А это уже другая задача. И более простая! Другого сосуда, кроме 4-литрового кувшина, у нас нет, значит, надо сделать так, чтобы в 4-литровом кувшине был 1 л вина. А это уж совсем простая задачка: надо наполнить 9-литровый кувшин и слить из него два раза по 4 л, а оставшийся литр вылить в 4-литровый кувшин (9-4-4 = 1). Когда в 4-литровом кувшине окажется 1 л, надо вторично наполнить 9-литровый кувшин и слить из него 3 л (9-3 = 6). Задача решена.
Решим еще несколько задачек, чтобы накопить кое-какой опыт, подвести итоги и сделать некоторые обобщения.
1. На столе стоят опрокинутыми пять одинаковых фарфоровых чашек. Известно, что под одной из них — орех. Определите, под какой чашкой орех? Ясно, чтобы надежно определить, под какой чашкой орех, надо поднять 4 чашки. Но, может, и повезет, и орех окажется под первой же поднятой чашкой.
2. Возьмите 12 спичек и выложите из них 4 одинаковых квадрата. Переложите спички так, чтобы получилось три таких же квадрата. Отметьте, с чего вы начали решать? Сразу начали перекладывать (МПиО) или сначала подумали (здравый смысл)? 3. А вот задачка, над которой без здравого смысла придется долго мучиться, перебирая варианты. Расставьте недостающие цифры в квадрате так, чтобы их сумма по всем направлениям была равна 9.

Используем цепное правило: «Операцию, которая приводит к однозначному ответу (без вариантов), надо делать сразу». Без вариантов заполняется второй столбец. В нижнюю строчку вписываем 0, в левый нижний угол 5. А потом? Придется подобрать цифры в оставшиеся четыре пустые клетки. Начать лучше с первой строки, так как вариантов тут меньше (3). 9-6 = 1+2.
Ставим в левый верхний угол 1, а в правый 2. Тогда в пустые клетки среднего ряда надо вписать две тройки. Задача решена. Кстати, она решается, если в левый верхний угол вписать 2.
4. В США имеются монеты достоинством 1, 5, 10, 25 и 50 центов. Как набрать 1 доллар из 13 монет? 1 доллар равен 100 центам. Для этой задачи известны, по крайней мере, три варианта решения. Найдите их.
Перечислим преимущества и недостатки МПиО и подведем некоторые итоги.
Достоинства МПиО:
1. Этому методу не надо учиться.
2. Методическая простота решения («А что, если попробовать сделать так?…»).
3. Удовлетворительно решаются простые задачи (не более 10 проб и ошибок).
4. Учит упорству и терпению, учит не отчаиваться при неудачах.
5. Вообще говоря, с каждым новым решением человек «становится умнее». Не случайно говорят, что на ошибках учатся.
Мы знаем, что учиться надо и на ошибках, и на успехах, и на победах, и на поражениях, своих и чужих.
Перебрать 1000 вариантов решений невозможно, но не надо считать позорным перебор вариантов, если их не много: 4-5-6… до 10.
Недостатки метода проб и ошибок. Обратите особое внимание на приведенные ниже недостатки, далее мы будем рассматривать много методов мышления, и все они будут исключать или уменьшать эти недостатки.
1. Плохо решаются задачи средней сложности (более 20-30 проб и ошибок) и практически не решаются сложные задачи (более 1000 проб и ошибок). Согласитесь, трудно предложить даже более 10 разных решений.
Вспомните, был ли случай в вашей практике, когда, решая какую-нибудь, даже серьезную проблему, вы предложили более 20 различных вариантов решений? Тем более это трудно, если вы думали в одиночку.
Если не верите — предложите 20 способов передачи простейшего сообщения (да — нет) на расстояние в полкилометра.
Я начну: дым костра, трембита, барабан, шест с флагом, забраться на дерево, веревка длиной 0,5 км, выстрел из ружья, почтовый голубь, собака…
А вот дети, у которых специально развивали воображение, предлагали более 20 способов. Почему? Потому что они умели управлять своим мышлением и не боялись фантазировать!
2. Нет никаких помощников мышления — приемов решения задач.
3. Нет алгоритма мышления, мы не управляем процессом думанья. Мы не знаем, как мы думаем. Мы не знаем, как нам в голову приходят новые варианты решений. Идет довольно хаотичный перебор вариантов.
4. Неизвестно, когда придет хорошая идея и придет ли вообще.
5. Отсутствуют критерии оценки силы решения, поэтому не ясно, когда прекращать думать. А вдруг в следующее мгновение придет гениальное решение?
6. Требуются большие волевые усилия и большие затраты времени при решении трудных задач.
7. МПиО часто дает усложненные, неоптимальные решения.
Считается, что для МПиО выполняется правило: «первое пришедшее в голову решение — слабое». Объясняют этот феномен тем, что человек старается поскорее освободиться от неопределенности и «брякает» то, что пришло в голову первым. МПиО сравнивают с ловлей мячика с закрытыми глазами или в темноте. Повезет — не повезет, придет хорошее решение — не придет хорошее решение. Чаще всего мы начинаем решать любые задачи, используя метод проб и ошибок. И только если решить с ходу не удается, мы обращаемся к другим методам, если, конечно, ими владеем. «Чем шкура красивей, тем охотник хитрей».
Вследствие своей врожденности, способ мышления методом проб и ошибок очень консервативен, трудно поддается изменению и переучиванию. Это последнее обстоятельство надо учитывать и сознательно прикладывать волевые усилия (и немалые!), заставляя себя осваивать другие, более эффективные методы мышления. Эффективность МПиО (число вариантов, быстроту и силу решений…) увеличивают использованием рассуждений на основании здравого смысла и напряжением мышления.
Напряжение мышления — это преодоление несоответствия между какой-либо потребностью, желательностью действия и ее удовлетворением, это недовольство ситуацией и желание исправить положение, что заставляет думать и действовать.
Можно составить своеобразную формулу нашего обычного мышления: Перебор вариантов + Здравый Смысл + Напряжение мышления.
Но основной недостаток МПиО заключается в том, что отсутствуют какие-либо более-менее надежные «помощники»: приемы, методики или способы, помогающие решать задачи, помогающие «прорваться» в подкорку и извлечь оттуда сильное решение.
Здравый смысл.
Что такое здравый смысл и чем он отличается от логики? Как отмечалось, здравый смысл — это логические операции в повседневной жизни, интуитивные суждения, это умение делать правильные выводы на основе недостаточно формализованного практического опыта, в условиях нечетких значений слов.
Можно сказать, что здравый смысл — это рационализм, умение принимать обдуманные, рациональные решения, в отличие от иррационального мышления — нелогичного, непонятного, необъяснимого на разумной основе.
Чем отличается строгое научное мышление от обычного, житейского — здравого смысла? Если здравый смысл построен на принципе интуитивной очевидности (это каждому дураку ясно!), то строгое логичное мышление построено на полной доказательности каждого положения, каждого шага, каждого суждения и вывода. Поэтому его называют научным, логическим.
Житейские суждения могут основываться на доверии к человеку, на симпатиях, на догмах, на правдоподобных рассуждениях, на лукавой заинтересованности, на привычках и обычаях, даже на преднамеренной лжи — то есть на основаниях, весьма далеких от достаточных, чтобы быть логически верными.
Отсюда вытекает, так сказать, «совет здравому смыслу» — ищи строгий научный закон, на который можно было бы смело опереться. А это нечто иное, как законы формальной логики.
Поэтому здравый смысл может дать досадные осечки.
1. Ответьте, например, на такой умозрительный вопрос: если земной шар и грецкий орех мысленно обтянуть нерастяжимыми нитями, а потом одну и другую нити удлинить на десять метров и опять обтянуть земной шар и орех, то в каком случае зазор (провисание) будет больше? Здравый смысл говорит, что в случае с грецким орехом. Ибо на такой огромной длине окружности земного шара равной 40 000 000 м удлинение на 10 метров просто не будет заметно (0,000025 %).
А теперь посчитаем. Длина окружности земного шара Lз = 2nRз, откуда Rз = Lз/2n. Длина окружности ореха Lо = 2nRо, откуда Rо = Lо/2n.
Увеличенная на 10 м длина окружности земли равна Lз+10 м = 2nRзу, откуда Rзу = (Lз+10 м)/2n. Увеличенная на 10 м длина окружности ореха Lо+10 м = 2nRоу, откуда Rоу = (Lо+10 м)/2n. Теперь найдем искомые зазоры: Rзу-Rз = (Lз+10 м)/2n-Lз/2n = 10 м/2n = 1,6 м; Rоу-Rо = (Lо+10 м)/2n-Lо/2n = 10 м/2n = 1,6 м!!! Столь странный результат вытекает из постоянства отношения длины окружности к своему радиусу L/R = 2n.
2. Очевидно, что через точку на плоскости можно провести одну и только одну прямую, параллельную заданной. Этому нас учили в школе. Так утверждал еще в III веке до н. э. великий греческий математик Евклид. Через 21 век(!) другой великий математик, Н. И. Лобачевский, совершил переворот в геометрии, доказав, что это не так, что через точку можно провести много прямых, параллельных исходной. Это привело к отличию многих теорем геометрии Лобачевского от аналогичных теорем геометрии Евклида. Например, сумма углов треугольника меньше 180°, подобные треугольники всегда равны между собой…
3. Согласно здравому смыслу, заливать пожар холодной водой эффективней, чем кипятком. Однако это не так. Удельная теплота парообразования много больше удельной теплоты нагревания.
4. Вряд ли на основании здравого смысла можно сказать, что диапазон слышимости человека от едва слышимого звука до невыносимого по своей громкости равен триллиону (числу с 12 нулями).
Несколько примеров правильных поступков, с позиций формальной логики (инструкций), но противоречащих здравому смыслу, что нередко приводит к глупости.
* В одном из павильонов научно-исследовательского института, где размещалась научная аппаратура, возник пожар.
Огнетушителей в павильоне не оказалось, и люди побежали в главный корпус института. Показали свои пропуска на проходной, взяли огнетушители и хотели идти тушить пожар, который, кстати, был хорошо виден из проходной. Однако не тут-то было, охрана потребовала предъявить пропуска на вынос материальных ценностей(!). Начальник охраны горячо поддержал своих бдительных вахтеров и пригрозил оружием. Только вмешательство генерального директора пресекло глупость, но для тушения пожара уже пришлось вызывать специалистов со шлангами, насосами и лестницами.
* Врач прописал больному, страдающему бессонницей, таблетки и попросил медсестру давать таблетки через каждые два часа. Придя к больному в очередной раз, сестра увидела, что больной крепко спит. Сестра его с трудом разбудила и заставила принять таблетку!!!
* Машенька написала в тетради «што» вместо «что».
Мама замечает:
— Ты же знаешь, как надо писать.
— А кого мы обманываем? Говорим «што», а писать надо «что»!
Тренинг здравого смысла.
Прекрасным тренингом здравого смысла является решение задач на смекалку.
1. Мама испекла кулич и дочка испекла кулич, из того же теста и точно совпадающий по форме с маминым, но его размеры в три раза меньше. Мамин кулич весит 1 кг, сколько весит кулич дочери?
2. Чему равна сумма чисел натурального ряда? 1 + 2 + 3 + 4 + 5 + 6 + Е = ? Здравый смысл совершенно правильно говорит — бесконечности.
3. А чему равна сумма убывающих правильных дробей? 1/2 +1/3+1/4+1/5+1/6+Е = ?
4. Чему равна сумма убывающих дробей такого ряда? 1/2+1/4+1/8+1/16+1/32+Е = ? Здравый смысл говорит — надо спросить математиков.
5. Решим такую задачку.
Можно ли написать пять нечетных цифр, таким образом, чтобы в сумме получить 14?
Ответы.
1. Здравый смысл вроде бы говорит — 333 г. Трудно поверить, но он весит менее 40 г. Для проверки посчитаем. Чтобы найти массу, надо объем умножить на плотность. Плотность у обоих куличей одинакова. Пусть кулич дочки имеет размеры 1x*1x*1x = 1x, тогда мамин кулич 3x*3x*3x = 27x. Если 1кг разделить на 27, то получится 37 г.
3. Бесконечности!
4. Математики говорят, что сумма приведенного ряда равна 1!
5. Что мы начинаем делать? Пытаемся подобрать нечетные цифры. 1 + 3 + 5 + 7 + 9 = 25.
Первая догадка: несколько цифр должны быть одинаковыми. 1 + 3 + 5 + 3 + 1 = 13.
Вторая догадка: сумма нечетного числа нечетных цифр никогда не может быть четным числом. «Спасительная» мысль: эта задача не решается! А если не сдаваться? Вчитаемся в условия задачи. Что они не запрещают? Они не запрещают, как угодно комбинировать, необязательно складывать, пять каких-то нечетных чисел, среди которых могут быть одинаковые. Третья догадка: 11+1+1+1 =
Нам удалось вырваться из стандартной ситуации, когда знания есть, а задачу не решить. В чем дело? Не можем догадаться.
Одним из недостатков здравого смысла является то, что он ставит вне закона фантазию и вообще «дикое мышление».
From Wikipedia, the free encyclopedia
Trial and error is a fundamental method of problem-solving[1] characterized by repeated, varied attempts which are continued until success,[2] or until the practicer stops trying.
According to W.H. Thorpe, the term was devised by C. Lloyd Morgan (1852–1936) after trying out similar phrases «trial and failure» and «trial and practice».[3] Under Morgan’s Canon, animal behaviour should be explained in the simplest possible way. Where behavior seems to imply higher mental processes, it might be explained by trial-and-error learning. An example is a skillful way in which his terrier Tony opened the garden gate, easily misunderstood as an insightful act by someone seeing the final behavior. Lloyd Morgan, however, had watched and recorded the series of approximations by which the dog had gradually learned the response, and could demonstrate that no insight was required to explain it.
Edward Lee Thorndike was the initiator of the theory of trial and error learning based on the findings he showed how to manage a trial-and-error experiment in the laboratory. In his famous experiment, a cat was placed in a series of puzzle boxes in order to study the law of effect in learning.[4] He plotted to learn curves which recorded the timing for each trial. Thorndike’s key observation was that learning was promoted by positive results, which was later refined and extended by B. F. Skinner’s operant conditioning.
Trial and error is also a method of problem solving, repair, tuning, or obtaining knowledge. In the field of computer science, the method is called generate and test (Brute force). In elementary algebra, when solving equations, it is guess and check.
This approach can be seen as one of the two basic approaches to problem-solving, contrasted with an approach using insight and theory. However, there are intermediate methods which for example, use theory to guide the method, an approach known as guided empiricism.
This way of thinking has become a mainstay of Karl Popper’s critical rationalism.
Methodology[edit]
The trial and error approach is used most successfully with simple problems and in games, and it is often the last resort when no apparent rule applies. This does not mean that the approach is inherently careless, for an individual can be methodical in manipulating the variables in an attempt to sort through possibilities that could result in success. Nevertheless, this method is often used by people who have little knowledge in the problem area. The trial-and-error approach has been studied from its natural computational point of view [5]
Simplest applications[edit]
Ashby (1960, section 11/5) offers three simple strategies for dealing with the same basic exercise-problem, which have very different efficiencies. Suppose a collection of 1000 on/off switches have to be set to a particular combination by random-based testing, where each test is expected to take one second. [This is also discussed in Traill (1978–2006, section C1.2]. The strategies are:
- the perfectionist all-or-nothing method, with no attempt at holding partial successes. This would be expected to take more than 10^301 seconds, [i.e., 2^1000 seconds, or 3·5×(10^291) centuries]
- a serial-test of switches, holding on to the partial successes (assuming that these are manifest), which would take 500 seconds on average
- parallel-but-individual testing of all switches simultaneously, which would take only one second
Note the tacit assumption here that no intelligence or insight is brought to bear on the problem. However, the existence of different available strategies allows us to consider a separate («superior») domain of processing — a «meta-level» above the mechanics of switch handling — where the various available strategies can be randomly chosen. Once again this is «trial and error», but of a different type.
Hierarchies[edit]
Ashby’s book develops this «meta-level» idea, and extends it into a whole recursive sequence of levels, successively above each other in a systematic hierarchy. On this basis, he argues that human intelligence emerges from such organization: relying heavily on trial-and-error (at least initially at each new stage), but emerging with what we would call «intelligence» at the end of it all. Thus presumably the topmost level of the hierarchy (at any stage) will still depend on simple trial-and-error.
Traill (1978–2006) suggests that this Ashby-hierarchy probably coincides with Piaget’s well-known theory of developmental stages. [This work also discusses Ashby’s 1000-switch example; see §C1.2]. After all, it is part of Piagetian doctrine that children learn first by actively doing in a more-or-less random way, and then hopefully learn from the consequences — which all has a certain resemblance to Ashby’s random «trial-and-error».
Application[edit]
Traill (2008, espec. Table «S» on p.31) follows Jerne and Popper in seeing this strategy as probably underlying all knowledge-gathering systems — at least in their initial phase.
Four such systems are identified:
- Natural selection which «educates» the DNA of the species,
- The brain of the individual (just discussed);
- The «brain» of society-as-such (including the publicly held body of science); and
- The adaptive immune system.
Features[edit]
Trial and error has a number of features:
- solution-oriented: trial and error makes no attempt to discover why a solution works, merely that it is a solution.
- problem-specific: trial and error makes no attempt to generalize a solution to other problems.
- non-optimal: trial and error is generally an attempt to find a solution, not all solutions, and not the best solution.
- needs little knowledge: trials and error can proceed where there is little or no knowledge of the subject.
It is possible to use trial and error to find all solutions or the best solution, when a testably finite number of possible solutions exist. To find all solutions, one simply makes a note and continues, rather than ending the process, when a solution is found, until all solutions have been tried. To find the best solution, one finds all solutions by the method just described and then comparatively evaluates them based upon some predefined set of criteria, the existence of which is a condition for the possibility of finding a best solution. (Also, when only one solution can exist, as in assembling a jigsaw puzzle, then any solution found is the only solution and so is necessarily the best.)
Examples[edit]
Trial and error has traditionally been the main method of finding new drugs, such as antibiotics. Chemists simply try chemicals at random until they find one with the desired effect. In a more sophisticated version, chemists select a narrow range of chemicals it is thought may have some effect using a technique called structure–activity relationship. (The latter case can be alternatively considered as a changing of the problem rather than of the solution strategy: instead of «What chemical will work well as an antibiotic?» the problem in the sophisticated approach is «Which, if any, of the chemicals in this narrow range will work well as an antibiotic?») The method is used widely in many disciplines, such as polymer technology to find new polymer types or families.
Trial and error is also commonly seen in player responses to video games — when faced with an obstacle or boss, players often form a number of strategies to surpass the obstacle or defeat the boss, with each strategy being carried out before the player either succeeds or quits the game.
Sports teams also make use of trial and error to qualify for and/or progress through the playoffs and win the championship, attempting different strategies, plays, lineups and formations in hopes of defeating each and every opponent along the way to victory. This is especially crucial in playoff series in which multiple wins are required to advance, where a team that loses a game will have the opportunity to try new tactics to find a way to win, if they are not eliminated yet.
The scientific method can be regarded as containing an element of trial and error in its formulation and testing of hypotheses. Also compare genetic algorithms, simulated annealing and reinforcement learning – all varieties for search which apply the basic idea of trial and error.
Biological evolution can be considered as a form of trial and error.[6] Random mutations and sexual genetic variations can be viewed as trials and poor reproductive fitness, or lack of improved fitness, as the error. Thus after a long time ‘knowledge’ of well-adapted genomes accumulates simply by virtue of them being able to reproduce.
Bogosort, a conceptual sorting algorithm (that is extremely inefficient and impractical), can be viewed as a trial and error approach to sorting a list. However, typical simple examples of bogosort do not track which orders of the list have been tried and may try the same order any number of times, which violates one of the basic principles of trial and error. Trial and error is actually more efficient and practical than bogosort; unlike bogosort, it is guaranteed to halt in finite time on a finite list, and might even be a reasonable way to sort extremely short lists under some conditions.
Jumping spiders of the genus Portia use trial and error to find new tactics against unfamiliar prey or in unusual situations, and remember the new tactics.[7] Tests show that Portia fimbriata and Portia labiata can use trial and error in an artificial environment, where the spider’s objective is to cross a miniature lagoon that is too wide for a simple jump, and must either jump then swim or only swim.[8][9]
See also[edit]
- Ariadne’s thread (logic)
- Brute-force attack
- Brute-force search
- Dictionary attack
- Empiricism
- Genetic algorithm
- Learning curve
- Margin of error
- Regula falsi
References[edit]
- ^ Campbell, Donald T. (November 1960). «Blind variation and selective retention in creative thoughts as in other knowledge processes». Psychological Review. 67 (6): 380–400. doi:10.1037/h0040373. PMID 13690223.
- ^ Concise Oxford Dictionary p1489
- ^ Thorpe W.H. The origins and rise of ethology. Hutchinson, London & Praeger, New York. p26. ISBN 978-0-03-053251-1
- ^ Thorndike E.L. 1898. Animal intelligence: an experimental study of the association processes in animals. Psychological Monographs #8.
- ^ X. Bei, N. Chen, S. Zhang, On the Complexity of Trial and Error, STOC 2013
- ^ Wright, Serwall (1932). «The roles of mutation, inbreeding, crossbreeding and selection in evolution» (PDF). Proceedings of the Sixth International Congress on Genetics. Volume 1. Number 6: 365. Retrieved 17 March 2014.
- ^ Harland, D.P. & Jackson, R.R. (2000). ««Eight-legged cats» and how they see — a review of recent research on jumping spiders (Araneae: Salticidae)» (PDF). Cimbebasia. 16: 231–240. Archived from the original (PDF) on 28 September 2006. Retrieved 5 May 2011.
- ^ Jackson, Robert R.; Fiona R. Cross; Chris M. Carter (2006). «Geographic Variation in a Spider’s Ability to Solve a Confinement Problem by Trial and Error». International Journal of Comparative Psychology. 19 (3): 282–296. doi:10.46867/IJCP.2006.19.03.06. Retrieved 8 June 2011.
- ^ Jackson, Robert R.; Chris M. Carter; Michael S. Tarsitano (2001). «Trial-and-error solving of a confinement problem by a jumping spider, Portia fimbriata«. Behaviour. Leiden: Koninklijke Brill. 138 (10): 1215–1234. doi:10.1163/15685390152822184. ISSN 0005-7959. JSTOR 4535886.
Further reading[edit]
- Ashby, W. R. (1960: Second Edition). Design for a Brain. Chapman & Hall: London.
- Traill, R.R. (1978–2006). Molecular explanation for intelligence…, Brunel University Thesis, HDL.handle.net
- Traill, R.R. (2008). Thinking by Molecule, Synapse, or both? — From Piaget’s Schema, to the Selecting/Editing of ncRNA. Ondwelle: Melbourne. Ondwelle.com — or French version Ondwelle.com.
- Zippelius, R. (1991). Die experimentierende Methode im Recht (Trial and error in Jurisprudence), Academy of Science, Mainz, ISBN 3-515-05901-6
Человечество берет свое начало несколько тысяч лет назад. И на протяжении всего этого времени оно неустанно развивается. Причин на это было всегда много, но без изобретательности человека это просто не представлялось бы возможным. Метод проб и ошибок был и является в настоящее время одним из основных.
Описание способа
Четко зафиксированного в исторических документах применения данного метода мало. Но, несмотря на это, он заслуживает особого внимания.
Метод проб и ошибок – это способ, при котором решение задачи достигается подбором вариантов до тех пор, пока результат не станет правильным (например, в математике) или приемлемым (при изобретении новых методов в науке).
Человечество всегда пользовалось данным методом. Ориентировочно век назад психологи пытались найти общее между людьми, которые использовали данный способ познания. И им это удалось. Человек, который ищет ответ на поставленную задачу, вынужден подбирать варианты, ставить эксперименты и смотреть на результат. Это продолжается до тех пор, пока не приходит озарение по данному вопросу. Экспериментатор выходит на новую ступень мышления в данном вопросе.
Метод в мировой истории
Одним из самых известных людей, кто применял данный способ, был Эдисон. Все знают его историю изобретения лампочки. Он экспериментировал до тех пор, пока не получилось. Но Эдисон усовершенствовал данный метод. При поиске решения он разделял задачи между людьми, которые работали на него. Соответственно материала по теме получалось намного больше, чем при работе одного человека. И на основании полученных данных метод проб и ошибок имел большой успех в деятельности Эдисона. Благодаря этому человеку появились исследовательские институты, которые применяют, в том числе, и этот метод.
Степени трудности
У данного метода есть несколько уровней сложности. Они были так разделены для лучшего усвоения. Задача первого уровня считается легкой, и на поиск ее решения затрачивается немного сил. Но и вариантов ответов она имеет не так много. С повышением степени трудности растет и сложность поставленной задачи. Метод проб и ошибок 5 класса – самый труднорешаемый и затратный по времени.
Необходимо учитывать, что при возрастании уровня сложности растет и объем знаний, которыми обладает человек. Чтобы лучше понимать, о чем идет речь, рассмотрим технику. Первый и второй уровни позволяют изобретателям ее усовершенствовать. На последней ступени сложности создается совершенно новый продукт.
Например, известен случай, когда молодые люди темой дипломной работы взяли труднорешаемую задачу из аэронавигации. Студенты не обладали такими же знаниями, как многие ученые, которые работали в данной области, но благодаря широкому спектру знаний ребят у них получилось найти ответ. И причем область решения оказалась в самом далеком от науки кондитерском деле. Казалось бы, что это невозможно, но это факт. Молодым людям было даже выдано авторское свидетельство на их изобретение.
Преимущества метода
Первым достоинством можно по праву считать творческий подход. Задачи методом проб и ошибок решаемые позволяют задействовать оба полушария головного мозга для поиска ответа.
Стоит привести в пример, как строились лодки. Раскопки показывают, как на протяжении столетий деталь за деталью менялась форма. Исследователи постоянно пробовали что-то новое. Если лодка тонула, то эту форму вычеркивали, если оставалась держаться на воде, то принимали это к сведению. Таким образом, в итоге было найдено компромиссное решение.
Если поставленная задача не слишком сложная, то данный метод занимает немного времени. У некоторых возникающих проблем может быть десять вариантов, один или два из которых окажутся правильными. Но если рассматривать, например, робототехнику, то в данном случае без применения других методов исследования могут затянуться на десятки лет и принесут миллионы вариантов.
Разделение задач на несколько уровней позволяет оценить, насколько быстрым и возможным представляется поиск решения. Это сокращает время для принятия решения. И при сложных задачах можно использовать метод проб и ошибок параллельно с другими.
Недостатки метода
С развитием технологий и науки данный метод начал терять свою популярность.
В некоторых областях просто нерационально создавать тысячи образцов, чтобы менять по одному элементу. Поэтому зачастую теперь используют другие методы, основанные на конкретных знаниях. Для этого стали изучаться природа вещей, взаимодействие элементов друг с другом. Стали использоваться математические расчеты, научные обоснования, эксперименты и опыт прошлого.
Метод проб и ошибок все так же отлично используется в творчестве. Но строить автомобиль таким способом уже кажется глупым и неактуальным. Поэтому теперь, при нынешнем уровне развития цивилизации, нужно в точных науках по большей части использовать другие методы.
Часто при рассматриваемом способе задача может описывать много совершенно незначительных вещей и не учитывать априори важные вещи. Например, изобретатель пенициллина (антибиотик) утверждал, что при правильном подходе лекарство могли изобрести лет на двадцать раньше его. Это поспособствовало бы спасению огромного количества жизней.
При сложных задачах часто бывают ситуации, когда сам вопрос лежит в одной области знаний, а его решение — совершенно в другой.
Не всегда исследователь уверен, что ответ вообще будет найден.
Автор метода проб и ошибок
Кто конкретно изобрел это способ познания, мы никогда не узнаем. Точнее мы знаем, что это явно был изобретательный человек, которым, скорее всего, руководило желание улучшить свою жизнь.
В древности люди были достаточно ограничены во многих вещах. Все изобреталось именно этим методом. Тогда еще не было каких-то фундаментальных знаний в области физики, математики, химии и прочих важных наук. Поэтому приходилось действовать наугад. Именно так добыли огонь, чтобы защищаться от хищников, готовить пищу и обогревать жилище. Оружие, чтобы добывать пропитание, лодки — для передвижения по рекам. Все было изобретено при столкновении человека с трудностью. Но каждый раз решаемая проблема приводила к более качественному уровню жизни.
Известно, что многие ученые использовали этот метод в своих трудах.
Однако именно описание метода и активное использование мы наблюдаем у физиолога Торндайка в конце девятнадцатого века.
Исследования Торндайка
Пример метода проб и ошибок можно рассмотреть в научных трудах ученого-физиолога. Он ставил различные поведенческие эксперименты с животными, помещая их в специальные коробки.
Один из экспериментов выглядел приблизительно следующим образом. Кошка, помещенная в ящик, ищет выход. Сама коробка может иметь 1 вариант открытия: нужно было нажать на пружинку — и дверца распахивалась. Животное применяло много действий (так называемых проб), и большинство из них оказывались неудачными. Кошка так и оставалась в коробке. Но после некоторого набора вариантов животному удавалось нажать на пружинку и выбраться из ящика. Таким образом, кошка, попадая в коробку, с течением времени запоминала варианты развития событий. И выбиралась из ящика за более короткое время.
Торндайк доказал, что метод действителен, и хоть результат не линеен, но со временем, при повторении аналогичных действий, решение приходит практически моментально.
Решение задач методом проб и ошибок
Примеров этого способа великое множество, однако стоит привести один очень интересный.
В начале двадцатого века жил известный конструктор двигателей для авиации Микулин. В то время наблюдалось огромное количество авиакатастроф из-за магнето, то есть искра зажигания через некоторое время полета исчезала. Много было экспериментов и размышлений о причине, но ответ пришел в совершенно неожиданной ситуации.
Александр Александрович встретил на улице мужчину с подбитым глазом. В тот момент к нему и пришло озарение, что человек без одного глаза видит намного хуже. Он поделился этим наблюдением с авиатором Уточкиным. Когда установили в самолеты второе магнето, количество авиакатастроф значительно уменьшилось. А Уточкин некоторое время выплачивал после каждого показательного полета Микулину денежные вознаграждения.
Применение способа в математике
Достаточно часто метод проб и ошибок в математике применяется в школах как способ развития логического мышления и проверки скорости поиска вариантов. Это позволяет разнообразить процесс обучения и внести элементы игры.
Часто можно встретить в школьных учебниках задания с формулировкой «реши уравнение методом проб и ошибок». В данном случае необходимо подбирать варианты ответа. Когда найден правильный ответ, он просто доказывается уже практически, то есть проводятся необходимые расчеты. В итоге мы удостоверяемся, что это единственно верный ответ.
Пример практической задачи
Метод проб и ошибок в математике 5 класса (в последних изданиях) часто фигурирует. Приведем пример.
Необходимо назвать, какие стороны могут быть у прямоугольника. При условии, что площадь (S) = 32 см, а периметр (P) = 24 см.
Решение данной задачи: предположим, что длина одной стороны 4. Значит и длина еще одной стороны такая же.
Получаем следующее уравнение:
24 – 4 – 4 = 16
16 делим на 2 = 8
8 см – это ширина.
Проверяем по формуле площади. S = A*B = 8*4 = 32 сантиметра. Как мы видим, решение верное. Так же можно вычислить и периметр. По формуле получается следующий расчет Р = 2* (А + В) = 2* (4 + 
В математике метод проб и ошибок не всегда отлично подходит для поиска решений. Зачастую можно использовать более подходящие способы, при этом затрачивается меньше времени. Но для развития мышления данный метод имеется в арсенале каждого педагога.
Теория решения изобретательских задач
В ТРИЗ метод проб и ошибок считается одним из самых неэффективных. Когда человек попадает в необычную для него затруднительную ситуацию, то действия наугад, скорее всего, будут безрезультатными. Можно потратить много времени и в результате не добиться успеха. Теория решения изобретательских задач основана на уже известных закономерностях, и обычно используются другие методы познания. Часто ТРИЗ используют в воспитании детей, делая этот процесс интересным и увлекательным для ребенка.
Выводы
Рассмотрев данный метод, можно с уверенностью сказать, что он достаточно интересный. Несмотря на недостатки, он часто используется в решении творческих задач.
Однако не всегда он позволяет добиться нужного результата. Никогда исследователь не знает, когда стоит прекратить поиски или, может, стоит сделать еще пару усилий и гениальное изобретение появится на свет. Также непонятно, сколько времени будет затрачено.
Если вы решили использовать данный метод для решения какой-либо проблемы, то должны понимать, что ответ порой может находиться в совершенно неожиданной области. Но это позволяет взглянуть на поиск с разных точек зрения. Возможно, придется набросать несколько десятков вариаций, а может, и тысячи. Но лишь упорство и вера в успех приведут к нужному результату.
Иногда этот метод используют как дополнительный. Например, на начальном этапе для сужения поиска. Либо когда исследование было проведено многими способами и зашло в тупик. В этом случае творческая составляющая метода позволит найти компромиссное решение проблемы.
Метод проб и ошибок часто применяют в педагогической деятельности. Он позволяет детям на собственном опыте находить решения в различных жизненных ситуациях. Это учит их запоминать правильные типы поведения, которые приняты в обществе.
Художники используют данный способ для поиска вдохновения.
Метод стоит опробовать в обыденной жизни при решении проблем. Возможно, какие-то вещи предстанут вам по-другому.