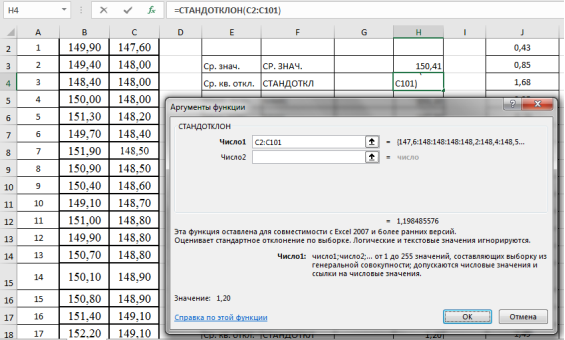
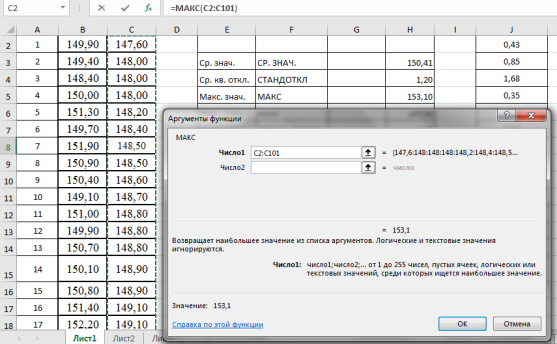
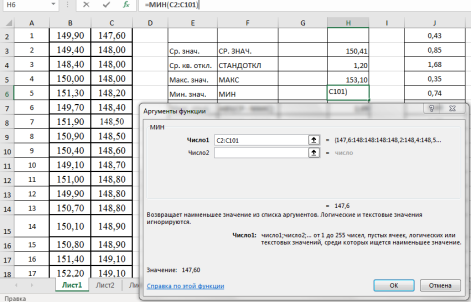
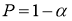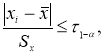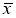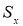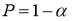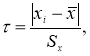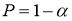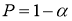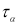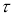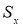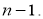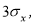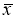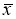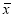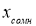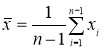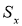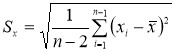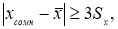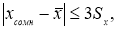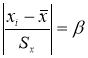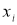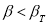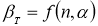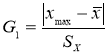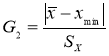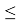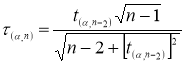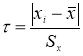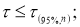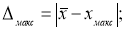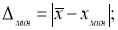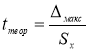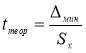Методы
исключения систематических погрешностей
В
теоретической метрологии принято
считать, что систематические погрешности
можно обнаружить и исключить из результата
измерения. Однако в реальных условиях
полностью исключить систематическую
составляющую погрешности невозможно.
Всегда остаются какие-то не исключенные
факторы, которые нужно учитывать и
которые будут вызывать систематическую
погрешность измерения. Это значит, что
систематическая погрешность тоже
случайна и ее определение обусловлено
лишь установившимися традициями
обработки и представления результатов
измерения.
Для
результата измерения не обнаруженная
систематическая составляющая погрешности
гораздо опаснее случайной погрешности:
если случайная составляющая вызывает
вариацию (разброс) результатов, то
систематическая — устойчиво их искажает
(смещает результаты измерений, содержащие
систематическую погрешность, относятся
к неисправленным. В любом случае
отсутствие или незначительность
(пренебрежение) систематической
погрешности надо доказать.
Постоянные
систематические погрешности можно
обнаружить только путем сравнения
результатов измерений с другими,
подученными с использованием более
точных методов и средств измерения. В
ряде случаев систематическую погрешность
можно исключить путем устранения
источников погрешности до начала
измерений (профилактика погрешности),
а в процессе измерений — внесением
известных поправок в результаты
измерений. Профилактика — наиболее
рациональный способ снижения погрешности,
который заключается в устранении
влияния, например, температуры
(термостатированием и термоизоляцией),
магнитных полей (магнитными экранами),
вибраций и т. п. Сюда же относятся
регулировка, ремонт и поверка средств
измерений.
Метод
замещения обеспечивает наиболее полную
компенсацию постоянной систематической
погрешности. Суть данного метода состоит
в такой замене измеряемой величины хи
известной величиной Δ, получаемой с
помощью регулируемой меры, чтобы
показание измерительного прибора
сохранилось неизменным. Значение
измеряемой величины считывают в этом
случае по указателю меры. При использовании
данного метода погрешность неточного
измерительного прибора устраняют, а
погрешность измерения определяют только
погрешностью самой меры и погрешностью
отсчета измеряемой величины по указателю
меры.
Метод
противопоставления применяется в
радиоизмерениях для уменьшения постоянных
систематических погрешностей при
сравнении измеряемой величины с известной
величиной примерно равного значения,
воспроизводимой соответствующей
образцовой мерой.
Оценки
случайных погрешностей (2.17), (2.18), (2.19)
среднего арифметического значения Х0
так же, как и оценки случайных погрешностей
отдельных измерений, не могут служить
в качестве поправок, как это имеет место
для систематических погрешностей.
Результат многократного измерения,
когда в качестве оценки, например,
принята вероятная погрешность, дается
в виде Х0 Е, где Х0 и Е выражаются в
абсолютных единицах.
Для
оценки случайных погрешностей производятся
многократные измерения, по результатам
которых определяются закон их распределения
и среднеквадратическое отклонение.
Для
оценки случайных погрешностей, кроме
среднего квадрати-ческого отклонения
о, иногда пользуются вероятной
погрешностью, равной ( 2 / 3) 0, и предельной
погрешностью, равной Зо. Отсюда следует,
что если произвести очень много измерений,
то при нормальном законе распределения
в среднем каждый из двух результатов
измерений будет иметь случайную
погрешность более ( 2 / 3) а, и только в
одном результате из 370 появится случайная
погрешность по значению большая За.
Обычно при точных измерениях предельная
погрешность За считается критерием
грубых погрешностей, поэтому результаты,
содержащие погрешности больше За,
исключают из рассмотрения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Существует две фундаментальные стратегии: обработка исправимых ошибок (исключения, коды возврата по ошибке, функции-обработчики) и неисправимых (assert(), abort()). В каких случаях какую стратегию лучше использовать?
Виды ошибок
Ошибки возникают по разным причинам: пользователь ввёл странные данные, ОС не может дать вам обработчика файла или код разыменовывает (dereferences) nullptr. Каждая из описанных ошибок требует к себе отдельного подхода. По причинам ошибки делятся на три основные категории:
- Пользовательские ошибки: здесь под пользователем подразумевается человек, сидящий перед компьютером и действительно «использующий» программу, а не какой-то программист, дёргающий ваш API. Такие ошибки возникают тогда, когда пользователь делает что-то неправильно.
- Системные ошибки появляются, когда ОС не может выполнить ваш запрос. Иными словами, причина системных ошибок — сбой вызова системного API. Некоторые возникают потому, что программист передал системному вызову плохие параметры, так что это скорее программистская ошибка, а не системная.
- Программистские ошибки случаются, когда программист не учитывает предварительные условия API или языка программирования. Если API требует, чтобы вы не вызывали
foo()с0в качестве первого параметра, а вы это сделали, — виноват программист. Если пользователь ввёл0, который был переданfoo(), а программист не написал проверку вводимых данных, то это опять же его вина.
Каждая из описанных категорий ошибок требует особого подхода к их обработке.
Пользовательские ошибки
Сделаю очень громкое заявление: такие ошибки — на самом деле не ошибки.
Все пользователи не соблюдают инструкции. Программист, имеющий дело с данными, которые вводят люди, должен ожидать, что вводить будут именно плохие данные. Поэтому первым делом нужно проверять их на валидность, сообщать пользователю об обнаруженных ошибках и просить ввести заново.
Поэтому не имеет смысла применять к пользовательским ошибкам какие-либо стратегии обработки. Вводимые данные нужно как можно скорее проверять, чтобы ошибок не возникало.
Конечно, такое не всегда возможно. Иногда проверять вводимые данные слишком дорого, иногда это не позволяет сделать архитектура кода или разделение ответственности. Но в таких случаях ошибки должны обрабатываться однозначно как исправимые. Иначе, допустим, ваша офисная программа будет падать из-за того, что вы нажали backspace в пустом документе, или ваша игра станет вылетать при попытке выстрелить из разряженного оружия.
Если в качестве стратегии обработки исправимых ошибок вы предпочитаете исключения, то будьте осторожны: исключения предназначены только для исключительных ситуаций, к которым не относится большинство случаев ввода пользователями неверных данных. По сути, это даже норма, по мнению многих приложений. Используйте исключения только тогда, когда пользовательские ошибки обнаруживаются в глубине стека вызовов, вероятно, внешнего кода, когда они возникают редко или проявляются очень жёстко. В противном случае лучше сообщать об ошибках с помощью кодов возврата.
Системные ошибки
Обычно системные ошибки нельзя предсказать. Более того, они недетерминистские и могут возникать в программах, которые до этого работали без нареканий. В отличие от пользовательских ошибок, зависящих исключительно от вводимых данных, системные ошибки — настоящие ошибки.
Но как их обрабатывать, как исправимые или неисправимые?
Это зависит от обстоятельств.
Многие считают, что ошибка нехватки памяти — неисправимая. Зачастую не хватает памяти даже для обработки этой ошибки! И тогда приходится просто сразу же прерывать выполнение.
Но падение программы из-за того, что ОС не может выделить сокет, — это не слишком дружелюбное поведение. Так что лучше бросить исключение и позволить catch аккуратно закрыть программу.
Но бросание исключения — не всегда правильный выбор.
Кто-то даже скажет, что он всегда неправильный.
Если вы хотите повторить операцию после её сбоя, то обёртывание функции в try-catch в цикле — медленное решение. Правильный выбор — возврат кода ошибки и цикличное исполнение, пока не будет возвращено правильное значение.
Если вы создаёте вызов API только для себя, то просто выберите подходящий для своей ситуации путь и следуйте ему. Но если вы пишете библиотеку, то не знаете, чего хотят пользователи. Дальше мы разберём подходящую стратегию для этого случая. Для потенциально неисправимых ошибок подойдёт «обработчик ошибок», а при других ошибках необходимо предоставить два варианта развития событий.
Обратите внимание, что не следует использовать подтверждения (assertions), включающиеся только в режиме отладки. Ведь системные ошибки могут возникать и в релизной сборке!
Программистские ошибки
Это худший вид ошибок. Для их обработки я стараюсь сделать так, чтобы мои ошибки были связаны только с вызовами функций, то есть с плохими параметрами. Прочие типы программистских ошибок могут быть пойманы только в runtime, с помощью отладочных макросов (assertion macros), раскиданных по коду.
При работе с плохими параметрами есть две стратегии: дать им определённое или неопределённое поведение.
Если исходное требование для функции — запрет на передачу ей плохих параметров, то, если их передать, это считается неопределённым поведением и должно проверяться не самой функцией, а оператором вызова (caller). Функция должна делать только отладочное подтверждение (debug assertion).
С другой стороны, если отсутствие плохих параметров не является частью исходных требований, а документация определяет, что функция будет бросать bad_parameter_exception при передаче ей плохого параметра, то передача — это хорошо определённое поведение (бросание исключения или любая другая стратегия обработки исправимых ошибок), и функция всегда должна это проверять.
В качестве примера рассмотрим получающие функции (accessor functions) std::vector<T>operator[] говорится, что индекс должен быть в пределах валидного диапазона, при этом at() сообщает нам, что функция кинет исключение, если индекс не попадает в диапазон. Более того, большинство реализаций стандартных библиотек обеспечивают режим отладки, в котором проверяется индекс operator[], но технически это неопределённое поведение, оно не обязано проверяться.
Примечание: необязательно бросать исключение, чтобы получилось определённое поведение. Пока это не упомянуто в исходных условиях для функции, это считается определённым. Всё, что прописано в исходных условиях, не должно проверяться функцией, это неопределённое поведение.
Когда нужно проверять только с помощью отладочных подтверждений, а когда — постоянно?
К сожалению, однозначного рецепта нет, решение зависит от конкретной ситуации. У меня есть лишь одно проверенное правило, которому я следую при разработке API. Оно основано на наблюдении, что проверять исходные условия должен вызывающий, а не вызываемый. А значит, условие должно быть «проверяемым» для вызывающего. Также условие «проверяемое», если можно легко выполнить операцию, при которой значение параметра всегда будет правильным. Если для параметра это возможно, то это получается исходное условие, а значит, проверяется только посредством отладочного подтверждения (а если слишком дорого, то вообще не проверяется).
Но конечное решение зависит от многих других факторов, так что очень трудно дать какой-то общий совет. По умолчанию я стараюсь свести к неопределённому поведению и использованию только подтверждений. Иногда бывает целесообразно обеспечить оба варианта, как это делает стандартная библиотека с operator[] и at().
Хотя в ряде случаев это может быть ошибкой.
Об иерархии std::exception
Если в качестве стратегии обработки исправимых ошибок вы выбрали исключения, то рекомендуется создать новый класс и наследовать его от одного из классов исключений стандартной библиотеки.
Я предлагаю наследовать только от одного из этих четырёх классов:
std::bad_alloc: для сбоев выделения памяти.std::runtime_error: для общих runtime-ошибок.std::system_error(производное отstd::runtime_error): для системных ошибок с кодами ошибок.std::logic_error: для программистских ошибок с определённым поведением.
Обратите внимание, что в стандартной библиотеке разделяются логические (то есть программистские) и runtime-ошибки. Runtime-ошибки — более широкое определение, чем «системные». Оно описывает «ошибки, обнаруживаемые только при выполнении программы». Такая формулировка не слишком информативна. Лично я использую её для плохих параметров, которые не являются исключительно программистскими ошибками, а могут возникнуть и по вине пользователей. Но это можно определить лишь глубоко в стеке вызовов. Например, плохое форматирование комментариев в standardese приводит к исключению при парсинге, проистекающему из std::runtime_error. Позднее оно ловится на соответствующем уровне и фиксируется в логе. Но я не стал бы использовать этот класс иначе, как и std::logic_error.
Подведём итоги
Есть два пути обработки ошибок:
- как исправимые: используются исключения или возвращаемые значения (в зависимости от ситуации/религии);
- как неисправимые: ошибки журналируются, а программа прерывается.
Подтверждения — это особый вид стратегии обработки неисправимых ошибок, только в режиме отладки.
Есть три основных источника ошибок, каждый требует особого подхода:
- Пользовательские ошибки не должны обрабатываться как ошибки на верхних уровнях программы. Всё, что вводит пользователь, должно проверяться соответствующим образом. Это может обрабатываться как ошибки только на нижних уровнях, которые не взаимодействуют с пользователями напрямую. Применяется стратегия обработки исправимых ошибок.
- Системные ошибки могут обрабатываться в рамках любой из двух стратегий, в зависимости от типа и тяжести. Библиотеки должны работать как можно гибче.
- Программистские ошибки, то есть плохие параметры, могут быть запрещены исходными условиями. В этом случае функция должна использовать только проверку с помощью отладочных подтверждений. Если же речь идёт о полностью определённом поведении, то функции следует предписанным образом сообщать об ошибке. Я стараюсь по умолчанию следовать сценарию с неопределённым поведением и определяю для функции проверку параметров лишь тогда, когда это слишком трудно сделать на стороне вызывающего.
Гибкие методики обработки ошибок в C++
Иногда что-то не работает. Пользователи вводят данные в недопустимом формате, файл не обнаруживается, сетевое соединение сбоит, в системе кончается память. Всё это ошибки, и их надо обрабатывать.
Это относительно легко сделать в высокоуровневых функциях. Вы точно знаете, почему что-то пошло не так, и можете обработать это соответствующим образом. Но в случае с низкоуровневыми функциями всё не так просто. Они не знают, что пошло не так, они знают лишь о самом факте сбоя и должны сообщить об этом тому, кто их вызвал.
В C++ есть два основных подхода: коды возврата ошибок и исключения. Сегодня широко распространено использование исключений. Но некоторые не могут / думают, что не могут / не хотят их использовать — по разным причинам.
Я не буду принимать чью-либо сторону. Вместо этого я опишу методики, которые удовлетворят сторонников обоих подходов. Особенно методики пригодятся разработчикам библиотек.
Проблема
Я работаю над проектом foonathan/memory. Это решение предоставляет различные классы выделения памяти (allocator classes), так что в качестве примера рассмотрим структуру функции выделения.
Для простоты возьмём malloc(). Она возвращает указатель на выделяемую память. Если выделить память не получается, то возвращается nullptr, то есть NULL, то есть ошибочное значение.
У этого решения есть недостатки: вам нужно проверять каждый вызов malloc(). Если вы забудете это сделать, то выделите несуществующую память. Кроме того, по своей натуре коды ошибок транзитивны: если вызвать функцию, которая может вернуть код ошибки, и вы не можете его проигнорировать или обработать, то вы тоже должны вернуть код ошибки.
Это приводит нас к ситуации, когда чередуются нормальные и ошибочные ветви кода. Исключения в таком случае выглядят более подходящим решением. Благодаря им вы сможете обрабатывать ошибки только тогда, когда вам это нужно, а в противном случае — достаточно тихо передать их обратно вызывающему.
Это можно расценить как недостаток.
Но в подобных ситуациях исключения имеют также очень большое преимущество: функция выделения памяти либо возвращает валидную память, либо вообще ничего не возвращает. Это функция «всё или ничего», возвращаемое значение всегда будет валидным. Это полезное следствие согласно принципу Скотта Майера «Make interfaces hard to use incorrectly and easy to use correctly».
Учитывая вышесказанное, можно утверждать, что вам следует использовать исключения в качестве механизма обработки ошибок. Этого мнения придерживается большинство разработчиков на С++, включая и меня. Но проект, которым я занимаюсь, — это библиотека, предоставляющая средства выделения памяти, и предназначена она для приложений, работающих в реальном времени. Для большинства разработчиков подобных приложений (особенно для игроделов) само использование исключений — исключение.
Каламбур детектед.
Чтобы уважить эту группу разработчиков, моей библиотеке лучше обойтись без исключений. Но мне и многим другим они нравятся за элегантность и простоту обработки ошибок, так что ради других разработчиков моей библиотеке лучше использовать исключения.
Так что же делать?
Идеальное решение: возможность включать и отключать исключения по желанию. Но, учитывая природу исключений, нельзя просто менять их местами с кодами ошибок, поскольку у нас не будет внутреннего кода проверки на ошибки — весь внутренний код опирается на предположение о прозрачности исключений. И даже если бы внутри можно было использовать коды ошибок и преобразовывать их в исключения, это лишило бы нас большинства преимуществ последних.
К счастью, я могу определить, что вы делаете, когда обнаруживаете ошибку нехватки памяти: чаще всего вы журналируете это событие и прерываете программу, поскольку она не может корректно работать без памяти. В таких ситуациях исключения — просто способ передачи контроля другой части кода, которая журналирует и прерывает программу. Но есть старый и эффективный способ передачи контроля: указатель функции (function pointer), то есть функция-обработчик (handler function).
Если у вас включены исключения, то вы просто их бросаете. В противном случае вызываете функцию-обработчика и затем прерываете программу. Это предотвратит бесполезную работу функции-обработчика, та позволит программе продолжить выполняться в обычном режиме. Если не прервать, то произойдёт нарушение обязательного постусловия функции: всегда возвращать валидный указатель. Ведь на выполнении этого условия может быть построена работа другого кода, да и вообще это нормальное поведение.
Я называю такой подход обработкой исключений и придерживаюсь его при работе с памятью.
Решение 1: обработчик исключений
Если вам нужно обработать ошибку в условиях, когда наиболее распространённым поведением будет «журналировать и прервать», то можно использовать обработчика исключений. Это такая функция-обработчик, которая вызывается вместо бросания объекта-исключения. Её довольно легко реализовать даже в уже существующем коде. Для этого нужно поместить управление обработкой в класс исключений и обернуть в макрос выражение throw.
Сначала дополним класс и добавим функции для настройки и, возможно, запрашивания функции-обработчика. Я предлагаю делать это так же, как стандартная библиотека обрабатывает std::new_handler:
class my_fatal_error
{
public:
// тип обработчика, он должен брать те же параметры, что и конструктор,
// чтобы у них была одинаковая информация
using handler = void(*)( ... );
// меняет функцию-обработчика
handler set_handler(handler h);
// возвращает текущего обработчика
handler get_handler();
... // нормальное исключение
};Поскольку это входит в область видимости класса исключений, вам не нужно именовать каким-то особым образом. Отлично, нам же легче.
Если исключения включены, то для удаления обработчика можно использовать условное компилирование (conditional compilation). Если хотите, то также напишите обычный подмешанный класс (mixin class), дающий требуемую функциональность.
Конструктор исключений элегантен: он вызывает текущую функцию-обработчика, передавая ей требуемые аргументы из своих параметров. А затем комбинирует с последующим макросом throw:
If```cpp #if EXCEPTIONS #define THROW(Ex) throw (Ex) #else #define THROW(Ex) (Ex), std::abort() #endif> Такой макрос throw также предоставляется [foonathan/compatiblity](https://github.com/foonathan/compatibility).
Можно использовать его и так:
```cpp
THROW(my_fatal_error(...))
Если у вас включена поддержка исключений, то будет создан и брошен объект-исключение, всё как обычно. Но если поддержка выключена, то объект-исключение всё равно будет создан, и — это важно — только после этого произойдёт вызов std::abort(). А поскольку конструктор вызывает функцию-обработчика, то он и работает, как требуется: вы получаете точку настройки для журналирования ошибки. Благодаря же вызову std::abort() после конструктора пользователь не может нарушить постусловие.
Когда я работаю с памятью, то при включённых исключениях у меня также включён и обработчик, который вызывается при бросании исключения.
Так что при этой методике вам ещё будет доступна определённая степень кастомизации, даже если вы отключите исключения. Конечно, замена неполноценная, мы только журналируем и прерываем работу программы, без дальнейшего продолжения. Но в ряде случаев, в том числе при исчерпании памяти, это вполне пригодное решение.
А если я хочу продолжить работу после бросания исключения?
Методика с обработчиком исключений не позволяет этого сделать в связи с постусловием кода. Как же тогда продолжить работу?
Ответ прост — никак. По крайней мере, это нельзя сделать так же просто, как в других случаях. Нельзя просто так вернуть код ошибки вместо исключения, если функция на это не рассчитана.
Есть только одно решение: сделать две функции. Одна возвращает код ошибки, а вторая бросает исключения. Клиенты, которым нужны исключения, будут использовать второй вариант, остальные — первый.
Извините, что говорю такие очевидные вещи, но ради полноты изложения я должен был об этом сказать.
Для примера снова возьмём функцию выделения памяти. В этом случае я использую такие функции:
void* try_malloc(..., int &error_code) noexcept;
void* malloc(...);
При сбое выделения памяти первая версия возвращает nullptr и устанавливает error_code в коде ошибки. Вторая версия не возвращает nullptr, зато бросает исключение. Обратите внимание, что в рамках первой версии очень легко реализовать вторую:
void* malloc(...)
{
auto error_code = 0;
auto res = try_malloc(..., error_code);
if (!res)
throw malloc_error(error_code);
return res;
}Не делайте этого в обратной последовательности, иначе вам придётся ловить исключение, а это дорого. Также это не даст нам скомпилировать код без включённой поддержки исключений. Если сделаете, как показано, то можете просто стереть другую перегрузку (overload) с помощью условного компилирования.
Но даже если у вас включена поддержка исключений, клиенту всё равно может понадобиться вторая версия. Например, когда нужно выделить наибольший возможный объём памяти, как в нашем примере. Будет проще и быстрее вызывать в цикле и проверять по условию, чем ловить исключение.
Решение 2: предоставить две перегрузки
Если недостаточно обработчика исключений, то нужно предоставить две перегрузки. Одна использует код возврата, а вторая бросает исключение.
Если рассматриваемая функция не имеет возвращаемого значения, то можете её использовать для кода ошибки. В противном случае вам придётся возвращать недопустимое значение для сигнализирования об ошибке — как nullptr в вышеприведённом примере, — а также установить выходной параметр для кода ошибки, если хотите предоставить вызывающему дополнительную информацию.
Пожалуйста, не используйте глобальную переменную errno или что-то типа GetLastError()!
Если возвращаемое значение не содержит недопустимое значение для обозначения сбоя, то по мере возможности используйте std::optional или что-то похожее.
Перегрузка исключения (exception overload) может — и должна — быть реализована в рамках версии с кодом ошибки, как это показано выше. Если компилируете без исключений, сотрите перегрузку с помощью условного компилирования.
std::system_error
Подобная система идеально подходит для работы с кодами ошибок в С++ 11.
Она возвращает непортируемый (non-portable) код ошибки std::error_code, то есть возвращаемый функцией операционной системы. С помощью сложной системы библиотечных средств и категорий ошибок вы можете добавить собственные коды ошибок, или портируемые std::error_condition. Для начала почитайте об этом здесь. Если нужно, то можете использовать в функции кода ошибки std::error_code. А для функции исключения есть подходящий класс исключения: std::system_error. Он берёт std::error_code и применяется для передачи этих ошибок в виде исключений.
Эту или подобную систему должны использовать все низкоуровневые функции, являющиеся закрытыми обёртками ОС-функций. Это хорошая — хотя и сложная — альтернатива службе кодов ошибок, предоставляемой операционной системой.
Да, и мне ещё нужно добавить подобное в функции виртуальной памяти. На сегодняшний день они не предоставляют коды ошибок.
std::expected
Выше упоминалось о проблеме, когда у вас нет возвращаемого значения, содержащего недопустимое значение, которое можно использовать для сигнализирования об ошибке. Более того, выходной параметр — не лучший способ получения кода ошибки.
А глобальные переменные вообще не вариант!
В № 4109 предложено решение: std::expected. Это шаблон класса, который также хранит возвращаемое значение или код ошибки. В вышеприведённом примере он мог бы использоваться так:
std::expected<void*, std::error_code> try_malloc(...);
В случае успеха std::expected будет хранить не-null указатель памяти, а при сбое — std::error_code. Сейчас эта методика работает при любых возвращаемых значениях. Комбинация std::expected и функции исключения определённо допускает любые варианты использования.
Заключение
Если вы создаёте библиотеки, то иногда приходится обеспечивать максимальную гибкость использования. Под этим подразумевается и разнообразие средств обработки ошибок: иногда требуются коды возврата, иногда — исключения.
Одна из возможных стратегий — улаживание этих противоречий с помощью обработчика исключений. Просто удостоверьтесь, что когда нужно, то вызывается callback, а не бросается исключение. Это замена для критических ошибок, которая в любом случае будет журналироваться перед прерыванием работы программы. Как таковой этот способ не универсален, вы не можете переключаться в одной программе между двумя версиями. Это лишь обходное решение при отключённой поддержке исключений.
Более гибкий подход — просто предоставить две перегрузки, одну с исключениями, а вторую без. Это даст пользователям максимальную свободу, они смогут выбирать ту версию, что лучше подходит в их ситуации. Недостаток этого подхода: вам придётся больше потрудиться при создании библиотеки.
Случайные, систематические и грубые ошибки
Под
случайными
понимают ошибки, значения которых
меняются от одного измерения к другому.
Они являются следствием случайных
ошибок контрольно – измерительных
приборов, случайных ошибок экспериментатора,
неточных соблюдений методики измерения,
непостоянством самой контролируемой
величины. Для количественной оценки
случайных ошибок применяют математический
аппарат теории вероятностей и
математической статистики.
Наиболее
полно случайные ошибки могут быть
оценены функцией их распределения,
получаемой многократными наблюдениями
с последующей статистической обработкой
полученных экспериментальных данных.
Отличие
систематических
ошибок от
случайных состоит в том, что их значение
остается постоянным при проведении
серии однотипных измерений; причины их
возникновения известны, следовательно,
они могут быть исключены из окончательного
результата, если их величина предварительно
определена. К систематическим ошибкам
можно отнести ошибки эталонов, по которым
проградуированы контрольно – измерительные
приборы, систематические ошибки,
связанные с принятой методикой измерения
(например, ошибки, возникшие вследствие
неучета температурных поправок,
применения приближенных формул расчета
и т.д.), “личные ошибки” экспериментатора,
т.е. присущие данному лицу и др. Различают
также постоянные (неизменные во времени)
и прогрессирующие (возрастающие или
убывающие во времени) систематические
ошибки.
Грубые
ошибки (промахи) являются результатом
нарушения условия и процесса измерений.
Их характерным признаком является
резкое отличие от результатов
предшествующих измерений. Повторение
эксперимента (если это возможно) является
наиболее надежным, достоверным и
эффективным способом обнаружения грубых
ошибок.
Современные
математические методы обработки
результатов эксперимента базируется
на вероятностном подходе и предполагают,
что ошибки измерения являются случайными.
При этом предполагается, что к началу
этой обработки все грубые и систематические
ошибки выявлены и устранены.
Рассмотрим
практические методы исключения грубых
ошибок, если их не удалось исключить в
процессе проведения экспериментов.
Методы исключения резко выделяющихся результатов эксперимента
1. Критерий
Романовского.
Имеется
упорядоченный статистический ряд
измеренных значений случайной величины
x:
x1,
x2,
…, xi,
…, xn.
Здесь:
х1
или хn
– значения, которые вызывают сомнения
(резко отличаются от остальных значений);
n
– объем выборки.
Сущность критерия:
а)
вычисляется
,
где
— резко выделяющее значение, в качестве
которого взято значение
или
;
и
— выборочные значения математического
ожидания и среднего квадратического
отклонения, вычисленные без значения
(при объеме выборки n-1);
б)
определяется
из табл. 1.
Таблица1
Табличные значения критерия Романовского
|
|
tтабл. |
|||||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
30 |
40 |
60 |
|
|
|
0.01 |
78 |
11.5 |
6.5 |
5 |
4.4 |
4 |
3.7 |
3.5 |
3.4 |
2.9 |
2.8 |
2.7 |
2.7 |
2.6 |
|
0.02 |
39 |
8 |
5.1 |
4.1 |
3.6 |
3.4 |
3.2 |
3.1 |
3 |
2.6 |
2.5 |
2.5 |
2.4 |
2.3 |
|
0.05 |
15.6 |
5 |
3.6 |
3 |
2.8 |
2.6 |
2.5 |
2.4 |
2.4 |
2.2 |
2.1 |
2.0 |
2.0 |
2.0 |
в)
сравнивается tрасч.
и tтабл.
Если
tрасч.
> tтабл.,
то с вероятностью P=1-
значение x1
или xn
статистического ряда не принадлежит к
рассматриваемой совокупности СВ X.
Пример.
При изучении
технологического процесса изготовления
электронного средства при n-1
независимых равноточных измерениях
некоторой физической величины было
получено среднее значение, равное m
= 8.6 и среднее
квадратическое значение S
= 0.121. Известно
также, что n
измерение дало результат x*
= 8.923. Необходимо
выяснить с вероятностью P
= 0.98, является
ли этот результат грубой ошибкой, если
n=61.
Решение.
Вычислим
.
Из
табл.1 tтабл.
(
= 0.02;60)
2.4.
Поскольку
2.67>2.4,
то этот означает, что измерение x*
= 8.923 содержит
грубую ошибку с вероятностью 0.98.
Вопрос
решался бы иначе, если бы, например,
число приемлемых измерений в результате
эксперимента равнялось 10.
В этом случае по табл.1 имеем tтабл.
(
= 0.02;10)
= 3.0. Поскольку
2.67 < 3.0, то
исключать x*
= 8.923 не
следует.
2.
Критерий Ирвина.
Сущность
критерия:
а) вычисляется расч.
по упорядоченному статистическому ряду
по формуле:
— если вызывает сомнение значение xn
или
— если вызывает сомнение значение x1
;
б) определяется
из табл.2.
Таблица 2.
|
|
расч. |
||||||||
|
2 |
3 |
10 |
20 |
30 |
50 |
100 |
400 |
1000 |
|
|
0.1 |
2.3 |
1.8 |
1.2 |
1.0 |
1.0 |
0.9 |
0.8 |
0.7 |
0.6 |
|
0.05 |
2.8 |
2.2 |
1.5 |
1.3 |
1.2 |
1.1 |
1.0 |
0.9 |
0.8 |
|
0.01 |
3.7 |
2.9 |
2.0 |
1.8 |
1.7 |
1.6 |
1.5 |
1.3 |
1.2 |
|
0.005 |
4.0 |
3.2 |
2.3 |
2.0 |
1.9 |
1.8 |
1.6 |
1.5 |
1.4 |
в)
сравнивается расч.
и табл.
Если
расч.
> табл.,
то с вероятностью P
= 1-
значение x1
или xn
относится к резко выделяющемуся значению,
и оно исключается при статистической
обработке результатов эксперимента.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что
такое генеральная совокупность и выборка
изделий ?
2. Какие
оценки называются состоятельными,
несмещенными и эффективными ?
3. Как
строится гистограмма ?
4. Назовите
характеристики положения и рассеяния
случайных величин.
5. В
чем заключается сущность проверки
гипотезы о равенстве средних с помощью
критерия Стьюдента ?
6. Сущность
критерия Колмогорова.
7.
Сущность критерия Пирсона.
8.
Понятия случайных, систематических и
грубых ошибок.
9.
Критерий Романовского.
10.
Критерий Ирвина.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Случайные, систематические и грубые ошибки
Под
случайными
понимают ошибки, значения которых
меняются от одного измерения к другому.
Они являются следствием случайных
ошибок контрольно – измерительных
приборов, случайных ошибок экспериментатора,
неточных соблюдений методики измерения,
непостоянством самой контролируемой
величины. Для количественной оценки
случайных ошибок применяют математический
аппарат теории вероятностей и
математической статистики.
Наиболее
полно случайные ошибки могут быть
оценены функцией их распределения,
получаемой многократными наблюдениями
с последующей статистической обработкой
полученных экспериментальных данных.
Отличие
систематических
ошибок от
случайных состоит в том, что их значение
остается постоянным при проведении
серии однотипных измерений; причины их
возникновения известны, следовательно,
они могут быть исключены из окончательного
результата, если их величина предварительно
определена. К систематическим ошибкам
можно отнести ошибки эталонов, по которым
проградуированы контрольно – измерительные
приборы, систематические ошибки,
связанные с принятой методикой измерения
(например, ошибки, возникшие вследствие
неучета температурных поправок,
применения приближенных формул расчета
и т.д.), “личные ошибки” экспериментатора,
т.е. присущие данному лицу и др. Различают
также постоянные (неизменные во времени)
и прогрессирующие (возрастающие или
убывающие во времени) систематические
ошибки.
Грубые
ошибки (промахи) являются результатом
нарушения условия и процесса измерений.
Их характерным признаком является
резкое отличие от результатов
предшествующих измерений. Повторение
эксперимента (если это возможно) является
наиболее надежным, достоверным и
эффективным способом обнаружения грубых
ошибок.
Современные
математические методы обработки
результатов эксперимента базируется
на вероятностном подходе и предполагают,
что ошибки измерения являются случайными.
При этом предполагается, что к началу
этой обработки все грубые и систематические
ошибки выявлены и устранены.
Рассмотрим
практические методы исключения грубых
ошибок, если их не удалось исключить в
процессе проведения экспериментов.
Методы исключения резко выделяющихся результатов эксперимента
1. Критерий
Романовского.
Имеется
упорядоченный статистический ряд
измеренных значений случайной величины
x:
x1,
x2,
…, xi,
…, xn.
Здесь:
х1
или хn
– значения, которые вызывают сомнения
(резко отличаются от остальных значений);
n
– объем выборки.
Сущность критерия:
а)
вычисляется
,
где
— резко выделяющее значение, в качестве
которого взято значение
или
;
и
— выборочные значения математического
ожидания и среднего квадратического
отклонения, вычисленные без значения
(при объеме выборки n-1);
б)
определяется
из табл. 1.
Таблица1
Табличные значения критерия Романовского
|
|
tтабл. |
|||||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
30 |
40 |
60 |
|
|
|
0.01 |
78 |
11.5 |
6.5 |
5 |
4.4 |
4 |
3.7 |
3.5 |
3.4 |
2.9 |
2.8 |
2.7 |
2.7 |
2.6 |
|
0.02 |
39 |
8 |
5.1 |
4.1 |
3.6 |
3.4 |
3.2 |
3.1 |
3 |
2.6 |
2.5 |
2.5 |
2.4 |
2.3 |
|
0.05 |
15.6 |
5 |
3.6 |
3 |
2.8 |
2.6 |
2.5 |
2.4 |
2.4 |
2.2 |
2.1 |
2.0 |
2.0 |
2.0 |
в)
сравнивается tрасч.
и tтабл.
Если
tрасч.
> tтабл.,
то с вероятностью P=1-
значение x1
или xn
статистического ряда не принадлежит к
рассматриваемой совокупности СВ X.
Пример.
При изучении
технологического процесса изготовления
электронного средства при n-1
независимых равноточных измерениях
некоторой физической величины было
получено среднее значение, равное m
= 8.6 и среднее
квадратическое значение S
= 0.121. Известно
также, что n
измерение дало результат x*
= 8.923. Необходимо
выяснить с вероятностью P
= 0.98, является
ли этот результат грубой ошибкой, если
n=61.
Решение.
Вычислим
.
Из
табл.1 tтабл.
(
= 0.02;60)
2.4.
Поскольку
2.67>2.4,
то этот означает, что измерение x*
= 8.923 содержит
грубую ошибку с вероятностью 0.98.
Вопрос
решался бы иначе, если бы, например,
число приемлемых измерений в результате
эксперимента равнялось 10.
В этом случае по табл.1 имеем tтабл.
(
= 0.02;10)
= 3.0. Поскольку
2.67 < 3.0, то
исключать x*
= 8.923 не
следует.
2.
Критерий Ирвина.
Сущность
критерия:
а) вычисляется расч.
по упорядоченному статистическому ряду
по формуле:
— если вызывает сомнение значение xn
или
— если вызывает сомнение значение x1
;
б) определяется
из табл.2.
Таблица 2.
|
|
расч. |
||||||||
|
2 |
3 |
10 |
20 |
30 |
50 |
100 |
400 |
1000 |
|
|
0.1 |
2.3 |
1.8 |
1.2 |
1.0 |
1.0 |
0.9 |
0.8 |
0.7 |
0.6 |
|
0.05 |
2.8 |
2.2 |
1.5 |
1.3 |
1.2 |
1.1 |
1.0 |
0.9 |
0.8 |
|
0.01 |
3.7 |
2.9 |
2.0 |
1.8 |
1.7 |
1.6 |
1.5 |
1.3 |
1.2 |
|
0.005 |
4.0 |
3.2 |
2.3 |
2.0 |
1.9 |
1.8 |
1.6 |
1.5 |
1.4 |
в)
сравнивается расч.
и табл.
Если
расч.
> табл.,
то с вероятностью P
= 1-
значение x1
или xn
относится к резко выделяющемуся значению,
и оно исключается при статистической
обработке результатов эксперимента.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что
такое генеральная совокупность и выборка
изделий ?
2. Какие
оценки называются состоятельными,
несмещенными и эффективными ?
3. Как
строится гистограмма ?
4. Назовите
характеристики положения и рассеяния
случайных величин.
5. В
чем заключается сущность проверки
гипотезы о равенстве средних с помощью
критерия Стьюдента ?
6. Сущность
критерия Колмогорова.
7.
Сущность критерия Пирсона.
8.
Понятия случайных, систематических и
грубых ошибок.
9.
Критерий Романовского.
10.
Критерий Ирвина.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Изучение всех влияющих на исследуемый объект факторов одновременно
провести невозможно, поэтому в эксперименте рассматривается их ограниченное
число. Остальные активные факторы стабилизируются, т.е. устанавливаются на
каких-то одинаковых для всех опытов уровнях.
Некоторые факторы не могут быть обеспечены системами стабилизации
(например, погодные условия, самочувствие оператора и т.д.), другие же
стабилизируются с какой-то погрешностью (например, содержание какого-либо
компонента в среде зависит от ошибки при взятии навески и приготовления
раствора). Учитывая также, что измерение параметра у осуществляется
прибором, обладающим какой-то погрешностью, зависящей от класса точности
прибора, можно прийти к выводу, что результаты повторностей одного и того же
опыта ук будут приближенными и должны
отличаться один от другого и от истинного значения выхода процесса.
Неконтролируемое, случайное изменение и множества других влияющих на процесс
факторов вызывает случайные отклонения измеряемой величины ук
от ее истинного значения – ошибку опыта.
Каждый эксперимент содержит элемент неопределенности вследствие
ограниченности экспериментального материала. Постановка повторных (или
параллельных) опытов не дает полностью совпадающих результатов, потому что
всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку и нужно
оценить по параллельным опытам. Для этого опыт воспроизводится по возможности в
одинаковых условиях несколько раз и затем берется среднее арифметическое всех
результатов. Среднее арифметическое у равно сумме всех n отдельных результатов, деленной на
количество параллельных опытов n:
Отклонение результата любого опыта от среднего арифметического
можно представить как разность y2–
, где y2 – результат отдельного
опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений
повторных опытов. Для измерения этой изменчивости чаще всего используют
дисперсию.
Дисперсией называется среднее значение квадрата отклонений
величины от ее среднего значения. Дисперсия обозначается s2 и
выражается формулой:
где (n-1)
– число степеней свободы, равное количеству опытов минус единица. Одна степень
свободы использована для вычисления среднего.
Корень квадратный из дисперсии, взятый с положительным знаком,
называется средним квадратическим отклонением, стандартом или квадратичной
ошибкой:
Ошибка опыта является суммарной величиной, результатом многих
ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др.
Каждую из этих ошибок можно, в свою очередь, разделить на составляющие.
Все ошибки принято разделять на два класса: систематические и
случайные (рисунок 1).
Систематические ошибки порождаются причинами, действующими
регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и
определить количественно. Систематическая ошибка – это ошибка,
которая остаётся постоянно или закономерно изменяется при повторных измерениях
одной и той же величины. Эти ошибки появляются вследствие неисправности
приборов, неточности метода измерения, какого либо упущения экспериментатора,
либо использования для вычисления неточных данных. Обнаружить систематические
ошибки, а также устранить их во многих случаях нелегко. Требуется тщательный
разбор методов анализа, строгая проверка всех измерительных приборов и
безусловное выполнение выработанных практикой правил экспериментальных работ.
Если систематические ошибки вызваны известными причинами, то их можно
определить. Подобные погрешности можно устранить введением поправок.
Систематические ошибки находят, калибруя измерительные приборы и
сопоставляя опытные данные с изменяющимися внешними условиями (например, при
градуировке термопары по реперным точкам, при сравнении с эталонным прибором).
Если систематические ошибки вызываются внешними условиями (переменной
температуры, сырья и т.д.), следует компенсировать их влияние.
Случайными ошибками называются
те, которые появляются нерегулярно, причины, возникновения которых неизвестны и
которые невозможно учесть заранее. Случайные ошибки вызываются и объективными
причинами и субъективными. Например, несовершенством приборов, их освещением,
расположением, изменением температуры в процессе измерений, загрязнением
реактивов, изменением электрического тока в цепи. Когда случайная ошибка больше
величины погрешности прибора, необходимо многократно повторить одно и тоже
измерение. Это позволяет сделать случайную ошибку сравнимой с погрешностью
вносимой прибором. Если же она меньше погрешности прибора, то уменьшать её нет
смысла. Такие ошибки имеют значение, которое отличается в отдельных измерениях.
Т.е. их значения могут быть неодинаковыми для измерений сделанных даже в
одинаковых условиях. Поскольку причины, приводящие к случайным ошибкам
неодинаковы в каждом эксперименте, и не могут быть учтены, поэтому исключить
случайные ошибки нельзя, можно лишь оценить их значения. При многократном
определении какого-либо показателя могут встречаться результаты, которые
значительно отличаются от других результатов той же серии. Они могут быть
следствием грубой ошибки, которая вызвана невнимательностью экспериментатора.
Систематические и случайные ошибки состоят из множества
элементарных ошибок. Для того чтобы исключать инструментальные ошибки, следует
проверять приборы перед опытом, иногда в течение опыта и обязательно после опыта.
Ошибки при проведении самого опыта возникают вследствие неравномерного нагрева
реакционной среды, разного способа перемешивания и т.п.
При повторении опытов такие ошибки могут вызвать большой разброс
экспериментальных результатов.
Очень важно исключить из экспериментальных данных грубые ошибки,
так называемый брак при повторных опытах. Грубые ошибки легко
обнаружить. Для выявления ошибок необходимо произвести измерения в других
условиях или повторить измерения через некоторое время. Для предотвращения
грубых ошибок нужно соблюдать аккуратность в записях, тщательность в работе и
записи результатов эксперимента. Грубая ошибка должна быть исключена из
экспериментальных данных. Для отброса ошибочных данных существуют определённые
правила.
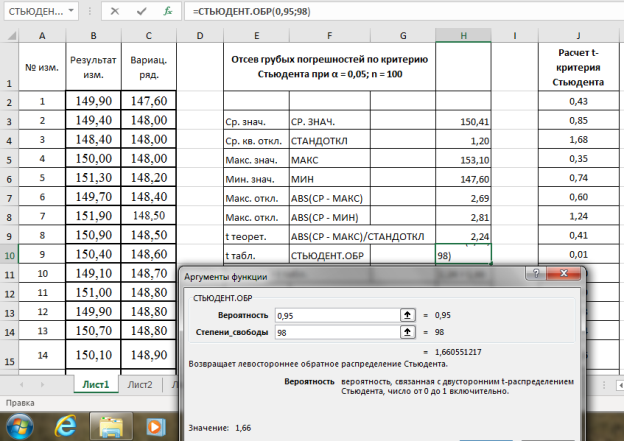
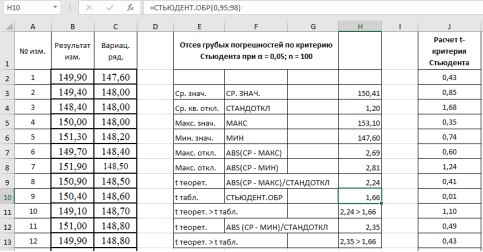
Например, используют критерий Стьюдента t (Р;
f):
Опыт считается бракованным, если экспериментальное значение критерия t по
модулю больше табличного значения t (Р; f).
Если в распоряжении исследователя имеется экспериментальная оценка
дисперсии S2(yk)
с небольшим конечным числом степеней свободы, то доверительные ошибки
рассчитываются с помощью критерий Стьюдента t (Р;
f):
ε()
= t (Р; f)* S(yk)/= t (Р; f)* S()
ε(yk) = t (Р; f)* S(yk)
Глава 1 Основные понятия статистики
Данная глава посвящена изложению основных понятий статистики эксперимента. Она может использоваться в качестве источника справочной информации.
1.1. Случайные ошибки результатов эксперимента
Говорят, что опыт эксперимента поставлен, когда необходимая аппаратура для его проведения была соответствующим образом настроена и функционировала при некотором заданном наборе определённых условий. Например, в химическом эксперименте опыт может быть проведён путём соединения в реакторе в определённых количествах химических реагентов, установки температуры и давления при определённых значениях и, позволив протекать реакции заданное время. В инженерной технологии опытом может быть обработка детали на станке при определённых технологических условиях. В психологическом эксперименте опыт может состоять в создании человеку некоторой управляемой стрессовой ситуации.
Вам также может быть полезна лекция «Лекция 2».
Результаты или данные эксперимента представляют собой результаты его опытов и обычно выражаются в виде чисел. Выполненные при одних и тех же условиях десять следующих один за другим опытов могут дать следующие результаты:
66,7 64,3 67,1 66,1 65,5 69,1 67,2 68,1 65,7 66,4
В химическом эксперименте данными могут быть процентный выход определённого вещества. В технологическом эксперименте данными могут быть значения шероховатости поверхности деталей при их обработке на станке, а в психологическом эксперименте данными могут быть периоды времени, затрачиваемые на выполнение определённого задания десятью подверженными стрессу персонами.
Однако, несмотря на то, что опыты эксперимента выполняются повторно при одних и тех же, как это только возможно сделать, условиях — результаты их выполнения всегда получаются разными. Происходящие при повторении опытов случайные изменения их результатов называются шумом, вариациями результатов эксперимента, ошибками эксперимента или просто ошибками. В этом случае ошибка используется в формальном и эмоционально нейтральном смысле. Она является выражением неустранимой в природе вариации. Такая статистическая ошибка не связана с порицанием, неодобрением или осуждением.
В дополнение к ошибкам измерения, округления и выборки ещё многие другие источники ошибок вносят вклад в вариацию результатов опытов эксперимента. Например, температура окружающей среды, мастерство или внимательность персонала, старение и чистота реагентов, эффективность или условия эксперимента – всё это может внести свои ошибки. Естественную вариацию результатов повторяемых опытов необходимо отличать от недоразумений или заблуждений, таких как неправильная постановка десятичной запятой во время записи результата или использование неправильного химического реагента.
Существенным недостатком многих экспериментаторов является отсутствие у них необходимых знаний, чтобы иметь дело с ситуациями, в которых нельзя безнаказанно игнорировать вариации результатов опытов эксперимента. Осведомлённость о возможных эффектах вариации результатов существенна не только при анализе данных, но является важной и при планировании получения данных, то есть при планировании экспериментов. Поэтому, элементарное понимание вариации результатов опытов и связанных с этим понятий теории вероятностей очень важно, чтобы иметь солидную базу, на которой строить практические приёмы планирования и анализа экспериментов.
Two Types of Experimental Error
No matter how careful you are, there is always error in a measurement. Error is not a «mistake»—it’s part of the measuring process. In science, measurement error is called experimental error or observational error.
There are two broad classes of observational errors: random error and systematic error. Random error varies unpredictably from one measurement to another, while systematic error has the same value or proportion for every measurement. Random errors are unavoidable, but cluster around the true value. Systematic error can often be avoided by calibrating equipment, but if left uncorrected, can lead to measurements far from the true value.
Key Takeaways
- Random error causes one measurement to differ slightly from the next. It comes from unpredictable changes during an experiment.
- Systematic error always affects measurements the same amount or by the same proportion, provided that a reading is taken the same way each time. It is predictable.
- Random errors cannot be eliminated from an experiment, but most systematic errors can be reduced.
Random Error Example and Causes
If you take multiple measurements, the values cluster around the true value. Thus, random error primarily affects precision. Typically, random error affects the last significant digit of a measurement.
The main reasons for random error are limitations of instruments, environmental factors, and slight variations in procedure. For example:
- When weighing yourself on a scale, you position yourself slightly differently each time.
- When taking a volume reading in a flask, you may read the value from a different angle each time.
- Measuring the mass of a sample on an analytical balance may produce different values as air currents affect the balance or as water enters and leaves the specimen.
- Measuring your height is affected by minor posture changes.
- Measuring wind velocity depends on the height and time at which a measurement is taken. Multiple readings must be taken and averaged because gusts and changes in direction affect the value.
- Readings must be estimated when they fall between marks on a scale or when the thickness of a measurement marking is taken into account.
Because random error always occurs and cannot be predicted, it’s important to take multiple data points and average them to get a sense of the amount of variation and estimate the true value.
Systematic Error Example and Causes
Systematic error is predictable and either constant or else proportional to the measurement. Systematic errors primarily influence a measurement’s accuracy.
Typical causes of systematic error include observational error, imperfect instrument calibration, and environmental interference. For example:
- Forgetting to tare or zero a balance produces mass measurements that are always «off» by the same amount. An error caused by not setting an instrument to zero prior to its use is called an offset error.
- Not reading the meniscus at eye level for a volume measurement will always result in an inaccurate reading. The value will be consistently low or high, depending on whether the reading is taken from above or below the mark.
- Measuring length with a metal ruler will give a different result at a cold temperature than at a hot temperature, due to thermal expansion of the material.
- An improperly calibrated thermometer may give accurate readings within a certain temperature range, but become inaccurate at higher or lower temperatures.
- Measured distance is different using a new cloth measuring tape versus an older, stretched one. Proportional errors of this type are called scale factor errors.
- Drift occurs when successive readings become consistently lower or higher over time. Electronic equipment tends to be susceptible to drift. Many other instruments are affected by (usually positive) drift, as the device warms up.
Once its cause is identified, systematic error may be reduced to an extent. Systematic error can be minimized by routinely calibrating equipment, using controls in experiments, warming up instruments prior to taking readings, and comparing values against standards.
While random errors can be minimized by increasing sample size and averaging data, it’s harder to compensate for systematic error. The best way to avoid systematic error is to be familiar with the limitations of instruments and experienced with their correct use.
Key Takeaways: Random Error vs. Systematic Error
- The two main types of measurement error are random error and systematic error.
- Random error causes one measurement to differ slightly from the next. It comes from unpredictable changes during an experiment.
- Systematic error always affects measurements the same amount or by the same proportion, provided that a reading is taken the same way each time. It is predictable.
- Random errors cannot be eliminated from an experiment, but most systematic errors may be reduced.
Sources
- Bland, J. Martin, and Douglas G. Altman (1996). «Statistics Notes: Measurement Error.» BMJ 313.7059: 744.
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. Taylor & Francis, Ltd. on behalf of American Statistical Association and American Society for Quality. 10: 637–666. doi:10.2307/1267450
- Dodge, Y. (2003). The Oxford Dictionary of Statistical Terms. OUP. ISBN 0-19-920613-9.
- Taylor, J. R. (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94. ISBN 0-935702-75-X.
Two Types of Experimental Error
No matter how careful you are, there is always error in a measurement. Error is not a «mistake»—it’s part of the measuring process. In science, measurement error is called experimental error or observational error.
There are two broad classes of observational errors: random error and systematic error. Random error varies unpredictably from one measurement to another, while systematic error has the same value or proportion for every measurement. Random errors are unavoidable, but cluster around the true value. Systematic error can often be avoided by calibrating equipment, but if left uncorrected, can lead to measurements far from the true value.
Key Takeaways
- Random error causes one measurement to differ slightly from the next. It comes from unpredictable changes during an experiment.
- Systematic error always affects measurements the same amount or by the same proportion, provided that a reading is taken the same way each time. It is predictable.
- Random errors cannot be eliminated from an experiment, but most systematic errors can be reduced.
Random Error Example and Causes
If you take multiple measurements, the values cluster around the true value. Thus, random error primarily affects precision. Typically, random error affects the last significant digit of a measurement.
The main reasons for random error are limitations of instruments, environmental factors, and slight variations in procedure. For example:
- When weighing yourself on a scale, you position yourself slightly differently each time.
- When taking a volume reading in a flask, you may read the value from a different angle each time.
- Measuring the mass of a sample on an analytical balance may produce different values as air currents affect the balance or as water enters and leaves the specimen.
- Measuring your height is affected by minor posture changes.
- Measuring wind velocity depends on the height and time at which a measurement is taken. Multiple readings must be taken and averaged because gusts and changes in direction affect the value.
- Readings must be estimated when they fall between marks on a scale or when the thickness of a measurement marking is taken into account.
Because random error always occurs and cannot be predicted, it’s important to take multiple data points and average them to get a sense of the amount of variation and estimate the true value.
Systematic Error Example and Causes
Systematic error is predictable and either constant or else proportional to the measurement. Systematic errors primarily influence a measurement’s accuracy.
Typical causes of systematic error include observational error, imperfect instrument calibration, and environmental interference. For example:
- Forgetting to tare or zero a balance produces mass measurements that are always «off» by the same amount. An error caused by not setting an instrument to zero prior to its use is called an offset error.
- Not reading the meniscus at eye level for a volume measurement will always result in an inaccurate reading. The value will be consistently low or high, depending on whether the reading is taken from above or below the mark.
- Measuring length with a metal ruler will give a different result at a cold temperature than at a hot temperature, due to thermal expansion of the material.
- An improperly calibrated thermometer may give accurate readings within a certain temperature range, but become inaccurate at higher or lower temperatures.
- Measured distance is different using a new cloth measuring tape versus an older, stretched one. Proportional errors of this type are called scale factor errors.
- Drift occurs when successive readings become consistently lower or higher over time. Electronic equipment tends to be susceptible to drift. Many other instruments are affected by (usually positive) drift, as the device warms up.
Once its cause is identified, systematic error may be reduced to an extent. Systematic error can be minimized by routinely calibrating equipment, using controls in experiments, warming up instruments prior to taking readings, and comparing values against standards.
While random errors can be minimized by increasing sample size and averaging data, it’s harder to compensate for systematic error. The best way to avoid systematic error is to be familiar with the limitations of instruments and experienced with their correct use.
Key Takeaways: Random Error vs. Systematic Error
- The two main types of measurement error are random error and systematic error.
- Random error causes one measurement to differ slightly from the next. It comes from unpredictable changes during an experiment.
- Systematic error always affects measurements the same amount or by the same proportion, provided that a reading is taken the same way each time. It is predictable.
- Random errors cannot be eliminated from an experiment, but most systematic errors may be reduced.
Sources
- Bland, J. Martin, and Douglas G. Altman (1996). «Statistics Notes: Measurement Error.» BMJ 313.7059: 744.
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. Taylor & Francis, Ltd. on behalf of American Statistical Association and American Society for Quality. 10: 637–666. doi:10.2307/1267450
- Dodge, Y. (2003). The Oxford Dictionary of Statistical Terms. OUP. ISBN 0-19-920613-9.
- Taylor, J. R. (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94. ISBN 0-935702-75-X.
Статьи
Главная страница

видно, что существует вероятность, пусть и очень маленькая, что наше единичное
измерение покажет результат, сколь угодно далеко отстоящий от истинного
значения. Выходом из положения является проведение серии измерений. Если на
разброс данных действительно влияет случай, то в результате нескольких
измерений мы скорее всего получим следующее (рис 2):
Будет ли
рассчитанное среднее значение нескольких измерений совпадать с истинным? Как
правило – нет. Но по теории вероятности, чем больше сделано измерений, тем
ближе найденное среднее значение к истинному. На языке математики это можно
записать так:
Но с бесконечностью у всех дело обстоит неважно. Поэтому на практике мы имеем дело
не со всеми возможными результатами измерений, а с некоторой выборкой из этого
бесконечного множества. Сколько же реально следует делать измерений? Наверное,
до тех пор, пока полученное среднее значение не будет отличаться от истинного
меньше чем точность отдельного измерения.
Следовательно,
когда наше среднее значение (рис. 2) отличается от истинного меньше чем
погрешность измерений, дальнейшее увеличение числа опытов бессмысленно. Однако
на практике мы не знаем истинного значения! Значит, получив среднее по
результатам серии опытов, мы должны определить, какова вероятность того, что
истинное значение находится внутри заданного интервала ошибки. Или каков тот
доверительный интервал, в который с заданной надежностью попадет истинное
значение (рис 3).
Рассмотрим
некоторый условный эксперимент, где в серии измерений получены некоторые
значения величины Х (см. табл. 1). Рассчитаем среднее значение и, чтобы оценить
разброс данных найдем величины DХ = Х –
Хср
|
Таблица |
||||||
|
№ |
Х |
Х ср |
DХ |
DХ2 |
s2 |
s |
|
1 |
130 |
143,5 » 144 |
-13,5 |
182,3 |
420 |
20,5 |
|
2 |
162 |
18,5 |
342,3 |
|||
|
3 |
160 |
16,5 |
272,3 |
s2ср |
sср |
|
|
4 |
122 |
-21,5 |
462,3 |
105 |
10,2 |
Ясно, что
величины DХ как-то характеризуют
разброс данных. На практике для усредненной характеристики разброса серии измерений используется
дисперсия выборки:
и среднеквадратичное или стандартное отклонение выборки:
Последнее
показывает, что каждое измерение в данной серии (в данной выборке) отличается
от другого в среднем на ± s.
Понятно, что каждое отдельное
значение оказывает влияние на средний результат. Но это влияние тем меньше, чем
больше измерений в нашей выборке. Поэтому дисперсия и стандартное отклонение
среднего значения, будет определяться по формулам:
Можем ли мы теперь определить вероятность того, что
истинное значение попадет в указанный интервал среднего? Или наоборот,
рассчитать тот доверительный интервал в который истинное значение
попадет с заданной вероятностью (95%)? Поскольку кривая на наших графиках это
распределение вероятностей, то площадь под кривой, попадающая в указанный
интервал и будет равна этой вероятности (доля площади, в процентах). А площади
математики научились рассчитывать хорошо, знать бы только уравнение этой
кривой.
И здесь мы сталкиваемся еще с одной сложностью. Кривая, которая описывает распределение
вероятности для выборки, для ограниченного числа измерений, уже не будет кривой нормального
распределения. Ее форма будет зависеть
не только от дисперсии (разброса данных) но и от степени свободы для выборки
(от числа независимых измерений) (рис 4):
Уравнения этих кривых впервые были предложены в 1908
году английским математиком и химиком Госсетом, который опубликовал их под
псевдонимом Student (студент), откуда пошло хорошо известные термины
«коэффициент Стьюдента» и аналогичные. Коэффициенты Стьюдента получены на
основе обсчета этих кривых для разных степеней свободы (f = n-1) и уровней
надежности (Р) и сведены в специальные таблицы. Для получения доверительного интервала необходимо
умножить уже найденное стандартное отклонение среднего на соответствующий
коэффициент Стьюдента. ДИ = sср*tf, P
Проанализируем, как меняется доверительный интервал
при изменении требований к надежности результата и числа измерений в серии.
Данные в таблице 2 показывают, что чем больше требование к надежности, тем
больше будет коэффициент Стьюдента и, следовательно, доверительный интервал. В большинстве случаев, приемлемым считают значение Р=95%
|
Таблица |
||||
|
P |
0,9 |
0,95 |
0,99 |
0,999 |
|
t5, |
2,02 |
2,57 |
4,03 |
6,87 |
|
Таблица |
|||||||
|
f= |
1 |
2 |
3 |
4 |
5 |
16 |
30 |
|
tf, |
12,7 |
4,3 |
3,18 |
2,78 |
2,57 |
2,23 |
2,04 |
Из таблицы 3 и графика
видно, что чем больше число измерений, тем меньше коэффициент и доверительный
интервал для данного уровня надежности. Особенно значительное падение
происходит при переходе от степени свободы 1 (два измерения) к 2 (три
измерения). Отсюда следует, что имеет смысл ставить не менее трех параллельных
опытов, проводить не менее трех измерений.
Окончательно
для измеряемой величины Х получаем значение Хсред±sср*tf,P. В
нашем случае получаем: f=3; t=3,18;
ДИ = 3,18*10,2 = 32,6; X = 143,5 ±32,6
Как правило,
значение доверительного интервала округляется до одной значащей цифры, а
значение измеряемой величины – в соответствии с округлением доверительного
интервала. Поэтому для нашей серии окончательно имеем: X = 140 ±30
Найденная
нами погрешность является абсолютной погрешностью и ничего не говорит еще о
точности измерений. Она свидетельствует о точности измерений только в сравнении
с измеряемой величиной. Отсюда представление об относительной ошибке:
Косвенные определения.
Исследуемая величина рассчитывается в этом случае с помощью
математических формул по другим величинам, которые были измерены
непосредственно. В этом случае для расчета ошибок можно использовать
соотношения, приведенные в таблице 4.
|
Таблица |
||
|
Формула |
Абсолютная |
Относительная |
|
x = a ± b |
Dx = Da+Db |
e = |
|
x = a* b; x = a* k |
Dx = bDa+aDb; Dx = kDa |
e = Da/a+Db/b = ea + e b |
|
x = a / b |
Dx = (bDa+aDb) / b2 |
e = Da/a+Db/b = ea + e b |
|
x = a*k; (x = a / k) |
Dx = Da*k; (Dx = Da/k ) |
e = ea |
|
x = a2 |
Dx = 2aDa |
e = 2Da/a = 2ea |
|
x = Öa |
Dx = Da/(2Öa) |
e = Da/2a = ea/2 |
Из таблицы видно, что относительная ошибка и точность определения не изменяются при умножении (делении) на некоторый постоянный коэффициент. Особенно сильно относительная ошибка может возрасти при вычитании
близких величин, так как при этом абсолютные ошибки суммируются, а значение Х
может уменьшиться на порядки.
Пусть например, нам необходимо определить
объем проволочки.
Если диаметр проволочки измерен с погрешностью 0,01 мм (микрометром) и равен 4 мм, то относительная погрешность составит 0,25% (приборная). Если
длину проволочки (200 мм) мы измерим линейкой с погрешностью 0,5 мм, то относительная погрешность также составит 0,25%. Объем можно рассчитать по формуле: V=(pd2/4)*L. Посмотрим, как будут меняться ошибки
по мере проведения расчетов (табл. 5):
|
Таблица 5. Расчет абсолютных и относительных ошибок. |
|||
|
Величина |
Значение |
Абсолютная |
Относительная |
|
d2 |
16 |
Dx = 2*4*0,01=0,08 |
e = 0,5% |
|
pd2 *) |
50,27 |
Dx = 0,08*3,14+0,0016*16 |
e = 0,55% |
|
pd2/4 |
12,57 |
Dx = 0,28/4 = 0,07 |
e = 0,55% |
|
(pd2/4)*L |
2513 |
Dx = 12,57*0,5+200*0,07=20 |
e = 0,8% |
|
*) Если мы возьмем привычное p=3,14, то Dp=0,0016 |
Окончательный
результат V=2510±20 (мм3) e
=0,8%. Чтобы повысить точность косвенного определения, нужно в первую очередь
повышать точность измерения той величины, которая вносит больший вклад в ошибку
(в данном случае – точность измерения диаметра проволочки).
План проведения измерений:
[1]
1. Знакомство
с методикой, подготовка прибора, оценка приборной погрешности d. Оценка возможных причин
систематических ошибок, их исключение.
2.
Проведение серии измерений. Если получены совпадающие результаты, можно
считать что случайная ошибка равна 0, DХ
= d. Переходим к пункту 7.
3.
Исключение промахов – результатов значительно отличающихся по своей
величине от остальных.
4.
Расчет
среднего значения Хср, и стандартного отклонение среднего
значения scp
5.
Задание значения уровня надежности P,
определение коэффициента Стьюдента t и
нахождение доверительного интервала ДИ= t*scp
6.
Сравнение случайной и приборной погрешности, при этом возможны варианты:
—
ДИ << d, можно
считать, что DХ = d, повысить точность измерения
можно, применив более точный прибор
—
ДИ >> d, можно
считать, что DХ = ДИ,
повысить точность можно, уменьшая случайную ошибку, повышая число измерений в
серии, снижая требования к надежности.
—
ДИ » d, в этом
случае расчитываем ошибку по формуле DХ
=
7.
Записывается окончательный результат Х = Хср ± DХ.
Оценивается относительная ошибка
измерения e = DХ/Хср
Если
проводится несколько однотипных измерений (один прибор, исследователь, порядок
измеряемой величины, условия) то подобную работу можно проводить один раз. В
дальнейшем можно считать DХ
постоянной и ограничиться минимальным числом измерений (два-три измерения
должны отличаться не более, чем на DХ)
Для косвенных
измерений необходимо провести обработку данных измерения каждой величины. При
этом желательно использовать приборы, имеющие близкие относительные погрешности
и задавать одинаковую надежность для расчета доверительного интервала. На
основании полученных значений Da, Db, определяется DХ
для результирующей величины (см табл. 4). Для повышения точности надо
совершенствовать измерение той величины, вклад ошибки которой в DХ наиболее существенен.
Изучение зависимостей.
Частым вариантом экспериментальной работы является
измерение различных величин с целью установления зависимостей. Характер этих
зависимостей может быть различен: линейный, квадратичный, экспоненциальный,
логарифмический, гиперболический. Для выявления зависимостей широко
используется построение графиков.
При построении графиков вручную важно правильно
выбрать оси, величины, масштаб, шкалы. Следует предупредить школьников, что
шкалы должны иметь равномерный характер, нежелательна как слишком детальная,
так и слишком грубая их разметка. Точки должны заполнять всю площадь графика,
их расположение в одном углу, или «прижатыми» к одной из осей, говорит о
неправильно выбранном масштабе и затрудняет определение характера зависимости.
При проведении линии по точкам надо использовать теоретические представление о
характере зависимости: является она непрерывной или прерывистой, возможно ли ее
прохождение через начало координат, отрицательные значения, максимумы и
минимумы.
Наиболее легко проводится и анализируется прямая
линия. Поэтому часто при изучении более сложных зависимостей часто используется
линеаризация зависимостей, которая достигается подходящей заменой переменных.
Например:
Зависимость . Вводя новую переменную
, получаем уравнение
a = bx, которое
будет изображаться на графике прямой линией. Наклон этой прямой позволяет
рассчитать константу диссоциации.
Разумеется и в этом случае полученные в эксперименте данные включают в себя различные ошибки, и точки редко лежат строго на прямой. Возникает
вопрос, как с наибольшей точностью провести прямую по экспериментальным точкам, каковы ошибки в определении
параметров.
Математическая статистика показывает, что наилучшим
приближением будет такая линия, для которой дисперсия (разброс) точек
относительно ее будет минимальным. А дисперсия определяется как средний квадрат
отклонений наблюдаемого положения точки от расчитанного:
Отсюда название этого метода – метод наименьших
квадратов. Задавая условие, чтобы величина s2
принимала минимальное значение, получают формулы для коэффициентов а и b в уравнении прямой у = а + bx:

и формулы для расчета соответствующих ошибок
[2].
Если
делать расчеты, используя калькулятор, то лучше оформлять их в виде таблицы:
|
x |
x2 |
y |
y2 |
xy |
|
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
|
Sx = |
Sx2 |
Sy = |
Sy2 |
Sxy = |
Подводя
итог, следует сказать, что обработка данных эксперимента достаточно сложный
этап работы ученого. Необходимость проведения большого числа измерений требует
большой затраты времени и материальных ресурсов. Громоздкость формул, необходимость
использования большого числа значащих цифр затрудняют вычисления. Поэтому, возможно,
не все рекомендации этой статьи применимы в рамках школьного исследования. Но
понимать их сущность, значимость, необходимость, и в соответствии с этим
адекватно оценивать свои результаты, должен любой исследователь.
В настоящее время обработку экспериментальных данных
существенно облегчают современные компьютерные технологии, современное
программное обеспечение. Об том, как их можно использовать – в следующей
статье.
Литература:
[1]
Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений, М., «Наука»,
1970, 194 с.
[2]
Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение – М.,: Химия,
1978, 816 с.
В статье рассмотрены различные критерии отбрасывания грубых погрешностей измерений, применяемые в практической деятельности, на основе рекомендаций ведущих специалистов-метрологов, а также с учетом действующих в настоящий момент нормативных документов.
Приведен пример использования Excel при оценке грубых погрешностей по критериям Стьюдента и Романовского при обработке реальных результатов измерений.
Ключевые слова:
грубые погрешности, критерии согласия, сомнительные значения, уровень значимости, нормальное распределение, критерий согласия Стьюдента, критерий Романовского, выборка, отклонения, Excel.
Одним из важнейших условий правильного применения статистических оценок является отсутствие грубых ошибок при наблюдениях. Поэтому все грубые ошибки должны быть выявлены и исключены из рассмотрения в самом начале обработки наблюдений.
Единственным достаточно надежным способом выявления грубых ошибок является тщательный анализ условий самих испытаний. При этом наблюдения, проводившиеся в нарушенных условиях, должны отбрасываться, независимо от их результата. Например, если при проведении эксперимента, связанного с электричеством, в лаборатории на некоторое время был выключен ток, то весь эксперимент обязательно нужно проводить заново, хотя результат, быть может, не сильно отличается от предыдущих измерений. Точно так же отбрасываются результаты измерений на фотопластинках с поврежденной эмульсией и вообще на любых образцах с обнаруженным позднее дефектом.
На практике, однако, не всегда удается провести подобный анализ условий испытания. Чаще всего приходится иметь дело с окончательным цифровым материалом, в котором отдельные данные вызывают сомнение лишь своим значительным отклонением от остальных. При этом сама «значительность» отклонения во многом субъективна — зачастую приходится сталкиваться со случаями, когда исследователь отбрасывает наблюдения, которые ему не понравились, как ошибочные исключительно по той причине, что они нарушают уже созданную им в воображении картину изучаемого процесса.
Строгий научный анализ готового ряда наблюдений может быть проведен лишь статистическим путем, причем должен быть достаточно хорошо известен характер распределения наблюдаемой случайной величины. В большинстве случаев исследователи исходят из нормального распределения. Каждая грубая ошибка будет соответствовать нарушению этого распределения, изменению его параметров, иными словами, нарушится однородность испытаний (или, как говорят
,
однородность наблюдений), поэтому выявление грубых ошибок можно трактовать как проверку однородности наблюдений.
Промахи, или грубые погрешности, возникают при единичном измерении и обычно устраняются путем повторных измерений. Причиной их возникновения могут быть:
- Объективная реальность (наш реальный мир отличается от идеальной модели мира, которую мы принимаем в данной измерительной задаче);
- Внезапные кратковременные изменения условий измерения (могут быть вызваны неисправностью аппаратуры или источников питания);
- Ошибка оператора (неправильное снятие показаний, неправильная запись и т. п.).
В третьем случае, если оператор в процессе измерения обнаружит промах, он вправе отбросить этот результат и провести повторные измерения.
В настоящее время определение грубой погрешности приведено в ГОСТ Р 8.736–2011: «Грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей» [1, с. 6].
Общие подходы к методам отсеивания грубых погрешностей, как это уже давно принято в практике измерений, заключаются в следующем.
Задаются вероятностью
Р
или уровнем значимости
α
(
) того, что результат наблюдения содержит промах. Выявление сомнительного результата осуществляют с помощью специальных критериев. Операция отбрасывания удаленных от центра выборки сомнительных значений измеряемой величины называется «цензурированием выборки».
Проверяемая гипотеза состоит в утверждении, что результат наблюдения
x
i
не содержит грубой погрешности, т. е. является одним из значений случайной величины
x
с законом распределения Fx(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший x
max
или наименьший xmin из результатов наблюдений.
Предложим для практического использования наиболее простые методы отсева грубых погрешностей.
Если в распоряжении экспериментатора имеется выборка небольшого объема
n
≤ 25, то можно воспользоваться методом вычисления максимального относительного отклонения [2, с. 149]:
(1)
где
x
i
— крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались оценки среднего значения
и среднеквадратичного отклонения
;
τ
1-
p
— табличное значение статистики
τ
, вычисленной при доверительной вероятности
.
Таким образом, для выделения аномального значения вычисляют значение статистики,
(2)
которое затем сравнивают с табличным значением
τ
1-α
:
τ
≤
τ
1-α
. Если неравенство
τ
≤
τ
1-α
соблюдается, то наблюдение не отсеивают, если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть пересчитаны по данным сокращенной выборки.
Квантили распределения статистики
τ
при уровнях значимости
α
= 0,10; 0,05; 0,025 и 0,01 или доверительной вероятности
=
0,90; 0,95; 0,975 и 0,99 приведены в таблице 1. На практике очень часто используют уровень значимости
α
= 0,05 (результат получается с 95 %-й доверительной вероятностью).
Функции распределения статистики
τ
определяют методами теории вероятностей. По данным таблицы, приведенной в источниках [2, с. 283; 3, с. 184] при заданной доверительной вероятности
или уровне значимости
α
можно для чисел измерения п = 3–25 найти те наибольшие значения
которые случайная величина
может еще принять по чисто случайным причинам.
Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать оценки среднего значения
и среднеквадратичного отклонения
для выборки нового объема
Таблица 1
Квантили распределения максимального относительного отклонения при отсеве грубых погрешностей [2, с. 283]
|
|
Уровень значимости |
|
Уровень значимости |
||||||
|
0,10 |
0,05 |
0,025 |
0,01 |
0,10 |
0,05 |
0,025 |
0,01 |
||
|
3 |
1,41 |
1,41 |
1,41 |
1,41 |
15 |
2,33 |
2,49 |
2,64 |
2,80 |
|
4 |
1,65 |
1,69 |
1,71 |
1,72 |
16 |
2,35 |
2,52 |
2,67 |
2,84 |
|
5 |
1,79 |
1,87 |
1,92 |
1,96 |
17 |
2,38 |
2,55 |
2,70 |
2,87 |
|
6 |
1,89 |
2,00 |
2,07 |
2,13 |
18 |
2,40 |
2,58 |
2,73 |
2,90 |
|
7 |
1,97 |
2,09 |
2,18 |
2,27 |
19 |
2,43 |
2,60 |
2,75 |
2,93 |
|
8 |
2,04 |
2,17 |
2,27 |
2,37 |
20 |
2,45 |
2,62 |
2,78 |
2,96 |
|
9 |
2,10 |
2,24 |
2,35 |
2,46 |
21 |
2,47 |
2,64 |
2,80 |
2,98 |
|
10 |
2,15 |
2,29 |
2,41 |
2,54 |
22 |
2,49 |
2,66 |
2,82 |
3,01 |
|
11 |
2,19 |
2,34 |
2,47 |
2,61 |
23 |
2,50 |
2,68 |
2,84 |
3,03 |
|
12 |
2,23 |
2,39 |
2,52 |
2,66 |
24 |
2,52 |
2,70 |
2,86 |
3,05 |
|
13 |
2,26 |
2,43 |
2,56 |
2,71 |
25 |
2,54 |
2,72 |
2,88 |
3,07 |
|
14 |
2,30 |
2,46 |
2,60 |
2,76 |
|||||
В литературе можно встретить большое количество методических рекомендаций для проведения отсева грубых погрешностей измерений, подробно рассмотренных в [4, с. 25]. Обратим внимание на некоторые из существующих критериев отсеивания грубых погрешностей.
-
Критерий «трех сигм» применяется для случая, когда измеряемая величина
x
распределена по нормальному закону. По этому критерию считается, что с вероятностью
Р
= 0,9973 и значимостью
α
= 0,0027 появление даже одной случайной погрешности, большей, чеммаловероятное событие и ее можно считать промахом, если
−
x
i
> 3
S
x
, где
S
x
—
оценка среднеквадратического отклонения (СКО) измерений. Величиныи
S
x
вычисляют без учета экстремальных значений
x
i
. Данный критерий надежен при числе измерений
n
≥ 20…50 и поэтому он широко применяется. Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при
6 <
n
≤100 она равна 4
S
x
; при 100 <
n
≤1000 − 4,5
S
x
; при 1000 <
n
≤10000–5
Sx
. Данное правило также используется только при нормальном распределении.
Практические вычисления проводят следующим образом [5, с. 65]:
- Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее, либо наименьшее значение наблюдения измеряемой величины.
-
Вычисляют среднее арифметическое значение выборки
без учета сомнительного значения
измеряемой величины.
(3)
-
Вычисляют оценку СКО выборки
без учета сомнительного значения
измеряемой величины.
(4)
- Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают.
Если
то сомнительное значение отбрасывают, как промах.
Если
то сомнительное значение оставляют как равноправное в ряду наблюдений.
Данный метод «трех сигм» среди метрологов-практиков является самым популярным, достаточно надежным и удобным, так как при этом иметь под рукой какие-то таблицы нет необходимости.
-
Критерий В. И. Романовского применяется, если число измерений невелико,
n
≤ 20. При этом вычисляется соотношение
(5)
где
— результат, вызывающий сомнение,
— коэффициент, предельное значение которого
определяют по таблице 2. Если
, сомнительное значение
исключают («отбрасывают») как промах. Если
,
сомнительное значение оставляют как равноправное в ряду наблюдений [5, с. 65].
Таблица 2
Значение критерия Романовского
|
Уровень значимости, |
Число измерений, |
||||||
|
|
|
|
|
|
|
|
|
|
0,01 |
1,73 |
2,16 |
2,43 |
2,62 |
2,75 |
2,90 |
3,08 |
|
0,02 |
1,72 |
2,13 |
2,37 |
2,54 |
2,66 |
2,80 |
2,96 |
|
0,05 |
1,71 |
2,10 |
2,27 |
2,41 |
2,52 |
2,64 |
2,78 |
|
0,10 |
1,69 |
2,00 |
2,17 |
2,29 |
2,39 |
2,49 |
2,62 |
Несмотря на многообразие существующих и применяемых на практике методов отсеивания грубых погрешностей в настоящее время действует национальный стандарт ГОСТ Р 8.736–2011, который является основным нормативным документом в данной области. В новом стандарте для исключения грубых погрешностей применяется критерий Граббса.
- Статистический критерий Граббса (Смирнова) исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению [1, с. 8]. Для этого вычисляют критерии Граббса (Смирнова) G1 и G2, предполагая, что наибольший хmax или наименьший xmin результат измерений вызван грубыми погрешностями.
и
(6)
Сравнивают G1 и G2 с теоретическим значением GT критерия Граббса (Смирнова) при выбранном уровне значимости α. Таблица критических значений критерия Граббса (Смирнова) приведена в приложении к стандарту [1, с. 12]. Следует отметить, что критические значения критерия Граббса (Смирнова) GT отличаются от критических значений критериев
t
-статистик или значений критериев Стьюдента при одних и тех же величинах уровней значимости, что может вызывать некоторые трудности у пользователей при выборе конкретного метода отсеивания погрешностей, соответствующего нормативным документам.
Если G1>GТ, то хmax исключают как маловероятное значение. Если G2>GТ, то xmin исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонение ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.
Если G1
GТ, то хmax не считают промахом и его сохраняют в ряду результатов измерений. Если G2
GТ, то xmin не считают промахом и его сохраняют в ряду результатов измерений.
Отсев грубых погрешностей можно производить и для больших выборок (
n
= 50…100). Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике, кроме того, распределение Стьюдента реализовано в пакете Excel. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике [3, с. 24].
Известно, что критическое значение
τ
p
(
p
— процентная точка нормирования выборочного отклонения) выражается через критическое значение распределения Стьюдента
t
α, n-2
[6, с. 26]:
(7)
Учитывая это, можно предложить следующую процедуру отсева грубых погрешностей измерения для больших выборок (
n
= 100):
1) из таблицы наблюдений выбирают наблюдение имеющее наибольшее отклонение;
2)
по формуле
вычисляют значение статистики
τ
;
3)
по таблице (или в программе Excel) находят процентные точки
t
-распределения Стьюдента
t
(
α,
n
-2
)
:
t
(95
%, 98)
= 1,6602, и
t
(
99
%, 98)
= 3,1737;
По предыдущей формуле в программе Excel вычисляют соответствующие точки
t
(95
%, 100)
= 1,66023и
t
(99
%, 100)
=3,17374.
Сравнивают значение расчетной статистики с табличными критическими значениями и принимают решение по отсеву грубых погрешностей.
Рекомендуемый метод отсева грубых погрешностей удобен еще тем, что максимальные относительные отклонения могут быть разделены на три группы: 1)
2)
3)
.
Наблюдения, попавшие в первую группу, нельзя отсеивать ни в коем случае. Наблюдения второй группы можно отсеять, если в пользу этой процедуры имеются еще и другие соображения экспериментатора (например, заключения, сделанные на основе изучения физических, химических и других свойств изучаемого явления). Наблюдения третьей группы, как правило, отсеивают всегда.
Рассмотрим далее пример с использованием средств программного пакета Excel, который позволяет снизить трудоемкость расчетов при осуществлении данной процедуры. К сожалению, в настоящее время средства Excel не позволяют автоматизировать расчеты по всем известным критериям отсеивания грубых погрешностей, поэтому проиллюстрируем рассмотренные методы с использованием доступных в Excel критериев Стьюдента.
Пример 1.
Имеется выборка из 100 шт. резисторов с номинальным сопротивлением
R
н
= (150,0 ± 5 %) кОм, которая используется для оценки качества партии резисторов (генеральная совокупность). Используя критерий Стьюдента, отсеем грубые погрешности (промахи) при измерениях.
- Заносим данные измерений в таблицу Excel в ячейки В2:В101
- Составляем вариационный ряд — располагаем данные в порядке возрастания с помощью функции «Сортировка по возрастанию» в ячейках С2:С101 (рис. 1)
Рис. 1. Фрагмент диалогового окна с данными измерений и вариационного ряда
3. Находим среднее значение выборки с помощью мастера функций в категории «Статистические» и функции — СРЗНАЧ, результат в ячейке Н3 (рис. 2).
Рис. 2. Фрагмент диалогового окна при нахождении среднего значения выборки
-
Находим среднеквадратическое отклонение —
S
x
. Выделяем ячейку Н4, вызываем «Мастер функций», категория «Статистические», функция — СТАНДОТКЛОН, результат в ячейке Н4–1,20 (рис. 3).
Рис. 3. Фрагмент диалогового окна при нахождении среднего квадратического отклонения
-
Находим максимальное значение в выборке —
x
макс
. Выделяем ячейку Н5, в категории «Статистические», функция — МАКС, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н5–153,10 (рис. 4).
Рис. 4. Фрагмент диалогового окна при нахождении максимального значения
-
Находим минимальное значение в выборке —
x
мин
. Выделяем ячейку Н6, в категории «Статистические», функция — МИН, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н6–147,6 (рис. 5).
Рис. 5. Фрагмент диалогового окна при нахождении минимального значения
-
Находим максимальное и минимальное отклонения — Δ
макс
и Δ
мин
. Вводим в ячейки Н7 и Н8 формулы:
-
Находим теоретическое значение —
t
теор
. для максимального и минимального отклонений. Вводим в ячейки Н9 и Н12 формулу
. и
-
Находим табличное значение
t
табл.
Выделяем ячейку Н10, вызываем в категории «Статистические» функцию — СТЬЮДЕНТ.ОБР, «Вероятность» — 0,95, степени свободы (
n
-2) — 98, результат в ячейке Н10–1,66 (рис. 6).
Рис. 6. Фрагмент диалогового окна при нахождении табличного значения критерия Стьюдента
-
Сравниваем теоретическое значение
t
теор
= 2,24 критерия Стьюдента для максимального значения — 153,1 кОм с табличным значением:
t
табл
.= 1,6605. - Аналогично п. 9 проверим на наличие грубой погрешности у минимального значения в выборке — 147,6 кОм. Результат в ячейке Н12–2,35 (рис. 7).
Рис. 7. Фрагмент диалогового окна при окончательном анализе данных
- Делаем вывод о наличии грубых ошибок в данных измерениях. Рассмотренная процедура подтвердила наши сомнения относительно достоверности максимального и минимального значений в данной выборке, т. е., указанные результаты могут быть отброшены из результатов измерений, и проверка может быть повторена снова без этих данных.
Пример расчета теоретического критерия Романовского по аналогичным формулам в Excel и диалоговое окно представлены на рис. 8, при условии α = 0,05, число измерений
n
= 20, β
табл
= 2,78 (из таблицы 2).
Рис. 8. Фрагмент диалогового окна при расчете критерия Романовского
Выводы
- Для использования различных критериев отбрасывания грубых погрешностей измерений необходимо учитывать требования действующих нормативных документов.
- Рассмотренный пример показал, что расчеты погрешностей по критерию Стьюдента с использованием таблиц и формул Excel значительно упрощаются, а процесс отбрасывания грубых погрешностей можно осуществить наиболее качественно и быстро.
Литература:
1. ГОСТ Р 8.736–2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. — М.: ФГУП Стандартинформ, 2013. — 24 с.
2. Пустыльник Е. И. Статистические методы анализа и обработки наблюдений. — М.: Наука, 1968. — 288 с.
3. Львовский Е. Н. Статистические методы построения эмпирических формул: Учеб. пособие. — М.: Высш. школа, 1982. — 224 с.
4. Фаюстов А. А. Ещё раз о критериях отсеивания грубых погрешностей. — Законодательная и прикладная метрология, 2016, № 5, с. 25–30.
5. Сергеев А. Г. Метрология: Учебник. — М.: Логос, 2005. — 272 с.
6. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, Главная редакция физико-математической литературы, 1983. — 416 с.
Основные термины (генерируются автоматически): диалоговое окно, сомнительное значение, уровень значимости, измеряемая величина, погрешность, критерий, нормальное распределение, ячейка, вариационный ряд, минимальное значение.
Первичная обработка опытных данных
Исключение ложных данных
Ложные результаты проникают в исходную совокупность случайным путем из-за действия достаточно большого числа случайных причин, которые не удается заранее предусмотреть при проведении измерений или при сборе статистических сведений (описки, опечатки). Не исключен случай, когда ошибки в статистические данные вносятся злонамеренно, к примеру, с целью искажения или сокрытия истинного положения вещей.
Процедура исключения ложных данных позволяет выявить такие данные в статистической совокупности с большой степенью вероятности.
К источникам ложных данных относятся:
— грубые (недостаточно точные) измерения;
— нарушение условий эксперимента;
— использование неисправного оборудования;
— ошибки при обработке информации и др.
Наличие ложных данных приводит к необоснованным выводам, поэтому ложные данные должны быть исключены из выборочной совокупности в процессе первичной обработки опытных данных [26,30,33,35].
Процедура исключения ложных данных для представленных совокупностей:
1. Имеющиеся значения совокупностей значений располагаются в порядке возрастания: х(1) ? х(2) ? х(m), и определяются крайние элементы представленной совокупности:
х(1) = хmin, х(n) = х(max).
Таблица 7 — Упорядоченные по возрастанию совокупности значений
|
L, чел. |
m1, чел. |
m2, чел. |
m3, чел. |
N, дни |
|
278200 |
625 |
10 |
18 |
29090 |
|
283730 |
725 |
12 |
18 |
29482 |
|
290000 |
858 |
13 |
32 |
35398 |
|
291008 |
899 |
17 |
36 |
35476 |
|
292200 |
912 |
18 |
36 |
35604 |
|
324500 |
1133 |
20 |
38 |
40278 |
|
339100 |
1313 |
28 |
40 |
40689 |
|
343600 |
1542 |
30 |
47 |
42046 |
|
351900 |
1650 |
31 |
51 |
47039 |
|
357900 |
1722 |
33 |
58 |
48838 |
|
390500 |
2059 |
44 |
63 |
52710 |
|
411700 |
2387 |
46 |
63 |
56094 |
|
427300 |
2540 |
51 |
65 |
58420 |
|
2,203 |
0,034 |
0,529 |
23,000 |
1527,6 |
|
2,500 |
0,041 |
0,621 |
23,500 |
1566,1 |
|
3,084 |
0,047 |
1,062 |
24,417 |
1778,3 |
|
3,089 |
0,052 |
1,150 |
24,660 |
2221,3 |
|
3,121 |
0,062 |
1,171 |
25,600 |
2519,4 |
|
3,492 |
0,070 |
1,237 |
26,121 |
3155,6 |
|
3,872 |
0,081 |
1,313 |
35,826 |
4194,5 |
|
4,308 |
0,085 |
1,369 |
38,899 |
4992,5 |
|
4,689 |
0,087 |
1,449 |
39,604 |
5488,4 |
|
5,012 |
0,097 |
1,474 |
40,665 |
7007,6 |
|
5,273 |
0,103 |
1,579 |
41,256 |
7306,8 |
|
5,586 |
0,118 |
1,613 |
43,105 |
8339,3 |
|
6,170 |
0,124 |
1,688 |
46,544 |
11161,5 |
|
17,8 |
10360 |
11,5 |
65,6 |
41400 |
|
18 |
10886 |
13,1 |
78,3 |
49800 |
|
18,2 |
11690 |
13,6 |
89 |
56900 |
|
18,5 |
11729 |
15,5 |
100,8 |
64800 |
|
20,5 |
11811 |
26,9 |
140 |
90400 |
|
20,8 |
11929 |
34,3 |
164,8 |
107000 |
|
23,3 |
12124 |
41,3 |
205,8 |
134100 |
|
25,8 |
12314 |
42,3 |
226,1 |
148200 |
|
26,5 |
12500 |
44,5 |
240,3 |
157200 |
|
26,5 |
12550 |
49,9 |
264,5 |
173800 |
|
30,9 |
12975 |
57,2 |
318,8 |
187300 |
|
33,3 |
13690 |
60,9 |
335,4 |
220800 |
|
33,5 |
14383 |
71,8 |
404,8 |
244700 |
2. Вычисляются значения , отклонений крайних значений случайной величины хmin, хmax от ее среднего значения с учетом разброса значений случайной величины x в выборке по следующим формулам:
, . (5)
Среднее значение опытных данных вычисляется по исходной совокупности объемом m по формуле:
(6)
Среднее значение для величины L:
Lср==337049,1
По исходной совокупности опытных данных вычисляется величина , характеризующая разброс опытных значений величины x вокруг среднего
Разброс опытных данных для величины L:
. (7)
1,18
1,80
3. Рассчитанные значения относительно отклонения (б;m) сравниваются с его критическими (теоретическими) значениями . Так как выборка небольшая (m?25) для исключения ложных данных используется таблица квантилей распределения максимального относительного отклонения . Значение квантиля максимального относительного отклонения для уровня значимости б=0,05 принимается равным 2,43. [30,35]
Таблица 8 -Квантили максимального относительного отклонения
|
б, % |
Объем выборочной совокупности m |
||||||||
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
1 |
2,37 |
2,46 |
2,54 |
2,61 |
2,66 |
2,71 |
2,76 |
2,8 |
2,84 |
|
5 |
2,17 |
2,24 |
2,29 |
2,34 |
2,39 |
2,43 |
2,46 |
2,49 |
2,52 |
Сравниваются расчетное и критическое значения по формуле:
?.
Оба значения и 1,80 меньше =2,43, следовательно, оба неравенства выполнены и оба значения не считаются ложными и остаются в выборке.
Таким образом, рассчитываются оставшиеся выборочные совокупности. Результаты расчетов представлены в таблице
Таблица 9 — Результаты расчетов , отклонений крайних значений случайных величин хmin, хmax от среднего значения
|
хmin |
хmax |
|||||
   
L |
278200 |
427300 |
337049,1 |
50071,51 |
1,18 |
1,80 |
|
m1 |
625,00 |
2540,00 |
1412,69 |
633,14 |
1,24 |
1,78 |
|
m2 |
10,00 |
51,00 |
27,15 |
13,63 |
1,26 |
1,75 |
|
m3 |
15,00 |
65,00 |
43,23 |
16,46 |
1,72 |
1,32 |
|
N |
29090,00 |
58420,00 |
42397,23 |
9609,77 |
1,38 |
1,67 |
|
Kч |
2,203 |
6,170 |
4,031 |
1,197 |
1,787 |
0,8 |
|
Kл |
0,034 |
0,124 |
0,077 |
0,028 |
1,685 |
0,02 |
|
Kп.з. |
0,529 |
1,688 |
1,250 |
0,341 |
1,285 |
0,25 |
|
Kт |
23,000 |
46,544 |
33,323 |
8,472 |
1,561 |
5,0 |
|
S |
1527,60 |
11161,50 |
4712,3 |
3024,73 |
1,05 |
2,13 |
|
D |
17,80 |
33,50 |
24,12 |
5,78 |
1,09 |
1,62 |
|
E |
10360,00 |
14383,00 |
12226,23 |
1065,65 |
1,75 |
2,02 |
|
I |
11,50 |
71,80 |
37,14 |
20,00 |
1,28 |
1,73 |
|
V |
65,50 |
404,80 |
202,70 |
108,25 |
1,27 |
1,87 |
|
Vp |
41400,00 |
244700,00 |
128953,8 |
66864,25 |
1,31 |
1,73 |
Как видно из таблицы все значения и выборочных совокупностей удовлетворяют неравенству ?. В результате проведенной процедуры можно утверждать, что в таблице значений случайных величин ложных данных нет.
При цитировании материалов в рефератах, курсовых, дипломных работах правильно указывайте источник цитирования, для удобства можете скопировать из поля ниже:
Комментарии к статье
Содержание
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Содержание
- 1 Методы обработки ошибок
- 2 Исключения
- 3 Классификация исключений
- 3.1 Проверяемые исключения
- 3.2 Error
- 3.3 RuntimeException
- 4 Обработка исключений
- 4.1 try-catch-finally
- 4.2 Обработка исключений, вызвавших завершение потока
- 4.3 Информация об исключениях
- 5 Разработка исключений
- 6 Исключения в Java7
- 7 Примеры исключений
- 8 Гарантии безопасности
- 9 Источники
Методы обработки ошибок
1. Не обрабатывать.
2. Коды возврата. Основная идея — в случае ошибки возвращать специальное значение, которое не может быть корректным. Например, если в методе есть операция деления, то придется проверять делитель на равенство нулю. Также проверим корректность аргументов a и b:
Double f(Double a, Double b) {
if ((a == null) || (b == null)) {
return null;
}
//...
if (Math.abs(b) < EPS) {
return null;
} else {
return a / b;
}
}
При вызове метода необходимо проверить возвращаемое значение:
Double d = f(a, b); if (d != null) { //... } else { //... }
Минусом такого подхода является необходимость проверки возвращаемого значения каждый раз при вызове метода. Кроме того, не всегда возможно определить тип ошибки.
3.Использовать флаг ошибки: при возникновении ошибки устанавливать флаг в соответствующее значение:
boolean error; Double f(Double a, Double b) { if ((a == null) || (b == null)) { error = true; return null; } //... if (Math.abs(b) < EPS) { error = true; return b; } else { return a / b; } }
error = false; Double d = f(a, b); if (error) { //... } else { //... }
Минусы такого подхода аналогичны минусам использования кодов возврата.
4.Можно вызвать метод обработки ошибки и возвращать то, что вернет этот метод.
Double f(Double a, Double b) {
if ((a == null) || (b == null)) {
return nullPointer();
}
//...
if (Math.abs(b) < EPS) {
return divisionByZero();
} else {
return a / b;
}
}
Но в таком случае не всегда возможно проверить корректность результата вызова основного метода.
5.В случае ошибки просто закрыть программу.
if (Math.abs(b) < EPS) { System.exit(0); return this; }
Это приведет к потере данных, также невозможно понять, в каком месте возникла ошибка.
Исключения
В Java возможна обработка ошибок с помощью исключений:
Double f(Double a, Double b) {
if ((a == null) || (b == null)) {
throw new IllegalArgumentException("arguments of f() are null");
}
//...
return a / b;
}
Проверять b на равенство нулю уже нет необходимости, так как при делении на ноль метод бросит непроверяемое исключение ArithmeticException.
Исключения позволяют:
- разделить обработку ошибок и сам алгоритм;
- не загромождать код проверками возвращаемых значений;
- обрабатывать ошибки на верхних уровнях, если на текущем уровне не хватает данных для обработки. Например, при написании универсального метода чтения из файла невозможно заранее предусмотреть реакцию на ошибку, так как эта реакция зависит от использующей метод программы;
- классифицировать типы ошибок, обрабатывать похожие исключения одинаково, сопоставлять специфичным исключениям определенные обработчики.
Каждый раз, когда при выполнении программы происходит ошибка, создается объект-исключение, содержащий информацию об ошибке, включая её тип и состояние программы на момент возникновения ошибки.
После создания исключения среда выполнения пытается найти в стеке вызовов метод, который содержит код, обрабатывающий это исключение. Поиск начинается с метода, в котором произошла ошибка, и проходит через стек в обратном порядке вызова методов. Если не было найдено ни одного подходящего обработчика, выполнение программы завершается.
Таким образом, механизм обработки исключений содержит следующие операции:
- Создание объекта-исключения.
- Заполнение stack trace’а этого исключения.
- Stack unwinding (раскрутка стека) в поисках нужного обработчика.
Классификация исключений
Класс Java Throwable описывает все, что может быть брошено как исключение. Наследеники Throwable — Exception и Error — основные типы исключений. Также RuntimeException, унаследованный от Exception, является существенным классом.
Иерархия стандартных исключений
Проверяемые исключения
Наследники класса Exception (кроме наслеников RuntimeException) являются проверяемыми исключениями(checked exception). Как правило, это ошибки, возникшие по вине внешних обстоятельств или пользователя приложения – неправильно указали имя файла, например. Эти исключения должны обрабатываться в ходе работы программы, поэтому компилятор проверяет наличие обработчика или явного описания тех типов исключений, которые могут быть сгенерированы некоторым методом.
Все исключения, кроме классов Error и RuntimeException и их наследников, являются проверяемыми.
Error
Класс Error и его подклассы предназначены для системных ошибок. Свои собственные классы-наследники для Error писать (за очень редкими исключениями) не нужно. Как правило, это действительно фатальные ошибки, пытаться обработать которые довольно бессмысленно (например OutOfMemoryError).
RuntimeException
Эти исключения обычно возникают в результате ошибок программирования, такие как ошибки разработчика или неверное использование интерфейса приложения. Например, в случае выхода за границы массива метод бросит OutOfBoundsException. Такие ошибки могут быть в любом месте программы, поэтому компилятор не требует указывать runtime исключения в объявлении метода. Теоретически приложение может поймать это исключение, но разумнее исправить ошибку.
Обработка исключений
Чтобы сгенерировать исключение используется ключевое слово throw. Как и любой объект в Java, исключения создаются с помощью new.
if (t == null) { throw new NullPointerException("t = null"); }
Есть два стандартных конструктора для всех исключений: первый — конструктор по умолчанию, второй принимает строковый аргумент, поэтому можно поместить подходящую информацию в исключение.
Возможна ситуация, когда одно исключение становится причиной другого. Для этого существует механизм exception chaining. Практически у каждого класса исключения есть конструктор, принимающий в качестве параметра Throwable – причину исключительной ситуации. Если же такого конструктора нет, то у Throwable есть метод initCause(Throwable), который можно вызвать один раз, и передать ему исключение-причину.
Как и было сказано раньше, определение метода должно содержать список всех проверяемых исключений, которые метод может бросить. Также можно написать более общий класс, среди наследников которого есть эти исключения.
void f() throws InterruptedException, IOException { //...
try-catch-finally
Код, который может бросить исключения оборачивается в try-блок, после которого идут блоки catch и finally (Один из них может быть опущен).
try { // Код, который может сгенерировать исключение }
Сразу после блока проверки следуют обработчики исключений, которые объявляются ключевым словом catch.
try { // Код, который может сгенерировать исключение } catch(Type1 id1) { // Обработка исключения Type1 } catch(Type2 id2) { // Обработка исключения Type2 }
Сatch-блоки обрабатывают исключения, указанные в качестве аргумента. Тип аргумента должен быть классом, унаследованного от Throwable, или самим Throwable. Блок catch выполняется, если тип брошенного исключения является наследником типа аргумента и если это исключение не было обработано предыдущими блоками.
Код из блока finally выполнится в любом случае: при нормальном выходе из try, после обработки исключения или при выходе по команде return.
NB: Если JVM выйдет во время выполнения кода из try или catch, то finally-блок может не выполниться. Также, например, если поток выполняющий try или catch код остановлен, то блок finally может не выполниться, даже если приложение продолжает работать.
Блок finally удобен для закрытия файлов и освобождения любых других ресурсов. Код в блоке finally должен быть максимально простым. Если внутри блока finally будет брошено какое-либо исключение или просто встретится оператор return, брошенное в блоке try исключение (если таковое было брошено) будет забыто.
import java.io.IOException; public class ExceptionTest { public static void main(String[] args) { try { try { throw new Exception("a"); } finally { throw new IOException("b"); } } catch (IOException ex) { System.err.println(ex.getMessage()); } catch (Exception ex) { System.err.println(ex.getMessage()); } } }
После того, как было брошено первое исключение — new Exception("a") — будет выполнен блок finally, в котором будет брошено исключение new IOException("b"), именно оно будет поймано и обработано. Результатом его выполнения будет вывод в консоль b. Исходное исключение теряется.
Обработка исключений, вызвавших завершение потока
При использовании нескольких потоков бывают ситуации, когда поток завершается из-за исключения. Для того, чтобы определить с каким именно, начиная с версии Java 5 существует интерфейс Thread.UncaughtExceptionHandler. Его реализацию можно установить нужному потоку с помощью метода setUncaughtExceptionHandler. Можно также установить обработчик по умолчанию с помощью статического метода Thread.setDefaultUncaughtExceptionHandler.
Интерфейс Thread.UncaughtExceptionHandler имеет единственный метод uncaughtException(Thread t, Throwable e), в который передается экземпляр потока, завершившегося исключением, и экземпляр самого исключения. Когда поток завершается из-за непойманного исключения, JVM запрашивает у потока UncaughtExceptionHandler, используя метод Thread.getUncaughtExceptionHandler(), и вызвает метод обработчика – uncaughtException(Thread t, Throwable e). Все исключения, брошенные этим методом, игнорируются JVM.
Информация об исключениях
-
getMessage(). Этот метод возвращает строку, которая была первым параметром при создании исключения; -
getCause()возвращает исключение, которое стало причиной текущего исключения; -
printStackTrace()печатает stack trace, который содержит информацию, с помощью которой можно определить причину исключения и место, где оно было брошено.
Exception in thread "main" java.lang.IllegalStateException: A book has a null property
at com.example.myproject.Author.getBookIds(Author.java:38)
at com.example.myproject.Bootstrap.main(Bootstrap.java:14)
Caused by: java.lang.NullPointerException
at com.example.myproject.Book.getId(Book.java:22)
at com.example.myproject.Author.getBookIds(Author.java:35)
Все методы выводятся в обратном порядке вызовов. В примере исключение IllegalStateException было брошено в методе getBookIds, который был вызван в main. «Caused by» означает, что исключение NullPointerException является причиной IllegalStateException.
Разработка исключений
Чтобы определить собственное проверяемое исключение, необходимо создать наследника класса java.lang.Exception. Желательно, чтобы у исключения был конструкор, которому можно передать сообщение:
public class FooException extends Exception { public FooException() { super(); } public FooException(String message) { super(message); } public FooException(String message, Throwable cause) { super(message, cause); } public FooException(Throwable cause) { super(cause); } }
Исключения в Java7
- обработка нескольких типов исключений в одном
catch-блоке:
catch (IOException | SQLException ex) {...}
В таких случаях параметры неявно являются final, поэтому нельзя присвоить им другое значение в блоке catch.
Байт-код, сгенерированный компиляцией такого catch-блока будет короче, чем код нескольких catch-блоков.
-
Tryс ресурсами позволяет прямо вtry-блоке объявлять необходимые ресурсы, которые по завершению блока будут корректно закрыты (с помощью методаclose()). Любой объект реализующийjava.lang.AutoCloseableможет быть использован как ресурс.
static String readFirstLineFromFile(String path) throws IOException { try (BufferedReader br = new BufferedReader(new FileReader(path))) { return br.readLine(); } }
В приведенном примере в качестве ресурса использутся объект класса BufferedReader, который будет закрыт вне зависимосити от того, как выполнится try-блок.
Можно объявлять несколько ресурсов, разделяя их точкой с запятой:
public static void viewTable(Connection con) throws SQLException { String query = "select COF_NAME, SUP_ID, PRICE, SALES, TOTAL from COFFEES"; try (Statement stmt = con.createStatement(); ResultSet rs = stmt.executeQuery(query)) { //Work with Statement and ResultSet } catch (SQLException e) { e.printStackTrace; } }
Во время закрытия ресурсов тоже может быть брошено исключение. В try-with-resources добавленна возможность хранения «подавленных» исключений, и брошенное try-блоком исключение имеет больший приоритет, чем исключения получившиеся во время закрытия. Получить последние можно вызовом метода getSuppressed() от исключения брошенного try-блоком.
- Перебрасывание исключений с улучшенной проверкой соответствия типов.
Компилятор Java SE 7 тщательнее анализирует перебрасываемые исключения. Рассмотрим следующий пример:
static class FirstException extends Exception { } static class SecondException extends Exception { } public void rethrowException(String exceptionName) throws Exception { try { if ("First".equals(exceptionName)) { throw new FirstException(); } else { throw new SecondException(); } } catch (Exception ex) { throw e; } }
В примере try-блок может бросить либо FirstException, либо SecondException. В версиях до Java SE 7 невозможно указать эти исключения в декларации метода, потому что catch-блок перебрасывает исключение ex, тип которого — Exception.
В Java SE 7 вы можете указать, что метод rethrowException бросает только FirstException и SecondException. Компилятор определит, что исключение Exception ex могло возникнуть только в try-блоке, в котором может быть брошено FirstException или SecondException. Даже если тип параметра catch — Exception, компилятор определит, что это экземпляр либо FirstException, либо SecondException:
public void rethrowException(String exceptionName) throws FirstException, SecondException { try { // ... } catch (Exception e) { throw e; } }
Если FirstException и SecondException не являются наследниками Exception, то необходимо указать и Exception в объявлении метода.
Примеры исключений
- любая операция может бросить
VirtualMachineError. Как правило это происходит в результате системных сбоев. -
OutOfMemoryError. Приложение может бросить это исключение, если, например, не хватает места в куче, или не хватает памяти для того, чтобы создать стек нового потока. -
IllegalArgumentExceptionиспользуется для того, чтобы избежать передачи некорректных значений аргументов. Например:
public void f(Object a) { if (a == null) { throw new IllegalArgumentException("a must not be null"); } }
IllegalStateExceptionвозникает в результате некорректного состояния объекта. Например, использование объекта перед тем как он будет инициализирован.
Гарантии безопасности
При возникновении исключительной ситуации, состояния объектов и программы могут удовлетворять некоторым условиям, которые определяются различными типами гарантий безопасности:
- Отсутствие гарантий (no exceptional safety). Если было брошено исключение, то не гарантируется, что все ресурсы будут корректно закрыты и что объекты, методы которых бросили исключения, могут в дальнейшем использоваться. Пользователю придется пересоздавать все необходимые объекты и он не может быть уверен в том, что может переиспозовать те же самые ресурсы.
- Отсутствие утечек (no-leak guarantee). Объект, даже если какой-нибудь его метод бросает исключение, освобождает все ресурсы или предоставляет способ сделать это.
- Слабые гарантии (weak exceptional safety). Если объект бросил исключение, то он находится в корректном состоянии, и все инварианты сохранены. Рассмотрим пример:
class Interval { //invariant: left <= right double left; double right; //... }
Если будет брошено исключение в этом классе, то тогда гарантируется, что ивариант «левая граница интервала меньше правой» сохранится, но значения left и right могли измениться.
- Сильные гарантии (strong exceptional safety). Если при выполнении операции возникает исключение, то это не должно оказать какого-либо влияния на состояние приложения. Состояние объектов должно быть таким же как и до вызовов методов.
- Гарантия отсутствия исключений (no throw guarantee). Ни при каких обстоятельствах метод не должен генерировать исключения. В Java это невозможно, например, из-за того, что
VirtualMachineErrorможет произойти в любом месте, и это никак не зависит от кода. Кроме того, эту гарантию практически невозможно обеспечить в общем случае.
Источники
- Обработка ошибок и исключения — Сайт Георгия Корнеева
- Лекция Георгия Корнеева — Лекториум
- The Java Tutorials. Lesson: Exceptions
- Обработка исключений — Википедия
- Throwable (Java Platform SE 7 ) — Oracle Documentation
- try/catch/finally и исключения — www.skipy.ru