Методы кодирования и защиты от ошибок - Oshibku.top - решение и исправление самых разных ошибок

оптическое волокно на кремниевой или пластмассовой основе, заключенное в материал с низким коэффициентом преломления света, который закрыт внешней оболочкой. Скорость передачи данных 3Гбит/c.

Радиоканалы наземной и спутниковой связи образуются с помощью передатчика и приемника радиоволн и относятся к технологии беспроводной передачи данных. Радиорелейные каналы связи состоят из последовательности станций, являющихся ретрансляторами. Связь осуществляется в пределах прямой видимости, дальности между соседними станциями — до 50 км. В спутниковых системах используются антенны СВЧ-диапазона частот для приема радиосигналов от наземных станций и ретрансляции этих сигналов обратно на наземные станции. Целесообразнее использоватьспутниковуюсвязьдляорганизацииканаласвязи междустанциями,расположенными на очень больших расстояниях, и возможности обслуживания абонентов в самых труднодоступных точках. Пропускная способность высокая – несколько десятков Мбит/c. Радиоканалы сотовой связи строятся по тем же принципам, что и сотовые телефонные сети. Радиоканалы передачи данных MMDS. Эти системы способна обслуживать территорию в радиусе 50—60 км, при этом прямая видимость передатчика оператора является не обязательной. Средняя гарантированная скорость передачиданныхсоставляет500Кбит/с-1 Мбит/с, но можно обеспечить до 56 Мбит/с на один канал. Радиоканалы передачи данных для локальных сетей. Стандартом беспроводной связи для локальных сетей является технология Wi-Fi. Скорость обмена данными до 11 Mбит/с при подключении точка-точка (для подключения двух ПК ) и до 54 Мбит/с при инфраструктурном соединении(дляподключениянесколькоПКкоднойточкедоступа).Радиоканалыпередачиданных Bluetooht-это технология передачи данных на короткие расстояния (не более 10 м) и мб использована для созд домашних сетей. Скорость передачи данных не превышает 1 Мбит/с.

Электронная почта(E-mail) является самой популярной и распространенной службой Internet. Для того чтобы иметь возможность обмениваться письмами по электронной почте, пользователь должен стать клиентом одной из компютерных сетей. Все письма, поступающие на некоторый почтовый адрес, записываются в выделенную для него область памяти сетевого компа. Сетевой комп, содержащий почтовые ящики абонентов носит название хост компа.

Кодирование и защита от ошибок

Существует три наиболее распространенных орудия борьбы с ошибками в процессе передачи данных:

•коды обнаружения ошибок;

•коды с коррекцией ошибок – схемы прямой коррекции ошибок (Forward Error Correction —

FEC);

•протоколы с автоматическим запросом повторной передачи (Automatic Repeat Request —

ARQ).

Код обнаружения ошибок позволяет довольно легко установить наличие ошибки. Как правило, подобные коды используются совместно с определенными протоколами канального или транспортного уровней, имеющими схему ARQ. В схеме ARQ приемник попросту отклоняет блок данных, в котором была обнаружена ошибка, после чего передатчик передает этот блок повторно. Коды с прямой коррекцией ошибок позволяют не только обнаружить ошибки, но и исправить их, не прибегая к повторной передаче. Схемы FEC часто используются в беспроводной передаче, где повторная передача крайне неэффективна, а уровень ошибок довольно высок.

1)Методы обнаружения ошибок

Методы обнаружения ошибок основаны на передаче в составе блока данных избыточной служебной информации, по которой можно судить с некоторой степенью вероятности о достоверности принятых данных.

Избыточную служебную информацию принято называть контрольной суммой, или контрольной последовательностью кадра (Frame Check Sequence, FCS). Контрольная сумма вычисляется как функция от основной информации, причем не обязательно путем суммирования. Принимающая сторона повторно вычисляет контрольную сумму кадра по известному алгоритму и в случае ее совпадения с контрольной суммой, вычисленной передающей стороной, делает вывод о том, что данные были переданы через сеть корректно.

2) Методы коррекции ошибок Наиболее часто в современных системах связи применяется тип кодирования, реализуемый

сверхточным кодирующим устройством (Сonvolutional coder), потому что такое кодирование несложно реализовать аппаратно с использованием линий задержки (delay) и сумматоров. В отличие от рассмотренного выше кода, который относится к блочным кодам без памяти, сверхточный код относится к кодам с конечной памятью (Finite memory code); это означает, что выходная последовательность кодера является функцией не только текущего входного сигнала, но также нескольких из числа последних предшествующих битов. Длина кодового ограничения (Constraint length of a code) показывает, как много выходных элементов выходит из системы в пересчете на один входной. Коды часто характеризуются их эффективной степенью (или коэффициентом) кодирования (Code rate). Вам может встретиться сверхточный код с коэффициентом кодирования 1/2. Этот коэффициент указывает, что на каждый входной бит приходится два выходных. Хотя коды с более высокой эффективной степенью кодирования позволяют передавать данные с более высокой скоростью, они, соответственно, более чувствительны к шуму.

Вбеспроводных системах с блочными кодами широко используется метод чередования блоков. Преимущество чередования состоит в том, что приемник распределяет пакет ошибок, исказивший некоторую последовательность битов, по большому числу блоков, благодаря чему становитсявозможнымисправлениеошибок.Чередованиевыполняетсяспомощьючтенияизаписи данных в различном порядке. Если во время передачи пакет помех воздействует на некоторую последовательность битов, то все эти биты оказываются разнесенными по различным блокам. Следовательно, от любой контрольнойпоследовательности требуется возможностьисправить лишь небольшую часть от общего количества инвертированных битов.

3) Методы автоматического запроса повторной передачи

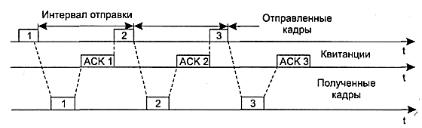
Впростейшем случае защита от ошибок заключается только в их обнаружении. Система должна предупредить передатчик об обнаружении ошибки и необходимости повторной передачи. Такие процедуры защиты от ошибок известны как методы автоматического запроса повторной передачи (Automatic Repeat Request — ARQ). В беспроводных локальных сетях применяется процедура «запрос ARQ с остановками» (stop-and-wait ARQ).

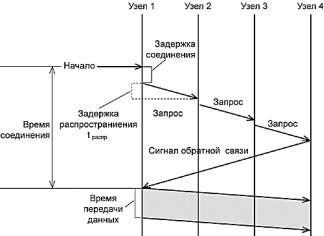
Рис. 1.13. Процедура запрос ARQ с остановками

В этом случае источник, пославший кадр, ожидает получения подтверждения (Acknowledgement — ACK), или, как еще его называют, квитанции, от приемника и только после этого посылает следующий кадр. Если же подтверждение не приходит в течение тайм-аута, то кадр (или подтверждение) считается утерянным и его передача повторяется. На рис. 1.13 видно, что в этом случае производительность обмена данными ниже потенциально возможной; хотя передатчик и мог бы послать следующий кадр сразу же после отправки предыдущего, он обязан ждать прихода подтверждения.

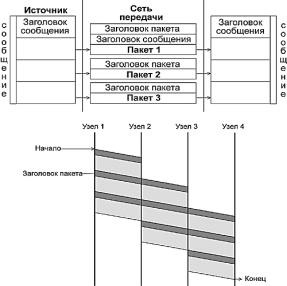
Структура пакета

Структураи размерыпакета в каждой сетижестко определены стандартом на даннуюсеть и связаны, прежде всего, с аппаратными особенностями данной сети, выбранной топологией и типом среды передачи информации. Кроме того, эти параметры зависят от используемого протокола (порядка обмена информацией).

Но существуют некоторые общие принципы формирования структуры пакета, которые учитывают характерные особенности обмена информацией по любым локальным сетям.

•Стартовая комбинация битов или преамбула, которая обеспечивает предварительную настройку аппаратурыадаптера или другого сетевого устройства на прием и обработку пакета. Это поле может полностью отсутствовать или же сводиться к единственному стартовому биту.

•Сетевой адрес (идентификатор) принимающего абонента, то есть индивидуальный или групповой номер, присвоенный каждому принимающему абоненту в сети. Этот адрес позволяет приемнику распознать пакет, адресованный ему лично, группе, в которую он входит, или всем абонентам сети одновременно (при широком вещании).

•Сетевой адрес (идентификатор) передающего абонента, то есть индивидуальный номер, присвоенный каждому передающему абоненту. Этот адрес информирует принимающего абонента, откуда пришел данный пакет. Включение в пакет адреса передатчика необходимо в том случае, когда одному приемнику могут попеременно приходить пакеты от разных передатчиков.

•Служебная информация, которая может указывать на тип пакета, его номер, размер, формат, маршрут его доставки, на то, что с ним надо делать приемнику и т.д.

•Данные (поле данных) – это таинформация, ради передачи которойиспользуется пакет.

Вотличие от всех остальных полей пакета поле данных имеет переменную длину, которая, собственно, и определяет полную длину пакета. Существуют специальные управляющие пакеты, которые не имеют поля данных. Их можно рассматривать как сетевые команды. Пакеты, включающие поле данных, называются информационными пакетами. Управляющие пакеты могут выполнять функцию начала и конца сеанса связи, подтверждения приема информационного пакета, запроса информационного пакета и т.д.

•Контрольная сумма пакета – это числовой код, формируемый передатчиком по определенным правилам и содержащий в свернутом виде информацию обо всемпакете. Приемник, повторяя вычисления, сделанные передатчиком, с принятым пакетом, сравнивает их результат с контрольной суммой и делает вывод о правильности или ошибочности передачи пакета. Если пакет ошибочен, то приемник запрашивает его повторную передачу. Обычно используется циклическая контрольная сумма (CRC). Подробнее об этом рассказано в главе 7.

•Стоповая комбинация служит для информирования аппаратуры принимающего абонента об окончании пакета, обеспечивает выход аппаратуры приемника из состояния приема. Это поле может отсутствовать, если используется самосинхронизирующийся код, позволяющий определять момент окончания передачи пакета.

Рис. Структура заголовка IP-пакета

Методы коммутации каналов, сообщений, пакетов

В общем случае решение каждой из частных задач коммутации — определение потоков и соответствующих маршрутов, фиксация маршрутов в конфигурационных параметрах и таблицах сетевых устройств, распознавание потоков и передача данных между интерфейсами одного устройства,мультиплексирование/демультиплексированиепотоковиразделение среды передачи— тесно связано с решением всех остальных. Комплекс технических решений обобщенной задачи коммутации в совокупности составляет базис любой сетевой технологии. От того, какой механизм прокладки маршрутов, продвижения данных и совместного использования каналов связи заложен в той или иной сетевой технологии, зависят ее фундаментальные свойства.

Среди множества возможных подходов к решению задачи коммутации абонентов в сетях выделяют два основополагающих:

•коммутация каналов ( circuit switching );

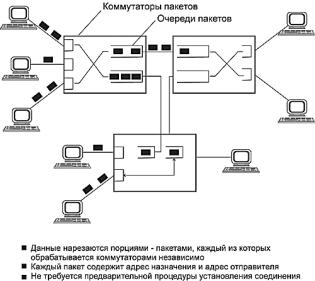
•коммутация пакетов ( packet switching ).

Внешне обе эти схемы соответствуют приведенной на рис. 6.1 структуре сети, однако возможности и свойства их различны.

Рис. 6.1. Общая структура сети с коммутацией абонентов Сети с коммутацией каналов имеют более богатую историю, они произошли от первых

телефонных сетей. Сети с коммутацией пакетов сравнительно молоды, они появились в конце 60- х годов как результат экспериментов с первыми глобальными компьютерными сетями. Каждая из этих схем имеет свои достоинства и недостатки, но по долгосрочным прогнозам многих специалистов, будущее принадлежит технологии коммутации пакетов, как более гибкой и универсальной.

Коммутация каналов При коммутации каналов коммутационная сеть образует между конечными узлами

непрерывный составной физический канал из последовательно соединенных коммутаторами

промежуточных канальных участков. Условием того, что несколько физических каналов при последовательном соединении образуют единый физический канал, является равенство скоростей передачи данных в каждом из составляющих физических каналов. Равенство скоростей означает, что коммутаторы такой сети не должны буферизовать передаваемые данные.

В сети с коммутацией каналов перед передачей данных всегда необходимо выполнить процедуру установления соединения, в процессе которой и создается составной канал. И только после этого можно начинать передавать данные.

Например, если сеть, изображенная на рис. 6.1, работает по технологии коммутации каналов, то узел 1, чтобы передать данные узлу 7, сначала должен передать специальный запрос на установление соединения коммутатору A, указав адрес назначения 7. Коммутатор А должен выбрать маршрут образования составного канала, а затем передать запрос следующему

коммутатору, в данном случае E. Затем коммутатор E передает запрос коммутатору F, а тот, в

свою очередь, передает запрос узлу 7. Если узел 7 принимает запрос на установление соединения, он направляет по уже установленному каналу ответ исходному узлу, после чего составной канал считается скоммутированным, и узлы 1 и 7 могут обмениваться по нему данными.

Рис. 6.2. Установление составного канала Техника коммутации каналов имеет свои достоинства и недостатки.

Достоинства коммутации каналов

1.Постоянная и известная скорость передачи данных по установленному между конечными узлами каналу. Это дает пользователю сети возможности на основе заранее произведенной оценки необходимой для качественной передачи данных пропускной способности установить в сети канал нужной скорости.

2.Низкий и постоянный уровень задержки передачи данных через сеть. Это позволяет качественно передавать данные, чувствительные к задержкам (называемые также трафиком реального времени) — голос, видео, различную технологическую информацию.

Недостатки коммутации каналов

1.Отказ сети в обслуживании запроса на установление соединения. Такая ситуация может сложиться из-за того, что на некотором участке сети соединение нужно установить вдоль канала, через который уже проходит максимально возможное количество информационных потоков. Отказ может случиться и на конечном участке составного канала — например, если абонент способен поддерживать только одно соединение, что характерно для многих телефонных сетей. При поступлении второго вызова к уже разговаривающему абоненту сеть передает вызывающему абоненту короткие гудки — сигнал «занято».

2.Нерациональное использование пропускной способности физических каналов. Та часть пропускной способности, которая отводится составному каналу после установления соединения, предоставляется ему на все время, т.е. до тех пор, пока соединение не будет разорвано. Однако абонентам не всегда нужна пропускная способность канала во время соединения, например

втелефонном разговоре могут быть паузы, еще более неравномерным во времени является взаимодействие компьютеров. Невозможность динамического перераспределения пропускной способности представляет собой принципиальное ограничение сети с коммутацией каналов, так как единицей коммутации здесь является информационный поток в целом.

3.Обязательная задержка перед передачей данных из-за фазы установления соединения. Достоинства и недостатки любой сетевой технологии относительны. В определенных

ситуациях на первый план выходят достоинства, а недостатки становятся несущественными. Так, техника коммутации каналов хорошо работает в тех случаях, когда нужно передавать только трафик телефонных разговоров. Здесь с невозможностью «вырезать» паузы из разговора и более рационально использовать магистральные физические каналы между коммутаторами можно мириться. Авотприпередачеочень неравномерного компьютерноготрафикаэтанерациональность уже выходит на первый план.

Коммутация пакетов Эта техника коммутации была специально разработана для эффективной передачи

компьютерного трафика. Первые шаги на пути создания компьютерных сетей на основе техники коммутации каналов показали, что этот вид коммутации не позволяет достичь высокой общей пропускной способности сети. Типичные сетевые приложения генерируют трафик очень неравномерно, с высоким уровнем пульсации скорости передачи данных. Например, при обращении к удаленному файловому серверу пользователь сначала просматривает содержимое

каталога этого сервера, что порождает передачу небольшого объема данных. Затем он открывает требуемый файл в текстовом редакторе, и эта операция может создать достаточно интенсивный обмен данными, особенно если файл содержит объемные графические включения. После отображения нескольких страниц файла пользователь некоторое время работает с ними локально, что вообще не требует передачи данных по сети, а затем возвращает модифицированные копии страниц на сервер — и это снова порождает интенсивную передачу данных по сети.

Коэффициент пульсации трафика отдельного пользователя сети, равный отношению средней интенсивностиобмена данными кмаксимально возможной, может достигать 1:50илидаже 1:100. Если для описанной сессии организовать коммутацию канала между компьютером пользователя и сервером, то большую часть времени канал будет простаивать. В то же время коммутационные возможности сети будут закреплены за данной парой абонентов и будут недоступны другим пользователям сети.

При коммутации пакетов все передаваемые пользователем сообщения разбиваются в исходном узле на сравнительно небольшие части, называемые пакетами. Напомним, что сообщением называется логически завершенная порция данных — запрос на передачу файла, ответ на этот запрос, содержащий весь файл и т.д. Сообщения могут иметь произвольную длину, от нескольких байт до многих мегабайт. Напротив, пакеты обычно тоже могут иметь переменную длину, но в узких пределах, например от 46 до 1500 байт. Каждый пакет снабжается заголовком, в котором указывается адресная информация, необходимая для доставки пакета на узел назначения, атакженомерпакета, которыйбудетиспользоватьсяузломназначениядлясборкисообщения(рис. 6.3). Пакеты транспортируются по сети как независимые информационные блоки. Коммутаторы сетипринимаютпакетыотконечныхузловинаосновании адреснойинформациипередаютихдруг другу, а в конечном итоге — узлу назначения.

Рис. 6.3. Разбиение сообщения на пакеты Коммутаторы пакетной сети отличаются от коммутаторов каналов тем, что они имеют

внутреннюю буферную память для временного хранения пакетов, если выходной порт коммутатора в момент принятия пакета занят передачей другого пакета (рис. 6.3). В этом случае пакет находится некоторое время в очереди пакетов в буферной памяти выходного порта, а когда до него дойдет очередь, он передается следующему коммутатору. Такая схема передачи данных позволяет сглаживать пульсацию трафика на магистральных связях между коммутаторами и тем самым наиболее эффективно использовать их для повышения пропускной способности сети в целом.

Действительно, для пары абонентов наиболее эффективным было бы предоставление им в единоличноепользование скоммутированногоканала связи, как это делается в сетях с коммутацией каналов. В таком случае время взаимодействия этой пары абонентов было бы минимальным, так как данные без задержек передавались бы от одного абонента другому. Простои канала во время пауз передачи абонентов не интересуют, для них важно быстрее решить свою задачу. Сеть с коммутацией пакетов замедляет процесс взаимодействия конкретной пары абонентов, так как их

пакеты могут ожидать в коммутаторах, пока по магистральным связям передаются другие

пакеты, пришедшие в коммутатор ранее.

Тем не менее, общий объем передаваемых сетью компьютерныхданных в единицу времени при технике коммутации пакетов будет выше, чем при технике коммутации каналов. Это происходит потому, что пульсации отдельных абонентов в соответствии с законом больших чисел распределяются во времени так, что их пики не совпадают. Поэтому коммутаторы постоянно и достаточно равномерно загружены работой, если число обслуживаемых ими абонентов действительно велико. На рис. 6.4 показано, что трафик, поступающий от конечных узлов на коммутаторы, распределен во времени очень неравномерно. Однако коммутаторы более высокого уровня иерархии, которые обслуживают соединения между коммутаторами нижнего уровня, загружены более равномерно, и поток пакетов в магистральных каналах, соединяющих коммутаторы верхнего уровня, имеет почти максимальный коэффициент использования. Буферизация сглаживает пульсации, поэтому коэффициент пульсации на магистральных каналах гораздо ниже, чем на каналах абонентского доступа — он может быть равным 1:10 или даже 1:2.

Рис. 6.4. Сглаживание пульсаций трафика в сети с коммутацией пакетов Более высокая эффективность сетей с коммутацией пакетов по сравнению с сетями с

коммутацией каналов (при равной пропускной способности каналов связи) была доказана в 60-е годы как экспериментально, так и с помощью имитационного моделирования. Здесь уместна аналогия с мультипрограммными операционными системами. Каждая отдельнаяпрограмма в такой системе выполняется дольше, чем в однопрограммной системе, когда программе выделяется все процессорное время, пока ее выполнение не завершится. Однако общее число программ, выполняемых за единицу времени, в мультипрограммной системе больше, чем в однопрограммной.

Сеть с коммутацией пакетов замедляет процесс взаимодействия конкретной пары абонентов, но повышает пропускную способность сети в целом.

Задержки в источнике передачи:

•время на передачу заголовков ;

•задержки, вызванные интервалами между передачей каждого следующего пакета.

Задержки в каждом коммутаторе:

•время буферизации пакета ;

•время коммутации, которое складывается из:

o времени ожидания пакета в очереди (переменная величина); o времени перемещения пакета в выходной порт. Достоинства коммутации пакетов

1.Высокая общая пропускная способность сети при передаче пульсирующего трафика.

2.Возможность динамически перераспределять пропускную способность физических каналов связи между абонентами в соответствии с реальными потребностями их трафика.

Недостатки коммутации пакетов

1.Неопределенность скорости передачи данных между абонентами сети, обусловленная тем, что задержки в очередях буферов коммутаторов сети зависят от общей загрузки сети.

2.Переменная величина задержки пакетов данных, которая может быть достаточно продолжительной в моменты мгновенных перегрузок сети.

3.Возможные потери данных из-за переполнения буферов.

В настоящее время активно разрабатываются и внедряются методы, позволяющие преодолеть указанные недостатки, которые особенно остро проявляются для чувствительного к задержкам трафика, требующего при этом постоянной скорости передачи. Такие методы называются методами обеспечения качества обслуживания (Quality of Service, QoS).

Сети с коммутацией пакетов, в которых реализованы методы обеспечения качества обслуживания, позволяют одновременно передавать различные виды трафика, в том числе такие важные как телефонный и компьютерный. Поэтому методы коммутации пакетов сегодня считаются наиболее перспективными для построения конвергентной сети, которая обеспечит комплексные качественные услуги для абонентов любого типа. Тем не менее, нельзя сбрасывать со счетов и методы коммутации каналов. Сегодня они не только с успехом работают в традиционных телефонных сетях, но и широко применяются для образования высокоскоростных постоянных соединений в так называемых первичных (опорных) сетях технологий SDH и DWDM, которые используются для создания магистральных физических каналов между коммутаторами телефонных или компьютерных сетей. В будущем вполне возможно появление новых технологий коммутации, в том или ином виде комбинирующих принципы коммутации пакетов и каналов.

Коммутация сообщений Коммутация сообщений по своим принципам близка к коммутации пакетов. Под

коммутацией сообщений понимается передача единого блока данных между транзитными компьютерами сети с временной буферизацией этого блока на диске каждого компьютера. Сообщение в отличие от пакета имеет произвольную длину, которая определяется не технологическими соображениями, а содержанием информации, составляющей сообщение.

Транзитные компьютеры могут соединяться между собой как сетью с коммутацией пакетов, так и сетью с коммутацией каналов. Сообщение (это может быть, например, текстовый документ, файл с кодом программы, электронное письмо) хранится в транзитном компьютере на диске, причем довольно продолжительное время, если компьютер занят другой работой или сеть временно перегружена.

По такой схеме обычно передаются сообщения, не требующие немедленного ответа, чаще всего сообщения электронной почты. Режим передачи с промежуточным хранением на диске называется режимом «хранения-и-передачи» (store-and-forward).

Режим коммутации сообщений разгружает сеть для передачи трафика, требующего быстрого ответа, например трафика службы WWW или файловой службы.

Количество транзитных компьютеров обычно стараются уменьшить. Если компьютеры подключены к сети с коммутацией пакетов, то число промежуточных компьютеров уменьшается до двух. Например, пользователь передает почтовое сообщение своему серверу исходящей почты, атот сразу старается передать его серверу входящей почтыадресата. Но если компьютеры связаны между собой телефонной сетью, то часто используетсянесколько промежуточных серверов, так как прямой доступ к конечному серверу может быть в данный момент невозможен из-за перегрузки телефонной сети (абонент занят) или экономически невыгоден из-за высоких тарифов на дальнюю телефонную связь.

Техника коммутации сообщений появилась в компьютерных сетях раньше техники коммутации пакетов, но потом была вытеснена последней, как более эффективной по критерию пропускной способности сети. Запись сообщения на диск занимает достаточно много времени, и кроме того, наличие дисков предполагает использование в качестве коммутаторов специализированных компьютеров, что влечет за собой существенные затраты на организацию сети.

Сегодня коммутация сообщений работает только для некоторых не оперативных служб, причем чаще всего поверх сети с коммутацией пакетов, как служба прикладного уровня.

Источник

Методы
защиты от ошибок при передаче информации
в ТКС.

Вопросы :

Методы защиты
от ошибок при передаче и информации.
Помехоустойчивое
(избыточное) кодирование
Системы передачи
с обратной связью.
Групповые методы
защиты от ошибок.

Цели
и задачи изучения темы:
получение
представления о методах обеспечения
достоверности передачи информации,
причинах возникновения ошибок, методах
защиты от ошибок – групповые методы,
помехоустойчивое кодирование, системы
передачи с обратной связью.

Изучив тему,
студент должен:

знать понятие и
сущность методов обеспечения достоверности
передачи информации, причин возникновения
ошибок, методов защиты от ошибок как
совокупности групповых методов,
помехоустойчивого кодирования и систем
передачи с обратной связью, проблем
современной теории и техники связи.
иметь представление
о методах защиты от ошибок, как
совокупности методов обеспечения
достоверности передачи информации, о
причинах возникновения ошибок, о
проблемах современной теории и техники
связи, системах с решающей обратной
связью, системах с информационной
обратной связью.

Изучая
тему, необходимо акцентировать внимание
на следующих понятиях:
достоверность передачи информации,
методы защиты от ошибок, помехоустойчивое
кодирование, системы передачи с обратной
связью, избыточность кода, корректирующая
способность кода, значимость кода,
системы с решающей обратной связью,
системы с информационной обратной
связью.

Тема №6. Методы
защиты от ошибок при передаче информации
в ТКС

1. Методы защиты от ошибок при передаче и информации

Проблема обеспечения
безошибочности (достоверности) передачи
информации в сетях имеет очень важное
значение. Если при передаче информации
обычной телеграммы возникает в тексте
ошибка или при разговоре по телефону
слышен треск, то в большинстве случаев
ошибки и искажения легко обнаруживаются
по смыслу. Но при передаче данных одна
ошибка (искажение одно бита) на тысячу
переданных сигналов может серьезно
отразится на качестве информации.

Существуют множество
методов обеспечения достоверности
передачи информации (методы защиты от
ошибок), отличающиеся по используемым
для их реализации средствам, по затратам
времени на их применение на передающем
и приемном пунктах, по затратам
дополнительного времени на передачу
фиксированного объема данных (оно
обусловлено объема трафика пользователя
при реализации данного метода), по
степени обеспечения достоверности
передачи информации. Практическое
воплощение метода состоит из двух
частей. – программной и аппаратной.
Соотношение между ними может быть самым
различным, вплоть до почти полного
отсутствия одной из частей. Чем больше
удельный вес аппаратурных средств по
сравнению с программными, тем при прочих
равных условиях сложнее оборудование,
реализующее метод, и меньше затрат
времени на его реализацию, и наоборот.

Выделяют две
основные причины
возникновения ошибок
при передаче информации в сетях:

сбои
в какой-то части оборудования сети или
возникновение неблагоприятных
объективных событий в сети. Как правило,
система передачи данных готова к такого
рода проявлениям и устраняет их с
помощью планово предусмотренных средств
помехи,
вызванные внешним источниками и
атмосферными явлениями. Помехи – это
электрические возмущения, возникающие
в аппаратуре или попадающие в нее извне.
Наиболее распространенными являются
флуктуационные (случайные) помехи. Они
представляют собой последовательность
импульсов, имеющих случайную амплитуду
и следующих друг за другом через
различные промежутки времени. Примерами
таких помех могут быть атмосферные и
индустриальные помехи, которые обычно
появляются в виде одиночных импульсов
малой длительности и большой амплитуды.
Возможны и сосредоточенные помехи в
виде синусоидальных колебаний к ним
относятся сигналы от посторонних
радиостанций, излучения генераторов
высокой частоты. Встречаются и смешенные
помехи. В приемнике помехи могут
настолько ослабить информационный
сигнал, что он либо вообще не будет
обнаружен, либо искажен так, что «единица»
может перейти в нуль и наоборот.

Трудности борьбы
с помехами заключается в беспорядочности,
нерегулярности и в структурном сходстве
помех с информационными сигналами.
Поэтому защита информации от ошибок и
вредного влияния помех имеет большое
практическое значение и является одной
из серьезных проблем современной теории
и техники связи.

Среди многочисленных
методов защиты от ошибок выделяют три
группы методов:

помехоустойчивое
кодирование;
методы защиты
от ошибок в системах передачи с обратной
связью;
групповые
методы.

Соседние файлы в папке Лекции Вссит

Защита от ошибок в сетях.

Проблема обеспечения безошибочности (достоверности) передачи информации в сетях имеет очень большое значение. Практическое воплощение методов состоит из двух частей — программной и аппаратной.

Выделяют две основные причины возникновения ошибок при передаче информации в сетях:

• сбои в какой-то части оборудования сети или возникновение неблагоприятных объективных событий в сети (например, коллизий при использовании метода случайного доступа в сеть). Как правило, система передачи данных готова к такого рода проявлениям и устраняет их с помощью предусмотренных планом средств;

• помехи, вызванные внешними источниками и атмосферными явлениями.

Помехи — это электрические возмущения, возникающие в самой аппаратуре или попадающие в нее извне.

Среди многочисленных методов защиты от ошибок выделяются три группы методов: групповые методы, помехоустойчивое кодирование и методы защиты от ошибок в системах передачи с обратной связью.

Из групповых методов получили широкое применение мажоритарный метод.

Рекомендация для Вас — 13. Математическая модель изменения уровня жидкости.

Суть мажоритарного метода, давно и широко используемого в телеграфии, состоит в следующем. Каждое сообщение ограниченной длины передается несколько раз, чаще всего три раза. Принимаемые сообщения запоминаются, а потом производится их поразрядное сравнение. Суждение о правильности передачи выносится по совпадению большинства из принятой информации методом «два из трех».

Другой групповой метод, также не требующий перекодирования информации, предполагает передачу данных блоками с количественной характеристикой блока. Такими характеристиками могут быть: число единиц или нулей в блоке, контрольная сумма передаваемых символов в блоке, остаток от деления контрольной суммы на постоянную величину и др.

Помехоустойчивое (избыточное) кодирование, предполагающее разработку и использование корректирующих (помехоустойчивых) кодов, применяется не только в ТКС, но и в ЭВМ для защиты от ошибок при передаче информации между устройствами машины. Оно позволяет получить более высокие качественные показатели работы систем связи. Его основное назначение заключается в обеспечении малой вероятности искажений передаваемой информации, несмотря на присутствие помех или сбоев в работе сети.

Системы передачи с обратной связью делятся на системы с решающей обратной связью и системы с информационной обратной связью.

Особенностью систем с решающей обратной связью (систем с перезапросом) является то, что решение о необходимости повторной передачи информации (сообщения, пакета) принимает приемник. Здесь обязательно применяется помехоустойчивое кодирование, с помощью которого на приемной станции осуществляется проверка принимаемой информации.

В системах с информационной обратной связью передача информации осуществляется без помехоустойчивого кодирования. Приемник, приняв информацию по прямому каналу и зафиксировав ее в своей памяти, передает ее в полном объеме по каналу обратной связи передатчику, где переданная и возвращенная информация сравниваются. При совпадении передатчик посылает приемнику сигнал подтверждения, в противном случае происходит повторная передача всей информации. Таким образом, здесь решение о необходимости повторной передачи принимает передатчик.

6.2.1. Связность оконечных устройств

6.2.2. Автоматический запрос повторной передачи

Перед тем как начать обсуждение структурированной избыточности, рассмотрим два основных метода использования избыточности для защиты от ошибок. В первом методе, обнаружение ошибок и повторная передача, для проверки на наличие ошибки используется контрольный бит четности (дополнительный бит, присоединяемый к данным). При этом приемное оконечное устройство не предпринимает попыток исправить ошибку, оно просто посылает передатчику запрос на повторную передачу данных. Следует заметить, что для такого диалога между передатчиком и приемником необходима двухсторонняя связь. Второй метод, прямое исправление ошибок (forward error correction — FEC), требует лишь односторонней линии связи, поскольку в этом случае контрольный бит четности служит как для обнаружения, так и исправления ошибок. Далее мы увидим, что не все комбинации ошибок можно исправить, так что коды коррекции классифицируются в соответствии с их возможностями исправления ошибок.

6.2.1. Связность оконечных устройств

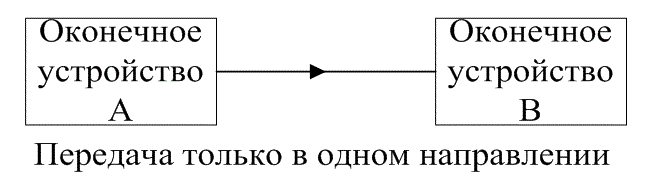
Оконечные устройства систем связи часто классифицируют согласно их связности с другими оконечными устройствами. Возможные типы соединения, показанные на рис. 6.6, называются симплексными (simplex) (не путайте с симплексными, или трансортогональными кодами), полудуплексными (half-duplex) и полнодуплексными (full-duplex). Симплексное соединение на рис. 6.6, а — это односторонняя линия связи.

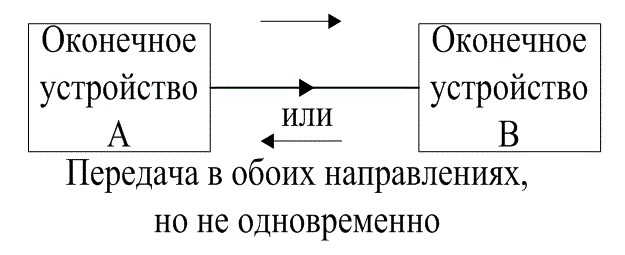
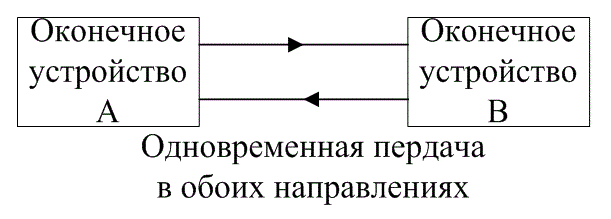
Передача сигналов производится только от оконечного устройства А к оконечному устройству В. Полудуплексное соединение на рис. 6.6,б это линии связи, посредством которой можно осуществлять передачи сигналов в обоих направлениях, но не одновременно. И наконец, полнодуплексное соединение (рис. 6.6, в) — это двусторонняя связь, где передача сигналов происходит одновременно в обоих направлениях.

Передача только в одном направлении а)

а)

б)

в)

Рис. 6.6. Классификация связности оконечных устройств: а) симплексная; б) полудуплексная; в) полнодуплексная

6.2.2. Автоматический запрос повторной передачи

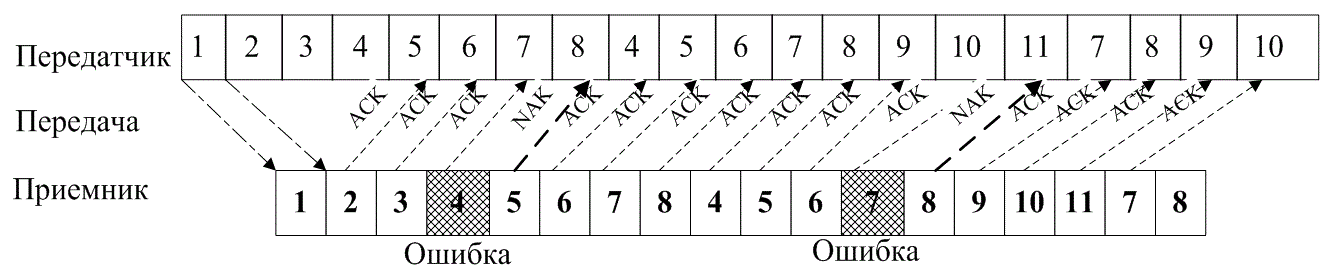
Если зашита от ошибок заключается только в их обнаружении, система связи должна обеспечить средства предупреждения передатчика об опасности, сообщающие, что была обнаружена ошибка и требуется повторная передача. Подобные процедуры защиты от ошибок известны как методы автоматического запроса повторной передачи (Automatic Repeat Request — ARQ). На рис. 6.7 показаны три наиболее распространенные процедуры ARQ. На каждой схеме ось времени направлена слева направо. Первая процедура ARQ, запрос ARQ с остановками (stop-and-wait ARQ), показана на рис. 6.7, а. Ее реализация требует только полудуплексного соединения, поскольку передатчик перед началом очередной передачи ожидает подтверждения об успешном приеме (acknowledgement — АСК) предыдущей. В примере, приведенном на рисунке, третий блок передаваемых данных принят с ошибкой. Следовательно, приемник передает отрицательное подтверждение приема (negative acknowledgment — NAK); передатчик повторяет передачу третьего блока сообщения и только после этого передает следующий по очередности блок. Вторая процедура ARQ, непрерывный запрос ARQ с возвратом (continuous ARQ with pullback), показана на рис. 6.7,б. Здесь требуется полно-дуплексное соединение. Оба оконечных устройства начинают передачу одновременно: передатчик отправляет информацию, а приемник передает подтверждение о приеме данных. Следует .отметить,„что каждому блоку передаваемых данных присваивается порядковый номер. Кроме того, номера кадров АСК и NAK должны быть согласованы; иначе говоря, задержка распространения сигнала должна быть известна априори, чтобы передатчик знал, к какому блоку сообщения относится данный кадр подтверждения приема. В примере на рис. 6,7,б время подобрано так, что между отправленным блоком сообщений и полученным подтверждением о приеме существует постоянный интервал в четыре блока. Например, после отправки сообщения 8, приводит сигнал NAK, сообщающий об ошибке в блоке 4. При использовании процедуры ARQ передатчик «возвращается» к сообщению с ошибкой и снова передает всю информацию, начиная с поврежденного сообщения. И наконец, третья процедура, именуемая непрерывным запросом ARQ с выборочным повторением (continuous ARQ with selective repeat), показана на рис. 6.7, в. Здесь, как и во второй процедуре, требуется полнодуплексное соединение. Впрочем, в этой процедуре повторно передается только искаженное сообщение; затем передатчик продолжает передачу с того места, где она прервалась, не выполняя повторной передачи правильно принятых сообщений.

а)

б)

в)

Рис. 6.7. Автоматический запрос повторной передачи (ARQ): а) запрос

ARQ с остановками (полудуплексная связь); б) непрерывный запрос ARQ с возвратом (полнодуплексная связь); в) непрерывный запрос ARQ с выборочным повторением (полнодуплексная связь)

Выбор конкретной процедуры ARQ является компромиссом между требованиями эффективности применения ресурсов связи и необходимостью полнодуплексной связи. Полудуплексная связь (рис. 6.7, а) требует меньших затрат, нежели полнодуплексная; в то же время она менее эффективна, что можно определить по количеству пустых временных интервалов. Более эффективная работа, показанная на рис. 6.7, б, требует более дорогой полнодуплексной связи.

Главное преимущество схем ARQ перед схемами прямого исправления ошибок (forward error correction — FEC) заключается в том, что «обнаружение ошибок требует более простого декодирующего оборудования и меньшей избыточности, чем коррекция ошибок. Кроме того, она гибче; информация передается повторно только при обнаружении ошибки. С другой стороны, метод FEC может оказаться более приемлемым (или дополняющим) по какой-либо из следующих причин.

1. Обратный канал недоступен или задержка при использовании ARQ слишком велика.

2. Алгоритм повторной передачи нельзя реализовать удобным образом.

3. При ожидаемом количестве ошибок потребуется слишком много повторных передач.

Эта статья — о работе с ошибками в данных при их хранении или передаче. О контроле фактических ошибок в текстах см. Проверка фактов; о проверке знаний и навыков при обучении см. Педагогическое тестирование; о методе обучения нейросети см. Метод коррекции ошибки.

Контроль ошибок — комплекс методов обнаружения и исправления ошибок в данных при их записи и воспроизведении или передаче по линиям связи.

Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI) в связи с тем, что в процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Различные области применения контроля ошибок диктуют различные требования к используемым стратегиям и кодам.

В системах связи возможны несколько стратегий борьбы с ошибками:

обнаружение ошибок в блоках данных и автоматический запрос повторной передачи^[⇨] повреждённых блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
упреждающая коррекция ошибок добавляет к передаваемой информации такие дополнительные данные, которые позволяют исправить ошибки без дополнительного запроса.

В контроле ошибок, как правило, используется помехоустойчивое кодирование — кодирование данных при записи или передаче и декодирование при считывании или получении при помощи корректирующих кодов, которые и позволяют обнаружить и, возможно, исправить ошибки в данных. Алгоритмы помехоустойчивого кодирования в различных приложениях могут быть реализованы как программно, так и аппаратно.

Современное развитие корректирующих кодов приписывают Ричарду Хэммингу с 1947 года^[1]. Описание кода Хэмминга появилось в статье Клода Шеннона «Математическая теория связи»^[2] и было обобщено Марселем Голеем^[3].

Стратегии исправления ошибокПравить

Упреждающая коррекция ошибокПравить

Упреждающая коррекция ошибок (также прямая коррекция ошибок, англ. Forward Error Correction, FEC) — техника помехоустойчивого кодирования и декодирования, позволяющая исправлять ошибки методом упреждения. Применяется для исправления сбоев и ошибок при передаче данных путём передачи избыточной служебной информации, на основе которой может быть восстановлено первоначальное содержание. На практике широко используется в сетях передачи данных, телекоммуникационных технологиях. Коды, обеспечивающие прямую коррекцию ошибок, требуют введения большей избыточности в передаваемые данные, чем коды, которые только обнаруживают ошибки.

Например, в спутниковом телевидении при передаче цифрового сигнала с FEC 7/8 передаётся восемь бит информации: 7 бит полезной информации и 1 контрольный бит^[4]; в DVB-S используется всего 5 видов: 1/2, 2/3, 3/4 (наиболее популярен), 5/6 и 7/8. При прочих равных условиях, можно утверждать, что чем ниже значение FEC, тем меньше пакетов допустимо потерять, и, следовательно, выше требуемое качество сигнала.

Техника прямой коррекции ошибок широко применяется в различных устройствах хранения данных — жёстких дисках, флеш-памяти, оперативной памяти. В частности, в серверных приложениях применяется ECC-память — оперативная память, способная распознавать и исправлять спонтанно возникшие ошибки.

Автоматический запрос повторной передачиПравить

Системы с автоматическим запросом повторной передачи (англ. Automatic Repeat Request, ARQ) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:

Идея запроса ARQ с остановками (англ. stop-and-wait ARQ) заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем, как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.

Для метода непрерывного запроса ARQ с возвратом (continuous ARQ with pullback) необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть передается ошибочный блок и все последующие).

При использовании метода непрерывного запроса ARQ с выборочным повторении (continuous ARQ with selective repeat) осуществляется передача только ошибочно принятых блоков данных.

Сетевое кодированиеПравить

Раздел теории информации, изучающий вопрос оптимизации передачи данных по сети с использованием техник изменения пакетов данных на промежуточных узлах называют сетевым кодированием. Для объяснения принципов сетевого кодирования используют пример сети «бабочка», предложенной в первой работе по сетевому кодированию «Network information flow»^[5]. В отличие от статического сетевого кодирования, когда получателю известны все манипуляции, производимые с пакетом, также рассматривается вопрос о случайном сетевом кодировании, когда данная информация неизвестна. Авторство первых работ по данной тематике принадлежит Кёттеру, Кшишангу и Силве^[6]. Также данный подход называют сетевым кодированием со случайными коэффициентами — когда коэффициенты, под которыми начальные пакеты, передаваемые источником, войдут в результирующие пакеты, принимаемые получателем, с неизвестными коэффициентами, которые могут зависеть от текущей структуры сети и даже от случайных решений, принимаемых на промежуточных узлах. Для неслучайного сетевого кодирования можно использовать стандартные способы защиты от помех и искажений, используемых для простой передачи информации по сети.

Энергетический выигрышПравить

При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом, при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.

Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.

ПримечанияПравить

↑ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, с. vii, ISBN 0-88385-023-0
↑ Shannon, C.E. (1948), A Mathematical Theory of Communication, Bell System Technical Journal (p. 418) Т. 27 (3): 379–423, PMID 9230594, DOI 10.1002/j.1538-7305.1948.tb01338.x
↑ Golay, Marcel J. E. (1949), Notes on Digital Coding, Proc.I.R.E. (I.E.E.E.) (p. 657) Т. 37
↑ Understanding Digital Television: An Introduction to Dvb Systems With … — Lars-Ingemar Lundström — Google Книги. Дата обращения: 19 мая 2020. Архивировано 11 ноября 2021 года.
↑ Ahlswede, R.; Ning Cai; Li, S.-Y.R.; Yeung, R.W., «Network information flow», Information Theory, IEEE Transactions on, vol.46, no.4, pp.1204-1216, Jul 2000
↑
Статьи:
- Koetter R., Kschischang F.R. Coding for errors and erasures in random network coding// IEEE International Symposium on Information Theory. Proc.ISIT-07.-2007.- P. 791—795.
- Silva D., Kschischang F.R. Using rank-metric codes for error correction in random network coding // IEEE International Symposium on Information Theory. Proc. ISIT-07. — 2007.
- Koetter R., Kschischang F.R. Coding for errors and erasures in random network coding // IEEE Transactions on Information Theory. — 2008- V. IT-54, N.8. — P. 3579-3591.
- Silva D., Kschischang F.R., Koetter R. A Rank-Metric Approach to Error Control in Random Network Coding // IEEE Transactions on Information Theory.- 2008- V. IT-54, N. 9.- P.3951-3967.

ЛитератураПравить

Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир, 1986. — 576 с.
Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева. — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.
Clark, George C., Jr., and J. Bibb Cain. Error-Correction Coding for Digital Communications. New York: Plenum Press, 1981. ISBN 0-306-40615-2.
Lin, Shu, and Daniel J. Costello, Jr. «Error Control Coding: Fundamentals and Applications». Englewood Cliffs, N.J.: Prentice-Hall, 1983. ISBN 0-13-283796-X.
Mackenzie, Dana. «Communication speed nears terminal velocity». New Scientist 187.2507 (9 июля 2005): 38-41. ISSN 0262-4079.
Wicker, Stephen B. Error Control Systems for Digital Communication and Storage. Englewood Cliffs, N.J.: Prentice-Hall, 1995. ISBN 0-13-200809-2.
Wilson, Stephen G. Digital Modulation and Coding, Englewood Cliffs, N.J.: Prentice-Hall, 1996. ISBN 0-13-210071-1.

СсылкиПравить

Charles Wang, Dean Sklar, and Diana Johnson. Forward Error-Correction Coding. The Aerospace Corporation. — Volume 3, Number 1 (Winter 2001/2002). Дата обращения: 24 мая 2009. Архивировано из оригинала 20 февраля 2005 года. (англ.)
Charles Wang, Dean Sklar, and Diana Johnson. How Forward Error-Correcting Codes Work (недоступная ссылка — история). The Aerospace Corporation. Дата обращения: 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
Morelos-Zaragoza, Robert The Error Correcting Codes (ECC) Page (недоступная ссылка — история) (2004). Дата обращения: 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)

Макеты страниц

При передаче данных по коротковолновым радиоканалам несмотря на применение разнесенного приема и методов модуляции, специально приспособленных к свойствам таких каналов, частота появления ошибок из-за многочисленных и разнообразных помех в среде распространения нередко оказывается недопустимо большой. Существенного повышения качества связи в этом случае можно достичь только с помощью специальных устройств защиты от ошибок (УЗО). Последние, в отличие от систем защитв от ошибок, применяемых при передаче данных по проводным линиям, обычно относятся к каналу связи, а не к оконечному оборудованию данных. Поэтому методы защиты от ошибок в радиоканалах, во многом сходные с некоторыми процедурами передачи данных, необходимо рассмотреть здесь несколько подробнее. Применяемый

в том или ином случае метод тесно связан с эксплуатационными требованиями к радиоаппаратуре и особенностями ее реализаций. В зависимости от вида радиоканала (см. разд. 4.2.3) различают следующие методы.

При использовании дуплексных каналов защита данных от ошибок осуществляется с помощью кодов, обнаруживающих ошибки; отрезок сообщения, оказавшийся искаженным помехой, повторяется по запросу, посылаемому на передающую сторону по постоянно действующему обратному каналу.

В случае симплексных каналов для защиты данных также используются коды, обнаруживающие ошибки, однако для посылки запроса или подтверждения приема передача основной информации периодически прерывается и производится переключение на работу в обратном направлении.

При передаче по каналам односторонней связи ошибки могут исправляться непосредственно в месте приема с помощью корректирующих кодов.

4.4.1. ПРИМЕНЕНИЕ КОДОВ, ОБНАРУЖИВАЮЩИХ ОШИБКИ

Системы защиты от ошибок, основанные на использовании кодов, обнаруживающих ошибки, и автоматического запроса на повторение, применяются при передаче данных и телеграфной связи уже многие годы и рекомендованы МККР [4.16]. Такие системы часто сокращенно называют системами АЗО (автоматический запрос при ошибке) или, от английского выражения «automatic request» — системами Для обнаружения ошибок применяется семиэлементный равновесный двоичный код. Из общего числа возможных семиэлементных комбинаций в нем используется только комбинаций равного веса, в каждой из которых четыре разряда всегда заняты нулями, а три — единицами из которых составлен, в частности, Алфавит № (см. том 1, разд. 2.4.4.2, а также [4.17]). Тридцати двум из них приведены в соответствие знаки Алфавита № 2, остальным трем соответствуют знаки холостого хода а и (3, которые служат для выполнения некоторых коммутационных функций, и знак запроса по каналу обратной связи на повторение Каждая кодовая комбинация, в которой соотношение числа единиц и нулей отличается от рассматривается на приемной стороне системы как ошибочная, и на передающую сторону автоматически посылается запрос на повторение.

Этот метод не дает результата при ошибках типа перестановок, когда одна пли несколько единиц перешли в нули, а точно такое же число нулей перешло в единицы, так что упомянутое весовое соотношение единиц и нулей остается равным 3: 4. Однако в коротковолновых радиоканалах, поскольку в них ошибки носят преимущественно односторонний характер и перестановки появляются крайне редко, равновесные коды оказываются при обнаружении ошибок весьма эффективными.

Используемая в коротковолновых каналах система АЗО в том виде, который описан выше, обеспечивает передачу только 32 комбинаций Алфавита № 2 МККТТ. Однако системы, работающие по такому принципу, применимы и .в случае кодирования источника с помощью кодов большего объема (например, Алфавита № 5). Эффективность подобных новых систем сравнима с эффективностью ныне действующих, систем АЗО [4.18].

Принцип автоматической коррекции ошибок путем повторения знаков, первоначально принятых ошибочно, предполагает, что во время повторения обычный обмен сообщениями между оконечными установками прерывается. Чтобы несмотря на это абоненты могли работать непрерывно, на входе передающей аппаратуры системы АЗО устанавливается буферное запоминающее устройство для сообщений, поступающих во время процесса повторения. Одновременно с помощью таких буферных накопителей — механических (с применением перфоленты) или электронных ЗУ — устраняются небольшие расхождения в скоростях работы оконечного оборудования, которые могут, например, иметь место при передаче между США (45, 46 Бод) и Европой (50 Бод), а также, разумеется, и другие малые отклонения скорости от ее номинального значения. Затем с помощью импульсов считывания, поступление которых на то время, пока шел процесс повторения, было прервано, накопленные в ЗУ знаки поочередно направляются на передающие блоки системы АЗО. Блоки подключения, специально разработанные для систем АЗО, вместе с буферными накопителями обеспечивают подсоединение таких систем к национальным сетям и их применение в международной сети Телекс [4.19, 4.20].

4.4.1.1. ДУПЛЕКСНЫЕ СИСТЕМЫ АЗО

Структурная схема системы передачи данных по коротковолновому каналу, работающей по методу АЗО с применением Алфавита № 2 МККТТ при скорости 50 Бод, приведена на рис. 4.8. Система защиты от ошибок типа АЗО включает в себя расположенные в каждой из оконечных установок устройства для преобразования кода ООД в помехоустойчивый канальный код и обратно, а также схемы для проверки весового соотношения 3:4 каждой принимаемой комбинации, управления процессом повторения и запоминания

Рис. 4.8. Система АЗО для дуплексных каналов: ИД — источник данных (периодически опрашиваемый); ПД — получатель данных; фазирование по знакам; Мод — модулятор; Дем — демодулятор; Рпрд — радиопередатчик; Рпрм — радиоприемник; система защиты от ошибок (автоматического запроса при ошибке}; Нрд — передающее устройство; приемное устройство

подлежащих повторению знаков. Согласно Рекомендации 342-2 МККР [4 16] и Рекомендациям [4.21, 4.17] длительность одного еемиэлементного кодового знака составляет ; таким образом, скорость передачи изохронной

Рис. 4.9. Ход процесса повторения в системе АЗО для дуплексных каналов: — ошибочный знак; знак запроса на повторение

последовательности битов по радиоканалу равна

Общий принцнп организации процесса повторения в дуплексном канале поясняет рис. 4.9. Сразу же после обнаружения ошибочного знака в приемнике установки II передача полученной информации на ООД прекращается на время, равное длительности нескольких знаков, и передатчик установки II с помощью сигнала запрашивает от установки I повторение ранее переданного знака (рис. 4.9, сигнал 1). В этой установке после получения упомянутого сигнала запроса дальнейшая передача сообщения прерывается и начинается процесс повторения. При этом сначала качестве квитирующей информации посылается сигнал (рис. 4.9, сигнал 2), а затем повторяются последние из переданных на установку II знаков. Первый повторяемый знак — это тот знак, который был принят установкой II с ошибкой. Длительность цикла повторения охватывает несколько знаков (в рекомендуемых МККР системах — четыре или восемь знаков). Она зависит от максимального времени распространения сигнала по каналу связи в прямом и обратном направлениях, а также от времени, которое необходимо на приеме для того, чтобы обнаружить ошибку и послать запрос.

Для организации нескольких каналов передачи данных в одном коротковолновом канале с АЗО используются методы временного разделения (см. раед. 1.4.2.3). В двухканальной системе сигналы отдельных каналов объединяются по знакам: сразу же за семью последовательно передаваемыми элементами знака из канала идут семь элементов знака из канала и т. д. Пару знаков двух объединенных каналов называют диплексом. Этот диплекс может объединяться с другим таким же диплексом, относящимся к каналам в поэлементном порядке в четырехканальный сигнал. Поскольку скорости передачи в отдельных каналах остаются неизменными, скорость общего потока битов в двухканальной системе равна двукратной, а в четырехканальной системе — четырехкратной скорости отдельного канала, которая составляет

Можно и наоборот, образовать подканалы с пониженной скоростью передачи с помощью сверхцикла, охватывающего четыре основных цикла. Подобная возможность представляет интерес для таких абонентов, которым постоянно нужен канал, хотя бы и со скоростью передачи меньше 50 Бод. Упорядочение (индикация номеров) подканалов при этом осуществляется путем периодического инвертирования (т. е. переключения полярностей) элементов, относящихся к тому или иному каналу, причем порядок этого изменения однозначно указывает и начало сверхцикла. Различают «полукана-лы» и «четвертьканалы»: при полной пропускной способности первоначального канала, составляющей, например, 400 знаков/мин (что соответствует скорости 50 Бод), пропускная способность

каждого такого подканала равна соответственно 200 или 100 знакам/мин (т. е. 25 или 12,5 Бод) [4.9, 4.22].

Оглавление

ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
1. АППАРАТУРА ПЕРЕДАЧИ ДАННЫХ
1.1. СТЫК МЕЖДУ АППАРАТУРОЙ ПЕРЕДАЧИ ДАННЫХ У АБОНЕНТА И ОКОНЕЧНЫМ ОБОРУДОВАНИЕМ ДАННЫХ
1.1.1. АБОНЕНТСКИЕ СТЫКИ АПД, ПРИМЕНЯЕМОЙ В ТЕЛЕФОННЫХ СЕТЯХ
1.1.2. АБОНЕНТСКИЙ СТЫК АППАРАТУРЫ ПЕРЕДАЧИ ДАННЫХ, ПРЕДНАЗНАЧЕННОЙ ДЛЯ СЕТИ ТЕЛЕКС
1.1.3. АБОНЕНТСКИЕ СТЫКИ АПД ДЛЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
1.1.4. ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ СТЫКОВ
1.2. АППАРАТУРА ПЕРЕДАЧИ ДАННЫХ ПО КОММУТИРУЕМЫМ ТЕЛЕФОННЫМ СЕТЯМ
1.2.1. МОДЕМЫ ДЛЯ ПОСЛЕДОВАТЕЛЬНОЙ ПЕРЕДАЧИ ДАННЫХ
1.2.1.2. МОДЕМ НА 1200/600 бит/с
1.2.1.3. МОДЕМ НА 2400/1200 бит/с
1.2.1.4. МОДЕМ НА 4800/2400 бит/с
1.2.2. МОДЕМЫ ДЛЯ ПАРАЛЛЕЛЬНОЙ ПЕРЕДАЧИ ДАННЫХ
1.2.2.2. УСТРОЙСТВА ПЕРЕДАЧИ ДАННЫХ С ПОМОЩЬЮ ЧАСТОТ КНОПОЧНОГО НАБОРА НОМЕРА
1.2.3. УСТРОЙСТВА АВТОМАТИЧЕСКОГО ВЫЗОВА ДЛЯ СИСТЕМ ПЕРЕДАЧИ ДАННЫХ ПО ТЕЛЕФОННЫМ СЕТЯМ
1.3. АППАРАТУРА ПЕРЕДАЧИ ДАННЫХ ДЛЯ НЕКОММУТИРУЕМЫХ КАНАЛОВ И ТРАКТОВ
1.3.1. МОДЕМЫ ДЛЯ РАБОТЫ ПО НИЗКОЧАСТОТНЫМ И ПУПИНИЗИРОВАННЫМ КАБЕЛЬНЫМ ЛИНИЯМ
1.3.2. МОДЕМЫ ДЛЯ КАНАЛОВ ТОНАЛЬНОЙ ЧАСТОТЫ
1.3.2.2. МОДЕМ НА 9600 бит/с
1.3.3. МОДЕМЫ ДЛЯ ШИРОКОПОЛОСНЫХ КАНАЛОВ
1.4. АППАРАТУРА ПЕРЕДАЧИ ДАННЫХ, ПРИМЕНЯЕМАЯ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
1.4.1. АППАРАТУРА ПЕРЕДАЧИ ДАННЫХ ПО АБОНЕНТСКИМ ЛИНИЯМ
1.4.1.2. ПОДКЛЮЧЕНИЕ К СЕТИ ОКОНЕЧНЫХ УСТАНОВОК РАБОТАЮЩИХ В СИНХРОННОМ РЕЖИМЕ СО СКОРОСТЯМИ ДО 9600 бит/с
1.4.2. КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
1.4.2.2. СИСТЕМЫ ПЕРЕДАЧИ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ
1.4.2.3. СИСТЕМЫ ПЕРЕДАЧИ С ВРЕМЕННЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ
1.4.2.4. АППАРАТУРА ДЛЯ ПЕРЕДАЧИ ГРУППОВЫХ ПОТОКОВ БИТОВ В СИСТЕМАХ С ВРЕМЕННЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ
2. КОММУТАЦИОННОЕ ОБОРУДОВАНИЕ СИСТЕМ ПЕРЕДАЧИ ДАННЫХ
2.1. КОММУТАЦИОННОЕ ОБОРУДОВАНИЕ УЗЛОВ СЕТИ
2.1.1.1. ОБОРУДОВАНИЕ КОММУТАЦИИ КАНАЛОВ
2.1.1.2. КОНЦЕНТРАТОРЫ С КОММУТАЦИЕЙ КАНАЛОВ
2.1.1.3. ОБОРУДОВАНИЕ КОММУТАЦИИ СООБЩЕНИЙ
2.1.2. ОБОРУДОВАНИЕ НЕКОММУТИРУЕМЫХ УЗЛОВ СЕТИ
2.2. КОММУТАЦИОННОЕ ОБОРУДОВАНИЕ ОКОНЕЧНЫХ УСТАНОВОК ПЕРЕДАЧИ ДАННЫХ
2.2.2. ПРИБОРЫ ПОДКЛЮЧЕНИЯ
3. СЕТИ ПЕРЕДАЧИ ДАННЫХ
3.1.2. СЕТИ СВЯЗИ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ПЕРЕДАЧИ ДАННЫХ
3.2. ХАРАКТЕРИСТИКИ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ ОБЩЕГО ПОЛЬЗОВАНИЯ
3.2.2. СЕТЕВЫЕ ПАРАМЕТРЫ
3.2.3. УСЛУГИ, ПРЕДОСТАВЛЯЕМЫЕ АБОНЕНТАМ
3.3. СЕТИ С КОММУТАЦИЕЙ КАНАЛОВ
3.3.2. СИНХРОННЫЕ СЕТИ С КОММУТАЦИЕЙ КАНАЛОВ
3.4. СЕТИ С КОММУТАЦИЕЙ СООБЩЕНИЙ
3.4.1. СЕТЬ С КОММУТАЦИЕЙ ПОЛНЫХ СООБЩЕНИЙ
3.4.2. СЕТЬ С ПАКЕТНОЙ КОММУТАЦИЕЙ
3.5. НЕКОММУТИРУЕМЫЕ СЕТИ
3.6. КОНФИГУРАЦИИ СЕТЕЙ
3.6.2. ОБЪЕДИНЕННАЯ СЕТЬ
3.6.3. СРАВНЕНИЕ И ОЦЕНКА СТРУКТУР СЕТЕЙ
4. ПЕРЕДАЧА ДАННЫХ ПО КОРОТКОВОЛНОВЫМ РАДИОКАНАЛАМ
4.2. ОСОБЕННОСТИ КОРОТКОВОЛНОВЫХ РАДИОКАНАЛОВ И СЕТЕЙ СВЯЗИ
4.2.2. СИСТЕМЫ РАДИОСВЯЗИ
4.2.3. РАДИОКАНАЛЫ
4.3. АППАРАТУРА ПЕРЕДАЧИ ДАННЫХ ПО РАДИОКАНАЛАМ
4.3.2. АППАРАТУРА ДЛЯ ОДНОПОЛОСНОЙ ПЕРЕДАЧИ
4.3.3. ПОВЫШЕНИЕ КАЧЕСТВА СВЯЗИ С ПОМОЩЬЮ РАЗНЕСЕННОГО ПРИЕМА
4.4. МЕТОДЫ ЗАЩИТЫ ОТ ОШИБОК
4.4.1.2. СИМПЛЕКСНЫЕ СИСТЕМЫ АЗО
4.4.2. МЕТОДЫ ЗАЩИТЫ ОТ ОШИБОК С ПРИМЕНЕНИЕМ КОРРЕКТИРУЮЩИХ КОДОВ
5. ИЗМЕРЕНИЯ В ТЕХНИКЕ ПЕРЕДАЧИ ДАННЫХ
5.2. МЕТОДЫ И АППАРАТУРА ДЛЯ ИЗМЕРЕНИЯ ХАРАКТЕРИСТИК КАНАЛОВ СВЯЗИ
5.2.2. ИЗМЕРЕНИЯ ЗАТУХАНИЯ И ГРУППОВОГО ВРЕМЕНИ ЗАМЕДЛЕНИЯ
5.2.3. ИЗМЕРЕНИЯ ИМПУЛЬСНЫХ ХАРАКТЕРИСТИК КАНАЛА СВЯЗИ
5.2.4. ИЗМЕРЕНИЯ ПОМЕХ
5.2.4.2. ИНТЕНСИВНОСТЬ ИМПУЛЬСНЫХ ПОМЕХ
5.2.5. ИЗМЕРЕНИЯ КРАТКОВРЕМЕННЫХ ПЕРЕРЫВОВ
5.2.6. ИЗМЕРЕНИЕ ФАЗОВОГО ДРОЖАНИЯ
5.3. МЕТОДЫ И АППАРАТУРА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ СИГНАЛОВ
5.3.2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ КРАЕВЫХ ИСКАЖЕНИЙ И КОЭФФИЦИЕНТА ОШИБОК
5.4. ЦЕНТРАЛИЗОВАННАЯ ИЗМЕРИТЕЛЬНАЯ АППАРАТУРА
ПРИЛОЖЕНИЕ. МЕЖДУНАРОДНЫЕ И НАЦИОНАЛЬНЫЕ СОГЛАШЕНИЯ И СТАНДАРТЫ; В ОБЛАСТИ ПЕРЕДАЧИ ДАННЫХ
2. МЕЖДУНАРОДНЫЕ И НАЦИОНАЛЬНЫЕ СОГЛАШЕНИЯ И СТАНДАРТЫ В ОБЛАСТИ ПЕРЕДАЧИ ДАННЫХ, УПОРЯДОЧЕННЫЕ ПО ОРГАНИЗАЦИЯМ-СОСТАВИТЕЛЯМ
СПИСОК ЛИТЕРАТУРЫ

Кодирование и защита от ошибок

Существует три наиболее распространенных орудия борьбы с ошибками в процессе передачи данных:

коды обнаружения ошибок;
коды с коррекцией ошибок, называемые также схемами прямой коррекции ошибок (Forward Error Correction — FEC);
протоколы с автоматическим запросом повторной передачи (Automatic Repeat Request — ARQ).

1) Методы обнаружения ошибок

Контроль по паритету представляет собой наиболее простой метод контроля данных. В то же время это наименее мощный алгоритм контроля, так как с его помощью можно обнаружить только одиночные ошибки в проверяемых данных. Метод заключается в суммировании по модулю 2 всех битов контролируемой информации. Нетрудно заметить, что для информации, состоящей из нечетного числа единиц, контрольная сумма всегда равна 1, а при четном числе единиц — 0. Например, для данных 100101011 результатом контрольного суммирования будет значение 1. Результат суммирования также представляет собой один дополнительный бит данных, который пересылается вместе с контролируемой информацией. При искажении в процессе пересылки любого бита исходных данных (или контрольного разряда) результат суммирования будет отличаться от принятого контрольного разряда, что говорит об ошибке.
Однако двойная ошибка, например 110101010, будет неверно принята за корректные данные. Поэтому контроль по паритету применяется к небольшим порциям данных, как правило, к каждому байту, что дает коэффициент избыточности для этого метода 1/8. Метод редко применяется в компьютерных сетях из-за значительной избыточности и невысоких диагностических способностей.

Вертикальный и горизонтальный контроль по паритету представляет собой модификацию описанного выше метода. Его отличие состоит в том, что исходные данные рассматриваются в виде матрицы, строки которой составляют байты данных. Контрольный разряд подсчитывается отдельно для каждой строки и для каждого столбца матрицы. Этот метод обнаруживает значительную часть двойных ошибок, однако обладает еще большей избыточностью. Он сейчас также почти не применяется при передаче информации по сети.

Циклический избыточный контроль (Cyclic Redundancy Check — CRC) является в настоящее время наиболее популярным методом контроля в вычислительных сетях (и не только в сетях; в частности, этот метод широко применяется при записи данных на гибкие и жесткие диски). Метод основан на рассмотрении исходных данных в виде одного многоразрядного двоичного числа. Например, кадр стандарта Ethernet, состоящий из 1024 байт, будет рассматриваться как одно число, состоящее из 8192 бит. Контрольной информацией считается остаток от деления этого числа на известный делитель R. Обычно в качестве делителя выбирается семнадцати- или тридцатитрехразрядное число, чтобы остаток от деления имел длину 16 разрядов (2 байт) или 32 разряда (4 байт). При получении кадра данных снова вычисляется остаток от деления на тот же делитель R, но при этом к данным кадра добавляется и содержащаяся в нем контрольная сумма.
Если остаток от деления на R равен нулю, то делается вывод об отсутствии ошибок в полученном кадре, в противном случае кадр считается искаженным.

Этот метод обладает более высокой вычислительной сложностью, но его диагностические возможности гораздо шире, чем у методов контроля по паритету. Метод CRC обнаруживает все одиночные ошибки, двойные ошибки и ошибки в нечетном числе битов. Метод также обладает невысокой степенью избыточности. Например, для кадра Ethernet размером 1024 байта контрольная информация длиной 4 байта составляет только 0,4 %.

2) Методы коррекции ошибок

Техника кодирования, которая позволяет приемнику не только понять, что присланные данные содержат ошибки, но и исправить их, называется прямой коррекцией ошибок (Forward Error Correction — FEC). Коды, обеспечивающие прямую коррекцию ошибок, требуют введения большей избыточности в передаваемые данные, чем коды, которые только обнаруживают ошибки.

При применении любого избыточного кода не все комбинации кодов являются разрешенными. Например, контроль по паритету делает разрешенными только половину кодов. Если мы контролируем три информационных бита, то разрешенными 4-битными кодами с дополнением до нечетного количества единиц будут:

000 1, 001 0, 010 0, 011 1, 100 0, 101 1, 110 1, 111 0, то есть всего 8 кодов из 16 возможных.

Для того чтобы оценить количество дополнительных битов, необходимых для исправления ошибок, нужно знать так называемое расстояние Хемминга между разрешенными комбинациями кода. Расстоянием Хемминга называется минимальное число битовых разрядов, в которых отличается любая пара разрешенных кодов. Для схем контроля по паритету расстояние Хемминга равно 2.

Можно доказать, что если мы сконструировали избыточный код с расстоянием Хемминга, равным n, такой код будет в состоянии распознавать (n-1) -кратные ошибки и исправлять (n-1)/2 -кратные ошибки. Так как коды с контролем по паритету имеют расстояние Хемминга, равное 2, они могут только обнаруживать однократные ошибки и не могут исправлять ошибки.

Коды Хемминга эффективно обнаруживают и исправляют изолированные ошибки, то есть отдельные искаженные биты, которые разделены большим количеством корректных битов. Однако при появлении длинной последовательности искаженных битов (пульсации ошибок) коды Хемминга не работают.

Наиболее часто в современных системах связи применяется тип кодирования, реализуемый сверхточным кодирующим устройством (Сonvolutional coder), потому что такое кодирование несложно реализовать аппаратно с использованием линий задержки (delay) и сумматоров. В отличие от рассмотренного выше кода, который относится к блочным кодам без памяти, сверточный код относится к кодам с конечной памятью (Finite memory code); это означает, что выходная последовательность кодера является функцией не только текущего входного сигнала, но также нескольких из числа последних предшествующих битов. Длина кодового ограничения (Constraint length of a code) показывает, как много выходных элементов выходит из системы в пересчете на один входной. Коды часто характеризуются их эффективной степенью (или коэффициентом) кодирования (Code rate). Вам может встретиться сверточный код с коэффициентом кодирования 1/2.
Этот коэффициент указывает, что на каждый входной бит приходится два выходных. При сравнении кодов обращайте внимание на то, что, хотя коды с более высокой эффективной степенью кодирования позволяют передавать данные с более высокой скоростью, они, соответственно, более чувствительны к шуму.

В беспроводных системах с блочными кодами широко используется метод чередования блоков. Преимущество чередования состоит в том, что приемник распределяет пакет ошибок, исказивший некоторую последовательность битов, по большому числу блоков, благодаря чему становится возможным исправление ошибок. Чередование выполняется с помощью чтения и записи данных в различном порядке. Если во время передачи пакет помех воздействует на некоторую последовательность битов, то все эти биты оказываются разнесенными по различным блокам. Следовательно, от любой контрольной последовательности требуется возможность исправить лишь небольшую часть от общего количества инвертированных битов.

3) Методы автоматического запроса повторной передачи

В простейшем случае защита от ошибок заключается только в их обнаружении. Система должна предупредить передатчик об обнаружении ошибки и необходимости повторной передачи. Такие процедуры защиты от ошибок известны как методы автоматического запроса повторной передачи (Automatic Repeat Request — ARQ). В беспроводных локальных сетях применяется процедура «запрос ARQ с остановками» (stop-and-wait ARQ).

В этом случае источник, пославший кадр, ожидает получения подтверждения (Acknowledgement — ACK), или, как еще его называют, квитанции, от приемника и только после этого посылает следующий кадр. Если же подтверждение не приходит в течение тайм-аута, то кадр (или подтверждение) считается утерянным и его передача повторяется. На
рис.
1.13 видно, что в этом случае производительность обмена данными ниже потенциально возможной; хотя передатчик и мог бы послать следующий кадр сразу же после отправки предыдущего, он обязан ждать прихода подтверждения.

Источник

Корректирующие коды «на пальцах»

Время на прочтение
11 мин

Количество просмотров 64K

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ( $A$ , $B$ , $C$ , …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой ( $\rightarrow$ ), а передачу по каналу связи — волнистой стрелкой ( $\rightsquigarrow$ ). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$ . В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$\begin{aligned} A &\to 0,\\ B &\to 1. \end{aligned}$

Передача по каналу, в котором возникла ошибка будет записана так:

$A \to 0 \rightsquigarrow \underline{1} \to B.$

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$ .

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$\begin{aligned} A &\to 00,\\ B &\to 11. \end{aligned}$

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

$A \to 00 \rightsquigarrow 0\underline{1} \to ?.$

Какие выводы мы можем сделать, когда получили $01$ ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$ . А может, во втором, и была передана $A$ .

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$\begin{aligned} A &\to 000,\\ B &\to 111. \end{aligned}$

Проверим в деле:

$A \to 000 \rightsquigarrow 0\underline{1}0 \to A?.$

Получили $010$ . Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$ . Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$ .

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$ , а получили $001$ . Видно, что эта цепочка больше похожа на исходные $000$ , чем на $111$ . А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину $d(\alpha, \beta)$ , равную количеству различающихся цифр в соответствующих разрядах цепочек $\alpha$ и $\beta$ . Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, , так как все цифры в соответствующих позициях равны, а вот .

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
Расстояние в обе стороны одинаково.
Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

$d(x, y) \geqslant 0,\quad d(x, y) = 0 \Leftrightarrow x = y;$
$d(x, z) + d(z, y) \geqslant d(x, y)$ .

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

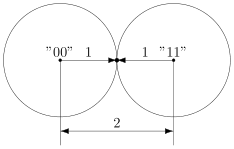
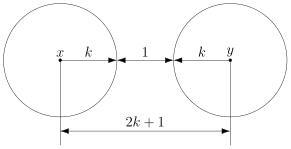
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

$\{000, 100, 010, 001\}.$

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$ ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$ , мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$ . Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{\min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$d_{\min} \geqslant 2k+1.$

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{\min}\geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$\begin{aligned} A \to 10100,\\ B \to 01000,\\ C \to 00111,\\ D \to 11011.\\ \end{aligned}$

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

	A	B	C	D
A	—	3	3	4
B	3	—	4	3
C	3	4	—	3
D	4	3	3	—

Минимальное расстояние $d_{\min}=3$ , а значит $3\geqslant2k+1$ , откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

$A \to 10100 \rightsquigarrow 101\underline{1}0.$

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$\begin{aligned} A:\, d(10110, 10100) &= 1,\\ B:\, d(10110, 01000) &= 4,\\ C:\, d(10110, 00111) &= 2,\\ D:\, d(10110, 11011) &= 3. \end{aligned}$

Минимальное расстояние получилось для символа $A$ , значит вероятнее всего передавался именно он:

$A \to 10100 \rightsquigarrow 101\underline{1}0 \to A?.$

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$\begin{aligned} 0 + 0 &= 0,\\ 0 + 1 &= 1,\\ 1 + 0 &= 1,\\ 1 + 1 &= 0. \end{aligned}$

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов $\{0, 1\}$ с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

Это свойство прямо следует из определения.

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$\begin{aligned} A &\to 000,\\ B &\to 111. \end{aligned}$

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

$\dots \rightsquigarrow x = (x_1, x_2, x_3).$

Математически равенство всех трёх цифр можно записать как систему:

$\left\{ \begin{aligned} x_1 &= x_2,\\ x_2 &= x_3. \end{aligned} \right.$

Или, если воспользоваться свойствами сложения в GF(2), получаем

$\left\{ \begin{aligned} x_1 + x_2 &= 0,\\ x_2 + x_3 &= 0. \end{aligned} \right.$

Или

$\left\{ \begin{aligned} 1\cdot x_1 + 1\cdot x_2 + 0\cdot x_3 &= 0,\\ 0\cdot x_1 + 1\cdot x_2 + 1\cdot x_3 &= 0. \end{aligned} \right.$

В матричном виде эта система будет иметь вид

где

$H = \begin{pmatrix} 1 & 1 & 0\\ 0 & 1 & 1 \end{pmatrix}.$

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$\left\{ \begin{aligned} x_1 + x_2 &= 0,\\ x_2 + x_3 &= 0. \end{aligned} \right.$

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$ ) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$H = \begin{pmatrix} 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1\\ 0 & 0 & 0 & 1 & 1 \end{pmatrix}.$

Соответствующая система имеет вид:

$\left\{ \begin{aligned} x_1 + x_3 &= 0,\\ x_2 + x_3 + x_5 &= 0,\\ x_4 + x_5 &= 0. \end{aligned} \right.$

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$\left\{ \begin{aligned} x_1 &= x_3,\\ x_2 &= x_3 + x_5,\\ x_4 &= x_5. \end{aligned} \right.$

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$\begin{aligned} x_3=1, x_5=0:\quad x_1=1, x_2=1, x_4=0 \Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\\ x_3=0, x_5=1:\quad x_1=0, x_2=1, x_4=1 \Rightarrow x^{(2)} = (0, 1, 0, 1, 1). \end{aligned}$

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$a_1 x^{(1)}+a_2 x^{(2)},$

где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$(a_1, a_2)\cdot \begin{pmatrix} 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 \end{pmatrix} = aG.$

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

$a \to aG.$

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$\begin{aligned} 00 &\to 00000,\\ 01 &\to 01011,\\ 10 &\to 11100,\\ 11 &\to 10111. \end{aligned}$

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$a=01 \to aG=01011 \rightsquigarrow x=01\underline{1}11 \to Hx^T = (110)^T \neq 0.$

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

$G=\begin{pmatrix}1&1&1\end{pmatrix}.$

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$ , а было отправлено кодовое слово $v$ . Тогда вектор ошибки по определению

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$\begin{aligned} v &= x + e,\\ x &= v + e. \end{aligned}$

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то $Hx^T\neq 0$ . Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

И заметим следующее

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.


	$\underline{00000}, 11100, 01011, 10111$
	$\underline{00010}, 11110, 01001, 10101$
	$\underline{01000}, 10100, 00011, 11111$
	$01010, 10110, \underline{00001}, 11101$
	$\underline{10000}, 01100, 11011, 00111$
	$\underline{10010}, 01110, 11001, \underline{00101}$
	$11000, \underline{00100}, 10011, 01111$
	$11010, \underline{00110}, \underline{10001}, 01101$

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$a=01 \to aG=01011 \rightsquigarrow x=01\underline{1}11 \to s(x)=Hx^T = (110)^T \to e=(00100).$

Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

6.2.1. Связность оконечных устройств

6.2.2. Автоматический запрос повторной передачи

6.2.1. Связность оконечных устройств

Передача только в одном направлении а)

а)

б)

в)

Рис. 6.6. Классификация связности оконечных устройств: а) симплексная; б) полудуплексная; в) полнодуплексная

6.2.2. Автоматический запрос повторной передачи

а)

б)

в)

Рис. 6.7. Автоматический запрос повторной передачи (ARQ): а) запрос

1. Обратный канал недоступен или задержка при использовании ARQ слишком велика.

2. Алгоритм повторной передачи нельзя реализовать удобным образом.

3. При ожидаемом количестве ошибок потребуется слишком много повторных передач.

Источник

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

где n – количество символов закодированного сообщения (результата кодирования);
m – количество проверочных символов, добавляемых при кодировании;
k – количество информационных символов.

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.

Рассчитаем скорость кода для:

1 1 0 0 0 1 0 0 | 1

Здесь R=8/9=0,88

И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.

Классификация помехоустойчивых кодов

Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.

По используемому алфавиту:

Двоичные. Оперируют битами.
Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.

Блочные коды делятся на

Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.

n — количество символов на входе.
k — количество символов на выходе.
t — кратность исправляемых ошибок.
Отношение k/n — скорость кода.
G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромисс:

Достоверность vs полоса пропускания.
Мощность vs полоса пропускания.
Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.

Источник

Кодирование и защита от ошибок

Структура пакета

Методы коммутации каналов, сообщений, пакетов

1. Методы защиты от ошибок при передаче и информации

6.2.1. Связность оконечных устройств

6.2.2. Автоматический запрос повторной передачи

Стратегии исправления ошибокПравить

Упреждающая коррекция ошибокПравить

Автоматический запрос повторной передачиПравить

Сетевое кодированиеПравить

Энергетический выигрышПравить

ПримечанияПравить

ЛитератураПравить

СсылкиПравить

4.4.1. ПРИМЕНЕНИЕ КОДОВ, ОБНАРУЖИВАЮЩИХ ОШИБКИ

4.4.1.1. ДУПЛЕКСНЫЕ СИСТЕМЫ АЗО

Кодирование и защита от ошибок

1) Методы обнаружения ошибок

2) Методы коррекции ошибок

3) Методы автоматического запроса повторной передачи

Корректирующие коды «на пальцах»

Каналы с ошибкой

Код с утроением

Расстояния между кодами

Окрестности

Сколько ошибок может исправить код?

Интерлюдия: поле GF(2)

Проверяем корректность

Кодирование

Ошибка по синдрому

Что же дальше?

6.2.1. Связность оконечных устройств

6.2.2. Автоматический запрос повторной передачи

Исправление ошибок в помехоустойчивом кодировании

Параметры помехоустойчивого кодирования

Контроль чётности

Классификация помехоустойчивых кодов

Код Хэмминга

Декодирование кода Хэмминга

Расстояние Хэмминга

Помехоустойчивые коды

Компромиссы при использовании помехоустойчивых кодов

Необходимость чередования (перемежения)

Интересное по теме: