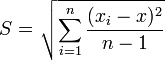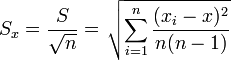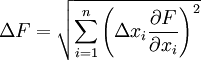Метрологическая ошибка это

Типовые ошибки, выявляемые при метрологической и стандартизационной экспертизе

Опыт
метрологической и стандартизационной
экспертизы позволяет утверждать, что
при экспертизе типовых объектов, наиболее
часто встречаются однотипные ошибки,
на выявление которых следует обратить
особое внимание. Перечни типовых ошибок
складываются при анализе накопленных
материалов многочисленных экспертиз
аналогичных объектов. Одним из примеров
таких перечней является классификатор
типовых ошибок для цифрового кодирования
замечаний нормоконтролера, который
применяется в подразделениях стандартизации
некоторых субъектов хозяйствования.

Наличие
перечня типовых ошибок позволяет
проводить профилактические работы для
их предупреждения или хотя бы для
снижения частоты их появления. Тем не
менее, даже при активном предупреждении
ошибок, анализ больших массивов экспертной
информации показывает, что типовые
ошибки встречаются всегда.

К
самым общим ошибкам, выявляемым при
совместной метрологической и
стандартизационной экспертизе можно
отнести:

• неконтролепригодность
  требований из-за некорректности их
  выражений, в том числе из-за противоречивости
  или неполноты информации;

• невозможность
  обеспечить достоверную оценку из-за
  отсутствия критериев, методов и
  инструментальных средств;

• противоречия
  в нормировании свойств или параметров.

Далее типовые
ошибки дифференцированы по видам
экспертиз.

К
типовым ошибкам, выявляемым при
стандартизационной экспертизе можно
отнести:

• несоответствие
  заглавия и содержания документа или
  его части;

• использование
  некорректных терминов и обозначений;

• неправильно
  использованные корректные термины и
  обозначения, включая неправильные
  обозначения требований к точности
  параметров на чертежах;

• неоднозначно
  сформулированные положения, требования;

• недостаток
  информации;

• избыточная
  информация в документе;

• использование
  нестандартных элементов при наличии
  стандартных без необходимости;

• отсутствие
  стандартных требований к точности
  параметров;

• ошибки
  в оформлении и содержании текстовых
  документов или записей технических
  требований или технических условий
  начертежах.

Наиболее
часто при формальной стандартизационной
экспертизе
(нормоконтроле) деталей обнаруживаются
следующие ошибки:

• неправильное
  оформление основной надписи (отсутствие
  необходимой информации, подписей с
  указанием дат);

• неправильные
  обозначения материала детали в основной
  надписи;

• неправильный
  порядок записи технических требований;

• обозначения
  единиц физических величин с нарушением
  требований ГОСТ 8.417;

• некорректные
  обозначения общих допусков;

• неправильные
  обозначения допусков формы и расположения
  поверхностей (например, стрелка от
  рамки допусков круглости, цилиндричности,
  радиального биения и некоторых других
  на продолжении размерной линии, или
  наоборот, для допусков соосности и
  иных, относящихся к оси цилиндрической
  поверхности, стрелка не на продолжении
  размерной линии);

• неправильные
  обозначения баз при назначении допусков
  расположения поверхностей, особенно
  при обозначении допусков биений;

• отсутствие
  всех установленных стандартом требований
  к поверхностям, сопрягаемым с подшипниками
  качения;

• некорректно
  проставленные размерные цепи, отсутствие
  размеров, необходимых для разработки
  чертежей деталей (для чертежа общего
  вида).

Каждый
нормоконтролер может составить подобный
перечень для себя, особенно если он
работает на конкретном предприятии.

Приведем примеры
типовых ошибок и пояснения к некоторым
их видам.

Несоответствие
заглавия и содержания документа или
его части встречаются как в текстовых
документах, так и в графических. Оно
может быть в виде неполного соответствия,
возникающего из-за слишком широкого
заголовка, не обеспеченного содержанием
текстового материала, либо из-за неполного
охвата заголовком его содержания.
Возможно также полное несоответствие
заглавия и содержания раздела документа
в ситуации, когда текст был радикально
переработан, а заголовок остался прежним.
В текстовых документах такие дефекты
легко выявляются сопоставлением
заголовка и содержания.

В графических
документах встречаются некорректные
наименования деталей типа «кронштейн»,
«рычаг» и некоторых других.

Некорректные
термины, в том числе зафиксированные в
стандартах как нерекомендуемые («замер»,
«забор пробы», «тарировка», «измерительный
инструмент», «измерительное усилие» и
др.) используются достаточно часто в
силу традиций, причем встречаются весьма
длительное время в литературе и
нормативной документации после отмены
или замены терминов. Например, официально
называемые «мерными сосудами» средства
измерения объема жидкостей («сосуды
измерительные»), жаргонные наименования
средств измерений типа «мерник»,
«измеритель» (измеритель – не прибор,
а субъект, осуществляющий измерения),
иные профессиональные жаргонизмы
(«допусковый контроль», «размер в
допуске» и др.).

Самостоятельно
сконструированные разработчиками
определения вводимых терминов часто
фактически не являются определениями.
К сожалению, примеры подобного подхода
можно найти в действующей нормативной
документации.

Из
РМГ 43: неопределенность
(измерений) – параметр, связанный с
результатом измерений и характеризующий
рассеяние значений, которые могли бы
быть обоснованно приписаны измеряемой
величине.

Неопределенность
измерений – сложное явление, а параметр
случайного распределения может дать
его количественную оценку. В определении
смешаны неопределенность (качественная
характеристика измерений) и количественные
оценки неопределенности.

Из
РМГ 29: случайная
погрешность измерения – составляющая
погрешности результата измерения,
изменяющаяся случайным образом (по
знаку и значению) при повторных измерениях,
проведенных с одинаковой тщательностью,
одной и той же физической величины.

Если
выделить суть «определения» получится,
что случайная погрешность измерения
та, которая изменяется случайным образом
– типичный случай определения через
определяемое. Требование одинаковой
тщательности невыполнимо
из-за неопределенности, отсутствия
критериев «одинаковости».

Погрешность
метода измерений – составляющая
систематической погрешности измерений,
обусловленная несовершенством принятого
метода измерений.
Снова определение через определяемое,
дополненное указанием на систематический
характер погрешности, что не является
ее обязательным атрибутом. Подтверждение
этого факта приведено в примечании к
определению: «Иногда
погрешность метода может проявляться
как случайная».

Погрешность
(измерения) из-за изменений условий
измерения – составляющая систематической
погрешности измерения, являющаяся
следствием неучтенного влияния отклонения
в одну сторону
какого-либо из параметров, характеризующих
условия измерений, от установленного
значения.
Оставляем без комментариев из-за явных
недостатков (обратите внимание на
выделенные нами слова).

Недостаток
информации в документе может выражаться
следующим образом:

• отсутствие
  на чертеже или рисунке минимально
  необходимого числа изображений
  (недостающие схемы, изображения,
  проекции, разрезы, сечения);

• отсутствие
  необходимых выносок, размеров (неполные
  размерные цепочки, отсутствие размеров
  на повторяющихся однотипных элементах
  чертежа, например одинаковых подшипниковых
  шейках вала и др.);

• отсутствие
  логически вытекающих необходимых
  положений или ссылок на иные источники.

Избыток
информации в документе может быть связан
с дублированием некоторых положений,
видов и размеров на чертежах, наличием
информации, которая не является
необходимой, не имеет непосредственного
отношения к объекту экспертизы.

Неправильное
использование терминов и обозначений
встречается и в текстовых, и в графических
документах. Множество типичных ошибок
связаны с метрологическими характеристиками
средств измерений, наименованиями
физических величин, обозначениями их
единиц, формами представления результатов
измерений. Часто путают диапазон
измерений с диапазоном показаний (у
измерительной головки нет диапазона
измерений, нет его и у многозначной
меры), обозначают диапазон одним пределом,
называют номинальную ступень квантования
«дискрета», «дискретность», «величина
отсчета», «разрешающая способность».

Очень
распространенным словосочетаниями
являются «величина силы», «величина
напряжения» и им подобные, в то время
как сила и напряжение (электрического
тока) сами являются физическими
величинами. В обозначениях единиц
физических величин отсутствуют пробелы
между числом и обозначением единицы,
обозначение единицы переносят на
следующую строку или страницу, некорректно
обозначают диапазоны величин. Правила
обозначения единиц физических величин
представлены в ГОСТ 8.417.

Обозначения
результатов измерений часто не
соответствует требованиям обеспечения
единства измерений в части представления
оценки погрешности или неопределенности
с указанием значения доверительной
вероятности.

Использование
нестандартных элементов конструкции
при наличии стандартных обычно
обнаруживается на чертежах и включает
неприменение нормальных линейных
размеров для несопрягаемых элементов
деталей, использование нестандартных
канавок, заплечиков, нестандартных
значений допусков и др.

Среди
неправильных обозначений требований
к точности параметров на чертежах
особенно часто встречаются неправильные
указания допусков формы и расположения
поверхностей (включая обозначения баз),
параметров шероховатости поверхностей,
неуказанных допусков размеров.
Разработчики часто забывают, что допуск
формы не может быть больше установленного
по уровню относительной точности А (60
% от допуска размера или 30 % для симметричных
поверхностей), что частные допуски формы
не могут быть больше интегрального.

Недостаточно
квалифицированные конструкторы не
различают в обозначениях допусков формы
и расположения те, что относятся к
поверхности элемента и те, что
распространяются на ось или плоскость
его симметрии. Те же ошибки характерны
для обозначения баз при назначении
допусков расположения.

Пока
еще часто используют устаревшие
обозначения параметров шероховатости
поверхностей и допусков размеров, не
указанных индивидуально (общие допуски).
В старых документах это не являлось
ошибками, но сегодня должно фиксироваться
как архаизм.

Знание
стандартных требований к точности
параметров составляют элементарную
профессиональную грамотность разработчика.
К ним относятся, например, требования
к поверхностям, сопрягаемым с подшипниками
качения (обязательное нормирование
допусков формы сопрягаемых цилиндрических
поверхностей, требований к их расположению,
требований к торцовому биению привалочных
плоскостей валов и корпусов, ограничение
высотных параметров шероховатости
сопрягаемых и привалочных поверхностей).
Не следует забывать также стандартные
требования к резьбовым посадкам с
натягом, к точности шпоночных сопряжений,
зубчатых колес и передач и многому
другому.

Часто
встречаются также ошибки в текстовых
записях технических требований или
технических условий (нарушение требований
ЕСКД), в том числе неправильный порядок
записей, наличие неконтролепригодных
требований, а также уже упоминавшиеся
ошибки в обозначениях физических величин
и их единиц.

К
типовым ошибкам, выявляемым при
метрологической экспертизе, можно
отнести:

• назначение
  недостаточно жестких допусков на
  функционально важные параметры;

• назначение
  необоснованно жестких допусков
  параметров (включая функционально
  важные и второстепенные);

• несогласованные
  допуски макрогеометрии (размеров, формы
  и/или расположения);

• несогласованные
  с допусками макрогеометрии (размеров,
  формы и/или расположения) высотные
  параметры шероховатости поверхностей;

• назначение
  в качестве конструкторских (а значит
  и измерительных) баз конструктивных
  элементов низкой точности;

• выбор
  в качестве конструкторских и измерительных
  баз осей или точек, получаемых
  геометрическими построениями, в том
  числе с использованием элементов,
  положение которых не ограничивается
  специальными точностными требованиями
  (допусками формы и расположения
  поверхностей)

• выбор
  в качестве измерительных баз поверхностей,
  не являющихся главными при функционировании
  детали (нарушение следствия из принципа
  инверсии).

Этот перечень
также может быть самостоятельно дополнен
экспертом метрологом на основании
собственного опыта экспертной работы.

Хотя
перечисленные ошибки являются типовыми,
примеры мы не приводим, поскольку
выявление таких ошибок требует проведения
функциональной экспертизы, реализация
которой в каждом конкретном случае
имеет свои особенности.

Любой перечень
типовых ошибок может быть самостоятельно
дополнен экспертом на основании
собственного опыта экспертной работы.

Соседние файлы в папке Лекции МЭиНК

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

МЕТРОЛОГИЧЕСКИЕ ОШИБКИ

Следствием наличия метрологических несоответствий в разрабатываемой
документации может быть не только увеличение ошибок первого и второго
рода при контроле готовых деталей, но и брак, обнаруживаемый только в
процессе испытаний или эксплуатации изделия. В зависимости от места,
назначения и функций детали в изделии, одно и тоже метрологическое
несоответствие может принести разный ущерб от простого увеличения
времени на изменение технологии и исправления терминологических
несоответствий до необходимости изменения конструкции готового изделия.

Для
особо ответственных деталей, разрушение или отказ которых может привести
к отказу изделия с опасными последствиями, метрологические
несоответствия имеют наибольшее влияние на качество. К этим деталям
предъявляются повышенные требования метрологического обеспечения. Для
всех остальных деталей изделия влияние качества метрологического
обеспечения на качество конечного продукта не является критическим, но
является важным в плане устранения издержек, вызванных наличием
метрологических несоответствий. Устранение несоответствия на любой
детали, узле, конструкции изделия до ее производства дает реальную
экономию за счет предотвращения несоответствий, которые могли бы
появиться при производстве, испытаниях, эксплуатации.

Метрологические
несоответствия, допускаемые при разработке технической документации,
влекут издержки для предприятия и снижают качество продукции.

Уже столетие не утихают споры вокруг раскола земной Науки на “старую”-классическую и “новую”-неклассическую. Начало ему было положено достаточно сплоченной группой физиков-“новаторов”, пожелавших приобрести независимость от “ретроградов” и “консерваторов”. Преимущества независимости оказались достаточным аргументом для присоединения к ним множества других ученых и не только ученых и завоевания ими господствующих позиций в физике. Пример успешного раскола физики оказался заразительным для остальных отраслей земной Науки. После многих лет борьбы и преследования инакомыслящих переворот в Науке был завершен по аналогии с подобными политическими переворотами принятием законов, переводящих всех противников на нелегальное положение. С середины ХХ столетия Академии Наук разных стран Земли принимают постановления о прекращении рассмотрения альтернативных гипотез. Все постулаты “новой науки” официально признаются бесспорными истинами в последней инстанции. В целом ситуация стала напоминать старую сказку о платье короля, хотя сказочник не мог иметь в виду именно эти события (по времени). Причины и возможность такой ситуации в “цивилизованном” обществе еще ждут своих исследователей – историков, психологов и организаторов Науки. Пока же для завершения сказки требуется мальчик, не обремененный титулами. Поскольку тупиковая ситуация зарождалась в физике и стала основным препятствием для техники, то в роли мальчика должен выступить простой инженер-“технарь”, знакомый с проблемами физики не понаслышке, и для которого конечный практический результат важнее любых исходных теоретических предпосылок. То есть, человек доверяющий (безусловно), но привычно проверяющий (по возможности) все, что видит и, особенно то, что слышит. Ибо таковы технические требования в технике.

Проверки (испытания и измерения) в технике обслуживает отдельный раздел науки и техники – метрология. Современная метрология владеет целым комплексом испытанных правил и методов проверок. Основным правилом метрологии является немедленное вычитание любых обнаруживаемых ошибок и действия помех из результатов любых измерений и наблюдений и определение степени доверия к полученным результатам. Поскольку это правило стало непреложным законом техники уже после раскола физики, то, похоже, никто не делал анализ исходных данных, использованных для обоснования раскола.

Объявленным аргументом раскола была “невозможность объяснения новых экспериментальных данных на основе классических представлений”. Поскольку в основе всех классических представлений лежит представление о Науке, как непрерывной совокупности человеческих представлений о непрерывном Мире, то основой раскола следует считать отход от этого представления и замену его представлением о Науке, как совокупности разрозненных представлений, группирующихся вокруг никак не связанных между собой и не вытекающих из чего-либо утверждений-постулатов. Именно последнее представление возобладало в современной Науке и было названо ее новейшим достижением, хотя, по сути, это был возврат к доклассическим представлениям, используемым еще доисторическими шаманами (Как тут не вспомнить утверждение философов о спиралях развития?). Поэтому, хотя начало раскола Науки часто связывают с появлением теории относительности Эйнштейна, в действительности отсчет времени отхода от классических позиций следует начинать значительно раньше. Эйнштейн и его последователи только довели этот процесс до логичного завершения. Попробуем сначала просто посмотреть на ситуацию с метрологической точки зрения, оставив достаточно нудную и трудоемкую полную метрологическую экспертизу другим, более терпеливым и дотошным исследователям.

Человеческий мозг, как измерительно-регистрационная система, имеет довольно ограниченные параметры. Удобная в других случаях дискретно-цифровая форма памяти ограничивает возможности счета только натуральными числами, требуя преобразования и сведения к ним результатов любого счета-наблюдения. Ограниченное количество довольно медлительных каналов однотипной информации (нервов, их чувствительных окончаний-датчиков и исполнителей-мышц) делает достаточной последовательную (поэлементную) обработку всей передаваемой по ним и запоминаемой информации ограниченным количеством более быстродействующих центральных процессоров и контроллеров. Поэтому в основе всей человеческой логики и, соответственно, всех человеческих рассуждений лежат простейшие представления о возможности натурального счета количества объектов и количественном сопоставлении (сравнении) любых двух (не больше и не меньше) однотипных объектов разной величины, отображаемое арифметическими знаками + (да), — (нет), > (больше), < (меньше) и = (равно). Эти знаки изначально предназначены людьми для логических операций только с парами (двойками) объектов, и использование их для одновременного сопоставления большего числа объектов без дополнительных оговорок некорректно. Поэтому любая попытка соединения одним таким знаком больше двух чисел или выражений заведомо обречена на полную неудачу. Поэтому же все, без исключения, используемые в Науке формулы (сокращенные записи утверждений) с этими знаками можно рассматривать только как утверждения, касающиеся только конкретных пар сопоставляемых объектов.

В основе всех “естественных” наук лежит довольно логичное представление о самопроизвольном взаимодействии любых объектов Мира. Представление о реальной множественности взаимодействующих объектов автоматически приводит к не менее логичному представлению о коллективности их взаимодействия, немедленно вступающему в противоречие с ограниченной человеческой возможностью его описания упрощенными формулами по-парного сопоставления объектов. Некоторое ослабление (но не полную ликвидацию) противоречия привносит отказ от очень сложного представления о дальнодействии объектов в пользу несравненно более простого представления об их близкодействии, разрешающем ограничивать неудобное описание коллективного взаимодействия бесконечного множества объектов более удобным описанием существенно меньшего количества соседних (соприкасающихся) объектов. Но это приводит к установлению полного запрета на непосредственное взаимодействие любых удаленных (не соседних) объектов и требует при описании пар таких объектов обязательно учитывать влияние разделяющих их цепочек других объектов. Последнее требование является универсальным, и оно совпадает с основным требованием метрологии. Поэтому все ошибки и неточности, обусловленные невыполнением этого требования можно считать чисто метрологическими ошибками конкретных описаний, но никак не дефектами классических представлений вообще, прямо запрещающих такие ошибки или разрешающих их только в рамках допустимых приближений. И, тем более, запрещающих подмены описаний одних взаимодействующих объектов описаниями других, имеющих к первым, в лучшем случае, косвенное отношение.

Только это противоречие и можно считать основной объективной причиной брожений в физике XIX-XX столетий, но никак не недееспособность классической методологии непрерывной увязки представлений о Мире. Наиболее известная попытка разрешить это противоречие была сделана Галилеем, опубликовавшим в 1636 году свою формулировку принципа относительности. Предложенное Галилеем представление о возможности пренебрежения коллективным (системным) взаимодействием при описании взаимодействия некоторых пар наблюдаемых объектов создавало такие удобства для ученых, что немедленно получило широкое распространение, а затем и громкое название теории (всеобщей, абсолютной и т.п.) относительности, несмотря на явно ограниченную только приближенными описаниями область применения. Такое необоснованно широкое распространение теории относительности (ТО) впоследствии, после выявления назревшей необходимости учета коллективных взаимодействий, создало проблему значительного психологического дискомфорта.

Опыты тех же Кулона, Фарадея и др. уже нарушали установившийся комфорт, но все описания их опытов еще выдержаны в духе по-парного описания объектов (см. формулы взаимодействия двух зарядов, двух токов, двух магнитов и т.п.). В порядке платы за спасение привычной формы описаний физике пришлось узаконить представления о передающих взаимодействие промежуточных третьих объектах-полях, фактически использованных еще Ньютоном в описании всемирного тяготения. Теоретические работы Максвелла по электромагнитным взаимодействиям потребовали придания воображаемым посредникам-полям и/или их носителям (эфиру, вакууму и т.п.) статуса реальных (материальных) объектов, отличающихся по форме, но равноправных с другими материальными объектами. Это возвращало физиков к дискомфортной метрологической проблеме учета коллективных взаимодействий и встретило психологически понятное сопротивление многих ученых. Опыты Майкельсона только подлили масла в огонь, но не результатами, а самой попыткой описания наблюдаемого коллективного взаимодействия нескольких объектов (двух лучей волн, эфира и интерферометра с тремя зеркалами) в представлениях по-парного взаимодействия. С этой точки зрения, Специальная Теория Относительности и Общая Теория Относительности Эйнштейна, как и широко разрекламированная впоследствии Единая Теория Поля, также являются только очередными попытками спасти субъективные удобства, пренебрегая реальной коллективностью и близкодействием взаимодействий наблюдаемых объектов. Все полученные в их рамках противоречия-парадоксы были неизбежной платой за пренебрежение простым метрологическим требованием учета влияния на результат наблюдения всех непосредственно взаимодействующих объектов. Поскольку по формальному определению гипотезами могут называться только непроверенные утверждения, а теориями – только подтвержденные опытами утверждения, то известность любых логических противоречий в любом умозрительном построении-утверждении автоматически означает невозможность опытного подтверждения этого утверждения и исключает его даже из числа гипотез. Поэтому применение названия теории к таким построениям с формальной точки зрения является неправомерным (некорректным, ошибочным). Так же некорректным будет название не только теорией, но даже гипотезой любого другого утверждения, основывающегося на таких самоопровергнутых своими парадоксами утверждениях. Однако, в отличие от простых ложных утверждений, опровергаемых только прямым опытом, любые противоречивые логические построения всегда сохраняют некоторое положительное значение для науки в качестве доказательств от противного, позволяющих оценивать ожидаемый результат без проведения дорогостоящих опытов и, тем самым, экономить материальные ресурсы.

Подобные противоречивые логические построения с времен Древней Греции принято называть софизмами. В основе софизмов всегда лежит малозаметная подмена одних объектов (предметов) рассуждения и/или логических действий другими. При таком определении любые утверждения, базирующиеся на умолчании о каком-либо взаимодействии, автоматически подпадают под определение софизма, та как в них реальная совокупность взаимодействующих объектов подменяется другой совокупностью. Любые существующие и возможные “теории” относительности и единого поля не могут составлять исключение, так как во всех них результат взаимодействия многих объектов всегда представляется как результат взаимодействия только двух избранных из них. То есть, налицо типичная подмена, формально относящая такие “теории” к обычным софизмам, пригодным только на роль доказательств от противного.

Но кроме логических подмен, сохраняющих некоторую ценность парадоксальных рассуждений-софизмов для науки, можно привести примеры и прямых (явных) подмен в физике, не связанных с объектами типа материального всеохватывающего эфира-вакуума или нематериальной, но сохраняющейся энергии-потенциала, недостаточно известными на момент проведения рассуждений конкретным рассуждающим ученым. К таким явным подменам можно отнести, например, подмену представления взаимодействия трех электрических зарядов (двух положительных и одного отрицательного) в описании опыта Кулона представлением о взаимодействии только двух одноименных зарядов.

Декларированной целью опытов Кулона было наблюдение взаимодействия пары электрически заряженных тел сферической формы, удаленных друг от друга на расстояние, предположительно достаточное для пренебрежения взаимными искажениями электрического поля вокруг них. Вследствие предполагаемой неуничтожимости электрических зарядов технология опыта предусматривала перенос части заряда конкретного знака с одного шарика крутильных весов на другой. Это предполагало оставление равного заряда противоположного знака на первом шарике. При прочих равных условиях это позволяет утверждать, что результат наблюдения практически соответствовал поставленной задаче – наблюдению взаимодействия двух электрических зарядов противоположного знака и равной величины.

Применение той же технологии для опытов по наблюдению взаимодействия зарядов с другим соотношением знаков и величины неизбежно требовало использования третьих тел для сбрасывания или заимствования нескомпенсированной разности зарядов. В качестве такого буферного тела использовался “заземленный” корпус весов. Таким образом, при декларированном наблюдении двух одноименных зарядов в действительности наблюдалось взаимодействие трех зарядов, двух одноименных и одного заряда, противоположного по знаку и равного по величине сумме двух первых. Результаты наблюдения этих трех зарядов потом без какого-либо обоснования выдавались за результаты взаимодействия только двух одноименных зарядов. Такая подмена уже не может быть оправдана неизвестностью каких-либо параметров опыта, как в предыдущем случае с эфиром, так как описание технологии опыта прямо использует представление о трех зарядах и их размещении на разных телах. Это позволяет говорить о явном пренебрежении метрологическим требованием учета влияния всех элементов опыта в процессе обработки полученных Кулоном результатов – прямых показаний крутильных весов. Все остальные результаты, включая известные “законы Кулона”, являются не результатами этих опытов, а результатами достаточно фривольной обработки результатов опытов и, поэтому, с метрологической точки зрения должны оцениваться как обладающие очень низкой достоверностью.

Если бы такая оценка была сделана 150-200 лет назад, то потребность в теории единого поля, как и во всех теориях относительности, возможно, и не возникла б. Классические представления о единстве мира и наблюдательских свойствах человека уже тогда могли бы прямо привести к представлению о существовании в Мире частиц, способных создать, по крайней мере, одну непрерывную мировую упаковку-среду, и позволили бы отождествить представление о такой среде с представлением о вакууме-эфире. Вытекающие представления о дефектах этой упаковки хорошо ассоциируются с представлениями о веществе как скоплениях элементарных дефектов этой упаковки, а представления о самопроизвольном однотипном сближении любых дефектов (и вакансий, и включений) хорошо соответствуют представлениям обо всех известных свойствах вещества и, к тому же, позволяют предвидеть неизвестные. Но на прямом пути такого классического развития событий оказалось несколько препятствий, способствовавших уводу авангардной части Науки (физики) в сторону с этого пути. Среди них основную роль сыграло представление об отталкивании одноименных электрических зарядов, полученное в результате банальной подмены представлений об опытах Кулона. Оно было чужеродным для физики и, естественно, не могло быть никак увязано с другими ее представлениями без появления противоречий. Его наличие привносило и устанавливало нереальные соотношения в системе физических представлений и заведомо обрекало на неудачу любые попытки построения даже приближенной общей теории, включая единую теорию поля.

Не намного меньшие отрицательные последствия для науки имело пренебрежение метрологическим требованием учета свойств измерительных инструментов при исследовании, например, спектра излучения газов. Все использованные инструменты (спектрофотометры) имеют одну особенность. Они измеряют не частоту падающей волны, а частоты многих составляющих ее гармоник. В результате, для этих инструментов любая одиночная несинусоидальная волна становится неотличимой от множества соответствующих независимых синусоидальных волн. Картина распределения волн по частоте, полученная с помощью такого спектрофотометра, является слишком неопределенной и не может быть (по правилам метрологии) использована для уверенного суждения о свойствах источника волн. Поэтому однозначный вывод Бора о наличии в атомах газа множества квантованных электронных энергетических уровней, сделанный на основании фотографии линейчатого спектра излучения газа, является необоснованным с метрологической точки зрения. Он должен был рассматриваться только как одно из многих неравноправных предположений. С большим правом можно было бы утверждать, что в каждом атоме имеется меньшее количество уровней, например, всего 2, но излучаемая волна является достаточно несинусоидальной, так как классическое представление об ограниченности перемещений электрона в атоме и, соответственно, об асимметрии его колебаний требует сделать однозначный выбор в сторону второго предположения. Принцип простоты (бритва Оккама) дополнительно усиливает этот выбор. Да и распределение энергии излучения по частоте (распределение Планка) для второго предположения получалось бы автоматически без “ультрафиолетовых катастроф” Вина как результат простого разложения в ряд Фурье реальной несинусоидальной функции излучения, а не на основе отвлеченных моделей для статистики шариков в ящиках. Но сделано то, что сделано. И сегодня вся Квантовая Механика построена на представлении о множестве квантовых состояний очень сложного атома, переходы между которыми сопровождаются излучением строго монохроматических волн, рассчитываемых с помощью “эмпирических” (подгоночных) коэффициентов.

Недостаточно обоснованным с метрологической точки зрения является и однозначный выбор объяснения “красного смещения” спектров далеких звезд их продолжающимся удалением. На момент обнаружения “красного смещения” классические представления о взаимодействии проходящих волн и осцилляторов позволяли предвидеть удлинение волны за счет отставания по фазе вынужденного последнего колебания осциллятора со средой относительно окончания вынуждающих исходных колебаний среды. Наличие отставания конца волны при совпадении начала первого колебания осциллятора с началом первого колебания пришедшей волны означает удлинение волны. Пропорциональность запаздывания конца конкретной волны количеству взаимодействий с осцилляторами и разности частоты волны и резонансной частоты осцилляторов приводит к примерно однотипному поведению наблюдаемых световых волн (одинаковому смещению частот и длин волн в % от их значений пропорционально расстоянию), делая его очень похожим на наблюдаемое. Такое “красное смещение” может наблюдаться и при неподвижных звездах, и даже при их движении в обратную сторону. Кроме того, в арсенале классической физики имелось еще, как минимум, одно представление, позволяющее ожидать похожий эффект. Это зависимость частоты колебаний излучающих волны осцилляторов от жесткости связи их частей, в свою очередь, зависящей от сжатия (давления) окружающей среды (эфира-вакуума). Наблюдаемое пропорциональное расстоянию “красное смещение” излученных когда-то удаленными источниками волн могло бы быть следствием равномерного сжатия этой среды в настоящее время и постоянного повышения частоты излучения используемых нами эталонов. При таком “красном смещении” далекие звезды и галактики должны приближаться к нам, а не удаляться.

Однозначный выбор объяснения “красного смещения” в пользу эффекта Доплера потребовал введения представления о начале движения, которое, в свою очередь, тоже без достаточного обоснования было использовано для утверждений о Большом Взрыве Проточастицы, создавшем видимую Вселенную. Совокупность этих представлений тоже без достаточного обоснования была объявлена Теорией Большого Взрыва. Необоснованность названия Теории Большого Взрыва сразу двойная. Во-первых, возможность удлинения световых волн атомами межзвездного газа и/или повышения частоты излучения наших измерительных эталонов делает недоказанным расширение видимой части вселенной и лишает права на звание теории любые умозрительные построения с их использованием. Во-вторых, даже в случае доказательства реального расширения Вселенной требуются веские доказательства начала расширения от нуля-Проточастицы, так как их отсутствие тоже возвращает Теорию Большого Взрыва в ранг рядовой рабочей гипотезы.

Количество примеров можно было бы увеличить, но и приведенных достаточно, чтобы уверенно утверждать, что основные представления и результаты экспериментов, положенные в основу “новой” физической науки, были использованы, как минимум, без учета метрологических требований. Поэтому в фундаменте официальной физики сейчас имеются грубые метрологические ошибки, приведшие к длительному застою в Науке и требующие немедленного пересмотра многих ее представлений.

Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».

Определение погрешности

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

• Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:

• Средняя квадратическая погрешность:

• Средняя квадратическая погрешность среднего арифметического:

Классификация погрешностей

По форме представления

• Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины X_meas. При этом равенство:

ΔX = | X_true − X_meas | ,

где X_true — истинное значение, а X_meas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина X_meas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

• Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:

.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

• Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

,

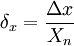
где X_n — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то X_n определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

Приведенная погрешность — безразмерная величина (может измеряться в процентах).

По причине возникновения

• Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
• Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
• Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.

Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.

По характеру проявления

• Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
• Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
• Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
• Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).

По способу измерения

• Погрешность прямых измерений
• Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:

Если F = F(x₁,x₂…x_n), где x_i — непосредственно измеряемые независимые величины, имеющие погрешность Δx_i, тогда:

См. также

• Измерение физических величин
• Класс точности
• Метрология
• Система автоматизированного сбора данных со счетчиков по радиоканалу
• Методы электроаналитической химии

Литература

• Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.

• Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.

Погрешность средств измерения и результатов измерения. 

Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.

Инструментальные и методические погрешности. 

Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности.

• Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.
  Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях.
• Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины. 

Систематическая и случайная погрешности. 

Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Причинами возникновения систематических составляющих погрешности измерения являются:

• отклонение параметров реального средства измерений от расчетных значений, предусмотренных схемой;
• неуравновешенность некоторых деталей средства измерений относительно их оси вращения, приводящая к дополнительному повороту за счет зазоров, имеющихся в механизме;
• упругая деформация деталей средства измерений, имеющих малую жесткость, приводящая к дополнительным перемещениям;
• погрешность градуировки или небольшой сдвиг шкалы;
• неточность подгонки шунта или добавочного сопротивления, неточность образцовой измерительной катушки сопротивления;
• неравномерный износ направляющих устройств для базирования измеряемых деталей;
• износ рабочих поверхностей, деталей средства измерений, с помощью которых осуществляется контакт звеньев механизма;
• усталостные измерения упругих свойств деталей, а также их естественное старение;
• неисправности средства измерений.

Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.

Погрешности адекватности и градуировки. 

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.

Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.

Абсолютная, относительная и приведенная погрешности. 

Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.

Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.

Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

– если шкала прибора односторонняя и нижний предел измерений равен нулю (например диапазон измерений 0…100), то Xn определяется равным верхнему пределу измерений (Xn=100);
– если шкала прибора односторонняя, нижний предел измерений больше нуля, то Xn определяется как разность между максимальным и минимальным значениями диапазона (для прибора с диапазоном измерений 30…100, Xn=Xmax-Xmin=100-30=70);
– если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора (диапазон измерений -50…+50, Xn=100).

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

Аддитивные и мультипликативные погрешности.

• Аддитивной погрешностью называется погрешность, постоянную в каждой точке шкалы.
• Мультипликативной погрешностью называется погрешность, линейно возрастающую или убывающую с ростом измеряемой величины.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.

Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).

Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:

– для аддитивной погрешности:
аддитивная погрешность 
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность 
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).