,
—
уравнение регрессии,
—
случайная ошибка (с ограничениями).
;
;
—
остатки регрессии. Надо различать
остатки и
ошибки регрессии.
Остатки в отличии от ошибок наблюдаемы.
Предположим,
что оценка σ2
связана с
суммой квадратов остатков регрессии

Вычислим:
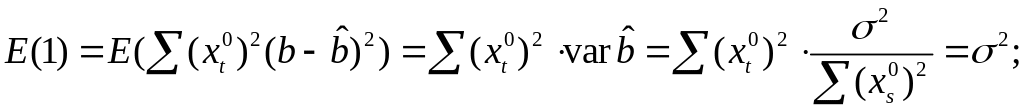
Используя,
получим

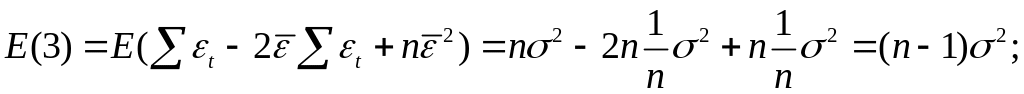
где
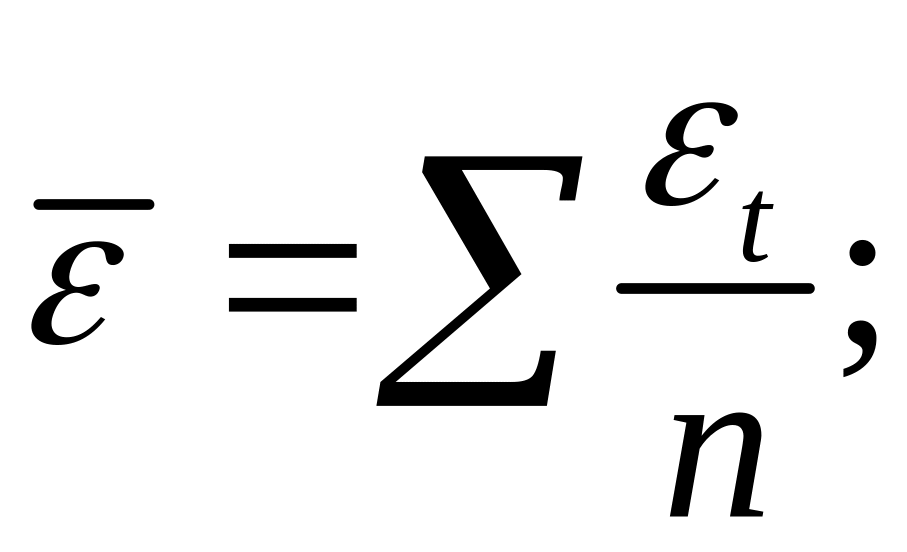
Таким образом
откуда следует,
что
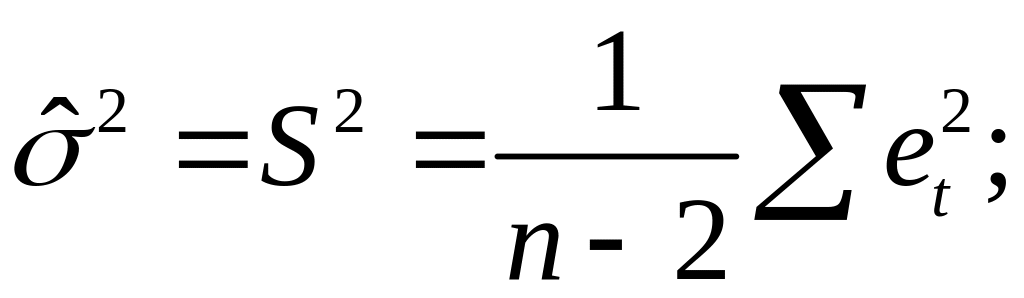
является
несмещенной оценкой дисперсии ошибок
σ2.
12. Оценка существенности параметров линейной регрессии и корреляции
Существенность
коэф-ов регрессии определяет можно ли
его заменить нулем. Если данный коэф-т
несуществ., то его можно заменить нулем.
При выполнении
дополнительного условия о совместном
нормальном распределении ошибок,
стандартная ошибка коэффициента
регрессии параметра Sb
рассчитывается
по формуле
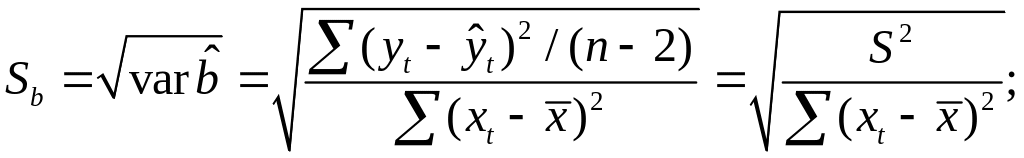
где S2
— остаточная
дисперсия на одну степень свободы.
Отношение коэф-та
регрессии к его стандартной ошибке дает
t-статистику,
кот. подчиняется статистике Стьюдента
при (n-2)
степенях свободы.
Эта статистика применяется для проверки
стат. значимости коэф-та
регрессии.
Для оценки значимости
коэф-та регрессии опр-ют фактическое
знач. t-критерия
Стьюдента: tb=b/Sb
, которое
затем сравнивают с табличным значением
при определенном уровне значимости
и числе степеней
свободы (n-2).
Если tb>tкр,
коэф-т b значим и
его нельзя заменить 0.
Доверительный
интервал для коэф-та регрессии опр-ся
как
.
Замечание: Т.к.
коэф-т регрессии b для эк. Исследований
имеет четкую интерпритацию доверит.
Интервалы не должны содержать
противоречивыхрезультатов, напр., от
«-10» до 20 , т.е. положит. и отрицат.
Значимость линейного
коэффициента корреляции r
проверяется на основе величины ошибки
коэффициента корреляции Sr=mr(заменить):
О
тсюда
фактическое значение
Данная формула
свидетельствует, что в парной лин.
регрессии
tr2=F
=>tr2=
tb2
.
Таким образом,
проверка гипотез о значимости коэффициентов
регрессии и корреляции равносильна
проверке гипотезы о значимости линейного
уравнения регрессии.
13. Интервалы прогноза по линейному уравнению регрессии
Основное назначение
ур-ия регрессии — прогноз возможных
знач. результата при заданном значении
фактора.
Этот прогноз
осущ-ся путем подстановки знач. фактора
х=хk
в ур-ние
регрессии
.
Но данный
точечный прогноз не всегда реален. Он
должен дополняться интервальной
оценкой прогноза значения результата
y*.
Т.е.
,
где
—
стандартная ошибка оценки
.
Получим данную
оценку для лин. регрессии
.
Подставим это
выражение в ур-ие
.
Отсюда следует,
что стандартная ошибка
зависит от
ошибки
и ошибки
коэффициента b,
т.е.
.
В курсе мат. стат.
получено:
=S2/n,где
S2
– оценка дисперсии рез-ого признака.
;Получим
Откуд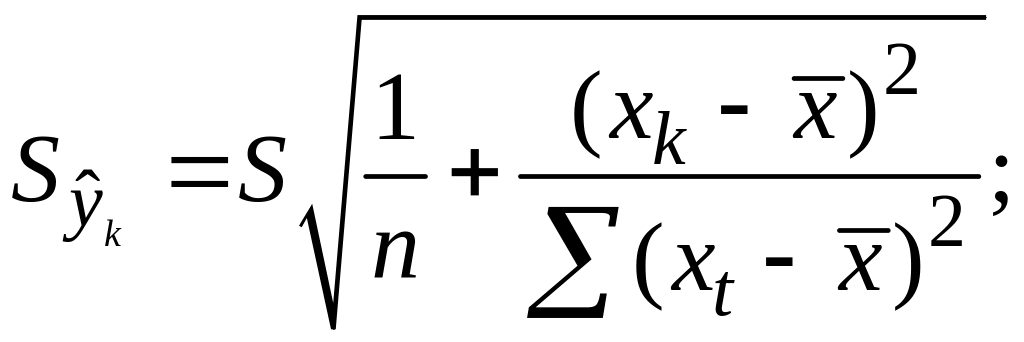
Где t=1,…n
– номера измерений, xk
не обязано совпадать с одним из xt.
Видно, что величина
стандартной ошибки xk
зависит от
.
Она достигает
мин. при xк=
и возрастает
по мере того, как «удаляется» от
в любом
направлении.
Т.е.
.
Можно строить
интервальные оценки рез-ого признака
при заданном xк
, которые
определяются как
,
где
—
критическое значение распределения
Стьюдента, при (n-2) степенями свободы.
На графике
доверительные границы для
представляют собой гиперболы,
расположенные по обе стороны от линии
регрессии.
Фактические знач.
yk
варьируют
около ср. знач.
на величину случ. ошибки ε, дисперсия
кот. оценивается как S2
, поэтому
ошибка предсказываемого индивид-ого
значения y
должно включать как станд.ошибку
так и случ.ошибку S.
Средняя ошибка
прогнозного индив.значения составит
.
На основе этой оценки м.также строить
интервальные оценки, кот. б. содержать
заданные доверительной вероятностью,
измеряемые значения рез-ого признака.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
Доказательство. Примем без доказательства справедливость следующих равенств:
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
– выборочная оценка дисперсии случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
,
—
уравнение регрессии,
—
случайная ошибка (с ограничениями).
;
;
—
остатки регрессии. Надо различать
остатки и
ошибки регрессии.
Остатки в отличии от ошибок наблюдаемы.
Предположим,
что оценка σ2
связана с
суммой квадратов остатков регрессии

Вычислим:
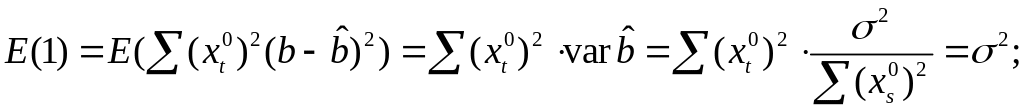
Используя,
получим

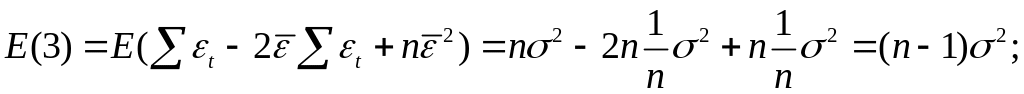
где
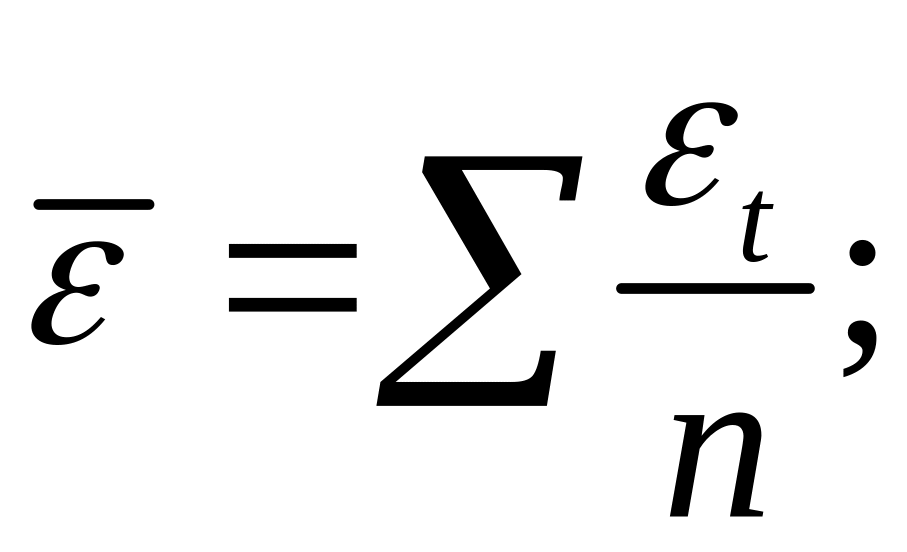
Таким образом
откуда следует,
что
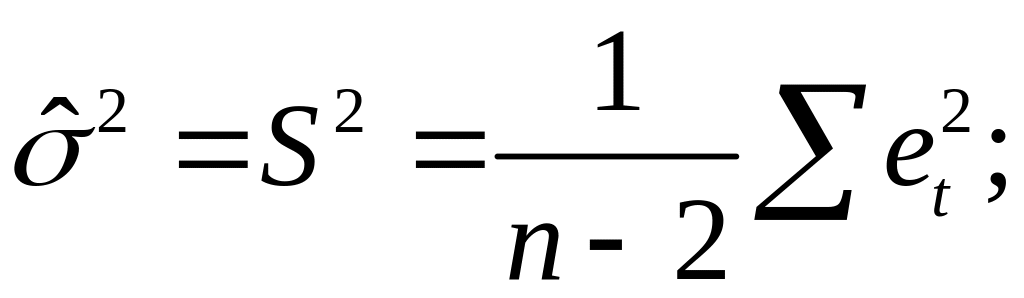
является
несмещенной оценкой дисперсии ошибок
σ2.
12. Оценка существенности параметров линейной регрессии и корреляции
Существенность
коэф-ов регрессии определяет можно ли
его заменить нулем. Если данный коэф-т
несуществ., то его можно заменить нулем.
При выполнении
дополнительного условия о совместном
нормальном распределении ошибок,
стандартная ошибка коэффициента
регрессии параметра Sb
рассчитывается
по формуле
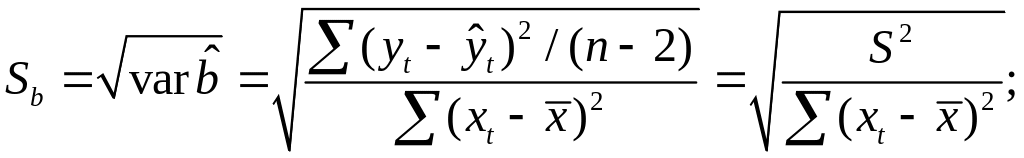
где S2
— остаточная
дисперсия на одну степень свободы.
Отношение коэф-та
регрессии к его стандартной ошибке дает
t-статистику,
кот. подчиняется статистике Стьюдента
при (n-2)
степенях свободы.
Эта статистика применяется для проверки
стат. значимости коэф-та
регрессии.
Для оценки значимости
коэф-та регрессии опр-ют фактическое
знач. t-критерия
Стьюдента: tb=b/Sb
, которое
затем сравнивают с табличным значением
при определенном уровне значимости
и числе степеней
свободы (n-2).
Если tb>tкр,
коэф-т b значим и
его нельзя заменить 0.
Доверительный
интервал для коэф-та регрессии опр-ся
как
.
Замечание: Т.к.
коэф-т регрессии b для эк. Исследований
имеет четкую интерпритацию доверит.
Интервалы не должны содержать
противоречивыхрезультатов, напр., от
«-10» до 20 , т.е. положит. и отрицат.
Значимость линейного
коэффициента корреляции r
проверяется на основе величины ошибки
коэффициента корреляции Sr=mr(заменить):
О
тсюда
фактическое значение
Данная формула
свидетельствует, что в парной лин.
регрессии
tr2=F
=>tr2=
tb2
.
Таким образом,
проверка гипотез о значимости коэффициентов
регрессии и корреляции равносильна
проверке гипотезы о значимости линейного
уравнения регрессии.
13. Интервалы прогноза по линейному уравнению регрессии
Основное назначение
ур-ия регрессии — прогноз возможных
знач. результата при заданном значении
фактора.
Этот прогноз
осущ-ся путем подстановки знач. фактора
х=хk
в ур-ние
регрессии
.
Но данный
точечный прогноз не всегда реален. Он
должен дополняться интервальной
оценкой прогноза значения результата
y*.
Т.е.
,
где
—
стандартная ошибка оценки
.
Получим данную
оценку для лин. регрессии
.
Подставим это
выражение в ур-ие
.
Отсюда следует,
что стандартная ошибка
зависит от
ошибки
и ошибки
коэффициента b,
т.е.
.
В курсе мат. стат.
получено:
=S2/n,где
S2
– оценка дисперсии рез-ого признака.
;Получим
Откуд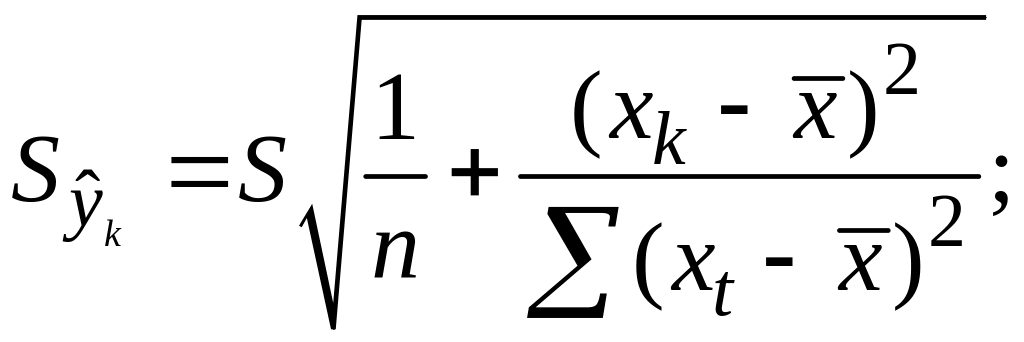
Где t=1,…n
– номера измерений, xk
не обязано совпадать с одним из xt.
Видно, что величина
стандартной ошибки xk
зависит от
.
Она достигает
мин. при xк=
и возрастает
по мере того, как «удаляется» от
в любом
направлении.
Т.е.
.
Можно строить
интервальные оценки рез-ого признака
при заданном xк
, которые
определяются как
,
где
—
критическое значение распределения
Стьюдента, при (n-2) степенями свободы.
На графике
доверительные границы для
представляют собой гиперболы,
расположенные по обе стороны от линии
регрессии.
Фактические знач.
yk
варьируют
около ср. знач.
на величину случ. ошибки ε, дисперсия
кот. оценивается как S2
, поэтому
ошибка предсказываемого индивид-ого
значения y
должно включать как станд.ошибку
так и случ.ошибку S.
Средняя ошибка
прогнозного индив.значения составит
.
На основе этой оценки м.также строить
интервальные оценки, кот. б. содержать
заданные доверительной вероятностью,
измеряемые значения рез-ого признака.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
Доказательство. Примем без доказательства справедливость следующих равенств:
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
– выборочная оценка дисперсии случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
Пусть мы имеем модель наблюдений в виде модели простой линейной регрессии
И хотим дать прогноз, каким будет значение объясняемой переменной при некотором выбранном (фиксированном) значении
объясняющей переменной
, если мы будем продолжать наблюдения.
Мы умеем оценивать коэффициенты и
методом наименьших квадратов, и естественно использовать для целей прогнозирования получаемую в результате такого оценивания (подобранную) модель линейной связи
Что приводит к Прогнозируемому значению Объясняемой переменной, равному
Вопрос только в том, Сколь надежным является выбор такого значения в качестве прогнозного. И здесь надо иметь в виду следующее.
Поскольку мы используем для прогноза оценки, полученные, исходя из модели наблюдений то для того, чтобы этот прогноз был осмысленным, нам по необходимости приходится предполагать, что структура модели наблюдений и ее параметры Не изменятся при переходе к новому наблюдению, так что соответствующее
значение
должно описываться Тем же линейным соотношением
. В таком случае, мы по-существу имеем дело с расширенной линейной моделью с
наблюдениями, в которой дополнительное наблюдение удовлетворяет соотношению
При этом, случайная величина должна иметь То же распределение, что и случайные величины
и должна образовывать вместе с ними множество случайных величин, независимых в совокупности.
Итак, мы договорились, что в расширенной модели
Выбирая в качестве прогноза для значение
Мы тем самым допускаем Ошибку прогноза, равную
Поскольку вычисленные оценки являются (как мы уже выяснили выше) реализациями случайных величин, наблюдаемая ошибка прогноза также является реализацией случайной величины
и включает два источника неопределенности:
· неопределенность, связанную с отклонением вычисленных значений случайных величин От истинных значений параметров
;
· неопределенность, связанную со случайной ошибкой в
— м наблюдении.
При наших Стандартных предположениях о линейной модели наблюдений ошибка прогноза является Случайной величиной , имеющей математическое ожидание
(Мы использовали здесь справедливые при выполнении стандартных предположений соотношения )
Точность прогноза характеризуется Дисперсией ошибки прогноза
Здесь использован тот факт, что сумма Неслучайна (хотя ее точное значение и не известно). Далее, из предположенной независимости случайных ошибок
и
вытекает независимость случайных величин
(эта величина зависит от случайных ошибок
) и
(последняя Не зависит от случайных ошибок
). В силу же независимости
и
,
(использовано правило сложения дисперсий). Остается заметить, что
Где, как обычно, (Мы не будем выводить эту формулу.) Таким образом,
Если случайные ошибки имеют Нормальное распределение, то тогда случайные величины
и
Также имеют нормальные распределения. При этом, ошибка прогноза имеет нормальное распределение с нулевым математическим ожиданием и дисперсией, вычисляемой по последней формуле.
Разделив разность на квадратный корень из ее дисперсии, получаем случайную величину
Имеющую Стандартное нормальное распределение . Заменяя в правой части выражения для
Неизвестное значение
его несмещенной оценкой
, получаем оценку дисперсии
в виде
Заменяя, наконец, в знаменателе отношения, имеющего стандартное нормальное распределение, неизвестное значение его оценкой
, приходим к
-статистике (
-отношению)
Имеющей При выполнении сделанных предположений о модели наблюдений -распределение Стьюдента
с
Степенями свободы.
Последний факт дает возможность построения -процентного доверительного интервала для значения
А именно,
На основании которого получаем -процентный доверительный интервал для
:
— здесь мы использовали то, что в силу симметрии распределения Стьюдента, .
Заметим, что при заданных значениях (по которым строится прогноз) доверительный интервал для
будет Тем длинее, чем больше значение
. Последнее же равно
при
и возрастает с ростом
. Это означает, что длина доверительного интервала Возрастает при удалении значения
, при котором строится прогноз, от среднего арифметического значений
.
Таким образом, прогнозы для значений , далеко отстоящих от
, становятся менее определенными, поскольку длина соответствующих доверительных интервалов для значений объясняемой переменной возрастает.
Пример. Для данных о размерах совокупного располагаемого дохода и совокупных расходах на личное потребление в США в период с 1970 по 1979 год (в млрд. долларов, в ценах 1972 года), оцененная модель линейной связи имеет вид .
Представим себе, что мы находимся в 1979 году и ожидаем увеличения в 1980 году совокупного располагаемого дохода (в тех же ценах) до млрд. долларов. Тогда прогнозируемый по подобранной модели объем совокупных расходов на личное потребление в 1980 году равен
Так что если выбрать уровень доверия , то
И доверительный интервал для соответствующего значения
имеет вид
Т. е.
Или
Заметим, что интервал достаточно широк и его нижняя граница допускает даже возможность некоторого снижения уровня потребления по сравнению с предыдущим годом.
В действительности, в 1980 г. совокупный располагаемый доход достиг 1021 млрд. долларов, а совокупное потребление — 931.8 млрд. долларов. Тем самым, ошибка прогноза составила
Если бы мы исходили при прогнозе из Действительного значения , а не из
, то прогнозируемое значение для
равнялось бы 931.94 и ошибка прогноза составила всего лишь
Проиллюстрируем, наконец, как изменяется в этом примере длина 95%-доверительных интервалов в интервале наблюдавшихся значений объясняющей переменной . На графике приведены отклонения нижней и верхней границ таких интервалов от центра интервала:
В случае модели Множественной линейной регрессии
Точечный прогноз значения соответствующего Фиксированному набору
значений объясняющих переменных, дается формулой
Где — оценки наименьших квадратов параметров
. Интервальный прогноз Имеет вид
Где
— оценка дисперсии ошибки прогноза, а — несмещенная оценка дисперсии
Случайных ошибок.
| < Предыдущая | Следующая > |
|---|
Определение дисперсии случайных величин
Дисперсия – норма, отражающая, с точки зрения теории, ожидаемое отклонение случайной величины от ее математического ожидания.
В математической статистике она определяется в качестве центрального момента второго порядка. Приведем формулу дисперсии:
где М(х) – математическое ожидание, а D(х) – дисперсия.
На основе данной формулы можно вывести другую, которая дает оценку дисперсии:
где S2— оценка дисперсии, Xi— наблюдаемые значения, n – объем собранных эмпирических значений, X—— оценка математического ожидания.
В первой формуле оценка математического ожидания не смещена, но во второй формуле дисперсия является выборочной. Т.е. эта оценка дает характеристику величине дисперсии данной выборки, не для популяции данных. Обычно для эксперимента необходимо оценить популяционный характер математического ожидания и дисперсию.
Так как вторая формула предполагает сравнение эмпирических знаний не с истинной величиной, а с оценочной, то происходит смещение оценки дисперсии. Способами дифференциального исчисления определено: ожидаемая величина оценки дисперсии по второй формуле описывает соотношение:
Данная формула отражает выборочную дисперсию. Из нее следует, что при наличии 10 выборочных значений случайной величины идет занижение значения. Получается 9/10 дисперсий анализируемой величины для генеральной совокупности. Если увеличить объем в десять раз, то уменьшиться величина смещения до одной сотой, и при этому полученный результат будет отличаться от ожидаемого значения. При помощи третьей формулы можно рассчитать несмещенную оценку дисперсии:
Данная формула называется популяционной дисперсией, или дисперсией генеральной совокупности. Эту формулу используют для расчета генеральной совокупности, третью – для определения вариантов внутри выборки и выход за пределы имеющихся значений, который не предполагается теорией.
Характеристика оценивания стандартного отклонения
Иногда для оценивания важна не сама дисперсия, а оценка стандартного отклонения. Эти две величины связаны однозначным соотношением. Оценивание стандартного отклонения также применяется для выборки и генеральной совокупности, как и дисперсия. Оценка данной величины является предпочтительной, так как она удобна для восприятия из-за своей размерности. Помимо этого, эту величину используют для вычисления стандартной ошибки. Формула выглядит следующим образом:
где SE – стандартная ошибка.
Данная статистика необходима для интервальной оценки исследуемой случайной величины.
Характеристика оценки полумежквартильного интервала
Это еще один способ оценивания вариантов в распределении случайной величины. Ее обозначают Q. Она используется в качестве альтернативы стандартного отклонения, несмотря на то, что они связаны соотношением Q = 0,67σ.
Квартиль – это вариант названия квантиля распределения.
При соответствии медианы с половиной распределения, то квартиль равен четверти. Т.е. первая четверть – это первый квартиль, половина – второй квартиль, три четвертых – третий, общая сумма величины – четвертый квартиль. Формула межквартильного интервала выглядит следующим образом:
Данную оценку используют, например, в сенсорной психофизике при оценивании порога способом констант.
Характеристика ковариации
Иногда необходимо оценить не одну дисперсию, а две (х,у). Такая статистика называется ковариацией. Ее формула выглядит следующим образом:
Она определяет степень связи между двумя переменами. Отличительная особенность ковариации – это ее выражение и в положительных и в отрицательных числах. Так как ковариация зависит от размерности, то оценить степень между переменными невозможно. Поэтому в качестве меры двух переменных используют термин «корреляция». Ее величина может быть определена за счет деления ковариации на произведение стандартных отклонений двух случайных величин, между которыми вычисляют ковариацию.
Преподаватель факультета психологии кафедры общей психологии. Кандидат психологических наук
При проведении регрессионного анализа
основная трудность заключается в том,
что генеральная дисперсия случайной
ошибки является неизвестной величиной,
что вызывает необходимость в расчёте
её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии(или
исправленной дисперсией) случайной
ошибки линейной модели парной регрессии
называется величина, рассчитываемая
по формуле:
где n
– это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной
регрессии несмещённая оценка дисперсии
случайной ошибки рассчитывается по
формуле:
где k
– число оцениваемых параметров модели
регрессии.
Оценка матрицы ковариаций случайных
ошибок Cov(ε) будет являться оценочная
матрица ковариаций:
где In
– единичная матрица.
Оценка дисперсии случайной
ошибки модели регрессии распределена
по ε2(хи-квадрат)
закону распределения с (n-k-1)
степенями свободы.
Для доказательства несмещённости оценки
дисперсии случайной ошибки модели
регрессии необходимо доказать
справедливость равенства
Доказательство. Примем без
доказательства справедливость следующих
равенств:
где G2(ε)
– генеральная дисперсия случайной
ошибки;
S2(ε)– выборочная дисперсия случайной
ошибки;
– выборочная оценка дисперсии
случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка
дисперсии случайной ошибки
является несмещённой оценкой
генеральной дисперсии случайной ошибки
модели регрессии G2(ε).
При условии извлечения из
генеральной совокупности нескольких
выборок одинакового объёма n
и при одинаковых значениях объясняющих
переменных х,
наблюдаемые значения зависимой переменной
у будут случайным образом колебаться
за счёт случайного характера случайной
компоненты β.
Отсюда можно сделать вывод, что будут
варьироваться и зависеть от значений
переменной у значения оценок коэффициентов
регрессии и оценка дисперсии случайной
ошибки модели регрессии.
Для иллюстрации данного утверждения
докажем зависимость значения МНК-оценки
от величины случайной ошибки
ε.
МНК-оценка коэффициента β1 модели
регрессии определяется по формуле:
В связи с тем, что переменная
у зависит от случайной компоненты ε
(yi=β0+β1xi+εi), то ковариация
между зависимой переменной у
и независимой переменной х
может быть представлена следующим
образом:
Для дальнейших преобразования используются
свойства ковариации:
1) ковариация между переменной
х и
константой С
равна нулю: Cov(x,C)=0,
C=const;
2) ковариация
переменной х
с самой собой равна дисперсии этой
переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации,
справедливы следующие равенства:
Cov(x,β0)=0
(β0=const);
Cov(x, β1x)=
β1*Cov(x,x)=
β1*G2(x).
Следовательно, ковариация
между зависимой и независимой переменными
Cov(x,y)
может быть записана как:
Cov(x,y)=
β1G2(x)+Cov(x,ε).
В результате МНК-оценка коэффициента
β1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух
компонент:
1) константы β1,
т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,ε),
вызывающей вариацию коэффициента модели
регрессии.
Однако на практике подобное разложение
МНК-оценки невозможно, потому что
истинные значения коэффициентов модели
регрессии и значения случайной ошибки
являются неизвестными. Теоретически
данное разложение можно использовать
при изучении статистических свойств
МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и
несмещённая оценка дисперсии случайной
ошибки
могут быть представлены как сумма
постоянной составляющей (константы) и
случайной компоненты, зависящей от
ошибки модели регрессии ε.
[c.85]
Основные положения теории Шарпа. Коэффициенты регрессии. Измерение ожидаемой доходности и риска портфеля. Дисперсия ошибок. Определение весов ценных бумаг в модели Шарпа. Нахождение оптимального портфеля. Сравнительный анализ методов Г. Марковица и В. Шарпа.
[c.335]
Наиболее хорошо изучены линейные регрессионные модели, удовлетворяющие условиям (1.6), (1.7) и свойству постоянства дисперсии ошибок регрессии, — они называются классическими моделями.
[c.19]
Очевидно, для продвижения к этой цели необходимы некоторые дополнительные предположения относительно характера гетероскедастичности. В самом деле, без подобных предположений, очевидно, невозможно было бы оценить п параметров (п дисперсий ошибок регрессии а ) с помощью п наблюдений.
[c.161]
Решение. Предположим, что дисперсии ошибок о, связаны уравнением регрессии
[c.163]
Вспомним, что наиболее часто употребляемые процедуры устранения гетероскедастичности так или иначе были основаны на предположении, что дисперсия ошибок регрессии ст2 является функцией от каких-то регрессоров. Если а2 существенно зависит от регрессора Z, а при спецификации модели регрессор Z не был включен в модель, стандартные процедуры могут не привести к устранению гетероскедастичности.
[c.250]
В случае постоянства дисперсии ошибок МНК необъясненная дисперсия для меньших значений X должна быть приблизительно равна необъясненной дисперсии для больших значений X, то есть должно быть справедливым следующее равенство [c.125]
Чем ближе к единице отношение / S2, тем больше оснований рассчитывать на то, что дисперсия ошибок МНК постоянна. Случайная величина F = Sl / S2 подчиняется F -распределению
[c.125]
Непостоянство дисперсии ошибок МНК возникает как правило в том случае, если неправильно выбран вид математической модели зависимости фактора X и отклика 7. Например, если нелинейную зависимость пытаются аппроксимировать линейной функцией.
[c.126]
Пятая часть полностью посвящена приложению матричного дифференциального исчисления к линейной регрессионной модели. Она содержит исчерпывающее изложение проблемы оценивания, связанной с неслучайной частью модели при различных предположениях о рангах и других ограничениях. Кроме того, она содержит ряд параграфов, связанных со стохастической частью модели, например оценивание дисперсии ошибок и прогноз ошибок. Включен также небольшой параграф, посвященный анализу чувствительности. Вводная глава содержит необходимые предварительные сведения из теории вероятностей и математической статистики.
[c.16]
Дисперсия ошибок прогноза в задаче (3.6) — (3.7) достигает минимума в точке , являющейся основанием перпендикуляра, опущенного из точки т] на подпространство Q, определяемое равенством (3.7). Соотношение (3.10) эквивалентно равенству
[c.309]
Ограничение (а) не вызывает претензий. Условие (б) также естественно. Ясно, что механизм сглаживания и прогноза, при котором математическое ожидание или дисперсия ошибок фильтрации или интенсивность искусственного рассеивания достаточно велики, вряд ли рационален и тем более не может быть признан оптимальным.
[c.320]
Задача прогнозирования по минимуму дисперсии ошибок при различных статистических характеристиках входных случайных процессов и ошибок измерений подробно обсуждалась в литературе. Имеются и стандартные аналоговые устройства и программы для ЦВМ, реализующие соответствующие схемы. Экстремальная задача, к которой сводится вычисление характеристик генераторов случайных шумов, несомненно, проще исходной вариационной задачи.
[c.334]
Матрица корреляции k j R регулируемых ошибок прогноза, оптимального в смысле показателя качества R( k ), может быть получена из корреляционной матрицы kff a ошибок прогноза, оптимальных в смысле минимума дисперсии ошибок в каждой координате в каждый момент времени, по следующей формуле [c.339]
Из (1.14), в частности, следует, что коэффициент корреляции признаков, на которые наложены ошибки измерения, всегда меньше по абсолютной величине, чем коэффициент корреляции исходных признаков. Другими словами, ошибки измерения всегда ослабляют исследуемую корреляционную связь между исходными переменными, и это искажение тем меньше, чем меньше отношения дисперсий ошибок к дисперсиям самих исходных переменных. Формула (1.14) позволяет скорректировать искаженное значение коэффициента корреляции для этого нужно либо знать разрешающие характеристики измерительных приборов (и, следовательно, величины дисперсий ошибок а и а ), либо провести дополнительное исследование по их выявлению.
[c.73]
Пример 7.4 ]. Известно, что дисперсия о2, вызванная ошибками измерения, при некоторых видах количественного анализа составляет 0,5. Если заменить измерительный прибор и произвести 10-кратное измерение одного и того же стандартного образца, а затем подсчитать дисперсию, то она составит s2 = 0,25. Может показаться, что дисперсия ошибок измерения изменилась, превысив 5%-ный уровень значимости. Так ли это [c.128]
Теорема Гаусса-Маркова. Оценка дисперсии ошибок сг2
[c.41]
Оценка дисперсии ошибок а2
[c.43]
Формулы (2.11), (2.13) дают дисперсии оценок о, Ь коэффициентов регрессии в том случае, если а2 известно. На практике, как правило, дисперсия ошибок а2 неизвестна и оценивается по наблюдениям одновременно с коэффициентами регрессии а, Ь. В этом случае вместо дисперсий оценок о, b мы можем получить лишь оценки дисперсий о, 6, заменив а2 на s2 из (2.15) в (2.11), (2.13), (2.14) [c.45]
Распределение оценки дисперсии ошибок s2
[c.47]
Так как оценка дисперсии ошибок s2 является функцией от остатков регрессии et, то для того чтобы доказать независимость s2 и (2,6), достаточно доказать независимость et и (2,6). Оценки 2, 6 так же, как и остатки регрессии et, являются линейными функциями ошибок t (см. (2.4а), (2.46), (2.20)) и поэтому имеют совместное нормальное распределение. Известно (приложение МС, п. 4, N4), что два случайных вектора, имеющие совместное нормальное распределение, независимы тогда и только тогда, когда они некоррелированы. Таким образом, чтобы доказать независимость s2 и (а, 6), нам достаточно доказать некоррелированность et и (2,6).
[c.48]
Значение Д2 увеличилось по сравнению с первой регрессией. Переход к удельным данным приводит к уменьшению дисперсии ошибок модели.
[c.58]
Пусть SML = Y et/ n и OLS — ] et/ (n — 1 — оценки методов максимального правдоподобия и наименьших квадратов для дисперсии ошибок <т2 в классической модели парной регрессии Yt =
[c.62]
Оценка дисперсии ошибок а1. Распределение s2
[c.72]
Сумма квадратов остатков е2 = е е является естественным кандидатом на оценку дисперсии ошибок а1 (конечно, с некоторым поправочным коэффициентом, зависящим от числа степеней свободы) [c.73]
Тест ранговой корреляции Спирмена использует наиболее общие предположения о зависимости дисперсий ошибок регрессии от значений регрессоров [c.158]
Тест Уайта. Тест ранговой корреляции Спирмена и тест Голдфелда—Квандта позволяют обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности.
[c.161]
Наиболее простой и часто употребляемый тест на гетероске-дастичность — тест Уайта. При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же функцию от наблюдаемых значений регрессоров, т.е.
[c.161]
Другим недостатком тестов Уайта и Глейзера является то, что факт невыявления ими гетероскедастичности, вообще говоря, не означает ее отсутствия. В самом деле, принимая гипотезу Щ, мы принимаем лишь тот факт, что отсутствует определенного вида зависимость дисперсий ошибок регрессии от значений регрессоров.
[c.166]
Построенные экологометрические модели требуют оценки их достоверности. При выполнении статистических исследований полученные данные тщательно анализируются на предмет удовлетворения их предположения о независимости случайных наблюдений, симметричности распределения, из которого получена выборка, равенства дисперсии ошибок, одинаковости распределения нескольких случайных величин и т.д. Все эти предположения могут рассматриваться как гипотезы, которые необходимо проверить.
[c.57]
Доказано (см., например, [37]), что приведенную задачу оптимального стохастического управления можно разделить на две задачу сглаживания и лрогноза по минимуму дисперсии ошибок и задачу оптимального детерминированного управления. При более сложном критерии качества управления и при дополнительных ограничениях на переменные состояния и управляющие параметры такое разделение не всегда удается я, его, по-видимому, не всегда целесообразно производить.
[c.44]
Здесь Paaa(tt, » ) — система функций веса, минимизирующих дисперсию ошибок За(/г-) прогноза W (ti, т) — тождественно не равные нулю функ-22 339
[c.339]
В ходе анализа финансовых данных любой ряд динамики, будь то процентные ставки или цены на финансовые активы, можно разбить на две компоненты, одна из которых изменяется случайным образом, а другая подчиняется определенному закону. Колебания финансовых переменных значительно изменяются во времени бурные периоды с высокой волатильностью переменных сменяют спокойные периоды и наоборот. В некоторых случаях вола-тильность играет ключевую роль в ценообразовании на финансовые активы. В частности, курсы акций напрямую зависят от ожидаемой волатильности доходов корпораций. Все финансовые учреждения без исключения стремятся адекватно оценить волатильность в целях успешного управления рисками. В свое время Трюгве Хаавельмо, нобелевский лауреат по экономике 1989 г., предложил рассматривать изменение экономических переменных как однородный стохастический (случайный) процесс. Вплоть до 1980-х гг. экономисты для анализа финансовых рынков применяли статистические методы, предполагавшие постоянную волатильность во времени. В 1982 г. Роберт Ингл развил новую эконометрическую концепцию, позволяющую анализировать периоды с разной волатильностью. Он ввел кластеризацию данных и условную дисперсию ошибок, которая завесит от времени. Свою разработку Ингл назвал авторегрессионной гетероскедастической моделью , с ее помощью можно точно описать множество временных рядов, встречающихся в экономике. Метод Ингла сегодня применяется финансовыми аналитиками в целях оценки финансовых активов и портфельных рисков.
[c.197]
Отметим, что оценки максимального правдоподобия параметров а, 6 совпадают с оценками метода наименьших квадратов OML = SOLS, ML OLS- Это легко видеть из того, что уравнения (2.37а) и (2.376) совпадают с соответствующими уравнениями метода наименьших квадратов (2.2). Оценка максимального правдоподобия для <т2 не совпадает с
несмещенной оценкой дисперсии ошибок. Таким образом, с = ((п — 2)/n)<7OLS является смещенной, но тем не менее состоятельной оценкой <т2.
[c.57]
В этом разделе мы рассмотрим частный случай обобщенной регрессионной модели, а именно, модель с гетероскедастичностъю, Это означает, что ошибки некоррелированы, но имеют непостоянные дисперсии. (Классическая модель с постоянными дисперсиями ошибок называется гомоскедастичной.) Как уже отмечалось, Гетероскедастичность довольно часто возникает, если анализируемые объекты, говоря нестрого, неоднородны. Например, если исследуется зависимость прибыли предприятия от каких-либо факторов, скажем, от размера основного фонда, то естественно ожидать, что для больших предприятий колебание прибыли будет выше, чем для малых.
[c.168]
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
Доказательство. Примем без доказательства справедливость следующих равенств:
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
– выборочная оценка дисперсии случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
Пусть
Поскольку
заменяются две величины (
и
),
то это вызывает смещение оценки
:
. (1.22)
Покажем
это .
Известно
что
.
Пусть
Х1,
Х2,…,
Хi
,…,Xn
— независимые случайные величины, каждая
из которых имеет один и тот же закон
распределения с числовыми характеристиками:
и D(Xi)=D0.
Пусть
подставим в (*), тогда:
Найдем
E[Dв]:
Итак
Что и требовалось доказать.
При
больших п
смещение невелико, им можно пренебречь,
но при малых выборках оно существенно.
Таким
образм,
есть несмещенная оценка дисперсии или
.
(1.23)
Тогда
исправленное среднее квадратическое
отклонение имеет вид:
.
(1.24)
Для
интервальной оценки используется
выражение
,
где
находится по формуле (1.24).
Замечание.
Однако для больших выборок можно считать,
что
.
В случае малых выборок (п
< 30) пользуются исправленной дисперсией
по формуле (1.24).
По
закону больших чисел
является состоятельной оценкой для
генеральной дисперсии. А так как множитель
при
,
то
также является состоятельной оценкой
для
.
Оценка
,
строго говоря, не является эффективной
оценкой для
,
однако при наличии нормального
распределения ее можно считать приближенно
эффективной.
Замечание.
Если известно точное значение
математического ожидания «
»
для n
измерений, то E(Xi)
=
где хi
– отдельные измерения. Исправленная
(несмещённая) дисперсия находится по
формуле
(1.25)
Действительно.
,
т.е. E(D*в)
= D0
.
Пример
1.19. В ящике содержатся стержни трех
размеров (N
= 3): 12 см, 14 см и 16 см с соответствующими
долями 0,1; 0,3; 0,6. Производится повторная
выборка двух стержней (n
= 2). Найти
все возможные выборочные распределения
и построить законы распределения для
и
.
Проверить на данном примере справедливость
равенств
.
Решение.
Определим
количество возможных выборок:
.
Закон
распределения генеральной совокупности
представлен в следующей в таблице
|
X |
12 |
14 |
16 |
|
P |
0,1 |
0,3 |
0,6 |
Вычислим
генеральные характеристики :
Все
выборочные законы представлены в
следующей таблице.
|
№ выборки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
12 12 |
12 14 |
12 16 |
14 12 |
14 14 |
14 16 |
16 12 |
16 14 |
16 16 |
|
|
2 |
1 1 |
1 1 |
1 1 |
2 |
1 1 |
1 1 |
1 1 |
2 |
|
|
12 |
13 |
14 |
13 |
14 |
15 |
14 |
15 |
16 |
|
|
0 |
1 |
4 |
1 |
0 |
1 |
4 |
1 |
0 |
|
|
0,01 |
0,03 |
0,06 |
0,03 |
0,09 |
0,18 |
0,06 |
0,18 |
0,36 |
Проверим,
что
.
По
данным последней таблицы получим строим
законы распределения для
и Dв
и находим соответствующие характеристики.
|
|
12 |
13 |
14 |
15 |
16 |
|
|
P |
0,01 |
0,06 |
0,21 |
0,36 |
0,36 |
1 |
,
|
|
0 |
1 |
4 |
|
|
|
0,46 |
0,42 |
0,12 |
1 |
E[Dв]=0,42+0,48=0.9/
Итак,
,
Откуда
следует:
и
при n
= 2.
Пример
1.20. Даны результаты 6 независимых
измерений одной и той же величины
прибором, не имеющим систематических
ошибок: 36; 37; 32; 43; 39; 41. Найдите несмещенную
оценку дисперсии ошибок измерений,
если истинная длина неизвестна.
Решение.
Представим исходные данные в виде
таблицы:
|
xi |
32 |
36 |
37 |
39 |
41 |
43 |
|
р |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
Вычислим
последовательно
;
Отсюда
Пример
1.21.
В условиях предыдущей задачи найдите
несмещённую оценку дисперсии ошибок
измерений, если истинная величина
известна и равна 37,8.
Решение
В этом случае в формулу подставляется
не выборочное среднее, а истинная
величина:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Несмещенная оценка выборочной дисперсии
Краткая теория
Пусть из генеральной совокупности в результате
независимых наблюдений над количественным
признаком
извлечена повторная выборка объема
:
При этом
Требуется по данным выборки оценить (приближенно найти) неизвестную
генеральную дисперсию
.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то
эта оценка будет приводить в систематическим ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная
дисперсия является смещенной оценкой
,
другими словами, математическое ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно:
Легко «исправить» выборочную дисперсию так, чтобы ее математическое
ожидание было равно генеральной дисперсии. Достаточно для этого умножить
на дробь
.
Сделав это, получим исправленную дисперсию, которую обычно обозначают через
:
Исправленная дисперсия является, конечно, несмещенной оценкой
генеральной дисперсии. Действительно:
Итак, в качестве оценки генеральной дисперсии принимают
исправленную дисперсию:
Для оценки среднего квадратического
отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню
из исправленной дисперсии:
При достаточно больших значениях
объема выборки выборочная и исправленная
дисперсия отличаются мало. На практике используются исправленной дисперсией,
если примерно
.
Пример решения задачи
Задача
Найти
несмещенную выборочную дисперсию на основании данного распределения выборки.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.
Сумма
частот:
Вычислим
среднюю:
Средняя квадратов:
Несмещенная
выборочная дисперсия:
Ответ:
Кроме этой задачи на другой странице сайта есть
пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда
|
Заблокирован |
|
|
1 |
|
Найти несмещенную оценку дисперсии ошибок измерений03.08.2016, 18:54. Показов 7812. Ответов 1
Даны результаты 5 независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 10, 9, 11, 8, 12. Найти несмещенную оценку дисперсии ошибок измерений, если истинная длина неизвестна. Правильно ли я нашел нужное значение? Несмещенная оценка дисперсии ошибок измерений вычисляется как: Найдем выборочное среднее: Используем формулу для Ответ 2 правильный?
__________________ 0 |
|
1941 / 1050 / 159 Регистрация: 06.12.2012 Сообщений: 4,598 |
|
|
03.08.2016, 19:07 |
2 |
|
1 |
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
Доказательство. Примем без доказательства справедливость следующих равенств:
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
– выборочная оценка дисперсии случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
В статистике , то несмещенная оценка дисперсии переменных возмущений , также называется несмещенной оценкой дисперсии ошибки , является точечной оценкой , что обладает свойством качества , что оценивает неизвестные дисперсии переменных возмущений в непредвзято , если предположениях Гаусса-Markow применяются.
Введение в проблему
Дисперсия ошибки , и остаточная дисперсия , экспериментальные ошибки , Störgrößenvarianz , дисперсия возмущений , необъяснимой дисперсии , необъясненные дисперсии называют , являются дисперсией функции регрессии в популяции и дисперсии условий ошибок или помех. Дисперсия ошибки — это неизвестный параметр, который необходимо оценить на основе информации о выборке. Он измеряет отклонения, которые можно проследить до ошибок измерения или переменных возмущений. Первый очевидный подход заключался бы в оценке дисперсии смешивающих переменных, как обычно, с оценкой максимального правдоподобия (см. Классическую линейную модель нормальной регрессии ). Однако эта оценка проблематична, как будет объяснено ниже.
Ожидаемая оценка дисперсии возмущающих переменных
Простая линейная регрессия
Хотя иногда предполагается, что гомоскедастическая дисперсия в генеральной совокупности известна, следует исходить из того, что она неизвестна в большинстве случаев использования (например, при оценке параметров спроса в экономических моделях или производственных функций ). Поскольку дисперсия переменной возмущения имеет неизвестное значение, численные значения дисперсии параметра наклона и абсолютного члена не могут быть оценены, поскольку формулы зависят от этого. Однако эти количества можно оценить по имеющимся данным. Очевидной оценкой переменных возмущения является невязка , которую представляет выборочная функция регрессии . Таким образом, информация, содержащаяся в остатках, может использоваться для оценки дисперсии возмущающей переменной. Из-за того, что , с частотной точки зрения, « среднее значение » равно . Однако размер не может быть соблюден, так как нельзя наблюдать переменные возмущения. Если вместо текущего используется наблюдаемый аналог , это приводит к следующей оценке дисперсии возмущающей переменной


-
,
где остаточная сумма квадратов. Эта оценка представляет собой выборочное среднее оцененных квадратов остатков и может использоваться для оценки смешанной дисперсии . Можно показать, что приведенное выше определение также соответствует оценке максимального правдоподобия ( ). Однако оценщик не соответствует общим критериям качества для точечных оценщиков и поэтому нечасто используется. Например, оценщик не беспристрастный для . Это связано с тем, что ожидаемое значение дает остаточную сумму квадратов и, следовательно, применяется к ожидаемому значению этого средства оценки . В простой линейной регрессии можно показать в предположениях классической модели единственной линейной регрессии, что несмещенная оценка , т.е. .h оценка, которой удовлетворяет

-
,
при условии, что . Эта несмещенная оценка представляет собой средний квадрат остаточной величины , которую иногда называют остаточной дисперсией . Корень квадратный из этого несмещенной оценки или остаточной дисперсии называется стандартной ошибкой регрессии . Остаточная дисперсия может быть интерпретирована как средняя модель оценки ошибка и формирует основу для всех дальнейших расчетов ( доверительных интервалов , стандартных ошибок в параметрах регрессии, и т.д.). Оно отличается от приведенного выше выражения тем, что остаточная сумма квадратов корректируется числом степеней свободы . Эту настройку можно интуитивно объяснить тем фактом, что одна теряет две степени свободы при оценке двух неизвестных параметров регрессии и .
Как упоминалось выше, несмещенная оценка для простой линейной регрессии дается выражением
-
,
где и являются методом наименьших квадратов для и .
Чтобы показать точность математического ожидания, используется свойство, заключающееся в том, что остатки могут быть представлены как функция переменных возмущения как . Кроме того, используется свойство, заключающееся в том, что дисперсия оценки KQ определяется выражением . Следует также отметить, что ожидаемое значение оценки KQ задается и то же самое относится к . Ожидание можно доказать следующим образом:

-
.
Дисперсии оценок KQ также могут быть оценены с помощью несмещенной оценки . Например, можно оценить , заменив на. Предполагаемая дисперсия параметра наклона тогда определяется выражением
-
.
Множественная линейная регрессия
В множественной линейной регрессии несмещенная оценка дисперсии возмущающих переменных или остаточной дисперсии дается выражением
-
,
в котором оценки по методу наименьших квадратов и -й строки из экспериментальной конструкции матрицы представляет. В качестве альтернативы несмещенная оценка дисперсии переменных возмущения в множественном случае может быть представлена как

-
.
Это представление является результатом того факта, что остаточная сумма квадратов может быть записана как . Другое альтернативное представление остаточной дисперсии является результатом того факта, что остаточная сумма квадратов также может быть представлена с использованием порождающей невязки матрицы как . Это приводит к остаточной дисперсии
Эта оценка, в свою очередь, может использоваться для вычисления ковариационной матрицы вектора оценки KQ . Если теперь заменить на , получается вектор оценки KQ для оцененной ковариационной матрицы.
-
.
Регрессия со стохастическими регрессорами
В случае регрессии со стохастическими регрессорами со стохастической матрицей регрессора , основанная на ожидании оценка дисперсии переменных возмущения также дается выражением
-
.
Верность ожиданиям можно показать с помощью закона повторного математического ожидания.
веб ссылки
- Ursa Pantle: Неожиданная оценка дисперсии σ² переменных возмущения. 2003 г., по состоянию на 10 апреля 2019 г. (конспект лекций Ульмского университета ).
Индивидуальные доказательства
- ↑ Людвиг фон Ауэр : Эконометрика. Введение. Springer, ISBN 978-3-642-40209-8 , с 6 по. u. обновленное издание. 2013.
- ↑ Людвиг фон Ауэр: Эконометрика. Введение. Springer, ISBN 978-3-642-40209-8 , с 6 по. u. обновленное издание. 2013. 191 с.
- ↑ Джордж Джадж, Р. Картер Хилл, В. Гриффитс, Гельмут Люткеполь , Т. С. Ли. Введение в теорию и практику эконометрики. 2-е издание. John Wiley & Sons, Нью-Йорк / Чичестер / Брисбен / Торонто / Сингапур 1988, ISBN 0-471-62414-4 , стр.170 .
- ^ Людвиг Фармейр , Томас Кнейб , Стефан Ланг, Брайан Маркс: Регрессия: модели, методы и приложения. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2 , стр.109.
- ^ Людвиг Фармейр, Томас Кнейб, Стефан Ланг, Брайан Маркс: Регрессия: модели, методы и приложения. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2 , стр.109.
- ^ Карл Мослер и Фридрих Шмид: расчет вероятности и окончательная статистика. Springer-Verlag, 2011, с. 308.
- ↑ Джеффри Марк Вулдридж: Вводная эконометрика: современный подход. 5-е издание. Нельсон Образование 2015
- ↑ Джеффри Марк Вулдридж : Вводная эконометрика: современный подход. 4-е издание. Nelson Education, 2015, стр. 55.
- ↑ Джеффри Марк Вулдридж: Вводная эконометрика: современный подход. 4-е издание. Nelson Education, 2015, стр. 55.

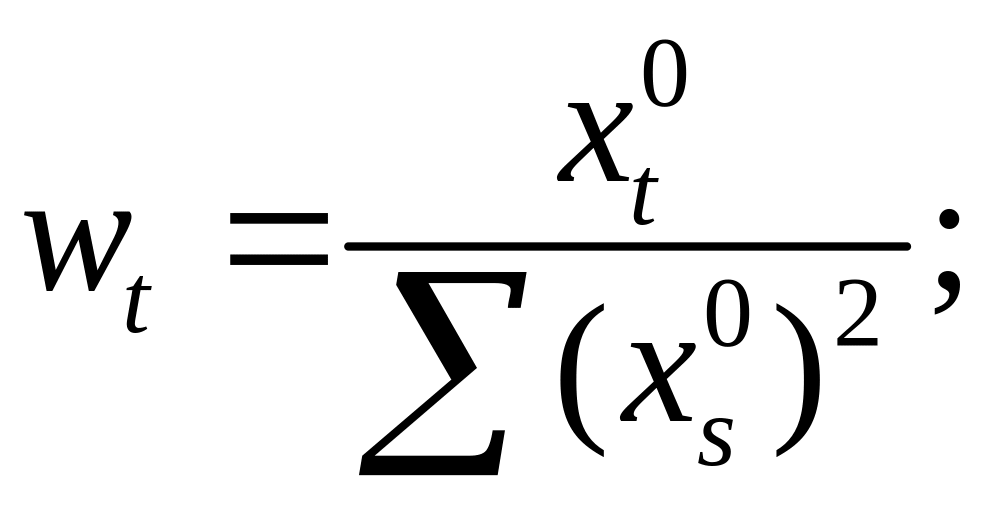
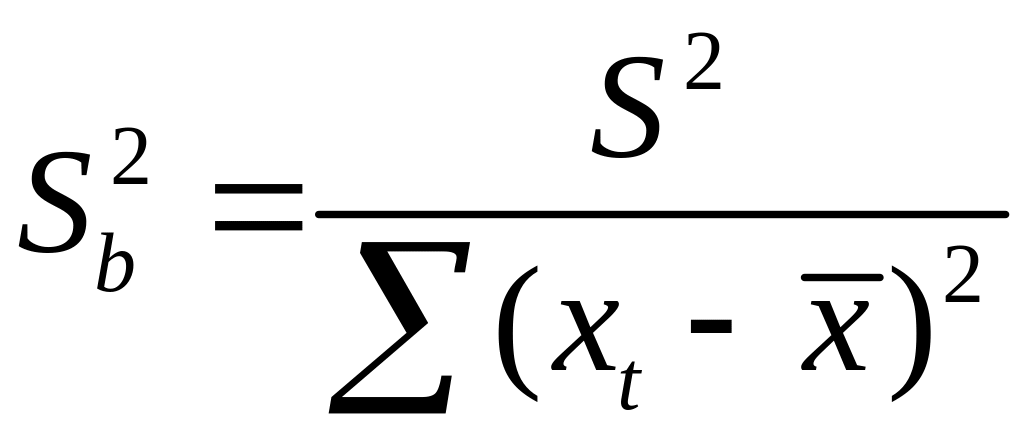
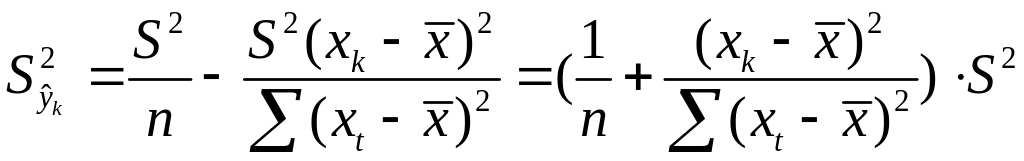
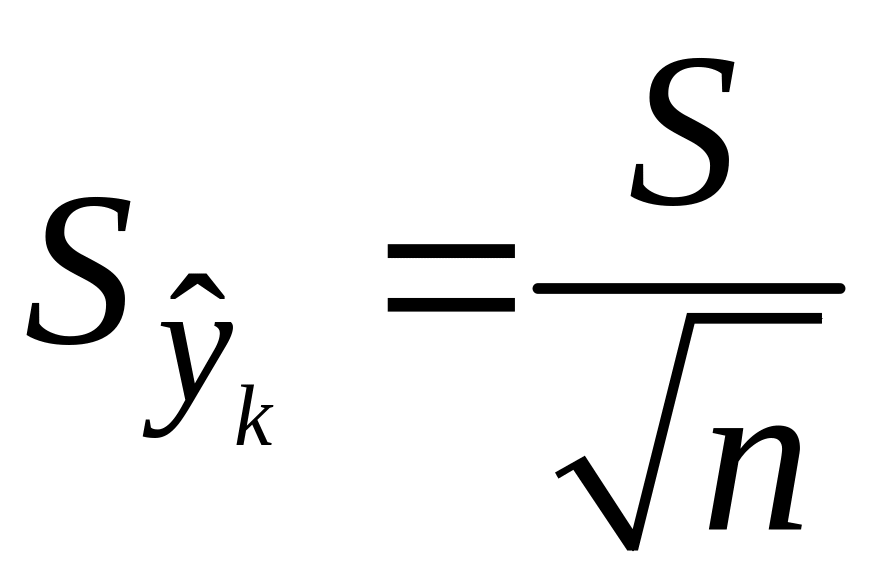
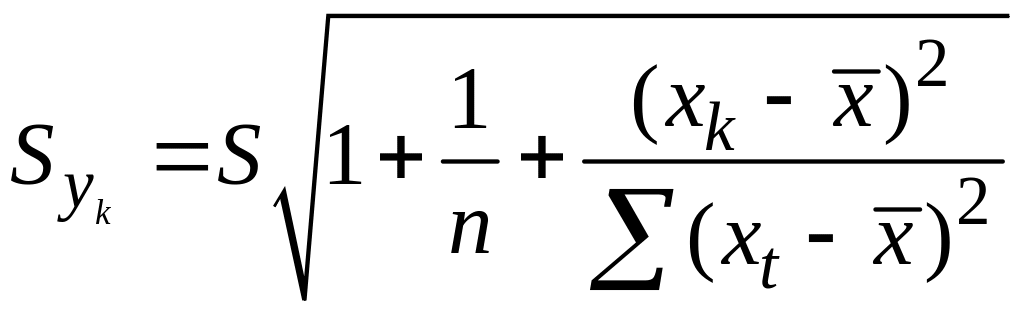
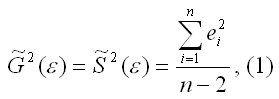
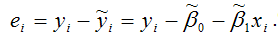
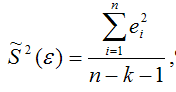
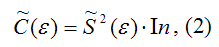
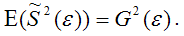
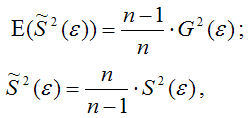
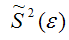
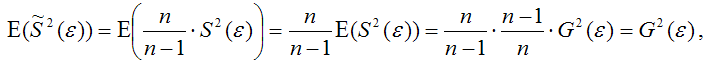
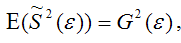
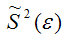
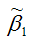
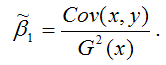
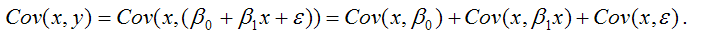
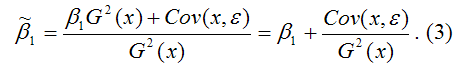
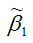
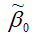
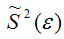






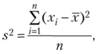
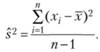
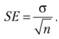
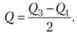
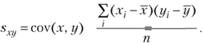
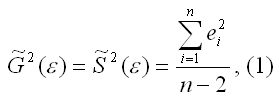




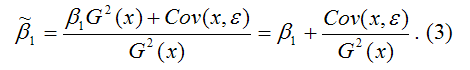
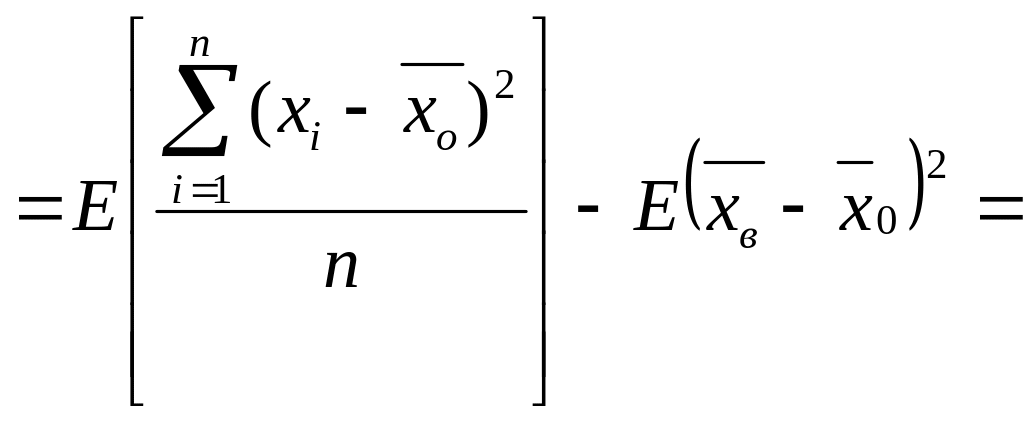
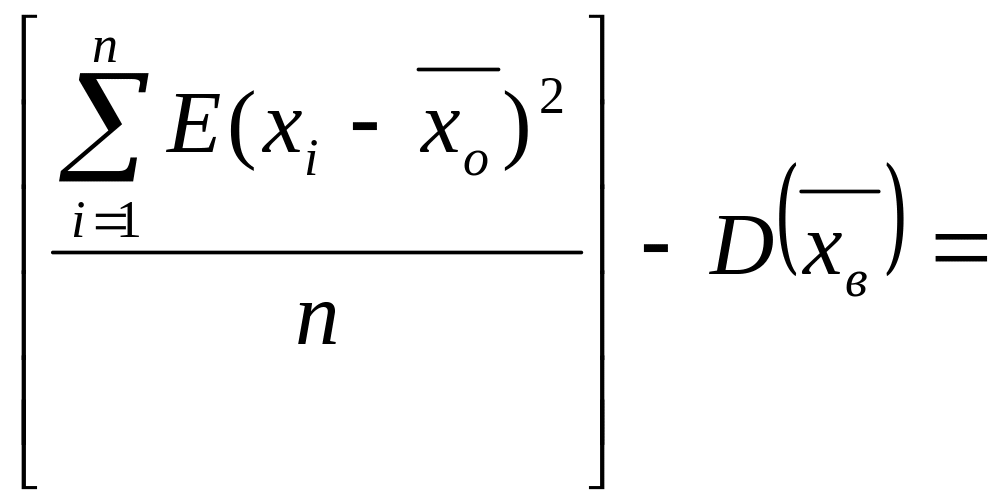
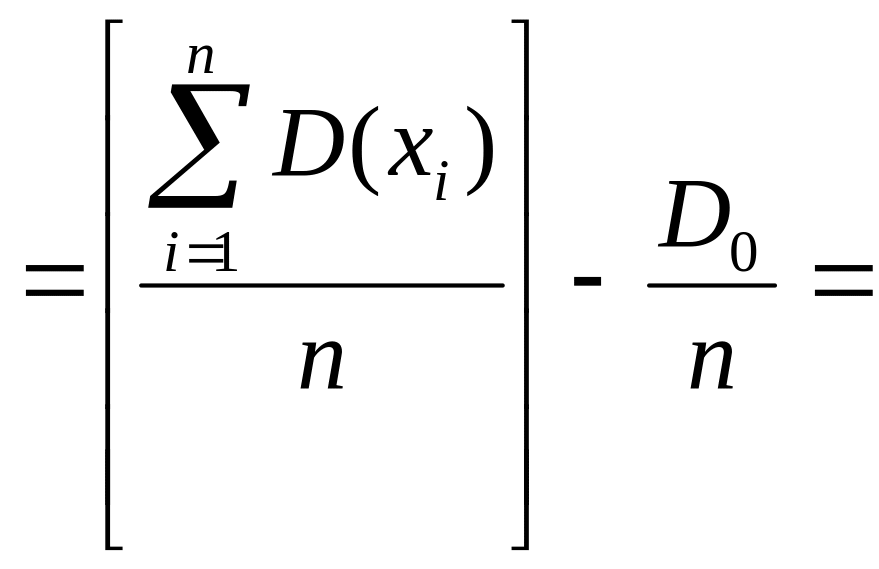
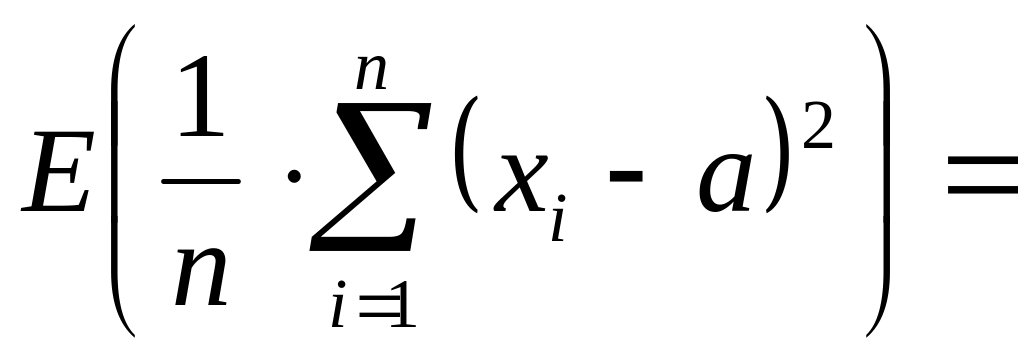
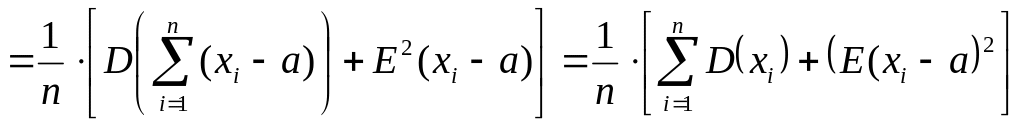
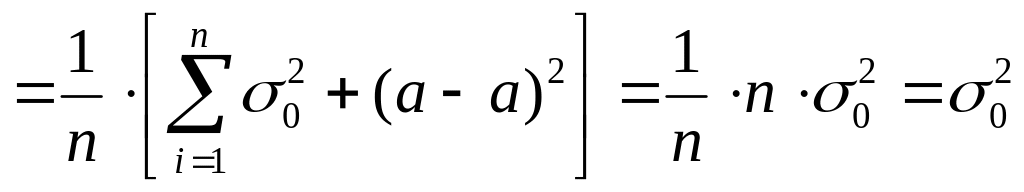
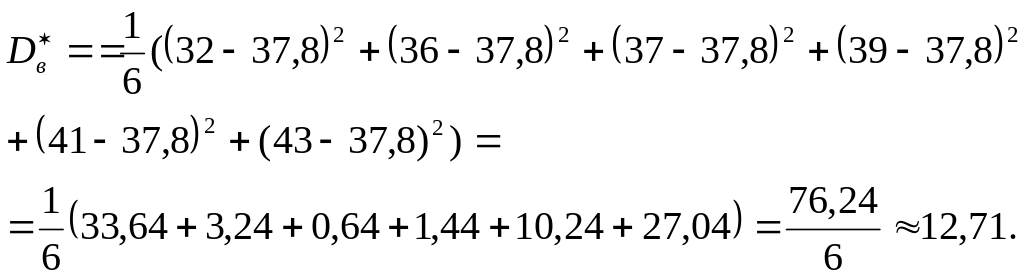
![{ displaystyle sigma ^ {2} = operatorname {E} [( varepsilon _ {i} - operatorname {E} ( varepsilon _ {i})) ^ {2}] quad, i = 1 ldots n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3d3236d5188541aa9126704580731209a9266cc)




































