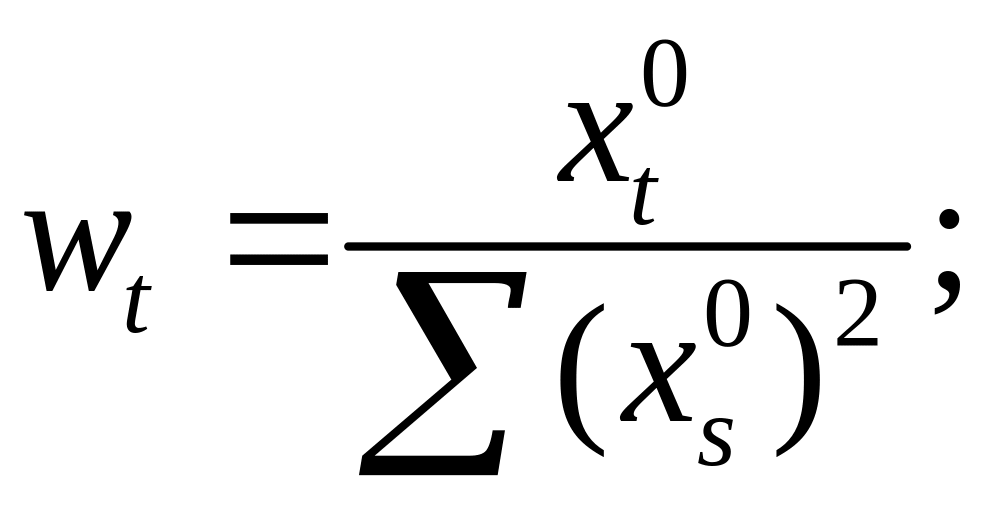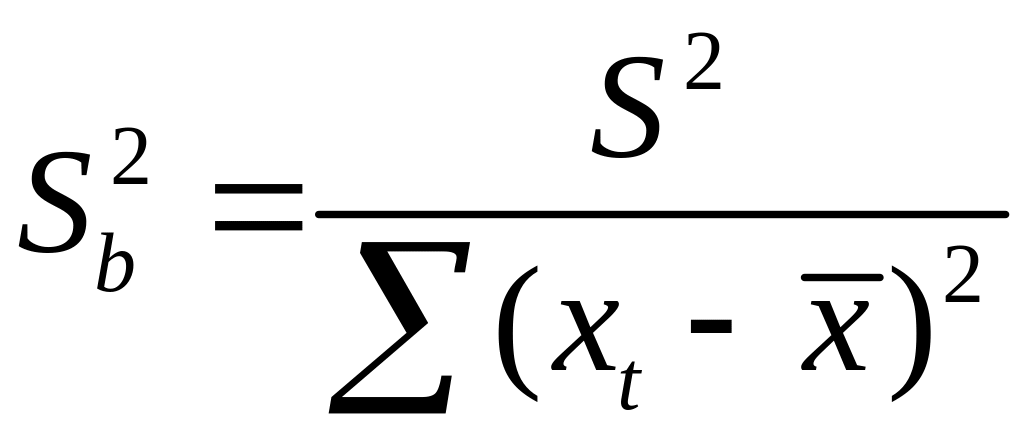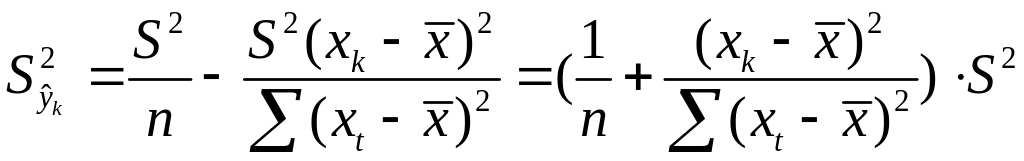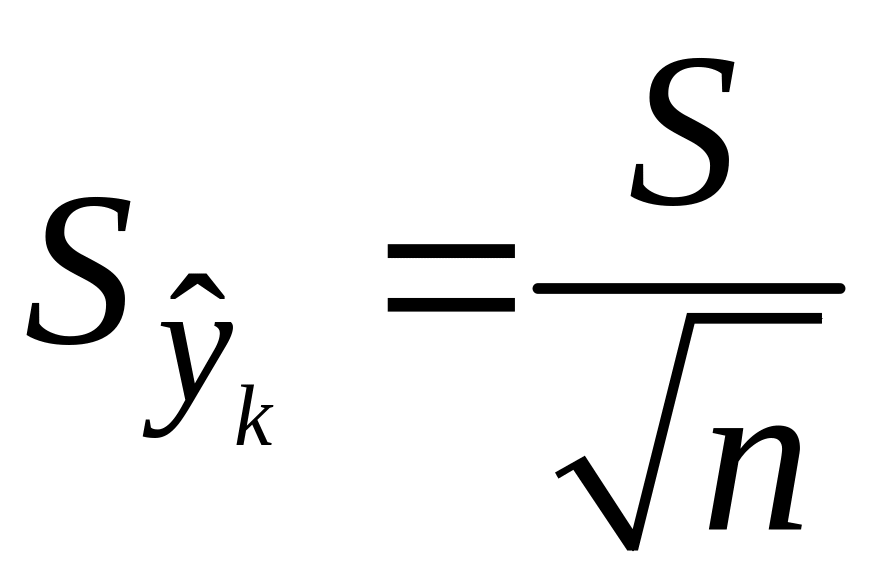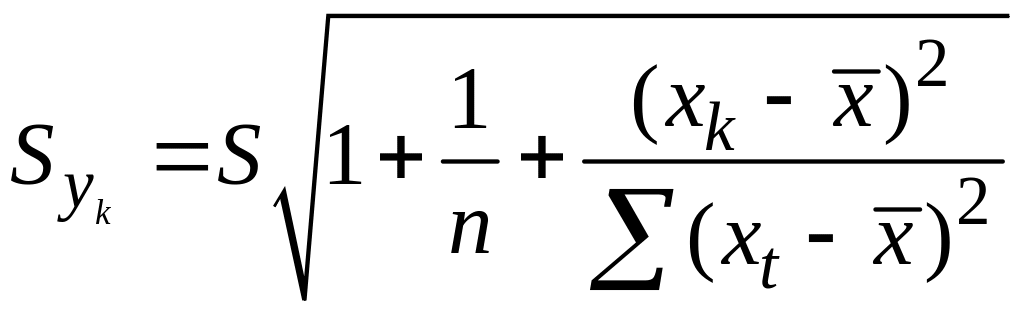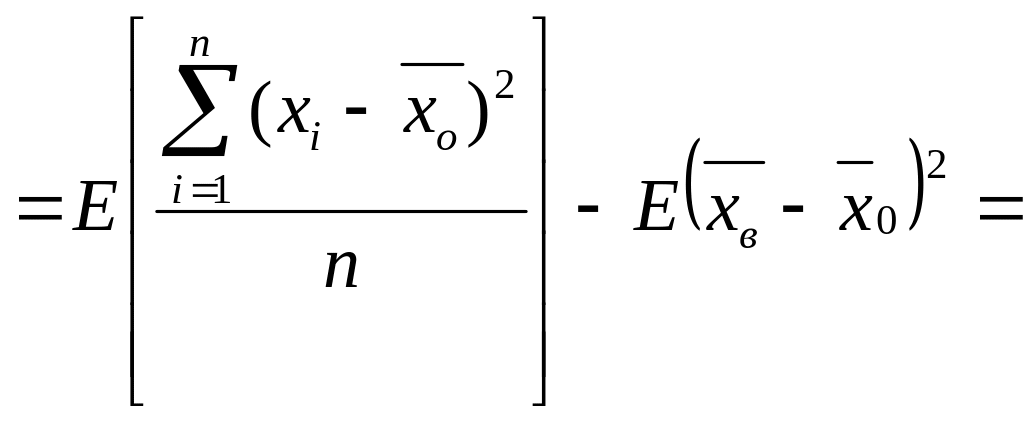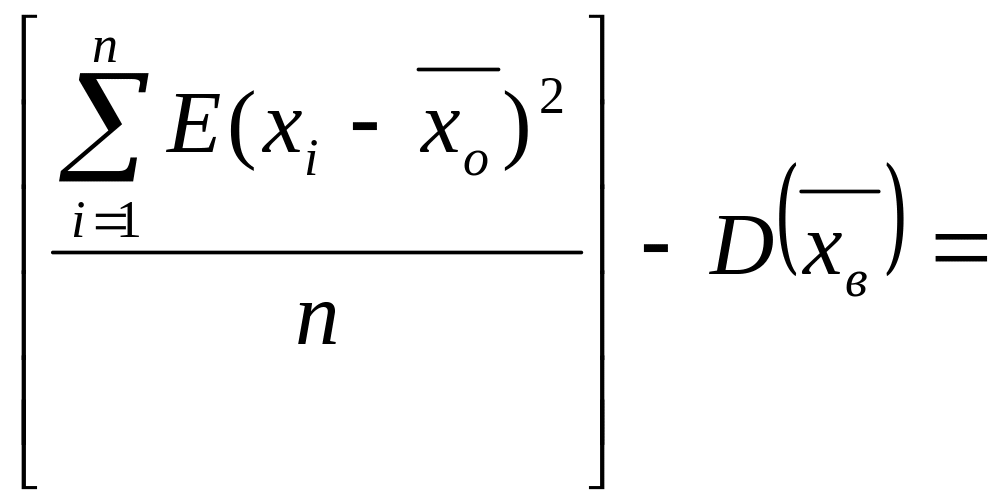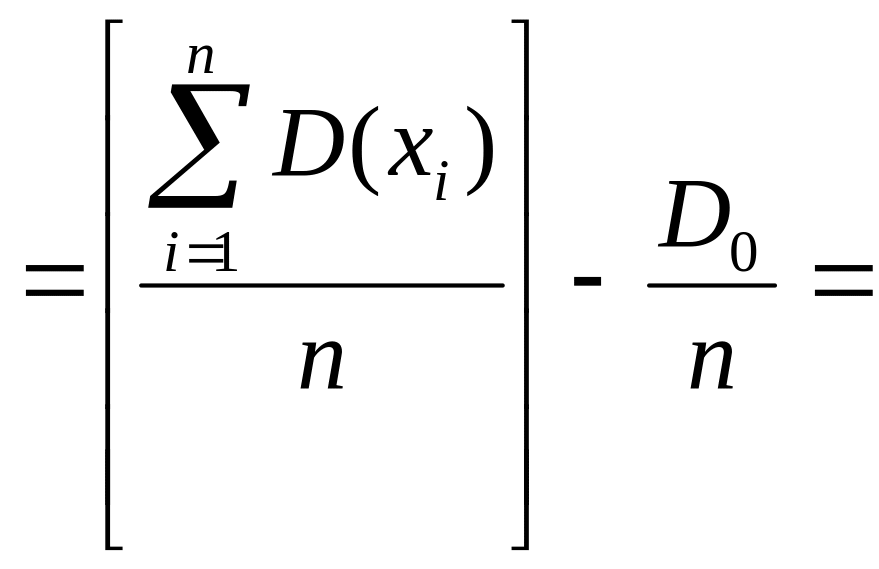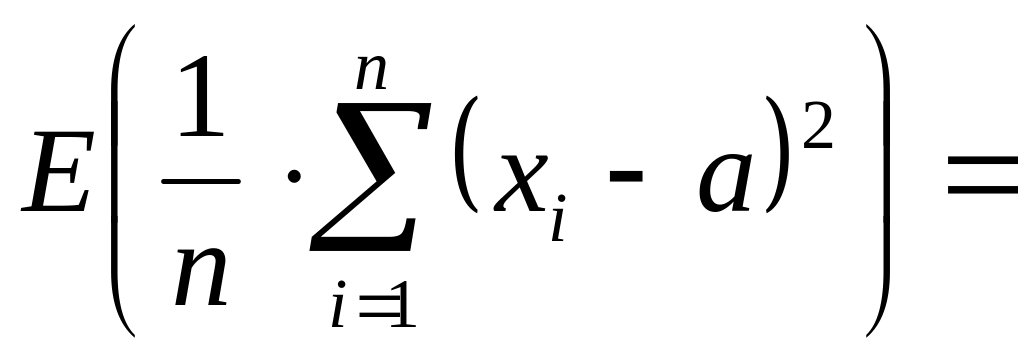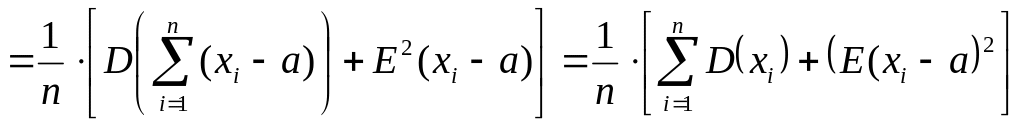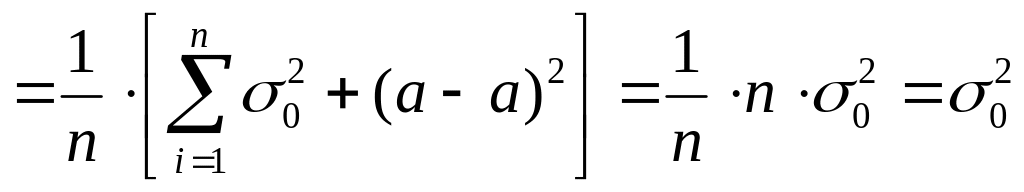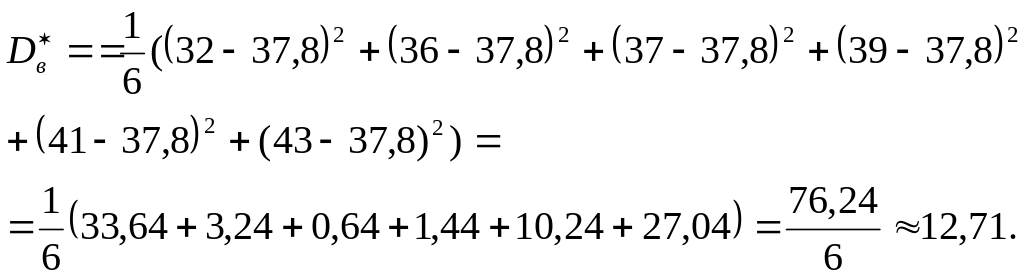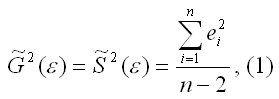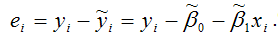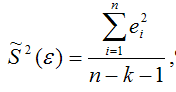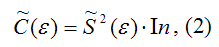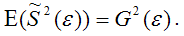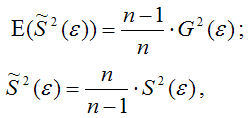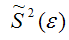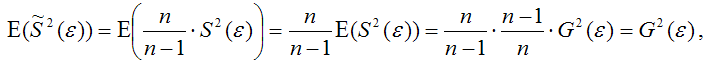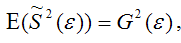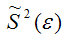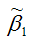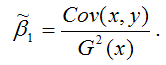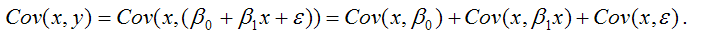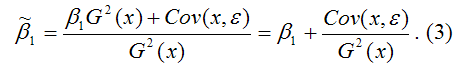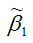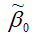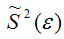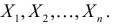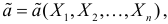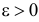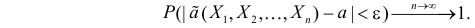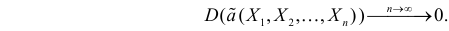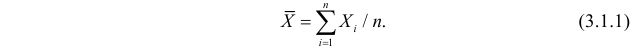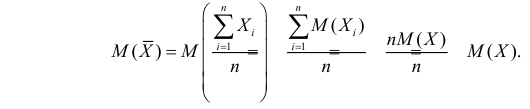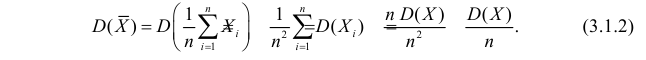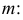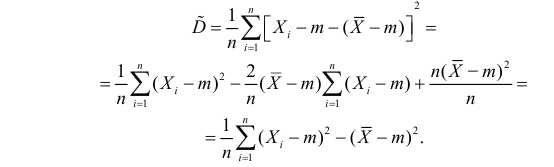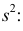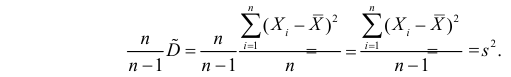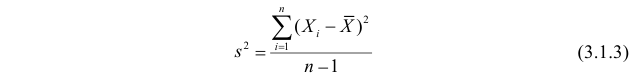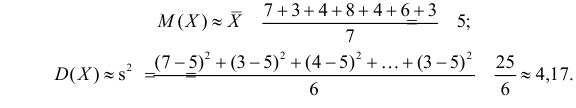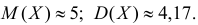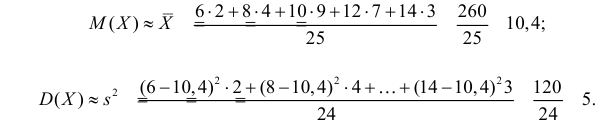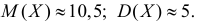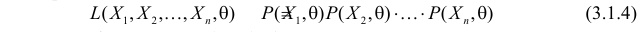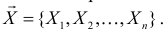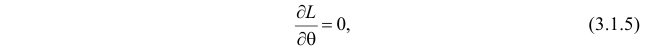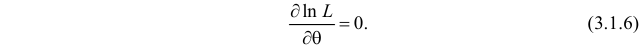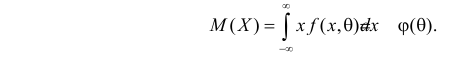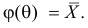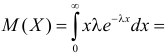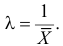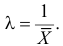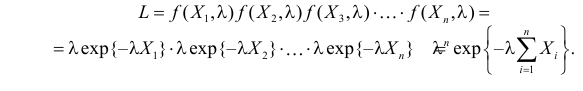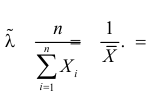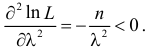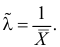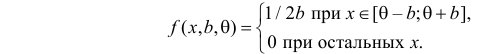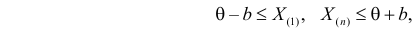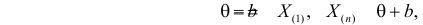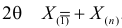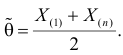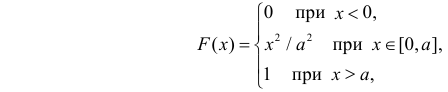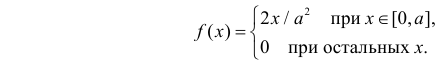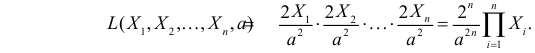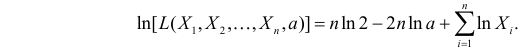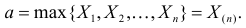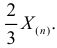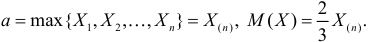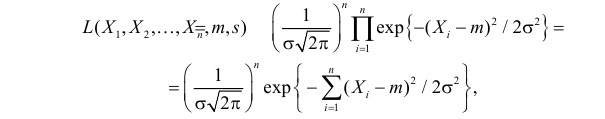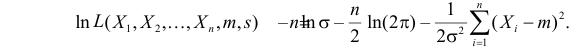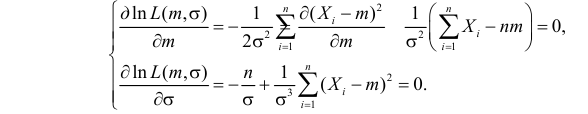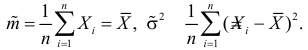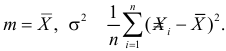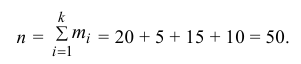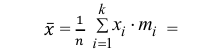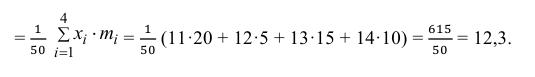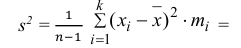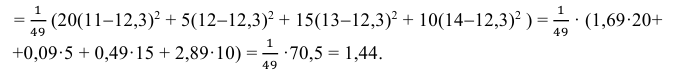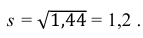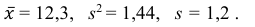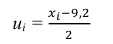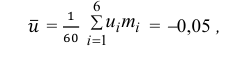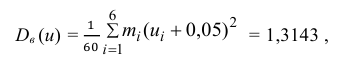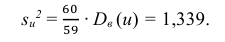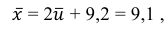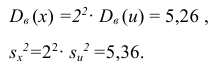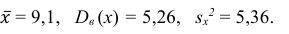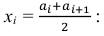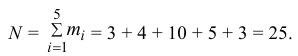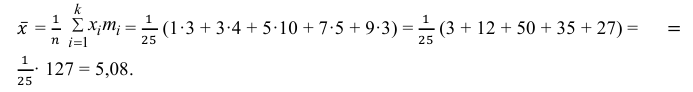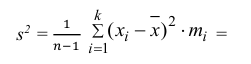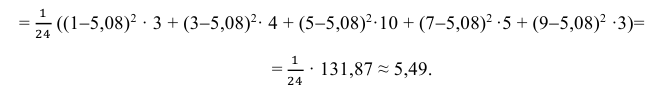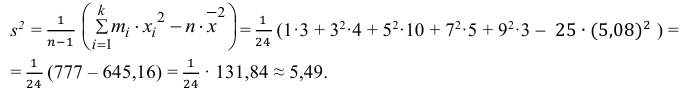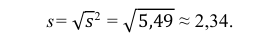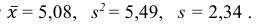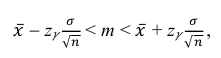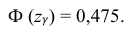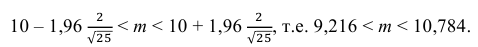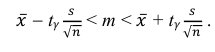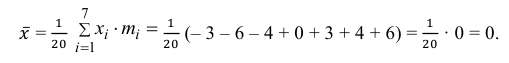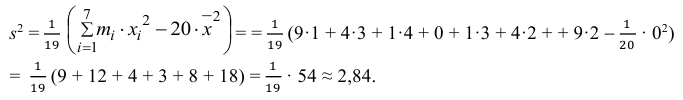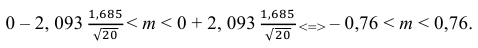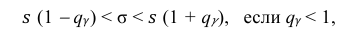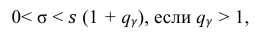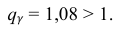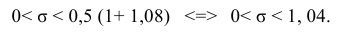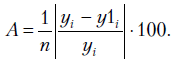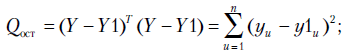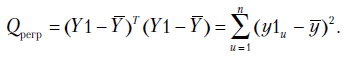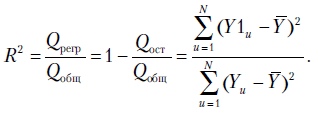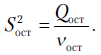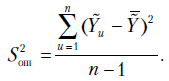Оценка дисперсии ошибок наблюдений - Oshibku.top - решение и исправление самых разных ошибок

,

—
уравнение регрессии,

—
случайная ошибка (с ограничениями).

;

;

—
остатки регрессии. Надо различать
остатки и
ошибки регрессии.
Остатки в отличии от ошибок наблюдаемы.

Предположим,
что оценка σ²
связана с
суммой квадратов остатков регрессии

Вычислим:

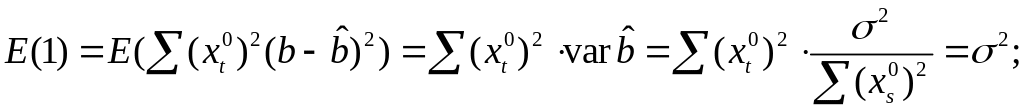
Используя,

получим

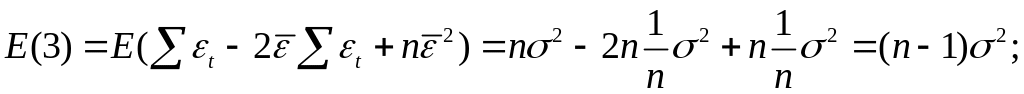
где

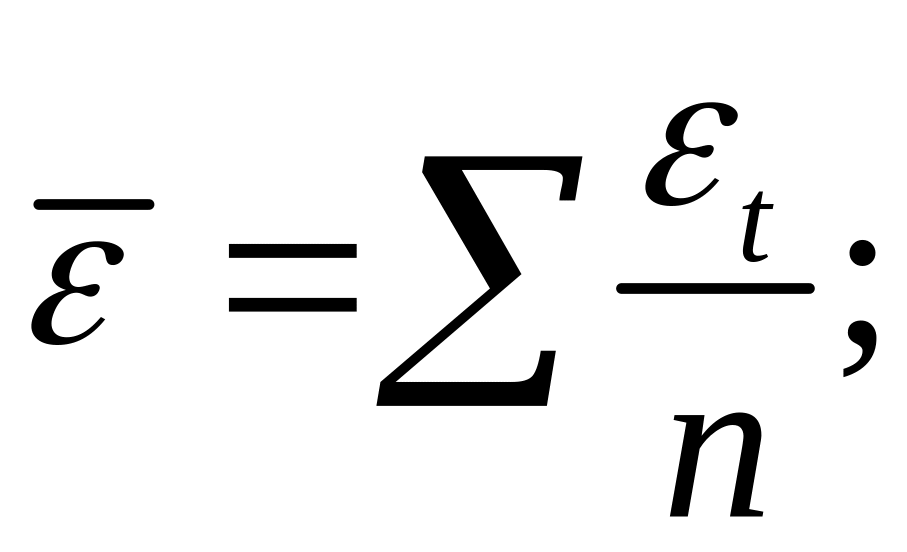
Таким образом

откуда следует,
что

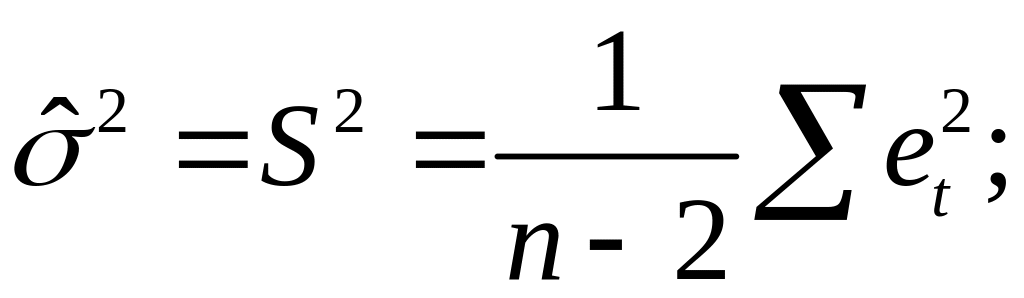
является
несмещенной оценкой дисперсии ошибок
σ².

12. Оценка существенности параметров линейной регрессии и корреляции

Существенность
коэф-ов регрессии определяет можно ли
его заменить нулем. Если данный коэф-т
несуществ., то его можно заменить нулем.

При выполнении
дополнительного условия о совместном
нормальном распределении ошибок,
стандартная ошибка коэффициента
регрессии параметра S_b
рассчитывается
по формуле

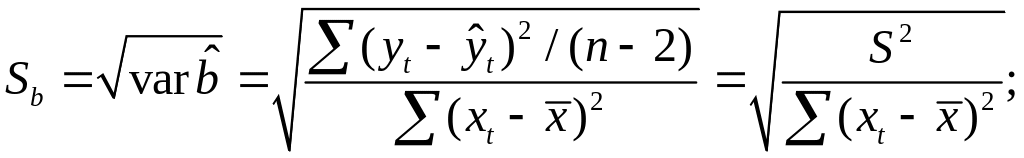
где S²
— остаточная
дисперсия на одну степень свободы.

Отношение коэф-та
регрессии к его стандартной ошибке дает
t-статистику,
кот. подчиняется статистике Стьюдента
при (n-2)
степенях свободы.
Эта статистика применяется для проверки
стат. значимости коэф-та
регрессии.

Для оценки значимости
коэф-та регрессии опр-ют фактическое
знач. t-критерия
Стьюдента: t_b=b/S_b
, которое
затем сравнивают с табличным значением
при определенном уровне значимости
и числе степеней
свободы (n-2).
Если t_b>t_кр,
коэф-т b значим и
его нельзя заменить 0.

Доверительный
интервал для коэф-та регрессии опр-ся
как

.

Замечание: Т.к.
коэф-т регрессии b для эк. Исследований
имеет четкую интерпритацию доверит.
Интервалы не должны содержать
противоречивыхрезультатов, напр., от
«-10» до 20 , т.е. положит. и отрицат.

Значимость линейного
коэффициента корреляции r
проверяется на основе величины ошибки
коэффициента корреляции S_r=m_r(заменить):

О
тсюда
фактическое значение

Данная формула
свидетельствует, что в парной лин.
регрессииt_r²=F
=>t_r²=
t_b²
.

Таким образом,
проверка гипотез о значимости коэффициентов
регрессии и корреляции равносильна
проверке гипотезы о значимости линейного
уравнения регрессии.

13. Интервалы прогноза по линейному уравнению регрессии

Основное назначение
ур-ия регрессии — прогноз возможных
знач. результата при заданном значении
фактора.

Этот прогноз
осущ-ся путем подстановки знач. фактора
х=х_k
в ур-ние
регрессии

.
Но данный
точечный прогноз не всегда реален. Он
должен дополняться интервальной
оценкой прогноза значения результата
y*.
Т.е.

,
где

—
стандартная ошибка оценки

.

Получим данную
оценку для лин. регрессии

.
Подставим это
выражение в ур-ие

.
Отсюда следует,
что стандартная ошибка

зависит от
ошибки

и ошибки
коэффициента b,
т.е.

.

В курсе мат. стат.
получено:

=S²/n,где
S²
– оценка дисперсии рез-ого признака.

;Получим

Откуд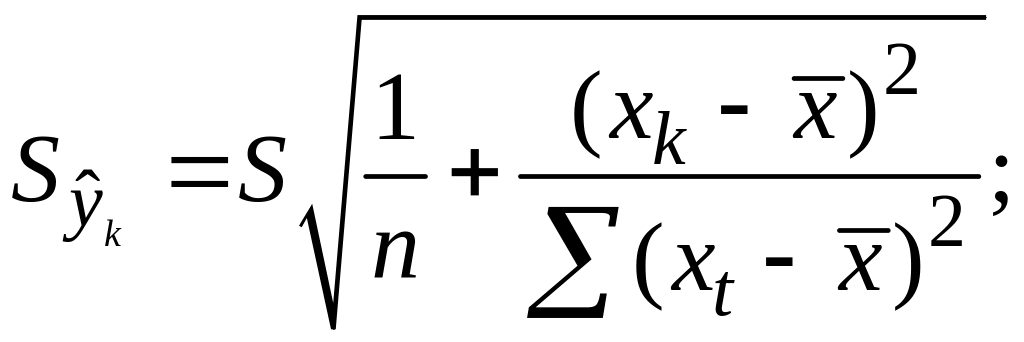

Где t=1,…n
– номера измерений, x_k
не обязано совпадать с одним из x_t_.

Видно, что величина
стандартной ошибки x_k
зависит от

.
Она достигает
мин. при x_к=

и возрастает
по мере того, как «удаляется» от

в любом
направлении.

Т.е.

.

Можно строить
интервальные оценки рез-ого признака
при заданном x_к

,которые
определяются как

,
где

—
критическое значение распределения
Стьюдента, при (n-2) степенями свободы.

На графике
доверительные границы для

представляют собой гиперболы,
расположенные по обе стороны от линии
регрессии.

Фактические знач.
y_k
варьируют
около ср. знач.

на величину случ. ошибки ε, дисперсия
кот. оценивается как S², поэтому
ошибка предсказываемого индивид-ого
значения y
должно включать как станд.ошибку

так и случ.ошибку S.

Средняя ошибка
прогнозного индив.значения составит

.
На основе этой оценки м.также строить
интервальные оценки, кот. б. содержать
заданные доверительной вероятностью,
измеряемые значения рез-ого признака.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пусть

Поскольку
заменяются две величины (

и

),
то это вызывает смещение оценки

:

. (1.22)

Покажем
это .

Известно
что

Пусть
Х₁,
Х₂,…,
Х_i
,…,X_n
— независимые случайные величины, каждая
из которых имеет один и тот же закон
распределения с числовыми характеристиками:

и D(X_i)=D₀.
Пусть

подставим в (*), тогда:

Найдем
E[D_в]:

Итак

Что и требовалось доказать.

При
больших п
смещение невелико, им можно пренебречь,
но при малых выборках оно существенно.

Таким
образм,

есть несмещенная оценка дисперсии или

.
(1.23)

Тогда
исправленное среднее квадратическое
отклонение имеет вид:

.
(1.24)

Для
интервальной оценки используется
выражение

,
где

находится по формуле (1.24).

Замечание.
Однако для больших выборок можно считать,
что

.
В случае малых выборок (п
< 30) пользуются исправленной дисперсией
по формуле (1.24).

По
закону больших чисел

является состоятельной оценкой для

генеральной дисперсии. А так как множитель

при

,
то

также является состоятельной оценкой
для

.
Оценка

,
строго говоря, не является эффективной
оценкой для

,
однако при наличии нормального
распределения ее можно считать приближенно
эффективной.

Замечание.
Если известно точное значение
математического ожидания «
»
для n
измерений, то E(X_i)
=

где х_i
– отдельные измерения. Исправленная
(несмещённая) дисперсия находится по
формуле

(1.25)

Действительно.

,
т.е. E(D^*_в)
= D₀
.

Пример
1.19. В ящике содержатся стержни трех
размеров (N
= 3): 12 см, 14 см и 16 см с соответствующими
долями 0,1; 0,3; 0,6. Производится повторная
выборка двух стержней (n
= 2). Найти
все возможные выборочные распределения
и построить законы распределения для

и

.
Проверить на данном примере справедливость
равенств

.

Решение.
Определим
количество возможных выборок:

Закон
распределения генеральной совокупности
представлен в следующей в таблице

X	12	14	16
P	0,1	0,3	0,6

Вычислим
генеральные характеристики :

Все
выборочные законы представлены в
следующей таблице.

№ выборки	1	2	3	4	5	6	7	8	9
	12 12	12 14	12 16	14 12	14 14	14 16	16 12	16 14	16 16
	2	1 1	1 1	1 1	2	1 1	1 1	1 1	2
	12	13	14	13	14	15	14	15	16
	0	1	4	1	0	1	4	1	0
	0,01	0,03	0,06	0,03	0,09	0,18	0,06	0,18	0,36

Проверим,
что

.

По
данным последней таблицы получим строим
законы распределения для

и D_в
и находим соответствующие характеристики.

	12	13	14	15	16
P	0,01	0,06	0,21	0,36	0,36	1

	0	1	4
	0,46	0,42	0,12	1

E[D_в]=0,42+0,48=0.9/

Итак,

Откуда
следует:

при n
= 2.

Пример
1.20. Даны результаты 6 независимых
измерений одной и той же величины
прибором, не имеющим систематических
ошибок: 36; 37; 32; 43; 39; 41. Найдите несмещенную
оценку дисперсии ошибок измерений,
если истинная длина неизвестна.

Решение.
Представим исходные данные в виде
таблицы:

x_i	32	36	37	39	41	43
р	1/6	1/6	1/6	1/6	1/6	1/6

Вычислим
последовательно

;

Отсюда

Пример
1.21.
В условиях предыдущей задачи найдите
несмещённую оценку дисперсии ошибок
измерений, если истинная величина
известна и равна 37,8.

Решение
В этом случае в формулу подставляется
не выборочное среднее, а истинная
величина:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

15. Оценка дисперсии случайной ошибки модели регрессии

При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.

Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:

где n – это объём выборочной совокупности;

еi– остатки регрессионной модели:

Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:

где k – число оцениваемых параметров модели регрессии.

Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:

где In – единичная матрица.

Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.

Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства

Доказательство. Примем без доказательства справедливость следующих равенств:

где G2(?) – генеральная дисперсия случайной ошибки;

S2(?) – выборочная дисперсия случайной ошибки;

– выборочная оценка дисперсии случайной ошибки.

Тогда:

т. е.

что и требовалось доказать.

Следовательно, выборочная оценка дисперсии случайной ошибки

является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).

При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.

Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки

от величины случайной ошибки ?.

МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:

В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:

Для дальнейших преобразования используются свойства ковариации:

1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;

2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).

Исходя из указанных свойств ковариации, справедливы следующие равенства:

Cov(x,?0)=0 (?0=const);

Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).

Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:

Cov(x,y)= ?1G2(x)+Cov(x,?).

В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:

Таким образом, МНК-оценка

может быть представлена как сумма двух компонент:

1) константы ?1, т. е. истинного значения коэффициента;

2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.

Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.

Аналогично доказывается, что МНК-оценка

коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки

могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.

Данный текст является ознакомительным фрагментом.

Читайте также

11. Критерии оценки неизвестных коэффициентов модели регрессии

11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные

14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии

14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии

18. Характеристика качества модели регрессии

18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии

22. Проверка гипотезы о значимости коэффициентов модели парной регрессии

22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки

25. Точечный и интервальный прогнозы для модели парной регрессии

25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных

32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации

32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для

35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом

35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости

39. Модели регрессии, нелинейные по факторным переменным

39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных

40. Модели регрессии, нелинейные по оцениваемым коэффициентам

40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по

41. Модели регрессии с точками разрыва

41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)

44. Методы нелинейного оценивания коэффициентов модели регрессии

44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида

Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических

46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии

46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все

57. Гетероскедастичность остатков модели регрессии

57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается

60. Устранение гетероскедастичности остатков модели регрессии

60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии

63. Устранение автокорреляции остатков модели регрессии

63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков

67. Модели регрессии с переменной структурой. Фиктивные переменные

67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую

Содержание:

Точечные оценки:

Пусть случайная величина имеет неизвестную характеристику а. Такой характеристикой может быть, например, закон распределения, математическое ожидание, дисперсия, параметр закона распределения, вероятность определенного значения случайной величины и т.д. Пронаблюдаем случайную величину n раз и получим выборку из ее возможных значений

Существует два подхода к решению этой задачи. Можно по результатам наблюдений вычислить приближенное значение характеристики, а можно указать целый интервал ее значений, согласующихся с опытными данными. В первом случае говорят о точечной оценке, во втором – об интервальной.

Определение. Функция результатов наблюдений

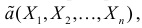
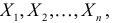
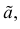
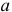
Для одной и той же характеристики можно предложить разные точечные оценки. Необходимо иметь критерии сравнения оценок, для суждения об их качестве. Оценка как функция случайных результатов наблюдений сама является случайной величиной. Значения найденные по разным сериям наблюдений, могут отличаться от истинного значения характеристики в ту или другую сторону. Естественно потребовать, чтобы оценка систематически не завышала и не занижала оцениваемое значение, а с ростом числа наблюдений становилась более точной. Формализация названных требований приводит к следующим понятиям.

Определение. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине: 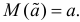В противном случае оценку называют смещенной.

Определение. Оценка называется состоятельной, если при увеличении числа наблюдений она сходится по вероятности к оцениваемой величине, т.е. для любого сколь угодно малого

Если известно, что оценка 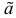несмещенная, то для ее состоятельности достаточно, чтобы

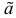
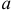
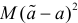
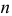
Последнее условие удобно для проверки. В качестве меры разброса значений оценки относительно можно рассматривать величину Из двух оценок предпочтительней та, для которой эта величина меньше. Если оценка имеет наименьшую меру разброса среди всех оценок характеристики, построенных по наблюдениям, то оценку называют эффективной.

Следует отметить, что несмещенность и состоятельность являются желательными свойствами оценок, но не всегда разумно требовать наличия этих свойств у оценки. Например, может оказаться предпочтительней оценка хотя и обладающая небольшим смещением, но имеющая значительно меньший разброс значений, нежели несмещенная оценка. Более того, есть характеристики, для которых нет одновременно несмещенных и состоятельных оценок.

Оценки для математического ожидания и дисперсии

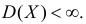
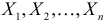
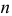
Пусть случайная величина имеет неизвестные математическое ожидание и дисперсию, причем Если – результаты независимых наблюдений случайной величины, то в качестве оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений

Несмещенность такой оценки следует из равенств

В силу независимости наблюдений

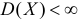
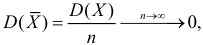
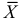
При условии имеем что означает состоятельность оценки .

Доказано, что для математического ожидания нормально распределенной случайной величины оценка 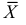еще и эффективна.

Оценка математического ожидания посредством среднего арифметического наблюдаемых значений наводит на мысль предложить в качестве оценки для дисперсии величину

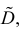
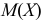
Преобразуем величину обозначая для краткости через

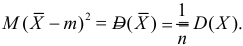
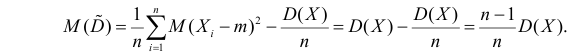
В силу (3.1.2) имеем Поэтому

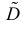
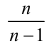
Последняя запись означает, что оценка имеет смещение. Она систематически занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку в виде множителя и полученную оценку обозначим через

Величина

является несмещенной и состоятельной оценкой дисперсии.

Пример:

Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.

Решение. По формулам (3.1.1) и (3.1.3) имеем

Ответ.

Пример:

Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде:

Требуется оценить математическое ожидание и дисперсию этой случайной величины.

Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы (3.1.1) и (3.1.3) дают следующие оценки:

Ответ.

Метод наибольшего правдоподобия для оценки параметров распределений

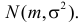
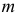
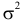
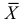
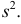
В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон распределения Его параметры и имеют смысл математического ожидания и дисперсии соответственно. Их можно оценить с помощью и В общем случае параметры законов распределения не всегда напрямую связаны со значениями числовых 179 характеристик. Поэтому практический интерес представляет следующая задача.

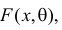
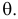
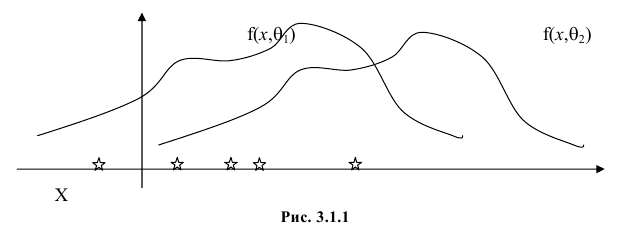
Пусть случайная величина Х имеет функцию распределения причем тип функции распределения F известен, но неизвестно значение параметра По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.

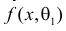
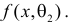
Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций плотности вероятности или

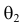
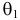
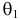
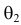
Из рисунка видно, что при значении параметра такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же эти результаты наблюдений вполне возможны. Поэтому значение параметра более правдоподобно, чем значение . Такая аргументация позволяет сформулировать принцип наибольшего правдоподобия: в качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.

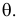
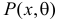
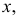
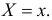
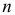
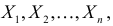
Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величины Х зависит от неизвестного значения параметра Обозначим через для непрерывной случайной величины плотность вероятности в точке а для дискретной случайной величины – вероятность того, что Если в независимых наблюдениях реализовались значения случайной величины то выражение

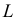
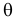
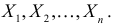
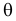
называют функцией правдоподобия. Величина зависит только от параметра при фиксированных результатах наблюдений При каждом значении параметра функция равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе наблюдений. Для непрерывной случайной величины равна плотности вероятности в точке выборочного пространства

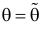
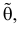
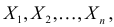
Сформулированный принцип предлагает в качестве оценки значения параметра выбрать такое при котором принимает наибольшее значение. Величина будучи функцией от результатов наблюдений называется оценкой наибольшего правдоподобия.

Во многих случаях, когда дифференцируема, оценка наибольшего правдоподобия находится как решение уравнения

которое следует из необходимого условия экстремума. Поскольку достигает максимума при том же значении , что и , то можно решать относительно эквивалентное уравнение

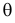
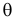
Это уравнение называют уравнением правдоподобия. Им пользоваться удобнее, чем уравнением (3.1.5), так как функция равна произведению, а – сумме, а дифференцировать проще.

Если параметров несколько (многомерный параметр), то следует взять частные производные от функции правдоподобия по всем параметрам, приравнять частные производные нулю и решить полученную систему уравнений.

Оценку, получаемую в результате поиска максимума функции правдоподобия, называют еще оценкой максимального правдоподобия.

Известно, что оценки максимального правдоподобия состоятельны. Кроме того, если для q существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой. Оценка максимального правдоподобия может оказаться смещенной.

Метод моментов

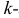
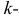
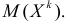
Начальным моментом го порядка случайной величины Х называется математическое ожидание й степени этой величины, т.е. Само математическое ожидание считается начальным моментом первого порядка.

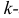
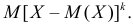
Центральным моментом го порядка называется Очевидно, что дисперсия – это центральный момент второго порядка. Если закон распределения случайной величины зависит от некоторых параметров, то от этих параметров зависят и моменты случайной величины.

Для оценки параметров распределения по методу моментов находят на основе опытных данных оценки моментов в количестве, равном числу оцениваемых параметров. Эти оценки приравнивают к соответствующим теоретическим моментам, величины которых выражены через параметры. Из полученной системы уравнений можно определить искомые оценки.

Например, если Х имеет плотность распределения 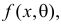то

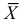
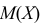
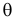
Если воспользоваться величиной как оценкой для на основе опытных данных, то оценкой по методу моментов будет решение уравнения

Пример:

Найти оценку параметра показательного закона распределения по методу моментов.

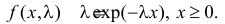
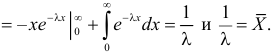
Решение. Плотность вероятности показательного закона распределения имеет вид Поэтому Откуда

Ответ.

Пример:

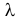
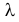
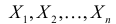
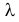
Пусть имеется простейший поток событий неизвестной интенсивности . Для оценки параметра проведено наблюдение потока и зарегистрированы – длительности последовательных интервалов времени между моментами наступления событий. Найти оценку для .

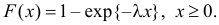
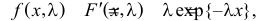
Решение. В простейшем потоке интервалы времени между последовательными моментами наступления событий потока имеют показательный закон распределения Так как плотность вероятности показательного закона распределения равна то функция правдоподобия (3.1.4) имеет вид

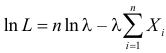
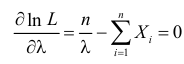
Тогда и уравнение правдоподобия имеет решение

При таком значении 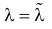функция правдоподобия действительно достигает наибольшего значения, так как

Ответ.

Определение. Пусть 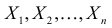– результаты n независимых наблюдений случайной величины X. Если расставить эти результаты в порядке возрастания, то получится последовательность значений, которую называют вариационным рядом и обозначают:

В этой записи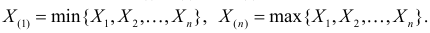

Величины 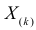называют порядковыми статистиками.

Пример:

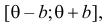
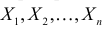
Случайная величина Х имеет равномерное распределение на отрезке где и неизвестны. Пусть – результаты независимых наблюдений. Найти оценку параметра .

Решение. Функция плотности вероятности величины Х имеет вид

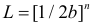
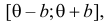
В этом случае функция правдоподобия от явно не зависит. Дифференцировать по такую функцию нельзя и нет возможности записать уравнение правдоподобия. Однако легко видеть, что возрастает при уменьшении . Все результаты наблюдений лежат в поэтому можно записать:

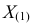
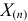
где – наименьший, а – наибольший из результатов наблюдений. При минимально возможном

откуда 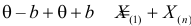или

Оценкой наибольшего правдоподобия для параметра будет величина

Ответ.

Пример:

Случайная величина X имеет функцию распределения

где 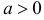неизвестный параметр.

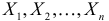
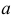
Пусть – результаты независимых наблюдений случайной величины X. Требуется найти оценку наибольшего правдоподобия для параметра и найти оценку для M(X).

Решение. Для построения функции правдоподобия найдем сначала функцию плотности вероятности

Тогда функция правдоподобия:

Логарифмическая функция правдоподобия:

Уравнение правдоподобия

не имеет решений. Критических точек нет. Наибольшее и наименьшее значения находятся на границе допустимых значений .

По виду функции можно заключить, что значение тем больше, чем меньше величина . Но не может быть меньше Поэтому наиболее правдоподобное значение

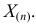
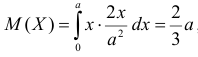
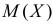
Так как , то оценкой наибольшего правдоподобия для будет величина
Ответ.

Пример:

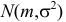
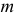
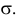
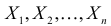
Случайная величина Х имеет нормальный закон распределения c неизвестными параметрами и По результатам независимых наблюдений найти наиболее правдоподобные значения этих параметров.

Решение. В соответствии с (3.1.4) функция правдоподобия имеет вид

а логарифмическая функция правдоподобия:

Необходимые условия экстремума дают систему двух уравнений:

Решения этой системы имеют вид:

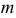
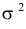
Отметим, что обе оценки являются состоятельными, причем оценка для несмещенная, а для смещенная (сравните с формулой (3.1.3)).

Ответ.

Пример:

По данным эксперимента построен статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. 1) Число экспериментальных данных вычисляется по формуле:

Значит, объем выборки n = 50.

2) Вычислим среднее арифметическое значение эксперимента:

Значит, найдена оценка математического ожидания 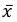= 12,3.

3) Вычислим исправленную выборочную дисперсию:

Значит, найдена оценка дисперсии: 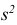= 1,44.

5) Вычислим оценку среднего квадратического отклонения:

Ответ:

Пример:

По данным эксперимента построен статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. По формуле

перейдем к условным вариантам:

Для них произведем расчет точечных оценок параметров:

Следовательно, вычисляем искомые точечные оценки:

Ответ:

Пример:

По данным эксперимента построен интервальный статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения.
Решение. 1) От интервального ряда перейдем к статистическому ряду, заменив интервалы их серединами

2) Объем выборки вычислим по формуле:

3) Вычислим среднее арифметическое значений эксперимента:

3) Вычислим исправленную выборочную дисперсию:

Можно было воспользоваться следующей формулой:

5) Вычислим оценку среднего квадратического отклонения:

Ответ:

Пример:

Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания M(X) нормально распределенной случайной величины X, если известно среднее квадратическое отклонение σ = 2, оценка математического ожидания 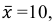объем выборки n = 25.

Решение. Доверительный интервал для истинного математического ожидания с доверительной вероятностью 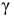= 0,95 при известной дисперсии σ находится по формуле:

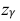
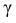
где m = M(X) – истинное математическое ожидание; 𝑥̅ − оценка M(X) по выборке; n – объем выборки; – находится по доверительной вероятности = 0,95 из равенства:

Из табл. П 2.2 приложения 2 находим: 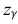= 1,96. Следовательно, найден доверительный интервал для M(X):

Ответ: (9,216 ; 10,784).

Пример:

По данным эксперимента построен статистический ряд:

Найти доверительный интервал для математического ожидания M (X) с надежностью 0,95.

Решение. Воспользуемся формулой для доверительного интервала математического ожидания при неизвестной дисперсии:

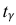
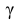
где n – объем выборки; 𝑥̅ оценка M(X); s – оценка среднего квадратического отклонения; − находится по доверительной вероятности = 0,95.

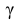
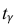
По числам = 0,95 и n = 20 находим: = 2,093.
Теперь вычисляем оценки для M(X) и D(X):

Следовательно, s ≈ 1,685. Поэтому искомый доверительный интервал математического ожидания задается формулой:

Ответ: (– 0,76; 0,76).

Пример:

По данным десяти независимых измерений найдена оценка квадратического отклонения 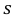= 0,5. Найти доверительный интервал точности измерительного прибора с надежностью 99 %.

Решение. Задача сводится к нахождению доверительного интервала для истинного квадратического отклонения, так как точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений.

Доверительный интервал для среднего квадратического отклонения находим по формуле:

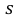
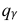
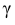
где = 0,5 − оценка среднего квадратического отклонения; – число, определяемое из табл. П 2.4 приложения 2 по заданной доверительной вероятности = 0,99 и заданному объему выборки n = 10.
Находим:
Тогда можно записать:

Ответ: (0; 1,04).

Доверительный интервал для вероятности события
Проверка гипотезы о равенстве вероятностей
Доверительный интервал для математического ожидания
Доверительный интервал для дисперсии
Системы случайных величин
Вероятность и риск
Определения вероятности событий
Предельные теоремы теории вероятностей

Источник

3.4. Оценка качества модели

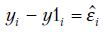
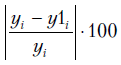
Отклонения называют абсолютной ошибкой аппроксимации в -м наблюдении, а величину — относительной ошибкой аппроксимации. О судят по средней относительной ошибке аппроксимации

Считается, что ошибка в 4-9% на контрольной выборке свидетельствует о хорошем качестве построенной модели. О качестве модели судят также и по результатам дисперсионного анализа модели.

Рассмотрим, как и для случая парной регрессии

(3.16)

(3.17)

(3.18)

Можно показать, что

$Q_{общ} = Q_{ост} + Q_{регр}$

(3.19)

Докажем это равенство:

$Q_{общ} = (Y - Y)^{T}(Y - Y) =\\ = (Y - Y1 + Y1 - Y)^{T}(Y - Y1 + Y1 - Y) =\\ =Q_{регл} + Q_{ост} + (Y - Y1)^{T}(Y1 - Y) + (Y1 - Y)^{T}(Y - Y1).$

Докажем, что две последние суммы равны нулю:

$(Y - Y1)^{T}(Y1 - Y) = (Y^{T}Y1 - Y1^{T}Y1) + (Y1^{T }Y - Y^{T}Y);\\ Y^{T}Y1 = Y^{T}Xb = Y^{T}X(X^{T}X)^{-1}X^{T}Y;\\ Y1^{T}Y1 = b^{T}X^{T}Xb = Y^{T}X(X^{T}X)^{-1}X^{T}X(X^{T}X)^{-1}X^{T}Y =\\ = Y^{T}X(X^{T}X)^{-1}X^{T}Y = Y^{T}Y^{1}$

Равенство $Y1^{T }Y - Y^{T }Y = 0$ эквивалентно равенству $\sum Y_{i}Y - \sum Y1_{i}Y$ , или $\sum Y1_{i} - \sum Y_{i}$ . Последнее равенство является первым равенством нормальной системы уравнений МНК (с учетом того, что $x_{0j} = 1, j = 1, 2, \dots , N$ ). Таким образом, равенство (3.19) доказано.

С вопросом об оценке качества модели тесно связано понятие коэффициента множественной корреляции. В главе 2 рассматривался коэффициент детерминации

Он показывает, насколько предсказания по уравнению регрессии лучше, чем по среднему значению отклика . Число $R=\sqrt{R^{2}}$ называют коэффициентом множественной корреляции. Оказывается, это число совпадает с коэффициентом корреляции между и , который отражает тесноту линейной связи между значениями выхода и их расчетными значениями . Докажем этот факт. Необходимо установить равенство

(3.20)

Для этого достаточно показать, что числитель равен $Q_{регр}$ , а знаменатель равен $\sqrt{Q_{общ}Q_{регл}}$ . Прежде всего заметим, что в силу ранее доказанного равенства $\sum Y1_{i} - \sum Y_{i}$ получаем Y - Y1 . Отсюда вытекает требуемое соотношение для знаменателя. Далее

Итак, из (3.6) последнее слагаемое равно нулю, что и требовалось.

Дисперсионный анализ для случая многих факторов проводится так же, как и для парной регрессии. Сделаем только замечания по поводу подсчета степеней свободы для $Q_{ост}$ и $Q_{регр}$ .

Обозначим 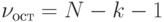$\nu _{ост} = N - k - 1$ . Это число степеней свободы остаточной суммы квадратов $Q_{ост}$ . Оно равно разности между числом наблюдений и числом линейных связей между ними, участвующими в определении $Q_{ост}$ (в сумме участвуют значения $Y1_{i}$ , которые, в свою очередь, зависят от вектора коэффициентов $b = b_{0}, b_{1}, \dots , b_{k})$ .

Несмещенная оценка дисперсии $\sigma ^{2 }$ ошибок наблюдений задается в этом случае формулой

(3.21)

Аналогично сумма $Q_{общ}$ имеет число степеней свободы $\nu _{общ}$ , равное N - 1, так как в этой сумме все наблюдения связаны одной связью (участвует одно значение ). Наконец, для суммы $Q_{регр }$ число степеней свободы $\nu _{регр} = (k + 1) - 1 = k$ , так как в выражение $Q_{регр}$ входят k + 1 оценок $b_{0}, b_{1}, \dots, b_{k}$ и одна линейная связь, определяемая . Очевидно, что $\nu _{общ},= \nu _{ост}+\nu _{регр}$ .

Проверку значимости уравнения регрессии проводим по уже знакомой нам схеме. Находим 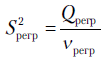и наблюдаемое значение критерия Фишера . Если уравнение регрессии незначимо, то в условиях Гаусса — Маркова числитель и знаменатель дроби являются несмещенными оценками для $\sigma^{2}$ и дробь подчиняется распределению Фишера — Снедекора. Затем по заданной надежности $g = 1 - \alpha$ , где $\alpha$ — уровень значимости, по таблицам данного распределения находим критическое значение $F_{krit}(\alpha ,\nu _{регр}., \nu _{ост})$ . Если $F_{набл} > F_{krit}(\alpha , \nu _{регр}., \nu _{ост}))$ , то нулевая гипотеза о незначимости уравнения регрессии отвергается и принимается гипотеза о значимости уравнения регрессии.

Формула (3.20) дает выборочное значение коэффициента множественной корреляции, являющейся оценкой фактического его значения $\rho$ . Иногда возникает необходимость проверить значимость этого коэффициента, т.е. проверить нулевую гипотезу: $\rho = 0$ . Это равнозначно проверке значимости уравнения регрессии. Для этого составляют соотношение

Далее проверка значимости коэффициента полностью совпадает с проверкой значимости уравнения регрессии.

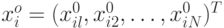
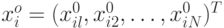
В случае когда наблюдения проводятся с повторениями, т.е. при некотором наборе $x^{o}_{i} = (x^{0}_{il}, x^{0}_{i2},\dots ,x^{0}_{iN})^{T}$ проводится дополнительных повторных опытов, появляется возможность проверить качество выбора модели, т.е. ее адекватность опытным данным. Пусть в дополнительной точке $x^{o}_{i} = (x^{0}_{il}, x^{0}_{i2},\dots ,x^{0}_{iN})^{T}$ получены $\tilde{Y} _{1}, \tilde{Y} _{2},\dots ,\tilde{Y}_{n }$ значения которые отражают лишь влияние случайных ошибок или в худшем случае влияние неучтенных факторов на результаты наблюдений. Оценим дисперсию ошибок по этим данным:

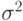
Если регрессия адекватна наблюдениям, то $S^{2}_{ош}$ и $S^{2}_{ост}$ являются несмещенными оценками одной и той же дисперсии случайных ошибок $\sigma ^{2}$ .

Итак, нулевая гипотеза в этом случае имеет вид

$M(S^{2}_{ост}) = M(S^{2}_{ош}) = \sigma ^{2}.$

(3.21)

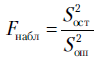
Согласно конкурирующей гипотезе, равенство (3.21) не выполняется, т.е. остатки модели слишком велики по сравнению с ошибками наблюдений, а следовательно, модель (3.1) неадекватна. Это позволяет использовать критерий Фишера для проверки адекватности регрессионной модели. Сначала выберем уровень значимости a в пределах от 0,01 до 0,1. Из таблиц распределения Фишера необходимо найти величину $F_{krit}(\alpha , \nu _{ост}, \nu _{ош})$ . Затем находят . Если $F_{набл} < F_{krit}$ , оснований отвергнуть гипотезу об адекватности нет. Если $F_{набл }> F_{krit}$ , гипотеза об адекватности модели отвергается.

Источник

15. Оценка дисперсии случайной ошибки модели регрессии

где n – это объём выборочной совокупности;

еi– остатки регрессионной модели:

где k – число оцениваемых параметров модели регрессии.

Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:

где In – единичная матрица.

Доказательство. Примем без доказательства справедливость следующих равенств:

где G2(?) – генеральная дисперсия случайной ошибки;

S2(?) – выборочная дисперсия случайной ошибки;

– выборочная оценка дисперсии случайной ошибки.

Тогда:

т. е.

что и требовалось доказать.

Следовательно, выборочная оценка дисперсии случайной ошибки

является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).

Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки

от величины случайной ошибки ?.

МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:

Для дальнейших преобразования используются свойства ковариации:

1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;

2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).

Исходя из указанных свойств ковариации, справедливы следующие равенства:

Cov(x,?0)=0 (?0=const);

Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).

Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:

Cov(x,y)= ?1G2(x)+Cov(x,?).

В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:

Таким образом, МНК-оценка

может быть представлена как сумма двух компонент:

1) константы ?1, т. е. истинного значения коэффициента;

2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.

Аналогично доказывается, что МНК-оценка

коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки

Данный текст является ознакомительным фрагментом.

12. Оценка существенности параметров линейной регрессии и корреляции

13. Интервалы прогноза по линейному уравнению регрессии

Читайте также

11. Критерии оценки неизвестных коэффициентов модели регрессии

14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии

18. Характеристика качества модели регрессии

22. Проверка гипотезы о значимости коэффициентов модели парной регрессии

25. Точечный и интервальный прогнозы для модели парной регрессии

35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом

39. Модели регрессии, нелинейные по факторным переменным

40. Модели регрессии, нелинейные по оцениваемым коэффициентам

41. Модели регрессии с точками разрыва

44. Методы нелинейного оценивания коэффициентов модели регрессии

46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии

57. Гетероскедастичность остатков модели регрессии

60. Устранение гетероскедастичности остатков модели регрессии

63. Устранение автокорреляции остатков модели регрессии

67. Модели регрессии с переменной структурой. Фиктивные переменные

Оценки для математического ожидания и дисперсии

Метод наибольшего правдоподобия для оценки параметров распределений

Метод моментов

3.4. Оценка качества модели

Читайте также

11. Критерии оценки неизвестных коэффициентов модели регрессии

14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии

18. Характеристика качества модели регрессии

22. Проверка гипотезы о значимости коэффициентов модели парной регрессии

25. Точечный и интервальный прогнозы для модели парной регрессии

35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом

39. Модели регрессии, нелинейные по факторным переменным

40. Модели регрессии, нелинейные по оцениваемым коэффициентам

41. Модели регрессии с точками разрыва

44. Методы нелинейного оценивания коэффициентов модели регрессии

46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии

57. Гетероскедастичность остатков модели регрессии

60. Устранение гетероскедастичности остатков модели регрессии

63. Устранение автокорреляции остатков модели регрессии

67. Модели регрессии с переменной структурой. Фиктивные переменные

Интересное по теме: