Оценка ошибки аппроксимации численного интегрирования

Оценим
погрешности методов вычисления. Для
разностных правой и левой производных
будут справедливы следующие выражения

(5.16)

, (5.17)

а
для центральной

. (5.18)

Для
оценки погрешностей левых и правых
разностных производных первую производную
можно получить из разложения в ряд
Тейлора в виде

. (5.19)

Здесь
и ниже

и

– некоторые точки, расположенные на
интервалах

и

соответственно. Откуда погрешности
этих методов будут иметь вид

, (5.20)

а
оценка абсолютных погрешностей будет
удовлетворять неравенству

, (5.21)

где

. (5.22)

Таким
образом, формулы (5.2) и (5.3) вычисления
правой и левой разностных производных
имеют первый порядок точности по
.

Для
центральной разностной производной
соответствующие разложения функций

в ряд Тейлора должны учитывать и
производную третьего порядка (вторая
производная при вычитании исчезает)

. (5.23)

Отсюда
получим

(5.24)

и
для оценки абсолютной погрешности будет
справедливо неравенство

, (5.25)

где

. (5.26)

Таким
образом, производная

вычисляется при помощи формул центральной
разностной производной со вторым
порядком точности по
,
т.е. точнее, чем по формулам (5.2) и (5.3).

Очень
часто уменьшение погрешности метода,
в данном случае метода численного
дифференцирования, сопровождается
ростом влияния погрешности исходных
данных и вычислительной погрешности.
Численное дифференцирование относится
именно к таким задачам, которые обычно
называют плохо обусловленными.

Оценим
совместное влияния погрешностей
вычисления и метода для вычисления
первой производной. Пусть значение
производной вычисляется по формуле
(5.3), тогда погрешность метода можно
оценить по соотношению (5.21). Если значения
функции

известны с некоторой погрешностью

(),
то погрешность вычисления

будет содержать дополнительное слагаемое

, (5.27)

Пренебрегая
для простоты погрешностью округления,
имеем оценку погрешности в следующем
виде

. (5.28)

Из
формулы (5.28) очевидно, что уменьшение

не приводит к увеличению точности
вычисления производной, так как возрастает
ошибка, связанная с погрешностью
определения функции (рисунок 5.1).
Погрешности

возникают вследствие ошибок измерения
или предыдущего вычисления по приближенным
формулам. Из соотношения (5.28) можно найти
оптимальное значение разбиения, находя
экстремум правой части, такое

будет равно

. (5.29)

Отметим,
что повышение точности метода лишь
отчасти повышает точность вычисления
производной.

Рисунок
5.1. Зависимость погрешности вычисления
первой производной от величины шага.

5.3. Численное интегрирование. Простейшие методы

К
численному интегрированию прибегают
в тех случаях, когда невозможно
аналитически получить первообразную,
или когда такая первообразная имеет
неудобный или слишком сложный для
вычисления вид. Основной задачей
численного интегрирования является
вычисление интеграла вида

, (5.29)

где

и

– нижний и верхний пределы интегрирования,
а функция

– непрерывная на отрезке
.

Сущность
большинства методов вычисления
определенных интегралов состоит в
замене подынтегральной функции

аппроксимирующей функцией
,
для которой можно легко записать
первообразную в элементарных функциях,
т.е.

, (5.30)

где

– погрешность вычисления.

Используемые
на практике методы численного
интегрирования можно условно сгруппировать
в зависимости от способа аппроксимации
подынтегральной функции.

Методы
полиномиальной аппроксимации
,
которые отличаются друг от друга
степенью используемого полинома, что
определяет количество узлов, где
необходимо вычислить подынтегральную
функцию. Это достаточно простые для
реализации методы. В частности к этим
методам относятся простейшие формулы
– прямоугольников, трапеций, Симпсона,
которые обобщаются формулами
Ньютона-Котеса.
Сплайновые
методы базируются на аппроксимации

сплайнами. Методы этого класса отличаются
по типу выбранных сплайнов и используются
в основном там, где применяются алгоритмы
сплайновой аппроксимации для обработки
данных.
Методы
наивысшей алгебраической точности,
использующие неравноотстоящие узлы,
расположенные по алгоритму, обеспечивающую
минимальную погрешность интегрирования,
используются для наиболее сложных
функций при заданном количестве узлов
вычисления функции
.
Методы,
основанные на случайном выборе узлов,
где определяются значения интегрируемой
функции. Эти методы (методы Монте-Карло)
используются для вычисления кратных
интегралов, для которых они наиболее
эффективны.

В
дальнейшем ограничимся методами первой
и второй группы, а также рассмотрим
алгоритмы метода Монте-Карло для кратных
интегралов.

Наиболее
широко на практике для вычисления
определенных интегралов используются
квадратурные формулы – приближенные
равенства вида

, (5.31)

что
соответствует разбиению полного
интеграла на сумму интегралов от функции
по элементарным отрезкам. Здесь

– некоторые точки (узлы) из отрезка
,
разбитого на

элементарных отрезков
,
при этом
,
а
,
а

– некоторые коэффициенты. Сумма, стоящая
в правой части выражения (5.31) называется
квадратурной суммой. Погрешность
вычисления по этой формуле определяется
выражением

. (5.32)

Заметим,
что интеграл вида (5.29) определяет площадь
фигуры ограниченной прямыми
,

и графиком функции
.
Для вычисления этой и площади и
соответственно интеграла ее можно
разбить на простые фигуры. На этом и
основаны простейшие методы вычисления
интеграла (5.29).

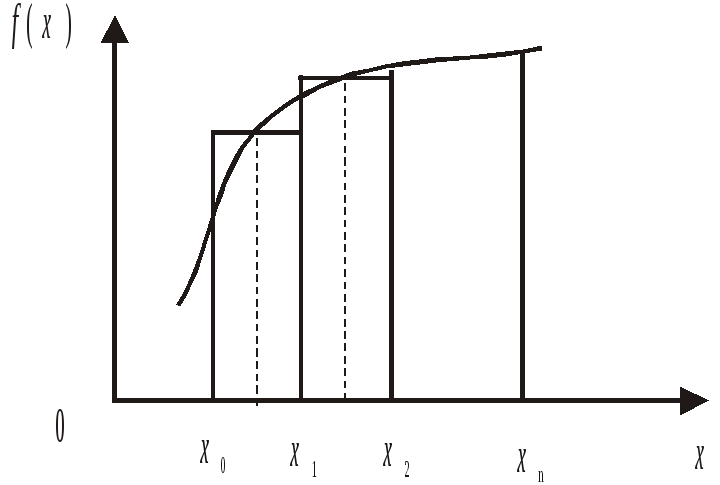
Формулы
прямоугольников.
Рассмотрим разбиение отрезка

на

элементарных отрезков
,
пусть для простоты
,
тогда каждому значению

можно поставить в соответствие значение
функции
.
Рассматривая

как высоту прямоугольника с основанием

можно получить две формулы: формулу
левых прямоугольников (рисунок 5.2)

(5.33)

и
формулу правых прямоугольников

. (5.34)

Аналогичным
образом за высоту прямоугольника можно
взять его середину. В этом случае отрезок
обычно разбивают на

отрезков и рассматривают только нечетные
узлы, что эквивалентно рассмотрению
прямоугольников высотой, равной значению
функции в середине элементарного
отрезка. Квадратурная формула называется
формулой средних прямоугольников
(рисунок 5.3) и имеет вид

. (5.35)

Рисунок
5.2. Интегрирование по формуле левых
прямоугольников

Интересно
отметить, что формулы левых и правых
прямоугольников фактически заменяют
интеграл верхними и нижними суммами
Дарбу и, к сожалению, имеют высокую
погрешность. Это в равной степени
относится и к формуле средних
прямоугольников.

Формула
трапеций.
Следующая простейшая формула получается,
если рассматривать в качестве приближения
не прямоугольник, а трапецию с высотами

и

(рисунок 5.4). В этом случае площадь
-ой
элементарной трапеции с основанием

будет иметь вид

. (5.36)

Рисунок
5.3. Интегрирование по формуле средних
прямоугольников

Приближенное
значение интеграла в свою очередь будет
определяться как

. (5.37)

Эта
формула соответствует приближенной
замене площади исходной криволинейной
трапеции площадью фигуры, ограниченной
ломаной линией.

Рисунок
5.4. Интегрирование по формуле трапеций

В
качестве примера приведена программа
вычисления интеграла от функции

на отрезке [-5,5] по формуле правых
прямоугольников.

Программа
5.2

x=-5:0.1:5;

f=(exp(x)+exp(-x))/2;

for
i=1:100,

inte(i)=f(i)*(x(i+1)-x(i));

end;

indeg=sum(inte)

end.

Соседние файлы в предмете Численные методы

Источник

Вычисление определённых интегралов: базовые алгоритмы

Время на прочтение
13 мин

Количество просмотров 85K

В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают «под капотом», и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.

Определение интеграла

Интегралом (по Риману) от функции $f(x)$ на отрезке $[a;b]$ называется следующий предел:

$\int_a^b f(x)dx = \lim_{\Delta x \to 0} \sum_{i=0}^{n-1} f(\xi_i)(x_{i+1} - x_i),~~(1)$

где $\Delta x = \max\lbrace x_{i+1} - x_i\rbrace$ — мелкость разбиения, , , $\xi_i$ — произвольное число на отрезке $[x_i; x_{i+1}]$ .

Если интеграл от функции существует, то значение предела одно и то же вне зависимости от разбиения, лишь бы оно было достаточно мелким.

Более наглядно геометрическое определение — интеграл равен площади криволинейной трапеции, ограниченной осью 0x, графиком функции и прямыми x = a и x = b (закрашенная область на рисунке).

Квадратурные формулы

Определение интеграла (1) можно переписать в виде

$I = \int_a^b f(x)dx \approx I_n = (b - a)\sum_{i=0}^{n-1} w_i f(\xi_i),~~(2)$

где $w_i$ — весовые коэффициенты, сумма которых должна быть равна 1, а сами коэффициенты — стремиться к нулю при увеличении числа $n$ точек, в которых вычисляется функция.

Выражение (2) — основа всех квадратурных формул (т.е. формул для приближенного вычисления интеграла). Задача состоит в том, чтобы выбрать точки $\lbrace \xi_i \rbrace$ и веса $w_i$ таким образом, чтобы сумма в правой части приближала требуемый интеграл как можно точнее.

Вычислительная задача

Задана функция $f(x)$ , для которой есть алгоритм вычисления значений в любой точке отрезка $[a;b]$ (имеются в виду точки, представимые числом с плавающей точкой — никаких там функций Дирихле!).

Требуется найти приближённое значение интеграла $\int_a^b f(x)dx$ .
Решения будут реализованы на языке Python 3.6.

Для проверки методов используется интеграл $\int_0^{3/2} \left[ 2x + \frac{1}{\sqrt{x + 1/16}}\right]dx = 17/4$ .

Кусочно-постоянная аппроксимация

Идейно простейшие квадратурные формулы возникают из применения выражения (1) «в лоб»:

$I_n = \sum_{i=0}^{n-1} f(\xi_i) (x_{i+1} - x_i)$

Т.к. от метода разбиения отрезка точками $\lbrace x_i\rbrace$ и выбора точек $\lbrace\xi_i\rbrace$ значение предела не зависит, то выберем их так, чтобы они удобно вычислялись — например, разбиение возьмём равномерным, а для точек вычисления функции рассмотрим варианты: 1) $\xi_i = x_i$ ; 2) $\xi_i = x_{i+1}$ ; 3) $\xi_i = (x_i + x_{i+1}) / 2$ .

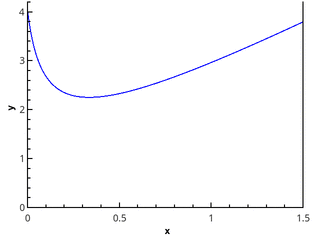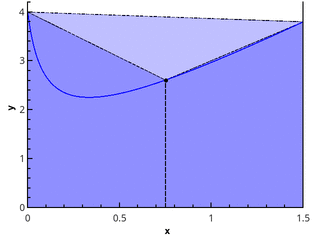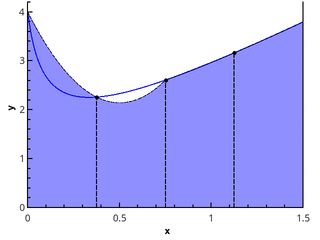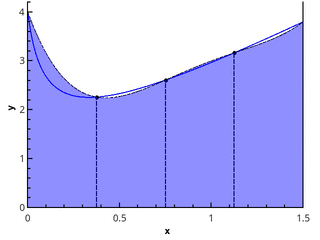
Получаем методы левых прямоугольников, правых прямоугольников и прямоугольников со средней точкой, соответственно.

Реализация

def _rectangle_rule(func, a, b, nseg, frac):
    """Обобщённое правило прямоугольников."""
    dx = 1.0 * (b - a) / nseg
    sum = 0.0
    xstart = a + frac * dx # 0 <= frac <= 1 задаёт долю смещения точки, 
                           # в которой вычисляется функция,
                           # от левого края отрезка dx
    for i in range(npoints):
        sum += func(xstart + i * dx)

    return sum * dx

def left_rectangle_rule(func, a, b, nseg):
    """Правило левых прямоугольников"""
    return _rectangle_rule(func, a, b, nseg, 0.0)

def right_rectangle_rule(func, a, b, nseg):
    """Правило правых прямоугольников"""
    return _rectangle_rule(func, a, b, npoints, 1.0)

def midpoint_rectangle_rule(func, a, b, nseg):
    """Правило прямоугольников со средней точкой"""
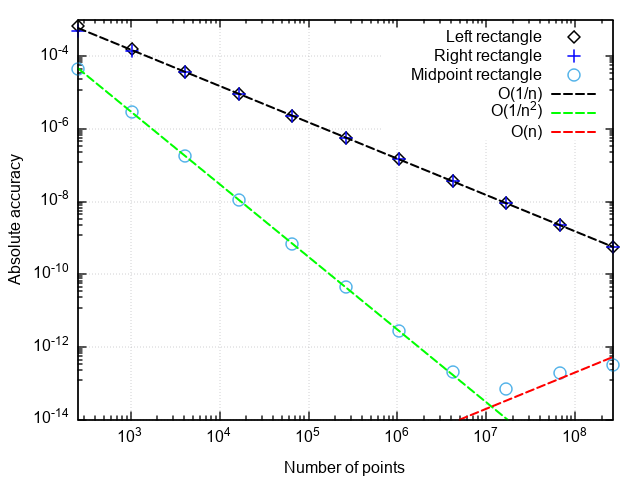
    return _rectangle_rule(func, a, b, nseg, 0.5)

Для анализа производительности квадратурных формул построим график погрешности в координатах «число точек — отличие численного результата от точного».

Что можно заметить:

Формула со средней точкой гораздо точнее, чем с правой или левой точками
Погрешность формулы со средней точкой падает быстрее, чем у двух остальных
При очень мелком разбиении погрешность формулы со средней точкой начинает возрастать
Первые два пункта связаны с тем, что формула прямоугольников со средней точкой имеет второй порядок аппроксимации, т.е. , а формулы правых и левых прямоугольников — первый порядок, т.е. .
Возрастание погрешности при измельчении шага интегрирования связано с нарастанием погрешности округления при суммировании большого числа слагаемых. Эта ошибка растёт как , что не даёт при интегрировании достигнуть машинной точности.
Вывод: методы прямоугольников с правой и левой точками имеют низкую точность, которая к тому же медленно растёт с измельчением разбиения. Поэтому они имеют смысл разве что в демонстрационных целях. Метод прямоугольников со средней точкой имеет более высокий порядок аппроксимации, что даёт ему шансы на использование в реальных приложениях (об этом чуть ниже).

Кусочно-линейная аппроксимация

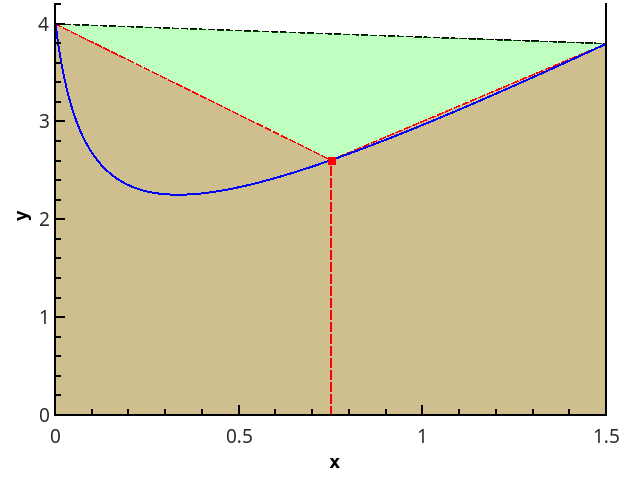
Следующий логический шаг — аппроксимировать интегрируемую функцию на каждом из подотрезков линейной функцией, что даёт квадратурную формулу трапеций:

$I_n = \sum_{i=0}^{n-1} \frac{f(x_i) + f(x_{i+1})}{2}(x_{i+1} - x_i)~~(3)$

Иллюстрация метода трапеций для n=1 и n=2.

В случае равномерной сетки длины всех отрезков разбиения равны, и формула имеет вид

$I_n = h\left(\frac{f(a) + f(b)}{2} + \sum_{i=1}^{n-1} f(a + ih)\right),~h=\frac{b-a}{n}~~(3a)$

Реализация

def trapezoid_rule(func, a, b, nseg):
    """Правило трапеций
       nseg - число отрезков, на которые разбивается [a;b]"""
    dx = 1.0 * (b - a) / nseg
    sum = 0.5 * (func(a) + func(b))
    for i in range(1, nseg):
        sum += func(a + i * dx)

    return sum * dx

Построив график ошибки от числа точек разбиения, убеждаемся, что метод трапеций тоже имеет второй порядок аппроксимации и вообще даёт результаты, слабо отличающиеся от метода прямоугольников со средней точкой (в дальнейшем — просто метод прямоугольников).

Контроль точности вычисления

Задание в качестве входного параметра числа точек разбиения не слишком практично, поскольку обычно требуется вычислить интеграл не с заданной плотностью разбиения, а с заданной погрешностью. Если подынтегральная функция известна наперёд, то можно оценить погрешность заранее и выбрать такой шаг интегрирования, чтобы заданная точность заведомо достигалась. Но так редко бывает на практике (и вообще, не проще ли при известной наперёд функции и сам интеграл протабулировать наперёд?), поэтому необходима процедура автоматической подстройки шага под заданную погрешность.

Как это реализовать? Один из простых методов оценки погрешности — правило Рунге — разность значений интегралов, рассчитанных по n и 2n точкам, даёт оценку погрешности: $\Delta_{2n} \approx |I_{2n} - I_n|$ . Метод трапеций удобнее для удвоения мелкости разбиения, чем метод прямоугольников с центральной точкой. При расчёте методом трапеций для удвоения числа точек нужны новые значения функции только в серединах отрезков предыдущего разбиения, т.е. предыдущее приближение интеграла можно использовать для вычисления следующего.

Чем ещё хорош метод прямоугольников

Метод прямоугольников не требует вычислять значения функции на концах отрезка. Это означает, что его можно использовать для функций, имеющих на краях отрезка интегрируемые особенности (например, sinx/x или x^-1/2 от 0 до 1). Поэтому показанный далее метод экстраполяции будет работать точно так же и для метода прямоугольников. Отличие от метода трапеций лишь в том, что при уменьшении шага вдвое отбрасывается результат предыдущих вычислений, однако можно утроить число точек, и тогда предыдущее значение интеграла также можно использовать для вычисления нового. Формулы для экстраполяции в этом случае необходимо скорректировать на другое соотношение шагов интегрирования.

Отсюда получаем следующий код для метода трапеций с контролем точности:

def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1):
    """Правило трапеций
       rtol - желаемая относительная точность вычислений
       nseg0 - начальное число отрезков разбиения"""
    nseg = nseg0
    old_ans = 0.0
    dx = 1.0 * (b - a) / nseg
    ans = 0.5 * (func(a) + func(b))
    for i in range(1, nseg):
        ans += func(a + i * dx)

    ans *= dx
    err_est = max(1, abs(ans))
    while (err_est > abs(rtol * ans)):
        old_ans = ans
        ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) # новые точки для уточнения интеграла
                                                                      # добавляются ровно в середины предыдущих отрезков
        nseg *= 2
        err_est = abs(ans - old_ans)

    return ans

С таким подходом подынтегральная функция не будет вычисляться по нескольку раз в одной точке, и все вычисленные значения используются для окончательного результата.

Но нельзя ли при том же количестве вычислений функции добиться более высокой точности? Оказывается, что можно, есть формулы, работающие точнее метода трапеций на той же самой сетке.

Кусочно-параболическая аппроксимация

Следующим шагом аппроксимируем функцию элементами парабол. Для этого требуется, чтобы число отрезков разбиения было чётным, тогда параболы могут быть проведены через тройки точек с абсциссами {(x₀=a, x₁, x₂), (x₂, x₃, x₄), …, (x_n-2, x_n-1, x_n=b)}.

Иллюстрация кусочно-параболического приближения на 3 и 5 точках (n=2 и n=3).

Приближая интеграл от функции на каждом из отрезков [x_k;x_k+2] интегралом от параболической аппроксимации на этом отрезке и считая точки равномерно распределенными (x_k+1=x_k+h), получаем формулу Симпсона:

$I_{Simps, n} = \sum_{i=0}^{n/2-1}\frac{h}{3}[f(x_{2i})+4f(x_{2i+1})+f(x_{2i + 2})] = \\ =\frac{h}{3}[f(a)+4f(a+h)+2f(a+2h) + ... +4f(b-h) + f(b)]~~(4)$

Из формулы (4) напрямую получается «наивная» реализация метода Симпсона:

Заголовок спойлера

def simpson_rule(func, a, b, nseg):
    """Правило трапеций
       nseg - число отрезков, на которые разбивается [a;b]"""
    if nseg%2 = 1:
        nseg += 1
    dx = 1.0 * (b - a) / nseg
    sum = (func(a) + 4 * func(a + dx) + func(b))
    for i in range(1, nseg / 2):
        sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx)

    return sum * dx / 3

Для оценки погрешности можно использовать точно так же вычисление интеграла с шагами h и h/2 — но вот незадача, при вычислении интеграла с более мелким шагом результат предыдущего вычисления придётся отбросить, хотя половина новых вычислений функции будет в тех же точках, что и раньше.

Бесполезной траты машинного времени, к счастью, можно избежать, если реализовать метод Симпсона более хитроумным образом. Присмотревшись повнимательнее, заметим, что интеграл по формуле Симпсона может быть представлен через два интеграла по формуле трапеций с разными шагами. Яснее всего это видно на базовом случае аппроксимации интеграла по трём точкам :

$I_{Simps,2} = \frac{h}{3}(f_0 + 4f_1 + f_2) = \frac{4}{3}h\left(\frac{f_0 + f_1}{2} + \frac{f_1 + f_2}{2}\right) - \frac{1}{3}\cdot2h\frac{f_0 + f_2}{2} = \\ =\frac{4I_{trap,2} - I_{trap,1}}{3}$

Таким образом, если реализовать процедуру уменьшения шага вдвое и хранить два последних вычисления методом трапеций, метод Симпсона с контролем точности реализуется более эффективно.

Как-то так…

class Quadrature:
    """Базовые определения для квадратурных формул"""
    __sum = 0.0
    __nseg = 1  # число отрезков разбиения
    __ncalls = 0 # считает число вызовов интегрируемой функции

    def __restart(func, x0, x1, nseg0, reset_calls = True):
        """Обнуление всех счётчиков и аккумуляторов.
           Возвращает интеграл методом трапеций на начальном разбиении"""
        if reset_calls:
            Quadrature.__ncalls = 0
        Quadrature.__nseg = nseg0
        # вычисление суммы для метода трапеций с начальным числом отрезков разбиения nseg0
        Quadrature.__sum = 0.5 * (func(x0) + func(x1))
        dx = 1.0 * (x1 - x0) / nseg0
        for i in range(1, nseg0):
            Quadrature.__sum += func(x0 + i * dx)

        Quadrature.__ncalls += 1 + nseg0
        return Quadrature.__sum * dx

    def __double_nseg(func, x0, x1):
        """Вдвое измельчает разбиение.
           Возвращает интеграл методом трапеций на новом разбиении"""
        nseg = Quadrature.__nseg
        dx = (x1 - x0) / nseg
        x = x0 + 0.5 * dx
        i = 0
        AddedSum = 0.0
        for i in range(nseg):
            AddedSum += func(x + i * dx)

        Quadrature.__sum += AddedSum
        Quadrature.__nseg *= 2
        Quadrature.__ncalls += nseg
        return Quadrature.__sum * 0.5 * dx

    def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1):
        """Интегрирование методом трапеций с заданной точностью.
           rtol - относительная точность,
           nseg0 - число отрезков начального разбиения"""
        ans = Quadrature.__restart(func, x0, x1, nseg0)
        old_ans = 0.0
        err_est = max(1, abs(ans))
        while (err_est > abs(rtol * ans)):
            old_ans = ans
            ans = Quadrature.__double_nseg(func, x0, x1)
            err_est = abs(old_ans - ans)

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

    def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1):
        """Интегрирование методом парабол с заданной точностью.
           rtol - относительная точность,
           nseg0 - число отрезков начального разбиения"""
        old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0)
        new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
        ans = (4 * new_trapez_sum - old_trapez_sum) / 3
        old_ans = 0.0
        err_est = max(1, abs(ans))
        while (err_est > abs(rtol * ans)):
            old_ans = ans
            old_trapez_sum = new_trapez_sum
            new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
            ans = (4 * new_trapez_sum - old_trapez_sum) / 3
            err_est = abs(old_ans - ans)

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

Сравним эффективность метода трапеций и парабол:

>>> import math
>>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 65537
4.250000001385811
>>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 2049
4.2500000000490985

Как видим, обоими методами ответ можно получть с достаточно высокой точностью, но количество вызовов подынтегральной функции разительно отличается — метод более высокого порядка эффективнее в 32 раза!

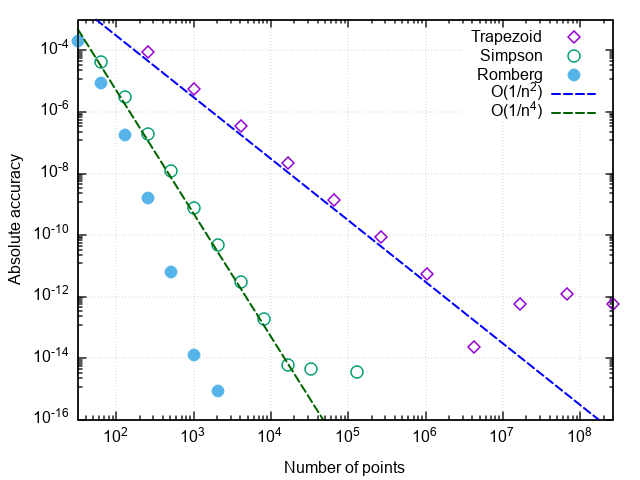
Построив график погрешности интегрирования от числа шагов, можно убедиться, что порядок аппроксимации формулы Симпсона равен четырём, т.е. ошибка численного интегрирования $|I_{Simps, n} - I| = O(1/n^4)$ (а интегралы от кубических многочленов с помощью этой формулы вычисляются с точностью до ошибок округления при любом чётном n>0!).

Отсюда и возникает такой рост эффективности по сравнению с простой формулой трапеций.

Что дальше?

Дальнейшая логика повышения точности квадратурных формул, в целом, понятна — если функцию продолжать приближать многочленами всё более высокой степени, то и интеграл от этих многочленов будет всё точнее приближать интеграл от исходной функции. Этот подход называется построением квадратурных формул Ньютона-Котеса. Известны формулы вплоть до 8 порядка аппроксимации, но выше среди весовых коэффициентов w_i в (2) появляются знакопеременные члены, и формулы при вычислениях теряют устойчивость.

Попробуем пойти другим путём. Ошибка квадратурной формулы представляется в виде ряда по степеням шага интегрирования h. Замечательное свойство метода трапеций (и прямоугольников со средней точкой!) в том, что для неё этот ряд состоит только из чётных степеней:

$I_{trap,n}[f, a, b] = \int_a^b f(x)dx + C_2h^2 + C_4h^4 + C_6h^6 + ...,~h = \frac{b-a}{n}~~~(5)$

На нахождении последовательных приближений к этому разложению основана экстраполяция Ричардсона: вместо того, чтобы приближать подынтегральную функцию многочленом, по рассчитанным приближениям интеграла $I(h)$ строится полиномиальная аппроксимация, которая при h=0 должна давать наилучшее приближение к истинному значению интеграла.

Разложение ошибки интегрирования по чётным степеням шага разбиения резко ускоряет сходимость экстраполяции, т.к. для аппроксимации порядка 2n нужно всего n значений интеграла методом трапеций.

Если считать, что каждое последующее слагаемое меньше предыдущего, то можно последовательно исключать степени h, имея приближения интеграла, рассчитанные с разными шагами. Поскольку приведённая реализация легко позволяет дробить разбиение вдвое, удобно рассматривать формулы для шагов h и h/2.

$I_{trap,n} - I \approx C_2h^2;~I_{trap,2n} - I \approx C_2\left(\frac{h}{2}\right)^2$

Легко показать, что исключение старшего члена погрешности формулы трапеций в точности даст формулу Симпсона:

$I = I_{trap,2n} - C_2\left(\frac{h}{2}\right)^2 + O(h^4) \approx I_{trap,2n} - \frac{I_{trap,2n}-I_{trap,n}}{1-2^2} = I_{Simps,2n}$

Повторяя аналогичную процедуру для формулы Симпсона, получаем:

$I_{Simps,2n} - I \approx C_4\left(\frac{h}{2}\right)^4;~I_{Simps,n} - I \approx C_4h^4$

$I = I_{Simps,2n} - C_4\left(\frac{h}{2}\right)^4 + O(h^6) \approx I_{Simps,2n} - \frac{I_{Simps,2n}-I_{Simps,n}}{1-2^4}$

Если продолжить, вырисовывается такая таблица:

2 порядок	4 порядок	6 порядок
I_0,0
I_1,0	I_1,1
I_2,0	I_2,1	I_2,2
…	…	…

В первом столбце стоят интегралы, вычисленные методом трапеций. При переходе от верхней строки вниз разбиение отрезка становится вдвое мельче, а при переходе от левого столбца вправо повышается порядок аппроксимации интеграла (т.е. во втором столбце находятся интегралы по методу Симпсона и т.д.).

Элементы таблицы, как можно вывести из разложения (5), связаны рекуррентным соотношением:

$I_{i,j} = I_{i,j-1} - \frac{I_{i,j-1}-I_{i-1,j-1}}{1-\left(\frac{h_{i-j}}{h_i}\right)^2} = I_{i,j-1} - \frac{I_{i,j-1}-I_{i-1,j-1}}{1-2^{2j}}~~~(6)$

Погрешность приближения интеграла можно оценить по разности формул разных порядков в одной строке, т.е.

$\Delta_{i,j} \approx I_{i,j} - I_{i,j-1}$

Применение экстраполяции Ричардсона вместе с интегрированием методом трапеций называется методом Ромберга. Если метод Симпсона учитывает два предыдущих значения по методу трапеций, то метод Ромберга использует все ранее вычисленные методом трапеций значения для получения более точной оценки интеграла.

Реализация

Дополнительный метод добавляется в класс Quadrature

class Quadrature:
    """Базовые определения для квадратурных формул"""
    __sum = 0.0
    __nseg = 1  # число отрезков разбиения
    __ncalls = 0 # считает число вызовов интегрируемой функции

    def __restart(func, x0, x1, nseg0, reset_calls = True):
        """Обнуление всех счётчиков и аккумуляторов.
           Возвращает интеграл методом трапеций на начальном разбиении"""
        if reset_calls:
            Quadrature.__ncalls = 0
        Quadrature.__nseg = nseg0
        # вычисление суммы для метода трапеций с начальным разбиением на nseg0 отрезков
        Quadrature.__sum = 0.5 * (func(x0) + func(x1))
        dx = 1.0 * (x1 - x0) / nseg0
        for i in range(1, nseg0):
            Quadrature.__sum += func(x0 + i * dx)

        Quadrature.__ncalls += 1 + nseg0
        return Quadrature.__sum * dx

    def __double_nseg(func, x0, x1):
        """Вдвое измельчает разбиение.
           Возвращает интеграл методом трапеций на новом разбиении"""
        nseg = Quadrature.__nseg
        dx = (x1 - x0) / nseg
        x = x0 + 0.5 * dx
        i = 0
        AddedSum = 0.0
        for i in range(nseg):
            AddedSum += func(x + i * dx)

        Quadrature.__sum += AddedSum
        Quadrature.__nseg *= 2
        Quadrature.__ncalls += nseg
        return Quadrature.__sum * 0.5 * dx

    def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True):
        """Интегрирование методом Ромберга
           nseg0 - начальное число отрезков разбиения
           maxcol - максимальный столбец таблицы"""
        # инициализация таблицы
        Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]]
        i = 0
        maxcol = max(0, maxcol)
        ans = Itable[i][i]
        error_est = max(1, abs(ans))
        while (error_est > abs(rtol * ans)):
            old_ans = ans
            i += 1
            d = 4.0
            ans_col = min(i, maxcol)
            Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1))
            for j in range(0, ans_col):
                diff = Itable[i][j] - Itable[i - 1][j]
                Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0)
                d *= 4.0

            ans = Itable[i][ans_col]
            if (maxcol <= 1): # методы трапеций и парабол обрабатываются отдельно
                error_est = abs(ans - Itable[i - 1][-1])
            elif (i > maxcol):
                error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)])
            else:
                error_est = abs(ans - Itable[i - 1][i - 1])

        print("Total function calls: " + str(Quadrature.__ncalls))
        return ans

Проверим, как работает аппроксимация высокого порядка:

>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) # трапеции
Total function calls: 65537
4.250000001385811
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) # параболы
Total function calls: 2049
4.2500000000490985
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4)
Total function calls: 257
4.250000001644076

Убеждаемся, что, по сравнению с методом парабол, число вызовов подынтегральной функции снизилось ещё в 8 раз. При дальнейшем увеличении требуемой точности преимущества метода Ромберга проявляются ещё заметнее:

Некоторые замечания

Замечание 1. Количество вызовов функции в этих задачах характеризует число суммирований при вычислении интеграла. Уменьшение числа вычислений подынтегрального выражения не только экономит вычислительные ресурсы (хотя при более оптимизированной реализации и это тоже), но и уменьшает влияние погрешностей округления на результат. Так, при попытке вычислить интеграл тестовой функции метод трапеций зависает при попытке достигнуть относительной точности 5×10^-15, метод парабол — при желаемой точности 2×10^-16(что является пределом для чисел в двойной точности), а метод Ромберга справляется с вычислением тестового интеграла вплоть до машинной точности (с ошибкой в младшем бите). То есть, повышается не только точность интегрирования при заданном числе вызовов функции, но и предельно достижимая точность вычисления интеграла.

Замечание 2. Если метод сходится при задании некоторой точности, это не означает, что вычисленное значение интеграла имеет ту же самую точность. В первую очередь, это относится к случаям, когда задаваемая погрешность близка к машинной точности.

Замечание 3. Хотя метод Ромберга для ряда функций работает почти магическим образом, он предполагает наличие у подынтегральной функции ограниченных производных высоких порядков. Это значит, что для функций с изломами или разрывами он может оказаться хуже простых методов. Например, проинтегрируем f(x)=|x|:

>>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5)
Total function calls: 9
5.0
>>> Quadrature.simpson(abs, -1, 3, rtol=1e-5)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3)
Total function calls: 33
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4)
Total function calls: 33
5.000001383269357

Замечание 4. Может показаться, что чем выше порядок аппроксимации, тем лучше. На самом деле, лучше ограничить число столбцов таблицы Ромберга на уровне 4-6. Чтобы понять это, посмотрим на формулу (6). Второе слагаемое представляет собой разность двух последовательных элементов j-1-го столбца, поделенную на примерно 4^j. Т.к. в j-1-м столбце находятся аппроксимации интеграла порядка 2j, то сама разность имеет порядок (1/n_i)^2j ~ 4^—ij. C учётом деления получается ~4^-(i+1)j ~ 4^—j². Т.е. при j~7 второе слагаемое в (6) теряет точность после приведения порядков при сложении чисел с плавающей точкой, и повышение порядка аппроксимации может вести к накоплению ошибки округления.

Замечание 5. Желающие могут ради интереса применить описанные методы для нахождения интеграла $\int_0^1\sqrt{x}\sin{x}dx$ и эквивалентного ему $\int_0^1 2t^2\sin{t^2}dt$ . Как говорится, почувствуйте разницу.

Заключение

Представлено описание и реализация базовых методов численного интегрирования функций на равномерной сетке. Продемонстрировано, как с помощью несложной модификации получить на базе метода трапеций класс квадратурных формул по методу Ромберга, что значительно ускоряет сходимость численного интегрирования. Метод хорошо работает для интегрирования «обычных» функций, т.е. слабо меняющихся на отрезке интегрирования, не имеющих особенностей на краях отрезка (см. Замечание 5), быстрых осцилляций и т.д.

Продвинутые методы численного интегрирования для более сложных случаев можно найти в книгах из списка литературы (в [3] — с примерами реализации на C++).

Литература

А.А. Самарский, А.В. Гулин. Численные методы. М.: Наука. 1989.
J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.

Источник

Numerical integration is used to calculate a numerical approximation for the value

, the area under the curve defined by f(x)

In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of definite integrals.

The term numerical quadrature (often abbreviated to quadrature) is more or less a synonym for numerical integration, especially as applied to one-dimensional integrals. Some authors refer to numerical integration over more than one dimension as cubature;^[1] others take quadrature to include higher-dimensional integration.

The basic problem in numerical integration is to compute an approximate solution to a definite integral

$\int _{a}^{b}f(x)\,dx$

to a given degree of accuracy. If f(x) is a smooth function integrated over a small number of dimensions, and the domain of integration is bounded, there are many methods for approximating the integral to the desired precision.

Reasons for numerical integration[edit]

There are several reasons for carrying out numerical integration, as opposed to analytical integration by finding the antiderivative:

The integrand f(x) may be known only at certain points, such as obtained by sampling. Some embedded systems and other computer applications may need numerical integration for this reason.
A formula for the integrand may be known, but it may be difficult or impossible to find an antiderivative that is an elementary function. An example of such an integrand is f(x) = exp(−x²), the antiderivative of which (the error function, times a constant) cannot be written in elementary form.
It may be possible to find an antiderivative symbolically, but it may be easier to compute a numerical approximation than to compute the antiderivative. That may be the case if the antiderivative is given as an infinite series or product, or if its evaluation requires a special function that is not available.

History[edit]

The term «numerical integration» first appears in 1915 in the publication A Course in Interpolation and Numeric Integration for the Mathematical Laboratory by David Gibb.^[2]

Quadrature is a historical mathematical term that means calculating area. Quadrature problems have served as one of the main sources of mathematical analysis. Mathematicians of Ancient Greece, according to the Pythagorean doctrine, understood calculation of area as the process of constructing geometrically a square having the same area (squaring). That is why the process was named quadrature. For example, a quadrature of the circle, Lune of Hippocrates, The Quadrature of the Parabola. This construction must be performed only by means of compass and straightedge.

The ancient Babylonians used the trapezoidal rule to integrate the motion of Jupiter along the ecliptic.^[3]

Antique method to find the Geometric mean

For a quadrature of a rectangle with the sides a and b it is necessary to construct a square with the side $x={\sqrt {ab}}$ (the Geometric mean of a and b). For this purpose it is possible to use the following fact: if we draw the circle with the sum of a and b as the diameter, then the height BH (from a point of their connection to crossing with a circle) equals their geometric mean. The similar geometrical construction solves a problem of a quadrature for a parallelogram and a triangle.

The area of a segment of a parabola

Problems of quadrature for curvilinear figures are much more difficult. The quadrature of the circle with compass and straightedge had been proved in the 19th century to be impossible. Nevertheless, for some figures (for example the Lune of Hippocrates) a quadrature can be performed. The quadratures of a sphere surface and a parabola segment done by Archimedes became the highest achievement of the antique analysis.

The area of the surface of a sphere is equal to quadruple the area of a great circle of this sphere.
The area of a segment of the parabola cut from it by a straight line is 4/3 the area of the triangle inscribed in this segment.

For the proof of the results Archimedes used the Method of exhaustion of Eudoxus.

In medieval Europe the quadrature meant calculation of area by any method. More often the Method of indivisibles was used; it was less rigorous, but more simple and powerful. With its help Galileo Galilei and Gilles de Roberval found the area of a cycloid arch, Grégoire de Saint-Vincent investigated the area under a hyperbola (Opus Geometricum, 1647), and Alphonse Antonio de Sarasa, de Saint-Vincent’s pupil and commentator, noted the relation of this area to logarithms.

John Wallis algebrised this method: he wrote in his Arithmetica Infinitorum (1656) series that we now call the definite integral, and he calculated their values. Isaac Barrow and James Gregory made further progress: quadratures for some algebraic curves and spirals. Christiaan Huygens successfully performed a quadrature of some Solids of revolution.

The quadrature of the hyperbola by Saint-Vincent and de Sarasa provided a new function, the natural logarithm, of critical importance.

With the invention of integral calculus came a universal method for area calculation. In response, the term quadrature has become traditional, and instead the modern phrase «computation of a univariate definite integral» is more common.

Methods for one-dimensional integrals[edit]

Numerical integration methods can generally be described as combining evaluations of the integrand to get an approximation to the integral. The integrand is evaluated at a finite set of points called integration points and a weighted sum of these values is used to approximate the integral. The integration points and weights depend on the specific method used and the accuracy required from the approximation.

An important part of the analysis of any numerical integration method is to study the behavior of the approximation error as a function of the number of integrand evaluations. A method that yields a small error for a small number of evaluations is usually considered superior. Reducing the number of evaluations of the integrand reduces the number of arithmetic operations involved, and therefore reduces the total round-off error. Also, each evaluation takes time, and the integrand may be arbitrarily complicated.

A ‘brute force’ kind of numerical integration can be done, if the integrand is reasonably well-behaved (i.e. piecewise continuous and of bounded variation), by evaluating the integrand with very small increments.

Quadrature rules based on interpolating functions[edit]

A large class of quadrature rules can be derived by constructing interpolating functions that are easy to integrate. Typically these interpolating functions are polynomials. In practice, since polynomials of very high degree tend to oscillate wildly, only polynomials of low degree are used, typically linear and quadratic.

Illustration of the rectangle rule.

The simplest method of this type is to let the interpolating function be a constant function (a polynomial of degree zero) that passes through the point ${\textstyle \left({\frac {a+b}{2}},f\left({\frac {a+b}{2}}\right)\right)}$ . This is called the midpoint rule or rectangle rule

$\int _{a}^{b}f(x)\,dx\approx (b-a)f\left({\frac {a+b}{2}}\right).$

Illustration of the trapezoidal rule.

The interpolating function may be a straight line (an affine function, i.e. a polynomial of degree 1)
passing through the points $\left(a,f(a)\right)$ and $\left(b,f(b)\right)$ .
This is called the trapezoidal rule

$\int _{a}^{b}f(x)\,dx\approx (b-a)\left({\frac {f(a)+f(b)}{2}}\right).$

Illustration of Simpson’s rule.

For either one of these rules, we can make a more accurate approximation by breaking up the interval [a,b] into some number of subintervals, computing an approximation for each subinterval, then adding up all the results. This is called a composite rule, extended rule, or iterated rule. For example, the composite trapezoidal rule can be stated as

$\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{n}}\left({f(a) \over 2}+\sum _{k=1}^{n-1}\left(f\left(a+k{\frac {b-a}{n}}\right)\right)+{f(b) \over 2}\right),$

where the subintervals have the form $[a+kh,a+(k+1)h]\subset [a,b],$ with ${\textstyle h={\frac {b-a}{n}}}$ and $k=0,\ldots ,n-1.$ Here we used subintervals of the same length but one could also use intervals of varying length $\left(h_{k}\right)_{k}$ .

Interpolation with polynomials evaluated at equally spaced points in [a,b] yields the Newton–Cotes formulas, of which the rectangle rule and the trapezoidal rule are examples. Simpson’s rule, which is based on a polynomial of order 2, is also a Newton–Cotes formula.

Quadrature rules with equally spaced points have the very convenient property of nesting. The corresponding rule with each interval subdivided includes all the current points, so those integrand values can be re-used.

If we allow the intervals between interpolation points to vary, we find another group of quadrature formulas, such as the Gaussian quadrature formulas. A Gaussian quadrature rule is typically more accurate than a Newton–Cotes rule that uses the same number of function evaluations, if the integrand is smooth (i.e., if it is sufficiently differentiable). Other quadrature methods with varying intervals include Clenshaw–Curtis quadrature (also called Fejér quadrature) methods, which do nest.

Gaussian quadrature rules do not nest, but the related Gauss–Kronrod quadrature formulas do.

Generalized midpoint rule formula[edit]

A generalized midpoint rule formula is given by

$\int _{0}^{1}f(x)\,dx=\sum _{m=1}^{M}{\sum _{n=0}^{\infty }{{\frac {\left({-1}\right)^{n}+1}{{\left(2M\right)^{n+1}}\left({n+1}\right)!}}{{\left.f^{(n)}(x)\right|}_{x={\frac {m-1/2}{M}}}}}}$

$\int _{0}^{1}{f(x)\,dx}=\lim _{N\to \infty }\sum _{m=1}^{M}{\sum _{n=0}^{N}{{\frac {\left({-1}\right)^{n}+1}{{{\left({2M}\right)}^{n+1}}\left({n+1}\right)!}}{\left.f^{(n)}(x)\right|_{x={\frac {m-1/2}{M}}}}}},$

where $f^{(n)}(x)$ denotes -th derivative.^[4] For example, substituting $M=1$ and

$f(x)={\frac {\theta }{1+\theta ^{2}x^{2}}}$

in the generalized midpoint rule formula, we obtain an equation of the inverse tangent

$\tan ^{-1}(\theta )=i\sum _{n=1}^{\infty }{\frac {1}{2n-1}}\left({\frac {1}{\left(1+2i/\theta \right)^{2n-1}}}-{\frac {1}{\left(1-2i/\theta \right)^{2n-1}}}\right)=2\sum _{n=1}^{\infty }{{\frac {1}{2n-1}}{\frac {a_{n}\left(\theta \right)}{a_{n}^{2}\left(\theta \right)+b_{n}^{2}\left(\theta \right)}}},$

where $i={\sqrt {-1}}$ is the imaginary unit and

${\begin{aligned}a_{1}(\theta )&={\frac {2}{\theta }},\\b_{1}(\theta )&=1,\\a_{n}(\theta )&=\left(1-{\frac {4}{\theta ^{2}}}\right)\,a_{n-1}(\theta )+{\frac {4}{\theta }}\,b_{n-1}(\theta ),\\b_{n}(\theta )&=\left(1-{\frac {4}{\theta ^{2}}}\right)\,b_{n-1}(\theta )-{\frac {4}{\theta }}\,a_{n-1}(\theta ).\end{aligned}}$

Since at each odd the numerator of the integrand becomes $(-1)^{n}+1=0$ , the generalized midpoint rule formula can be reorganized as

$\int _{0}^{1}f(x)\,dx=2\sum _{m=1}^{M}{\sum _{n=0}^{\infty }{{\frac {1}{{\left(2M\right)^{2n+1}}\left({2n+1}\right)!}}{{\left.f^{(2n)}(x)\right|}_{x={\frac {m-1/2}{M}}}}}}\,\,.$

The following example of Mathematica code generates the plot showing difference between inverse tangent and its approximation truncated at $M=5$ and $N=10$ :

f[theta_, x_] := theta/(1 + theta^2 * x^2);

aTan[theta_, M_, nMax_] := 
    2*Sum[(Function[x, Evaluate[D[f[theta, x], {x, 2*n}]]][(m - 1/2)/
        M])/((2*n + 1)!*(2*M)^(2*n + 1)), {m, 1, M}, {n, 0, nMax}];

Plot[{ArcTan[theta] - aTan[theta, 5, 10]}, {theta, -Pi, Pi}, 
 PlotRange -> All]

For a function g(t) defined over interval (a,b) , its integral is

$\int _{a}^{b}g(t)\,dt=\int _{0}^{b-a}g(\tau +a)\,d\tau =(b-a)\int _{0}^{1}g((b-a)x+a)\,dx.$

Therefore, we can apply the generalized midpoint integration formula above by assuming that $f(x)=(b-a)\,g((b-a)x+a)$ .

Adaptive algorithms[edit]

If f(x) does not have many derivatives at all points, or if the derivatives become large, then Gaussian quadrature is often insufficient. In this case, an algorithm similar to the following will perform better:

def calculate_definite_integral_of_f(f, initial_step_size) -> float:
    """
    This algorithm calculates the definite integral of a function
    from 0 to 1, adaptively, by choosing smaller steps near
    problematic points.
    """
    x = 0.0
    h = initial_step_size
    accumulator = 0.0
    while x < 1.0:
        if x + h > 1.0:
            h = 1.0 - x  # At end of unit interval, adjust last step to end at 1.
        if error_too_big_in_quadrature_of_f_over_range(f, [x, x + h]):
            h = make_h_smaller(h)
        else:
            accumulator += quadrature_of_f_over_range(f, [x, x + h])
            x += h
            if error_too_small_in_quadrature_of_over_range(f, [x, x + h]):
                h = make_h_larger(h)  # Avoid wasting time on tiny steps.
    return accumulator

Some details of the algorithm require careful thought. For many cases, estimating the error from quadrature over an interval for a function f(x) isn’t obvious. One popular solution is to use two different rules of quadrature, and use their difference as an estimate of the error from quadrature. The other problem is deciding what «too large» or «very small» signify. A local criterion for «too large» is that the quadrature error should not be larger than t ⋅ h where t, a real number, is the tolerance we wish to set for global error. Then again, if h is already tiny, it may not be worthwhile to make it even smaller even if the quadrature error is apparently large. A global criterion is that the sum of errors on all the intervals should be less than t. This type of error analysis is usually called «a posteriori» since we compute the error after having computed the approximation.

Heuristics for adaptive quadrature are discussed by Forsythe et al. (Section 5.4).

[edit]

The accuracy of a quadrature rule of the Newton–Cotes type is generally a function of the number of evaluation points. The result is usually more accurate as the number of evaluation points increases, or, equivalently, as the width of the step size between the points decreases. It is natural to ask what the result would be if the step size were allowed to approach zero. This can be answered by extrapolating the result from two or more nonzero step sizes, using series acceleration methods such as Richardson extrapolation. The extrapolation function may be a polynomial or rational function. Extrapolation methods are described in more detail by Stoer and Bulirsch (Section 3.4) and are implemented in many of the routines in the QUADPACK library.

Conservative (a priori) error estimation[edit]

Let have a bounded first derivative over [a,b], i.e. $f\in C^{1}([a,b]).$ The mean value theorem for $f,$ where $x\in [a,b),$ gives

$(x-a)f'(\xi _{x})=f(x)-f(a),$

for some $\xi _{x}\in (a,x]$ depending on .

If we integrate in from to on both sides and take the absolute values, we obtain

$\left|\int _{a}^{b}f(x)\,dx-(b-a)f(a)\right|=\left|\int _{a}^{b}(x-a)f'(\xi _{x})\,dx\right|.$

We can further approximate the integral on the right-hand side by bringing the absolute value into the integrand, and replacing the term in by an upper bound

$\left|\int _{a}^{b}f(x)\,dx-(b-a)f(a)\right|\leq {(b-a)^{2} \over 2}\sup _{a\leq x\leq b}\left|f'(x)\right|,$

(1)

where the supremum was used to approximate.

Hence, if we approximate the integral ${\textstyle \int _{a}^{b}f(x)\,dx}$ by the quadrature rule $(b-a)f(a)$ our error is no greater than the right hand side of 1. We can convert this into an error analysis for the Riemann sum, giving an upper bound of

${\frac {n^{-1}}{2}}\sup _{0\leq x\leq 1}\left|f'(x)\right|$

for the error term of that particular approximation. (Note that this is precisely the error we calculated for the example f(x)=x .) Using more derivatives, and by tweaking the quadrature, we can do a similar error analysis using a Taylor series (using a partial sum with remainder term) for f. This error analysis gives a strict upper bound on the error, if the derivatives of f are available.

This integration method can be combined with interval arithmetic to produce computer proofs and verified calculations.

Integrals over infinite intervals[edit]

Several methods exist for approximate integration over unbounded intervals. The standard technique involves specially derived quadrature rules, such as Gauss-Hermite quadrature for integrals on the whole real line and Gauss-Laguerre quadrature for integrals on the positive reals.^[5] Monte Carlo methods can also be used, or a change of variables to a finite interval; e.g., for the whole line one could use

$\int _{-\infty }^{\infty }f(x)\,dx=\int _{-1}^{+1}f\left({\frac {t}{1-t^{2}}}\right){\frac {1+t^{2}}{\left(1-t^{2}\right)^{2}}}\,dt,$

and for semi-infinite intervals one could use

${\begin{aligned}\int _{a}^{\infty }f(x)\,dx&=\int _{0}^{1}f\left(a+{\frac {t}{1-t}}\right){\frac {dt}{(1-t)^{2}}},\\\int _{-\infty }^{a}f(x)\,dx&=\int _{0}^{1}f\left(a-{\frac {1-t}{t}}\right){\frac {dt}{t^{2}}},\end{aligned}}$

as possible transformations.

Multidimensional integrals[edit]

The quadrature rules discussed so far are all designed to compute one-dimensional integrals. To compute integrals in multiple dimensions, one approach is to phrase the multiple integral as repeated one-dimensional integrals by applying Fubini’s theorem (the tensor product rule). This approach requires the function evaluations to grow exponentially as the number of dimensions increases. Three methods are known to overcome this so-called curse of dimensionality.

A great many additional techniques for forming multidimensional cubature integration rules for a variety of weighting functions are given in the monograph by Stroud.^[6]
Integration on the sphere has been reviewed by Hesse et al. (2015).^[7]

Monte Carlo[edit]

Monte Carlo methods and quasi-Monte Carlo methods are easy to apply to multi-dimensional integrals. They may yield greater accuracy for the same number of function evaluations than repeated integrations using one-dimensional methods.^{[citation needed]}

A large class of useful Monte Carlo methods are the so-called Markov chain Monte Carlo algorithms, which include the Metropolis–Hastings algorithm and Gibbs sampling.

Sparse grids[edit]

Sparse grids were originally developed by Smolyak for the quadrature of high-dimensional functions. The method is always based on a one-dimensional quadrature rule, but performs a more sophisticated combination of univariate results. However, whereas the tensor product rule guarantees that the weights of all of the cubature points will be positive if the weights of the quadrature points were positive, Smolyak’s rule does not guarantee that the weights will all be positive.

Bayesian Quadrature[edit]

Bayesian quadrature is a statistical approach to the numerical problem of computing integrals and falls under the field of probabilistic numerics. It can provide a full handling of the uncertainty over the solution of the integral expressed as a Gaussian process posterior variance.

Connection with differential equations[edit]

The problem of evaluating the integral

$F(x)=\int _{a}^{x}f(u)\,du$

can be reduced to an initial value problem for an ordinary differential equation by applying the first part of the fundamental theorem of calculus. By differentiating both sides of the above with respect to the argument x, it is seen that the function F satisfies

${\frac {dF(x)}{dx}}=f(x),\quad F(a)=0.$

Methods developed for ordinary differential equations, such as Runge–Kutta methods, can be applied to the restated problem and thus be used to evaluate the integral. For instance, the standard fourth-order Runge–Kutta method applied to the differential equation yields Simpson’s rule from above.

The differential equation has a special form: the right-hand side contains only the independent variable (here ) and not the dependent variable (here ). This simplifies the theory and algorithms considerably. The problem of evaluating integrals is thus best studied in its own right.

References[edit]

^ Weisstein, Eric W. «Cubature». MathWorld.
^ «Earliest Known Uses of Some of the Words of Mathematics (Q)». jeff560.tripod.com. Retrieved 31 March 2018.
^ Mathieu Ossendrijver (Jan 29, 2016). «Ancient Babylonian astronomers calculated Jupiter’s position from the area under a time-velocity graph». Science. 351 (6272): 482–484. Bibcode:2016Sci…351..482O. doi:10.1126/science.aad8085. PMID 26823423. S2CID 206644971.
^ S. M. Abrarov and B. M. Quine (2018), «A formula for pi involving nested radicals», The Ramanujan Journal, 46 (3): 657–665, arXiv:1610.07713, doi:10.1007/s11139-018-9996-8, S2CID 119150623
^ Leader, Jeffery J. (2004). Numerical Analysis and Scientific Computation. Addison Wesley. ISBN 978-0-201-73499-7.
^ Stroud, A. H. (1971). Approximate Calculation of Multiple Integrals. Cliffs, NJ: Prentice-Hall Inc. ISBN 9780130438935.
^ Kerstin Hesse, Ian H. Sloan, and Robert S. Womersley: Numerical Integration on the Sphere. In W. Freeden et al. (eds.), Handbook of Geomathematics, Springer: Berlin 2015, doi:10.1007/978-3-642-54551-1_40

Philip J. Davis and Philip Rabinowitz, Methods of Numerical Integration.
George E. Forsythe, Michael A. Malcolm, and Cleve B. Moler, Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice-Hall, 1977. (See Chapter 5.)
Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007), «Chapter 4. Integration of Functions», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
Josef Stoer and Roland Bulirsch, Introduction to Numerical Analysis. New York: Springer-Verlag, 1980. (See Chapter 3.)
Boyer, C. B., A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach, New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7).
Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0,

External links[edit]

Integration: Background, Simulations, etc. at Holistic Numerical Methods Institute
Lobatto Quadrature from Wolfram Mathworld
Lobatto quadrature formula from Encyclopedia of Mathematics
Implementations of many quadrature and cubature formulae within the free Tracker Component Library.
SageMath Online Integrator

Источник

5.3. Численное интегрирование. Простейшие методы

Вычисление определённых интегралов: базовые алгоритмы

Определение интеграла

Квадратурные формулы

Вычислительная задача

Кусочно-постоянная аппроксимация

Кусочно-линейная аппроксимация

Контроль точности вычисления

Кусочно-параболическая аппроксимация

Что дальше?

Некоторые замечания

Заключение

Литература

Reasons for numerical integration[edit]

History[edit]

Methods for one-dimensional integrals[edit]

Quadrature rules based on interpolating functions[edit]

Generalized midpoint rule formula[edit]

Adaptive algorithms[edit]

[edit]

Conservative (a priori) error estimation[edit]

Integrals over infinite intervals[edit]

Multidimensional integrals[edit]

Monte Carlo[edit]

Sparse grids[edit]

Bayesian Quadrature[edit]

Connection with differential equations[edit]

See also[edit]

References[edit]

External links[edit]

Интересное по теме: