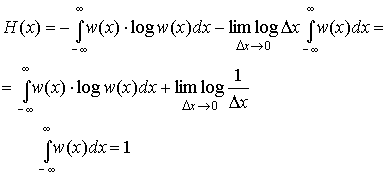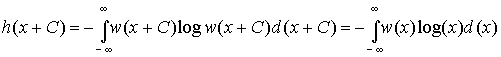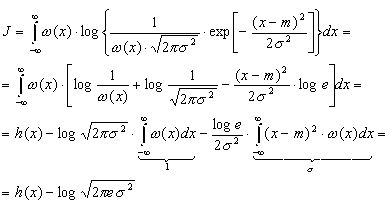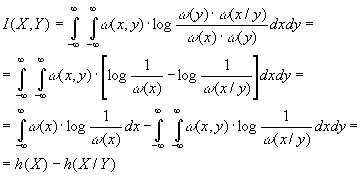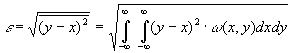Оценка ошибки квантования - Oshibku.top - решение и исправление самых разных ошибок

Будем
рассматривать квантование
с равномерным шагом x=const, т.е. равномерное
квантование.

Как было отмечено в §
3.1.1. в процессе квантования неизбежно
возникает ошибка квантования .
Последовательность ошибок квантования
(kt), возникающая при квантовании
процесса с дискретным временем, называется
шумом квантования. Обычно шум квантования
предполагают стационарным эргодическим
случайным процессом.

Чаще всего
интерес представляют максимальное
значение ошибки квантования, ее среднее
значение , равное математическому
ожиданию шума и среднеквадратическое
отклонение _,
равное квадратному корню из дисперсии
шума
(она характеризует мощность шума
квантования). Все эти величины зависят
от способа округления, применяемого
при квантовании, кроме того

и
_
зависят от закона распределения w()
мгновенных значений сигнала в пределах
шага квантования.

Считая шаг квантования
x малым по сравнению с диапазоном
изменения сигнала, плотность w(x) в
пределах этого шага можно принять
равномерной, т.е.

.

Различают
квантование с округлением, с усечением
и с усечением модуля.

При квантовании
с округлением истинному значению отсчета
приписывает ближайший разрешенный
уровень квантования независимо от того,
находится он сверху или снизу. Очевидно,
что при этом

_max=0.5x;

(3.31а)

Квантование
с округлением требует определенной
сложности в реализации. Проще выполняется
квантование с усечением, при котором
истинному значению отсчета приписывается
ближайший нижний уровень. При
этом

_max=x;

т.е.
максимальное значение погрешности в 2
раза больше, а

,
что приводит к накоплению погрешности
квантования при дальнейшей обработке
квантованной последовательности.

Промежуточное
положение по точности и сложности
реализации занимает квантование с
усечением модуля, которое для положительных
отсчетов является таким же, как и
квантование с усечением. Отрицательным
отсчетам приписывается ближайший
верхний уровень. При этом

то
есть накопление погрешностей не
происходит, но в 2 раза увеличивается
максимальная погрешность, и в 2 раза —
мощность шума квантования

.
Выбирая достаточно большее число уровней
квантования N, шаг квантования.

,
а следовательно и все рассмотренные
погрешности можно сделать необходимо
малыми. При неравномерном законе
распределения мгновенных значений
сигнала квантования с постоянным шагом

не
является оптимальным по критерию
минимума среднеквадратической ошибки

.
Квантуя участки с менее вероятными
значениями сигнала с большим шагом
значение

можно
уменьшить, при этом же количестве уровней
квантования.

3.3. Информация в непрерывных сообщениях

Для
того, чтобы оценить потенциальные
возможности передачи сообщений
по непрерывным каналам, необходимо
вести количественные информационные
характеристики непрерывных сообщений
и каналов.
Обобщим с этой целью понятие энтропии
и взаимной
информации
на ансамбли непрерывных сигналов.

Пусть
Х — случайная величина (сечение или
отсчет случайного процесса), определенная
в некоторой непрерывной области и ее
распределение вероятностей характеризуется
плотностью w(х).

Разобьем область
значений Х на небольшие интервалы
протяженностью x. Вероятность Р_к
того, что х_к<x<x_к+
x, приблизительно равна w(х_к)
x т.е.

Р_к=Р(
х_к<x<x_к+x)

w(х_к)x,

(3.32)

причем
приближение тем точнее, чем меньше
интервал x. Степень положительности
такого события.

Если
заменить истинные значения Х в пределах
интервала x значениями х_к
в начале интервала, то непрерывный
ансамбль заменится дискретным и его
энтропия в соответствии с (1.4)
определится, как

или
с учетом (3.32)

(3.33)

Будем
теперь увеличивать точность определения
значения х, уменьшения интервал x. В
пределе при x0 получим
энтропию непрерывной случайной величины.

(3.34)

Второй
член в полученном выражении стремится
к

и
совершенно не зависит от распределения
вероятностей Х. Это означает, что
собственная информация любой непрерывной
случайной величины бесконечно велика.
Физический смысл такого результата
становиться понятным, если учесть, что
в конечном диапазоне непрерывная
величина может принимать бесконечное
множество значений, поэтому вероятность
того, что ее реализация будет точно
равна какому-то наперед заданному
конкретному значению является бесконечно
малой величиной 0. В результате энтропия,
определенная в соответствии с (1.4),
характеризующая среднюю степень
неожиданности появления возможных
реализаций для любой непрерывной
случайной величины не зависит от ее
закона распределения и всегда равна
бесконечности. Поэтому для описания
информационных свойств непрерывных
величин необходимо ввести другие
характеристики. Это можно сделать, если
обратить внимание на то, что первое
слагаемое выражении (3.34) является
конечным и однозначно определяется
плотностью распределения вероятности
w(x). Его называют дифференциальной
энтропией и обозначают h(x):

(3.35)

Дифференциальная
энтропия обладает следующими свойствами.

1.
Дифференциальная энтропия в отличии
от обычной энтропии дискретного источника
не является мерой собственной информации,
содержащейся в ансамбле значений
случайной величины Х. Она зависит от
масштаба Х и может принимать отрицательные
значения. Информационный смысл имеет
не сама дифференциальная энтропия, а
разность двух дифференциальных энтропий,
чем и объясняется ее название.

2.
Дифференциальная энтропия не меняется
при изменении всех возможных значений
случайной величины Х на постоянную
величину. Действительно, масштаб Х при
этом не меняется и
справедливо равенство

(3.36)

Из
этого следует, что h(x) не зависит от
математического ожидания случайной
величины, т.к. изменяя все значения Х на
С мы тем самым изменяем на С и ее среднее,
то есть математическое ожидание.

3.
Дифференциальная энтропия аддитивна,
то есть для объединения ХY независимых
случайный величин Х и Y справедливо:

h(XY)=
h(X)+ h(Y).

Доказательство этого свойства
аналогично доказательству (1.8) аддитивности
обычной энтропии.

4. Из всех
непрерывных величин Х с фиксированной
дисперсией ²
наибольшую дифференциальную энтропию

имеет
величина с гауссовским распределением,
т.е.

(3.37)

Доказательство
свойства проведем в два этапа: сначала
вычислим h(x) для гауссовского распределения,
задаваемого плотностью.

где
м — математическое ожидание,

а затем
докажем неравенство (3.37).

Подставив
(3.38) в (3.35) найдем<

Для
доказательства неравенства (3.37) зададимся
произвольным распределением (х) с
дисперсией ²
и математическим ожиданием m и вычислим
интеграл J вида

Но
в силу неравенства (1.7)
с учетом правила изменения основания
логарифмов (log t = log e  ln t)
имеем:

так
как подинтегральное выражение —
гауссовская плотность распределения
см.(3.38).

Таким
образом

,
откуда

.

Но
как только что было показано,

—
это дифференциальная энтропия гауссовского
распределения. Доказанное неравенство
и означает, что энтропия
гауссовского распределения
максимальна.

Попытаемся теперь
определить с помощью предельного
перехода взаимную
информацию между двумя непрерывными
случайными величинами X и Y. Разбив
области определения Х и Y соответственно
на небольшие интервалы x и y, заменим
эти величины дискретными так же, как
это делалось при выводе формулы
(3.34).

Исходя из выражения
(1.14) можно определить взаимную информацию
между величинами Х и Y .

(3.39)

При
этом предельном переходе никаких явных
бесконечностей не появилось, т.е. взаимная
информация оказывается величиной
конечной, имеющей тот же смысл, что и
для дискретных сообщений.

С
учетом того, что

(x,y)= (y)

(x/y)

равенство
(3.39) можно представить в виде

(3.40)

Здесь
h(X) — определенная выражением (3.35)
дифференциальная энтропия Х, а

(3.41)

h(X/Y)
— условная дифференциальная энтропия.
Можно показать, что во всех случаях
h(X/Y)h(X).

Формула
(3.40) имеет ту же форму, что и (1.13), а
отличается лишь заменой энтропии
дифференциальной энтропией. Легко
убедиться, что основные свойства 1 и 2
(см. пункт 1.3) взаимной информации,
описываемые равенствами (1.15)(1.17),
остаются справедливыми и в этом случае.

3.4 -энтропия
и -производительность
источника непрерывных сообщений

Как
было показано в § 3.3, в одном отсчете
любого непрерывного сообщения содержится
бесконечное количество собственной
информации. И тем не менее, непрерывные
сообщения (телефонные разговоры,
телепередачи) успешно передаются по
каналам связи. Это объясняется тем, что
на практике никогда не требуется
абсолютно точного воспроизведения
переданного сообщения, а для передачи
даже с очень высокой, но ограниченной
точностью, требуется конечное количество
информации, также как и при передаче
дискретных сообщений. Данное обстоятельство
и положено в основу определения
количественной меры собственной
информации, источников непрерывных
сообщений. В качестве такой меры,
принимается минимальное количество
информации, необходимое для воспроизведения
непрерывного сообщения с заданной
точностью. Очевидно, что при таком
подходе собственная информация зависит
не только от свойств источника сообщений,
но и от выбора параметра , характеризующего
точность воспроизведения. Возможны
различные подходы к определению  в
зависимости от вида и назначения
передаваемой информации. Наиболее часто
в информационной технике в качестве 
используют среднеквадратическое
отклонение между принятым у и переданным
х сигналами, отражающими непрерывные
сообщения, т.е.

(3.42)

где
Х и Y – ансамбли сигналов, отражающих
исходное и воспроизведенное сообщения.

Два
варианта сообщения или сигнала,
различающиеся не более, чем на заданное
значение ₀,
называются эквивалентными. Взаимная
информация
I(X,Y) между двумя эквивалентными процессами
X(t) и Y(t) может быть определена в соответствии
с (3.40) как

I(X,Y)=h(X)-h(X/Y),

где
h(X) и h(X/Y) – соответственно дифференциальная
и условная дифференциальная энтропии.

Из приведенного выражения видно,
что величина I(X,Y) зависит не только от
собственного распределения (х) ансамбля
Х (см. (3.35)), но и от условного распределения
(x/y) (см. (3.41)), которое определяется
способом преобразования процесса X в
Y. Для характеристики собственной
информации, содержащейся в одном отсчете
процесса Х, нужно устранить ее зависимость
от способа преобразования сообщения Х
в эквивалентное ему сообщение Y. Этого
можно добиться, если под количеством
собственной информации или  — энтропией
H_(Х)
процесса Х понимать минимизированную
по всем распределениям (X/Y) величину
I(X,Y), при которой сообщения Х
и Y еще эквивалентны, т.е.

(3.43)

Таким
образом, 
— энтропия
определяет минимальное количество
информации, содержащейся в одном отсчете
непрерывного
сообщения,
необходимое для воспроизведения его с
заданной верностью.

Если ансамбль
сообщений Х представляет собой процесс
с дискретным
временем
с непрерывными отсчетами, то под 
— производительностью источника понимают
величину

(3.44)

где
_с
– количество отсчетов сообщения,
выдаваемых в единицу времени.

В том
случае, когда Х — непрерывный случайный
процесс с ограниченным спектром, вся
информация, содержащаяся в его значениях,
эквивалентна информации, содержащейся
в отсчетах процесса, следующих друг за
другом с интервалом

,
(f_m-граничная
частота спектра), т.е. со
скоростью

_c=2
_m.

(3.45)

При
этом 
— производительность
источника или процесса по-прежнему
определяется выражением (3.44), где величина
_с
рассчитывается из условия (3.45).

В том
случае, если следующие друг за другом
отсчеты процесса коррелированны
(взаимозависимы), величина Н_(Х)
в (3.43) должна вычисляться с учетом
вероятностных связей между отсчетами.

Итак,
 — производительность источника
непрерывных сообщений представляет
собой минимальное количество информации,
которое нужно создать источнику в
единицу времени, для воспроизведения
его сообщений с заданной верностью.


— производительность называют также
скоростью создания информации при
заданном критерии верности.

Максимально
возможная  — производительность

непрерывного
источника Х обеспечивается при гауссовском
распределении Х с дисперсией

(при
этом условии h(X) максимальна (см. (3.37)).
Оценим значение

.
Рассмотрим случай, когда непрерывное
сообщение X(t) представляет собой
стационарный гауссовский процесс с
равномерным энергетическим спектром,
ограниченным частотой F_c,
и с заданной мощностью (дисперсией) Р_х,
а критерий эквивалентности  задан в
виде (3.42).
Будем считать, что заданная верность
воспроизведения обусловлена действием
аддитивной статистически не связанной
с сигналом помехи (t) с математическим
ожиданием М[]=0 и дисперсией (мощностью)

.
Исходный сигнал Х рассматриваем
как сумму воспроизводящего сигнала Y и
помехи:

X=Y+.

При
этом, поскольку (x/y)= (y+/y)= (/y)=
(), то h(X/Y) полностью определяется
шумом воспроизведения (t). Поэтому max
h(X/Y)=max h(). Так как шум воспроизведения
имеет фиксированную дисперсию

,
то дифференциальная энтропия имеет
максимум (3.37) при гауссовском
распределении шума

В
свою очередь дифференциальная энтропия
гауссовского источника с дисперсией

.

Следовательно,
 — энтропия на один отсчет
сообщения

(3.46)

Величина

характеризует
минимальное отношение сигнал-шум, при
котором сообщения X(t) и Y(t) еще
эквивалентны.

Согласно теореме
Котельникова
шаг
дискретизации

,
а _c=2
F_c.
При этом равномерность спектра сообщения
обеспечивает некоррелированность
отстоящих на t друг от друга отсчетов,
а гауссовский характер распределения
X(t) — их независимость. Следовательно,
в соответствии с (3.44)

или с учетом (3.46)

(3.47)

Количество
информации,
выданное таким источником за время Т_с

(3.48)

Интересно
отметить, что правая часть выражения
(3.48) совпадает с наиболее общей
характеристикой сигнала, называемой
его объемом, если принять динамический
диапазон сигнала D=log 
₀.
Это означает, что объем сигнала равен
максимальному количеству информации,
которое может содержаться в сигнале
длительностью Т_с.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Sensors

Andrea Colagrossi, … Matteo Battilana, in Modern Spacecraft Guidance, Navigation, and Control, 2023

Quantization errors

Quantization error is a systematic error resulting from the difference between the continuous input value and its quantized output, and it is like round-off and truncation errors. This error is intrinsically associated with the AD conversion that maps the input values from a continuous set to the output values in a countable set, often with a finite number of elements. The quantization error is linked to the resolution of the sensor. Namely, a high-resolution sensor has a small quantization error. Indeed, the maximum quantization error is smaller than the resolution interval of the output, which is associated to the least significant bit representing the smallest variation that can be represented digitally:

LSB=FSR2NBIT

where FSR is the full-scale range of the sensor, and NBIT is the number of bits (i.e., the resolution) used in the AD converter to represent the sensor’s output. Quantization errors are typically not corrected, and the discrete values of the output are directly elaborated by the GNC system, which is designed to operate on digital values.

Fig. 6.9 shows a convenient model block to simulate quantization errors.

Figure 6.9. Quantization error model.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780323909167000068

Digital Filters

Marcio G. Siqueira, Paulo S.R. Diniz, in The Electrical Engineering Handbook, 2005

2.11 Quantization in Digital Filters

Quantization errors in digital filters can be classified as:

•: Round-off errors derived from internal signals that are quantized before or after more down additions;
•: Deviations in the filter response due to finite word length representation of multiplier coefficients; and
•: Errors due to representation of the input signal with a set of discrete levels.

A general, digital filter structure with quantizers before delay elements can be represented as in Figure 2.23, with the quantizers implementing rounding for the granular quantization and saturation arithmetic for the overflow nonlinearity.

FIGURE 2.23. Digital Filter Including Quantizers at the Delay Inputs

The criterion to choose a digital filter structure for a given application entails evaluating known structures with respect to the effects of finite word length arithmetic and choosing the most suitable one.

2.11.1 Coefficient Quantization

Approximations are known to generate digital filter coefficients with high accuracy. After coefficient quantization, the frequency response of the realized digital filter will deviate from the ideal response and eventually fail to meet the prescribed specifications. Because the sensitivity of the filter response to coefficient quantization varies with the structure, the development of low-sensitivity digital filter realizations has raised significant interest (Antoniou, 1993; Diniz et al., 2002).

A common procedure is to design the digital filter with infinite coefficient word length satisfying tighter specifications than required, to quantize the coefficients, and to check if the prescribed specifications are still met.

2.11.2 Quantization Noise

In fixed-point arithmetic, a number with a modulus less than one can be represented as follows:

(2.84)x=b0b1b2b3…bb,

where b₀ is the sign bit and where b₁b₂b₃ … b_b represent the modulus using a binary code. For digital filtering, the most widely used binary code is the two’s complement representation, where for positive numbers b₀ = 0 and for negative numbers b₀ = 1. The fractionary part of the number, called x₂ here, is represented as:

(2.85)x2={xif b0=0.2−|x|if b0=1.

The discussion here concentrates in the fixed-point implementation.

A finite word length multiplier can be modeled in terms of an ideal multiplier followed by a single noise source e(n) as shown in Figure 2.24.

FIGURE 2.24. Model for the Noise Generated after a Multiplication

For product quantization performed by rounding and for signal levels throughout the filter much larger than the quantization step q = 2^−b, it can be shown that the power spectral density of the noise source e_i(n) is given by:

(2.86)Pei(z)=q212=2−2b12.

In this case, e_i(n) represents a zero mean white noise process. We can consider that in practice, e_i(n) and e_k(n + l) are statistically independent for any value of n or l (for i ≠ k). As a result, the contributions of different noise sources can be taken into consideration separately by using the principle of superposition.

The power spectral density of the output noise, in a fixed-point digital-filter implementation, is given by:

(2.87)Py(z)=σe2Σi=1KGi(z)Gi(z−1),

where Pei(ejw)=σe2, for all i, and each G_i(z) is a transfer function from multiplier output (g_i(n)) to the output of the filter as shown in Figure 2.25. The word length, including sign, is b + 1 bits, and K is the number of multipliers of the filter.

FIGURE 2.25. Digital Filter Including Scaling and Noise Transfer Functions.

2.11.3 Overflow Limit Cycles

Overflow nonlinearities influence the most significant bits of the signal and cause severe distortion. An overflow can give rise to self-sustained, high-amplitude oscillations known as overflow limit cycles. Digital filters, which are free of zero-input limit cycles, are also free of overflow oscillations if the overflow nonlinearities are implemented with saturation arithmetic, that is, by replacing the number in overflow by a number with the same sign and with maximum magnitude that fits the available wordlength.

When there is an input signal applied to a digital filter, overflow might occur. As a result, input signal scaling is required to reduce the probability of overflow to an acceptable level. Ideally, signal scaling should be applied to ensure that the probability of overflow is the same at each internal node of the digital filter. This way, the signal-to-noise ratio is maximized in fixed-point implementations.

In two’s complement arithmetic, the addition of more than two numbers will be correct independently of the order in which they are added even if overflow occurs in a partial summation as long as the overall sum is within the available range to represent the numbers. As a result, a simplified scaling technique can be used where only the multiplier inputs require scaling. To perform scaling, a multiplier is used at the input of the filter section as illustrated in Figure 2.25.

It is possible to show that the signal at the multiplier input is given by:

(2.88)xi(n)=12πj∮cXi(z)zn−1dz=12π∫02πFi(ejω)X(ejω)ejωndω,

where c is the convergence region common to F_i(z) and X(z).

The constant λ is usually calculated by using L_p norm of the transfer function from the filter input to the multiplier input F_i(z), depending on the known properties of the input signal. The L_p norm of F_i(z) is defined as:

(2.89)‖Fi(ejω)‖p=[12π∫02π|Fi(ejω)|pdω]1p,

for each p ≥ 1, such that ∫02π|Fi(ejω)|pdω≤∞. In general, the following inequality is valid:

(2.90)|xi(n)| ≤ ‖Fi‖p‖X‖q, (1p+1q=1),

for p, q = 1, 2 and ∞.

The scaling guarantees that the magnitudes of multiplier inputs are bounded by a number M_max when |x(n)| ≤ M_max. Then, to ensure that all multiplier inputs are bounded by M_max we must choose λ as follows:

(2.91)λ=1Max{‖F1‖p,…,‖F1‖p,…, ‖FK‖p},

which means that:

(2.92)‖F′i(ejω)‖p≤1, for‖X(ejω)‖q ≤ Mmax.

The K is the number of multipliers in the filter.

The norm p is usually chosen to be infinity or 2. The L_∞ norm is used for input signals that have some dominating frequency component, whereas the L₂ norm is more suitable for a random input signal. Scaling coefficients can be implemented by simple shift operations provided they satisfy the overflow constraints.

In case of modular realizations, such as cascade or parallel realizations of digital filters, optimum scaling is accomplished by applying one scaling multiplier per section.

As an illustration, we present the equation to compute the scaling factor for the cascade realization with direct-form second-order sections:

(2.93)λi=1‖∏j=1i−1Hj(z)Fi(z)‖p,

where:

Fi(z)=1z2+m1iz+m2i.

The noise power spectral density is computed as:

(2.94)Py(z)=σe2[3+3λ12∏i=1mHi(z)Hi(z−1)+5Σj=2m1λj2∏i=jmHi(z)Hi(z−1)],

whereas the output noise variance is given by:

(2.95)σo2=σe2[3+3λ12||∏i=1mHi(ejω)||22+5Σj=2m1λj2||∏i=jmHi(ejω)||22].

As a design rule, the pairing of poles and zeros is performed as explained here: poles closer to the unit circle pair with closer zeros to themselves, such that ||H_i(z)||_p is minimized for p = 2 or p = ∞.

For ordering, we define the following:

(2.96)Pi=| |Hi(z)| |∞| |Hi(z)| |2.

For L₂ scaling, we order the section such that P_i is decreasing. For L_∞ scaling, P_i should be increasing.

2.11.4 Granularity Limit Cycles

The quantization noise signals become highly correlated from sample to sample and from source to source when signal levels in a digital filter become constant or very low, at least for short periods of time. This correlation can cause autonomous oscillations called granularity limit cycles.

In recursive digital filters implemented with rounding, magnitude truncation,⁷² and other types of quantization, limitcycles oscillations might occur.

In many applications, the presence of limit cycles can be harmful. Therefore, it is desirable to eliminate limit cycles or to keep their amplitude bounds low.

If magnitude truncation is used to quantize particular signals in some filter structures, it can be shown that it is possible to eliminate zero-input limit cycles. As a consequence, these digital filters are free of overflow limit cycles when overflow nonlinearities, such as saturation arithmetic, are used.

In general, the referred methodology can be applied to the following class of structures:

•: State-space structures: Cascade and parallel realization of second-order state-space structures includes design constraints to control nonlinear oscillations (Diniz and Antoniou, 1986).
•: Wave digital filters: These filters emulate doubly terminated lossless filters and have inherent stability under linear conditions as well as in the nonlinear case where the signals are subjected to quantization (Fettweis, 1986).
•: Lattice realization: Modular structures allowing easy limit cycles elimination (Gray and Markel, 1975).

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780121709600500621

Biomedical signals and systems

Sri Krishnan, in Biomedical Signal Analysis for Connected Healthcare, 2021

2.2.1 Noise power

The quantization error (e) or noise tends to have a random behavior, and they could be mathematically represented using statistical variables. Power of a random variable with a probability density function of p(e) could be obtained by computing the second-order statistics of variance, and it is denoted by

σ2=∫−q/2q/2e2p(e)de

A good assumption for p(e) is a uniform probability density function which will have a value of 1/q over the range of −q/2 to q/2.

=∫−q/2q/2e2·1qde=q212

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128130865000049

Measurement of high voltages

E. Kuffel, … J. Kuffel, in High Voltage Engineering Fundamentals (Second Edition), 2000

Static errors

The quantization error is present because the analogue value of each sample is transformed into a digital word. This A-to-D conversion entails a quantization of the recorder’s measuring range into a number of bands or code bins, each represented by its central value which corresponds to a particular digital code or level. The number of bands is given by 2^N, where N is the resolution of the A-to-D converter. The digital output to analogue input relationship of an ideal digitizer is shown diagrammatically in Fig. 3.49. For any input in the range (iΔV_av – 0.5 * ΔV_av to iΔV_av + 0.5 * ΔV_av), where iΔV_av is the voltage corresponding to the width of each code bin, or one least significant bit (LSB), and iΔV_av is the centre voltage corresponding to the i th code, an ideal digitizer will return a value of I_i. Therefore, the response of an ideal digitizer to a slowly increasing linear ramp would be a stairway such as that shown in Fig. 3.50. A quick study of these figures reveals the character of the quantization error associated with the ideal A-to-D conversion process. The maximum error possible is equivalent to a voltage corresponding to ±(½) of an LSB. For an ideal digital recorder, this quantization would be the only source of error in the recorded samples. For a real digital recorder, this error sets the absolute upper limit on the accuracy of the readings. In the case of an 8-bit machine, this upper limit would be 0.39 per cent of the recorder’s full-scale deflection. The corresponding maximum accuracy (lowest uncertainty) of a 10-bit recorder is 0.10 per cent of its full-scale deflection.

Figure 3.49. Analogue input to digital output relation of an ideal A/D converter

Figure 3.50. Response of an ideal A/D converter to a slowly rising ramp

The error caused by discrete time sampling is most easily demonstrated with reference to the recording of sinusoidal signals. As an example we can look at the discrete time sampling error introduced in the measurement of a single cycle of a pure sine wave of frequency f, which is sampled at a rate of four times its frequency. When the sinusoid and the sampling clock are in phase, as shown in Fig. 3.51, a sample will fall on the peak value of both positive and negative half-cycles. The next closest samples will lie at π/2 radians from the peaks. As the phase of the clock is advanced relative to the input sinusoid the sample points which used to lie at the peak values will move to lower amplitude values giving an error (Δ) in the measurement of the amplitude (A) of

Figure 3.51. Sample points with sinusoid and sampling clock in phase. (Error in peak amplitude = 0)

Δ = A(1 − cos ϕ)

where ϕ is the phase shift in the sample points. This error will increase until ϕ – π/4 (Fig. 3.52). For ϕ > π/4 the point behind the peak value will now be closer to the peak and the error will decrease for a ϕ in the range of π/4 to π/2. The maximum per unit value of the discrete time sampling error is given by eqn 3.93,

Figure 3.52. Sample points with sampling clock phase advanced to π/4 with respect to the sinusoid. Error in peak amplitude (Δ) is at a maximum

(3.93)Δmax=I−cos(πfts)

where t_s is the recorder’s sampling interval and f the sinewave frequency.

The maximum errors obtained through quantization and sampling when recording a sinusoidal waveform are shown in Fig. 3.53. The plotted quantities were calculated for an 8-bit 200-MHz digitizer.

Figure 3.53. Sampling and quantization errors of an ideal recorder

In a real digital recorder, an additional two categories of errors are introduced. The first includes the instrument’s systematic errors. These are generally due to the digitizer’s analogue input circuitry, and are present to some degree in all recording instruments. They include such errors as gain drift, linearity errors, offset errors, etc. They can be compensated by regular calibration without any net loss in accuracy. The second category contains the digitizer’s dynamic errors. These become important when recording high-frequency or fast transient signals. The dynamic errors are often random in nature, and cannot be dealt with as simply as their systematic counterparts and are discussed below.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780750636346500046

Remaining useful life prediction

Yaguo Lei, in Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery, 2017

6.3.4.3 RUL Prediction

The constructed indicator WMQE is further input into the RUL prediction module. In this module, a PF-based prediction algorithm is utilized to predict RUL of the rotating machinery whose degradation processes are described using a variant of Paris–Erdogan model. The Paris–Erdogan model is formulated as

(6.96)dxdt=c(Δδ)γ, Δδ=mx

where x represents the semicrack length, t is the number of stress cycles (i.e., the fatigue life), c, γ, and m are material constants which are determined by tests, and Δδ is amplitude of stress intensity factor roughly proportional to the square root of x.

It is seen from Eq. (6.96) that there are several model parameters in the Paris–Erdogan model, that is, c, γ, and m, which are difficult to measure during the operation process of the rotating machinery. For convenient application, the Paris–Erdogan model is transformed into the following format with α=cmγ and β = γ/2.

(6.97)dxdt=αxβ.

Then, the above function is rewritten into the following state space model.

(6.98)xk=xk−1+αk−1xk−1βΔtkαk=αk−1zk=xk+νk,

where α_k−1 is a random variable following a normal distribution of Nμα,σα2, β is a constant parameter, Δtk=tk−tk−1, z_k is the measured WMQE value at t_k and ν_k is the measurement noise following the normal distribution of N0,σν2. With the transformation of the Paris–Erdogan model, the model parameters are more convenient to estimate according to the measurements. In addition, the state space model inherits the superiority of the Paris–Erdogan model in describing the general degradation processes. Therefore, it is supposed to be a good model for a general degradation process.

After the transformation, the unknown model parameters are changed to be Θ=μα,σα2,β,σν2′, where (·)′ denotes the vector transposition. Then, the measured WMQE values constructed from vibration signals are input into the model, and the model parameters are initialized using MLE. It is assumed that there are a series of measurements z0:M=z0,…,zM′ at ordered times t₀,…,t_M. According to Eq. (6.98), z_k is formulated as follows:

(6.99)zk=xk−1+αkxk−1βΔtk+νk.

The degradation state x_k−1 has the following relationship with the measurement z_k−1.

(6.100)xk−1=zk−1−νk−1.

The degradation state x_k−1 is hard to be acquired in real applications. If the measurement noise ν_k−1 is small enough compared with the measurement itself, it is negligible and x_k−1 is approximated by z_k−1. Let T=z0βΔt1,…,zM−1βΔtM′. z1:M=z1,…,zM′ is multivariate normally distributed, which is denoted as follows:

(6.101)z1:M∼Nz0:M−1+μαT,σα2TT′+σν2IM,

where I_M is an identity matrix of order M.

Let Δz1:M=z1−z0,…,zM−zM−1′, and the log-likelihood function of the unknown parameters based on the measurements is expressed as

(6.102)ℓΘ|z0:M=−M2ln2π−12lnσα2TT′+σν2IM −12Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT =−M2ln2π−M2lnσα2−12lnTT′+σ˜ν2IM −12σα2Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT,

with σ~ν2=σν2/σα2. The first partial derivatives of ℓΘ|z0:M with respect to μ_α and σα2 are calculated and formulated with

(6.103)∂ℓΘ|z0:M∂μα=1σα2T′TT′+σ~ν2IM-1Δz1:M−μαT,

(6.104)∂ℓΘ|z0:M∂σα2=−M2σα2+12σα4Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαT.

Let ∂ℓΘ|z0:M/∂μα=0 and ∂ℓΘ|z0:M/∂σα2=0. The MLE results of μ_α and σα2 are

(6.105)μα=T′TT′+σ~ν2IM−1Δz1:MT′TT′+σ~ν2IM−1T,

(6.106)σα2=Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαTM.

With Eqs. (6.105) and (6.106) substituted into Eq. (6.102), the log-likelihood function is reduced into a two-variable function about β and σ~ν2, which is denoted by

(6.107)ℓΘ|z0:M=−M2ln2π−M2lnσα2−12lnTT′+σ~ν2IM−M2.

The MLE values of β and σ~ν2 are obtained by maximizing the log-likelihood function (6.107) through two-dimensional optimizing. Then the MLE values of β and σ~ν2 are substituted into Eqs. (6.105) and (6.106), and the MLE values of μ_α and σα2 are acquired. The value of σν2 is calculated with σ~ν2 multiplied by σα2. Finally, all of the unknown parameters Θ=μα,σα2,β,σν2′ are initialized.

After parameter initialization, the model parameters are further updated and the RUL is predicted using a PF-based prediction algorithm. Based on the initialized parameters, a series of initial particles y0nn=1:Ns are sampled from the initial PDF of the system state p(y0n|Θ0)∼N(y0,Q0) with

(6.108)y0=x0μα and Q0=000σα2.

Ns is the number of particles and the weight of each particle is set to be 1/Ns. Then new particles ykni=1:Ns are obtained following

(6.109)ykn=xknμαn=xk−1n+μαnxk−1nβΔtkμαn.

When the new measurement z_k at t_k is available, each particle weight is updated and normalized by

(6.110)wkn=wk−1npzk|ykn, w~kn=wkn∑n=1Nswkn,

where

(6.111)pzk|ykn=12πσνexp−12zk−xknσν2.

The particles are resampled according to the particle weights and their weights are reset to be 1/Ns. After that, the RUL is predicted based on the resampled particles. The RUL l_k at t_k is defined as

(6.112)lk=inflk:xlk+tk≥λ|x1:k,

where λ is a prespecified failure threshold. Each particle is transmitted following the transition function of Eq. (6.98) from current state until the state value exceeds the failure threshold, and the RUL lknn=1:Ns predicted using each particle is acquired. Then the PDF of the RUL is approximated by

(6.113)plk|z0:k=∑n=1Nsw~knδlk−lkn.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128115343000068

Orbit and Attitude Sensors

Enrico Canuto, … Carlos Perez Montenegro, in Spacecraft Dynamics and Control, 2018

Exercise 1

Prove that the quantization error defined by Eq. (8.6) is bounded by |n˜y(i)|≤ρy/2 and under the random assumption has zero mean and variance equal to ρy2/12. □

A typical model of the random error d˜ in Eq. (8.4), which includes quantization errors, is the linear continuous-time stochastic state equation

(8.7)x˜˙(t)=A˜x˜+G˜w˜d˜(t)=C˜x˜+D˜w˜E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=S˜w2δ(τ)E{x˜(0)}=x˜0,E{(x˜(0)−x˜0)(x˜(0)−x˜0)T}=P˜0≥0E{(x˜(0)−x˜0)w˜T(0)}=0,

which is similar to the DT Eq. (4.159) of Section 4.8.1. Eq. (8.7) being continuous-time, the eigenvalues of the state matrix A˜ are assumed to lie on the imaginary axis and when equal to zero may be multiple. The statistics in Eq. (8.7) assumes that w˜ is a zero-mean second-order stationary white noise with constant spectral density S˜w2, and impulsive covariance, where δ(τ) denotes a Dirac delta (see Sections 13.2.1 and 13.7.3Section 13.2.1Section 13.7.3). The initial state may be modeled as a random vector with mean value x˜0 and covariance matrix P˜0, but is uncorrelated from any simultaneous white noise as expressed by the last identity in Eq. (8.7). This uncorrelation has been already referred to as the causality constraint. In principle, Eq. (8.7) may be unobservable from the output d˜ and uncontrollable by the noise w˜, because the output d˜ may include polynomial and trigonometric components (deterministic signals) just driven by the initial state x˜0. For instance, a trigonometric component tuned to the angular frequency ω˜ corresponds to a second-order subsystem with eigenvalues ±jω˜. A first-order polynomial corresponds to a second-order subsystem with a pair of zero eigenvalues and a single eigenvector. The mixed case of stochastic processes and deterministic signals can be simplified by assuming that trigonometric and polynomial components are the free response of the equations driven by w˜, and that Eq. (8.7) is observable and controllable.

The simplest model of the class in Eq. (8.7), which is common to inertial sensors (accelerometers in Section 8.4 and gyroscopes in Section 8.5), is the scalar first-order random drift [32]:

(8.8)x˜˙(t)=w˜x,x˜(0)=x˜0d˜(t)=x˜+w˜dE{x˜(0)}=x˜0,var{x˜}=σ02,E{(x˜−x˜0)w˜T(0)}=0w˜=[w˜xw˜d],E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=[S˜wx200S˜wd2]δ(τ),

where, if [unit] denotes the unit of measurement of x˜, we find S˜wx2 in [(unit/s)2Hz−1] and S˜wd2 in [unit2Hz−1]. The initial state x˜0 accounts for a constant bias and is uncorrelated with any simultaneous noise; the scalar input noise w˜x and the output noise w˜d in Eq. (8.8) are uncorrelated with each other. The output process d˜ is nonstationary and the autocorrelation is given by

(8.9)R˜d(t,t+τ)=S˜wx2min(t,t+τ)+S˜wd2δ(τ).

Although x˜ is nonstationary, the spectral density S˜x2(f) can be defined through the AS equation x˜˙=−εx˜+w˜x, where ε > 0 must be sufficiently smaller than the cutoff frequency f₀ to be defined in the next paragraph. We can write the following identities:

(8.10)S˜d2(f)=S˜x2(f)+S˜wd2=S˜wx2(2πf)2+S˜wd2,f>ε2π=fεσ˜x2=limf→∞∫0fS˜x2νdν<∞,

where if, for f < ε, S˜x2(f) is bounded, also the variance σ˜x2 is bounded. The Bode plot of S˜d(f) is approximately flat for f>f0=2π−1S˜wx/S˜wd>fε and has a −20 dB/decade slope for f_ε < f < f₀. The first PSD in the first row of Eq. (8.10) is a first-order random walk, which is known, in the realm of inertial sensors, as the (long-term) bias instability of the sensor. The name is appropriate because it describes the long-term fluctuations—bounded because of ε—around the mean sensor bias x˜0. The square root of the second term S˜wd corresponds to the minimum-valued profile of the overall spectral density. Let us call it, as already anticipated, noise floor, although the name sometimes refers to the whole instrument noise (here referred to as the background noise). In the realm of inertial sensors, it is known as the velocity random walk in the case of linear accelerometers, the unit being [m/(s2Hz)], and the angular random walk (ARW) in the case of gyroscopes, the unit being[rad/(sHz)]. The name, which may cause same confusion, is justified by the fact that when either of the two measurements (linear acceleration and angular rate) is time integrated for generating either velocity or attitude measurements, the integrated noise floor becomes a random walk. By restricting to gyroscopes, the ARW unit [rad/(sHz)] is usually simplified to [rad/s], de facto to the non-SI unit [degree/hour]. Indeed, the simplified unit is at the same time the unit of S˜wd and the unit of the root mean square (RMS) σ¯w(t,Δt) of the random walk increment w¯d(t,Δt)=∫tt+Δtw˜d(τ)dτ, namely:

(8.11)σ¯w(t,Δt)=E{1Δt(∫tt+Δtw˜d(τ)dτ)2}=S˜wd.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780081007006000088

Sampling Theory

Luis Chaparro, in Signals and Systems Using MATLAB (Second Edition), 2015

8.3.2 Quantization and Coding

Amplitude discretization of the sampled signal x_s(t) is accomplished by a quantizer consisting of a number of fixed amplitude levels against which the sample amplitudes {x(nT_s)} are compared. The output of the quantizer is one of the fixed amplitude levels that best represents {x(nT_s)} according to some approximation scheme. The quantizer is a non-linear system.

Independent of how many levels or, equivalently, of how many bits are allocated to represent each level of the quantizer, in general there is a possible error in the representation of each sample. This is called the quantization error. To illustrate this, consider the 2-bit or four-level quantizer shown in Figure 8.12. The input of the quantizer are the samples {x(nT_s)}, which are compared with the values in the bins [-2Δ,-Δ],[-Δ,0],[0,Δ], and [Δ,2Δ]. Depending on which of these bins the sample falls in it is replaced by the corresponding levels -2Δ,-Δ,0, or Δ, respectively. The value of the quantization step Δ for the four-level quantizer is

Figure 8.12. Four-level quantizer and coder.

(8.23)Δ=dynamic range of signal2b=2max|x(t)|22

where b = 2 is number of bits of the code assigned to each level. The bits assigned to each of the levels uniquely represents the different levels [-2Δ,-Δ,0,Δ]. As to how to approximate the given sample to one of these levels, it can be done by rounding or by truncating. The quantizer shown in Figure 8.12 approximates by truncation, i.e., if the sample kΔ≤x(nTs)<(k+1)Δ, for k = −2, −1,0,1, then it is approximated by the level kΔ.

To see how quantization and coding are done, and how to obtain the quantization error, let the sampled signal be

x(nTs)=x(t)|t=nTS

The given four-level quantizer is such that if the sample x(nT_s) is such that

(8.24)kΔ≤x(nTs)<(k+1)Δ⇒xˆ(nTs)=kΔk=-2,-1,0,1

The sampled signal x(nT_s) is the input of the quantizer and the quantized signal xˆ(nTs) is its output. So that whenever

-2Δ≤x(nTs)<-Δ⇒xˆ(nTs)=-2Δ-Δ≤x(nTs)<0⇒xˆ(nTs)=-Δ0≤x(nTs)<Δ⇒xˆ(nTs)=0Δ≤x(nTs)<2Δ⇒xˆ(nTs)=Δ

To transform the quantized values into unique binary 2-bit values, one could use a code such as

xˆ(nTs)⇒binary code-2Δ10-Δ110Δ00Δ01

which assigns a unique 2 bit binary number to each of the 4 quantization levels. Notice that the first bit of this code can be considered a sign bit, “1” for negative levels and “0” for positive levels.

If we define the quantization error as

ε(nTs)=x(nTs)-xˆ(nTs)

and use the characterization of the quantizer given by Equation (8.24) as

xˆ(nTs)≤x(nTs)≤xˆ(nTs)+Δ

by subtracting xˆ(nTs) from each of the terms gives that the quantization error is bounded as follows

(8.25)0≤ε(nTs)≤Δ

i.e., the quantization error for the four-level quantizer being considered is between 0 and Δ. This expression for the quantization error indicates that one way to decrease the quantization error is to make the quantization step Δsmaller. Increasing the number of bits of the A/D converter makes Δ smaller (see Equation (8.23) where the denominator is 2 raised to the number of bits) which in turn makes smaller the quantization error, and improves the quality of the A/D converter.

In practice, the quantization error is random and so it needs to be characterized probabilistically. This characterization becomes meaningful when the number of bits is large, and when the input signal is not a deterministic signal. Otherwise, the error is predictable and thus not random. Comparing the energy of the input signal to the energy of the error, by means of the so-called signal to noise ratio (SNR), it is possible to determine the number of bits that are needed in a quantizer to get a reasonable quantization error.

Example 8.5

Suppose we are trying to decide between an 8 and a 9 bit A/D converter for a certain application where the signals in this application are known to have frequencies that do not exceed 5 kHz. The dynamic range of the signals is 10 volts, so that the signal is bounded as −5 ≤ x(t) ≤ 5. Determine an appropriate sampling period and compare the percentage of error for the two A/Ds of interest.

Solution

The first consideration in choosing the A/D converter is the sampling period, so we need to get an A/D converter capable of sampling at f_s = 1/T_s > 2 f_max samples/second. Choosing f_s = 4 f_max = 20 k samples/second then T_s = 1/20 msec/sample or 50 microseconds/sample. Suppose then we look at the 8-bit A/D converter, the quantizer has 2⁸ = 256 levels so that the quantization step is Δ=10/256 volts and if we use a truncation quantizer the quantization error would be

0≤ε(nTs)≤10/256

If we find that objectionable we can then consider the 9-bit A/D converter, with a quantizer of 2⁹ = 512 levels and the quantization step Δ=10/512 or half that of the 8-bit A/D converter, and

0≤ε(nTs)≤10/512

So that by increasing one bit we cut the quantization error in half from the previous quantizer. Inputting a signal of constant amplitude 5 into the 9-bit A/D gives a quantization error of [(10/512)/5] × 100% = (100/256)% ≈ 0.4% in representing the input signal. For the 8-bit A/D it would correspond to 0.8% error. ▪

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123948120000085

Compression

StéphaneMallat , in A Wavelet Tour of Signal Processing (Third Edition), 2009

Weighted Quantization and Regions of Interest

Visual distortions introduced by quantization errors of wavelet coefficients depend on the scale 2^j. Errors at large scales are more visible than at fine scales [481]. This can be taken into account by quantizing the wavelet coefficients with intervals Δj=Δwj that depend on the scale 2^j. For R¯≤1 bit/pixel, w_j = 2^−j is appropriate for the three finest scales. The distortion in (10.34) shows that choosing such weights is equivalent to minimizing a weighted mean-square error.

Such a weighted quantization is implemented like in (10.35) by quantizing weighted wavelet coefficients f_B[m]/w_j with a uniform quantizer. The weights are inverted during the decoding process. JPEG-2000 supports a general weighting scheme that codes weighted coefficients w[m]f_B[m] where w[m] can be designed to emphasize some region of interest Ω ⊂ [0, 1]² in the image. The weights are set to w[m] = w > 1 for the wavelet coefficients fB[m]=〈f,ψj,p,q1〉 where the support of ψj,p,q1 intersects Ω. As a result, the wavelet coefficients inside Ω are given a higher priority during the coding stage, and the region Ω is coded first within the compressed stream. This provides a mechanism to more precisely code regions of interest in images—for example, a face in a crowd.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123743701000148

Signal and Image Representation in Combined Spaces

Zoran. Cvetković, Martin. Vetterli, in Wavelet Analysis and Its Applications, 1998

6.1 Two lemmas on frames of complex exponentials

Estimates of bounds on the quantization error in Subsection 4.3 are derived from the next two lemmas [5].

Lemma 1

Letejλnωbe a frame in L²[− σ, σ]. If M is any constant and {μ_n} is a sequence satisfying |μ_n − λ_n| ≤ M, for all n, then there is a number C = C(M, σ, {λ_n}) such that

(6.1.1)∑n|fμn|2∑n|fλn|2≤C

for every cr-bandlimited signal f(x).

Lemma 2

Letejλnωbe a frame in L²[− σ, σ], with bounds 0 < A ≤ B < ∞ and δ a given positive number. If a sequence { μ_n } satisfies | λ_n − μ_n \ < δ for all n, then for every σ-bandlimited signal f(x)

(6.1.2)A1−C2||f||2≤∑n|fμn|2≤B(1+C)2||f||2,

where

(6.1.3)C=BAeγδ−12

Remark 1

If δ in the statement of Lemma 2 is chosen small enough, so that C is less then 1, then ejμnω is also a frame in L²[− σ, σ]. Moreover, there exists some δ _1/4 ({λ_n},σ), such that whenever δ < δ _1/4 ({λ_n }, σ), ejμnω is a frame with frame bounds A/A and 9B/4.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/S1874608X98800125

Live HDR Video Broadcast Production

I.G. Olaizola, … J. Gorostegui, in High Dynamic Range Video, 2017

1.4.1 Banding

Banding effects are directly related to quantization errors. As the dynamic range increases, the quantization effects become more noticeable and banding artifacts arise. To avoid this, smaller quantization steps must be taken, but this requires a higher bitdepth (from 8 to 10 or 12 in order to have backwards compatibility with existing infrastructures, and ideally 14 or 16 bits) and nonlinear transform functions based on the HVS that minimize the observable banding effects. Nowadays, this is partially solved by the electro-optical transfer function (EOTF) and opto-electronic transfer function (OETF) mapping curves that will be introduced in a further section.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B978012809477800008X

Источник

This example shows how to compute and compare the statistics of the signal quantization error when using various rounding methods. Quantization occurs when a data type cannot represent a value exactly. In these cases, the value must be rounded to the nearest value that can be represented by the data type.

First, a random signal is created that spans the range of the quantizer object. Next, the signal is quantized, respectively, with rounding methods 'fix', 'floor', 'ceil', 'nearest', and 'convergent', and the statistics of the signal are estimated.

The theoretical probability density function of the quantization error is computed with the errpdf function, the theoretical mean of the quantization error is computed with the errmean function, and the theoretical variance of the quantization error is computed with the errvar function.

Create Uniformly Distributed Random Signal

Create a uniformly distributed random signal that spans the domain -1 to 1 of the fixed-point quantizer object q.

q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1);
xi = linspace(-2*eps(q),2*eps(q),256);

Fix: Round Towards Zero

With 'fix' rounding, the probability density function is twice as wide as the others. For this reason, the variance is four times that of the others.

q = quantizer('fix',[8 7]);
err = quantize(q,u) - u;    
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);

qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -46.8586
Theoretical error variance (dB) = -46.9154
Estimated   mean = 7.788e-06
Theoretical mean = 0

The theoretical variance is eps(q)^2/3 and the theoretical mean is 0.

Floor: Round Towards Negative Infinity

'floor' rounding is often called truncation when used with integers and fixed-point numbers that are represented using two’s complement notation. It is the most common rounding mode of DSP processors because it requires no hardware to implement. 'floor' does not produce quantized values that are as close to the true values as 'round' will, but it has the same variance. Using 'floor', small signals that vary in sign will be detected, whereas in 'round' they will be lost.

q = quantizer('floor',[8 7]);
err = quantize(q,u) - u;    
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);

qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9148
Theoretical error variance (dB) = -52.936
Estimated   mean = -0.0038956
Theoretical mean = -0.0039062

The theoretical variance is eps(q)^2/12 and the theoretical mean is -eps(q)/2.

Ceil: Round Towards Positive Infinity

q = quantizer('ceil',[8 7]);
err = quantize(q,u) - u;    
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);

qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9148
Theoretical error variance (dB) = -52.936
Estimated   mean = 0.0039169
Theoretical mean = 0.0039062

The theoretical variance is eps(q)^2/12 and the theoretical mean is eps(q)/2.

Round: Round to Nearest; In a Tie Round to Largest Magnitude

'round' is more accurate than 'floor', but all values smaller than eps(q) get rounded to zero and are lost.

q = quantizer('nearest',[8 7]);
err = quantize(q,u) - u;    
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);

qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9579
Theoretical error variance (dB) = -52.936
Estimated   mean = -2.212e-06
Theoretical mean = 0

The theoretical variance is eps(q)^2/12 and the theoretical mean is 0.

Convergent: Round to Nearest; In a Tie Round to Even

'convergent' rounding eliminates the bias introduced by ordinary 'round' caused by always rounding the tie in the same direction.

q = quantizer('convergent',[8 7]);
err = quantize(q,u) - u;    
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);

qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9579
Theoretical error variance (dB) = -52.936
Estimated   mean = -2.212e-06
Theoretical mean = 0

The theoretical variance is eps(q)^2/12 and the theoretical mean is 0.

Compare Nearest and Convergent Rounding

The error probability density function for convergent rounding is difficult to distinguish from that of round-to-nearest by looking at the plot.

The error probability density function of convergent is

f(err) = 1/eps(q),  for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise

while the error probability density function of round is

f(err) = 1/eps(q),  for -eps(q)/2 <  err <= eps(q)/2, and 0 otherwise

The error probability density function of convergent is symmetric, while round is slightly biased towards the positive.

The only difference is the direction of rounding in a tie.

x = (-3.5:3.5)';
[x convergent(x) nearest(x)]

ans = 8×3

   -3.5000   -4.0000   -3.0000
   -2.5000   -2.0000   -2.0000
   -1.5000   -2.0000   -1.0000
   -0.5000         0         0
    0.5000         0    1.0000
    1.5000    2.0000    2.0000
    2.5000    2.0000    3.0000
    3.5000    4.0000    4.0000

Ошибки квантования

В реальных
устройствах цифровой обработки сигналов
необходимо учитывать
эффекты, обусловленные квантованием
входных сигналов
и конечной разрядностью всех регистров.
Источниками ошибок
в процессах обработки сигналов являются
округление (усечение)
результатов арифметических операций,
шум аналого-цифрового квантования
входных аналоговых сигналов, неточность
реализации характеристик цифровых
фильтров из-за округления их коэффициентов
(параметров). В дальнейшем с целью
упрощения анализа предполагается, что
вес источники ошибок независимы и не
коррелируют с входным сигналом (хотя
мы и рассмотрим явление предельных
циклов, обусловленных коррелированным
шумом округления).

Эффект квантования
приводят в конечном итоге к погрешностями выходных сигналах цифровых фильтров
(ЦФ), а в некоторыхслучаяхи к неустойчивым
режимам. Выходную ошибку ЦФ будем
рассчитыватькаксуперпозицию ошибок, обусловленных
каждым независимымисточником.

Квантование
чисел– нелинейная операция;m-разрядное
двоичное числоА
представляетсяb-разрядным
двоичнымчислом
B=F(A),
причем b
< m. В
результате квантования число А
представляется
с ошибкой

е
=B–А= F(А)
–А.

Шаг квантования
Q
=
2^–^b
определяется весом младшего
числовогоразряда.
При квантовании
используется усечение или округление.

Усечение
числаА
состоит в отбрасываниит
– b
младших разрядов числа, при этом
ошибка усечения
e_ус=
F_ус(А) –А.

Оценим величину
ошибки в предположении m
» b.
Для положительных чисел при любом
способе кодирования –2^–^b
<е_ус0. Для
отрицательных чисел при использовании
прямого и обратного кодов ошибка усечения
неотрицательна: 0е_ус< 2^–^b,
а в дополнительном коде эта ошибка
неположительна: 0е_ус> –2^–^b.
Таким образом, во всех случаях
абсолютное значение ошибки усечения
не превосходит шага квантования:maxe_ус
< 2^–^b
=Q.

Округление
m-разрядного
числаA
доb
разрядов (b «
m)b-й
разряд остается неизменным или
увеличивается на единицув
зависимости от соотношения (больше –
меньше) между отбрасываемой дробью
0,а_b+₁…а_т
и величиной
,
гдеа_i–i-й
разряд числаA;
i =
b+1,
…,m.
Округление можно практически выполнить
путемприбавления
единицы к (b+1)-му
разряду и усечения полученного числа
до b разрядов.
В таком случае ошибка округления е_oк
=
f_ок(А)–
А
при всех способах кодирования лежит в
пределах

–2^–⁽^b⁺¹⁾
<
е_o_к
< 2^–⁽^b⁺¹⁾
(1.11)

и, следовательно,
max<2^–^b
= Q/2.
(1.12)

В задачах ЦОС
ошибки квантования чисел рассматриваются
как стационарный
шумоподобный процесс с равномерным
распределением
вероятности по диапазону распределения
ошибок квантования.



(nT)

x(nT)

e(nT)

Рис. 3. Линейная модель квантования
сигналов:

(nT) —дискретный
или m-разрядный
цифровой сигнал (m
> b);

x(nT) —квантованный
b-разрядный
цифровой сигнал;

e(nT)
= x(nT)
–f(nT)
— ошибка
квантования.

Квантование
дискретных сигналов состоит в
представлении отсчета
(выборки сигнала) числамиx(nT),
содержащими b
числовых разрядов. Квантование сигналов,
как и квантование
чисел – нелинейная операция. Однако
при анализе процессов в ЦФ целесообразно
использовать линейную модель квантования
сигналов – рис. 3.

Верхнее значение ошибки квантования
определяетсясоотношением
(1.11) или (1.12).

Вероятностные
оценки ошибок квантования основаны на
предположениях о том, что
последовательностье(пТ)являетсястационарным
случайным процессом с равномерным
распределением вероятности по
диапазону ошибок квантования ие(пТ)
не коррелирован
с f(nT).
Математическое
ожидание (среднее значение) _e
и дисперсия
ошибки квантованияе
определяются
по формулам:

=E(е)
=,

===E(е²)
–,

где р_е
— плотность вероятности ошибки. По
этим формуламвычисляются
математическое ожидание и дисперсия
для ошибок
округления и усечения:

В логарифмическоммасштабе

Лекция 2

Ошибки квантования

е
=B–А= F(А)
–А.

Усечение
числаА
состоит в отбрасываниит
– b
младших разрядов числа, при этом
ошибка усечения
e_ус=
F_ус(А) –А.

–2^–⁽^b⁺¹⁾
<
е_o_к
< 2^–⁽^b⁺¹⁾
(1.11)

и, следовательно,
max<2^–^b
= Q/2.
(1.12)



(nT)

x(nT)

e(nT)

Рис. 3. Линейная модель квантования
сигналов:

(nT) —дискретный
или m-разрядный
цифровой сигнал (m
> b);

x(nT) —квантованный
b-разрядный
цифровой сигнал;

e(nT)
= x(nT)
–f(nT)
— ошибка
квантования.

Верхнее значение ошибки квантования
определяетсясоотношением
(1.11) или (1.12).

=E(е)
=,

===E(е²)
–,

В логарифмическоммасштабе

Лекция 2

Вычислите ошибку квантования

В этом примере показано, как вычислить и сравнить статистику ошибки квантования сигнала при использовании различных методов округления.

Во-первых, случайный сигнал создается, который порождает линейную оболочку столбцов квантизатора.

Затем сигнал квантуется, соответственно, с округлением методов ‘фиксируют’, ‘ставят в тупик’, ‘перекрывают’, ‘самый близкий’, и ‘конвергентный’, и статистические данные сигнала оцениваются.

Теоретическая функция плотности вероятности ошибки квантования будет вычислена с ERRPDF, теоретическое среднее значение ошибки квантования будет вычислено с ERRMEAN, и теоретическое отклонение ошибки квантования будет вычислено с ERRVAR.

Равномерно распределенный случайный сигнал

Сначала мы создаем равномерно распределенный случайный сигнал, который охватывает область-1 к 1 из квантизаторов фиксированной точки, на которые мы посмотрим.

q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1);        % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);

Фиксация: вокруг по направлению к нулю.

Заметьте, что с округлением ‘фиксации’, функция плотности вероятности вдвое более широка, чем другие. Поэтому отклонение в четыре раза больше чем это других.

q = quantizer('fix',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance = eps(q)^2 / 3
% Theoretical mean     = 0
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -46.8586
Theoretical error variance (dB) = -46.9154
Estimated   mean = 7.788e-06
Theoretical mean = 0

Пол: вокруг к минус бесконечность.

Пол, округляющийся, часто называется усечением, когда используется с целыми числами и числами фиксированной точки, которые представлены в дополнении two. Это — наиболее распространенный режим округления процессоров DSP, потому что это требует, чтобы никакое оборудование не реализовало. Пол не производит квантованные значения, которые являются как близко к истинным значениям, когда ROUND будет, но это имеет то же отклонение, и маленькие сигналы, которые варьируются по знаку, будут обнаружены, тогда как в ROUND они будут потеряны.

q = quantizer('floor',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance =  eps(q)^2 / 12
% Theoretical mean     = -eps(q)/2
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9148
Theoretical error variance (dB) = -52.936
Estimated   mean = -0.0038956
Theoretical mean = -0.0039062

Потолок: вокруг к плюс бесконечность.

q = quantizer('ceil',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance = eps(q)^2 / 12
% Theoretical mean     = eps(q)/2
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9148
Theoretical error variance (dB) = -52.936
Estimated   mean = 0.0039169
Theoretical mean = 0.0039062

Вокруг: вокруг к самому близкому. Вничью, вокруг к самой большой величине.

Вокруг более точно, чем пол, но все значения, меньшие, чем eps (q), округлены, чтобы обнулить и потеряны — также.

q = quantizer('nearest',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance = eps(q)^2 / 12
% Theoretical mean     = 0
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9579
Theoretical error variance (dB) = -52.936
Estimated   mean = -2.212e-06
Theoretical mean = 0

Конвергентный: вокруг к самому близкому. Вничью, вокруг к даже.

Конвергентное округление устраняет смещение, введенное обычным «раундом», вызванным, всегда округляя связь в том же направлении.

q = quantizer('convergent',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance = eps(q)^2 / 12
% Theoretical mean     = 0
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9579
Theoretical error variance (dB) = -52.936
Estimated   mean = -2.212e-06
Theoretical mean = 0

Сравнение самых близких по сравнению с конвергентным

Функция плотности вероятности появления ошибки для конвергентного округления затрудняет, чтобы различать от того из раунда-к-самому-близкому путем рассмотрения графика.

Ошибка p.d.f. из конвергентных

f(err) = 1/eps(q),  for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise

в то время как ошибка p.d.f. из раунда

f(err) = 1/eps(q),  for -eps(q)/2 <  err <= eps(q)/2, and 0 otherwise

Обратите внимание на то, что ошибка p.d.f. из конвергентных симметрично, в то время как вокруг немного склоняется к положительному.

Единственной разницей является направление округления вничью.

x=(-3.5:3.5)';
[x convergent(x) nearest(x)]

ans =

   -3.5000   -4.0000   -3.0000
   -2.5000   -2.0000   -2.0000
   -1.5000   -2.0000   -1.0000
   -0.5000         0         0
    0.5000         0    1.0000
    1.5000    2.0000    2.0000
    2.5000    2.0000    3.0000
    3.5000    4.0000    4.0000

Постройте функцию помощника

Функция помощника, которая использовалась, чтобы сгенерировать графики в этом примере, описана ниже.

type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m'))
%#ok<*NOPTS>

function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT  Plot function for QERRORDEMO.
%    QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
%    used by the example function QERRORDEMO, where Q is the quantizer
%    whose attributes are being analyzed; F_T is the theoretical
%    quantization error probability density function for quantizer Q
%    computed by ERRPDF; XI is the domain of values being evaluated by
%    ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
%    computed by ERRMEAN; V_T is the theoretical quantization error
%    variance of quantizer Q computed by ERRVAR; and ERR is the error
%    generated by quantizing a random signal by quantizer Q.
%
%    See QERRORDEMO for examples of use.

%    Copyright 1999-2014 The MathWorks, Inc.

v=10*log10(var(err));
disp(['Estimated   error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated   mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')

Ошибка квантования E = em — ea — это разность между реальной продолжительностью события ea и его измеренной продолжительностью em. У вас нет возможности узнать реальную продолжительность события, следовательно, нельзя и обнаружить ошибку квантования, основываясь на отдельном значении. Однако можно доказать наличие ошибки квантования, исследуя группы родственных статистик. Мы уже рассматривали пример, в котором удалось выявить ошибку квантования. В примере 7.5 наличие ошибки квантования удалось определить, заметив, что:

Ошибку квантования легко выявить, исследуя вызов базы данных и выполняемые им события ожидания в системе с низкой загрузкой, где минимизировано влияние других факторов, способных нарушить отношение e и c + Eela.

Рассмотрим фрагмент файла трассировки Oracle8i, который демонстрирует эффект ошибки квантования:

Данный вызов выборки инициировал ровно три события ожидания. Мы знаем, что приведенные значения c, e и ela должны быть связаны таким приблизительным равенством:

В системе с низкой загрузкой величина, на которую отличаются левая и правая части приблизительного равенства, указывает на общую ошибку квантования, присутствующую в пяти измерениях (одно значение c, одно значение e и три значения ela):

С учетом того, что отдельному вызову gettimeofday в большинстве систем соответствует лишь несколько микросекунд ошибки, вызванной влиянием измерителя, получается, что ошибка квантования вносит значительный вклад в «разность» длиной в одну сантисекунду в данных трассировки.

Следующий фрагмент файла трассировки Oracle8i демонстрирует простейший вариант избыточного учета продолжительности, в результате которого возникает отрицательная величина неучтенного времени:

WAIT #96: nam=’db file sequential read’ ela= 0 p1=1 p2=1691 p3=1

FETCH #96:c=1,e=0,p=1,cr=4,cu=0,mis=0,r=1,dep=1,og=4,tim=116694789 В данном случае E = -1 сантисекунда:

При наличии «отрицательной разности» (подобного только что рассмотренному) невозможно все объяснить эффектом влияния измерителя, ведь этот эффект может быть причиной появления только положительных значений неучтенного времени. Можно было бы подумать, что имел место двойной учет использования процессора, но и это не соответствует действительности, т. к. нулевое значение ela свидетельствует о том, что время занятости процессора вообще не учитывалось для события ожидания. В данном случае ошибка квантования имеет преобладающее влияние и приводит к излишнему учету времени для выборки.

В данном случае E = 640 мкс:

В Oracle9i разрешение временной статистики улучшено, но и эта версия отнюдь не защищена от воздействия ошибки квантования, что видно в предложенном ниже фрагменте файла трассировки для E > 0:

Некоторая часть этой ошибки, несомненно, является ошибкой квантования (невозможно, чтобы общее время использования процессора данной выборкой действительно равнялось нулю). Несколько микросекунд следует отнести на счет эффекта влияния измерителя.

Наконец, рассмотрим пример ошибки квантования E < 0 в данных трассировки Oracle9i:

Возможно, в данном случае имел место двойной учет использования процессора. Также вероятно, что именно ошибка квантования внесла основной вклад в полученное время вызова выборки. Избыточный учет 8784 микросекунд говорит о том, что фактический общий расход процессорного времени вызовом базы данных составил, вероятно, всего около (10000 — 8784) мкс = 1,216 мкс.

Диапазон значений ошибки квантования

Величину ошибки квантования, содержащейся во временных статистиках Oracle, нельзя измерить напрямую. Зато можно проанализировать статистические свойства ошибки квантования в данных расширенной трассировки SQL. Во-первых, величина ошибки квантования для конкретного набора данных трассировки ограничена сверху. Легко представить ситуацию, в которой ошибка квантования, вносимая такими характеристиками продолжительности, как e и ela, будет максимальной. Наибольшего значения данная ошибка достигает в том случае, когда в последовательности значений e и ela все отдельные ошибки квантования имеют максимальную величину и их знаки совпадают.

На рис. 7.9 показан пример возникновения описанной ситуации: имеется восемь очень непродолжительных системных вызовов, причем все они попадают на такты интервального таймера. Фактическая длительность каждого события близка к нулю, но измеренная длительность каждого такого события равна одному такту системного таймера. В итоге суммарная фактическая продолжительность всех вызовов близка к нулю, а общая измеренная продолжительность равна 8 тактам. Для такого набора из n = 8 системных вызовов ошибка квантования по существу равна nrx, где rx — это разрешение интервального таймера, с помощью которого измеряется характеристика x.

Думаю, вы обратили внимание, что изображенный на рис. 7.9 случай выглядит надуманно и изобретен исключительно для прояснения вопроса. В реальной жизни подобная ситуация чрезвычайно маловероятна. Вероятность, что n ошибок квантования будут иметь одинаковые знаки, равна всего 0,5n. Вероятность того, что n=8 последовательных

Рис. 7.9. Наихудший вариант накопления ошибки квантования для последовательности измеренных продолжительностей

ошибок квантования будут отрицательными, равна всего 0,00390625 (т. е. приблизительно четыре шанса из тысячи). Для 266 значений шанс совпадения знаков у всех ошибок квантования меньше, чем один из 1080.

Для больших наборов значений длительностей совпадение знаков всех ошибок квантования практически невозможно. Но это не единственное, в чем состоит надуманность ситуации, изображенной на рис. 7.9. Она также предполагает, что абсолютная величина каждой ошибки квантования максимальна. Шансы наступления такого события еще более иллюзорны, чем у совпадения всех знаков ошибок. Например, вероятность того, что величина каждой из n имеющихся ошибок квантования превышает 0,9, равна (1 — 0,9)n. Вероятность того, что величина каждой из n = 266 ошибок квантования превысит 0,9, составляет всего 1 из 10266.

Вероятность того, что все n ошибок квантования имеют одинаковый знак и абсолютная величина всех из них больше m, чрезвычайно мала и равна произведению рассмотренных ранее вероятностей:

P (значения всех n ошибок квантования больше m или меньше -m)=

= (0.5)n(1- m)n

Ошибки квантования для продолжительностей (например, значений e и ela в Oracle) — это случайные числа в диапазоне:

-rx < E < rx где rx — это разрешение интервального таймера, с помощью которого измеряется характеристика x (x- это e или ela).

Так как положительные и отрицательные ошибки квантования возникают c равной вероятностью, средняя ошибка квантования для выбранного набора статистик стремится к нулю даже для больших файлов трассировки. Опираясь на теорему Лапласа (Pierre Simon de Laplace, 1810), можно предсказать вероятность того, что ошибки квантования для статистик e и ela будут превышать указанное пороговое значение для файла трассировки, содержащего определенное количество статистик.

Я начал работать над вычислением вероятности того, что общая ошибка квантования файла трассировки (включая ошибку, вносимую статистикой c) будет превышать заданную величину, однако мое исследование еще не завершено. Мне предстоит получить распределение ошибки квантования для статистики c, что, как я уже говорил, осложняется особенностями получения этой статистики в процессе опроса. Результаты этих изысканий планируется воплотить в одном из будущих проектов.

К счастью, относительно ошибки квантования есть и оптимистические соображения, которые позволяют не слишком расстраиваться по поводу невозможности определения ее величины:

• Во многих сотнях файлов трассировки Oracle, проанализированных нами в hotsos.com, общая продолжительность неучтенного вре-

Что означает «один шанс из десяти в [очень большой] степени»?

Для того чтобы представить себе, что такое «один шанс из 1080», задумайтесь над следующим фактом: ученые утверждают, что в наблюдаемой вселенной содержится всего около 1080 атомов (по данным http:// www.sunspot.noao.edu/sunspot/pr/answerbook/universe.html#q70, http:/ /www.nature.com/nsu/020527/020527-16.html и др.). Это означает, что если бы вам удалось написать на каждом атоме нашей вселенной 266 равномерно распределенных случайных чисел от -1 до +1, то лишь на одном из этих атомов можно было бы ожидать наличия всех 266 чисел с одинаковым знаком.

Представить вторую упомянутую вероятность — «один шанс из 10266»-еще труднее. На этот раз представим себе три уровня вложенных вселенных. То есть что каждый из 1080 атомов нашей вселенной сам по себе является вселенной, состоящей из 1080 вселенных, каждая из которых в свою очередь содержит 1080 атомов. Теперь у нас достаточно атомов для того, чтобы представить себе возможность возникновения ситуации с вероятностью «один из 10240». Даже во вселенных третьего уровня вложенности вероятность появления атома, для которого все 266 его случайных чисел по абсолютной величине больше 0,9, составит один из 100 000 000 000 000 000 000 000 000.

мени в случае корректного сбора данных (см. главу 6) чрезвычайно редко превышала 10% общего времени отклика.

Несмотря на то, что и ошибка квантования, и двойной учет использования процессора могут привести к такому результату, файл трассировки чрезвычайно редко содержит отрицательное неучтенное время, абсолютная величина которого превышала бы 10% общего времени отклика.

В случаях, когда неучтенное время оценивается более чем в 25% времени отклика для корректно собранных данных трассировки, такой объем неучтенного времени почти всегда объясняется одним из двух явлений, описанных в последующих разделах.

Наличие ошибки квантования не лишает нас возможности правильно диагностировать основные причины проблем производительности при помощи файлов расширенной трассировки SQL в Oracle (даже в файлах трассировки Oracle8i, в которых вся статистика приводится с точностью лишь до сотых долей секунды).

Ошибка квантования становится еще менее значимой в Oracle9i благодаря повышению точности измерений.

В некоторых случаях влияние ошибки квантования способно привести к утрате доверия к достоверности данных трассировки Oracle. Наверное, ничто не может так подорвать боевой дух, как подозрение в недостоверности данных, на которые вы полагаетесь. Думаю, что лучшим средством, призванным укрепить веру в получаемые данные, должно служить четкое понимание влияния ошибки квантования.

Следующая >

Погрешность восстановления сигнала. Информационный расчёт системы. Квантование сообщений. Ошибки квантования

Мы охотно слушаем музыку, пение птиц, приятный человеческий голос. Напротив, тарахтенье телеги, визг пилы, мощные удары молота нам неприятны и нередко раздражают и утомляют.
Таким образом, по действию, производимому на нас, все звуки делятся на две группы: музыкальные звуки и шумы. Чем отличаются они друг от друга?
Чистый музыкальный звук всегда имеет определённую высоту. Это как бы организованная звуковая волна. Напротив, в шуме царит полный беспорядок. Прислушайтесь, например, к дневному шуму городской улицы. В нём вы услышите и краткие быстро исчезающие высокие звуки, и длительный низкий гул, и резкий лязг. Шум-это множество самых различных, одновременно несущихся звуков. Чем быстрее и резче изменяются их высота и сила, тем неприятнее на нас действует шум.
Каждый из вас легко обнаружит разницу между звуком рояля и скрипом сапога. Но не всегда можно провести резкую границу между музыкальным звуком и шумом. В шуме очень часто можно уловить музыкальные звуки. В свою очередь, и к музыкальным звукам всегда примешивается шум. От него не свободно даже самое искусное музыкальное исполнение. Попробуйте внимательно прислушаться к игре на рояле, и вы услышите, кроме звуков музыки, и стук клавишей, и удары пальцев по ним, и шелест переворачиваемых нотных листов. Точно так же и к пению всегда примешивается шум дыхания певца. Но обычно мы сосредоточиваем своё внимание на звуках самой музыки и не замечаем этого шума.Получить чистый звук со строго определённой частотой колебания, даже при полном отсутствии посторонних шумов, очень трудно, и вот почему. Любое колеблющееся тело издаёт не только один основной звук. Его постоянно сопровождают звуки других частот. Эти «спутники» всегда выше основного звука и называются поэтому обертонами, то есть верхними тонами. Однако не стоит огорчаться существованием этих «спутников». Именно они-то и позволяют нам отличать звук одного инструмента от другого и голоса различных людей, если даже они равны по высоте. Каждому звуку обертоны придают своеобразную окраску или, как говорят, тембр. И если основной звук сопровождается близкими ему по высоте обертонами, то сам звук кажется нам мягким, «бархатным». Когда же обертоны значительно выше основного тона, мы говорим о неприятном «металлическом» голосе или звуке.
Причина появления обертонов сложна. Она лежит в физической природе колебания тел, и мы не станем её здесь рассматривать.
Шум вредно отражается на здоровье и работоспособности людей. Человек может работать при шуме, привыкает к нему, но продолжительное действие шума вызывает утомление, часто приводит к понижению остроты слуха, а в отдельных случаях и к глухоте. Поэтому борьба с шумом — очень важная задача.
Развивая технику, человек старается свой мускульный труд заменить работой машины. А применение машин, как иногда представляют себе, влечёт за собой увеличение шума. Неверно, однако, думать, что чем выше техника и чем больше механических средств применяет человек, тем больше он подвергает себя воздействию шума. История развития техники показывает, что с улучшением действия отдельных механизмов снижается или совсем устраняется шум при их работе. Вместе с изобретением новых машин открываются и новые пути борьбы с шумом. Действительно, паровая машина уступает своё место бесшумной турбине, грохочущий локомотив старой конструкции — менее шумному современному паровозу и электровозу. На смену звуковым сигналам, гудкам, свисткам, звонкам, там, где это возможно, приходят световые сигналы. Моторы, машины, дающие много шума, закрываются поглощающими звук оболочками, ставятся на особые фундаменты и т. д. Чтобы ослабить шум внутри помещений, на стены вешают ковры, драпируют двери и окна. Телефонные будки обивают войлоком или прессованными пробковыми плитами.
Но защититься полностью от внешнего шума очень трудно. Ведь звук проникает внутрь зданий не только по воздуху. Он пробирается и через стены, по водопроводным и канализационным трубам, через вентиляторы. Когда нужно полностью устранить всякий шум, например, при граммофонной записи или записи звуковых кинофильмов, строят специальные здания с особым фундаментом. В этих зданиях отдельные комнаты как бы «плавают» на упругих прокладках или пружинах. Двойные стены, изолированные одна от другой, двойные или даже тройные окна и двери, полное отсутствие щелей- вот какие сложные меры приходится применять для полного ограждения от шума.

А. Т. Бизин

Сибирская Государственная Академия телекоммуникаций и информатики

Новосибирск 1998 г.

Последовательность кодовых слов на выходе цифрового фильтра необходимо преобразовать в аналоговый сигнал. Преобразование осуществляется с помощью двух устройств: ЦАП и ФНЧ. В ЦАП происходит преобразование каждого кодового слова в узкий импульс, амплитуда которого соответствует значению кодового слова. В ФНЧ происходит выделение той части спектра, которая соответствует спектру аналогового сигнала.

Характеристики ЦАП

Цап преобразует отсчеты сигнала в виде кодовых слов в отсчеты сигнала в виде импульсов. Преобразование происходит с постоянным коэффициентом преобразования, не зависящим от величины отсчета. Следовательно ЦАП является линейной системой, импульсная характеристика которой совпадает с формой импульсов на выходе ЦАП. Поэтому сигнал на выходе ЦАП можно определить по формуле свертки аналоговых сигналов

yцап(t) = y(t) Е hцап(t) (5.1)

где y(t)=y(nT) — дискретный сигнал на входе ЦАП,

hцап(t) — импульсная характеристика ЦАП.

На рис. 5.1, а,в показана форма сигналов на входе и выходе ЦАП на примере импульсной характеристики в форме прямоугольного импульса длительностью t (Рис. 5.1, б)

В частотной области свертке (5.1) соответствует произведение спектров

Yцап (jw) = Y (jw) * Hцап (jw)
(5.2)

где, согласно (1.3),

Y (jw) =

Yа(jw) — спектр аналогового сигнала, подлежащего восстановлению,

Hцап(jw) — передаточная функция ЦАП.

Множитель Т-1 в формуле Y (jw) принято относить к передаточной функции ЦАП, поэтому передаточная функция ЦАП для случая, соответствующего импульсу на Рис. 5.1, б, запишется так

Hцап(jw) = (5.3)

Отсюда, если t << Т, получаем

Hцап(jw) » t / Т
(5.4)

что подтверждается известным фактом спектральной теории: спектр короткого импульса равен его площади и не зависит от формы импульса.

Погрешности восстановления

Аналоговый сигнал ya(t) обращается на выходе ФНЧ, который выделяет спектр частот , соответствующий спектру Yа(jw).

Yа(jw) = Y (jw) * Hцап (jw) * Hфнч (jw) (5.5)

Неравномерность реальных частотных характеристик ЦАП и ФНЧ приводит к искажениям восстанавливаемого непрерывного сигнала. На рис. 5.2 показаны характерные особенности реальных АЧХ восстанавливающих устройств.

Искажения ЦАП обусловлены наклоном АЧХ. На Рис. 5.2 АЧХ соответствует импульсной характеристике в форме прямоугольного импульса длительностью t. Но с уменьшением t, согласно (5.3) и (5.4), падает усиление ЦАП, что приводит к малым уровням сигнала и, соответственно, к низкой помехозащищенности сигнала по отношению к собственным помехам системы.

Искажения ФНЧ увеличиваются по мере приближения к частоте среза ФНЧ wс = 0,5wд. Поэтому рабочую полосу частот сигнала Y (jw) целесообразно размещать на неискаженном участке полосы пропускания ФНЧ, что можно сделать увеличением тактовой частоты wд цифрового фильтра. Таким образом, если имеется возможность увеличить тактовую частоту, то в качестве ФНЧ можно использовать простую цепочку RC. В противном случае качественные показатели восстанавливающего устройства приходится улучшать усложнением схемы ФНЧ. Наконец, погрешности восстановления можно скомпенсировать, если создавать соответствующие предыскажения в ЦФ. В этом случае нормы на проектируемый ЦФ необходимо поправить в расчете на реальные характеристики ЦАП и ФНЧ.

Частота дискретизации Fд >= 2Fв. Для восстановления непрерывного сигнала из последовательности его дискретных отсчетов в пункте приема используется ФНЧ (фильтр низких частот) с частотой среза равной Fв. На выходе фильтра в результате суммирования отдельных откликов переданный сигнал непрерывный сигнал вновь восстанавливается. При амплитудно-импульсной модуляции (АИМ) по закону модулирующего

стемы. Содержание Нормативные ссылки Введение 1 Расчет информационных характеристик источников дискретных сообщений 2 Расчет информационных характеристик дискретного канала 3 Согласование дискретного источника с дискретным каналом 4 Дискретизация и квантование Заключение Нормативные ссылки В настоящем отчете использованы ссылки на следующие стандарты: — ГОСТ 1.5 – 93 …

Кодовыми словами конечной размерности (ошибки квантования). Поэтому сигнал на выходе цифровой цепи отличается от идеального варианта на величину погрешности квантования. Цифровая техника позволяет получить высокое качество обработки сигналов несмотря на ошибки квантования: ошибки (шумы) квантования можно привести в норму увеличением разрядности кодовых слов. Рациональные способы конструирования…

Функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой…

При
выборе шага дискретизации непрерывных процессов, в частности сигналов и помех,
необходимо оценить погрешность замены непрерывных процессов дискретными. В
настоящем параграфе рассматриваются вопросы оценки этой погрешности.

Пусть
непрерывный процесс изображается,
на ЦВМ. в виде последовательности его значений в равноотстоящих точках . Ясно, что дискретный
процесс лишь приближенно изображает непрерывный процесс. Требуется найти
количественную меру этого приближения, т. е. найти погрешность дискретизации. Величина
погрешности дискретизации, очевидно, зависит от того, что понимается под
погрешностью. Определение погрешности дискретизации зависит от той задачи, в
которой используется дискретный процесс вместо непрерывного. При рассмотрении некоторой
конкретной задачи погрешность дискретизации целесообразно определить как
величину отклонения результата ее решения при использовании дискретного
процесса от результата решения этой же задачи при использовании непрерывного
процесса. Поскольку задачи могут быть самыми разнообразными, то определить
заранее, к чему может привести дискретизация, не представляется возможным.
Поэтому обычно под погрешностью дискретизации процессов понимается та
погрешность, с которой может быть восстановлен непрерывный процесс по его
дискретным значениям, т. е. понимается погрешность в задаче интерполяции непрерывного
процесса по дискретным точкам.

Восстановление
непрерывного процесса по соответствующему ему дискретному
процессу обычно
можно представить как пропускание последовательности «мгновенных» импульсов (-функций) с огибающей и периодом через линейный
интерполирующий фильтр (ИФ) (восстанавливающий элемент) с некоторой импульсной
переходной характеристикой (интерполирующей функцией) . Этому соответствует схема
восстановления, показанная на рис. 1.4. Она содержит ключ, замыкающийся в
моменты времени ,
и интерполирующий фильтр (восстановление как процесс прерывания и сглаживания
). В результате восстановления образуется сигнал

(1.34)

В
соответствии с данной схемой осуществляется восстановление процессов при
наиболее распространенных видах интерполяции: ступенчатой несимметричной и симметричной
(метод прямоугольников, рис. 1.5 а, б), линейной (метод трапеций, рис. 1.5, в)
и др.

Ошибку
интерполяции

(1.35)

можно рассматривать как выходной
сигнал схемы, представленной на рис. 1.6, при воздействии на входе сигнала .

Ниже
найдены достаточно простые общие выражения для корреляционной функции,
энергетического спектра и дисперсии ошибки в предположении, что — стационарный центрированный
случайный процесс. Из общих соотношений в качестве примеров выведены частные
соотношения, соответствующие наиболее распространенным типам интерполирующих
фильтров.

Аналогичная
задача, но иными методами, решалась в работах . Однако в них получены более сложные, а в
ряде случаев лишь частные и приближенные решения. Здесь предложен новый подход
к рассматриваемой задаче, позволяющий найти ее общее точное решение,
отличающееся, кроме того, тем, что из него следует простое решение задачи
оптимизации характеристик интерполирующих фильтров по критерию минимума
среднеквадратической ошибки интерполяции.

Для информационного расчёта в качестве исходного критерия будем использовать допустимую среднеквадратическую погрешность системы, которая определяется через погрешность отдельных узлов. В нашем случае она определяется по следующей формуле:

где — среднеквадратическая погрешность АЦП, возникающая за счёт шума квантования (погрешность квантования АЦП);

Погрешность восстановления сигнала.

Для упрощения расчётов все указанные погрешности предварительно принимаются равными. Таким образом, из формулы (1) следует, что

В соответствии с техническим заданием погрешность преобразования

1%, следовательно

Расчет разрядности АЦП

АЦП преобразуют аналоговые сигналы в цифровую форму и являются оконечными устройствами в интерфейсе ввода информации в ЭВМ. Основными характеристиками АЦП являются: разрешающая способность, точность и быстродействие. Разрешающая способность определяется разрядностью и максимальным диапазоном входного аналогового напряжения.

Относительная среднеквадратическая погрешность, вносимая за счет квантования АЦП, вычисляется по формуле

где — среднеквадратическое значение шума квантования.

Шаг квантования АЦП, определяемый диапазоном изменения сигнала U с. и числом разрядов АЦП n.

Таким образом, погрешность квантования АЦП

Из этого выражения можно определить минимально необходимую разрядность АЦП:

Исходя из,

Следовательно, минимальная разрядность АЦП для решения поставленной задачи — 6 разрядов. Но поскольку АЦП в модуле ADAM-6024 имеет 16 разрядов, то его реальная погрешность преобразования будет равна

Расчет максимально возможной погрешности восстановления

Так как в задании указано, что максимальная погрешность преобразования составляет 1%, то для удовлетворения этому условию погрешность восстановления должна быть меньше либо равна

Восстановление непрерывного сигнала U(t) с помощью интерполяционного метода

Интерполяционный метод восстановления очень широко распространён в наши дни. Этот метод наиболее приспособлен для обработки сигналов с помощью средств вычислительной техники. Этот метод восстановления основан на использовании интерполяционного многочлена Лагранжа. Из соображений простоты реализации интерполирующих устройств обычно используют многочлен не выше второго порядка, применяя в основном интерполяцию нулевого и первого порядка (ступенчатая и линейная). Восстановление сигналов с помощью ступенчатой (а) и линейной (б) интерполяции поясняется на рисунке 13.

Рисунок 13. Восстановление сигналов с помощью ступенчатой (а) и линейной (б) интерполяции

При ступенчатой интерполяции мгновенные значения U(kT) дискретного сигнала U(t) сохраняются постоянными на всём интервале дискретизации Т (рисунок 13, а).

Линейная интерполяция заключается в соединении отрезками прямых мгновенных значений U(kT), как показано на рисунке 13, б.

Интерполяционный способ восстановления обладает погрешностью, которую на практике часто выражают через максимальное относительное значение

где — восстановленный интерполяционным способом сигнал (при ступенчатой интерполяции, при линейной); — диапазон изменения дискретного сигнала U(t).

Период дискретизации выбирается с учетом допустимой погрешности из формулы.

· для ступенчатого интерполятора

· при линейной интерполяции

при параболической интерполяции

Определим период дискретизации для одного канала по Котельникову:

По заданию дипломного проекта частота процессов должна быть меньше 0,1 Гц. Модуль аналогового ввода-вывода ADAM-6024 имеет fmax = 10 Гц (на 1 канал). Так как в разрабатываемой системе используются 4 канала аналогового ввода, то предельная частота дискретизации по каждому из каналов составит fmax = 2,5 Гц. Тогда необходимая частота дискретизации при ступенчатой интерполяции составит:

Следовательно, для удовлетворения требованиям к разрабатываемой системе ступенчатая интерполяция не подходит, так как частота дискретизации при ступенчатой интерполяции существенно больше 2,5 Гц.

Частота дискретизации при линейной интерполяции составляет

Частота дискретизации при параболической интерполяции равна

Можно заметить, что частота дискретизации при линейной и параболической интерполяции меньше предельной частоты дискретизации модуля на канал. Но интерполяция второго и большего порядков практически не используют, так как её реализация усложняется, поэтому для восстановления сигналов будем использовать линейную интерполяцию.

Теорема
Котельникова точно справедлива только
для сигналов с финитным (конечным)
спектром. На рис. 4.15 показаны некоторые
варианты финитных спектров.

Однако
спектры реальных информационных сигналов
бесконечны (рис. 4.16). В этом случае теорема
Котельникова справедлива с погрешностью.

Погрешность
дискретизации определяется энергией
спектральных составляющих сигнала,
лежащих за пределами частоты

(рис. 4.16).

Вторая причина
возникновения погрешностей — неидеальность
восстанавливающего ФНЧ.

Таким
образом? погрешность дискретизации и
восстановления непрерывного сигнала
определяется следующими причинами:

Спектры реальных
сигналов не финитны.

АЧХ реальных ФНЧ
неидеальны.

Рис.4.17.
Структурная схема RC-фильтра

Например,
если в качестве ФНЧ использовать
RC-фильтр
(рис.4.17), то восстановленный сигнал на
его выходе будет иметь вид, представленный
на рис.4.18.

Импульсная
реакция RC-фильтра
равна:

Вывод:
чем выше

и чем ближе характеристики ФНЧ к
идеальным, тем ближе восстановленный
сигнал к исходному.

4.6. Квантование сообщений. Ошибки квантования

Итак
показано, что передачу практически
любых сообщений

можно свести к передаче их отсчетов,
или чисел
,
следующих друг за другом с интервалом
дискретности
.
Тем самым непрерывное (бесконечное
)
множество возможных значений сообщения

заменяетсяконечным

числом его дискретных значений

.
Однако сами эти числа имеют непрерывную
шкалу уровней (значений), то есть
принадлежат опять же континуальному
множеству. Дляабсолютно
точного

представления таких чисел, к примеру,
в десятичной (или двоичной) форме,
необходимо теоретически бесконечное

число разрядов. Вместе с тем, на практике
нет необходимости в абсолютно точном
представлении значений

,
как и любых чисел вообще.

Во-первых,
сами источники сообщений обладают
ограниченным динамическим диапазоном
и вырабатывают исходные сообщения с
определенным уровнем искажений и ошибок.
Этот уровень может быть большим или
меньшим, но абсолютной точности
воспроизведения достичь невозможно.

Во-вторых,
передача сообщений по каналам связи
всегда производится в присутствии
различного рода помех. Поэтому, принятое
(воспроизведенное) сообщение (оценка
сообщения

)
всегда в определенной степени отличается
от переданного, то есть на практикеневозможна
абсолютно точная передача
сообщений
при наличии помех в канале связи.

Наконец,
сообщения передаются для их восприятия
и использования получателем. Получатели
же информации — органы чувств человека,
исполнительные механизмы и т.д. — также
обладают конечной разрешающей
способностью, то есть не замечают
незначительной разницы между абсолютно
точным
и
приближенным

значениями
воспроизводимого сообщения. Порог
чувствительности к искажениям также
может быть различным, но он всегда есть.

С
учетом этих замечаний процедуру
дискретизации сообщений можно продолжить,
а именно подвергнуть отсчеты

квантованию.

Процесс
квантования состоит в замене непрерывного
множества значений отсчетов

дискретным
множеством

.
Тем самым точные значения чисел
заменяются их приблизительными
(округленными до ближайшего разрешенного
уровня) значениями. Интервал между
соседними разрешенными уровнями,
или уровнями квантования,
называетсяшагом
квантования
.

Различают
равномерное и неравномерное квантование.
В большинстве случаев применяется и
далее подробно рассматривается
равномерное квантование (рис. 4.19), при
котором шаг квантования постоянный:
;
однако иногда определенное преимущество
дает неравномерное квантование, при
котором шаг квантования
разный
для различных
(рис. 4.20).

Квантование
приводит к искажению сообщений. Если
квантованное сообщение, полученное в
результате квантования отсчета

,
обозначить как
,

то

где

— разность между истинным значением
элементарного сообщения

и
квантованным
сообщением (ближайшим разрешенным
уровнем)
,
называемая ошибкой
квантования, или
шумом
квантования
.
Шум квантования оказывает на процесс
передачи информации по существу такое
же влияние, как и помехи в канале связи.
Помехи, так же как и квантование, приводят
к тому, что оценки
,
получаемые на приемной стороне системы
связи, отличаются на некоторую величину
от истинного значения.

Поскольку
квантование сообщений приводит к
появлению ошибок и потере некоторой
части информации, можно определить
цену таких потерь

и среднюю величину ошибки, обусловленной
квантованием:

Чаще
всего в качестве функции потерь (цены
потерь) используется квадратичная
функция вида

В
этом случае мерой ошибок квантования
служит дисперсия этих ошибок. Для
равномерного

-уровневого
квантования с шагом

дисперсия ошибок квантования определяется
следующим образом:

Абсолютное
значение ошибки квантования не превосходит
половины шага квантования
,

и
тогда при
достаточно большом числе уровней
квантования

и малой величине
плотность
распределения вероятностей ошибок
квантования

можно
считать равномерной на интервале +
…

—:

В
результате величина ошибки квантования
определится соотношением

и
соответствующим выбором шага квантования

может быть сделана сколь угодно малой
или сведена к любой наперед заданной
величине.

Относительно
требуемой точности передачи отсчетов
сообщений можно высказать те же
соображения, что и для ошибок временной
дискретизации: шумы квантования или
искажения, обусловленные квантованием,
не имеют существенного значения, если
эти искажения меньше ошибок, обусловленных
помехами и допустимых техническими
условиями.

Template:Unreferenced

The difference between the actual analog value and quantized digital value due is called quantization error. This error is due either to rounding or truncation.

Many physical quantities are actually quantized by physical entities. Examples of fields where this limitation applies include electronics (due to electrons), optics (due to photons), biology (due to DNA), and chemistry (due to molecules). This is sometimes known as the «quantum noise limit» of systems in those fields. This is a different manifestation of «quantization error,» in which theoretical models may be analog but physics occurs digitally. Around the quantum limit, the distinction between analog and digital quantities vanishes.

Quantization noise model of quantization error[]

File:Quanterr.png

Quantization noise. The difference between the blue and red signals in the upper graph is the quantization error, which is «added» to the original signal and is the source of noise.

Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC) process in telecommunication systems and signal processing. It is a rounding error between the analogue input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent. It can be modelled in several different ways.

In an ideal analog-to-digital converter, where the quantization error is uniformly distributed between −1/2 LSB and +1/2 LSB, and the signal has a uniform distribution covering all quantization levels, the signal-to-noise ratio (SNR) can be calculated from

${displaystyle mathrm {SNR_{ADC}} =20log _{10}(2^{Q})approx 6.0206cdot Q mathrm {dB} ,!}$

The most common test signals that fulfil this are full amplitude triangle waves and sawtooth waves.

In this case a 16-bit ADC has a maximum signal-to-noise ratio of 6.0206 · 16=96.33 dB.

When the input signal is a full-amplitude sine wave the distribution of the signal is no longer uniform, and the corresponding equation is instead

${displaystyle mathrm {SNR_{ADC}} =left(1.761+6.0206cdot Qright) mathrm {dB} ,!}$

Here, the quantization noise is once again assumed to be uniformly distributed. When the input signal has a high amplitude and a wide frequency spectrum this is the case.^[1]

In this case a 16-bit ADC has a maximum signal-to-noise ratio of 98.09 dB.

For complex signals in high-resolution ADCs this is an accurate model. For low-resolution ADCs, low-level signals in high-resolution ADCs, and for simple waveforms the quantization noise is not uniformly distributed, making this model inaccurate.^[2] In these cases the quantization noise distribution is strongly affected by the exact amplitude of the signal.

Template:Listen

References[]

↑ Template:Cite book
↑ Template:Cite book

External links[]

Quantization noise in Digital Computation, Signal Processing, and Control, Bernard Widrow and István Kollár, 2007.
The Relationship of Dynamic Range to Data Word Size in Digital Audio Processing
Round-Off Error Variance — derivation of noise power of q²/12 for round-off error
Dynamic Evaluation of High-Speed, High Resolution D/A Converters Outlines HD, IMD and NPR measurements, also includes a derivation of quantization noise
Signal to quantization noise in quantized sinusoidal

de:Quantisierungsrauschen
es:Ruido de cuantificación
ja:量子化雑音
ja:量子化誤差
pl:Szum kwantyzacji
ru:Шум квантования

Вычислите ошибку квантования

Во-первых, случайный сигнал создается, который порождает линейную оболочку столбцов квантизатора.

Равномерно распределенный случайный сигнал

q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1);        % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);

Фиксация: вокруг по направлению к нулю.

q = quantizer('fix',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance = eps(q)^2 / 3
% Theoretical mean     = 0
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -46.8586
Theoretical error variance (dB) = -46.9154
Estimated   mean = 7.788e-06
Theoretical mean = 0

Пол: вокруг к минус бесконечность.

q = quantizer('floor',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance =  eps(q)^2 / 12
% Theoretical mean     = -eps(q)/2
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9148
Theoretical error variance (dB) = -52.936
Estimated   mean = -0.0038956
Theoretical mean = -0.0039062

Потолок: вокруг к плюс бесконечность.

q = quantizer('ceil',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance = eps(q)^2 / 12
% Theoretical mean     = eps(q)/2
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9148
Theoretical error variance (dB) = -52.936
Estimated   mean = 0.0039169
Theoretical mean = 0.0039062

Вокруг: вокруг к самому близкому. Вничью, вокруг к самой большой величине.

Вокруг более точно, чем пол, но все значения, меньшие, чем eps (q), округлены, чтобы обнулить и потеряны — также.

q = quantizer('nearest',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance = eps(q)^2 / 12
% Theoretical mean     = 0
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9579
Theoretical error variance (dB) = -52.936
Estimated   mean = -2.212e-06
Theoretical mean = 0

Конвергентный: вокруг к самому близкому. Вничью, вокруг к даже.

q = quantizer('convergent',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t  = errvar(q);
% Theoretical variance = eps(q)^2 / 12
% Theoretical mean     = 0
fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)

Estimated   error variance (dB) = -52.9579
Theoretical error variance (dB) = -52.936
Estimated   mean = -2.212e-06
Theoretical mean = 0

Сравнение самых близких по сравнению с конвергентным

Ошибка p.d.f. из конвергентных

f(err) = 1/eps(q),  for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise

в то время как ошибка p.d.f. из раунда

f(err) = 1/eps(q),  for -eps(q)/2 <  err <= eps(q)/2, and 0 otherwise

Единственной разницей является направление округления вничью.

x=(-3.5:3.5)';
[x convergent(x) nearest(x)]

ans =

   -3.5000   -4.0000   -3.0000
   -2.5000   -2.0000   -2.0000
   -1.5000   -2.0000   -1.0000
   -0.5000         0         0
    0.5000         0    1.0000
    1.5000    2.0000    2.0000
    2.5000    2.0000    3.0000
    3.5000    4.0000    4.0000

Постройте функцию помощника

Функция помощника, которая использовалась, чтобы сгенерировать графики в этом примере, описана ниже.

type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m'))
%#ok<*NOPTS>

function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT  Plot function for QERRORDEMO.
%    QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
%    used by the example function QERRORDEMO, where Q is the quantizer
%    whose attributes are being analyzed; F_T is the theoretical
%    quantization error probability density function for quantizer Q
%    computed by ERRPDF; XI is the domain of values being evaluated by
%    ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
%    computed by ERRMEAN; V_T is the theoretical quantization error
%    variance of quantizer Q computed by ERRVAR; and ERR is the error
%    generated by quantizing a random signal by quantizer Q.
%
%    See QERRORDEMO for examples of use.

%    Copyright 1999-2014 The MathWorks, Inc.

v=10*log10(var(err));
disp(['Estimated   error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated   mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')

Рассмотрим фрагмент файла трассировки Oracle8i, который демонстрирует эффект ошибки квантования:

WAIT #96: nam=’db file sequential read’ ela= 0 p1=1 p2=1691 p3=1

FETCH #96:c=1,e=0,p=1,cr=4,cu=0,mis=0,r=1,dep=1,og=4,tim=116694789 В данном случае E = -1 сантисекунда:

В данном случае E = 640 мкс:

Наконец, рассмотрим пример ошибки квантования E < 0 в данных трассировки Oracle9i:

Диапазон значений ошибки квантования

P (значения всех n ошибок квантования больше m или меньше -m)=

= (0.5)n(1- m)n

Ошибки квантования для продолжительностей (например, значений e и ela в Oracle) — это случайные числа в диапазоне:

Что означает «один шанс из десяти в [очень большой] степени»?

мени в случае корректного сбора данных (см. главу 6) чрезвычайно редко превышала 10% общего времени отклика.

Ошибка квантования становится еще менее значимой в Oracle9i благодаря повышению точности измерений.

Следующая >

Источник

3.3. Информация в непрерывных сообщениях

Sensors

Quantization errors

Digital Filters

2.11 Quantization in Digital Filters

2.11.1 Coefficient Quantization

2.11.2 Quantization Noise

2.11.3 Overflow Limit Cycles

2.11.4 Granularity Limit Cycles

Biomedical signals and systems

2.2.1 Noise power

Measurement of high voltages

Static errors

Remaining useful life prediction

6.3.4.3 RUL Prediction

Orbit and Attitude Sensors

Exercise 1

Sampling Theory

8.3.2 Quantization and Coding

Compression

Weighted Quantization and Regions of Interest

Signal and Image Representation in Combined Spaces

6.1 Two lemmas on frames of complex exponentials

Live HDR Video Broadcast Production

1.4.1 Banding

Create Uniformly Distributed Random Signal

Fix: Round Towards Zero

Floor: Round Towards Negative Infinity

Ceil: Round Towards Positive Infinity

Round: Round to Nearest; In a Tie Round to Largest Magnitude

Convergent: Round to Nearest; In a Tie Round to Even

Compare Nearest and Convergent Rounding

See Also

Ошибки квантования

Ошибки квантования

Вычислите ошибку квантования

Равномерно распределенный случайный сигнал

Фиксация: вокруг по направлению к нулю.

Пол: вокруг к минус бесконечность.

Потолок: вокруг к плюс бесконечность.

Вокруг: вокруг к самому близкому. Вничью, вокруг к самой большой величине.

Конвергентный: вокруг к самому близкому. Вничью, вокруг к даже.

Сравнение самых близких по сравнению с конвергентным

Постройте функцию помощника

Погрешность восстановления сигнала. Информационный расчёт системы. Квантование сообщений. Ошибки квантования

Расчет разрядности АЦП

Расчет максимально возможной погрешности восстановления

Восстановление непрерывного сигнала U(t) с помощью интерполяционного метода

4.6. Квантование сообщений. Ошибки квантования

Quantization noise model of quantization error[]

References[]

See also[]

External links[]

Вычислите ошибку квантования

Равномерно распределенный случайный сигнал

Фиксация: вокруг по направлению к нулю.

Пол: вокруг к минус бесконечность.

Потолок: вокруг к плюс бесконечность.

Вокруг: вокруг к самому близкому. Вничью, вокруг к самой большой величине.

Конвергентный: вокруг к самому близкому. Вничью, вокруг к даже.

Сравнение самых близких по сравнению с конвергентным

Постройте функцию помощника

Интересное по теме: