Оценка точности прогноза модельная ошибка

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

---

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

1. Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
2. Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
3. Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error

---

MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
2. Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
3. Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

---

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
2. Находится сумма всех фактов по всем позициям  (общий фактический объем)
3. Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

---

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

1. Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
2. Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
3. Извлекаем корень из полученного результат — RMSE
4. Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
   1. Разделить на разницу между максимальным и минимальным значением показателей
   2. Разделить на разницу между третьим и первым квартилем значений показателей
   3. Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)

---

MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

---

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Об авторе

HeinzBr

Автор статей и создатель сайта SHTEM.RU

Методы оценки качества прогноза

Часто при составлении любого прогноза — забывают про способы оценки его результатов. Потому как часто бывает, прогноз есть, а сравнение его с фактом отсутствует. Еще больше ошибок случается, когда существуют две (или больше) модели и не всегда очевидно — какая из них лучше, точнее. Как правило одной цифрой (R²) сложно обойтись. Как если бы вам сказали — этот парень ходит в синей футболке. И вам сразу все стало про него ясно )

В статьях о методах прогнозирования при оценке полученной модели я постоянно использовал такие аббревиатуры или обозначения.

• R²
• MSE
• MAPE
• MAD
• Bias

Попробую объяснить, что я имел в виду.

Остатки

Итак, по порядку. Основная величина, через которую оценивается точность прогноза это остатки (иногда: ошибки, error, e). В общем виде это разность между спрогнозированными значениями и исходными данными (либо фактическими значениями). Естественно, что чем больше остатки тем сильнее мы ошиблись. Для вычисления сравнительных коэффициентов остатки преобразуют: либо берут по модулю, либо возводят в квадрат (см. таблицу, колонки 4,5,6). В сыром виде почти не используют, так как сумма отрицательных и положительных остатков может свести суммарную ошибку в ноль. А это глупо, сами понимаете.

Суровые MSE и R²

Когда нам требуется подогнать кривую под наши данные, то точность этой подгонки будет оцениваться программой по среднеквадратической ошибке (mean squared error, MSE). Рассчитывается по незамысловатой формуле

где n-количество наблюдений.

Соотвественно, программа, рассчитывая кривую подгонки, стремится минимизировать этот коэффициент. Квадраты остатков в числителе взяты именно по той причине, чтобы плюсы и минусы не взаимоуничтожились. Физического смысла MSE не имеет, но чем ближе к нулю, тем модель лучше.

Вторая абстрактная величина это R² — коэффициент детерминации. Характеризует степень сходства исходных данных и предсказанных. В отличии от MSE не зависит от единиц измерения данных, поэтому поддается сравнению. Рассчитывается коэффициент по следующей формуле:

где Var(Y) — дисперсия исходных данных.

Безусловно коэффициент детерминации — важный критерий выбора модели. И если модель плохо коррелирует с исходными данными, она вряд ли будет иметь высокую предсказательную силу.

MAPE и MAD для сравнения моделей

Статистические методы оценки моделей вроде MSE и R², к сожалению, трудно интерпретировать, поэтому светлые головы придумали облегченные, но удобные для сравнения коэффициенты.

Среднее абсолютное отклонение (mean absolute deviation, MAD) определяется как частное от суммы остатков по модулю к числу наблюдений. То есть, средний остаток по модулю. Удобно? Вроде да, а вроде и не очень. В моем примере MAD=43. Выраженный в абсолютных единицах MAD показывает насколько единиц в среднем будет ошибаться прогноз.

MAPE призван придать модели еще более наглядный смысл. Расшифровывается выражение как средняя абсолютная ошибка в процентах (mean percentage absolute error, MAPE).

где Y — значение исходного ряда.

Выражается MAPE в процентах, и в моем случае означает, что в модель может ошибаться в среднем на 16%. Что, согласитесь, вполне допустимо.

Наконец, последняя абсолютно синтетическая величина — это Bias, или просто смещение. Дело в том, что в реальном мире отклонения в одну сторону зачастую гораздо болезненнее, чем в другую. К примеру, при условно неограниченных складских помещениях, важнее учитывать скачки реального спроса вверх от спрогнозированных значений. Поэтому случаи, где остатки положительные относятся к общему числу наблюдений. В моем случае 44% спрогнозированных значений оказались ниже исходных. И можно пожертвовать другими критериями оценки, чтобы минимизировать этот Bias.

Можете попробовать это сами в Excel и Numbers

Интересно узнать — какие методы оценки качества прогнозирования вы используете в своей работе?

Подробности на блоге

Оценка ошибки прогнозирования временного ряда

Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE.
Пусть ошибка есть разность:
     ,
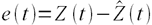
где Z(t) – фактическое значение временного ряда, а – прогнозное.
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.

MAPE – средняя абсолютная ошибка в процентах

     
.

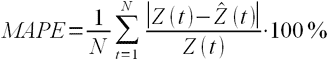
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.

Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.

MAE – средняя абсолютная ошибка

     
.

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.

После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.

Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.

MSE – среднеквадратичная ошибка

     
.

RMSE – квадратный корень из среднеквадратичной ошибки

     
.

ME – средняя ошибка

     
.

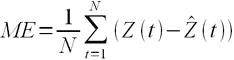
SD – стандартное отклонение

     
, где ME – есть средняя ошибка, определенная по формуле выше.

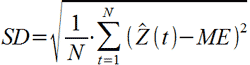
Связь точности и ошибки прогнозирования

Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.

Точность прогноза в % = 100% – MAPE

Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.

При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.

Важным этапом прогнозирования
социально-экономических явлений
является оценка точности и надежности
прогнозов.

Эмпирической мерой точности прогноза,
служит величина его ошибки, которая
определяется как разность между
прогнозными ()
и фактическими (у_t)
значениями исследуемого показателя.
Данный подход возможен только в двух
случаях:

а) период упреждения известен, уже
закончился и исследователь располагает
необходимыми фактическими значениями
прогнозируемого показателя;

б) строится ретроспективный прогноз,
то есть рассчитываются прогнозные
значения показателя для периода времени
за который уже имеются фактические
значения. Это делается с целью проверки
разработанной методики прогнозирования.

В данном случае вся имеющаяся информация
делится на две части в соотношении 2/3
к 1/3. Одна часть информации (первые 2/3
от исходного временного ряда) служит
для оценивания параметров модели
прогноза. Вторая часть информации
(последняя 1/3 части исходного ряда)
служит для реализации оценок прогноза.

Полученные, таким образом, ретроспективно
ошибки прогноза в некоторой степени
характеризуют точность предлагаемой
и реализуемой методики прогнозирования.
Однако величина ошибки ретроспективного
прогноза не может в полной мере и
окончательно характеризовать используемый
метод прогнозирования, так как она
рассчитана только для 2/3 имеющихся
данных, а не по всему временному ряду.

В случае если, ретроспективное
прогнозирование осуществлять по связным
и многомерным динамическим рядам, то
точность прогноза, соответственно,
будет зависеть от точности определения
значений факторных признаков, включенных
в многофакторную динамическую модель,
на всем периоде упреждения. При этом,
возможны следующие подходы к
прогнозированию по связным временным
рядам: можно использовать как фактические,
так и прогнозные значения признаков.

Все показатели оценки точности
статистических прогнозов условно можно
разделить на три группы:

• аналитические;

• сравнительные;

• качественные.

Аналитические показатели точности
прогноза позволяют количественно
определить величину ошибки прогноза.
К ним относятся следующие показатели
точности прогноза:

Абсолютная ошибка прогноза (D^*)
определяется как разность между
эмпирическим и прогнозным значениями
признака и вычисляется по формуле:

, (16.1)

где у_t– фактическое
значение признака;

—
прогнозное значение признака.

Относительная ошибка прогноза (d^*_отн)
может быть определена как отношение
абсолютной ошибки прогноза (D^*):

• к
  фактическому значению признака (у_t):

(16.2)

— к прогнозному
значению признака ()

(16.3)

Абсолютная и относительная ошибки
прогноза являются оценкой проверки
точности единичного прогноза, что
снижает их значимость в оценке точности
всей прогнозной модели, так как на
изучаемое социально-экономическое
явление подвержено влиянию различных
факторов внешнего и внутреннего
свойства. Единично удовлетворительный
прогноз может быть получен и на базе
реализации слабо обусловленной и
недостаточно адекватной прогнозной
модели и наоборот – можно получить
большую ошибку прогноза по достаточно
хорошо аппроксимирующей модели.

Поэтому на практике иногда определяют
не ошибку прогноза, а некоторый
коэффициент качества прогноза (К_к),
который показывает соотношение между
числом совпавших (с) и общим числом
совпавших (с) и несовпавших (н) прогнозов
и определяется по формуле:

(16.4)

Значение К_к= 1 означает, что имеет
место полное совпадение значений
прогнозных и фактических значений и
модель на 100% описывает изучаемое
явление. Данный показатель оценивает
удовлетворительный вес совпавших
прогнозных значений в целом по временному
ряду и изменяющегося в пределах от 0 до
1.

Следовательно, оценку точности получаемых
прогнозных моделей целесообразно
проводить по совокупности сопоставлений
прогнозных и фактических значений
изучаемых признаков.

Средним показателем точности прогноза
является средняя абсолютная ошибка
прогноза (),
которая определяется как средняя
арифметическая простая из абсолютных
ошибок прогноза по формуле вида:

, (16.5)

де n– длина временного
ряда.

Средняя абсолютная ошибка прогноза
показывает обобщенную характеристику
степени отклонения фактических и
прогнозных значений признака и имеет
ту же размерность, что и размерность
изучаемого признака.

Для оценки точности прогноза используется
средняя квадратическая ошибка прогноза,
определяемая по формуле:

(16.6)

Размерность средней квадратической
ошибки прогноза также соответствует
размерности изучаемого признака. Между
средней абсолютной и средней квадратической
ошибками прогноза существует следующее
примерное соотношение:

(16.7)

Недостатками средней абсолютной и
средней квадратической ошибками
прогноза является их существенная
зависимость от масштаба измерения
уровней изучаемых социально-экономических
явлений.

Поэтому на практике в качестве
характеристики точности прогноза
определяют среднюю ошибку аппроксимации,
которая выражается в процентах
относительно фактических значений
признака, и определяется по формуле
вида:

(16.8)

Данный показатель является относительным
показателем точности прогноза и не
отражает размерность изучаемых
признаков, выражается в процентах и на
практике используется для сравнения
точности прогнозов полученных как по
различным моделям, так и по различным
объектам. Интерпретация оценки точности
прогноза на основе данного показателя
представлена в следующей таблице:

,%	Интерпретация точности
< 10 10 – 20 20 – 50 > 50	Высокая Хорошая Удовлетворительная Не удовлетворительная

В качестве сравнительного показателя
точности прогноза используется
коэффициент корреляции между прогнозными
и фактическими значениями признака,
который определяется по формуле:

, (16.9)

где
—
средний уровень ряда динамики прогнозных
оценок.

Используя данный коэффициент в оценке
точности прогноза следует помнить, что
коэффициент парной корреляции в силу
своей сущности отражает линейное
соотношение коррелируемых величин и
характеризует лишь взаимосвязь между
временным рядом фактических значений
и рядом прогнозных значений признаков.
И даже если коэффициент корреляции R= 1, то это еще не предполагает полного
совпадения фактических и прогнозных
оценок, а свидетельствует лишь о наличии
линейной зависимости между временными
рядами прогнозных и фактических значений
признака.

Одним из показателей оценки точности
статистических прогнозов является
коэффициент несоответствия (КН), который
был предложен Г. Тейлом и может
рассчитываться в различных модификациях:

1. Коэффициент несоответствия (КН₁),
   определяемый как отношение средней
   квадратической ошибки к квадрату
   фактических значений признака:

(16.10)

КН = о, если
,
то есть полное совпадение фактических
и прогнозных значений признака.

КН = 1, если при прогнозировании получают
среднюю квадратическую ошибку адекватную
по величине ошибке, полученной одним
из простейших методов экстраполяции
неизменности абсолютных цепных
приростов.

КН > 1, когда прогноз дает худшие
результаты, чем предположение о
неизменности исследуемого явления.
Верхней границы коэффициент несоответствия
не имеет.

2.Коэффициент несоответствия КН₂определяется как отношение средней
квадратической ошибки прогноза к сумме
квадратов

отклонений
фактических значений признака от
среднего уровня исходного временного
ряда за весь рассматриваемый период:

, (16.11)

где — средний уровень исходного ряда
динамики.

Если КН > 1, то прогноз на уровне среднего
значения признака дал бы лучший
результат, чем имеющийся прогноз.

3.Коэффициент несоответствия (КН₃),
определяемый как отношение средней
квадратической ошибке прогноза к сумме
квадратов отклонений фактических
значений признака от теоретических,
выравненных по уравнению тренда:

, (16.12)

где — теоретические уровни временного ряда,
полученные по

модели тренда.

Если КН > 1, то прогноз методом
экстраполяции тренда дает хороший
результат.

Существует множество моделей прогноза, но как выбрать среди них ту, которая наиболее точно сделает прогноз?

Из данной статьи вы узнаете:

1. Какие способы оценки прогноза вы можете использовать?
2. Как выбрать оптимальную модель, которая поможет вам сделать максимально точный прогноз?
3. Как рассчитать показатель «Точность прогноза»?

Какие способы оценки прогнозной модели вы можете использовать:

1.  Оценить отношение фактических продаж к прогнозу;

2. Расчет показателя точность прогноза — оценка на сколько точно выбранная модель описывает анализируемые данные;

3. Графический анализ — строим график и визуально оцениваем адекватность модели прогноза относительно фактических продаж за последний период ;
 

1-й способ — Расчет отношения фактических продаж к прогнозу.

Сначала рассчитываем прогноз разными способами и оцениваем отношение фактических продаж к прогнозу. ВАЖНО протестировать модели не по одному товару или направлению продаж, а сразу взять 10 и более товарных позиций или направлений продаж и рассчитать прогноз по ним на минимум на 3 периода вперед (количество периодов и направления прогноза зависят от ваших задач. Если задача — сделать точный прогноз на 6 месяцев, то рассчитываем прогноз на 6 месяцев несколькими вариантами и оцениваем отношение факта к прогнозу по сумме полугода).

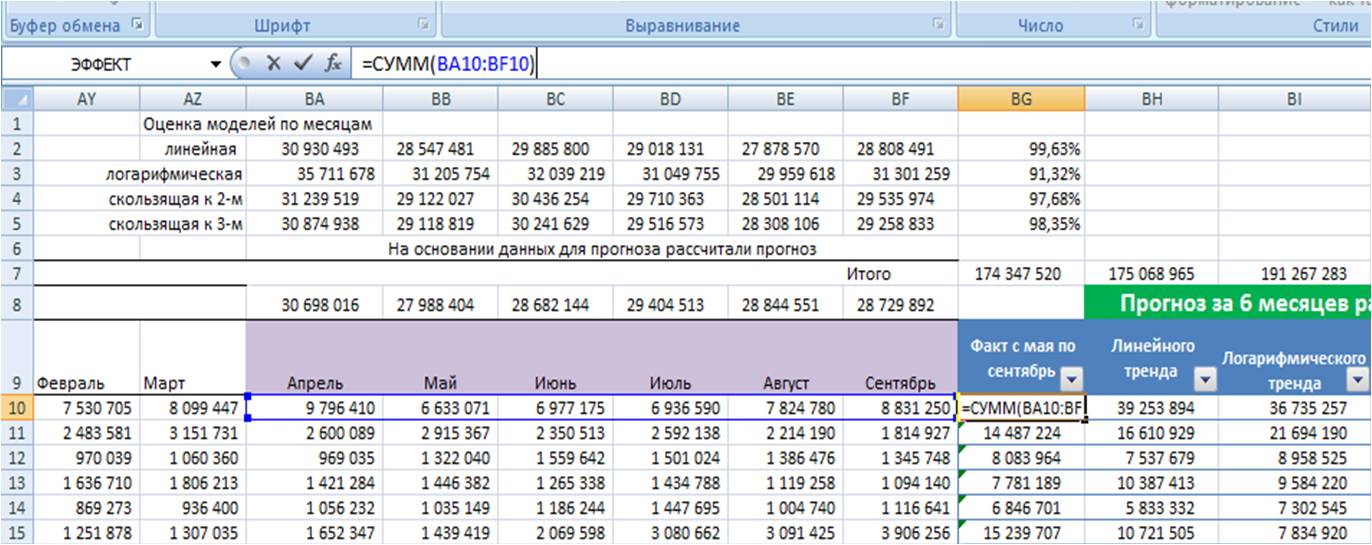
Рассчитаем прогноз 4 способами на полгода. Протестируем следующие модели:

1. Линейный тренд + сезонность — лист «Линейный» в приложенном файле (см. статью «Как рассчитать прогноз с учетом роста и сезонности в Excel»)

2. Логарифмический тренд + сезонность — лист «Логарифмический» в приложенном файле (см. статью «5 способов расчета значений логарифмического тренда»)

3. Скользящая средняя с сезонностью к 2-м месяцам — лист «Скользящая к 2-м» (см. статью «Как рассчитать прогноз по методу скользящей средней»);

4. Скользящяя средняя с сезонностью к 3-м месяцам — лист «Скользящая к 3-м»;

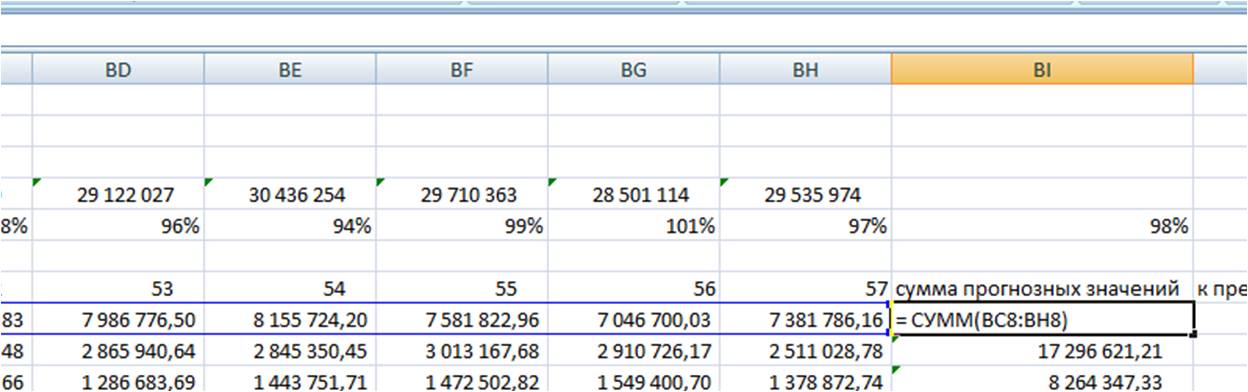
Для каждой из 4-х прогнозных моделей в листе «Оценка моделей»:

• Суммируем прогноз по каждой модели за 6 месяцев;

• Суммируем фактические продажи, которые мы будем сравнивать с прогнозом;

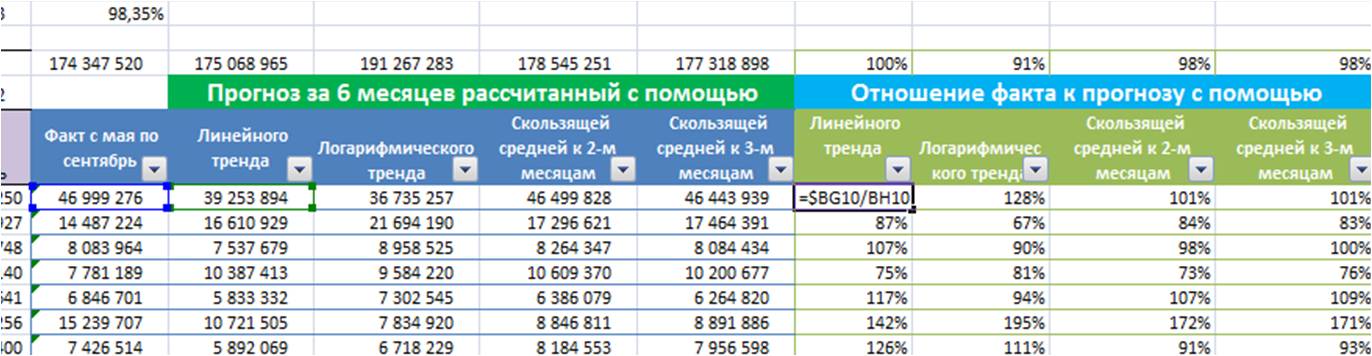
• Рассчитываем отношение факта к прогнозу по каждой позиции для каждой модели;

 

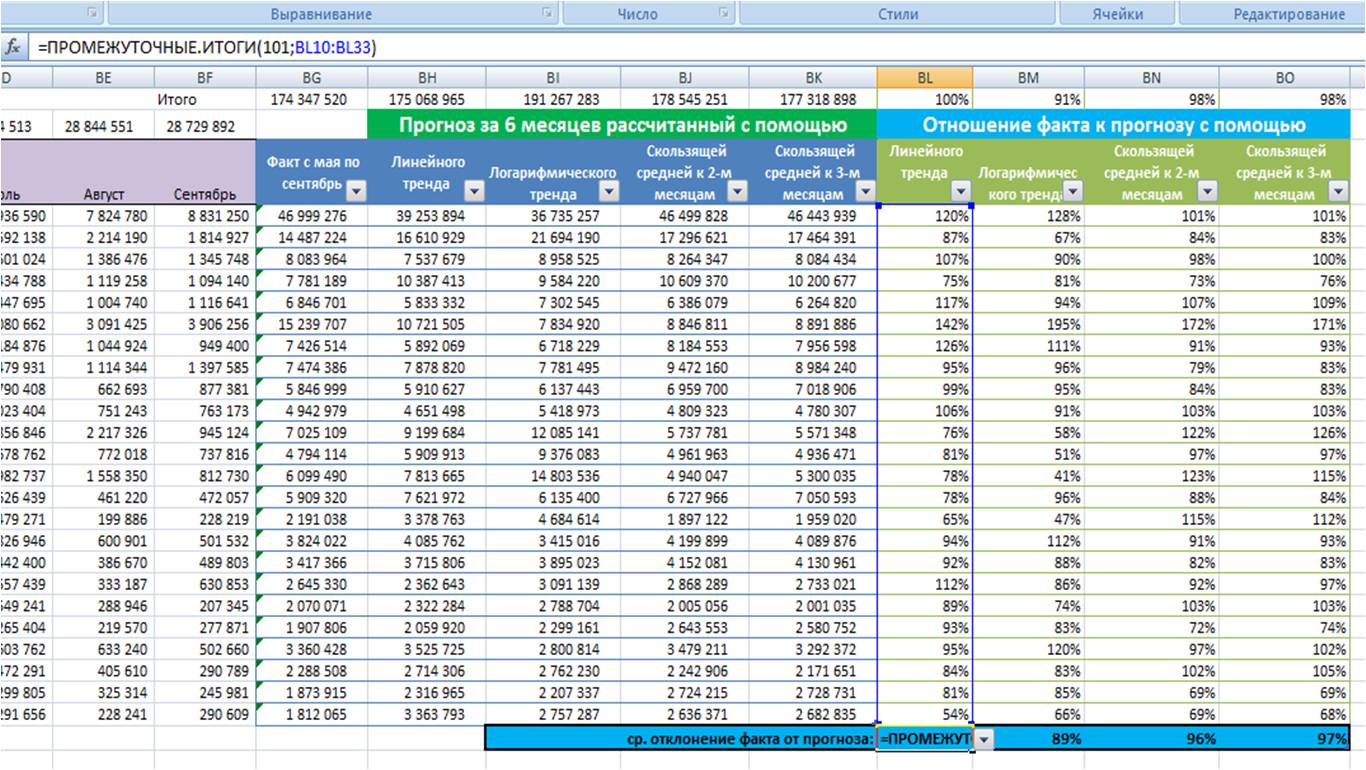
• Рассчитываем по каждой модели среднее отношение факта к прогнозу;

 

• Выбираем модель прогноза, которая по показателю «среднее отношение факта к прогнозу» оказалась максимально приближена к 100%;

 

Для наших данных самой точной моделью оказалась скользящая средняя к 3-м месяцам с сезонностью, среднее отклонение факта от прогноза 97%.

Мы протестировали каждую модель прогноза на реальных данных и выбрали для себя оптимальную, которая в среднем показала минимальное отклонение от факлических продаж.

2-й способ оценки модели прогноза — расчет показателя точность прогноза.

Показатель точность прогноза показывает, на сколько точно выбранная модель прогноза описывает данные. Идея в том, чем точнее выбранная модель описывает фактические данные, тем точнее она сделает прогноз.

Как рассчитать точность прогноза? Рассмотрим на примере расчета для модели прогноза с линейным трендом и сезонностью.

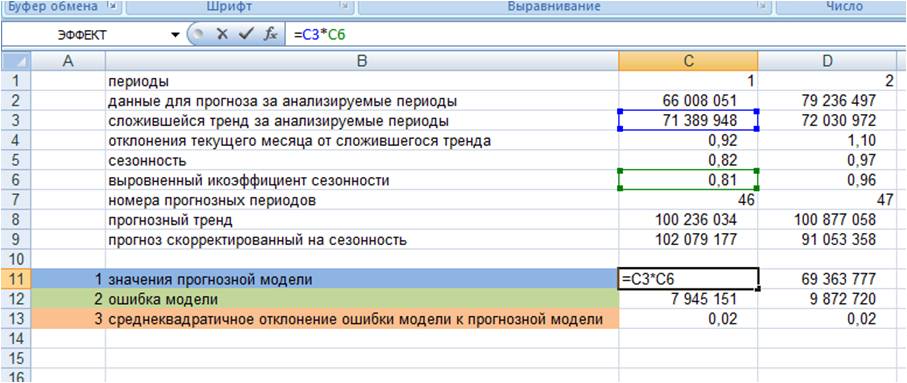
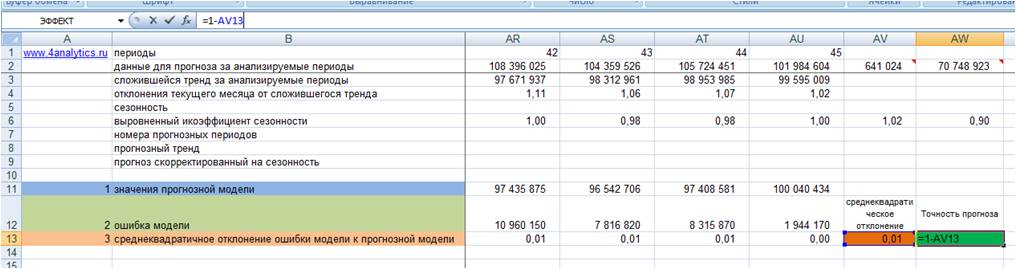
1. Рассчитываем значения прогнозной модели для каждого анализируемого момента времени в прошлом.

Для этого значения тренда для анализируемых периодов умножаем на выровненные коэффициенты сезонности (см. файл с примером)

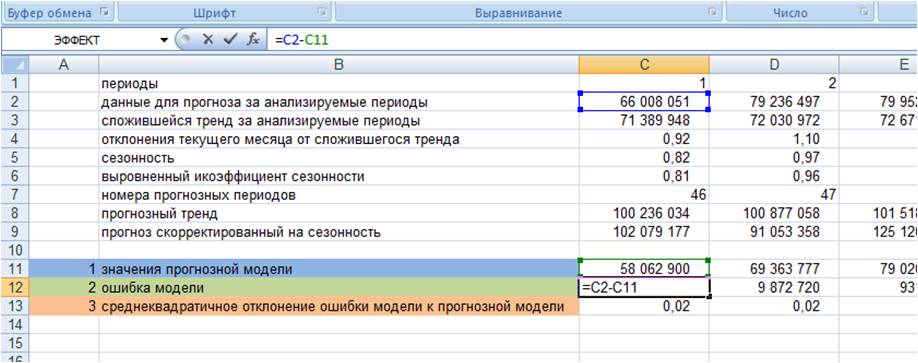
2. Рассчитываем ошибку прогнозной модели. Для этого за каждый период от фактических значений вычитаем значения прогнозной модели.

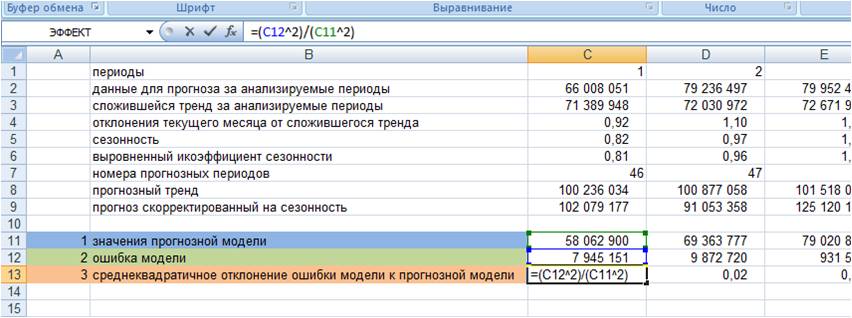
3. Рассчитываем квадратическое отклонение ошибки от значений прогнозной модели (см. файл с примером);

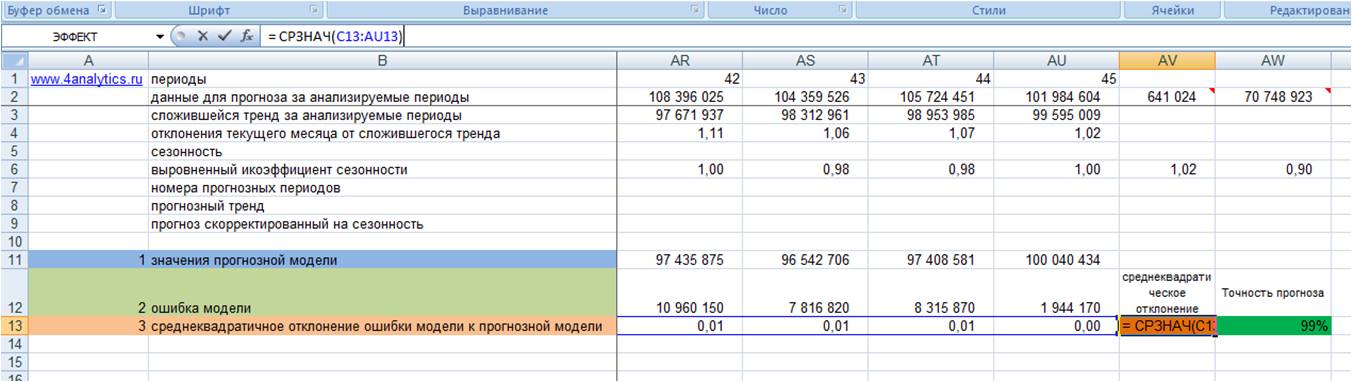
4. Рассчитываем среднее значение квадратического отклонения, т.е. среднеквадратическое отклонение

5. Точность прогноза = (1- среднеквадратическое отклонение ошибки прогнозной модели)*100 (см. файл с примером).

Показатель точности прогноза выражается в процентах:

• Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно.

• Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.

 Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.

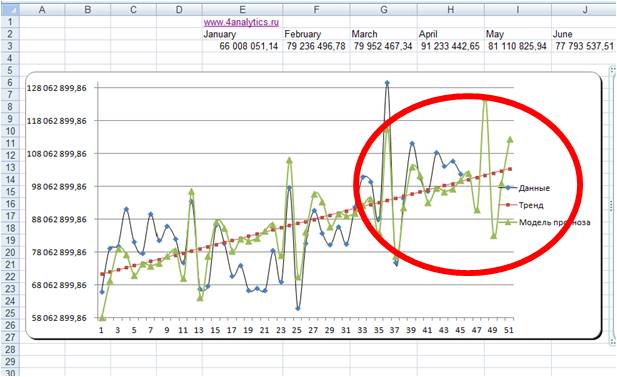
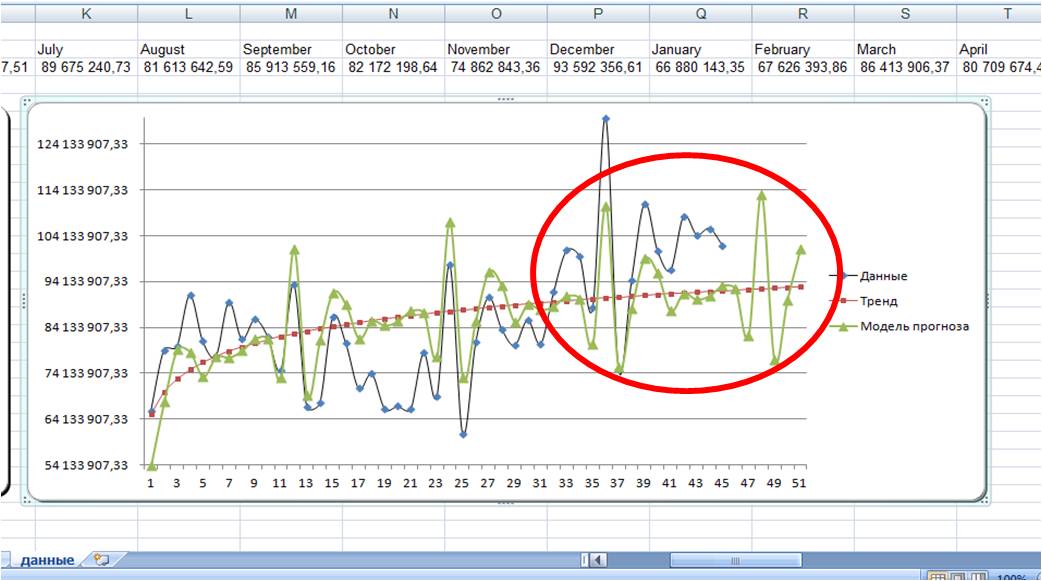
3. Способ оценки прогнозной модели — визуальный.

На график выводим анализируемые данные, тренд, значение модели и прогноз (см. вложенный файл). Обычно визуально видно, какая модель адекватнее строит прогноз . 3-й способ по своей сути схож с 1-м и вторым, только мы верим не цифрам, а тому что мы видим на графике.

Линейная модель:

 

Логарифмическая модель:

 

По последним периодам видно, что линейная модель более точно описывает данные за последние месяцы, и она, вероятнее всего, сделает более точный прогноз.

Какую модель прогноза выбрать?

1. Которая на основании тестирования на реальных данных для выбранного промежутка времени (месяца, 3-х месяцев, полугода, года) будет делать максимально точный прогноз, т.е. отношение факта к прогнозу будет близко к 1 или 100%.

2. Модель, которая будет максимально точно описывать фактические данные, т.е. показатель точность прогноза будет приближаться к 1, но не всегда модели точно описывающие данные делают адекватные прогнозы (это надо понимать и оценивать графически).

3. Модель, которой визуально вы больше доверяете с точки зрения описания входящих данных и продления прогнозной модели в будущее.

Для повышения точности прогноза я в своей практике стараюсь использовать 3 этих способа параллельно:

• По завершении прогнозного периода и в промежутках всегда оцениваю отношение фактических продаж к прогнозу.

• При построении прогноза анализирую показатель «среднеквадратическое отклонение» и рассчитываю показатель «точность прогноза» для оценки данных и модели.

• А также на график вывожу анализируемые данные и прогнозную модель, для визуального контроля.

Оценивая прогноз по факту или в промежуточные периоды в случае значительных отклонений фактических продаж от прогнозных, разбираю ситуацию и выясняю причины, в случае необходимости вношу корректировки в прогнозную модель.

С помощью программы Forecast4AC PRO вы можете рассчитать показатель точность прогноза автоматически.

Также Forecast4AC умеет автоматически выбирать оптимальную модель прогноза для каждого временного ряда.

+ одним нажатием строить график «Анализируемые данные + модель прогноза», на котором вы можете оценить, как соотносятся между собой:

• анализируемые данные;

• выбранный тренд;

• модель прогноза;

как в анализируемом периоде, так и в будущем. 

Точных прогнозов!

Статья полезная? Поделитесь с друзьями