Определение объема выборки ошибка выборки - Oshibku.top - решение и исправление самых разных ошибок

Один из первых шагов при планировании количественного маркетингового исследования – определение объема выборки.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних

1. Формула (даже две)

Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).

Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.

На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).

В таких случаях для расчета объема выборки используется следующая формула:

где

n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.

Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.

Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.

Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.

Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне

Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.

ШПАРГАЛКА (скопируйте ссылку или текст)

Подходы к решению проблемы:

Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,

N – объем генеральной совокупности,

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,

p – доля респондентов с наличием исследуемого признака,

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)

∆ – предельная ошибка выборки.

Например,

рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:

Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%

При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.

2. Причины «раздувать» выборку

Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).

Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок

Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра

При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).

Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:

увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).

Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ

Доверительный уровень:

Ошибка выборки (?):
%

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

РЕЗУЛЬТАТ

Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.

Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.

Объем выборки рассчитывается по следующим формулам

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.

Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.

ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:

Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:

n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек

Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Доля признака (p):
%

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для доли признака рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

Δ– предельная ошибка выборки.

Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:

Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%

Рассчитаем доверительный интервал:

(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)

Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).

Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Среднее значение (x̄):

Стандартное отклонение (s):

РЕЗУЛЬТАТ

Ошибка выборки для среднего значения рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Δ– предельная ошибка выборки.

Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:

Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44

Рассчитаем доверительный интервал:

(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)

Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ

Доверительный уровень:

	Измерение 1	Измерение 2
Доля признака (p):	%	%
Объём выборки (n):

РЕЗУЛЬТАТ

Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ

Доверительный уровень:

	Измерение 1	Измерение 2
Среднее значение (x̄):
Стандартное отклонение (s):
Объём выборки (n):

РЕЗУЛЬТАТ

Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?

В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Распределения значений в выборках близки к нормальному распределению.

В калькуляторе используются следующие вводные данные:

Среднее значение ( ̅x) – среднее арифметическое показателя.

Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

Вы можете подписаться на уведомления о новых материалах СканМаркет

Источник

Размер
выборки
– это количество элементов, которые
необходимо отобрать из генеральной
совокупности для проведения выборочного
исследования.

Определение
размера выборки для вероятностного
метода отбора представляет собой сложный
процесс, включающий ряд этапов: 1) оценка
факторов, влияющих на объем выборки; 2)
выбор метода расчета размера выборки;
3) расчет размера выборки; 4) оценка
стандартного отклонения среднего в
выборочной совокупности; 5) расчет
предельной ошибки выборки; 6) оценка
среднего значения признака в генеральной
совокупности (см. рис. 4.8).

В
случае применения детерминированного
метода отбора используются только
приблизительные методы расчета размера
выборки и оценить объективно точность
результатов исследования не представляется
возможным.

1.
Оценка факторов, влияющих на размер
выборки.
К наиболее важным факторам, определяющим
объем выборки, относятся следующие:
важность принимаемого решения, характер
исследования, бюджет исследования,
стоимость сбора информации, число групп
и подгрупп в генеральной совокупности,
коэффициенты охвата и завершенности,
размер генеральной совокупности и
требуемая точность исследования (см.
рис. 4.9). На размер ошибки выборки и,
соответственно, точность результатов
исследования влияют применяемая
процедура отбора и степень вариации
признака в совокупности.

Как
правило, для
принятия важных решений
необходима детальная, максимально
точная информация. Ее получение
предусматривает создание больших
выборок, но при увеличении объема выборки
возрастает и стоимость каждой
дополнительной единицы информации.

На
величину объема выборки влияет также
характер
исследования.
В поисковых исследованиях, изучающих
качественные характеристики, объем
выборки, как правило, невелик. Для
исследований, предусматривающих
статистическое заключение, таких как
дескриптивные, необходим больший объем
выборки. Кроме того, большие выборки
нужны, когда информация собирается
с учетом большого количества переменных.
Большой объем выборки позволяет снизить
общий эффект от ошибок выборки по всем
переменным.

Принимая
решения об объеме выборки, нужно учитывать
фактор ограниченности ресурсов или
располагаемый
бюджет исследования.
В любом исследовательском проекте
существуют временные и финансовые
ограничения. При жестких бюджетных
ограничениях исследователь будет стоять
перед выбором: использовать более
дешевые методы сбора информации или
ограничить размер выборки, допуская
снижение точности результатов.

Р
исунок
4.8.
Этапы расчета необходимого размера
выборки и оценки значения признака в
генеральной совокупности

Р
исунок
4.9.
Факторы, учитываемые при определении
размера выборки и взаимосвязи между
ними

Чем
больше размер выборки
(чем
он ближе к размерам генеральной
совокупности в целом), тем надежнее и
достовернее полученные данные, однако
стоимость
сбора информации
(включающая в себя расходы на размножение
инструментария, оплату труда интервьюеров,
супервайзеров и операторов компьютерного
набора данных) при этом значительно
возрастает;

При
проведении углубленного анализа данных
с использованием разнообразных
методов многомерного статистического
анализа необходим большой объем выборки.
Это же касается данных, которые
анализируются с особой точностью. Таким
образом, для
анализа данных на уровне группы или
подгруппы
потребуется больший объем выборки, чем
для анализа общей или генеральной
совокупности.

К примеру, мы хотим
исследовать потребительское поведение
населения города. Перед нами – структура
генеральной совокупности, которая
представляет распределение в целом
населения города и по трем квотным
признакам: район города, пол, возраст.
Совершенно очевидно, что если в
исследовании ставится задача изучить
мнения населения города в целом — это
одна ситуация; если в том числе и по
возрастным группам – это другая (здесь
мы имеем 3 группы); если необходимо
выявить распределения мнений по
возрастным и половым группам — это третья
ситуация (здесь мы имеем уже шесть
групп); наконец, если в исследовании нас
интересует распределение информации
по возрастным, половым группам и районам
города (к примеру, мы хотим определить,
как к покупкам того или иного товара
относятся молодые женщины, проживающие
во Фрунзенском районе г. Минска), то
здесь мы имеем дело уже с четвертой
ситуацией (54 группы). Для получения
репрезентативной информации в последним
случае необходимо обеспечить
представительство в минимальной из
этих пятидесяти четырех групп 25-30 чел.
Следовательно, минимальный объем
выборочной совокупности здесь будет
находиться в пределах 1600 чел.

Статистически
определенный объем выборки представляет
собой конечный, или чистый объем выборки,
который необходимо получить, чтобы
обеспечить расчет параметров с желательной
степенью точности и заданным уровнем
достоверности. При проведении опросов
он выражается в количестве завершенных
интервью. Для получения конечного объема
выборки необходимо связаться с большим
количеством потенциальных респондентов.
Другими словами, начальный объем выборки
должен намного превышать конечный,
поскольку коэффициенты охвата и
завершенности обычно составляют меньше
100%.

Коэффициентом
охвата
называется степень наличия или процент
людей, подходящих для участия в
исследовании. Коэффициент охвата
определяет, какое количество контактов
с людьми необходимо осуществить, чтобы
в итоге получить объем выборки,
соответствующий заданным критериям.

Предположим,
что для исследования характеристик
моющих средств необходимо создать
выборку из женщин – глав семьи в возрасте
от 25 до 55 лет. Приблизительно 75% женщин
в возрасте от 20 до 60 лет, к которым можно
обратиться, – это женщины – главы семьи
в возрасте от 25 до 55 лет. Это означает,
что, в среднем, необходимо обратиться
к 1,33 женщин, чтобы получить одного
подходящего респондента. Дополнительные
критерии для отбора респондентов
(например, каким образом использовался
продукт) увеличивают необходимое
количество контактов. Предположим, что
дополнительным критерием является
использование женщиной моющего средства
для пола в течение последних двух
месяцев. Предполагается, что 60% женщин,
к которым обратятся исследователи,
будут соответствовать этому критерию.
Тогда коэффициент охвата составит 0,75
х 0,60 = 0,45. Таким образом, конечный объем
выборки следует увеличить на 2,22 (1/0,45).

Точно
так же при определении объема выборки
необходимо учитывать ожидаемые отказы
людей, соответствующих критериям
исследования. Коэффициент
завершенности
указывает на процент респондентов,
соответствующих критериям отбора,
которые полностью прошли интервью.
Например, если исследователь предполагает,
что коэффициент завершенности интервью
составит 80% от числа подходящих
респондентов, необходимое количество
контактов следует умножить на коэффициент
1,25. Применение коэффициентов охвата и
завершенности означает, что число
контактов с потенциальными респондентами,
т.е. начальный объем выборки, должно
быть в 2,22 х 1,25 (или 2,77) раз больше
необходимого объема выборки.

Заранее
заданная точность
результатов исследования или допустимая
ошибка выборки
позволяют рассчитать необходимый размер
выборочной совокупности, используя
статистические методы, которые будут
рассмотрены далее.

Ошибкой
выборочного исследования
называется
любая ошибка, возникающая в результате
опроса или наблюдения и являющаяся
следствием использования выборки, а не
всей генеральной совокупности. Ошибки
выборочного исследования обусловлены
процедурой формирования выборки и
объемом выборки. Крупные выборки
порождают меньшую ошибку выборочного
исследования, чем малые.

Чтобы
извлечь выборку, как уже отмечалось в
предыдущем параграфе, сначала необходимо
определит: основу
выборки,
представляющую собой сводный список
все членов генеральной совокупности.
Как известно, списки не всегда полно
представляют генеральную совокупность,
поскольку в ней постоянно происходят
изменения: одни члены появляются, другие
– уходят. Кроме того, списки не застрахованы
от ошибок и опечаток. Таким образом,
ошибка
основы выборки
выражается
в неправильном описании всей генеральной
совокупности. Независимо от способа
формирования выборки, исследователь
должен учитывать ошибку основы. Иногда
в распоряжении исследователя оказывается
основа, лишь приблизительно описывающая
всю генеральную совокупность, однако,
если альтернативы нет, приходится
использовать и такие списки. Исследователь
должен тщательно выбирать основу
выборки, стремясь минимизировать
ошибки. Кроме того, исследователь должен
предупредить клиента о том, что
используемая основа выборки может
содержать ошибки.

Далее
будет идти речь только о случайных
ошибках выборочного
исследования, которые не связанны с
основой выборки и могут быть оценены
статистически. Иначе говоря, будем
предполагать, что основа выборки является
достаточно качественной и обеспечивает
низкий уровень ошибок, так что мы можем
извлечь из нее репрезентативную выборку.

Ошибка
выборки
зависит
не
только от ее величины, но и от
степени различий между отдельными
единицами внутри данной генеральной
совокупности.
Например, если нужно узнать, средний
размер потребления пива молодежью г.
Минска в возрасте 18-25 лет, то обнаружится,
что внутри имеющейся генеральной
совокупности нормы потребления у
различных людей существенно различны
(гетерогенная
генеральная
совокупность). Если же необходимо узнать
размер потребления хлеба в той же
генеральной совокупности, то он будет
различаться значительно меньше
(гомогенная
генеральная
совокупность). Чем больше различия
(гетерогенность) внутри генеральной
совокупности, тем больше возможная
ошибка выборки.

Некоторые
методы выборочного исследования
минимизируют ошибку выборки, другие –
никак на нее не влияют.
Например, использование стратифицированного
отбора может дать выигрыш в точности
при оценивании характеристик всей
совокупности. Часто неоднородную
совокупность удается расслоить на
подсовокупности (страты), каждая из
которых внутренне однородна. Если каждая
страта однородна в том смысле, что
результаты измерений в ней мало изменяются
от единицы к единице, то можно получить
точную оценку среднего значения для
любой страты по небольшой выборке в
этой страте. Затем эти оценки можно
объединить в одну точную оценку для
всей совокупности.

2. Выбор метода
расчета размера выборки.
Если специалист из опыта знает, какой
размер выборки следует использовать,
или же существуют различные ограничения
(например, связанные с бюджетом),
используют приблизительные
методы расчета размера выборки,
к которым относятся следующие:

— произвольный
метод расчета.
В этом случае объем выборки определяется
на уровне 5-10 % от генеральной совокупности.

— по
эмпирическим правилам.
Рекомендуется
выбирать размер выборки таким образом,
чтобы при ее разделении на группы в
каждой группе было не меньше 100 элементов.
Кроме сопоставления основных групп
анализ часто может потребовать
использования подгрупп. Размеры таких
подгрупп должны составлять от 20 до 50
человек. Это основано на том, что для
подгрупп требуется меньшая точность.

Если
одна из групп или подгрупп составляет
сравнительно небольшой процент
совокупности, то будет разумно использовать
непропорциональную выборку. Допустим,
что только 10% совокупности смотрит
образовательные телепередачи, и мнения
представителей этой группы требуется
сопоставить с мнениями других членов
совокупности. Если используются
телефонные интервью, контакты с жителями
могут устанавливаться случайно до тех
пор, пока не будут набраны 100 человек,
которые не смотрят образовательные
телепередачи. Далее опрос продолжается,
однако уже опрашиваются лишь те
респонденты, кто образовательные
телепередачи смотрит. В результате
будет получена выборка из 200 человек,
половина из которых смотрят образовательные
телепередачи.

— традиционный
метод расчета
связан с проведением периодических
ежегодных исследований, охватывающих,
например, 500, 1000 или 1500 респондентов.

— на
основе опыта сопоставимых исследований.
Таблица
4.7 дает представление об объемах выборок,
используемых в различных маркетинговых
исследованиях. Эти величины установлены
опытным путем и могут использоваться
в качестве ориентировочных данных,
особенно при детерминированных методах
формирования выборки.

— затратный
метод основан
на размере расходов, которые допустимо
затратить на проведение исследования.

Статистический
метод определения объема выборки
основан на традиционном статистическом
заключении. В соответствии с этим методом
заранее определяется уровень (степень)
точности.

Рассмотрение
данного метода начнем с краткой
характеристики базовых
понятий математической статистики.

Наиболее
важным понятием, позволяющим делать
заключения о свойствах генеральной
совокупности на основе выборочных
методов является кривая нормального
распределения.

Таблица
4.7.
Объемы выборок, используемых в
маркетинговых исследованиях

Вид исследования	Минимальный объем	Обычный диапазон
Исследование, цель которого – определить проблему (например, изучение потенциала рынка)	500	1000-2500
Исследование, цель которого – решить проблему (например, определить цену)	200	300-500
Тестирование товара	200	300-500
Пробный маркетинг	200	300-500
Теле- радио- и печатная реклама (в расчете на одно рекламное объявление, эффективность которого исследуется)	150	200-300
Аудит на пробном рынке	10 магазинов	10-20 магазинов
Фокус-группы	2 группы	10-15 групп

Кривая нормального
распределения
– это теоретическая модель, представляющая
собой абсолютно симметричный и гладкий
вид полигона частот. Она имеет форму
колокола и одну вершину, а ее концы
уходят в бесконечность в обоих
направлениях. Важнейшим свойством,
которым обладает кривая нормального
распределения, является то, что расстояние
по абсциссе (горизонтальная ось)
распределения, измеренное в единицах
стандартного отклонения от среднего
арифметического распределения, всегда
дает одинаковую общую площадь под
кривой: между ±1 стандартным отклонением
находится 68,3% площади; между ±2 стандартными
отклонениями – 95,4% площади; между ±3
стандартными отклонениями – 99,7% площади
(см. рис. 4.10).

Рисунок
4.10. Области
под теоретической кривой нормального
распределения

C
понятием кривой нормального распределения
связана центральная
предельная теорема, которая
гласит:
«Если
из генеральной совокупности, имеющей
любое распределение со средним μ
и
стандартным отклонением σ,
многократно извлекать случайные выборки
объема n,
то
при большом n
распределение всех возможных выборочных
средних будет стремиться к нормальному
распределению со средним μ
и
стандартным
отклонением σ
/
».

Таким
образом, центральная предельная теорема
позволяет распространять данные,
полученные в результате выборочного
исследования на всю генеральную
совокупность с определенной степенью
допущения при условии достаточно
большого объема выборки.

Конечно,
остается вопрос о том, что же такое
большой объем выборки. Полезное
эмпирическое правило гласит: если объем
выборки (n)
равен
100 или более, то применима центральная
предельная теорема и вы можете принять
допущение о нормальности распределения
всех возможных выборочных средних. Если
же n
меньше
100, то вы должны иметь веские доказательства
нормальности распределения генеральной
совокупности, и только после этого вы
можете полагать, что распределение,
которому подчиняются выборочные
статистики, является нормальным.
Следовательно, нормальность распределения
выборочных статистик гарантируется
путем использования довольно больших
выборок.

3.
Выбор требуемой степени точности и
достоверности результатов исследования.
При проведении любого выборочного
опроса или наблюдения перед исследователем
ставится задача оценить, каково истинное
значение во всей генеральной совокупности
либо среднего
значения
абсолютного
признака (доход
потребителей, размер потребления
конкретного товара), либо доли
единиц в совокупности, обладающих
каким-либо
признаком
(доля постоянных потребителей конкретного
товара; доля потребителей, удовлетворенных
уровнем обслуживания). Точность
выборки
в первом случае будет представлена в
виде абсолютной величины со знаком ±
(например, ±100 тыс. руб.; ±1 кг), или в виде
процента, во втором случае – только в
виде процента с тем же знаком (например,
±1% или ±5%).

Интерпретация
точности выборки подчиняется следующей
логике: если объем выборки обеспечивает
точность ±5%, то результаты опроса или
наблюдения, полученные с помощью выборки,
отличаются от результатов полной
переписи не более чем на 5%.

Еще одним фактором,
влияющим на объем выборки является
заданная исследователем степень
достоверности
(надежности)
оценки,
то есть степень
уверенности в том, что оценка близка к
истинному значению.

Для выборки
фиксированного объема степень точности
и степень достоверности являются
связанными величинами. На деле определение
объема выборки предполагает достижение
известного баланса между двумя этими
принципами.

Зависимость
точности выборки от ее объема для 95,4% и
99,7% уровня надежности представлена на
рисунке 4.11. Объем выборок на графике
колеблется от 50 до 2000. График демонстрирует,
что при увеличении объема выборки
ее ошибка уменьшается. Однако, как видим,
зависимость ошибки выборки от ее объема
не является прямолинейной. Иначе говоря,
удвоение объема выборки, не приводит к
существенному уменьшению ошибки.

исунок
4.11. Зависимость
точности и достоверности от объема
выборки

Если
объем выборки превышает 500, ошибка
выборки для 95,4% надежности падает ниже
±4% и продолжает очень медленно снижаться.
С другой стороны, анализ графика в
области малых выборок показывает, что
относительно небольшое изменение объема
выборки позволяет значительно повысить
их точность. Например, если объем выборки
равен 50, то ее уровень точности равен
±13,9%, а увеличение их объема до 250 позволяет
уменьшить ошибку выборки до ±6,2%. Иными
словами, точность выборки, объем которой
равен 25 примерно вдвое выше, чем точность
выборки, объем которой равен 50. Однако
в области крупных выборок это правило
не выполняется.

4. Определение
t
параметра, связанного с уровнем
надежности.
Определить значение t,
связанное с уровнем надежности можно
воспользовавшись таблицей 1 приложения.
Как видно по данным таблицы, при объеме
выборки больше 100 для 95,4% надежности
t≈2,
для 99,7% надежности t≈3.

5. Поиск информации
об уровне стандартного отклонения
среднего значения признака в генеральной
совокупности.
Здесь возможны
две различные ситуации: 1) стандартное
отклонение среднего значения признака
(σ)
в генеральной совокупности известно и
2) стандартное отклонение среднего
значения признака в генеральной
совокупности неизвестно.

В
первом случае можно приступить к расчету
объема
выборки с помощью формулы стандартной
ошибки выборки.

6.
Определение
объема выборки с помощью формулы
стандартной ошибки с учетом корректировки
на охват и завершенность.

Принято различать
среднюю и предельную ошибки выборки.
Предельная ошибка выборки определяется
следующим образом:

где
∆
— предельная ошибка выборки;

t
– параметр, связанный с уровнем
надежности;

μ
– средняя ошибка выборки.

Формулы расчета
средней ошибки
выборки для средней и для доли с учетом
способа отбора приведены в таблице 4.8.

Доверительные
интервалы для генеральной средней
можно установить на основе соотношений

Доверительные
интервалы для генеральной доли
устанавливаются на основе соотношений

Далее
для вычисления объема выборки применяется
формула
вычисление объема выборки по заданному
доверительному интервалу.
Формулы
расчета численности выборки
для определения средней и доли с учетом
способа отбора приведены в таблице 4.9.

Например,
для обследования, преследующего цель
выявить мнение потребителей о новом
товаре, в регионе, насчитывающем 10 тыс.
семей, необходимо провести анкетирование.
Условно принимается, что в каждой
квартире проживает одна семья и на нее
будет выделена одна анкета. Предварительные
исследования установили, что дисперсия
среднего размера покупки составляет
24 тыс. руб.; σ²
= 2; предельная ошибка не должна превышать
0,5 тыс. руб. Отсюда численность выборки
(п)
составит:

Эта
величина округляется до 400 семей
(квартир), т.е. установлена 4%-я выборка.
Однако практика показывает, что некоторая
часть анкет не возвращается (предположим
каждая пятая), поэтому увеличиваем число
анкет до 500. Следовательно, необходимо
включить в выборку каждую 20-ю квартиру
(10000 : 500).

Все
вышеприведенные формулы применимы для
большой выборки.
Кроме большой выборки используются так
называемые малые
выборки (n
< 30), которые могут иметь место в случаях
нецелесообразности использования
больших выборок.

При
расчете ошибок малой
выборки
необходимо учесть два момента:

1) формула средней
ошибки имеет вид

2)
при определении доверительных интервалов
исследуемого показателя в генеральной
совокупности или при нахождении
вероятности допуска той или иной ошибки
необходимо использовать таблицы
вероятности Стьюдента. При этом
вероятность
определяется
в зависимости от объема выборки и t
(см. табл.
прил. 1).

Таблица 4.8.
Формулы определения стандартной ошибки
выборки при различных способах отбора

Виды выборки Способы отбора	Повторная выборка	Бесповторная выборка
	Для средней
Простая случайная выборка
Стратифицированная или типическая выборка
Кластерная, гнездовая или серийная выборка	—
	Для доли
Простая случайная выборка
Стратифицированная или типическая выборка
Кластерная, гнездовая или серийная выборка	—	—

В
таблице используются следующие условные
обозначения:

N
– объем генеральной совокупности;

п
– объем выборочной совокупности;

– средняя в
генеральной совокупности;

–
средняя в выборочной
совокупности;

р
– доля единиц в генеральной совокупности;

w
– доля единиц в выборочной совокупности;

– генеральная
дисперсия (заменяется на выборочную
(S²) в случае, если она
не известна);

– межсерийная
дисперсия

;

r
— число отобранных серий;

R—
число серий в генеральной совокупности.

Таблица 4.9.
Формулы определения численности выборки
(n)
при различных способах отбора

Виды выборки Способы отбора	Повторная выборка	Бесповторная выборка
	Для средней
Простая случайная выборка
Стратифицированная или типическая выборка
Кластерная, гнездовая или серийная выборка	—
	Для доли
Простая случайная выборка
Стратифицированная или типическая выборка
Кластерная, гнездовая или серийная выборка	—	—

Например, для
разработки бизнес-плана нового ресторана,
который открывается в центральной части
г. Минска необходимо узнать ожидаемый
диапазон расходов одного посетителя в
вечернее время. Удалось получить
информацию о том, что стандартное
отклонение расходов посетителей близкого
по уровню и месту расположения ресторана
составляет 30$. Существует возможность
опросить около 26 посетителей ресторана.
С какой достоверностью можно получить
результат при заданной точности ±10$?

Рассчитаем среднюю
ошибку выборки:

Тогда

Из
таблицы приложения 1 для n=26
и t=1,66
можно определить, что при допуске ошибки
±10$ достоверность
результатов составит менее 90%. Более
точное значение достоверности для тех
же параметров можно получить, например,
при помощи функции СТЬЮДРАСП в Microsoft
Excel
— 89,2%.

С 95,4% надежностью
будет обеспечена меньшая точность:

7. Отбор
произвольной пробной выборки.
В случае если стандартное
отклонение среднего значения признака
в генеральной совокупности неизвестно,
необходимо сформировать произвольную
пробную выборку.

8. Расчет
стандартного отклонения средней в
выборочной совокупности.
На основе полученных данных рассчитывается
стандартное отклонение признака в
выборочной совокупности и, затем –
необходимый размер выборки по приведенным
выше формулам.

9. Расчет точности
полученных результатов по формуле
предельной ошибки выборки.По
данным, собранным в ходе проведенного
выборочного исследования, рассчитывается
точность результатов. Если полученная
точность не устраивает исследователя,
может возникнуть необходимость увеличить
размер выборки с учетом рассчитанного
стандартного отклонения и коэффициентов
отклика и завершенности.

Предположим, что
в предыдущем примере не было возможности
узнать стандартное отклонение расходов
посетителей ресторана. По данным опроса
30 случайно отобранных респондентов
получены следующие данные: 25$ – 2 чел.;
30$ – 3 чел.; 45$ – 7 чел.; 55$ – 6 чел.; 70$ – 3
чел.; 85$ – 5 чел.; 110$ – 2 чел.; 150$ – 2 чел.

Определяем среднее
значение по формуле средней взвешенной:

Далее
рассчитываем дисперсию (квадрат
стандартного отклонения) расходов
посетителей ресторана по выборочной
совокупности.

Тогда
точность полученных результатов с
достоверностью 95,4%:

Для
того, чтобы обеспечить заданную точность
(±10$) рассчитываем
необходимый размер выборки:

В
целом, для принятия взвешенного решения
по размеру выборки наряду со статистическими
методами расчета следует применить
рассмотренные ранее приблизительные
методы и сравнить полученные результаты.

10. Оценка значения
признака в генеральной совокупности.
Основными
методами распространения выборочного
наблюдения на генеральную совокупность
являются прямой пересчет и способ
коэффициентов.

Прямой
пересчет есть
произведение среднего значения признака
на объем генеральной совокупности.
Однако большое число факторов не
позволяет в полной мере использовать
точечную оценку прямого пересчета при
распространении результатов выборки
на генеральную совокупность. На практике
чаще пользуются интервальной оценкой,
которая дает возможность учитывать
размер предельной ошибки выборки,
которая рассчитана для средней или для
доли признака.

Оценка
среднего по совокупности при использовании
стратифицированной выборки является
взвешенным средним средних значений
по каждой страте выборки.

Например,
производителю пива для оценки емкости
внутреннего рынка в частности необходимо
определить долю потребителей пива в
общей численности населения региона в
возрасте от 20 до 60 лет с точностью ±5%.
Можно предположить, что данный показатель
будет варьировать по полу и возрасту.
В таблице 4.10 представлена информация
о численности и структуре населения
региона в возрасте от 20 до 60 лет.

Таблица
4.10. Численность
населения региона в возрасте от 20 до 60
лет

Возрастные категории населения	Всего, тыс. чел.	В том числе
мужчины	женщины
20-29	1576,0	802,0	774,0
30-39	1357,3	671,4	685,9
40-49	1559,6	751,9	807,7
50-59	1276,1	582,7	693,4
Всего	5769,0	2807,9	2961,1

Ранее
проведенный опрос 200 респондентов в
возрасте от 20 до 60 лет показал, что доля
потребителей пива в общей численности
населения региона составляет 83%. По
имеющейся информации был рассчитан
необходимый объем выборки:

С
учетом необходимости обеспечить
необходимый минимальный размер подгрупп
округляем полученный результат до 300
человек и рассчитываем объем выборки
для каждой из страт по полу и возрасту
пропорционально соответствующей
численности населения. Результаты
расчета представлены в таблице 4.11.

Таблица
4.11. Структура
населения региона в возрасте от 20 до 60
лет и численность выборки.

Возрастные категории населения	В % к общей численности населения	Численность выборки
всего	мужчины	женщины	мужчины	женщины
20-29	27,3	13,9	13,4	42	40
30-39	23,6	11,7	11,9	35	36
40-49	27,0	13,0	14,0	39	42
50-59	22,1	10,1	12,0	30	36
Всего	100,0	48,7	51,3	146	154

В
результате опроса получены данные,
представленные в таблице 4.12.

Таблица
4.12. Доля
потребителей пива в общей численности
населения в разрезе возрастных категорий
по данным выборочного опроса.

Возрастные категории населения	Доля потребителей пива
мужчины	женщины
20-29	0,812	0,795
30-39	0,855	0,743
40-49	0,848	0,683
50-59	0,867	0,542

Определяем долю
потребителей пива по формуле средней
взвешенной:

Средняя
ошибка выборки:

Предельная ошибка
выборки для 95,4% надежности составит:

Таким
образом, с 95,4% надежностью можно
утверждать, что доля потребителей пива
в общей численности населения региона
в возрасте от 20 до 60 лет находится в
интервале от 71,8% (76,6% — 4,8%) до 81,4% (76,6% +
4,8%).

Опрос
обычно не ограничивается одним вопросом
–
иногда их сотни. Поэтому повторять
подобный процесс для каждого вопроса
смысла не имеет. Разумный подход –
выбрать несколько репрезентативных
вопросов и по ним определить размер. В
этот набор следует включить наиболее
критичные вопросы с максимальным уровнем
ожидаемой дисперсии.

В таком случае
может оказаться полезным подход
к расчету объема выборки, основанный
на сценарии максимально возможной
вариации признака в совокупности. Как
видно на рисунке 6, вариант,
когда w=
0,5 (50%) является наиболее консервативным,
поскольку он порождает максимальный
размер ошибки и, соответственно,
максимальный объем выборки. Следовательно,
его следует выбирать, когда изменчивость
не известна. Тогда формула размера
выборки упрощается:

Для 95% уровня
надежности и 5% уровня точности:

Р
исунок
4.12.
График

Использование
номограмм для
расчета
объема выборки. Стремление
упростить процедуру расчета объема
выборки приводит к созданию таблиц,
шкал или программ, которые ориентированы
на обеспечение статистической
надежности информации, но при этом не
обременяют пользователя знаниями
специальных формул из области статистики.
Например, существует калькулятор выборки
(www.
shortway.
to/few/calculator,
htm).

Номограмма является
графическим способом определения
размера выборки. Номограмма включает
три шкалы (рис. 7). На шкале слева
устанавливается разметка показателя
среднеквадратического отклонения
или распределения доли признака. На
правой шкале наносится разметка точности
измерения в виде допустимой ошибки при
заданной доверительной вероятности
95,4% или 99,7%. На средней шкале делается
разметка, соответствующая требуемому
объему выборки. На правой и левой
шкалах делаются отметки на уровне
желаемых значений показателей (доли
признака и допустимой ошибки). Линейкой
эти две отметки соединяются, на пересечении
линейки со средней шкалой делается
отметка, соответствующая тому объему
выборки, который отвечает пожеланиям
исследователя.

Источник

Ядгаров М.Я.

НИИ Общей реаниматологии ФНКЦ РР

Берикашвили Л.Б.

НИИ Общей реаниматологии ФНКЦ РР

Каданцева К.К.

НИИ Общей реаниматологии ФНКЦ РР;
ГБУЗ «Московский клинический научный центр им. А.С. Логинова» Департамента здравоохранения Москвы

Определение объема выборки

Авторы:

Лихванцев В.В., Ядгаров М.Я., Берикашвили Л.Б., Каданцева К.К., Кузовлев А.Н.

Как цитировать:

Лихванцев В.В., Ядгаров М.Я., Берикашвили Л.Б., Каданцева К.К., Кузовлев А.Н. Определение объема выборки. Анестезиология и реаниматология.
2020;(6):77‑86.
Likhvantsev VV, Yadgarov MYa, Berikashvili LB, Kadantseva KK, Kuzovlev AN. Sample size estimation. Russian Journal of Anesthesiology and Reanimatology. 2020;(6):77‑86. (In Russ.)
https://doi.org/10.17116/anaesthesiology202006177

Данная статья открывает цикл публикаций, посвященных общим проблемам выбора и практического применения методов статистического анализа в клинических исследованиях. Мнения о ценности такого (статистического) подхода к оценке результатов исследования колеблются в диапазоне от «отсутствие грамотного статистического анализа приводит к утрате научной ценности исследования в целом» до «статистика — это некие «фантики», которыми принято декорировать исследование для пущей привлекательности и наукообразия». Последнее утверждение верно в той мере, в какой манипуляция статистикой или добросовестное заблуждение при выборе метода действительно могут изменить результат исследования, иногда на прямо противоположный. Однако необходимо отдавать себе отчет в том, что это проблема не статистики, а добросовестности и (или) полноты знания проблемы со стороны исследователя.

В эпоху доказательной медицины, в которую мы, хорошо ли, плохо ли, проживаем, статистический анализ, наряду с эпидемиологическим подходом к проведению исследования, стал обязательным элементом любой клинической работы, претендующей на звание научной. Раз так, а это именно так, то знание (в прагматически необходимом объеме!) статистики становится неотъемлемым элементом подготовки каждого научного сотрудника и обязательным квалификационным признаком состоявшегося специалиста. Однако на практике дела обстоят не настолько хорошо.

Последнее, к сожалению, становится все более и более заметно для авторов настоящей публикации, которые на протяжении многих лет являются рецензентами ряда ведущих отечественных журналов анестезиолого-реаниматологической тематики. Растущее количество работ с досадными, иногда нелепыми ошибками, допущенными по незнанию или недоразумению, заставляет каждый раз вновь обращаться к вопросам планирования исследования вообще и правилам проведения статистического анализа в частности.

Ряд ошибок, допущенных на этапе планирования, как мины замедленного действия, «срабатывают» в тот момент, когда менять что-либо уже поздно. Уже рекрутировано достаточное количество пациентов, и вдруг становится очевидно, что необходимо было мониторировать еще и «этот» показатель, без которого исследование «рассыпается», становится малоинформативным и бездоказательным. Рано или поздно авторы оказываются перед дилеммой: прервать исследование и начать все заново (жалко: столько сил и средств уже потрачено!) или продолжить, отдавая себе отчет в том, что цель достигнута быть не может, а единственное, что остается — это рассчитывать на получение некоего суррогата сомнительного качества. Именно поэтому крайне необходимым является проведение тщательного анализа предстоящей работы на этапе планирования, определение цели и задач, формулировка первичной, вторичной и т.д. конечных точек, адекватных поставленной цели; подбор методов не из арсенала того, «что у нас есть», а в соответствии с тем, «что необходимо, чтобы ответить на главный вопрос исследования». Жесткое соблюдение протокола и наличие CRF (Case Report Form — форма наблюдения за пациентом) являются абсолютными признаками качественного планирования. Все это в комплексе позволяет определить метод статистического анализа не «после», а еще «до» начала исследования, хотя некоторые коррективы, по-видимому, неизбежны (например, сообразно различному характеру распределения данных).

Маленькая иллюстрация вышесказанного. Допустим, вы собираетесь исследовать эффективность и безопасность разработанного Вами метода анестезии. Сделать это Вы планируете на основе анализа интраоперационных изменений уровня артериального давления (АД) и динамики активности ряда ферментов, обычно используемых для предварительной оценки функции некоторых органов и систем (аспартатаминотрансферазы — АсАТ, аланинаминотрансферазы — АлАТ, лактатдегидрогеназы — ЛДГ и т.д.). Вы справедливо полагаете, что для изучения летальности или частоты встречаемости жизнеугрожающих осложнений понадобится многосотенная, а то и многотысячная выборка, что нереально в рамках вашего учреждения, на что уйдут многие годы, и к окончанию работы либо «осел сдохнет», либо… далее по известной притче.

В итоге Вы получаете какой-то статистически значимый результат, например, тот, что уровень АД на неких, выбранных Вами, дискретных точках оказался несколько выше в контрольной группе, а значение некоторых ферментов — ниже. Радостно потирая руки, Вы пишете, что разработали более совершенный метод анестезии. Вся беда заключается в том, что полученный Вами результат говорит лишь о том, что наблюдается некоторое влияние метода на уровень АД в определенных фиксированных точках (и еще стоит подумать, положительное ли?), и уменьшается активность некоторых ферментов, что может указывать на меньший риск развития органной недостаточности, не более того. Утверждать, что предложенный Вами метод эффективнее и безопаснее существующих, без изучения частоты осложнений, летальности, времени пребывания в палате интенсивной терапии и других клинических исходов — невозможно.

Означает ли это, что проделанная Вами работа бессмысленна? Вовсе нет. Вы показали хотя бы то, что предложенный метод интересен, и следует подумать о его дальнейшем изучении. Можно ли рекомендовать предложенный Вами метод для широкого клинического применения? Увы, нет — недостаточно оснований. Таким образом, если Вы сформулировали цель исследования как «изучение эффективности и безопасности…», то Вы ее не достигли. И не могли достичь, так как выбрали методы, не отвечающие поставленной цели.

Авторы настоящей статьи осознают, насколько предложенный пример условен, ограничен и не детализирован, хотя и типичен. Тем не менее представляется, что он позволяет указать на один из многих «подводных камней», которые ждут исследователя на этапе планирования работы. В этой связи многие ученые обоснованно полагают, что время и усилия, затраченные на планирование, должны быть сопоставимы со временем и усилиями при выполнении работы. Только такой подход если и не гарантирует качество исследования, то определенно создает к тому серьезные предпосылки.

Первая, но далеко не единственная, проблема, которую необходимо решить до начала исследования — определение размера выборки. В отечественной и зарубежной литературе описано множество методик определения оптимального объема выборки, однако отсутствует четко установленная единая методология их применения.

Цель данной статьи — попытка предоставить неискушенному читателю общие сведения и один из возможных алгоритмов действия при определении размера выборки в ходе организации клинического исследования.

Варианты ошибок и их последствия

Ошибка в определении размера выборки одинаково нежелательна как в меньшую, так и в большую сторону.

При выборке меньшего объема мы с большей долей вероятности можем столкнуться с ошибками первого и второго родов. Для понимания сути таких ошибок нам необходимо ввести понятие нулевой гипотезы. Нулевая гипотеза — принимаемое по умолчанию предположение о том, что между двумя явлениями не существует никакой связи. В действительности нулевая гипотеза похожа на презумпцию невиновности. Мы всегда изначально считаем, что экспериментальная стратегия никак не может повлиять на исходы группы (то есть эффективность экспериментальной стратегии равна эффективности плацебо или отсутствию вмешательства, что зависит от дизайна исследования). Теперь вернемся к возможным ошибкам. Ошибкой первого рода называется отказ от правильной нулевой гипотезы (например, мы установили, что препарат эффективен, хотя в действительности его эффект такой же, как у плацебо). Ошибкой второго рода называется принятие неправильной нулевой гипотезы (например, мы установили, что препарат неэффективен, хотя в действительности он оказывает значительный положительный эффект).

При выборке большего объема (по сравнению с необходимым) большее количество больных будет подвергнуто неоправданному риску при испытании нового препарата или методики. А это недопустимо в соответствии со стандартами GCP (Good Clinical Practice) [1]. Кроме того, в случае избыточно большой выборки возможно обнаружение несуществующих в генеральной совокупности взаимосвязей, что вновь является ошибкой первого рода [2].

Важность определения объема выборки можно проиллюстрировать на следующем «доведенном до абсурда» примере. Скажем, Вы запланировали исследование, при котором в экспериментальной и контрольной группах по одному пациенту. Пациент контрольной группы получает плацебо, в то время как пациент экспериментальной группы получает препарат, об эффективности которого мы ничего не знаем. Если мы зададимся целью проанализировать летальность в таком исследовании, то обнаружим, что возможны 4 варианта развития событий.

Представим, что пациент контрольной группы умирает, а пациент экспериментальной группы выздоравливает. Вы даете абсолютно обоснованное заключение, что «все пациенты контрольной группы умерли, а все пациенты, которым применен тестируемый препарат, поправились, следовательно, методика эффективна». Интересно не то, что Вы с большой долей вероятности выдали ошибочное заключение, а то, что Вы, возможно, и правы. Дело в том, что объем выборки, в данном случае, не позволяет сделать никакого заключения вовсе!

Теперь представим, что оба больных поправились или оба погибли. Следуя простой логике, должно появиться заключение об отсутствии положительного эффекта у тестируемого препарата. Здесь Вы также обоснованно можете заключить, что препарат не отличается от плацебо. Но вся проблема снова в том, что объем выборки не позволяет сделать никакого заключения.

Вариант «пациент контрольной группы выжил, пациент экспериментальной группы погиб» приведет к рекомендации не использовать препарат (запрет) ввиду безусловного вреда здоровью. Но мы ведь с Вами понимаем, что ни о какой достоверности подобного заключения речи быть не может.

Остается удивительным, насколько люди не готовы допустить вероятность подобных ошибок при размере выборки в 15—20—30 человек. Мало того, иногда 100—200 и более пациентов недостаточно для обоснованного заключения. Очень многое, как будет показано далее, зависит от выбора первичной конечной точки, гетерогенности групп, возможных bias (перевод с английского — смещение в исходах, связанное с влиянием субъективного фактора) и т.д.

Пренебрегая предварительным расчетом размера выборки, авторы никогда не могут быть уверены в статистической значимости полученного результата [3]. Однако некоторые обзоры наглядно демонстрируют, что далеко не все исследователи понимают важность обозначенной проблемы [4, 5].

Определение объема выборки

Исследователь, ставящий перед собой цель определить размер выборки планируемого исследования, должен свободно оперировать следующими понятиями:

— Статистическая мощность (1-β), под которой понимают вероятность отклонить неверную нулевую гипотезу. Чем выше мощность статистического теста, тем меньше вероятность совершить ошибку второго рода. При планировании исследования желаемая мощность, как правило, принимается равной 0,8—0,9.

— Уровень статистической значимости (α) — вероятность ошибки первого рода — допускаемая исследователем вероятность ошибочного отклонения верной нулевой гипотезы (гипотезы об отсутствии различия между группами, об отсутствии взаимосвязи признаков и т.д.). Это постоянная величина, которая произвольно принимается автором за допустимую границу значимости полученных результатов. Именно с этой величиной будет производиться сравнение полученных данных. Как правило, за величину уровня значимости принимаются значения 0,05; 0,01 или 0,001.

— p-уровень значимости — рассчитанная в ходе статистического анализа вероятность ошибочного отклонения некоторой предполагаемой гипотезы. Если рассчитанный p-уровень меньше принятого уровня значимости (α), то предполагаемая гипотеза (нулевая гипотеза) отклоняется. Чем меньше p-уровень значимости, тем более значимой является тестовая статистика.

— Генеральная совокупность — совокупность всех возможных объектов данного рода, для которых будут справедливы результаты проведенного исследования. Скажем, вы исследуете эффективность препарата для лечения ишемической болезни сердца (ИБС) у пожилых пациентов. В этом случае генеральной совокупностью будут все пациенты с установленным диагнозом ИБС старшей возрастной группы.

— Выборка — часть генеральной совокупности (например, используя вышеприведенный пример, — пожилые пациенты с ИБС), полученная путем отбора. По результатам анализа выборки делают выводы о всей популяции (генеральной совокупности), что правомерно в случае, если отбор был случайным. Ввиду того, что случайный отбор из популяции осуществить практически невозможно, необходимо стремиться к тому, чтобы выборка была репрезентативна по отношению ко всей совокупности (популяции).

— Гетерогенность в таком случае относится к выборке. Гетерогенный означает неоднородный по составу (в противоположность понятию «гомогенный»). Чем менее гетерогенна выборка, тем менее выраженным является «разброс» значений изучаемого показателя в исходе, тем меньшие отличия, обнаруженные в результате исследования, могут иметь статистическую значимость. Обратная сторона этого утверждения заключается в том, что достаточно гомогенную выборку можно получить только ценой ужесточения критериев включения/исключения. Следовательно, полученный результат можно будет экстраполировать на ограниченную группу пациентов. В качестве примера: вы можете ограничить выборку пациентов, в которой планируете изучать эффективность нового препарата для лечения ИБС, вводя следующие критерии включения: возраст от 65 до 80 лет; впервые выявленная ИБС, «не получавшие ранее кардиотропной терапии». Но тогда и обнаруженный эффект (в случае его выявления) можно будет распространить только на выделенную когорту больных. Проведенное исследование не позволит вам рекомендовать тестируемый препарат у пациентов с «ИБС в анамнезе» или у пациентов в возрасте 40—50 лет и т.д.

Определение размера выборки всегда является неким компромиссом между необходимой мощностью исследования и возможностью ее практической реализации с учетом имеющихся ресурсов.

Метод расчета размера выборки во многом зависит от объема знаний о характеристиках изучаемого параметра.

Еще раз вынуждены оговориться: все примеры, иллюстрирующие данную статью, в той или иной мере условны; необходимо с пониманием отнестись к тому, что строгое и детальное описание настоящего (а не выдуманного) клинического примера займет слишком много места и, скорее всего, отвлечет от предмета обсуждения настоящей статьи.

Начнем с самого неприятного случая: нам ничего не известно ни о генеральной совокупности, ни о параметре, который мы собираемся изучать. Например, мы изобрели новый метод анестезии, который не имеет даже близкого аналога (изобретение эфирного наркоза, открытие хлороформа, более близкий пример — ксенон) и работа будет проходить в клинике, проводящей уникальные операции в гериатрии. Первичной конечной точкой исследования выбрана 28-дневная летальность. Допустим, что никто и никогда не изучал летальность после выбранного типа операций, тем более в гериатрии, т.е. Вам неизвестны характеристики основного изучаемого параметра (среднее (медиана) и разброс данных) и невозможно предположить эффективность нашего метода по сравнению с известным (т.е. какая летальность будет при применении нашего метода относительно летальности при использовании эталонного метода анестезии). Это достаточно редкая ситуация, так как:

— если неизвестна летальность при точно такой же операции, как у нас, то, скорее всего, есть какой-то очень близкий аналог;

— если неизвестна летальность, предположим, у лиц «90 лет и старше», то известна у лиц «пожилого и старческого возраста» («60 лет и старше»);

— и даже такой, несомненно, новый анестетик, как ксенон, можно как-то, в первом приближении (при оценке анальгетической активности, например), соотнести с закисью азота.

Следует иметь в виду, что всегда предпочтительнее иметь хотя бы крайне ненадежный ориентир в размере выборки, чем не иметь никакого, так как при использовании рекомендованных в этой ситуации методов объем выборки, как правило, получается завышенным.

Но, допустим, мы имеем дело с истинно «пилотным» исследованием — никто и никогда ничего похожего не изучал. В таком случае планирование объема выборки возможно исключительно с использованием табличных методов (табл. 1—4), не требующих от исследователя информации о распределении изучаемых параметров. Выбор алгоритма из предложенных четырех будет определяться особенностями исследования и/или пожеланиями авторов [6]:

— методика К.А. Отдельновой [7] требует информации о желаемом уровне значимости и «уровне точности» исследования (см. табл. 1);

— метод В.И. Паниотто [8] требует от исследователей лишь информации об объеме генеральной совокупности (см. табл. 2);

— методика N. Fox [9] определяет объем выборки в зависимости от требуемой величины возможной ошибки (см. табл. 3);

— и наиболее «продвинутый» способ определения объема выборки, предложенный S. Das, K. Mitra, M. Mandal [10], принимает на входе информацию о предполагаемой величине эффекта, мощности и уровне значимости исследования (см. табл. 4).

Таблица 1. Определение требуемого размера выборки по методике К.А. Отдельновой [7]

Уровень значимости	Уровень точности
ориентировочное знакомство	исследование средней точности	исследование повышенной точности
0,05	44	100	400
0,01	100	225	900

Примечание. Уровень значимости: безразмерная величина, указан размер выборки как абсолютное значение количества пациентов в группе.

Таблица 2. Определение требуемого размера выборки по методике В.И. Паниотто [8]

Объем генеральной совокупности (единиц)	500	1000	2000	3000	4000	5000	10000	100000	∞
Объем выборки (единиц)	222	286	333	350	360	370	385	398	400

Таблица 3. Определение объема выборки по методике N. Fox [9]

Величина допускаемой ошибки, %	Объем выборки, единиц
10	88
5	350
3	971
2	2188
1	8750

Таблица 4. Способ определения объема выборки, предложенный S. Das, K. Mitra, M. Mandal [10]

Величина различий (между контрольной и основной группами)	Мощность (1-β)	Уровень значимости (α)	Размер выборки, единиц
0,2	80	0,5	586
0,2	80	0,1	773
0,2	90	0,5	746
0,4	80	0,5	146
0,4	80	0,1	193
0.4	90	0,5	186
0,6	80	0,5	65
0,6	80	0,1	86
0,6	90	0,5	83

Еще пример. Другая ситуация несколько лучше: операции, которые выполняются в клинике, не уникальны; летальность и ее разброс при эталонном методе анестезии известны, однако отсутствует информация о характеристиках распределения изучаемых количественных параметров, влияющих на летальность в генеральной совокупности, а предлагаемая методика действительно аналогов не имеет. В такой ситуации можно продолжать пользоваться «табличными» методами, но предпочтительнее все же взять на вооружение статистические формулы (Приложение: см. табл. 5, формулы 3—15). Последний подход позволит получить искомый показатель с большей точностью и, вероятно, использовать меньший объем выборки. Например, изучается послеоперационная летальность пациентов группы высокого риска (возраст 60 лет и старше, наличие хронических заболеваний) при применении нового метода анестезии. Необходимо определить объем выборки с принимаемым исследователем уровнем значимости 0,05 и предельно допустимой ошибкой 5%. Так как информация о распределении количественных параметров, влияющих на летальность, неизвестна, подходящей является формула 4 (см. Приложение, табл. 5). Допустим, что по данным литературы, 28-дневная летальность среди пациентов старшего возраста при применении стандартной анестезии составляет 9%, а исследователи предполагают, что предлагаемая ими методика позволит уменьшить обсуждаемый показатель в полтора раза (т.е. летальность может составить около 6%). Критическое значение нормального стандартного распределения при заданном уровне значимости α=0,05 принято равным 1,96. В соответствии с имеющимися условиями, для последующего сравнения летальности в контрольной и основной группах объем каждой выборки рассчитывается следующим образом:

Это означает, что для решения поставленной исследователем задачи достаточно сформировать выборку, включающую по 126 пациентов в основной и в контрольной группах.

Третий пример — вам известны все необходимые параметры: исходная летальность, характеристики распределения изучаемых параметров в генеральной совокупности; операции рутинные, кроме того, предлагаемый метод является близким аналогом другого, эффективность которого является секретом Полишинеля. Как и в предыдущем примере, изучается послеоперационная летальность у пациентов группы высокого риска (возраст 60 лет и старше, наличие хронических заболеваний) при применении нового метода анестезии, однако теперь исследователи имеют информацию практически обо всех влияющих на летальность факторах, распределение параметров соответствует нормальному закону, известен также объем генеральной совокупности (например, 1000 пациентов с равной вероятностью входят в группу риска в календарном году). Тогда в соответствии с формулой 17:

Как видим, в связи с появлением дополнительной информации необходимый объем выборки снизился со 126 до 112 пациентов.

Возможно, вы обратили внимание, что, в соответствии с формулой 17, при увеличении объема генеральной совокупности необходимый объем выборки также увеличивается. В этой связи бытует распространенное заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки. Проще говоря, исследователь попадает в ловушку: с одной стороны, чем больше больных с искомой патологией (или операцией) проходит через стационар, тем быстрее можно набрать достаточное количество пациентов. С другой стороны, увеличение размера генеральной совокупности (количества больных с искомой патологией, проходящих лечение или оперируемых в клинике) влечет за собой необходимость увеличения размера выборки (количества больных, рекрутируемых в исследование). Ложный вывод: чем реже встречается в клинике какая-то патология или тип оперативного вмешательства, тем быстрее можно выполнить исследование — меньшая выборка будет признана достаточной. Однако эта закономерность (чем больше генеральная совокупность, тем больше должен быть объем выборки) справедлива лишь отчасти (а вывод и вовсе вводит в заблуждение), и то лишь в ситуации, когда объем выборки сопоставим с размером генеральной совокупности. Возникает дилемма: сколько должно продолжаться проспективное исследование, чтобы объем выборки был репрезентативен по отношению ко всей совокупности пациентов, но в то же время исследование не продолжалось бы бесконечно долго.

Иными словами, как определить ту точку, когда погоня за точностью перестает реально влиять на результат и становится, скорее всего, самоцелью.

В соответствии с исследованием В.И. Паниотто [8], с ростом объема выборки значение получаемой ошибки уменьшается все медленнее (см. рисунок). Так, при объеме выборки 400 человек предельная ошибка для доли встречаемости признака 50% составит ±5%, а при объеме 1000 человек — ±3%. То есть возникает ситуация, когда при определенном объеме выборки дальнейшее ее увеличение не дает значительного выигрыша в точности.

Зависимость ошибки выборки от ее объема при 95% доверительном уровне.

Иная ситуация возникает, если изучаемая когорта пациентов имеет низкую распространенность в популяции, а критерии формирования выборки достаточно жесткие (что ограничивает подходящий контингент пациентов). Тогда все отобранные в ходе проспективного исследования пациенты, составляющие генеральную совокупность, будут попадать в исследуемую выборку, т.е. они будут сопоставимы по размеру.

В нашем примере, в соответствии с рисунком, при уровне летальности 9% и объеме выборки 50 человек предельная ошибка будет составлять примерно 10%. Для клинических исследований это недопустимо низкий уровень точности. Увеличение выборки до 200 человек приведет к уменьшению предельной ошибки до 4%, а при объеме выборки 400 пациентов ошибка составит всего 3%. Исходя из требований к клиническим исследованиям точность, при которой ошибка составляет 4%, считается допустимой, поэтому размер выборки можно ограничить 200 больными. Увеличивать объем выборки в два раза, по-видимому, в таком случае нецелесообразно.

Таким образом, в похожих ситуациях исследователи могут планировать продолжительность проспективного исследования исходя из требуемого и допустимого уровня ошибки.

Следует принять во внимание, что для медицинских исследований допустимой ошибкой считается 5%, если же удается получить результат с точностью до 1%, то исследование можно признать крайне убедительным.

Однако даже самое тщательное планирование не позволяет получить размер выборки, гарантирующий получение статистически значимого результата. Два приема используются порознь или вместе:

— автоматическое увеличение размера выборки на 10—15% по отношению к расчетному (особенно популярно при одноцентровых исследованиях небольшой мощности);

— коррекция размера выборки после получения первых данных о показателях, необходимых для более точного математического анализа.

Чем менее точно определен размер выборки при планировании (что не всегда является дефектом работы составителя плана, но, как показано выше, может быть и следствием отсутствия необходимых данных), тем насущнее становится необходимость коррекции данного показателя после появления первичных, предварительных данных, характеризующих исследуемый показатель и его изменения в результате предпринятых воздействий. Как правило, проведение повторного, уточняющего расчета размера выборки планируется до начала исследования и проводится после набора 50—75% от первоначально определенного количества больных.

Некоторые дополнительные замечания относительно определения размера выборки

Принято использовать два подхода к структурированию выборки — вероятностный и детерминированный (стратифицированный) [11]. Первый связан с формированием случайной выборки в процессе рандомизации (каждый элемент выборки включается с равной, ненулевой вероятностью); при использовании второго подхода элементы выборки отбираются субъективно в случае, если они отвечают целям исследования — выборка, основывается на неких частных предпочтениях или суждениях исследователя (например, ограничения по полу, возрасту, массе тела и т.д.).

Вероятностная выборка во многих случаях является предпочтительной, однако ее реализация в практической медицине может быть ограничена. Использование же детерминированного подхода в общем случае предполагает и использование иного математического аппарата или эмпирической методики [12].

Отдельную сложность представляет планирование объема выборки в условиях несоответствия распределения генеральной совокупности нормальному закону, а также при необходимости формирования различных по численности опытной и контрольной групп. Значительная вариабельность характеристик генеральной совокупности, а также многообразие вариантов клинических исследований предъявляют определенные требования к используемым методам планирования объема выборки.

Математический подход к определению размера выборки

Все математические методы определения объема выборки можно классифицировать на несколько групп:

— табличные методы, не требующие априорного представления об изучаемом факторе и о характеристиках генеральной совокупности (совокупности всех объектов или наблюдений, которые подлежат изучению). Описаны ранее;

— методы, требующие от исследователя некоторого представления об изучаемом признаке (количественный, порядковый (шкала), номинальный и т.д.);

— методы, требующие предварительной информации как о признаке, так и о генеральной совокупности (ее размере, нормальности распределения данных).

В медицине и анестезиологии-реаниматологии, в частности, авторы нередко сталкиваются с ситуацией, при которой невозможно оценить распределение исследуемого признака в генеральной совокупности и потому приходится использовать табличные методы при планировании объема выборки. Размер выборки может быть уточнен по мере получения предварительных результатов исследования, что сделает возможным использование математических формул. Это, в свою очередь, в некоторых случаях позволяет снизить риск необоснованного применения тестируемой методики у большего количества больных и уменьшить материальные затраты и нагрузку на медицинский персонал.

Экспертный подход к планированию объема выборки

Как отмечено ранее, в процессе набора данных возможен момент, когда большее количество данных (наблюдений) не обязательно приводит к большему количеству информации. А поскольку качественные исследования очень трудоемки, анализ значительной по размерам выборки может занять много времени, а зачастую и просто будет нецелесообразен [5]. Как правило, для непрерывной оценки размера выборки при проведении клинических исследований используется концепция насыщения выборки данными, позволяющая принимать обоснованные решения о необходимости прекращения процесса набора данных или о продолжении исследования.

Принципы определения насыщенности данных

В зарубежной литературе предложено несколько принципов, относящихся к концепции «насыщенности» в планировании исследования [13]. Согласно J. Francis и соавт., прежде всего необходимо учесть, какого размера будет выборка по завершении первого этапа исследования, чтобы определить основу для прогрессивных суждений о насыщенности данными и оценить наблюдаемую тенденцию, в том числе методами экстраполяции. Объем выборки будет зависеть от особенностей организации исследования, разнообразия выборки и способа ее формирования. Второй принцип заключается в том, что исследователи должны заранее знать продолжительность всего исследования (время набора данных). Важно также, чтобы методы насыщения данных были подробно описаны в тексте статьи, и коллеги имели возможность оценить доказательную базу исследования [13].

Концепция насыщения является в настоящее время спорной ввиду наличия более объективных методик оценки размера выборки [14]. В частности, указывается на тот факт, что для получения представления о размере выборки и мощности исследования приходится делать большое количество допущений. Информацию, необходимую для оценки объема выборки, получают либо из результатов собственных предыдущих исследований (пилотных исследований), либо из источников литературы. Возможны ситуации, при которых исследователь не имеет ни того, ни другого. Тем не менее необходимо заранее знать минимальную величину эффекта, которая в данном исследовании будет считаться достаточной, и на ее основании можно будет сделать предположение о мощности исследования.

Обсуждение

Определение размера выборки — важнейший этап планирования научной работы. Кроме того, это не просто формальный пункт, обязательный к исполнению по прихоти какого-то чиновника от науки. Это инструмент, позволяющий, с одной стороны, не делать лишнюю работу, с другой,— не сомневаться по окончании этой работы при получении отрицательного результата: «что это, реальное отсутствие эффекта или что «не хватило буквально каких-то …дцать больных»? Действительно, задача не так проста, как может показаться, но, соблюдая предложенный алгоритм, можно получить искомый результат с известной точностью [15—26].

Несколько полезных замечаний:

— при анализе пилотных исследований и сопоставимых работ других авторов необходимо обратить внимание не только на схожесть дизайна, но и на факторы, которые послужили причиной разброса данных. К таким факторам можно отнести демографические сведения о пациентах (половозрастные характеристики, прогностические факторы и т.д.), методы сбора информации, погрешности инструментальных и лабораторных методов исследования и прочее;

— необходимо помнить и о том, что мощность исследования зависит не только и не столько от объема выборки, сколько от предполагаемой величины эффекта и разброса данных. Возможно определение объема выборки исходя из априорных представлений об анализируемых параметрах, однако эмпирический подход является субъективным и проигрывает при равных условиях математическому подходу;

— возможны ситуации, при которых исследователь в силу определенных обстоятельств (финансовых, этических, организационных) не способен увеличить или изменить численность групп. В такой ситуации необходимо учитывать, что размер выборки не является единственным фактором качества исследования. И по сей день подходы к анализу объема выборки расширяются. В частности, показано использование однофакторного дисперсионного анализа ANOVA для определения объема выборки [15].

Таким образом, грамотному исследователю доступен широкий функционал математических методов определения требуемого объема выборки, руководствуясь которым в совокупности с собственным опытом и эмпирической методикой можно оптимально спланировать исследование и получить статистически обоснованные выводы.

Заключение

На современном этапе развития науки отсутствует четко установленная, единая методология определения минимально необходимого объема выборки для клинических исследований. В данной работе представлены наиболее часто применяемые методы определения необходимого объема выборки, которые могут быть применены при планировании исследований. Результатом анализа стало формирование единого алгоритма, позволяющего выбрать наиболее подходящую методику определения искомого показателя.

Приложение

Методы, требующие информации о типе анализируемого признака. Эта группа методов определения объема выборки зависит от ряда факторов: вида признаков, связанности выборок, количества предполагаемых групп и подхода к их формированию — вероятностного или детерминированного (стратифицированного). Формулы для расчетов приведены в табл. 5 (формулы 3—15). Использование приведенных формул дает значительно меньшие объемы выборок по сравнению с методами, не требующими информации о характеристиках распределения и типе анализируемого фактора, однако в некоторых случаях это может привести к неоправданному занижению необходимого объема выборки [6].

Таблица 5. Выбор метода планирования объема выборки (математический подход)

Нет информации о признаке/информация неполная Нет информации о генеральной совокупности	Есть информация о признаке. Нет информации о генеральной совокупности	Есть информация о признаке Есть информация о генеральной совокупности (распределение соответствует нормальному закону)	Есть информация о признаке. Есть информация о генеральной совокупности (распределение не соответствует нормальному закону)
Две выборки: односторонние тесты	Две выборки: двусторонние тесты	Одна выборка (вероятностный подход)	Одна выборка (детерминированный подход)	Одна выборка (погрешность измерений)	Одна выборка (вероятностный подход)	Одна выборка (детерминированный подход)
Методика К.А. Отдельновой [6, 7]	Количественный признак [24]: (3)	Количественный признак [25]: (7) (8)	Количественный признак [26]: (11)	Количественный признак [26]: (13)	[20] (15)	Количественный признак [26]: (16)	Количественный признак [26]: (18)	Лог-нормальное распределение, Hale W. E. [22]: (20)
Методика В.И. Паниотто [8]	Качественный признак [25]: (4)	Качественный признак [25]: (9) (10)	Оценка доли (частоты признака) [26]: (12)	Оценка доли (частоты признака) [26]: (14)		Номинальный/порядковый признак [26]: (17)	Качественный признак [26]: (19)	Распределение Пуассона [21]: (21)
Метод Монте-Карло [23]
Методика N. Fox [9] и S. Das, K. Mitra, M. Mandal [10]	Известна численность одной из групп [17]: (5)	Примечание. * — Использовать в случае несвязанных выборок; для связанных выборок расчет обеих групп проводить по формулам 7 и 9; n — рассчитанный объем выборки; N — объем генеральной совокупности; ????² — критическое значение критерия Стьюдента при соответствующем уровне значимости; d² — предельно допустимая ошибка (минимальная, клинически значимая величина различий, которую необходимо обнаружить, как правило — 5%); ???? — стандартное отклонение признака, который будет изучаться в исследовании (????²— дисперсия); ???? — доля случаев, в которых встречается анализируемый признак; Q — доля случаев, в которых не встречается анализируемый признак (100—????); Zα, — критические значения нормального стандартного распределения для заданных α и β; α/2 — желаемый уровень значимости; 1-β — желаемая мощность; p — доля признака в группе; σ⁽^d^{^}²⁾ — средняя внутригрупповая дисперсия, pq^d — средняя внутригрупповая дисперсия; X — среднее арифметическое изучаемого признака; E — погрешность измерения прибора
Определение Х выборки [6]: (1)	Сравнение долей (частот признаков) [24]: (6)
Определение выборки [16]: (2)	Номограммы [6, 18, 19]

Возможны ситуации, при которых оценить некоторые характеристики признака (такие как среднее арифметическое, стандартное отклонение) определить невозможно по причине отсутствия пилотного исследования или сопоставимых исследований в литературе — в данном случае возможно определение параметров с использованием расчетных формул (см. табл. 5, формулы 1—2). Эти формулы требуют наличия экспертных навыков и опыта у исследователя для предварительного определения размаха вариабельности исследуемого признака. Расчет размаха признака основывается на предположении о том, что расстояние между максимальным и минимальным значениями признака приблизительно равно шести стандартным отклонениям, что вытекает из правила трех сигм, и отсюда возможно определение стандартного отклонения (см. табл. 5, формула 2). В частности, если распределение генеральной совокупности соответствует нормальному закону, ее размах приблизительно равен 6σ, а следовательно, стандартное отклонение приблизительно равно одной шестой диапазона [16].

Весьма распространенной является задача планирования объема для последующего сравнения медианного значения определенного параметра между выборками в случае, если распределение признака уже известно, а информация о всей генеральной совокупности еще не получена. Например, необходимо определить объем выборки при сравнении уровня С-реактивного белка (СРБ) в одной группе пациентов с разлитым фибринозно-гнойным перитонитом в 1-е сутки и через 7 суток. Различия считаются статистически значимыми при уровне p<0,05, предельно допустимая ошибка равна 5%. По результатам предварительного (пилотного) исследования известно, что стандартное отклонение σ в первой группе составило 11,5, во второй — 16,2, а разница средних значений уровня СРБ в группах (X1—X2) по модулю составила 2. Так как СРБ является количественным параметром, выборки зависимы (связанные), а объем генеральной совокупности неизвестен, подходящими являются формулы 3 и 7. Однако в связи с тем, что стандартные отклонения в двух выборках различны, воспользуемся формулой 4, так как она учитывает стандартные отклонения обеих выборок.

(4)

Отметим, что при уменьшении разницы X1—X2 (например, в пилотном исследовании ввиду неэффективной терапии уровень СРБ снизился менее чем на 1 единицу) объем выборки будет увеличиваться, что необходимо для выявления незначительных различий в уровне СРБ.

Ввиду финансовых, этических или иных соображений возможна ситуация, при которой требуется формирование различных по объему основной и контрольной групп [17]. Такое часто встречается в обсервационном исследовании или в рандомизированном контролируемом исследовании с неравной рандомизацией. Разработан математический аппарат, позволяющий оценить требуемую численность одной группы при известной фиксированной численности другой группы для формирования заключения о наличии/отсутствии статистически значимых различий между ними (см. табл. 5, формула 5).

Актуальной является задача определения объема выборки для дальнейшей оценки (сравнения) долей (частот встречаемости) признаков в одной или нескольких группах с использованием хи-квадрат критерия Пирсона — для этого случая также представлено несколько методик. Первая связана с использованием критических значений стандартного нормального распределения для оценки объема выборки (см. табл. 5, формулы 6, 12, 14). Вторая методика предполагает использование номограмм [18, 19]. Номограмма представляет собой диаграмму с двумя осями: осью стандартизованной разности и осью величины мощности; на пересечении приведенной прямой с необходимым уровнем значимости находится требуемый объем выборки. Расчет стандартизованной разности предполагает расчет отношения разности средних арифметических значений признака между группами к стандартному отклонению анализируемого признака, а уровень мощности в клинических исследованиях принимается, как правило, равным 0,8—0,9 [6]. В случае связанных выборок стандартизованная разность умножается на 2. В некоторых ситуациях может потребоваться расчет объема выборки с учетом прямой погрешности измерения прибора [20]. Тогда становится возможным заменить t-статистику Стьюдента на Z-оценку стандартного нормального распределения (см. табл. 5, формула 15).

Методы, требующие предварительной информации о виде признака и о генеральной совокупности. Наилучшая ситуация с точки зрения планирования объема выборки возникает при наличии информации о типе признака и о характеристиках распределения совокупности, при этом предпочтительно наличие нормально распределенных данных. В таком случае возможно использование статистических формул с учетом подхода к формированию выборки и использованием t-статистики (см. табл. 5, формулы 16—19). Этот математический аппарат широко описан в литературе, однако он неприменим к данным, распределение которых отлично от нормального [21]. Достаточно давно известен подход к планированию размера выборки для данных, распределение которых близко к лог-нормальному [22] (см. табл. 5, формула 20). По результатам исследования B. Cundill и N. Alexander, описанный выше подход к анализу лог-нормального распределения хорошо работал и для рассмотренных отрицательных биномиальных и гамма-распределений и превосходил по качеству методы, используемые при нормально распределенных данных [21]. Тем не менее он показал лишь незначительное преимущество для пуассоновского распределения, в связи с чем авторами предложен отдельных подход к расчету объема выборки для частного случая — Пуассоновского распределения данных (см. табл. 5, формула 21). В качестве альтернативного подхода к планированию объема выборки описано использование методов Монте-Карло, в частности, модели подтверждающего факторного анализа и модели роста [23]. В исследованиях данные генерируются из совокупности с гипотетическими значениями параметров, выбирается большое количество наблюдений и для каждого образца оценивается модель; значения параметров и стандартные ошибки усредняются по выборкам. Для определения объема выборки требуется соблюдение трех критериев. Первый критерий остановки алгоритма срабатывает в случае отклонения параметров и стандартных ошибок более 10% для любого параметра в модели. Второй критерий — стандартное смещение ошибки для параметра, для которого оценивается мощность, не превышает 5%. Третий критерий — оценка доверительных интервалов находится в интервале между 0,91 и 0,98. В случае, если эти три условия выполнены, размер выборки выбирается так, чтобы мощность была близка к 0,80. В целом такой подход может быть использован и при соответствии распределения совокупности нормальному закону.

Авторы заявляют об отсутствии конфликта интересов.

Источник

Приведенная ниже формула для расчета объема выборки используется в тех случаях, когда опрашиваемым (респондентам) задается только один вопрос, на который существует только два варианта ответа. Например: «Да» и «Нет», «Покупаю» и «Не покупаю», «Пользуюсь» и «Не пользуюсь». Конечно, данную формулу можно применять только при проведении простейших исследований. Если Вам нужно определить объем выборочной совокупности при проведении более масштабных исследований, например анкетирования, то следует использовать другие формулы.

Содержание:

формула с пояснениями;
пример расчета объема выборки;
нормированное отклонение (таблица);
область применения;
особенности формулы.

Простая формула для расчета объема выборки

Ниже приведена простая формула для расчета объема выборки для тех случаев когда на заданный вопрос возможны лишь два варианта ответа:

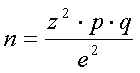
где: n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности (доверительного интервала, доверительной вероятности).

Этот показатель характеризует вероятность попадания ответов в специальный доверительный интервал — диапазон, границам которого соответствует определенный процент определенных ответов на некоторый вопрос.

Можно сказать, что уровень доверительности выражает вероятность того, что респонденты генеральной совокупности ответят так же, как и представители анализируемой выборки.

На практике доверительный интервал при проведении маркетинговых исследований часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58.

Также существует специальная таблица «Значение интеграла вероятностей», используя которую можно найти значение z для различных доверительных интервалов. Сокращенный вариант такой таблицы приведен ниже;

p – вариация для выборки, в долях.

Вариация характеризует величину схожести / несхожести ответов респондентов на вопрос. По сути, p — вероятность того, что респонденты выберут той или иной вариант ответа.

Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;

q = 1 — p.

Можно сказать, что q — это вероятность того, что респонденты не выберут анализируемый вариант ответа (в нашем примере ответят «Нет»). Например, если p = 0,25, то q = 1 — 0,25 = 0,75;

e – допустимая ошибка, в долях.

Значение допустимой ошибки заранее определяют исследователь и заказчик маркетингового исследования.

Пример расчета объема выборочной совокупности

Маркетинговая компания получила заказ на проведение социологического исследования с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».

Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95% (одно из стандартных значений для маркетинговых исследований), тогда нормированное отклонение z = 1,96. Проведя предварительный анализ населения города, вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они — «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. исходя из требуемой заказчиком точности, допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.

Подставляем эти данные в формулу и считаем:

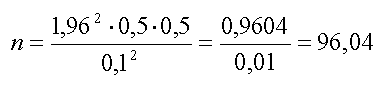
Округлив расчетное значение, получаем объем выборки n = 96 человек.

Следовательно, для проведения исследования с заданными параметрами (уровень доверительности, допустимая ошибка) компании необходимо опросить 96 человек.

Значение нормированного отклонения для различных доверительных интервалов

В таблице приведены некоторые значения нормированного отклонения (z) для важнейших уровней доверительности, или, иначе, доверительной вероятности (α):

α (%)	60	70	80	85	90	95	97	99	99,7
z	0,84	1,03	1,29	1,44	1,65	1,96	2,18	2,58	3,0

Конечно, в таблице приведены значения z только для основных уровней доверительности. Полную версию таблицы можно найти в интернете.

Область применения простой формулы выборки

При проведении простых исследований, когда нужно получить ответ всего на один простой вопрос. При этом шкала ответов, как правило, дихотомического характера. То есть предлагаются (или подразумеваются) варианты ответов по типу «Да» — «Нет», «Черное» — «Белое», «Куплю» — «Не куплю», и т. д. Иными словами возможны лишь два варианта ответа на заданный вопрос.

Особенности формулы расчета размера выборки

Для рассмотренной нами простой формулы определения объема выборки можно выделить несколько характерных особенностей:

перед тем, как рассчитывать объем выборки в данном случае желательно предварительно провести качественный анализ изучаемой генеральной совокупности. В частности установить степень схожести, близости изучаемых единиц совокупности в части их социальных, демографических, географических, иных характеристик. Также полезно провести пилотное (разведочное) исследование, чтобы установить приблизительную величину p;
нужно иметь в виду, что максимальная изменчивость (вариация ответов) соответствует значению p = 50%, так как тогда q = 50% и p × q = 0,5 × 0,5 = 0,25. Это наихудший случай, все другие значения p дадут изменчивость меньшего размера (например, при p = 80%, p × q = 0,8 × 0,2 = 0,16; а при p = 10%, p × q = 0,1 × 0,9 = 0,09). Впрочем, данный показатель влияет на объем выборки не очень сильно.

Также стоит отметить, что существует ряд иных формул для определения объема выборки в случаях с дихотомической шкалой ответов на единственный вопрос. Для более сложных маркетинговых исследований применяются другие формулы.

Источники

Голубков Е. П. Маркетинговые исследования: теория, методология и практика. — М.: Издательство «Финпресс», 1998.

Статья дополнена и доработана автором 10 дек 2020 г.

Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.

Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Формула выборки — простая // Сайт преподавателя экономики. [2020]. URL: https://galyautdinov.ru/post/formula-vyborki-prostaya (дата обращения: 22.09.2023).

Источник

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

Варианты ошибок и их последствия

Определение объема выборки

Некоторые дополнительные замечания относительно определения размера выборки

Математический подход к определению размера выборки

Экспертный подход к планированию объема выборки

Принципы определения насыщенности данных

Обсуждение

Заключение

Приложение

Простая формула для расчета объема выборки

Пример расчета объема выборочной совокупности

Значение нормированного отклонения для различных доверительных интервалов

Область применения простой формулы выборки

Особенности формулы расчета размера выборки

Интересное по теме: