Определение статистических ошибок

Статистические ошибки

Использование
методов биометрии позволяет исследователю
на ограниченном по численности материале
делать заключения о проявлении признака,
его изменчивости и других параметрах
в генеральной совокупности. Но так
как выборочная совокупность — часть
генеральной и ее формируют методом
случайного отбора, то в выборку могут
попасть животные с более низкими
продуктивными качествами, или несколько
лучшие особи. В этом случае вычисленные
значения M, б, C_v и
других биометрических величин будут
отличаться от значений этих величин в
генеральной совокупности, то есть
выборка отражает генеральную совокупность
с ошибкой. Эти ошибки, связанные с
методом выборочности, называются
статистическими и устранить их нельзя.
Ошибки не будет лишь в том случае, когда
в обработку включаются все члены
генеральной совокупности. Величины
статистических ошибок зависят от
изменчивости признаков и объема выборки:
чем более изменчив признак, тем больше
ошибка, и чем больше объем выборки, тем
она меньше. Ошибки статистических
величин в биометрии принято обозначать
буквой m.

Ошибки
имеют все статистические величины.
Вычисляют их по формулам:

Все
ошибки измеряют в тех же единицах, что
и сами показатели, и записывают обычно
рядом с ними.

Статистические
ошибки указывают интервал, в котором
находится величина того или иного
статистического показателя в генеральной
совокупности. Зная среднее значение
признака (М) и его ошибку (m), можно
установить доверительные границы
средней величины в генеральной
совокупности по формуле: М_ген.=М_в. 
tm, где t — нормированное отклонение,
которое зависит от уровня вероятности
и объема выборки. Цифровое значение t
для каждого конкретного случая находят
с помощью специальной таблицы. Например,
нас интересует средняя частота пульса
у овец породы прекос. Для изучения этого
показателя была сформирована выборка
в количестве 50 голов и определена у
этих животных средняя частота пульса.
Оказалось, что этот показатель равен
75 ударов в минуту, изменчивость его б =
12 ударов. Ошибка средней арифметической
величины в этом случае составит:

б
12

m
= ──── = ──── = 1,7 (уд./мин).

n
50

Итоговая
запись будет иметь вид: М 
m или 75 
1,7, то есть частота пульса 75 ударов в
минуту — среднее значение для 50 голов.
Чтобы определить среднюю частоту пульса
в генеральной совокупности животных,
возьмем в качестве доверительной
вероятности P = 0,95. В этом случае, исходя
из таблицы, t = 2,01. Определим доверительные
границы частоты пульса в генеральной
совокупности M 
tm.

75,0
+ 2,01 x 1,7 = 75,0 + 3,4 = 78,4 (уд./мин)

75,0
— 2,01 x 1,7 = 75,0 — 3,4 = 71,6 (уд./мин)

Таким
образом, средняя частота пульса для
генеральной совокупности будет в
пределах от 71,6 до 78,4 ударов в минуту.

Зная
величину статистических ошибок,
устанавливают также, правильно ли
выборочная совокупность отражает тот
или иной параметр генеральной, то есть
устанавливают критерий доверительности
выборочных величин.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its «true value» (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the estimated value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals.
In econometrics, «errors» are also called disturbances.^[1]^[2]^[3]

Introduction[edit]

Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors are the deviations of the observations from the population mean, while the residuals are the deviations of the observations from the sample mean.

A statistical error (or disturbance) is the amount by which an observation differs from its expected value, the latter being based on the whole population from which the statistical unit was chosen randomly. For example, if the mean height in a population of 21-year-old men is 1.75 meters, and one randomly chosen man is 1.80 meters tall, then the «error» is 0.05 meters; if the randomly chosen man is 1.70 meters tall, then the «error» is −0.05 meters. The expected value, being the mean of the entire population, is typically unobservable, and hence the statistical error cannot be observed either.

A residual (or fitting deviation), on the other hand, is an observable estimate of the unobservable statistical error. Consider the previous example with men’s heights and suppose we have a random sample of n people. The sample mean could serve as a good estimator of the population mean. Then we have:

The difference between the height of each man in the sample and the unobservable population mean is a statistical error, whereas
The difference between the height of each man in the sample and the observable sample mean is a residual.

Note that, because of the definition of the sample mean, the sum of the residuals within a random sample is necessarily zero, and thus the residuals are necessarily not independent. The statistical errors, on the other hand, are independent, and their sum within the random sample is almost surely not zero.

One can standardize statistical errors (especially of a normal distribution) in a z-score (or «standard score»), and standardize residuals in a t-statistic, or more generally studentized residuals.

In univariate distributions[edit]

If we assume a normally distributed population with mean μ and standard deviation σ, and choose individuals independently, then we have

$X_{1},\dots ,X_{n}\sim N\left(\mu ,\sigma ^{2}\right)\,$

and the sample mean

$\overline{X}={X_1 + \cdots + X_n \over n}$

is a random variable distributed such that:

${\overline {X}}\sim N\left(\mu ,{\frac {\sigma ^{2}}{n}}\right).$

The statistical errors are then

$e_{i}=X_{i}-\mu ,\,$

with expected values of zero,^[4] whereas the residuals are

$r_{i}=X_{i}-{\overline {X}}.$

The sum of squares of the statistical errors, divided by σ², has a chi-squared distribution with n degrees of freedom:

${\frac {1}{\sigma ^{2}}}\sum _{i=1}^{n}e_{i}^{2}\sim \chi _{n}^{2}.$

However, this quantity is not observable as the population mean is unknown. The sum of squares of the residuals, on the other hand, is observable. The quotient of that sum by σ² has a chi-squared distribution with only n − 1 degrees of freedom:

${\frac 1{\sigma ^{2}}}\sum _{{i=1}}^{n}r_{i}^{2}\sim \chi _{{n-1}}^{2}.$

This difference between n and n − 1 degrees of freedom results in Bessel’s correction for the estimation of sample variance of a population with unknown mean and unknown variance. No correction is necessary if the population mean is known.

[edit]

It is remarkable that the sum of squares of the residuals and the sample mean can be shown to be independent of each other, using, e.g. Basu’s theorem. That fact, and the normal and chi-squared distributions given above form the basis of calculations involving the t-statistic:

$T={\frac {{\overline {X}}_{n}-\mu _{0}}{S_{n}/{\sqrt {n}}}},$

where ${\overline {X}}_{n}-\mu _{0}$ represents the errors, $S_{n}$ represents the sample standard deviation for a sample of size n, and unknown σ, and the denominator term $S_n/\sqrt n$ accounts for the standard deviation of the errors according to:^[5]

$\operatorname {Var} \left({\overline {X}}_{n}\right)={\frac {\sigma ^{2}}{n}}$

The probability distributions of the numerator and the denominator separately depend on the value of the unobservable population standard deviation σ, but σ appears in both the numerator and the denominator and cancels. That is fortunate because it means that even though we do not know σ, we know the probability distribution of this quotient: it has a Student’s t-distribution with n − 1 degrees of freedom. We can therefore use this quotient to find a confidence interval for μ. This t-statistic can be interpreted as «the number of standard errors away from the regression line.»^[6]

Regressions[edit]

In regression analysis, the distinction between errors and residuals is subtle and important, and leads to the concept of studentized residuals. Given an unobservable function that relates the independent variable to the dependent variable – say, a line – the deviations of the dependent variable observations from this function are the unobservable errors. If one runs a regression on some data, then the deviations of the dependent variable observations from the fitted function are the residuals. If the linear model is applicable, a scatterplot of residuals plotted against the independent variable should be random about zero with no trend to the residuals.^[5] If the data exhibit a trend, the regression model is likely incorrect; for example, the true function may be a quadratic or higher order polynomial. If they are random, or have no trend, but «fan out» — they exhibit a phenomenon called heteroscedasticity. If all of the residuals are equal, or do not fan out, they exhibit homoscedasticity.

However, a terminological difference arises in the expression mean squared error (MSE). The mean squared error of a regression is a number computed from the sum of squares of the computed residuals, and not of the unobservable errors. If that sum of squares is divided by n, the number of observations, the result is the mean of the squared residuals. Since this is a biased estimate of the variance of the unobserved errors, the bias is removed by dividing the sum of the squared residuals by df = n − p − 1, instead of n, where df is the number of degrees of freedom (n minus the number of parameters (excluding the intercept) p being estimated — 1). This forms an unbiased estimate of the variance of the unobserved errors, and is called the mean squared error.^[7]

Another method to calculate the mean square of error when analyzing the variance of linear regression using a technique like that used in ANOVA (they are the same because ANOVA is a type of regression), the sum of squares of the residuals (aka sum of squares of the error) is divided by the degrees of freedom (where the degrees of freedom equal n − p − 1, where p is the number of parameters estimated in the model (one for each variable in the regression equation, not including the intercept)). One can then also calculate the mean square of the model by dividing the sum of squares of the model minus the degrees of freedom, which is just the number of parameters. Then the F value can be calculated by dividing the mean square of the model by the mean square of the error, and we can then determine significance (which is why you want the mean squares to begin with.).^[8]

However, because of the behavior of the process of regression, the distributions of residuals at different data points (of the input variable) may vary even if the errors themselves are identically distributed. Concretely, in a linear regression where the errors are identically distributed, the variability of residuals of inputs in the middle of the domain will be higher than the variability of residuals at the ends of the domain:^[9] linear regressions fit endpoints better than the middle. This is also reflected in the influence functions of various data points on the regression coefficients: endpoints have more influence.

Thus to compare residuals at different inputs, one needs to adjust the residuals by the expected variability of residuals, which is called studentizing. This is particularly important in the case of detecting outliers, where the case in question is somehow different from the others in a dataset. For example, a large residual may be expected in the middle of the domain, but considered an outlier at the end of the domain.

Other uses of the word «error» in statistics[edit]

The use of the term «error» as discussed in the sections above is in the sense of a deviation of a value from a hypothetical unobserved value. At least two other uses also occur in statistics, both referring to observable prediction errors:

The mean squared error (MSE) refers to the amount by which the values predicted by an estimator differ from the quantities being estimated (typically outside the sample from which the model was estimated).
The root mean square error (RMSE) is the square-root of MSE.
The sum of squares of errors (SSE) is the MSE multiplied by the sample size.

Sum of squares of residuals (SSR) is the sum of the squares of the deviations of the actual values from the predicted values, within the sample used for estimation. This is the basis for the least squares estimate, where the regression coefficients are chosen such that the SSR is minimal (i.e. its derivative is zero).

Likewise, the sum of absolute errors (SAE) is the sum of the absolute values of the residuals, which is minimized in the least absolute deviations approach to regression.

The mean error (ME) is the bias.
The mean residual (MR) is always zero for least-squares estimators.

References[edit]

^ Kennedy, P. (2008). A Guide to Econometrics. Wiley. p. 576. ISBN 978-1-4051-8257-7. Retrieved 2022-05-13.
^ Wooldridge, J.M. (2019). Introductory Econometrics: A Modern Approach. Cengage Learning. p. 57. ISBN 978-1-337-67133-0. Retrieved 2022-05-13.
^ Das, P. (2019). Econometrics in Theory and Practice: Analysis of Cross Section, Time Series and Panel Data with Stata 15.1. Springer Singapore. p. 7. ISBN 978-981-329-019-8. Retrieved 2022-05-13.
^ Wetherill, G. Barrie. (1981). Intermediate statistical methods. London: Chapman and Hall. ISBN 0-412-16440-X. OCLC 7779780.
^ ^a ^b Frederik Michel Dekking; Cornelis Kraaikamp; Hendrik Paul Lopuhaä; Ludolf Erwin Meester (2005-06-15). A modern introduction to probability and statistics : understanding why and how. London: Springer London. ISBN 978-1-85233-896-1. OCLC 262680588.
^ Peter Bruce; Andrew Bruce (2017-05-10). Practical statistics for data scientists : 50 essential concepts (First ed.). Sebastopol, CA: O’Reilly Media Inc. ISBN 978-1-4919-5296-2. OCLC 987251007.
^ Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, with Special Reference to Biological Sciences. McGraw-Hill. p. 288.
^ Zelterman, Daniel (2010). Applied linear models with SAS ([Online-Ausg.]. ed.). Cambridge: Cambridge University Press. ISBN 9780521761598.
^ «7.3: Types of Outliers in Linear Regression». Statistics LibreTexts. 2013-11-21. Retrieved 2019-11-22.

Cook, R. Dennis; Weisberg, Sanford (1982). Residuals and Influence in Regression (Repr. ed.). New York: Chapman and Hall. ISBN 041224280X. Retrieved 23 February 2013.
Cox, David R.; Snell, E. Joyce (1968). «A general definition of residuals». Journal of the Royal Statistical Society, Series B. 30 (2): 248–275. JSTOR 2984505.
Weisberg, Sanford (1985). Applied Linear Regression (2nd ed.). New York: Wiley. ISBN 9780471879572. Retrieved 23 February 2013.
«Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]

External links[edit]

Media related to Errors and residuals at Wikimedia Commons

Источник

Статистическая погрешность — это та неопределенность в оценке истинного значения измеряемой величины, которая возникает из-за того, что несколько повторных измерений тем же самым инструментом дали различающиеся результаты. Возникает она, как правило, из-за того, что результаты измерения в микромире не фиксированы, а вероятностны. Она тесно связана с объемом статистики: обычно чем больше данных, тем меньше статистическая погрешность и тем точнее результат измерения. Среди всех типов погрешностей она, пожалуй, самая безобидная: понятно, как ее считать, и понятно, как с ней бороться.

Статистическая погрешность: чуть подробнее

Предположим, что ваш детектор может очень точно измерить какую-то величину в каждом конкретном столкновении. Это может быть энергия или импульс какой-то родившейся частицы, или дискретная величина (например, сколько мюонов родилось в событии), или вообще элементарный ответ «да» или «нет» на какой-то вопрос (например, родилась ли в этом событии хоть одна частица с импульсом больше 100 ГэВ).

Это конкретное число, полученное в одном столкновении, почти бессмысленно. Скажем, взяли вы одно событие и выяснили, что в нём хиггсовский бозон не родился. Никакой научной пользы от такого единичного факта нет. Законы микромира вероятностны, и если вы организуете абсолютно такое же столкновение протонов, то картина рождения частиц вовсе не обязана повторяться, она может оказаться совсем другой. Если бозон не родился сейчас, не родился в следующем столкновении, то это еще ничего не говорит о том, может ли он родиться вообще и как это соотносится с теоретическими предсказаниями. Для того, чтобы получить какое-то осмысленное число в экспериментах с элементарными частицами, надо повторить эксперимент много раз и набрать статистику одинаковых столкновений. Всё свое рабочее время коллайдеры именно этим и занимаются, они накапливают статистику, которую потом будут обрабатывать экспериментаторы.

В каждом конкретном столкновении результат измерения может быть разный. Наберем статистику столкновений и усредним по ней результат. Этот средний результат, конечно, тоже не фиксирован, он может меняться в зависимости от статистики, но он будет намного стабильнее, он не будет так сильно прыгать от одной статистической выборки к другой. У него тоже есть некая неопределенность (в статистическом анализе она так и называется: «неопределенность среднего»), но она обычно небольшая. Вот эта величина и называется статистической погрешностью измерения.

Итак, когда экспериментаторы предъявляют измерение какой-то величины, то они сообщают результат усреднения этой величины по всей набранной статистике столкновений и сопровождают его статистической погрешностью. Именно такие средние значения имеют физический смысл, только их может предсказывать теория.

Есть, конечно, и иной источник статистической погрешности: недостаточный контроль условий эксперимента при повторном измерении. Если в физике частиц этот источник можно попытаться устранить, по крайней мере, в принципе, то в других разделах естественных наук он выходит на первый план; например, в медицинских исследованиях каждый человек отличается от другого по большому числу параметров.

Как считать статистическую погрешность?

Существует теория расчета статистической погрешности, в которую мы, конечно, вдаваться не будем. Но есть одно очень простое правило, которое легко запомнить и которое срабатывает почти всегда. Пусть у вас есть статистическая выборка из N столкновений и в ней присутствует n событий какого-то определенного типа. Тогда в другой статистической выборке из N событий, набранной в тех же условиях, можно ожидать примерно n ± √n таких событий. Поделив это на N, мы получим среднюю вероятность встретить такое событие и погрешность среднего: n/N ± √n/N. Оценка истинного значения вероятности такого типа события примерно соответствует этому выражению.

Сразу же, впрочем, подчеркнем, что эта простая оценка начинает сильно «врать», когда количество событий очень мало. В науке обсчета маленькой статистики есть много дополнительных тонкостей.

Более серьезное (но умеренно краткое) введение в методы статистической обработки данных в применении к экспериментам на LHC см. в лекциях arXiv.1307.2487.

Именно поэтому эксперименты в физике элементарных частиц стараются оптимизировать не только по энергии, но и по светимости. Ведь чем больше светимость, тем больше столкновений будет произведено — значит, тем больше будет статистическая выборка. И уже это позволит сделать измерения более точными — даже без каких-либо улучшений в эксперименте. Примерная зависимость тут такая: если вы увеличите статистику в k раз, то относительные статистические погрешности уменьшатся примерно в √k раз.

Этот пример — некая симуляция того, как могло бы происходить измерение массы ρ-мезона свыше полувека назад, на заре адронной физики, если бы он был вначале обнаружен в процессе e⁺e^– → π⁺π^–. А теперь перенесемся в наше время.

Сейчас этот процесс изучен вдоль и поперек, статистика набрана огромная (миллионы событий), а значит, и масса ρ-мезона сейчас определена несравнимо точнее. На рис. 3 показано современное состояние дел в этой области масс. Если ранние эксперименты еще имели какие-то существенные погрешности, то сейчас они практически неразличимы глазом. Огромная статистика позволила не только измерить массу (примерно равна 775 МэВ с точностью в десятые доли МэВ), но и заметить очень странную форму этого пика. Такая форма получается потому, что практически в том же месте на шкале масс находится и другой мезон, ω(782), который «вмешивается» в процесс и искажает форму ρ-мезонного пика.

Другой, гораздо более реальный пример влияния статистики на процесс поиска и изучения хиггсовского бозона обсуждался в новости Анимации показывают, как в данных LHC зарождался хиггсовский сигнал.

Источник

2.4. Точность статистического наблюдения

Под точностью статистического наблюдения понимают степень соответствия значения наблюдаемого показателя, вычисленного по материалам обследования, его действительной величине. Расхождение, или разница, между ними называется ошибкой статистического наблюдения.

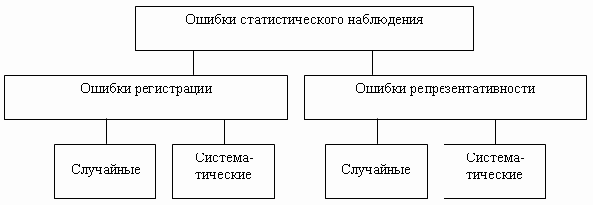
Различают две группы ошибок:

ошибки регистрации;
ошибки репрезентативности.

Ошибки регистрации присущи любому статистическому наблюдению, как сплошному, так и несплошному. Они делятся на случайные ошибки регистрации и систематические ошибки регистрации.

Случайными ошибками регистрации называют ошибки, возникающие вследствие действия случайных факторов. К ним можно отнести различного рода непреднамеренные описки: например, вместо возраста человека «15 лет» указано «5 лет», у Ивановой Марии Петровны в графе пол отмечен «Мужской» и т. п. Такие ошибки легко выявляются методом логического анализа, например, если человеку 8 лет, но имеется высшее образование, а в графе «Семейное положение» указано «Состоит в браке», то, естественно, следует исправить возраст. Если объем исследуемой совокупности велик или велика доля отбора при выборочном наблюдении, случайные ошибки регистрации имеют тенденцию взаимопогашаться вследствие действия закона больших чисел, поскольку ошибки, как правило, разнонаправлены и искажают статистический показатель как в большую, так и в меньшую сторону. При небольшом объеме наблюдения требуется тщательная выверка его результатов — логический анализ данных.

Систематические ошибки регистрации чаще всего имеют однонаправленные искажения: они либо увеличивают, либо уменьшают статистический показатель, и, что характерно, подобная ситуация повторяется от обследования к обследованию. Так, по результатам переписей (практически всех!) число замужних женщин превышает число женатых мужчин — мужчинам приятнее ощущать себя неженатыми, а для женщины как бы «стыдно» быть не замужем. Другой пример, когда человек округляет свой возраст — вместо 32 лет говорит 30, вместо 79-80 и т. п. (это явление широко известно и даже получило свое название — «аккумуляция возрастов»). Систематические ошибки регистрации могут возникать и из-за неточностей измерительных приборов, если сбор информации проводят путем непосредственного наблюдения.

Ошибки репрезентативности присущи только несплошному обследованию. Они также делятся на случайные и систематические ошибки.

Случайные ошибки репрезентативности возникают из-за того, что обследованию подвергается не вся совокупность в целом, а только ее часть, и, следовательно, при несплошном наблюдении они присутствуют всегда. В теории статистики разработаны специальные методы для оценки величин таких ошибок, на их основе для наблюдаемых показателей строят доверительные интервалы, т.д. эти ошибки вычисляются и находятся как бы «под контролем».

Хуже обстоит дело, если наряду со случайными ошибками имеются и ошибки систематические.

Систематические ошибки репрезентативности возникают, если при несплошном наблюдении кардинально нарушаются технологии отбора единиц из генеральной совокупности объектов, но чаще — если в ходе обследования не удается получить информацию обо всех отобранных для наблюдения единицах, например, вследствие отказа отвечать на вопросы анкеты, или если человека не удалось застать дома и т. п.

Ошибки статистического наблюдения для наглядности можно изобразить в виде схемы (рис. 2.1).

Рис.
2.1.
Виды ошибок статистического наблюдения

Для повышения точности наблюдения необходимо:

правильно разработать формуляр статистического наблюдения: вопросы должны быть четкими, однозначными, не допускающими двойного толкования;
иметь хорошо обученный персонал для проведения обследования;
строго придерживаться выбранной технологии обследования (если проводится несплошное наблюдение) и помнить, что если не удается опросить какую-то конкретную единицу, отобранную для наблюдения, замена ее на другую единицу может привести к возникновению систематической ошибки репрезентативности;
провести логический анализ данных, основанный на логических взаимосвязях показателей, после сбора всей совокупности анкет или формуляров;
целесообразно провести и арифметический контроль данных, т.д. заново пересчитать расчетные величины, если какие-либо показатели получаются в результате определенных арифметических действий;
предпринять определенные меры по восстановлению данных при наличии незаполненных анкет или формуляров либо при получении результатов обследования сделать поправку на неответы респондентов.

Источник

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Колмогоров и Прохоров (1984) определили математическую статистику как ветвь математики, систематизирующую, обрабатывающую и применяющую статистические данные, под которыми понимается число объектов в некоторых совокупностях. Разумеется, они исключили сбор данных и их предварительное исследование, которое по существу появилось в середине ХХ в. и является важной главой теоретической статистики. Споры о различии между математической и теоретической статистиками можно решить, полагая, что именно сбор и исследование данных относятся к последней и определяют ее отличие от первой.

Первое достойное определение теории статистики (которая, видимо, почти совпадает с теоретической статистикой) предложил Butte: это – наука о понимании и оценке статистических данных, их сбору и систематизации. Неясно, включал ли он в свое определение и приложения статистики.

Громадное количество определений статистики (без каких-либо прилагательных) было предложено начиная со Шлёцера, но указанного выше достаточно. Впрочем, упомянем еще Гаттерера, у которого цели статистики частично относились к новому государствоведению: понять состояние государства, исходя из его прежних состояний.

Статистический метод – это метод исследования, основанный на математической обработке количественных данных, и в основном его имеют в виду в связи с естествознанием. Его первая стадия была характерна выявлением статистических закономерностей, основанных на общих представлениях; вот афоризм Гиппократа (1952): полные люди склонны умирать в более раннем возрасте, чем остальные.

Здесь можно усмотреть качественную корреляцию, вполне совместимую с качественным характером древней науки. Во время второй стадии выводы основывались на статистических данных (Граунт). Нынешняя, третья стадия началась в середине XIX в. с появлением первых стохастических критериев для проверки статистических выводов, см. Пуассон (1837), Sheynin. Впрочем, эти стадии не отделены друг от друга полностью: даже древние астрономы накапливали свои количественные наблюдения [1].

Исключительно важные открытия удалось сделать без применения критериев. Оказалось, например, что очистка питьевой воды в восемь раз снижала смертность от холеры, что объясняло пути распространения холерных эпидемий. Аналогично, проявился полный успех оспопрививания (Дженне, в 1798 г.), хотя потребовались дополнительные статистические исследования технологии прививок и без разочарований обойтись не удалось.

Теория ошибок относится к статистическому методу. Ее основная особенность – применение истинного значения измеряемых констант. Фурье определил его как предел среднего арифметического из измерений, что эвристически схоже с частотным определением вероятности по Мизесу и означает, что остаточные систематические ошибки включаются в это значение.

С момента своего зарождения во второй половине XVIII в. Т. Симпсон (1756; 1757) и Ламберт, который и ввел термин теория ошибок до 1920-х годов эта теория оставалась основным полем приложения теории вероятностей, а математическая статистика переняла у нее принципы наибольшего правдоподобия и наименьшей дисперсии.

Первое гауссово обоснование метода (точнее, принципа) наименьших квадратов (1809) для уравнивания косвенных наблюдений (т. е. для оценивания неизвестных, входящих в избыточную систему линейных уравнений, коэффициенты которой задаются соответствующей теорией, а свободные члены – результаты непосредственных наблюдений) было основано на (независимо введенном им) принципе наибольшего правдоподобия и на предположении о том, что среднее арифметическое – лучшая оценка истинного значения непосредственных наблюдений [2].

Его второе обоснование 1823 г., весьма тяжело написанное, было основано на принципе наименьшей дисперсии искомых оценок. Колмогоров (1946) мимоходом заметил, что можно было бы принять выведенную Гауссом формулу выборочной дисперсии за её определение. Во всяком случае, её вывод несложен, а принцип наименьших квадратов последует сразу же, потому что указанный вывод требует только линейности и независимости исходных уравнений и несмещённости оценок неизвестных. Можно предположить, что Гаусс это прекрасно знал и ввёл два независимых обоснования принципа наименьших квадратов. Оставив только второе, можно будет отказаться от рассуждений 1809 г., которые ввиду своего изящества и сравнительной простоты оставались основными.

Многие авторы предпочли обоснование 1823 г., и в том числе Марков, который тем не менее отрицал всякую оптимальность метода наименьших квадратов (МНК) в и тем самым обесценил своё предпочтение. Вопреки его мнению, в случае нормального распределения ошибок наблюдения МНКв обеспечивает совместную эффективность оценок (Петров 1954).

Один из первых методов уравнивания косвенных наблюдений предложил Бошкович, который участвовал в прокладке градусного измерения в Италии. В некотором смысле его рекомендация приводила к выбору медианы.

Уже Кеплер считал среднее арифметическое буквой закона. Уравнивая косвенные наблюдения, он, видимо, применял элементы принципа минимакса (выбора решения избыточной системы уравнений, соответствующего наименьшему абсолютному максимальному остаточному свободному члену) и метода Монте-Карло: он искажал наблюдения произвольными малыми поправками так, чтобы они соответствовали друг другу.

Древние астрономы считали непосредственные наблюдения своей собственностью; они не сообщали об отброшенных результатах и выбирали любую разумную оценку. Погрешности наблюдений были значительными, и теперь известно, что при плохих распределениях среднее арифметическое не лучше отдельного наблюдения, а иногда хуже его.

Бируни, арабский учёный X – XI вв., который превзошёл Птолемея, ещё не придерживался среднего арифметического, а выбирал различные оценки (Шейнин 1992).

Существует и детерминированная теория ошибок, которая исследует весь процесс наблюдений без применения стохастических представлений и близка к предварительному исследованию данных и планированию эксперимента. Уже древние астрономы умели выбирать наилучшие моменты наблюдений, чтобы неизбежные ошибки меньше всего влияли на результаты.

Не позднее XVII в. естествоиспытатели включая Ньютона начали учитывать подобные соображения. Даниил Бернулли чётко определил случайные и систематические ошибки, Гаусс и Бессель породили новую стадию экспериментальной науки, предполагая, что каждый инструмент должен быть полностью исследован и отъюстирован. Бессель (1839) определял, в каких двух точках должны находиться опоры измерительного жезла, чтобы он в наименьшей степени изгибался (и изменял свою длину) под влиянием собственного веса.

Последний пример: выбор исходных данных. Некоторые естествоиспытатели XIX в. полагали, что можно надежно использовать разнородные данные. Английский хирург Дж. Симпсон тщетно изучал смертность от ампутации конечности по данным многих больниц за 45 лет. С другой стороны, заключения иногда делались при отсутствии данных. У. Гершель заявил, что размер звезды, случайно отобранной из многих тысяч, вряд ли будет существенно отличаться от их среднего размера. Он не знал, что размеры звезд чудовищно различны, так что их среднее не имеет смысла, да и вообще нельзя ничего узнать из незнания[3].

Список используемых источников

Статистические методы. [Электронный ресурс] – Режим доступа: http://diplomba.ru/work/74016

Теория статистических методов. [Электронный ресурс] – Режим доступа:http://www.0zd.ru/ekonomika_i_ekonomicheskaya_teoriya/teoriya_statisticheskix_metodov.html

Теория статистики. [Электронный ресурс] – Режим доступа: http://www.e-reading.club/bookreader.php/99603/Burhanova_Teoriya_statistiki.html

Источник

Статистические ошибки

Introduction[edit]

In univariate distributions[edit]

[edit]

Regressions[edit]

Other uses of the word «error» in statistics[edit]

See also[edit]

References[edit]

External links[edit]

Статистическая погрешность: чуть подробнее

Как считать статистическую погрешность?

2.4. Точность статистического наблюдения

Интересное по теме: