Ошибка линейного предсказания - Oshibku.top - решение и исправление самых разных ошибок

Speech Synthesis Based on Linear Prediction

Power Spectral Density

V-Vector Algebra and Volterra Filters

Multiple Random Variables

Electron dipole‐dipole interaction in ESEEM of biradicals

Time Series Analysis

Reconstruction Theory and Nonlinear Time Series Analysis

Restricted maximum likelihood and inference of random effects in linear mixed models

Patterns of residual covariance structure

Multiple Random Variables

Сжатие речевого сигнала на основе линейного предсказания

Speech Synthesis Based on Linear Prediction

Power Spectral Density

V-Vector Algebra and Volterra Filters

Multiple Random Variables

Electron dipole‐dipole interaction in ESEEM of biradicals

Time Series Analysis

Reconstruction Theory and Nonlinear Time Series Analysis

Restricted maximum likelihood and inference of random effects in linear mixed models

Patterns of residual covariance structure

Multiple Random Variables

Сжатие речевого сигнала на основе линейного предсказания

I Introduction

Section 10.4 Spectral Estimation

A Nonlinear Prediction of Speech by Using V-Vector Algebra

5.7 Covariance and Correlation Coefficient

Example 5.12

Example 5.13

3.1 Two‐pulse ESEEM of biradical toluene solution

Example 4

Local linear predictors

4.7 Summary

5.5.1 Least squares means

6.6 Engineering Application: Linear Prediction of Speech

I Introduction

Section 10.4 Spectral Estimation

A Nonlinear Prediction of Speech by Using V-Vector Algebra

5.7 Covariance and Correlation Coefficient

Example 5.12

Example 5.13

3.1 Two‐pulse ESEEM of biradical toluene solution

Example 4

Local linear predictors

4.7 Summary

5.5.1 Least squares means

6.6 Engineering Application: Linear Prediction of Speech

Интересное по теме:

Solution:

Solution:

Упрощенная дискретная модель речевого сигнала

Коэффициенты линейного предсказания (Linear Prediction Coding Coefficients или просто LPC)

Нахождение LPC-коэффициентов

Краткий итог по модели LPC

Применение LPC для анализа речевого тракта

Выводы

Solution:

Solution:

Упрощенная дискретная модель речевого сигнала

Коэффициенты линейного предсказания (Linear Prediction Coding Coefficients или просто LPC)

Нахождение LPC-коэффициентов

Краткий итог по модели LPC

Применение LPC для анализа речевого тракта

Выводы

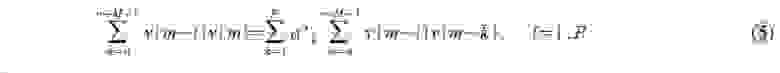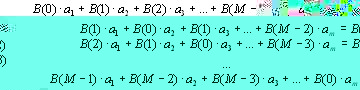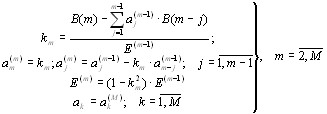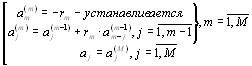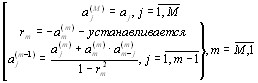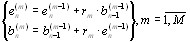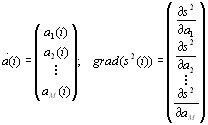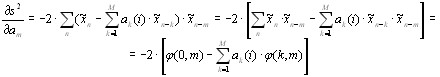
оценивании коэффициента отражения по этим отсчетам на каждом шаге рекурсии Левинсона.

Подставляя в уравнения (2.20) и (2.25) значения a p [n ] , определяемые выражением

(2.26), можно получить рекурсивные соотношения:
e pf [n] = e pf −1[n] + K p ebp−1[n − 1],	(2.31)
ebp [n] = ebp−1[n − 1] + K p*e pf −1[n] ,	(2.32)

которые связывают ошибки предсказания порядка p с ошибками предсказания порядка (p- 1), с начальными условиями e0f[n]= e0b[n] = x[n]. Показано [1], что коэффициенты

отражения можно рассматривать как взятый со знаком минус нормированный коэффициент корреляции между ошибками линейного предсказания вперед и назад с единичным временным сдвигом:

Km =

— áemf

−1[n]emb*−1[n —1]ñ

emf −1[n]

emb −1[n —1]

(2.33)

ñ á

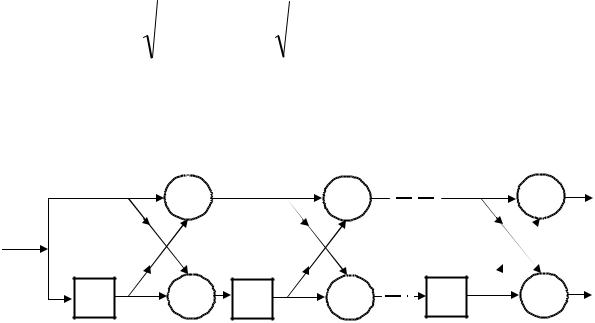
Соотношения (2.31) и (2.32) позволяют реализовать КИХ—фильтр ошибки линейного предсказания с помощью коэффициентов отражения в форме, называемой решетчатым

фильтром, представленным на рис.2.5.

x[n]		+ e1f [n]
K1			K2
	K1	+	e1b[n]	K	2
	z-1	z-1

e2f [n]		+	emf	[n]

	K m		emb
e2b[n]	K m	+	[n]
	z-1

Рис.2.5. Решетчатая реализация фильтра ошибки линейного предсказания: z-1 означает

задержку на один отсчет

Параметрами каждой ступени решетчатого фильтра являются коэффициенты отражения. В этой структуре одновременно распространяются ошибки предсказания вперед и назад, причем ошибки предсказания назад на выходе каждой ступени взаимно ортогональны.

1≤n≤N.

В алгоритме Берга используется оценка коэффициента отражения, методу наименьших квадратов. При каждом значении порядка p в нем

среднее арифметическое мощности ошибок линейного предсказания (выборочная дисперсия ошибки предсказания):

ρ pfb =

e pf [n]

ebp [n]

+ å

2N ên= p+1

n= p+1

определяемая по минимизируется вперед и назад

2 ù

ú , úû

и решая полученное уравнение относительно Kp, получаем следующее выражение для оценки по методу наименьших квадратов:

			N
€		− 2 å e pf −1 [n]e bp*−1 [n	− 1]
=		n = p +1
K p					.	(2.34)
N	\| e pf −1 [n] \|2	N
		å	+ å \| e bp −1[n − 1] \|2
		n = p +1		n = p +1

В (2.34) предполагается, что имеется N отсчетов данных x[1], …, x[N] и ошибки предсказания формируются в диапазоне индексов от n=p+1 до n=N, поскольку используются только имеющиеся отсчеты данных. Таким образом, алгоритм Берга использует рекурсивный алгоритм Левинсона, в котором вместо Kp, вычисляемого по АКП используется его оценка (2.34). Базовый алгоритм Левинсона дополняется уравнениями (2.31) и (2.32), вычисления по которым начинаются с e0f[n]= e0b[n] = x[n],

Начальное значение дисперсии ошибки предсказания равно

		1	N		2

ρ0	=		å	x[n]	.

		N n=1

Последовательность действий в рекуррентной процедуре вычисления коэффициентов ap[k], k=1,2,…,p будет следующей.

1). Положив m=1, из (2.34) найдем

N
− 2 å x[n]x [n −1]
n=2
N	2 + x[n −1]	2}
å{ x[n]
n=2

, ρ1 = ρ0 (1 −		^	2	^

	K1		), a1[1] = K1 .

2). После определения K1 по соотношениям (2.31) и (2.32) вычисляются ошибки прямого ef1[n] и обратного eb1[n] предсказания на выходе 1-й ступени решетчатого фильтра

(рис.2.5).

3). Положив m=2, из (2.34) найдем оценку коэффициента отражения K2 . На основе

соотношений Левинсона найдем коэффициенты фильтра ошибки линейного предсказания 2-го порядка в виде:

(1 −

(1) = a [1] + K1 a

[1]

= K1

+ K1

K1 , a

[2]

= K 2 ,

= ρ

K 2

4). По известной оценке

вычислим ошибки ef2[n]

и eb2[n]

на выходе 2-й ступени

решетчатого фильтра. Далее, полагая m=3, определяем

K3 и т.д. для более высоких

значений m. Вычисления закончим для m=p.

5). Имея полный набор коэффициентов ap[k], k=1,2,…,p и ρp

вычисляем

СПМ по

соотношению (2.14).

Оценка коэффициента отражения (2.34) представляет собой гармоническое среднее коэффициентов частной корреляции ошибок предсказания вперед и назад. Рекурсивная формула, которая упрощает вычисление знаменателя в выражении для оценки (2.34)

e pf

−1[n]

ebp−1[n —1]

DENP = å

ý;

n= p+1 î

(2.35)

e pf −1[n]

ebp−1[N]

2 .

DENP = (1—

K p

)DENP−1 —

—

Гармонический метод дает несколько смещенные оценки частоты синусоид. Для

уменьшения этого смещения предложено взвешивание среднего квадрата ошибки предсказания:

2 ü

ρ p

W p [n]í

e p [n]

(2.36)

2N n= p+1

что приводит к следующей оценке коэффициента отражения:

		N
	— 2 å Wp−1[n]epf −1[n]ebp*−1[n —1]
€	n= p+1
K p =						(2.37)
N	f	2	b	2	,
å	Wp−1[n](\| ep−1[n] \|	+ \| ep−1[n —1] \|	)
	n= p+1

где Wp−1[n] — определяет весовую функцию. Показано [1], что частотное смещение

уменьшается при использовании окна Хэмминга. В [1] приведена программа BURG , реализующая метод Берга.

2.3.3.Ковариационный метод

Налагая на АР — коэффициенты ограничения, с тем чтобы они удовлетворяли рекурсивному соотношению Левинсона, Бергу удалось осуществить оптимизацию по методу наименьших квадратов единственного параметра — коэффициента отражения.

Другой подход состоит в минимизации в методе наименьших квадратов одновременно по всем коэффициентам линейного предсказания, что позволяет полностью устранить ограничение, налагаемое рекурсией Левинсона. Такой подход будет несколько улучшать характеристики спектральной оценки.

Предположим, что для оценивания АР— параметров порядка р используется N—точечная последовательность данных x[1],…x[N]. Оценка линейного предсказания вперед для отсчета x[n] будет иметь форму

	p
	x€f [n] = − åa f [k]x[n − k].	(2.38)
	k=1
Ошибка линейного предсказания вперед определяется выражением:
e pf	p
[n] = x[n] − x€f [n] = x[n] + åa pf [k]x[n − k],	(2.39)

k=1

Ошибку линейного предсказания вперед можно определить в диапазоне временных индексов от n = 1 до n = N + p , если предположить, что данные до первого и после последнего отсчетов равны нулю (т.е. x[n] = 0, при n <1, n > N ). N + p — членов

ошибки линейного предсказания вперед, определяемых выражением (2.39), можно записать, используя матрично—векторное обозначение, в следующем виде:

[1]

x[1]

e p

ê e

[ p + 1]

x[ p + 1]

x[1]

f [1]

ê x[ N — p ] .

x[ p + 1]

× ê

ê e

[ N — p ]ú

[ N ]

x[ N ]

x[ N — p ]ú

e p

êe

[ N + p ]ú

x[ N ]

ë a

f [ p ]û

где XP — прямоугольная теплицева (N + p) × ( p + 1) — матрица данных. Модуль среднего

квадрата ошибки линейного предсказания вперед, который необходимо минимизировать, это величина:

ρ pf = å	e pf [n]	2 .	(2.41)

n

Поделив (2.41) на N, получим выборочную дисперсию. Выбор диапазона суммирования в (2.41) зависит от конкретного применения. Выбирая полный диапазон суммирования от

e pf [1] до e pf [N + p], получаем так называемый взвешенный случай, поскольку отсутствующие значения данных приравниваются к нулю. Выбирая диапазон суммирования от e pf [1] до e pf [N ], получаем предвзвешенный случай, поскольку при этом полагается, что значения данных, предшествующие отсчету x[1], равны нулю.

Диапазон суммирования от e pf [ p + 1] до e pf [N ] соответствует невзвешенному

случаю, поскольку используются только имеющиеся отсчеты данных. Взвешенный случай получил название автокорреляционного метода линейного предсказания. Случай отсутствия взвешивания называется ковариационным методом линейного предсказания.

Показано [1], что нормальные уравнения для нахождения коэффициентов линейного предсказания в автокорреляционном методе, совпадают с уравнениями Юла—Уолкера, в которых используются смещенные оценки АКП. Обработка данных с помощью окна, применяемая в этом методе, ухудшает разрешение по сравнению с другими методами спектрального оценивания на основе линейного предсказания, поэтому для коротких записей данных автокорреляционный метод редко применяется.

Соотношение между ошибками линейного предсказания вперед и коэффициентами линейного предсказания для ковариационного (т.е. без взвешивания) метода, можно в матричной форме записать в следующем виде:

é e pf [ p +1]	ù	é x[ p + 1] .
ê	.	ú	ê	.	.
ê	ú	ê
ê	.	ú	ê	.
ê		ú	ê
êe pf [N — p]ú	= êx[N — p] .
ê	.	ú	ê	.	.
ê	.	ú	ê	.
ê	ú	ê
ê	f	ú	ê	x[N ]	.
ë	e p [N ]	û	ë

x[1]

x[ p +

x[N —

	ù		é		1	ù
	ú		ê			ú
	ú		ê			ú
	ú		ê			ú
1]	ú	×	ê a f [1]	ú.	(2.42)
	ú		ê		.	ú
	ú		ê		ú
	ú		ê		.	ú
	ú		ê	f	ú
	ú		ê		ú
p]û		ëa		[ p]û

Нормальные уравнения, минимизирующие средний квадрат ошибки:

порядка p, имеют вид:

ö	æ	ρ f
÷	= ç	p
÷	ç	0 p
ø	è

Элементы эрмитовой ( p +1) × ( p +1) матрицы Rp имеют вид корреляционных форм

N
rp[i, j] = åx*[n − i]x[n − j], 0	≤ i, j ≤ p .	(2.45)
n= p+1

Элементы матрицы Rp в ковариационном методе не могут быть записаны как функции разности (i-j), а это означает, что Rp не является теплицевой матрицей. Однако тот факт, что матрица является произведением теплицевых матриц, все же обеспечивает возможность построения быстрого алгоритма, аналогичного алгоритму Левинсона [1]. Необходимым, но недостаточным условием того, чтобы матрица была невырожденной,

является условие N — p ³ p или p ≤ N / 2. Отсюда следует, что выбранный порядок

модели не должен превышать половины длины записи данных. Аналогичное рассмотрение можно провести применительно и к оценке линейного предсказания назад. В [1] приведена программа COVAR , реализующая ковариационный метод. Быстрый

алгоритм для ковариационного метода одновременно решает нормальные уравнения относительно коэффициентов линейного предсказания вперед и назад при всех промежуточных значениях порядка модели, поэтому оба набора коэффициентов получаются здесь без дополнительных вычислительных затрат.

Коэффициенты линейного предсказания вперед и назад, определяемые с помощью ковариационного метода, вообще говоря, не гарантируют получение устойчивого фильтра. Однако это не приводит к каким—либо затруднениям, если их значения используются только для целей спектрального оценивания. В действительности спектральные оценки, получаемые по оценкам АР— коэффициентов с помощью

ковариационного метода обычно имеют меньшие искажения, чем спектральные оценки, получаемые с помощью методов, гарантирующих устойчивость фильтра.

2.3.4.Модифицированный ковариационный метод

Для стационарного случайного процесса авторегрессионные коэффициенты линейного предсказания вперед и назад представляют собой комплексно — сопряженные величины, поэтому ошибку линейного предсказания назад можно записать в следующем виде:

p
ebp [n] = x[n − p] + åa pf *[k]x[n − p + k].	(2.46)

k=1

Поскольку оба направления предсказания обеспечивают получение одинаковой статистической информации, представляется целесообразным объединить статистики ошибок предсказания вперед и назад с тем, чтобы получить большее число точек, в которых определяются ошибки, и улучшить оценку АР — параметров.

Минимизируя среднее значение квадратов ошибок предсказания вперед и назад:

ρ pfb =	1	é	N	epf [n]	2	N	ebp[n]		2 ù
ê	å	+ å			ú
2
	ê				n= p+1			ú

		ën= p+1					û

по коэффициентам линейного предсказания, получаем систему нормальных уравнений:

R	æ	1	ö	æ	2	ρ fb ö
ç		÷	= ç	p	÷	(2.47)
	p ç	fb ÷	ç	0 p	÷ ,
	èa p	ø	è	ø

где элементы матрицы R p имеют вид:
	N
rp[i, j] =	å(x[n —i]x[n — j]+ x[n — p +i]x[n — p + j]),	(2.48)
	n=p+1
где 0 ≤ i, j ≤ p .	Процедура, основанная на совместном использовании	ошибок

линейного предсказания вперед и назад по методу наименьших квадратов, получила название модифицированного ковариационного метода.

Модифицированный ковариационный метод и гармонический метод Берга основаны на минимизации средних квадратов ошибок линейного предсказания вперед и назад. В первом из них минимизация выполняется по всем коэффициентам предсказания, во втором выполняется условная (т.е. с наложенным ограничением) минимизация только по

одному коэффициенту предсказания a p [ p] (т.е. по коэффициенту отражения K p ).

При использовании метода Берга возникает ряд проблем, включая расщепление спектральных линий и смещение частотных оценок, которые устраняются при использовании модифицированного ковариационного метода.

Необходимым условием	невырожденности матрицы R p является условие
2(N − p) > p или p ≤	2N	, т.е. порядок модели не должен превышать две трети
3

длины записи данных. В [1] приведена программа MODCOVAR, реализующая модифицированный ковариационный метод.

2.3.5. Выбор порядка модели

Поскольку наилучшее значение порядка модели заранее, как правило, не известно, на практике приходится испытывать несколько порядков модели.. При слишком низком порядке модели получаются сильно сглаженные спектральные оценки, при излишне высоком – увеличивается разрешение, но в спектре появляются ложные пики. Интуитивно ясно, что следует увеличивать порядок АР–модели до тех пор, пока вычисляемая ошибка предсказания не достигнет минимума. Однако во всех процедурах

оценивания по методу наименьших квадратов мощности ошибок предсказания монотонно уменьшаются с увеличением порядка модели p. Так, например, в алгоритме Берга и в уравнениях Юла—Уолкера используется соотношение

ρ p = ρ p −1 (1 − a p [ p ] 2 ) .

До тех пор, пока величина ap[p] отлична от нуля (она должна быть равной или меньше

1), мощность ошибки предсказания уменьшается. Следовательно, сама по себе мощность

ошибки предсказания не может служить достаточным критерием окончания процедуры изменения порядка модели.

Для выбора порядка АР–модели предложено несколько целевых критериев. Акаике предложил два критерия. Первым из них является величина окончательной ошибки предсказания (ООП). Согласно этому критерию, порядок АР –процесса выбирается таким образом, чтобы средняя дисперсия ошибки на каждом шаге предсказания была минимальна. Акаике рассматривал ошибку как сумму мощностей в непредсказуемой (или не обновляемой) части процесса и как некоторую величину, характеризующую неточность

оценивания АР–параметров. Окончательная ошибка предсказания для АР–процесса

определяется

æ N + p +1ö ООПp = ρ€p ççè N — p +1÷÷ø,

где N – число отсчетов данных, p – порядок АР—процесса, ρ€p —оценочное значение

дисперсии шума (дисперсии ошибки предсказания). Член в круглых скобках увеличивает оконечную ошибку предсказания по мере того, как p приближается к N, характеризуя тем самым увеличение неопределенности оценки ρ€ p для дисперсии ошибки предсказания.

Выбирается порядок р, при котором величина оконечной ошибки предсказания минимальна. Критерий на основе оконечной ошибки предсказания исследовался в различных приложениях, и для идеальных АР–процессов он обеспечивает хорошие результаты. Однако при обработке реальных сигналов этот критерий приводит к выбору слишком малого порядка модели.

Второй критерий Акаике основан на методе максимального правдоподобия и получил название информационного критерия Акаике (ИКА). Согласно этому критерию, порядок модели выбирается посредством минимизации некоторой теоретико—информационной функции. Если исследуемый процесс имеет гауссовы статистики, то ИКА определяется

выражением

ИКА[ p] = N ln(ρ€p ) + 2 p .

И здесь выбирается порядок модели, при котором ИКА минимален.

Третий метод выбора критерия предложен Парзеном и получил название авторегрессионой передаточной функции критерия (АПФК). Порядок модели р выбирается в этом случае равным порядку, при котором оценка разности среднеквадратичных ошибок между истинным фильтром предсказания ошибки (его длина может быть бесконечной) и оцениваемым фильтром минимальна. Парзен показал, что эту разность можно вычислить, даже если истинный предсказывающий ошибку фильтр точно не известен:

	1	p	1			1
АПФК[ p] = (		å			) −		,

	ρ j
	N j=1			ρ p

где ρ j = [N(N − j)]ρ€j . И здесь р выбирается так, чтобы минимизировать АПФК.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Bishnu S. Atal, in Encyclopedia of Physical Science and Technology (Third Edition), 2003

Linear prediction has become an important method for speech analysis and synthesis. Although the basic mathematical foundations of the theory of linear prediction were established in the early 1940s, the method did not find widespread use for speech analysis and synthesis until the mid-1960s. Most speech analysis until then was based exclusively on frequency-domain techniques. Since then, the linear prediction has become the predominant method of speech processing. What are the reasons linear prediction has become so important for speech processing?

The reasons will become evident if we look briefly at how the speech signals are produced by the human vocal system. There are many different modes in which speech is produced. One important mode—vowel production—relies on the regular and almost periodic opening and closing of the vocal cords to convert the steady air flow from the lungs into a wideband signal rich in harmonics. This wideband signal excites the resonances of the vocal cavities, which are then radiated from the mouth into the open air. The waveform of sound pressure for a short speech segment is illustrated in Fig. 1, where the regular motion of the vocal cords appears as periodic variations in the sound pressure and the vocal resonances appear as oscillations within each period.

FIGURE 1. Sound pressure for a short segment of speech signal, about 60 ms in duration.

Digitized speech waveform, produced by sampling natural speech at 8000 samples/s (0.125 ms time intervals), provides a fairly accurate representation of the original speech signal. In speech analysis, our goal is to represent speech by a small number of slowly varying parameters reflecting the changing nature of the shape of the vocal cavities and the motion of the vocal cords. The theory of linear prediction provides an accurate representation of speech in terms of a few (as low as 12) parameters specified once every 10 ms.

One is often interested in identifying vocal resonances independent of the motion of the vocal cords. It is difficult to determine these resonances in a spectrum obtained by using Fourier transforms or bandpass filters. This is illustrated in Fig. 2, which shows the distribution of energy in different frequency components of the speech waveform of Fig. 1. It is obvious that the harmonic structure in the spectrum introduced by the vocal cords makes it very difficult to identify vocal resonances. The linear prediction methods take account of resonances directly in the analysis procedure and are thus able to provide a smooth spectrum with well-defined peaks corresponding to the resonances. Such a spectrum for the speech waveform of Fig. 1 is shown in Fig. 3.

FIGURE 2. Energy in different frequency components of the speech waveform shown in Fig. 1. The abscissa represents the frequency in kilohertz (kHz) and the ordinate represents the energy in decibels (dB).

FIGURE 3. Spectrum of the speech waveform of Fig. 1 using linear prediction techniques. The abscissa and ordinate are the same as in Fig. 2.

Consider now an application such as digital speech coding. Here, linear prediction offers an easy solution. The speech waveform is a continuously varying (analog) signal. In speech coding, we are interested in transmitting speech over a digital communication channel that can carry only the binary digits zero and one. How can we convert the analog speech signal into a digital form using as few binary digits (bits) as possible? We can reduce the bit rate needed to transmit the speech signal significantly by sending only new information on the digital channel. If we look at the speech waveform of Fig. 1, we notice that there is considerable similarity between the signal and its preceding values. Now, it would be wasteful to send that information on the digital channel that can be predicted from the past. The theory of linear prediction allows us to determine exactly what is predictable in the signal and remove that information from the speech signal before transmission on the digital channel.

Speech signals can be analyzed using both the frequency-domain approach based on Fourier transforms and the time-domain approach based on linear prediction. Although the frequency- and time-domain approaches appear different from each other, there is a close connection between the two for stationary signals. This connection is carried over only loosely to nonstationary signals, such as speech, whose characteristics vary slowly with time.

We shall discuss in this article the basic concept of linear prediction, the merit of using linear prediction for speech analysis and synthesis, and the differences between linear prediction and more traditional spectral estimation techniques. We will also discuss some important applications of linear prediction in the coding and synthesis of speech signals.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B0122274105007201

Scott L. Miller, Donald Childers, in Probability and Random Processes (Second Edition), 2012

10.21

Consider the linear prediction random process X[n] = (1/2)X[n − 1] + E[n], n = 1, 2, 3, …, where X[0] = 0 and E[n] is a zero-mean, IID random process.

(a): Find the mean and autocorrelation functions for X[n]. Is X[n] WSS?
(b): Find the PSD of X[n].

10.22

Consider an AR(2) process which is described by the recursion

Y[n]=a1Y[n-1]+a2Y[n-2]+X[n]

where X[n] is an IID random process with zero-mean and variance σ²_X.

(a)

Show that the autocorrelation function of the AR(2) process satisfies the difference equation,

RYY[k]=a1RYY[k-1]+a2RYY[k-2], k=2,3,4,….

(b)

Show that the first two terms in the autocorrelation function satisfy

(1-a12-a22)RYY[0]-2a1a2RYY[1]=σX2,and (1-a2)RYY[1]=a1RYY[0].

From these two equations, solve for R_YY[0] and R_YY[1] in terms of a₁, a₂, and σ²_X

(c)

Using the difference equation in part (a) together with the initial conditions in part (b), find a general expression for the autocorrelation function of an AR(2) process.

(d)

Use your result in part (c) to find the PSD of an AR(2) process.

10.23

Suppose we use an AR(2) model to predict the next value of a random process based on observations of the two most recent samples. That is, we form

Yˆ[n+1]=a1Y[n]+a2Y[n-1].

(a)

Derive an expression for the mean-square estimation error,

E[ɛ2]=E[(Y[n+1]-Yˆ[n+1])2].

(b)

Find the values of the prediction coefficients, a₁ and a₂, that minimize the mean-square error.

10.24

Extend the results of Exercise 10.23 to a general AR(p) model. That is, suppose we wish to predict the next value of a random process by forming a linear combination of the p most recent samples:

Yˆ[n+1]=∑k=1pakY[n-k+1].

Find an expression for the values of the prediction coefficients which minimize the mean-square prediction error.

10.25

Show that the estimator for the autocorrelation function,

_XX(τ), described in Equation (10.26) is unbiased. That is, show that E[_XX(τ)] = R_XX(τ).

10.26

Suppose X(t) is a zero-mean, WSS, Gaussian random process. Find an expression for the variance of the estimate of the autocorrelation function,

XX(τ), given in Equation (10.26). That is, find Var(XX(τ). Hint: Remember xx(i) is unbiased (see Exercise 10.25) and you might find the Gaussian moment factoring theorem (see Exercise 6.18) useful.

10.27

Using the expression for Var(

_XX(τ)) found in Exercise 10.26, show that as |τ|→2t_o, Var(_XX(τ))> Var(X(t)) and therefore, the estimate of the autocorrelation function is at least as noisy as the process itself as |τ|→2t_o.

10.28

Determine whether or not the periodogram is an unbiased estimate of the PSD.

10.29

Suppose we form a smoothed periodogram of the PSD,

^(wp)_XX(f), as defined in Equation (10.35), using a rectangular smoothing function,

w˜(f)=1fΔrect(ffΔ),

where f_Δ is the width of the rectangle. If we want to form the same estimator using a windowed correlation-based estimate, what window function (in the time domain) should we use?

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123869814500138

Alberto Carini, … Giovanni L. Sicuranza, in Advances in Imaging and Electron Physics, 2002

Many authors have pointed out that nonlinear prediction of speech greatly outperforms linear prediction in terms of prediction gain. In this subsection, we focus on nonlinear prediction implemented with discrete Volterra series truncated to the second term, as described in Section II. A quadratic Volterra predictor has a linear term, which is related to the vocal-tract resonances, and a quadratic term that can model the nonlinearities related to the mechanisms of speech production. Therefore, the Volterra predictor appears as a natural extension of the linear predictors well described by Markel and Gray (1976); in fact, the predictor is the following simple parametric model:

(91)x^(n)=∑i=1N1h1(i)x(n-i)+∑i=1N2∑j=iN2h2(i,j)x(n-1)x(n-j)

where N₁ and N₂ are called linear and quadratic orders in the following discussion. In principle, we can thus define an analysis model,

(92)e(n)=x(n)-∑i=1NIh1(i)x(n-i)-∑i=1N2∑j=iN2h2(i,j)x(n-i)x(n-j)

and a synthesis model,

(93)x(n)=e(n)+∑i=1N1h1(i)x(n-i)+∑i=1N2∑j=iN2h2(i,j)x(n-i)x(n-j)

The prediction error shown in Eq. (92) is the instantaneous prediction error. Identification of the Volterra coefficients can be performed by means of the minimization of the mean squared prediction error over a frame of data; the related equations are simple to derive because the predictor is nonlinear in the signal values but it is linear in the filter coefficients. This problem thus requires the solution of a linear system in which statistical moments up to the fourth order are involved. Such block-based approaches have been worked out by Mumolo and Francescato (1993), and some results are reported subsequently. The prediction gain is very good; however, the inversion problem— namely, the reconstruction of the input signal by using a quantized residual signal—is very critical, because even a soft quantization of the residual signal leads to an unstable inverted Volterra filter. Therefore, the block-based configuration is unsuitable for coding applications. Moreover, the numerical complexity of such block-based approaches is very high.

Adaptive identification of the Volterra filter coefficients yields the possibility of reducing the computational burden. The algorithms can be divided into least mean square (LMS) and RLS approaches; a thorough discussion of these adaptive techniques applied to discrete Volterra filters can be found in Mathews and Sicuranza (2000). Although the LMS approach is a simple stochastic- gradient adaptive technique, it only approximately solves the problem depicted in Eq. (44) of Section V, and its convergence to the final coefficient values is very slow. A much faster convergence is obtained by using RLS algorithms, which are recursive solutions of Eq. (44) of Section V. In these algorithms, care must be taken to ensure that the autocorrelation matrix does not lose its symmetry and positiveness during the adaptation, so that numerical instabilities can be avoided in limited-precision environments. Therefore, the problem is to derive low-complexity RLS algorithms which ensure numerical stability. Mumolo and Carini (1995) derived stable RLS algorithms for Volterra filters by using SQR techniques; however, their computational complexity is quite high.

The RLS algorithm for Volterra filters described in Section V and based on V-vector algebra is very attractive as regards numerical stability and computational complexity. It is worth recalling that, as shown in Section V, besides computing the prediction error, the algorithm does not compute the Volterra filter coefficients but a lattice realization of the filter; the filter coefficients can be computed at the expense of additional computations. Therefore, it is better to use this algorithm in prediction-based applications, such as adaptive coding, which requires the computation of only a good prediction of the input sample, rather than in system identification applications.

Moreover, two interpretations of the instantaneous prediction error are considered in the algorithm—namely, the forward a priori and a posteriori prediction errors. In any case, a direct dependency of the input signal to the Volterra filter is shown. The a priori prediction error is the error involved in the prediction of the ith channel input value v_n,i before the coefficients of the lattice Volterra representation are updated. Similarly, the a posteriori prediction error arises from predicting the input value after the Volterra filter is updated. As shown in Section V, the two forms of prediction errors are related by the likelihood variable. Because the a priori prediction can be viewed as a tentative prediction, it is not suitable to demonstrate that a Volterra model is able to describe speech nonlinearities. Rather, the a posteriori prediction error should be used. However, for coding purposes the question of which type of prediction error should be used is a matter of how well the quantizer is able to adaptively track the error; this topic is further discussed in Sections VI.E and VI.F.

The question of how well a Volterra filter can model speech nonlinearities can be answered only experimentally. The following discussion details a series of experimental investigations pefformed by the authors to assess the modeling capability of Volterra filters when they are applied to speech signals.

The adaptive prediction algorithm, based on V-vector algebra and proposed in Section V, was used in these nonlinear prediction experiments. The algorithm is implemented according to the following pseudo-code using a scripting- like language (for better clarity, the pseudo-code can be compared with the algorithm description reported in Section V):

A data set composed of 10 different sentences, each spoken by 10 speakers, 5 males and 5 females, sampled at 48 kHz and downsampled at 8 kHz, was used in the authors’ experiments. The data set was large because it involved 10 speakers and more than 8 min of natural speech; for this reason significant mean results could be obtained. Figure 9 shows the mean squared a posteriori error, averaged over all the sentences and the speakers, versus the total number of Volterra coefficients. The first curve, denoted with asterisks, is the a posteriori linear prediction error for all the linear orders from 10 to 46. The second curve, indicated with plus signs, is related to Volterra predictions with a linear order equal to 8; the first point is related to a quadratic order equal to 2 (11 coefficients total), the second to 3 (14 coefficients total), and so on, up to the 8th quadratic order. The mean squared prediction error with a nonlinear predictor is less than the corresponding linear predictor with the same total number of coefficients up to the 7th quadratic order. The third curve, denoted with multiplication signs, is related to a 10th linear order and quadratic orders from 1 to 8. The best prediction gain was obtained for a quadratic order equal to 2. The last curve, denoted by triangles, was obtained with a 12th linear order and quadratic orders from 1 to 7. The third and fourth curves show that the mean squared prediction error in the case of a quadratic Volterra model is always significantly less than in the linear case. In conclusion, the nonlinearities in speech are relevant and are well gathered by Volterra predictors. Moreover, a good choice of linear and quadratic orders is (10,2); in any case, good values of the quadratic orders are small, in the range of 2–3.

Figure 9. Mean squared a posteriori prediction error versus the total number of filter coefficients. See text for a description of the curves.

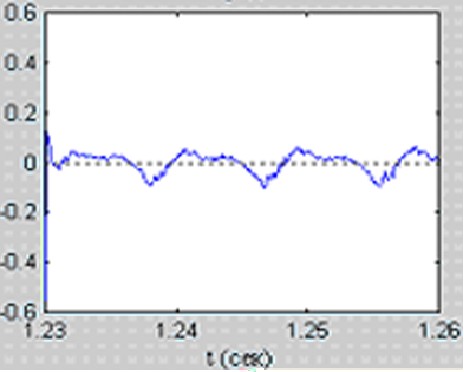
The performance of the nonlinear predictor depends on the characteristics of the nonlinear mechanisms involved in the signal production; thus they arenot uniform during a sentence. In general, they are more evident for vowel sounds. For example, in Figure 10, the a posteriori prediction error for a vowellike segment extracted from the sentence “Nanny may know my meaning” is reported. In the upper and lower panels, respectively, the predictor error corresponding to a 46th- order linear predictor and the prediction error for a filter with the orders 10 for the linear part and 8 for the quadratic part (i.e., with the same number of coefficients) are reported. As is shown graphically, the error variance is greatly reduced for the Volterra model with the same number of predictor coefficients; this indicates that a Volterra predictor is able to model speech nonlinearities.

Figure 10. Prediction error for the sentence “Nanny may know my meaning” for (top) a 46th-order linear predictor and (bottom) a 10th/8th-order Volterra predictor.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/S1076567002800416

Oliver C. Ibe, in Fundamentals of Applied Probability and Random Processes (Second Edition), 2014

Consider two random variables X and Y with expected values EX=μX and EY=μY, respectively, and variances σX2 and σY2, respectively. The covariance of X and Y, which is denoted by Cov(X, Y) or σ_XY is defined by

(5.17)CovXY=σXY=E[(X−μX)(Y−μY)]=EXY−μYX−μXY+μXμY=EXY−μYE[X]−μXE[Y]+μXμY=EXY−μXμY−μXμY+μXμY=EXY−μXμY

If X and Y are independent, then E[XY] = μ_Xμ_Y and Cov(X, Y) = 0. However, the converse is not true; that is, if the covariance of X and Y is zero, it does not mean that X and Y are independent random variables. If the covariance of two random variables is zero, we define the two random variables to be uncorrelated.

We define the correlation coefficient of X and Y, denoted by ρ(X, Y) or ρ_XY, as follows:

(5.18)ρXY=CovXYVarXVarY=σXYσXσY

The correlation coefficient has the property that

(5.19)−1≤ρXY≤1

This can be proved as follows. Since the variance is always nonnegative, we have that if X and Y have variances given by σX2 and σY2 respectively, then

0≤VarXσX+YσX=VarXσX2+VarYσY2+2CovXYσXσY=21+ρXY

which implies that − 1 ≤ ρ_XY. Also,

0≤VarXσX−YσX=VarXσX2+VarYσY2−2CovXYσXσY=21−ρXY

which implies the ρ_XY ≤ 1. Thus,

−1≤ρXY≤1

The correlation coefficient ρ_XY provides a measure of how good a linear prediction of the value of one of the two random variables can be formed based on an observed value of the other. Thus, if we represent the relationship between X and Y by the linear equation Y = a + bX, a value of ρ_XY near − 1 or + 1 indicates a high degree of linearity between X and Y. In particular, a positive ρ_XY implies that b > 0, and a negative ρ_XY implies that b < 0. That is, a positive ρ_XY implies that as X increases, Y also tends to increase; and a negative ρ_XY implies that as X increases, Y tends to decrease. A value of ρ_XY = 0 means that there is no linear correlation between X and Y. However, it does not mean that there is no correlation at all between them because there may still be a high nonlinear correlation between them. In general, ρ_XY measures the goodness of fit of the equation that expresses Y as a function of X to actual (or measured) values of Y. That is, it indicates how closely the equation that expresses Y as a function of X matches measured (or observed) values of Y.

The joint PDF of the random variables X and Y is defined as follows:

fXYxy=25e−5y0≤x<0.2;y≥00otherwise

a.: Find the marginal PDFs of X and Y.
b.: What is the covariance of X and Y?

a.

The marginal PDFs are obtained as follows:

fXx=∫0∞fXYxydy=∫0∞25e−5ydy=50≤x<0.20otherwisefYy=∫00.2fXYxydx=∫00.225e−5ydx=5e−5yy≥00otherwise

Thus, X has a uniform distribution and Y has an exponential distribution.

b.

The expected values of X and Y are given by

EX=μX=0+0.22=0.1EY=μY=15=0.2

Also,

EXY=∫x=00.2∫y=0∞xyfXYxydydx=∫x=00.2∫y=0∞25xye−5ydydx=∫x=00.2x∫y=0∞25ye−5ydydx=∫x=00.2xdx=x2200.2=0.02

Thus, the covariance of X and Y is given by

σXY=EXY−μXμY=0.02−0.10.2=0

This means that X and Y are uncorrelated. Note that the reason why σ_XY = 0 is because X and Y are independent. This follows from the fact that f_XY(x, y) is separable into a function x and a function of y, and the region of interest is rectangular. Thus, f_XY(x, y) = f_X(x)f_Y(y).

Hans and Ann planned to meet at their favorite restaurant on a date at about 6:30 pm. Both of them will arrive at the restaurant separately by train. They live in different parts of the city and so will be arriving on different trains that operate independently of each other’s schedule. Hans’ train will arrive at a stop by the restaurant at a time that is uniformly distributed between 6:00 pm and 7:00 pm. Ann’s train will arrive at the same stop at a time that is uniformly distributed between 6:15 pm and 6:45 pm. They agreed that whoever arrives at the restaurant first will wait up to 5 minutes before leaving.

a.: What is the probability that they meet?
b.: What is the probability that Ann arrives before Hans?

Let X be the random variable that denotes Hans’ arrival time, and let Y be the random variable that denotes Ann’s arriving time. As stated in the problem, X and Y are independent random variables. If we consider the time from 6:00 pm to 7:00 pm, we see that we can represent the PDFs of X and Y as follows:

fXx=1600≤x≤600otherwisefYy=13015≤x≤450otherwise

Thus, the joint PDF f_XY(x, y), which is the product of the above marginal PDFs, has a uniform distribution over the rectangle shown in Figure 5.3.

a.

The probability that they meet is given by P[|X − Y| ≤ 5], which is the probability of being in the shaded area of the rectangle. Now, the total area of the rectangle is 60 × 30 = 1800. The area of section A is 10 × 30 = 300, which is also the area of section D. The area of section B is 30 × 30/2 = 450, which is also the area of section C. Thus, the area of the shaded section is 1800 − 2(450 + 300) = 300. This means that

p=3001800=16

b.

The probability that Ann arrives before Hans is P[Y < X], which is the probability of being in the portion of the rectangle above the line Y = X. From the symmetry of the diagram, this can be seen to be equal to 1/2.

Figure 5.3. Domain of the Joint Distribution

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128008522000055

S.A. Dzuba, L.V. Kulik, in EPR in the 21st Century, 2002

Primary ESEEM time‐domain traces for the biradical solution were extrapolated to zero τ value, using a linear prediction method. It was fitted by an exponential function, which was then subtracted before Fourier transformation. The resulting modulus Fourier spectrum is given in Fig 2a. One can see peaks around the single and double proton Larmor frequencies (14 MHz and 28 MHz). In addition, a shallow but sharp negative peak with the minimum at 7.3 MHz is seen. This peak is absent for the spectrum of nitroxide monoradical TEMPON in toluene obtained in the same way (data not shown). One may suggests that this negative peak is induced by electron dipole‐dipole interaction representing the singularity (θ=π/2) in the Pake spectrum. Its unusual shape we ascribe to interference of the weak electron‐electron dipolar line with the huge wing of the electron‐nuclear peak having a comparable intensity at this spectral position. This is readily supported by model calculation employing modulus Fourier transform of several damped harmonics differing in amplitudes [27].

Figure 2. Modulus ESEEM frequency spectra of biradical in toluene glass. The time‐domain signal within the dead time (72 ns) was restored (a) and dropped (b). The asterisks mark the the Pake spectrum singularity.

The sign of the electron dipole‐dipole peak in Fig. 2a may be corrected by dropping some initial data points of ESEEM time‐domain traces prior to Fourier transform. Variation of initial τ value changes the relative phase of electron‐electron and electron‐nuclear contributions in the frequency spectrum. Fig. 2b presents the modulus ESEEM spectrum with the data points omitted for the initial time interval τ_d=72 ns (which exactly corresponds to our experimental dead time). The Pake spectrum singularity appears now as a positive peak with the maximum at 7.1±0.2 MHz. Numerical calculation with two damped harmonics indicates that the positive peak in the modulus Fourier transform spectrum obtained in such way reflects the correct value of the frequency of the weak harmonic.

We assumed that J=0 because substantial overlap of the unpaired electron orbitals is not expected for the biradical of such structure. The corresponding interspin distance calculated by Eq. (2) is 19.6±0.2 Å.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780444509734501086

P.J. Brockwell, in International Encyclopedia of Education (Third Edition), 2010

In order to predict future values of the causal AR[1] process defined in example 3, we can make use of the fact that linear prediction is a linear operation and that P_nZ_t = 0 for t > n to deduce that

PnYn+b=ϕPnYn+h−1=ϕ2PnYn+h−2=⋯=ϕhYn,h≥1.

with mean squared error,

E(Yn+h−PnYn+h)2=σ21−ϕh1−ϕ2.

In order to obtain forecasts and prediction bounds for the original series which were transformed to generate the residuals, we simply apply the inverse transformations to the forecasts and prediction bounds for the residuals.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780080448947013725

Floris Takens, in Handbook of Dynamical Systems, 2010

As we mentioned before, the above procedure of using the past to predict the future is rather primitive. We discuss here briefly a refinement which is based on a combination of optimal linear prediction and the above procedure. This type of prediction was the subject of [8] which appeared in [50]. In this case we start in the same way as above, but now we collect all the segments from the past which are ε-close to the last segment of k elements. Let m1,…,ms be the first indices of these segments. We have then s different values, namely ym1+k,…,yms+k, which we can use as predictions for yN+1. This collection of possible predictions already gives a better idea of the variance of the possible prediction errors.

We can however go further. Assuming that there should be some functional dependence yn=F(yn−1,…,yn−k) with differentiable F (and such an assumption is justified by the reconstruction theorem if we have a time series which is generated by a smooth and deterministic dynamical system and if k is sufficiently big), then F admits locally a good linear, or rather affine, approximation (given by its derivative). In the case that s, the number of nearby segments of length k, is sufficiently large, one can estimate such a linear approximation. This means estimating the constants α0,…,αk such that the variance of {(yˆmi+k−ymi+k)} is minimal, where yˆmi+k=α0+α1ymi+k−1+⋯+αkymi. The determination of the constants α0,…,αk is done by linear regression. The estimation of the next value is then yˆN+1=α0+α1yN+⋯+αkyN−k+1. This means that we use essentially a linear predictor, which is however only based on ‘nearby segments’ (the fact that we have here a term α0, which was absent in the discussion of optimal linear predictors, comes from the fact that here there is no analogue of the assumption that the average is zero).

Finally we note that if nothing is known about how a (stationary) time series is generated, it is not a priori clear that this method of local linear estimation will give better results. Also, a proper choice of k and ε is less obvious in that case; the [8].

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/S1874575X10003152

Xian Liu, in Methods and Applications of Longitudinal Data Analysis, 2016

In longitudinal data analysis, one of the most remarkable progresses in the past three decades is the widespread application of the Bayes-type techniques. Bayes’ theorem and Bayesian inference provide a strong theoretical foundation for approximating unobservable parameters in mixed-effects models. The REML approach, which corrects the downward bias in the ML variance estimates, is an empirical Bayes method that models the marginal posterior predictive density for the variance components while formally integrating out the regression coefficient vector, β. Therefore, in this chapter I first described the basic specifications of Bayesian inference prior to the introduction of the REML estimator. The REML method is arguably a more reliable estimator to find parameter estimates in linear mixed models; nevertheless, for large samples the ML and REML estimators usually yield very close or even identical parameter estimates and approximates, as empirically evidenced in the Section 4.6.

In this chapter, the statistical techniques for predicting the random effects were delineated and discussed. In longitudinal data analysis, linear predictions are often required to generate the trajectory of individuals in the continuous response variable. Population-averaged growth curves can also be predicted from averaging over the random effects. In linear predictions, the BLUP and the shrinkage approach are regularly applied to approximate the random effects and predict the outcomes for each subject. In Section 4.6, a technique was delineated to adjust for potential confounding effects when creating population-averaged trajectories. In particular, a scoring dataset was constructed by retaining the variables of interest and creating some others for representing a hypothetical population.

Given the iid assumption for random errors in linear mixed models, linear predictions with adjustments for the confounding effects can also be conducted by using the least squares means, as will be described and illustrated in the next chapter. Briefly, least squares means are obtained by using the estimated regression coefficients, the selected covariates’ values, and the averages over the distribution of the random effects. While the scoring data approach directly computes the mean of BLUPs with shrinkage, the model-based approach in least squares means assumes longitudinal data to be balanced, and thus can generate different predictions for population groups. The two approaches, however, are expected to yield exactly the same predicted values of the response for the entire population given the condition that Ebˆ=EBLUP bˆ=0. At the same time, as the BLUP bˆi is shrunk toward the population average X′iβˆ, varBLUP bˆ<varbˆ, and therefore, the least squares means are associated with greater standard error estimates than the scoring data approach. These issues will be further discussed in Chapter 7.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128013427000046

Xian Liu, in Methods and Applications of Longitudinal Data Analysis, 2016

The computation of least squares means starts with the construction of a design matrix or a row vector for covariates with the GLM coding, containing specific values for the time factor and one or more other covariates. The design matrix or the row vector is referred to as the L˜ matrix or vector, as briefly described in Chapter 3. As indicated earlier, a combination of the fixed-effects vector and the L˜ matrix derives robust linear predictions on the longitudinal outcomes.

For example, by constructing a specific row vector L˜, a population marginal mean can be predicted. The specification of the vector L˜ defines which population the estimates or predictions refer to. The researcher can set a given element in L˜ to one, which corresponds to a level of interest in a classification factor, and all other elements of the factor as 0. Consequently, the sum of the Xs within any classification effect is one. At the same time, the control variables can be set at mean values to represent a general population, as regularly applied in linear predictions. Consequently, corresponding to the specified values of covariates, the marginal means for a population or a population subgroup can be predicted over a balanced population. In the literature of general linear modeling, such predicted marginal means are referred to as least squares means.

By using matrix notations, each least square mean can be expressed in terms of L˜βˆ where βˆ contains estimates of the fixed-effects parameters from maximum likelihood estimate or the restricted maximum likelihood (REML) estimator. The variance–covariance matrix of the least square means can be approximated by

(5.16)varL˜βˆ=L˜X′ Rˆ−1X−1L˜′.

Equation (5.16), also presented in Chapter 3, indicates that the estimation of the variance for least squares means is based on the R estimate from the maximum likelihood or the REML estimator. Therefore, without the application of shrinkage, the variance of least squares means differs from the variance of the best linear unbiased predictors (BLUPs). As defined, the square root of varL˜βˆ yields the standard error approximate for least square means. Given the standard error approximate, an approximate t test can be performed on the null hypothesis that L˜βˆ=0.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128013427000058

Scott L. Miller, Donald Childers, in Probability and Random Processes (Second Edition), 2012

In many applications, we are interested in predicting future values of a waveform given current and past samples. This is used extensively in speech coders where the signal-to-quantization noise associated with a quantizer can be greatly increased if only the prediction error is quantized. A fairly simple speech coder which utilizes this idea is illustrated in Figure 6.2. In Section 4.11, we introduced the idea of scalar quantization. The process of sampling (at or above the Nyquist rate), quantizing, and then encoding each quantization level with some binary codeword is known as pulse code modulation (PCM). In Figure 6.2, we consider a slight modification to the basic PCM technique known as differential PCM (or DPCM). The basic idea here is that if we can reduce the range of the signal that is being quantized, then we can either reduce the number of quantization levels needed (and hence reduce the bit rate of the speech coder) or reduce the amount of quantization noise and hence increase the SQNR.

Figure 6.2. Block diagram of a simple speech coder using differential pulse code modulation.

A typical speech signal has a frequency content in the range from about 300 to 3500 Hz. In order to be able to recover the signal from its samples, a typical sampling rate of 8 kHz is used which is slightly higher than the Nyquist rate. However, much of the energy content of a speech signal lies in a frequency band below about 1 kHz; thus, when sampled at 8 kHz, a great deal of the speech signal does not change substantially from one sample to the next. Stated another way, when the speech signal is sampled at 8 kHz, we should be able to predict future sample values from current and past samples with pretty good accuracy. The DPCM encoder does exactly that and then only quantizes and encodes the portion of the signal that it is not able to predict.

In Figure 6.2, the X_n represent samples of a speech waveform. These samples are input to the predictor whose job is to make its best estimate of X_n given X_n−1, X_n−2, X_n−3, … as inputs. It is common to use linear prediction, in which case the predictor output is a linear combination of the inputs. That is, assuming the predictor uses the last m samples to form its estimate, the predictor output is of the form

where the a_i are constants that we select to optimize the performance of the predictor. The quantity Z_n = X_n − Y_n is the predictor error, which we want to make as small as possible. This error is quantized with a scalar quantizer which uses 2^b levels and each level is encoded with a b bit codeword. The overall bit rate of the speech coder is b*f_s bits/second, where f_s is the rate (in Hz) at which the speech is sampled. For example, if a 16-level quantizer were used with a speech sampling rate of 8 kHz, the DPCM speech coder would have a bit rate of 32 kbits/second.

An important question is “Can the original samples be recovered from the binary representation of the signal?” Given the encoded bit stream, we can construct the sequence of quantizer outputs, Q_n. As with any quantization scheme, we can never recover the exact quantizer input from the quantizer output, but if we use enough levels in the quantizer, the quantization noise can be kept fairly small. The speech samples are reconstructed according to X_n = Y_n + Z_n. Since we do not have Z_n we use Q_n in its place and form

where ɛ_n = Q_n − Z_n is the quantization noise in the n th sample. To complete the process of recovering the sample values, the decoder must also form the Y_n. It can do this by employing an identical predictor as used at the encoder. Unfortunately, the predictor at the decoder does not have access to the same input as the predictor at the encoder. That is, at the decoder we cannot use the true values of the past speech samples, but rather must use the quantized (noisy) versions. This can be problematic since the predictor at the decoder will now form

If the

_n are noisy versions of the X_n, then the _n will also be noisy. Now, not only do we have quantization noise, but that noise propagates from one sample to the next through the predictor. This leads to the possibility of a snowballing effect, where the noise in our recovered samples gets progressively larger from one sample to the next.

The above problem is circumvented using the modified DPCM encoder shown in Figure 6.3; the corresponding decoder is shown in the figure as well. The difference between this DPCM system and the one in Figure 6.2 is that now the predictor used in the encoder bases its predictions on the quantized samples rather than on the true samples. By doing this, the predicted value may be slightly degraded (but not much if the number of quantization levels is sufficient), but there will be no propagation of errors in the decoder, since the predictor at the decoder now uses the same inputs as the predictor at the encoder.

Figure 6.3. Block diagram of a modified speech coder using differential pulse code modulation.

Now that we have the design of the speech encoder and decoder squared away, we shift our attention to the problem of designing the predictor. Assuming a linear predictor, the problem is essentially to choose the coefficients a_i in Equation (6.67) to minimize the prediction error:

(6.70)Zn=Xn-Yn=Xn-∑i=1maiXn-i.

Following the theory developed in Section 6.5.3, we choose the predictor coefficients to minimize the MSE:

(6.71)E[Zn2]=E[(Xn-∑i=1maiXn-i)2].

Define the correlation parameter r_k = E[X_nX_n−k] to be the correlation between two samples spaced by k sampling intervals. Then the system of equations in Equation (6.65) can be expressed in matrix form as

(6.72)[r0r1r2…rm-1r1r0r1…rm-2r2r1r0…rm-3…………rm-1rm-2rm-3…r0][a1a2a3…am]=[r1r2r3…rm],

and the predictor coefficients are simply the solution to this set of linear equations.

Example 6.14

Figure 6.4 shows a segment of speech that has a duration of about 2 s, which was sampled at a rate of 8 kHz. From this data, (using MATLAB) we estimated the correlation parameters r_k = E[X_nX_{n + k}]; found the linear prediction coefficients, a_i, i = 1,2, …, m, and then calculated the mean squared estimation error, MSE = E[(X_n − Y_n)²]. The results are shown in Table 6.1. We should note a couple of observations. First, even with a simple one-tap predictor, the size of the error signal is much smaller than the original signal (compare the values of MSE with r₀ in the table). Second, we note that (for this example) there does not seem to be much benefit gained from using more than two previous samples to form the predictor.

Figure 6.4. Speech segment used in Example 6.7. (For color version of this figure, the reader is refered to the web version of this chapter.)

Table 6.1. Results of linear prediction of speech segment form Figure 6.4

r₀ = 0.0591 r₁ = 0.0568 r₂ = 0.0514 r₃ = 0.0442 r₄ = 0.0360
m = 1	a₁ = 0.9615				MSE = 0.004473
m = 2	a₁ = 1.6564	a₂ = −0.7228			MSE = 0.002144
m = 3	a₁ = 1.7166	a₂ = −0.8492	a₃ = 0.0763		MSE = 0.002132
m = 4	a₁ = 1.7272	a₂ = −1.0235	a₃ = 0.4276	a₄ = −0.2052	MSE = 0.002044

Finally, in Figure 6.5 we compare the quality of the encoded speech as measured by the SQNR for PCM and the DPCM scheme of Figure 6.3 using the two-tap predictor specified in Table 6.1. For an equal number of bits per sample, the DPCM scheme improves the SQNR by more than 20 dB. Alternatively, the DPCM scheme can use 3 bits/sample fewer than the PCM scheme and still provide better SQNR.

Figure 6.5. SQNR comparison of PCM and DPCM speech coders for the speech segment in Figure 6.4. (For color version of this figure, the reader is refered to the web version of this chapter.)

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123869814500096

Источник

Время на прочтение
15 мин

Количество просмотров 16K

Продолжаем цикл статей, посвященных задаче изменения человеческого голоса, над решением которой мы работаем в компании i-Free. В предыдущей статье я попытался кратко рассказать о математическом аппарате, применяемом для описания сложных физических процессов, происходящих в речевом тракте человека при произнесении звуков. Были затронуты вопросы, связанные с моделированием акустики речевого тракта. Были описаны допустимые во многих случаях упрощения и аппроксимации. Итогом статьи было приведение физической модели распространения звука в речевом тракте к простому дискретному фильтру.

В данной статье хочется с одной стороны продолжить предыдущие начинания, а с другой — немного отойти от фундаментальной теории и поговорить о более практических (более «инженерных») вещах. Кратко будет рассмотрена одна из прикладных моделей, часто применяемая при работе с речевым сигналом. Математическая база этого подхода, как это часто бывает, изначально была заложена в рамках исследований совершенно другой направленности. Тем не менее физические особенности речевого сигнала позволили применить данные идеи именно для его эффективного анализа и модификации.

Предыдущая статья, в силу специфики рассматриваемого вопроса, была перенасыщена научными терминами и формулами. В данной — мы постараемся вместо детального описания математических построений сделать акцент на идеологическую концепцию и качественные характеристики описываемой модели.

Далее будет более подробно рассмотрена теория модели LPC (Linear Prediction Coding) – замечательный стройных подход к описанию речевого сигнала, в прошлом определивший направление развития речевых технологий на несколько десятилетий и до сих пор часто применяемый, как один из базовых инструментов при анализе и описании речевого сигнала.

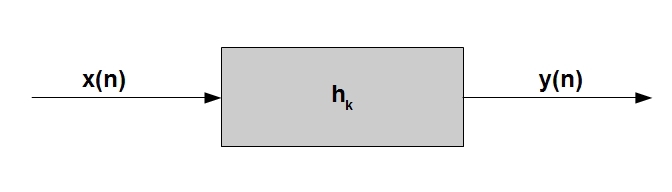
В данном пункте мы сделаем переход от дискретной модели речевого тракта из прошлой статьи, (та модель описывала только распространение звука в трубах с постоянной площадью поперечного сечения), к более полной модели, описывающей весь артикуляционный процесс. Основная идея модели формулируется достаточно просто — представим себе, что анализируемый нами дискретный сигнал y(n)* является выходом линейного цифрового фильтра** h, через который проходит некоторый «возбуждающий» сигнал x(n):
_____________________________
* — здесь и далее мы будет говорить только о дискретных сигналах и переменную времени t будем заменять на индекс дискретного отсчета n
** — сразу приносим извинения за некоторые ссылки на англоязычные источники, но нередко в них требуемый вопрос раскрыт более полно и в одном месте, надеемся языковой барьер не будет большой преградой.

Логично предположить, что, изменяя коэффициенты фильтра h_k, а, возможно, в некоторых случаях сам «возбуждающий» сигнал, можно добиться другого звучания выходного звука*. На словах все весьма просто, но теперь попробуем разобраться, какое отношение эта совершенно абстрактная обобщенная идея может иметь к речевому сигналу.
_____________________________
* — как и в предыдущей статье, символом « _ » мы будем обозначать операцию индексирования, а символом « ^ » — операцию возведения в степень.

Кратко напомним, а заодно немного обобщим рассказанное в самой первой статье. Формирование звуков речи можно, с небольшими оговорками, описать следующим образом:

1) голосовая щель в гортани является «базовым» источником звука (здесь с участием голосовых связок порождается тот самый вокализованный или невокализованный сигнала возбуждения из 1-й статьи)

2) органы речевого тракта выше гортани являются одним сложным акустическим фильтром, усиливающим одни и ослабляющим другие частоты

3) «последний штрих» к конечному звуку добавляет процесс излучения звуковых волн ртом или носом

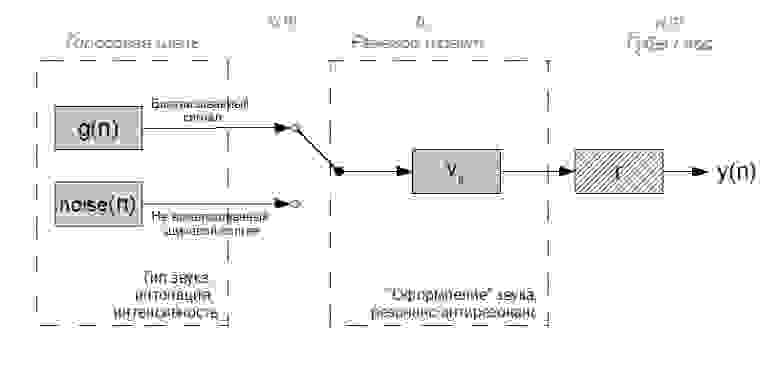
Последний пунктом можно в некотором роде пренебречь, т.к. данное преобразование над сигналом можно аппроксимировать дифференцированием и, соответственно, сравнительно просто обратить его воздействие на сигнал. С первыми двумя история несколько сложнее. Оба данных процесса не стационарны во времени. При генерации вокализованного сигнала возбуждения, период смыкания и степень смыкания складок голосовой щели в гортани непрерывно меняется, что порождает изменение в длительности и в форме «гортанных» воздушных импульсов: как следствие, меняется интонация и интенсивность звука, эмоциональный окрас речи. Речевой тракт выше гортани является одним большим подвижным акустическим фильтром, его камеры и смычки, изменяя свою геометрию, меняют положение резонансных (формантных) и антирезонансных частот — меняется тип произносимого вокализованного звука с точки зрения фонетики. При произнесении невокализованного звука голосовые складки не работают, и гортань является источником шумового сигнала. Работа остального речевого тракта при этом принципиально не меняется и, как следствие, спектр шумных звуков речи также имеет формантную структуру, хоть и несколько менее «заметную». Сказанное выше можно проиллюстрировать следующей упрощенной схемой:

Соответствующие элементы из 1-го рисунка обозначены серым шрифтом вверху.

В реальной жизни существует масса нюансов и механизмов взаимного влияния речевого тракта на гортань и наоборот, а также дыхательного аппарата на всю аккустику речевого тракта в момент, когда речевая щель разомкнута. Однако рассматривая несколько «идеализированные» процессы, можно сказать, что данный рисунок адаптирует предыдущую абстрактную идею «возбуждающий сигнал — фильтр — звук» к артикуляции звуков речи и при этом достаточно хорошо учитывает основные свойства реального речевого сигнала.

Преимущества, которые дает данный взгляд на процесс звукообразования:

— возможность рассматривать сигнал возбуждения речевого тракта и его дальнейшее распространение по речевому тракту независимо друг от друга (в действительности они все-таки взаимосвязаны, однако данная взаимосвязь не всегда ярко выражена и в некоторых случаях ей можно пренебречь)

— возможность анализа речевого тракта как линейной стационарной (на коротких временных интервалах) системы

— возможность хорошо аппроксимировать большинство звуков в речевом сигнале

Конечно, как это всегда бывает в реальной жизни, данный упрощенный подход не так прост для практического применения. Множество неопределенностей возникает даже на этапе разбиения анализируемого сигнала на вокализованные/невокализованные сегменты. Только для этой задачи в общем случае требуется непростая обработка сигнала с привлечением серьезного мат. аппарата. Следующим сложным моментом является нестационарность рассматриваемых процессов, и при этом x(n) меняется гораздо более стремительно, нежели h(n). Для получения достоверных оценок параметров данной модели наиболее оптимальной является обработка сигнала на временных сегментах, длительность которых кратна периоду основного тона, что не просто, с учетом того, что этот период постоянно меняется. Также стоит упомянуть ограниченную применимость данной модели для описания некоторых согласных звуков, в частности фрикативных и «взрывных». При произнесении звонкого фрикативного звука, вокализованный возбуждающий сигнал проходит через значительное сужение в той или иной части речевого тракта, что приводит к формированию сильного турбулентного шума. Глухой фрикативный произносится аналогично, с тем различием, что возбуждающий сигнал изначально шумовой. Таким образом, шумовая составляющая фрикативных звуков в значительной мере формируется уже в речевом тракте, а не только в гортани, что не учитывается данной моделью. «Взрывные» звуки — особый случай, рассмотрение которого мы пока что опустим.

Перейдем теперь от обобщенной дискретной модели к конкретным прикладным моделям, позволяющим оценить те или иные параметры речевого сигнала.

Метод LPC бесхитростно подходит к описанной выше обобщенной дискретной модели речевого сигнала. А именно — LPC-коэффициенты непосредственно описывают речевой тракт V (см. предыдущий рисунок). Данное описание конечно же не является исчерпывающим и является некой аппроксимацией реальной акустической системы. Однако, как утверждается теорией, и как многократно доказано практикой (взять хотя бы алгоритмы CELP, применяемые в современных сетях сотовой связи), эта аппроксимация является вполне достаточной для многих и многих случаев. Белым пятном в LPC-модели остается сигнал возбуждения речевого тракта, который на практике либо никак существенно не меняется, либо, например, заменяется на какой-либо заранее рассчитанный, как в CELP.

Опишем более формально, какое именно место занимают LPC-коэффициенты в рассматриваемой системе. Cигнал на входе речевого тракта (на выходе голосовой щели) будем далее обозначать как g[n]. Пока что не будем заострять внимание на природе этого сигнала – шумовой или гармонической. Сигнал на выходе дискретного фильтра, которым мы аппроксимируем речевой тракт будем обозначать v[n]. LPC-модель таким образом решает обратную задачу — мы будем искать g[n], а также параметры фильтра, который превратил g[n] в v[n], имея в своем распоряжении только v[n].

Вспомним предыдущую статью, и описываемую в ней идею представления речевого тракта последовательностью соединенных труб. Главным результатом подобного подхода является удобное представление речевого тракта в виде дискретного фильтра (системы, состоящей из операций сложения/умножения/задержки). С помощью алгебраических преобразований возможно вывести из разностных уравнений, описывающих подобную модель, ее передаточную характеристику вида:

где G – некоторый сложный многочлен, зависящий от коэффициентов отражения r_k, a_k — некоторые действительные коэффициенты, также зависящие от r_k, P – количество труб в рассматриваемой модели. Поскольку мы рассматриваем сигнал на коротких временных интервалах, справедливо предположить «неподвижность» речевого тракта во время анализа, и, соответственно, постоянные значения площадей сочлененных труб, которыми мы аппроксимируем речевой тракт (см. предыдущую статью). Исходя из этого, коэффициенты отражения r_k мы полагаем постоянными, что, в частности, приводит к постоянному значению многочленов G и a_k на анализируемом сегменте речи.

Алгебру приведения разностных уравнений, описывающих состояние каждой трубы в составе речевого тракта (см. предыдущую статью), к данному простому на вид уравнению мы приводить не будем по понятным причинам. Само же данное уравнение представляет собой важный фундаментальный результат — при рассмотрении речевого тракта как системы сочлененных труб возможно привести его к виду линейной стационарной системы (ЛТС), а именно к БИХ-фильтру, содержащему только полюсы (забегая вперед сразу скажем, что эти полюсы и соответствуют так «горячо любимым» нами формантным частотам). Схема работы подобной системы изображена ниже:

Используя указанную выше передаточную характеристику речевого тракта, можно показать, что сигнал на выходе системы имеет нижеследующий вид во временной области:

Весьма интересный результат: сложный процесс звукообразования в речевом тракте сводится к тому, сигнал на выходе системы в момент времени n является суперпозицией входного сигнала в момент n, домноженного на константу, и линейной комбинации предыдущих выходных отсчетов в моменты n — 1, n — 2 … n — p. Но не будем забывать, что это конечно же всего лишь аппроксимация, игнорирующая многие детали.

Чтобы получить описание состояния речевого тракта на анализируемом сегменте речи, необходимо решить задачу оценки коэффициентов a_k и G. Теория адаптивной фильтрации в целом, и модель LPC в частности, позволяют решить данную задачу сравнительно просто и вычислительно эффективно. Полученное описание речевого тракта будет далеко не исчерпывающим, но достаточным для многих задач.

Для решения задачи оценки коэффициентов a_k удобно ввести понятие фильтра линейного предсказания, задача которого получить достоверные оценки искомых коэффициентов (оценки будем далее обозначать как a’_k). Выход фильтра предсказания (v'(n)) можно вычесть из сигнала на выходе речевого тракта (полученную разность будем далее называть «сигнал-ошибка»):

e(n) — сигнал-ошибка. Коэффициенты a’_k вместе с G и называют коэффициентами линейного предсказания, LPC-коэффициентами. В случае, когда оценки a’_k близки к истинным значениям a_k, e(n) будет стремиться к G∙g(n). Отметим, что фильтр линейного предсказания является в данной задаче обратным фильтром к нашей аппроксимации речевого тракта. Если оценки a’_k близки к истинным a_k, то данный фильтр (обозначим как v^(-1)_k) способен обратить воздействие речевого тракта на сигнал g(n) с точностью до константы G:

Вернемся к оценкам a’_k. Выбрав некий сегмент сигнала для анализа (предположим длины M), с помощью выражения (3) можно получить вектор сигнала-ошибки аналогичной длины. Вопрос — как теперь имея данный вектор сформировать состоятельные оценки a’_k? Данную задачу можно решить, применяя метод наименьших квадратов. Для этого производится поиск минимума функции E_n, значение которой равно среднему от суммы квадратов значений сигнала-ошибки на некотором анализируемом временном интервале (функция E_n является ничем иным, как среднеквадратическай ошибкой). Другими словами — ищутся такие параметры a’_k, при которых функция среднеквадратической ошибки E_n принимает минимальное значение. Сама среднеквадратическая ошибка в нашем случае выражается формулой:

Нахождение среднего подразумевает деление на количество элементов (умножение на 1/М), однако данный множитель никак не повлияет на решение искомой системы, поэтому его можно опустить.

Ещё раз для ясности опишем, что выражает формула (4):

1) в окрестности момента времени ‘n’ берется M отсчетов сигнала (как правило, от n до n + M – 1).Число М зависит от частоты дискретизации сигнала и о наших предположениях о длине интервала стационарности этого сигнала.

2) Для выбранных отсчетов составляется выражение, соответствующее ошибке предсказания e(m), m = n: n+M-1

3) Находится среднее от квадратов e(m) (в выражении для среднего опускаем деление на количество членов суммы).

4) Полученное среднее E_n (являющееся функцией от номера отсчета n) мы и будем минимизировать.

Почему в качестве меры достоверности нашего фильтра предсказания применяется именно среднеквадратическая ошибка? Во-первых, она является неплохой численной аппроксимацией дисперсии случайного процесса в некоторых случаях. Если предположить, что наша ошибка распределена нормально и наш фильтр предсказания не сильно смещен, то среднеквадратическая ошибка будет стремиться к дисперсии D[e(m)] и мы, таким образом, ищем минимум дисперсии нашего сигнала-ошибки. Во-вторых (правда, это скорее не причина, а удобное следствие), данную функцию весьма удобно дифференцировать по искомым a’_k, а именно с помощью дифференцирования удобно искать минимум функции.

Раскрыв знак квадрата под суммой в (4) и приравняв нулю значения производных E_n по каждому a’_k, возможно получить систему из P линейных уравнений вида:

Подробный вывод (5) из (4) приводить также не будем — для этого нужно применить несколько формул из школьной алгебры и некоторые формулы для преобразования определенных сумм. Система уравнений (5) является «основным ядром» в алгоритме LPC. Индекс i соответствует номеру уравнения в системе (номеру a’_k, по которому брали производную) и, так же, как и индекс k, проходит все значения от 1 до P. Напомним, что P соответствует числу труб в модели, аппроксимирующей речевой тракт. Это же число называют порядком линейного предсказания. Решение систем линейных алгебраических уравнений — отдельная прикладная область со своим математическим аппаратом, поэтому в данную задачу углубляться мы не будем. Скажем лишь, что для решения конкретно системы (5) с учетом её свойств как правило применяют разложение Холецкого или рекурсию Левинсона-Дарбина

Решив систему из P уравнений от P неизвестных, мы получаем оценки a’_k, и остается только найти коэффициент усиления G. В методе LPC оценка G находится после оценки a’_k, исходя из предположения, что сигнала на входе фильтра V является либо смещенной в момент времени n дискретной дельта-функцией (единичный импульс в момент n), либо белым шумом. В обоих случаях G можно найти из соотношения:

Сам вывод этой формулы исключительно математический (что в случае дельта-функции, что в случае белого шума) и как объяснить популярно физический смысл данной формулы автор статьи не представляет — оставим её как есть. Однако само предположение, что входной сигнал вдруг стал единичным импульсом или белым шумом стоит объяснить более подробно.

Строго говоря, на выходе голосовой щели в гортани — на входе речевого тракта, мы имеем либо «гортанный» импульс, либо окрашенный шумовой сигнал, но никак не дельта-функцию или белый шум. И вот тут в теории LPC делается весьма хитрый «финт ушами». Мы воображаемо представляем гортань частью речевого тракта и говорим, что вот именно в гортань-то якобы входил как раз либо единичный импульс, либо белый шум. Понятие речевого тракта, таким образом, несколько расширяется в рамках нашей модели, и чтобы учесть новой моделью эффекты, которые делают из единичного импульса «гортанный» импульс, а из белого шума окрашенный шум, мы увеличиваем порядок линейного предсказания P. Более того, мы идем дальше и включаем в наш «LPC-фильтр» эффекты, связанные с излучением сигнала, что также компенсируем добавлением дополнительных коэффициентов. Данные операции соответствуют увеличению длины нашего полюсного фильтра, которым мы аппроксимируем речевой тракт, что приведет к росту числа его полюсов, и именно эти дополнительные полюсы отвечают за означенное выше воображаемое превращение. Очевидно, что в таком случае модель LPC уже не вполне соответствует изначальному дискретному фильтру, аппроксимирующему речевой тракт. Однако идеологически эти два подхода остаются весьма близкими, если не сказать «родственными». Восстановить с помощью LPC сигнал возбуждения речевого тракта g[n], в том виде, как мы этого хотели вначале, не представляется возможным. Тем не менее, итоговая аппроксимация частотной характеристики речевого тракта (коэффициенты a’_k), полученная с помощью LPC, достаточно точна для многих задач.

Раз заговорили о выборе порядка P, логично дать какие-то общие рекомендации по его выбору. Считается, что в среднем формантные частоты в речевом сигнале располагаются с плотностью примерно 1 форманта на килогерц. Тогда, поскольку каждый комплексный полюс нашего модельного фильтра соответствует одной формантной частоте, удобно выбирать порядок, как:

где [] — округление до ближайшего целого числа, Fs — частота дискретизации сигнала в герцах. Для компенсации эффекта совмещения гортани и речевого тракта, а также для учета в модели эффекта излучения сигнала губами/носом, различные источники рекомендуют увеличить P дополнительно на 2-4 коэффициента. Т. е. для работы, например, с 10 КГц сигналом, порядок P можно выбрать равным 12-14 коэффициентов. Некоторые авторы также советуют применять плотность «1 форманта на 1200-1300 Гц», когда анализируется женский голос. Это связано с меньшей длиной речевого тракта у женщин и, как следствие, более высокими значениями формантных частот в женских голосах.

Что в итоге нам дает расчет LPC-коэффициентов для некоторого сигнала:

1) Выходом алгоритма расчета LPC является набор числовых коэффициентов, которые описывают полюсный фильтр. Данные коэффициенты в чистом виде позволяют получить выражение для выхода данного фильтра во временной области (выражение (2)), а также общий вид его z-характеристики (выражение (1)). Поскольку данный фильтр является полюсным, то в его основе лежит рекурсия и выразить импульсную характеристику для такого фильтра не представляется возможным. С помощью z-характеристики, тем не менее, возможен полноценный анализ полученного фильтра как во временной, так и в частотной областях.

2) Если разложить на множители знаменатель полученной z-характеристики, становится возможным найти численные значения частот, соответствующих полюсам данного фильтра. Эти же значения хорошо аппроксимируют формантные частоты речевого тракта на анализируемом сегменте речи. (Правда стоит добавить, что точность аппроксимации зависит от грамотного выбора базовых параметров LPC — порядка P, длительности анализируемого интервала M, времени начала анализа n. Для общего случая автоматизировать этот выбор не так просто.)

3) Полученный с помощью LPC сигнал-ошибка (сигнал возбуждения дискретного фильтра, которым мы аппроксимируем процесс звукообразования) выходит похожим либо на белый шум, либо на смещенную во времени дельта-функцию. (данный пункт наиболее активно эксплуатируется при сжатии речи)

Ниже для примера приведен логарифмический спектр сигнала, полученный обычным БПФ, и с помощью LPC. Обрабатывалась гласная «А», произнесенная мужским голосом.

Как видно, «LPC-спектр» является некоторой сглаженной версией обычного «БПФ-спектра». При этом формантные частоты проявляются «яркими» локальными максимумами, что является хорошим «стартом» для их обнаружения и слежения за ними.

Как было сказано в предыдущей статье, при представлении речевого тракта в виде сочлененных труб фиксированного диаметра возможно аппроксимировать процессы, происходящие внутри каждой трубы при распространении по тракту звука, с помощью разностных уравнений. При этом уравнения будут зависеть от коэффициентов отражения r_k, где k – номер рассматриваемой трубы. Данные коэффициенты в свою очередь зависят от отношения площади рассматриваемой трубы к площади следующей за ней трубы. Граничные условия (первая труба после гортани и последняя перед губами) берутся из особых формул, зависящих от соответствующих акустических импедансов, которые в свою очередь могут в большинстве случаев быть табличными функциями. Ранее в статье без доказательства приводился тот факт, что из совокупности дискретных разностных уравнений, описывающих такую систему, можно вывести соотношение (1), которое можно принять удобной отправной точкой LPC-анализа.

Сам по-себе LPC-анализ – достаточно «прямолинейный» и эффективный метод. Сразу может появиться вопрос, а возможно ли, рассчитав LPC-коэффициенты некоторого сигнала, каким-то образом восстановить параметры речевого тракта? На данный вопрос нельзя дать на 100% положительный ответ. С одной стороны, LPC-коэффициенты являются многочленами от r_k, и практически возможно проделать обратную операцию – восстановить r_k из a’_k. Для этого можно применить переходный этап в виде PARCOR (partial correlation) коэффициентов. Т. е. из LPC-коэффициентов рассчитать PARCOR-коэффициенты, а уже из них r_k. Однако есть одно осложняющее обстоятельство: в модель LPC включаются эффекты, связанные с прохождением сигнала через гортань и его излучением в районе губ, что никак не соответствует модели речевого тракта в виде дискретного фильтра из предыдущей статьи (число труб в модели речевого тракта уже не равно порядку линейного предсказания P). В случае, если каким-то образом обратить воздействие на сигнал гортани и излучения, и проводить LPC-анализ этого модифицированного сигнала, то возможно получить более состоятельные оценки коэффициентов отражения на основе LPC. Опять же стоит помнить, что даже в таком случае, коэффициенты отражения могут показать лишь отношения площадей соседствующих труб в модели речевого тракта — не имея никаких начальных приближений, не удастся восстановить абсолютные значения площадей. Т. е. мы сможем восстановить некоторую функцию, повторяющую площадь речевого тракта, однако отличающуюся от неё на некоторый масштабирующий множитель.

Существует немало работ, авторы которых решают задачу восстановления функции площади речевого тракта, и в данных работах LPC-коэффициенты занимают не последнее место в используемом математическом инструментарии. В частности, LPC нередко применяется в качестве базового метода для определения значений формантных частот, с помощью которых уже восстанавливается функция площади речевого тракта.

Сам по себе подход к анализу площади речевого тракта с помощью LPC имеет множество погрешностей, связанных с допущениями, которые мы изначально делаем, полагая в качестве модели речевого тракта линейный дискретный фильтр — об этом много было сказано в предыдущей статье. Исследования на данную тему велись и ведутся, неплохие результаты достигнуты, но действительно точно восстановить функцию площади речевого тракта на сегодняшний день в общем случае невозможно, ни с применением LPC, ни с помощью каких-либо принципиально иных подходов.

В данной статье кратко описаны основные идеи и идеология LPC-модели представления речевого сигнала. Данная модель является одной из наиболее часто применяемых в области обработки речи и, несмотря на свои фундаментальные ограничения, дает весьма неплохие оценки реальных физических феноменов. Наиболее часто данная модель применяется для задач:

— сжатия речи

— анализа формантных частот

— анализа речевого тракта (в качестве вспомогательного инструмента)

В следующей статье мы расскажем про HPN-модель (Harmonics-plus-noise) речевого сигнала, в рамках которой речевой сигнал в явном виде разделяется на вокализованную и невокализованную составляющие.

Использованная литература:
[1] J.L. Flanagan. Speech Analysis, Synthesis and Perception.
[2] L.R. Rabiner, R.W. Schafer, Digital Processing of Speech Signals // (основной первоисточник данной статьи)
[3] Солонина И.А. Основы цифровой обработки сигналов, 2-е издание // (хорошее краткое, но немного «сухое» объяснение, как инструкция к применению )
[4] Mark Hasegawa-Johnson, Lecture Notes in Speech Production, Speech Coding, and Speech Recognition
[5] G. Fant. Speech Acoustics and Phonetics. Selected Writings.

Источник

Введение

Одной из задач такого обширного раздела как ВлЦифровая обработка речевых сигналовВ», входящего в состав науки, занимающейся цифровой обработкой сигналов или просто обработкой сигналов является сжатие или кодирование речевого сигнала (РС). Сжатие РС может быть как без потерь (архивация), так и с потерями. Причем в последнем случае это кодирование можно подразделить на три вида:

кодирование непосредственно реализации РС (Wave Form Codec);
измерение, кодирование и передача на приемную сторону параметров РС, по которым уже на приемной стороне производится синтез этого (искусственного) РС. Такие системы называют вокодерными (Source Codec);
гибридные способы кодирования, т.е. сочетание первого и второго способов кодирования. В задачу данной работы входит рассмотрение первого способа кодирования.

Под кодированием подразумевается преобразование РС в некоторый ВлдругойВ» сигнал, который можно представить с меньшим числом разрядов, что в итоге повысит скорость передачи данных. Одним из видов такого кодирования является дифференциальная импульсно-кодовая модуляция (ДИКМ), о которой и пойдет речь в дальнейшем.

Дифференциальная импульсно-кодовая модуляция

В обычной импульсно-кодовой модуляции каждый отсчет кодируется независимо от других. Однако у многих источников сигнала при стробировании с частотой Найквиста или быстрее проявляется значительная корреляция между последовательными отсчетами [1] (в частности, источник РС является квазистационарным источником и может относиться к рассматриваемым видам источников). Другими словами, изменение амплитуды между последовательными отсчетами в среднем относительно малы. Следовательно, схема кодирования, которая учитывает избыточность отсчетов, будет требовать более низкой битовой скорости.

Суть ДИКМ заключается в следующем. Предсказывается текущее значение отсчета на основе предыдущих M отсчетов. Для конкретности предположим, что означает текущий отсчет источника, и пусть обозначает предсказанное значение (оценку) для , определяемое как

Таким образом, является взвешенной линейной комбинацией M отсчетов, а являются коэффициентами предсказания. Величины выбираются так, чтобы минимизировать некоторую функцию ошибки между и . Проиллюстрируем вышесказанное на отрезке РС:

Прежде чем идти дальше, рассмотрим виды предсказания. ВлЛинейноеВ» предсказание означает, что является линейной функцией предыдущих отсчетов; при ВлнелинейномВ» предсказании тАУ это нелинейная функция. Порядок предсказания определяется количеством используемых предыдущих отсчетов. То есть, предсказание нулевого и первого порядка является линейным, а второго и более высокого порядка — нелинейным. При линейном предсказании восстановить сигнал значительно проще, чем при нелинейном предсказании. Будем рассматривать только линейное предсказание.

Виды линейных предсказаний

Предсказание нулевого порядка.

В этом случае для предсказания текущего отсчета используется только предыдущий отсчет РС, т.е.

Предсказание первого порядка (линейная экстраполяция).

В этом случае для предсказания текущего отсчета используется не только предыдущий отсчет, но и разница между предпоследним и последним отсчетами, которая суммируется к общему результату:

Коэффициенты линейного предсказания (получение и расчет)

Формирование сигнала ошибки при использовании линейного предсказания эквивалентно прохождению исходного сигнала через линейный цифровой фильтр. Этот фильтр называется фильтром сигнала ошибки (ФСО) или обратным фильтром.

Обозначим передаточную функцию такого фильтра как А(z):

где E(z) и X(z) тАУ прямое z — преобразование от сигнала ошибки и входного сигнала соответственно.

На приемной стороне при прохождении сигнала ошибки через формирующий фильтр (ФФ) мы в идеале получим исходный сигнал. Обозначим передаточную функцию формирующего фильтра как K(z).

Т.е. передаточная функция K(z) связана с A(z) следующим соотношением:

Рассмотрим последовательно соединенные кодер и декодер:

При условии, что A(z)K(z) = 1, будет обеспечено абсолютно точное восстановление сигнала, т.е. . Но это в идеале, на самом деле такого быть не может по причинам, о которых скажем ниже.

Для примера, найдем передаточные функции ФСО и ФФ для разных типов линейного предсказания.

а) предсказание нулевого порядка;

; ;

Получили, что такой фильтр неустойчив (граница устойчивости), так как полюс находится на единичной окружности.

б) предсказание первого порядка;

;;

Получили, что и такой фильтр тоже неустойчив (граница устойчивости).

в) общая форма предсказания;

Было получено, что => .

; ;

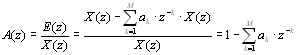
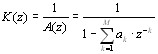
На основании рассмотренных примеров можно сделать следующие выводы.

Фильтр сигнала ошибки всегда является КИХ фильтром, а формирующий фильтр тАУ БИХ фильтром. Коэффициенты передаточной функции ФФ, которые, как уже было сказано выше, являются коэффициентами линейного предсказания (LPC: Linear Prediction Coefficients), должны быть такими, чтобы:

формирующий фильтр был устойчивым;
ошибка была минимальна.

Для получения передаточной функции ФФ, наиболее точно воспроизводящего частотную характеристику голосового тракта для данного звука, следует определять коэффициенты передаточной функции исходя из условия наименьшей ошибки линейного предсказания речевого сигнала (по условию минимума среднего квадрата ошибки).

Запишем выражение для оценки дисперсии сигнала ошибки, которую надо свести к минимуму:

; ;

Получили, что — функция нескольких переменных. Продифференцируем ее и приравняем частные производные для нахождения экстремума:

; ,

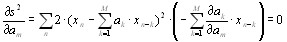
где — символ Кронекера. Следовательно: ;

; => ;

Получили нормальные уравнения или уравнения Юла-Волкера. Введем обозначение: , где — есть ни что иное, как корреляционная функция. Перепишем полученное выражение с учетом принятого обозначения:

(*)

Для вычисления функции необходимо определить пределы суммирования по n: , где N тАУ количество отсчетов в сегменте РС, а M — количество отсчетов, необходимых для расчета коэффициентов предсказания (M + 1)-го отсчета. Значит, первое предсказанное значение запишется так: , где n = M + 1.

Получили:

;

Обозначим n тАУ k = j => n = k + j, n тАУ m = k + j тАУ m <=> n тАУ m = i + j, где i = k тАУ m. Следовательно:

Таким образом, получается выражение, имеющее структуру кратковременной ненормированной АКФ, но зависящей не только от относительного сдвига последовательности i, но и от положения этих последовательностей внутри сегмента РС, которые определяются индексом k, входящим в пределы суммирования. Такой метод определения функции называется ковариационным.

Выражение (*) представляет собой систему линейных алгебраических уравнений (СЛАУ) относительно , у которых все коэффициенты различны.

При использовании ковариационного метода получаются несмещенные оценки коэффициентов линейного предсказания, то есть E{ak}= ak.ист, где ak.ист тАУ истинные значения коэффициентов линейного предсказания.

Другой способ определения коэффициентов системы (*) состоит в том, что вместо функции используется некоторая другая функция , которая определяется как

где — ненормированная кратковременная АКФ. Поскольку определение функции сводится к расчету АКФ, то такой метод называется автокорреляционным. При использовании этого метода мы получаем смещенные оценки коэффициентов линейного предсказания (однако, при M << N смещение пренебрежимо мало).

Перепишем СЛАУ (*) с учетом введенной функции :

При использовании автокорреляционного метода вся информация о сигнале, необходимая для определения коэффициентов линейного предсказания, содержится в кратковременной ненормированной АКФ B(i).

Распишем полученную систему линейных алгебраических уравнений (СЛАУ) в явном виде:

Перепишем ее в матричной форме:

;

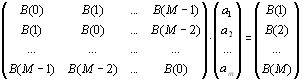
Свойства матрицы коэффициентов системы:

матрица симметрична;
матрица Теплица (матрица, в пределах каждой диагонали которой все элементы равны);

Для решения СЛАУ с такой матрицей используется алгоритм Левинсона тАУ Дурбина, который требует меньших вычислительных затрат, чем стандартные алгоритмы. Он выглядит следующим образом.

Начальные значения для алгоритма:

Алгоритм:

Решетчатый фильтр сигнала ошибки предсказания

В предыдущем разделе приводилась процедура вычисления коэффициентов предсказания Левинсона-Дурбина. В этой процедуре, как промежуточные величины, используются некоторые коэффициенты km, которые называются коэффициентами отражения. Их физический смысл заключается в следующем. Голосовой тракт человека представляет собой трубу, состоящую из секций, соединенных последовательно, но имеющих разный диаметр. При прохождении звуковой волны через такую систему, возникают отражения на стыках секций, т.к. каждый стык является неоднородностью. Коэффициент отражения характеризует величину проходимости стыка двух секций (сред). Коэффициент отражения равен:

Поясним его смысл на следующем рисунке (ВлжирнымВ» показана m тАУ секция голосового тракта):

Если rm = -1, то произойдет обрыв в цепи передачи сигнала (обрыв прямой ветви). Такого быть не должно, поэтому необходимо следить за этим.

Модель акустических труб может быть представлена в виде фильтра, имеющего решетчатую (или лестничную) структуру. Основными параметрами такого фильтра являются коэффициенты отражения.

Система акустических труб тАУ резонансная система, поэтому если фильтр без потерь, то на его АЧХ будут наблюдаться разрывы (всплески в бесконечность). Реально на месте этих всплесков будут резонансные пики, и резонансные частоты таких пиков называются формантными. Обычно в реальных голосовых трактах человека формантных частот (или формант) не более трех. Более подробно о коэффициентах отражения и решетчатых фильтрах можно прочитать в [2, глава 3].

Так как коэффициенты отражения и коэффициенты предсказания вычисляются в рамках одной и той же процедуры алгоритма Левинсона-Дурбина, то они могут быть выражены друг через друга. Приведем здесь эти алгритмы.

Прямая рекурсия (коэффициенты отражения а коэффициенты предсказания):

Обратная рекурсия (коэффициенты предсказания а коэффициенты отражения):

Как уже было сказано, фильтры сигнала ошибки представляют собой КИХ фильтры или нерекурсивные фильтры, что означает отсутствие ветвей обратной связи. Системы с КИХ также могут обладать строго линейной ФЧХ. Линейность ФЧХ является очень важным обстоятельством применительно к РС в тех случаях, когда требуется сохранить взаимное расположение элементов сигнала. Это существенно облегчает задачу их проектирования и позволяет уделять лишь внимание аппроксимации их АЧХ. За это достоинство приходится расплачиваться необходимостью аппроксимации протяженной импульсной реакции в случае фильтров с крутыми АЧХ [2].

Изобразим граф фильтра, имеющего решетчатую структуру, на примере фильтра 3тАУго порядка:

В отличие от формирующего фильтра этот фильтр имеет один вход и два выхода:

1) ei тАУ последовательность отсчетов сигнала ошибки прямого линейного предсказания;

2) bi тАУ последовательность отсчетов сигнала ошибки обратного линейного предсказания.

Важность bi определяется тем, что по нему совместно с сигналом ошибки ei могут быть оценены коэффициенты отражения.

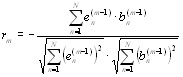
где N тАУ количество отсчетов в сегменте.

Полученная формула для расчета коэффициентов отражения имеет также другой физический смысл. Это не что иное, как коэффициент корреляции между последовательностью отсчетов сигнала ошибки прямого и обратного линейных предсказаний.

Приведем также рекуррентные разностные уравнения решетчатого фильтра сигнала ошибки:

выход фильтра;

Начальные условия для этой рекуррентной процедуры:

Реализация ДИКМ

Имея метод определения коэффициентов предсказания, рассмотрим блок-схему практической системы ДИКМ, показанную ниже.

В этой схеме предсказатель стоит в цепи обратной связи, охватывающей квантователь. Вход предсказателя обозначен . Он представляет собой сигнальный отсчет , искаженный в результате квантования сигнала ошибки. Выход предсказателя равен:

; (**)

Разность является входом квантователя, а обозначает его выход. Величина квантованной ошибки предсказания кодируется последовательностью двоичных символов и передается через канал в пункт приема. Квантованная ошибка также суммируется с предсказанной величиной , чтобы получить .

В месте приема используется такой же предсказатель, как на передаче, а его выход суммируется с , чтобы получить (см. рис. ниже).

Сигнал является входным воздействием для предсказателя и в то же время образует входную последовательность, по которой с помощь ЦАП восстанавливается сигнал x(t). Использование обратной связи вокруг квантователя обеспечивает то, что ошибка в — просто ошибка квантования и что здесь нет накопления предыдущих ошибок квантования при декодировании. Имеем

Следовательно, . Это означает, что квантованный отсчет отличается от входа ошибкой квантования независимо от использования предсказателя. Значит, ошибки квантования не накапливаются.

В рассмотренной выше системе ДИКМ оценка или предсказанная величина отсчета сигнала получается посредством линейной комбинации предыдущих значений , k = 1, 2, тАж, M, как показано в формуле (**). Улучшение качества оценки можно получить включением в оценку линейно отфильтрованных последних значений квантованной ошибки.

Конкретно, оценку можно выразить так:

где {} тАУ коэффициенты фильтра для квантованной последовательности ошибок . Блок-схемы кодера на передаче и декодера на приеме приведены ниже.

Здесь два ряда коэффициентов {} и {} выбираются так, чтобы минимизировать некоторую функцию ошибки , например среднеквадратическую ошибку.

Адаптивная дифференциальная импульсно-кодовая модуляция

Многие реальные источники (например, источники РС), как уже было сказано выше, являются квазистационарными по своей природе. Одно из свойств квазистационарности характеристик случайного выхода источника заключается в том, что его дисперсия и автокорреляционная функция медленно меняются со временем. Кодеры ИКМ и ДИКМ, однако, проектируются в предположении, что выход источника стационарен. Эффективность и рабочие характеристики таких кодеров могут быть улучшены, если они будут адаптироваться к медленно меняющейся во времени статистике источника. Как в ИКМ, так и в ДИКМ ошибка квантования , возникающая в равномерном квантователе, работающем с квазистационарным входным сигналом, будет иметь меняющуюся во времени дисперсию (мощность шума квантования).

Одно улучшение, которое уменьшает динамический диапазон шума квантования, — это использование адаптивного квантователя. Другое тАУ сделать адаптивным предсказатель в ДИКМ. При этом коэффициенты предсказателя могут время от времени меняться, чтобы отразить меняющуюся статистику источника сигнала. И полученная СЛАУ, для решения которой используется алгоритм Левинсона тАУ Дурбина, остается справедливой и с краткосрочной оценкой автокорреляционной функции B(i) (при принятых обозначениях B(i) тАУ уже кратковременная АКФ), поставленной вместо оценки функции корреляции по ансамблю. Определенные таким образом коэффициенты предсказателя могут быть вместе с ошибкой квантования переданы приемнику, который использует такой же предсказатель. К сожалению, передача коэффициентов предсказателя приводит к увеличению необходимой битовой скорости, частично компенсируя снижение скорости, достигнутое посредством квантователя с немногими битами (немногими уровнями квантования) для уменьшения динамического диапазона ошибки , получаемой при адаптивном предсказании.

В качестве альтернативы предсказатель приемника может вычислить свои собственные коэффициенты предсказания через и , где

;

Если пренебречь шумом квантования, эквивалентно . Следовательно, можно использовать для оценки АКФ B(i) в приемнике, и результирующие оценки могут быть использованы в СЛАУ вместо B(i) при нахождении коэффициентов предсказателя. При достаточно большом числе уровней квантования разность между и очень мала. Следовательно, оценка B(i), полученная через , может быть использована для определения коэффициентов предсказателя. Выполненный таким образом адаптивный предсказатель приводит к низкой скорости кодирования данных источника.

Вместо использования блоковой обработки для нахождения коэффициентов предсказателя {}, как описано выше, мы можем адаптировать коэффициенты предсказателя поотсчетно, используя алгоритм градиентного типа, который мы и рассмотрим.

Основное преимущество такого метода адаптации тАУ это отказ от решения СЛАУ, что значительно уменьшает вычислительные затраты.

Запишем оценку среднего квадрата ошибки предсказания:

Изобразим два графика, объясняющих функциональную зависимость в одномерном случае () и в двумерном случае ():

Очевидно, что в общем случае, т.е. при фигура, полученная при двух коэффициентах предсказания, превратится в многомерный параболоид. Цель градиентного метода состоит в том, чтобы найти такой вектор аорt, при котором функция s2 будет иметь наименьшее значение, т.е. после определенных итераций необходимо достичь вершины этого параболоида. Алгоритм такого градиентного метода выглядит так:

где i тАУ номер шага, Ој тАУ шаг алгоритма.

При малом шаге алгоритма мы практически полностью устраняем возможность расхождения алгоритма, но при этом проигрываем в скорости сходимости или в скорости нахождения коэффициентов предсказателя. И наоборот.

Следует сказать, что такой алгоритм сходится при очень большом количестве итераций, в общем случае, при количестве итераций стремящемся к бесконечности. Поэтому необходимо также перед началом вычислений задаться допустимой погрешностью, которая нас может устроить.

Найдем частную производную:

Тогда алгоритм адаптации коэффициентов линейного предсказания примет следующий вид:

Иллюстрации

Ниже приводятся иллюстрации одного из опытов, проделанного в лабораторной работе.

Обрабатываемый сегмент речевого сигнала:

Ошибка предсказания:

Коэффициенты отражения и Импульсная характеристика формирующего фильтра:

Передаточные функции ФФ и ФСО и Диаграмма полюсов:

Полученный (синтезированный) сегмент РС:

Ошибка предсказания:

В проделанной работе проводились исследования влияния разрядности коэффициентов предсказания / отражения и сигнала ошибки на синтезированный сигнал в системе с АДИКМ, полученный по этим величинам на приемной стороне декодером. Как уже ясно из названия коэффициентов, исследовались и сравнивались два типа фильтров: стандартный и решетчатый.

В результате можно сделать следующие выводы.

Решетчатый фильтр всегда устойчив и коэффициенты отражения всегда меньше 1, потому что коэффициенты отражения являются также и коэффициентами корреляции. Устойчивость решетчатого фильтра инвариантна к разрядности коэффициентов отражения. Разрядность коэффициентов отражения сказывается лишь на форме передаточной функции и, как следствие, на диаграмме полюсов и импульсной характеристике, а на форму синтезированного РС влияет очень незначительно, при условии постоянной, довольно высокой (12) разрядности сигнала ошибки.

В случае фиксированной, довольно низкой, разрядности коэффициентов отражения (4) и уменьшающейся разрядности сигнала ошибки до значения (6), ухудшение синтезированного РС незначительно. При числе разрядов меньше (6) уже начинают наблюдаться значительные искажения. Если сравнить эти опыты с опытами, проделанными над стандартным фильтром, то для того же сегмента и при значении разрядности (8), наблюдалась неустойчивость синтезированного фильтра и, как следствие, полное искажение РС.

В случае, если два фильтра были устойчивы и разрядность их коэффициентов, а также разрядность сигнала ошибки была одинаковой, то синтезированный сигнал оказывался идентичным.

Следует также отметить не только влияние разрядности коэффициентов предсказания / отражения на синтезированный сигнал, но и, прежде всего, саму реализацию исходного аналогового РС, как основы, по которой рассчитываются сами коэффициенты. Поэтому необходимо иметь запас по разрядности коэффициентов предсказания, чтобы стандартный фильтр для некоторых реализаций не оказался неустойчив (решетчатый фильтр устойчив в любом случае). Экспериментально был подобран вариант выбора разрядности коэффициентов предсказания (12), а сигнала ошибки (8) (разрядность коэффициентов отражения не играет почти никакой роли). Это достаточно хорошо различимая речь.

Заключение

В данной работе достаточно подробно изложен метод цифрового сжатия речевого сигнала на основе линейного предсказания. Показано, что существуют несколько подходов к решению этой задачи. Приведены иллюстрации из проделанной лабораторной работы со всеми необходимыми комментариями и выводами.

Список литературы

Прокис Дж., ВлЦифровая связьВ», — М: Радио и связь, 2000.
Рабинер Л.Р., Шафер Р.В., ВлЦифровая обработка РСВ», — М: Радио и связь, 1981.
Конспект лекций по курсу ВлЦифровая обработка РСВ», 2004.

Вместе с этим смотрят:

Синтез цифрового конечного автомата Мили
Система бесперебойного электропитания телекоммуникационного узла
Система сжатия и уплотнения каналов
Системы подвижной спутниковой связи на основе низкоорбитальных ИСЗ

Источник

— является функцией только одного параметра комплексного коэффициента

отражения Kp. Приравнивая комплексную производную от ρ pfb к нулю:

d Re{K p }

d Im{K p }