Ошибка первого рода это риск поставщика - Oshibku.top - решение и исправление самых разных ошибок

При
приемке партии продукции контроль может
быть сплошным,
когда
контролируется каждая единица продукции
(например, подшипник, бутылка воды,
моток провода и т.п.). Такой контроль
чаще всего экономически необоснован,
а иногда и невозможен. Более распространен
выборочный
контроль,
когда заключение о качестве партии
продукции делается на основе анализа
выборки ограниченного объема. Выборочный
контроль подразделяется:

по
времени проведения: на входной (закупочный
контроль сырья и полуфабрикатов),
промежуточный (межоперационный) и
выходной (приемка и сертификация готовой
продукции);
по
изменениям в результате контроля: на
разрушающий и неразрушающий (например,
для контроля прочности изделия его
необходимо довести до разрушения);
по
жесткости: на нормальный, усиленный
(более сложный) и облегченный; переход
с одного вида контроля на другой
производится в зависимости от количества
партий, которые были последовательно
приняты, или наоборот, отклонены
потребителем;
по
контролируемому параметру: на
количественный (в этом случае производится
измерение контролируемого показателя
качества продукции) и качественный (в
частности, наиболее распространен
контроль по альтернативному признаку,
когда о каждом контролируемом объекте
делается заключение, годен он или
негоден, соответствует предъявляемым
требованиям или не соответствует).

План
контроля
–
это система правил по отбору изделий
для проверки (формированию выборок) и
принятию решения относительно всей
партии –
партию принять или забраковать.
Забракованная партия или возвращается
поставщику, или производится ее сплошной
контроль. Применение плана статистического
контроля по существу является проверкой
статистической гипотезы H₀:.
качество партии соответствует
предъявляемым требованиям при
альтернативной гипотезе H₁:
качество партии не соответствует
предъявляемым требованиям.

Наиболее
распространен контроль по альтернативному
признаку. Предположим, что в партии из
N изделий имеется М
дефектных
изделий (М
неизвестно).
Требуется оценить генеральную долю
дефектных изделий q
=
M/N.

по
результатам контроля выборки объемом
n
изделий, из которых m
дефектных.

Различают
следующие типы планов контроля:

одноступенчатый:
если
среди п
изделий
число дефектных т
не
превышает приемочное
число с (т < с),
то партия принимается, в противном
случае партия бракуется;
двухступенчатый:
на
первой ступени, если среди n₁
изделий в выборке число дефектных т₁
не
превышает приемочное число с₁
(m
< с₁),
то партия принимается; если т₁
> d₁,
где
d₁
— браковочное число, то
партия бракуется; если же с₁
< m₁<
d₁,
то принимается решение о взятии второй
выборки; на второй ступени объемом
п₂
с
приемочным числом с₂,
если суммарное число дефектных изделий
не превышает с₂
(m₁
+ т₂)
< с₂,
то
партия принимается, в противном случае
партия бракуется;
многоступенчатые
планы
—
обобщение двухступенчатого плана.
Берется выборка объемом п₁
и
определяется число дефектных изделий
т₁;
при
m₁
< с₁,
партия принимается, при с₁
< m₁
< d₁(d₁>
с₁
+ 1) принимается решение о взятии второй
выборки объемом п₂.
Пусть
среди (п₁
+ п₂)
изделий
имеется (m₁
+ т₂)
дефектных,
тогда если (m₁
+ т₂)
< с₂
(с₂
—
приемочное число второй ступени), то
партия принимается, при с₂
< (m₁+
т₂)
< d₂(d₂>
с₂+1),
принимается решение о взятии третьей
выборки, и т.д. На заключительном k-том
шаге,
если среди суммы (п₁
+ п₂
+ +
… + n_k)
проконтролированных
изделий оказалось (т_{
+ т₂
+ + … + т_к)
дефектных
и (т₁+
т₂
+ … + т_к)
с_к,
то
партия принимается, в противном случае
партия бракуется. В многоступенчатых
планах число шагов к
задается
заранее. Обычно п₁
= п₂
= … = п_к.;
последовательный
контроль,
при
котором решение принимается после
оценки ряда выборок, общее число которых
заранее не
устанавливается, а
определяется в процессе контроля по
результатам предыдущих выборок.
Принимается одно из трех решений –
принять партию, забраковать партию,
продолжить контроль.

Оперативная
характеристика плана

Решение
о качестве всей партии изделий принимается
по данным выборочных наблюдений. При
этом существует два вида рисков:

в
выборке оказалось большое число
дефектных изделий, а во всей партии их
доля допустима (партия хорошая, а выборка
плохая). В этом случае годная партия
будет ошибочно забракована –
это ошибка первого рода. Вероятность
такой ошибки α –
риск
поставщика.
Вероятность
приемки партии в этом случае равна (1 –
α);
при
сильной засоренности партии дефектными
изделиями в выборке может оказаться
небольшое количество дефектов (партия
плохая, а выборка хорошая) и партия
будет ошибочно принята –
ошибка второго рода. Вероятность такой
ошибки β
–
риск
потребителя.

Требуется
дать заключение о качестве партии
продукции на основе доли дефектов q
(групповой
показатель качества продукции).
Предположим, что задано нормативное
значение этого показателя q₀,
обозначаемое
в стандартах NQL:
NQL
= q₀(Normative
Quality
Level).
Нормативный
уровень несоответствий NQL
–
это граничное значение уровня
несоответствий: партия продукции
считается годной к поставке и к
использованию потребителем по назначению,
если фактический уровень несоответствий
не превышает нормативного значения
NQL.

Тогда
задача состоит в проверке гипотезы о
том, что доля дефектных изделий q
в
партии равна допустимой величине q₀,
т.е.
Н₀:
q
= q₀
и
при этом сделать риски поставщика и
потребителя маловероятными.

Основной
вероятностный показатель плана
статистического контроля — оперативная
характеристика. Это
функция P(q),
определяющая
вероятность приемки партии продукции
в зависимости от доли дефектных изделий
q
= М / N. Очевидно,
для каждого плана будет своя оперативная
характеристика.

Пусть
установлено, что если q
< q₀,
то
качество партии считается хорошим
и партию следует принять. При q
> q₀
партию
следует забраковать. В идеальном случае
оперативной характеристикой будет
функция P(q)
=
1 при 0 < q
< q₀,
P{q)
=
0 при q₀<
q
< 1
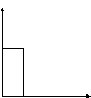
(рис. 5.2). Такая характеристика соответствует
плану сплошного контроля при условии,
что во время контроля дефект не может
быть пропущен.

При
выборочном контроле оперативная
характеристика –
гладкая кривая (см. рис.), при этом Р(0) =
1, т.е. партия, у которой все изделия
годные, не может быть забракована; Р(1)
=
0: партия, у которой все изделия дефектные,
не может быть принята.

P(q)

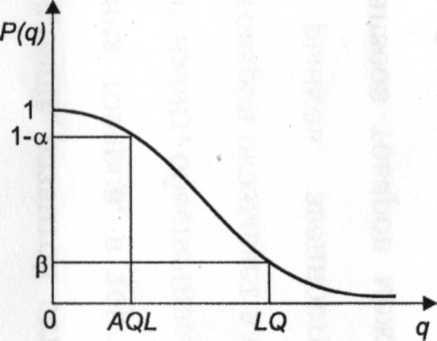
Рис.

0
q

Обычно
партии разделяют на «хорошие» и «плохие»
с помощью двух чисел: q₀
= AQL
(Acceptable
Quality
Level)
–
приемлемый уровень качества, q₁=
LQ
(Limiting
Quality)
–
предельное качество.

Приемлемый
уровень качества AQL
–
максимальный
уровень несоответствий в партии
продукции, который считается
удовлетворительным при приемке (по
устаревшей, но используемой на практике
терминологии –
приемочный уровень дефектности). При
контроле на основе этого показателя
большинство предъявленных партий будет
принято, если их уровень несоответствий
не превышает заданного значения AQL.

Предельное
качество LQ
(в
устаревшей терминологии –
браковочный уровень дефектности) –
это минимальный уровень несоответствий,
который рассматривается как
неудовлетворительный при приемке. При
контроле на основе показателя LQ
обеспечивается
низкая вероятность приемки отдельной
партии.

Партии
считаются хорошими при q
< AQL
и
плохими при q
> LQ.
При
AQL
< q
< LQ
качество
партии считается еще допустимым.

К
плану предъявляются требования:
вероятность приемки для хорошей партии
должна быть не ниже, чем 1 – α, для плохой
– не выше риска потребителя β (см. рис.):

P(q)
>1–
α при q
< AQL;

Р(q)
< β
при q
> LQ,

т.е.
план сводится к тому, чтобы риски
поставщика и потребителя не превышали
аиβ.

Пример

При
α = 0,05, β =0,1, AQL
=
0,003, LQ
=
0,02 — для этого плана в среднем из каждых
100 партий, имеющих засоренность не выше
0,3% будет забраковано не более пяти, а
из 100 партий, содержащих более 2% дефектных
изделий будет принято не более 10 партий.

Контроль
по альтернативному признаку – это такой
контроль, при котором о каждом
контролируемом объекте делается
заключение годен он или не годен,
соответствует предъявляемым требованиям
или не соответствует.

Предположим,
что контролируется партия из N изделий.
Для контроля делается случайная выборка
объемом п.
Количество
способов, которыми можно выбрать п
изделий
из N без учета порядка следования — это
число сочетаний

Пусть
случайная величина X–
количество
дефектных (несоответствующих) изделий
в выборке. Известно, что во всей партии
изделий доля несоответствий составляет
q.
Тогда
число дефектных изделий в партии равно
Nq,
число
годных изделий составит N
–
Nq.
Рассмотрим
событие X
= т –
взято
ровно т
дефектных
изделий. Это возможно, если из Nq
дефектных
изделий взято т
изделий,
а из оставшихся годных N
–
Nq
взято
п
–
т изделий
(всего в выборке п
изделий).
Тогда вероятность рассматриваемого
события

(5.1)

Формула
(5.1) описывает гипергеометрическое
распределение.

Как
правило, объем выборки составляет не
более 10% от объема всей партии, в этом
случае гипергеометрическое распределение
может быть аппроксимировано биномиальным

P(X
= m) =C^m_nq^m(1-q)^n-m. (5.1)

На
практике доля несоответствий обычно
составляет менее 10%, в этом случае в свою
очередь биномиальное распределение
может быть аппроксимировано распределением
Пуассона:

(5.3)

Рассмотрим
одноступенчатый контроль по альтернативному
признаку [30, 44]. Вероятность приемки
партии P(q)
в
этом случае — это вероятность того, что
количество дефектных изделий т
в
выборке не превысит приемочное число
с. Используя формулу сложения вероятностей
несовместных событий, получим уравнение
оперативной характеристики одноступенчатого
плана контроля:

^P⁽^q^{)

= Р(т <}^с)

–^Р(Х^{=

0) +}^Р(Х^=

1)+…+^Р(Х^{=

с) =}

Подставляя
в полученное выражение вместо Р(q) формулу
соответствующего распределения
(биномиального или гипергеометрического
или распределения Пуассона) получают
уравнение оперативной характеристики
одноступенчатого плана. Подставляя
известные значения AQL
и
LQ,
а
также заданные риски α и β получают
систему нелинейных уравнений, решая
которую находят параметры плана — объем
выборки п
и
приемочное число с.

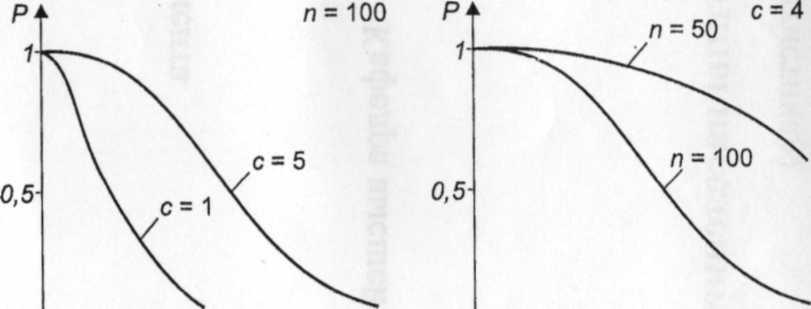
Анализ
соответствующих зависимостей показывает,
что при постоянном объеме выборки п
с
возрастанием приемочного числа с
вероятность принятия партии с заданным
приемлемым уровнем качества AQL
возрастает
(рис. 5.4, а),
а
с возрастанием п
при
постоянном с
вероятность
приемки партии уменьшается (рис. 5.4, б).
Можно
подобрать такой план контроля (п,с),
который
бы обеспечивал значения рисков аир
при заданных значениях уровней качества
AQL
и
LQ.

Рис.
5.4. Оперативные
характеристики при п
= const
(а) и с
=
const
(б)

По
результатам контроля множества партий
продукции могут быть найдены некоторые
полезные характеристики, в частности,
средняя доля несоответствующих единиц
продукции в принятых партиях (средний
уровень выходного качества) и среднее
число проконтролированных изделий в
партии.

Рассмотрим
одноступенчатый план, при котором
забракованные партии изделий подвергаются
сплошному контролю, т.е. контролируются
все оставшиеся (N-
п)
изделия
партии, а выявленные дефектные изделия
заменяют годными. Предположим, что доля
дефектных изделий постоянна и равна q.
Тогда
с вероятностью P(q)
партии
изделий принимаются (доля дефектных
изделий в ней приблизительно равна q),
а
с вероятностью [1 — P(q)]
партии
подвергаются сплошному контролю; доля
дефектных изделий в этих партиях равна
нулю. Тогда средняя доля дефектных
изделий в принятых партиях по формуле
математического ожидания для дискретной
случайной величины равна:

q_cp=qP(q)
+
0[1-
P(q)]
=
qP(q). (5.7)

Величина
q_cp
и
называется средним
уровнем выходного качества. Из
формулы (5.7) видно, что при q
=
0 значение q_c
=
0 и при q
=
1 также q_cp
— 0,
поскольку вероятность Р(1)
= 0.
Так как q_cp
— неотрицательная
функция от q,
равная
нулю при q
= 0
и q
=
1, то внутри интервала 0 < q
< 1
средний выходной уровень дефектности
имеет максимум q_max
(рис.
5.5). Максимальный для заданного плана
контроля средний уровень q_max
называют
пределом
среднего уровня выходного качества.

При
использовании рассмотренного выше
плана, когда забракованные партии
изделий подвергаются сплошному контролю,
число проконтролированных в партии
объемаN
изделий
есть случайная величина, принимающая
значение п
с
вероятностью Р(q)
и
значение N
(сплошной
контроль) с вероятностью [1 — P(q)].
Поэтому
среднее
число проконтролированных изделий в
партии равно:

n_cp
= nP(q)
+
N(1
-P(q)). (5.8)

Если
же принято решение о возврате забракованной
партии поставщику, то объем контроля в
этом случае постоянен и равен объему
выборки п.

Для
уменьшения объема контроля используют
многоступенчатые и в частности
двухступенчатые планы. Двухступенчатый
контроль уменьшает риск поставщика.

При
последовательном контроле проверяются
изделия, отбираемые из партии случайным
образом, и на каждом шаге принимается
одно из трех решений: принять партию,
отклонить партию или продолжить контроль
— взять на контроль следующее изделие.
Контроль продолжается до тех пор, пока
не накопится информация, достаточная
для принятия решения.

При
последовательном контроле по
альтернативному признаку в качестве
исходных данных принимаются риски
поставщика α
и
потребителя Р,
приемлемый
уровень качества AQL
= q₀
и
предельное качество LQ=
q_v.
После
задания этих параметров проверяются
гипотезы Н₀:
q<
q₀
или
H₁:
q>
q₁
Используются
методы последовательного анализа,
которые уже применялись при выводе
основных соотношений для контрольных
карт кумулятивных сумм. Определяется
вероятность P(q₀,n)
того,
что «проконтролированных изделий
принадлежат партии с долей несоответствий,
не превышающей q₀;
или
вероятность P(q_l,n)
того,
что они принадлежат партии с долей
несоответствий не ниже, чем q_v.
Для
принятия решения находят отношение
правдоподобия P(q₁,n)
/ P(q₀,n).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Вероятность того, что, отвергая нулевую гипотезу, мы совершаем ошибку (первого рода), которая численно равна уровню значимости а, задаваемому при проверке гипотезы. [c.205]

52. [c.80]

Случай, когда РН, п> РНО,П определены, называется случаем двух простых гипотез. В [12] показано, что для данного случая существует наилучший критерий, т. е. что всегда можно определить с как функцию ошибки первого рода и что [c.89]

Очевидно, что уровень значимости q — это вероятность ошибки первого рода. Если он чрезмерно велик, то в основном ущерб будет связан с ошибочным отклонением верной гипотезы Н0, если же он чрезмерно мал, то ущерб будет возникать от ошибочного принятия ложной гипотезы Н0. На практике в качестве [c.70]

Ошибки первого рода определяются на уровне менеджмента, реально сложившемся на [c.37]

Если qn > q, то возникает ошибка первого рода и, наоборот. [c.155]

Вероятность совершить ошибку первого рода принято обозна- [c.63]

Ошибка первого рода возникает, когда процесс находится в [c.149]

При проверке гипотезы Я0 против Я, возможны два рода ошибок. Ошибки первого рода — это ошибка, когда принимается не- [c.58]

Все выборочные методы контроля качества связаны с риском ошибок. Существует риск ошибочного отклонения годной партии (в терминах статистики ошибка первого рода) и риск ошибочного принятия негодной партии (ошибка второго рода). Поскольку в первом случае дополнительные расходы несет производитель, риск называется риском производителя. Принятие бракованной партии имеет те же последствия для другой стороны, поэтому риск второго рода называют риском покупателя. [c.250]

Ошибка первого рода 256 [c.480]

Ошибки первого рода должны предотвращаться агентствами-исполнителями с ошибками второго рода сложнее, так как исполнителю их трудно об- [c.31]

Задача правильного выбора плана статистического контроля состоит в том, чтобы сделать ошибки первого и второго рода маловероятными. Напомним, что ошибки первого рода связаны с возможностью ошибочно забраковать партию изделий, ошибки второго рода связаны с возможностью ошибочно пропустить бракованную партию. [c.225]

При использовании критерия К. Пирсона, как и в случае применения других критериев, возможны два рода ошибок. Ошибка первого рода состоит в отклонении верной гипотезы, а ошибка второго рода — в принятии неправильной. Для иллюстрации на рис. 43 показаны кривые плотности распределения вероятности величины х2 в случаях, когда проверяемая гипотеза верна — кривая 1, и когда неверна — кривая 2. Если вероятности, с которой выносится решение, соответствует значение х20 ю при всех Х < х о гипотеза будет приниматься, а при всех х2 > х.2, — отклоняться. Вероятности ошибок первого и второго родов при этом [c.108]

Мы проанализируем АЩ1)-разности логарифмических прибылей для рынков капитала. АК(1)-разности используются для устранения — или, по крайней мере, для сведения к минимуму — линейной зависимости. Как мы видели в Главе 5, линейная зависимость может сместить показатель Херста (и может заставить его выглядеть значимым, когда нет процесса с долговременной памятью) т.е. вызвать ошибку первого рода. Используя АК(1)-разности, мы сводим смещение к минимуму, и, будем надеяться, делаем результаты незначительными. Такой процесс часто называют, предварительным отбеливанием или удалением трендов. Мы будем использовать последний термин. Удаление трендов не подходит для всех статистических испытаний, хотя кажется, что оно используется почти волей-неволей. Для некоторых испытаний удаление трендов может скрыть значимую информацию. Однако в случае R/S-анализа удаление трендов устранит сериальную корреляцию, или кратковременную память, а также инфляционный рост. Сериальная корреляция представляет проблему для очень высокочастотных данных, таких как пятиминутные прибыли. Инфляционный рост является проблемой для низкочастотных данных, таких как 60 лет месячных прибылей. Однако, как мы увидим, для R/S-анализа процесс с кратковременной памятью представляет гораздо большую проблему, чем проблема инфляционного роста. Мы начинаем с ряда логарифмической доходности [c.110]

Как видно по таблице, для реально встречающихся на практике распределений (см. [14, п. 6.1.11]) истинная ошибка первого рода может быть очень большой, в несколько раз превышая нормальную ошибку в 5%. [c.397]

Применительно к задаче статистического регулирования ошибка первого рода состоит в том, что налаженный процесс будет принят за разлаженный и он будет необоснованно остановлен для корректировки, когда в этом нет необходимости. Ошибка второго рода в этой задаче состоит в том, что разлаженный процесс будет принят за налаженный, что приведет к выпуску бракованной продукции. [c.25]

Вероятность совершить ошибку первого рода принято обозначать через а, а вероятность совершить ошибку второго рода — через р. Для задачи статистического регулирования а называется риском излишней наладки, ар — риском незамеченной разладки. Критическими точками (границами) называют точки, отделяющие критическую область от интервала — области принятия гипотезы. Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области. Правосторонней называют критическую область, определяемую неравенством К>Ккр, где К — статистика критерия, Кщ, — положительное число (рис. 2.3). [c.25]

С этой целью задаются достаточной малой вероятностью — уровнем значимости а (это то же, что и вероятность совершения ошибки первого рода). Затем ищут критическую точку Ккр, исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий К примет значение большее /СкР, была бы равна принятому уровню значимости [c.26]

Как следует из неравенства (3.89) и (3.93), события Л и S не являются независимыми (поскольку в указанные неравенства входит одна и та же величина Дт). Поэтому на основании выражений (3.90) и (3.93) вероятность ошибки первого рода определится как [c.161]

Поэтому, несмотря на отсутствие отклонений в технологическом процессе, границы регулирования на контрольной карте могут быть нарушены вследствие ошибочной оценки ( риск излишней наладки ). Это называется ошибкой первого рода. Поскольку расстояние между средней линией и границами регулирования обычно составляет 3 сигмы (три средних квадратических отклонения), вероятность риска ошибки первого рода составляет 0,3%. [c.74]

Если сузить диапазон границ регулирования, то ошибки второго рода сократятся, однако ошибки первого рода увеличатся. Если же расширить границы регулирования, то ошибки первого рода уменьшатся, тогда как ошибки второго рода возрастут. Отсюда вытекает, что рациональное и экономичное сочетание этих двух аспектов является сущностью установления границ регулирования. [c.74]

Последствия ошибок первого и второго рода весьма различны. Ошибка первого рода требует от аудитора или экономического субъекта дополнительной работы по уточнению факта и характера обнаруженных недостатков бухгалтерского учета или системы внутреннего контроля. После дополнительных исследований истина обычно устанавливается. [c.216]

Ошибка первого рода — ошибка биометрической системы, принявшей зарегистрированного легального пользователя за злоумышленника. [c.449]

Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза. [c.71]

Гипотеза Но отклоняется Ошибка первого рода Правильный вывод [c.72]

В большинстве случаев последствия указанных ошибок неравнозначны. Первая приводит к более осторожному, консервативному решению, вторая — к неоправданному риску. Что лучше или хуже — зависит от конкретной постановки задачи и содержания нулевой гипотезы. Например, если Н0 состоит в признании продукции предприятия качественной, и допущена ошибка первого рода, то будет забракована годная продукция. Допустив ошибку второго рода, мы отправим потребителю брак. Очевидно, последствия второй ошибки более серьезны с точки зрения имиджа фирмы и ее долгосрочных перспектив. [c.72]

Вероятность совершить ошибку первого рода принято обозначать буквой а, и ее называют уровнем значимости. Вероятность совершить ошибку второго рода обозначают / . Тогда вероятность несовершения ошибки второго рода (1 — р) называется мощностью критерия. [c.72]

Обычно значения а задают заранее круглыми числами (например, 0.1 0.05 0.01 и т. п.), а затем стремятся построить критерий наибольшей мощности. Таким образом, если а = 0.05, то это означает, что исследователь не хочет совершить ошибку первого рода более чем в 5 случаях из 100. [c.72]

На практике для построения тестов часто используют следующий подход. Предположим, что можно найти такую статистику tn = tn(Xi,…, Хп), что если гипотеза Щ верна, то распределение случайной величины tn известно (например, табулировано). Тогда для заданного значения а ошибки первого рода можно найти такую область Ка, что P(in Ка] = 1 — а (подчеркнем, что вероятность вычисляется в предположении, что верна нулевая гипотеза). Тогда тест определяется следующим образом [c.540]

При желании можно повысить «подозрительность» нейросети, обеспечив точность выявления банкротов вплоть до 99% — за счет снижения требований к ошибкам второго рода (класификации нормальной фирмы как банкрота). Это достигается путем увеличения веса ошибки первого рода (класификации банкрота как нормальной фирмы). В зависимости от конкретной практической задачи «подозрительность» сети можно произвольно регулировать. [c.188]

Вероятность ошибки первого рода, т.е. вероятность попада- [c.65]

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Введение
2 Одноступенчатый и двухступенчатый планы ВКК
3 Оперативная характеристика плана контроля
4 Парадоксы ВКК
5 Ссылки
6 Литература

Введение

Статистический контроль качества продукции широко применяется в промышленности индустриально развитых стран. Большая роль статистических методов в управлении производством и в первую очередь качества продукции объясняется целым рядом моментов, из которых выделим два.

Во-первых, статистический контроль – база научно обоснованного получения, накопления и обработки информации о качестве продукции, состоянии технических процессов и производства.

Во-вторых, статистический контроль позволяет построить конкретные производственные отношения между изготовителями и потребителями продукции, обеспечивая достоверность и доказательность принимаемых решений, затрагивающих интересы обоих сторон.

По способу отбора изделий, подвергаемых контролю качества, различают тотальный (стопроцентный) и выборочный контроль.

Для сокращения затрат на контроль в крупносерийном и массовом производстве больших партий изделий (генеральной совокупности) контролю подвергают только часть партии — выборку. Очевидно, что выборка должно производиться случайным образом.

Если уровень качества изделий в выборке соответствует установленным требованиям, то считают, что всю партию можно принять как годную. В противном случае партия бракуется.

В ряде случаев вся партия может быть ошибочно забракована, и это считается ошибкой первого рода, или риском поставщика. Ошибка противоположного свойства называется ошибкой второго рода или риском заказчика. Обе ошибки выражаются в процентах и оговариваются при совершении торговых сделок.

Одноступенчатый и двухступенчатый планы ВКК

d(X^n) — количество дефектных деталей в выборке X^n .

Одноступенчатый план :

1. Взять $X^n\subset X^N$

методом простого случайного выбора;

2. Если $d(X^n)\le c$

, то принимаем всю партию, иначе не принимаем.

Двухступенчатый план $(n,a,b)+(m,c),\ a\le b$ :

1. Взять $X^n\subset X^N$

методом простого случайного выбора;

2. Если $d(X^n)\le a$

, то принимаем партию, иначе: если $d(X^n)\ge b$

, то бракуем патрию, иначе

3. Взять $X^m\subset X^N$

; если $d(X^m)\le c$

, то принимаем, иначе нет.

Оперативная характеристика плана контроля

f(p) — вероятность приемки.

$p=\frac{D}{N}$ — входной уровень дефектности, — количество бракованных экземпляров.

$\alpha$ — вероятность ошибки первого рода (риск поставщика забраковать хорошую партию).

$\beta$ — вероятность ошибки второго рода (риск потребителя принять плохую партию).

Утв. $\forall \alpha,\beta,\ p_{pr}<p_{br}\ \ \exists (n,c):\ f(p_{pr})>1-\alpha,\ f(p_{br})<\beta$

Парадоксы ВКК

1. «Догма»: план контроля у поставщика и потребителя должен быть одинаков.

На самом деле приемка у поставщика должна быть строже!!!

Рекомендации: $p_{br}^{post}=p_{pr}^{potr}$ .

2. Чем меньше

, тем больше

Пример: план (n,0)

$(1-p_{br})^n=\beta=0.1\ \Rightarrow\ n=\frac{2.3}{-ln(1-p_{br})}\approx\frac{2.3}{p_{br}}$

$p_{br}\sim 0.01\ \rightarrow\ n=230$

$p_{br}\sim 0.0001\ \rightarrow\ n=23000$

Ссылки

Статистический анализ данных (курс лекций, К.В.Воронцов)/2009

Литература

Статистический анализ данных (курс лекций, К.В.Воронцов)

Данная статья является непроверенным учебным заданием.

Студент: Участник:Аманжолов Рустем

Преподаватель: Участник:Vokov

Срок: 6 января 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru.
По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник

Материал из MachineLearning.

Содержание

Введение

Одноступенчатый и двухступенчатый планы ВКК

Оперативная характеристика плана контроля

Парадоксы ВКК

Ссылки

Литература

Интересное по теме: