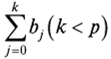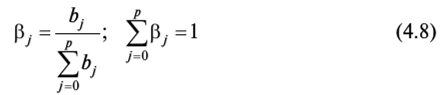1. Отбрасывание
значимой переменной.
Оценки, получен.
по такому урав-ию являются смещенными
и несостоятельными, интервальные оценки
и рез-ты проверки гипотез будут
ненадежными.
2. Добавление
незначимой переменной.
Оценки остаются,
как правило, несмещенными и состоятельными.
Однако их точность уменьшится, т.е.
оценки становятся неэффективными, что
отразится на их устойчивости.
3. Выбор
неправильной функциональной формы.
Приводит либо к
получ. смещенных оценок, либо к ухудшению
статистич. св-в оценок коэф-тов регрессии
и других показателей качества ур-ия.
Прогнозные качества модели очень низки.
13. Эконометрический анализ при нарушении классических предположений. Гетероскедастичность и ее последствия.
Гетероскедастичность
Зависимость
потребления от дохода
-
дисперсия потребления
остается одной и той же для различных
уровней дохода -
дисперсия потребления
увеличивается с ростом дохода
Последствия
гетероскедастичности:
-
оценки коэф
по-прежнему останутся несмещенными и
линейными -
неэффективно
-
дисперсия
рассчитывается со смещением -
выводы ненадежны
14. Обнаружение гетероскедастичности, методы ее устранения.
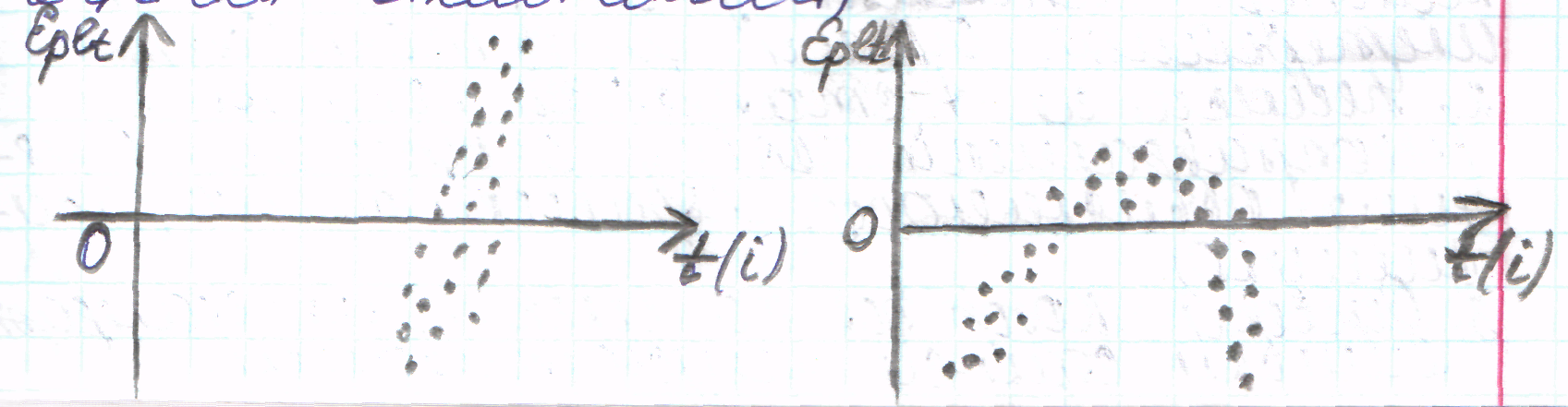
Графический анализ
остатков.
Графич. представления
поведения остаточного члена позволяет
проанализировать наличие автокорреляции
и гетероскедастичности, может быть
обнаружена неправильная спецификация
ур-ия.
По оси абсцисс –
значения объясняющей переменной X
(либо линейной комбинации объясняющей
переменной), по оси ординат – отклонения
(либо их квадраты)
Методы смягчения
проблемы гетероскедастичности:
Метод взвешенных
наименьших квадратов (ВНК).
Устранить
гетероскедастичность, разделив каждое
наблюдаемое значение на соответсвующее
ему значение среднего квадрат отклонения.
15. Автокорреляция, ее основные причины и последствия.
Автокорреляция-
это корреляция между наблюдаемыми
показателями, упорядоченными во времени
или в пространстве.
Спрос У на
прохладительные напитки в зависимости
от дохода Х по ежемесячным данным.
Фактические точки
наблюд. обычно будут превышать трендовую
линию в летние периоды.
Зависимость
предельных издержек МС от объема выпуска
Q.
Если вместо реальной квадратической
модели выбрать линейную модель, то
совершается ошибка спецификации.
Основные причины
автокорреляции:
-
ошибка спецификации
-
инерция в изменении
экономических показателей(цикличность,связанная
с волнообразной деловой активн., обладает
определенной активностью) -
эффект паутины(эконом.
показатели реагир. на изменен экономич
условий с запаздыванием ) -
сглаживание данных
Последствия
автокорреляции: 1) оценки неэффективны
2)дисперсии смещены 3)оценка дисперсий
регрессии смещена 4)выводы неверны
5)ухудшаются прогнозные качества модели.
16. Обнаружение и устранение автокорреляции
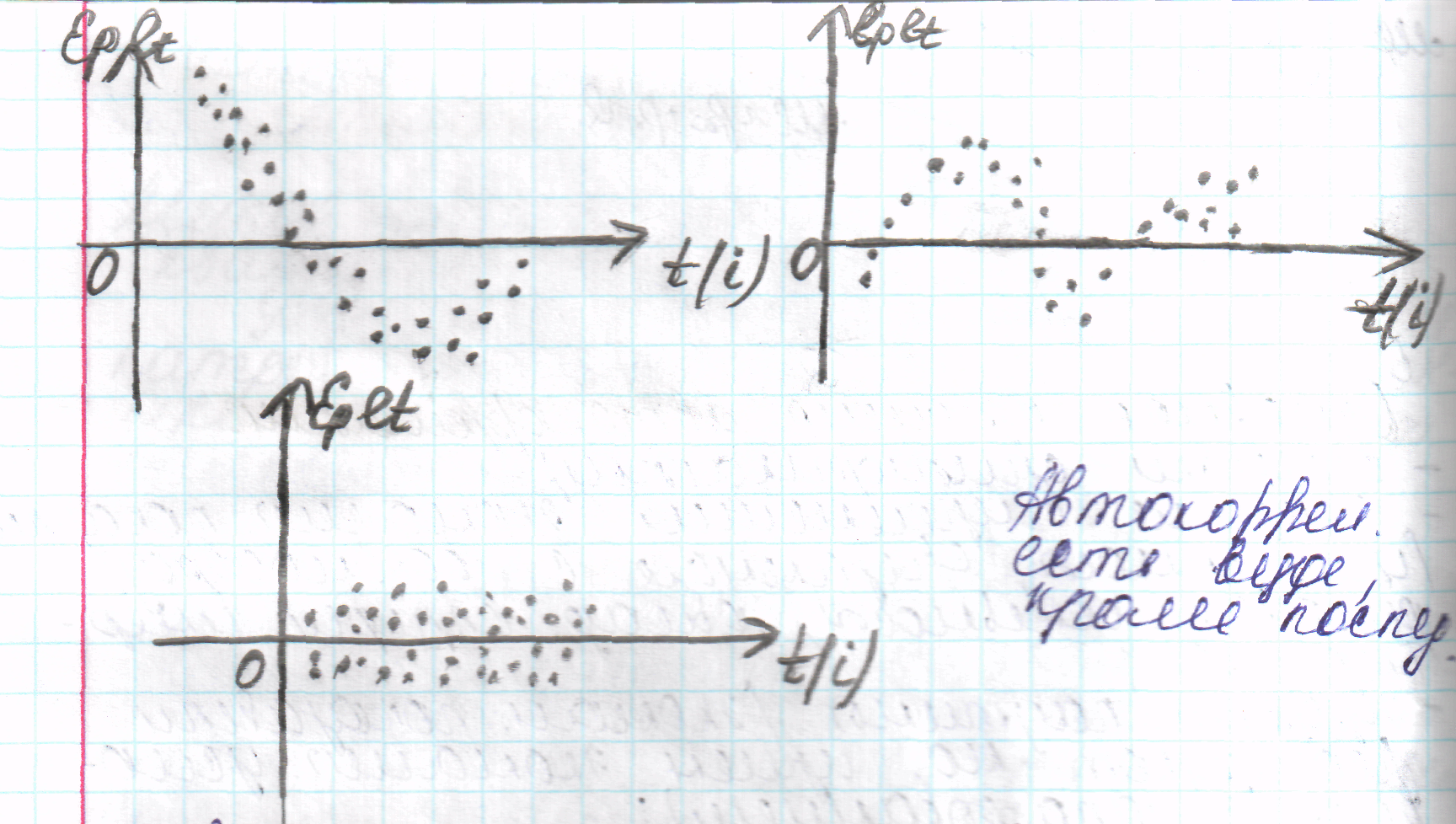
Графический метод
По оси абсцисс
отклад-ся либо время (момент) полученных
данных, либо порядковый номер наблюдения,
а по оси ординат – отклонения (либо
оценки отклонений)
Методы устранения
автокорреляции:
-
Возможно отсутствие
в модели некоторой важной объясняющей
переменной:
— определить данный
фактор и учесть его в уравнении регрессии;
2. Попробовать
изменить формулу зависимости (например
линейную на логлинейную, гиперболическую
и т.д.)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
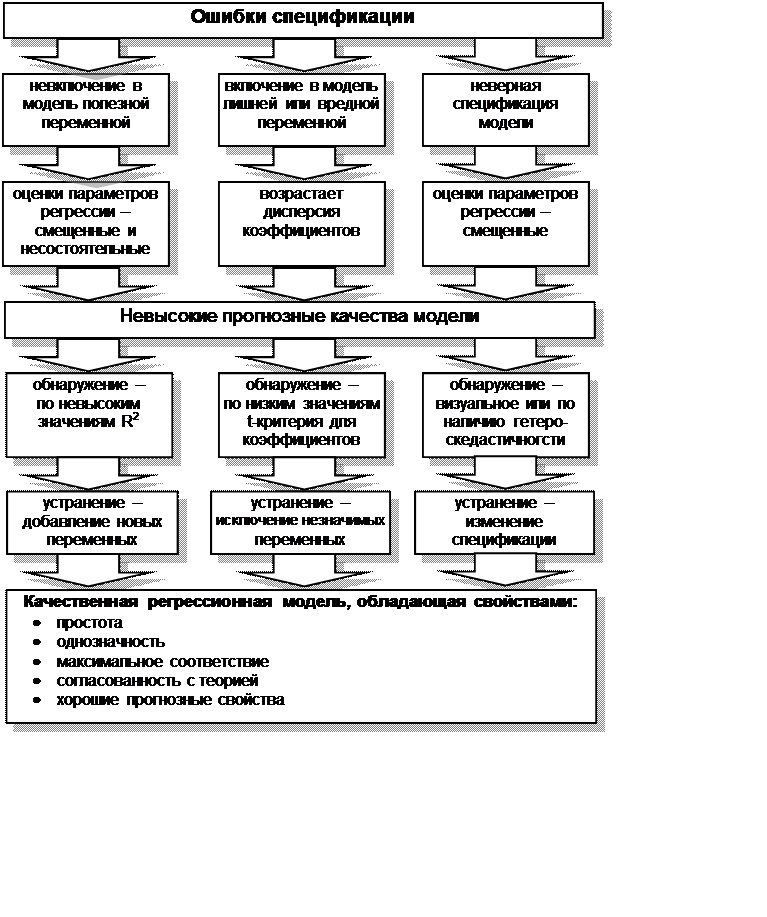
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. [c.36]
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при ис- [c.36]
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели. [c.37]
В чем состоят ошибки спецификации модели [c.88]
Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о [c.204]
Иллюстрация возможного появления ошибки спецификации приводится на рис. 5.4. [c.239]
| Рис. 5.4. Ошибка спецификации при выборе уравнения тренда |  |
Ошибкой спецификации называются неправильный выбор типа связей и соотношений между элементами модели, а также выбор в качестве существенных таких переменных и параметров, которые на самом деле таковыми не являются, и наконец, отсутствие в модели некоторых существенных переменных. [c.338]
Следовательно, шаг 4 заключается в вычислении (50), (53), (59) — (60). Таким образом, для регрессионных уравнений первого порядка с запаздывающей переменной продолжение итеративного процесса от первичных обобщенных оценок наименьших квадратов приводит к асимптотическим оценкам наибольшего правдоподобия, а последующее применение техники оценки ошибки спецификации дает возможность получить оценки и доверительные интервалы прогноза также и при наличии ошибок в переменных. [c.80]
Даже если бы удалось получить программы, свободные от ошибок, то возникает необходимость учитывать некоторый переходный период, в течение которого структура системы не должна основываться на предположении об отсутствии ошибок в отдельных модулях, но должна допускать возможность неправильного функционирования компонентов ПО вследствие внутренней ошибки. Спецификации модуля должны закреплять за каждым из них функцию выполнения определенных проверок модулей, с которыми последний взаимодействует. Кроме того, если даже ПО было написано корректно, более ранние ошибки оборудования могли сделать его некорректным. [c.15]
Оценки с ограниченной информацией оказываются более устойчивыми к ошибкам спецификации модели. Наоборот, оценки с полной информацией весьма чувствительно реагируют на изменения структуры. [c.424]
Какие ошибки спецификации встречаются, и каковы последствия данных ошибок [c.190]
Как обнаружить ошибку спецификации [c.190]
Каким образом можно исправить ошибку спецификации и перейти к лучшей (качественной) модели [c.190]
Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками спецификации. Рассмотрим основные типы ошибок спецификации. [c.192]
При построении уравнений регрессии, особенно на начальных этапах, ошибки спецификации весьма нередки. Они допускаются обычно из-за поверхностных знаний об исследуемых экономических процессах, либо из-за недостаточно глубоко проработанной теории, или из-за погрешностей при сборе и обработке статистических данных при построении эмпирического уравнения регрессии. Важно уметь [c.195]
Как можно обнаружить ошибки спецификации [c.202]
Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена [c.202]
Совершается ли при этом ошибка спецификации Если да, то каковы ее последствия Что можно сказать, если указанные модели поменять ролями [c.203]
Совершается ли при этом ошибка спецификации и каковы ее последствия [c.203]
Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных. [c.228]
Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может привести к автокорреляции. [c.228]
PiQ + выбрать линейную модель МС = ро + PiQ + s, то совершается ошибка спецификации. Ее можно рассматривать как неправильный выбор формы модели или как отбрасывание значимой переменной при линеаризации указанных моделей. Последствия данной ошибки выразятся в системном отклонении точек наблюдений от прямой регрессии (рис. 9.3) и существенном преобладании последовательных отклонений одинакового знака над соседними отклонениями противоположных знаков. Налицо типичная картина, характерная для положительной автокорреляции. [c.228]
Однако необходима определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации. Например, при исследовании спроса на некоторое благо в качестве объясняющих переменных можно использовать цену данного блага и цены заменителей данного блага, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, скорее всего, допустим ошибку спецификации. Вследствие этого возможно получение смещенных оценок и осуществление необоснованных выводов. Таким образом, в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой. [c.252]
Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, т. к. в этом случае вполне вероятны ошибки спецификации. Наиболее рациональной практической стратегией выбора модели является следующая схема. [c.267]
Однако применение этого метода весьма ограничено в силу постоянно уменьшающегося числа степеней свободы, сопровождающегося увеличением стандартных ошибок и ухудшением качества оценок, а также возможности мультиколлинеарности. Кроме этого, при неправильном определении количества лагов возможны ошибки спецификации. [c.279]
Мы видим, что квадраты остатков регрессии е2, которыми оперируют тесты на гетероскедастичность, зависят от значения переменной xt, и, соответственно, тесты отвергают гипотезу гомоскедастичности, что в данном случае является следствием ошибки спецификации модели. [c.181]
Теперь оба коэффициента значимо отличаются от нуля и имеют правильные знаки . Тест Уайта показывает отсутствие гетероскедастичности. Из последнего уравнения можно также получить, что возраст, при котором достигается максимальная зарплата, равен примерно 54 годам, что согласуется со здравым смыслом. По-видимому следует заключить, что в первом уравнении результат теста указывал на ошибку спецификации. Пример показывает, что при эконометрическом анализе полезна любая дополнительная информация (в нашем случае — механизм формирования зарплаты). [c.183]
Следовательно, влияние ошибочной спецификации на смещение и среднеквадратичное отклонение оценки ш /З проявляется через величину с /ф2 72> которая, конечно, неизвестна. Заметим, что абсолютная величина смещения оценки и ее среднеквадратичное отклонение в результате ошибки спецификации могут как возрасти, так и уменьшиться. [c.430]
Другой важный вопрос связан с устойчивостью оценок по отношению к ошибкам спецификации, т. е. к неправильно выбранной форме связи, автокоррелированности или гетеро-скедастичности отклонений, нарушениям гипотезы о нормальности возмущений и т. д. [c.423]
Совершается ли ошибка спецификации при использовании следующей ре грессии [c.203]
Из таблицы видно, что коэффициенты при интересующих нас переменных AGE и AGE2 не значимы. Тест Уайта показывает наличие гетероскедастичности. Прежде чем начать коррекцию гетероскедастичности, вспомним, что тест может давать такой результат при ошибке спецификации функциональной формы. В самом деле, поскольку, как правило, все надбавки к зарплате формулируются в мультипликативной форме ( увеличение на 5% ), то более естественно взять в качестве зависимой переменной логарифм зарплаты InW. Результаты регрессии In W на остальные переменные приведены в таблице 6.4. [c.183]
Этот разрыв между теорией и практикой имеет довольно интересные последствия. Одно из них то, что прикладные эконо-метристы чувствуют необходимость проверки гипотез, потому что они проходили курс Теория эконометрики и хотят использовать свои знания. Однако они редко могут объяснить, почему они тестируют конкретную гипотезу, скажем, однородность или выпуклость. Если гипотеза отклоняется, как и происходит в большинстве случаев, они видят в этом свидетельство ошибки спецификации. Зачем же тогда проводить тестирование, если его логические следствия игнорируются Размышление о последствиях тестирования перед его выполнением было бы разумным, но редко встречается в эконометрической практике. [c.477]
В этой книге мы будем различать понятия спецификация ошибки i ошибка спецификации. Первое понятие относится к выбору неко-горого типа ошибок при спецификацииУмодели, подлежащей оцени-занию, а второе понятие означает, властности, ошибку спецификации матрицы X1. Предположим, как обычно, что истинная модель шеет вид [c.168]
Рассмотрим оценку Ъг параметра 32, полученную простой регрес сией у на xz на основе таблицы, построенной в результате классифи кации данных по переменной Xz, и оценку Ь3 параметра р3, получен ную в результате простой регрессии у на ха на основе таблицы, соот ветствующей классификации по Xs. Обе оценки окажутся смещенными поскольку в каждом случае допущена ошибка спецификации из-з исключения из регрессии существенной переменной. Поэтому [c.234]
Любое ранжирование остальных четырех методов должно рассматриваться как пробное. Первым рассмотрим наименее противоречивый случай. В экспериментах, содержащих ошибку спецификации, двухшаговый метод наименьших квадратов показывает заметно худшие результаты по сравнению с остальными тремя методами, если предопределенные переменные не сильно коррелированы друг с другом, и его качества становятся относительно лучшими, когда такая корреляция присутствует. В итоге представляется правильным присвоение этому методу наименьшего рангового значения. Неожиданно метод максимального правдоподобия с полной информацией оказался лучше других. Можно было ожидать, что он более других методов пострадает от ошибочной спецификации. Конечно, для достаточно больших значений у21 это вполне может произойти. Также неожиданным оказалось и то, что метод наименьших квадратов, без ограничений не проявил себя в этих экспериментах. Это произошло потому, что при работе с малыми выборками использование априорной информации «о модели, которое достигается с помощью метода максимального правдоподобия с полной информацией и метода ограниченной информации для отдельного урав нения, дает больший вклад в качество оценок, чем уменьшение ошибок спецификации этой модели. Метод наименьших квадратов без ограничений не введен нас в заблуждение из-за неправильных ограничений на элементы матрицы П, не в то же время он не способен воспринять верные ограничения. В результате ov. не выдерживает конкуренции с двумя методами, использующими априорнук информацию, когда степень неточности ограничений не очень велика. [c.422]
Возможные ошибки спецификации модели:
1. Неправильный выбор вида уравнения
регрессии
2. В уравнение регрессии включена лишняя
(незначимая) переменная
3. В уравнении регрессии пропущена
значимая переменная
-
Неправильный выбор вида функции в
уравнении
Пусть на первом этапе была сделана
спецификация модели в виде:
в
которой функция fF(x,a0,a1)
выбрана не верно. Предположим, что
yT=fT(x,a0,a1)+v
– правильный вид функции регрессии.
Тогда справедливо выражение:
И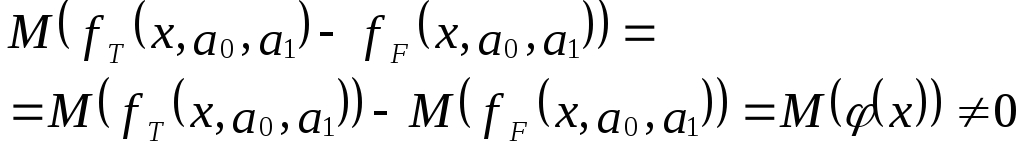
выражения следует:
Иными словами, математические ожидания
эндогенной переменной, полученные с
помощью функций fT
и fF
не совпадают, т.е. первая предпосылка
теоремы Гаусса-Маркова M(ulx)=0
не выполняется
Следовательно, в результате оценивания
такой модели параметры а0 и а1
будут смещенными
Симптомы наличия ошибки спецификации
первого типа:
1. Несоответствие диаграммы рассеяния,
построенной по имеющейся выборке виду
функции, принятой в спецификации
2. В динамических моделях длительно
сохраняется знак значений оценок
случайных возмущений у смежных (по
номеру t ) уравнений
наблюдений
Именно этот симптом и улавливается
статистикой DW Дарбина–Уотсона!
В силу данного обстоятельства тесту
Дарбина–Уотсона в эконометрике придается
большое значение.
Способ устранения: выбор другой формы
спецификации модели. Например, нелинейная
вместо линейной и т.д.
2. В уравнение регрессии включена
лишняя переменная
П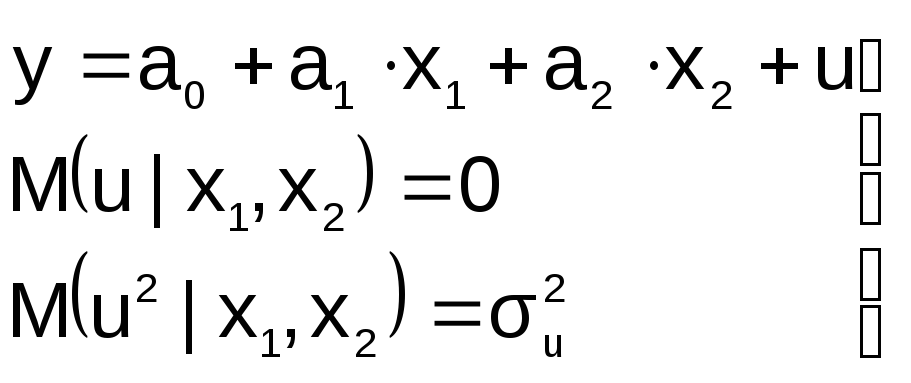
на этапе спецификации в модель включена
«лишняя» переменная, например, X2
«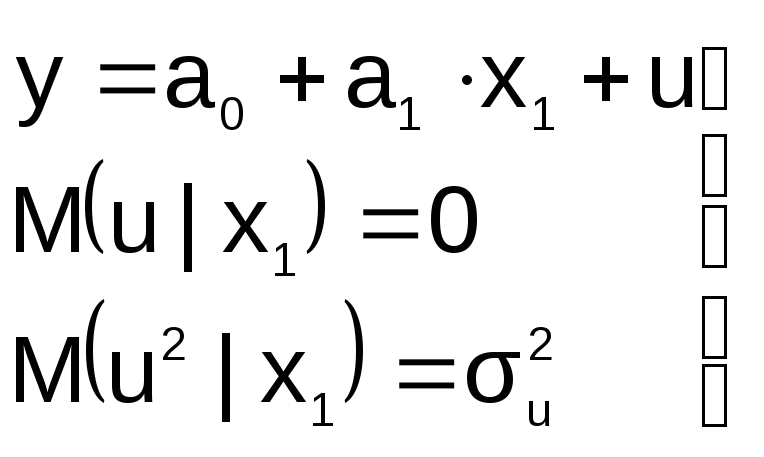
спецификация должна иметь вид:
Последствия:
1.
Оценки параметров а0, а1, а2
останутся несмещенными, но потеряют
свою эффективность (точность)
2. Увеличивается ошибка прогноза по
модели
как за счет ошибок оценок коэффициентов
и σu,
так и за счет последнего слагаемого.
Это особенно опасно при больших абсолютных
значениях регрессора
Диагностика:
В моделях множественной регрессии
необходимо для каждого коэффициента
уравнения проверять статистическую
гипотезу H0: ai=0.
Вспомним, что для этого достаточно
оценить дробь Стьюдента и сравнить ее
значение с критическим значением
распределения Стьюдента, которое
вычисляется по значению доверительной
вероятности и значению степени свободы
n2 = n – (k+1)
3.
В модели не достает важной переменной
Последствия такие же, как и в первом
случае: получаем смещенные оценки
параметров модели
Для устранения необходимо вернуться к
изучению особенностей поведения
экономического объекта, выявить опущенные
переменные и дополнить ими модель
29. Фиктивные переменные и особенности их использования в моделях.
На практике приходится учитывать в
моделях факторы, носящие качественный
характер, значения которых в наблюдениях
не возможно измерить с помощью числовой
шкалы.
Примеры.
Моделирование влияния пола специалистов
на уровень зарплаты.
Моделирование доходов граждан от типа
учебного заведения, в котором он получил
образование (государственное, частное,
специализированное,…)
Модель инфляции с учетом различных
видов регулирования со стороны государства
Возможны два подхода к решению задачи:
— построить несколько моделей отдельно
для каждого значения (градации)
качественной переменной
— учесть влияние качественного фактора
в одной модели
Второй способ представляется более
прогрессивным, т.к в этом случае появляется
возможность оценить статистическую
значимость влияния данного фактора на
поведение эндогенной переменной на
фоне других факторов, внесенных в
спецификацию модели
Пример. Изучается зависимость
расходов на образование «С» в «обычных»
и «специализированных» школах в
зависимости от числа учащихся N
Предположим:
-
Зависимость затрат на обучение от
количества учащихся N в
обоих типах школ одинакова
2. Разница в затратах объясняется
необходимостью приобретения
специализированного оборудования для
обучения специальным дисциплинам
Тогда если строить различные модели
для каждого типа школ, то спецификацию
моделей можно записать в виде:
Yo
= a0 +
a1N +u
Ys
= b0 +
a1N +
v
О
модели можно объединить, если ввести
переменную d, область
определения которой два целых числа :
0 и 1. При этом:
Спецификация такой модели имеет вид:
Y = a0
+ a1N
+ δd + u
Тогда при d=0 получим Yo
= a0 + a1N
+ u
при d=1 получим Ys
= (a0+δ)
+a1N +
v
d – фиктивная переменная
сдвига
Фиктивные переменные часто применяются
при построении динамических моделей,
когда с определенного момента времени
начинает действовать какой-либо
качественный фактор
Пусть некоторый качественный фактор
имеет несколько градаций (более 2-х)
Введение в модель фиктивных переменных
с несколькими градациями рассмотрим
на примере шанхайских школ, где имеются
4 категории школ: общеобразовательные,
технические, ПТУ и специализированные
Казалось достаточно ввести фиктивную
переменную сдвига d, придав
ей четыре различных значения и проблема
будет решена
Такой подход мало эффективен, т.к не
удается оценить статистическую значимость
влияния каждой градации на значения
эндогенной переменной
В этом случае имеет смысл ввести отдельную
переменную для каждой градации фактора
Н
Однако, если взять спецификацию модели
в виде:
Y=a0
+ a1d1+a2d2+a3d3+a4d4+a5N+u
при этом всегда верно тождество
d1+d2+d3+d4=1
Это означает, что матрица Х коэффициентов
системы уравнений наблюдений будет
коллинеарной т.к в ней присутствует
столбец из 1, и как следствие отсутствует
возможность применения МНК для оценки
параметров модели.
Предлагается в спецификацию ввести
(к-1) фиктивную переменную (к- кол-во
градаций), сделав одну из градаций
базовой, относительно которой изучать
влияние остальных градаций. Проблемы
мультиколинеарности в этом случае не
возникает
Для учета возможного изменения наклона
графика модели при изменении градации
качественного фактора предлагается
ввести в спецификацию модели еще одно
слагаемое вида «d умноженное
на x»
Вернемся к примеру изучения зависимости
расходов на образование в различных
школах. Для простоты ограничимся лишь
двумя градациями фактора «тип школы»:
d=0 – обычная школа;
d=1 – профессиональная
школа
Спецификацию модели следует записать
в виде:
Y = a0
+ a1N
+ a2*d
+ a3dN
+U
50
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
анастасия александровна янченко
Эксперт по предмету «Эконометрика»
Задать вопрос автору статьи
Проблема спецификации эконометрической модели
Проблема спецификации эконометрической модели предполагает определение:
- конечной цели моделирования;
- набора эндогенных и экзогенных переменных;
- состава и структуры системы уравнений, набора переменных;
- первоначальных ограничений стохастических составляющих.
Спецификация в эконометрике является важнейшим этапом исследования, эффективность решения влияет на успех исследования в целом. В основе спецификации — имеющиеся теории, интуиция и специальные знания.
Проблема идентифицируемости
В эконометрике проблема идентифицируемости сводится к следующему: нас интересует такие эндогенные переменные, которые относятся к случайным величинам.
Уравнение структурной формы является точно идентифицируемым тогда, когда каждый участвующий неизвестный коэффициент однозначно восстанавливается по коэффициентам приведенной формы, не ограничивая значения последних.

Учим создавать игры
Создавай 3D-графику и концепты, придумывай персонажей, учись программировать с нуля
Записаться на курс
Определение 1
Эконометрическую модель можно назвать точно идентифицируемой, если каждое уравнение ее структурной формы является точно идентифицируемым.
Если какой-либо коэффициент не может быть восстановлен, не идентифицируемо и уравнение, и модель. Проблемы идентификации сводятся к «настройкам» модели по реальным статистическим данным.
Проблема верификации
Замечание 1
Проблема верификации применительно к эконометрическим моделям заключается в разрешении вопросов относительно возможностей использования модели.
Иными словами эта проблема сводится к точности имитационных и прогнозных расчетов. Верификация подразумевает статистическую проверку гипотез и анализ параметров точности оценки. Зачастую применяется ретроспективный расчет: исходные данные делятся на части: обучающая выборка и экзаменующая выборка.
«Проблемы эконометрики» 👇
Обучающая выборка позволяет определить значения неизвестных параметров и получить модельные значения для экзаменующей выборки, которые затем подлежат сравнению с реальными значениями.
Недостаточный набор данных
Замечание 2
Проблема недостаточности данных заключается в том, что имеющиеся данные могут быть недостаточны для определения функциональной связи между переменными, или они мало варьируются для выявления отличий влияния одних факторов от влияния других.
Последнюю проблему в эконометрическом моделировании часто называют «мультиколлинеарностью».
В отличие от экспериментальной науки, отдельный исследователь, изучающий экономические процессы обычно не имеет возможности заметно повлиять на них.
Для восполнения недостатка данных, исследователь должен принимать определенные априорные допущения, которые часто могут быть недостаточно обоснованными.
Обычно функциональная форма эконометрической модели неизвестна заранее. В таком случае целесообразно использовать непараметрические методы оценивания. Но применение подобных методов требует достаточно значительного набора данных. На практике поэтому, как правило, предполагается, что зависимость двумя переменных линейна. Это связано с тем, что линейная зависимость подразумевает хороший уровень аппроксимации гладкой зависимости в определенной окрестности. Однако нет никаких гарантий, что истинная зависимость не будет нелинейной в интервале, к которому отнесены данные.
В случае применении методов эконометрики следует понимать, что обычно постулируемые свойства имеют асимптотический характер, или проявляются при стремлении числа наблюдений к бесконечности. Например, если линейная регрессия подразумевает использование в качестве регрессоров лагов (запаздывания) зависимых переменных, то, даже при выполнении стандартных предположений регрессионного анализа, итоговые оценки будут смещенными, но состоятельными.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Шпоры по эконометрике.
№ 1. СПЕЦИФИКАЦИЯ МОДЕЛИ
Простая регрессия представляет собой регрессию между двумя переменными у и х, т.е. модель вида , где у результативный признак; х — признак-фактор.
Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида
Спецификация модели — формулировка вида модели, исходя из соответствующей теории связи между переменными. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. где yj фактическое значение результативного признака;
yxj -теоретическое значение результативного признака.
случайная величина, характеризующая отклонения реального значения результативного признака от теоретического.
Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака подходят к фактическим данным у.
К ошибкам спецификации относятся неправильный выбор той или иной математической функции для, и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.
Ошибки выборки — исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками.
Ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.
В парной регрессии выбор вида математической функции может быть осуществлен тремя методами: графическим, аналитическим и экспериментальным.
Графический метод основан на поле корреляции. Аналитический метод основан на изучении материальной природы связи исследуемых признаков.
Экспериментальный метод осуществляется путем сравнения величины остаточной дисперсии Dост, рассчитанной при разных моделях. Если фактические значения результативного признака совпадают с теоретическими у =, то Docm =0. Если имеют место отклонения фактических данных от теоретических (у ) то .
Чем меньше величина остаточной дисперсии, тем лучше уравнение регрессии подходит к исходным данным. Число наблюдений должно в 6 7 раз превышать число рассчитываемых параметров при переменной х.
№ 2 ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ: СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ.
Линейная регрессия сводится к нахождению уравнения вида или .
Уравнение вида позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.
Построение линейной регрессии сводится к оценке ее параметров а и в.
Оценки параметров линейной регрессии могут быть найдены разными методами.
1.
2.
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Формально а значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а < 0.
Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Существуют разные модификации формулы линейного коэффициента корреляции.
Линейный коэффициент корреляции находится и границах: -1≤.rxy ≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к линейной. Если r в точности =1или -1 все точки лежат на одной прямой. Если коэф. регрессии b>0 то 0 ≤.rxy ≤ 1 и наоборот при b<0 -1≤.rxy ≤0. Коэф. корреляции отражает степени линейной зависимости м/у величинами при наличии ярко выраженной зависимости др. вида.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака y, объясняемую регрессией. Соответствующая величина характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.
№ 3. МНК.
МНК позволяет получить такие оценки параметров а и b, которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) минимальна:
Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной. Решается система нормальных уравнений
№ 4. ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от средне го значения у на две части — «объясненную» и «необъясненную»:
— общая сумма квадратов отклонений
— сумма квадратов отклонения объясненная регрессией — остаточная сумма квадратов отклонения.
Любая сумма квадратов отклонений связана с числом степеней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых отклонений из п возможных требуется для образования данной суммы квадратов.
Дисперсия на одну степень свободы D.
F-отношения (F-критерий):
Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется.
Если же величина окажется меньше табличной Fфакт ‹, Fтабл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.
Стандартная ошибка коэффициента регрессии
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: которое
затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n- 2).
Стандартная ошибка параметра а:
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции тr:
Общая дисперсия признака х:
Коэф. регрессии Его величина показывает ср. изменение результата с изменением фактора на 1 ед.
Ошибка аппроксимации:
№ 5. ИНТЕРВАЛЫ ПРОГНОЗА ПО ЛИНЕЙНОМУ УРАВНЕНИЮ
РЕГРЕССИИ
Оценка стат. значимости параметров регрессии проводится с помощью t статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н0 о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактич. знач. t критерия Стьюдента.
Определяется стат. значимость параметров.
ta ›Tтабл — a стат. значим
tb ›Tтабл — b стат. значим
Находятся границы доверительных интервалов.
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что п
Анализ ошибок спецификации модели.
допускаемых при построении регрессионной модели
ошибок спецификации второго вида
Методы линеаризации нелинейных моделей.Линеаразиция — один из наиболее распространенных методов анализа нелинейных систем. Идея линеаризации — использование линейной системы для аппроксимации поведения решений нелинейной системы в окрестности точки равновесия. Линеаризация позволяет выявить большинство качественных и особенно количественных свойств нелинейной системы. Методы линеаризации имеют ограниченный характер, то есть эквивалентность исходной нелинейной системы и ее линейного приближения сохраняется лишь для ограниченных пространственных или временных масштабов системы, или для определенных процессов, причем, если система переходит из одного режима работы в другой, то следует изменить и ее линеаризованную модель. Рассмотрим такие методы линеаризации нелинейных моделей, как замена переменных; логарифмирование обеих частей уравнения и комбинированные методы. Суть первого метода состоит в замене нелинейных объясняющих переменных новыми линейными переменными и сведении нелинейной регрессии к линейной. Например, полиномиальная модель которого порядка может быть приведена к линейному виду путем замены переменных. Среди нелинейных полиномиальных регрессионных моделей чаще всего используются параболические модели второго и третьего порядка. Ограничения в использовании полиномов более высоких порядков связаны с содержательной интерпретацией коэффициентов регрессии. Линеаризация системы нелинейных уравнений в окрестности точки равновесия может быть достигнута путем замены переменных так, чтобы точка равновесия превратилась в начало координат. Уравнения, полученные в результате указанного действия, будут линейными и называться линеаризацией исходной системы. Точки исходной системы, находящиеся в окрестности точки равновесия, будут соответствовать точкам в окрестности начала координат новой системы. Нас будет интересовать: значение новых переменных, близкие к нулю; при каких условиях нелинейными выражениями можно пренебречь. Замену переменных можно использовать и при другой организации линеаризации. Производят замену: |
Временные ряды: аддитивные и мультипликативные модели тренда и сезонности.В теории временных рядов чаще всего применяются два способа записи моделей временных рядов. Первый способ основывается на предположении, что влияние всех его компонент на значения элементов временного ряда носит аддитивный характер. В этом случае модель временного ряда называется аддитивной и имеет вид Второй способ записи модели основан на предположении о мультипликативном характере воздействия компонент временного ряда на x(t). В этом случае модель временного ряда называется мультипликативной и записывается в виде произведения: Выбор в пользу аддитивной или мультипликативной модели осуществляется на основе анализа динамики временного ряда. Если периодические колебания значений временного ряда имеют относительно постоянную амплитуду, то предпочтительнее использовать аддитивную модель. Мультипликативную модель логичнее использовать в ситуациях, когда амплитуда колебаний изменяется с течением времени. Такими свойствами, как правило, обладают развивающиеся экономические процессы. Пример такого процесса — динамика инвестиций в основной капитал в Российской Федерации. Далее будем рассматривать анализ только аддитивной модели, так как мультипликативная модель может быть сведена к аддитивному виду посредством логарифмирования левой и правой частей. Отметим также, что присутствие в модели всех четырех компонент не является обязательным. Например, временной ряд может не содержать тренда или циклических колебаний. Единственная компонента, которая всегда присутствует в модели временного ряда, — это случайная функция Е. Процесс анализа временного ряда предполагает последовательное выполнение следующих этапов. Этап 1. Определение структуры временного ряда, т.е. формирование набора неслучайных функций, которые должны присутствовать в разложении. Этап 2. Оценивание неслучайных функций, присутствие которых в модели было доказано на первом этапе. Этап 3. Построение модели для Е(?)> описывающей влияние случайных факторов (построение модели остатков). Простейшую ситуацию для анализа представляет собой модель, содержащая только случайную компоненту. Построение таких моделей, как правило, проводится в рамках теории стационарных временных рядов. |
Системы одновременных эконометрических уравнений.Не всегда получается описать адекватно сложное социально-экономическое явление с помощью только одного соотношения (уравнения). Кроме того, некоторые переменные могут оказывать взаимные воздействия и трудно однозначно определить, какая из них является зависимой, а какая независимой переменной. Поэтому при построении эконометрической модели прибегают к системам уравнений. Экзогенные (независимые) – значения которых задаются «извне», автономно, в определенной степени они являются управляемыми (планируемыми) (X). Экзогенные переменные модели характеризуются тем, что они являются независимыми и определяются вне системы; Эндогенные (зависимые) — значения которых определяются внутри модели, или взаимозависимые (Y). Лаговые – экзогенные или эндогенные переменные эконометрической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Например: Предопределенные переменные – переменные, определяемые вне модели. К ним относятся лаговые и текущие экзогенные переменные (xt , xt-1), а также лаговые эндогенные переменные (yt-1). Все эконометрические модели предназначены для объяснения текущих значений эндогенных переменных по значениям предопределенных переменных. |
Динамические эконометрические модели.Теперь рассмотрим модели временных рядов, где в качестве исходных статистических данных мы располагаем наблюдениями двух временных рядов: *1, *2, •?•> х„ иуь У2,уЦелью регрессионного анализа в данном случае является построение линейной регрессионной модели, позволяющей с наименьшими ошибками прогнозировать значения у, по значениям х, для t > п. Подобные модели естественны в ситуациях, когда две переменные х и у связаны так, что воздействия единовременного изменения одной из них (х) на другую (у) сказываются в течение достаточно продолжительного времени, т.е. наблюдается распределенный во времени эффект воздействия. В частности, такие связи возникают между регистрируемыми во времени входными и выходными характеристиками процессов накопления и распределения ресурсов (например, процессов преобразования доходов населения в его расходы) или процессов трансформации затрат в результаты (например, процессов воспроизводства основных доходов). Эконометрическая модель является динамической, если в данный момент 1 она учитывает значения входящих в нее переменных, относящихся как к текущему, так и к предыдущим моментам времени, т.е. модель учитывает, отражает динамику исследуемых переменных в каждый момент времени. Переменные, влияние которых характеризуется определенным запаздыванием, называются лаговыми переменными. Динамические модели классифицируются по-разному. Приведем один из вариантов классификации. 1. Модели с распределенными лагами. Они содержат в качестве ла- говых переменных лишь независимые (объясняющие) переменные, например: 2. Авторегрессионные модели, уравнения которых включают в качестве объясняющих переменных лаговые значения зависимых переменных, например: Рассмотрим модель (4.7), приняв, что р — конечное число. Модель говорит о том, что, если в некоторый момент t происходит изменение x, это изменение будет влиять на значение у в течение р последующих моментов времени. Коэффициент Ь0 называется краткосрочным мультипликатором, так как он характеризует изменение среднего значения у при единичном изменении х в тот же самый момент. Сумма мультипликатором. Относительные коэффициенты модели (4.7) с распределенным лагом определяются выражениями: (условие нормировки имеет место, только если все bj имеют одинаковые знаки). Значения ру в (4.8) являются весами для соответствующих коэффициентов bj. Каждый из них измеряет долю общего изменения y, приходящегося на момент (/ + j). |
Одной из основных ошибок, , является ошибка спецификации (рис. 4.3). Под ошибкой спецификации понимается неправильный выбор функциональной формы модели или набора объясняющих переменных.Различают следующие виды ошибок спецификации:1. Невключение в модель полезной (значимой) переменной.2. Добавление в модель лишней (незначимой) переменной3. Выбор неправильной функциональной формы моделиПоследствия ошибки первого вида (невключение в модель значимой переменной) заключаются в том, что полученные по МНК оценки параметров являются смещенными и несостоятельными, а значение коэффициента детерминации значительно снижаются.При добавлении в модель лишней переменной (ошибка второго вида) ухудшаются статистические свойства оценок коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели и затрудняет содержательную интерпретацию параметров, однако по сравнению с другими ошибками ее последствия менее серьезны.Если же осуществлен неверный выбор функциональной формы модели, то есть допущена ошибка третьего вида, то получаемые оценки будут смещенными, качество модели в целом и отдельных коэффициентов будет невысоким. Это может существенно сказаться на прогнозных качествах модели.Ошибки спецификации первого вида можно обнаружить только по невысокому качеству модели, низким значениям R2.Обнаружение , если лишней является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент будет статистически незначим.Если же таких переменных несколько, целесообразно прибегнуть к сравнению значений коэффициентов детерминации модели до и после исключения из модели переменных, которые считаются лишними, при помощи расчета F-критерия.Полученное значение сравнивается с критическим F α;m1–m2;n–m1–1. Если расчетное значение меньше, то считается, что исключенные из модели переменные являются лишними.Ошибки третьего вида можно обнаружить только при помощи содержательной интерпретации модели или визуально анализируя данные или по наличию гетероскедастичности.Комплексный анализ ошибок спецификации можно провести, выполнив один или несколько из следующих тестов:1) Тест Рамсея (Regression specification error test – RESET);2) Тест максимального правдоподобия (The Likelihood Ratio test);3) Тест Валда (The Wald test);4) Тест множителя Лагранжа (The Lagrange multiplier test);5) Тест Хаусманна (The Hausmann test)6) Преобразование Бокса-Кокса (Box-Cox transformation)





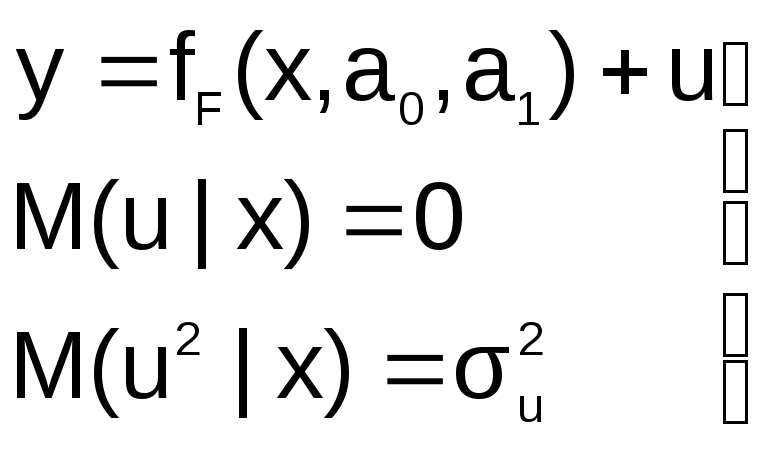
 где
где  Это может быть записано в виде:
Это может быть записано в виде:  где
где 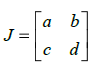 называется якобиан.
называется якобиан.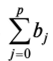 называется долгосрочным мультипликатором, который характеризует изменение у под воздействием единичного изменения х в каждом из моментов времени. Любая сумманазывается промежуточным
называется долгосрочным мультипликатором, который характеризует изменение у под воздействием единичного изменения х в каждом из моментов времени. Любая сумманазывается промежуточным