Дан ряд результатов
неравноточных измерений
x1
, x2
, . . . , xn
;
m1
, m2
, . . . , mn
.
Cоответственно
(2.22)
Как видим из
равенств (2.22) , всегда найдется такое
соотношение, когда
,
т.е. коэффициент С есть не что иное,
как средняя квадратическая ошибка
измерения, вес которой равен единице и
которая в отличие от остальных средних
квадратических ошибок обозначается
и называется ошибкой единицы веса.
Тогда
(2.23)
Следовательно,
(2.24)
В соответствии с
(2.24) можно записать
(2.25)
или
(2.26)
т.е.
cредняя квадратическая ошибка любого
результата измерения равна ошибке
единицы веса, деленной на корень
квадратный из веса соответствующего
результата.
2.4. Вычисление весов функций
2.4.1. Вес
функции независимых величин
Определим вес
функции
(2.27)
При этом известны
веса аргументов p1
, p2
, . . . , pn.
В случае независимых величин имеем
(2.28)
Разделим обе части
равенства (2.28) на 2
так как
то окончательно имеем
(2.29)
2.4.2. Вес функции
неравноточных слагаемых
Дана функция вида
F
= x1
+ x2
+ . . . + xn
, (2.30)
где xi
— результаты
неравноточных измерений с соответствующими
весами: p1,
p2
, . . . , pn
.
Требуется определить
вес функции F
. Cогласно
(2.29) будем иметь
(2.31)
Обратный вес
суммы неравноточных слагаемых равен
сумме обратных весов.
2.4.3. Вес суммы
равноточных слагаемых
Дана функция вида
(2.30), в которой xi
являются результатами равноточных
измерений, т.е. p1
= p2
= . . . = pn
= p. Тогда
вес такой функции определится из
равенства (2.31)
(2.32)
Откуда
(2.33)
Вес суммы
равноточных слагаемых в n раз меньше
веса одного измерения.
2.4.4. Вес простой
арифметической средины
Поскольку простая
арифметическая средина вычисляется
согласно формуле
(2.34)
ее средняя
квадратическая ошибка будет равна
,
откуда
Переходя к весам,
получим
или
(2.35)
Вес простой
арифметической средины в n раз больше
веса одного измерения.
2.4.5. Вес и
средняя квадратическая ошибка
общей
арифметической средины
Представив общую
арифметическую средину в виде линейной
функции
,
(2.36)
cогласно равенства
(2.29) получим
или
откуда
(2.37)
Вес общей
арифметической средины равен сумме
весов результатов измерений.
Средняя квадратическая ошибка
M
среднего весового согласно формуле
(2.26) вычислится
(2.38)
или
(2.39)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.
По своей природе ошибки бывают грубые, систематические и случайные.
Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.
Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.
Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.
Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
(1.25)
Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:
1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.
Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.
Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
(1.27)
где: ;
n – количество измерений одной величины.
Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.
Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.
Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.
Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:
F = f( X, Y, Z … ), (1.28)
здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.
В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.
Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:
Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
(1.30)
Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)
Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим
В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
(1.32)
Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:
Если функция имеет вид произведения нескольких аргументов,
F = x * y * z,
то для нее можно записать выражение относительной ошибки функции:
(1.33)
которое в некоторых случаях оказывается более удобным, чем формула (1.32).
Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.
Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)
Величина (1.36)
называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде
по третьему свойству ошибок (1.26) можно написать:
что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.
Запишем формулу (1.36) в виде
и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:
или
Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:
M2 = m2/n
или
(1.37)
то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.
Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.
Пусть имеется ряд равноточных измерений величины X:
l1, l2 , …, ln .
Вычислим арифметическую середину X0 = [1]/n и образуем разности:

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:
[V] = 0. (1.39)
Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
(1.40)
Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:

Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):

Возведем все уравнения (1.42) в квадрат, сложим их и получим:
.
Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.
Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)
Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ; такая замена практически не изменит правой части формулы (1.43). Итак,
,
откуда ;
после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).
Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
(1.44)
Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.
Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:
p = C/m2 (1.45)
где C – в общем случае произвольное положительное число.
При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
(1.46)
или X0 = [l*p] / [p] .
Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем
откуда (1.47)
то-есть, за число C принимают квадрат ошибки единицы веса.
Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)
Согласно (1.46) и (1.32) напишем:
Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:
Подставим это выражение в формулу (1.48) и получим,
P = [p], (1.49)
то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.
В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:
P = n. (1.50)
При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
(1.51)
где pi – вес i-того элемента.
Слайд 1Контроль:
[ ] = 0, (31)
[ 2] = [d ]. (32)
Систематическую ошибку можно не исключать и делать оценку по формуле (27), если выполняется условие
|[d]|≤0,25 [|d|]. (33)

Слайд 2ЛЕКЦИЯ 3
«ВЕСА ИЗМЕРЕНИЙ И ИХ ФУНКЦИЙ. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ
ИЗМЕРЕНИЙ».

Слайд 31. Веса измерений и их свойства. Соотношение между весами и
средними квадратическими ошибками. Вес среднего арифметического.
2. Веса функций измеренных величин.
3.
Средняя квадратическая ошибка единицы веса.
4. Среднее весовое. Средняя квадратическая ошибка и вес среднего весового.

Слайд 45.Поправки неравноточных измерений одной и той же величины и их
свойства. Оценка точности неравноточных измерений и среднего весового по поправкам.
6.
Определение средней квадратической ошибки единицы веса по разностям двойных неравноточных измерений.
7. Оценка точности измерения углов и превышений по невязкам в полигонах и ходах.

Слайд 51.Веса измерений и их свойства. Соотношение между весами и средними
квадратическими ошибками. Вес среднего арифметического.
При
обработке неравноточных измерений пользуются дополнительной характеристикой точности измерений, называемой весом измерения.

Слайд 6 Вес измерения р – величина обратно-пропорциональная квадрату средней
квадратической ошибки этого измерения:
(1)
В этой формуле k произвольное число, но при решении конкретной задачи одинаковое для всех измерений. Его стремятся выбрать таким, чтобы веса были близкими к 1.

Слайд 7Поскольку k выбирается произвольно, при решении данной задачи все веса
можно увеличивать или уменьшать в одно и то же число
раз. Это является первым свойством весов.
Пусть сделано два измерения с весами

Слайд 8
т.е. веса двух измерений обратно пропорциональны квадратам их средних квадратических
ошибок. Это второе свойство весов.
Отсюда
(2)

Слайд 9Найдем вес среднего арифметического, принимая вес р отдельного измерения равным
единице.
Обозначим вес среднего арифметического через Р. На основании
формулы (2) запишем

Слайд 10Подставляя р =1 и
Р = п, (3)
,
получим
т.е. вес среднего арифметического равен числу равноточных измерений из которого
оно получено, если вес каждого измерения принят равным единице.

Слайд 11 На этом основании любой результат измерений c
весом p можно понимать как среднее арифметическое из ряда воображаемых
равноточных измерений, каждое с весом единица, число которых было р.

Слайд 122. Веса функций измеренных величин.
Ранее были выведены формулы для нахождения
СКО функций. Веса и СКО измерений связаны зависимостью

Слайд 13Принимая k=1, получим
Величину
называют обратным весом.

Слайд 14Если в ранее выведенные формулы подставить вместо квадратов СКО соответствующие
обратные веса, то получим формулы для нахождения весов функций
1.
(4)
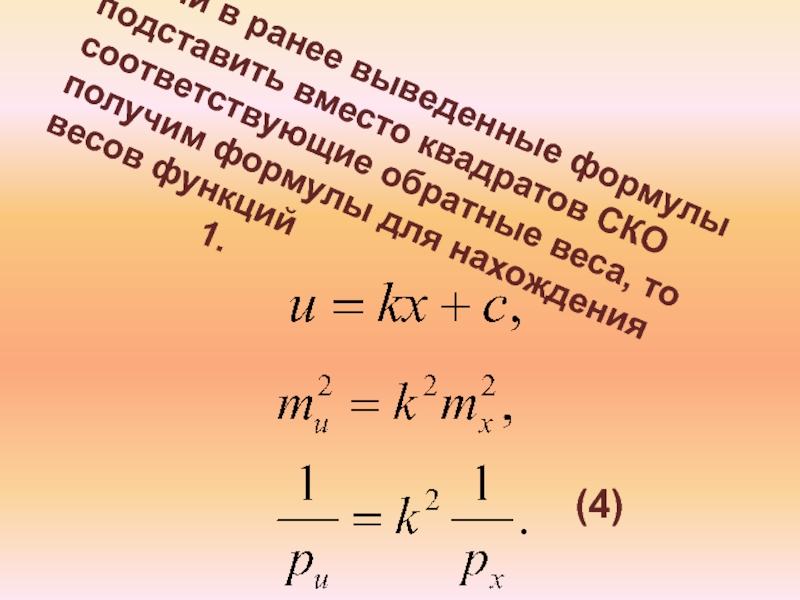
Слайд 18Если измерения равноточные, то
откуда
т.е. вес суммы n равноточных слагаемых в n раз меньше веса одного измерения.
(8)

Слайд 203. Средняя квадратическая ошибка единицы веса.
Средней квадратической
ошибкой единицы веса μ называют СКО измерения, вес которой равен
единице.

Слайд 21Выразим μ через истинные ошибки Δ.
Пусть измерению с весом
p соответствует СКО m. На основании свойства весов можно написать

Слайд 23Пусть имеется ряд измерений l1, l2, …, ln, с весами
p1, p2, …, pn. Составим вспомога-тельные функции, найдем их истинные
и СКО
(i=1, 2, …, n).
Следовательно, функции равноточные и имеют веса, равные единице.
В соответствии с (12)

Слайд 24Для равноточных измерений можно записать
или

Слайд 254. Среднее весовое. Средняя квадратическая ошибка и вес среднего весового.
Рассмотрим обработку результатов неравноточных измерений одной и той
же величины.
Пусть получено n измерений l1, l2, …, ln, с весами p1, p2, …, pn.

Слайд 26Результат любого измерения li можно рассматривать как среднее арифметическое из
pi воображаемых измерений
каждое с весом единица, т. е.
(14)

Слайд 27Таким образом, измерения можно свести к равноточным и окончательное значение
вычислить по формуле среднего арифме- тического
(15)

Слайд 28Из (14) следует, что
Подставляя в (15), получим
(16)
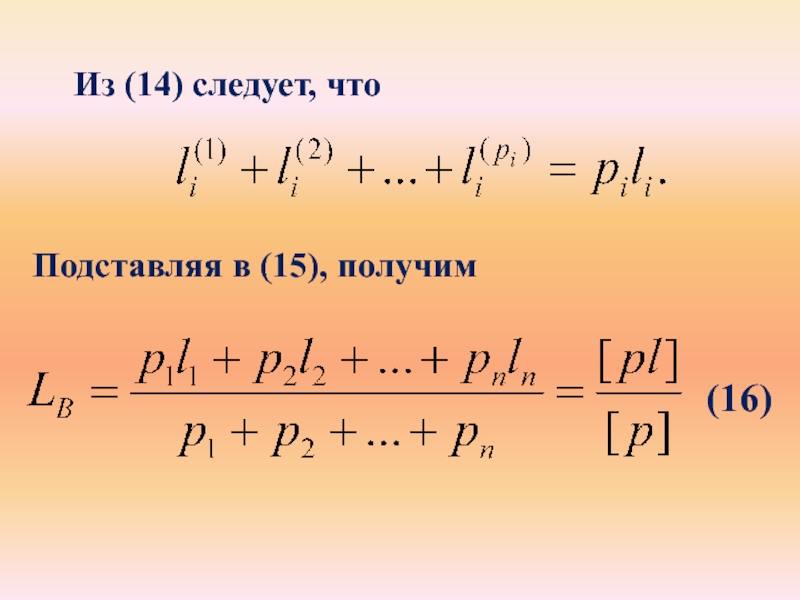
Слайд 29Величину LB называют средним весовым значением (весовым средним, средневзве- шенным,
общей арифметической срединой).
Для упрощения расчетов вводят приближенное значение l0, находят
остатки εi=li– l0, а затем среднее весовое по формуле
(17)

Слайд 30Величина [p] – сумма весов, а следовательно, общее число измерений
с весом единица, из которых получено среднее арифметическое. Поэтому вес
среднего весового
PB = [p]. (18)
Для нахождения средней квадратической ошибки среднего весового воспользуемся формулой
![ВЕСА ИЗМЕРЕНИЙ И ИХ ФУНКЦИЙ. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ Величина [p] – сумма весов, а следовательно, общее число измерений с Величина [p] – сумма весов, а следовательно, общее число измерений с весом единица, из которых получено среднее](https://theslide.ru/img/thumbs/a4cc9de6c93bda25043586aea680871f-800x.jpg)
Слайд 325. Поправки неравноточных измерений одной и той же величины и
их свойства. Оценка точности неравноточных измерений и среднего весового по
поправкам.
Поправки неравноточных измерений одной и той же величины определяют по формуле
(20)

Слайд 33Запишем поправки для всех n измерений, умножим на соответствующие веса
и сложим
[pv] = LB [p] – [pl].
![ВЕСА ИЗМЕРЕНИЙ И ИХ ФУНКЦИЙ. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ Запишем поправки для всех n измерений, умножим на соответствующие веса и Запишем поправки для всех n измерений, умножим на соответствующие веса и сложим [pv] = LB [p] –](https://theslide.ru/img/thumbs/8ed93c5700739cec582ab62d42dc3e54-800x.jpg)
Слайд 34Подставляя
[pv] = 0.
(21)
Это первое свойство поправок неравноточных измерений. Равенство (21) контролирует правильность
вычисления LB и v.
При округлении LB получим равенство
[pv] = [p] w , (22)
где w – ошибка округления.
![ВЕСА ИЗМЕРЕНИЙ И ИХ ФУНКЦИЙ. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ Подставляя [pv] = 0. (21)Это первое свойство поправок неравноточных Подставляя [pv] = 0. (21)Это первое свойство поправок неравноточных измерений. Равенство (21)](https://theslide.ru/img/thumbs/fc8dfb2a955bb48b25f51f74e5b3fa16-800x.jpg)
Слайд 35Второе свойство поправок для неравноточных измерений одной и той же
величины выражается равенством
[pv2] = min.
(23)
Для оценки точности неравноточных измерений по поправкам используют формулы
где μ – СКО единицы веса;
MB – СКО среднего весового.
(25)
![ВЕСА ИЗМЕРЕНИЙ И ИХ ФУНКЦИЙ. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ Второе свойство поправок для неравноточных измерений одной и той же величины Второе свойство поправок для неравноточных измерений одной и той же величины выражается равенством [pv2] =](https://theslide.ru/img/thumbs/c04cec8ab31ceaf8c7134946da28d36a-800x.jpg)
Слайд 36Вычисления контролируются по формуле
[p v2] = – [pvl] =
– [pvε].
Если LB округлено, то
[p v2] = – [pvε]
+ (LB – l0)[pv].
Для приближенного контроля можно пользоваться неравенством |[p v2]+[pvε]| ≤ 0,5 |[pε]| единицы последнего знака LB.
![ВЕСА ИЗМЕРЕНИЙ И ИХ ФУНКЦИЙ. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ Вычисления контролируются по формуле [p v2] = – [pvl] = – Вычисления контролируются по формуле [p v2] = – [pvl] = – [pvε].Если LB округлено, то [p v2]](https://theslide.ru/img/thumbs/3f10e4fdaeb334f46786615ce5103e23-800x.jpg)
Слайд 376. Определение средней квадратической ошибки единицы веса по разностям двойных
неравноточных измерений.
Пусть при двойном измерении n величин получены результаты
l1, l1/ каждое с весом p1 ,
l2, l2/ -“- p2,
…. … … … …
ln, ln/ -“- pn.

Слайд 38Составим разности
d1 = l1 – l1/,
d2 = l2 –
l2/,
…. …. … …
dn = ln – ln/.
Полученные разности являются
истинными ошибками самих разностей, поэтому можно записать

Слайд 39Каждая разность di = li – li/ является функцией
равноточных измерений с весом pi.
Следовательно,
При наличии систематических ошибок их
предва-рительно исключают по формуле
и формула примет вид
(26)
(27)

Слайд 40После исключения систематических ошибок СКО единицы веса находят по формуле

Слайд 417. Оценка точности измерения углов и превышений по невязкам в
полигонах и ходах
Во всех замкнутых и разомкнутых теодолитных ходах и
полигонах угловые невязки являются истинными ошибками суммы измеренных углов. Поэтому для оценки точности можно воспользоваться формулой

Слайд 42Если вес измерения одного угла принять равным единице, то вес
суммы n углов найдется по формуле
Подставляя в предыдущую формулу это
значение веса, заменяя Δ на f и n на число полигонов N, получим
(29)

Слайд 43Здесь μ является СКО измерения одного угла, т.к. за единицу
веса принят вес одного угла. Поэтому формулу (29) можно записать
иначе
где f β– невязки в полигонах или ходах;
n – число углов в полигоне или ходе;
N – число полигонов или ходов.
(30)

Слайд 44Для триангуляции n =3, поэтому
Для четырехугольников
(32)
(31)

Слайд 45Аналогичными рассуждениями можно получить формулу для оценки точности превышений геометрического
нивелирования.
Если сумме превышений на 1 км хода придать вес,
равный единице, то вес суммы превышений хода длиной L км определится по формуле

Слайд 46СКО единицы веса (СКО в сумме превышений
на 1 км
хода) найдется по формуле
где fh – невязки в превышениях;
L – длины ходов в км;
N – число полигонов или ходов.
(33)

Слайд 47В качестве единицы веса можно взять вес превышения на одной
станции. Тогда вес суммы превышений из п станций будет равен
и формула примет вид
Если на 1 км хода приходится k станций, то
(35)
(34)





