Часто
при проведении тех или других испытаний
необходимо знать, достаточно ли проведено
испытаний или их необходимо увеличить.
Для этого необходимо знать относительную
ошибку, доверительную вероятность и
коэффициент вариации.
Абсолютная
доверительная ошибка, допущенная
при определении среднего значения
генеральной совокупности для нормального
распределения в симметричном доверительном
интервале определяется по формуле:
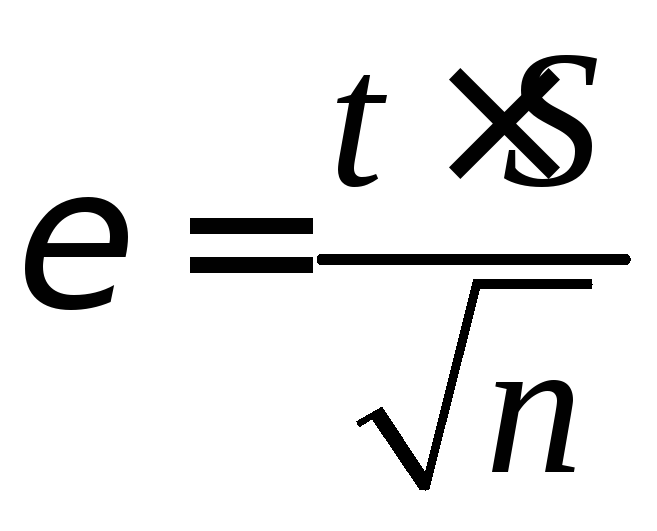
где
t
– коэффициент Стьюдента, выбираемый
по таблице в зависимости от числа
испытаний.
Относительная
доверительная ошибка
Коэффициент
вариации
Подставляя
формулы для определения абсолютной
ошибки выборки коэффициента вариации
в формулу относительной ошибки выборки,
получим
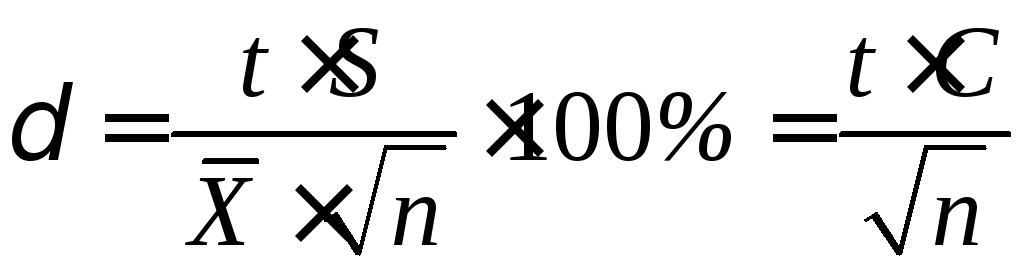
t
C
/
n
(45)
Выразив
из формулы (45) n,
получим
(46)
7. Сравнение двух выборок
7.1. Сравнение двух средних независимых выборок (критерий Стьюдента)
Часто
в процессе проведения испытаний
необходимо сравнить результаты двух
независимых выборок с тем, чтобы оценить
достоверность разности Х1
– Х2.
Если эта разность недостаточно значима,
то средние Х1
и Х2
могут относиться к одной и той же
генеральной совокупности. Если же эта
разность достаточно значима, то средние
Х1
и
Х2
относятся
к разным генеральным совокупностям или
к одной совокупности, но при измерении
величин Х1
и Х2
имеется достаточная разница в методах
их определения.
При
большом числе испытаний n>30
и m>30
критерий достоверности определяется
по формуле:
(47)
где
S1,
S2
– среднее
квадратическое отклонение в первой и
второй выборке;
n,
m
– число значений в первой и второй
выборке.
Полученное
значение сравнивают с табличными
значениями критерия Стьюдента.
При
малом числе испытаний n+m<60
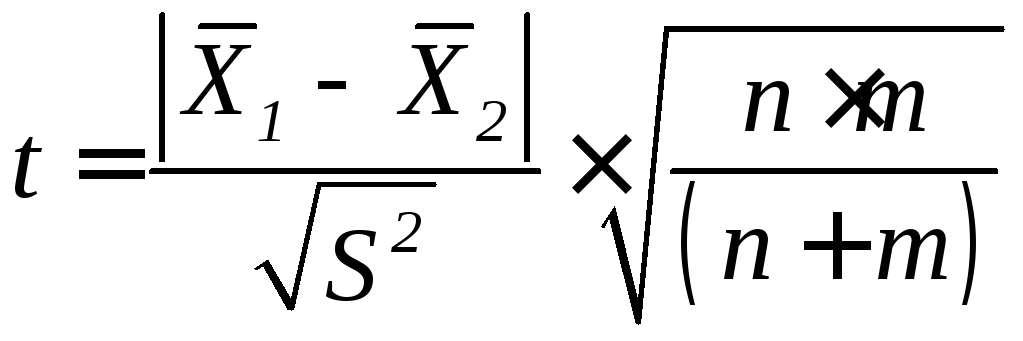
При
числе испытаний n=m<30
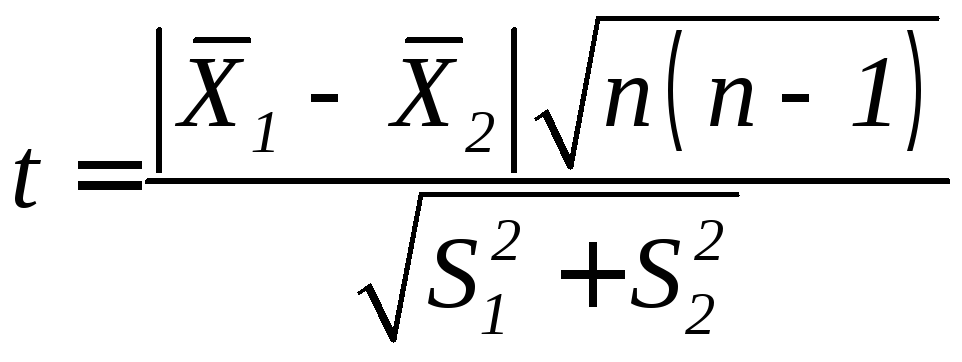
где
σ1,
σ2
– среднее
квадратическое отклонение в первой и
второй выборке.
При
использовании формулы (48) находят
значение
k
= n
+ m
-2 (50)
и
по таблице 14 для найденной величины k
и при вероятности 95% определяют табличное
значение t.
При
использовании формулы (49) находят
значение
k
= 2 .(n
— 1)
(51)
и
по таблице 14 для найденной величины k
и при вероятности 95% определяют табличное
значение t.
Если
tр
> t,
то разность средних Ха
–Хв
при нормальном распределении достоверна
более чем на 95%. Если tр
< t
, то разность средних не считается
достаточно достоверной.
Таблица
14
|
k |
t |
k |
t |
k |
t |
k |
t |
|
1 |
12,78 |
10 |
2,23 |
19 |
2,09 |
28 |
2,05 |
|
2 |
4,30 |
11 |
2,20 |
20 |
2,09 |
29 |
2,05 |
|
3 |
3,18 |
12 |
2,18 |
21 |
2,08 |
30 |
2,04 |
|
4 |
2,78 |
13 |
2,16 |
22 |
2,07 |
40 |
2,02 |
|
5 |
2,57 |
14 |
2,14 |
23 |
2,07 |
60 |
2,00 |
|
6 |
2,45 |
15 |
2,13 |
24 |
2,06 |
120 |
1,98 |
|
7 |
2,37 |
16 |
2,12 |
25 |
2,06 |
|
1,96 |
|
8 |
2,30 |
17 |
2,11 |
26 |
2,06 |
— |
— |
|
9 |
2,26 |
18 |
2,10 |
27 |
2,05 |
— |
— |
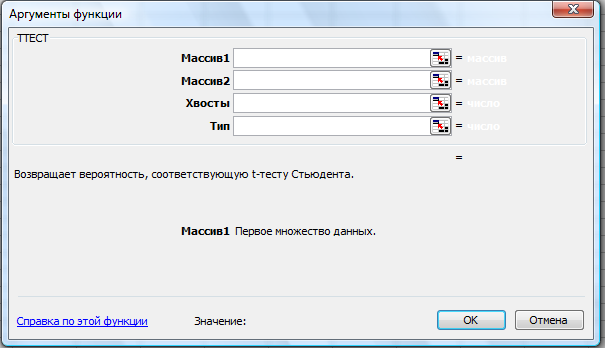
В
программе Excel применяется функция ТТЕСТ
(рис. 25). Она возвращает вероятность,
соответствующую критерию Стьюдента.
Функция ТТЕСТ используется, чтобы
определить, насколько вероятно, что две
выборки взяты из генеральных совокупностей,
которые имеют одно и то же среднее.
Рис.
25. Функция ТТЕСТ
ТТЕСТ(массив1;массив2;хвосты;тип)
Массив1
— первое множество данных.
Массив2
— второе множество данных.
Хвосты
— число хвостов распределения. Если
хвосты = 1, то функция ТТЕСТ использует
одностороннее распределение. Если
хвосты = 2, то функция ТТЕСТ использует
двустороннее распределение.
Тип
— вид исполняемого t-теста.
|
Тип |
Выполняемый |
|
1 |
Парный |
|
2 |
Двухвыборочный |
|
3 |
Двухвыборочный |
Если
массив1 и массив2 имеют различное число
точек данных, а тип = 1 (парный), то функция
ТТЕСТ возвращает значение ошибки #Н/Д.
Аргументы
хвосты и тип усекаются до целых.
Если
хвосты или тип не является числом, то
функция ТТЕСТ возвращает значение
ошибки #ЗНАЧ!.
Если
хвосты имеет значение, отличное от 1 и
2, то функция ТТЕСТ возвращает значение
ошибки #ЧИСЛО!.
TTEСT
использует данные массива1 и массива2
для вычисления неотрицательной
t-статистики. Если хвосты = 1, TTEСT возвращает
вероятность более высокого значения
t-статистики, исходя из предположения,
что массив1 и массив2 являются выборками,
принадлежащими одной и той же генеральной
совокупности. Значение, возвращаемое
функцией TTEСT в случае, когда хвосты = 2,
является двусторонним значением,
возвращаемым, когда хвосты = 1 и представляет
собой вероятность более высокого
абсолютного значения t-статистики,
исходя из предположения, что массив1 и
массив2 являются выборками, принадлежащими
одной и той же генеральной совокупности.
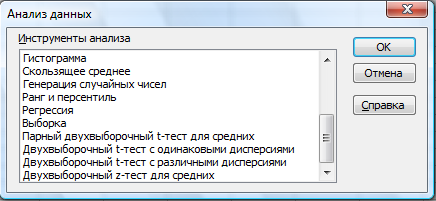
В
надстройке АНАЛИЗ
ДАННЫХ
представлено несколько типов теста для
сравнения выборочных средних (рис. 26).
Рис.
26. Пакет анализа
Двухвыборочный
t-тест проверяет равенство средних
значений генеральной совокупности по
каждой выборке. Эти три средства допускают
следующие условия: равные дисперсии
генерального распределения, дисперсии
генеральной совокупности не равны, а
также представление двух выборок до и
после наблюдения по одному и тому же
субъекту.
Для
всех трех средств, перечисленных ниже,
значение t-статистики t вычисляется и
отображается как «t-статистика» в
выводимой таблице. В зависимости от
данных, это значение t может быть
отрицательным или неотрицательным.
Если предположить, что средние генеральной
совокупности равны, при t < 0 “P(T <= t)
одностороннее” дает вероятность того,
что наблюдаемое значение t-статистики
будет более отрицательным, чем t. При t
>=0 “P(T <= t) одностороннее” делает
возможным наблюдение значения
t-статистики, которое будет более
положительным чем t. “t критическое
одностороннее” выдает пороговое
значение, так что вероятность наблюдения
значения t-статистики большего или
равного “t критическое одностороннее”
равно Alpha. “P(T <= t) двустороннее” дает
вероятность наблюдения значения
t-статистики по абсолютному значению
большего чем t. “P критическое двустороннее”
выдает пороговое значение, так что
значение вероятности наблюдения значения
t- статистики по абсолютному значению
большего “P критическое двустороннее”
равно Alpha.
Двухвыборочный
t-тест с одинаковыми дисперсиями.
Двухвыборочный t-тест Стьюдента служит
для проверки гипотезы о равенстве
средних для двух выборок. Эта форма
t-теста предполагает совпадение значений
дисперсии генеральных совокупностей
и обычно называется гомоскедастическим
t-тестом.
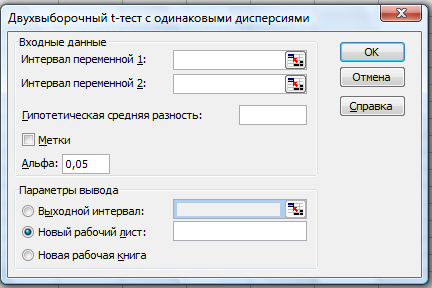
Элементы
диалогового окна «Двухвыборочный t-тест
с одинаковыми дисперсиями» приведены
на рис. 27.
Рис.
27. Двухвыборочный
t-тест с одинаковыми дисперсиями
Интервал
переменной 1. Дается ссылка на первый
диапазон анализируемых данных. Диапазон
должен состоять из одного столбца или
одной строки.
Интервал
переменной 2. Дается ссылка на второй
диапазон анализируемых данных. Диапазон
должен состоять из одного столбца или
одной строки.
Гипотетическая
средняя разность. Вводится число, равное
предполагаемой разности средних.
Значение 0 (нуль) указывает, что средние
принимаются равными.
Заголовки.
Если первая строка или первый столбец
входного интервала содержит заголовки,
то устанавливается флажок. Флажок
снимается, если заголовки отсутствуют;
в этом случае подходящие названия для
данных выходного диапазона будут созданы
автоматически.
Альфа.
Вводится уровень надежности для теста.
Его значение должно находиться в
диапазоне 0…1. Уровень альфа связан с
вероятностью возникновения ошибки типа
I (опровержение верной гипотезы).
Выходной
диапазон. Вводится ссылка на левую
верхнюю ячейку выходного диапазона.
Размер выходного диапазона будет
определен автоматически, и на экран
будет выведено сообщение в случае
возможного наложения выходного диапазона
на исходные данные.
Новый
лист. Устанавливается переключатель
таким образом, чтобы открыть новый лист
в книге и вставить результаты анализа,
начиная с ячейки A1. Если в этом есть
необходимость, введите имя нового листа
в поле, расположенном напротив
соответствующего положения переключателя.
Новая
книга. Устанавливается переключатель
таким образом, чтобы открыть новую книгу
и вставить результаты анализа в ячейку
A1 на первом листе в этой книге.
Результаты
расчетов выводятся в виде таблицы (табл.
15).
Таблица
15
|
Заголовок |
Объяснение |
|
Среднее |
Средние |
|
Дисперсия |
Дисперсии |
|
Наблюдения |
Число |
|
Объединенная |
Выборочная |
|
Гипотетическая |
Гипотетическая |
|
df |
Число |
|
t |
Расчетное |
|
P(T≤t) |
Значимость |
|
t |
Критическое |
|
P(T≤t) |
Значимость |
|
t |
Критическое |
Двухвыборочный
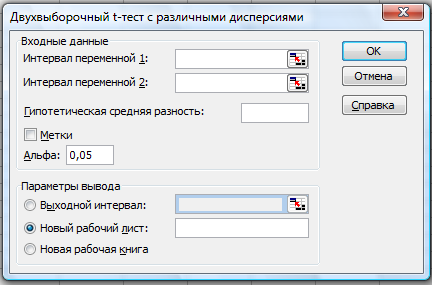
t-тест с разными дисперсиями.
Двухвыборочный t-тест Стьюдента (рис.
28) используется для проверки гипотезы
о равенстве средних для двух выборок
данных из разных генеральных совокупностей.
Эта форма t-теста предполагает несовпадение
дисперсий генеральных совокупностей
и обычно называется гетероскедастическим
t-тестом. Если тестируется одна и та же
генеральная совокупность, используется
парный тест.
Рис.
28.
Двухвыборочный
t-тест с разными дисперсиями
Для
определения тестовой величины t
используется следующая формула.
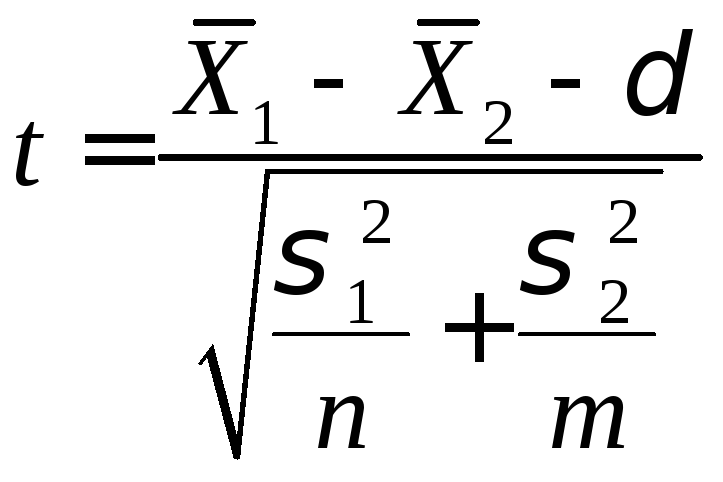
где
δ
— гипотетическая разность средних; .
Так
как результат вычисления обычно не
бывает целым числом, значение df
округляется до целого для получения
порогового значения из t-таблицы. Функция
Excel ТТЕСТ
по возможности использует вычисленные
значения без округления для вычисления
значения ТТЕСТ
с нецелым значением df. Из-за разницы
подходов к определению степеней свободы,
результаты функций ТТЕСТ
и t-тест будут различаться в случае с
разными дисперсиями. Следующая формула
используется для вычисления степени
свободы df.
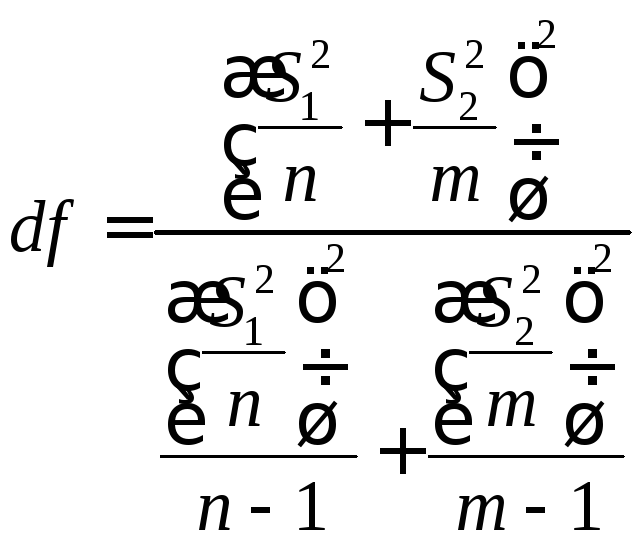
Элементы
диалогового окна «Двухвыборочный t-тест
с различными дисперсиями» совпадают с
элементами диалогового окна «Двухвыборочный
t-тест с одинаковыми дисперсиями»
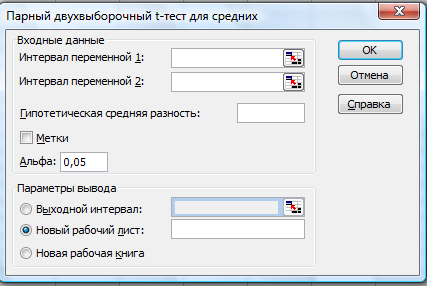
Парный
двухвыборочный t-тест для средних.
Парный двухвыборочный t-тест Стьюдента
(рис. 29) используется для проверки
гипотезы о различии средних для двух
выборок данных. В нем не предполагается
равенство дисперсий генеральных
совокупностей, из которых выбраны
данные. Парный тест используется, когда
имеется естественная парность наблюдений
в выборках, например, когда генеральная
совокупность тестируется дважды — до
и после эксперимента.
Рис.
29. Парный двухвыборочный t-тест для
средних
Одним
из результатов теста является совокупная
дисперсия (совокупная мера распределения
данных вокруг среднего значения),
вычисляемая по следующей формуле.
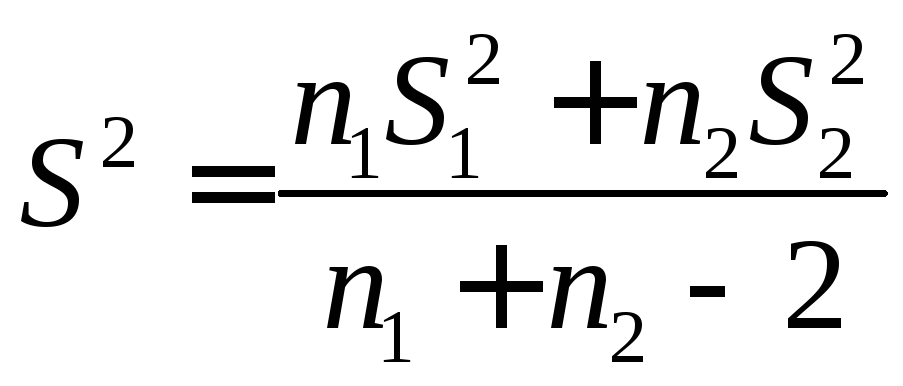
Элементы
диалогового окна «Парный двухвыборочный
t-тест для средних» совпадают с элементами
диалогового окна «Двухвыборочный t-тест
с одинаковыми дисперсиями».
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вероятность попадания средней или относительной величины в доверительный интервал называется доверительной вероятностью.
Доверительные границы средней арифметической генеральной совокупности определяют по формуле:
Мген = Мвыб ± t · mM
Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:
Рген = Рвыб ± t · mр
Где: Мген и Рген — значения средней и относительной величин, полученных для генеральной совокупности;
Мвыб и Рвыб — значения средней и относительной величин, полученных для выборочной совокупности;
mM и mр— ошибки репрезентативности выборочных величин;
t — доверительный критерий, который зависит от величины безошибочного прогноза, устанавливаемого при планировании исследования.
Произведение t · m (Δ) — предельная ошибка показателя, полученного при данном выборочном исследовании.
Размеры предельной ошибки зависят от коэффициента t, который избирает сам исследователь, исходя из заданной вероятности безошибочного прогноза.
Величина критерия t связана с вероятностью безошибочного прогноза (Р) и числом наблюдений в выборочной совокупности (табл. 4.1).
Таблица 4.1. Зависимость доверительного критерия t от степени вероятности безошибочного прогноза Р (при n > 30)
| Степень вероятности безошибочного прогноза (Р %) | Доверительный критерий t |
| 95,0 | |
| 99,0 | 2,6 |
| 99,9 | 3,3 |
Для большинства медико-биологических и социальных исследований
достоверными считаются доверительные границы, установленные с
вероятностью безошибочного прогноза = 95% и более.
Чтобы найти критерий t при числе наблюдений (n) < 30, необходимо
пользоваться специальной таблицей Н.А.Плохинского (табл. 4.2), в которой
слева показано число наблюдений — единица (n — 1), а сверху (Р) —
степень вероятности безошибочного прогноза.
При определении доверительных границ сначала надо решить вопрос о
том, с какой степенью вероятности безошибочного прогноза необходимо
представить доверительные границы средней или относительной величины.
Избрав определенную степень вероятности, соответственно этому находят
величину доверительного критерия t при данном числе наблюдений. Таким
образом, доверительный критерий устанавливается заранее, при
планировании исследования.
Таблица 4.2. Значение критерия t для трех степеней вероятности (по Н.А.Плохинскому)
| Р n = n-1 |
95% | 99% | 99,9% |
| 12,7 | 63,7 | 37,0 | |
| 4,3 | 9,9 | 31,6 | |
| 3,2 | 5,8 | 12,9 | |
| 2,8 | 4,6 | 8,6 | |
| 2,6 | 4,0 | 6,9 | |
| 2,4 | 3,7 | 6,0 | |
| 2,4 | 3,5 | 5,3 | |
| 2,3 | 3,4 | 5,0 | |
| 2,3 | 3,3 | 4,8 | |
| 2,2 | 3,2 | 4,6 | |
| 2,2 | 3,1 | 4,4 | |
| 2,2 | 3,1 | 4,3 | |
| 2,3 | 3,0 | 4,1 | |
| 14-15 | 2,1 | 3,0 | 4,1 |
| 16-17 | 2,1 | 2,9 | 4,0 |
| 18-20 | 2,1 | 2,9 | 3,9 |
| 21-24 | 2,1 | 2,8 | 3,8 |
| 25-29 | 2,0 | 2,8 | 3,7 |
Любой параметр (средняя или относительная величина) может оцениваться с учетом доверительных границ, полученных при расчете.
Например: требуется определить
доверительные границы среднего уровня пепсина у больных гипертериозом с
95% вероятностью безошибочного прогноза. Если известно, что:
n = 49;
Мвыб =1г%;
mм = ± 0,05г%
- Определение доверительных границ средней величины в генеральной совокупности:
Мген = Мвыб ± t · mM = 1г% ± 2 · 0,05г%
1г% + 0,1г% = 1,1 г%
Мген =
1г% — 0,1г% = 0,9 г%
Заключение: установлено с вероятностью
безошибочного прогноза 95%, что средний уровень пепсина в генеральной
совокупности у больных гипертериозом находится в пределах от 1,1 г% до
0,9 г%.
Как видно, доверительные границы зависят от размера доверительного интервала.
Анализ доверительных интервалов указывает, что при заданных степенях
вероятности и n > 30 — t имеет неизменную величину и при этом
доверительный интервал зависит от величины ошибки репрезентативности.
С уменьшением величины ошибки суживаются доверительные границы
средних и относительных величин, полученных на выборочной совокупности,
т.е. уточняются результаты исследования, которые приближаются к
соответствующим величинам генеральной совокупности. Если ошибка большая,
то получают для выборочной величины большие доверительные границы,
которые могут противоречить логической оценке искомой величины в
генеральной совокупности. В подобном случае надо искать резервы
сокращения размаха доверительных границ в размере величины ошибки
репрезентативности.
Доверительные границы Мвыб и Рвыб
зависят не только от средних ошибок этих величин, но и от избранной
исследователем степени вероятности безошибочного прогноза. При большой
степени вероятности размах доверительных границ увеличивается.
3. Определение достоверности разности средних (или относительных) величин (по критерию t — Стъюдента).
В медицине и здравоохранении по разности параметров оценивают
средние и относительные величины, полученные для разных групп населения
по полу, возрасту, а также групп больных и здоровых и т.д. Во всех
случаях при сопоставлении двух сравниваемых величин возникает
необходимость не только определить их разность, но и оценить ее
достоверность.
Достоверность разности величин, полученных при выборочных
исследованиях, означает, что вывод об их различии может быть перенесен
на соответствующие генеральные совокупности.
Достоверность разности выборочной совокупности измеряется доверительным критерием, который рассчитывается по специальным формулам для средних и относительных величин.
Формула оценки достоверности разности сравниваемых средних величин:
M1 — M2
m12 + m22
Для относительных величин:
Р1 — Р2
m12 + m22
Где: M1; M2 ; Р1; Р2 — параметры, полученные при выборочных исследованиях;
m1; m2 — их средние ошибки;
t — критерий достоверности (Стъюдента).
Разность статистически достоверна при t ≥ 2, что соответствует вероятности безошибочного прогноза, равной 95% и более.
Для большинства исследований, проводимых в медицине и здравоохранении, такая степень вероятности является вполне достаточной.
При величине критерия достоверности t < 2 степень вероятности
безошибочного прогноза составляет Р < 95%. При такой степени
вероятности нельзя утверждать, что полученная разность показателей
достоверна с достаточной степенью вероятности. В этом случае необходимо
получить дополнительные данные, увеличив число наблюдений.
Иногда при увеличении численности выборки разность продолжает
оставаться не достоверной. Если при повторных исследованиях разность
остается недостоверной, можно считать доказанным, что между
сравниваемыми совокупностями не обнаружено различий по изучаемому
признаку.
Например: требуется определить, достоверны ли
различия в уровне пепсина в желудочном соке больных гипертериозом и
здоровых лиц. Обследуются на пепсин две группы: 49 больных гипертериозом
и 50 здоровых людей (контрольная группа). Результаты представлены в
таблице 4.3.
Таблица 4.3. Сравнение среднего уровня пепсина в желудочном соке больных гипертериозом и здоровых лиц
| Сравниваемые группы |
N |
М |
m |
t |
Уровень вероятности безошибочного прогноза (Р) |
| Больные гипертериозом | 1,0 | ± 0,3 | 10,0 |
< 99,9 |
|
| Здоровые (контрольная группа) | 4,0 | ± 0,1 |
M1 — M2
m12 + m22
4 — 1
t = —————- = 10,0
0,32 + 0,12
Погрешность и доверительный интервал: в чем разница?
читать 2 мин
Часто в статистике мы используем доверительные интервалы для оценки значения параметра совокупности с определенным уровнем достоверности.
Каждый доверительный интервал принимает следующий вид:
Доверительный интервал = [нижняя граница, верхняя граница]
Погрешность равна половине ширины всего доверительного интервала.
Например, предположим, что у нас есть следующий доверительный интервал для среднего значения генеральной совокупности:
95% доверительный интервал = [12,5, 18,5]
Ширина доверительного интервала составляет 18,5 – 12,5 = 6. Допустимая погрешность равна половине ширины, которая будет равна 6/2 = 3 .
В следующих примерах показано, как рассчитать доверительный интервал вместе с погрешностью для нескольких различных сценариев.
Пример 1: Доверительный интервал и допустимая погрешность для среднего значения генеральной совокупности
Мы используем следующую формулу для расчета доверительного интервала для среднего значения генеральной совокупности:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: z-критическое значение
- s: стандартное отклонение выборки
- n: размер выборки
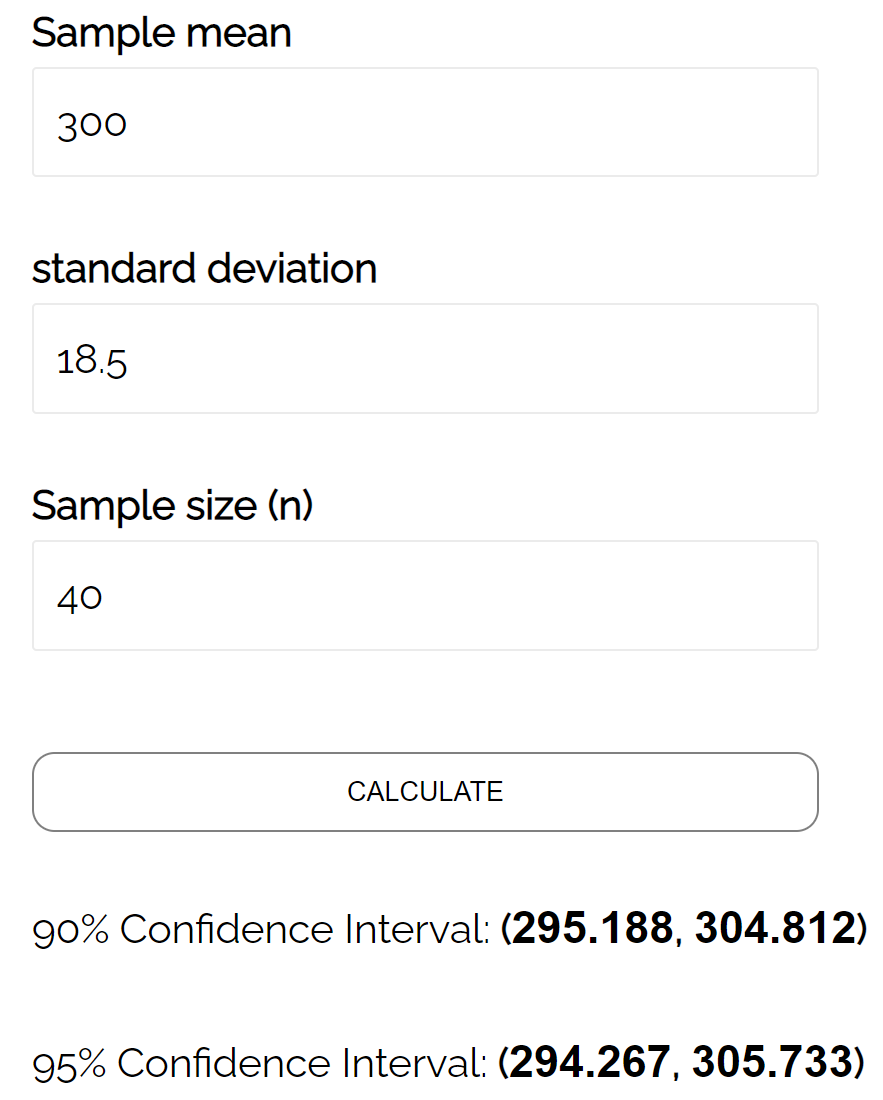
Пример: Предположим, мы собираем случайную выборку дельфинов со следующей информацией:
- Размер выборки n = 40
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
Мы можем подставить эти числа в калькулятор доверительного интервала , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинного среднего веса популяции черепах составляет [294,267, 305,733] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (305,733 – 294,267) / 2 = 5,733 .
Пример 2: Доверительный интервал и допустимая погрешность для доли населения
Мы используем следующую формулу для расчета доверительного интервала для доли населения:
Доверительный интервал = p +/- z * (√ p (1-p) / n )
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Пример: Предположим, мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:
- Размер выборки n = 100
- Доля в пользу закона p = 0,56
Мы можем подставить эти числа в доверительный интервал для калькулятора пропорций , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинной доли населения составляет [0,4627, 0,6573] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (0,6573 – 0,4627) / 2 = 0,0973 .
Дополнительные ресурсы
Погрешность и стандартная ошибка: в чем разница?
Как найти погрешность в Excel
Как найти погрешность на калькуляторе TI-84

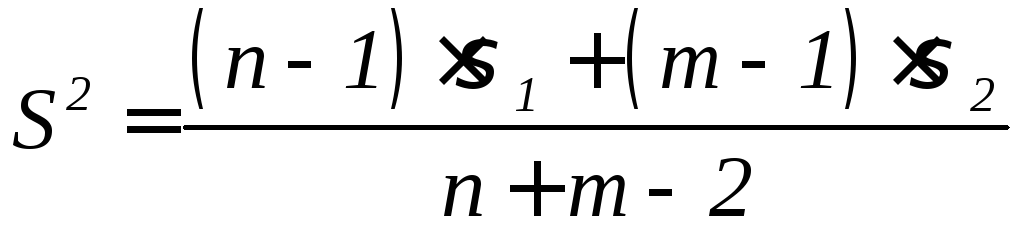
 ,
,