Относительная ошибка буква - Oshibku.top - решение и исправление самых разных ошибок

Абсолютная и относительная погрешности

Пусть X–
некоторая физическая величина,x–
результат её измерения,х– истинное значение. Так как не существуют
идеальные измерительные приборы, и
человек, проводящий измерения, тоже
далёк от совершенства, то ясно, чтоxx.
Повторное измерение величиныX,
произведённое в тех же условиях и с
помощью тех же измерительных приборов,
даст другое значениеx,
которое тоже не равно истинному значениюx.

Область значений, в которой лежат
возможные результаты измерения величины
Xдля данной методики измерений и
при данных измерительных приборах,
называетсядоверительным интерваломвеличиныX.

Доверительный
интервал изображён на рисунке 1.1.

Чем меньше
ширина доверительного интервала 2(x),
тем точнее можно измерить величинуXи тем меньшепогрешность.

Абсолютной погрешностью(x)
измерения величиныXназываетсяполуширина доверительного интервала.

Относительной погрешностьюизмерения
величиныXназываетсяотношение
абсолютной погрешности(x)к результату измеренияx.
Относительная погрешность обозначается
буквами(x)
или(x).

.(1.1)

Часто относительную
погрешность измеряют в процентах.
Тогда формулу (1.1) пишут в виде:

. (1.2)

Приборная и случайная погрешности

Погрешность
измерения величины Xможно разделить
на сумму двух составляющих –приборную
погрешность_п(x)
ислучайную_с(x):

. (1.3)

Приборная
погрешность определяется классом
точностиприборов, применяемых для
измеренияX, случайная погрешность
определяется действиемслучайных
факторов– неточностью действий
человека, производящего измерения, и
колебаний параметров среды, в том числе
параметров измерительной установки
(давления, температуры, освещённости,
напряжения в сети и т.д.).

Оценка приборной
погрешности зависит от того, к какому
из двух классов относится способ
измерения величины X. Первый класс
– этопрямые измерения, второй класс
–косвенные измерения.

Прямые и косвенные измерения

Результат
прямого измерения – это отсчёт по
шкалеизмерительного прибора. Результат
косвенного измерения получается в два
этапа: на первом из них производится
одно или несколькопрямых измерений,
на втором этапе проделывается некоторыйрасчёт, использующий результаты
прямых измерений первого этапа. Например,
если измерить глубину пустого колодца,
спускаясь в него с рулеткой в руках, то
это будетпрямое измерение. Если же
сбросить в колодец камень, измерить по
секундомерувремя падениякамня на
дноt, а затем вычислить глубину по
формуле,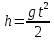
то полученное число будет результатомкосвенного измеренияглубины колодцаh.

Приборная погрешность прямого измерения

Для того чтобы
оценить приборную погрешность прямого
измерения, достаточно знать класс
точностиприменяемого прибора, который указывается
на шкале или корпусе прибора либо в виде
числа с указанием единиц измерения,
либо в виде одного из чисел: 0,01; 0,02; 0,1;
0,5; 1,0; 1,5; 2,5; 4,0 без единиц измерения. Смысл
термина «класс точности» зависит от
типа прибора. Отличить эти типы друг от
друга можнопо способу указанияна
них класса точности.

1 тип. Класс
точностиуказан
на приборе в виде числа с указанием
единиц измерения. Примером является
штангенциркуль, фрагмент которого
показан на рисунке 1.2.

Для такого
прибора класс точности – это абсолютнаяприборная погрешность:.
Для любого результата измеренияабсолютнаяприборная погрешность
– одна и та же, но относительная
погрешность
уменьшается с ростомx. Для
штангенциркуля, показанного на рисунке
1.2,.

2 тип. Класс
точностиуказан
на приборе в виде одного из чисел 0,01;
0,02; 0,1; 0,5; 1,0; 1,5; 2,5; 4,0 без каких-либо
дополнительных значков.

Пример:
микроамперметр, шкала которого изображена
на рисунке 1.3, обладает классом точности
1,5.

Приборы этого
типа выполнены так, что их абсолютнаяприборная погрешность_п(x)не зависитот результата измеренияx, и поэтому относительная погрешностьуменьшается с ростомx. При этом под
классом точности понимается следующая
величина:

, (1.4)

где
x_N– так называемое «нормирующее значение».
Для всех приборов, которые применяются
в учебной лаборатории, нормирующее
значение – это предел измерения, то
есть максимальное значение величины,
которое может показать прибор. Например,
у микроамперметра на рисунке 1.2 нормирующее
значениеx_N= 100 мкА.

Зная класс
точности и нормирующее
значениеx_N,
можно определить абсолютную приборную
погрешность_п(x)
по формуле

. (1.5)

Относительная
приборная погрешность, как указывалось
выше, зависит от результата измерения
x.

Микроамперметр,
показанный на рисунке 1.3, обеспечивает
абсолютную приборную погрешность
измерения тока
,
относительная приборная погрешность
того результата, который показывает
микроамперметр, то естьI= 30 мкА,
составляет.

3 тип. Класс
точностиуказан
на приборе в виде одного из чисел 0,01;
0,02; 0,1; 0,5; 1,0; 1,5; 2,5; 4,0, причём это числообведёно кружком. Пример такого
прибора показан на рисунке 1.4.

Приборы этого
типа выполнены так, что их относительнаяприборная погрешностьδ_п(x)
не зависит от результата измеренияx.
Класс точностив этих приборах – это относительная
приборная погрешностьδ_п(x),
измеренная в процентах. Абсолютная
приборная погрешность при этом зависит
от результата измеренияx– чем
большеx, тем больше_п(x):

(1.6)

Например,
относительная погрешность измерения
напряжения с помощью вольтметра,
изображённого на рисунке 1.4, равна 2,5%,
а абсолютная погрешность того результата,
который показывает вольтметр, то есть
U= 45 В, составляет.

4 тип. Класс
точностине указан. В этом случае,
как и для приборов 1 типа,абсолютнаяпогрешность_п(x)
не зависит от результата измеренияx.
Если прибор – цифровой, то_п(x)
равна 1 вмладшемразряде прибора.
Если прибор – не цифровой, например,
миллиметровая линейка или бытовой
уличный термометр, то_п(x)
равнаполовине цены деленияприбора.

Правда, это
правило не следует применять как догму.
Пример: необходимо линейкой измерить
размер Lнекоторого
предмета. Процедура измерения состоит
в том, что линейку располагают вдоль
предмета, причём один край предмета
совмещают с нулём линейки. Тогда размер
предметаLравен тому
показанию линейки, которое находится
против другого края предмета. В этом
случае погрешность измерения связана
не только с погрешностью отсчёта по
линейке, но и с погрешностью нулевого
деления. Поэтому рекомендуется считать
приборную погрешность в подобных
ситуациях равной не половине деления
шкалы, а целому делению. Если, например,
линейка миллиметровая, то_п(L)
= 1 мм.

Соседние файлы в папке Пособия к лаб. работам

Источник

Погрешность средств измерения и результатов измерения.

Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.

Инструментальные и методические погрешности.

Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.
Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях.
Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Систематическая и случайная погрешности.

Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Причинами возникновения систематических составляющих погрешности измерения являются:

отклонение параметров реального средства измерений от расчетных значений, предусмотренных схемой;
неуравновешенность некоторых деталей средства измерений относительно их оси вращения, приводящая к дополнительному повороту за счет зазоров, имеющихся в механизме;
упругая деформация деталей средства измерений, имеющих малую жесткость, приводящая к дополнительным перемещениям;
погрешность градуировки или небольшой сдвиг шкалы;
неточность подгонки шунта или добавочного сопротивления, неточность образцовой измерительной катушки сопротивления;
неравномерный износ направляющих устройств для базирования измеряемых деталей;
износ рабочих поверхностей, деталей средства измерений, с помощью которых осуществляется контакт звеньев механизма;
усталостные измерения упругих свойств деталей, а также их естественное старение;
неисправности средства измерений.

Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.

Погрешности адекватности и градуировки.

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.

Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.

Абсолютная, относительная и приведенная погрешности.

Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.

Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.

Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

– если шкала прибора односторонняя и нижний предел измерений равен нулю (например диапазон измерений 0…100), то Xn определяется равным верхнему пределу измерений (Xn=100);
– если шкала прибора односторонняя, нижний предел измерений больше нуля, то Xn определяется как разность между максимальным и минимальным значениями диапазона (для прибора с диапазоном измерений 30…100, Xn=Xmax-Xmin=100-30=70);
– если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора (диапазон измерений -50…+50, Xn=100).

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

Аддитивные и мультипликативные погрешности.

Аддитивной погрешностью называется погрешность, постоянную в каждой точке шкалы.
Мультипликативной погрешностью называется погрешность, линейно возрастающую или убывающую с ростом измеряемой величины.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.

Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).

Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:

– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).

Источник

ГОССТАНДАРТ РОССИИ

НПО «ВНИИМ им. Д.И. Менделеева»

РЕКОМЕНДАЦИЯ

Государственная система обеспечения единства измерений

Погрешности измерений. Обозначения

МИ 2246-93

Группа Т80

Введены в действия с 01.07.93

Рекомендация распространяется на нормативно-техническую документацию (далее — НТД) и устанавливает обозначения погрешностей измерений физических величин.

1.1 Погрешность измерения — отклонение результата измерения от действительного значения измеряемой величины — может состоять из инструментальной погрешности, погрешности метода, погрешности оператора и др. погрешностей.

Погрешность измерения и ее составляющие представлены на схеме в приложении 1.

1.2 Погрешность измерения при воспроизведении единицы физической величины называют погрешностью воспроизведения единицы, а при передаче размера единицы физической величины называют погрешностью передачи размера единицы величины или погрешностью поверки (погрешностью аттестации).

1.3 Погрешности измерений подразделяют:

в зависимости от характера проявления на систематические, случайные;

в зависимости от характера их изменения в диапазоне измеряемой величины на аддитивные и мультипликативные;

по форме представления на абсолютные и относительные.

1.4 Погрешность измерения может быть выражена в виде:

доверительного интервала;

пределов погрешности;

комплекса характеристик распределения погрешностей (среднее квадратическое отклонение, размах, среднее арифметическое и др. характеристики).

Примечание: задаваемые или допускаемые характеристики погрешностей измерений могут быть выражены в соответствии с требованиями, установленными в МИ 1317-86, в форме

предела допускаемых значений характеристики;

нижнего и верхнего пределов допускаемых значений характеристики;

1.5 Наибольший вклад в погрешность измерений, как правило, вносит инструментальная погрешность, обусловленная погрешностью применяемого средства измерений (далее — СИ).

Инструментальная погрешность и ее составляющие приведены в приложении 2.

2. Обозначения погрешностей

2.1 Для обозначения какой-либо погрешности используют букву греческого алфавита «дельта» — Δ (прописная), δ (строчная).

Прописной буквой Δ обозначают абсолютную погрешность измерения и строчной буквой δ — относительную погрешность измерения.

2.2 Неисключенную систематическую погрешность измерения рекомендуется обозначать буквой греческого алфавита «тэта» — θ.

2.3 Среднее квадратическое отклонение и размах — характеристики случайной погрешности — рекомендуется обозначать буквами латинского алфавита S и R, соответственно.

2.4 Поправку, которую вводят в неисправленный результат измерения с целью исключения одной или нескольких систематических погрешностей, обозначают символом (перевернутой буквой греческого алфавита «дельта»).

2.5 Метрологические характеристики СИ — нестабильность и вариацию — рекомендуется обозначать буквой греческого (ню) и латинского V алфавитов соответственно.

2.6 Для наглядности вышеизложенное сведено в табл. 1.

3.1 При необходимости конкретизации погрешности измерения (указания ее составляющей, формы представления или внесения других уточняющих данных) рекомендуется символ погрешности сопровождать индексом (индексами).

Если текст НТД не вызывает затруднений при прочтении обозначений погрешностей измерений, индексация необязательна.

3.2 В качестве индексов используют первую букву, несколько букв того слова, которое определяет или источник погрешности, или форму представления ее, или другие особенности погрешности.

3.3 Для индексации рекомендуется применять буквы русского, латинского и греческого алфавитов. (Например, Δ_ε — суммарная погрешность результата измерения). Индексы пишутся как прописными, так и строчными буквами.

3.4 При необходимости указания физической величины, погрешность которой оценивается, в качестве индекса рекомендуется использовать символ этой физической величины. (Например, Δ_L — абсолютная погрешность измерений длины, δ_M — относительная погрешность измерения массы и т.д.).

Обозначения (символы) наиболее распространенных физических величин представлены в приложении 3.

Примечание: если в тексте измеряемую величину обозначают символом х, у и т д., то и погрешность измерения этих величин обозначают соответственно Δ_х или δ_х, Δ_у или δ_у и т.д.

3.5 Дополнительную погрешность средств измерений, возникающую вследствие изменения показаний последних из-за воздействия влияющих величин, обозначают либо Δ_доп — (дополнительная абсолютная погрешность СИ), либо δ_доп — (дополнительная относительная погрешность СИ).

Дополнительную погрешность результата измерения, возникающую вследствие воздействия влияющих величин на измеряемую величину, обозначают либо Δ_ВВ, либо δ_ВВ.

3.6 В приложении 4 дан перечень допускаемых сокращений слов, применяемых в метрологической практике для указания источника погрешности (составляющих погрешности измерений).

3.7 Для индексации символов при обозначении погрешности средств измерений рекомендуется использовать аббревиатуру, уточняющую вид средства измерений. (Например, Δ_СИ — абсолютная погрешность средства измерений, δ_ИИС — относительная погрешность измерительной информационной системы и т.д.).

В приложении 5 приведена аббревиатура для обозначения некоторых средств измерений.

4.1 При необходимости указания нескольких индексов у одного символа сначала указывается индекс, характеризующий источник погрешности (составляющую погрешности), а потом — индекс, характеризующий форму ее представления, (например, предел погрешности метода, заданной в абсолютной форме, должен быть выражен как Δм,пр).

4.2 Если наличие нескольких индексов у одного символа приводит к затруднению их раздельного прочтения, их разделяют запятой. (Например, Δо,пр — предел допускаемой основной погрешности средства измерений в абсолютной форме, δ_{дин,макс} максимальное значение динамической погрешности средства измерений в относительной форме).

4.3 Допустимо применять символы погрешностей, опуская некоторые индексы, если это не приводит к затруднению понимания текста. (Например, если речь идет о конкретном средстве измерений, то индекс в виде аббревиатуры, конкретизирующий средство измерений, можно опускать.

Если в НТД речь идет об измерении конкретной физической величины и ее погрешности измерения, то индекс, конкретизирующий измеряемую величину, можно опустить.

Наличие индексов «о» (основная), «доп» (дополнительная), «прв» (приведенная) снимает необходимость дополнительного указания индекса «СИ».

4.4 Для пояснения того, характеристику какой погрешности представляет среднее квадратическое отклонение «S», рекомендуется сразу после символа «S» указывать в круглых скобках эту погрешность. (Например, S (Δдоп) — среднее квадратическое отклонение дополнительной погрешности средства измерений).

Среднее квадратическое отклонение единичного результата измерений рекомендуется обозначать только символом «S».

При обозначении среднего квадратического отклонения результата многократных измерений (среднего арифметического) сразу после символа «S» в круглых скобках указывают символ результата измерений. (Например, S() — среднее квадратическое отклонение среднего арифметического группы экспериментальных данных).

4.5 При указании нестабильности «v» метрологической характеристики последнюю указывают в круглых скобках после символа нестабильности. (Например, v(Δсист) — нестабильность систематической погрешности).

Время, в течение которого фиксируется нестабильность, чаще всего указывается в тексте документа или в техническом тексте.

При необходимости указания времени нестабильности в обозначении, оно указывается символом «τ» в качестве индекса к символу нестабильности v. (Например, v_τ (Δсист) — нестабильность систематической погрешности за время τ).

4.6 Доверительную погрешность рекомендуется обозначать соответствующим символом погрешности с указанием вероятности в круглых скобках после символа этой погрешности. (Например, Δ(0.95) — абсолютная доверительная погрешность измерения при вероятности Р = 0.95).

4.7 Структура обозначений наиболее часто употребляемых погрешностей приведена в виде примера ниже.

Приложение 1

ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ И ЕЕ СОСТАВЛЯЮЩИЕ*

* Примечание: на рисунке приведены в качестве примеров возможные составляющие погрешности измерения для лучшего понимания принципов индексации.

Приложение 2

ИНСТРУМЕНТАЛЬНАЯ ПОГРЕШНОСТЬ И ЕЕ СОСТАВЛЯЮЩИЕ *

* Примечание: на рисунке приведены в качестве примеров возможные составляющие инструментальной погрешности для лучшего понимания индексации.

Приложение 3

Обозначения (символы) наиболее распространенных

физических величин

Приложение 4

Перечень допускаемых сокращений слов,

используемых в качестве индекса

для метрологической практики

Примечание: предлагаемые сокращения не всегда совпадают с правилами сокращений в русском языке, но авторы ориентировались на краткость сокращений с целью удобства индексации.

Приложение 5

Аббревиатура для обозначений некоторых средств измерений

Источник

ВИДЕО УРОК

Абсолютная погрешность.

Разность между истинным значением измеряемой величины
и её приближённым значением называется абсолютной погрешностью.

Для подсчёта
абсолютной погрешности необходимо из большего числа вычесть меньшее число.

Существует формула
абсолютной погрешности. Обозначим точное число буквой А, а буквой а –
приближение к точному числу. Приближённое число – это число, которое
незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда
формула будет выглядеть следующим образом:

∆а = А – а.

ПРИМЕР:

В школе учится 374 ученика. Если округлить это число до 400,
то абсолютная погрешность измерения равна:

400 – 374 = 26.

ПРИМЕР:

На предприятии 1284 рабочих и
служащих. При округлении этого числа до 1300 абсолютная
погрешность составляет

1300 – 1284 = 16.

При округлении до 1280 абсолютная
погрешность составляет

1284 – 1280 = 4.

Редко когда можно
точно знать значение измеряемой величины, чтобы рассчитать абсолютную
погрешность. Но при выполнении различных измерений мы обычно представляем себе
границы абсолютной погрешности и всегда можем сказать, какого определённого
числа она не превосходит.

ПРИМЕР:

Торговые весы могут дать абсолютную погрешность, не
превышающую 5 г, а аптекарские – не превышающую одной сотой грамма.

Записывают
абсолютную погрешность числа, используя знак
±.

ПРИМЕР:

Длина рулона обоев составляет.

30 м ± 3
см.

Границу абсолютной
погрешности называют предельной абсолютной погрешностью.

Но абсолютная
погрешность не даёт нам представление о качестве измерения, то есть о том,
насколько тщательно это измерение выполнено. Чтобы понять эту мысль, достаточно
разобраться в таком примере.

ПРИМЕР:

Допустим, что при измерении коридора длиной в 20
м мы допустили абсолютную погрешность
всего только в 1 см. Теперь представим себе, что, измеряя корешок книги,
имеющий 18
см длины, мы тоже допустили абсолютную
погрешность в 1 см. Тогда понятно, что первое измерение нужно признать
превосходным, но зато второе – совершенно неудовлетворительным. Это значит, что
на 20
м ошибка в 1
см вполне допустима и неизбежна, но
на 18
см такая ошибка является очень грубой.

Отсюда ясно, что для оценки качества измерения
существенна не сама абсолютная погрешность, а та доля, какую она составляет от
измеряемой величины. При измерении коридора длиной в 20 м погрешность в 1 см
составляет

долю
измеряемой величины, а при измерении корешка книги погрешность в 1 см составляет

долю
измеряемой величины.

Делаем вывод, что измеряя корешок книги, имеющий 18
см длины и допустив погрешность в 1
см, можно считать измерение с большой ошибкой. Но если погрешность в 1
см была допущена при измерении коридора
длиной в 20
м, то это измерение можно считать максимально точным.

Если ошибка,
возникающая при измерении линейкой или каким либо другим измерительным
инструментом, значительно меньше, чем деления шкалы этой линейки, то в качестве
абсолютной погрешности измерения обычно берут половину деления. Если деления на
линейке нанесены достаточно точно, то ошибка при измерении близка к нулю.

Тогда
значение измеряемой длины предмета будет значение ближайшей метки линейки.
Поэтому, если измерение выполнено аккуратно, то истинная длина предмета может
отличаться от измеренной длины не более чем на половину деления шкалы, то есть 0,5 мм.

ПРИМЕР:

Для измерения длины болта использованы метровая линейка с
делениями 0,5 см и линейка с
делениями 1 мм. В обоих случаях получен результат 3,5
см. Ясно, что в первом случае отклонение найденной длины 3,5
см от истинной, не
должно по модулю превышать 0,5 см, во втором случае
0,1 см.

Если этот же результат получится при измерении
штангенциркулем, то

p(l; 3,5) = |l – 3,5 ≤ 0,01|.

Данный пример показывает зависимость абсолютной
погрешности и границ, в которых находится точный результат, от точности
измерительных приборов. В одном случае ∆l = 0,5 и, следовательно,

3
≤ l ≤ 4,

в другом – ∆l = 0,1 и

3,4
≤ l ≤ 3,6.

ПРИМЕР:

Длина листа бумаги формата А4 равна (29,7 ± 0,1)
см. А расстояние от Санкт-Петербурга до Москвы равно (650 ± 1) км. Абсолютная погрешность в первом случае
не превосходит одного миллиметра, а во втором – одного километра. Необходимо
сравнить точность этих измерений.

РЕШЕНИЕ:

Если вы думаете, что длина листа измерена точнее потому,
что величина абсолютной погрешности не
превышает 1 мм, то вы ошибаетесь.
Напрямую сравнить эти величины нельзя. Проведём некоторые рассуждения.

При измерении длины листа абсолютная погрешность не
превышает 0,1 см на 29,7 см, то есть в процентном отношении это составляет

0,1
: 29,7 ∙ 100% ≈ 0,33%

измеряемой величины.

Когда мы измеряем расстояние от Санкт-Петербурга до
Москвы, то абсолютная погрешность не превышает
1 км
на 650 км, что в процентном соотношении составляет

1
: 650 ∙ 100% ≈ 0,15%

измеряемой величины.

Видим, что расстояние между городами измерено точнее, чем
длинна листа формата А4.

Истинное значение
измеряемой величины известно бывает лишь в очень редких случаях, а поэтому и
действительная величина абсолютной погрешности почти никогда не может быть вычислена.
На практике абсолютной погрешности недостаточно для точной оценки измерения.
Поэтому на практике более важное значение имеет определение относительной
погрешности измерения.

Относительная погрешность.

Абсолютная
погрешность, как мы убедились, не даёт возможности судить о качестве измерения.
Поэтому для оценки качества приближения вводится новое понятие – относительная
погрешность. Относительная погрешность позволяет судить о качестве измерения.

Относительная погрешность –
это частное от деления абсолютной погрешности на модуль приближённого значения
измеряемой величины, выраженная в долях или процентах.

Относительная
погрешность величина всегда положительная. Это следует из того, что абсолютная погрешность
всегда положительная величина, и мы делим её на модуль приближённого значения
измеряемой величины, а модуль тоже всегда положителен.

ПРИМЕР:

Округлим дробь 14,7 до целых и найдём относительную погрешность приближённого
значения:

14,7 ≈ 15,

Для вычисления
относительной погрешности, кроме приближённого значения, нужно знать ещё и
абсолютную погрешность. Обычно абсолютная погрешность неизвестна, поэтому
вычислить относительную погрешность нельзя. В таких случаях ограничиваются
оценкой относительной погрешности.

ПРИМЕР:

При измерении в (сантиметрах) толщины
b
стекла и длины l книжной полки
получили следующие результаты:

b ≈ 0,4 с
точностью до 0,1,

l ≈ 100 с
точностью до 0,1.

Абсолютная погрешность каждого из этих измерений не
превосходит 0,1. Однако 0,1 составляет
существенную часть числа 0,4 и
ничтожную часть числа 100. Это показывает, что качество второго
измерения намного выше, чем первого.

В результате измерения нашли,
что b ≈ 0,4 с точностью до 0,1, то
есть абсолютная погрешность измерения не превосходит 0,1.
Значит, отношение абсолютной погрешности к приближённому значению меньше или равно

то есть относительная погрешность приближения не превосходит 25%.

Аналогично найдём, что
относительная погрешность приближения, полученного при измерении длины полки,
не превосходит

Говорят, что в первом случае измерение выполнено с
относительной точностью до 25%,
а во втором – с относительной точностью до 0,1%.

ПРИМЕР:

Если взять абсолютную погрешность в 1
см, при измерении длины отрезков 10
см и 10
м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для
отрезка длиной в 10 см погрешность
в 1
см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, эта ошибка всего в 0,1%.

Чем меньше относительная погрешность
измерения, тем оно точнее.

Различают
систематические и случайные погрешности.

Систематической погрешностью называют ту погрешность, которая остаётся неизменной при
повторных измерениях.

Случайной погрешностью называют ту погрешность, которая возникает в результате
воздействия на процесс измерения внешних факторов и может изменять своё
значение.

В большинстве
случаев невозможно узнать точное значение приближённого числа, а значит, и
точную величину погрешности. Однако почти всегда можно установить, что
погрешность (абсолютная или относительная) не превосходит некоторого числа.

ПРИМЕР:

Продавец взвешивает арбуз на чашечных весах. В наборе
наименьшая гиря – 50
г. Взвешивание показало 3600 г. Это число – приближённое. Точный вес арбуза
неизвестен. Но абсолютная погрешность не превышает 50
г. Относительная погрешность не превосходит

⁵⁰/₃₆₀₀ ≈
1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной
погрешностью.

Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной
погрешностью.

В предыдущем примере
за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность 1,4%.

Величина предельной
погрешности не является вполне определённой. Так в предыдущем примере можно
принять за предельную абсолютную погрешность
100 г, 150 г и вообще всякое
число, большее чем 50 г.
На практике берётся по возможности меньшее значение предельной погрешности. В
тех случаях, когда известна точная величина погрешности, эта величина служит
одновременно предельной погрешностью. Для каждого приближённого числа должна
быть известна его предельная погрешность (абсолютная или относительная). Когда
она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено
приближённое число 4,78 без указания предельной погрешности, то подразумевается,
что предельная абсолютная погрешность составляет 0,005. В следствии этого соглашения всегда можно обойтись без указания
предельной погрешности числа.

Предельная
абсолютная погрешность обозначается греческой буквой ∆ (<<дельта>>),
предельная относительная погрешность – греческой буквой δ
(<<дельта малая>>). Если приближённое число обозначить буквой а,

Правила округления.

На практике
относительную погрешность округляют до двух значащих цифр, выполняя округление
с избытком, то есть, всегда увеличивая последнюю значащую цифру на единицу.

ПРИМЕР:

Для х = 1,7 ± 0,2 относительная погрешность измерений равна:

ПРИМЕР:

Длина карандаша измерена линейкой с миллиметровым
делением. Измерение показало 17,9 см. Какова предельная относительная погрешность этого
измерения ?

РЕШЕНИЕ:

Здесь а =
17,9 см. Можно принять ∆ = 0,1 см, так как с точностью
до 1 мм
измерить карандаш нетрудно, а значительно уменьшить предельную
погрешность не удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но
у самого карандаша рёбра могут отличаться на большую величину). Относительная погрешность равна

Округляя, находим

ПРИМЕР:

Цилиндрический поршень имеет около 35
мм в диаметре. С какой точностью нужно
его измерить микрометром, чтобы предельная относительная погрешность составляла 0,05% ?

РЕШЕНИЕ:

По условию, предельная относительная
погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная абсолютная
погрешность равна

или, усиливая, 0,02
мм.

Можно воспользоваться
формулой

Подставляя в формулу

а = 35,

𝛿 = 0,0005,

имеем

Значит,

∆
= 35 × 0,0005 = 0,0175 мм.

Действия над приближёнными числами.

Сложение и вычитание приближённых чисел.

Абсолютная погрешность суммы двух величин равна сумме
абсолютных погрешностей отдельных слагаемых.

ПРИМЕР:

Складываются приближённые числа

265 и 32.

РЕШЕНИЕ:

Пусть предельная погрешность первого есть 5,
а второго 1. Тогда предельная погрешность суммы равна

5
+ 1 = 6.

Так, если истинное значение первого есть 270,
а второго 33, то приближённая сумма

265
+ 32 = 297

на 6 меньше истинной

270
+ 33 = 303.

ПРИМЕР:

Найти сумму приближённых чисел:

0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667

+ 0,0625 + 0,0588 + 0,0556 + 0,0526.

РЕШЕНИЕ:

Сложение даёт следующий результат – 0,6187.

Предельная погрешность каждого слагаемого

0,00005.

Предельная погрешность суммы:

0,00005
∙ 9 = 0,00045.

Значит, в последнем (четвёртом) знаке суммы возможна ошибка до 5
единиц. Поэтому округляем сумму до третьего знака, то есть до тысячных.
Получаем 0,619,
здесь все знаки верные.

При значительном
числе слагаемых обычно происходит взаимная компенсация погрешностей, поэтому
истинная погрешность суммы лишь в исключительных случаях совпадает с предельной
погрешностью или близка к ней. Насколько редки эти случаи, видно из предыдущего
примера, где 9 слагаемых. Истинная величина каждого из них может
отличаться в пятом знаке от взятого приближённого значения на 1, 2, 3, 4 или даже на 5 единиц в ту и в другую сторону.

Например, первое
слагаемое может быть больше своего истинного значения на 4 единицы пятого знака, второе – на две, третье – меньше
истинного на одну единицу и так далее.

Расчёт показывает,
что число всех возможных случаев распределения погрешностей составляет около
одного миллиарда. Между тем лишь в двух случаях погрешность суммы может
достигнуть предельной погрешности 0,00045,
это произойдёт:

– когда истинная величина каждого слагаемого больше
приближённой величины на 0,00005;

– когда истинная величина каждого слагаемого меньше
приближённой величины на 0,00005.

Значит, случаи,
когда погрешность суммы совпадает с предельной, составляют только 0,0000002% всех возможных случаев.

Дальнейший расчёт
показывает, что случаи, когда погрешность суммы девяти слагаемых может
превысить три единицы последнего знака, тоже очень редки. Они составляют
лишь 0,07%
из числа всех
возможных. Две единицы последнего знака погрешность может превысить 2% всех возможных случаев, а одну единицу –
примерно в 25%.
В остальных 75% случаев погрешность девяти слагаемых не
превышает одной единицы последнего знака.

ПРИМЕР:

Найти сумму точных чисел:

0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667

+ 0,0625 + 0,0588 + 0,0556 + 0,0526.

РЕШЕНИЕ:

Сложение даёт следующий результат – 0,6187.

Округлим их до тысячных и сложим:

0,091
+ 0,083 + 0,077 + 0,071 + 0,067

+ 0,062 + 0,059 + 0,056 + 0,053 = 0,619.

Предельная погрешность суммы:

0,0005
∙ 9 = 0,0045.

Приближённая сумма отличается от истинной на 0,0003,
то есть на треть единицы последнего знака приближённых чисел. Все три знака
приближённой суммы верны, хотя теоретически последняя цифра могла быть грубо
неверной.

Произведём в наших слагаемых округление до сотых. Теперь
предельная погрешность суммы будет:

0,005
∙ 9 = 0,045.

Между тем получим:

0,09
+ 0,08 + 0,08 + 0,07 + 0,07

+ 0,06 + 0,06 + 0,06 + 0,05 = 0,62.

Истинная погрешность составляет только 0,0013.

Предельная абсолютная погрешность разности двух величин
равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.

ПРИМЕР:

Пусть предельная погрешность приближённого
уменьшаемого 85 равна 2,
а предельная погрешность вычитаемого 32 равна 3.
Предельная погрешность разности

85
– 32 = 53

есть

2
+ 3 = 5.

В самом деле, истинное значение уменьшаемого и
вычитаемого могут равняться

85
+ 2 = 87 и

32
– 3 = 29.

Тогда истинная разность есть

87
– 29 = 58.

Она на 5 отличается от
приближённой разности 53.

Относительная погрешность суммы и разности.

Предельную
относительную погрешность суммы и разности легко найти, вычислив сначала
предельную абсолютную погрешность.

Предельная
относительная погрешность суммы (но не разности!) лежит между наименьшей и
наибольшей из относительных погрешностей слагаемых. Если все слагаемые имеют
одну и ту же (или примерно одну и ту же) предельную относительную погрешность,
то и сумма имеет ту же (или примерно ту же) предельную относительную
погрешность. Другими словами, в этом случае точность суммы (в процентном
выражении) не уступает точности слагаемых. При значительном же числе слагаемых
сумма, как правило, гораздо точнее слагаемых.

ПРИМЕР:

Найти предельную абсолютную и предельную относительную
погрешность суммы чисел:

24,4
+ 25,2 + 24,7.

РЕШЕНИЕ:

В каждом слагаемом суммы

24,4
+ 25,2 + 24,7 = 74,3

предельная относительная погрешность примерно одна и та
же, а именно:

0,05
: 25 = 0,2%.

Такова же она и для суммы.

Здесь предельная абсолютная погрешность равна 0,15,
а относительная

0,15
: 74,3 ≈ 0,15 : 75 = 0,2%.

В противоположность
сумме разность приближённых чисел может быть менее точной, чем уменьшаемое и
вычитаемое. <<Потеря точности>> особенно велика в том случае, когда
уменьшаемое и вычитаемое мало отличаются друг от друга.

Относительные погрешности при сложении и вычитании
складывать нельзя.

Умножение и деление приближённых чисел.

При делении и умножении чисел требуется сложить
относительные погрешности.

ПРИМЕР:

Пусть перемножаются приближённые числа 50 и 20, и пусть предельная относительная погрешность первого
сомножителя есть 0,4%, а второго
0,5%.

Тогда предельная относительная погрешность произведения

50
× 20 = 1000

приближённо равна 0,9%.
В самом деле предельная абсолютная погрешность первого сомножителя есть

50
× 0,004 = 0,2,

а второго

20
× 0,005 = 0,1.

Поэтому истинная величина произведения не больше чем

(50
+ 0,2)(20 + 0,1) = 1009,02,

и не меньше, чем

(50
– 0,2)(20 – 0,1) = 991,022.

Если истинная величина произведения есть 1009,2,
то погрешность произведения равна

1009,2
– 1000 = 9,02,

а если 991,02, то погрешность произведения равна

1000
– 991,02 = 8,98.

Рассмотренные два случая – самые неблагоприятные. Значит,
предельная абсолютная погрешность произведения есть 9,02.
Предельная относительная погрешность равна

9,02
: 1000 = 0,902%,

то есть приближённо 0,9%.

Задания к уроку 16

Задание 1

Задание 2

Задание 3

Урок 1. Числовые неравенства
Урок 2. Свойства числовых неравенств
Урок 3. Сложение и умножение числовых неравенств
Урок 4. Числовые промежутки
Урок 5. Линейные неравенства
Урок 6. Системы линейных неравенств
Урок 7. Нелинейные неравенства
Урок 8. Системы нелинейных неравенств
Урок 9. Дробно-рациональные неравенства
Урок 10. Решение неравенств с помощью графиков
Урок 11. Неравенства с модулем
Урок 12. Иррациональные неравенства
Урок 13. Неравенства с двумя переменными
Урок 14. Системы неравенств с двумя переменными
Урок 15. Приближённые вычисления

Источник

Абсолютная и относительная погрешность

4.2

Средняя оценка: 4.2

Всего получено оценок: 2248.

4.2

Средняя оценка: 4.2

Всего получено оценок: 2248.

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Опыт работы учителем математики — более 33 лет.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
при делении и умножении чисел требуется сложить относительные погрешности;
при возведении в степень относительную погрешность умножают на показатель степени.

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.