
Относительная ошибка
В практике геодезических измерений о точности измерений судят не только по абсолютной величине средней квадратической или предельной
погрешности, но и по величине относительной погрешности.
Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины.
Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух — трех значащих цифр с нулями.
отн = тl /l =1/(l / тl ), где l — значение измеряемой величины.
Относительная предельная ошибка:
отн. пр. = пр / l, где пр = 2(3)m
Например, относительная средняя квадратическая погрешность измерения линии длиной l = 110 м при тl = 2 см равна тl /l = 1/5500, а
|
относительная предельная погрешность при пр = 3m = 6 см, |
пр /l= |
|
1/1800. |
12

Пример. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность выполненных измерений. Результаты измерений и вычислений записывают по форме, приведенной в таблице
|
№ п/п |
l, м |
, см |
2 ,см2 |
Вычисления |
|
1 |
121,75 |
-1 |
1 |
|
|
2 |
121,81 |
+5 |
25 |
|
|
3 |
121,77 |
+ 1 |
1 |
|
|
4 |
121,70 |
-6 |
36 |
|
|
5 |
121,73 |
-3 |
9 |
6121,79 +3 9
|
Среднее 121,76 Σ =-1 |
Σ = |
|
|
значени |
81 |
=12см |
|
е |
пр |
|
13

Вычислительная обработка результатов геодезических измерений
Для производства топографической съемки создается геодезическое съемочное обоснование в виде закрепленных на местности пунктов, координаты которых определены из геодезических линейно-угловых построений (сети триангуляции, теодолитные, тахеометрические, мензульные ходы, геодезические засечки). Высоты точек съемочных сетей определяются тригонометрическим или геометрическим нивелированием.
Съемочное обоснование развивается от пунктов опорной геодезической сети более высокого класса путем сгущения геодезической основы до плотности, обеспечивающей выполнение топографической съемки.
Самый распространенный вид съемочного планового обоснования – теодолитные ходы, опирающиеся на один или два исходных пункта.
Теодолитные ходы привязываются к пунктам опорной геодезической сети. Это выполняется для того, чтобы вершины теодолитных ходов были определены в существующей системе координат. Привязка выполняется различными способами. В результате ее выполнения на стороны и вершины теодолитного хода должны быть переданы дирекционный угол и координаты x, y.
Теодолитный ход не привязанный к пунктам опорной геодезической сети, носит название свободного, привязанный лишь в начальной точке – висячим.
14

Вычисление координат пунктов разомкнутого теодолитного хода
Исходными данными в теодолитном ходе являются координаты XA, YA пункта A и дирекционный угол αBA линии BA, который называется начальным
исходным дирекционным углом; этот угол может задаваться неявно через координаты пункта B, путем решения обратной геодезической задачи.
Измеряемые величины — это горизонтальные углы β1, β2,…, βn-1, βn и расстояния S1, S2,…, Sn-1, Sn.
Дирекционные углы сторон хода вычисляют последовательно по формулам передачи дирекционного угла через угол поворота.
Координаты пунктов хода получают из решения прямой геодезичеcкой задачи сначала от пункта A к пункту 2, затем от пункта 2 к пункту 3 и так далее до конца хода.
15

Прямая геодезическая задача
Дано:
координаты точки А (ХА ;YА ),
дирекционный угол направления АВ (αАВ),
горизонтальная проекция направления АВ (dАВ ).
Найти: координаты точки В (хВ уВ).
Решение:
Δх=± dАВ·cos rАВ= dАВ·cos αАВ;
Δу=± dАВ·sinrАВ= dАВ·sin αАВ.
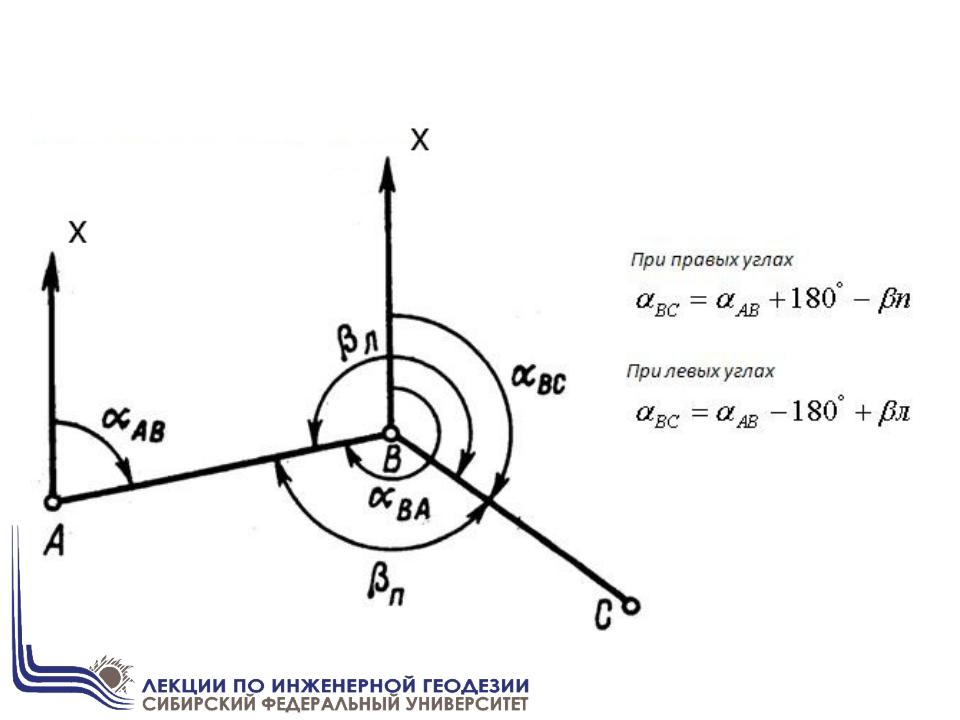
Контроль вычисления приращений координат: d АВ 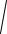
Координаты искомой точки В определяются по формулам:
хВ=хА+Δх; уВ=уА+Δу.

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Дано:
Координаты точек А (ХА ;YА ), В (ХВ; YВ).
Найти:
дирекционный угол направления АВ (αАВ),
горизонтальную проекцию направления АВ (dАВ ).
|
Решение: |
|
|
ΔХ = ХВ — ХА; |
ΔY = YВ — YА. |
По найденным значениям приращений координат ΔХ и ΔY в прямоугольном
|
треугольнике, вычисляют табличный угол |
||
|
(румб): |
tgr |
|
|
отсюда |
r arctg |
|
Зная дирекционный. угол направления и приращения координат, определяют горизонтальную проекцию направления:
|
d АВ |
d АВ |
d АВ 2 . 2 |
||||
|
; |
; |
|||||
|
sin АВ |
||||||
|
cos АВ |
ПЕРЕДАЧА ДИРЕКЦИОННОГО УГЛА НА СТОРОНУ ТЕОДОЛИТНОГО ХОДА
В общем виде:
n n 1 180 прn n 1 180 л

180 л
В разомкнутом теодолитном ходе должны выполняться три условия: условие дирекционных углов и два координатных условия.
Вычислим последовательно дирекционные углы всех сторон хода,
используя формулу передачи дирекционного угла на последующую сторону хода: n n 1 180 пр или n n 1 .
Математическая запись условия дирекционных углов в разомкнутом теодолитном ходе для левых углов поворота:
(1)
Для правых углов поворота оно запишется так:
(2)
где αн , αк – дирекционные углы начальной и конечной выходных сторон,
между которыми прокладывается ход, n – число углов хода, включая
примычные.
Сумма углов, подсчитанная по формулам (1) и (2), называется теоретической суммой углов хода. Сумма измеренных углов вследствие
ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую fβ:
(3)
19

|
f доп 2 m |
. |
|||
|
Допустимое значение угловой невязки: |
n |
(4) |
||
|
где n – число углов хода. |
|
Для теодолитных ходов mβ = 30″, поэтому: |
(5) |
|||
|
f доп 1 n. |
Присутствие ошибок в результатах измерений является причиной возникновения задачи уравнивания. Целью уравнивания является устранение невязок и повышение точности всех измеренных величин.
Обозначим поправку в измеренный угол Vβ и запишем условие:
откуда следует, что сумма угловых поправок равна угловой невязке с противоположным
|
знаком: |
V f . |
(7) |
|
При условии, что поправки в измеренные углы одинаковы, |
решение уравнения (7) |
|
|
получается в виде: |
V f / n. |
|
|
Исправленные значения углов вычисляются по формуле: |
||
|
i i(изм) V . |
(8) |
По исправленным углам поворота вычисляют дирекционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем правильности обработки угловых измерений.
20

Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и ΔYi :
|
Xвыч d cos d cos r |
(9) |
|||
|
Yвыч d sin d sin r |
(10) |
|||
|
где r – румб соответствующего дирекционного угла. |
X n X n 1 X |
|||
|
Координаты пунктов хода получим по формулам : |
(11) |
|||
|
Для конечной точки хода: Xкон Xнач Xi |
Yn Yn 1 Y |
(12) |
||
|
(13) |
||||
|
или |
Xi Xкон Xнач . |
(14) |
||
Аналогичная формула для суммы приращений ΔY имеет вид:
i кон нач . (15)
Получились еще два условия (14) и (15), которые называются координатными. Суммы приращений координат, подсчитанные по этим формулам, называются теоретическими суммами приращений. Вследствие ошибок измерения сторон суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам.
21
Соседние файлы в папке геодезия. все лекции
- #
- #
- #
- #
- #
- #
- #
Добро пожаловать!
Войдите или зарегистрируйтесь сейчас!
Войти
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
какую информацию можно извлечь из относительной ошибки? например линейная погрешность или что то в этом роде. пожалуйста привидите пример.
#1
-
Форумчанин
- Регистрация:
- 16 авг 2008
- Сообщения:
- 5.141
- Симпатии:
- 631
- Адрес:
-
Химки
1/2000 = 1 м на 2 км
То есть, линейная погрешность в 1 м на 2 км хода дает 1/2000.#2
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
это я знаю, а еще что нибудь из нее нельзя извлечь?
#3
-
Форумчанин
- Регистрация:
- 16 авг 2008
- Сообщения:
- 5.141
- Симпатии:
- 631
- Адрес:
-
Химки
Попробуйте, может, получится;)
#4
-
Форумчанин
а вы что хотите извлечь то, вы расскажите причину столь странного интереса…
#5
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
нам преподаватель говорит, что относительная ошибка дает много информации, но не рассказывает, мол мы сами все знаем. а я кроме линейной погрешности ничего незнаю
#6
-
Форумчанин
- Регистрация:
- 5 мар 2010
- Сообщения:
- 175
- Симпатии:
- 4
- Адрес:
-
Москва
ну, скажем, на первый взгляд: в теодолитном ходе если угловая невязка в допуске а относительная ошибка слишком большая, то это логично говорит о том что у вас есть ошибка в длинах линий, если же вы проверили все длины линий и поняли что они все верны, а относительная ошибка хода по-прежнему вас не устраивает, то у вас ошибка как минимум в двух углах поворота, причем эти ошибки взаимно исключают друг друга.. (а преподаватели, к слову, пользуются относительной ошибкой часто для того что бы определить подгонялись ли углы в ходе или нет.. )
Случай с ошибкой в исходных данных тоже может быть выявлен таким образом..
#7
-
Форумчанин
Самую полезную для студента информацию несет не относительная ошибка, а абсолютные ошибки приращений координат. В случае, если в небольшом ходе Вы где-то пролетели с измерением длин линий лентой (на метр, двадцать метров, остаток до другого края ленты), ним легко узнать дир. угол линии, в которой сидит промах. Как — не скажу, сами догадайтесь.
И тогда в поисках ошибки не придется перемерять весь полигон.
#8
-
Форумчанин
Для теодолитного хода относительная ошибка вычисляется по формуле =√ΣΔX²+ ΣΔY²/P<1/2000, где ΣΔX, ΣΔY — суммы приращений координат, Р — периметр полигона, т.е. относительная ошибка позволяет определить еще и ошибку в вычислениях превышений.
Относительная ошибка как правило характеризует точность линейных измерений. Например, относительная ошибка нитяного дальномера составляет 1/300, ошибка измерения рулеткой 1/2000, значит линия в 50 м в первом случае будет определена с точностью ±17 см, а во втором ±2,5см#9
-
Форумчанин
- Регистрация:
- 5 мар 2010
- Сообщения:
- 175
- Симпатии:
- 4
- Адрес:
-
Москва
не понял.. а это то откуда?
#10
-
Форумчанин
- Регистрация:
- 30 ноя 2007
- Сообщения:
- 2.717
- Симпатии:
- 2.460
- Адрес:
-
Сибирь
А если промахнулись в двух линиях?
#11
-
Форумчанин
Извините приращений координат
#12
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
спасибо за участие в этом вопросе.
#13
-
Форумчанин
Тогда уже не узнать
Если трасса, и углы близки к 180 градусам, то тоже.
Но в теодолито-рулеточную эпоху этим методом пользовались частенько. Помогало.
#14
Поделиться этой страницей

Относительная ошибка
В практике геодезических измерений о точности измерений судят не только по абсолютной величине средней квадратической или предельной
погрешности, но и по величине относительной погрешности.
Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины.
Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух — трех значащих цифр с нулями.
отн = тl /l =1/(l / тl ), где l — значение измеряемой величины.
Относительная предельная ошибка:
отн. пр. = пр / l, где пр = 2(3)m
Например, относительная средняя квадратическая погрешность измерения линии длиной l = 110 м при тl = 2 см равна тl /l = 1/5500, а
|
относительная предельная погрешность при пр = 3m = 6 см, |
пр /l= |
|
1/1800. |
12

Пример. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность выполненных измерений. Результаты измерений и вычислений записывают по форме, приведенной в таблице
|
№ п/п |
l, м |
, см |
2 ,см2 |
Вычисления |
|
1 |
121,75 |
-1 |
1 |
|
|
2 |
121,81 |
+5 |
25 |
|
|
3 |
121,77 |
+ 1 |
1 |
|
|
4 |
121,70 |
-6 |
36 |
|
|
5 |
121,73 |
-3 |
9 |
6121,79 +3 9
|
Среднее 121,76 Σ =-1 |
Σ = |
|
|
значени |
81 |
=12см |
|
е |
пр |
|
13

Вычислительная обработка результатов геодезических измерений
Для производства топографической съемки создается геодезическое съемочное обоснование в виде закрепленных на местности пунктов, координаты которых определены из геодезических линейно-угловых построений (сети триангуляции, теодолитные, тахеометрические, мензульные ходы, геодезические засечки). Высоты точек съемочных сетей определяются тригонометрическим или геометрическим нивелированием.
Съемочное обоснование развивается от пунктов опорной геодезической сети более высокого класса путем сгущения геодезической основы до плотности, обеспечивающей выполнение топографической съемки.
Самый распространенный вид съемочного планового обоснования – теодолитные ходы, опирающиеся на один или два исходных пункта.
Теодолитные ходы привязываются к пунктам опорной геодезической сети. Это выполняется для того, чтобы вершины теодолитных ходов были определены в существующей системе координат. Привязка выполняется различными способами. В результате ее выполнения на стороны и вершины теодолитного хода должны быть переданы дирекционный угол и координаты x, y.
Теодолитный ход не привязанный к пунктам опорной геодезической сети, носит название свободного, привязанный лишь в начальной точке – висячим.
14

Вычисление координат пунктов разомкнутого теодолитного хода
Исходными данными в теодолитном ходе являются координаты XA, YA пункта A и дирекционный угол αBA линии BA, который называется начальным
исходным дирекционным углом; этот угол может задаваться неявно через координаты пункта B, путем решения обратной геодезической задачи.
Измеряемые величины — это горизонтальные углы β1, β2,…, βn-1, βn и расстояния S1, S2,…, Sn-1, Sn.
Дирекционные углы сторон хода вычисляют последовательно по формулам передачи дирекционного угла через угол поворота.
Координаты пунктов хода получают из решения прямой геодезичеcкой задачи сначала от пункта A к пункту 2, затем от пункта 2 к пункту 3 и так далее до конца хода.
15

Прямая геодезическая задача
Дано:
координаты точки А (ХА ;YА ),
дирекционный угол направления АВ (αАВ),
горизонтальная проекция направления АВ (dАВ ).
Найти: координаты точки В (хВ уВ).
Решение:
Δх=± dАВ·cos rАВ= dАВ·cos αАВ;
Δу=± dАВ·sinrАВ= dАВ·sin αАВ.
Контроль вычисления приращений координат: d АВ 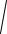
Координаты искомой точки В определяются по формулам:
хВ=хА+Δх; уВ=уА+Δу.

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Дано:
Координаты точек А (ХА ;YА ), В (ХВ; YВ).
Найти:
дирекционный угол направления АВ (αАВ),
горизонтальную проекцию направления АВ (dАВ ).
|
Решение: |
|
|
ΔХ = ХВ — ХА; |
ΔY = YВ — YА. |
По найденным значениям приращений координат ΔХ и ΔY в прямоугольном
|
треугольнике, вычисляют табличный угол |
||
|
(румб): |
tgr |
|
|
отсюда |
r arctg |
|
Зная дирекционный. угол направления и приращения координат, определяют горизонтальную проекцию направления:
|
d АВ |
d АВ |
d АВ 2 . 2 |
||||
|
; |
; |
|||||
|
sin АВ |
||||||
|
cos АВ |

ПЕРЕДАЧА ДИРЕКЦИОННОГО УГЛА НА СТОРОНУ ТЕОДОЛИТНОГО ХОДА
В общем виде:
n n 1 180 прn n 1 180 л

180 л
В разомкнутом теодолитном ходе должны выполняться три условия: условие дирекционных углов и два координатных условия.
Вычислим последовательно дирекционные углы всех сторон хода,
используя формулу передачи дирекционного угла на последующую сторону хода: n n 1 180 пр или n n 1 .
Математическая запись условия дирекционных углов в разомкнутом теодолитном ходе для левых углов поворота:
(1)
Для правых углов поворота оно запишется так:
(2)
где αн , αк – дирекционные углы начальной и конечной выходных сторон,
между которыми прокладывается ход, n – число углов хода, включая
примычные.
Сумма углов, подсчитанная по формулам (1) и (2), называется теоретической суммой углов хода. Сумма измеренных углов вследствие
ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую fβ:
(3)
19

|
f доп 2 m |
. |
|||
|
Допустимое значение угловой невязки: |
n |
(4) |
||
|
где n – число углов хода. |
|
Для теодолитных ходов mβ = 30″, поэтому: |
(5) |
|||
|
f доп 1 n. |
Присутствие ошибок в результатах измерений является причиной возникновения задачи уравнивания. Целью уравнивания является устранение невязок и повышение точности всех измеренных величин.
Обозначим поправку в измеренный угол Vβ и запишем условие:
откуда следует, что сумма угловых поправок равна угловой невязке с противоположным
|
знаком: |
V f . |
(7) |
|
При условии, что поправки в измеренные углы одинаковы, |
решение уравнения (7) |
|
|
получается в виде: |
V f / n. |
|
|
Исправленные значения углов вычисляются по формуле: |
||
|
i i(изм) V . |
(8) |
По исправленным углам поворота вычисляют дирекционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем правильности обработки угловых измерений.
20

Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и ΔYi :
|
Xвыч d cos d cos r |
(9) |
|||
|
Yвыч d sin d sin r |
(10) |
|||
|
где r – румб соответствующего дирекционного угла. |
X n X n 1 X |
|||
|
Координаты пунктов хода получим по формулам : |
(11) |
|||
|
Для конечной точки хода: Xкон Xнач Xi |
Yn Yn 1 Y |
(12) |
||
|
(13) |
||||
|
или |
Xi Xкон Xнач . |
(14) |
||
Аналогичная формула для суммы приращений ΔY имеет вид:
i кон нач . (15)
Получились еще два условия (14) и (15), которые называются координатными. Суммы приращений координат, подсчитанные по этим формулам, называются теоретическими суммами приращений. Вследствие ошибок измерения сторон суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам.
21
Соседние файлы в папке геодезия. все лекции
- #
- #
- #
- #
- #
- #
- #
Человеку свойственно ошибаться. Это касается не только общих вопросов и знаний жизни. Но и распространяется на любые сферы его деятельности, в том числе в области геодезии. В ней все проводимые измерения выполняются с ошибками. Значительная часть работ в геодезическом производстве основывается на измерениях. А измерения — своего рода сравнение с какой-то эталонной или истинной величиной. Если понимать, что истинного значения в идеале не существует, то все сравнения в измерениях сводятся к сравнению с конкретно полученным значением и принятому, как верное. Одним из наиболее приближенных к истинному значению, считается среднее арифметическое.
Понятие погрешности, её абсолютная и относительная величины
Если переходить на понятие погрешности, то отклонение отдельного замера от среднего арифметического из выполненных измерений и считается абсолютной его ошибкой. Числовая форма погрешности не дает представления о качестве произведенного измерения. Для этого существует понятие относительной погрешности. Под ним понимают отношение значения собственно ошибки к замеренной величине. Применяется этот параметр в определении точности работ при линейных замерах в полигонометрических и теодолитных ходах.
В нивелирных ходах для его оценки точности существует так называемая приведенная погрешность. Это тоже своего рода относительный показатель. Только он подразумевает под собой отношение абсолютного значения ошибки к конкретному принятому значению определяемой величины (для нивелировок на 1 км хода).
Погрешности по источникам возникновения
При производстве геодезических работ после окончания каждой выполненной операции в полевых условиях можно говорить об ошибках. Присутствуют они и при проведении камеральных работ. Так при установке приборов в рабочее положение возникают отклонения в центрировании инструмента над центром знака. Также возникают неточности при выставлении прибора в отвесное состояние, когда выводим его цилиндрический уровень в верхнее горизонтальное положение и круглый уровень на середину. Следующими причинами возникновения погрешностей считаются визирование и снятие отсчетов в момент исполнения наблюдений. Влияние внешних условий окружающей среды: рефракция воздуха, дымка, туман, осадки, формирует еще одну группу ошибок. Помимо человеческого фактора и влияния внешней среды существуют конструктивные особенности приборов, с заложенными в них вероятностными составляющими точности измерений. Еще одной из причин возникновения погрешностей считается несовершенство методик их определений. Резюмируя выше сказанное, можно выделить следующий перечень ошибок по источникам их возникновения:
- инструментальные;
- индивидуальные;
- из-за условий окружающей среды;
- методические.
Погрешности по характеру действий
По данному признаку все ошибки можно разделить на следующие отклонения:
- грубые, то есть значительно превышающие ожидаемые ошибки, возникающие в результате просчетов, неверных действий и обнаруженные при дополнительном контроле;
- систематические отклонения, отличающиеся постоянством возникновения и закономерностями изменений при повторных операциях; к ним можно отнести периодические и функциональные погрешности;
- случайные, значения величин, которых не значительны, большая часть их мала, чем велика, встречаются как с положительными, так и с отрицательными значениями, в каждом конкретном случае они возникают отдельно случайным образом и в своей массе подчинены определенным вероятностным закономерностям;
Именно изучение случайных погрешностей в геодезии дает возможность производить оценки точности и получать наиболее надежные результаты.
Предельные и допустимые отклонения
При определенных факторах случайные ошибки по абсолютному значению своей величины не могут превышать определенного предела. Этот предел в геодезической и маркшейдерской практике имеет название предельной погрешности.
В строительном производстве нормативными документами введен термин предельного отклонения, который может иметь как положительное, так и отрицательное значения. Алгебраическая сумма этих параметров (предельных отклонений) имеет название допуска.
В геодезии крайние предельные значения отклонений, допускаемые нормативной документацией, называются допустимыми.
Средние, вероятные и средне квадратические погрешности
При различных оценках точности выполненных замеров применяются некоторые критерии случайных ошибок. К таким мерилам оценки относятся понятия:
- средне арифметического отклонения от всех случайных ошибок, имеющее название среднего уклонения;
- срединного отклонения, то есть находящегося в середине измеренного ряда по абсолютным значениям с учетом убывания и возрастания, именуемое вероятной ошибкой;
- средне квадратическое отклонение (СКО) – это параметр функции дисперсии (рассеивания) случайных величин результатов измерений. Он равен математическому ожиданию (среднему арифметическому значению) квадратов отклонений в измерениях от математического ожидания (среднего арифметического значения) результатов замеров.
Случайные погрешности подчиняются нормальному закону распределения и находятся в интервале от нуля до трех СКО. Большинство из них в пределах шестидесяти восьми процентов находятся в интервале до одного СКО. Девяносто пять процентов случайных величин попадает в интервал от нуля до двух СКО. Девяносто девять процентов случайных ошибок находится в интервале от нуля до трех СКО.
На основании этого в теоретических расчетах при предварительных оценках точности выполнения работ за предельные принимаются три средне квадратические ошибки. При геодезических и маркшейдерских работах на практике к расчетам принимаются двойные величины средне квадратических отклонений.
Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.
По своей природе ошибки бывают грубые, систематические и случайные.
Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.
Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.
Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.
Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
(1.25)
Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:
1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.
Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.
Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
(1.27)
где: ;
n – количество измерений одной величины.
Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.
Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.
Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.
Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:
F = f( X, Y, Z … ), (1.28)
здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.
В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.
Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:
Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
(1.30)
Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)
Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим
В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
(1.32)
Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:
Если функция имеет вид произведения нескольких аргументов,
F = x * y * z,
то для нее можно записать выражение относительной ошибки функции:
(1.33)
которое в некоторых случаях оказывается более удобным, чем формула (1.32).
Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.
Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)
Величина (1.36)
называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде
по третьему свойству ошибок (1.26) можно написать:
что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.
Запишем формулу (1.36) в виде
и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:
или
Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:
M2 = m2/n
или
(1.37)
то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.
Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.
Пусть имеется ряд равноточных измерений величины X:
l1, l2 , …, ln .
Вычислим арифметическую середину X0 = [1]/n и образуем разности:

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:
[V] = 0. (1.39)
Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
(1.40)
Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:

Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):

Возведем все уравнения (1.42) в квадрат, сложим их и получим:
.
Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.
Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)
Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ; такая замена практически не изменит правой части формулы (1.43). Итак,
,
откуда ;
после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).
Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
(1.44)
Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.
Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:
p = C/m2 (1.45)
где C – в общем случае произвольное положительное число.
При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
(1.46)
или X0 = [l*p] / [p] .
Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем
откуда (1.47)
то-есть, за число C принимают квадрат ошибки единицы веса.
Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)
Согласно (1.46) и (1.32) напишем:
Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:
Подставим это выражение в формулу (1.48) и получим,
P = [p], (1.49)
то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.
В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:
P = n. (1.50)
При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
(1.51)
где pi – вес i-того элемента.






