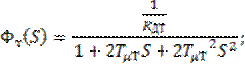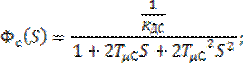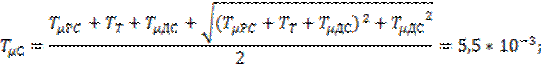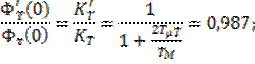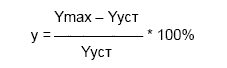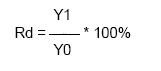Относительная величина ошибки регулирования

Одним
из основных показателей, характеризующих
регулирование скорости электропривода,
является диапазон регулирования.
Диапазон регулированияD
— это отношение максимальной установившейся
скорости электропривода к минимальной
при изменении нагрузки на валу двигателя
в заданных пределах. Определение величины
диапазона регулирования показано на
рис.4.2.

Положим, что
электропривод имеет прямолинейные
механические характеристики. Прямая 1
соответствует максимальной по скорости
механической характеристике.

Положим, что
регулировочные характеристики привода
будут перемещаться вниз параллельно
характеристике 1, имея ту же жесткость
,
что характерно для большинства современных
систем регулируемого электропривода.
Нижняя предельная характеристика,
которая будет обеспечивать требуемый
максимальный момент, будет характеристика
2. Диапазон регулирования будет равен
отношению максимальной скорости к
минимальной, которые определяются по
среднему моменту из заданных минимального
и максимального его значений [8]

.

.

(4.1)

Из графиков рис.4.2.
найдем:

Подставляя
эти значения в (4.1), получим:

(4.2)

Здесь
и далее β
– абсолютное значение жесткости.

Из
формулы (4.2) следует, что диапазон
регулирования зависит от жесткости
механических характеристик привода:
чем больше жесткость, тем больше диапазон
регулирования.

Вторым важным
показателем качества регулирования
является точность регулирования
скорости. Статическая ошибка
характеризует реакцию электропривода
на приложение (снятие) нагрузки. Если
мы анализируем регулируемый электропривод,
имеющий линейные (линеаризованные)
механические характеристики, которые
в зависимости от управляющего воздействия
могут плавно перемещаться вниз от
основной с постоянной жесткостью
(рис.4.3), то абсолютная статическая ошибка
будет равна:

.

(4.3)

Эта
ошибка при постоянной жесткости
механических характеристик будет одна
и та же во всем диапазоне регулирования.

Относительная
величина ошибки находится как отношение
абсолютной ошибки к базовой (заданной)
скорости. Она тем больше, чем меньше
заданная скорость.

.

(4.4)

Из
(4.3) и (4.4) следует, что величина статической
ошибки, связанной с возмущением по
нагрузке, обратно пропорциональна
жесткости механических характеристик:
чем больше жесткость, тем меньше
статическая ошибка.

Нижнее
значение скорости
заданного диапазона регулирование
скорости может ограничиваться также
требуемой точностью регулирования
(статизмом). В соответствии с (4.4) точность
поддержания заданной скорости, как
величина относительная, будет тем хуже,
чем меньше заданная минимальная скорость.
Поэтому условие выполнения заданной
точности будет

.

Учитывая,
что

,

получим

.

Тогда
диапазон регулирования скорости из
условия обеспечения заданной точности
будет

.
(4.5)

Обычно
жесткость механических характеристик
электропривода с разомкнутой системой
управления недостаточна для достижения
требуемого диапазона регулирования и
требуемой статической точности. Потому
в регулируемых электроприводах, как
правило, используются замкнутые по
скорости системы регулирования.

Рассмотрим
влияние отрицательной обратной связи
по скорости на механические характеристики
электропривода.

На
рис.4.4 представлена структурная схема
электропривода с разомкнутой системой
управления (рис.4.4,а) и с системой
управления, включающей в себя отрицательную
жесткую обратную связь по скорости,
т.е. с замкнутой по скорости системой
управления (рис.4.4,б). При разомкнутой
системе управления заданная скорость
определяется как
(см. рис.4.4,а).

Величина статической
ошибки, возникающей при приложении
момента нагрузки М_с,
будет зависеть от жесткости механических
характеристик (см. 4.3). Разомкнутая
система управления не может автоматически
компенсировать или уменьшить ошибку
по возмущению.

В замкнутой системе
управления с жесткой отрицательной
обратной связью по контролируемому
параметру (в рассматриваемом случае по
скорости) величина этого параметра
через датчик скорости с передаточным
коэффициентом к_с
подается с отрицательным знаком на вход
системы регулирования

.

(4.6)

Таким образом,
регулирование скорости производится
по величине ошибки, т.е. разности между
заданным и действующим значениями
скорости

.

(4.7)

Рассмотрим механизм
действия отрицательной обратной связи
(рис. 4.5). Пусть характеристики 1 —
механические характеристики привода
с разомкнутой системой управления. Если
задано значение скорости _0зад,
то при М_с=0
привод будет работать с заданной
скоростью. При приложении нагрузки М_с
и разомкнутой системе регулирования
скорость двигателя снизится на величину
,
пропорциональную отрезкуав.
При этом двигатель работает на механической
характеристике, определяемой прямой
_0зад-в,
имеющей жесткость ,
и просадка скорости определяется
величиной
.

В замкнутой системе
регулирования процесс изменения скорости
протекает иначе. После приложения
нагрузки скорость начнет снижаться.
При этом будет уменьшаться сигнал
обратной связи по скорости к_с,
в результате чего разность (х_зад-х_осс)
увеличится, а, следовательно, увеличится
сигнал задания скорости _зад

.

(4.8)

Увеличение сигнала
задания скорости холостого хода
произойдет до величины _об,
и двигатель автоматически перейдет на
механическую характеристику _об-б
и после завершения переходного процесса
будет работать в точке б.
В результате установившаяся ошибка
скорости составит
,
определяемую отрезкомаб,
существенно меньшим, чем это было бы в
разомкнутой системе

.

(4.9)

Если статический
момент равен М_сг,
то привод будет работать в точке г,
если М_с=М_се,
то привод будет работать в точке е.

Мы видим, что
механическая характеристика замкнутой
системы представляет собой совокупность
точек _0зад-г-б-д-е,
принадлежащих механическим характеристикам
разомкнутой системы с различными
значениями скорости холостого хода.
Жесткость
механической характеристики замкнутой
системы (прямая 2) будет выше жесткости
характеристик разомкнутой системы.

Механическая
характеристика замкнутой системы будет

,

где ₀
определяется
из (4.8)

,

,

откуда
,

обозначив к_ук_с=К
– коэффициент усиления разомкнутой
системы (при разрыве обратной связи по
скорости), получим

или

,

где:
(4.10)

Мы видим, что
жесткость механических характеристик
в замкнутой системе увеличивается по
сравнению с жесткостью механических
характеристик разомкнутой системы в
(1+К)
раз.

Следовательно,
статическая ошибка уменьшается в (1+К)
раз

.

(4.11)

Сопоставив с (4.9),
получим (см. рис.4.5)

.

Таким образом,
введение отрицательной обратной связи
по скорости повышает жесткость
механических характеристик привода,
уменьшает статическую ошибку, расширяет
диапазон регулирования скорости.
Введение обратной связи по скорости
также сказывается на динамических
характеристиках привода – повышается
быстродействие привода. Показатели
качества регулирования, характеризующие
динамические свойства привода, рассмотрены
в главе 8.

Пример 4.1.
Электропривод
имеет линейные механические характеристики
с жесткостью
Нм.с. Номинальный моментМ_н=50
Нм. Наибольшее значение скорости
холостого хода ω₀=104,6
1/с. Найти величину диапазона регулирования
скорости, который обеспечивает данный
электропривод, если момент на валу
двигателя может изменяться в пределах
0,15М_н≤М_с≤1,2М_н
и требуемая
точность поддержания заданной скорости
составляет 10%. Какой должна быть жесткость
механических характеристик, чтобы
достичь диапазона регулирования D=100.

Решение. Диапазон
регулирования определим по формуле
(4.5):

Для того, чтобы
достичь диапазона регулирования D₁=100,
жесткость механических характеристик
нужно повысить до значения

Увеличения жесткости
механических характеристик можно
добиться, применив замкнутую по скорости
систему регулирования и повысив общий
коэффициент усиления разомкнутой
системы.

Соседние файлы в папке Главы по ЭП

• #
• #
• #
• #
• #
• #
• #
• #
• #

1. Рассчитать и построить
механические характеристики системы регулирования скорости типа вентильный
преобразователь – двигателя постоянного тока.

2. Определить диапазон
регулирования скорости, если допустимая относительная величина ошибки
регулирования равна 30%.

Исходный данные:

— Тип системы управления –
однократноинтегрирующая двухконтурная система подчиненного управления;

— Тип двигателя – П21;

— Тип вентильного преобразователя –
ШИП;

— Частота коммутации
преобразователя fшип=1500Гц;

— Внутреннее сопротивление
вентильного преобразователя Rип = Rя;

— Коэффициент усиления вентильного
преобразователя Квп =22;

— Коэффициент передачи датчика
скорости Кдс = ;

— Коэффициент передачи датчика тока
Кдт
= ;

— Малые постоянные времени датчиков
тока и скорости равны 0,0005 С;

— Индуктивность якорной цепи
двигателя определяется по формуле ;

-Суммарная индуктивность якорной
цепи 3,
где коэффициент 3 учитывает индуктивность цепей вентильного преобразователя и
соединительных проводов.

Паспортные данные электрической машины типа П21:

Мощность
Рн=1500 Вт;

Частота
вращения n=3000 об/мин;

Ток
Iн=9 А;

Напряжение
Uн=220 В;

Сопротивление
Rя+Rд.п.=1,99 Ом;

Сопротивление
Rпар=600 Ом;

Число
активных проводников якоря N=1224;

Число
параллельных ветвей якоря 2а=2;

Магнитный
поток полюса Ф=3,2 м Вб;

Номинальный
ток возбуждения параллельной обмотки Iн=0,3
А;

Максимальная допустимая частота
вращения =3450 об/мин;

Момент инерции якоря J=0,042 кгм^2;

Масса двигателя Q=38 кг

Решение:

Однократноинтегрирующая
система с обратной связью по скорости:

Контур регулирования тока:

;

;

  постоянная интегрирования
оптимизированного контура;

;

Передаточная функция  замкнутого контура по току:

Передаточная функция замкнутого контура по скорости:

 — электромеханическая постоянная времени;

Учет влияния ЭДС на контур регулирования тока:

Скорость холостого хода:

;

Механическая характеристика:

Диапазон регулирования скорости при допустимом значении
статической ошибки регулирования равной 30%:

Диапазон регулирования:

К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.

Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).

Классификация показателей качества состоит из нескольких групп:

• прямые — определяемые непосредственно по переходной характеристике процесса,
• корневые — определяемые по корням характеристического полинома,
• частотные — по частотным характеристикам,
• интегральные — получаемые путем интегрирования функций.

Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:

1. Установившееся значение выходной величины Yуст,
2. Степень затухания ?,
3. Время достижения первого максимума tmax,
4. Время регулирования tp,
5. Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
6. Перерегулирование у,
7. Динамический коэффициент регулирования Rd,
8. Показатель колебательности М.

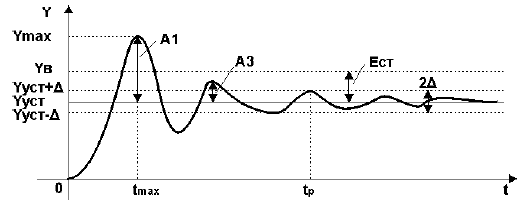
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.

Рисунок 1 — Определение показателей качества по переходной характеристике

Установившееся значение выходной величины Yуст

Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.

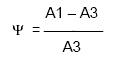
Степень затухания ?

Степень затухания ? определяется по формуле:

где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.

Время достижения первого максимума tmax

Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.

Время регулирования tp

Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.

В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.

Ошибка регулирования Ест

Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.

Перерегулирование у

Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:

где значения величин Ymax и Yуст определяются согласно рис.1.

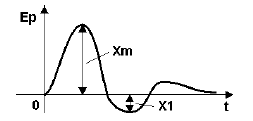
При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:

где значения величин Xm и X1 определяются согласно рис. 2.

Рисунок 2 — График переходного процесса при отработке возмущения

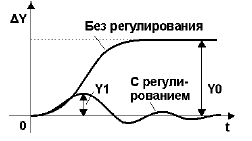
Динамический коэффициент регулирования Rd

Динамический коэффициент регулирования Rd определяется из формулы:

где значения величин Y1 и Y0 определяются согласно рис. 3.

Рисунок 3 — К понятию динамического коэффициента регулирования

Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.

Показатель колебательности М

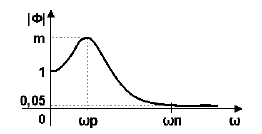
Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.

Рисунок 4 — График модуля частотной передаточной функции замкнутой системы

Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.

В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.