Урок по теме «Работа над ошибками» 7 класс
Цели урока
- Развивать у учащихся критическое мышление, навыки самостоятельной работы, культуру математической речи.
- Способствовать развитию мыслительных операций (сравнения, абстрагирования, обобщения, конкретизации, анализа, синтеза);
- Закрепить знания и умения учащихся при решении задач составлением уравнений, нестандартных задач;
Оборудование:
1. Компьютер
2. Мультимедийный проектор
3. Лист заданий
Тип урока: коррекция и систематизация знаний
Ход урока.
- Вступительное слово учителя. Постановка цели урока.
Два человека стоят у подножия красивейшей горы. Один думает:
«Хочется приблизиться к этой красоте, но вдруг я упаду. Нет, не пойду»
А другой размышляет: «Страшно, опасно, но даже если я упаду, встану,
поднимусь и снова пойду вперед, навстречу прекрасному».
Какова мораль? Ошибся, оступился, исправляй ошибку и двигайся вперед.
Наш урок сегодня обычен. Главная его цель: проанализировать ошибки,
допущенные в контрольной работе по теме «Решение уравнений» и
скорректировать знания по теме.
- Работа по теме урока
I. Напомните:
— Что называется уравнением? (Равенство, содержащее букву)
— Что значит решить уравнение? (Решить уравнение – значит найти все его корни или доказать, что корней нет)
— Что такое корень уравнения? (Корнем уравнения называется число, при подстановке которого в уравнение получается верное равенство)
— Сформулируйте правило переноса слагаемых из одной части в другую.
II. На доске: устно: письменно:
Дима: 1/6х = 18 (у) 6х – (2х – 5) = 2 (3х – 2)
Рита: 7х + 11,9 = 0
Сережа: 6х – (2х -5) = 2 (2х – 4)
Юлиана: 5х – (7х + 7) = 9
Вадим: 8х – (2х + 4) = 2 (3х – 2)
Саша: 3х – 0,5 = 2х + 1,3
Дана – консультант
Никита, Рита, Саша решают задачу:
Саша решил две задачи за 35 мин. Первую задачу он решал на 7 мин. дольше, чем вторую. Сколько мин Саша решал вторую задачу?
III. Прочитать задачу по краткой записи (на доске), составить уравнение и решить задачу:
Навага — ?
Треска — ?, в 1,5 раз больше наваги всего 520 тонн
Окунь — ? на 16 тонн больше трески
На базе хранится 520 тонн рыбы. При этом трески в 1,5 раза больше, чем наваги. Окуня на 16 тонн больше, чем трески. Сколько тонн трески, наваги и окуня находится на складе?
уравнения?
- Работа в тетрадях и у доски
Юлиана (у доски)
- 2х – 15 = 3х – 7 (-8)
- у + 6 = 2у – 5 (11)
Сережа (у доски)
1. 4у – 10 = -6у (1)
- 3х +2 = 6х + 2 (0)
Вадим (у доски)
- 2(1,1 – 5у) = 6у – 1 (0,2)
- 29 – 13х = 17 – 3х (1,2)
Ряд у окна
1. 7х – 18 = 3х + 22 (10)
2. 0,3х – 17 = -1,4х (10)
Ряд к двери
1. 1,3х + 2,5 = 0,3х – 1,5 (-4)
2. 18 – 5у = 6у – 15 (3)
- Необычная задача
Отцу 32 года, сыну 5 лет. Через сколько лет отец будет в 10 раз старше сына?
(решить самостоятельно, сделать вывод)
(Решение.
Обозначим искомый срок через х. Спустя х лет отцу будет (32 + х) лет, сыну (5 + х) лет.
Так как отец должен быть в 10 раз старше сына, то получим уравнение 32 + х = 10(5 + х). Решив его, получаем: х = -2).
Итак, через минус два года. Как вы это можете объяснить?
(Через «минус 2 года» означает «два года назад»).
4. Самостоятельная работа с последующей самопроверкой (10 мин)
Решите уравнение:
I. а) 12х – 21 = 11х + 2(3х + 2); б) 5х – 4(2х – 1) = 2(2х – 5);
в) 0,4 (х – 1,2) + 1,6 = — 2; г) 10х – 2,5(0,6х – 3) = — 1.
II. а) (х + 5) / 6 =(3 – х) /4 б) (1,5х -3,6) / 5 = (- 2,4 + х) / 2
III. а) (3х + 3)(6 – 2х) = 0; б) (2х – 4)(х + 5) = 0;
в) (4х – 8)(х + 3) = 0; г) (х – 2)(2х + 6) = 0;
IV. а) 5х = 3х*х – х; б) 2х *х = 10х.
V. При каких значениях буквенной переменной уравнение
(6 – 4х) / (х – 4) = 0 не имеет корней?
(самооценки по самостоятельной работе)
- Математические фокусы – задача из занимательной алгебры Перельмана (если останется время)
Задумайте число, прибавьте 2, умножьте на 3, отнимите 5, отнимите задуманное число, умножьте на 2, отнимите 1, сообщите окончательный результат. Я легко угадаю, какое число было задумано. Как? Это задание на дом.
(Решение.
Составим таблицу:
|
Задумайте число |
х |
|
Прибавьте 2 |
х + 2 |
|
Умножьте результат на 3 |
3(х + 2) = 3х + 6 |
|
Отнимите 5 |
3х + 6 – 5 = 3х + 1 |
|
Отнимите задуманное число |
3х + 1 – х = 2х + 1 |
|
Умножьте на 2 |
2(2х + 1) = 4х + 2 |
|
Отнимите 1 |
4х + 2 – 1 = 4х + 1 |
Пусть, например, в результате операций получилось число 33, тогда необходимо решить уравнение: 4х + 1 = 33.) О других способах отгадывать числа можно узнать из книги Я.И. Перельмана «Занимательная алгебра».
- Итог урока (2 мин)
|
Посмотрите на уравнение: 4х + 2х *х = 10х |
|
|
Встречались с ним ранее? |
нет |
|
Попробуем решить |
|
|
Какие правила мы применяем при решении уравнений? |
Перенос слагаемых c переменной в одну сторону, а известных слагаемых в другую сторону |
|
Что получилось? |
4х + 2х *х — 10х = 0 |
|
Что заметили? |
Можно привести подобные слагаемые |
|
2х*х -6х = 0 |
|
|
Что общего у каждого из слагаемых? |
общий множитель х |
|
Что с ним можно сделать? |
2х(х – 3) = 0 |
|
Назовите корни |
0 или 3 |
Если вы стоите у подножия горы и видите, какая прекрасная перед вами открывается панорама, не стойте на месте, поднимитесь хотя бы на несколько шагов и красоты преумножатся.
Сегодня мы познакомились с Я.И. Перельманом.
(Учитель сообщает ребятам отметки, заработанные ими на уроке).
- Задание на дом.
Составить уравнение по задаче (текст на столах), найти информацию по Перельману, решить из самостоятельной работы то, что не успели решить.
Алгебра 8 класс.
Работа над ошибками по теме:»Преобразование выражений, содержащих
квадратные корни».
Цель урока: закрепление знаний и
формирование практических навыков.
Задачи урока:
Образовательные:
- повторить и закрепить правила вынесения
множителя из-под знака корня; внесения множителя под знак корня; - отработать навык освобождения от
иррациональности в знаменателе; - закрепить умение упрощать сложные радикалы;
- сравнивать выражения, содержащие квадратные
корни.
Развивающие:
- расширение кругозора;
- быстрота реакции;
- развитие математической речи при
комментировании решений.
Воспитательные:
- воспитание взаимопомощи в процессе
выполнения коллективной работы; - воспитание чувства ответственности в
процессе индивидуальной работы, от которой зависит общий результат; - воспитание внимательности, собранности и
аккуратности; - формирование у учащихся адекватной
самооценки при выборе отметки за работу на уроке.
Оборудование:
- Карточки с индивидуальными заданиями;
- Таблица ответов к математическому диктанту;
Ход урока
Главные этапы урока:
1. Организация начала занятия.
Цель: подготовка
учащихся к работе на занятии.
Человек… родился быть господином, повелителем, царём природы,
но мудрость, с которой он должен править…, не дана ему от рождения; она
приобретается учением.
Лобачевский Н.И.
1 этап
Приветствие. Вступление.
Эпиграф: Хочется сказать крылатую фразу «У желания 1000
возможностей. У нежелания – 1000 причин».
Вводное слово учителя:
– Давайте вспомним сюжет сказки Валентина Катаева «Цветик
семицветик», где девочка неожиданно получила цветок с семью разноцветными
лепестками. Каждый лепесток означал исполнение желания. Она загадала следующие
желания:
- Вернуться домой вместе с баранками, которые
съела собака. - Разбив любимую вазу мамы, она попросила,
чтобы чашка восстановилась. - Захотела много игрушек. И все игрушки мира
слетелись к ней. - Попросила игрушки вернуть назад.
- Отправилась на север. Где ее чуть не съели
белые медведи. - Вернулась назад.
И только после этого, когда у нее остался один лепесток, она
задумалась, и поняла, что лепестки израсходовала без пользы. И решила сделать
что-то важное. Она начала думать, как же поступить с 7 лепестком, и загадала
желание о здоровье мальчика. Поняла, когда увидела счастье этого мальчика, что
самое главное для человека – это здоровье. И сама была счастлива. Ребята план
сегодняшнего урока я расположила на лепестках семицветика.
И, конечно, от каждого из вас будет зависеть, как будут
израсходованы лепестки с пользой или нет. А еще это ваш оценочный лист. На
каждом лепестке должна появиться оценка, а в середине итоговая.
2.Проблемная ситуация.
Задание называется «Скорость счета». Задача учащихся решить 12
примеров за 1 минуту. В тетради записывать только ответы.
На доске даны примеры:
Приложение 2
Алгоритм
Вынести множитель из-под корня Внести
множитель под корень
1. Разложить подкоренное
выражение 1. Число, стоящее перед
корнем, на множители удобным способом.
представить в виде корня.
2.Применить
теорему 2. Применить теорему «корень
из произведения». «произведение корней».
Работа над ошибками.
1.
Вынести множитель из-под
корня:
;
;
.
2.
Внести множитель под
корень: ;
;
;
.
3.
Вычислить: а); б)
.
Внести множитель под знак корня или вынести множитель из-под
знака корня (на этом этапе можно обращаться за помощью).
|
Задания I команде |
Задания II команде |
|
1. |
1. |
|
2. |
2. |
|
3. |
3. |
|
4. |
4. |
|
5. |
5. |
|
6. |
6. |
|
7. |
7. |
|
8. |
8. |
|
9. |
9. |
|
10. |
10. |
|
11. |
11. |
|
12. |
12. |
|
13. |
13. |
Проверяем, помогаем, исправляем по ходу решения.
А теперь работаем самостоятельно.
Контроль и проверка по вариантам. Самостоятельная
работа.
Цель — выявление
качества и уровня овладения знаниями и способами действий, обеспечение их
коррекции.
В-1.
1. Выполните действия:
а) 3√2-5√8+√32;
б) √3*√15;
в) 2√5-√125+3√80;
г) √6*7√54.
- Упростите выражение, считая, что все
переменные принимают только неотрицательные значения:4√t-3 ∕4√16t-12√t ∕ 9.
В-2.
1. Упростите выражение:
а) 7√3+2√27-√75;
б) 2√7*√21;
в) 5√6-√216+3√24;
г) √10*6√15.
- Упростите выражение, считая, что все
переменные принимают только неотрицательные значения:6√x-2∕3√9x+10√x∕4.
Задание по вариантам.
- При каких значениях a имеет смысл выражение:
;[
]
- Сравнить числа:
и
[
и
]
- Сократить дробь:
; [
]
- Освободиться от иррациональности в
знаменателе:; [
]
- Найти значение выражения:
[
]
III
Работа по карточкам.
По найденному значению выражения определить соответствующую букву.
В результате должно получиться высказывание известного философа.
|
1 |
|
14 |
|
|
2 |
|
15 |
|
|
3 |
|
16 |
|
|
4 |
|
17 |
|
|
5 |
|
18 |
|
|
6 |
|
19 |
|
|
7 |
|
20 |
|
|
8 |
|
21 |
|
|
9 |
|
22 |
|
|
10 |
|
23 |
|
|
11 |
|
24 |
|
|
12 |
|
25 |
|
|
13 |
|
4 ступень.
Подведение итогов.
За работу на уроке ребята сами выставляют себе оценки
(критерии выставления оценок вывешиваются на доску).
«отлично» — все задания
выполнял самостоятельно;
«хорошо» — иногда прибегал
к помощи товарища;
«удовлетворительно» —
получать верный ответ не удавалось, но было велико желание разобраться в
решении.
V ступень.
Домашнее задание. тест стр. 37
Цели и задачи урока «Работа над ошибками»:
- Разобрать, проработать погрешности, допущенные в контрольной работе.
- Сформировать умение работать в роли проверяемого и проверяющего.
- Формировать умение систематизировать и обобщать, закреплять и проводить
анализ по данной теме. - Научить правильно относиться к ошибке, умело и грамотно ее использовать.
Выделим основные компоненты урока:
- Консультация;
- Коррекция знаний и умений;
- Диагностика результатов;
- Оценочная деятельность.
В начале урока(15минут) учащиеся делятся на две группы:
- первая — учащиеся, получившие за контрольную работу «4» и «5»;
- вторая –«3» и «2».
Первая группа работает в парах, в тройках: отличник плюс хорошист,
отличник плюс два хорошиста. Вначале в этих группах идет работа над ошибками,
допущенными хорошистами, затем они вспоминают все правила, которые применяются
при выполнении всех заданий. Заключительный этап их совместной работы —
составление аналогичных заданий, предлагаемых в контрольной работе, которые
потом будут использованы хорошистами, когда они будут работать в роли
консультантов.
Параллельно идет работа учителя со второй группой учащихся. Учитель
подробно останавливается на часто встречающихся ошибках данной темы, допущенных
этой группой учащихся. Идет беседа между учителем и учеником, ответы на вопрос
«А почему?», причем не только со стороны учителя, но и со стороны учащихся
(задача учителя научить задавать вопросы). Прорешивается каждое задание, но не
из контрольной работы, а аналогичное ему, в конце которого учитель обязательно
делает вывод.
В основной части урока (20 минут), идет перераспределение
обязанностей: «хорошисты» становятся консультантами для «троечников» и
«двоечников», у которых идет работа в парах и тройках. Сколько бывает радости у
заядлого «троечника», когда он попадает в разряд консультантов.
Основная цель их совместной работы — провести работу над допущенными
ошибками в контрольной работе: консультируемый решает, проговаривает правила,
применяемые при решении заданий, задает вопросы по непонятым темам; консультант
анализирует, отвечает на вопросы, предлагает аналогичные задания, проверяет их,
оценивает работу над ошибками.
Работа консультанта оценивается учителем в зависимости от понимания материала
их консультируемого (индивидуальные способности консультируемого учитель
учитывает).
«Отличники» получают творческое задание, чаще всего им предстоит поработать
над составлением заданий «со звездочкой» по данной теме. Некоторое время ученики
работают самостоятельно, затем объединяются в группу и под руководством учителя,
а чаще сами, объединяют свои наработки, идеи и получают интересные, а порой
очень оригинальные задания. Эти задания могут быть использованы учителем для
работы с учащимися — участниками олимпиад, для индивидуальной работы на уроке, в
контрольных работах в параллельных классах (как дополнительные задания).
В конце урока подводится итог, в журнале появляется очередной столбик оценок,
причем, на ряд выше предыдущих и обязательно, всем классом, прорешиваем самую
интересную задачу урока, составленную творческой группой.
Итогом урока является тщательно проработанная и усвоенная тема.
Т.о. урок работы над ошибками позволяет индивидуально и дифференцированно
подойти к процессу обучения. У учащихся формируется умение делать самоанализ,
умение работать в группах, умение применять полученные знания на практике.
Разработка урока-путешествия после контрольной работы,работа над ошибками допущенных при выполнении работы
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок -путешествие «Работа над ошибками.Решение заданий на сложение и вычитание смешанных чисел»»
Урок путешествие 5 класс
5 класс
Работа над ошибками
Билеты на поезд :
- А).половина от 1 часа
- Б).четверть от 1 килограмма
- В).восьмушка от 1 километра
- Г).треть от года
- Д)десятая часть от сентября
Ответы билеты на поезд
- А) 30 минут
- Б) 250 грамм
- В) 125 метров
- Г) 4 месяца
- Д) 3 дня
Найдите ошибку
- 1) 3:4 = 2)9:6=
- 3)5:2= 4)28:31=
- 5)70:12=
Ответ «Найди ошибку»
- Это 5 вопрос:
- 70:12=
- Должно быть:
- 70:12=
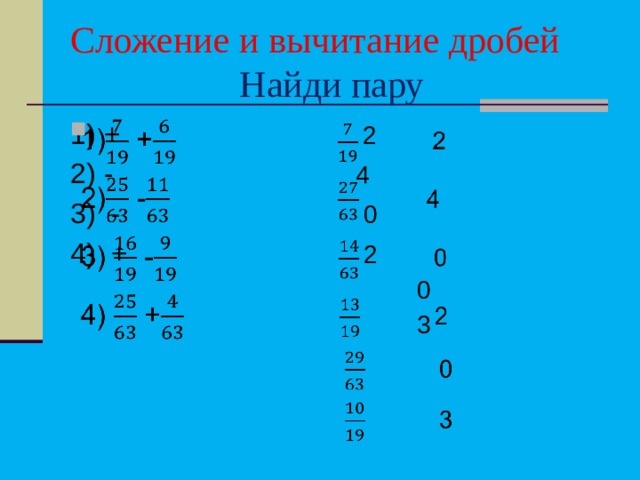
Сложение и вычитание дробей Найди пару
1) + 2
2) — 4
3) — 0
4) + 2
0
3
Ответ «Найди пару»
1) + = 2
2) — = 0
3) — = 2
4) + 0
2020 год-
- Год развития науки, просвещения и цифровой экономики
Найдите правильный ответ
- 1)м=4см 2)час=8мин
- 3) год=3мес 4)ц=50кг
- 5)т=4000кг
Найдите правильный ответ -это 3ответ
- 1)м=5см 2)час=4мин
- 3) год=3мес 4)ц=60кг
- 5)т=40кг
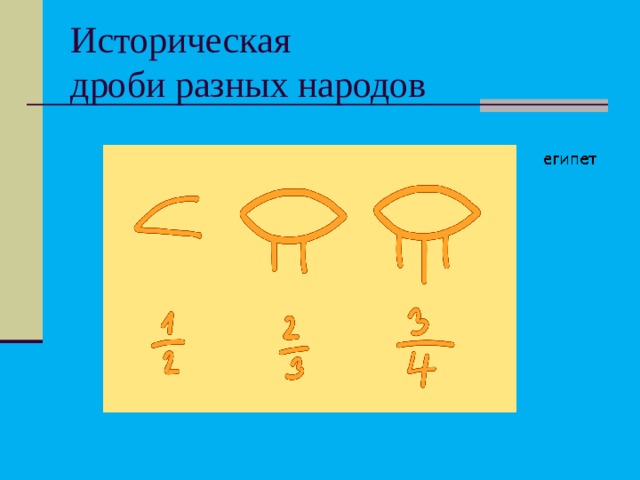
Историческая дроби разных народов
египет
В Греции
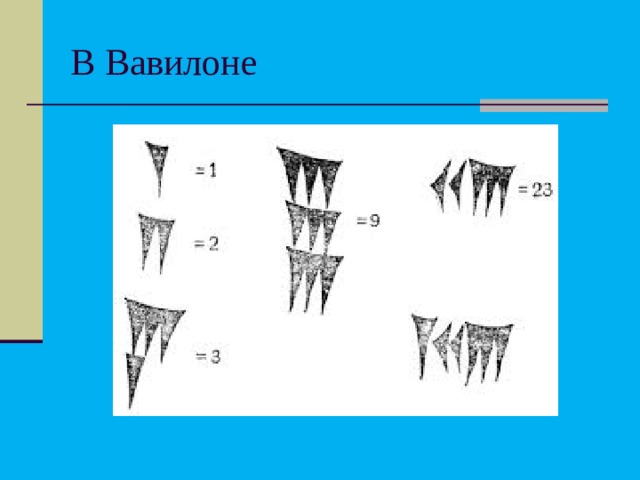
В Вавилоне
В древней Руси
Февраль
Захир-ад-дин Мухаммад Бабу́р ( 14февраля 1483 — 26 декабря 1530 ) —среднеазиатский и тимуридский правитель Индии и Афганистана, полководец, основатель династии Бабуридов и империи Великих Моголов . Известен также как узбекский поэт и писатель
Самое маленькое натуральное число
- 1
Правильные и неправильные дроби
- А)все правильные дроби со знаменателем 8
- Б) все неправильные дроби с числителем 5
- В)записать в виде неправильной дроби
- 2 ,3 ,6, 9
- Г)записать в виде смешанного числа
- , , , ,
Сложение и вычитание смешанных чисел
- А) 9+4 Б)28 -19
- В)26-4 Г)8 +9
- Д)47 — 35 Е)1+
Ответы -Сложение и вычитание смешанных чисел
- А) 9+4= 13 Б)28 -19=9
- В)26-4 =21 Г)8 +9=18
- Д)47 — 35=11 Е)1+=2
спортивная
- 1)7 +2 17 -17
- 7 — 3 4+
- — 9 -8
- + 7 1 +16
спортивная
- 1)7 +2 = 9 2) 9 -8 = 1
- 3)1 +16 = 17 4) 17 -17=
- 5) — = 6) + 7 = 7
- 7) 7 — 3 = 4
4+ =5
Спасибо
Желаю всем успехов
и хорошего настроения!
В этом разделе сайта разбираются ошибки, наиболее часто встречающиеся в работах учащихся. Освоив материал ниже перечисленных разделов, можно избежать многих ошибок в будущем.
Для удобства ошибки разбираются по темам:
Тождественные преобразования
Решение уравнений
Решение систем уравнений
Решение неравенств
Упражнения с параметрами
Функции и свойства функций
Начала анализа
Геометрия
Существует мнение, что такие итоговые письменные работы, как ЕГЭ, невозможно выполнить успешно из-за слишком высоких требований. Действительно, предъявляемые требования, несколько выше требований, предъявляемых на обычном школьном уроке. И максимальных результатов могут достичь разве что победители математических олимпиад. При этом гибкая система оценивания ЕГЭ специально разработана для того, чтобы все учащиеся были оценены объективно, и те, кто хорошо знают математику в пределах школьной программы, могут претендовать на высокий результат, вполне достаточный для поступления в высшее учебное заведение.
К сожалению, при выполнении работ разного уровня, в том числе и ЕГЭ, учащиеся все чаще демонстрируют слабые знания школьного курса математики. И именно это является основной причиной «провалов». В подтверждение приведем примеры элементарных ошибок, допущенных учащимися при выполнении проверочных работ по математике.
|
L Неправильное решение |
J Правильное решение |
|
\[ \frac{x}{2x^2+3x}=2x+3 \] |
\[ \frac{x}{2x^2+3x}=\frac{1}{2x+3} \] |
|
\[ \left(1+x\right)^{3}=\left(1+x\right)(1-x+x^2) \] |
\[ \left(1+x\right)^{3}=1+3x+3x^2+x^3 \] |
|
\[ \left(x^{\sqrt{3}} \right)^{2}=x^3 \] |
\[ \left(x^{\sqrt{3}} \right)^{2}=x^{2\sqrt{3}} \] |
|
\[ \frac{4^x}{2^x}=2 \] |
\[ \frac{4^x}{2^x}=\frac{2^{2x}}{2^x}=2^x \] |
|
\[ 2^x+4^x=6^x \] |
\[ 2^x+4^x=2^x+2^{2x}=2^x(1+2^x) \] |
|
\[ 4\cdot 2^x=8^x \] |
\[ 4\cdot 2^x=2^2\cdot 2^x=2^{2+x} \] |
|
\[ \sqrt{x^6}=x^3 \] |
\[ \sqrt{x^6}=\left| x^3\right| \] |
|
\[ \sqrt{a^2+b^2}=a+b \] |
\[ \sqrt{a^2+b^2}=\sqrt{a^2+b^2} \] |
|
\[ 3x^{\frac{1}{2}}=\sqrt{3x} \] |
\[ 3x^{\frac{1}{2}}=3\sqrt{x} \] |
|
\[ {(\lg x^3)}^2=\lg x^6 \] |
\[ {(\lg x^3)}^2=\lg^2 x^3 \] |
|
\[ \lg x^2=2\lg x \] |
\[ \lg x^2=2\lg \left| x\right| \] |
|
\[ -\lg x=\lg (-x) \] |
\[ -\lg x=\lg x^{-1} \] |
|
\[ \lg^2 {3x}=\lg^2 {3}+\lg^2 {x} \] |
\[ \lg^2 {3x}=\left(\lg 3+\lg x \right)^2 \] |
|
\[ \lg^2 {x^3}=3\lg^2 {x} \] |
\[ \lg^2 {x^3}=9\lg^2 {x} \] |
|
\[ 10^{-\lg 7}=-7 \] |
\[ 10^{-\lg 7}=10^{\lg 7^{-1}}=\frac{1}{7} \] |
|
\[ \arccos \frac{\pi }{3}=\frac{1}{2} \] |
\[ \arccos \frac{1}{2}=\frac{\pi }{3} \] |
Прежде чем перейти к разбору конкретных ошибок, обратите внимание на проблемы, возникающие из-за недостатка общей математической культуры.
Во-первых, многие испытывают затруднения при переводе словесного условия задания на язык математических формул, уравнений или неравенств. Например:
L выражение «доказать, что функция f(x) неотрицательна» записывается f(x) > 0 вместо f(x) > 0;
L выражение «при каких значениях х значение функции f(x) равно 2,5» не ассоциируется с уравнением
f(x) = 2,5;
L выражение «найдите радиус шара, объем которого равен объему куба с ребром а» не записывается соотношением 4/3πr3 = a3, хотя каждая из этих формул учащимся очевидно известна;
L выражение «треугольник, образованный осями координат и прямой, их пересекающей» не вызывает необходимости найти точки пересечения этой прямой с осями координат и т.д.
Во-вторых, некоторые учащиеся путаются в элементарных понятиях, например, не могут четко разделить понятия целого и натурального, положительного и неотрицательного чисел. В результате при выборе из множества решений решения, удовлетворяющего условию (например, при выборе наименьшего целого числа промежутка (a; b)), допускаются ошибки.
В-третьих, часто при отборе корней не учитывается область допустимых значений переменной и т.д.
При подготовке данного раздела сайта использовано учебное пособие «Математика. Репетитор» Будная Е.С., Будная С.Н. (Харьков, «Факт», 2008)

























 4+ =5
4+ =5 
