Построение
математической модели — это скорее
искусство, чем наука, и, прежде всего,
требует глубоких знаний предметной
области. Социально-экономические системы
имеют чрезвычайно сложную структуру,
со многими явными и неявными взаимосвязями
между элементами системы, подвержены
влиянию многих скрытых факторов,
относятся к классу так называемых
больших систем. Стечением
времени меняются не только их
характеристики, учитываемые в модели
в виде отдельных параметров, но и
структура самих уравнений, которые
описывают процесс. Для их адекватного
описания требуется соответствующий
математический аппарат. Однако, даже
самые сложные математические методы
не в состоянии описать реальную систему
во всех ее деталях, да это и не нужно.
Модель не должна быть слишком сложной.
Излишняя детализация и учет второстепенных
факторов затрудняет
исследование
и не дает существенной информации об
изучаемой системе. Если модель слишком
сложна, то ее трудно использовать и
интерпретировать на практике.
Относительная
простота — важная характеристика
удачно построенной модели.
С другой стороны, слишком упрощенная
модель не будет адекватно описывать
реальную систему. Таким образом, сложность
модели должна соответствовать сложности
изучаемого экономического объекта.
В связи
с этим возникает необходимость
формулировки некоторых разумных
упрощающих гипотез (предположений),
исключения из анализа второстепенных
факторов и т. п., с тем, чтобы была
возможность описать процесс математически.
При этом существенные для
данного
социально-экономического процесса
характерные черты
должны
быть учтены в модели в соответствии с
поставленной целью исследования.
Другой
характерной проблемой, с которой
сталкивается эконометрист, является
то, что часто приходится довольствоваться
неточными
данными,
которые имеются в наличии и быстро
устаревают. Этих данных не всегда
хватает, а провести управляемый
эксперимент с целью получения
дополнительной информации невозможно.
В подобном случае целесообразно сочетание
количественных методов с привлечением
экспертных знаний и суждений.
Таким
образом, при создании эконометрической
модели возникают следующие вопросы.
1.
Какую модель желательно построить —
статическую или динамическую (с
учетом фактора времени), нелинейную или
линеаризованную? Как учесть влияние
внешней среды (возмущений)? (Ответ на
эти вопросы определяет желаемую точность
и сложность модели, выбор адекватного
математического аппарата и т. д.)
2.
Достаточно
ли имеющихся данных, необходимых для
построения адекватной модели,
насколько они достоверны? Существует
ли возможность получения дополнительной
информации, если это необходимо? Следует
ли привлечь экспертную информацию?
3. Как
оценить качество модели, т. е. определить,
насколько адекватно (правильно) она
описывает поведение реального объекта?
В
рамках эконометрического подхода
существует мощный арсенал средств,
который включает многие современные
эффективные
математические методы,
такие, например, как аппарат
нейронных сетей,
и разработанные на их основе компьютерные
технологии, в известной степени помогающие
справиться с этими проблемами. Но
решающая
роль принадлежит специалисту —
эконометристу.
Окончательный успех зависит от его
способности к неформальному анализу
проблемной ситуации, адекватной оценке
возможностей современных эконометрических
методов, от их правильного применения
и интерпретации полученных результатов.
Построив
удачную математическую модель и оценив
ее количественно с использованием
эконометрических методов, экономист-аналитик
получает в распоряжение эффективнейшее
средство анализа и прогноза, а
управляющий-практик — инструмент для
обоснования управленческих решений.
Такие модели широко применяются на
практике.
Практически
величина y
складывается из двух слагаемых:
,
где
— фактическое
значение, результат признака;
— теоретическое
значение результата признака, найденное
из математической модели или уравнения
регрессии;
— СВ, характерное
отклонение реального значения результата
признака от теоретического.
СВ
называется
возмущением. Она включает влияние
неучтённых в модели факторов, случайных
ошибок и особенно измерения. Её присутствие
в модели порождено тремя источниками:
-
спецификацией
модели; -
выборочным
характером исходных данных; -
особенностями
измерения.
От правильно
выбранной спецификации модели зависит
величина случайных ошибок: они тем
меньше, чем больше теоретические
значения результативного признака
подходит к фактическим данным y.
К ошибкам спецификации
будут относиться не только неправильный
выбор той или иной математической
функции для
,
но и недоучет в УР какого-либо существенного
фактора (например, использование парной
регрессии вместо множественной).
Наряду с ошибками
спецификации могут иметь место ошибки
выборки (неоднородность данных в исходной
статистической совокупности). Если
совокупность неоднородна, то УР не имеет
практического смысла.
Для получения
хорошего результата обычно исключают
из совокупности единицы с аномальными
значениями исследуемых признаков, то
есть результаты регрессии представляют
собой выборочные характеристики.
Наибольшую опасность
в практическом использовании методов
регрессии представляют ошибки
измерения.
Если ошибки спецификации можно уменьшить,
изменяя форму модели, а ошибки выборки
– увеличивая объём исходных данных, то
ошибки измерения практически сводят
на нет все усилия по количественной
оценке связи между признаками. Особенно
велика роль ошибок измерения при
исследовании на макроуровне.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
04.08.2019218.11 Кб2kv.doc
- #
- #
- #
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
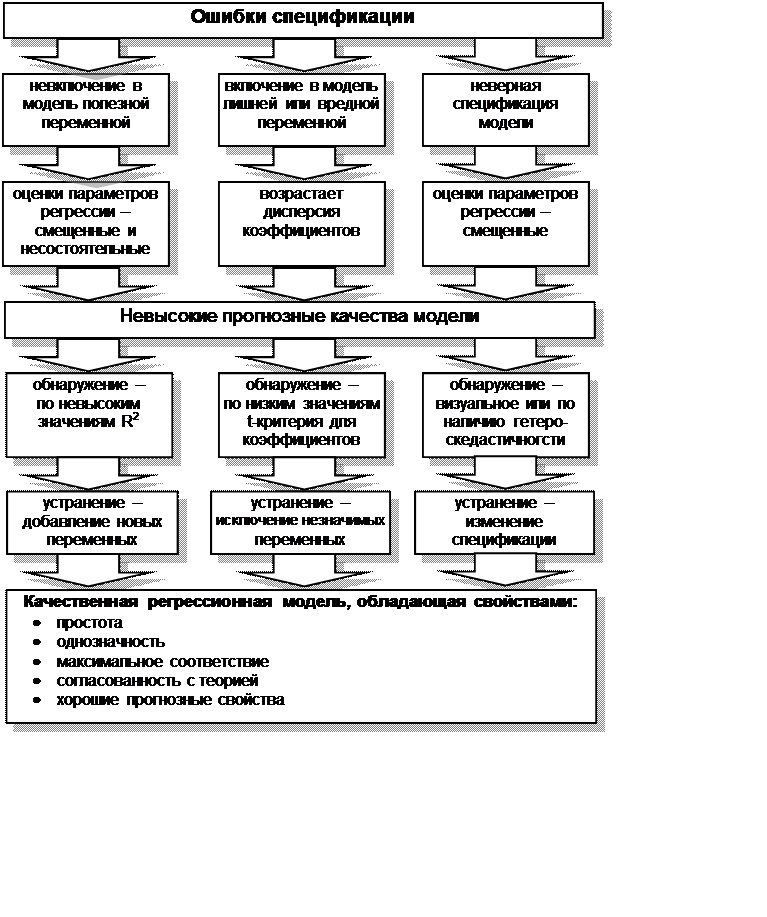
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ТВЕРСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА «БУХГАЛТЕРСКИЙ УЧЕТ, АНАЛИЗ И АУДИТ»
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Тверь 2009
________________________________________________________________________________
Раздел 4. Спецификация переменных
в уравнениях регрессии
Тематические вопросы: Эконометрические модели: общая характеристика,
различия статистического и эконометрического подхода к моделированию.
Спецификация
переменных
в
уравнениях
регрессии.
Ошибки
спецификации. Обобщенная линейная модель множественной регрессии.
Обобщенный
метод
наименьших
квадратов.
Проблема
гетероскедастичности.
Автокорреляция.
Анализ
линейной
модели
множественной регрессии при гетероскедастичности и автокорреляции.
Фиктивные переменные: общий случай. Множественные совокупности
фиктивных переменных. Фиктивные переменные для коэффициентов
наклона. Тест Чоу. Моделирование: влияние отсутствия переменной,
которая должна быть включена; влияние включения в модель переменной,
которая не должна быть включена. Замещающие переменные.
Минимум содержания в соответствии с ГОС: линейные регрессионные
модели с гетероскедастичными и автокоррелированными остатками;
регрессионные модели с переменной структурой (фиктивные переменные).
4.1.Выбор формы модели регрессии: проблемы спецификации, основные
регрессионные модели………………………………………………………………..2
4.2.Ошибки спецификации: виды, обнаружение, корректировка……………5
4.3.Проблема автокорреляции остатков в моделях регрессии………………..6
4.4.Проблема гетероскедастичности остатков
в моделях регрессии………………………………………………………………….12
4.5.Обобщенный метод наименьших квадратов………………………………..18
4.6.Фиктивные переменные в регрессионных моделях……………………….18
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
4.1.Выбор формы модели регрессии: проблемы спецификации,
основные регрессионные модели
Многообразие и сложность экономических процессов предопределяет
многообразие моделей, используемых для эконометрического анализа. С
другой стороны, это существенно усложняет процесс нахождения
максимально адекватной формулы зависимости. Для случая парной
регрессии подбор модели обычно осуществляется по виду расположения
наблюдаемых точек на корреляционном поле. Однако нередки ситуации,
когда расположение точек приблизительно соответствует нескольким
функциям и необходимо из них выявить наилучшую. Например,
криволинейные зависимости могут аппроксимироваться полиномиальной,
показательной, степенной, логарифмической функциями. Еще более
неоднозначна ситуация для множествен-нои регрессии, так как наглядное
представление статистических данных в этом случае невозможно.
◊Эконометрическая модель – экономико-математическая модель,
параметры которой оцениваются с помощью методов математической
статистики; выступает в качестве средства анализа и прогнозирования
конкретных экономических процессов как на макро-, так и на
микроэкономическом
уровне
на
основе
реальной
статистической
информации. ◊Экономико-статистическая модель – вид экономикоматематической модели; описывает зависимости, носящие вероятностный
(стохастический) характер и возникающие под воздействием множества
причин и следствий в массовых, повторяющихся явлениях; предназначена
прежде всего для выявления тенденций и закономерностей, которые были
в прошлом, чтобы с их помощью оценивать будущее
Стандартная схема эконометрического исследования
осуществлении ряда последовательных процедур:
состоит
в
•
Подбор
начальной
модели:
осуществляется
на
экономической теории, предыдущих знаний об
исследования, опыта исследователя и его интуиции.
•
Оценка
параметров
статистических данных.
•
Осуществление тестов проверки качества модели (обычно
используются t-статистики для коэффициентов регрессии, Fстатистика для коэффициента детерминации и ряд других
тестов).
•
При наличии хотя бы одного неудовлетворительного ответа по
какому-либо тесту модель совершенствуется с целью устранения
выявленного недостатка.
•
При положительных ответах по всем проведенным тестам модель
считается качественной. Она используется для анализа и
модели
2
на
основе
основе
объекте
имеющихся
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
прогноза объясняемой переменной.
Основные проблемы спецификации модели регрессии:
•
Качественная модель является подгонкой спецификации модели
под имеющийся набор данных. Поэтому вполне реальна картина,
когда исследователи, обладающие разными наборами данных,
строят разные модели для объяснения одной и той же
переменной.
•
Использование
модели
для
прогнозирования
значений
объясняемой переменной. Иногда хорошие с точки зрения
диагностических тестов модели обладают весьма низкими
прогнозными качествами.
Признаки «хорошей» модели:
•
Скупость (простота): модель должна быть максимально простой,
т.е. из двух моделей, приблизительно одинаково отражающих
реальность, предпочтение
отдается
модели,
содержащей
меньшее число объясняющих переменных.
•
Единственность: для любого набора статистических данных
определяемые коэффициенты регрессии должны вычисляться
однозначно.
•
Максимальное соответствие: уравнение тем лучше, чем большую
часть разброса зависимой переменной оно может объяснить, т.е.
с максимально возможным скорректированным коэффициентом
детерминации.
•
Согласованность с теорией: модель обязательно должна
опираться на теоретический фундамент, т.к. в противном случае
результат использования регрессионного уравнения может быть
неадекватным.
•
Прогнозные
качества:
модель
может
быть
признана
качественной, если: полученные на ее основе прогнозы
подтверждаются реальностью; модель имеет малое значение
относительной ошибки прогноза ( V = S y ) при отсутствии
автокорреляции остатков.
Основные регрессионные модели:
◊Коэффициент эластичности переменной Y по переменной Х (Э) как
относительное изменение Y вследствие единичного относительного
изменения X, часто на практике, как процентное изменение Y для
однопроцентного изменения X.
3
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
Функционал
ьная форма
Уравнение
Линейная
модель
Y = β 0+ β 1 X 1 + β 2 X 2 +
Двойная
логарифм
ическая
модель
ln Y = β 0 + β 1 ln X 1 +
Логлинейная
модель
ln Y = β 0 + β 1 X 1 +
Линейнологарифм
ическая
модель
Y = β 0 + β 1 ln X 1 +
Обратная
модель
Степенная
модель
+ … + β m X m + ε
+ β 2 ln X 2 + … +
+ β m ln X m + ε
+ β 2 X 2 + … +
+ β mXm + ε
+ β 2 ln X 2 + … +
+ β m ln X m + ε
Y = β0 + β1
1
+
X1
+ β2
1
+ … +
X2
+ βm
1
+ ε
Xm
Интерпретация
коэффициента (ов) регрессии
предельный
эффект
независимого
фактора,
т.е.
прирост зависимой переменной
при изменении независимого
фактора на единицу
процентное
изменение
зависимой
переменной
вследствие
единичного
относительного прироста (напр.,
однопроцентного) независимого
фактора
темп
прироста
зависимой
переменной по объясняющей
переменной, т.е. процентное
изменение
зависимой
переменной
при
изменении
независимого
фактора
на
единицу (при интерпретации
коэффициент следует умножать
на 100%)
изменение
зависимой
переменной
вследствие
единичного
относительного
прироста
(напр.,
однопроцентного) независимого
фактора (при интерпретации
коэффициент следует делить на
100%)
скорость
асимптотического
приближения
зависимой
переменной
к
некоторому
пределу
(напр.,
β0 )
при
увеличении
объясняющей
переменной
Y = β 0 + β 1 X + β 2 X 2 + аналогично
+ … + β m X m + ε
(после
линейной
X = X1, X 2 = X 2 ,
…, X m = X m
Показател
ьная
модель
Y = β 0aβ X eε
модели
замены:
Э= β
X
Y
Э= β ,
эластичность
постоянна
Э = βX,
эластичность
растет
с
ростом Y
Э= β
1
,
Y
эластичность
убывает
с
ростом Y
1
Э = β−
XY
аналогично
линейной
модели
)
аналогично
лог-линейной
модели
(после
логарифмирования)
4
Коэффициент
эластичности,
Э
аналогично
лог-линейной
модели
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
4.2.Ошибки спецификации: виды, обнаружение, корректировка
◊Ошибка спецификации как неправильный выбор функциональной
формы или набора объясняющих переменных в регрессионной модели.
Основные типы ошибок спецификации:
•
Отбрасывание значимой переменной: в результате оценки,
полученные с помощью МНК по уравнению, являются
смещенными и несостоятельными, следовательно, интервальные
оценки и результаты проверки соответствующих гипотез будут
ненадежными.
•
Добавление незначимой переменной: в результате оценки
коэффициентов, найденные с помощью МНК для модели,
остаются, как правило, несмещенными и состоятельными; однако
их точность уменьшится, увеличивая при этом стандартные
ошибки, т.е. оценки становятся неэффективными, что отразится
на их устойчивости; увеличение дисперсии оценок может
привести
к
ошибочным
результатам
проверки
гипотез
относительно значений коэффициентов регрессии, расширению
интервальных оценок.
•
Выбор неправильной функциональной формы: в результате
оценки коэффициентов, найденные с помощью МНК для модели,
как
правило,
являются
смещенными,
либо
ухудшаются
статистические свойства оценок коэффициентов регрессии и
других показателей качества уравнения; прогнозные качества
модели в этом случае очень низки.
•
Проблемы в использовании переменных: невозможно получение
данных по переменной, невозможно измерить количественно
переменную; такие ситуации характерны для переменных
социально-экономического
характера
(напр.,
качество
образования).
Обнаружение и корректировка ошибок спецификации:
Примеры обнаружения ошибок
спецификации
Примерная корректировка ошибок
спецификации
Если в уравнении регрессии В дальнейшем эту переменную
имеется одна несущественная следует
исключить
из
переменная, то она обнаружит рассмотрения
себя по низкой t-статистике
Если в уравнении несколько
статистически
незначимых
объясняющих
переменных,
обнаруженных по низкой tстатистике
Следует
построить
другое
уравнение
регрессии
без
незначимых
переменных
и
провести анализ качества с
помощью F-статистики.
5
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
Проверить
наличие
мультиколлинеарности
и
провести
соответствующие
меры.
Невозможность
получения Подбор
переменной
данных (количественных) по заместителя:
◊Замещающие
переменной.
переменные
переменные,
которые
вводятся
в
эконометрические
модели
вместо
тех
переменных,
которые
не
поддаются
измерению.
Замещающая
переменная
должна
коррелировать с переменной,
которую она замещает.
Существует ряд тестов обнаружения ошибок спецификации, среди
которых можно выделить:
•
Тест Рамсея RESET
•
Тест (критерий) максимального правдоподобия
•
Тест Валда
•
Тест множителя Лагранжа
•
Тест Хаусмана
•
Box-Сох преобразование
Суть данных тестов состоит либо в осуществлении преобразований
случайных отклонений, либо масштаба зависимой переменной с тем,
чтобы можно было сравнить начальное и преобразованное уравнения
регрессии на основе известного критерия. Подробное описание данных
тестов выходит за рамки данного курса и может быть найдено в
дополнительной литературе.
4.3.Проблема автокорреляции остатков в моделях регрессии
Автокорреляция остатков в моделях регрессии как нарушение важной
предпосылки построения качественной регрессионной модели по МНК
(одного из условий Гаусса-Маркова): «Случайные отклонения являются
независимыми друг от друга: cov(εi,εj)=0, i‡j, cov(εi,εj)=σ2, i=j».
◊Автокорреляция
(последовательная
корреляция)
остатков
определяется
как
корреляция
между
остатками
(отклонениями),
6
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
упорядоченными во времени (временные ряды) или в пространстве
(перекрестные данные): cov(εt-1,εt)<>0.
Автокорреляция остатков (отклонений) обычно встречается в
регрессионном анализе при использовании данных временных рядов. При
использовании
перекрестных
данных
наличие
автокорреляции
(пространственной корреляции) крайне редко. В экономических задачах
значительно
чаще
встречается
так
называемая
положительная
автокорреляция (cov(εt-1,εt) > 0), чем отрицательная автокорреляция
(cov(εt-1,εt)< 0).
Примечание:
Порядок автокорреляции определяется периодом (p) прошлых
значений случайного члена εt-p, относительно периода (t) значения
случайного члена εt , между которыми обнаружена корреляция: cov(εtНапример, автокорреляция первого порядка формализуется
p,εt)<>0.
следующим образом: εt=ρεt-1+ ut, где ρ – коэффициент автокорреляции
первого порядка (-1;1).
Основные причины, вызывающие появление автокорреляции:
•
Ошибки спецификации: неучет в модели какой-либо важной
объясняющей переменной либо неправильный выбор формы
зависимости обычно приводит к системным отклонениям точек
наблюдений от линии регрессии, что может привести к
автокорреляции.
•
Инерция:
многие
экономические
показатели
(например,
инфляция, безработица, ВНП и т.п.) обладают определенной
цикличностью,
связанной
с
волнообразностью
деловой
активности.
•
Эффект паутины: во многих сферах экономики экономические
показатели реагируют на изменение экономических условий с
запаздыванием (временным лагом), в связи с чем неадекватно
предполагать случайность отклонений друг от друга.
7
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
• Сглаживание данных: зачастую данные по некоторому
продолжительному временному периоду получают усреднением
данных по составляющим его подынтервалам, что может
привести к определенному сглаживанию колебаний, которые
имелись внутри рассматриваемого периода.
Последствия автокорреляции:
•
Истинная автокорреляция не приводит к смещению оценок
коэффициентов регрессии. Оценки параметров, оставаясь
линейными и несмещенными, перестают быть эффективными.
Следовательно, они перестают обладать свойствами наилучших
линейных несмещенных оценок (BLUE-оценок).
•
Дисперсии оценок являются смещенными. Зачастую дисперсии,
вычисляемые
по
стандартным
формулам,
являются
заниженными, что приводит к увеличению t-статистик. Это
может привести к признанию статистически значимыми
объясняющие
переменные,
которые
в
действительности
таковыми могут и не являться.
•
Оценка дисперсии регрессии S2 является смещенной оценкой
истинного значения, во многих случаях заниженной, что
вызывает
занижение
оценок
стандартных
ошибок
коэффициентов.
•
В силу вышесказанного выводы по t- и F-статистикам,
определяющим
значимость
коэффициентов
регрессии
и
коэффициента детерминации, возможно, будут неверными.
Вследствие этого ухудшаются прогнозные качества модели.
Методы обнаружения автокорреляции:
•
Графический метод: 1) последовательно-временные графики,
увязывающие отклонения с моментами их получения, т.е. по оси
абсцисс обычно откладываются либо момент получения
статистических данных, либо порядковый номер наблюдения, а по
оси ординат отклонения (оценки отклонений); 2) наложение на
график реальных колебаний зависимой переменной графика
колебаний
переменной
по
уравнению
регрессии
и
сопоставление: если эти графики пересекаются редко, то можно
предположить наличие положительной автокорреляции остатков,
и др. варианты.
•
Метод рядов: последовательно определяются знаки отклонений,
причем ряд определяется как непрерывная последовательность
одинаковых знаков, количество знаков в ряду называется
длиной
ряда.
Визуальное
распределение
знаков
свидетельствует о характере связей между отклонениями. Если
рядов слишком мало по сравнению с количеством наблюдений, то
8
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
вполне вероятна положительная автокорреляция. Если же рядов
слишком много, то вероятна отрицательная автокорреляция. Для
более
детального
анализа
имеются
формализованные
процедуры.
•
Критерий Дарбина-Уотсона: суть состоит в вычислении
статистики Дарбина-Уотсона (в случае неприменимости –
статистики Дарбина) и на основе ее величины осуществлении
выводов об автокорреляции.
◊Статистика Дарбина-Уотсона предназначена для обнаружения
автокорреляции первого порядка, основана на изучении остатков
уравнения регрессии:
T
DW =
∑ (e
t=2
− et − 1 )
t
T
∑
2
≈ 2(1 − ret ,et − 1 ) ,
2
t
e
t=1
где T – число наблюдений (обычно временных периодов), et – остатки
уравнения регрессии, ret ,et − 1 – выборочный коэффициент автокорреляции
T
первого порядка:
ret ,et − 1 =
∑
t=1
T
∑
t=1
et et − 1
2
t
e
T
∑
t=1
.
2
t−1
e
Ограничения использования статистики Дарбина-Уотсона:
•
Критерий DW применяется лишь для тех моделей, которые
содержат свободный член.
•
Предполагается, что случайные отклонения определяются по
следующей
итерационной
схеме:
εt=ρ εt-1+ ut, называемой авторегрессионной схемой первого
порядка AR(1), где ut — случайный член.
•
Статистические
данные
должны
иметь
одинаковую
периодичность (т. е. не должно быть пропусков в наблюдениях).
•
Критерий Дарбина-Уотсона не применим для регрессионных
моделей, содержащих в составе объясняющих переменных
зависимую переменную с временным лагом в один период, т. е.
для так называемых авторегрессионных моделей вида:
y t = β 0 + β 1 x t1 + … + β m x tm + γ y t − 1 + ε t .
9
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
Общая схема использования статистики Дарбина-Уотсона:
•
По
построенному
эмпирическому
уравнению
регрессии
ˆt = b0 + b1 x t1 + … + bm x tm определяются значения отклонений
y
ˆt для каждого наблюдения t=1,2…T.
et = y t − y
•
Рассчитывается статистика DW:
T
DW =
∑ (e
t=2
t
− et − 1 )
T
∑
t=1
•
2
et2
По таблице критических точек Дарбина-Уотсона определяются
границы приемлемости (dl,du) и осуществляются выводы по
правилу:
dl < DW < du
вывод о наличии автокорреляции
не определен
du < DW < 4 — du
автокорреляция отсутствует
4 — du < DW < 4 — dl
вывод о наличии автокорреляции
не определен
4 — dl < DW < 4
существует
автокорреляция
отрицательная
Или применяется грубое правило: «автокорреляция остатков
отсутствует, если 1,5 < DW < 2,5».
◊Статистика Дарбина используется для обнаружения автокорреляции
в авторегрессионных моделях вида y t = β 0 + β 1 x t1 + … + β m x tm + γ y t − 1 + ε t :
h = ρˆ
n
n
≈
(
1
−
,
5
DW
)
1 − nSy2t − 1
1 − nSy2t − 1
,
2
где ρˆ — оценка автокорреляции первого порядка, Syt − 1 — выборочная
дисперсия коэффициента при лаговой переменной yt-1 , n -число
наблюдений. При большом объеме выборки n и ρ=0 статистика h имеет
стандартизированное нормальное распределение (h~N(0,1)).
Ограничения использования статистики Дарбина: только одна лаговая
переменная, только автокорреляция первого порядка, невозможность
2
вычисления при nS yt − 1 = 1 .
10
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
Общая схема использования статистики Дарбина:
•
По
построенному
эмпирическому
уравнению
регрессии
y t = β 0 + β 1 x t1 + … + β m x tm + γ y t − 1 + ε t определяются значения для
расчета h-статистики.
•
Рассчитывается h-статистика:
h = (1 − 0,5DW )
•
n
1 − nSy2t − 1
По
таблицам
критических
точек
стандартизированного
нормального распределения (функции Лапласа) по заданному
уровню значимости α определяется критическая точка uα/2 из
условия Ф(uα/2) = (1-α)/2 и сравнивается h с uα/2: если h < uα/2, то
делается вывод об отсутствии автокорреляции, в противном
случае – гипотеза об отсутствии автокорреляции должна быть
отклонена.
Устранение автокорреляции:
•
При установлении автокорреляции необходимо в первую
очередь проанализировать правильность спецификации модели.
Если после ряда возможных усовершенствований регрессии
(уточнения состава объясняющих переменных либо изменения
формы зависимости) автокорреляция по-прежнему имеет место,
то, возможно, это связано с внутренними свойствами ряда
отклонений.
•
В случае, если наличие автокорреляции связано с внутренними
свойствами
ряда
отклонений,
возможны
определенные
преобразования, устраняющие автокорреляцию. Среди них
выделяется авторегрессионная схема первого порядка AR(1),
которая, в принципе, может быть обобщена в AR(p), p = 2, 3, …
•
Для
применения
указанных
схем
необходимо
оценить
коэффициент корреляции между отклонениями. Это может быть
сделано различными методами: на основе статистики ДарбинаУотсона, Кохрана-Оркатта, Хилдрета-Лу и др.
•
В случае наличия среди объясняющих переменных лаговой
зависимой переменной наличие автокорреляции устанавливается
с помощью h-статистики Дарбина. А для ее устранения в этом
случае предпочтителен метод Хилдрета-Лу.
11
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
Авторегрессионная схема первого порядка AR(1):
•
Оценивается регрессия Y = b0 + b1 X + e и находятся остатки et ,
тогда наблюдениям t и (t-1) соответствуют формулам:
y t = b0 + b1 x t + et , y t − 1 = b0 + b1 x t − 1 + et − 1 .
•
По остаткам, подверженным воздействию авторегрессии первого
порядка
εt=ρ εt-1+ ut,
находится
оценка
коэффициента
автокорреляции первого порядка: напр., на основе статистики
Дарбина-Уотсона ρˆ ≈ ret , et − 1 = 1 − 0,5DW .
•
Оценка автокорреляции используется для пересчета данных для
*
*
*
уравнения регрессии: y t = b0 + b1 x t + v t ,
y t* = y t − ρˆy t − 1 ,
x t* = x t − ρˆx t − 1 ,
b0* = b0 (1 − ρˆ) ,
где
v t = et − ρˆet − 1 ; причем для первого наблюдения выборки обычно
используется
y1* =
•
поправка
Прайса-Винстена:
x1* =
1 − ρˆ2 ⋅ x1 ,
1 − ρˆ2 ⋅ y1 .
Цикл повторяется (процесс останавливается, как только
обеспечивается
достаточная
сходимость,
т.е.
результаты
перестают существенно улучшаться).
4.4.Проблема гетероскедастичности остатков
в моделях регрессии
Гетероскедастичность остатков в моделях регрессии как нарушение
важной предпосылки построения качественной регрессионной модели по
МНК (одного из условий Гаусса-Маркова): «Дисперсия случайных
отклонений εi
постоянна для всех наблюдений: D(εi)=D(εj)=σ2».
Выполнимость данной предпосылки называется гомоскедастичностъю
(постоянством
дисперсии
отклонений).
Невыполнимость
данной
предпосылки
называется
гетероскедастичностъю
(непостоянством
дисперсий отклонений).
◊Гетероскедастичность остатков определяется как различные
вероятностные распределения случайных отклонений при различных
наблюдениях, что основывается на априорной причине, вызывающей
большую ошибку (отклонение) при одних наблюдениях и меньшую — при
других.
Проблема гетероскедастичности в большей степени характерна для
перекрестных данных и довольно редко встречается при рассмотрении
временных рядов.
12
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
Виды гетероскедастичности:
•
истинная (вызывается непостоянством дисперсии случайного
члена, ее зависимостью от различных факторов),
•
ложная (вызывается ошибочной спецификацией модели).
Последствия гетероскедастичности:
•
Истинная гетероскедастичность не приводит к смещению оценок
коэффициентов регрессии. Оценки коэффициентов по-прежнему
остаются несмещенными и линейными.
•
Оценки не будут эффективными (т.е. они не будут иметь наименьшую
дисперсию по сравнению с другими оценками данного параметра).
Они не будут даже асимптотически эффективными. Увеличение
дисперсии оценок снижает вероятность получения максимально
точных оценок.
•
Дисперсии
оценок
будут
рассчитываться
со
смещением.
Смещенность появляется вследствие того, что необъясненная
уравнением регрессии дисперсия, которая используется при
вычислении оценок дисперсий всех коэффициентов, не является
более несмещенной. Как правило, гетероскедастичность увеличивает
дисперсию распределения оценок коэффициентов.
•
Гетероскедастичность
вызывает
тенденцию
к
недооценке
стандартных ошибок коэффициентов. Вполне вероятно, что
стандартные
ошибки
коэффициентов
будут
занижены,
а
следовательно, t-статистики будут завышены. Это может привести к
признанию статистически значимыми коэффициентов, таковыми на
самом деле не являющимися.
•
Вследствие вышесказанного все выводы, получаемые на основе
соответствующих t- и F-статистик, а также интервальные оценки
будут ненадежными. Следовательно, статистические выводы,
получаемые при стандартных проверках качества оценок, могут
быть ошибочными и приводить к неверным заключениям по
построенной модели.
Обнаружение гетероскедастичности. В ряде случаев на базе знаний
характера данных появление проблемы гетероскедастичности можно
предвидеть и попытаться устранить этот недостаток еще на этапе
спецификации. Однако значительно чаще эту проблему приходится решать
после построения уравнения регрессии. В последнем случае наиболее
популярные и наглядные методы: графический анализ отклонений, тест
ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест
Голдфелда-Квандта.
Графический анализ остатков: в этом случае по оси абсцисс
откладывается объясняющая переменная X (либо линейная комбинация
13
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
объясняющих переменных Ŷ, в случае множественной регрессии), а по оси
ординат либо отклонения (остатки) et, либо их квадраты e2t; на основе
визуального анализа формируются суждения: напр., если наблюдаются
некоторые систематические изменения в соотношениях между значениями
переменной и квадратами отклонений, то можно с большой вероятностью
предполагать наличие гетероскедастичности остатков.
Тест ранговой корреляции Спирмена: при использовании данного
теста
предполагается,
что
дисперсия
отклонения
будет
либо
увеличиваться, либо уменьшаться с увеличением значения X; поэтому для
регрессии, построенной по МНК, абсолютные величины отклонений
(остатков) и значения переменной X будут коррелированны.
Схема теста ранговой корреляции Спирмена (проверка осуществляется
по каждой объясняющей переменной отдельно):
•
Выборка упорядочивается по фактору X, при этом определяются
ранги (порядковый номер) pXi, i=1,…,n.
•
Оценивается уравнение регрессии и вычисляются остатки ei, i=1,
…,n.
•
Выборка упорядочивается по величине остатков ei, при этом
определяются ранги (порядковый номер) pei, i=1,…,n.
•
Рассчитывается коэффициент ранговой корреляции Спирмена
между рангами фактора и остатков:
n
rx , e = 1 − 6
•
∑
d
i=1
2
n(n − 1)
= 1− 6
∑
i=1
( p Xi − pei )2
rx , e n − 2
1 − rx2, e
.
2
n(n − 1)
Рассчитывается
t-статистика,
имеющая
Стьюдента с числом степеней свободы (n-2):
t =
•
n
2
i
распределение
.
Формируется суждение по правилу: если наблюдаемое значение
t α / 2, n − 2
t-статистики
превышает
критическое
значение
(определяемое по таблице критических точек распределения
Стьюдента), то необходимо отклонить гипотезу о равенстве нулю
коэффициента корреляции, а следовательно, и об отсутствии
гетероскедастичности. В противном случае гипотеза об
отсутствии гетероскедастичности принимается.
Тест
Парка:
дополняет
графический
метод
некоторыми
формальными зависимостями; может приводить к необоснованным
14
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
выводам, поэтому дополняется другими тестами; включает следующие
этапы:
•
Строится уравнение регрессии y i = b0 + b1 x i + ei .
•
ˆi )2 .
Для каждого наблюдения определяются ln ei2 = ln(y i − y
•
ln ei2 = α + β ln x i + υ i ;
Строится
регрессия:
в
случае
множественной регрессии зависимость строится для каждой
объясняющей переменной.
•
Проверяется
статистическая
значимость коэффициента
β
β
уравнения на основе t-статистики t =
. Если коэффициент
Sβ
статистически
значим,
то
это
означает
гетероскедастичности в статистических данных.
наличие
Тест Глейзера: по своей сути аналогичен тесту Парка и дополняет
его анализом других (возможно, более подходящих) зависимостей между
k
дисперсиями отклонений И значениями переменной: ei = α + β x i + υ i , где
k=…,-1,-0.5,0.5,1,… Так же, как и в тесте Парка, в тесте Глейзера для
отклонений υ i может нарушаться условие гомоскедастичности. Однако во
многих случаях предложенные модели являются достаточно хорошими для
определения гетероскедастичности.
Тест Голдфелда-Квандта: предполагается, что СКО отклонения
пропорционально значению переменной X в i-наблюдении, отклонение
имеют нормальное распределение и отсутствует автокорреляция остатков в
i-наблюдении; состоит в следующем:
•
Все n наблюдений упорядочиваются по величине X.
•
Вся упорядоченная выборка после этого разбивается на три
подвыборки размерностей k, (n – 2k), k соответственно. Для
парной регрессии предлагаются следующие пропорции: n=30 и
k=11, n=60 и k=22; для множественной регрессии k>(m+1).
•
Оцениваются отдельные регрессии для первой подвыборки (k
первых наблюдений) и для третьей подвыборки (k последних
наблюдений). Если предположение о пропорциональности
дисперсий отклонений значениям X верно, то дисперсия
регрессии по первой подвыборке S1 =
k
∑
ei2 будет существенно
i=1
меньше
S3 =
•
дисперсии
n
∑
регрессии
по
третьей
подвыборке
ei2 .
i = n− k + 1
Для сравнения соответствующих дисперсий строится следующая
F-статистика:
15
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
S3
S
(k − m − 1)
F =
= 3,
S1
S1
(k − m − 1)
где (k-m-1) — число степеней свободы соответствующих выборочных дисперсий (m- количество объясняющих переменных в
уравнении
регрессии).
При
сделанных
предположениях
относительно случайных отклонений построенная F-статистика
имеет распределение Фишера с числами степеней свободы v1=
v2 = k-m-1.
•
S3
> Fα , k − m − 1, k − m − 1 , то
S1
гетероскедастичности отклоняется
значимости α.
Если
F =
гипотеза
при
об
отсутствии
выбранном
уровне
Для множественной регрессии данный тест обычно проводится для той
объясняющей переменной, которая в наибольшей степени связана с СКО
отклонения. Если нет уверенности относительно выбора переменной, то
данный тест может осуществляться для каждой из объясняющих
переменных. Этот же тест может быть использован при предположении об
обратной пропорциональности между СКО отклонения и значениями
объясняющей переменной; при этом статистика Фишера примет вид: F =
S1/S3.
Устранение проблемы гетероскедастичности. В случае установления
наличия гетероскедастичности ее корректировка представляет довольно
серьезную проблему. Одним из возможных решений является метод
взвешенных наименьших квадратов (при этом необходима определенная
информация либо обоснованные предположения о величинах дисперсий
отклонений). На практике имеет смысл попробовать несколько методов
определения
гетероскедастичности и способов ее корректировки
(преобразований, стабилизирующих дисперсию). Во многих случаях
дисперсии отклонений зависят не от включенных в уравнение регрессии
объясняющих переменных, а от тех, которые не включены в модель, но
играют существенную роль в исследуемой зависимости, в этом случае они
должны быть включены в модель. В ряде случаев для устранения
гетероскедастичности необходимо изменить
спецификацию
модели
(например,
линейную
на
лог-линейную,
мультипликативную
на
аддитивную и т. п.).
Метод взвешенных наименьших квадратов (ВНК): применяется при
2
известных для каждого наблюдения значениях дисперсии отклонения σ i ;
в этом случае можно устранить гетероскедастичность, разделив каждое
наблюдаемое значение на соответствующее ему значение дисперсии.
16
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
Схема метода взвешенных наименьших квадратов:
•
•
•
Каждую из пар наблюдений (хi, yi) делят на известную величину
СКО отклонения σ i в i-наблюдении. Тем самым наблюдениям с
наименьшими дисперсиями придаются наибольшие «веса», а с
максимальными
дисперсиями –
наименьшие
«веса»;
так,
наблюдения с меньшими дисперсиями отклонений будут более
значимыми
при
оценке
коэффициентов
регрессии,
чем
наблюдения с большими дисперсиями, что увеличивает
вероятность получения более точных оценок.
1 xi yi
строится
,
,
По МНК для преобразованных значений
σ
σ
σ
i
i
i
уравнение регрессии без свободного члена с гарантированными
y i* = y i
y i* = β 0 z i + β 1 x i* + υ i , где
качествами оценок:
σi,
z = 1 , υi = εi
x i* = x i
σi
σi , i
σi.
После определения по МНК оценок коэффициентов β0 и β1 для
преобразованного
уравнения
возвращаются
к
исходному
уравнению регрессии y i = β 0 + β 1 x i + ε i .
Для применения ВНК необходимо знать фактические значения дисперсий
отклонений. На практике такие значения известны крайне редко.
Следовательно, чтобы применить ВНК, необходимо сделать реалистические
2
предположения о значениях σ i :
•
дисперсии
отклонений
пропорциональны
значениям
2
2
2
объясняющей переменной: σ i = σ x i , где σ — коэффициент
пропорциональности, тогда уравнение преобразуется по схеме
1
x
y
, i , i . Если в уравнении регрессии присутствует
x
xi
x i
i
несколько
объясняющих
переменных,
можно
поступить
1
x
y
, i , i , где ŷ — исходное
следующим образом:
y
ˆi
ˆi
y
y
ˆi
уравнение
множественной
регрессии
как
комбинация
объясняющих переменных.
•
дисперсии отклонений пропорциональны квадрату значений
σ i2 = σ 2 x i2 ,
объясняющей
переменной:
тогда
уравнение
1 xi y i
,
,
преобразуется по схеме
xi xi xi
17
.
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
4.5.Обобщенный метод наименьших квадратов
Невозможность или нецелесообразность использования традиционного
МНК по причине проявляющихся в той или иной степени проблем
автокорреляции или гетероскедастичности обуславливает использование
обобщенного метода наименьших квадратов (ОМНК), при котором
корректируется модель, изменяются ее спецификации, преобразуются
исходные данные для обеспечения несмещенности, эффективности и
состоятельности оценок коэффициентов регрессии.
Обобщенный МНК в чистом виде практически не применяется:
•
Подход к реализации ОМНК в виде авторегрессионных
преобразований является целесообразным при наличии проблем
автокорреляции остатков.
•
Подход к реализации ОМНК в виде взвешенного МНК является
достаточно
практичным
при
наличии
проблем
гетероскедастичности;
иногда
его
называют
доступный
обобщенный МНК.
Суть обобщенного МНК: Пусть ковариационная матрица ошибок имеет
T
следующий вид: E (ε ε ) = λ W , где W-известная матрица (симметричная и
положительно определенная), представленная в виде W = АT А , матрица А
– квадратная невырожденная матрица (напр., разложение Холецкого).
Коэффициенты β в этом случае можно оценить по формуле:
βˆ = ( X T W − 1 X )− 1 X TW − 1Y . Обобщенный МНК эквивалентен следующей
~
~
~
~
вспомогательной регрессии: Y = Xβ + ~
ε , где Y = ( A − 1 )T Y , X = ( A − 1 )T X ,
~
ε = ( A − 1 )T ε . Геометрически задача состоит в том, чтобы найти такой
~
~ , чтобы расстояние было минимальным: Y − Y
→ min .
вектор Y
При этом следует учитывать, что коэффициент детерминации не может
служить удовлетворительной мерой качества подгонки при использовании
ОМНК. На практике достаточную общность имеет критерий стандартных
отклонений (стандартных ошибок) регрессии.
4.6.Фиктивные переменные в регрессионных моделях
◊Фиктивная переменная формализует в регрессионных моделях
влияние качественного фактора, отражая два противоположных состояния
фактора: «фактор действует» — «фактор не действует». Как правило,
фиктивная переменная выражается в двоичной форме:
0, фактор не действует
D =
.
1, фактор действует
Регрессионные модели, содержащие лишь качественные объясняющие
переменные, называются ANOVA-моделями (моделями дисперсионного
18
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
анализа): Y = β 0 + γ D + ε , где γ
указывает величину, на которую
отличаются средние значения зависимой переменной Y при отсутствии или
наличии
фактора,
выраженного
переменной
D:
M(Y | D = 0) = β 0 , M(Y | D = 1) = β 0 + γ .
Модели, в которых объясняющие переменные носят как количественный,
так и качественный характер, называются ANCOVA-моделями (моделями
ковариационного анализа):
•
Правило
формализации
качественного
фактора:
«Если
качественная переменная имеет k альтернативных значений, то
при моделировании используются только (k-1) фиктивных
переменных»; если не следовать данному правилу, то при
моделировании исследователь попадает в ситуацию совершенной
мультиколлинеарности или так называемую ловушку фиктивной
переменной.
•
Значение фиктивной переменной, для которого принимается D=0,
называется базовым или сравнительным. Выбор базового значения
обычно диктуется целями исследования, но может быть и произвольным.
•
При наличии у фиктивной переменной двух альтернатив:
Y = β 0 + β 1X + γ D + ε ,
M(Y | x , D = 0) = β 0 + β 1 x ,
M(Y | x, D = 1) = (β 0 + γ ) + β 1 x ; где коэффициент γ называется
дифференциальным коэффициентом свободного члена, т. к. он
показывает, на какую величину отличается свободный член модели
при значении фиктивной переменной, равном единице, от
свободного члена модели при базовом значении фиктивной
переменной.
•
При наличии у фиктивной переменной более двух альтернатив:
Y = β 0 + β 1 X + γ 1D1 + γ 2 D2 + ε , M(Y | x, D1 = 0, D2 = 0) = β 0 + β 1 x ,
M(Y | x , D1 = 1, D2 = 0) = (β 0 + γ 1 ) + β 1 x ,
M(Y | x , D1 = 1, D2 = 1) = (β 0 + γ 1 + γ 2 ) + β 1 x ,
где
коэффициент
γ 1 , γ 2 — дифференциальные коэффициенты свободного члена.
•
Модель регрессии с одной количественной и двумя качественными
Y = β 0 + β 1 X + γ 1D1 + γ 2 D2 + ε ,
переменными:
M(Y | x, D1 = 0, D2 = 0) = β 0 + β 1 x ,
M(Y | x, D1 = 0, D2 = 1) = (β 0 + γ 2 ) + β 1 x ,
M(Y | x , D1 = 1, D2 = 0) = (β 0 + γ 1 ) + β 1 x ,
M(Y | x , D1 = 1, D2 = 1) = (β 0 + γ 1 + γ 2 ) + β 1 x ,
где
коэффициент
γ 1 , γ 2 — дифференциальные коэффициенты свободного члена.
19
Конспект лекций по дисциплине «Эконометрика» для студентов специальности
«Бухгалтерский учет, анализ и аудит»
Составитель: Коновалова А.С.
Раздел 4. Спецификация переменных в уравнениях регрессии
________________________________________________________________________________
• Модель регрессии, где изменение качественного фактора может
привести как к изменению свободного члена уравнения, так и
Y = β 0 + β 1 X + γ 1D1 + γ 2 D1 X + ε ,
наклона
прямой
регрессии:
M(Y | x, D1 = 0) = β 0 + β 1 x , M(Y | x, D1 = 1) = (β 0 + γ 1 ) + (β 1 + γ 2 )x
, где γ 1 — дифференциальный коэффициент свободного члена, γ 2 дифференциальный угловой коэффициентом соответственно.
Представленные выше схемы могут быть распространены на ситуации с
произвольным числом количественных и качественных факторов.
Модели, в которых фиктивная зависимая переменная:
•
Y = β 0 + β 1X + ε ,
Линейные
вероятностные
модели
(LPM):
M(Y | x ) = P (Y = 1 | x ) = β 0 + β 1 x , применимость МНК к которым
имеет определенные ограничения: случайные отклонения в данных
моделях не являются нормальными случайными величинами, а
скорее всего, имеют биноминальное распределение; случайные
отклонения не обладают свойством постоянства дисперсии
(гомоскедастичности); нарушается неравенство 0 ≤ P(Y =1| х) ≤ 1;
применение модели проблематично с содержательной точки зрения;
так непосредственное использование МНК в модели LPM приводит к
серьезным
погрешностям
и
необоснованным
выводам.
Использование
обыкновенного
МНК
в
данном
случае
нецелесообразно.
•
Logit модель для преодоления недостатков модели LPM: такие
модели, в которых не нарушается неравенство 0 ≤ P(Y=1|х) ≤ 1, и
зависимость между P(Y=1|х) и х не имеет линейный характер
pi
= z i = β 0 + β 1 x i , где
(закон убывающей эффективности): ln
1 − pi
условная
pi = M(Y = 1 | x i ) =
вероятность
1
.
1+ e
Использование
обыкновенного
МНК
в
данном
случае
нецелесообразно в силу проблемы гетероскедастичности. Поэтому
при расчетах коэффициентов обычно используется взвешенный
МНК, устраняющий указанный недостаток.
20
− ( β 0 + β 1xi )