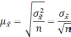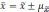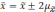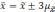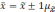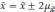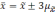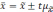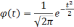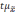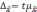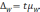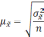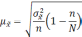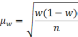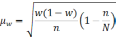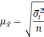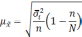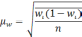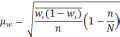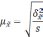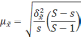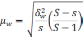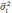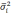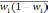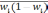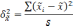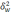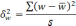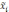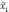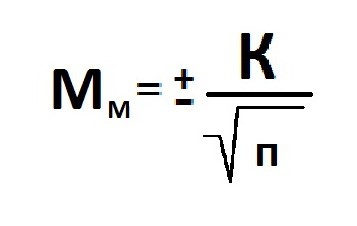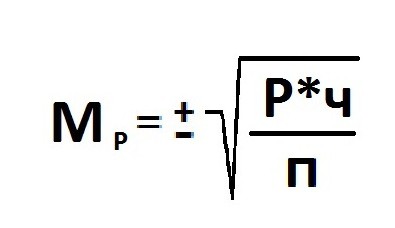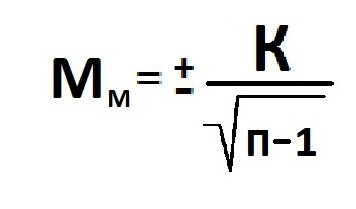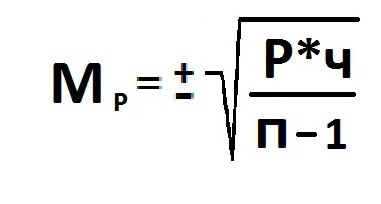Репрезентативные ошибки это

Ошибка
репрезентативности
— расхождение между выборочной
характе­ристикой и характеристикой
генеральной совокупности.

Ошибки
репрезентативности

1. Систематические
   — возникают в результате нарушения
   научных принципов отбора единиц
   совокупности (преднамеренные и
   непреднамеренные).

2. Случайные
   возникают в результате несплошного
   характера наблюде­ния (средняя и
   предельная ошибки выбора).

Случайные
ошибки могут быть доведены до незначительных
размеров, а главное, их размеры и пределы
можно определить с достаточной точностью
на основании закона больших чисел.

Средняя
ошибка выборки
— такое расхождение между средними
вы­борочной и генеральной совокупностями,
которое не превышает ±.

В
математической статистике доказывается,
что значения средней ошибки выборки
определяются по формулам:

Формула
для определения величины средней ошибки
выборки для количественного признака:

Формула
для определения величины средней ошибки
выборки для альтернативного признака:

Полученное
значение средней ошибки необходимо для
установления возможного значения .
Которое определяется по формуле:

Но
такое суждение можно гарантировать не
с абсолютной
достоверностью, а лишь с определенной
степенью
вероятности.

В
математической статистике доказывается,
что пределы значений характеристик
генеральной совокупности отличаются
от характеристик выборочной совокупности
лишь с вероятностью, которая определена
числом 0,683.

Это
означает, что в 683 случаях из 1000 генеральная
средняя будет находиться в установленных
пределах, т.е. отклонение ГС от ВС не
превысит однократной средней ошибки
выборки. В остальных 317 случаях они могут
выйти за эти пределы. Вероятность можно
повысить, если расширить пределы
отклонений. Так, при удвоенном значении
,
вероятность достигает 0,954 ().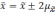
Если утроить значение то вероятность
увеличится до 0,997 ().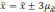

Возможное значение генеральной средней	Вероятность
	0,683
	0,954
	0,997

Если
обозначить значение увеличения
за
t,
то можно записать в общем виде:

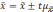
Множитель
t
называется коэффициентом
доверия.
Известный русский математик А.М.Ляпунов
дал выражение конкретных значений
множителя t
для различных степеней вероятности в
виде функции:

На
практике пользуются готовыми таблицами
этой функции.

t	0	0,1	0,5	1	1,5	2	2,5	2,6	3	4
(t)	0,1	0,0797	0,3829	0,6827	0,8664	0,9545	0,9876	0,9907	0,9973	0,99994

Из
вышесказанного следует, что лишь с
определенной степенью вероятности
можно утверждать, что показатели
генеральной совокупности и их отклонения
не превысят величину .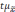
Полученную величину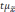называетсяпредельной
ошибкой выборки.

Предельная
ошибка выборки
—
максимально
возможное расхождение вы­борочной и
генеральной средних,
т.е.
максимум ошибки при заданной ве­роятности
ее появления.

Предельная
ошибка выборки для количественного
признака:

Предельная
ошибка выборки для альтернативного
признака:

В
связи с тем, что существуют различные
методы, виды и способы отбора единиц из
генеральной совокупности формулы для
расчета средней ошибки выборки также
будут различаться:

Способ отбора	Оцениваемый параметр	Повторный отбор	Бесповторный отбор
Собственно случайный и механи­ческий	Средняя
Доля
Типический	Средняя
Доля
Серийный	Средняя
Доля

— средняя из групповых дисперсий;

w_i

— доля
единиц совокупности, обладающих изучаемым
признаком в i-й
типической
группе;

— средняя из групповых дисперсий для
доли. В табл. 6.6 представлены формулы
для исчисления средней ошибки выборки
при типическом отборе;

S
– общее число серий;

s
– число отобранных серий;

—
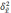
межгрупповая дисперсия средних,
определяемая по формуле:

—
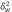
межгрупповая дисперсия доли, определяемая
по формуле:

— средняя
i-й
серии;

—
средняя по всей выборочной совокупности;

w
— доля признака i-й
серии;

— общая доля признака во всей выборочной
совокупности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Лекция 2. Ошибка репрезентативности и доверительный интервал для
генерального параметра
Выборочные характеристики, представляющие собой числа (точки на
шкале) называют точечными оценками (существуют также и интервальные
оценки). Оценки должны удовлетворять следующим требованиям: быть
состоятельными, эффективными, несмещенными. Только при удовлетворении
этих требований оценки хорошо представляют соответствующие параметры.
В математической статистике введено понятие статистической ошибки
или ошибки репрезентативности; она связана с точностью, с которой
выборочная оценка представляет, репрезентирует свой параметр.
Когда ошибка оценивания генерального параметра стремится к нулю при
возрастании объема выборки, т.е. значение оценки стремится к значению
параметра, то такая оценка называется состоятельной. Оценка называется
эффективной,
если
она
имеет
наименьшую
дисперсию
выборочного
распределения по сравнению с другими аналогичными оценками.
К примеру,
из трех показателей, описывающих положение центра
нормального распределения (средняя, медиана, мода), наиболее эффективной
является средняя арифметическая, наименее эффективной — мода.
Оценка
ожидание)
называется
ее
несмещенной,
выборочного
если
распределения
среднее
совпадает
(математическое
со
значением
генерального параметра. Выборочная средняя является несмещенной оценкой
генеральной средней, а тогда как выборочная дисперсия представляет собой
смещенную оценку.
Например, чтобы получить несмещенную оценку, надо при вычислении
выборочной дисперсии использовать формулу, где в знаменателе (N — 1):
D=S2=
1
2
( Xi  X )

N 1
Для понимания смысла этих требований нужно рассмотреть понятие
выборочного распределения оценок какого-либо параметра.
Рассмотрим
условный
пример
для
такого
понятия,
как
арифметическое среднее: пусть ГС представляет собой 5 результатов
выполнения некоторого психологического теста: 8 16 20 24 32:
=
8  16  20  24  32
= 20
5
Таким образом, 20 — это значение генерального параметра.
Заменим изучение генеральной совокупности изучением выборок объемом
n = 4. Рассмотрим все возможные варианты таких выборок:
1) 8
16 20 24
 = 17
2) 16 20 24 32
 = 23
3) 8
16 24 32
 = 20
4) 8
16 20 32
 = 19
Из нашего примера видно, что из 5 оценок средних лишь одна совпала
с параметром. Заранее мы не можем знать, как составить (отобрать) выборку,
чтобы оценка параметра по ней была близка к параметру.
Однако очевидно, что чем больше объем выборки, тем меньше вероятность
того, что  , определяемое по выборке, будет значительно отличаться от
генерального среднего (крайние случаи n=N-1 и n=2 ,т.е. N>>n) .
Когда
генеральная совокупность велика и, соответственно, число
возможных выборок велико, то совокупность выборочных оценок средних для
каждой
из
этих
концентрирующееся
выборок
вокруг
«концентрация» (дисперсия)
Дисперсия
образует
генерального
тем
выше,
нормальное
среднего,
чем
больше
распределение,
причем
эта
объемы выборок.
распределения средних имеет особое название, она именуется
ошибкой репрезентативности.
Выше речь шла о распределении выборочных средних.
Это же
рассуждение можно повторить для оценок дисперсии, моды, коэффициентов
корреляции и т.д.
В теории математической статистики доказано, что нормального
распределения при достаточном объеме выборки (на практике n  30),
стандартное отклонение среднего арифметического равно:
Sx =
S
N
; где
S — стандартное отклонение
N — объем выборки.
Эту величину называют также статистической ошибкой или ошибкой
репрезентативности, т.е. это средняя ошибка, которая допускается, когда 
рассматривается как генеральный параметр.
Для других параметров ошиб ки репрезентативности таковы:
Ошибка репрезентативности дисперсии:
Ss2=S2/ 2N
Ошибка репрезентативности стандартного отклонения
Ss=S/ 2N
Ошибка репрезентативности показателя асимметрии:
Sa= 6 / N
Ошибка репрезентативности показателя эксцесса:
Se= 24 / N
Теперь перейдем к понятию доверительного интервала, которое применяется
для любого параметра. Мы рассмотрим его для генеральной средней. По
известным выборочным характеристикам можно построить интервал, в котором
с той или иной степенью вероятности находится генеральное среднее. Понятие
доверительного интервала связано с понятием доверительной вероятности.
Согласно этому принципу, маловероятные события считаются практически
невозможными,
а
события,
вероятность
которых
близка
к
единице,
принимаются за почти достоверные. Обычно в психологии в качестве
доверительных используют вероятности р = 0,95 и р = 0,99. Это означает, что
при оценивании генерального параметра по известной выборочной оценке риск
ошибиться в первом случае — один раз на 20 испытаний, во втором случае 1 раз
на 100 испытаний.
С доверительной вероятностью связано понятие уровня значимости
 = 1- р
Геометрически — это площадь под нормальной кривой выборочного
распределения, выходящая за пределы той его части, которая соответствует
Р%, поскольку в сумме они соответствуют всей площади под кривой. Иначе
говоря,

означает площадь двух хвостов под кривой нормального
распределения. При при р = 0,95 и  = 0, 05 на каждый «хвост» приходится
по 2,5 % площади.
Вероятность того, что  будет находиться в пределах
доверительного интервала x — t SX     + t SX,
описывается
особой функцией, которая сведена в таблице (обычно это таблица 1 в
приложении учебников по математической статистике)
для р= 0,95
t=1,96
для р=0,99
t = 2,58
для p=0, 999 t =3,29
График нормальной кривой
Выбор того или иного уровня доверительной вероятности зависит от
исследователя, от его оценки ответственности за ошибочность выводов
относительно генерального параметра .
Пример: При измерении объема памяти у 100 испытуемых
получено среднее значение числа запоминаемых сигналов
было
= 9 и
стандартное отклонение S = 3. 27. Построить доверительный
интервал для генеральной средней .
Вычисления проводятся по формуле:
x — t SX     + t SX
9 — 1,96
3271
.
327
.
   92+1,96
100
100
или 9+ 0.196  3,27    9 + 1..96  3,27 или 8. 36    9.64.
Таким образом, с вероятностью р = 0.95 генеральный параметр 
находится в интервале 8.36 — 9.64.
95%

Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.

Репрезентативность — что это?

Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.

Другие определения

Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.

Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.

Репрезентативная выборка

Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.

Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.

Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.

Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.

Вероятностная выборка

Вероятностные выборки также могут подразделяться на несколько видов:

• Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
• Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
• Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.

Вероятностные выборки

Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:

• Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.

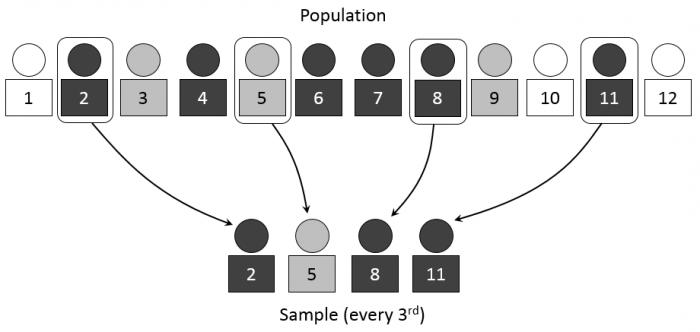
• Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.

Выборка потребителей

Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.

Размер выборки

Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.

Понятие ошибки репрезентативности

Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.

Виды ошибок

Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:

• Систематические.
• Случайные.
• Преднамеренные.
• Непреднамеренные.
• Стандартные.
• Предельные.

Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.

Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.

Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.

Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.

Преднамеренные и непреднамеренные ошибки репрезентативности

Ошибки смещения данных бывают преднамеренными и непреднамеренными.

Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.

Валидность, надежность, репрезентативность. Расчет ошибок

Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).

Среднее квадратическое отклонение: численность выборки (>30).

Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).

В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.

Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.

Репрезентативные системы

Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:

• Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
• Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
• Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.

• Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.

Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.

Ошибки репрезентативности

Полезное