В
реальных опытах присутствуют как
систематические, так и случайные ошибки.
Пусть они характеризуются стандартными
погрешностями сист
и случ
. Суммарная погрешность находится по
формуле
(30)
Поясним
эту формулу. Систематическая и случайная
ошибки могут, в зависимости от случая,
складываться или вычитаться друг из
друга. Как уже говорилось, точность
опытов принято характеризовать не
максимальной (и не минимальной), а
среднеквадратичной погрешностью.
Поэтому правильно рассчитанная
погрешность должна быть меньше суммы
случ
+ сист
и больше их разности случ
— сист
. Легко видеть, что полн
, определенная формулой (30), удовлетворяет
этому условию. В самом деле, все величины
положительные. Поэтому
Знак равенства
возникает только в том случае, когда
одна из погрешностей равна нулю.
Аналогично имеем
Формула (30)
показывает, что при наличии как случайной,
так и систематической погрешности
полная ошибка опыта больше, чем каждая
из них в отдельности, что также является
вполне естественным.
Обратим
внимание на ещё одну важную особенность
формулы (30). Пусть одна из ошибок, например
случ
, в 2 раза меньше другой. Тогда
Как
мы уже говорили, погрешности редко
удается оценить с точностью лучше
20%.
Но в нашем примере с точностью 20% полн
= сист
. Таким образом, меньшая погрешность
почти ничего не добавляет к большей,
даже если она составляет половину от
нее.
Этот
вывод очень важен. В том случае, если
случайная ошибка опытов вдвое меньше
систематической, нет смысла производить
многократные измерения, так как полная
погрешность опыта при этом практически
не уменьшается. Измерения достаточно
произвести 2
3 раза, чтобы убедиться, что случайная
ошибка действительно мала.
1.3.2. Обработка результатов при косвенных измерениях
Если
исследуемая величина равна сумме или
разности двух измеренных величин,
А
=В
С, (31)
то
наилучшее значение величины А равно
сумме (или разности) наилучших значений
слагаемых: Анаил
= Внаил
+ Снаил
, или, как рекомендовано выше,
(32)
Здесь
и в дальнейшем угловые скобки (или черта
сверху) означают усреднение: вместо
того, чтобы писать Аср,
будем пользоваться обозначением А
(или
),
и т. д.
Среднеквадратичная
погрешность А,
если величины В и С независимы, находится
по формуле
(33)
т. е. погрешности, как
всегда, складываются квадратично. (Иначе
говоря, складываются не погрешности, а
дисперсии результатов измерений.) При
обсуждении формулы (33) следует использовать
те же аргументы, которые были приведены
в связи с формулой (30).
В
том случае, если искомая величина равна
произведению или частному двух других,
А
= ВС
или А = В/С, (34)
то
(35)
Относительная
среднеквадратичная погрешность
произведения и частного
независимых величин находится по формуле
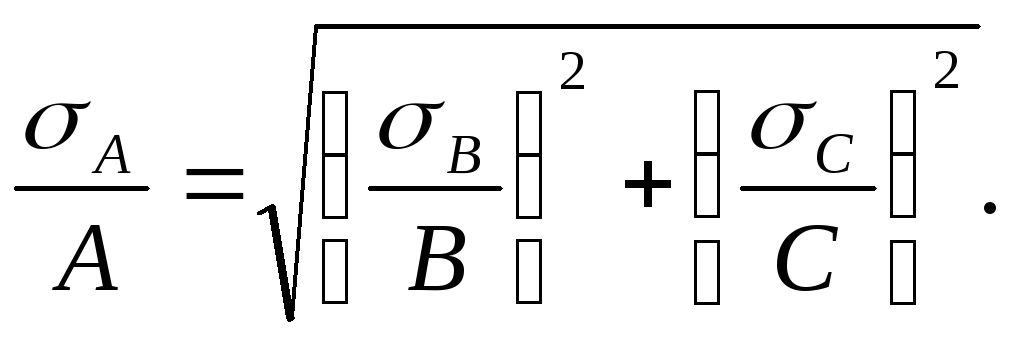
Приведем расчетные
формулы для случая, когда
А
= ВCE……
(37)
Наилучшее
значение А связано с наилучшими значениями
В, С, Е и т. д. той же формулой (24), что и
каждое конкретное значение. Относительная
среднеквадратичная погрешность величины
А при
независимых В, С, Е… находится по формуле
(38)
Наконец, приведем
для справок общую расчетную формулу.
Пусть
А
= f
(В, С, Е, …),
(39)
где
f
— произвольная функция величин В, С, Е и
т. д. Тогда
Анаил=
f
(Внаил ,
Снаил ,
Енаил ,
…) (40)
Формула
(40) справедлива как в том случае, когда
Внаил ,
Снаил ,
и т.д. непосредственно измерены, так и
в том случае, если они найдены по
измеренным значениям других величин.
В первом случае значения Внаил
, Снаил
, и т.д., как
уже указывалось, равны В,
С
и т. д. Погрешность А находится по формуле
(41)
Частные
производные следует вычислять при
наилучших значениях аргументов. Все
приведенные в этом параграфе формулы
являются частными случаями (40) и (41).
Рассмотрим
некоторые следствия, которые могут быть
получены из анализа формул, приведенных
в этом разделе. Прежде всего, заметим,
что следует
избегать измерений, при которых искомая
величина находится как разность двух
больших чисел.
Так, толщину стенки трубы не следует
определять, вычитая ее внутренний
диаметр из внешнего диаметра и конечно
деля результат пополам. Относительная
погрешность измерения, которая обычно
представляет главный интерес, при этом
сильно увеличивается, так как измеряемая
величина
в нашем случае толщина стенки
мала, а ошибка в ее определении находится
путем сложения погрешностей измерения
обоих диаметров и поэтому возрастает.
Следует
также помнить, что погрешность измерения,
которая составляет, например, 0.5% от
величины внешнего диаметра, может
составить 5% и более от толщины стенки.
При
измерениях, которые затем обрабатываются
по формуле
(34) (например, при определении плотности
тела по его массе и объему), следует
определять все измеряемые величины с
приблизительно одинаковой относительной
точностью.
Так, если объем тела измерен с погрешностью
1%, то при взвешивании с погрешностью
0.5% его плотность определяется с точностью
1.1%, а при взвешивании с погрешностью
0.01% — с точностью 1%, т. е. с той же,
практически, точностью. Тратить силы и
время на измерение массы тела с точностью
0.01% в этом случае, очевидно, не имеет
смысла.
При
измерениях, которые обрабатываются по
формуле (41),
следует
обращать главное внимание на точность
измерения величины, входящей в расчетную
формулу с наибольшим показателем
степени.
Прежде
чем приступать к измерениям, всегда
нужно подумать о последующих расчетах
и выписать формулы, по которым будут
рассчитываться погрешности. Эти формулы
позволят понять, какие измерения следует
производить особенно тщательно, а на
какие не нужно тратить больших усилий.
Соседние файлы в папке AttaМетрология
- #
13.05.201546.08 Кб241.doc
- #
13.05.201517.83 Mб1393.doc
- #
- #
- #
- #
Виды лексических ошибок
1. Смешение слов,
близких по значению: крайний
и последний,
любить
и уважать,
спать
и отдыхать,
профессия и
специальность,
новорождённый
и именинник,
учитель
и преподаватель,
годовщина
и юбилей.
2. Смешение слов,
близких по звучанию:
индейка – индианка, одинарный –
ординарный, экскаватор – эскалатор,
декрет – кредит, фауна – флора, Австрия
– Австралия,
Швеция – Швейцария, нотариальная
(контора) – натуральная и
т.д.
3. Смешение слов,
близких по значению и по звучанию
(паронимов):
командировочный – командированный,
дипломат – дипломант, одеть – надеть,
представить – предоставить, главный –
заглавный, сытый – сытный, невежа –
невежда, туристский – туристический и
т.д.
4. Словосочинительство
(словотворчество) – замена «законной»
морфемы синонимичной «незаконной»:
грузинец
(грузин),
благородность
(благородство), волнительный
(волнующий), плагиаторство
(плагиат), нервенный
(нервный) и
т.д.
5. Нарушение правил
семантического (смыслового) согласования
слов: Я поднимаю
тост (поднимать
– «перемещать куда-либо наверх», тост
– «застольное пожелание чего-либо,
здравица»); Живописца поразила поза
её лица;
Базаров отрастил
длинные волосы и красные обветренные
руки;
большая
половина и
т.д.
6. Плеоназмы (от
греческого pleonasmos
– переизбыток)
– словосочетания, в которых значение
одного компонента (слова) полностью
входит в значение другого (смысловое
дублирование): март
месяц, лично я (ты, он), период времени,
прейскурант цен, адрес местожительства,
основной костяк, памятные сувениры,
мемориальный памятник, народный фольклор,
свободная вакансия, внутренний интерьер,
продолжай дальше, вдруг неожиданно,
очень сильно
и т.п.
7. Тавтология (от
греческих tauto
– то же самое и logos
– слово) – крайняя форма, разновидность
плеоназма – непреднамеренное употребление
в пределах фразы однокоренных слов;
более грубая ошибка, так как происходит
дублирование и на уровне содержания, и
на уровне формы: проливной
ливень, гостеприимно приняли, соединить
воедино, вновь возобновить, бездонная
бездна, заданное задание
и т.п. Тавтологию не следует смешивать
с повторами. Тавтология
– это
словосочетание, состоящее из двух
однокоренных слов (заданное
задание), а
повторы –
это многократное использование на
небольшом отрезке речи одного и того
же слова, словоформы, фразеологизма: Я
записал задание.
Придя домой, я
стал выполнять
задание. Я
легко справился с этим заданием.
Повторы создают однообразие речи, т.е.
делают ее бедной, следовательно, это не
лексическая, а стилистическая ошибка
– нарушение принципа богатства речи.
Далеко не все плеоназмы и тавтологии
являются нарушением нормы (см.: Аникин,
А.И. Употребление
однокоренных слов в предложении. – М.,
1965).
8. Неустраненная
(неснятая) многозначность, порождающая
двоякое осмысление высказывания: Это
предложение следует оставить
(сохранить или отбросить?); Ты уже
отходишь?
(выздоравливаешь или умираешь?); Студенты
разбирают книги
(перебирают или берут себе?) и т.п.
9. Лексические
анахронизмы – слова, не соответствующие
изображаемой (описываемой) эпохе: Анна
Павловна Шерер часто устраивала в своем
доме дискотеки;
Герасим
уволился по собственному желанию; Чацкий
вернулся из
командировки;
В Древней Руси выходила
газета «Русская
правда» и т.п.
К лексическим
ошибкам следует отнести и употребление
в речи слов-сорняков
(паразитов),
поскольку они не несут никакой смысловой
нагрузки, т.е. семантически опустошенных
слов, засоряющих речь и затрудняющих
ее понимание: как
бы, ну, это, это самое, так сказать, как
говорится
и др.
Соседние файлы в папке Русский
- #
- #
- #
- #
- #
- #
- #
Закон сложения случайных ошибок
- Пусть измеряемая величина Z является суммой (или разностью) двух величин X и Y, результаты измерений которых независимы. Тогда, если , , – дисперсии величин X, Y и Z, то можно доказать, что
- Если Z является суммой не двух, а большего числа слагаемых, то закон сложения ошибок будет таким же, т. е. средняя квадратичная ошибка суммы или разности двух (или нескольких) независимых величин равна корню квадратному из суммы дисперсий отдельных слагаемых
- или
- Для нахождения суммарной ошибки нужно складывать не сами ошибки, а их квадраты
- 1: роль каждой из ошибок в общей ошибке результата. Значение отдельных ошибок очень быстро падает по мере их уменьшения
- Пример: пусть X и Y – два слагаемых, определенных со средними квадратичными ошибками и , причем, известно, что В два раза меньше, чем . Тогда ошибка суммы будет
- Из закона сложения ошибок следуют два чрезвычайно важных вывода
- В первую очередь надо уменьшать ошибку, имеющую наибольшую величину
- будет тем больше, чем меньше , и относительная погрешность возрастает до бесконечности, если
- Если нужная величина Z является разностью двух независимо измеряемых величин X и Y, то из выражения для среднего значения следует, что ее относительная погрешность
- Невозможно добиться хорошей точности измерений какой-либо величины, строя измерения так, что она находится как небольшая разность результатов независимых измерений двух величин, существенно превышающих искомую. В противоположность этому относительная погрешность суммы
- очевидно, не зависит от соотношения величин X и Y
- 2: средняя квадратическая погрешность среднего арифметического равна средней квадратической погрешности отдельного результата, деленная на корень квадратный из числа измерений
- согласно закону сложения случайных погрешностей
- – средняя квадратичная погрешность отдельного измерения
- Cреднеарифметическое ряда измерений
- Это рассуждение относится лишь к измерениям, при которых точность результата полностью определяется случайной ошибкой
- В тех случаях, когда требуется характеризовать точность применяемого способа измерений, следует характеризовать его ошибкой .
- При практической работе очень важно строго разграничивать применение средней квадратичной ошибки отдельного измерения и средней квадратичной среднего арифметического
- применяется всегда, когда нужно оценить погрешность того числа, которое получили в результате всех произведенных измерений
- Обозначим истинное значение измеряемой величины через x, погрешность измерения этой величины – . Среднее арифметическое значение, полученное в результате измерений, будет . Пусть означает вероятность того, что результат измерений отличается от истинного значения на величину, не большую, чем .
- Доверительный интервал и доверительная вероятность
- Вероятность называется доверительной вероятностью, или коэффициентом надежности. Интервал значений от до называется доверительным интервалом
- или
- Для характеристики величины случайной ошибки необходимо задать два числа, а именно: величину самой ошибки (или доверительного интервала) и величину доверительной вероятности
- При обычных измерениях можно ограничиться доверительной вероятностью 0,9 или 0,95
- Для измерений, по условиям которых требуется чрезвычайно высокая степень надежности, иногда задают доверительную вероятность 0,997
- Удобство применения стандартной ошибки в качестве основного численного выражения погрешности наблюдений заключается в том, что этой величине соответствует вполне определенная доверительная вероятность, равная 0,68. (Здесь и дальше полагаем, что ошибки распределены по нормальному закону)
- Средней квадратичной ошибке соответствует доверительная вероятность 0,68, удвоенной средней квадратичной ошибке (2 ) – доверительная вероятность 0,95, утроенной (3 ) – 0,997
- Определение доверительного интервала и доверительной вероятности
- При определении среднеквадратичной ошибки из малого числа наблюдений находим последнюю с малой точностью
- Заменяя на , мы уменьшаем надежность нашей оценки. Чтобы учесть это обстоятельство, будем записывать вероятность через коэф. Стьюдента, найденные по
- Группы систематических погрешностей и методы их компенсации
- При измерениях необходимо учитывать и исключать систематические ошибки, которые иногда могут быть так велики, что совершенно исказят результаты измерений
- Их можно разделить на четыре группы:
- 1. Погрешности, природа которых нам известна, и их величина может быть достаточно точно определена
- Такие ошибки могут быть устранены введением соотв-щих поправок. Источники таких ошибок нужно тщательно анализировать, величины поправок определять и учитывать в окончательном результате
- ПРАВИЛО: если поправка не превышает 0,005 от средней квадратической ошибки результата измерений , то ею следует пренебречь
- 2. Погрешности известного происхождения, но неизвестной величины
- К числу таких погрешностей относится погрешность измерительных приборов, которая определяется иногда классом точности прибора. Если на приборе указан класс точности 0,5, то это означает, что показания прибора правильны с точностью до 0,5% от всей действующей шкалы прибора
- Электроизмерительные приборы характеризуются обычно классом точности в пределах от 0,05 до 4. Менее точные приборы обозначения класса не имеют
- Максимальные погрешности, даваемые измерительными линейками, микрометрами и некоторыми другими приборами, иногда наносят на самом приборе, иногда указывают в прилагаемом к нему паспорте. Обычно дается наибольшая абсолютная погрешность, которую вынуждены считать постоянной по всей шкале прибора, если последний не сопровождается специальной таблицей поправок для каждого деления шкалы. Последняя прилагается только к наиболее точным измерительным приборам
- 3. Ошибки, природа которых неизвестна, но которые могут иметь существенное значение
- Один из наиболее надежных способов убедиться в отсутствии таких погрешностей – провести измерения интересующей величины совсем другим методом и в других условиях. Совпадение полученных результатов служит известной, хотя, к сожалению, не абсолютной, гарантией их правильности. Бывает, что и при измерении разными методами в результатах присутствует ускользнувшая от наблюдателя систематическая ошибка, и в этом случае оба совпавшие друг с другом результата окажутся одинаково неверными
- Эта группа систематических ошибок самая опасная. Это ошибки, о существовании которых мы не подозреваем, но их величина может быть значительной. Они чаще всего проявляются при сложных измерениях, и иногда бывает, что какая-нибудь величина, которая считается определенной с точностью, например, до 2 3%, в действительности оказывается в 2 раза больше измеренного значения
- 4. Ошибки, обусловленные свойствами измеряемого объекта
- Эта группа ошибок, хотя и не связана непосредственно с измерительными операциями, может существенным образом искажать результат измерений
- Систематическая ошибка, связанная со свойствами измеряемого объекта, часто может быть переведена в случайную. Перевод систематических ошибок в случайные часто оказывается полезным, так как позволяет улучшить точность получаемых результатов
- Можно перевести систематическую ошибку в случайную, организовав измерения таким образом, что постоянный фактор, влияющий на результат измерений, в каждом из них действует разным образом, т.е. результат его действий носит случайный характер. Этот прием называется рандомизацией. Он позволяет практически исключить многие неизвестные систематические ошибки
- Определение грубых погрешностей
- Можно считать какое-то измерение промахом, если вероятность случайного появления такого значения в данном ряду измерений является достаточно малой
- Если известно точное значение , то вероятность появления значения, уклоняющегося от среднего арифметического более чем на 3 , равна 0,003; и все измерения, отличающиеся от на эту (или большую) величину, могут быть отброшены как очень маловероятные
- Алгоритм определения грубых погрешностей
- Пусть известен ряд измерений случайных величин:
- Установим, есть ли среди этих значений измерения, проведенные с грубыми погрешностями (промахами)
- Пусть – первое подозреваемое на грубую погрешность
- Вычисляем среднеарифметическое с учетом подозреваемой величины xk и оценку СКО . Определяем величину максимального отклонения в долях среднеквадратической ошибки:
- По таблице оценки выскакивающих измерений, зная число измерений n и Vmax, находим вероятность β того, что данное измерение содержит случайную погрешность
- 0,10
- β
- Отбросить
- Оставить
- 0
- 0,01
- Определение числа измерений
- Допустим, что все систематические ошибки учтены, т.е. поправки, которые следовало определить, вычислены, класс точности прибора известен и есть уверенность, что отсутствуют какие-либо существенные и неизвестные источники систематических ошибок
- Если случайная ошибка окажется меньше систематической, то очевидно, что нет смысла пытаться еще уменьшить величину случайной ошибки: все равно результаты измерений не станут от этого заметно точнее, и, желая получить большую точность, нужно искать пути к уменьшению систематической ошибки. Наоборот, если случайная ошибка больше систематической, то именно случайную ошибку нужно уменьшать в первую очередь
- Для уменьшения случайной ошибки следует произвести ряд измерений, тем больший, чем меньшую величину случайной ошибки хотим получить. Но нет смысла производить измерений больше, чем это необходимо, чтобы систематическая ошибка существенно превышала случайную
- ПРАВИЛА
- 1. Если систематическая ошибка является определяющей, т.е. ее величина существенно больше величины случайной ошибки, присущей данному методу, то достаточно выполнить измерение один раз
- 2. Если случайная ошибка является определяющей, то измерения следует производить несколько раз. Число измерений целесообразно выбирать таким, чтобы случайная ошибка среднего арифметического была меньше систематической ошибки с тем, чтобы последняя опять определяла окончательную ошибку результата
- Для уменьшения случайной ошибки результата могут быть использованы два пути: улучшение точности измерений, т.е. уменьшение величины σ, и увеличение числа измерений, т.е. использование соотношения
- Считаем, что все возможности совершенствования техники измерений уже использованы
- Пусть систематическая ошибка измерений, определяемая классом точности прибора или другими аналогичными обстоятельствами, будет δ
- Уменьшать случайную ошибку целесообразно только до тех пор, пока общая погрешность измерений не будет полностью определяться систематической ошибкой. Для этого необходимо, чтобы доверительный интервал, определенный с выбранной степенью надежности, был бы существенно меньше величины систематической ошибки. Иначе говоря,
- Нет необходимости определять общую ошибку с точностью большей 10%.
- Надежность α с какой хотим установить доверительный интервал, в большинстве случаев не должна превышать 0,95, хотя иногда требуются и более высокие значения α
- Суммарная погрешность
- Если систематическая и случайная погрешности измерений близки друг к другу, они обе в одинаковой степени определяют точность результата. Значение суммарных ошибок можно оценить так: обозначим величину систематической ошибки δ, дисперсию измерений – σ2, тогда в качестве верхней границы суммарной ошибки можно принять
- Вопрос о сложении систематических и случайных ошибок актуален только тогда, когда одна из них не более чем в несколько раз превышает другую. В противном случае в качестве меры погрешности измерения следует указывать только большую ошибку
Ошибки первого и второго рода
- В тех случаях, когда измеряются какие-то свойства готовой продукции (диаметр подшипника, состав металла, и т.п.), задача измерений обычно состоит не в получении точного значения измеряемой величины, а в необходимости уложиться в определенные допуски, установленные для данной продукции. Те изделия, которые не укладываются в эти допуски, будем называть браком. Но следствием ошибок измерений могут быть два обстоятельства: 1) хорошее изделие бракуется и 2) брак пропускается
- В той или иной мере ошибки Ι и ΙΙ рода всегда наблюдаются
- Ввиду того, что ошибки Ι и ΙΙ рода всегда обусловлены многочисленными факторами, их количественные характеристики могут носить только статистический характер и задаваться как вероятности РI и РII
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
- Графическое изображение дает наиболее наглядное представление о результатах экспериментов, позволяет лучше понять физическую сущность исследуемого процесса, выявить общий характер функциональных зависимостей изучаемых переменных величин, установить наличие максимума или минимума функции
- Методы графического изображения результатов измерений
- 1
- 2
- x6y6
- x5y5
- x4y4
- x3y3
- x2y2
- x1y1
- x
- y
- Правильно подобранный масштаб позволяет существенно повысить точность результатов исследований.
- Расчетные графики, имеющие максимум (минимум) функции или какой-либо сложный вид, особо тщательно необходимо вычерчивать в зонах изгиба. Количество точек на таких участках должно быть значительно больше, чем на плавных
- Из неравномерных координатных сеток наиболее распространены полулогарифмические, логарифмические, вероятностные.
- Назначение неравномерных сеток различное. В большинстве случаев их применяют для более наглядного изображения функций. Функция имеет различную форму на различных сетках. Так, многие криволинейные функции спрямляют на логарифмических сетках.
- При графическом изображении результатов экспериментов большую роль играет выбор систем координат или координатной сетки. Координатные сетки бывают равномерными и неравномерными
Методы подбора эмпирических формул
- На основе экспериментальных данных можно подобрать алгебраические выражения, которые называют эмпирическими формулами. Такие формулы подбирают лишь в пределах измерений значений аргумента x1,…,xn. Эмпирические формулы имеют тем большую ценность, чем больше они соответствуют результатам эксперимента
- Эмпирические формулы часто незаменимы для анализа измеренных величин. К эмпирическим формулам предъявляют два основных требования:
- по возможности они должны быть наиболее простыми и
- точно соответствовать экспериментальным данным в пределах изменения аргумента
- Процесс подбора эмпирических формул состоит из двух этапов
- Эмпирические формулы являются приближенными выражениями аналитических формул. Замену точных аналитических выражений приближенными, более простыми называют аппроксимацией, а функции –аппроксимирующими
- данные измерений наносят на сетку прямоугольных координат, соединяют экспериментальные точки плавной кривой и выбирают ориентировочно вид формулы
- вычисляют параметры формул, которые наилучшим образом соответствовали бы принятой формуле
- Метод выравнивания заключается в том, что кривую, построенную по экспериментальным точкам, представляют линейной функцией
- Линеаризацию кривых можно легко осуществить на полу- или логарифмических координатных сетках, которые применяют при графическом методе подбора эмпирических формул
Do’stlaringiz bilan baham:
Речевые ошибки – это
любые случаи отклонения от действующих языковых норм. Без их знания человек
может нормально жить, работать и настраивать коммуникацию с другими. Но вот
эффективность совершаемых действий в определённых случаях может страдать. В
связи с этим возникает риск быть недопонятым или понятым превратно. А в
ситуациях, когда от этого зависит наш личный успех, подобное недопустимо.
Автором приведённой ниже классификации
речевых ошибок является доктор филологических наук Ю. В. Фоменко. Его деление,
по нашему мнению, наиболее простое, лишённое академической вычурности и, как
следствие, понятное даже тем, кто не имеет специального образования.
Виды речевых ошибок:
С. Н. Цейтлин пишет: «В качестве
фактора, способствующего возникновению речевых ошибок, выступает сложность
механизма порождения речи». Давайте рассмотрим частные случаи, опираясь на
предложенную выше классификацию видов речевых ошибок.
Произносительные ошибки
Произносительные или орфоэпические
ошибки возникают в результате нарушения правил орфоэпии. Другими словами,
причина кроется в неправильном произношении звуков, звукосочетаний, отдельных
грамматических конструкций и заимствованных слов. К ним также относятся
акцентологические ошибки – нарушение норм ударения. Примеры:
Произношение: «конечно» (а не «конешно»), «пошти» («почти»), «плотит»
(«платит»), «прецендент» («прецедент»), «иликтрический» («электрический»),
«колидор» («коридор»), «лаболатория» («лаборатория»), «тыща» («тысяча»), «щас»
(«сейчас»).
Неправильное ударение: «зво́нит», «диа́лог», «до́говор», «ката́лог», «путепро́вод»,
«а́лкоголь», «свекла́», «феноме́н», «шо́фер», «э́ксперт».
Лексические ошибки
Лексические ошибки – нарушение правил
лексики, прежде всего – употребление слов в несвойственных им значениях,
искажение морфемной формы слов и правил смыслового согласования. Они бывают
нескольких видов.
Употребление слова в несвойственном ему
значении. Это самая распространённая лексическая речевая
ошибка. В рамках этого типа выделяют три подтипа:
·
Смешение слов, близких по
значению: «Он обратно прочитал книжку».
·
Смешение слов, близких по
звучанию: экскаватор – эскалатор, колос – колосс,
индианка – индейка, одинарный – ординарный.
·
Смешение слов, близких по значению и
звучанию: абонент – абонемент, адресат – адресант,
дипломат – дипломант, сытый – сытный, невежа – невежда.
Словосочинительство. Примеры ошибок: грузинец, героичество, подпольцы,
мотовщик.
Нарушение правил смыслового согласования
слов. Смысловое согласование – это взаимное приспособление слов по линии их
вещественных значений. Например, нельзя сказать «Я поднимаю этот тост»,
поскольку «поднимать» значит «перемещать», что не согласовывается с пожеланием.
«Через приоткрытую настежь дверь» – речевая ошибка, потому что дверь не может
быть и приоткрыта (открыта немного), и настежь (широко распахнута)
одновременно.
Сюда же относятся плеоназмы и
тавтологии. Плеоназм – словосочетание, в котором значение одного компонента
целиком входит в значение другого. Примеры: «май месяц», «маршрут
движения», «адрес местожительства», «огромный мегаполис», «успеть вовремя». Тавтология
– словосочетание, члены которого имеют один корень: «Задали задание», «Организатором выступила одна общественная
организация», «Желаю долгого творческого долголетия».
Фразеологические ошибки
Фразеологические ошибки возникают, когда
искажается форма фразеологизмов или они употребляются в несвойственном им
значении. Ю. В. Фоменко выделяет 7 разновидностей:
·
Изменение лексического состава
фразеологизма: «Пока суть да дело» вместо «Пока суд да дело»;
·
Усечение фразеологизма: «Ему было впору биться об стенку» (фразеологизм: «биться головой
об стенку»);
·
Расширение лексического состава
фразеологизма: «Вы обратились не по правильному адресу»
(фразеологизм: обратиться по адресу);
·
Искажение грамматической формы
фразеологизма: «Терпеть не могу сидеть сложив руки».
Правильно: «сложа»;
·
Контаминация (объединение)
фразеологизмов: «Нельзя же все делать сложа рукава»
(объединение фразеологизмов «спустя рукава» и «сложа руки»);
·
Сочетание плеоназма и
фразеологизма: «Случайная шальная пуля»;
·
Употребление фразеологизма в
несвойственном значении: «Сегодня мы будем говорить о
фильме от корки до корки».
Морфологические ошибки
Морфологические ошибки – неправильное
образование форм слова. Примеры таких речевых ошибок: «туфель», «полотенцев», «дешевше», «в полуторастах километрах».
Синтаксические ошибки
Синтаксические ошибки связаны с
нарушением правил синтаксиса – конструирования предложений, правил сочетания
слов. Их разновидностей очень много, поэтому приведём лишь некоторые примеры.
·
Неправильное согласование: «В шкафу стоят много книг»;
·
Неправильное управление: «Оплачивайте за проезд»;
·
Синтаксическая двузначность: «Чтение Маяковского произвело сильное впечатление» (читал
Маяковский или читали произведения Маяковского?);
·
Смещение конструкции: «Первое, о чём я вас прошу, – это о внимании». Правильно: «Первое,
о чём я вас прошу, – это внимание»;
·
Лишнее соотносительное слово в главном
предложении: «Мы смотрели на те звёзды, которые усеяли всё
небо».
Орфографические ошибки.
Этот вид ошибок возникает из-за незнания правил написания, переноса,
сокращения слов. Характерен для письменной речи.
Например: «сабака лаяла», «сидеть на стули», «приехать
на вогзал», «русск. язык», «грамм. ошибка».
Пунктуационные ошибки
Пунктуационные ошибки – неправильное
употребление знаков препинания при письме.
Пути исправления и предупреждения
речевых ошибок
Как предупредить речевые ошибки? Работа
над своей речью должна включать:
·
Чтение художественной литературы.
·
Посещение театров, музеев, выставок.
·
Общение с образованными людьми.
·
Постоянная работа над совершенствованием
культуры речи.
https://4brain.ru/blog/
Вопрос о классификации ошибок в речи
школьников продолжает оставаться одной из
болевых точек преподавания русского языка в
школе. Данная проблема является болезненной не
только для учителей, методистов, специалистов по
культуре речи, она актуальна и для всех людей,
пишущих и читающих по-русски.
Грамматические ошибки — это
нарушение грамматических норм образования
языковых единиц и их структуры.
Анализ грамматических ошибок помогает
учителю определить, какими нормами языка
(словообразовательными, морфологическими,
синтаксическими) не владеет ученик.
|
№ п/п |
Вид ошибки |
Примеры |
|
Словообразовательные |
||
| 1 | Нарушение норм русского литературного словообразования: Ошибочное Искажение слов |
Трудолюбимый, надсмехаться, надсмешка, подчерк, нагинаться, пинжак, беспощадство, публицизм разночинская интеллигенция; полность |
| 2 | “Заменительное” словообразование, проявляющееся в замене какой-либо морфемы. |
Укидываться (вместо раскидываться), отвесить (от повесить); |
| 3 | Словосочинительство (создание несуществующей производной единицы, которую нельзя рассматривать как окказиональную) |
мотовщик, рецензист, не оглядаемая. |
|
Морфологические
Неправильное формообразование, |
||
| 4 | Ошибочное образование формы существительного |
Многие чуда техники, не хватает время |
| 5 | образование формы В.п. неодушевленного существительного, как у одушевленного |
Я попросила ветерка (вместо: ветерок); |
| 6 | образование формы В.п. одушевленного существительного, как у неодушевленного |
Запрягли в сани два медведя (вместо: двух медведей); |
| 7 | изменение рода при образовании падежных форм: |
пирожок с повидлой, февральский лазурь; |
| 8 | склонение несклоняемых существительных |
играть на пианине; |
| 9 | образование форм множественного числа у существительных, имеющих только единственное, и наоборот |
поднос чаев, небо затянулось облаком. |
|
Ошибочное |
||
| 10 | Неправильный выбор полной и краткой форм |
Шляпка была полная воды, мальчик был очень полон |
| 11 | Неправильное образование форм степеней сравнения: |
новенькие становятся боевее, она была послабже Пети; более интереснее, красивше |
| 12 | Нарушение норм формообразования глагола |
Человек метается по комнате; |
| 13 | Нарушение образования деепричастий и причастий |
Ехавши в автобусе, охотник шел, озирая по сторонам |
| 14 | Ошибочное образование формы числительного |
С пятистами рублями |
| 15 | Ошибочное образование формы местоимения |
Ихнего пафоса, ихи дети, не хотелось от ее (книги) оторваться |
| 16 | Ошибочное образование формы глагола | Они ездиют, хочут, пиша о жизни природы |
|
||
| 17 | Нарушение согласования | Я знаком с группой ребят, серьёзно увлекающемися джазом, Базаров не может побороть По обоим сторонам дороги тянулись холмы; Базаров говорит Аркадию, что твой отец — |
| 18 | Нарушение управления | Нужно сделать свою природу более красивую, повествует читателей, согласно закона, он особое внимание было уделено на составление |
| 19 |
Ошибки в структуре простого нарушение связи между подлежащим и |
Солнце села; но не вечно ни юность, ни лето; это было моей единственной книгой в дни войны; |
| 20 |
Нарушение границы |
Собаки напали на след зайца. И |
| 21 | Неудачное употребление местоимений | Приезжий снял со стула тяжелый сверток и отодвинул его в сторону. Манилов попросил Собакевич потребовал у Чичикова написать себе |
| 22 | Нарушение связи между подлежащим и сказуемым |
Большинство возражали против такой оценки его творчества. Обычно молодежь является Произошло еще ряд событий.
Чтобы приносить пользу Родине, нужно |
| 23 | Нарушение способа выражения сказуемого в отдельных конструкциях |
Он написал книгу, которая эпопея. Все были рады, счастливы и весёлые. |
| 24 | Ошибки в построении предложения, ведущие к искажению его смысла, структуры |
В своей пьесе Чехов показал также трудовую часть интеллигенции с ее мечтами о светлой и прекрасной жизни, представителем которой является Трофимов. Порфирий был Она уговорила отдать подводы для раненых, на |
| 25 | Ошибки, связанные с употреблением частиц |
Хорошо было бы, если бы на В тексте всего раскрываются две |
| 26 | Ошибки в построении предложения с однородными членами |
Страна любила и гордилась поэтом. В сочинении я хотел сказать о значении спорта и почему я его люблю. |
| 27 |
Разрушение ряда однородных |
Настоящий учитель верен |
| 28 |
Ошибки в построении |
Читая текст, возникает такое чувство… На картине “Вратарь” изображен мальчик, широко расставив ноги, упершись руками в колени. |
| 29 | Ошибки в построении предложения с причастным оборотом |
Узкая дорожка была покрыта проваливающимся снегом под ногами; причалившая лодка к берегу. |
| 30 |
Местоименное дублирование |
Кусты, они покрывали берег реки. |
| 31 |
Пропуски необходимых слов. |
Владик прибил доску и побежал |
| 32 |
Ошибки в структуре сложного смешение сочинительной и |
Эта книга научила меня ценить Ум автор текста понимает не только как |
| 33 |
Отрыв придаточного от |
Сыновья Тараса только что |
| 34 | Смешение прямой и косвенной речи | Автор сказал, что я не согласен с мнением рецензента. |
| 35 |
Разрушение |
Терпеть не могу сидеть сложив руки; хохотала как резаная. |
| 36 |
Неоправданный пропуск |
Его храбрость — постоять за честь и справедливость привлекают автора текста. |
| 37 | Нарушение видовременной соотнесённости глагольных форм |
Замирает на мгновение сердце и вдруг застучит вновь. |

