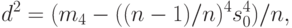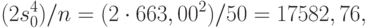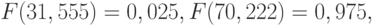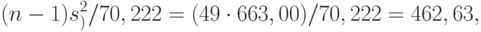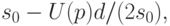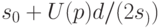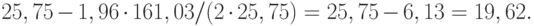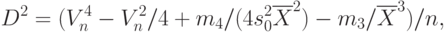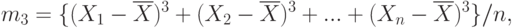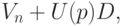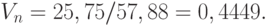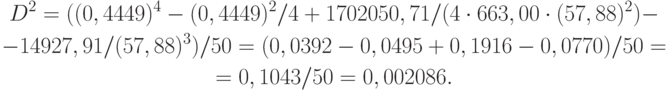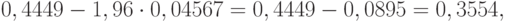Корреляция и регрессия
Линейное уравнение регрессии имеет вид y=bx+a+ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид:
10a + 356b = 49
356a + 2135b = 9485
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17
Уравнение регрессии:
y = 68.16 x — 11.17
1. Параметры уравнения регрессии.
Выборочные средние.
1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Линейное уравнение регрессии имеет вид y = 68.16 x -11.17
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько ед. изменится результат при изменении фактора на 1 ед.
Коэффициент b = 68.16 показывает среднее изменение результативного показателя (в единицах измерения у ) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 68.16.
Коэффициент a = -11.17 формально показывает прогнозируемый уровень у , но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений x , то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения x , можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами — Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.
1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.98 2 = 0.9596, т.е. в 95.96 % случаев изменения x приводят к изменению у . Другими словами — точность подбора уравнения регрессии — высокая. Остальные 4.04 % изменения Y объясняются факторами, не учтенными в модели.
| x | y | x 2 | y 2 | x·y | y(x) | (yi— y ) 2 | (y-y(x)) 2 | (xi— x ) 2 | |y — yx|:y |
| 0.371 | 15.6 | 0.1376 | 243.36 | 5.79 | 14.11 | 780.89 | 2.21 | 0.1864 | 0.0953 |
| 0.399 | 19.9 | 0.1592 | 396.01 | 7.94 | 16.02 | 559.06 | 15.04 | 0.163 | 0.1949 |
| 0.502 | 22.7 | 0.252 | 515.29 | 11.4 | 23.04 | 434.49 | 0.1176 | 0.0905 | 0.0151 |
| 0.572 | 34.2 | 0.3272 | 1169.64 | 19.56 | 27.81 | 87.32 | 40.78 | 0.0533 | 0.1867 |
| 0.607 | 44.5 | .3684 | 1980.25 | 27.01 | 30.2 | 0.9131 | 204.49 | 0.0383 | 0.3214 |
| 0.655 | 26.8 | 0.429 | 718.24 | 17.55 | 33.47 | 280.38 | 44.51 | 0.0218 | 0.2489 |
| 0.763 | 35.7 | 0.5822 | 1274.49 | 27.24 | 40.83 | 61.54 | 26.35 | 0.0016 | 0.1438 |
| 0.873 | 30.6 | 0.7621 | 936.36 | 26.71 | 48.33 | 167.56 | 314.39 | 0.0049 | 0.5794 |
| 2.48 | 161.9 | 6.17 | 26211.61 | 402 | 158.07 | 14008.04 | 14.66 | 2.82 | 0.0236 |
| 7.23 | 391.9 | 9.18 | 33445.25 | 545.2 | 391.9 | 16380.18 | 662.54 | 3.38 | 1.81 |
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=7 находим tкрит:
tкрит = (7;0.05) = 1.895
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 94.6484 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
Sy = 9.7287 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bxp ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx i ± ε)
где
| xi | y = -11.17 + 68.16xi | εi | ymin | ymax |
| 0.371 | 14.11 | 19.91 | -5.8 | 34.02 |
| 0.399 | 16.02 | 19.85 | -3.83 | 35.87 |
| 0.502 | 23.04 | 19.67 | 3.38 | 42.71 |
| 0.572 | 27.81 | 19.57 | 8.24 | 47.38 |
| 0.607 | 30.2 | 19.53 | 10.67 | 49.73 |
| 0.655 | 33.47 | 19.49 | 13.98 | 52.96 |
| 0.763 | 40.83 | 19.44 | 21.4 | 60.27 |
| 0.873 | 48.33 | 19.45 | 28.88 | 67.78 |
| 2.48 | 158.07 | 25.72 | 132.36 | 183.79 |
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (7;0.05) = 1.895
Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(68.1618 — 1.895 • 5.2894; 68.1618 + 1.895 • 5.2894)
(58.1385;78.1852)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — ta)
(-11.1744 — 1.895 • 5.3429; -11.1744 + 1.895 • 5.3429)
(-21.2992;-1.0496)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения ei с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения ei (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости ei от ei-1.
Случайная ошибка модели регрессии в уравнении регрессии
Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования зависимостей между социально-экономическими переменными. Эту задачу мы рассмотрим в рамках самой распространенной в статистических пакетах классической модели линейной регрессии.
Специфика социологических исследований состоит в том, что очень часто необходимо изучать и предсказывать социальные события. Вторая часть данной главы будет посвящена логистической регрессии, целью которой является построение моделей, предсказывающих вероятности событий.
Линейная модель связывает значения зависимой переменной Y со значениями независимых показателей X k (факторов) формулой:
Y=B 0 +B 1 X 1 +:+B p X p + e
где e — случайная ошибка. Здесь X k означает не «икс в степени k «, а переменная X с индексом k .
Традиционные названия «зависимая» для Y и «независимые» для X k отражают не столько статистический смысл зависимости, сколько их содержательную интерпретацию.
Величина e называется ошибкой регрессии. Первые математические результаты, связанные с регрессионным анализом, сделаны в предположении, что регрессионная ошибка распределена нормально с параметрами N(0,? 2 ) , ошибка для различных объектов считаются независимыми. Кроме того, в данной модели мы рассматриваем переменные X как неслучайные значения, Такое, на практике, получается, когда идет активный эксперимент, в котором задают значения X (например, назначили зарплату работнику), а затем измеряют Y (оценили, какой стала производительность труда). За это иногда зависимую переменную называют откликом. Теория регрессионных уравнений со случайными независимыми переменными сложнее, но известно, что, при большом числе наблюдений, использование метода разработанного для неслучайных X корректно.
Благодаря полученным оценкам коэффициентов уравнения регрессии могут быть оценены прогнозные значения зависимой переменной , причем они могут быть вычислены и там, где значения y определены, и там где они не определены. Прогнозные значения являются оценками средних, ожидаемых по модели значений Y , зависящих от X .
Поскольку коэффициенты регрессии — случайные величины, линия регрессии также случайна. Поэтому прогнозные значения случайны и имеют некоторое стандартное отклонение , зависящее от X . Благодаря этому можно получить и доверительные границы для прогнозных значений регрессии (средних значений y ).
Кроме того, с учетом дисперсии остатка могут быть вычислены доверительные границы значений Y (не средних, а индивидуальных!).
Для каждого объекта может быть вычислен остаток e i = 
Для изучения отклонений от модели удобно использовать стандартизованный остаток — деленный на стандартную ошибку регрессии.
Случайность оценки прогнозных значений Y вносит дополнительную дисперсию в регрессионный остаток, из-за этого дисперсия остатка зависит от значений независимых переменных ( 

Таким образом, мы можем получить: оценку (прогнозную) значений зависимой переменной Unstandardized predicted value), ее стандартное отклонение (S.E. of mean predictions), доверительные интервалы для среднего Y(X) и для Y(X) (Prediction intervals — Mean, Individual).
Это далеко не полный перечень переменных, порождаемых SPSS.
Пусть прогнозируется вес ребенка в зависимости от его возраста. Ясно, что дисперсия веса для четырехлетнего младенца будет значительно меньше, чем дисперсия веса 14-летнего юноши. Таким образом, дисперсия остатка e i зависит от значений X , а значит условия для оценки регрессионной зависимости не выполнены. Проблема неоднородности дисперсии в регрессионном анализе называется проблемой гетероскедастичности.
В SPSS имеется возможность корректно сделать соответствующие оценки за счет приписывания весов слагаемым минимизируемой суммы квадратов. Эта весовая функция должна быть равна 1/? 2 (x) , где ? 2 (x) — дисперсия y как функция от x . Естественно, чем меньше дисперсия остатка на объекте, тем больший вес он будет иметь. В качестве такой функции можно использовать ее оценку, полученную при фиксированных значениях X .
Например, в приведенном примере на достаточно больших данных можно оценить дисперсию для каждой возрастной группы и вычислить необходимую весовую переменную. Увеличение влияния возрастных групп с меньшим возрастом в данном случае вполне оправдано.
В диалоговом окне назначение весовой переменной производится с помощью кнопки WLS (Weighed Least Squares — метод взвешенных наименьших квадратов).
В меню — это команда Linear Regression. В диалоговом окне команды:
— Назначаются независимые и зависимая переменные,
— Назначается метод отбора переменных. STEPWISE — пошаговое включение/удаление переменных. FORWARD — пошаговое включение переменных. BACKWARD — пошаговое исключение переменных. При пошаговом алгоритме назначаются значимости включения и исключения переменных (OPTIONS). ENTER — принудительное включение.
— Имеется возможность отбора данных, на которых будет оценена модель (Selection). Для остальных данных могут быть оценены прогнозные значения функции регрессии, его стандартные отклонения и др.
— Назначения вывода статистик (Statistics) — доверительные коэффициенты коэффициентов регресии, их ковариационная матрица, статистики Дарбина-Уотсона и пр.
— Задаются графики рассеяния остатков, их гистограммы (Plots)
— Назначаются сохранение переменных(Save), порождаемых регрессией.
— Если используется пошаговая регрессия, назначаются пороговые значимости для включения (PIN) и исключения (POUT) переменных (Options).
— Если обнаружена гетероскедастичность, назначается и весовая переменная.
Обычно демонстрацию модели начинают с простейшего примера, и такие примеры Вы можете найти в Руководстве по применению SPSS. Мы пойдем немного дальше и покажем, как получить полиномиальную регрессию.
Курильский опрос касался населения трудоспособного возраста. Как показали расчеты, в среднем меньшие доходы имеют молодые люди и люди старшего возраста. Поэтому, прогнозировать доход лучше квадратичной кривой, а не простой линейной зависимостью. В рамках линейной модели это можно сделать, введя переменную — квадрат возраста. Приведенное ниже задание SPSS предназначено для прогноза логарифма промедианного дохода (ранее сформированного).
REGRESSION /DEPENDENT lnv14m /METHOD=ENTER v9 v9_2
/SAVE PRED MCIN ICIN.
*регрессия с сохранением предсказанных значений и доверительных интервалов средних и индивидуальных прогнозных значений.
Таблица 5.1 показывает, что уравнение объясняет всего 4.5% дисперсии зависимой переменной (коэффициент детерминации R 2 =.045), скорректированная величина коэффициента равна 0.042, а коэффициент множественной корреляции равен 0.211. Много это или мало, трудно сказать, поскольку у нас нет подобных результатов на других данных, но то, что здесь есть взаимосвязь, можно понять, рассматривая таблицу 6.2.
Таблица 6.1. Общие характеристики уравнения
Adjusted R Square
Std. Error of the Estimate
a Predictors: (Constant), V9_2, V9 Возраст
b Dependent Variable: LNV14M логарифм промедианного дохода
Результаты дисперсионного анализа уравнения регрессии показывает, что гипотеза равенства всех коэффициентов регрессии нулю должна быть отклонена.
Таблица 6.2. Дисперсионный анализ уравнения
Основы линейной регрессии
Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Остатки нормально распределены с нулевым средним значением;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:
Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:
Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии
Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .
Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»
Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.
Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости
Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
источники:
http://masters.donntu.org/2005/fvti/scherbak/library/doc_1.htm
http://statistica.ru/theory/osnovy-lineynoy-regressii/
В
линейной регрессии обычно оценивается
значимость не только уравнения в целом,
но и отдельных его параметров. С этой
целью по каждому из параметров определяется
его стандартная ошибка: тb
и
та.
Стандартная
ошибка коэффициента регрессии параметра
b
рассчитывается
по формуле:
Где
остаточная дисперсия на одну степень
свободы.
Отношение
коэффициента регрессии к его стандартной
ошибке дает t-статистику,
которая подчиняется статистике Стьюдента
при
степенях
свободы. Эта статистика применяется
для проверки статистической значимости
коэффициента регрессии и для расчета
его доверительных интервалов.
Для
оценки значимости коэффициента регрессии
его величину сравнивают с его стандартной
ошибкой, т.е. определяют фактическое
значение t-критерия
Стьюдента:
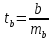
которое затем сравнивают с табличным
значением при определенном уровне
значимостиα
и
числе степеней свободы
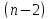
Справедливо
равенство
Доверительный
интервал для коэффициента регрессии
определяется как
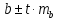
Стандартная
ошибка параметра а
определяется
по формуле
Процедура
оценивания значимости данного параметра
не отличается от рассмотренной выше
для коэффициента регрессии: вычисляется
t-критерий:
Его
величина сравнивается с табличным
значением при
степенях свободы.
Значимость
линейного коэффициента корреляции
проверяется на основе величины ошибки
коэффициента корреляции mr:
Фактическое
значение t-критерия
Стьюдента определяется как
Данная
формула свидетельствует, что в парной
линейной регрессии
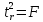
ибо как уже указывалось,
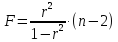
Кроме того,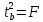
следовательно,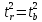
Таким
образом, проверка гипотез о значимости
коэффициентов регрессии и корреляции
равносильна проверке гипотезы о
значимости линейного уравнения регрессии.
Рассмотренную
формулу оценки коэффициента корреляции
рекомендуется применять при большом
числе наблюдений, а также если r
не близко к +1 или –1.
2.3 Интервальный прогноз на основе линейного уравнения регрессии
В
прогнозных расчетах по уравнению
регрессии определяется предсказываемое
yр
значение
как точечный прогноз
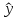
при
хр
= хk
т.
е. путем подстановки в линейное уравнение
регрессии
соответствующего
значения х.
Однако
точечный прогноз явно нереален, поэтому
он дополняется расчетом стандартной
ошибки
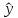
т.
е.
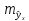
и
соответственно мы получаем интервальную
оценку прогнозного значения у*:
Считая,
что прогнозное значение фактора хр
= хk
получим
следующую формулу расчета стандартной
ошибки предсказываемого по линии
регрессии значения, т. е.
имеет выражение:
Рассмотренная
формула стандартной ошибки предсказываемого
среднего значения у
при
заданном значении хk
характеризует
ошибку положения линии регрессии.
Величина стандартной ошибки
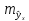
минимума при
и
возрастает по мере того, как «удаляется»
от
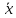
больше разность между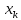
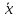
тем больше ошибка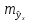
с
которой предсказывается среднее значение
у
для
заданного значения
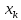
Можно ожидать наилучшие результаты
прогноза, если признак-фактор х находится
в центре области наблюдений х, и нельзя
ожидать хороших результатов прогноза
при удалении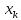
от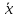
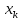
оказывается за пределами наблюдаемых
значенийх,
используемых при построении линейной
регрессии, то результаты прогноза
ухудшаются в зависимости от того,
насколько
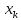
отклоняется от области наблюдаемых
значений факторах.
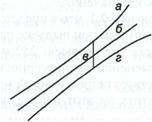
На
графике, приведенном на рис. 1, доверительные
границы для
представляют
собой гиперболы, расположенные по обе
стороны от линии регрессии. Рис. 1
показывает, как изменяются пределы в
зависимости от изменения
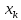
две гиперболы по обе стороны от линии
регрессии определяют 95 %-ные доверительные
интервалы для среднего значенияу
при
заданном значении х.
Однако
фактические значения у
варьируют
около среднего значения
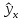
Индивидуальные
значения у
могут
отклоняться от
на
величину случайной ошибки ε, дисперсия
которой оценивается как остаточная
дисперсия на одну степень свободы
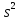
Поэтому ошибка предсказываемого
индивидуального значенияу
должна включать не только стандартную
ошибку
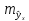
но и случайную ошибкуs.
Рис.
1. Доверительный интервал линии регрессии:
а
— верхняя
доверительная граница; б
— линия
регрессии;
в
— доверительный
интервал для
при
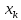
г
— нижняя
доверительная граница.
Средняя
ошибка прогнозируемого индивидуального
значения у
составит:
При
прогнозировании на основе уравнения
регрессии следует помнить, что величина
прогноза зависит не только от стандартной
ошибки индивидуального значения у,
но
и от точности прогноза значения фактора
х.
Его
величина может задаваться на основе
анализа других моделей исходя из
конкретной ситуации, а также анализа
динамики данного фактора.
Рассмотренная
формула средней ошибки индивидуального
значения признака у
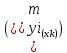
быть использована также для оценки
существенности различия предсказываемого
значения и некоторого гипотетического
значения.
11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аннотация: Описывается точечное и интервальное оценивание основных параметров распределений (математического ожидания, медианы, дисперсии и др). Большая часть лекции посвящена методам проверки однородности характеристик двух независимых или связанных выборок.
8.1. Оценивание основных характеристик распределения
Одна из основных задач прикладной статистики — оценивание по выборочным данным характеристик генеральной совокупности, таких, как математическое ожидание, медиана, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Точечные оценки строятся очевидным образом — используют выборочные аналоги теоретических характеристик. Для получения интервальных оценок приходится использовать асимптотическую нормальность выборочных моментов и функций от них.
Пусть исходные данные — это выборка 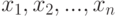

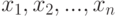
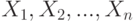
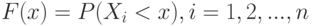
В расчетах будут использоваться выборочное среднее арифметическое
выборочная дисперсия
и некоторые другие выборочные характеристики, которые мы введем позже.
Точечное и интервальное оценивание математического ожидания. Точечной оценкой для математического ожидания в силу закона больших чисел является выборочное среднее арифметическое 
Нижняя доверительная граница для математического ожидания имеет вид
где:
Верхняя доверительная граница для математического ожидания имеет вид
Выражения для верхней и нижней доверительных границ получены с помощью Центральной предельной теоремы теории вероятностей, теоремы о наследовании сходимости и других результатов
«Теоретическая база прикладной статистики»
. Они являются асимптотическими, т.е. становятся тем точнее, чем больше объем выборки. В частности, вероятность попадания истинного значения математического ожидания между нижней и верхней доверительными границами асимптотически приближается к доверительной вероятности, но, вообще говоря, может отличаться от нее. Это — недостатки непараметрического подхода. Достоинством же является то, что его можно применять всегда, когда случайная величина имеет математическое ожидание и дисперсию, что в силу финитности (ограниченности шкал) имеет быть практически всегда в реальных ситуациях.
Интересно сопоставить с параметрическим подходом. Обычно в таких случаях предполагают нормальность результатов наблюдений (которой, как уже было обосновано в
«Описание данных»
, практически никогда нет). Тогда формулы для нижней и верхней доверительных границ для математического ожидания имеют похожий вид, только вместо 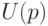
Пример 1. Рассмотрим данные о наработке резцов до отказа (см. 6.1, табл.6.2). Для них выборочное среднее арифметическое 

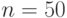
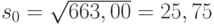
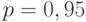
а верхняя доверительная граница есть 57,88 + 7,14 = 65,02.
Если заранее известно, что результаты наблюдения имеют нормальное распределение, то нижняя и верхняя доверительная границы для математического ожидания определяются по формулам
соответственно. Эти формулы отличаются от предыдущих тем, что квантиль нормального распределения 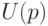
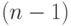
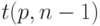


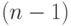
Для доверительной вероятности 
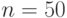
[
2.1
]
] имеем 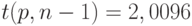
а верхняя доверительная граница есть 57,88 + 7,32 = 65,20. Таким образом, длина доверительного интервала увеличилась с 14,28 до 14,64, т.е. на 2,5%.
Отметим, что рассматриваемые данные согласуются с гамма-распределением (см. 7.1), а не с нормальным распределением, поэтому использование распределения Стьюдента для получения доверительных границ явно некорректно.
Иногда рекомендуют сначала проверить нормальность результатов наблюдений, а потом, в случае принятия гипотезы нормальности, рассчитывать доверительные границы с использованием квантилей распределения Стьюдента. Однако проверка нормальности — более сложная статистическая процедура, чем оценивание математического ожидания. Кроме того, применение одной статистической процедуры, как правило, нарушает предпосылки следующей процедуры, в частности, независимость результатов наблюдений (см. 7.5). Поэтому цепочка статистических процедур, следующих друг за другом, как правило, образует статистическую технологию, свойства которой неизвестны на современном уровне развития прикладной статистики.
Из сказанного вытекает, что только непараметрическую статистическую процедуру, основанную на асимптотических результатах
«Теоретическая база прикладной статистики»
, следует применять для анализа реальных данных. Как правило, встречающиеся на практике распределения не являются нормальными (см. 5.1), а потому применение квантилей распределения Стьюдента неправомерно.
Точечное и интервальное оценивание медианы. Точечной оценкой для медианы является выборочная медиана.
Пример 2. Для данных о наработке резцов до отказа объем выборки — четное число, поэтому выборочной медианой является полусумма 25-го и 26-го членов вариационного ряда, т.е. (56 + 56,5)/2 = 56,25.
Чтобы построить доверительные границы для медианы, по доверительной вероятности 
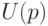
где [.] — знак целой части числа. Нижняя доверительная граница для медианы имеет вид
где 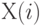


Теоретическое основание для приведенных доверительных границ содержится в литературе по порядковым статистикам (см., например, монографию [
[
8.11
]
, с.68]).
Пример 3. Для данных о наработке резцов до отказа 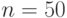
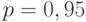
Следовательно, нижней доверительной границей является 
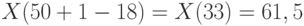
Поскольку в случае нормального распределения медиана совпадает с математическим ожиданием, то каких-либо специальных способов ее оценивания в классическом случае нет.
Точечное и интервальное оценивание дисперсии. Точечной оценкой дисперсии является выборочная дисперсия 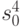
где 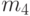

Нижняя доверительная граница для дисперсии случайной величины имеет вид
где:
Верхняя доверительная граница для дисперсии случайной величины имеет вид
где все составляющие имеют тот же смысл, что и выше.
При выводе приведенных соотношений используется асимптотическая нормальность выборочной дисперсии, установленная, например, в учебнике по математической статистике [
[
8.2
]
, с.419]. Соответственно доверительный интервал является непараметрическим и асимптотическим. В классическом случае точечная оценка имеет тот же вид, а вот доверительные границы находят с помощью квантилей распределения хи-квадрат с числом степеней свободы, на 1 меньшим объема выборки. Отметим, что в случае нормального распределения четвертый момент в 3 раза больше квадрата дисперсии, а потому можно оценить 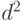
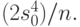
Пример 4. Для данных о наработке резцов до отказа объем выборки 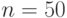


Тогда 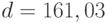
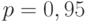
а верхняя доверительная граница для дисперсии — 663,00+315,63=978,63.
Пример 5. В случае нормального распределения с целью быстрого получения доверительного интервала величина 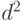
а потому 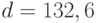
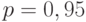
а верхняя доверительная граница — на 663,00+259,90=922,9.
Сужение границ для дисперсии вполне естественно. Данные о наработке резцов до предельного состояния (т.е. до отказа) соответствуют гамма-распределению, а это распределение является асимметричным, с «тяжелым» правым «хвостом». Последнее означает, что плотность убывает заметно медленнее, чем для нормального распределения. Как следствие, четвертый момент заметно больше, чем для нормального распределения с теми же математическим ожиданием и дисперсией. А потому больше и параметр 
Пример 6. В классическом случае нормального распределения исходят из того, что величина 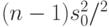
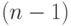
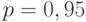
справедливое с вероятностью 0,95, поскольку
где 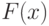
а верхняя доверительная граница есть
Полученный доверительный интервал не является симметричным относительно точечной оценки. Нижняя доверительная граница больше, чем в примерах 4 и 5, но и верхняя доверительная граница тоже больше. Несимметричность доверительного интервала в примере 6 приводит к тому, что его трудно сопоставить с симметричными интервалами примеров 4 и 5. Что же касается практических рекомендаций, то они однозначны: поскольку обычно нет основания считать данные имеющими нормальное распределение, то при анализе реальных данных надо пользоваться непараметрическими методами, не предполагающими нормальность, т.е. методами, примененными в примере 4.
Точечное и интервальное оценивание среднего квадратического отклонения. Точечной оценкой является выборочное среднее квадратическое отклонение, т.е. неотрицательный квадратный корень из выборочной дисперсии. Дисперсия рассматриваемой случайной величины — выборочного среднего квадратического отклонения 
Нижняя доверительная граница для среднего квадратического отклонения исходной случайной величины имеет вид
где:
Верхняя доверительная граница для среднего квадратического отклонения исходной случайной величины имеет вид
, где все составляющие имеют тот же смысл, что и выше.
Пример 7. Для данных о наработке резцов до отказа точечной оценкой для среднего квадратического отклонения является 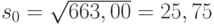
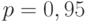
Соответственно верхняя доверительная граница симметрична нижней относительно точечной оценки и равна 25,75+6,13=31,88.
Правила интервального оценивания для среднего квадратического отклонения получены из аналогичных правил для оценивания дисперсии с помощью метода линеаризации (см.
«Теоретическая база прикладной статистики»
или, например, [
[
1.15
]
, п.2.4]). Как и раньше, доверительный интервал является симметричным, непараметрическим и асимптотическим.
Поскольку среднее квадратическое отклонение — это квадратный корень их дисперсии, то доверительные границы можно получить, извлекая квадратные корни из одноименных границ для дисперсии.
Пример 8. Для данных о наработке резцов до отказа при доверительной вероятности 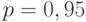
Классический подход, основанный на гипотезе нормальности распределения результатов наблюдения, связан с использованием распределения хи-квадрат и сводится к извлечению квадратных корней из доверительных границ для дисперсии.
Пример 9. Применяя формально классический подход к данным о наработке резцов до отказа, исходим из доверительного интервала для дисперсии [462,63; 1029,54], соответствующего доверительной вероятности 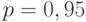
Точечное и интервальное оценивание коэффициента вариации. Коэффициент вариации 

Дисперсия выборочного коэффициента вариации состоятельно оценивается с помощью вспомогательной величины
где:
Нижняя доверительная граница для (теоретического) коэффициента вариации исходной случайной величины имеет вид
где:
Верхняя доверительная граница для (теоретического) коэффициента вариации исходной случайной величины имеет вид
где все составляющие имеют тот же смысл, что и выше.
Как и в предыдущих случаях, доверительный интервал является непараметрическим и асимптотическим. Он получен в результате применения специальной технологии вывода асимптотических соотношений прикладной статистики (см.
«Теоретическая база прикладной статистики»
). Напомним, что эта технология в качестве первого шага использует многомерную центральную предельную теорему, примененную к сумме векторов, координаты которых — степени исходных случайных величин. Второй шаг — преобразование предельного многомерного нормального вектора с целью получения интересующего исследователя вектора. При этом используются соображения линеаризации и отбрасываются бесконечно малые величины. Третий шаг — строгое обоснование полученных результатов на стандартном для асимптотических математико-статистических рассуждений уровне.
При этом обычно приходится использовать необходимые и достаточные условия наследования сходимости, полученные в монографии [
[
1.15
]
, п.2.4]. Именно таким образом были получены приведенные выше результаты для выборочного коэффициента вариации. Формулы оказались существенно более сложными, чем в предыдущих случаях. Это объясняется тем, что выборочный коэффициент вариации — функция двух выборочных моментов, а ранее рассматривались либо выборочные моменты поодиночке, либо функция от одного выборочного момента — выборочной дисперсии.
Пример 10. Для данных о наработке резцов до отказа выборочное среднее арифметическое 




Рассчитаем значение вспомогательной величины
Следовательно, 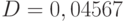
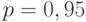
а верхняя доверительная граница такова:
Среди классических результатов математической статистики, основанных на гипотезе нормальности результатов наблюдений, нет методов построения доверительных границ для коэффициента вариации, поскольку задача построения таких границ не выражается в терминах обычно используемых распределений, например, распределений Стьюдента и хи-квадрат.
Примеры применения доверительных границ для коэффициентов вариации при решении прикладных задач приведены, например, в работе [
[
8.9
]
], посвященной анализу технических характеристик и показателей качества.








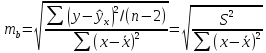
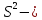
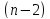
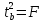
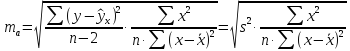
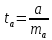
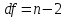
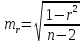
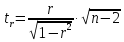
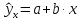
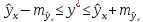
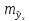
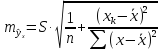
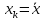
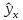
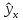
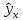
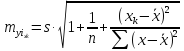

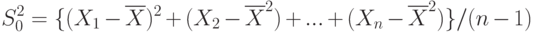
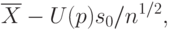
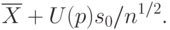

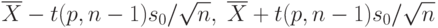

![C(p)=[n/2-U(p)n^{1/2}/2]](https://new2.intuit.ru/sites/default/files/tex_cache/28aa233e9bc3c93de7b1031c31ecbd6c.png)
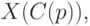
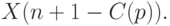
![C(p)=[50/2-1,96\sqrt{50}/2]=[18,07]=18.](https://new2.intuit.ru/sites/default/files/tex_cache/8e37ec54ba483aebf81eba6df5e204d3.png)