Случайные ошибки
Предмет
Механика
Разместил
🤓 GinniWag
👍 Проверено Автор24
ошибки, которые проявляются в разбросе результатов при повторных измерениях; случайные ошибки обусловливаются большим числом случайных причин, которые действуют в каждом отдельном измерении различным неизвестным образом.
Научные статьи на тему «Случайные ошибки»
Регрессия в эконометрике
ошибки должны быть равны нулю;
Дисперсия случайной ошибки для всех наблюдений должна быть постоянной…
;
Случайные ошибки не должны иметь между собой статической зависимости;
Объясняющая переменная x должна…
Согласно первому условию, случайная ошибка не должна систематически смещаться….
Второе условие – это наличие в каждом наблюдении только одного значения дисперсии случайной ошибки….
Дисперсия – это возможное изменение случайной ошибки до проведения выборки.

Статья от экспертов
Исследование составляющих ошибки для решения обратной задачи с использованием случайных проекций
Проведен сравнительный анализ решений дискретных некорректных обратных задач, полученных в результате оцифровки интегрального уравнения (задача Carasso, Delves, Phillips). Использовались методы псевдообращения и регуляризации Тихонова и эти же методы с использованием дополнительного проецирования случайной матрицей. Исследована зависимость составляющих ошибки решение (смещение и дисперсия) от размерности матрицы проектора. При использовании проецирования метод псевдообращения продемонстрировал точность на уровне регуляризации Тихонова
Статистические методы определения ожидаемой ошибки в аудите
, содержащиеся в генеральной совокупности, равновозможные и распределяются случайным образом….
берется нормальное распределение вероятностей случайной величины — размера ошибки элементов выборки….
Согласно теории вероятности известна информация о случайной величине….
величину, то случайная величина считается распределенной по нормальному закону….
Но для того чтобы определить ожидаемую ошибку потребуется большое количество расчетов.

Статья от экспертов
Применение фильтра Калмана для решения задачи численного дифференцирования при случайных ошибках измерений
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек
From Wikipedia, the free encyclopedia
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its «true value» (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the estimated value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals.
In econometrics, «errors» are also called disturbances.[1][2][3]
Introduction[edit]
Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors are the deviations of the observations from the population mean, while the residuals are the deviations of the observations from the sample mean.
A statistical error (or disturbance) is the amount by which an observation differs from its expected value, the latter being based on the whole population from which the statistical unit was chosen randomly. For example, if the mean height in a population of 21-year-old men is 1.75 meters, and one randomly chosen man is 1.80 meters tall, then the «error» is 0.05 meters; if the randomly chosen man is 1.70 meters tall, then the «error» is −0.05 meters. The expected value, being the mean of the entire population, is typically unobservable, and hence the statistical error cannot be observed either.
A residual (or fitting deviation), on the other hand, is an observable estimate of the unobservable statistical error. Consider the previous example with men’s heights and suppose we have a random sample of n people. The sample mean could serve as a good estimator of the population mean. Then we have:
- The difference between the height of each man in the sample and the unobservable population mean is a statistical error, whereas
- The difference between the height of each man in the sample and the observable sample mean is a residual.
Note that, because of the definition of the sample mean, the sum of the residuals within a random sample is necessarily zero, and thus the residuals are necessarily not independent. The statistical errors, on the other hand, are independent, and their sum within the random sample is almost surely not zero.
One can standardize statistical errors (especially of a normal distribution) in a z-score (or «standard score»), and standardize residuals in a t-statistic, or more generally studentized residuals.
In univariate distributions[edit]
If we assume a normally distributed population with mean μ and standard deviation σ, and choose individuals independently, then we have
and the sample mean
is a random variable distributed such that:
The statistical errors are then
with expected values of zero,[4] whereas the residuals are
The sum of squares of the statistical errors, divided by σ2, has a chi-squared distribution with n degrees of freedom:
However, this quantity is not observable as the population mean is unknown. The sum of squares of the residuals, on the other hand, is observable. The quotient of that sum by σ2 has a chi-squared distribution with only n − 1 degrees of freedom:
This difference between n and n − 1 degrees of freedom results in Bessel’s correction for the estimation of sample variance of a population with unknown mean and unknown variance. No correction is necessary if the population mean is known.
[edit]
It is remarkable that the sum of squares of the residuals and the sample mean can be shown to be independent of each other, using, e.g. Basu’s theorem. That fact, and the normal and chi-squared distributions given above form the basis of calculations involving the t-statistic:
where 


The probability distributions of the numerator and the denominator separately depend on the value of the unobservable population standard deviation σ, but σ appears in both the numerator and the denominator and cancels. That is fortunate because it means that even though we do not know σ, we know the probability distribution of this quotient: it has a Student’s t-distribution with n − 1 degrees of freedom. We can therefore use this quotient to find a confidence interval for μ. This t-statistic can be interpreted as «the number of standard errors away from the regression line.»[6]
Regressions[edit]
In regression analysis, the distinction between errors and residuals is subtle and important, and leads to the concept of studentized residuals. Given an unobservable function that relates the independent variable to the dependent variable – say, a line – the deviations of the dependent variable observations from this function are the unobservable errors. If one runs a regression on some data, then the deviations of the dependent variable observations from the fitted function are the residuals. If the linear model is applicable, a scatterplot of residuals plotted against the independent variable should be random about zero with no trend to the residuals.[5] If the data exhibit a trend, the regression model is likely incorrect; for example, the true function may be a quadratic or higher order polynomial. If they are random, or have no trend, but «fan out» — they exhibit a phenomenon called heteroscedasticity. If all of the residuals are equal, or do not fan out, they exhibit homoscedasticity.
However, a terminological difference arises in the expression mean squared error (MSE). The mean squared error of a regression is a number computed from the sum of squares of the computed residuals, and not of the unobservable errors. If that sum of squares is divided by n, the number of observations, the result is the mean of the squared residuals. Since this is a biased estimate of the variance of the unobserved errors, the bias is removed by dividing the sum of the squared residuals by df = n − p − 1, instead of n, where df is the number of degrees of freedom (n minus the number of parameters (excluding the intercept) p being estimated — 1). This forms an unbiased estimate of the variance of the unobserved errors, and is called the mean squared error.[7]
Another method to calculate the mean square of error when analyzing the variance of linear regression using a technique like that used in ANOVA (they are the same because ANOVA is a type of regression), the sum of squares of the residuals (aka sum of squares of the error) is divided by the degrees of freedom (where the degrees of freedom equal n − p − 1, where p is the number of parameters estimated in the model (one for each variable in the regression equation, not including the intercept)). One can then also calculate the mean square of the model by dividing the sum of squares of the model minus the degrees of freedom, which is just the number of parameters. Then the F value can be calculated by dividing the mean square of the model by the mean square of the error, and we can then determine significance (which is why you want the mean squares to begin with.).[8]
However, because of the behavior of the process of regression, the distributions of residuals at different data points (of the input variable) may vary even if the errors themselves are identically distributed. Concretely, in a linear regression where the errors are identically distributed, the variability of residuals of inputs in the middle of the domain will be higher than the variability of residuals at the ends of the domain:[9] linear regressions fit endpoints better than the middle. This is also reflected in the influence functions of various data points on the regression coefficients: endpoints have more influence.
Thus to compare residuals at different inputs, one needs to adjust the residuals by the expected variability of residuals, which is called studentizing. This is particularly important in the case of detecting outliers, where the case in question is somehow different from the others in a dataset. For example, a large residual may be expected in the middle of the domain, but considered an outlier at the end of the domain.
Other uses of the word «error» in statistics[edit]
The use of the term «error» as discussed in the sections above is in the sense of a deviation of a value from a hypothetical unobserved value. At least two other uses also occur in statistics, both referring to observable prediction errors:
The mean squared error (MSE) refers to the amount by which the values predicted by an estimator differ from the quantities being estimated (typically outside the sample from which the model was estimated).
The root mean square error (RMSE) is the square-root of MSE.
The sum of squares of errors (SSE) is the MSE multiplied by the sample size.
Sum of squares of residuals (SSR) is the sum of the squares of the deviations of the actual values from the predicted values, within the sample used for estimation. This is the basis for the least squares estimate, where the regression coefficients are chosen such that the SSR is minimal (i.e. its derivative is zero).
Likewise, the sum of absolute errors (SAE) is the sum of the absolute values of the residuals, which is minimized in the least absolute deviations approach to regression.
The mean error (ME) is the bias.
The mean residual (MR) is always zero for least-squares estimators.
See also[edit]
- Absolute deviation
- Consensus forecasts
- Error detection and correction
- Explained sum of squares
- Innovation (signal processing)
- Lack-of-fit sum of squares
- Margin of error
- Mean absolute error
- Observational error
- Propagation of error
- Probable error
- Random and systematic errors
- Reduced chi-squared statistic
- Regression dilution
- Root mean square deviation
- Sampling error
- Standard error
- Studentized residual
- Type I and type II errors
References[edit]
- ^ Kennedy, P. (2008). A Guide to Econometrics. Wiley. p. 576. ISBN 978-1-4051-8257-7. Retrieved 2022-05-13.
- ^ Wooldridge, J.M. (2019). Introductory Econometrics: A Modern Approach. Cengage Learning. p. 57. ISBN 978-1-337-67133-0. Retrieved 2022-05-13.
- ^ Das, P. (2019). Econometrics in Theory and Practice: Analysis of Cross Section, Time Series and Panel Data with Stata 15.1. Springer Singapore. p. 7. ISBN 978-981-329-019-8. Retrieved 2022-05-13.
- ^ Wetherill, G. Barrie. (1981). Intermediate statistical methods. London: Chapman and Hall. ISBN 0-412-16440-X. OCLC 7779780.
- ^ a b Frederik Michel Dekking; Cornelis Kraaikamp; Hendrik Paul Lopuhaä; Ludolf Erwin Meester (2005-06-15). A modern introduction to probability and statistics : understanding why and how. London: Springer London. ISBN 978-1-85233-896-1. OCLC 262680588.
- ^ Peter Bruce; Andrew Bruce (2017-05-10). Practical statistics for data scientists : 50 essential concepts (First ed.). Sebastopol, CA: O’Reilly Media Inc. ISBN 978-1-4919-5296-2. OCLC 987251007.
- ^ Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, with Special Reference to Biological Sciences. McGraw-Hill. p. 288.
- ^ Zelterman, Daniel (2010). Applied linear models with SAS ([Online-Ausg.]. ed.). Cambridge: Cambridge University Press. ISBN 9780521761598.
- ^ «7.3: Types of Outliers in Linear Regression». Statistics LibreTexts. 2013-11-21. Retrieved 2019-11-22.
- Cook, R. Dennis; Weisberg, Sanford (1982). Residuals and Influence in Regression (Repr. ed.). New York: Chapman and Hall. ISBN 041224280X. Retrieved 23 February 2013.
- Cox, David R.; Snell, E. Joyce (1968). «A general definition of residuals». Journal of the Royal Statistical Society, Series B. 30 (2): 248–275. JSTOR 2984505.
- Weisberg, Sanford (1985). Applied Linear Regression (2nd ed.). New York: Wiley. ISBN 9780471879572. Retrieved 23 February 2013.
- «Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
External links[edit]
Media related to Errors and residuals at Wikimedia Commons
11
ГОСУДАРСТВЕННОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛОРУССКО-РОССИЙСКИЙ
УНИВЕРСИТЕТ»
Кафедра
«Автоматизированные системы управления»
Эконометрика
и экономико-математические
методы и модели
Методические
указания
к лабораторным и
практическим занятиям для студентов
специальностей
1-25 01 04 «Финансы и кредит»,
1-25 01 08 «Бухгалтерский
учет, анализ и аудит»,
1-25 01 10 «Коммерческая
деятельность»
Часть 1
Могилев 2012
У
004.65
ББК 32.81
Э 11
Рекомендовано к
опубликованию
учебно-методическим
управлением
ГУ ВПО
«Белорусско-Российский университет»
Одобрено кафедрой
«Автоматизированные системы управления»
«20» марта 2012 г., протокол № 7
Составитель: канд.
техн. наук, доц. Т. В. Мрочек
Рецензент канд.
техн. наук, доц. В. А. Широченко
Описаны основные
этапы выполнения лабораторных и
практических работ по первой части
изучаемой дисциплины – эконометрике.
Приведены основные понятия, расчетные
зависимости и примеры выполнения
наиболее распространенных задач по
рассматриваемым темам.
Учебное издание
Эконометрика и
экономико-математические методы
и модели
Ответственный за
выпуск С. К. Крутолевич
Технический
редактор А. Т. Червинская
Компьютерная
верстка И. А. Алексеюс
Подписано в печать . Формат 60х84/16.
Бумага офсетная. Гарнитура Таймс.
Печать трафаретная. Усл.-печ. л. .
Уч.-изд. л. . Тираж 66 экз. Заказ №
Издатель и полиграфическое исполнение
Государственное учреждение высшего
профессионального образования
«Белорусско-Российский университет»
ЛИ № 02330/375 от 29.06.2004 г.
212000, Г. Могилев, пр. Мира, 43
© ГУ ВПО «Белорусско-Российский
университет», 2012
1 Парная регрессия и корреляция
Цель: определение
характеристик уравнений парной линейной
и нелинейной регрессий, оценка значимости
параметров и корреляции и выбор наилучшего
уравнения регрессии.
1.1 Расчетные формулы
Регрессия –
это модель вида
,
где y
– зависимая
переменная (результативный признак,
функция отклика, эндогенная (внутренняя)
переменная). Термин «внутренний» отражает
тот факт, что значения зависимой
переменной у
определяются
только значениями независимых переменных
x;
х –
независимая переменная (объясняющая
переменная, фактор, входная переменная,
внешняя или экзогенная переменная).
Термин «внешний» говорит о том, что
значения переменных х
определяются
вне рассматриваемой модели, для которой
они являются заданными.
Знак «ˆ»
(«ридж») означает, что между переменными
х и
у
нет строгой функциональной зависимости,
поэтому практически в каждом отдельном
случае величина у
складывается из двух слагаемых:
,
где у
– фактическое (экспериментальное)
значение результативного признака;
–теоретическое
значение результативного признака,
найденное из уравнения регрессии;
–случайная
величина, характеризующая отклонения
фактического значения у
от
.
Случайная величина
i
включает влияние не учтенных в модели
факторов, случайных ошибок и особенностей
измерения [5, с. 44].
В
случае единственной входной переменной
регрессию называютпарной
(простой),
если переменных
две и более –множественной.
В зависимости от
типа выбранного уравнения различают
линейную и
нелинейную
регрессию
(экспоненциальную, логарифмическую и
т. д.).
При изучении
регрессии выполняют следующие этапы:
-
спецификация
уравнения регрессии
и определение параметров регрессии;
-
определение
степени стохастической взаимосвязи
результативного признака и факторов,
проверка общего качества уравнения
регрессии; -
проверка
статистической значимости каждого
коэффициента уравнения регрессии и
определение их доверительных интервалов.
Спецификация
уравнения регрессии – это выбор вида
аналитической зависимости
.
В случае парной регрессии спецификация
осуществляется по графическому
изображению реальных статистических
данных в виде точек в декартовой системе
координат, которое называется
корреляционным
полем
(диаграммой рассеивания) (рисунок 1.1).
От правильно
выбранной спецификации модели зависит
величина случайных ошибок: они тем
меньше, чем в большей мере теоретические
значения результативного признака
подходят к фактическим даннымy.
Парная регрессия
применяется, если имеется доминирующий
фактор, который и используется в качестве
объясняющей переменной х.
Простейшей является
линейная
взаимосвязь
между x
и y,
описываемая линейной функцией регрессии
вида
.
Для вычисления
коэффициентов a,
b
используется метод
наименьших квадратов
(МНК), который позволяет получить
такие оценки параметров а
и b,
при которых
сумма квадратов отклонений фактических
значений зависимой переменной у
от теоретических
минимальна, т. е.
Это означает, что
линейная регрессия на диаграмме
рассеивания будет проходить «достаточно
близко» к точкам (xi,
yi).
Теснота
связи изучаемых явлений оценивается
при использовании линейной регрессии
с помощью линейного
коэффициента корреляции
.
Линейный коэффициент
корреляции
принимает значение в пределах от (–1)
до 1, т. е. (–1) < rху
< 1. Чем ближе
к единице,
тем связь теснее.
Качественная
оценка тесноты связи величин x
и y
может быть выявлена на основе шкалы
Чеддока.
Линейный
коэффициент корреляции
характеризует
степень тесноты не всякой, а только
линейной зависимости. При нелинейной
зависимости между явлениями линейный
коэффициент корреляции теряет смысл,
и для измерения тесноты связи применяют
так называемый индекс
корреляции
.
Для оценки
качества подбора линейной регрессии
рассчитывается квадрат линейного
коэффициента корреляции, называемый
коэффициентом
детерминации
,
а для нелинейной регрессии – квадрат
индекса корреляции, называемыйиндексом
детерминации
.
Коэффициент
детерминации характеризует долю
дисперсии
результативного признакаy,
объясняемую регрессией, в общей дисперсии
результативного признака. Чем больше
доля объясненной вариации, тем меньше
роль прочих факторов и тем лучше уравнение
регрессии описывает исходные данные.
Чем ближеR2
к 1, тем лучше
модель описывает (аппроксимирует)
исходные данные, и, значит, ее можно
использовать для оценки качества
построенной модели.
Средняя ошибка
аппроксимации
– среднее
отклонение расчётных значений от
фактических. Построенное уравнение
регрессии считается хорошего качества,
если значение
не превышает
8–10 % [5, с.
107].
Средний коэффициент
эластичности
показывает,
на сколько процентов в среднем изменится
результат у
от своей
средней величины при изменении фактора
х на
1 % от своего среднего значения:
,
где
– первая
производная уравнения регрессии,
характеризующая соотношение приростов
результата у
и фактора х.
После того, как
найдено уравнение линейной регрессии,
проводится:
1) оценка
значимости уравнения в целом с помощью
F-критерия
Фишера;
2) оценка
значимости коэффициентов регрессии с
помощью t-критерия
Стьюдента.
F-критерий
Фишера дает
ответ на вопрос, при каких значениях R2
уравнение
регрессии следует считать статистически
незначимым, что делает необоснованным
его использование. Согласно F-критерию
Фишера, выдвигается «нулевая» гипотеза
Н0
о
статистической
незначимости уравнения регрессии (т.
е. о статистически незначимом отличии
величины F
от нуля).
Если расчетное значение F-критерия
превышает табличное
,
т. е.
,
то гипотеза
Н0
отклоняется
и принимается статистическая значимость
и надежность уравнения регрессии. Если
,
то гипотеза Н0
не отклоняется
и признается статистическая незначимость,
ненадежность уравнения регрессии.
Табличное значение
F-критерия
определяется
по таблицам F-критерия
Фишера при числе степеней свободы
m
(m
– число
параметров при переменных х),
(n
– число наблюдений) и заданному уровню
значимости α.
Уровнем значимости
α
в статистических гипотезах называется
вероятность отвергнуть верную гипотезу.
Уровень значимости α
обычно принимает значения 0,05 и 0,01, что
соответствует вероятности отвергнуть
верную гипотезу 5 и 1 %.
Возможна ситуация,
когда часть вычисленных коэффициентов
регрессии не обладает необходимой
степенью значимости, т. е. значения этих
коэффициентов будут меньше их стандартной
ошибки. В этом случае такие коэффициенты
должны быть исключены из уравнения
регрессии. Поэтому проверка адекватности
построенного уравнения регрессии,
наряду с проверкой значимости коэффициента
детерминации R2,
включает в
себя также и проверку значимости каждого
коэффициента регрессии.
Для оценки
статистической значимости коэффициентов
регрессии применяется t-критерий
Стьюдента,
согласно которому выдвигается «нулевая»
гипотеза Н0
о статистической
незначимости коэффициента уравнения
регрессии (т. е. о статистически
незначимом отличии a
и b
от нуля). Эта
гипотеза отвергается при выполнении
условия
,
при этом принимается статистическая
значимость и надежность проверяемого
коэффициента регрессии, т. е. считается,
что отличие рассматриваемого коэффициента
уравнения регрессии от нуля статистически
значимо. Табличное значениеt-критерия
определяется
по таблице t-критерия
Стьюдента по числу степеней свободы
и заданному уровню значимости α. Расчетные
значения-критерия
для каждого коэффициента регрессии
(-статистики
Стьюдента) представляют собой отношение
оценки коэффициента регрессии к его
стандартной ошибке.
Стандартные
ошибки коэффициентов
линейной регрессии позволяют получить
представление о точности полученных
оценок коэффициентов регрессии
и
,
о том, насколько далеко они могут
отклониться от истинных значений
коэффициентов.
Общая
дисперсия
результативного
признака у
отображает
влияние как основных, так и остаточных
факторов. Остаточная
дисперсия
результативного
признака у
отображает
влияние только остаточных факторов.
Рассчитанные
значения оценок коэффициентов регрессии
являются приближенными, полученными
на основе имеющихся выборочных данных.
Для оценки того, насколько точные
значения оценок коэффициентов могут
отличаться от рассчитанных, осуществляется
построение доверительных интервалов.
Доверительные интервалы определяют
пределы, в которых лежит точное значение
определяемого показателя с заданной
вероятностью
[1,
с. 131].
Доверительные
интервалы для оценок коэффициентов
линейной регрессии рассчитываются по
формулам:
,
,
где
,
– предельные ошибки, рассчитываемые
по формулам
,
.
В таблице 1.1
представлены формулы для вычисления
основных характеристик линейной и
различных нелинейных регрессий.
В
MS
Excel
для построения функции линейной регрессии
используются команда «Добавить линию
тренда» и инструмент анализа «Регрессия».
Таблица 1.1 – Основные
характеристики
линейной и различных нелинейных регрессий
|
Функция |
линейная |
логарифмическая |
степенная |
экспоненциальная |
|
Среднеквадратические |
|
|||
|
Линейный |
(–1) < rху< 1 |
– |
||
|
Индекс корреляции |
– |
|
||
|
Коэффициент детерминации |
|
– |
||
|
Индекс детерминации |
– |
|
||
|
Табличное |
|
|||
|
Расчетное |
|
|||
|
Средняя |
|
|||
|
Коэффициент |
|
|
|
|
|
Общая |
|
|||
|
Остаточная |
|
|||
|
Стандартная ошибка коэффициента |
|
|||
|
Стандартная ошибка коэффициента |
|
|||
|
Расчетные значения
|
a |
|
||
|
b |
|
|||
|
Табличное |
|
Для построения
функций линейной и нелинейной регрессий
используется команда «Добавить линию
тренда». На рабочий лист MS
Excel вводятся
исходные данные, после чего строится
точечная диаграмма, представляющая
собой поле
корреляции (диаграмму
рассеивания). Если щелкнуть правой
кнопкой мыши на любой точке данных и в
контекстном меню выбрать команду
«Добавить линию тренда…», то появится
диалоговое окно. В диалоговом окне на
вкладке «Тип» необходимо щелкнуть по
пиктограмме, например, «Линейная».
Далее необходимо
открыть вкладку «Параметры» и в области
«Название аппроксимирующей (сглаженной)
кривой» выбрать опцию «автоматическое:».
Следует убедиться, что опция «пересечение
кривой с осью Y в точке:» не отмечена.
Далее следует включить опции «показывать
уравнение на диаграмме» и «поместить
на диаграмму величину достоверности
аппроксимации (R^2)»
и щелкнуть на кнопке ОК. После этого
необходимо выделить текст с уравнением
регрессии и значением R2
и перетащить на свободное место диаграммы.
Построить линейное
уравнение регрессии и выполнить расчет
его характеристик можно с помощью режима
Регрессия
модуля Анализ
данных
надстройки «Пакет
анализа» процессора MS
Excel
следующим образом:
1) проверить доступ
к пакету анализа. В главном меню выбирается
Сервис/Надстройки
и устанавливается флажок Пакет
анализа;
2) в главном меню
выбрать Сервис/Анализ
данных/Регрессия;
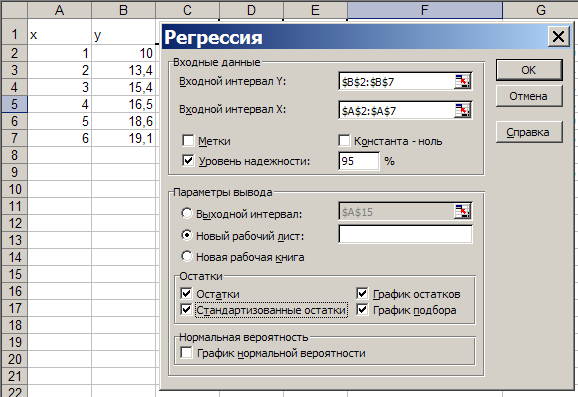
3) заполнить
диалоговое окно ввода данных и параметров
вывода (рисунок 1.2).
В
диалоговом окне режима Регрессия
(см. рисунок 1.2) задаются следующие
параметры.
Входные данные:
– Входной интервал
Y
– вводится
диапазон адресов ячеек, содержащих
значения уi
(ячейки
должны составлять один столбец);
– Входной интервал
X
– вводится диапазон адресов ячеек,
содержащих значения независимых
переменных. Значения каждой переменной
представляются одним столбцом. Количество
переменных – не более 16;
– Метки
– флажок включается, если первая строка
во входном диапазоне содержит заголовок.
В этом случае автоматически будут
созданы стандартные названия;
– константа-ноль
– при
включении этого параметра коэффициент
а =
0;
– уровень
надежности. Данный
флажок устанавливается в активное
состояние, если в поле, расположенное
напротив флажка, необходимо ввести
уровень надежности, отличный от уровня
95 %, применяемого по умолчанию. Принятый
уровень надежности используется для
проверки значимости коэффициента
детерминации R2
и
коэффициентов регрессии
.
Параметры
вывода:
– Выходной
интервал – при
включении активизируется поле, в которое
необходимо ввести адрес левой верхней
ячейки выходного диапазона, который
содержит ячейки с результатами вычислений
режима Регрессия;
– Новый рабочий
лист – при
включении этого параметра открывается
новый лист, в который, начиная с ячейки
А1, вставляются результаты работы режима
Регрессия;
– Новая рабочая
книга – при
включении этого параметра открывается
новая книга, на первом листе которой,
начиная с ячейки А1, вставляются результаты
работы режима Регрессия.
остатки:
– остатки
– при
включении вычисляется столбец, содержащий
невязки
,
;
– стандартизованные
остатки – при
включении вычисляется столбец, содержащий
стандартизованные остатки;
– график
остатков –
при включении выводятся точечные графики
невязки
,
в зависимости
от значений переменных
.
Количество графиков равно числуm
переменных
.
Далее рассмотрены
показатели, объединенные названием
Регрессионная
статистика (см.
ВЫВОД ИТОГОВ к примеру расчета) (рисунок
1.3).
Множественный
R
– коэффициент
корреляции
.
R-квадрат
– коэффициент
детерминации R2.
Нормированный
R-квадрат
– приведенный
коэффициент детерминации R2.
Стандартная
ошибка – оценка
s
для
среднеквадратического отклонения.
Наблюдения –
число
наблюдений п.
Далее рассмотрены
показатели,
объединенные названием Дисперсионный
анализ
(см.
ВЫВОД
ИТОГОВ к примеру расчета) (см. рисунок 1.3).
Столбец df
– это число
степеней свободы, которое для строкиРегрессия
определяется
числом параметров при
переменных х
в уравнении
регрессии и равно т.
Для строки
Остаток число
степеней свободы определяется числом
наблюдений n
и количеством переменных в уравнении
регрессии т + 1:
.
Для строкиИтого
число степеней
свободы определяется суммой чисел
и
.
Столбец SS
– сумма
квадратов отклонений. Для строки
Регрессия –
это сумма квадратов отклонений
теоретических данных от среднего. Для
строки Остаток
– это сумма
квадратов отклонений экспериментальных
данных от теоретических.
Для строки
Итого –
это сумма квадратов отклонений
экспериментальных данных от среднего.
Столбец MS
– дисперсии.
Для строки Регрессия
– факторная
дисперсия, для строки Остаток
– остаточная
дисперсия.
Столбец F –
расчетное значение F-критерия
Фишера
.
Столбец
Значимость
F
– значение
уровня значимости, соответствующее
вычисленному значению
.
Определяется
с помощью функции = FРАСП(Fp;
df(регрессия);
df(остаток)).
Если
значимость
F
меньше уровня значимости α (обычно α =
0,05), то построенная регрессия является
значимой.
Столбец Коэффициенты
– значения
коэффициентов a,
b.
Столбец Стандартная
ошибка – значения
.
t-статистика
– расчетные
значения t-критерия.
Р-значение
– значения
уровней значимости, соответствующие
вычисленным значениям tр.
Определяются с помощью функции =
СТЬЮДРАСП(tр;
n–m–1).
Если
Р-значение
меньше уровня значимости α,
то
принимается гипотеза о значимости
соответствующего коэффициента регрессии.
Нижние 95 % и
Верхние 95 %
– соответственно
нижние и верхние границы доверительных
интервалов для коэффициентов регрессии.
Далее рассмотрены
показатели, объединенные названием
Вывод
остатка
(см. ВЫВОД
ИТОГОВ к примеру расчета) (см. рисунок
1.3).
Столбец «Наблюдение»
содержит номера наблюдений.
Столбец «Предсказанное
y»
содержит значения
,
вычисленные по построенному уравнению
регрессии.
Столбец «Остатки»
содержит значения невязок
,
которые вычисляются как разность между
эмпирическимиу
и теоретическими
значениями результативного признакаy.
Пример –
Зависимость
доли расходов
у на товары
длительного пользования в общих расходах
семьи в процентах от среднемесячных
доходов х
семьи (млн р.)
представлена полем
корреляций
на рисунке 1.1, а [5, с. 85]. Построить
уравнения линейной и логарифмической
регрессий и выбрать регрессию, наилучшим
образом описывающую исходные данные.
На основе рисунка
1.1, а можно выдвинуть гипотезу о том, что
наилучшим образом описывать исходные
данные будет, скорее всего, логарифмическая
функция. Проверим это утверждение.
С помощью команды
«Добавить линию тренда» на
рисунке 1.1, б
построены линии линейного и логарифмического
трендов.
Параметры полученных уравнений регрессий
представлены в таблице 1.2.
По формулам,
представленным в таблице 1.1, рассчитаны
основные характеристики построенных
регрессий. Результаты расчетов
представлены таблицами 1.3 и 1.4.
Результаты
построения линейного уравнения регрессии
и расчета его характеристик с помощью
режима Регрессия
модуля Анализ
данных
надстройки «Пакет анализа» представлены
на рисунках 1.3 и 1.4.
Сравнение
результатов, полученных с помощью
расчетных формул, с результатами
применения инструментальных средств
Excel
показывает их близость, что свидетельствует
о правильном понимании методики
построения линейных регрессионных
уравнений и оценки их качества.
а) б)
а – пары чисел
,
которые представляют собой поле
корреляции; б – графики линейной (1) и
логарифмической (2) регрессий
Рисунок 1.1 – Графики поля корреляций,
линейной и логарифмической регрессий
Таблица 1.2 – Уравнения линейной и
логарифмической регрессий
|
Функция |
линейная |
логарифмическая |
|
a |
9,28 |
9,8759 |
|
b |
1,7771 |
5,1289 |
|
Уравнение |
|
|
Далее необходимо
выбрать регрессию, наилучшим образом
описывающую исходные данные.
Из расчетов видно,
что наименьшая остаточная дисперсия –
в логарифмической функции (0,0811).
Индекс корреляции
= 0,9916превышает значение
линейного коэффициента корреляции
= 0,9742.
При этом 97%
вариации результативного признака y
логарифмической регрессии объясняется
вариацией фактора х,
а 3 % приходится на долю прочих факторов.
Наименьшая средняя
ошибка аппроксимации ,
задающая среднее отклонение расчетных
значений от фактических, содержится в
логарифмической регрессии:
=1,3
(что не выходит за пределы интервала в
8–10 %).
Таким образом,
наилучшим образом описывать исходные
данные будет логарифмическая регрессия,
что подтверждается значениями
,
,
.

1.3 – Исходные данные к расчетам
|
Номер наблюдения |
х |
y |
|
xy |
|
линейная |
|
|
логарифми-ческая |
|
|
|
1 |
1 |
10 |
1 |
10 |
100 |
11,0571 |
1,1175 |
10,5710 |
9,8759 |
0,0154 |
1,2410 |
|
2 |
2 |
13,4 |
4 |
26,8 |
179,56 |
12,8342 |
0,3201 |
4,2224 |
13,4310 |
0,0010 |
0,2312 |
|
3 |
3 |
15,4 |
9 |
46,2 |
237,16 |
14,6113 |
0,6220 |
5,1214 |
15,5106 |
0,0122 |
0,7180 |
|
4 |
4 |
16,5 |
16 |
66 |
272,25 |
16,3884 |
0,0125 |
0,6764 |
16,9861 |
0,2363 |
2,9458 |
|
5 |
5 |
18,6 |
25 |
93 |
345,96 |
18,1655 |
0,1888 |
2,3360 |
18,1305 |
0,2204 |
2,5239 |
|
6 |
6 |
19,1 |
36 |
114,6 |
364,81 |
19,9426 |
0,7100 |
4,4115 |
19,0657 |
0,0012 |
0,1798 |
|
Среднее |
3,5 |
15,5 |
15,1667 |
59,4333 |
249,9567 |
– |
– |
4,5565 |
– |
– |
1,3066 |
Т
1.4 – Результаты расчетов
|
Функция |
линейная |
логарифмическая |
|
|
Среднеквадратическая |
|
||
|
Среднеквадратическая |
|
||
|
Линейный корреляции |
|
– |
|
|
Индекс корреляции |
– |
|
|
|
Коэффициент |
|
– |
|
|
Индекс детерминации |
– |
|
|
|
Табличное значение |
|
||
|
|
|||
|
Функция |
линейная |
логарифмическая |
|
|
Расчетное значение |
|
|
|
|
Средняя ошибка |
|
|
|
|
Коэффициент |
|
|
|
|
Общая дисперсия |
|
||
|
Остаточная признака у |
|
|
|
|
Стандартная коэффициента а |
|
|
|
|
Стандартная коэффициента b |
|
|
|
|
Расчетные
|
a |
|
|
|
b |
|
|
|
|
Табличное Стьюдента |
|
Рисунок 1.2 – Диалоговое окно режима
Регрессия
Рисунок 1.3 – Вывод итогов к расчету
















 Окончание таблицы 1.4
Окончание таблицы 1.4 

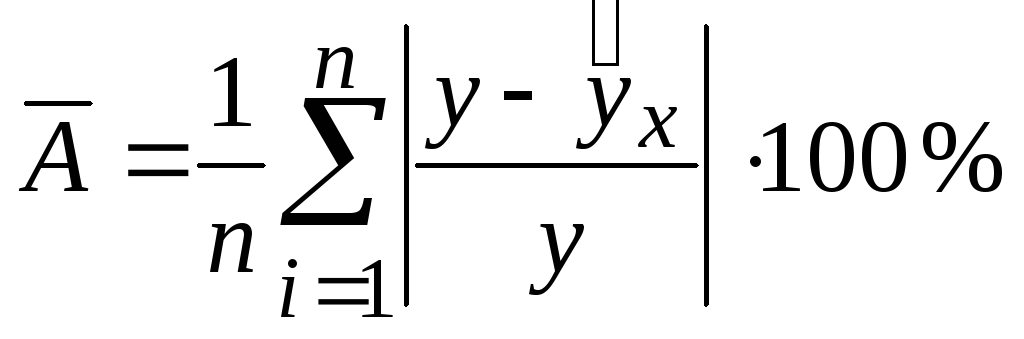 =4,5565
=4,5565 =0,0811
=0,0811