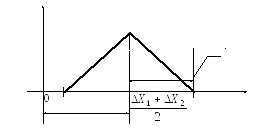Случайная ошибка измерения это

Случайные
погрешности вызываются большой
совокупностью причин, остающихся при
проведении измерений неизвестными.
Случайные погрешности неизбежны
и неустранимы.
Случайная погрешность, как и всякая
случайная величина, наиболее полно
характеризуется законом распределения.
В практике встречаются различные законы
распределения случайных погрешностей.
Наиболее часто приходиться иметь дело
с нормальным законом распределения, но
встречаются также: равномерный закон
распределения; треугольный закон (закон
Симпсона) и др. [6,
8].

Таким
образом, погрешность результата измерений
в общем случае включает систематическую
и случайную составляющие

(1.5)

(грубая
погрешность

входит в состав случайной погрешности).

В
выражении (1.5) перед составляющими
погрешности оставлен только знак “+”,
но и здесь,
и далее
следует иметь ввиду что

может иметь как знак “+”, так и знак
“-“, а если систематическая погрешность
задана в виде границ (как чаще всего и
бывает для неисключенных остатков
систематической погрешности), то перед
значением

подразумевается знак “”
(т.е.
).
Значение случайной погрешности всегда
указывается в виде границ (т.е.
).

В
соответствии с законами теории
вероятностей погрешность
,
записанная в форме (1.5), также становиться
случайной величиной, имеющей тот же
закон распределения, что и
.
Все сказанное в равной мере относится
и к результату измерения, если на
основании (1.2) и (1.5) его записать в виде

(1.6)

Из
теории вероятностей известно, что закон
распределения можно охарактеризовать
числовыми характеристиками, которые
являются уже неслучайными
величинами.
Эти характеристики и используются для
количественной оценки случайной
погрешности.

Основными
числовыми характеристиками законов
распределения погрешности
,
записанной в виде (1.5), являются

Математическое
ожидание —

, (1.7)

где

— плотность вероятности погрешности
;

и
дисперсия —

. (1.8)

Математическое
ожидание погрешности измерений,
вычисляемое в соответствии с (1.7) есть
неслучайная величина, она характеризует
систематическую составляющую погрешности
измерения. Т.е.
,
для чисто случайной погрешности (когда

)

.

Дисперсия
характеризует степень разброса отдельных
значений погрешности относительно

и может служить характеристикой точности
проведенных измерений, но имеет
размерность в единицах измеряемой
величины в
квадрате.
Поэтому в качестве числовой характеристики
случайной погрешности чаще используют
средне
квадратическое отклонение

(1.9)

Положительное
значение
,
вычисленное в соответствии с (1.9),
называется средним квадратическим
отклонением (СКО) случайной величины

,
а применительно к погрешностям измерений
ее следует называть средней
квадратической погрешностью (СКП)
результата измерений.

Графическое
представление нормального закона
распределения случайных погрешностей
(дифференциальная функция распределения

или плотность вероятностей) приведена
на рисунке 1.5, а аналитическое выражение
этого закона имеет вид:

(1.10)

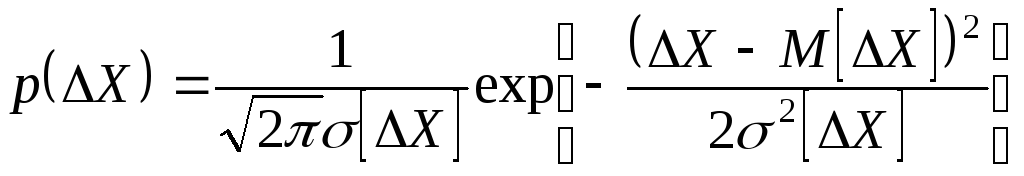
В
такой форме записи вид кривой распределения
будет изменяться в зависимости от
величины

(см. рис. 1.5), но если характеризовать
случайную погрешность безразмерным
нормированным числом

(нормировка относительно СКП), то получим
кривую
нормированного нормального распределения

, (1.11)

с аргументом

. (1.12)

Вид
кривой нормированного нормального
распределения чисто случайной погрешности
()
приведен на рисунке 1.6.

Графическое
представление дифференциальной функции
равномерного и треугольного законов
распределения приведены на рисунке 1.7
и рисунке 1.8. Аналитическая запись этих
законов распределения представлена
выражениями (1.13) и (1.14) соответственно.

Часто
по условиям измерительной задачи
требуется найти максимальную (предельную)
случайную погрешность, которая может
иметь место. Максимальная случайная
погрешность ()
связана с

и зависит
от закона распределения.
Так, например, для нормального закона
максимальная случайная погрешность
часто принимается равной (см. рис. 1.6):

. (1.15)

Для
других законов распределения соотношения
между

и

отличаются от (1.15). Так для равномерного
закона распределения
;
для треугольного

соответственно и т.д. [8].

Определить
числовые характеристики случайной
погрешности воспользовавшись (1.7) и
(1.8) можно только в том случае, если
известно аналитическое описание закона
распределения
.

Рисунок 1.5

Рисунок 1.6

(1.13)

Рисунок 1.7

(1.14)

Рисунок 1.8

На
практике числовые характеристики
случайной погрешности приходится
находить путем соответствующей
математической обработки результатов
измерений. Для нахождения числовых
характеристик случайной погрешности
измерения должны быть многократными
(статистическими), т.е. необходимо n
раз провести измерение одного и того
же значения измеряемой ФВ и получить
ряд результатов измерений в виде:
.

Если
все результаты полученного ряда
исправлены
(т.е. не содержат систематических
погрешностей), то пользуясь правилами
теории вероятностей можно найти
действительное значение измеряемой ФВ
и числовые характеристики случайной
погрешности. При этом следует учитывать
тот факт, что числовые характеристики

и

находятся всегда на основании ограниченного
ряда результатов измерений (на практике
n
всегда конечное число, т.е.
).
Поэтому в результате вычислений при
обработке результатов измерений находим
не теоретические значения

и
,
а их оценки.
Для того, чтобы подчеркнуть этот факт,
оценки, в отличии от теоретических
значений числовых характеристик,
обозначаются другими символами. Для
вычисления оценок в соответствии с ГОСТ
8.207-76 используются следующие формулы:

; (1.16)

. (1.17)

где
— среднее арифметическое значение
результатов серии из n
измерений (оценка математического
ожидания результата измерений), оценка
действительного
значения измеряемой ФВ;

— оценка средней квадратической
погрешности единичного измерения в
ряду равноточных измерений.

Средняя
квадратическая погрешность

и ее оценка
,
полученная путем обработки опытных
данных, является основным показателем
точности применительно к случайным
погрешностям измерений. Но кроме этого
показателя иногда (например, в
экспериментальной физике) применяются
и другие показатели точности: средняя
абсолютная погрешность (САП), мера
точности. Соотношения между этими
показателями для нормального распределения
следующие:

Вероятная
погрешность —
,

,

погрешность,
соответствующая доверительному интервалу
при
;

Средняя
арифметическая погрешность (САП) —
,

(теоретическое значение),

оценка САП по экспериментальным данным
для большого количества наблюдений,
или

оценка САП при малом количестве
экспериментальных данных;

Мера
точности —
,

.

Точность
оценок, полученных по формулам (1.16) и
(1.17) растет с увеличением n
и в пределе (при
)
они стремятся к теоретическим значениям
числовых характеристик.

Поскольку
при вычислении по формуле (1.16) получаем
оценку математического ожидания

и эту оценку принимаем
за результат измерения,
необходимо знать степень разброса
величины

относительно
.
Характеристикой меры разброса служит
оценка средней
квадратической погрешности среднего
арифметического
—
,
вычисляемая по формуле:

. (1.18)

Как
следует из (1.18) средняя квадратическая
погрешность среднего арифметического

в

раз меньше средней квадратической
погрешности единичного измерения
.

Полученные
в соответствии с (1.17) и (1.18) оценки СКП
имеют
размерность измеряемой ФВ,
т.е. выражены в абсолютной форме. Для
выражения этих оценок в относительной
форме следует поступать по общему
правилу (см.(1.3)), т.е.:

; .

и

могут быть выражены как безразмерным
числом, так и в процентах, что чаще всего
и бывает.

Полученные
по формулам (1.16 — 1.18) числовые характеристики
выражаются определенным числом и
называются точечными
оценками.

С
использование точечных оценок результат
измерения с учетом случайной погрешности
может быть представлен в виде :

. (1.19)

Такая
запись говорит о том, что действительное
значение измеряемой ФВ может находиться
в интервале значений

до
.
Вероятность этого события пока не
определена. Более того, результат
измерения может находиться и вне
интервала ограниченного значения

и
.
Вероятность этого события также пока
не определена. Более полную информацию
о действительном значении измеряемой
величины дает представление результата
измерения в виде доверительного
интервала
при заданной доверительной
вероятности

.

Для
результата измерения доверительным
называется интервал, который с заданной
вероятностью, называемой доверительной
вероятностью (),
включает действительное значение
измеряемой ФВ, т.е. это интервал значений
(,

),
для которого

(1.20)

Для
случайной погрешности доверительным
интервалом называется интервал значений
случайной погрешности, внутри которого
с заданной вероятностью находится
искомое значение погрешности
,
т.е.

. (1.21)

При
определении доверительных интервалов
доверительной вероятностью задаются
(если она не задана условиями измерительной
задачи). В зависимости от условий
измерений и конкретных требований

принимают, например, равной от 0.9 до
0.999. Чем больше принятое значение
,
тем более надежно будет оценен интервал,
но тем шире будут его границы, т.е.
надежность оценок (,

)
будет выше. Для технических измерений
при нормальном законе распределения в
большинстве случаев достаточной
считается величина
.

Следует
заметить, что точечная оценка
,
полученная на основании экспериментальных
данных при ограниченном числе измерений
n
остается случайной величиной (так,
например, если обработать другую выборку
результатов измерения той же ФВ с другим
числом измерений
,
то получим новую оценку
,
немного отличающуюся от
).
Следовательно может быть рассмотрена
задача о определении доверительного
интервала для оценки средней квадратической
погрешности
среднего арифметического

при некоторой доверительной вероятности.
Методику определения доверительного
интервала для
,
при необходимости, можно найти в [5, 6].

При
определении характеристик случайной
погрешности приходиться решать как
задачи определения доверительных границ
СКП при заданной доверительной
вероятности, так и обратную задачу,
определения доверительной вероятности

с которой СКП не выйдет за границы
заданного (симметричного или
несимметричного) интервала при заданном
законе распределения случайной
погрешности.

Границы
симметричного доверительного интервала
(),
за пределы которого с заданной
доверительной вероятностью не выходят
случайные погрешности результата
статистических измерений, определяют
в соответствии с выражением:

, (1.22)

где
— безразмерный коэффициент, определяемый
задаваемой доверительной вероятностью
()
и видом
закона распределения
случайных погрешностей.

При
несимметричном задании доверительного
интервала говорят о нижней —

и верхней —

границах интервала для случайной
погрешности результата измерений.
Выражение (1.21) в этом случае следует
записать в виде:

,

а
вероятность того, что случайная
погрешность окажется внутри указанного
интервала определяется в общем случае
в соответствии с выражением

(1.23)

Для
случайной погрешности, распределенной
по нормальному закону, выражение (1.23),
с использованием нормированной функции
нормального распределения (1.11), можно
записать в виде:

, (1.24)

где

— значение безразмерного коэффициента
для нижней границы доверительного
интервала;

— значение того же коэффициента для
верхней границы доверительного интервала.
Для симметричного интервала ()
(1.24) можно переписать в виде:

. (1.25)

Интеграл вида:

(1.26)

называется
нормированной функцией Лапласа или
интегралом вероятностей. Значения этого
интеграла или интеграла вида (1.25) для
различных значений аргумента приводятся
в справочных таблицах (см. таблицу 1
приложения в методических указаниях),
с использованием которых можно решить
прямую и обратную задачи определения
характеристик случайной погрешности,
распределенной
по нормальному закону.
При этом не следует забывать, что
пользуясь табличными значениями
интеграла вида (1.25) находим полную
вероятность
попадания в симметричный интервал с
границами
,
а пользуясь табличными значениями
интеграла вида (1.26) — только половину
полной вероятности для одной части
симметричного доверительного интервала.
При решении этих задач можно использовать
также таблицы значений нормированной
интегральной функции нормального
распределения вида:

(1.27)

С
использованием табличных значений
функции

(см. таблицу 2 приложения в методических
указаниях) выражение (1.24) для доверительной
вероятности нахождения случайной
погрешности внутри несимметричного
интервала от

до

записывается следующим образом:

(1.28)

Табличными
значениями нормированной функции
Лапласа удобно пользоваться для решения
задач при симметричном задании
доверительного интервала, а табличными
значениями нормированной интегральной
функции — при несимметричном.

При
определении числовых характеристик
случайной погрешности по результатам
эксперимента табличные значения
интегралов вида (1.25) и (1.28) следует
использовать в том случае, если количество
наблюдений в выборке достаточно велико
().
При малом n
точечные оценки случайной погрешности
сами становятся случайными величинами.
Учитывая это, выражение (1.12) для
нормированного отклонения результата
измерений от действительного значения
при

следует записать в виде:

. (1.29)

Использование
символа

в (1.29) подчеркивает тот факт, что
нормированное отклонение определено
с использованием оценок (
и
)
полученных при обработке выборки малого
объема.

Величина

,
таким образом, является некоторой
функцией числа наблюдений в выборке n.
Следовательно и границы доверительного
интервала определяемые в соответствии
с (1.22) будут зависеть не только от
доверительной вероятности, но и от числа
наблюдений n.
Закон распределения случайной величины

отличается от нормального и называется
распределением Стьюдента. Это различие
существенно при малых n,
а при

распределение Стьюдента полностью
совпадает с нормальным. Таким образом,
при обработке
результатов статистических измерений
при малом количестве наблюдений ()
доверительный интервал следует определять
с использованием распределения Стьюдента.
Чтобы подчеркнуть, что в этом случае
коэффициент t
в (1.22) зависит не только от доверительной
вероятности
,
но и от числа наблюдений n,
выражение (1.22) записывается в виде:

(1.30)

где
— коэффициент, определяемый по таблицам
распределения Стьюдента при выбранной
доверительной вероятности для конкретного
количества наблюдений n.

Распределение
Стьюдента также табулировано и значения
коэффициента

при выбранной доверительной вероятности
для каждого конкретного значения n
можно определить по таблице 4 (см.
приложение в методических указаниях).

Формулой
(1.22) для определения границ симметричного
доверительного интервала можно
пользоваться при любом законе распределения
случайной погрешности,
если имеются таблицы соответствующего
закона распределения
аналогичные таблицам 1 и 2 (см. приложение
в методических указаниях). К сожалению,
для других законов распределения (кроме
нормального) такие таблицы не получили
широкого применения. Но анализ интегральных
кривых различных законов распределения
обнаружил уникальное свойство
доверительного интервала, соответствующего
доверительной вероятности
.
Оказалось, что для широкого класса
симметричных распределений (нормального,
равномерного, треугольного, трапецеидального,
экспоненциального и даже ряда двухмодальных
законов) с погрешностью не более 10%
границы симметричного доверительного
интервала при

равны

[8]. Поэтому ГОСТ 11.001-73 предписывает при
отсутствии данных о виде закона
распределения
определять симметричный доверительный
интервал только при

пользуясь соотношением:

.

Таким
же образом следует определять
доверительный интервал для перечисленных
выше законов распределение при отсутствии
таблиц соответствующего распределения.

Результат измерений
с многократными наблюдениями, при
указании случайной погрешности в виде
симметричного доверительного интервала
должен быть представлен в виде:

(1.31)

Как
уже отмечалось, ряд экспериментальных
данных, полученных при многократном
измерении одного и того же значения
измеряемой ФВ, может содержать результаты,
имеющие в своем составе грубые погрешности.
Для того, чтобы эти данные не искажали
результат измерений, их следует исключить
до того, как будет определяться оценка

и доверительный интервал
(или

).
Эта процедура называется исключением
грубых погрешностей.
Статистический критерий обнаружения
грубых погрешностей разработан для
случая, когда группа обрабатываемых
данных подчиняется
нормальному закону распределения.
В этом случае теория вероятностей
позволяет при выбранной доверительной
вероятности

рассчитать теоретически допустимые
границы максимальных (по модулю)
нормированных отклонений для выборки
из n
наблюдений

(1.32)

Теоретически
допустимые границы

табулированы для различных значений n
при разных уровнях доверительной
вероятности

(или разных уровнях значимости g,
где
).
Табличные значения

приведены в таблице 3 приложения в
методических указаниях.

Применение
статистического критерия обнаружения
грубых погрешностей регламентировано
ГОСТ 11.002-73 и состоит в следующем. После
определения

и

для некоторого
,
который резко выделяется из общей
совокупности обрабатываемых результатов,
определяют величину нормированного
отклонения

. (1.33)

Задав
уровень доверительной вероятности

по таблице 3 (см. приложение в методических
указаниях) для числа n,
соответствующего обрабатываемой
выборке, находят допустимое нормированное
отклонение
.

Если

,
то результат

можно отбросить. В противном случае
результат должен быть оставлен.

Если
после исключения

вызывает сомнение какое-либо другое
данное, то указанный порядок
действий(определение
;

и
)
повторяют, но уже не учитывая исключенное
данное
.

Следует
подчеркнуть, что
если нет достаточных оснований считать
обрабатываемую совокупность результатов
нормально распределенной, описанный
критерий
обнаружения
грубых погрешностей применять
нельзя.

Если
о виде распределения опытных данных
заранее ничего определенного сказать
нельзя, то прежде чем исключать грубые
погрешности, определять

и

необходимо проверить гипотезу о
принадлежности группы экспериментальных
данных нормальному распределению.
Проверить гипотезу о том, что распределение
опытных данных не противоречит
теоретическому, можно по ряду критериев.
Но следует иметь ввиду, что при
n<10
проверить
гипотезу
о виде
распределения экспериментальных данных
невозможно.
При

проверка гипотезы затруднена, в этом
случае пользуются, как правило, составным
критерием [5]. При достаточно большом
числе данных ()
лучшим критерием проверки гипотезы о
виде распределения является критерий

(или критерий согласия К. Пирсона) [5, 6].

Критерий
Пирсона используется для проверки
согласия распределения предварительно
сгруппированных по интервалам опытных
данных теоретическому распределению.
Идея метода состоит в контроле отклонения
гистограммы опытных данных от гистограммы
с таким же числом интервалов, построенной
на основе теоретического распределения.
Мерой
расхождения
служит сумма квадратов разностей
экспериментального количества
результатов, попавших в соответствующий
интервал, и количества результатов,
которые
теоретически должны попадать
в этот интервал. Сумма квадратов разностей
()
не должна выходить за границы
(),определенные
по таблицам
-распределения
(таблица 5 см. приложение в методических
указаниях) при заданном уровне
доверительной вероятности (или уровне
значимости
).
Положительный ответ, полученный при
использовании критерия согласия
,
следует трактовать так, что
распределение опытных данных не
противоречит теоретическому
(на соответствие которому проверялось).
Но это не
означает что оно полностью соответствует
теоретическому.
При определенной доверительной
вероятности критерийможет
дать положительный результат и для
некоторого другого теоретического
закона распределения. Однозначным
ответом является лишь отрицательный
результат применения критерия
,
который трактуется так: распределение
опытных данных не
соответствует
теоретическому, на соответствие которому
проверялось. Таким образом при
использовании критерия согласия Пирсона
следует помнить следующее.

Критерий

позволяет проверить соответствие
опытных данных любому (выбранному
заранее по каким либо признакам)
теоретическому распределению, а не
только нормальному. Однако этот критерий
(как, впрочем, и другие критерии согласия)
не позволяет
однозначно установить вид распределения
этих данных.

Методика
использования критерия
с
необходимыми пояснениями приводится
на примере в п.1.3.4.

Соседние файлы в папке Метролоия

• #
• #

Случайная погрешность — это ошибка в измерениях, которая носит неконтролируемый характер и очень труднопредсказуема. Так происходит из-за того, что существует огромное количество параметров, находящихся вне контроля экспериментатора, которые влияют на итоговые показатели. Случайные погрешности с абсолютной точностью вычислить невозможно. Они вызваны не сразу очевидными источниками и требуют много времени на выяснение причины их возникновения.

Как определить наличие случайной погрешности

Непредсказуемые ошибки присутствует не во всех измерениях. Но для того чтобы полностью исключить ее возможное влияние на результаты измерений, необходимо повторить эту процедуру несколько раз. Если итог не меняется от эксперимента к эксперименту либо изменяется, но на определенное относительное число — величина этой случайной погрешности равна нулю, и о ней можно не думать. И, наоборот, если полученный результат измерений каждый раз другой (близкий к какому-то среднему значению, но отличный), и отличия носят неопределенный характер, следовательно, на него влияет непредсказуемая ошибка.

Пример возникновения

Случайная составляющая погрешности возникает вследствие действия различных факторов. Например, при измерении сопротивления проводника, необходимо собрать электрическую цепь, состоящую из вольтметра, амперметра и источника тока, которым служит выпрямитель, подключенный в осветительную сеть. Первым делом нужно измерить напряжение, записав показания с вольтметра. Затем перенести взгляд на амперметр, чтобы зафиксировать его данные о силе тока. После использовать формулу, где R = U / I.

Но может случиться так, что в момент снятия показаний с вольтметра в соседней комнате включили кондиционер. Это довольно мощный прибор. В результате этого напряжение сети немного уменьшилось. Если бы не пришлось отводить взгляд на амперметр, можно было заметить, что показания вольтметра изменились. Поэтому данные первого прибора уже не соответствуют записанным ранее значениям. Из-за непредсказуемого включения кондиционера в соседней комнате получается результат уже со случайной погрешностью. Сквозняки, трения в осях измерительных приборов — потенциальные источники ошибок в измерениях.

Как проявляется

Допустим, необходимо рассчитать сопротивление круглого проводника. Для этого нужно знать его длину и диаметр. Помимо этого, учитывается удельное сопротивление материала, из которого он изготовлен. При измерении длины проводника случайная погрешность себя проявлять не будет. Ведь этот параметр всегда один и тот же. Но вот при измерении диаметра штангенциркулем или микрометром окажется, что данные разняться. Так происходит потому, что идеально круглый проводник невозможно изготовить в принципе. Поэтому, если измерить диаметр в нескольких местах изделия, то он может оказаться разным вследствие действия непредсказуемых факторов в момент его изготовления. Это случайная погрешность.

Иногда она также называется статистической погрешностью, поскольку эту величину можно уменьшить, увеличив количество экспериментов при одинаковых условиях их проведения.

Природа возникновения

В отличие от систематической ошибки, простое усреднение нескольких итоговых показателей одной и той же величины компенсирует случайные погрешности результатов измерений. Природа их возникновения определяется очень редко, и поэтому никогда не фиксируется, как постоянная величина. Случайная погрешность — это отсутствие каких-либо природных закономерностей. Например, она не пропорциональна измеряемой величине или никогда не остается постоянной при проведении нескольких измерений.

Может существовать ряд возможных источников случайных ошибок в экспериментах, и он полностью зависит от типа эксперимента и используемых приборов.

Например, биолог, изучающий размножение конкретного штамма бактерии, может столкнуться с непредсказуемой ошибкой из-за небольшого изменения температуры или освещения в помещении. Однако когда эксперимент будет повторяться в течение определенного периода времени, он избавится от этих различий в результатах путем их усреднения.

Формула случайной погрешности

Допустим, нужно определить какую-то физическую величину x. Чтобы исключить случайную погрешность необходимо провести несколько измерений, итогом которых будет серия результатов N количества измерений — x_1, x_2,…, x_n.

Чтобы обработать эти данные следует:

1. За результат измерений х₀ принять среднее арифметическое х̅. Иными словами, х₀ = (x₁ + x₂ +… + x_n) / N_.
2. Найти стандартное отклонение. Обозначается оно греческой буквой σ и вычисляется следующим образом: σ = √((х₁ — х̅ )² + (х₂-х̅ )² + … + (х_n — х̅ )² / N — 1). Физический смысл σ состоит в том, что если провести еще одно измерение (N+1), то оно с вероятностью 997 шансов из 1000 ляжет в интервал х̅ -3σ < х_n+1 < с + 3σ.
3. Найти границу абсолютной погрешности среднего арифметического х̅. Находится она по следующей формуле: Δх = 3σ / √N.
4. Ответ: х = х̅ + (-Δх).

Относительная погрешность будет равна ε = Δх /х̅.

Пример вычисления

Формулы расчета случайной погрешности достаточно громоздкие, поэтому, чтобы не запутаться в вычислениях, лучше использовать табличный способ.

Пример:

При измерении длины l, были получены следующие значения: 250 см, 245 см, 262 см, 248 см, 260 см. Количество измерений N = 5.

N п/п	l, см	I ср. арифм., см	|l-l ср. арифм.|	(l-l ср. арифм.)2	σ, см	Δ l, см
1	250	253,0	3	9	7,55	10,13
2	245	8	64
3	262	9	81
4	248	5	25
5	260	7	49
	Σ = 1265			Σ = 228

Относительная погрешность равна ε = 10,13 см / 253,0 см = 0,0400 см.

Ответ: l = (253 + (-10)) см, ε = 4 %.

Практическая польза высокой точности измерений

Следует учитывать, что достоверность результатов тем выше, чем большее количество измерений проводится. Чтобы повысить точность в 10 раз, необходимо провести в 100 раз больше измерений. Это достаточно трудоемкое занятие. Однако оно может привести к очень важным результатам. Иногда приходится иметь дело со слабыми сигналами.

Например, в астрономических наблюдениях. Допустим, необходимо изучить звезду, блеск которой изменяется периодически. Но это небесное тело настолько далеко, что шум электронной аппаратуры или датчиков, принимающих излучения, может быть во много раз больше, чем сигнал, который необходимо обработать. Что же делать? Оказывается, если проводить миллионы измерений, то возможно среди этого шума выделить необходимый сигнал с очень большой достоверностью. Однако для этого потребуется совершать огромное количество измерений. Такая методика используется, чтобы различать слабые сигналы, которые едва заметны на фоне различных шумов.

Причина, по которой случайные погрешности могут быть решены путем усреднения, заключается в том, что они имеют нулевое ожидаемое значение. Они действительно непредсказуемы и разбросаны по среднему значению. Исходя из этого, среднее арифметическое ошибок ожидается равным нулю.

Случайная погрешность присутствуют в большинстве экспериментов. Поэтому исследователь должен быть подготовлен к ним. В отличие от систематических, случайные погрешности не предсказуемы. Это затрудняет их обнаружение, но от них легче избавиться, поскольку они являются статистическими и удаляются математическим методом, таким как усреднение.

Полученное из опыта значение измеряемой величины может
отличаться от ее действительного (истинного) значения.

Погрешность измерения – отклонение результата измерения от истинного (действительного) значения измеряемой
величины.

Это может быть обусловлено конструктивными недостатками прибора, несовершенством технологии его
изготовления, а также влиянием различных внешних факторов.

Таким образом, погрешности классифицируют:

1. По источнику возникновения (метод, инструмент, субъект)

   -Методические (зависят от метода измерения и способа включения приборов в электрическую цепь)

   -Инструментальные (зависят от средства измерения)

   -Субъективные (зависят от измерителя)

2. По условиям проведения измерений (температура, давление, влажность)

   -Основные (измерения проводятся в нормальных условиях — при нормальной температуре, давлении,
   влажности)

   -Дополнительные (условия отличны от нормальных)

3. По характеру проявления (систематические, случайные, промахи)

   Систематические – погрешности, остающиеся постоянными или закономерно изменяющимися при повторных
   измерениях тем же способом и средствами. Т.е. они заранее известны и их легко исключить.

   Случайные – погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же
   величины.  Обычно выявляются в результате многократных измерений (не менее 10).

   Промах – грубая ошибка, обусловленная неправильным отсчетом или расчетом, небрежностью измеряющего,
   поломки прибора, неправильно собранной схемы, невнимательности и т.д. Такие данные необходимо исключать.

4. По временному поведению измеряемой величины (статическая, динамическая)

   Статическая – когда измеряемая величина не меняется за время измерения

   Динамическая – когда прибор не успевает реагировать на изменения измеряемой величины.

5. По способу выражения измеряемой величины

   • абсолютная;

   • относительная;

   • приведенная.

     Абсолютной погрешностью
     DХ называется разность между измеренным и действительным значениями.

      – измеренное значение;

     – действительное значение измеряемой величины.

     Выражается
     DХ в единицах измеряемой величины.

     Относительная погрешность
      – отношение абсолютной погрешности к действительному значению измеряемой величины.

     Выражается в процентах или относительных единицах. Относительная погрешность характеризует
     точность измерений.

     Приведенная погрешность
     g_пр – отношение абсолютной погрешности к номинальному (нормированному) значению – верхнему пределу диапазона
     или поддиапазона измерения прибора.

     Пределом измерения прибора называется наибольшая величина, на которую рассчитан данный
     прибор.

     Прибор может иметь несколько пределов измерений (например, вольтметр).

     Чем меньшую погрешность дает прибор, тем он точнее.

   • Выражается в процентах.

     Максимальная приведенная погрешность определяет класс точности прибора.

   • Электроизмерительные приборы изготавливаются нескольких классов точности

0,01
0,02	0,2	1,5
0,05	0,5	2,5
0,1	1,0	4

Эти числа определяют максимальную погрешность прибора при полном отклонении указателя (стрелки).

Определяют также среднеквадратическую погрешность результата измерения по формуле:

Выражается  в единицах измеряемой величины.

За действительное значение измеряемой величины принимается обычно среднее арифметическое из ряда
измерений.

Хд = Х_СР =  (Х₁ + Х₂ +
Х₃ + … + Хn)/n,

где Х₁, Х₂,… , Хn – результаты измерений

       n – количество измерений