Если
повторять несколько раз измерения одной
и той же физической величины (например,
веса или, скажем, времени падения
грузика), стараясь при этом сохранить
все условия опыта постоянными, то, тем
не менее, полученные результаты будут
обязательно несколько отличаться друг
от друга (если, конечно, для результатов
каждого измерения записать достаточное
количество значащих цифр). Тому существует
множество разных причин, которые
практически невозможно учесть. Как
пример: неточности в фиксации времени
включения и выключения секундомера,
которые, кстати, важны для точного
определения интервалов времени не
только при физических измерениях, но и
во многих других случаях, в частности,
на спортивных соревнованиях. Как уже
указывалось ранее, соответствующие
ошибки называют случайными
ошибками.
Со
случайными изменениями некоторых
величин мы встречаемся и в повседневной
жизни, например, многократно отмечая
время, которое требуется, чтобы доехать
до нужного пункта. Случайные величины
важны для многих разделов естествознания,
например, для молекулярной физики при
измерениях скорости теплового движения
молекул газа или в ядерной физике при
изучении закономерностей радиоактивности.
Для количественного описания всех таких
случайно изменяющихся величин используют
хорошо разработанные методы теории
вероятностей. Эти методы позволяют
строго определить не только средние и
наиболее вероятные значения величин,
но и вероятности отклонений от этих
значений.
Среднее
значение любой случайной величины х,
а в данном случае результатов нескольких
последовательных её измерений (x1,
x2,
x3…xn),
определяют как среднее
арифметическое значение x
по формуле:

(5)
где
n
– число
измерений.
Далее
необходимо установить тот интервал
значений (—x
≤ x
≤
+x),
так называемый доверительный
интервал, в
пределах которого с обусловленной
доверительной
вероятностью
P(Δx)
(определяющей коэффициент надежности
полученных результатов измерения)
должны находиться значения x.
Доверительная
вероятность P(Δx)
в случае непрерывного распределения
значений x
определяется как:

(6)
где ρ(x)
– плотность вероятности реализации
значений x
в диапазоне от x
до x + dx,
причем знаменатель в этом выражении
обычно принимается равным 1 (условие
нормировки).
Еще
важнее, что эти две величины (доверительный
интервал и доверительная вероятность)
однозначно определяют отличие измеренного
значения x
от истинного значения той же физической
величины a.
Именно в их определении и состоит
основная задача математической обработки
результатов измерений.
Для
решения этой задачи необходимо, помимо
,
найтисреднюю
квадратичную ошибку измерений
в
данной серии опытов, которая определяется
по следующей формуле:

(7)
Вычисление
средней квадратичной, а не, как часто
делается, средней арифметической ошибки
измерений:

позволяет
более корректно и просто определить
затем доверительный интервал и
доверительную вероятность, как это
будет показано в дальнейшем.
При
большом числе измерений (n
> 30) можно воспользоваться и более
простым расчётом средней арифметической
ошибки, так как в этом случае: ()ср≈0,8
.
Таким
образом, при n
,
0
и случайную ошибку измерения можно в
принципе сделать столь угодно малой
величиной, что однако потребует бесконечно
долгого процесса измерения.
Определение
доверительного интервала для случайной
ошибки и, соответственно, отличие
среднего значения
от истинного значения этой величиныа
для заданного значения доверительной
вероятности P(x)
очевидно требует знания конкретного
вида функции распределения ρi(xi),
т.е. функции реализации определенных
значений xi.
Рассмотрим
вначале наиболее простой для математической
обработки, но сложный для практического
осуществления случай достаточно большого
числа измерений. Строго говоря, для
этого необходимо, чтобы n
и дискретная функция распределения
ρi(xi)
переходила в непрерывную функцию
плотности вероятности ρ(x).
Однако, как будет показано далее, для
этого достаточно n100
или даже n30.
При этом обычно реализуется функция
нормального распределения или функция
Гаусса, названная так в честь великого
немецкого математика, впервые установившего
вид этой функции:
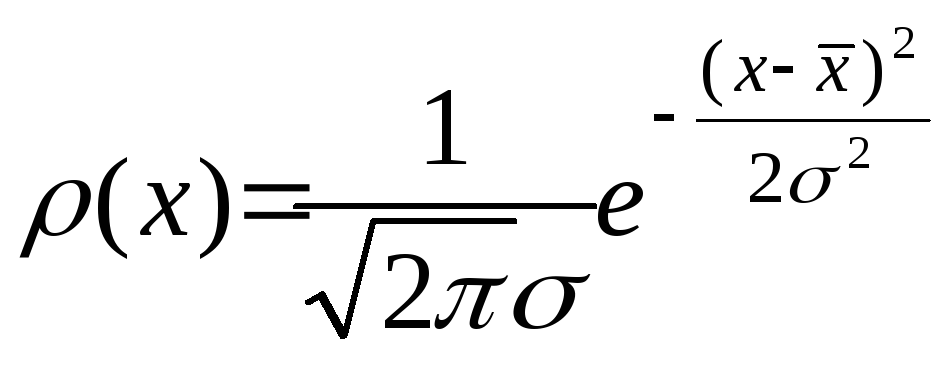
(9)
Здесь
использована новая величина
– среднестатистический предел средней
квадратичной ошибки одного измерения
при очень большом количестве измерений.
Квадрат этой величины 2,
однозначно определяющей ширину функции
распределения для ошибок измерения и
вообще распределения случайных величин,
называют нормой или дисперсией
распределения.
Для
обоснования применимости формулы Гаусса
необходимо выполнение трех положений,
а именно:
— ошибки
измерений могут принимать непрерывный
ряд значений,
— при
достаточно большом числе измерений
ошибки одинаковой абсолютной величины,
но разного знака, встречаются одинаково
часто
— большие
ошибки наблюдается реже, чем меньшие.
Тогда
измеренные значения величины x,
будут находиться внутри доверительного
интервала (-x
≤ x
≤
+x)
с доверительной вероятностью P(x),
определяемой по формуле:

(10)
При
этом, чем больше требуется доверительная
вероятность P(x)
и, соответственно, надежность того, что
измеренные значения x
отличаются
от истинного значения этой величины а
не более, чем на x,
тем шире по отношению к
становится доверительный интервал.
Так, если, например, требуется, чтобы
P(x)
= 0,7; 0,95; 0,98 или 0,999, то соответствующие
доверительные интервалы будут равны
;
2;
2,3
или 3,3.
В учебных лабораториях достаточно
выбирать доверительный интервал не
более 2σ, то есть брать доверительную
вероятность не более 0,95.
Для
выбора конкретного значения доверительной
вероятности P(x),
определяющей значения доверительного
интервала x,
необходимо понимать, насколько опасен
выход за пределы этого интервала,
вероятность которого, очевидно, равна
1 – P(x).
Такие задачи возникают на практике,
например, при отбраковке изделий,
выпускаемых в машиностроительной
промышленности, по их габаритам или
другим параметрам.
Реально
очень трудно осуществить (по причинам
большой длительности и малой продуктивности)
вышеуказанный идеализированный случай,
требующий, чтобы число измерений было,
по крайней мере, больше тридцати. Поэтому
необходимо рассмотреть реальный, но
более сложный для анализа случай
относительно небольшого числа измерений
(3
n
10).
Интуитивно понятно, что в этом случае
возникают повышенные требования к
доверительному интервалу (-x
;
+x)
при заданном значении P(x),
то есть он становится шире. Увеличение
числа измерений, наоборот, сужает этот
интервал.
На
опыте часто измеряют физические величины,
которые могут принимать лишь дискретные
значения, а число этих измерений конечно.
В ряде случаев вероятность реализации
определенных значений таких величин
хорошо описывается распределением
Пуассона (знаменитый французский
математик и физик).
Коэффициенты
Стьюдента .
Таблица №1.
|
n (число измерений) |
Доверительная вероятность |
||||||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
|
|
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21-24 25 26-27 28 29 30 40 60 120
|
0,16 0,14 0,14 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 |
0,33 0,29 0,28 0,27 0,27 0,27 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,25 0,25 0,25 |
0,51 0,45 0,42 0,41 0,41 0,40 0,40 0,40 0,40 0,40 0,40 0,40 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 |
0,73 0,62 0,58 0,57 0,56 0,55 0,55 0,54 0,54 0,54 0,54 0,54 0,54 0,54 0,54 0,54 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,52 |
1,00 0,82 0,77 0,74 0,73 0,72 0,71 0,71 0,70 0,70 0,70 0,70 0,69 0,69 0,69 0,69 0,69 0,69 0,69 0,69 0,69 0,68 0,68 0,68 0,68 0,68 0,68 0,68 0,67 |
1,38 1,06 0,98 0,94 0,92 0,90 0,90 0,90 0,88 0,88 0,87 0,87 0,87 0,87 0,87 0,86 0,86 0,86 0,86 0,86 0,86 0,86 0,86 0,86 0,85 0,85 0,85 0,85 0,84 |
2,0 1,3 1,3 1,2 1,2 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,0 1,0 1,0 |
3,1 1,9 1,6 1,5 1,5 1,4 1,4 1,4 1,4 1,4 1,4 1,4 1,4 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 |
6,3 2,9 2,4 2,1 2,0 1,9 1,9 1,9 1,8 1,8 1,8 1,8 1,8 1,8 1,8 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,6 |
12,7 4,3 3,2 2,8 2,6 2,4 2,4 2,3 2,3 2,2 2,2 2,2 2,2 2,1 2,1 2,1 2,1 2,1 2,1 2,1 2,1 2,1 2,0 2,0 2,0 2,0 2,0 2,0 2,0 |
31,8 7,0 4,5 3,7 3,4 3,1 3,0 2,9 2,8 2,8 2,7 2,7 2,7 2,6 2,6 2,6 2,6 2,6 2,5 2,5 2,5 2,5 2,5 2,5 2,5 2,4 2,4 2,4 2,3 |
63,7 9,9 5,8 4,6 4,0 3,7 3,5 3,4 3,3 3,2 3,1 3,1 3,0 3,0 2,9 2,9 2,9 2,9 2,9 2,8 2,8 2,8 2,8 2,8 2,8 2,7 2,7 2,6 2,6 |
636,6 31,6 12,9 8,6 6,9 6,0 5,4 5,0 4,8 4,6 4,5 4,3 4,2 4,1 4,0 4,0 4,0 3,9 3,9 3,8 3,7 3,7 3,7 3,7 3,7 3,6 3,5 3,4 3,3 |
Для
многих лабораторных работ, когда число
измерений не велико, распределение
погрешностей описывается еще более
сложными, специальными гамма–функциями
(распределение Стьюдента или “t”–
распределение. “Стьюдент” – это
псевдоним английского математика
Уильяма Сита Госсета.). Для такого
распределения с высокой точностью
вычислены и затабулированы так называемые
коэффициенты Стьюдента
(таблица №1). Они определяют отношение
доверительного интервала x
к средней квадратичной ошибке
для данной серии измерений и определенных
значенийn
и P(x),
то есть:
.
(11)
Из
таблицы 1 следует, что при доверительной
вероятности P(x)
0,7 доверительный интервал x
всегда несколько превышает значение
,
но дляP(x)=0,7
по мере увеличения числа измерений n
стремится
к этому значению, причем их различие
становится незначительным (меньше 10%)
уже при n
7. Аналогичное, но более медленное
уменьшение
наблюдается и для более высоких значений
P(x)=
0,95; 0,98; 0,999. Для этих значений P,
чтобы достаточно приблизиться к
предельным значениям
(2; 2,3; 3,3), соответствующим функции Гаусса,
необходимо значительно большее число
измерений (n
15,
20 и 40). В большинстве лабораторных работ
число измерений (3
n
10), а доверительная вероятность P(x)
принимается равной 0,95, так что
соответствующие коэффициенты Стьюдента
изменяются от 4,3 до 2,3. Если значения
доверительной вероятности не указаны,
то её обычно выбирают равной 0,7.
Таким
образом, окончательный результат
измерений с указанием доверительной
вероятности P
в лабораторных практикумах следует
представлять в виде:
,
(12)
где за
скобкой указывают единицу измерения
данной величины в общепринятой
международной системе единиц (СИ).
При
этом необходимо, чтобы среднее значение
и доверительный интервалx
были записаны в одних и тех же единицах
и с одинаковой точностью. Доверительный
интервал x
обычно
записывают в виде двух (реже одной)
значащих цифр, округляя последующие
цифры. Если число n
измерений невелико (менее 5 – 6), что
имеет место в большинстве лабораторных
работ, то достаточно округления
доверительного интервала до первой
значащей цифры, и только если она является
единицей – до двух значащих цифр. При
большем числе измерений (n
> 10) одна значащая цифра в доверительном
интервале оставляется только, когда
она больше трёх. При ещё большем числе
измерений (n
30 и более) оставляются две значащие
цифры. Предварительные вычисления
и
следует
проводить, разумеется, с несколько более
высокой точностью.
Таким
же образом округляются и приборные
абсолютная xпр
и относительная
пр
ошибки: с точностью до двух значащих
цифр, если первая значащая цифра равна
1, и до одной значащей цифры, если она
больше единицы.
При
округлении последняя из оставляемых
цифр в доверительном интервале x
всегда увеличивается на 1 (округление
с избытком).
Среднее
значение измеряемой величины
округляется до того же порядка величины,
что и значение x,
при этом
и x
должны быть
выражены в одинаковых единицах измерения.
Если в значении
первая отбрасываемая цифра, следующая
за последней оставляемой, больше или
равна 5 (но только, если за этой пятёркой
есть ещё цифры), то последняя из оставляемых
цифр увеличивается на 1 (округление с
избытком). Если же первая отбрасываемая
цифра меньше 5, то последняя из оставляемых
цифр не изменяется (округление с
недостатком).
Так,
если полученные при вычислении значения
∆x
составляют,
например, в одном случае: 1,255, а в другом
случае: 2,455, то, округляя их, в первом
случае следует записать: x
= 1,3 (округление с избытком до двух
значащих цифр, т.к. первая значащая цифра
— единица), а во втором – x
= 3
(округление с избытком до одной значащей
цифры, т.к. она – больше единицы). Если
при этом результат измерения составил,
скажем,
= 40,71 , то окончательно правильная запись:
в
первом случае x
= 40,7
1,3,
во
втором случае x
= 41
3.
Если
же в полученном результате измерения
первая
отбрасываемая цифра равна 5, а других
цифр после неё нет, то можно как оставить
предыдущую цифру неизменной, так и
увеличить её на 1. Часто для удобства
расчётов делают эту последнюю из
оставленных цифр чётной. Если, скажем,
получено значение тока 2,375 А, а погрешность
0,125 А, то результат удобнее записать
так:
I
= (2,38
0,13) A.
В
случае приборных погрешностей допустима
запись, когда в самой величине и
погрешности не совпадают разряды, в
которых стоят последние оставленные
цифры, например:
I
= (2,38 ± 0,005) А.
Если
случайная ошибка xсл
заметно превосходит приборную xnp
(приблизительно, раза в три и более), то
последней можно пренебречь, и, наоборот.
Если случайные и приборные ошибки
сравнимы, то они складываются по общему
закону сложения всех случайных величин,
а именно:
.
Рассмотрим
как пример расчёта случайных ошибок, а
также учета приборных ошибок и правильной
записи окончательного результата,
измерение величины тока I
через фотоэлемент, возникающего при
его освещении. Опыт повторялся пять раз
(n
= 5) при одинаковых условиях освещения
и были зафиксированы следующие результаты:
I1
= 0,292 мА; I2
= 0,284 мА; I3
= 0,305 мА; I4
= 0,293 мА; I5
= 0,290 мА. Измерения проводились цифровым
миллиамперметром, приборная ошибка
которого составляет единицу последнего
разряда цифрового табло индикатора
миллиамперметра: ∆Iпр
= 0,001 мА
Среднее
значение
= 0,2928 мА. Для доверительной вероятности
P
= 0,95 в таблице находится коэффициент
Стьюдента α = 2,8. Тогда доверительный
интервал: ∆I
= 2,8·
·=0,009594 мА.
Так
как ∆I
>> ∆Iпр,
то окончательный результат с учётом
округления: I
= 0,293±0,010 мА.
Всё
вышесказанное справедливо, прежде
всего, для прямых измерений, когда на
опыте непосредственно измеряется
интересующая нас физическая величина.
При косвенных
измерениях,
когда эта величина определяется по
известной формуле, в которую входят
несколько других измеряемых на опыте
независимых величин, необходимо провести
дополнительный анализ общей ошибки
измерения. Если искомая величина y
= (x1,
x2….xk),
то есть является известной функцией
нескольких непосредственно измеряемых
величин xi,
то её среднее значение определяется,
как.
Если в данном опыте преобладают приборные
ошибки, то
оценку
абсолютной y
ошибки
измерения следует производить по
формуле:
,
(13)
Если,
наоборот, в измерениях преобладают
случайные ошибки, то расчет общей ошибки
производят по формуле:

(14)
Вопрос
о том, какими формулами пользоваться,
решают при анализе результатов измерений.
Если отклонения большинства из результатов
измерений от среднего арифметического
значения не превышает абсолютную ошибку
используемых приборов, то расчет
производят по формуле (13), а в противоположном
случае, по формуле (14).
В
общем случае случайные xсл
и приборные ошибки xnp
складываются по общему закону сложения
всех случайных величин, а именно:
(15)
и расчёт
абсолютной ошибки ∆y
косвенных измерений производят по
формуле (14).
Поэтому,
если одна из этих ошибок в три и более
раз превышает другую ошибку, то последняя
из этих ошибок будет очень слабо влиять
на общую точность измерения. Исходя из
этих соображений, обычно и выбирается
необходимое число измерений n,
поскольку нет никакого смысла стремиться
получить случайную ошибку значительно
меньше приборной ошибки.
Наглядной
иллюстрацией систематических и случайных
ошибок могут служить результаты стрельбы
из различных видов оружия, в том числе
на спортивных соревнованиях. Так, если
имеется только систематическая ошибка
(сбит прицел, неправильное прицеливание
или расчеты), то все пули (снаряды, стрелы,
бомбы и т.д.) попадут в одно и то же место,
но смещенное от центра мишени или цели.
Наоборот, если существуют только
случайные ошибки, то будет значительный
разброс в местах попадания («плохая
кучность»), но усредненное отклонение
от центра мишени (или цели) будет
стремиться к нулю. Реально, конечно,
наблюдаются оба вида ошибок, но один из
них обычно существенно преобладает над
другим.
Разберём
пример нахождения плотности ρ материала
шара по измерениям его массы m
и объёма V
(объём шара находится через его диаметр
D:
V
= πD3/6):
ρ = 6m/πD3.
Если
масса шара была измерена на отъюстированных
рычажных весах с точностью 0,02 г и
составила m
= 11,20 г, то результат измерения запишется:
m
= 11,20 ± 0,02 г.
Диаметр
шара измерялся штангенциркулем, имеющем
погрешность ∆Dпр
= 0,05 мм. Десятикратное (n
= 10) повторение измерений диаметра даёт
среднее значение диаметра

13,615 мм.При
этом для случайных ошибок измерений
доверительный интервал ∆D
находится по формуле (11):
=

гдеn
= 10, и для доверительной вероятности P
= 0,95 по таблице №1 коэффициент Стьюдента
α = 2,3.
Произведённый
подсчёт показывает, что ∆D
= 0,1676 мм, то есть случайная ошибка более
чем в три раза превосходит приборную
ошибку ∆Dпр
= 0,05 мм, и последнюю можно не учитывать:
D
= 13,62 ± 0,17 мм.
Среднее
значение плотности находится из:
= 6m/π
=
8,480 г/см3.
А ошибка в определении плотности
находится по формуле (14):=
.
Подставляя
полученные ранее значения
,
,
,
∆m,
∆D,
находится ∆ρ = 0,1069 г/см3.
Округляя результаты, окончательный
результат записывается: ρ = 8,48 ± 0,11 г/см3.
При
сложении (вычитании) неточных значений
величин в окончательной записи полученной
суммы следует оставлять только те
разряды, которые имеются во всех
складываемых величинах, проводя
соответствующее округление. При умножении
(делении) неточных значений величин в
результате оставляется только то число
значащих цифр, которое имеется в
перемножаемой величине с наименьшим
их количеством.
Как
пример: нужно записать результат
вычислений с неточно полученными
величинами x
= 8,232 + 0,31π = 8,232 + 0,97 = 9,20.
Теория
вероятностей полезна и для правильного
построения
графиков на
основе полученных экспериментальных
данных. Недопустимо рисовать изломанную
кривую, точно проходящую через
экспериментальные точки: следует
провести такую плавную линию, чтобы
отклонение экспериментальных точек от
нее в разные стороны приблизительно
компенсировали друг друга. По методу
наименьших квадратов построение графика
экспериментальной зависимости y=(x)
следует проводить таким образом, чтобы
свести к минимуму сумму квадратичных
отклонений
экспериментальных точек yi
от
проводимой кривой f(xi),
где i
— номер
экспериментальной точки, n
– число
экспериментальных точек.
Для
построения графика кривой по
экспериментальным точкам вначале
подбирается функциональная зависимость
определённого вида (линейная: y=a+bx,
квадратичная: y=a+bx+cx2,
экспоненциальная: y
= a+bex
и т.д.),
которая предположительно наилучшим
образом соответствует экспериментальным
данным, и определяются значения её
параметров a,b,c.
При этих значениях функция S
должна быть минимальна, то есть её
частные производные по этим параметрам
должны быть равны нулю:.
Решая полученную систему уравнений,
сначала находят значения этих параметров,
а затем и значениеS.
Сравнивая значения S,
полученные таким образом для разного
вида функций f(x),
выбирают функцию, для которой S
будет
минимальна – этой функцией и
аппроксимируются полученные
экспериментальные данные.
Следует
отметить, что разработаны способы, с
помощью которых можно достаточно просто
оценить наиболее подходящую функцию y
= f(x)
для описания известных экспериментальных
данных. Кроме того, существует компьютерная
программа Grapher,
которая даёт возможность подбирать
необходимые функции с соответствующими
параметрами для приближения экспериментально
полученных точек xi
и yi.
Добавим, что удобно использовать для
построения графиков такие координаты,
при которых график функции представляет
собой прямую (эти координаты следует
выбирать на основании подобранной
функции y=f(x)).
Методы
теории вероятностей успешно используют
и для планирования различных экспериментов,
например по разработке технологии
синтеза многокомпонентных материалов
с оптимальными свойствами (электрическими,
оптическими, механическими и др.),
требующимися для их практических
применений.
Прогресс
физики и других разделов естествознания
во многом определяется точностью
экспериментов. В настоящее время
достигнута поразительная точность при
измерении ряда физических величин
(расстояние, время и др.). Так, с помощью
молекулярных генераторов и стандартов
частоты удается осуществить такие
молекулярные часы, что их ошибка
составляет всего одну секунду за 106
лет, т.е. относительная погрешность
равна 10-12%.
С
очень высокой точностью измерена и
такая важнейшая физическая величина
как скорость распространения света в
вакууме с = (299792458,0
1,2) м/с. Это позволяет производить очень
точные измерения больших расстояний:
до Луны, планет Солнечной системы и
других космических объектов.
На
смену общеизвестного эталона метра в
виде стержня, изготовленного из
платиноиридиевого сплава и хранящегося
в международной Палате мер и весов
вблизи Парижа, пришел «оптический
эталон». Он равен 1650763,73 длин волн
оранжевой линии излучения атомов
криптона, то есть на одном метре должно
укладываться ровно столько длин волн
этого излучения. Такой эталон примерно
в 100 раз точнее прежнего и может быть
легче воспроизведен в научных лабораториях.
При обычных измерениях, например в
физическом практикуме, конечно, не
удается достичь таких прецизионных
точностей измерений, которые во многом
определяются погрешностью используемых
приборов. Вместе с тем при работе в
практикуме нужно стремиться к уменьшению
ошибок измерения, правильно производить
их оценки и грамотно оформлять
промежуточные и окончательные результаты
измерений.
Свойства физического объекта (явления, процесса) определяются набором
количественных характеристик — физических величин.
Как правило, результат измерения представляет
собой число, задающее отношение измеряемой величины к некоторому эталону.
Сравнение с эталоном может быть как
прямым (проводится непосредственно
экспериментатором), так и косвенным (проводится с помощью некоторого
прибора, которому экспериментатор доверяет).
Полученные таким образом величины имеют размерность, определяемую выбором эталона.
Замечание. Результатом измерения может также служить количество отсчётов некоторого
события, логическое утверждение (да/нет) или даже качественная оценка
(сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем,
когда результат измерения может быть представлен в виде числа или набора чисел.
Взаимосвязь между различными физическими величинами может быть описана
физическими законами, представляющими собой идеализированную
модель действительности. Конечной целью любого физического
эксперимента (в том числе и учебного) является проверка адекватности или
уточнение параметров таких моделей.
1.1 Результат измерения
Рассмотрим простейший пример: измерение длины стержня
с помощью линейки. Линейка проградуирована производителем с помощью
некоторого эталона длины — таким образом, сравнивая длину
стержня с ценой деления линейки, мы выполняем косвенное сравнение с
общепринятым стандартным эталоном.
Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат
x=xизм. Можно ли утверждать, что xизм — это длина
стержня?
Во-первых, значение x не может быть задано точно, хотя бы
потому, что оно обязательно округлено до некоторой значащей
цифры: если линейка «обычная», то у неё
есть цена деления; а если линейка, к примеру, «лазерная»
— у неё высвечивается конечное число значащих цифр
на дисплее.
Во-вторых, мы никак не можем быть уверенны, что длина стержня на
самом деле такова хотя бы с точностью до ошибки округления. Действительно,
мы могли приложить линейку не вполне ровно; сама линейка могла быть
изготовлена не вполне точно; стержень может быть не идеально цилиндрическим
и т.п.
И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной
точности измерения, теряет смысл само понятие «длины стержня». Ведь
на масштабах атомов у стержня нет чётких границ, а значит говорить о его
геометрических размерах в таком случае крайне затруднительно!
Итак, из нашего примера видно, что никакое физическое измерение не может быть
произведено абсолютно точно, то есть
у любого измерения есть погрешность.
Замечание. Также используют эквивалентный термин ошибка измерения
(от англ. error). Подчеркнём, что смысл этого термина отличается от
общеупотребительного бытового: если физик говорит «в измерении есть ошибка»,
— это не означает, что оно неправильно и его надо переделать.
Имеется ввиду лишь, что это измерение неточно, то есть имеет
погрешность.
Количественно погрешность можно было бы определить как разность между
измеренным и «истинным» значением длины стержня:
δx=xизм-xист. Однако на практике такое определение
использовать нельзя: во-первых, из-за неизбежного наличия
погрешностей «истинное» значение измерить невозможно, и во-вторых, само
«истинное» значение может отличаться в разных измерениях (например, стержень
неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности.
Об измеренной величине также часто говорят как об оценке, подчеркивая,
что эта величина не точна и зависит не только от физических свойств
исследуемого объекта, но и от процедуры измерения.
Замечание.
Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3, но для более серьезного понимания следует обратиться к [5].
Для оценки значения физической величины корректно использовать
не просто некоторое фиксированное число xизм, а интервал (или
диапазон) значений, в пределах которого может лежать её
«истинное» значение. В простейшем случае этот интервал
может быть записан как
где δx — абсолютная величина погрешности.
Эта запись означает, что исследуемая величина лежит в интервале
x∈(xизм-δx;xизм+δx)
с некоторой достаточно большой долей вероятности (более подробно о
вероятностном содержании интервалов см. п. 2.2).
Для наглядной оценки точности измерения удобно также использовать
относительную величину погрешности:
Она показывает, насколько погрешность мала по сравнению с
самой измеряемой величиной (её также можно выразить в процентах:
ε=δxx⋅100%).
Пример. Штангенциркуль —
прибор для измерения длин с ценой деления 0,1мм. Пусть
диаметр некоторой проволоки равен 0,37 мм. Считая, что абсолютная
ошибка составляет половину цены деления прибора, результат измерения
можно будет записать как d=0,40±0,05мм (или
d=(40±5)⋅10-5м).
Относительная погрешность составляет ε≈13%, то
есть точность измерения весьма посредственная — поскольку
размер объекта близок к пределу точности прибора.
О необходимости оценки погрешностей.
Измерим длины двух стержней x1 и x2 и сравним результаты.
Можно ли сказать, что стержни одинаковы или различны?
Казалось бы,
достаточно проверить, справедливо ли x1=x2. Но никакие
два результата измерения не равны друг другу с абсолютной точностью! Таким
образом, без указания погрешности измерения ответ на этот вопрос дать
невозможно.
С другой стороны, если погрешность δx известна, то можно
утверждать, что если измеренные длины одинаковы
в пределах погрешности опыта, если |x2-x1|<δx
(и различны в противоположном случае).
Итак, без знания погрешностей невозможно сравнить между собой никакие
два измерения, и, следовательно, невозможно сделать никаких
значимых выводов по результатам эксперимента: ни о наличии зависимостей
между величинами, ни о практической применимости какой-либо теории,
и т. п. В связи с этим задача правильной оценки погрешностей является крайне
важной, поскольку существенное занижение или завышение значения погрешности
(по сравнению с реальной точностью измерений) ведёт к неправильным выводам.
В физическом эксперименте (в том числе лабораторном практикуме) оценка
погрешностей должна проводиться всегда
(даже когда составители задания забыли упомянуть об этом).
1.2 Многократные измерения
Проведём серию из n одинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений
Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?
Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.
В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. 2.
По набору результатов 𝐱 можно вычислить их среднее арифметическое:
| ⟨x⟩=x1+x2+…+xnn≡1n∑i=1nxi. | (1.1) |
Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.
Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как
Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:
| s=Δx12+Δx22+…+Δxn2n=1n∑i=1nΔxi2 | (1.2) |
или кратко
Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.
Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δxi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении (1.1)
почти все отклонения Δxi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:
Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.
Предельную величину среднеквадратичного отклонения при n→∞
обозначим как
Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.
Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы (1.3) использовать
исправленную формулу (подробнее см. п. 5.2):
sn-12=1n-1∑i=1nΔxi2,
(1.4)
где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.
Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.
Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу 2). Для таких величин
могут быть строго доказаны следующие свойства:
-
•
при многократном повторении эксперимента бо́льшая часть измерений
(∼68%) попадает в интервал x¯-σ<x<x¯+σ
(см. п. 2.2). -
•
выборочное среднее значение ⟨x⟩ оказывается с большей
вероятностью ближе к истинному значению x¯, чем каждое из измерений
{xi} в отдельности. При этом ошибка вычисления среднего
убывает пропорционально корню из числа опытов n
(см. п. 2.4).
Упражнение. Показать, что
s2=⟨x2⟩-⟨x⟩2.
(1.5)
то есть дисперсия равна разности среднего значения квадрата
⟨x2⟩=1n∑i=1nxi2
и квадрата среднего ⟨x⟩2=(1n∑i=1nxi)2.
1.3 Классификация погрешностей
Чтобы лучше разобраться в том, нужно ли многократно повторять измерения,
и в каком случае это позволит улучшить результаты опыта,
проанализируем источники и виды погрешностей.
В первую очередь, многократные измерения позволяют проверить
воспроизводимость результатов: повторные измерения в одинаковых
условиях, должны давать близкие результаты. В противном случае
исследование будет существенно затруднено, если вообще возможно.
Таким образом, многократные измерения необходимы для того,
чтобы убедиться как в надёжности методики, так и в существовании измеряемой
величины как таковой.
При любых измерениях возможны грубые ошибки — промахи
(англ. miss). Это «ошибки» в стандартном
понимании этого слова — возникающие по вине экспериментатора
или в силу других непредвиденных обстоятельств (например, из-за сбоя
аппаратуры). Промахов, конечно, нужно избегать, а результаты таких
измерений должны быть по возможности исключены из рассмотрения.
Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма
непрост. В литературе существуют статистические
критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем
пользоваться (по крайней мере, без серьезного понимания последствий
такого отбора). Отбрасывание аномальных данных может, во-первых, привести
к тенденциозному искажению результата исследований, а во-вторых, так
можно упустить открытие неизвестного эффекта. Поэтому при научных
исследованиях необходимо максимально тщательно проанализировать причину
каждого промаха, в частности, многократно повторив эксперимент. Лишь
только если факт и причина промаха установлены вполне достоверно,
соответствующий результат можно отбросить.
Замечание. Часто причины аномальных отклонений невозможно установить на этапе
обработки данных, поскольку часть информации о проведении измерений к этому моменту
утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего
процесса измерений в лабораторном журнале. Подробнее об этом
см. п. 4.1.1.
При многократном повторении измерении одной и той же физической величины
погрешности могут иметь систематический либо случайный
характер. Назовём погрешность систематической, если она повторяется
от опыта к опыту, сохраняя свой знак и величину, либо закономерно
меняется в процессе измерений. Случайные (или статистические)
погрешности меняются хаотично при повторении измерений как по величине,
так и по знаку, и в изменениях не прослеживается какой-либо закономерности.
Кроме того, удобно разделять погрешности по их происхождению. Можно
выделить
-
•
инструментальные (или приборные) погрешности,
связанные с несовершенством конструкции (неточности, допущенные при
изготовлении или вследствие старения), ошибками калибровки или ненормативными
условиями эксплуатации измерительных приборов; -
•
методические погрешности, связанные с несовершенством
теоретической модели явления (использование приближенных формул и
моделей явления) или с несовершенством методики измерения (например,
влиянием взаимодействия прибора и объекта измерения на результат измерения); -
•
естественные погрешности, связанные со случайным
характером
измеряемой физической величины — они являются не столько
«ошибками» измерения, сколько характеризуют
природу изучаемого объекта или явления.
Замечание. Разделение погрешностей на систематические и случайные
не является однозначным и зависит от постановки опыта. Например, производя
измерения не одним, а несколькими однотипными приборами, мы переводим
систематическую приборную ошибку, связанную с неточностью шкалы и
калибровки, в случайную. Разделение по происхождению также условно,
поскольку любой прибор подвержен воздействию «естественных»
случайных и систематических ошибок (шумы и наводки, тряска, атмосферные
условия и т. п.), а в основе работы прибора всегда лежит некоторое
физическое явление, описываемое не вполне совершенной теорией.
1.3.1 Случайные погрешности
Случайный характер присущ большому количеству различных физических
явлений, и в той или иной степени проявляется в работе всех без исключения
приборов. Случайные погрешности обнаруживаются просто при многократном
повторении опыта — в виде хаотичных изменений (флуктуаций)
значений {xi}.
Если случайные отклонения от среднего в большую или меньшую стороны
примерно равновероятны, можно рассчитывать, что при вычислении среднего
арифметического (1.1) эти отклонения скомпенсируются,
и погрешность результирующего значения ⟨x⟩ будем меньше,
чем погрешность отдельного измерения.
Случайные погрешности бывают связаны, например,
-
•
с особенностями используемых приборов: техническими
недостатками
(люфт в механических приспособлениях, сухое трение в креплении стрелки
прибора), с естественными (тепловой и дробовой шумы в электрических
цепях, тепловые флуктуации и колебания измерительных устройств из-за
хаотического движения молекул, космическое излучение) или техногенными
факторами (тряска, электромагнитные помехи и наводки); -
•
с особенностями и несовершенством методики измерения (ошибка
при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером); -
•
с несовершенством объекта измерений (неровная поверхность,
неоднородность состава); -
•
со случайным характером исследуемого явления (радиоактивный
распад, броуновское движение).
Остановимся несколько подробнее на двух последних случаях. Они отличаются
тем, что случайный разброс данных в них порождён непосредственно объектом
измерения. Если при этом приборные погрешности малы, то «ошибка»
эксперимента возникает лишь в тот момент, когда мы по своей
воле совершаем замену ряда измеренных значений на некоторое среднее
{xi}→⟨x⟩. Разброс данных при этом
характеризует не точность измерения, а сам исследуемый объект или
явление. Однако с математической точки зрения приборные и
«естественные»
погрешности неразличимы — глядя на одни только
экспериментальные данные невозможно выяснить, что именно явилось причиной
их флуктуаций: сам объект исследования или иные, внешние причины.
Таким образом, для исследования естественных случайных процессов необходимо
сперва отдельно исследовать и оценить случайные инструментальные погрешности
и убедиться, что они достаточно малы.
1.3.2 Систематические погрешности
Систематические погрешности, в отличие от случайных, невозможно обнаружить,
исключить или уменьшить просто многократным повторением измерений.
Они могут быть обусловлены, во-первых, неправильной работой приборов
(инструментальная погрешность), например, сдвигом нуля отсчёта
по шкале, деформацией шкалы, неправильной калибровкой, искажениями
из-за не нормативных условий эксплуатации, искажениями из-за износа
или деформации деталей прибора, изменением параметров прибора во времени
из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации
результатов (методическая погрешность), например, из-за использования
слишком идеализированной физической модели явления, которая не учитывает
некоторые значимые факторы (так, при взвешивании тел малой плотности
в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических
цепях может быть необходим учет неидеальности амперметров и вольтметров
и т. д.).
Систематические погрешности условно можно разделить на следующие категории.
-
1.
Известные погрешности, которые могут быть достаточно точно вычислены
или измерены. При необходимости они могут быть учтены непосредственно:
внесением поправок в расчётные формулы или в результаты измерений.
Если они малы, их можно отбросить, чтобы упростить вычисления. -
2.
Погрешности известной природы, конкретная величина которых неизвестна,
но максимальное значение вносимой ошибки может быть оценено теоретически
или экспериментально. Такие погрешности неизбежно присутствуют в любом
опыте, и задача экспериментатора — свести их к минимуму,
совершенствуя методики измерения и выбирая более совершенные приборы.Чтобы оценить величину систематических погрешностей опыта, необходимо
учесть паспортную точность приборов (производитель, как правило, гарантирует,
что погрешность прибора не превосходит некоторой величины), проанализировать
особенности методики измерения, и по возможности, провести контрольные
опыты. -
3.
Погрешности известной природы, оценка величины которых по каким-либо
причинам затруднена (например, сопротивление контактов при подключении
электронных приборов). Такие погрешности должны быть обязательно исключены
посредством модификации методики измерения или замены приборов. -
4.
Наконец, нельзя забывать о возможности существования ошибок, о
которых мы не подозреваем, но которые могут существенно искажать результаты
измерений. Такие погрешности самые опасные, а исключить их можно только
многократной независимой проверкой измерений, разными методами
и в разных условиях.
В учебном практикуме учёт систематических погрешностей ограничивается,
как правило, паспортными погрешностями приборов и теоретическими поправками
к упрощенной модели исследуемого явления.
Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.
Пример.
Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами:
•
Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях.
•
Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока.
В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.
Пример.
Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности:
1.
Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления.
2.
Систематическая погрешность, связанная с неправильной установкой нуля.
3.
Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).
Статья рассмотрит определение, причины, типы и способы учета ошибок измерения, а также приведет примеры для лучшего понимания.
О чем статья
Введение
В теории вероятности существует понятие ошибки измерения, которое играет важную роль в оценке и предсказании случайных событий. Ошибка измерения возникает, когда результаты измерений отличаются от истинных значений. В данной лекции мы рассмотрим определение ошибки измерения, причины ее возникновения, типы ошибок и способы учета и уменьшения ошибок измерения. Также мы рассмотрим примеры ошибок измерения и их влияние на результаты исследований. Понимание ошибок измерения поможет нам более точно и надежно оценивать вероятности и принимать решения на основе статистических данных.
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Определение ошибки измерения
Ошибкой измерения называется расхождение между полученным результатом измерения и истинным значением величины, которую требуется измерить. Она возникает из-за неполноты или неточности используемых методов и средств измерения.
Ошибки измерения могут быть вызваны различными факторами, такими как:
- Неточность измерительных приборов и средств.
- Неправильная калибровка или настройка приборов.
- Влияние окружающей среды на измеряемую величину.
- Недостаточная квалификация оператора, осуществляющего измерение.
Ошибки измерения могут быть как систематическими, так и случайными. Систематические ошибки возникают вследствие постоянного смещения результатов измерений в одну сторону, например, из-за неправильной калибровки прибора. Случайные ошибки, в свою очередь, являются непредсказуемыми и могут возникать из-за различных факторов, таких как шумы в измерительной системе или неправильное чтение показаний прибора.
Для учета и уменьшения ошибок измерения используются различные методы, такие как повторные измерения, усреднение результатов, использование более точных приборов и т.д. Также важно проводить калибровку и проверку приборов регулярно, чтобы минимизировать возможные систематические ошибки.
Причины ошибок измерения
Ошибки измерения могут возникать по разным причинам. Рассмотрим некоторые из них:
Систематические ошибки
Систематические ошибки возникают из-за неправильной калибровки или неисправности измерительных приборов. Эти ошибки имеют постоянное значение и могут приводить к смещению результатов измерений в одну сторону. Например, если весы не откалиброваны правильно, то все измерения будут иметь постоянное смещение в большую или меньшую сторону.
Случайные ошибки
Случайные ошибки возникают из-за непредсказуемых факторов, таких как внешние воздействия, шумы в измерительной системе или неправильное чтение показаний прибора. Эти ошибки имеют случайное значение и могут приводить к разбросу результатов измерений. Например, при измерении температуры в помещении могут возникать случайные изменения из-за колебаний внешней температуры или воздушных потоков.
Человеческий фактор
Человеческий фактор также может быть причиной ошибок измерения. Неправильное обращение с приборами, неправильное чтение показаний, неправильное выполнение измерений – все это может привести к ошибкам. Например, неправильное установление шкалы на измерительном приборе или неправильное чтение показаний на цифровом дисплее.
Важно учитывать все эти причины ошибок измерения и принимать меры для их учета и уменьшения. Это поможет получить более точные и надежные результаты измерений.
Типы ошибок измерения
Ошибки измерения могут быть различными и классифицируются на несколько типов:
Систематические ошибки
Систематические ошибки возникают из-за постоянных и повторяющихся причин и приводят к постоянному смещению результатов измерений относительно истинного значения. Эти ошибки могут быть вызваны неправильной калибровкой прибора, несоответствием шкалы измерения или неправильным условиям эксперимента. Систематические ошибки могут быть учтены и скорректированы, если известна их природа и величина.
Случайные ошибки
Случайные ошибки возникают из-за случайных факторов, которые не могут быть полностью контролируемыми или предсказуемыми. Они могут быть вызваны флуктуациями внешних условий, неправильным чтением показаний прибора или неправильным обработкой данных. Случайные ошибки могут быть уменьшены путем повторения измерений и использования статистических методов для оценки их влияния.
Грубые ошибки
Грубые ошибки возникают из-за серьезных и очевидных ошибок в процессе измерения. Они могут быть вызваны неправильной установкой прибора, неправильным выбором метода измерения или неправильным обращением с образцом. Грубые ошибки обычно очевидны и могут быть легко обнаружены и исправлены.
Важно учитывать все эти типы ошибок измерения и принимать меры для их учета и уменьшения. Это поможет получить более точные и надежные результаты измерений.
Способы учета и уменьшения ошибок измерения
Ошибки измерения могут быть неизбежными, но существуют способы учета и уменьшения их влияния на результаты измерений. Вот некоторые из них:
Калибровка и контрольные измерения
Калибровка – это процесс сопоставления измеряемой величины с известным эталоном. Путем проведения контрольных измерений с использованием эталонов можно установить и скорректировать систематические ошибки измерения.
Использование повторных измерений
Повторные измерения позволяют учесть случайные ошибки и уменьшить их влияние на результаты. Чем больше повторных измерений проводится, тем более точные результаты можно получить путем усреднения значений.
Использование статистических методов
Статистические методы позволяют анализировать и оценивать ошибки измерения. Например, можно использовать методы регрессионного анализа для определения зависимостей между измеряемыми величинами и их ошибками.
Проверка и обслуживание измерительного оборудования
Регулярная проверка и обслуживание измерительного оборудования помогают обнаружить и исправить возможные неисправности, которые могут привести к ошибкам измерения.
Обучение и квалификация персонала
Обучение и квалификация персонала, работающего с измерительным оборудованием, играют важную роль в учете и уменьшении ошибок измерения. Правильное обращение с оборудованием и соблюдение методик измерения помогают минимизировать возможные ошибки.
Все эти способы помогают учесть и уменьшить ошибки измерения, что в свою очередь позволяет получить более точные и надежные результаты измерений.
Примеры ошибок измерения
Систематическая ошибка
Систематическая ошибка возникает, когда измерения смещены относительно истинного значения вследствие постоянного фактора или неправильной калибровки прибора. Например, если прибор для измерения длины имеет неправильно установленную шкалу, то все измерения будут смещены на одну и ту же величину.
Случайная ошибка
Случайная ошибка возникает вследствие непредсказуемых факторов, таких как шумы, вибрации, температурные изменения и т.д. Эта ошибка не имеет постоянного характера и может меняться при каждом измерении. Например, при измерении температуры в помещении с непостоянной температурой воздуха, каждое измерение может давать разные результаты.
Погрешность округления
Погрешность округления возникает при округлении чисел до определенного количества знаков после запятой. Например, если при измерении длины округлить результат до двух знаков после запятой, то возможна погрешность, так как истинное значение может быть ближе к следующему числу.
Погрешность параллакса
Погрешность параллакса возникает при измерении с помощью приборов, где наблюдатель не находится в одной плоскости с измеряемым объектом. Например, при измерении длины с помощью линейки, если наблюдатель не смотрит перпендикулярно к линейке, то измерение может быть неточным.
Погрешность прибора
Погрешность прибора возникает из-за неточности самого измерительного прибора. Каждый прибор имеет свою погрешность, которая указывается в его технических характеристиках. Например, если прибор для измерения массы имеет погрешность ±0.1 г, то результат измерения будет иметь погрешность в этом диапазоне.
Это лишь некоторые примеры ошибок измерения, которые могут возникать в различных ситуациях. Важно помнить, что ошибки измерения неизбежны, но с помощью правильных методов и техник их можно учесть и уменьшить, чтобы получить более точные результаты.
Таблица сравнения типов ошибок измерения
| Тип ошибки | Описание | Причины | Способы учета и уменьшения |
|---|---|---|---|
| Систематическая ошибка | Ошибка, которая возникает при измерении и всегда приводит к одному и тому же отклонению от истинного значения | Неправильная калибровка прибора, неправильная техника измерения | Повторное калибрование прибора, использование более точных методов измерения |
| Случайная ошибка | Ошибка, которая возникает при измерении и может приводить к различным отклонениям от истинного значения | Внешние факторы, такие как шум, вибрации, неправильное чтение прибора | Повторное измерение, усреднение результатов, использование статистических методов для оценки погрешности |
| Грубая ошибка | Очевидная ошибка, которая сильно отклоняется от истинного значения и может быть вызвана человеческим фактором или технической неисправностью | Неправильная установка прибора, неправильное чтение, неправильная обработка данных | Проверка и повторное измерение, исправление ошибки, обучение и обучение персонала |
Заключение
Ошибки измерения являются неизбежной частью любого измерительного процесса. Они могут возникать по разным причинам, таким как неточность приборов, неправильная калибровка или неправильное использование. Важно учитывать и уменьшать ошибки измерения, чтобы получить более точные результаты. Существуют различные способы учета и уменьшения ошибок, такие как повторные измерения, использование более точных приборов или применение математических методов коррекции. Понимание и учет ошибок измерения является важным навыком для всех, кто работает с данными и проводит измерения.
19. Методы определения и учета погрешностей
Методы определения и учета погрешностей измерений используются для того, чтобы:
1) на основании результатов измерений получить настоящее (действительное) значение измеряемой величины;
2) определить точность полученных результатов, т. е. степень их соответствия настоящему (действительному) значению.
В процессе определения и учета погрешностей оцениваются:
1) математическое ожидание;
2) среднеквадратическое отклонение.
Точечная оценка параметра (математического ожидания или среднеквадратического отклонения) – это оценка параметра, которая может быть выражена одним числом. Точечная оценка является функцией от экспериментальных данных и, следовательно, сама должна быть случайной величиной, распределенной по закону, зависящему от закона распределения для значений исходной случайной величины Закон распределения значений точечной оценки будет зависеть также от оцениваемого параметра и от числа испытаний (экспериментов).
Точечная оценка бывает следующих видов:
1) несмещенная точечная оценка;
2) эффективная точечная оценка;
3) состоятельная точечная оценка.
Несмещенная точечная оценка – это оценка параметра погрешности, математическое ожидание которой равно этому параметру.
Эффективная точечная оценка – это точечная оценка. дисперсия которой меньше, чем дисперсия другой какой угодно оценки этого параметра.
Состоятельная точечная оценка – это оценка, которая при увеличении числа испытаний стремится к значению параметра, подвергающегося оценке.
Основные методы определения оценок:
1) метод максимального правдоподобия (метод Фишера);
2) метод наименьших квадратов.
1. Метод максимального правдоподобия основывается на идее, что сведения о действительном значении измеряемой величины и рассеивании результатов измерений, полученные путем многократных наблюдений, содержатся в ряде наблюдений.
Метод максимального правдоподобия состоит в поиске оценок, при которых функция правдоподобия проходит через свой максимум.
Оценки максимального правдоподобия – это оценки сред—неквадратического отклонения и оценки истинного значения.
Если случайные погрешности распределены по нормальному закону распределения, то оценка максимального правдоподобия для истинного значения представляет собой среднее арифметическое результатов наблюдений, а оценка дисперсии является средним арифметическим квадратов отклонений значений от математического ожидания.
Преимущества оценок максимального правдоподобия заключается в том, что данные оценки:
1) несмещенные асимптотически;
2) асимптотически эффективные;
3) асимптотически распределены по нормальному закону.
2. Метод наименьших квадратов состоит в том, что из определенного класса оценок берут ту оценку, у которой минимальная дисперсия (самую эффективную). Из всех линейных оценок действительного значения, где присутствуют некоторые постоянные, только среднее арифметическое сводит к наименьшему значению дисперсии. В связи с этим при условии распределения значений случайных погрешностей по нормальному закону распределения оценки, полученные с использованием метода наименьших квадратов, идентичны оценкам максимального правдоподобия. Оценка параметров с помощью интервалов проводится посредством нахождения доверительных интервалов, в пределах которых с заданными вероятностями располагаются действительные значения оцениваемых параметров.
Доверительная граница случайного отклонения – это число, представляющее собой длину доверительного интервала, разделенную пополам.
При достаточно большом количестве испытаний доверительный интервал существенно уменьшается. Если увеличивается число испытаний, то допустимо увеличить число доверительных интервалов.
Обнаружение грубых погрешностей
Грубые погрешности – это погрешности, намного превышающие предполагаемые в данных условиях проведения измерений систематические и случайные погрешности. Промахи и грубые погрешности могут появляться из—за грубых ошибок в процессе проведения измерения, технической неисправности средства измерения, неожиданного изменения внешних условий. Для того чтобы исключить грубые погрешности, рекомендуется до начала измерений приближенно определить значение измеряемой величины.
В случае, если при проведении измерений выясняется, что результат отдельного наблюдения сильно отличается от других полученных результатов, нужно обязательно установить причины такого отличия. Результаты, полученные с резким отличием, можно отбросить и повторно измерить данную величину. Однако в некоторых случаях отбрасывание таких результатов может вызвать ощутимое искажение рассеивания ряда измерений. В связи с этим рекомендуется не отбрасывать необдуманно отличающиеся результаты, а дополнять их результатами повторных измерений.
Если необходимо исключить грубые погрешности в процессе обработки полученных результатов, когда уже нельзя скорректировать условия проведения измерений и провести повторные измерения, то применяются статистические методы.
Общий метод проверки статистических гипотез позволяет выяснить, присутствует ли в данном результате измерений грубая погрешность.
Данный текст является ознакомительным фрагментом.
Читайте также
Организация технического учета электроэнергии
Организация технического учета электроэнергии
Вопрос. С какой целью устанавливают счетчики технического учета на электростанциях?Ответ. На всех электростанциях мощностью более 10 МВт устанавливают счетчики технического учета, чтобы обеспечивать возможность
Автоматизация контроля и учета электроэнергии
Автоматизация контроля и учета электроэнергии
Вопрос. В каких целях создаются автоматизированные системы контроля и учета электроэнергии и мощности (АСКУЭ)?Ответ. АСКУЭ создаются в целях:повышения точности измерений для учета электроэнергии и мощности при ее
14. Методы определения движения жидкости
14. Методы определения движения жидкости
Гидростатика изучает жидкость в ее равновесном состоянии.Кинематика жидкости изучает жидкость в движении, не рассматривая сил, порождавших или сопровождавших это движение.Гидродинамика также изучает движение жидкости, но в
14. Виды погрешностей
14. Виды погрешностей
Выделяют следующие виды погрешностей:1) абсолютная погрешность;2) относительна погрешность;3) приведенная погрешность;4) основная погрешность;5) дополнительная погрешность;6) систематическая погрешность;7) случайная
19. Методы определения и учета погрешностей
19. Методы определения и учета погрешностей
Методы определения и учета погрешностей измерений используются для того, чтобы:1) на основании результатов измерений получить настоящее (действительное) значение измеряемой величины;2) определить точность полученных
11. Методы определения показателей качества
11. Методы определения показателей качества
Показателями качества продукции являются числовые характеристики одного или многих свойств продукции, определяющих ее качество, и взятые в установленных условиях ее изготовления и эксплуатации.Выделяют следующие показатели
14. Виды погрешностей
14. Виды погрешностей
Выделяют следующие виды погрешностей:Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.Абсолютная погрешность меры –
44. Методы определения показателей качества
44. Методы определения показателей качества
Показателями качества продукции являются числовые характеристики одного или многих свойств продукции, определяющих ее качество, и взятые в установленных условиях ее изготовления и эксплуатации.Критерием разделения методов
ПРАВИЛА УЧЕТА ТЕПЛОВОЙ ЭНЕРГИИ И ТЕПЛОНОСИТЕЛЯ
ПРАВИЛА УЧЕТА ТЕПЛОВОЙ ЭНЕРГИИ И ТЕПЛОНОСИТЕЛЯ
МИНИСТЕРСТВО ЭНЕРГЕТИКИ РОССИЙСКОЙ ФЕДЕРАЦИИУТВЕРЖДЕНО Первый заместитель министра топлива и энергетики Российской Федерации В. Н. Костюнин 12 сентября 1995 г.СОГЛАСОВАНО Заместитель председателя Комитета Российской
14.1. Правила учета электрической энергии
14.1. Правила учета электрической энергии
Расчеты за потребляемую электроэнергию являются одной из основополагающих позиций договорных взаимоотношений между потребителем и энергоснабжающей организацией, учитывающих интересы обеих сторон.Требования к расчетным
14.2. Приборы учета электрической энергии
14.2. Приборы учета электрической энергии
В качестве расчетных и технических (контрольных) средств учета на предприятиях (организациях) используются электросчетчики одно-и трехфазного тока в основном двух типов: индукционные и электронные (1-, 2– и многотарифные),
19. Методы определения первичныхошибок
19. Методы определения первичныхошибок
Первичной ошибкой является неточность геометрической формы рабочих поверхностей узлов (звеньев). Подобными ошибками могут считаться отклонения разного рода: геометрические параметры, связанные с формой и поверхностью узлов, а
50. Причины начальных погрешностей
50. Причины начальных погрешностей
Начальные погрешности в измерение могут вноситься по следующим причинам.1.Удельный вес:1) степень однородности среды нарушена вследствие нахождения в ней примесей (в том числе и растворимых газов; такие жидкостные среды в гидравлике
16. Методы определения электрических свойств
16. Методы определения электрических свойств
Металлы с высокой электропроводностью (медь, алюминий) используются в электромашиностроении, для устройства линий электропередачи, а сплавы с высоким электросопротивлением – для ламп накаливания электронагревательных
18. Дилатометрия. Магнитные свойства металлов и сплавов. Методы определения
18. Дилатометрия. Магнитные свойства металлов и сплавов. Методы определения
Дилатометрия – раздел физики; основная задача: изучение влияния внешних условий (температуры, давления, электрического, магнитного полей, ионизирующих излучений) на размеры тел. Главный предмет
49. Химический состав, методы получения порошков, свойства и методы их контроля
49. Химический состав, методы получения порошков, свойства и методы их контроля
Порошковые материалы – материалы, получаемые в результате прессования металлических порошков в изделия необходимой формы и размеров и последующего спекания сформованных изделий в вакууме
