2. Пусть [math]X[/math]— ошибка измерения, [math]\sigma = 10[/math] – среднеквадратичное отклонение. Тогда вероятность того, что ошибка измерения не превзойдёт 2, равна
[math]p = P\left( {\left| X \right| < 2} \right) = P\left( {\left| {\frac{X}{\sigma }} \right| < \frac{2}{\sigma }} \right) = \Phi \left( {0.2} \right) — \Phi \left( { — 0.2} \right) = 2 \cdot \Phi \left( {0.2} \right) — 1 = 2 \cdot 0.57926 — 1 = 0.15852[/math]
Вероятность противоположного события равна [math]q = 1 — p = 0.84148[/math]
Следовательно, вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдёт по абсолютной величине 2, равна
[math]1 — q^3 = 0.404158[/math]
Отмечу, что здесь функция Лапласа [math]\Phi \left( x \right)[/math] отличается от функции, которую использовал Alexdemath
3. Пусть [math]T[/math] – время службы мотора. Далее есть два пути решения этой задачи.
а) Предположим, что эта случайная величина имеет показательный закон распределения (этот закон часто используют для величин такого типа). Тогда параметр этого закона равен [math]\lambda = 1/8[/math] и вероятность того, что данный мотор не прослужит 15 лет, равна
[math]P\left( {X < 15} \right) = \int\limits_0^{15} {\lambda \cdot e^{ — \lambda x} dx} = 1 — e^{ — 15\lambda } = 0.846645[/math]
б) Пусть закон распределения случайной величины [math]T[/math] неизвестен. Обозначим через [math]p\left( t \right)[/math] – плотность распределения этого закон. Тогда, используя приём из доказательства неравенства Чебышёва, получим
[math]P\left( {X < 15} \right) = 1 — P\left( {X > 15} \right) = 1 — \int\limits_{15}^\infty {p\left( t \right)dt} = 1 — \int\limits_{15}^\infty {\frac{t}{t}p\left( t \right)dt} \geqslant 1 — \frac{1}{{15}}\int\limits_0^\infty t p\left( t \right)dt = 1 — \frac{8}{{15}} = \frac{7}{{15}}[/math]
Скорее всего, именно это решение ожидается проверяющими.
Нормальным называют распределение вероятностей непрерывной случайной величины
, плотность которого имеет вид:
где
–
математическое ожидание,
–
среднее квадратическое отклонение
.
Вероятность того, что
примет
значение, принадлежащее интервалу
:
где
– функция Лапласа:
Вероятность того, что абсолютная
величина отклонения меньше положительного числа
:
В частности, при
справедливо
равенство:
Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:
, где
Правило трех сигм
Преобразуем формулу:
Положив
. В итоге получим
если
, и, следовательно,
, то
то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.
Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.
На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.
Смежные темы решебника:
- Таблица значений функции Лапласа
- Непрерывная случайная величина
- Показательный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Пример 2
Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.
а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.
б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?
в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину
:
В нашем
случае получаем:
б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:
Пусть событие
– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм
– ошибка не
превзошла 5 мм;
– ошибка не
превзошла 15 мм
в)
Для заданной нормальной величины получаем следующее правило трех сигм:
Ошибка высотометра будет лежать в интервале:
Функция плотности вероятностей:
График плотности распределения нормально распределенной случайной величины
Функция распределения:
График функции
распределения нормально распределенной случайной величины
Задача 1
Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?
Задача 2
Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?
Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).
Задача 3
Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.
Задача 5
Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.
Задача 6
Заданы
математическое ожидание ax=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.
Задача 7
Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см2.
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.
Задача 8
Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.
Задача 9
Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).
а) Написать
плотность распределения вероятностей и функцию распределения.
б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).
в) Определить
приближенно минимальное и максимальное значения случайной величины X.
г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.
a=5; σ=1.3;
α=4; β=6
Задача 10
Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σx=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.
Задача 11
Высота
стебля озимой пшеницы — случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.
Задача 12
Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.
а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.
б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?
в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.
Задача 13
Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?
Задача 15
Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.
Задача 16
В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).
Задача 17
Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:
а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;
б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.
Задача 18
Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?
Задача 19
Случайная
величина X~N(1,22). Найти P{2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 20
Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.
Задача 21
Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.
Задача 21
Найти
вероятность попадания снарядов в интервал (α1=10.7; α2=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.
Задача 22
Плотность
вероятности распределения случайной величины имеет вид
Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).
Задача 23
Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)
Задача 24
Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.
Задача 25
В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.
Задача 26
Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.
Условие
4. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением сигма =1 мм и математическим ожиданием а = 0. Найти вероятность того, что из двух независимых наблюдений ошибка хотя бы одного из них не превзойдет по абсолютной величине 1,28 мм.
Отв. 0,96.
математика ВУЗ
11305
Решение
★
Пусть случайная величина Х — ошибка измерения.
Так как вероятность отклонения нормально распределенной случайной величины Х от ее математического ожидания а по абсолютной величине меньше заданного положительного числа ε вычисляется по формуле:
P(|X-a| < ε) =2Ф(ε/σ)
и
по условию
σ=1
a=0
ε=1,28
ε/σ=1,28
Ф(1,28/1)=Ф(1,28)=0,3997 ( см. приложение),
то
вероятность ошибки в одном наблюдении
2Ф(ε/σ)=2*Ф(1,28)=2*0,3997=0,7994
p=0,7994
Найдем вероятность противоположного события:, что ошибка превзойдет 1,28 мм
q=1 — p =1 — 0,7994 = 0,2006
Вероятность того, что ошибка превзойдет 1,28 в двух испытаниях
q*q=q^2=0,2006^2≈0,04
Тогда вероятность того, что из двух независимых испытаний ошибка [b] хотя бы в одном из них [/b] не превзойдет 1,28
равна
1-q^2=1-0,2006^2≈1-0,04=0,96
О т в е т. 0,96
Написать комментарий
СВ Х подчинена
нормальному
закону
распределения,
если ее
плотность распределения вероятностей
имеет вид:

(5.14)
где
a ‑ математическое
ожидание,
‑среднее
квадратичное отклонение
Х.
Интегральная
функция нормального распределения
имеет вид
;
(5.15)
где

Лапласа, или интеграл вероятностей.
Основные
свойства
функции Лапласа:
-
(0)
= 0;
2)
(нечетная функция);
3) ()=0,5
Таблица значений
функции (х)
для
приведена в приложении, поскольку она
является нечетной, то для отрицательных
значенийх
пользуются теми же таблицами, что и для
положительных.
Вероятность
попадания Х в заданный интервал значений
:
,
(5.16)
Вероятность того,
что абсолютная величина отклонения
нормальной СВХ
от ее математического ожидания меньше
положительного числа ,
определяется выражением:
.
(5.17)
В частности, при
а=0,
P(Х
<)
=2().
Если
в равенстве 5.17.
взять
,
получимтак
называемое
«правило
трёх сигм»,
которое является одним из необходимых
условий
того, что СВ имеет нормальный закон
распределения. В самом деле,
т.е.
отклонение нормальной
СВ от своего математического ожидания
а
на
величину,
равную
является событием практически достоверным.
Асимметрия,
эксцесс, мода и медиана
нормального
распределения соответственно равны:
а
еk=0,
Mo=a,
Me=a,
где
a=M[X].
График плотности
вероятности нормального распределения
(рис.5.5) называют нормальной
кривой
(кривой Гаусса).
Пример 5.6.
Ошибка измерения длины платформы станции
метро подчинена нормальному закону.
Математическое ожидание этой ошибки
равно 5см, а среднее квадратичное
отклонение равно 10см. Найти вероятность
того, что измеряемое значение длины
платформы будет отклоняться от истинного
не более чем на 20см.
Решение задачи
сводится к определению вероятности
попадания СВ Х
(ошибка
измерения) с математическим ожиданием
а=5см
и средним квадратичным отклонением
=10см
в интервал значений (‑20, 20).
По формуле
вычисления вероятности попадания Х
в заданный интервал имеем:
P(‑20<Х<20)
=
=
.
Пример 5.7.
Доказать, что параметр а
нормальной плотности распределения СВ
Х является математическим ожиданием
Х.
Доказательство.
По определению:
.
Для нормального распределения получим:

=
==
+
=a
(так
как
=0,
а интеграл Пуассона:).
Задачи
Биномиальный
закон.
-
Вероятность
выигрыша по облигации займа за все
время его действия равна 0,1. Составить
закон распределения числа выигравших
облигаций среди приобретенных 19. Найти
математическое ожидание, дисперсию,
среднее квадратическое отклонение.
Ответ:
-
Партия из 10 изделий
проверяется на стандартность. Вероятность
того, что изделие стандартно, равна
0.8. Определить математическое ожидание
и дисперсию СВ Х = {число стандартных
изделий в партии}.
Ответ:
-
В большой партии
20% нестандартных деталей. Из них наудачу
отобраны 5 деталей. а) написать биномиальный
закон распределения дискретной СВ Х —
числа нестандартных деталей среди пяти
отобранных; б) построить многоугольник
распределения; в) найти математическое
ожидание и среднее квадратичное
отклонение.
|
Ответ: |
Х |
0 |
1 |
2 |
3 |
4 |
5 |
|
p |
0.328 |
0.41 |
0.205 |
0.051 |
0.0064 |
0.00032 |
M(X)
= 1;
-
Написать биномиальный
закон распределения дискретной СВ Х
‑ числа появлений “герба” при двух
бросках монеты. Построить функцию
распределения.
|
Ответ: |
Х |
0 |
1 |
2 |
|
p |
0,25 |
0,5 |
0,25 |
Гипергеометрическое
распределение
-
В партии из 10
деталей имеется 8 стандартных. Наугад
отобраны 2 детали. Составить закон
распределения числа стандартных деталей
среди отобранных. Определить вероятность
того, что число стандартных деталей
среди отобранных будет меньше двух.
|
Ответ: |
Х |
0 |
1 |
2 |
|
p |
|
|
|
; Р(Х<2)
=
.
-
В партии из 6
деталей имеется 4 стандартных. Наудачу
отобраны 3 детали. Составить закон
распределения СВ Х ‑ числа стандартных
деталей среди отобранных. Построить
функцию распределения. Найти M[X],
D[X], x.
|
Ответ: |
Х |
0 |
1 |
2 |
3 |
|
p |
0 |
0.2 |
0.6 |
0.2 |
|
|
M(X) |
-
Партия из 20 деталей
содержит 16 стандартных. Наугад отобраны
4 детали. Составить закон распределения
СВ Х = {число стандартных деталей среди
четырёх отобранных}. Определить
вероятность того, что среди отобранных
деталей число стандартных будет не
меньше двух.
|
Ответ: |
Х |
0 |
1 |
2 |
3 |
4 |
|
p |
0.0002 |
0.013 |
0.149 |
0.462 |
0.376 |
Р(2<Х<4)
= 0.987.
-
В партии из 10
деталей содержится 4 нестандартных.
Наугад отобраны 2 детали. Найти дисперсию
и среднее квадратичное отклонение СВ
Х={число
стандартных деталей среди отобранных}.
Ответ:
-
В партии из 10
деталей содержится 4 нестандартных.
Наугад отобраны 3 детали. Записать закон
распределения СВ Х={число
стандартных деталей среди отобранных}.
Определить вероятность того, что число
нестандартных деталей среди отобранных
будет не меньше двух.
|
Ответ: |
Х |
0 |
1 |
2 |
3 |
|
p |
|
|
|
|
p=1/3.
-
Н
а
складе магазина имеется 10 телевизоров,
среди которых 3 бракованных, что визуально
не определяется. Наугад берутся 4
телевизора и подключаются к сети. Найти
и построить (в виде многоугольника
распределения) ряд распределе-ния числа
телевизоров Х, которые будут работать.
Найти математическое ожидание, дис-персию
и среднее квадратичное отклонение СВХ.
Ответ:
M(X)
= 2.8;
Распределение
Пуассона
-
СВ Х представляет
число бракованных деталей из возвратной
выборки в 50 штук. Вероятность брака
одной детали p=0,06.
Найти математическое ожидание, дисперсию
и средне квадратичное отклонение числа
бракованных деталей в выборке.
Ответ:
-
Устройство состоит
из 1000 элементов, работающих независимо
один от другого. Вероятность отказа
любого элемента в течение времени Т
равна 0,002. Найти вероятность того, что
за время Т откажут : а) ровно три; б) менее
трех; в) более трех; г) хотя бы одно.
Ответ:
-
Найти среднее
число
— бракованных изделий в партии изделий,
если вероятность того, что в этой партии
содержится хотя бы одно бракованное
изделие, равна 0,95. Предполагается, что
число бракованных изделий распределено
по закону Пуассона.
Ответ:
Равномерное
распределение
-
Предполагая, что
индекс цен на продовольственные товары
равномерно распределен в пределах от
110 до 150%, найти вероятность того, что он
не превысит 135%, а также вычислить
характеристики его разброса.
Ответ:
-
Коммерческая
маржа Х посреднической фирмы равномерно
распределена с параметрами
=20
тыс. гривень
в месяц и
=3,464
тыс. гривень
в месяц. Найти вероятность того, что в
следующем месяце она превысит 25 тыс.
гривень.
Ответ:
-
Минутная стрелка
электрических часов передвигается
скачками поминутно. Вы бросили взгляд
на часы. Они показывают
минут. Тогда для вас истинное время в
данный момент будет случайной величиной.
Найти её функцию распределения, считая,
что время течёт равномерно.
Ответ:

-
Автобусы некоторого
маршрута идут строго по расписанию.
Интервал движения 5 мин. Найти вероятность
того, что пассажир, подошедший к
остановке, будет ожидать очередной
автобус менее 3 мин.
Ответ:
0,6.
Показательное
распределение
-
Регулярным
контролем состояния овощей, завезенных
на склад, определяется срок их годности.
В среднем он равен 125 дням. Описать этот
срок с помощью показательного закона
распределения и найти вероятность
того, что он превысит средний.
Ответ:
-
Плотность
показательного распределения имеет
вид:
;
. Найтипостоянную
С
Ответ:
-
Дана плотность
вероятности СВ:
.
Найти коэффициента
и вероятность того, что
.
Ответ:
а = 2; Р()=
0,75.
-
Время, необходимое
для устранения неисправностей в
телевизоре, есть СВ Т. Найти математическое
ожидание, дисперсию и среднее квадратичное
отклонение времени обслуживания, если
.
Ответ:
-
Найти математическое
ожидание, дисперсию, асимметрию и
эксцесс СВ Х,
подчиненной показательному распределению:
Ответ:
-
СВ Х
распределена по показательному закону,
заданному функцией распределения:
.
Найти вероятность того, что в результате
испытания Х попадет в интервал (2, 5).
Ответ:
0,251.
-
СВ Х
— продолжительность жизни мужчин в
некотором регионе – задана функцией
распределения
.
Найти вероятность того, что случайно
выбранный мужчина доживет до 60 лет.
Ответ:
0,091.
Нормальное
распределение СВ.
-
Текущая цена акции
моделируется нормальным законом
распределения с математ. ожиданием 15
ден. ед. и средним квадратическим
отклонением 0,2 ден. ед. Найти: 1 вероятность
того, что цена акции: а) не выше 15,3 ден.
ед.; б) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3
ден. ед. 2. С помощью правила
найти границы, в которых будет находиться
текущая цена акции.
Ответ:
1. а) 0,4332;
б) 0,0228;
в) 0,6246;
2.
.
-
Цена акции
распределена нормально. В течение
последнего года 20% рабочих дней она
была ниже 88 ден. ед., а 75% — выше 90 ден. ед.
Найти: а) математическое ожидание и
среднее квадратическое отклонение
цены ценной бумаги; б) вероятность того,
что в день покупки цена будет заключена
в пределах от 83 до 96 ден. ед.; в) с
надежностью 0,95 определить максимальное
отклонение цены от среднего (прогнозного)
значения по абсолютной величине.
Ответ: а)
М(х) = 98;
σ = 12;
б) 0,33;
в)
.
-
По многолетним
наблюдениям за балансовой прибылью
фирмы установлено, что эта прибыль
меняется в пределах от 10000 до 40000грив.
в месяц. Считая, что она распределена
нормально, определить параметры этого
распределения и найти вероятность
того, что балансовая прибыль в следующем
месяце составит 24000-28000 гривен. Указание.
Из неравенства
,
предварительно найти
Ответ:
-
Система, «следящая»
за процессом ценообразования, содержит
систематические и случайные ошибки.
Систематическая ошибка равна 0,5 цента
в сторону занижения. Случайные ошибки
подчиняются нормальному закону
распределения со средним квадратичным
отклонением =1цент.
Найти а) вероятность фиксации цены по
абсолютной величине 1,5 цента; б)
вероятность того, что фиксированная
цена не превзойдет истинной.
Ответ:
.
-
Производится
взвешивание некоторого вещества без
систематических ошибок. Случайные
ошибки взвешивания подчинены нормальному
закону со средним квадратичным
отклонением =20г.
Найти вероятность того, что взвешивание
будет произведено с ошибкой, не
превосходящей по абсолютной величине
10г.
Ответ:
-
Фирма изготавливает
железобетонные изделия, используя в
качестве основного сырья цемент. В
связи с неопределенностью спроса на
эти изделия потребность в цементе
меняется из месяца в месяц, причем в
среднем она составляет 2500 т/мес., а ее
разброс характеризуется среднеквадратичным
отклонением 600 т/мес. Считая распределение
потребности в цементе нормальным,
определить вероятность того, что в
следующем месяце она не выйдет за
пределы 2200-2700 т.
Ответ:
-
Деталь, изготовленная
автоматом, считается годной, если
отклонение ее контролируемого размера
от проектного не превышает 10 мм. Случайные
отклонения контролируемого размера
от проектного подчинены нормальному
закону со средним квадратичным
отклонением =5мм.
и математическим ожиданием а=0.
Сколько процентов годных деталей
изготавливает автомат?
Ответ:
,
т.е. автомат изготовил примерно 95%.
-
Нормально
распределенная СВ Х
задана плотностью вероятности
.
Найти моду и медиану.
Ответ:
-
СВ Х
распределена нормально с математическим
ожиданием а=10 и средним квадратичным
отклонением =5.
Найти интервал, симметричный относительно
математического ожидания, в который с
вероятностью 0,9973 попадет величина Х в
результате испытания.
Ответ:
.
Другие законы
распределения
-
СВ Х
задана функцией распределения Рэлея:
Найти плотность распределения
величиныХ.
Ответ:
-
Дана функция
распределения Рэлея:
Найти моду и медиану этого распределения.
Ответ:
-
Дана плотность
вероятности СВ Х:
.
Найти математическое ожидание.
Ответ:
-
Дана плотность
вероятности СВ:
.
Найти коэффициента
и моду.
Ответ:
а
= 0,25;
Соседние файлы в папке ФУБ 4 семестр ТВ
- #
- #
- #
- #
- #
- #
- #
- #
Некоторые законы распределения непрерывных случайных
величин
Многие
случайные величины, такие как ошибки при измерениях, величины износа деталей
некоторых механизмов, отклонения точки попадания от некоторого центра при
стрельбе, отклонения размеров от номинальных у животных, растений и т.п.,
подчиняются нормальному распределению. Нормальный закон распределения
вероятностей имеет очень важное значение и широкое распространение.
Широкое распространение нормального распределения объясняется тем,
что оно проявляется там, где случайная величина представлена суммой большого
числа независимых случайных величин (что чаще всего встречается на практике),
влияние каждой из которых на всю сумму не представляется существенным.
Нормальная (гауссовская) случайная величина является предельной
для многих случайных величин.
В теории надежности нормальное распределение применяется при
оценке надежности элементов, подверженных действию старения и изнашивания, а
также разрегулировки, т.е. при оценке постепенных отказов.
Нормальным называется распределение плотностей вероятностей
непрерывных случайных величин, которое имеет вид:
Функция
распределения нормального закона имеет вид:
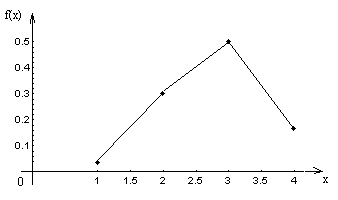
Кривая нормального распределения f(x) имеет
колоколообразную форму и называется нормальной кривой или кривой Гаусса.
При изменении параметра s изменяется
форма нормальной кривой. Изменение параметра а (математического
ожидания) влияет на положение (увеличение или уменьшение а сдвигает
график вправо или влево). Нормальная кривая в точках х = a-s и х = a+s имеет
перегиб. График функции f(x) симметричен относительно прямой х = а.
Нормальный закон распределения СВ с параметрами а=0 и s2=1
называется стандартным или нормированным, а соответствующая
нормальная кривая стандартной или нормированной
Математическое ожидание, дисперсия и среднее квадратическое
отклонение:
M(X) = a
D(X) = s2 s(X) = s
Для вычисления вероятности попадания случайной
величины в интервал (a;b)
можно воспользоваться функцией Лапласа:
P(a< Х <b) = Ф ,
где Ф(х)
=
нечетная, ее значения приведены в таблице)
Вероятность того, что непрерывная
случайная величина отклонится от своего среднего значения не более чем на
заданное положительное число d,
равна:
Р(÷Х-а÷< d) = 2Ф
Пример. Затаривание мешков с мукой производится без систематических
ошибок. Случайные ошибки подчинены нормальному закону со среднеквадратическим
отклонением s = 200г. Найти вероятность того, что
затаривание будет проведено с ошибкой, не превосходящей по абсолютной величине
100г.
В задаче рассматривается случайная величина-ошибка
взвешивания, то есть разность между случайным значением веса мешка муки и его
нормативным значением а — математическим ожиданием.
Правило трёх сигм (3s): P(ôX—aô< 3s) = 0.9973 » 1
c2 (хи –квадрат) распределение
Пусть Х1,Х2,Х3, .. Хr
распределены с параметрами М(Хi) = 0 и s(Xi) =1 (такие величины называются нормированными).
Тогда сумма квадратов этих величин распределена по закону c2
(хи-квадрат) с k степенями свободы:
c2
=
Параметр k называется числом степеней свободы и
только от k зависит распределение c2.
Плотность вероятности c2 распределения имеет вид:
f(x) =
где Г(k/2) –
гамма функция.
C
увеличением числа степеней свободы распределение медленно приближается к
нормальному. При k>30 кривая хи-квадрат сливается с кривой
нормального распределения.
Для хи-квадрат распределения:
М(c2) = k D(c2) = 2k s(c2)
=
Равномерное непрерывное распределение
Непрерывная случайная величина распределена равномерно в интервале [а;b], если все ее возможные значения сосредоточены на этом
интервале и если плотность распределения на этом интервале постоянна и равна
1/(b—a).
f(x) =
Равномерная случайная величина – это идеальная
случайная величина (скорость неизменна), встречается довольно редко.
Каждая случайная величина имеет единственную функцию
распределения, но не наоборот. Разные случайные величины могут иметь одну и ту
же функцию распределения.
M(Х) =
Вероятность попадания
СВ Х в интервал [a; b] : P(a < Х < b) =
Показательное распределение
Показательное
распределение играет важную роль в теории надежности систем, т.к. является
основной моделью так называемых внезапных (не связанных с процессом старения и
износа) отказов.
Непрерывная случайная величина распределена в интервале [0;¥] по
показательному закону, если плотность распределения f(х)
имеет вид:
где l=const
M(X) = s(X)= 1\l D(X) = 1\l2
Вероятность попадания
СВ Х в интервал [a; b] : P(a< X < b)= e —la – e —lb
Логарифмически нормальное распределение
Неотрицательная случайная величина Х называется
распределенной логарифмически нормально, если логарифм этой величины lnX
распределен нормально.
Функция распределения имеет вид:
F(x)=
Плотность вероятности:
f (x) =
Логарифмически нормальное распределение полностью определяется двумя
параметрами а и s, где s— среднее
квадратическое отклонение, а –медиана
Логнормальное распределение используется для
описания распределения доходов, банковских вкладов, долговечности изделий в
режиме износа и старения.
При малых s логарифмически
нормальное распределение близко к нормальному.
Гамма – распределение
Гамма — распределением случайной величины Х называется
распределение плотности вероятности:
f(x)=
Г(m)= 
Гамма – распределение описывает время, необходимое для появления
ровно m независимых испытаний, если эти события происходят с
постоянной интенсивностью l. Например, если
поставка какой-нибудь детали производится партиями объемом m
деталей каждая, а заявки на отдельные детали поступают независимо друг от друга
с постоянной интенсивностью l, то промежуток времени,
за который будет израсходована вся партия, является случайной величиной,
имеющей гамма-распределение.
При m=1 из гамма -распределения получается показательное
распределение. При m=2 гамма-распределение может быть описана нормальным
распределением.
Гамма-распределение позволяет описывать широкий класс случайных
величин.
Для гамма-распределения: M(X) =
Распределение Вейбулла-Гнеденко
Распределение Вейбулла-Гнеденко имеет следующую
плотность распределения:
f (x) = 
где b и а— параметры распределения
При b=1 распределение Вейбулла — Гнеденко совпадает с
показательным распределением. Распределение Вейбулла – Гнеденко используется в
теории надежности. Функция
распределения: F(x) =
Пример. Автобусы маршрута № 1 идут строго по расписанию.
Интервал движения пять минут. Найти вероятность того, что пассажир, подошедший
к остановке, будет ожидать очередной автобус этого маршрута не больше трех
минут. Найти среднее время ожидания автобуса.
Время ожидания автобуса на временном (в минутах) отрезке [0; 5] можно
рассматривать как случайную величину X, которая распределена равномерно:
b—a —
длина интервала, в котором заключены возможные значения Х. b=5,
a=2. P(0<X£ 3) =
Определим среднее время
ожидания автобуса по формуле:
М(Х)=
Пример. Перекресток оборудован автоматическим светофором, в
котором зеленый и красный свет горят соответственно в течение одной минуты и
0,5 минут. Автолюбитель подъезжает к перекрестку в случайный момент времени, не
связанный с работой светофора. Найти вероятность того, что он проедет
перекресток не останавливаясь.
Случайная величина Х, обозначающая момент проезда автомашины
через перекресток распределена равномерно в интервале ] 0; 1,5 [.
]0;1,5[ — период смены цветов в светофоре. Для того, чтобы
автолюбитель проехал перекресток не останавливаясь, нужно, чтобы момент проезда
перекрестка пришелся на интервал времени ] 0; 1
[.
Для случайной величины, распределенной равномерно в ]0;1,5[ вероятность
того, что она примет значение из ] 0; 1 [, равна 2/3, т.к.
P(0<x<1)=

Пример. Время
безотказной работы электродвигателя подчинено экспоненциальному
(показательному) закону распределения с параметром
l=2,5 × 10-5
Требуется определить среднюю наработку до первого отказа Т1
и вероятность безотказной работы Р(t) за время t = 1000 ч и t = Т1
Функцией надежности Р(t) = e—lt называют функцию определяющую вероятность
безотказной работы элемента за время длительностью t.
Вероятность безотказной работы элемента не зависит от
времени предшествующей работы до начала рассматриваемого интервала, а зависит
только от длительности интервала t (при заданной интенсивности отказов l).
Если Т – случайная величина времени работы элемента, то
Р(t) = P(T>t)=e—lt, тогда Р(1000) = е — 2,5×10 × 10
= е — 0,025 = 0,9753
Так как Т1 = m t = получим: Р(Т)= е —l×Т1
= е —l/l = е -1 = 0,3679 »0,37
Средняя наработка до первого отказа Т1 определяет время, в
течение которого вероятность безотказной работы элемента составляет всего лишь
0,37.
Т1 = =
= 40 000 часов
Пример . Длительность времени безотказной работы элемента
имеет показательное распределение, интегральная функция которого имеет вид:
F(t) = 1- e –0,02t
(t>0). Найти вероятность того, что за время длительностью t= 6
часов элемент откажет.
Так как интегральная функция F(t) = P(T<t) = 1 –
e —l t определяет вероятность отказа элемента за
время длительностью t, то подставив t = 6 в интегральную
функцию, получим вероятность отказа.
F(60)=
Литература
1.Е.С. Кочетков,
С.О. Смерчинская Теория вероятностей в задачах и упражнениях / М. ИНФРА-М
2005.

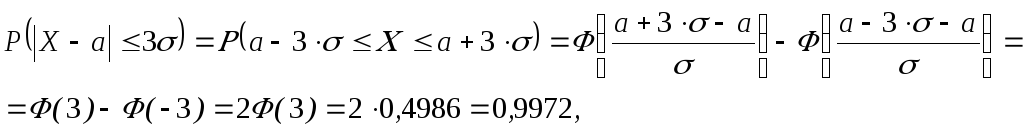


 а
а
 ;
; .
.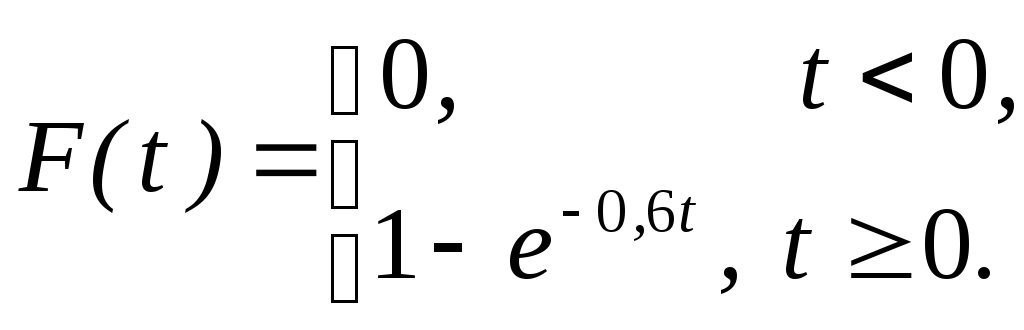 .
.
 .
.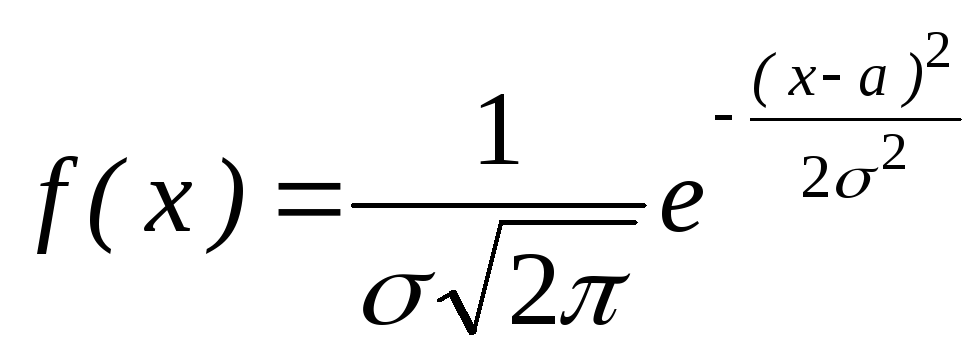 .
. Найти плотность распределения
Найти плотность распределения
 Найти моду и медиану этого распределения.
Найти моду и медиану этого распределения. .
. .
.








