При
выборе единиц наблюдения возможны
ошибки смещения, т.е. такие события,
появление которых не может быть точно
предсказуемым. Эти ошибки являются
объективными и закономерными. При
определении степени точности выборочного
исследования оценивается величина
ошибки, которая может произойти в
процессе выборки. Такие ошибки носят
название случайных ошибок
репрезентативности
(m),
На практике для определения средней
ошибки выборки при проведении
статистических исследований, используются
следующие Формулы:
для
расчета средней ошибки (mР)
относительной величины (Р):
,
где Ρ
— соответствующая относительная величина
(рассчитанная, например, в процентах
(%));
q
— 100 — Ρ;
n
— численность выборки.
96 Определение доверительных границ относительных показателей. Понятие о вероятности безошибочного прогноза.
Для
опред точности, с которой исследователь
желает получить результат, в статистике
исп-ся такое понятие, как вероятность
безошибочного прогноза,
кот является характеристикой надежности
результатов выборочных мед-биолог стат
исс-ий. Обычно, при проведении мед-биолог
стат исс-ий использ вероятность
безошибочного прогноза 95% или 99%. В
наиболее ответственных случаях, когда
необходимо сделать особенно важные
выводы в теоретическом или практическом
отношении, используют вероятность
безошибочного прогноза 99,7%
Определенной
степени вероятности безошибочного
прогноза соответствует определенная
величина предельной ошибки случайной
выборки (Δ)
Определяется эта величина по формуле:
Δ=t
* m
,
где
t
— доверительный коэффициент, который
при вероятности безошибочного
прогноза 95% равен 2. при вероятности
безошибочного прогноза 99% — 3,. и при
вероятности безошибочного прогноза
99,7% — 3,3.
Используя
предельную ошибку выборки (Δ),
можно определить доверительные
границы, в которых с опред вероятностью
безошиб прогноза заключено
действительное значение стат величины,
характериз
всю ген. совокупность (средней или
относительной).
Для опред доверительных
границ использ следующие Формулы:
,
где
— доверительные границы относ величины
в ген совокупности;
—
относ величина, полученная при проведении
исслед-я на выбороч совокупности;
t
— доверит коэффициент;
mP
— ошибка репрезентативности относ
величины.
При
малом числе наблюдений (n<30), для
вычисления доверительных границ
значение коэффициента t
находят по спец табл Стьюдента (Значения
t
расположены в таблице на пересечении
с избранной вероятностью безошибочного
прогноза и строки,
указывающей
на имеющееся число степеней свободы
(n`),
которое
равно n-1.
97 Оценка достоверности разности относительных величин. Критерий “t” (Стьюдента).
При
проведении медико-биологических
исследований на двух сравниваемых
совокупностях возникает необходимость
определить не только их различие, но и
его достоверность.
Для
оценки достоверности различия сравниваемых
относительных величин:
,
где,
P1
и P2
— относительные величины, полученные
при проведении выборочных исследований:
m1
и m2
— их ошибки репрезентативности; t
— коэффициент достоверности. Различие
достоверно при t>2.
что соответствует вероятности
безошибочного прогноза равной или более
95%. При величине коэффициента достоверности
t<2
степень вероятности безошибочного
прогноза менее 95%. При такой степени
вероятности мы не можем утверждать, что
полученная разность показателей
достоверна с достаточной степенью
вероятности. В этом случае необходимо
получить дополнительные данные, увеличив
число наблюдений. Если после увеличения
численности выборки, и. соответственно,
уменьшения
ошибки репрезентативности, различие
продолжает оставаться недостоверным,
можно считать доказанным, что между
сравниваемыми совокупностями не
обнаружено различий по изучаемому
признаку.
Соседние файлы в папке Шпора к госкзамену
- #
- #
In statistics, a relative standard error (RSE) is equal to the standard error of a survey estimate divided by the survey estimate and then multiplied by 100. The number is multiplied by 100 so it can be expressed as a percentage. The RSE does not necessarily represent any new information beyond the standard error, but it might be a superior method of presenting statistical confidence.
Relative Standard Error vs. Standard Error
Standard error measures how much a survey estimate is likely to deviate from the actual population. It is expressed as a number. By contrast, relative standard error (RSE) is the standard error expressed as a fraction of the estimate and is usually displayed as a percentage. Estimates with an RSE of 25% or greater are subject to high sampling error and should be used with caution.
Survey Estimate and Standard Error
Surveys and standard errors are crucial parts of probability theory and statistics. Statisticians use standard errors to construct confidence intervals from their surveyed data. The reliability of these estimates can also be assessed in terms of a confidence interval. Confidence intervals are important for determining the validity of empirical tests and research.
A confidence interval is a type of interval estimate, computed from the statistics of the observed data, that might contain the true value of an unknown population parameter. Confidence intervals represent the range in which the population value is likely to lie. They are constructed using the estimate of the population value and its associated standard error. For example, there is approximately a 95% chance (i.e. 19 chances in 20) that the population value lies within two standard errors of the estimates, so the 95% confidence interval is equal to the estimate plus or minus two standard errors.
In layman’s terms, the standard error of a data sample is a measurement of the likely difference between the sample and the entire population. For example, a study involving 10,000 cigarette-smoking adults may generate slightly different statistical results than if every possible cigarette-smoking adult was surveyed.
Smaller sample errors are indicative of more reliable results. The central limit theorem in inferential statistics suggests that large samples tend to have approximately normal distributions and low sample errors.
Standard Deviation and Standard Error
The standard deviation of a data set is used to express the concentration of survey results. Less variety in the data results in a lower standard deviation. More variety is likely to result in a higher standard deviation.
The standard error is sometimes confused with the standard deviation. The standard error actually refers to the standard deviation of the mean. Standard deviation refers to the variability inside any given sample, while a standard error is the variability of the sampling distribution itself.
Relative Standard Error
The standard error is an absolute gauge between the sample survey and the total population. The relative standard error shows if the standard error is large relative to the results; large relative standard errors suggest the results are not significant. The formula for relative standard error is:
Relative Standard Error
=
Standard Error
Estimate
×
1
0
0
where:
Standard Error
=
standard deviation of the mean sample
Estimate
=
mean of the sample
begin{aligned} &text{Relative Standard Error} = frac { text{Standard Error} }{ text{Estimate} } times 100 \ &textbf{where:} \ &text{Standard Error} = text{standard deviation of the mean sample} \ &text{Estimate} = text{mean of the sample} \ end{aligned}
Relative Standard Error=EstimateStandard Error×100where:Standard Error=standard deviation of the mean sampleEstimate=mean of the sample
Оценка достоверности результатов статистического исследования
В
практической и научно-практической
работе врачи обобщают результаты,
полученные, как правило, на выборочных
совокупностях. Для более
широкого распространения и применения
полученных при изучении
репрезентативной выборочной совокупности
данных и выводов надо уметь
по части явления судить о явлении и его
закономерностях в целом.
Учитывая,
как правило, что врачи проводят
исследования на выборочных совокупностях,
теория статистики позволяет с помощью
математического аппарата (формул)
переносить данные с выборочного
исследования на генеральную совокупность.
При этом врач должен уметь не только
пользоваться математическими формулами,
но и делать выводы, соответствующие
каждому способу оценки достоверности
полученных данных. С
этой целью врач должен знать способы
оценки достоверности.
В статистических
исследованиях применяются 2 вида
наблюдений — сплошное и выборочное.
Самые надежные результаты можно получить
при применении сплошного метода, т.е.
при изучении генеральной совокупности.
Между тем изучение
генеральной совокупности связано со
значительной трудоемкостью. Поэтому в
медико-биологических исследованиях,
как правило, проводятся выборочные
наблюдения. С тем, чтобы полученные при
изучении выборочной совокупности данные
можно было перенести на генеральную
совокупность, необходимо провести
оценку достоверности результатов
статистического исследования. Выборочная
совокупность может недостаточно полно
представлять генеральную совокупность,
поэтому выборочным наблюдениям всегда
сопутствуют ошибки
репрезентативности.
По размерам средней
ошибки ( m
) можно судить, насколько найденная
выборочная средняя величина отличается
от средней генеральной совокупности.
Малая ошибка указывает на близость этих
показателей, большая ошибка такой
уверенности не дает.
На величину средней
ошибки средней арифметической влияют
следующие два обстоятельства:
-
однородность
собранного материала
чем меньше разбросанность вариант
вокруг своей средней, тем меньше ошибка
репрезентативности. -
число наблюдений
средняя ошибка будет тем меньше, чем
больше число наблюдений.
Средняя ошибка
средней арифметической
вычисляется по формуле:
Средняя ошибка
для относительных величин вычисляется
по формуле:
, где
Р — величина
показателя в расчете на 100, 1000, 10 000 и т.д.
q
— разность между основанием, на которое
рассчитывается показатель, и его
конкретным числовым значением (100 — Р,
1000 — Р, 10 000 — Р и т.д.).
При n
< 30 в
знаменателе n
— 1.
Пример 8.
Средний рост
восьмилетних мальчиков составил — 125,5
см, среднее квадратическое отклонение
=±3,4
см , n=73
mм=
±
=±0,4
см
Пример 9.
Численность детей
в возрасте до года по данным детской
поликлиники составила 450 ,из них ни разу
не болели 100 детей. Необходимо определить
«Индекс здоровья» (процент ни разу
не болевших детей) и вычислить ошибку
для данного показателя.
Индекс здоровья
Оценка достоверности средних и относительных величин
При оценке
достоверности средних или относительных
величин руководствуются следующим
правилом:средняя
арифметическая или относительная
величина при числе наблюдений в выборочной
совокупности 30 и более должны превышать
свою ошибку не менее чем в 2 раза.
>
2 или
>
2
В рассматриваемых
примерах средняя арифметическая,
характеризующая рост восьмилетних
мальчиков и показатель „индекс
здоровья”
превышают свои ошибки соответственно:
раз,
раз, что соответствует высокой степени
их статистической достоверности с
вероятностью более чем 99,7 %.
Высказанное
положение вытекает из теории «вероятности»,
под которой понимается числовая мера
объективной возможности появления
случайного события.
Вероятность —
число, которое находится между 0 и 1, или
между 0% и 100%. Математиками определено,
что той или иной вероятности, выраженной
в процентах, соответствует определенное
значение критерия t
Стьюдента.
Так, например,
вероятности равной Р
= 68,3%
соответствует t=
1,0,
вероятности равной
Р = 95,5 %
соответствует
t
= 2,0
вероятности равной
Р = 99,7 % соответствует
t
= 3,0 .
В медико-биологических
исследованиях событие является
статистически достоверным, если
вероятность его появления соответствует
значению критерия t
Стьюдента, равное 2.
Средняя ошибка
позволяет не только оценить достоверность
относительного показателя или средней
величины, но и найти доверительные
границы средней величины или относительного
показателя в генеральной совокупности
М ген.=
М выб.
±
t
m
Р ген.
= Р выб
. ±
t
m
Как уже было
сказано, величина средней ошибки
указывает, насколько средняя величина
и относительный показатель выборочной
совокупности отличаются от соответствующих
величин в генеральной совокупности.
Величина t*m
является тем доверительным интервалом
по отношению к средней или относительной
величине, в котором с определенной
степенью вероятности можно ожидать
нахождение средней или относительной
величины в генеральной совокупности.
Пример 10.
М выб
.= 125,5 см;
m
= ±
0,4 см.
При 95% вероятности
t
=2, при 99,7 % — t
= 3 .
М ген.=
125,5 см ±
2
0,4 см = 124,7 — 126,3 см
М ген.=
125,5 см ±
3
0,4 см = 124,3 — 126,7 см.
Таким образом, с
вероятностью 95% можно ожидать, что
средняя будет находиться в пределах от
124,7 до 126,3 см и с вероятностью 99,7% — в
пределах от 124,3 до 126,7 см.
Понятно, что
действительное значение средней можно
получить только при обследовании всех
8-летних мальчиков, но как это очевидно
из полученных данных, подобное исследование
нецелесообразно, т.к. средняя арифметическая
статистически достоверна (Р >
99,7%), а доверительный интервал для средней
в генеральной совокупности является
весьма незначительным -t
m-
= 3
0,4 т.е. всего по 1,2 см от средней выборочной
совокупности в большую и меньшую
сторону.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статистике относительная стандартная ошибка (RSE) равна стандартной ошибке оценки обследования, деленной на оценку обследования, а затем умноженной на 100. Число умножается на 100, чтобы его можно было выразить в процентах. RSE не обязательно представляет какую-либо новую информацию, выходящую за рамки стандартной ошибки, но это может быть лучшим методом представления статистической достоверности.
Относительная стандартная ошибка против стандартной ошибки
Стандартная ошибка определяет, насколько оценка обследования может отличаться от фактической совокупности.Он выражается числом.Напротив, относительная стандартная ошибка (RSE) – это стандартная ошибка, выраженная как часть оценки и обычно отображается в процентах.Оценки с RSE 25% или более подвержены большой ошибке выборки и должны использоваться с осторожностью.
Оценка опроса и стандартная ошибка
Опросы и стандартные ошибки – важнейшие части теории вероятностей и статистики. Статистики используют стандартные ошибки для построения доверительных интервалов на основе своих обследованных данных. Достоверность этих оценок также можно оценить с помощью доверительного интервала. Доверительные интервалы важны для определения достоверности эмпирических тестов и исследований.
Доверительный интервал – это тип интервальной оценки, вычисляемой на основе статистики наблюдаемых данных, которая может содержать истинное значение неизвестного параметра совокупности.Доверительные интервалы представляют собой диапазон, в котором, вероятно, находится значение генеральной совокупности.Они построены с использованием оценки значения генеральной совокупности и связанной с ней стандартной ошибки.Например, вероятность того, что значение генеральной совокупности находится в пределах двух стандартных ошибок оценок, составляет приблизительно 95% (т.е. 19 из 20), поэтому 95% доверительный интервал равен оценке плюс или минус две стандартные ошибки.
С точки зрения непрофессионала, стандартная ошибка выборки данных – это измерение вероятной разницы между выборкой и всей совокупностью. Например, исследование с участием 10 000 взрослых, курящих сигареты, может дать несколько иные статистические результаты, чем при опросе всех возможных курящих сигареты взрослых.
Меньшие ошибки выборки указывают на более надежные результаты. Центральная предельная теорема в умозаключениях статистиков показывает, что большие выборки, как правило, имеют приблизительно нормальное распределение и низкие ошибки выборки.
Стандартное отклонение и стандартная ошибка
Стандартное отклонение набора данных используется для выражения концентрации результатов обследования. Меньшее разнообразие данных приводит к более низкому стандартному отклонению. Чем больше разнообразия, тем выше стандартное отклонение.
Стандартную ошибку иногда путают со стандартным отклонением. Стандартная ошибка фактически относится к стандартному отклонению среднего значения. Стандартное отклонение относится к изменчивости внутри любой данной выборки, тогда как стандартная ошибка – это изменчивость самого распределения выборки.
Относительная стандартная ошибка
Стандартная ошибка – это абсолютная мера между выборочным обследованием и генеральной совокупностью. Относительная стандартная ошибка показывает, велика ли стандартная ошибка по сравнению с результатами; большие относительные стандартные ошибки предполагают, что результаты незначительны. Формула относительной стандартной ошибки:
Стандартная ошибка
Стандартная ошибка — это стандартное отклонение выборочного распределения статистики. Этот термин также может использоваться для оценки (хорошего предположения) этого стандартного отклонения, взятого из выборки всей группы.
Среднее значение некоторой части группы (называемой выборкой) является обычным способом оценки среднего значения для всей группы. Часто бывает слишком сложно или стоит слишком много денег, чтобы измерить всю группу. Но если измерить другую выборку, то ее среднее значение будет немного отличаться от первой выборки. Стандартная ошибка среднего — это способ узнать, насколько близка средняя по выборке к средней по всей группе. Это способ узнать, насколько вы можете быть уверены в среднем значении по выборке.
В реальных измерениях истинное значение стандартного отклонения среднего для всей группы обычно неизвестно. Поэтому термин стандартная ошибка часто используется для обозначения близкого к истинному значению для всей группы. Чем больше измерений в выборке, тем ближе к истинному значению для всей группы.
Для значения, отобранного с несмещенной нормально распределенной ошибкой, выше показана доля выборок, которые будут находиться в пределах 0, 1, 2 и 3 стандартных отклонений выше и ниже фактического значения.
Как найти стандартную ошибку среднего значения
Один из способов найти стандартную ошибку среднего — это множество выборок. Сначала находят среднее значение для каждой выборки. Затем находят среднее и стандартное отклонение этих средних по выборкам. Стандартное отклонение для всех средних по выборке и есть стандартная ошибка среднего. Это может быть большой объем работы. Иногда иметь большое количество образцов слишком сложно или стоит слишком много денег.
Другой способ найти стандартную ошибку среднего — использовать уравнение, для которого нужна только одна выборка. Стандартная ошибка среднего обычно оценивается по стандартному отклонению для выборки из всей группы (стандартное отклонение выборки), деленному на квадратный корень из размера выборки.
S E x ¯ = s n {displaystyle SE_{bar {x}} ={frac {s}{sqrt {n}}}}
где
s — стандартное отклонение выборки (т.е. выборочная оценка стандартного отклонения популяции), и
n — количество измерений в выборке.
Насколько большой должна быть выборка, чтобы оценка стандартной ошибки среднего была близка к фактической стандартной ошибке среднего для всей группы? В выборке должно быть не менее шести измерений. Тогда стандартная ошибка среднего для выборки будет находиться в пределах 5% от стандартной ошибки среднего, если бы измерялась вся группа.
Исправления для некоторых случаев
Существует еще одно уравнение, которое можно использовать, если количество измерений составляет 5% или более от всей группы:
Существуют специальные уравнения, которые необходимо использовать, если образец имеет менее 20 измерений.
Иногда выборка поступает из одного места, хотя вся группа может быть рассредоточена. Кроме того, иногда выборка может быть сделана за короткий промежуток времени, когда вся группа охватывает более длительный период. В этом случае числа в выборке не являются независимыми. Тогда используются специальные уравнения, чтобы попытаться исправить это.
Полезность
Практический результат: Можно быть более уверенным в среднем значении, если провести больше измерений в выборке. Тогда стандартная ошибка среднего значения будет меньше, поскольку стандартное отклонение делится на большее число. Однако, чтобы сделать неопределенность (стандартную ошибку среднего) среднего значения в два раза меньше, размер выборки (n) должен быть в четыре раза больше. Это происходит потому, что стандартное отклонение делится на квадратный корень из размера выборки. Чтобы сделать неопределенность на одну десятую больше, размер выборки (n) должен быть в сто раз больше!
Стандартные ошибки легко вычисляются и часто используются, потому что:
- Если известна стандартная ошибка нескольких отдельных величин, то во многих случаях можно легко рассчитать стандартную ошибку некоторой функции этих величин;
- Если вероятностное распределение значения известно, его можно использовать для расчета хорошего приближения к точному доверительному интервалу; и
- Если распределение вероятности неизвестно, для оценки доверительного интервала можно использовать другие уравнения
- Когда размер выборки становится очень большим, принцип центральной предельной теоремы показывает, что числа в выборке очень похожи на числа во всей группе (они имеют нормальное распределение).
Относительная стандартная ошибка
Относительная стандартная ошибка (RSE) — это стандартная ошибка, деленная на среднее значение. Это число меньше единицы. Умножение его на 100% дает его в процентах от среднего значения. Это помогает показать, является ли неопределенность важной или нет. Например, рассмотрим два исследования доходов домохозяйств, в результате которых среднее значение по выборке составляет $50 000. Если стандартная ошибка одного опроса составляет $10 000, а другого — $5 000, то относительные стандартные ошибки равны 20% и 10% соответственно. Опрос с меньшей относительной стандартной ошибкой лучше, потому что он имеет более точное измерение (неопределенность меньше).
На самом деле, люди, которым необходимо знать средние значения, часто решают, насколько мала должна быть неопределенность, прежде чем они решат использовать информацию. Например, Национальный центр статистики здравоохранения США не сообщает среднее значение, если относительная стандартная ошибка превышает 30%. NCHS также требует не менее 30 наблюдений для того, чтобы оценка была представлена в отчете. []
Пример
Например, в воде Мексиканского залива водится много красной рыбы. Чтобы узнать, сколько в среднем весит красноперка длиной 42 см, невозможно измерить всех красноперок длиной 42 см. Вместо этого можно измерить некоторых из них. Рыба, которую измеряют, называется образцом. В таблице показан вес двух образцов красноперки длиной 42 см. Средний (средний) вес первого образца составляет 0,741 кг. Средний (средний) вес второго образца — 0,735 кг, что немного отличается от первого образца. Каждое из этих средних значений немного отличается от среднего значения, которое было бы получено при измерении каждой красной рыбы длиной 42 см (что в любом случае невозможно).
Неопределенность среднего значения можно использовать для того, чтобы узнать, насколько близки средние значения выборок к среднему значению, которое было бы получено в результате измерения всей группы. Неопределенность среднего оценивается как стандартное отклонение для выборки, деленное на квадратный корень из числа выборок минус один. Из таблицы видно, что неопределенности в средних для двух выборок очень близки друг к другу. Кроме того, относительная неопределенность — это неопределенность среднего значения, деленная на среднее значение, умноженное на 100%. Относительная неопределенность в данном примере составляет 2,38% и 2,50% для двух образцов.
Зная неопределенность среднего, можно узнать, насколько близко выборочное среднее к среднему, которое было бы получено в результате измерения всей группы. Среднее по всей группе находится между а) средним по выборке плюс неопределенность в среднем и б) средним по выборке минус неопределенность в среднем. В данном примере средний вес всей красноперки длиной 42 см в Мексиканском заливе, как ожидается, составит 0,723-0,759 кг по первой выборке и 0,717-0,753 по второй выборке.
Пример красной рыбы (также известной как красный барабан, Sciaenops ocellatus), используемой в примере.
Содержание
- Расчет ошибки средней арифметической
- Способ 1: расчет с помощью комбинации функций
- Способ 2: применение инструмента «Описательная статистика»
- Вопросы и ответы
Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.
Расчет ошибки средней арифметической
Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.
В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.
Способ 1: расчет с помощью комбинации функций
Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.
Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.
- Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».
- Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».
- Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:
=СТАНДОТКЛОН.В(число1;число2;…)«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.
Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».
- В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».
- Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».
- Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:
=КОРЕНЬ(число)Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.
Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».
- В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».
- Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:
=СЧЁТ(значение1;значение2;…)В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».
- После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13))Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1)
Урок: Статистические функции в Экселе
Способ 2: применение инструмента «Описательная статистика»
Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.
Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.
- После того, как открыт документ с выборкой, переходим во вкладку «Файл».
- Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».
- Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».
- В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.
- Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.
- После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».
- После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.
- Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.
- Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.
В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.
Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.
Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:
- На новый лист;
- В новую книгу (другой файл);
- В указанный диапазон текущего листа.
Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.
Далее следует блок настроек определяющий, какие именно данные нужно вводить:
- Итоговая статистика;
- К-ый наибольший;
- К-ый наименьший;
- Уровень надежности.
Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.
После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.
- После этого инструмент «Описательная статистика» выводит результаты обработки выборки на текущий лист. Как видим, это довольно много разноплановых статистических показателей, но среди них есть и нужный нам – «Стандартная ошибка». Он равен числу 0,505793. Это в точности тот же результат, который мы достигли путем применения сложной формулы при описании предыдущего способа.
Урок: Описательная статистика в Экселе
Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.
In statistics, a relative standard error (RSE) is equal to the standard error of a survey estimate divided by the survey estimate and then multiplied by 100. The number is multiplied by 100 so it can be expressed as a percentage. The RSE does not necessarily represent any new information beyond the standard error, but it might be a superior method of presenting statistical confidence.
Relative Standard Error vs. Standard Error
Standard error measures how much a survey estimate is likely to deviate from the actual population. It is expressed as a number. By contrast, relative standard error (RSE) is the standard error expressed as a fraction of the estimate and is usually displayed as a percentage. Estimates with an RSE of 25% or greater are subject to high sampling error and should be used with caution.
Survey Estimate and Standard Error
Surveys and standard errors are crucial parts of probability theory and statistics. Statisticians use standard errors to construct confidence intervals from their surveyed data. The reliability of these estimates can also be assessed in terms of a confidence interval. Confidence intervals are important for determining the validity of empirical tests and research.
A confidence interval is a type of interval estimate, computed from the statistics of the observed data, that might contain the true value of an unknown population parameter. Confidence intervals represent the range in which the population value is likely to lie. They are constructed using the estimate of the population value and its associated standard error. For example, there is approximately a 95% chance (i.e. 19 chances in 20) that the population value lies within two standard errors of the estimates, so the 95% confidence interval is equal to the estimate plus or minus two standard errors.
In layman’s terms, the standard error of a data sample is a measurement of the likely difference between the sample and the entire population. For example, a study involving 10,000 cigarette-smoking adults may generate slightly different statistical results than if every possible cigarette-smoking adult was surveyed.
Smaller sample errors are indicative of more reliable results. The central limit theorem in inferential statistics suggests that large samples tend to have approximately normal distributions and low sample errors.
Standard Deviation and Standard Error
The standard deviation of a data set is used to express the concentration of survey results. Less variety in the data results in a lower standard deviation. More variety is likely to result in a higher standard deviation.
The standard error is sometimes confused with the standard deviation. The standard error actually refers to the standard deviation of the mean. Standard deviation refers to the variability inside any given sample, while a standard error is the variability of the sampling distribution itself.
Relative Standard Error
The standard error is an absolute gauge between the sample survey and the total population. The relative standard error shows if the standard error is large relative to the results; large relative standard errors suggest the results are not significant. The formula for relative standard error is:
Relative Standard Error
=
Standard Error
Estimate
×
1
0
0
where:
Standard Error
=
standard deviation of the mean sample
Estimate
=
mean of the sample
begin{aligned} &text{Relative Standard Error} = frac { text{Standard Error} }{ text{Estimate} } times 100 &textbf{where:} &text{Standard Error} = text{standard deviation of the mean sample} &text{Estimate} = text{mean of the sample} end{aligned}
Relative Standard Error=EstimateStandard Error×100where:Standard Error=standard deviation of the mean sampleEstimate=mean of the sample
In statistics, a relative standard error (RSE) is equal to the standard error of a survey estimate divided by the survey estimate and then multiplied by 100. The number is multiplied by 100 so it can be expressed as a percentage. The RSE does not necessarily represent any new information beyond the standard error, but it might be a superior method of presenting statistical confidence.
Relative Standard Error vs. Standard Error
Standard error measures how much a survey estimate is likely to deviate from the actual population. It is expressed as a number. By contrast, relative standard error (RSE) is the standard error expressed as a fraction of the estimate and is usually displayed as a percentage. Estimates with an RSE of 25% or greater are subject to high sampling error and should be used with caution.
Survey Estimate and Standard Error
Surveys and standard errors are crucial parts of probability theory and statistics. Statisticians use standard errors to construct confidence intervals from their surveyed data. The reliability of these estimates can also be assessed in terms of a confidence interval. Confidence intervals are important for determining the validity of empirical tests and research.
A confidence interval is a type of interval estimate, computed from the statistics of the observed data, that might contain the true value of an unknown population parameter. Confidence intervals represent the range in which the population value is likely to lie. They are constructed using the estimate of the population value and its associated standard error. For example, there is approximately a 95% chance (i.e. 19 chances in 20) that the population value lies within two standard errors of the estimates, so the 95% confidence interval is equal to the estimate plus or minus two standard errors.
In layman’s terms, the standard error of a data sample is a measurement of the likely difference between the sample and the entire population. For example, a study involving 10,000 cigarette-smoking adults may generate slightly different statistical results than if every possible cigarette-smoking adult was surveyed.
Smaller sample errors are indicative of more reliable results. The central limit theorem in inferential statistics suggests that large samples tend to have approximately normal distributions and low sample errors.
Standard Deviation and Standard Error
The standard deviation of a data set is used to express the concentration of survey results. Less variety in the data results in a lower standard deviation. More variety is likely to result in a higher standard deviation.
The standard error is sometimes confused with the standard deviation. The standard error actually refers to the standard deviation of the mean. Standard deviation refers to the variability inside any given sample, while a standard error is the variability of the sampling distribution itself.
Relative Standard Error
The standard error is an absolute gauge between the sample survey and the total population. The relative standard error shows if the standard error is large relative to the results; large relative standard errors suggest the results are not significant. The formula for relative standard error is:
Relative Standard Error
=
Standard Error
Estimate
×
1
0
0
where:
Standard Error
=
standard deviation of the mean sample
Estimate
=
mean of the sample
begin{aligned} &text{Relative Standard Error} = frac { text{Standard Error} }{ text{Estimate} } times 100 &textbf{where:} &text{Standard Error} = text{standard deviation of the mean sample} &text{Estimate} = text{mean of the sample} end{aligned}
Relative Standard Error=EstimateStandard Error×100where:Standard Error=standard deviation of the mean sampleEstimate=mean of the sample
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
a:
В статистике относительная стандартная ошибка или RSE равна стандартной ошибке оценки опроса, деленной на оценку опроса, а затем умножается на 100. Число умножается на 100 так его можно выразить в процентах. RSE не обязательно представляет какую-либо новую информацию за пределами стандартной ошибки, но это может быть превосходный метод представления статистической достоверности.
Оценка и стандартная ошибка
Обследования и стандартные ошибки являются важными частями теории вероятностей и статистики. Статистики используют стандартные ошибки для построения доверительных интервалов из своих опрошенных данных. Доверительные интервалы важны для определения действительности эмпирических тестов и исследований.
В условиях непрофессионала стандартная ошибка выборки данных — это измерение вероятной разницы между выборкой и всей совокупностью. Например, исследование с участием 10 000 взрослых, курящих сигареты, может генерировать несколько иные статистические результаты, чем если бы были опрошены все возможные взрослые курильщики сигарет.
Меньшие ошибки выборки свидетельствуют о более надежных результатах. Центральная предельная теорема в статистических выводах показывает, что большие образцы имеют тенденцию иметь приблизительно нормальные распределения и низкие ошибки выборки.
Стандартное отклонение и стандартная ошибка
Стандартное отклонение набора данных используется для выражения концентрации результатов опроса. Меньшее разнообразие данных приводит к более низкому стандартным отклонениям. Больше разнообразия, вероятно, приведет к более высокому стандартным отклонениям.
Стандартная ошибка иногда путается со стандартным отклонением. Стандартная ошибка на самом деле относится к стандартным отклонениям среднего значения. Стандартное отклонение относится к изменчивости внутри любого данного образца, в то время как стандартная ошибка — это изменчивость самого распределения выборки.
Относительная стандартная ошибка
Стандартная ошибка — это абсолютная величина между выборочным обследованием и общей численностью населения. Относительная стандартная ошибка показывает, является ли стандартная ошибка большой по сравнению с результатами; большие относительные стандартные ошибки предполагают, что результаты не значительны. Формула относительной стандартной ошибки (стандартная ошибка / оценка) x 100.
Стандартная ошибка
Стандартная ошибка — это стандартное отклонение выборочного распределения статистики. Этот термин также может использоваться для оценки (хорошего предположения) этого стандартного отклонения, взятого из выборки всей группы.
Среднее значение некоторой части группы (называемой выборкой) является обычным способом оценки среднего значения для всей группы. Часто бывает слишком сложно или стоит слишком много денег, чтобы измерить всю группу. Но если измерить другую выборку, то ее среднее значение будет немного отличаться от первой выборки. Стандартная ошибка среднего — это способ узнать, насколько близка средняя по выборке к средней по всей группе. Это способ узнать, насколько вы можете быть уверены в среднем значении по выборке.
В реальных измерениях истинное значение стандартного отклонения среднего для всей группы обычно неизвестно. Поэтому термин стандартная ошибка часто используется для обозначения близкого к истинному значению для всей группы. Чем больше измерений в выборке, тем ближе к истинному значению для всей группы.
Для значения, отобранного с несмещенной нормально распределенной ошибкой, выше показана доля выборок, которые будут находиться в пределах 0, 1, 2 и 3 стандартных отклонений выше и ниже фактического значения.
Как найти стандартную ошибку среднего значения
Один из способов найти стандартную ошибку среднего — это множество выборок. Сначала находят среднее значение для каждой выборки. Затем находят среднее и стандартное отклонение этих средних по выборкам. Стандартное отклонение для всех средних по выборке и есть стандартная ошибка среднего. Это может быть большой объем работы. Иногда иметь большое количество образцов слишком сложно или стоит слишком много денег.
Другой способ найти стандартную ошибку среднего — использовать уравнение, для которого нужна только одна выборка. Стандартная ошибка среднего обычно оценивается по стандартному отклонению для выборки из всей группы (стандартное отклонение выборки), деленному на квадратный корень из размера выборки.
S E x ¯ = s n {displaystyle SE_{bar {x}} ={frac {s}{sqrt {n}}}}
где
s — стандартное отклонение выборки (т.е. выборочная оценка стандартного отклонения популяции), и
n — количество измерений в выборке.
Насколько большой должна быть выборка, чтобы оценка стандартной ошибки среднего была близка к фактической стандартной ошибке среднего для всей группы? В выборке должно быть не менее шести измерений. Тогда стандартная ошибка среднего для выборки будет находиться в пределах 5% от стандартной ошибки среднего, если бы измерялась вся группа.
Исправления для некоторых случаев
Существует еще одно уравнение, которое можно использовать, если количество измерений составляет 5% или более от всей группы:
Существуют специальные уравнения, которые необходимо использовать, если образец имеет менее 20 измерений.
Иногда выборка поступает из одного места, хотя вся группа может быть рассредоточена. Кроме того, иногда выборка может быть сделана за короткий промежуток времени, когда вся группа охватывает более длительный период. В этом случае числа в выборке не являются независимыми. Тогда используются специальные уравнения, чтобы попытаться исправить это.
Полезность
Практический результат: Можно быть более уверенным в среднем значении, если провести больше измерений в выборке. Тогда стандартная ошибка среднего значения будет меньше, поскольку стандартное отклонение делится на большее число. Однако, чтобы сделать неопределенность (стандартную ошибку среднего) среднего значения в два раза меньше, размер выборки (n) должен быть в четыре раза больше. Это происходит потому, что стандартное отклонение делится на квадратный корень из размера выборки. Чтобы сделать неопределенность на одну десятую больше, размер выборки (n) должен быть в сто раз больше!
Стандартные ошибки легко вычисляются и часто используются, потому что:
- Если известна стандартная ошибка нескольких отдельных величин, то во многих случаях можно легко рассчитать стандартную ошибку некоторой функции этих величин;
- Если вероятностное распределение значения известно, его можно использовать для расчета хорошего приближения к точному доверительному интервалу; и
- Если распределение вероятности неизвестно, для оценки доверительного интервала можно использовать другие уравнения
- Когда размер выборки становится очень большим, принцип центральной предельной теоремы показывает, что числа в выборке очень похожи на числа во всей группе (они имеют нормальное распределение).
Относительная стандартная ошибка
Относительная стандартная ошибка (RSE) — это стандартная ошибка, деленная на среднее значение. Это число меньше единицы. Умножение его на 100% дает его в процентах от среднего значения. Это помогает показать, является ли неопределенность важной или нет. Например, рассмотрим два исследования доходов домохозяйств, в результате которых среднее значение по выборке составляет $50 000. Если стандартная ошибка одного опроса составляет $10 000, а другого — $5 000, то относительные стандартные ошибки равны 20% и 10% соответственно. Опрос с меньшей относительной стандартной ошибкой лучше, потому что он имеет более точное измерение (неопределенность меньше).
На самом деле, люди, которым необходимо знать средние значения, часто решают, насколько мала должна быть неопределенность, прежде чем они решат использовать информацию. Например, Национальный центр статистики здравоохранения США не сообщает среднее значение, если относительная стандартная ошибка превышает 30%. NCHS также требует не менее 30 наблюдений для того, чтобы оценка была представлена в отчете. []
Пример
Например, в воде Мексиканского залива водится много красной рыбы. Чтобы узнать, сколько в среднем весит красноперка длиной 42 см, невозможно измерить всех красноперок длиной 42 см. Вместо этого можно измерить некоторых из них. Рыба, которую измеряют, называется образцом. В таблице показан вес двух образцов красноперки длиной 42 см. Средний (средний) вес первого образца составляет 0,741 кг. Средний (средний) вес второго образца — 0,735 кг, что немного отличается от первого образца. Каждое из этих средних значений немного отличается от среднего значения, которое было бы получено при измерении каждой красной рыбы длиной 42 см (что в любом случае невозможно).
Неопределенность среднего значения можно использовать для того, чтобы узнать, насколько близки средние значения выборок к среднему значению, которое было бы получено в результате измерения всей группы. Неопределенность среднего оценивается как стандартное отклонение для выборки, деленное на квадратный корень из числа выборок минус один. Из таблицы видно, что неопределенности в средних для двух выборок очень близки друг к другу. Кроме того, относительная неопределенность — это неопределенность среднего значения, деленная на среднее значение, умноженное на 100%. Относительная неопределенность в данном примере составляет 2,38% и 2,50% для двух образцов.
Зная неопределенность среднего, можно узнать, насколько близко выборочное среднее к среднему, которое было бы получено в результате измерения всей группы. Среднее по всей группе находится между а) средним по выборке плюс неопределенность в среднем и б) средним по выборке минус неопределенность в среднем. В данном примере средний вес всей красноперки длиной 42 см в Мексиканском заливе, как ожидается, составит 0,723-0,759 кг по первой выборке и 0,717-0,753 по второй выборке.
Пример красной рыбы (также известной как красный барабан, Sciaenops ocellatus), используемой в примере.
Оценка достоверности результатов статистического исследования
В
практической и научно-практической
работе врачи обобщают результаты,
полученные, как правило, на выборочных
совокупностях. Для более
широкого распространения и применения
полученных при изучении
репрезентативной выборочной совокупности
данных и выводов надо уметь
по части явления судить о явлении и его
закономерностях в целом.
Учитывая,
как правило, что врачи проводят
исследования на выборочных совокупностях,
теория статистики позволяет с помощью
математического аппарата (формул)
переносить данные с выборочного
исследования на генеральную совокупность.
При этом врач должен уметь не только
пользоваться математическими формулами,
но и делать выводы, соответствующие
каждому способу оценки достоверности
полученных данных. С
этой целью врач должен знать способы
оценки достоверности.
В статистических
исследованиях применяются 2 вида
наблюдений — сплошное и выборочное.
Самые надежные результаты можно получить
при применении сплошного метода, т.е.
при изучении генеральной совокупности.
Между тем изучение
генеральной совокупности связано со
значительной трудоемкостью. Поэтому в
медико-биологических исследованиях,
как правило, проводятся выборочные
наблюдения. С тем, чтобы полученные при
изучении выборочной совокупности данные
можно было перенести на генеральную
совокупность, необходимо провести
оценку достоверности результатов
статистического исследования. Выборочная
совокупность может недостаточно полно
представлять генеральную совокупность,
поэтому выборочным наблюдениям всегда
сопутствуют ошибки
репрезентативности.
По размерам средней
ошибки ( m
) можно судить, насколько найденная
выборочная средняя величина отличается
от средней генеральной совокупности.
Малая ошибка указывает на близость этих
показателей, большая ошибка такой
уверенности не дает.
На величину средней
ошибки средней арифметической влияют
следующие два обстоятельства:
-
однородность
собранного материала
чем меньше разбросанность вариант
вокруг своей средней, тем меньше ошибка
репрезентативности. -
число наблюдений
средняя ошибка будет тем меньше, чем
больше число наблюдений.
Средняя ошибка
средней арифметической
вычисляется по формуле:
Средняя ошибка
для относительных величин вычисляется
по формуле:
, где
Р — величина
показателя в расчете на 100, 1000, 10 000 и т.д.
q
— разность между основанием, на которое
рассчитывается показатель, и его
конкретным числовым значением (100 — Р,
1000 — Р, 10 000 — Р и т.д.).
При n
< 30 в
знаменателе n
— 1.
Пример 8.
Средний рост
восьмилетних мальчиков составил — 125,5
см, среднее квадратическое отклонение
=±3,4
см , n=73
mм=
±
=±0,4
см
Пример 9.
Численность детей
в возрасте до года по данным детской
поликлиники составила 450 ,из них ни разу
не болели 100 детей. Необходимо определить
«Индекс здоровья» (процент ни разу
не болевших детей) и вычислить ошибку
для данного показателя.
Индекс здоровья
Оценка достоверности средних и относительных величин
При оценке
достоверности средних или относительных
величин руководствуются следующим
правилом:средняя
арифметическая или относительная
величина при числе наблюдений в выборочной
совокупности 30 и более должны превышать
свою ошибку не менее чем в 2 раза.
>
2 или
>
2
В рассматриваемых
примерах средняя арифметическая,
характеризующая рост восьмилетних
мальчиков и показатель „индекс
здоровья”
превышают свои ошибки соответственно:
раз,
раз, что соответствует высокой степени
их статистической достоверности с
вероятностью более чем 99,7 %.
Высказанное
положение вытекает из теории «вероятности»,
под которой понимается числовая мера
объективной возможности появления
случайного события.
Вероятность —
число, которое находится между 0 и 1, или
между 0% и 100%. Математиками определено,
что той или иной вероятности, выраженной
в процентах, соответствует определенное
значение критерия t
Стьюдента.
Так, например,
вероятности равной Р
= 68,3%
соответствует t=
1,0,
вероятности равной
Р = 95,5 %
соответствует
t
= 2,0
вероятности равной
Р = 99,7 % соответствует
t
= 3,0 .
В медико-биологических
исследованиях событие является
статистически достоверным, если
вероятность его появления соответствует
значению критерия t
Стьюдента, равное 2.
Средняя ошибка
позволяет не только оценить достоверность
относительного показателя или средней
величины, но и найти доверительные
границы средней величины или относительного
показателя в генеральной совокупности
М ген.=
М выб.
±
t
m
Р ген.
= Р выб
. ±
t
m
Как уже было
сказано, величина средней ошибки
указывает, насколько средняя величина
и относительный показатель выборочной
совокупности отличаются от соответствующих
величин в генеральной совокупности.
Величина t*m
является тем доверительным интервалом
по отношению к средней или относительной
величине, в котором с определенной
степенью вероятности можно ожидать
нахождение средней или относительной
величины в генеральной совокупности.
Пример 10.
М выб
.= 125,5 см;
m
= ±
0,4 см.
При 95% вероятности
t
=2, при 99,7 % — t
= 3 .
М ген.=
125,5 см ±
2
0,4 см = 124,7 — 126,3 см
М ген.=
125,5 см ±
3
0,4 см = 124,3 — 126,7 см.
Таким образом, с
вероятностью 95% можно ожидать, что
средняя будет находиться в пределах от
124,7 до 126,3 см и с вероятностью 99,7% — в
пределах от 124,3 до 126,7 см.
Понятно, что
действительное значение средней можно
получить только при обследовании всех
8-летних мальчиков, но как это очевидно
из полученных данных, подобное исследование
нецелесообразно, т.к. средняя арифметическая
статистически достоверна (Р >
99,7%), а доверительный интервал для средней
в генеральной совокупности является
весьма незначительным -t
m-
= 3
0,4 т.е. всего по 1,2 см от средней выборочной
совокупности в большую и меньшую
сторону.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статистике относительная стандартная ошибка (RSE) равна стандартной ошибке оценки обследования, деленной на оценку обследования, а затем умноженной на 100. Число умножается на 100, чтобы его можно было выразить в процентах. RSE не обязательно представляет какую-либо новую информацию, выходящую за рамки стандартной ошибки, но это может быть лучшим методом представления статистической достоверности.
Относительная стандартная ошибка против стандартной ошибки
Стандартная ошибка определяет, насколько оценка обследования может отличаться от фактической совокупности.Он выражается числом.Напротив, относительная стандартная ошибка (RSE) — это стандартная ошибка, выраженная как часть оценки и обычно отображается в процентах.Оценки с RSE 25% или более подвержены большой ошибке выборки и должны использоваться с осторожностью.
Оценка опроса и стандартная ошибка
Опросы и стандартные ошибки — важнейшие части теории вероятностей и статистики. Статистики используют стандартные ошибки для построения доверительных интервалов на основе своих обследованных данных. Достоверность этих оценок также можно оценить с помощью доверительного интервала. Доверительные интервалы важны для определения достоверности эмпирических тестов и исследований.
Доверительный интервал — это тип интервальной оценки, вычисляемой на основе статистики наблюдаемых данных, которая может содержать истинное значение неизвестного параметра совокупности.Доверительные интервалы представляют собой диапазон, в котором, вероятно, находится значение генеральной совокупности.Они построены с использованием оценки значения генеральной совокупности и связанной с ней стандартной ошибки.Например, вероятность того, что значение генеральной совокупности находится в пределах двух стандартных ошибок оценок, составляет приблизительно 95% (т.е. 19 из 20), поэтому 95% доверительный интервал равен оценке плюс или минус две стандартные ошибки.
С точки зрения непрофессионала, стандартная ошибка выборки данных — это измерение вероятной разницы между выборкой и всей совокупностью. Например, исследование с участием 10 000 взрослых, курящих сигареты, может дать несколько иные статистические результаты, чем при опросе всех возможных курящих сигареты взрослых.
Меньшие ошибки выборки указывают на более надежные результаты. Центральная предельная теорема в умозаключениях статистиков показывает, что большие выборки, как правило, имеют приблизительно нормальное распределение и низкие ошибки выборки.
Стандартное отклонение и стандартная ошибка
Стандартное отклонение набора данных используется для выражения концентрации результатов обследования. Меньшее разнообразие данных приводит к более низкому стандартному отклонению. Чем больше разнообразия, тем выше стандартное отклонение.
Стандартную ошибку иногда путают со стандартным отклонением. Стандартная ошибка фактически относится к стандартному отклонению среднего значения. Стандартное отклонение относится к изменчивости внутри любой данной выборки, тогда как стандартная ошибка — это изменчивость самого распределения выборки.
Относительная стандартная ошибка
Стандартная ошибка — это абсолютная мера между выборочным обследованием и генеральной совокупностью. Относительная стандартная ошибка показывает, велика ли стандартная ошибка по сравнению с результатами; большие относительные стандартные ошибки предполагают, что результаты незначительны. Формула относительной стандартной ошибки:
Согласно теории выборочного метода, неоднократно подтвержденной практикой, опрашивать всех нет необходимости, а можно опросить лишь часть группы, которая может быть в тысячи раз меньше. Эта маленькая часть называется выборкой (или выборочной совокупностью), а большая группа, которую она представляет, называется генеральной совокупностью.
При этом если выборка сформирована правильно, выводы, полученные на основе изучения выборки, могут быть перенесены и на генеральную совокупность. Например, если в выборке женщины значимо чаще, чем мужчины, пользуются дезодорантами, то делается вывод, что и в генеральной совокупности (например, в исследованном городе) присутствует такая закономерность.
Процесс переноса выводов с выборки на генеральную совокупность называется генерализацией. А свойство выборки отражать характеристики генеральной совокупности называется репрезентативностью. Для более комфортного запоминания термина на рис.1.
приведены иллюстрации, когда выборка отражает свойства генеральной совокупности и когда свойства выборки отличаются от свойств генеральной совокупности.



Рис.1. Иллюстративные примеры соответствия (несоответствия) свойств генеральной совокупности и выборки
Не стоит путать понятие репрезентативности с такими понятиями как валидность и релевантность, хотя они тоже относятся к характеристикам качества исследования. В социальных науках валидность понимается довольно широко, но чаще всего – как обоснованность.
Понятие валидности относится не к выборке, а к исследовательской методике. Методика или измерение (анкета, блок вопросов, тест) считается валидным, если фиксирует именно то понятие или свойство, которое планируется измерить.
Например, если мы захотим оценить уровень лояльности клиента к магазину и выберем для этого лишь показатель частоты посещения магазина, валидность этого подхода будет неполной: возможно, респондент часто заходит в магазин только из-за банкомата, который там установлен.
Валидная методика в данном примере должна включать и другие показатели: предпочтение магазина, суммы покупок в этом и других магазинах, готовность переключиться на другие магазины, готовность рекомендовать магазин и др.
При установлении валидности решающую роль играет обоснование и последующая проверка гипотезы релевантности, то есть соответствия измеряемых параметров характеристикам исследуемого объекта.
Житейский пример нерелевантности – измерять уровень счастья человека количеством денег у него (хотя, наверное, не все с этим согласятся).
Очевидный пример нерелевантности – попытка измерить массу тела по его температуре.
Но вернемся к понятию репрезентативности. В то время как точность измерений зависит от размера выборки, размер выборки не гарантирует ее репрезентативности.
Репрезентативность выборки главным образом обеспечивается способом отбора ее участников (респондентов).
Примером явного нарушения репрезентативности может послужить шутка о том, что интернет-опрос показал, что 100% людей пользуется интернетом.
Можно выделить несколько вариантов нарушения репрезентативности выборки: когда опрошены не те люди и когда опрошено слишком много (или мало) определенных людей (например, женщин намного больше, чем мужчин). Кроме того, чем меньше размер выборки, тем меньше вероятность того, что она будет репрезентативной. Например, допустим, 1% населения мог бы заинтересоваться новой услугой.
Это 1 из 100 людей. Если размер выборки составляет всего 60 человек, то в вашей выборке может отсутствовать человек, который, скорее всего, будет заинтересован в услуге. Ваша выборка менее репрезентативна, потому что она меньше. Ваши результаты будут разными в зависимости от того, содержит ли ваша выборка одного из этих людей или нет.
Пример репрезентативной и нерепрезентативной выборки показан на рис.2.

Рис.2. Пример репрезентативной и нерепрезентативной выборки
На рис.3 показана та же по составу генеральная совокупность, но с другим расположением объектов внутри круга.

Рис.3. Пример репрезентативной и нерепрезентативной выборки при другом расположении объектов генеральной совокупности
Говоря простым языком, репрезентативная выборка – это такая выборка, в которой представлены все подгруппы, важные для исследования. Помимо этого, характер распределения рассматриваемых параметров в выборке должен быть таким же, как в генеральной совокупности.
Простой случайный отбор респондентов представляется оптимальным способом формирования репрезентативной выборки.
Поскольку в этом случае у любого представителя генеральной совокупности одинаковая вероятность попасть в выборку, в нее попадут люди с разными характеристиками пропорционально их долям в генеральной совокупности.
В итоге выборка будет представлять собой нечто вроде уменьшенной копии генеральной совокупности.
Случайность отбора респондентов в выборку обеспечивается разными способами.
Например, для телефонного опроса жителей города берется база данных всех телефонных номеров, и номера респондентов случайным образом выбираются компьютером (с использованием генератора случайных чисел).
При уличном опросе интервьюеров распределяют по случайно выбранным точкам и инструктируют опрашивать каждого N-ного прохожего.
Наглядным примером репрезентативной выборки может служить пицца. Если целая пицца – это генеральная совокупность, которую мы хотим изучить, то кусок пиццы – это выборка.
Как правило, достаточно одного куска пиццы, чтобы судить обо всей пицце (при условии, что ингредиенты равномерно распределены по ее поверхности). Таким образом, кусок пиццы пиццы на рис.
4 – это репрезентативная выборка из пиццы.

Рис.4. Наглядный пример репрезентативной выборки (пицца)
Важно отметить, что не любой кусок пиццы будет репрезентативной выборкой. Разные способы получения куска пиццы могут принципиально повлиять на качество исследования и выводы, которые будут получены при анализе каждого варианта выборки (рис.4)
(рисунок в сушильной камере, готовится к публикации)
Рис.5. Наглядный пример формирования репрезентативной и нерепрезентативной выборки.
Еще один показательный пример формирования репрезентативной выборки – кастрюля, содержимое которой мы должны узнать (допустим, там скрывается борщ). Мы только один раз можем зачерпнуть из кастрюли ложкой (провести исследование). В нашем примере ложка – это выборка, а содержимое кастрюли – генеральная совокупность.
Если мы зачерпнем сверху, то придем к выводу, что в кастрюле бульон. Если снизу – решим, что в кастрюле мясо. Зачерпнув где-то посередине, мы получим картошку или капусту. В любом из трех случаев выводы будут неверны.
Чтобы получить достоверный результат, нам стоит хорошенько перемешать содержимое кастрюли, перед тем как пробовать его.
Перемешивание в данном случае – аналог процедуры простого случайного отбора, поскольку оно предоставляет всем ингредиентам примерно равную вероятность попадания в ложку-выборку (или тарелку-выборку).

Рис.6. Борщ как модель, демонстрирующая репрезентативность выборки.
В реальности применить простой случайный отбор респондентов не всегда удается в полной мере. Например, мы можем абсолютно корректно отобрать в выборку нужное количество номеров домашних телефонов случайным образом, но при их прозвоне выяснится, что дозвониться и поговорить удается преимущественно с пенсионерами, а «поймать» дома молодежь и работающих людей получается плохо.
Возвращаясь к примеру с борщом, если у нас вместо кастрюли – огромный ресторанный котел, а в руках все та же обычная ложка, перемешивание будет неэффективным. Чтобы решить задачу, потребуются иные подходы.
Например, мы можем теоретически разделить глубину котла на несколько слоев и постараться зачерпнуть содержимое из каждого слоя (из случайного места слоя: не только в центре, но и по краям). Таким образом, наша итоговая выборка будет состоять уже из нескольких выборок и при этом адекватно отражать содержимое всех слоев котла.
Подобные альтернативные подходы называются типами выборки, которых придумано достаточно много для того, чтобы максимизировать репрезентативность выборки в сложных условиях реального мира.
Последствия нарушения репрезентативности выборки: некорректные выводы исследования, выброшенный на ветер бюджет исследования, финансовые потери вследствие применения неправильных выводов.
Вы можете выбрать валидную исследовательскую методику, рассчитать объем выборки, обеспечивающий приемлемую точность измерений, но, если выборка исследования нерепрезентативна, получить достоверную информацию не удастся.
- ПРИМЕРЫ НАРУШЕНИЯ РЕПРЕЗЕНТАТИВНОСТИ ВЫБОРКИ
- ПРЕДВЫБОРНЫЙ ОПРОС
- Самым известным примером нарушения репрезентативности выборки является история провала американского журнала «Литературный дайджест».
В 1936 году журнал в очередной раз провел почтовый опрос общественного мнения о вероятных результатах грядущих президентских выборов в США. До 1936 года опрос всегда правильно предсказывал победителя. Опрос 1936 года показал, что победителем с большим отрывом станет кандидат от республиканцев, но в итоге победителем оказался представитель демократов.
Таким образом, гигантская выборка (около 2,4 млн. человек) не обеспечила достоверных результатов. В чем же заключалась причина ошибки?
Называются две основные причины провала: смещение при формировании выборки и смещение вследствие отказа респондентов от участия в опросе.
Прежде всего, журнал включил своих подписчиков в список для рассылки анкет и, желая расширить выборку, использовал два других доступных тогда списка граждан: зарегистрированных автовладельцев и пользователей телефонов.
Во времена Великой Депрессии представители этих групп отличались от остального населения более высоким доходом, как и подписчики самого журнала.
Таким образом, полученная база для рассылки не являлась корректным отражением структуры населения США.
Вторая проблема с опросом заключалась в том, что из 10 миллионов человек, чьи имена были в первоначальном списке рассылки, только 2,4 миллиона ответили на опрос. Вероятно, высокий процент отказов был связан с тем, что опрос проводился по почте.
Уже в те времена американцы относились к почтовым рассылкам как к спаму. Таким образом, размер выборки составил примерно одну четверть от того, что первоначально планировалось.
Когда доля ответивших низка (как это было в данном случае), считается, что исследование страдает от необъективности ответов.
У этой истории две морали: Большая, но неправильно сформированная выборка гораздо хуже маленькой, но правильно сформированной выборки. При проведении опроса не упускайте из внимания смещение отбора и смещение в результате отказов.
СИСТЕМАТИЧЕСКАЯ ОШИБКА ВЫЖИВШЕГО
Пример из военной практики. Во Вторую мировую войну американские военные столкнулись со следующей проблемой. Не все американские бомбардировщики после задания возвращались на базу.
На вернувшихся самолетах оставалось множество пробоин от выстрелов противника, но распределены они были неравномерно: больше всего на фюзеляже и прочих частях, меньше в топливной системе и гораздо меньше — в двигателе.
Командованию казалось логичным, что в наиболее поврежденных местах нужно установить больше брони. Привлеченный к решению задачи математик возразил: данные как раз показывают, что самолет, получивший пробоины в этих местах, еще может вернуться на базу.
А самолет, которому попали в бензобак или двигатель, выходит из строя и не возвращается. Поэтому укреплять следует те места, которые у вернувшихся самолетов повреждены меньше всего.

Рис .7. Пробоины на вернувшихся самолётах. Получившие повреждения в других местах не смогли вернуться на базу
Эта задача служит примером нарушения репрезентативности выборки, когда в нее включены не те респонденты: в данном случае, вернувшиеся самолеты, в то время как не вернувшиеся проигнорированы.
Применительно к маркетинговым исследованиям, эта ситуация подобна следующей. При опросе клиентов бизнеса будет ошибкой опрашивать только текущих клиентов и не опрашивать потерянных клиентов (а какие «пробоины» получили они?).
НЕПРАВИЛЬНЫЕ МЕСТА ОПРОСА
При опросе посетителей ТРЦ важно правильно расставить интервьюеров. Например, если поставить интервьюеров только у главного входа, в выборку не попадут посетители, приехавшие в ТРЦ на автомобиле и попавшие в него через парковку.
Как следствие, выводы, полученные на собранных данных, будут корректны только для той части посетителей, которые приходят в ТРЦ пешком, а значит, делают меньше покупок, не покупают габаритные товары, живут ближе к ТРЦ, чем приезжающие на автомобиле.
ОТСУТСТВИЕ КВОТИРОВАНИЯ
Другой пример. Бывает, что в разных районах города сбор анкет идет с разной скоростью: где-то (например, в центре города) большой пешеходный поток и у людей есть время на участие в опросе (отдыхающие, в отпуске, офисные сотрудники на обеде), а на окраинах либо мало людей на улицах, либо все спешат на работу и отказываются участвовать.
В результате, если не ограничивать доли районов, в выборке будут преобладать люди из центрального района, которые могут значимо отличаться от остальных людей родом занятий, уровнем дохода и образования, уровнем осведомленности о магазинах и др.
Таким образом, собранная выборка уже не будет репрезентативной по отношению к населению всего города.
ОНЛАЙН-ОПРОСЫ (ОНЛАЙН-ПАНЕЛИ)
Несмотря на многие положительные стороны онлайн-опросов, такие как экономичность, оперативность сбора информации, удобство ее обработки и т. д., некоторые их особенности напрямую угрожают репрезентативности исследования:
- Во-первых, участники онлайн-опросов – это, как правило, активные пользователи интернета, хорошо в нем разбирающиеся и больше подверженные влиянию интернет-культуры, чем обычные люди.
- Во-вторых, люди, у которых есть время и желание регулярно участвовать в онлайн-опросах за небольшое вознаграждение, скорее всего, значительно отличаются от остальных людей как по социально-демографическим, так и по психографическим характеристикам.
- В-третьих, профессиональное участие в опросах приводит к так называемой профессиональной деформации, когда ответы респондентов на вопросы новых исследований обусловлены предыдущим опытом, но не жизненным, а опытом участия в других опросах.
- Таким образом, в данном случае возникает та ситуация, когда опрашиваются не те люди, хотя по формальным характеристикам они подходят под описание целевой аудитории.
- ВЫВОДЫ
- Итак, чтобы получить достаточно точные данные об интересующей нас группе людей, необязательно опрашивать их всех, благодаря свойству репрезентативности выборки.
- «Чем больше, тем лучше» – неправильный подход к формированию выборки.
Небольшая репрезентативная выборка лучше большой, но нерепрезентативной выборки. Применительно к выборке не стоит пугаться слова «случайная». Это вовсе не значит, что в исследовании будут получены случайные результаты. Напротив, случайный подход к формированию выборки делает ее максимально похожей на генеральную совокупность, а значит, репрезентативной.
При проектировании выборки следует учитывать опасность смещения структуры выборки вследствие особенностей сбора информации и других условий.
Источник: https://scanmarket.ru/blog/reprezentativnost-vyborki
Ошибки выборки
Чтобы оценить степень точности выборочного наблюдения, необходимо оценить величину ошибок, которые могут возникнуть в процессе проведения выборочного наблюдения.
Статистическое исследование может осуществляться по данным несплошного наблюдения, основная цель которого состоит в получении характеристик изучаемой совокупности по обследованной ее части. Одним из наиболее распространенных в статистике методов, применяющих несплошное наблюдение, является выборочный метод.
Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора.
При выборочном методе обследованию подвергается сравнительно небольшая часть всей изучаемой совокупности (обычно до 5 — 10%, реже до 15 — 25%). При этом подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью.
Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью
или просто выборкой.
Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.
В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции (товара), если проверка сопровождается уничтожением или разложением на составные части обследуемых образцов (определение сахаристости фруктов, клейковины печеного хлеба, установление носкости обуви, прочности тканей на разрыв и т.д.).
- Проведение исследования социально — экономических явлений выборочным методом складывается из ряда последовательных этапов:
- 1) обоснование (в соответствии с задачами исследования) целесообразности применения выборочного метода;
- 2) составление программы проведения статистического исследования выборочным методом;
- 3) решение организационных вопросов сбора и обработки исходной информации;
4) установление доли выборки, т.е. части подлежащих обследованию единиц генеральной совокупности;
- 5) обоснование способов формирования выборочной совокупности;
- 6) осуществление отбора единиц из генеральной совокупности для их обследования;
- 7) фиксация в отобранных единицах (пробах) изучаемых признаков;
-
статистическая обработка полученной в выборке информации с определением обобщающих характеристик изучаемых признаков;
- 9) определение количественной оценки ошибки выборки;
- 10) распространение обобщающих выборочных характеристик на генеральную совокупность.
- В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей (обозначается р), а средняя величина изучаемого варьирующего признака — генеральной средней (обозначается ).
- В выборочной совокупности долю изучаемого признака называют выборочной долей, или частостью (обозначается ), а среднюю величину в выборке — выборочной средней (обозначается ).
- Пример.
При контрольной проверке качества хлебобулочных изделий проведено 5%-ное выборочное обследование партии нарезных батонов из муки высшего сорта. При этом из 100 отобранных в выборку батонов 90 шт. соответствовали требованиям стандарта. Средний вес одного батона в выборке составлял 500,5 г при среднем квадратическом отклонении г.
- На основе полученных в выборке данных нужно установить возможные значения доли стандартных изделий и среднего веса одного изделия во всей партии.
- Прежде всего устанавливаются характеристики выборочной совокупности. Выборочная доля, или частость, определяется из отношения единиц, обладающих изучаемым признаком m, к общей численности единиц выборочной совокупности n:
Поскольку из 100 изделий, попавших в выборку n, 90 ед. оказались стандартными m, то показатель частости равен: = 90:100=0,9.
Средний вес изделия в выборке х = 500,5 г определен взвешиванием. Но полученные показатели частости (0,9) и средней величины (500,5 г) характеризуют долю стандартной продукции и средний вес одного изделия лишь в выборке. Дляопределения соответствующих показателей для всей партии товара надо установить возможные при этом значения ошибки выборки.
Ошибка выборки — это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методом отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.
- Определение ошибки выборочной средней.
- При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:
- ,
- где — средняя ошибка выборочной средней;
- — дисперсия выборочной совокупности;
- n — численность выборки.
- При бесповторном отборе она рассчитывается по формуле:
,
- где N — численность генеральной совокупности.
- Определение ошибки выборочной доли.
- При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:
- где — выборочная доля единиц, обладающих изучаемым признаком;
- — число единиц, обладающих изучаемым признаком;
- — численность выборки.
- При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:
- Предельная ошибка выборки связана со средней ошибкой выборки отношением:
- .
- При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.
- Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:
Предельная ошибка выборки при повторном отборе определяется по формуле:
.
Источник: https://www.ekonomstat.ru/lektsii-po-distsipline-statistika/36-obshhaja-teorija-statistiki-lekcii/834-oshibki-vyborki.html
116. Ошибка репрезентативности, методика вычисления ошибки средней и относительной величины
В статистике выделяют два основных метода исследования – сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений.
При выборе единиц наблюдения возможны Ошибки смещения, т. е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными.
При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки – Случайная ошибка репрезентативности (M) – Является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности.
- Оценка достоверности результатов исследования предусматривает определение:
- 1. ошибки репрезентативности
- 2. доверительных границ средних (или относительных) величин в генеральной совокупности
- 3. достоверности разности средних (или относительных) величин (по критерию t)
- Расчет ошибки репрезентативности (mм) средней арифметической величины (М):
- , где σ – среднее квадратическое отклонение; n – численность выборки (>30).
- Расчет ошибки репрезентативности (mР) относительной величины (Р):
- , где Р – соответствующая относительная величина (рассчитанная, например, в %);
- Q =100 – Ρ% – величина, обратная Р; n – численность выборки (n>30)
В клинических и экспериментальных работах довольно часто приходится использовать Малую выборку, Когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, Число наблюдений уменьшается на единицу, т. е.
Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным.
Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности.
Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований.
Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%.
В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7%
- Определенной степени вероятности безошибочного прогноза соответствует определенная величина Предельной ошибки случайной выборки (Δ – дельта), которая определяется по формуле:
- Δ=t * m, где t – доверительный коэффициент, который при большой выборке при вероятности безошибочного прогноза 95% равен 2,6; при вероятности безошибочного прогноза 99% – 3,0; при вероятности безошибочного прогноза 99,7% – 3,3, а при малой выборке определяется по специальной таблице значений t Стьюдента.
- Используя предельную ошибку выборки (Δ), можно определить Доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, Характеризующей всю генеральную совокупность (средней или относительной).
- Для определения доверительных границ используются следующие формулы:
- 1) для средних величин:
Мвыб – средняя величина, Полученная при проведении исследования на выборочной совокупности; t – доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; mM – ошибка репрезентативности средней величины.
2) для относительных величин:
Доверительные границы показывают, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера.
При малом числе наблюдений (n
Источник: https://uchenie.net/116-oshibka-reprezentativnosti-metodika-vychisleniya-oshibki-srednej-i-otnositelnoj-velichiny/
Ошибки репрезентативности. Ошибки выборки
Любое выборочное наблюдение ставит своей задачей определение среднего размера признака или доли единиц, обладающих данным признаком, и распространение полученных характеристик выборочной совокупности на генеральную совокупность.
Ошибки репрезентативности возникают вследствие различия структуры выборочной и генеральной совокупности.
Структура генеральной совокупности вполне однозначна, и ей соответствует вполне определенное значение среднего размера (или доли) изучаемого признака. Выборочная же совокупность формируется на основе случайного отбора, в силу этого ее состав отличается от состава генеральной совокупности, отличается, естественно, и значение среднего размера (или доли) изучаемого признака.
Если из одной и той же генеральной совокупности производится несколько выборок, то в каждую из них попадут разные единицы и, следовательно, каждой выборочной совокупности будет соответствовать своя средняя. Отсюда следует важный вывод: выборочная средняя, в отличие от генеральной, – величина переменная. Переменной или случайной величиной будет и ошибка репрезентативности.
В практических статистических работах выборочное наблюдение проводится один раз, поэтому фактически приходится иметь дело с одной из множества выборочных средних, но с какой именно – сказать невозможно.
Чтобы получить суждение о точности результатов выборочного наблюдения, математическая статистика дает формулу средней ошибки, т.е.
средней величины из всех возможных ошибок при бесчисленном множестве случайных выборок.
При бесконечно большом числе выборок получится кривая частот, которая представляет кривую выборочного распределения.
Рассмотрим выборочное распределение средней величины.
Такое распределение будет являться нормальным или приближаться к нему по мере увеличения объема выборки независимо от того, имеет или не имеет нормальное распределение та генеральная совокупность, из которой взяты выборки.
С увеличением числа выборок средняя для всех выборок будет приближаться к генеральной средней. По выборочному распределению может быть рассчитана средняя квадратическая ошибка репрезентативности:
Среднее квадратическое отклонение выборочных средних от генеральной средней называется средней ошибкой выборочной средней (средней ошибкой выборки для средней величины признака):

Поскольку, как правило, генеральная средняя неизвестна, этой формулой нельзя воспользоваться. Кроме того, в социально-экономических исследованиях выборки из одной и той же совокупности не производятся многократно. Поэтому используют нижеприведенную формулу, исходя из того, что средняя ошибка выборки зависит от колеблемости признака в генеральной совокупности и числа отобранных единиц.
Средняя ошибка выборки для средней величины признака определяется по формуле:
где s2г – дисперсия количественного признака в генеральной совокупности.
Следовательно, средняя ошибка выборки тем больше, чем больше вариация в генеральной совокупности, и тем меньше, чем больше объем выборки.
Т.о. можно утверждать, что отклонение выборочной средней от генеральной средней в среднем равно . Ошибка конкретной выборки может принимать различные значения, но ее отношение к средней ошибке практически не превышает , если величина объема выборки достаточно большая .
- Отношение ошибки конкретной выборки к средней квадратической ошибке называется нормированным отклонением :
- .
- Распределение нормированного отклонения выборочной средней от генеральной средней при численности выборки определяется следующим уравнением:
- (1)
Данное уравнение называют стандартным уравнением нормальной кривой. Величина достигает максимума при , в этом случае .
На рис. приведен график кривой распределения нормированных отклонений ошибок выборочных средних .
Рис.
Ординаты соответствуют плотностям вероятности при том или ином значении . Для того, чтобы определить вероятность значений в интервале от до , следует найти отношение части площади кривой, заключенной между ординатами, соответствующими и ко всей площади кривой. Вся площадь под кривой нормального распределения вероятностей принимается за единицу.
- Площадь нормальной кривой, заключенную между ординатами и , определяют, интегрируя функцию (1) – интеграл Лапласа.
- Имеются таблицы интеграла Лапласа, которые содержат значения вероятностей для нормированных отклонений . Значения функции Ф(t) табулированы при разных значениях, например:
- при t=1 P(D£ m) = Ф(1) = 0,683;
- при t=2 P(D£2m) = Ф(2) = 0,9545;
при t=3 P(D£3m) = Ф(3) = 0,9973 и т.д.
- Это вероятность того, что ошибка попадет в заданные пределы.
- В общем виде
- D=tm
характеризует предельную ошибку выборки, показывающую максимально возможное расхождение выборочной и генеральной характеристик при заданной вероятности этого утверждения. Т.о. о величине ошибки можно судить с определенной вероятностью.
- Так, при t=2 возможная ошибка D не превысит 2m, что гарантируется с вероятностью 0,9545. Это значит, что в 9545 выборках из 10000 подобных максимальная ошибка не выйдет за пределы ±2m,
- где – это коэффициент доверия.
- При проведении выборочного учета массовых социально-экономических явлений считается достаточным максимальный размах ошибки выборки ±3m.
- На практике наиболее часто пользуются значениями вероятности Р=0,95 (t=1,96), Р=0,99 (t=2,58) и Р=0,999 (t=3,28), гарантирующими репрезентативность выборки соответственно с ошибкой 5; 1; 0,1%.
Предельная ошибка выборки позволяет определять предельные значения характеристик генеральной совокупности при заданной вероятности, т.е. их доверительные интервалы.
Поэтому вероятность Р называется доверительной, она представляет собой вероятность того, что ошибка выборки не превысит некоторую заданную величину D, т.е. генеральная средняя находится где-то в пределах
- (от до ),
- генеральная доля – в пределах
- (от w–D до w+D).
- Как мы определили выше, средняя ошибка выборки для средней величины признака определяется по формуле:
- ,
- где s2г – дисперсия количественного признака в генеральной совокупности.
- Если при выборочном наблюдении изучению подлежит альтернативный признак, то средняя ошибка выборки для доли единиц, обладающих данным признаком, определяется по теореме Я. Бернулли:
- ,
- где p – доля единиц, обладающих данным качеством, в генеральной совокупности; p(1-p) – дисперсия альтернативного признака в генеральной совокупности.
Приведенные формулы средних ошибок выборки практически непригодны для расчета. В них фигурирует дисперсия признака в генеральной совокупности, которая неизвестна, как неизвестна и генеральная доля, генеральная средняя. Поскольку в теории вероятности доказано, что
,
то при большом объеме выборки дисперсии генеральной s2г и выборочной s2 совокупностей равны. ( ). Это дает основание исчислять среднюю ошибку выборки по значениям выборочной дисперсии s2 для средней и w(1–w) для доли признака:
- , ,
- где w – доля признака в выборочной совокупности.
- Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется отношением предельной ошибки средней или доли к соответствующей характеристике выборочной совокупности:
- ; .
При проведении выборочного наблюдения в экономических исследованиях преимущественно стремятся к тому, чтобы относительная ошибка репрезентативности выборки не превышала 5 … 10%.
Вывод формул , ,
исходит из схемы повторной выборки. На практике повторная выборка, при которой численность генеральной совокупности остается неизменной (т.е.отобранная единица возвращается в генеральную совокупность и снова может быть отобрана), встречается редко (например, при изучении населения в качестве пользователей, пациентов, избирателей).
- Обычно отбор организуется по схеме бесповторной выборки, при которой отобранная единица после обследования в генеральную совокупность не возвращается и в дальнейшей выборке не участвует.
- При бесповторной выборке численность генеральной совокупности в процессе отбора сокращается на
- 1–n/N, где n/N – доля отобранных единиц.
- В связи с этим формулы ошибки выборки приобретают следующий вид:
- ; .
- Так как доля единиц генеральной совокупности, не попавших в выборку (1–n/N), всегда меньше единицы, то ошибка выборки при бесповторном отборе при прочих равных условиях меньше, чем при повторном отборе.
Источник: https://infopedia.su/10x41a.html
2.2.2. Стихийная выборка
Исследователь при
применении данного метода в некоторой
степени контролирует выборку (например,
публикуя анкету в журнале, он обращается
только к читателям этого журнала), но
решение о включении в выборку принимает
сам респондент.
То есть, её размер заранее
часто не известен, а определяется
конкретным условием — активностью
респондентов. Значит, нельзя и заранее
определить структуру массива респондентов,
которые заполнят и вернут анкеты.
Поэтому
этот метод не претендует на репрезентативность
выборки, а выводы исследования очень
часто распространяются только на
опрошенную совокупность.
Сферы применения
стихийной выборки:
-
анкеты, публикуемые в газетах и журналах;
-
почтовые опросы1;
-
опросы покупателей в залах супермаркетов;
-
опрос пассажиров на остановках и в общественном транспорте2.
2.3. Многоступенчатая и одноступенчатая выборки
Выборка делится
на одноступенчатую и многоступенчатую
по количеству ступеней в отборе.
Одноступенчатая выборка предполагает,
что из генеральной совокупности сразу
осуществляется отбор респондентов для
опроса.
Процедура же многоступенчатой
выборки включает несколько ступеней,
при этом на каждой из них единица отбора
меняется. «Различают единицы отбора
первой ступени (первичные единицы),
единицы отбора вторичной ступени
(вторичные единицы) и так далее.
Объекты
самой нижней ступени, с которых ведется
непосредственный сбор информации,
называются единицами наблюдения»3.
Например, задача исследования – изучение
свободного времени студентов всей
страны.
Процедура будет
строиться следующим образом:
-
отбор регионов;
-
отбор города в них, где есть вузы;
-
отбор учебных заведений, в которых будет проводиться исследование;
-
выбор академических групп;
-
отбор студентов.
Многоступенчатая
выборка осуществляется не в локальных
масштабах, а в региональных, общенациональных,
международных. Использовать одноступенчатую
выборку в таких масштабах нерационально,
да и очень дорого обойдётся такое
исследование. Многоступенчатая выборка
в этом плане экономична и упрощает
подход к выбору объекта.
- Но нужно
учитывать, что чем больше ступеней в
выборке, тем больше будет ошибка
репрезентативности, возрастёт вероятность
погрешностей, что приведёт к искажению
результатов исследования4. - Рассмотрев
некоторые типы выборок, необходимо
также уяснить, что такое объем выборки
и какие бывают ошибки выборки и как их
избежать. - В
формировании выборочной совокупности
важную роль играет определение ее объема
и обеспечение репрезентативности.
«Если тип выборки
говорит о том, как попадают люди в
выборочную совокупность, то объём
выборки сообщает о том, какое их
количество попало сюда»2. То есть объем выборки – это количество
единиц попавших в выборочную совокупность.
И очень важно, чтобы выборка была
репрезентативной, то есть не искажала
представлений о генеральной совокупности
вцелом3.
«Требования репрезентативности выборки
означают, что по выделенным параметрам
(критериям) состав обследуемых должен
приближаться к соответствующим пропорциям
в генеральной совокупности»4.
Одна из ключевых
проблем, встающих, как правило, перед
социологом, решающим: доверять полученным
в ходе него данным или нет, это то, сколько
же человек должно быть опрошено для
того, чтобы получить действительно
репрезентативную информацию.
К сожалению,
единой и четкой формулы, используя
которую можно было бы рассчитать
оптимальный объем выборочной совокупности,
не существует в природе. И объясняется
это весьма просто.
Дело в том, что
определение объема выборочной совокупности
– это проблема не столько статистическая,
сколько содержательная.
Иными словами,
объем выборочной совокупности зависит
от множества факторов, основные из них
следующие:
-
затраты на сбор информации, включая временные;
-
стремление к определённой статистической достоверности результатов, которую надеется получить исследователь;
-
ценность и новизна информации, получаемой в результате опроса5.
Объем
выборки обусловлен степенью однородности
или неоднородности, генеральной
совокупности, количеством характеризующих
ее признаков.
Однородной считается совокупность,
в которой контролируемый признак,
например уровень грамотности, распределён
равномерно, то есть не образует пустот
и сгущений, тогда опросив лишь несколько
человек, можно сделать вывод о том, что
большинство людей грамотны.
Чем более
однородна генеральная совокупность,
тем меньше объем выборки. Например,
«допустим, мы осуществляем отбор из
генеральной совокупности в 2000 человек,
контролируя состав выборочной совокупности
по признаку «пол»»: 70% мужчин и 30% женщин.
Согласно теории вероятности, можно
предположить, что примерно среди каждых
десяти отбираемых респондентов встретятся
три женщины. Если мы хотим опросить по
крайней мерее 90 женщин, то исходя из
вышеупомянутого соотношения, нам
необходимо отобрать не менее 300 человек.
А теперь предположим, что в генеральной
совокупности 90% мужчин и 10% женщин. В
этом случае, чтобы в выборочную
совокупность попало 90 женщин, необходимо
отобрать уже не менее 900 человек»1.
Из примера видно, что объем выборки
зависит от разброса признака (дисперсии),
и его нужно вычислять по признаку,
дисперсия значений которого наибольшая.
«Степень
однородности социального объекта
зависит, в сущности, от того, насколько
детально мы намерены его исследовать.
Практически любой, самый «элементарный»
объект оказывается чрезвычайно сложным.
Лишь в анализе мы представляем его как
относительно простой, выделяя те или
иные его свойства.
Чем более основательным
и детальным будет анализ, чем больше
свойств данного объекта мы намерены
принять во внимание в их сочетании, а
не изолированно, тем больше должен быть
объем выборки»2.
Существуют, так
называемые «правила левой руки» для
определения размера выборки (таблица
1)»3:
| Размер выборки растёт | Размер выборки уменьшается |
| — при необходимости опубликовать данные для отдельных подгрупп (размеры подвыборок при этом суммируются, и выборка в целом растёт пропорционально числу подгрупп); | — при исследовании организаций, институтов и прочих «первичных единиц отбора», если сравнительно невелика величина генеральной совокупности, из которой производится отбор(например, совокупности сотрудников рекламных агентств, школьников, пациентов и т.п.); |
| — при проведении общенациональных обследований, когда велика генеральная совокупность; | — при проведении локальных и региональных исследований; |
Источник: https://studfile.net/preview/5996791/page:7/
Ошибки выборки
Расхождения между величиной какого-либо показателя, найденного посредством статистического наблюдения, и действительными его размерами называются ошибками наблюдения. В зависимости от причин возникновения различают ошибки регистрации и ошибки ре- пр ез ентативн о сти.
Ошибки регистрации возникают в результате неправильного установления фактов или ошибочной записи в процессе наблюдения или опроса. Они бывают случайными или систематическими.
Случайные ошибки регистрации могут быть допущены как опрашиваемыми в их ответах, так и регистраторами. Систематические ошибки могут быть и преднамеренными, и непреднамеренными. Преднамеренные — сознательные, тенденциозные искажения действительного положения дела.
Непреднамеренные вызываются различными случайными причинами (небрежность, невнимательность).
Ошибки репрезентативности (представительности) возникают в результате неполного обследования и в случае, если обследуемая совокупность недостаточно полно воспроизводит генеральную совокупность. Они могут быть случайными и систематическими.
Случайные ошибки репрезентативности — это отклонения, возникающие при несплошном наблюдении из-за того, что совокупность отобранных единиц наблюдения (выборка) неполно воспроизводит всю совокупность в целом. Систематические ошибки репрезентативности — это отклонения, возникающие вследствие нарушения принципов случайного отбора единиц.
Ошибки репрезентативности органически присущи выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную.
Избежать ошибок репрезентативности нельзя, однако, пользуясь методами теории вероятностей, основанными на использовании предельных теорем закона больших чисел, эти ошибки можно свести к минимальным значениям, границы которых устанавливаются с достаточно большой точностью.
Ошибки выборки — разность между характеристиками выборочной и генеральной совокупности. Для среднего значения ошибка будет определяться по формуле
Величина называется предельной ошибкой выборки.
Предельная ошибка выборки — величина случайная. Исследованию закономерностей случайных ошибок выборки посвящены предельные теоремы закона больших чисел. Наиболее полно эти закономерности раскрыты в теоремах П.Л. Чебышева и А.М. Ляпунова.
Теорему П.Л. Чебышева применительно к рассматриваемому методу можно сформулировать следующим образом: при достаточно большом числе независимых наблюдений можно с вероятностью, близкой к единице (т.е.
почти с достоверностью), утверждать, что отклонение выборочной средней от генеральной будет сколько угодно малым. В теореме П.Л. Чебышева доказано, что величина ошибки не должна превышать tp .
В свою очередь величина Р, выражающая среднее квадратическое отклонение выборочной средней от генеральной средней, зависит от колеблемости признака в генеральной совокупности о- и числа отобранных единиц п. Эта зависимость выражается формулой
- где Р зависит также от способа производства выборки.
- Величину М = о2 называют средней ошибкой выборки. В этом V п
- выражении а2 — генеральная дисперсия, п — объем выборочной совокупности.
Рассмотрим, как влияет на величину средней ошибки число отбираемых единиц п. Логически нетрудно убедиться, что при отборе большого числа единиц расхождения между средними будут меньше, т.е.
существует обратная связь между средней ошибкой выборки и числом отобранных единиц.
При этом здесь образуется не просто обратная математическая зависимость, а такая зависимость, которая показывает, что квадрат расхождения между средними обратно пропорционален числу отобранных единиц.
Увеличение колеблемости признака влечет за собой увеличение среднего квадратического отклонения, а, следовательно, и ошибки. Если предположить, что все единицы будут иметь одинаковую величину признака, то среднее квадратическое отклонение станет равно нулю и ошибка выборки также исчезнет.
Тогда нет необходимости применять выборку. Однако следует иметь в виду, что величина колеблемости признака в генеральной совокупности не известна, поскольку не известны размеры единиц в ней. Можно рассчитать лишь колеблемость признака в выборочной совокупности.
Соотношение между дисперсиями генеральной и выборочной совокупности выражается формулой
Поскольку величина п при достаточно больших п близка к 1, п — 1
можно приближенно считать, что выборочная дисперсия равна генеральной дисперсии, т.е. Орен ж •
Следовательно, средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Однако о величине этой ошибки можно судить с определенной вероятностью. На величину вероятности указывает множитель t.
Теорема А.М. Ляпунова. А.М. Ляпунов доказал, что распределение выборочных средних (следовательно, и их отклонений от генеральной средней) при достаточно большом числе независимых наблюдений приближенно нормально при условии, что генеральная совокупность обладает конечной средней и ограниченной дисперсией.
Математически теорему Ляпунова можно записать так:
- Где
- где я = 3,14 — математическая постоянная;
- — предельная ошибка выборки, которая дает возможность выяснить, в каких пределах находится величина генеральной средней.
- Значения этого интеграла для различных значений коэффициента доверия t вычислены и приводятся в специальных математических таблицах. В частности, при:
Поскольку t указывает на вероятность расхождения х — х , т.е.
на вероятность того, на какую величину генеральная средняя будет отличаться от выборочной средней, то это может быть прочитано так: с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превышает одной величины средней ошибки выборки.
Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы ±Ц. С вероятностью 0,954 можно утверждать, что ошибка репрезентативности не превышает ± 2р (т.е. в 95% случаев). С вероятностью 0,997, т.е.
довольно близкой к единице, можно ожидать, что разность между выборочной и генеральной средней не превзойдет трехкратной средней ошибки выборки и т.д.
- Логически связь здесь выглядит довольно ясно: чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью судят о ее величине.
- Зная выборочную среднюю величину признака (х) и предельную ошибку выборки можно определить границы (пределы), в
- которых заключена генеральная средняя
Источник: https://bstudy.net/710108/ekonomika/oshibki_vyborki





.jpg)

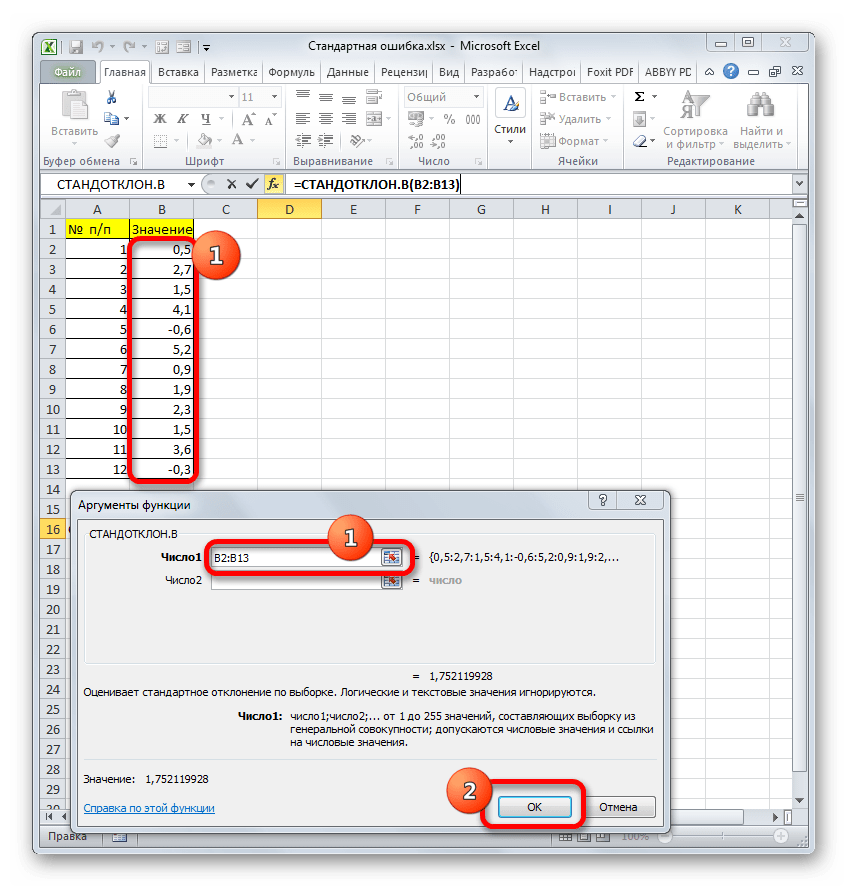
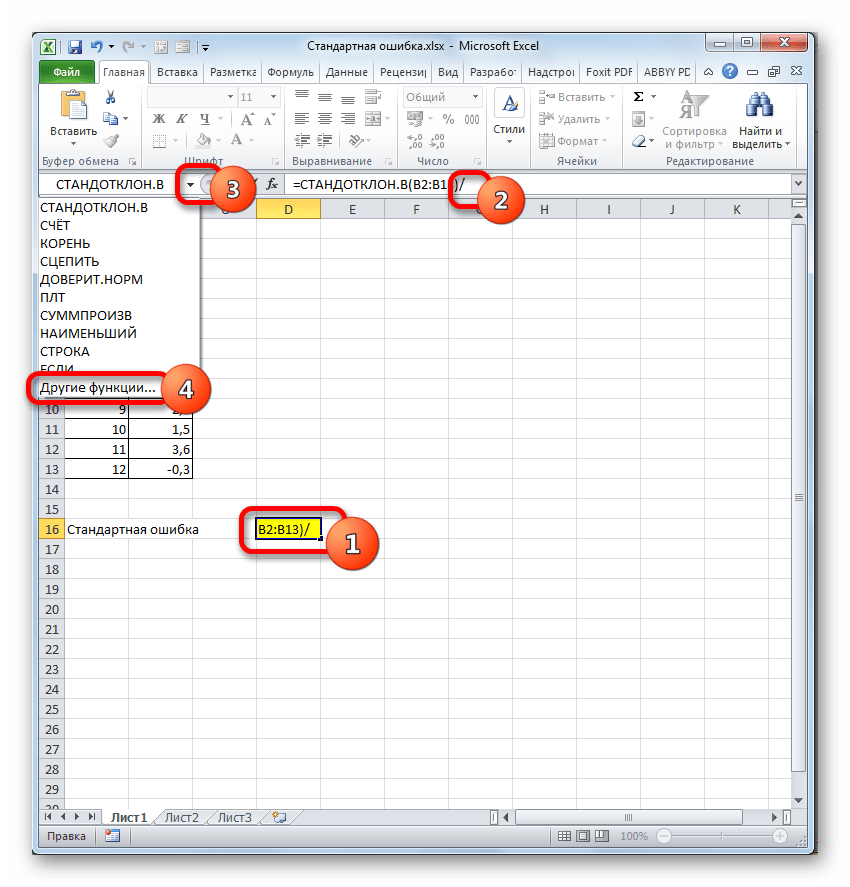
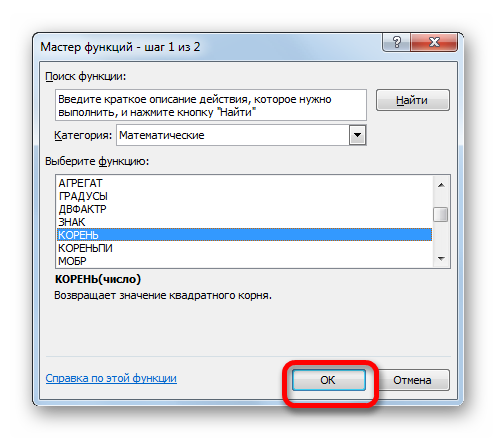

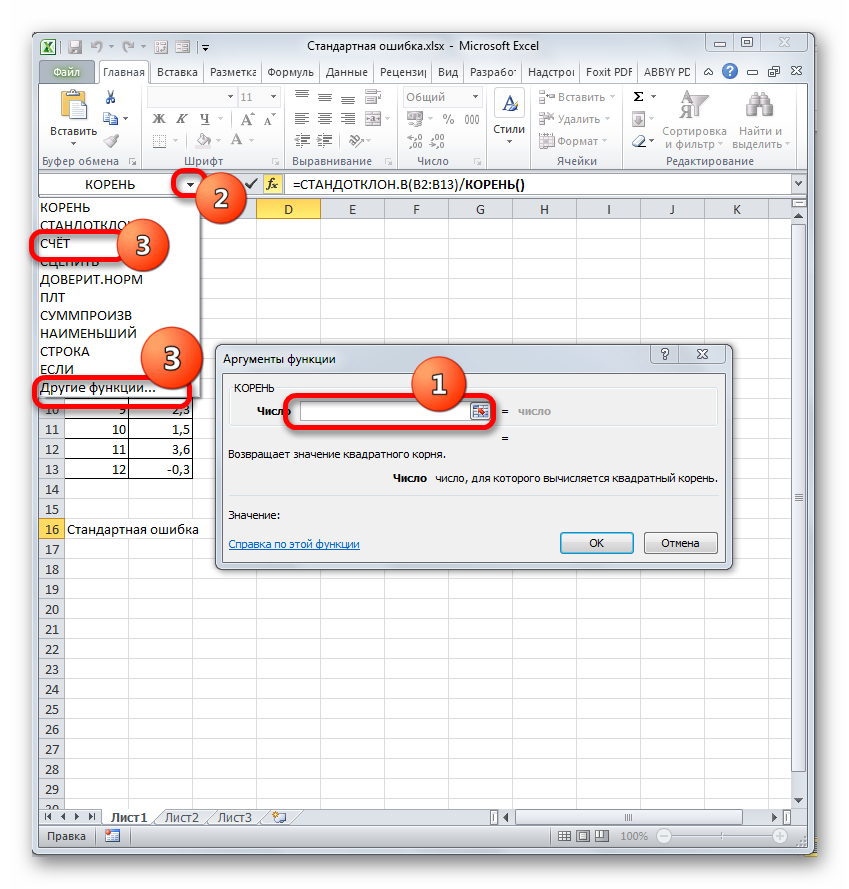
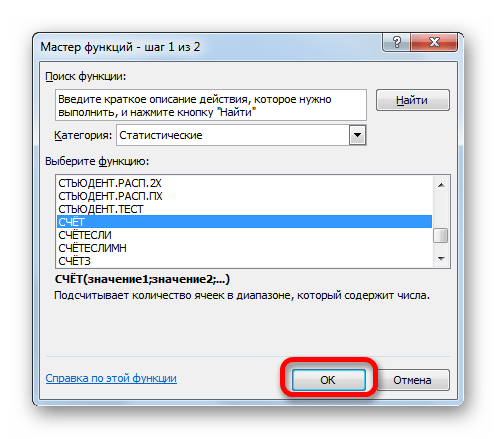
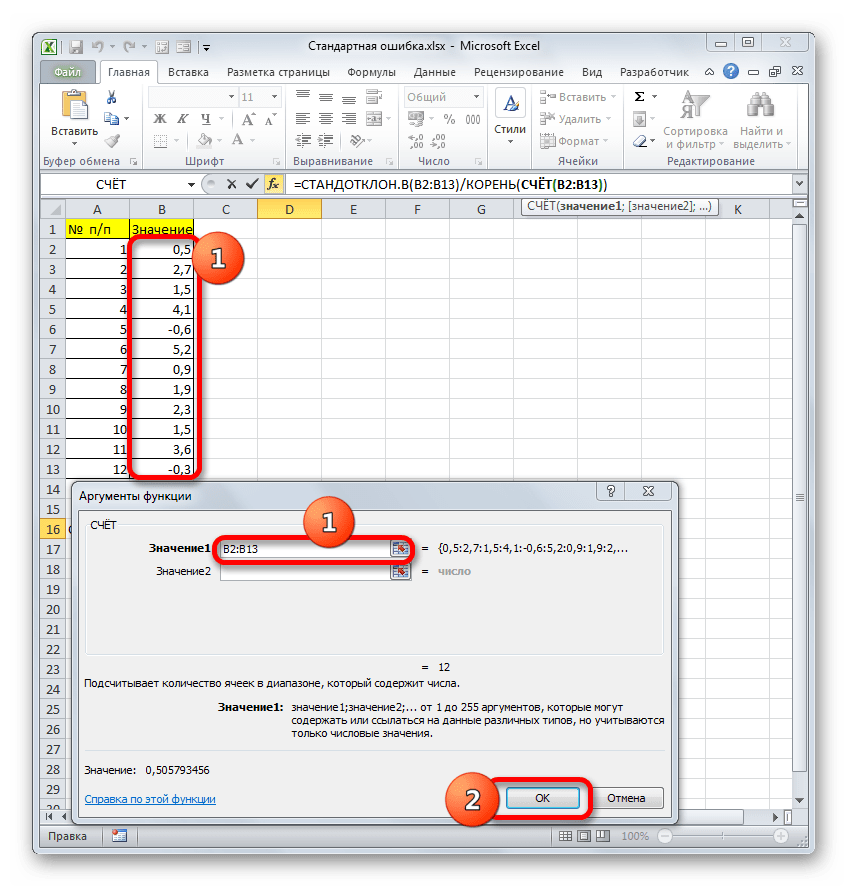
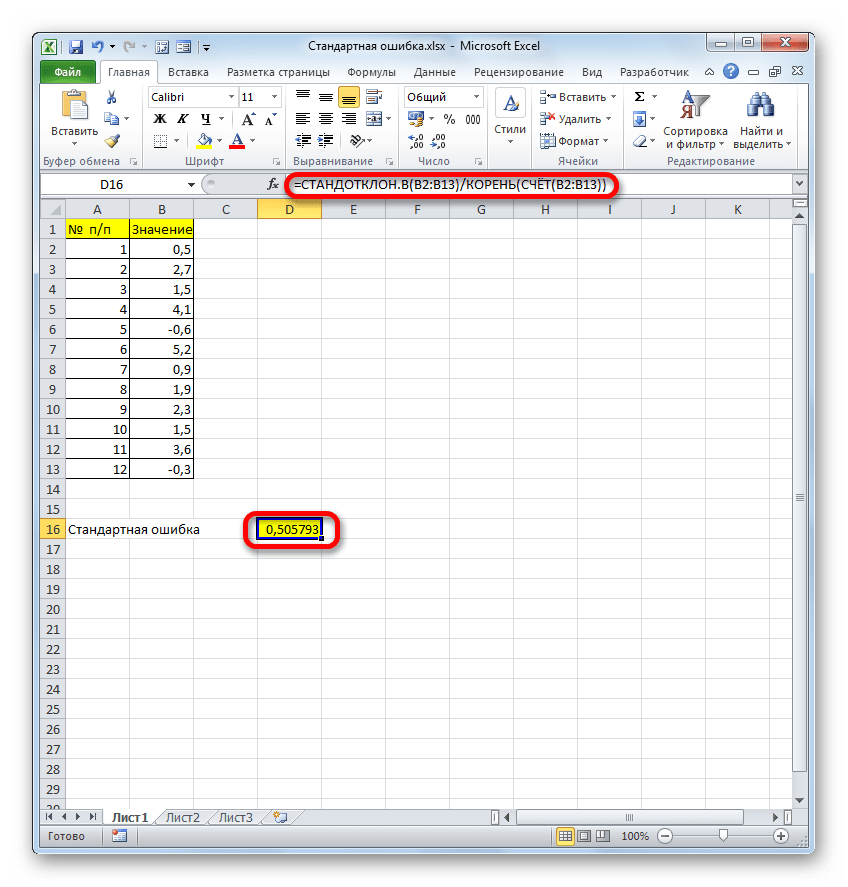
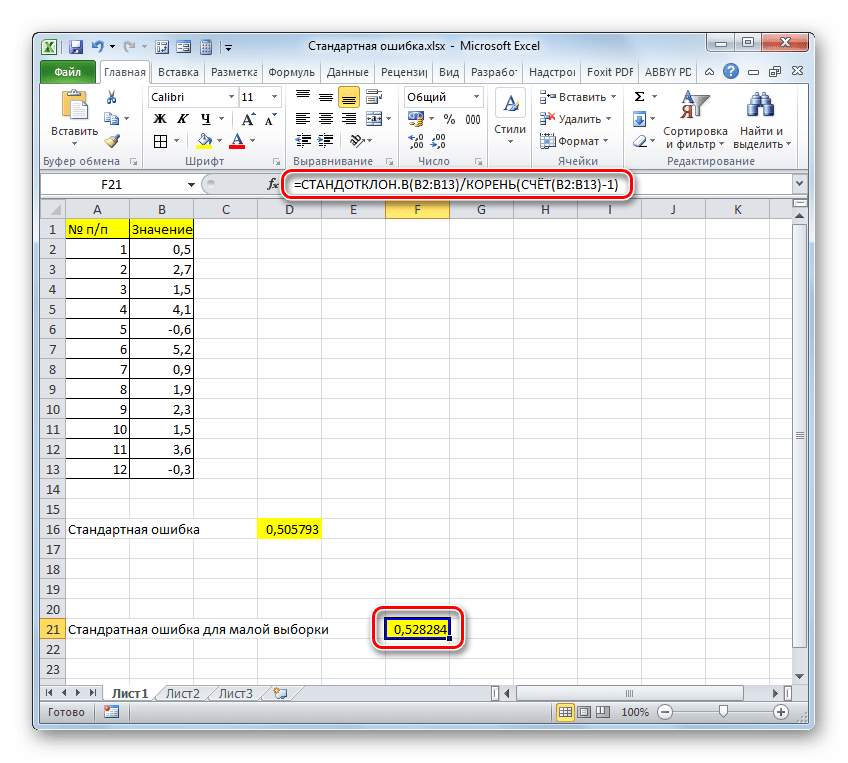
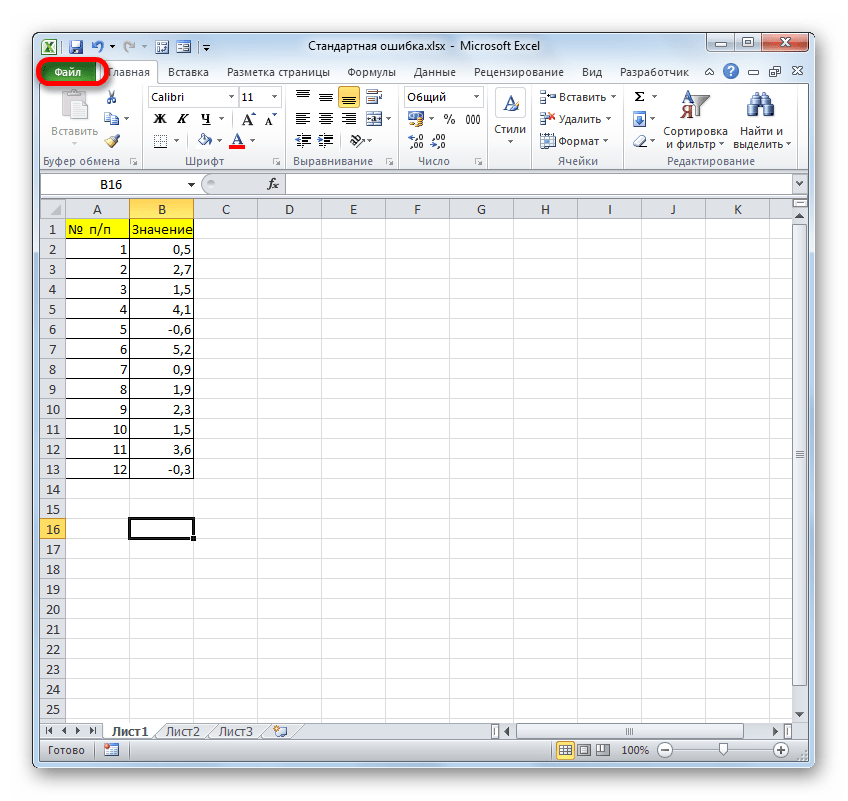
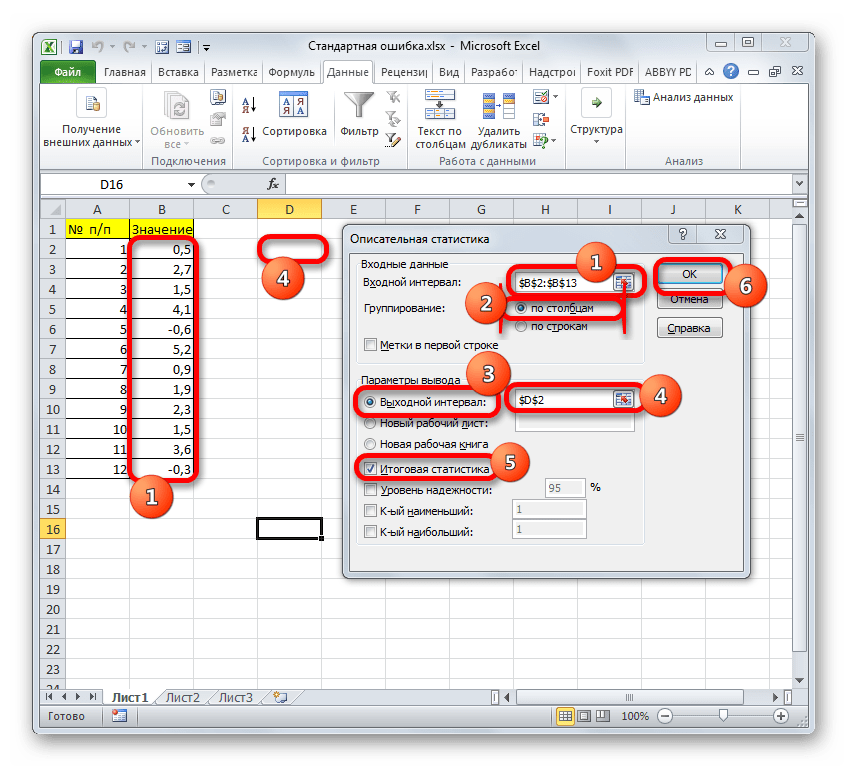
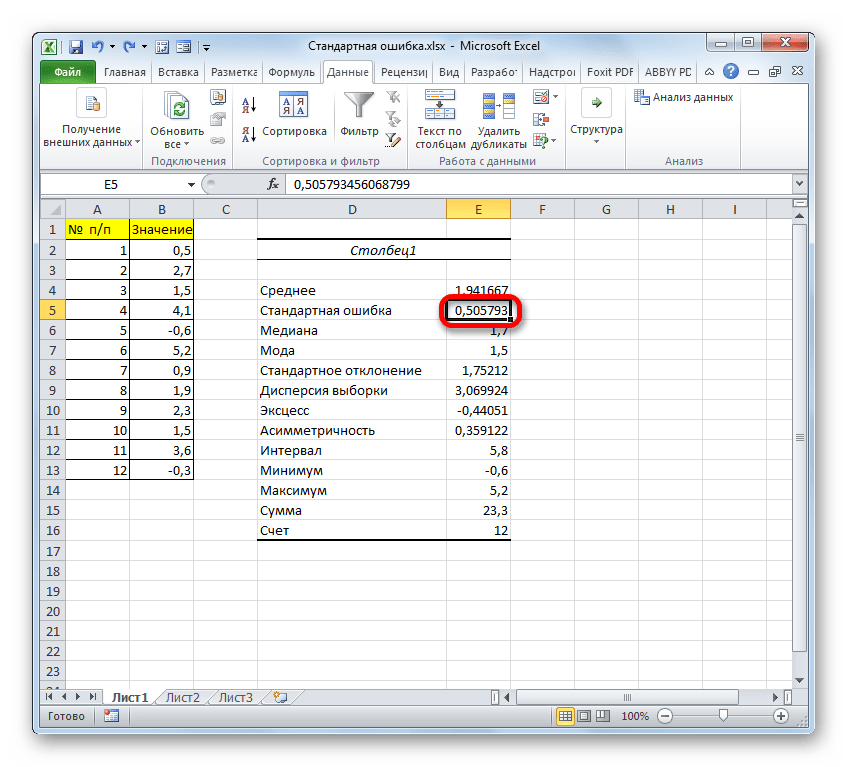



 ,
,

