From Wikipedia, the free encyclopedia
Human error assessment and reduction technique (HEART) is a technique used in the field of human reliability assessment (HRA), for the purposes of evaluating the probability of a human error occurring throughout the completion of a specific task. From such analyses measures can then be taken to reduce the likelihood of errors occurring within a system and therefore lead to an improvement in the overall levels of safety. There exist three primary reasons for conducting an HRA: error identification, error quantification, and error reduction. As there exist a number of techniques used for such purposes, they can be split into one of two classifications: first-generation techniques and second generation techniques. First generation techniques work on the basis of the simple dichotomy of ‘fits/doesn’t fit’ in the matching of the error situation in context with related error identification and quantification and second generation techniques are more theory based in their assessment and quantification of errors. HRA techniques have been used in a range of industries including healthcare, engineering, nuclear, transportation, and business sectors. Each technique has varying uses within different disciplines.
HEART method is based upon the principle that every time a task is performed there is a possibility of failure and that the probability of this is affected by one or more Error Producing Conditions (EPCs) – for instance: distraction, tiredness, cramped conditions etc. – to varying degrees. Factors which have a significant effect on performance are of greatest interest. These conditions can then be applied to a «best-case-scenario» estimate of the failure probability under ideal conditions to then obtain a final error chance. This figure assists in communication of error chances with the wider risk analysis or safety case. By forcing consideration of the EPCs potentially affecting a given procedure, HEART also has the indirect effect of providing a range of suggestions as to how the reliability may therefore be improved (from an ergonomic standpoint) and hence minimising risk.
Background[edit]
HEART was developed by Williams in 1986.[1] It is a first generation HRA technique, yet it is dissimilar to many of its contemporaries in that it remains to be widely used throughout the UK. The method essentially takes into consideration all factors which may negatively affect performance of a task in which human reliability is considered to be dependent, and each of these factors is then independently quantified to obtain an overall Human Error Probability (HEP), the collective product of the factors.
HEART methodology[edit]
1. The first stage of the process is to identify the full range of sub-tasks that a system operator would be required to complete within a given task.
2. Once this task description has been constructed a nominal human unreliability score for the particular task is then determined, usually by consulting local experts. Based around this calculated point, a 5th – 95th percentile confidence range is established.
3. The EPCs, which are apparent in the given situation and highly probable to have a negative effect on the outcome, are then considered and the extent to which each EPC applies to the task in question is discussed and agreed, again with local experts. As an EPC should never be considered beneficial to a task, it is calculated using the following formula:
- Calculated Effect = ((Max Effect – 1) × Proportion of Effect) + 1
4. A final estimate of the HEP is then calculated, in determination of which the identified EPC’s play a large part.
Only those EPC’s which show much evidence with regards to their affect in the contextual situation should be used by the assessor.[2]
Worked example[edit]
Context[edit]
A reliability engineer has the task of assessing the probability of a plant operator failing to carry out the task of isolating a plant bypass route as required by procedure. However, the operator is fairly inexperienced in fulfilling this task and therefore typically does not follow the correct procedure; the individual is therefore unaware of the hazards created when the task is carried out
Assumptions[edit]
There are various assumptions that should be considered in the context of the situation:
- the operator is working a shift in which he is in his 7th hour.
- there is talk circulating the plant that it is due to close down
- it is possible for the operator’s work to be checked at any time
- local management aim to keep the plant open despite a desperate need for re-vamping and maintenance work; if the plant is closed down for a short period, if the problems are unattended, there is a risk that it may remain closed permanently.
Method[edit]
A representation of this situation using the HEART methodology would be done as follows:
From the relevant tables it can be established that the type of task in this situation is of the type (F) which is defined as ‘Restore or shift a system to original or new state following procedures, with some checking’. This task type has the proposed nominal human unreliability value of 0.003.
Other factors to be included in the calculation are provided in the table below:
| Factor | Total HEART Effect | Assessed Proportion of Effect | Assessed Effect |
|---|---|---|---|
| Inexperience | x3 | 0.4 | (3.0-1) x 0.4 + 1 =1.8 |
| Opposite technique | x6 | 1.0 | (6.0-1) x 1.0 + 1 =6.0 |
| Risk Misperception | x4 | 0.8 | (4.0-1) x 0.8 + 1 =3.4 |
| Conflict of Objectives | x2.5 | 0.8 | (2.5-1) x 0.8 + 1 =2.2 |
| Low Morale | x1.2 | 0.6 | (1.2-1) x 0.6 + 1 =1.12 |
Result[edit]
The final calculation for the normal likelihood of failure can therefore be formulated as:
- 0.003 x 1.8 x 6.0 x 3.4 x 2.2 x 1.12 = 0.27
Advantages[edit]
- HEART is very quick and straightforward to use and also has a small demand for resource usage [3]
- The technique provides the user with useful suggestions as to how to reduce the occurrence of errors[4]
- It provides ready linkage between Ergonomics and Process Design, with reliability improvement measures being a direct conclusion which can be drawn from the assessment procedure.
- It allows cost benefit analyses to be conducted
- It is highly flexible and applicable in a wide range of areas which contributes to the popularity of its use [3]
Disadvantages[edit]
- The main criticism of the HEART technique is that the EPC data has never been fully released and it is therefore not possible to fully review the validity of Williams EPC data base. Kirwan has done some empirical validation on HEART and found that it had «a reasonable level of accuracy» but was not necessarily better or worse than the other techniques in the study.[5][6][7] Further theoretical validation is thus required.[2]
- HEART relies to a high extent on expert opinion, first in the point probabilities of human error, and also in the assessed proportion of EPC effect. The final HEPs are therefore sensitive to both optimistic and pessimistic assessors
- The interdependence of EPCs is not modelled in this methodology, with the HEPs being multiplied directly. This assumption of independence does not necessarily hold in a real situation.[2]
See also[edit]
- The curse of expertise
- Threat and error management
- Expert witnesses in English law
- Winner’s curse
- Sports Illustrated cover jinx
References[edit]
- ^ WILLIAMS, J.C. (1985) HEART – A proposed method for achieving high reliability in process operation by means of human factors engineering technology in Proceedings of a Symposium on the Achievement of Reliability in Operating Plant, Safety and Reliability Society (SaRS). NEC, Birmingham.
- ^ a b c Kirwan, B. (1994) A Guide to Practical Human Reliability Assessment. CPC Press.
- ^ a b Humphreys. P. (1995). Human Reliability Assessor’s Guide. Human Reliability in Factor’s Group.
- ^ «FAA Human Factors Workbench Display Page». Archived from the original on 2009-05-10. Retrieved 2008-08-27.
- ^ Kirwan, B. (1996) The validation of three human reliability quantification techniques — THERP, HEART, JHEDI: Part I — technique descriptions and validation issues. Applied Ergonomics. 27(6) 359-373.
- ^ Kirwan, B. (1997) The validation of three human reliability quantification techniques — THERP, HEART, JHEDI: Part II — Results of validation exercise. Applied Ergonomics. 28(1) 17-25.
- ^ Kirwan, B. (1997) The validation of three human reliability quantification techniques — THERP, HEART, JHEDI: Part III — practical aspects of the usage of the techniques. Applied Ergonomics. 28(1) 27-39.
External links[edit]
- HEART technique for Quantitative Human Error Assessment
- Human error analysis and reliability assessment — Michael Harrison
7.3. Оценка бухгалтерского риска
При оценке бухгалтерского риска в отношении отдельных статей баланса и показателей бухгалтерской отчетности организации в бухгалтерском деле необходимо принимать во внимание следующие факторы.
1. Условия и методы ведения производства
1.1 Жесткая конкуренция. Предприятие вынуждено быстро перестраиваться на производство конкурентоспособного продукта, а бухгалтеры могут быть еще не осведомлены о том, как правильно вести учет в новых условиях. Поэтому высок риск ошибки с их стороны. Это положение справедливо и для п. 1.2.
1.2 Быстрые изменения в технологии производства, установление новых информационных систем.
1.3. Изменение рынков сбыта и смена спроса клиентов.
1.4. Общее состояние отрасли и количество банкротств. В этом случае возможно возникновение нескольких причин. Причина первая – квалифицированные бухгалтеры перешли работать в более процветающие отрасли. Причина вторая – бухгалтеры умышленно стараются приукрасить положение предприятия и вуалируют убытки в публикуемой отчетности.
1.5. Национализация. Следствием этого процесса является не только смена прежнего руководства новым, которое обычно не знает специфики ведения производства, но и замена бухгалтеров, хорошо знакомых со своим делом.
1.6. Быстрые изменения в законодательстве, которые не успевают отслеживать бухгалтеры.
1.7. Законодательные ограничения по политическим причинам или ограничения, связанные с охраной окружающей среды, или др. Политические мотивы могут послужить причиной составления отчетности, которая не будет отражать финансовое положение предприятия, а будет отвечать политическим требованиям правящей партии, служить для рекламы экономических достижений установившегося политического режима и привлечения иностранных инвесторов.
Аналогична ситуация и с охраной окружающей среды. Если сильно влияние «зеленых» и предприятие выпускает отчетность, в которой показан ущерб, причиняемый природе, оно может потерять как фактических, так и потенциальных инвесторов.
2. Месторасположение (географическое)
2.1. Политическая нестабильность. В этом случае присутствует риск смены правительства, что, как правило, влечет за собой экономические реформы. Кроме того, руководители предприятия, понимая политическую несостоятельность для внешних инвесторов, могут постараться завуалировать отчетность с целью привлечения инвесторов.
2.2. Осуществление больших объемов реализации в районах с нестабильной экономической ситуацией. Возможные политические изменения могут привести к существенным суммам убытков и, как следствие, к поиску путей их сокрытия со стороны бухгалтеров.
2.3. Транспортные проблемы. Они могут стать причиной несвоевременной доставки требуемого количества товаров в определенные сроки, что приведет к срыву условий договора и снижению конкурентоспособности предприятия. Руководство в этом случае также может поставить бухгалтеру задачу «корректировки» результатов отдельных операций.
3. Штат и организация бизнеса
3.1. Доминирующая роль президента фирмы и неэффективная деятельность совета директоров предприятия. В этом случае главный бухгалтер должен составить отчетность, которая требуется с точки зрения президента фирмы. И совет директоров вряд ли будет осуществлять контроль за правильностью составления отчетности работы отдела.
3.2 Переоценка руководством фирмы внутреннего контроля. Слишком большое доверие отделу внутреннего контроля может отрицательно сказаться на подборе кадров в бухгалтерию. Ведущим будет принцип: зачем тратить деньги на квалифицированного бухгалтера, если есть качественный внутренний контроль, который позволит обнаружить все имеющиеся ошибки.
3.3. Личные проблемы финансового характера у президента фирмы. Он может использовать кассу фирмы для пополнения недостач в личном бюджете и порекомендовать главному бухгалтеру все это «прикрыть».
3.4. Проблемы и постоянные споры между акционерами и руководством фирмы. Это означает, что руководство действует не в интересах собственников, а преследует свои цели, что может привести к мошенничеству и злоупотреблениям.
3.5. Невысокий квалификационный уровень руководства и персонала фирмы, что сказывается на эффективности производства.
3.6. Слишком оптимистичный прогноз на будущее. Недооценка отрицательных фактов в настоящем может привести к их накоплению и превалированию в будущем. С экономической точки зрения это чревато банкротством, с бухгалтерской – тем, что пренебрежение незначительными признаками несостоятельности может отразиться в бухгалтерской отчетности.
3.6. Слишком большая децентрализация руководства. Не существует единого контроля за работой бухгалтерии. Каждый перекладывает ответственность на другого, а на самом деле ее нет.
3.7. Нехватка персонала. Это приводит к сверхурочной работе сотрудников и лишению их отпуска, что свидетельствует, с одной стороны, о нерациональной политике в отношении работы с персоналом, с другой – о том, что большая загруженность работой может стать причиной пропуска ошибки работником бухгалтерии.
3.8. Слишком большая ротация кадров на такой ключевой позиции, как финансовый директор. Финансовый директор определяет всю политику фирмы по ведению учета и составлению отчетности. И в случае быстрой и частой смены стратегии тактика может оставаться старой, что неизбежно повлечет за собой ошибки при оценке имущества, обязательств и составлении отчетности.
3.9. Частая смена бухгалтеров или юристов. Обычно это происходит в том случае, когда на фирме не все благополучно (в смысле злоупотреблений) и бухгалтеры (юристы), обнаружив это, стремятся как можно скорее найти выход.
3.10. Наем новых работников, плохо знакомых со спецификой производства и ведением учета.
3.11. Мошенничество и злоупотребления.
3.12. Наличие существенных операций, по которым возникают конфликты. Причины конфликтов могут быть разными, но чаще всего кто-то старается скрыть мошенничество путем, например, вуалирования отчетности, а кто-то пытается или не допустить этого, или своевременно обнаружить.
3.13 Необычно высокая плата за ординарные услуги (юристов, консультантов, агентов и др.). Возникает подозрение, не связано ли это с тем, что данным специалистам платят за молчание по поводу обнаруженных в отчетности фактов мошенничества и злоупотреблений?
3.14. Сложности с получением аудиторских доказательств при проведении аудита по следующим причинам:
а) наличие необычных или необъяснимых операций;
б) неполнота документов и отсутствие на документах санкций руководства;
в) исправления в документах.
Все это может указывать как на недобросовестность и небрежность руководства, так и на желание спрятать «лишнюю» информацию. И тот и другой случай свидетельствуют о наличии неверной информации в бухгалтерской документации.
3.15. Непредвиденные аудиторские проблемы, например:
а) давление со стороны клиента в целях быстрого завершения проверки;
б) неблагоприятные условия работы;
в) неожиданные отсрочки;
г) нереалистичные ответы руководства на запросы аудитора. Это свидетельствует о нежелании руководства допускать аудитора к самым важным данным об операциях клиента.
3.16. Крупные непредвиденные сделки по реализации продукции. Это говорит о нестабильности экономической политики фирмы, особенно в части деятельности отдела реализации. Вместе с тем данный факт может оказаться признаком или прикрытия крупных убытков, или продажи фирмы с целью ее последующей ликвидации.
3.17. Необычное ведение операций (новые агенты, новые условия сделки). Частота смены условий хозяйствования свидетельствует или о нестабильности экономического положения на фирме и стремлениях руководства исправить ситуацию, или о желании скрыть злоупотребления.
3.18. Распродажа продукции по демпинговым ценам за границей. Вероятнее всего, это может быть желание завоевать западный рынок, поскольку на нем ситуация более-менее стабильная, и перевод средств за границу с последующим «переводом» туда и руководства фирмы. Значит, в бухгалтерском учете и отчетности фирмы уже сейчас не все в порядке.
3.19. Ориентация на поглощение других фирм (или фирма сама является возможным объектом поглощения). Это указывает на нестабильность финансового положения фирмы. В первом варианте еще не известно, достоверны ли данные о положении поглощаемой фирмы, а во втором невозможно предсказать ее эффективную работу в рамках холдинга.
3.20. В деятельности фирмы наибольший удельный вес занимают операции с дочерними фирмами. Данный факт свидетельствует о возможности мошенничества и «перекачки» денег.
3.21. Зависимость вознаграждения руководства от финансовых показателей деятельности фирмы. В этом случае высока вероятность завышения доходности.
3.22. Плохая репутация руководства фирмы в деловых кругах.
3.23. Наличие фиктивных неработающих филиалов, секретных банковских счетов, неразрешенных фондов. Это уже нелегальная деятельность, и внутренний риск при ней очень высок.
4. Доходы и планы оперативной деятельности
4.1. Снижение количества и (или) качества реализуемой продукции. Сложности с производством и сбытом обычно влекут за собой вуалирование отчетности для привлечения инвесторов.
4.2. Значительные изменения процесса производства. Причины аналогичны причинам, приведенным в п. 1.2.
4.3. Зависимость от производства одного или нескольких продуктов, операций, дебиторов, кредиторов. Неудачная операция по реализации одного продукта, с одним клиентом может привести к полному краху фирмы.
4.4. Неэффективная маркетинговая политика. Она может привести к тому, что фирма потеряет свою нишу на рынке, а в дальнейшем – к банкротству фирмы, в ближайшем же будущем – к вуалированию отчетности для акционеров.
4.5. Неполное использование мощностей. Низкие показатели эффективности использования основного и оборотного капитала, которые следует скрыть от акционеров.
4.6. Нереальные цели развития производства. Основные причины: или недооценка деятельности конкурентов, или переоценка собственных возможностей, или непродуманная политика развития. В любом случае высока вероятность убытков, которые обычно стараются не афишировать.
4.7. Медленная замена устаревшего оборудования и снижение темпов начисления амортизационных отчислений. Это приведет к последствиям, описанным в комментариях к п. 4.5, но только в отношении основного капитала.
4.8. Спорные положения, которые не могут найти объяснения, например, необычные суммы сальдо по счетам, необычные отклонения по результатам инвентаризации, необычные коэффициенты оборачиваемости. Все это свидетельствует о наличии скрытых действий.
5. Имущество
5.1. Значительное снижение стоимости имущества. Свидетельствует или о близком банкротстве фирмы из-за обесценения имущества, или о его распродаже (хищении). И в том и в другом случае высок риск сокрытия ошибки в бухгалтерском учете.
5.2. Недостаточная сохранность имущества. Результат – его хищение и вуалирование баланса.
6. Ликвидность и финансирование
6.1. Неадекватный денежный поток. Когда фактическая сумма денежных поступлений не соответствует количеству реализованной продукции, это свидетельствует о наличии «подпольных» операций. Конечно, в этом случае не может быть все «верно и объективно» (принцип «true and fair view») в бухгалтерской отчетности.
6.2. Недостаток оборотного капитала. Указывает на нерациональность и неэффективность управления производством. Вероятным следующим этапом будет снижение объема производства и реализации из-за нехватки средств и запасов сырья для производства. В этом случае бухгалтеры, скорее всего, тоже не захотят терять акционеров и будут вуалировать отчетность.
6.3. Недостаточная гибкость в привлечении заемных средств. Связано с п. 6.2. Последствия могут быть аналогичными.
6.4. Нехватка акционерного капитала и проблемы его привлечения. Это свидетельствует уже о реальных, а не потенциальных проблемах на фирме. Люди не хотят вкладывать деньги в данную фирму, поскольку не доверяют ее управляющим.
7. Неожиданные убытки, возникшие в связи со следующим
7.1. С договорами на покупку и реализацию. Это означает потерю деловых партнеров, т. е. места и имиджа на рынке услуг. Далее следует потеря существующих и потенциальных акционеров.
7.2. С гарантиями третьим лицам: если фирма дала гарантии третьим лицам и из-за несостоятельности последних вынуждена была оплатить за них долги, результатом чего стали собственные убытки, то это говорит о недостаточно продуманной рыночной стратегии. Руководство фирмы, вероятно, не захочет афишировать этот факт, чтобы не отпугнуть клиентов и акционеров, и постарается не отражать его в отчетности.
7.3. С договорами аренды. В этом случае велик риск неверного отражения доходов в бухгалтерской отчетности.
7.4. С операциями с иностранными партнерами. Данные прблемы и подходы к ним аналогичны изложенным в п. 7.2.
7.5. С форс-мажорными обстоятельствами, связанными с природными катаклизмами.
Что касается оценки бухгалтерского риска в отношении конкретных счетов учета и однотипных групп фактов хозяйственной жизни, то бухгалтеру необходимо принимать во внимание следующие факторы.
Отдельные счета учета, данные которых чаще всего оказываются непреднамеренно искаженными. Повышающим бухгалтерский риск обстоятельствами могут быть: наличие у учетного персонала экономического субъекта проблем с отражением отдельных операций и сделок (возможность ошибок); необычные суммы сальдо по счетам (вероятность ошибок, возможность мошенничества); существенные отклонения по результатам инвентаризации (возможность хищения, отсутствие внутреннего контроля); исправления в документах (попытки скрыть факты мошенничества и злоупотреблений, сокрытие или занижение финансовых результатов в целях уменьшения налогооблагаемой базы).
Отдельные счета учета, в которых чаще всего появляются преднамеренные искажения вследствие высокой вероятности их использования для совершения злоупотреблений. Повышающим риск обстоятельствами могут быть операции между взаимозависимыми сторонами (сторона является зависимой, если другая сторона контролирует либо оказывает воздействие на ее финансовые и иные решения). Бухгалтер должен выявить и оценить признаки взаимозависимости: а) условия сделок, существенно отличающиеся от типичных (условия платежей, цены, гарантии и т. п.), б) отсутствие логической причины для совершения той или иной операции, в) отличный от обычного порядок оформления и отражения сделок, г) противоречия между формой и содержанием сделок, д) приоритет, отдаваемый без очевидных оснований определенным экономическим субъектам и поставщикам; отсутствие оправдательных документов либо визы руководства на них (неэффективность системы внутреннего контроля, возможность мошенничества); операции, в которых лично заинтересовано руководство или к которым оно проявляет повышенный и необычный интерес (возможность мошенничества).
Сложность учитываемых фактов хозяйственной жизни, которая требует для их правильного оформления высокой квалификации исполнителей (если квалификация специалистов не соответствует сложности операций, возрастает вероятность ошибки).
Наличие фактов хозяйственной жизни, бухгалтерское оформление которых может быть основано полностью или частично на субъективном мнении исполнителей. Повышающими риск обстоятельствами могут быть: необычные суммы сальдо по счетам; наличие необычных или необъяснимых операций.
Наличие фактов хозяйственной жизни, порядок правильного оформления которых неоднозначно трактуется действующим законодательством. Повышающими риск обстоятельствами могут быть: неоднозначный, а порой и противоречивый характер положений нормативных документов (высокая вероятность ошибок); наличие «неотрегулированных» операций.
Наличие редких, необычных, нестандартных фактов хозяйственной жизни, которые носят несистематический, разовый характер, требуют особого внимания и соответствующих знаний и устанавливаются во время краткого анализа бухгалтерской отчетности. Повышающими риск обстоятельствами могут быть: слишком высокая оплата ординарных услуг; наличие нестандартных сторнировочных записей; необычные суммы сальдо по счетам; исправления в документах; операции, редко встречающиеся в деятельности экономического субъекта; регулирующие записи, в том числе начисление резервов, и записи, связанные с окончанием периода (ошибки в исчислении, желание скрыть прибыль от налогообложения).
Основными источниками информации о факторах, оказывающих влияние на уровень бухгалтерского риска на фирме, являются:
а) официальные публикации в юридических изданиях, профессиональных, отраслевых и региональных журналах и монографиях;
б) статистические данные, официальные отчеты экономических субъектов, банковские отчеты;
в) нормативные и законодательные акты, регламентирующие деятельность проверяемого экономического субъекта;
г) результаты посещения специальных семинаров, конференций, других аналогичных мероприятий;
д) разъяснения и подтверждения, полученные от персонала проверяемого экономического субъекта, беседы с внутренним аудитором и другими компетентными лицами;
е) запросы третьим лицам;
ж) консультации аудитора, который проводил аудит в предыдущие периоды;
з) учредительные документы, протоколы собраний совета директоров и акционеров, контракты и договоры, бухгалтерская отчетность прошлых периодов, планы и бюджеты: положения о бухгалтерии, учетной политике, документообороте; рабочий план счетов и проводок; схема организационной и производственной структур;
и) результаты осмотра цехов, складов и служб проверяемого экономического субъекта, а также опрос персонала, непосредственно не связанного со сферой учета;
к) идентификация филиалов и структурных подразделений, выделенных на отдельный баланс, фактов хозяйственной жизни, методов учета и налогообложения в них;
л) результаты работы с привлеченными специалистами – экспертами;
м) реестр акционеров;
н) предыдущий опыт бухгалтера;
о) материалы налоговых проверок и судебных процессов. Основными методами сбора информации для оценки бухгалтерского риска являются:
а) изучение общеэкономических условий деятельности проверяемого экономического субъекта (например, национальная экономическая политика, система налогообложения и таможенного контроля, установление лимитов и квот);
б) анализ региональных особенностей, влияющих на деятельность экономического субъекта (например, географическое положение, экономические и налоговые условия региона);
в) учет отраслевых особенностей сферы деятельности экономического субъекта;
г) знакомство с организацией и технологией производства;
д) сбор информации о персонале экономического субъекта, ассортименте выпускаемой продукции, применяемых методах ведения бухгалтерского учета (форме, учетной политике, степени автоматизации);
е) сбор информации о структуре собственного капитала, анализ размещения и котировок акций;
ж) сбор информации об организационной и производственной структурах, проводимой маркетинговой политике, основных поставщиках и покупателях;
з) анализ деятельности экономического субъекта на рынке ценных бумаг (например, выдача векселей, операции с финансовыми векселями, покупка и продажа акций);
и) учет наличия и взаимоотношений с филиалами и дочерними (зависимыми) обществами и методов консолидации бухгалтерской отчетности, порядка распределения прибыли, остающейся в распоряжении экономического субъекта;
к) сбор информации о юридических и финансовых обязательствах экономического субъекта.
Таким образом, в основе оценки бухгалтерского риска лежит вероятность появления существенных искажений в данном бухгалтерском счете, статье баланса, однотипной группе фактов хозяйственной жизни. Для оценки бухгалтерского риска с учетом перечисленных факторов важно идентифицировать и правильно оценивать события, операции, используемые методы учета, которые могут оказывать существенное влияние на достоверность бухгалтерской отчетности экономического субъекта.
Данный текст является ознакомительным фрагментом.
Читайте также
91. Оценка уровня риска
91. Оценка уровня риска
Оценка уровня риска является одним из важнейших этапов риск – менеджмента, так как для управления риском его необходимо прежде всего проанализировать и оценить. В экономической литературе существует множество определения этого понятия, однако в
1. Оценка системы бухгалтерского учета
1. Оценка системы бухгалтерского учета
Информационной базой финансового контроля, т. е. источником сведений для финансового контроля над деятельностью организаций и индивидуальных предпринимателей, является бухгалтерский учет, который они ведут в соответствии с
17. Оценка системы бухгалтерского учета
17. Оценка системы бухгалтерского учета
Основными задачами учета являются:1) формирование полной и достоверной информации о деятельности организации и ее имущественном положении, необходимой внутренним и внешним пользователям бухгалтерской отчетности;2) обеспечение
68. Оценка уровня риска
68. Оценка уровня риска
Оценка уровня риска является одним из важнейших этапов риск – менеджмента, так как для управления риском его необходимо прежде всего проанализировать и оценить.В экономической литературе существует множество определения этого понятия, однако в
Оценка рыночного риска
Оценка рыночного риска
Рыночный риск – это риск изменения стоимости вашего актива в зависимости от рыночных колебаний цены актива. Другими словами, чем сильнее колеблется цена, тем выше рыночный риск.Здесь необходимо сказать о волатильности как об одном из показателей
Оценка валютного риска
Оценка валютного риска
Валютный риск – это риск изменения стоимости ваших активов в зависимости от колебаний курсов валют.Думаю, что все уже ощутили на себе, что такое валютный риск. Возможно, некоторые из вас пытались ловить выгодные курсы, чтобы купить или продать
64. Оценка уровня риска
64. Оценка уровня риска
Оценка уровня риска является одним из важнейших этапов риск – менеджмента, так как для управления риском его необходимо прежде всего проанализировать и оценить. В экономической литературе существует множество определения этого понятия, однако в
Оценка кредитного риска
Оценка кредитного риска
Кредитный риск – опасность несвоевременной или неполной уплаты долга и/или процентов, которая выражается в возможности возникновения убытков у кредитора.Основные причины кредитных рисков:1.отрецательные изменения в экономике страны, региона,
Оценка рыночного риска
Оценка рыночного риска
Рыночный риск – это риск изменения стоимости вашего актива в зависимости от рыночных колебаний цены актива. Другими словами, чем сильнее колеблется цена, тем выше рыночный риск.Здесь необходимо сказать о волатильности как об одном из показателей
Оценка валютного риска
Оценка валютного риска
Валютный риск – это риск изменения стоимости ваших активов в зависимости от колебаний курсов валют.Думаю, что все уже ощутили на себе, что такое валютный риск. Возможно, некоторые из вас пытались ловить выгодные курсы, чтобы купить или продать
31. ОЦЕНКА АУДИТОРСКОГО РИСКА И СИСТЕМЫ ВНУТРЕННЕГО КОНТРОЛЯ У СУБЪЕКТОВ, ИСПОЛЬЗУЮЩИХ ОБСЛУЖИВАЮЩИЕ ОРГАНИЗАЦИИ
31. ОЦЕНКА АУДИТОРСКОГО РИСКА И СИСТЕМЫ ВНУТРЕННЕГО КОНТРОЛЯ У СУБЪЕКТОВ, ИСПОЛЬЗУЮЩИХ ОБСЛУЖИВАЮЩИЕ ОРГАНИЗАЦИИ
Обслуживающая организация – это фирма, которая оказывает различные услуги по ведению бухгалтерского учета, подготовке финансовой отчетности. В этих
47. Оценка риска
47. Оценка риска
Анализ внешней бизнес-среды позволяет определить возможности и угрозы компании при решении воплотить в жизнь свои предпринимательские замыслы. Возможностями компании являются возможности удовлетворения потребностей потребителей. Угрозы внешней
4. Оценка риска
4. Оценка риска
Оценить ожидаемый риск в предпринимательской деятельности может только высококвалифицированный и опытный бизнесмен. Богатый опыт проведения бизнес-операций позволяет предпринимателю чувствовать степень риска на уровне интуиции.Научный расчет
76. Оценка организационной системы бухгалтерского учета
76. Оценка организационной системы бухгалтерского учета
Система бухгалтерского учета является и объектом, и составной частью системы внутреннего контроля, поскольку система двойной записи, применяемая в бухгалтерском учете, уже сама по себе выступает одним из средств
77. Оценка системы бухгалтерского учета (начало)
77. Оценка системы бухгалтерского учета (начало)
Ознакомление с системой бухгалтерского учета может быть произведено на основании устного опроса, просмотра необходимых документов, обработки и оценки сведений о различных сторонах хозяйственной деятельности
78. Оценка системы бухгалтерского учета (окончание)
78. Оценка системы бухгалтерского учета (окончание)
– организованы ли хранение и сохранность материально-производственных запасов, денежных средств: имеется ли склад с соответственно оборудованными местами для хранения материально-производственных запасов; склад
В работе рассмотрены вопросы составления рабочих документов при оценке
рисков существенного искажения вследствие ошибок или недобросовестных действий
на уровне отчетности в целом, а также на уровне видов
операций, сальдо счетов, раскрытий информации. Предложены рекомендации по
документированию, исходя из требований международных стандартов аудита и
рекомендаций Совета по аудиторской деятельности при Минфине России.
Основные обязанности аудитора по выявлению
и оценке рисков существенного искажения финансовой отчетности аудируемого лица определяет МСА 315 “Выявление и оценка рисков существенного
искажения посредством изучения
организации и ее окружения”. Стандарт обязывает аудитора оценивать
риски существенного искажения, возникшие в результате ошибок или недобросовестных действий, причем эта
оценка, согласно стандарту, должна осуществляться:
- в отчетности в целом;
- на уровне предпосылок в отношении видов операций (оборотов счетов),
сальдо счетов, раскрытий информации.
Установив подобное требование, МСА 315 далее указывает на
факторы, определяющие только риск существенного искажения
вследствие ошибок, а особенностям оценки риска существенного искажения, возникающего вследствие недобросовестных действий,
посвящены разделы 12-27 МСА 240 “Обязанности
аудитора в отношении недобросовестных действий при
проведении аудита финансовой отчетности”.
Поскольку, согласно МСА 230 “Аудиторская
документация”, аудитор должен документировать доказательства выполнения требований каждого применимого
МСА, то следует осуществлять отдельную оценку риска
существенного искажения вследствие ошибок и отдельную оценку риска существенного искажения вследствие недобросовестных
действий. На необходимость отдельной оценки риска существенного искажения вследствие недобросовестных действий
указывает также ряд разделов МСА 240 (разделы 25-27).
Согласно требованиям МСА 240, при выявлении
и оценке рисков существенного искажения аудитор должен оценить, свидетельствует ли полученная информация о присутствии факторов риска недобросовестных действий (п. 24 МСА 240) .
Напомним, что факторы риска недобросовестных
действий — это события или обстоятельства, которые свидетельствуют о наличии “треугольника
мошенничества” (стимул для совершения недобросовестных
действий, возможность их совершения, способность их
оправдания). Перечень факторов риска недобросовестных действий
(заключающихся в фальсификации отчетности и в присвоении активов),
классифицированных по трем причинам “треугольника мошенничества”, приведен
в Приложении 1 к МСА 240.
Советом по аудиторской деятельности при Минфине России разработаны Методические рекомендации по организации и осуществлению аудиторскими
организациями и индивидуальными аудиторами
противодействия коррупции (Протокол № 34 от
06.06.2017). Согласно этим рекомендациям, при оценке наличия
факторов риска недобросовестных действий аудиторам
следует также анализировать наличие факторов риска коррупционных правонарушений. В Приложениях 2 и 3 к указанным Методическим рекомендациям
приведен перечень таких факторов (осуществление деятельности в странах и
регионах с высоким уровнем коррупции; существенные суммы
госконтрактов; осуществление деятельности в отраслях с высокой
степенью государственного регулирования и др.).
Оценка наличия факторов риска недобросовестных
действий, указанных в МСА 240, а также в Методических рекомендациях Совета по аудиторской деятельности, может быть осуществлена с
помощью формы, представленной в табл. 1.
Таблица 1
Оценка наличия факторов риска недобросовестных действий
|
Факторы риска недобросовестных действий |
Наличие |
||
|
Да |
Нет |
||
|
1 |
2 |
3 |
4 |
|
1 |
Фальсификация финансовой |
||
|
1.1 |
Стимулы для совершения недобросовестных |
||
|
1.1.1 |
снижение доходности вследствие ситуации |
||
|
1.1.2 |
зависимость финансового благополучия |
||
|
1.1.3 |
давление на руководство |
||
|
1.1.4 |
|||
|
1.1.5 |
|||
|
1.2 |
Возможности совершения недобросовестных |
||
|
1.2.1 |
доминирующая позиция организации в |
||
|
1.2.2 |
недостаточная надежность внутреннего |
||
|
1.2.3 |
совершение международных операций в |
||
|
1.2.4 |
|||
|
1.2.5 |
|||
|
1.3 |
Способность оправдания недобросовестных |
||
|
1.3.1 |
низкое моральное состояние высшего |
||
|
1.3.2 |
разногласия между собственниками; |
||
|
1.3.3 |
отсутствие различий у |
||
|
1.3.4 |
|||
|
1.3.5 |
|
2 |
Незаконное присвоение активов |
||
|
2.1 |
Стимулы для совершения недобросовестных |
||
|
2.1.1 |
ожидаемые увольнения работников; |
||
|
о1 о 2.1.2 |
изменения в системе оплаты труда; |
||
|
2.1.3 |
наличие затруднительных жизненных или |
||
|
2.1.4 |
|||
|
2.1.5 |
|||
|
2.2 |
Возможности совершения недобросовестных |
||
|
2АЛ |
нерациональное распределение |
||
|
2А2 |
слабый контроль за работниками, |
||
|
2А3 |
ненадежные меры защиты денежных |
||
|
2 2 4 |
|||
|
2 2 5 |
|||
|
2 3 |
Способность оправдания недобросовестных |
||
|
0 0 |
поведение работников, демонстрирующее |
||
|
2.3.2 |
терпимость к мелким |
||
|
2.3.3 |
|||
|
2.3.4 |
|||
|
3 |
Коррупционные нарушения |
||
|
3.1 |
Стимулы для совершения коррупционных |
||
|
3.1.1 |
деятельность в странах или регионах с |
||
|
3.1.2 |
деятельность в отраслях с высокой |
||
|
3.1.3 |
осуществление операций с существенными |
||
|
3.1.4 |
|||
|
3.1.5 |
|||
|
3.2 |
Возможности совершения коррупционных |
||
|
3.2.1 |
необеспечение руководством соблюдения |
||
|
3.2.2 |
отсутствие процедур внутреннего |
||
|
3.2.3 |
|||
|
3.2.4 |
|||
|
3.3 |
Способность оправдания коррупционных |
||
|
3.3.1 |
позиция руководства, заключающаяся в |
||
|
3.3.2 |
|||
|
3.3.3 |
При выявлении факторов риска недобросовестных действий аудитор осуществляет оценку
рисков существенного искажения отчетности в результате недобросовестных
действий.
МСА 200 “Основные цели независимого аудитора и
проведение аудита в соответствии с международными стандартами аудита” указывает, что
оценка рисков может производиться в количественных величинах (например,
в процентах) либо в терминах, не носящих количественного характера.
При выборе способа оценки рисков в неколичественных
величинах, прежде всего, следует установить единицы оценки и их градацию,поскольку прямых указаний на то, в каких неколичественных величинах
может производиться оценка риска, стандарт не
содержит.
В свое время федеральный стандарт — ФП(С)АД № 8 “Понимание деятельности аудируемого лица,
среды, в которой она осуществляется, и оценка рисков существенного искажения аудируемой финансовой (бухгалтерской) отчетности” предусматривал
качественную оценку риска существенного искажения,
исходя из трех градаций: низкий, средний, высокий риск.
Анализ же содержания международных стандартов указывает на следующие
возможные градации качественной оценки рисков:
- приемлемо
низкий риск (уровень аудиторского риска, при котором
возможно получение достаточных надлежащих
аудиторских доказательств и, соответственно, разумное подтверждение достоверности отчетности
— МСА 200, п. 17; МСА 330, п. А43; МСА 500, п. А3); - низкий
риск (уровень
риска существенного искажения, при котором применение соответствующих мероприятий и дополнительных аудиторских процедур не является необходимым
— МСА 330, п. 10; МСА 505, п. 15); - высокий
риск (уровень
риска существенного искажения, при котором необходимо применение соответствующих мероприятий
и дополнительных аудиторских процедур — МСА 330, п.п. А9, А19); - чрезмерно
(крайне) высокий риск (уровень риска существенного искажения, при
котором аудитор может прийти к выводу о невозможности проведения
аудита — МСА 315, п. А120; МСА 580, п. А24).
Эти градации и могут быть установлены при
выборе способа оценки рисков в неколичественном измерении.
Оценка рисков существенного искажения вследствие недобросовестных
действий на уровне отчетности в целом, а также на уровне
видов операций, сальдо счетов, раскрытий информации может быть
совершена путем анализа обстоятельств, приведенных в Приложении 3 к МСА 240 и в Приложении 4 к Методическим рекомендациям
Совета по аудиторской деятельности (в части обстоятельств, указывающих на риск коррупционных нарушений). Подобная оценка может быть осуществлена с помощью форм, представленных в табл. 2 и 3.
Таблица 2
Оценка риска существенного искажения вследствие недобросовестных
действий на уровне отчетности в целом
|
№ |
Обстоятельства, указывающие на риск |
Оценка риска существенного искажения |
||
|
Низкий |
Высокий |
Чрезмерно высокий |
||
|
1 |
2 |
3 |
4 |
5 |
|
1 |
Стремление руководства ограничить объем |
|||
|
2 |
Несвоевременность (задержка) |
|||
|
3 |
Отрицательная реакция руководства на |
|||
|
4 |
Претензии руководства к проведению |
|||
|
5 |
Нежелание руководства принимать |
|||
|
6 |
Наличие информации о фактах |
|||
|
7 |
Внеплановые проверки организации со |
|
8 |
Существенные суммы представительских |
|||
|
9 |
Расходы на комиссионные (агентские) |
|||
|
10 |
||||
|
11 |
Таблица 3
Оценка риска существенного искажения вследствие недобросовестных
действий на уровне видов операций, сальдо счетов, раскрытий информации
|
№ |
Обстоятельства, указывающие на риск |
Вид операций, сальдо счета |
Оценка риска |
||
|
Низкий |
Высокий |
Чрезмерно высокий |
|||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
Наличие неподтвержденных |
||||
|
2 |
Наличие операций, учтенных ненадлежащим |
||||
|
3 |
Наличие ненадлежащих корректировок |
||||
|
4 |
Отсутствие |
||||
|
6 |
Нетипичные расхождения между учтенными документами и ответами на запросы |
||||
|
7 |
Излишне осложненное осуществление |
||||
|
8 |
Привлечение к выполнению определенных операций лиц, не имеющих возможностей (производственных, финансовых) для такого участия |
||||
|
9 |
Осуществление операций разового |
||||
|
10 |
Избыточное внимание руководства к |
||||
|
11 |
Необычно крупные операции в конце года |
||||
|
12 |
Неофициальный учет каких-либо операций |
||||
|
13 |
Осуществление каких-либо операций не в |
||||
|
14 |
Наличие сделок с лицами, зарегистрированными в юрисдикциях с низкими уровнями налогообложения |
||||
|
15 |
Наличие сделок с лицами, которые могут |
|
16 |
Неоправданное отсутствие мер по возврату займов, авансов, просроченной задолженности |
||||
|
17 |
Нетипичные выплаты компенсационного |
||||
|
18 |
Заключение контрактов на существенные суммы не в соответствии с общим порядком (конкурсы, тендеры) |
||||
|
19 |
|||||
|
20 |
По результатам анализа (табл. 3) выявляются
операции, сальдо счетов, раскрытия информации, в отношении которых риск существенного искажения в результате недобросовестных
действий отличен от низкого (оценен как высокий или
чрезмерно высокий).
Оценка риска существенного искажения вследствие ошибок на уровне
отчетности в целом должна осуществляться путем анализа указанных в МСА 315 факторов, характеризующих:
- внешние условия (отраслевые, регуляторные и иные);
- характер деятельности организации;
- информационную систему, связанную с финансовой отчетностью, а также
выбор и применение учетной политики; - бизнес-риски организации и процессы их оценки;
- контрольную среду;
- контрольные мероприятия;
- мониторинг средств контроля.
С учетом предусмотренных МСА градаций рисков оценка риска существенного
искажения вследствие ошибок на уровне отчетности
в целом может проводиться с помощью формы,
представленной в табл. 4.
Оценка рисков существенного искажения вследствие ошибок на уровне видов
операций, сальдо счетов, раскрытий информации должна осуществляться путем
анализа представленных в Приложении 2 к МСА 315 условий и событий, обусловливающих искажения в конкретном виде операций,
сальдо счета, раскрытии информации. Для подобного
анализа может быть использована форма, приведенная в табл. 5.
По результатам анализа выявляются операции,
сальдо счетов, раскрытия информации,
в отношении которых риск существенного искажения в результате ошибок
отличен от низкого (оценен как высокий или чрезмерно высокий).
Напомним, что при оценках рисков существенного
искажения, отличных от низких, аудитор должен запланировать
дополнительные мероприятия и дополнительные
аудиторские процедуры,
предусмотренные МСА 330 “Аудиторские процедуры в ответ на
оцененные риски” и снижающие риск необнаружения.
Дополнительные мероприятия по противодействию
выявленному риску (процедуры общего характера) осуществляются аудитором
при выявлении высокого риска существенного искажения на уровне финансовой отчетности в целом. Эти мероприятия
могут включать:
- привлечение более опытных аудиторов;
- привлечение экспертов;
- увеличение элементов непредсказуемости
при выборе последующих аудиторских процедур; - осуществление более тщательного контроля
со стороны руководителя проверки за членами аудиторской команды; - снижение уровней существенности для отчетности в целом.
Известно (на это указывает МСА 520, п. А16), что снижение уровня
существенности снижает риск необнаружения. В частности, ФП(С)АД 4 в свое время
пояснял, что аудитор может понижать уровень существенности
“в целях уменьшения вероятности необнаружения искажений”(п. 10 ФП(С)АД 4), т.е. в целях уменьшения риска необнаружения.
Уменьшение риска необнаружения при снижении уровня существенности
обусловлено, в частности, тем обстоятельством, что необнаружения
аудитором
различных существенных искажений — события независимые. Очевидно, что
чем больше количество
независимых событий, тем меньше вероятность одновременного их
появления.
Таблица 4
Оценка риска существенного искажения вследствие ошибок на уровне
отчетности в целом
|
№ |
Условия и события, свидетельствующие о |
Оценка риска существенного искажения |
||
|
Низкий |
Высокий |
Чрезмерно высокий |
||
| 1 |
2 |
3 |
4 |
5 |
|
1. |
Внешние условия: |
|||
|
1.1 |
экономическая стабильность в регионе; |
|||
|
1.2 |
экономическая стабильность в стране; |
|||
|
1.3 |
сложность нормативно-правового |
|||
|
1.4 |
доступность капитала и кредитов |
|||
|
1.5 |
||||
|
1.6 |
||||
|
2 |
Характер деятельности организации: |
|||
|
2Л |
реализация новых видов деятельности; |
|||
|
2.2 |
территориальное расширение |
|||
|
2.3 |
реорганизация; |
|||
|
2.4 |
использование сложных финансовых |
|||
|
2.5 |
||||
|
2.6 |
||||
|
3. |
Информационная система, связанная с |
|||
|
3.1 |
наличие персонала с надлежащим опытом в |
|||
|
3.2 |
надежность информационных систем, |
|||
|
3.3 |
наличие нововведений в сфере |
|||
|
3.4 |
||||
|
3.5 |
||||
|
4. |
Бизнес-риски и их оценка: |
|||
|
4.1 |
наличие судебных процессов и условных |
|||
|
4.2 |
проблемы, связанные с непрерывностью |
|||
|
4.3 |
наличие расчетных оценок со значительной неопределенностью; |
|||
|
4.4 |
наличие крупных сделок со связанными |
|||
|
4.5 |
||||
|
4.6 |
||||
|
5 |
Контрольная среда: |
|||
|
5.1 |
основные принципы и стиль работы |
|||
|
5.2 |
распределение полномочий и |
|||
|
5.3 |
кадровая политика |
|||
|
5.4 |
||||
|
5.5 |
|
6 |
Контрольные действия: |
|||
|
6.1 |
обзорные проверки результатов |
|||
|
6.2 |
надежность средств контроля за |
|||
|
6 3 6.3 |
надежность физических средств контроля; |
|||
|
6Л |
||||
|
7 |
||||
|
7.1 |
Мониторинг средств контроля: |
|||
|
7.2 |
периодическая проверка руководством |
|||
|
7.3 |
||||
|
7.4 |
Таблица 5
Оценка риска существенного искажения
вследствие ошибок на уровне видов операций, сальдо счетов, раскрытий информации
|
№ |
Условия и события, свидетельствующие о |
Вид операций, сальдо счета |
Оценка риска существенного искажения |
||
|
Низкий |
Высокий |
Чрезмерно высокий |
|||
|
1 |
Наличие нестандартных или нерегулярных операций |
||||
|
2 |
Наличие операций, учтенных по особым |
||||
|
3 |
Наличие операций со значительной |
||||
|
4 |
Наличие операций, учет которых подвергался корректировке |
||||
|
5 |
|||||
|
6 |
При выявлении высоких рисков существенного искажения на уровне видов
операций, сальдо счетов, раскрытий информации
аудитор должен разработать и выполнить
дополнительные аудиторские процедуры, направленные на снижение
риска необнаружения.
Снижение риска необнаружения при этом может быть обеспечено выбором:
- вида аудиторских процедур (процедуры
инвентаризации активов обеспечивают более высокую надежность аудиторских
доказательств, чем процедуры просмотра документов; запросы к внешним источникам обеспечивают более высокую надежность
аудиторских доказательств, чем запросы к руководству организации); - сроков выполнения аудиторских процедур
(риск необнаружения снижается при выполнении процедур проверки по существу ближе к концу отчетного
периода, поэтому чем выше риск существенного искажения в отношении какого-либо вида операций, тем более эффективно выполнение процедур по существу в конце года); - объема аудиторских процедур (увеличение
объема выборки снижает риск выборки, а следовательно, и риск
необнаружения, таким образом, чем выше риск существенного искажения, тем больше следует увеличивать объем выборки).
Очевидно, что в том случае, когда уровень риска существенного искажения
высок, но применение дополнительных мероприятий и
дополнительных аудиторских процедур позволяет обеспечить низкий риск необнаружения, то, соответственно,
аудиторский риск может быть оценен как приемлемо низкий,
при котором возможно разумное подтверждение достоверности
отчетности.
Если же применение указанных мероприятий
и аудиторских процедур согласно профессиональному
суждению аудитора не позволяет обеспечить приемлемо низкий
аудиторский риск (обеспечить получение достаточных надлежащих аудиторских
доказательств), то согласно МСА 330 аудитор должен модифицировать
аудиторское заключение оговоркой или отказом от выражения мнения (п. 27 МСА 330 “Аудиторские риски в
ответ на оцененные риски”).
Литература
- Устинова Я.И. Переход к МСА: изменения в практике документирования аудита // Аудитор.
— 2017. — № 8. — С. 3-14. - Козменкова С.В., Кемаева С.А. Аудит: проблемные
вопросы и пути развития // Международный бухгалтерский учет. — 2015. — № 2. —
С. 46-57. - Турищева Т.Б. Внедрение международных стандартов аудита в России // Аудитор. — 2015.
— № 12. — С. 12-17.
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Онлайн-тестыТестыМатематика и статистикаЭконометрикавопросы
241. При построении отдельных уравнений регрессии для каждого из 4-х кварталов сумма сезонных отклонений должна равняться:
• 0
242. При проведении теста Голдфелда-Квандта из рассмотрения исключаются __________________ наблюдений.
• средние (n-2n’)
243. При проведении теста Голдфелда-Квандта предполагается, что стандартное отклонение остаточного члена регрессии растет с __________________ переменной.
• ростом объясняющей
244. При рассмотрении спектральной плотности ограничиваются значениями ω, лежащими в пределах
• от 0 до π
245. При снижении уровня значимости риск совершить ошибку I рода
• уменьшается
246. При стремлении размера выборки к бесконечности стандартное отклонение математического ожидания стремится к:
• 0
247. При увеличении размера выборки оценка математического ожидания
• становится более точной
248. Проблема, связанная со смещением оценки коэффициентов регрессии, в одном случае, или с утратой эффективности этих оценок в другом случае неправильной спецификации переменных, перестает существовать, если коэффициент парной корреляции между переменными равен:
• 0
249. Проверка гипотезы Н0: R2 = 0 происходит с помощью теста
• Фишера
250. Процесс АР (2) имеет автокорреляционную функцию, которая:
• имеет бесконечную протяженность
251. Процесс выбора необходимых для регрессии переменных и отбрасывание лишних переменных называется:
• спецификацией переменных
252. Процесс смешанного типа имеет вид
•
253. Процесс СС (2) имеет автокорреляционную функцию, которая:
• обращается в ноль после некоторой точки
254. Процесс Юла описывается моделью
• АР (2)
255. Пусть имеется матрица исходных статистических данных 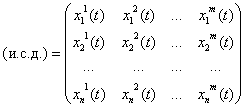
• одного из элементов
Финансовые аналитики часто сталкиваются с конкурирующими идеями о том, как работают финансовые рынки. Некоторые из этих идей развиваются через личные исследования или опыт работы с рынками; другие появляются благодаря взаимодействию с коллегами; и многие другие появляются в результате публикаций в профессиональной литературе по финансам и инвестициям.
Но как может аналитик определить насколько истинны или ложны те или иные идеи?
Когда мы можем свести идею или предположение к определенному утверждению о значении величины, такому как среднее значение совокупности, идея становится статистически проверяемым утверждением или гипотезой.
Аналитик может захотеть исследовать такие вопросы, как:
- Отличается ли средняя доходность данного взаимного фонда от средней эталонной доходности?
- Изменится ли волатильность доходности акции, после того как эта акция будет добавлена в рыночный индекс акций?
- Влияет ли разница между ценами продажи и покупки акции, связанная с числом дилеров, на рынок этой акции?
- Поддерживают ли данные национального рынка облигаций прогноз, полученный на основе экономической теории о временной структуре процентных ставок (связь между доходностью и сроком погашения)?
Для решения этих вопросов, мы используем концепцию и методы проверки статистических гипотез.
Проверка статистических гипотез (англ. ‘hypothesis testing’) является частью статистического вывода, и представляет собой процесс принятия суждений о более крупной группе (совокупности) на основе небольшой фактически наблюдаемой группе (выборке).
Концепции и методы проверки гипотез обеспечивают объективные средства для оценки того, подтверждают ли имеющиеся доказательства гипотезу. После статистической проверки гипотезы мы должны иметь четкое представление о вероятности того, верна ли гипотеза или нет.
Проверка статистических гипотез была мощным инструментом в научном развитии инвестиций. Как написал Роберт Л. Кан (Robert L. Kahn) из Института социальных исследований (Анн-Арбор, штат Мичиган):
«Мельница науки перемалывает только тогда, когда гипотезы и данные находятся в непрерывном и тесном контакте».
Основные акценты этого чтения сосредоточены на основах проверки гипотез и проверке гипотез, касающихся среднего значения и дисперсии, — двух величин, весьма часто использующихся в инвестициях.
Сначала мы приведем обзор процедуры проверки гипотез. Затем обратимся проверке гипотез о среднем, гипотез о разнице между средними и среднем значении разности. В следующем разделе этого чтения, мы рассмотрим проверку гипотез о дисперсии и различиях между дисперсиями, а также проверку гипотез о значении коэффицента корреляции.
В завершение мы рассмотрим непараметрические методы статистического вывода.
Проверка гипотезы, как мы уже упоминали, является частью области статистики, известной как статистический вывод. Традиционно область статистического вывода имеет два направления: статистическая оценка и проверка гипотез.
Статистическая оценка отвечает вопрос:
«Чему равно значение этого параметра (например, среднего значения по совокупности)?»
Ответ на этот вопрос дается в виде доверительного интервала, построенного вокруг точечной оценки. В случае со средним значением, мы строим доверительный интервал для среднего значения совокупности вокруг выборочного среднего, полученного в результате точечной оценки.
Например, предположим, что выборочное среднее равно 50 и 95-процентный доверительный интервал для среднего населения составляет (50 pm 10) (доверительный интервал составляет от 40 до 60). Если доверительный интервал правильно построен, то есть 95-процентная вероятность того, что интервал от 40 до 60 содержит среднее значение совокупности.
Мы обсуждали построение и интерпретацию доверительных интервалов в чтении о выборочном методе и статистической оценке.
Вторая ветвь статистического вывода, проверка гипотез, имеет несколько иную направленность.
Проверка статистических гипотез отвечает на вопрос:
«Равно ли значение параметра (например, среднего значения по совокупности) 45 (или другому конкретному значению)?»
Утверждение «среднее совокупности равно 45» является гипотезой. Статистическая гипотеза (англ. ‘hypothesis’) определяется как утверждение об одной или нескольких совокупностях.
Этот раздел посвящен концепции проверки гипотез. Процесс проверки гипотезы является частью строгого подхода к получению знаний, известного как научный метод (англ. ‘scientific method’).
Научный метод начинается с наблюдений и формулировки теории организации и объяснения наблюдений. Мы судим о правильности теории по ее способности давать точные прогнозы — например, предсказывать результаты новых наблюдений.
Чтобы быть проверяемой, теория должна быть способна делать предсказания, ошибочность которых можно показать.
Если прогнозы верны, мы продолжаем поддерживать теорию, как возможно правильное объяснение наших наблюдений. Когда в результатах наблюдений важна оценка риска, как в области финансов, мы можем попытаться сделать объективное, основанное на вероятности, суждение о том, поддерживают ли новые данные прогноз.
Проверка статистических гипотез играет ключевую роль, когда важна оценка риска.
В своей ежедневной работе финансовый аналитик может сталкиваться с вопросами, на которые он может дать ответы различного качества.
Когда аналитик правильно формулирует проверяемую гипотезу, проверяет ее и составляет отчет о проверке гипотезы, он следует нормам научного метода.
Конечно, логика аналитика, экономическое обоснование, источники информации, и, возможно, другие факторы также оказывают определенное влияние на качество ответа на заданный вопрос.
См. работу Freeley и Steinberg (2008) для обсуждения влияния критического мышления на мотивированное принятие решений.
Мы начнем изучение проверки гипотез со следующего списка из семи шагов.
Этапы проверки статистических гипотез.
Этапы проверки гипотезы заключаются в следующем:
- Формулировка гипотезы.
- Определение соответствующей тестовой статистики (статистики критерия) и ее распределения вероятностей.
- Определение уровня значимости.
- Формулировка правила принятия решения.
- Сбор данных и расчет тестовой статистики.
- Принятие статистического решения.
- Принятие экономического или инвестиционного решения.
Этот список этапов основан на списке из работы Daniel и Terrell (1995).
Мы расскажем о каждом из этих этапов, используя в качестве иллюстрации проверку гипотезы о премии за риск для американских акций. Описанный процесс представляет собой традиционный подход к проверке гипотез.
В завершении мы рассмотрим часто используемую альтернативу этих шагов — подход, основанный на p-значении.
1 этап. Формулировка гипотезы.
Первым шагом в проверке гипотезы является формулировка гипотезы. Мы всегда формулируем две гипотезы: нулевую гипотезу (или нуль), обозначаемую как (H_0), и альтернативную гипотезу, обозначаемую как (H_a).
Определение нулевой гипотезы.
Нулевая гипотеза — это гипотеза, которую нужно проверить. Например, мы могли бы предположить, что среднее по совокупности премии за риск для американских акций меньше или равно нулю.
Нулевая гипотеза (нуль, англ. ‘null hypothesis’) — это утверждение, которое считается истинным, если только используемая для проверки гипотезы выборка не дает убедительные доказательства того, что нулевая гипотеза неверна. Когда такие доказательства присутствуют, мы переходим к альтернативной гипотезе.
Определение альтернативной гипотезы.
Альтернативная гипотеза (альтернатива или конкурирующая гипотеза, англ. ‘alternative hypothesis’) — это гипотеза, которая принимается, когда нулевая гипотеза отвергается. Наша альтернативная гипотеза заключается в том, что среднее по совокупности премии за риск для американских акций больше нуля.
Предположим, что наш вопрос касается значения параметра совокупности (theta), по отношению к одному возможному значению параметра, (theta_0) (они читаются, соответственно, как «тета» и «тета ноль»).
Греческие буквы, такие как (sigma), зарезервированы для параметров совокупности. Римские курсивные буквы, например, (s), используются для выборочных статистик.
Примерами параметра совокупности являются среднее по совокупности (mu) и дисперсия совокупности (sigma^2). Мы можем сформулировать три различные пары нулевых и альтернативных гипотез и обозначить их согласно утверждению альтернативной гипотезы.
Формулировки гипотез.
Мы можем сформулировать нулевые и альтернативные гипотезы тремя различными способами:
- 1-я формулировка: (H_0: theta = theta_0) (нулевая гипотеза) и (H_a: theta neq theta_0) (альтернативная гипотеза «не равно»).
- 2-я формулировка: (H_0: theta leq theta_0) (нулевая гипотеза) и (H_a: theta > theta_0) (альтернативная гипотеза «больше чем»).
- 3-я формулировка: (H_0: theta geq theta_0) (нулевая гипотеза) и (H_a: theta < theta_0) (альтернативная гипотеза «меньше, чем»).
В нашем примере с американскими акциями, (theta = mu_{RP} ), что представляет собой среднее по совокупности премии за риск для американских акций. Кроме того, (theta_0 = 0 ), и мы используем вторую из указанных выше трех пар гипотез.
1-я формулировка представляет собой двустороннюю проверку гипотезы (англ. ‘ two-sided hypothesis test’ или ‘two-tailed hypothesis test’): Мы отвергаем нуль в пользу альтернативы, если данные свидетельствуют о том, что параметр совокупности либо меньше, либо больше, чем (theta_0 ).
В отличие от этого, 2-я и 3-я формулировки являются односторонней проверкой гипотезы (англ. ‘one-sided hypothesis test’ или ‘one-tailed hypothesis test’).
В формулировках 2 и 3 мы отвергаем нуль только тогда, когда данные свидетельствуют о том, что параметр совокупности соответственно, либо больше, либо меньше, чем (theta_0 ). Альтернативная гипотеза имеет только одну сторону.
Обратите внимание, что в каждом из описанных выше случаев, мы формулируем нулевые и альтернативные гипотезы так, что они учитывают все возможные значения параметра. В формулировке 1, например, параметр или равен гипотетическому значению (theta_0 ) (по нулевой гипотезе) или не равен гипотетическому значению (theta_0 ) (по альтернативной гипотезе).
Эти два утверждения логически исчерпывают все возможные значения параметра.
Несмотря на то, что формулировать гипотезы можно различными способами, мы всегда проводим проверку нулевой гипотезы в точке равенства, (theta = theta_0 ). Если нуль это (H_0: theta = theta_0), (H_0: theta leq theta_0) или (H_0: theta geq theta_0), мы на самом деле проверяем (theta = theta_0 ). Логика проста.
Предположим, что гипотетическое значение параметра равно 5.
Рассмотрим нулевую гипотезу (H_0: theta leq 5), с альтернативной гипотезой «больше чем» (H_a: theta > 5) .
Если у нас есть достаточно доказательств, чтобы отклонить (H_a: theta = 5) в пользу (H_a: theta > 5), то у нас, безусловно, также есть достаточные доказательства, чтобы отвергнуть гипотезу о том, что параметр (theta) равен некоторому меньшему значению, например, 4.5 или 4.
Напомним, что расчет для проверки нулевой гипотезы является одинаковым для всех трех формулировок. Различия в трех формулировках мы увидим в ближайшее время, — они заключаются в определении того, следует ли отклонить нулевую гипотезу.
Как мы выбираем нулевые и альтернативные гипотезы?
Вероятно, наиболее распространенными являются альтернативные гипотезы «не равно». Мы отвергаем нуль, поскольку данные свидетельствуют о том, что параметр больше или меньше, чем (theta_0).
Иногда, однако, у нас могут быть условия, имеющие вид «ожидаем», «подозреваем» или «надеемся на то, что», которые означают, что мы хотим найти благоприятные доказательства.
Часть этого обсуждения выбора гипотез взята из работы Bowerman, O’Connell и Murphree (2016).
В этом случае, мы можем сформулировать альтернативную гипотезу, как утверждение о том, что это условие является истинным. При этом нулевой гипотезой будет утверждение о том, что это условие не истинно. Если данные подтверждают отклонение нуля и принятие альтернативы, то мы статистически подтвердили наши ожидания того, что было истиной.
Например, экономическая теория предполагает, что инвесторы требуют положительную премию за риск по акциям (премия за риск определяется как ожидаемая доходность акций за вычетом безрисковой ставки).
Следуя принципу с формулировки альтернативы в виде условия «надеемся на то, что», сформулируем следующие гипотезы:
- (H_0:) Среднее по совокупности премии за риск для американских акций меньше или равно 0.
- (H_a:) Среднее по совокупности премии за риск для американских акций положительно.
Обратите внимание, что альтернативные гипотезы «больше чем» и «меньше чем» отражают убеждения исследователя сильнее, чем альтернативная гипотеза «не равно».
Для того, чтобы подчеркнуть свое нейтральное отношение к гипотезам, исследователь может иногда выбрать альтернативную гипотезу «не равно», когда выбор односторонней альтернативной гипотезы также разумен.
2 этап. Определение тестовой статистики и ее распределения вероятностей.
Второй этап проверки гипотез заключается в определении соответствующей тестовой статистики и ее распределения вероятностей.
Определение тестовой статистики.
Тестовая статистика, тест-статистика или статистика критерия (т.е. статистика, лежащая в основе критерия, англ. ‘test statistic’) является величиной, рассчитанной на основе выборки, значение которой является основанием для принятия решения о том, следует ли отклонить нулевую гипотезу.
Средоточием нашего статистического решения является значение тестовой статистики. Очень часто (во всех случаях, которые мы рассмотрим в этом чтении) тестовая статистика имеет следующий вид:
( Large stBf{Тестовая}{статистика} = { stRm{Выборочная}{статистика} — stRm{Значение параметра}{совокупности при $H_0$} over text{Стандартная ошибка выборочной статистики}} ) (Формула 1)
Для нашей премии за риск, например, интересующий параметр совокупности — это средняя по совокупности премия за риск (mu_{RP}). Мы обозначаем гипотетическое значение среднего по совокупности населения для (H_0) как (mu_0). Переформулировав гипотезу с использованием символов, мы проверяем нуль (H_0: mu_{RP} leq mu_0 ) и альтернативу (H_a: mu_{RP} > mu_0 ).
Однако, поскольку в соответствии с нулем мы проверяем условие ( mu_0 = 0), то мы пишем (H_0: mu_{RP} leq 0 ) и (H_a: mu_{RP} > 0 ).
Выборочное среднее обеспечивает оценку среднего по совокупности. Таким образом, мы можем использовать выборочное среднее премии за риск ( overline X_{RP}), рассчитанное на основе исторических данных, в качестве выборочной статистики в Формуле 1.
Стандартное отклонение выборочной статистики, известное как «стандартная ошибка» статистики, является знаменателем в Формуле 1.
В этом примере выборочной статистикой является выборочное среднее. Для выборочного среднего ( overline X ), рассчитанного по выборке, отобранной из совокупности со стандартным отклонением ( sigma ), стандартная ошибка определяется по одной из двух формул:
(large dst
sigma_{overline X} = {sigma over sqrt n} ) (Формула 2)
если нам известно стандартное отклонение совокупности (sigma), или
(large dst
s_{overline X} = {s over sqrt n} ) (Формула 3)
когда мы не знаем стандартное отклонение совокупности и нам необходимо использовать стандартное отклонение выборки (s) оценки стандартной ошибки.
В этом примере, поскольку мы не знаем стандартное отклонение совокупности, порождающей доходность, мы используем Формулу 3.
Таким образом, тестовая статистика определяется по формуле:
( large dst
{overline X_{RP} — mu_0 over s_{overline X}} = {overline X_{RP} — 0 over s big / sqrt n } )
Заменяя (mu_0) на 0, мы используем тот уже отмеченный факт, что мы тестируем любую нулевую гипотезу в точке равенства, а также тот факт, что здесь (mu_0 = 0).
Итак, мы определили тестовую статистику, чтобы проверить нулевую гипотезу.
Какому распределению вероятностей она соответствует?
В этом чтении мы будет использовать четыре распределения вероятности для тестовых статистик:
- t-распределение Стьюдента (для t-теста);
- Стандартное нормальное или z-распределение (для z-теста);
- Распределение хи-квадрат (( chi^2 )) (для хи-квадрат теста); а также
- F-распределение (для F-теста).
Мы обсудим детали этих вариантов позже, но предположим, что мы можем провести z-тест, основанный на центральной предельной теореме, потому что наша выборка американских акций имеет много наблюдений.
Центральная предельная теорема говорит о том, что выборочное распределение выборочного среднего будет приблизительно нормальным со средним (mu) и дисперсией (sigma^2 / n), когда выборка имеет большой размер.
Выборка, которую мы будем использовать для этого примера, содержит 118 наблюдений.
В итоге, тестовая статистика для проверки гипотезы о средней премии за риск равна ( overline X_{RP} big / s_{overline X}).
Мы можем выполнить z-тест, поскольку мы можем правдоподобно предположить, что тестовая статистика следует стандартному нормальному распределению.
3 этап. Определение уровня значимости.
Третьим этапом проверки гипотез является определение уровня значимости. Когда тестовая статистика рассчитана, возможны два действия:
- Мы отвергаем нулевую гипотезу или
- Мы не отвергаем нулевую гипотезу.
Выбор действия основан на сравнении вычисленной тестовой статистики с заданным возможным значением или значениями. Значения, которые мы выбираем, основаны на выбранном уровне значимости. Уровень значимости отражает то, какие основанные на выборке доказательства нам необходимы, чтобы отвергнуть нуль.
По аналогии с судом, необходимая доказательная база может меняться в зависимости от характера гипотез и серьезности последствий совершения ошибки.
Возможны четыре результата при проверке нулевой гипотезы:
- Мы отвергаем ложную нулевую гипотезу. Это правильное решение.
- Мы отвергаем истинную нулевую гипотезу. Это называется ошибкой I рода (англ. ‘Type I error’).
- Мы не отвергаем ложную нулевую гипотезу. Это называется ошибкой II рода (англ. ‘Type II error’).
- Мы не отвергаем истинную нулевую гипотезу. Это правильное решение.
Проиллюстрируем эти результаты в Таблице 1.
Таблица 1. Ошибки I и II рода при проверке гипотез.
|
Решение |
Ситуация |
|
|---|---|---|
|
(H_0) Истина |
(H_0) Ложь |
|
|
(H_0) не отвергается |
Правильное решение |
Ошибка II рода |
|
(H_0) отвергается (принимается (H_a)) |
Ошибка I рода |
Правильное решение |
Когда мы принимаем решение при проверке гипотезы, мы рискуем допустить ошибку I или II рода. Это взаимоисключающие ошибки:
- Если мы ошибочно отвергаем нуль, мы можем допустить только ошибку I рода.
- Если мы ошибочно не отвергаем нуль, мы можем допустить только ошибку II рода.
Вероятность ошибки I рода при проверке гипотезы обозначается греческой буквой альфа: (alpha). Эта вероятность также известна как уровень значимости проверки (англ. ‘level of significance’).
Например, уровень значимости 0.05 для проверки означает, что есть 5-процентная вероятность отклонения истинной нулевой гипотезы.
Вероятность ошибки II рода обозначается греческой буквой бета: (beta).
Управление вероятностью ошибок двух типов предполагает компромисс. При прочих равных, если мы уменьшаем вероятность ошибки I рода, задав меньший уровень значимости (скажем, 0.01, а не 0.05), мы увеличиваем вероятность совершить ошибку II рода, потому что мы отвергаем нуль реже, в том числе, когда он является ложным.
Единственным способом уменьшить вероятность ошибок обоих типов одновременно является увеличение размера выборки (n).
Количественный компромисс между двумя типами ошибок на практике, как правило, невозможен, потому что вероятность ошибки II рода очень трудно определить количественно.
Рассмотрим пример с парой гипотез: (H_0: theta leq 5) и (H_a: theta > 5).
Поскольку каждое истинное значение (theta) больше 5 делает нулевую гипотезу ложной, каждое значение (theta) больше 5 имеет различную (beta) (вероятность ошибки II рода).
В отличие от этого, нам достаточно только констатировать вероятность ошибки I рода при (theta = 5). Таким образом, как правило, мы указываем только вероятность ошибки I рода, когда выполняем проверку гипотезы.
В то время как уровень значимости проверки является вероятностью ошибочно отвергнуть нулевую гипотезу, то мощностью критерия или мощностью проверки (англ. ‘power of a test’) является вероятность правильного отклонения нулевой гипотезы — то есть вероятность отвергнуть нуль, если он ложный.
Мощность критерия, на самом деле, равна 1 минус вероятность ошибки II рода.
Когда при проведении проверки имеется более одной статистики критерия, мы должны предпочесть самую мощную из них, при прочих равных условиях.
Тем не менее, у нас не всегда есть информация об относительной мощности критерия для конкурирующих статистик критерия.
В итоге, стандартный подход к проверке гипотез включает только определение уровня значимости (вероятности ошибки I рода). Наиболее целесообразно устанавливать этот уровень значимости до расчета тестовой статистики (статистики критерия). Если мы указываем его после вычисления тестовой статистики, на нас может повлиять результат расчета, что умаляет объективность проверки.
Мы можем использовать три наиболее распространенных уровня значимости для проведения проверки гипотезы: 0.10, 0.05 и 0.01.
Если мы можем отклонить нулевую гипотезу на уровне значимости 0.10, то у нас есть доказательства того, что нулевая гипотеза неверна.
Если мы можем отклонить нулевую гипотезу на уровне значимости 0.05, то у нас есть убедительные доказательства того, что нулевая гипотеза неверна.
И если мы можем отклонить нулевую гипотезу на уровне значимости 0.01, то у нас есть очень убедительные доказательства того, что нулевая гипотеза неверна.
Для нашего примера с премией за риск, мы установим уровень значимости 0.05.
4 этап. Формулировка правила принятия решения.
Четвертый этап проверки гипотезы заключается в формулировке правила принятия решения (англ. ‘decision rule’).
Общий принцип формулируется просто.
Когда мы проверяем нулевую гипотезу, если мы находим, что рассчитанное значение статистики критерия (тестовой статистики) является экстремальным или более экстремальным, чем заданное значение или значения, определенные установленным уровнем значимости (alpha), то мы отвергаем нулевую гипотезу. Мы говорим, что результат является статистически значимым (англ. ‘statistically significant’).
В противном случае, мы не отвергаем нулевую гипотезу, и говорим, что результат не является статистически значимым. Значение или значения, с которым мы сравниваем вычисленную статистику критерия, чтобы принять наше решение, являются точками отклонения (критическими значениями) для проверки гипотезы.
Термин «точка отклонения» (англ. ‘rejection point’) является описательным синонимом для более традиционного термина «критическое значение» (англ. ‘critical value’).
Определение критического значения для статистики критерия.
Критическое значение или точка отклонения (англ. ‘critical value’) для тестовой статистики (статистики критерия) представляет собой значение, с которой сравнивается вычисленная тестовая статистика, чтобы решить, следует ли отклонять или не отклонять нулевую гипотезу.
Для односторонней проверки, мы указываем критическое значение, используя символ для тестовой статистики с индексом (alpha), обозначающим заданную вероятность ошибки I рода, например, (z_alpha).
Для двусторонней проверки, мы указываем критическое значение (z_{alpha/2}).
Для того, чтобы проиллюстрировать применение критических значений, предположим, что мы используем z-тест и выбрали уровень значимости 0.05.
Для проверки пары гипотез (H_0: theta = theta_0) и (H_a: theta neq theta_0), существуют два критических значения, — одно отрицательное и одно положительное.
Для двухсторонней проверки при уровне значимости 0.05, суммарная вероятность ошибки I рода должна быть равна 0.05. Таким образом, 0.05 / 2 = 0.025 вероятности должно быть в каждом хвосте распределения тестовой статистики при нулевой гипотезе.
Следовательно, двумя критическими значениями будут (z_{0.025} = 1.96) и (-z_{0.025} = -1.96). Пусть (z) является вычисленным значением тестовой статистики. Мы отвергаем нуль, если находим, что (z < -1.96) или (z > 1.96). И мы не отвергаем нуль, если (-1.96 leq z leq 1.96).
Для проверки пары гипотез (H_0: theta leq theta_0) и (H_a: theta > theta_0) при уровне значимости 0.05, критическим значением будет (z_{0.05} = 1.645). Мы отвергаем нулевую гипотезу, если (z > 1.645). Значение стандартного нормального распределения таково, что 5% результатов лежат правее точки (z_{0.05} = 1.645).
Для проверки пары гипотез (H_0: theta geq theta_0) и (H_a: theta < theta_0), критическим значением будет (-z_{0.05} = -1.645). Мы отвергаем нулевую гипотезу, если (z < -1.645).
График 2 иллюстрирует проверку (H_0: mu = mu_0) и (H_a: mu neq mu_0) при уровне значимости 0.05 с использованием z-теста.
Термин «область принятия гипотезы» (англ. ‘acceptance region’) является традиционным названием для множества значений тестовой статистики, при которых мы не отвергаем нулевую гипотезу.
Традиционное название, однако, неточное. Мы должны избегать использования таких фраз, как «принять нулевую гипотезу», потому что такое утверждение подразумевает неоправданно большую степень убежденности в нуле, когда мы не отвергаем его.
Аналогия с некоторыми судами (например, в Соединенных Штатах) заключается в том, что если присяжные не выносят вердикт о виновности (альтернативная гипотеза), наиболее точным будет сказать, что жюри не удалось отклонить нулевую гипотезу о невиновности обвиняемого (что следует из принципа презумпции невиновности).
По обеим сторонам от области принятия решения находятся области отклонения или критические области (англ. ‘rejection region’ или ‘critical region’).
Если нулевая гипотеза заключается в том, что ( mu = mu_0 ) истинно, тестовая статистика имеет 2.5-процентный шанс попадания в левую критическую область и 2.5-процентный шанс попадания в правую критическую область.
Любое вычисленное значение тестовой статистики, которое попадает в любую из этих двух областей, заставляет нас отвергнуть нулевую гипотезу при уровне значимости 0.05. Критические значения 1.96 и -1.96 рассматриваются как разделительные линии между областями принятия и отклонения гипотезы.
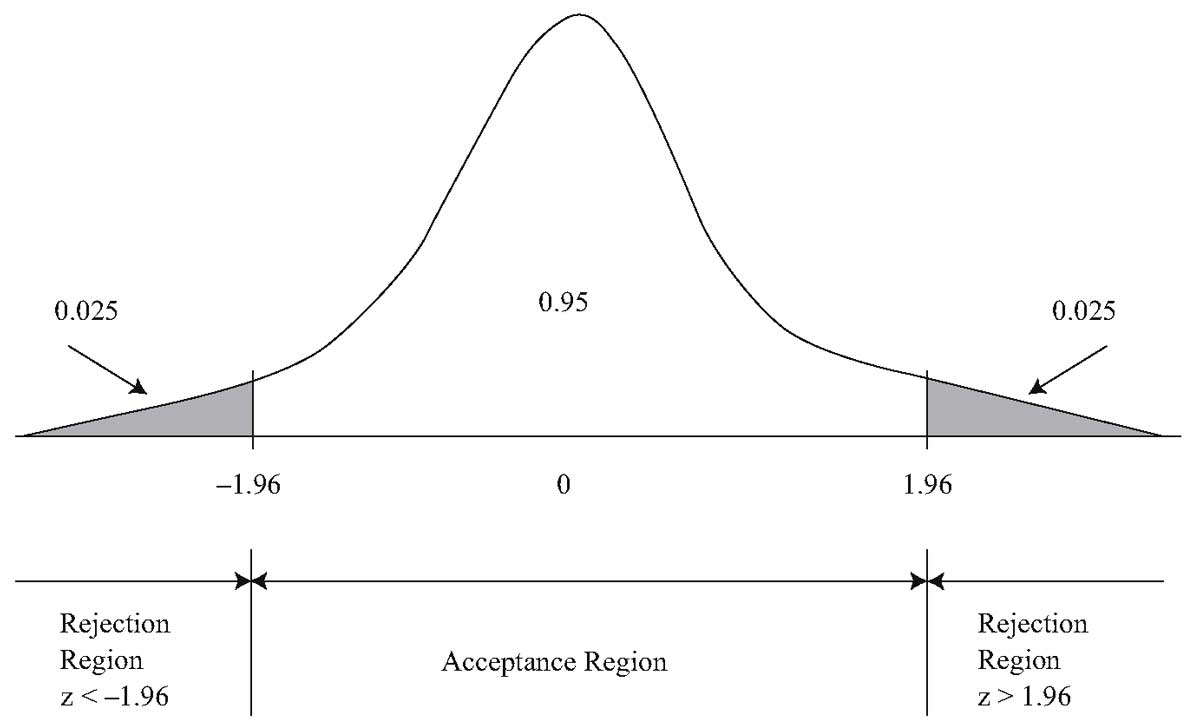
График 2 дает хорошую возможность подчеркнуть взаимосвязь между доверительными интервалами и проверкой гипотез. 95-процентный доверительный интервал для среднего по совокупности (mu), основанного на выборочном среднем (overline X), задается диапазоном от (overline X — 1.96s_{overline X}) до (overline X + 1.96s_{overline X}), где (s_{overline X}) является стандартной ошибкой выборочного среднего (Формула 3).
Так же, как и при проверке гипотезы, мы можем использовать этот доверительный интервал, основанный на стандартном нормальном распределении, когда у нас есть большая выборка.
Альтернативная проверка гипотезы и доверительный интервал используют t-распределение. Мы рассмотрим эти концепции в следующем разделе.
Теперь рассмотрим одно из условий для отклонения нулевой гипотезы:
( dst {overline X — mu_0 over s_{overline X}} > 1.96)
Здесь (mu_0) является гипотетическим значением среднего по совокупности. Условие гласит, что отклонение гипотезы является оправданным, если тестовая статистика превышает 1.96.
Умножив обе стороны неравенства на (s_{overline X}), мы получим ( overline X — mu_0 > 1.96 s_{overline X}), или после преобразования, ( overline X — 1.96 s_{overline X} > mu_0), что можем также записать в виде ( mu_0 < overline X — 1.96 s_{overline X}).
Это выражение означает, что если гипотетическое среднее по совокупности (mu_0), меньше нижнего предела 95-процентного доверительного интервала, основанного на выборочном среднем, мы должны отвергнуть нулевую гипотезу при уровне значимости 5% (тестовая статистика попадает в критическую область справа).
Теперь мы можем взять другое условие для отклонения нулевой гипотезы:
( dst {overline X — mu_0 over s_{overline X}} < -1.96)
и, используя алгебру, как и ранее, мы преобразуем его к виду:
( dst mu_0 > overline X — 1.96 s_{overline X})
Если гипотетическое среднее по совокупности больше, чем верхний предел 95-процентного доверительного интервала, мы отвергаем нулевую гипотезу при уровне значимости 5% (тестовая статистика попадает в критическую область слева).
Таким образом, уровень значимости в двусторонней проверке гипотезы можно интерпретировать точно так же, как доверительный интервал (1 — alpha).
Таким образом, когда гипотетическое значение параметра совокупности для нулевой гипотезы находится вне соответствующего доверительного интервала, то нулевая гипотеза отвергается. Мы могли бы использовать доверительные интервалы для проверки гипотез, но на практике финансовые аналитики, как правило, этого не делают.
Вычисление тестовой статистики (одно число, по сравнению с двумя числами для обычного доверительного интервала) более эффективно. Также, на практике аналитики редко сталкиваются с односторонними доверительными интервалами.
Кроме того, только вычислив тестовую статистику, мы можем получить p-значение, полезный показатель значимости результатов (мы обсудим p-значение далее).
Вернемся к нашей проверке премии за риск.
Мы сформулировали гипотезы (H_0: mu_{RP} leq 0) и (H_a: mu_{RP} > 0). Мы определили тестовую статистику как ( overline X_{RP} / s_{overline X}) и определили, что она следует стандартному нормальному распределению.
Таким образом, мы выполняем односторонний z-тест.
Мы определили уровень значимости 0.05. Для этого одностороннего z-теста, критическая точка при уровне значимости 0.05 составляет 1.645. Мы отвергаем нуль, если вычисленная z-статистика больше, чем 1.645.
График 3 иллюстрирует эту проверку.
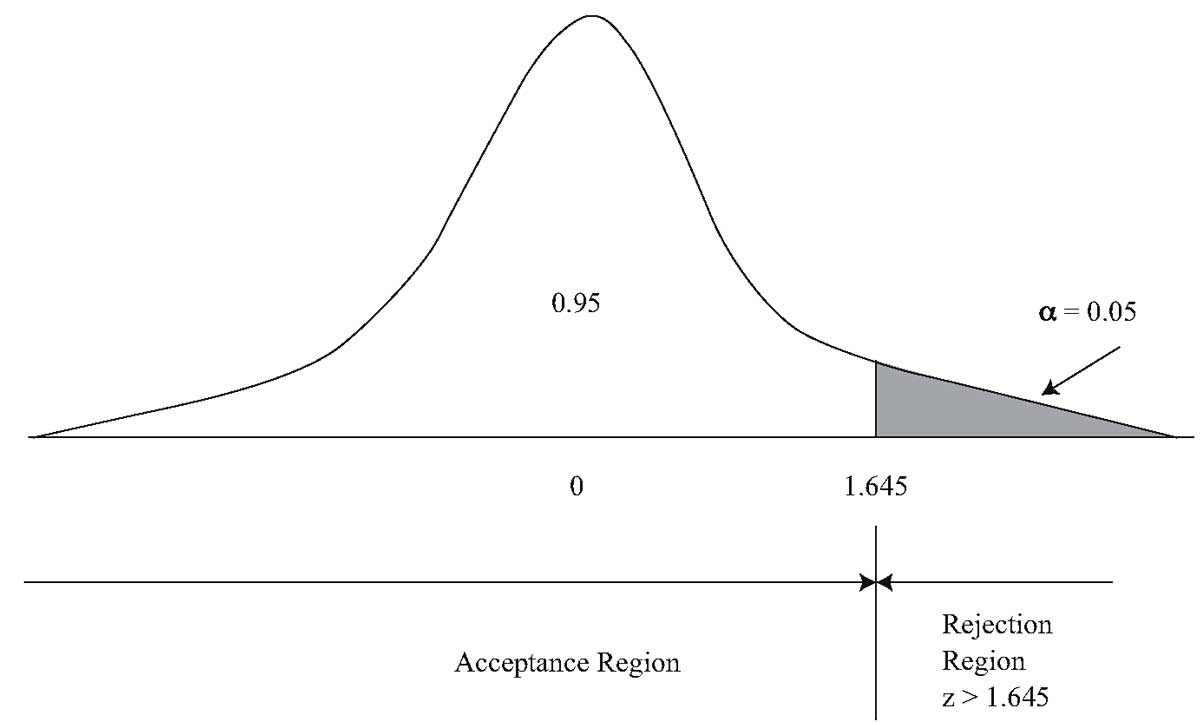
5 этап. Сбор данных и расчет тестовой статистики.
Пятый шаг в проверке гипотез заключается в сборе данные и расчете тестовой статистики. Качество наших выводов зависит не только от уместности статистической модели, но и от качества данных, которые мы используем при проведении проверки.
В первую очередь мы должны проверить данные на наличие ошибок измерений. Нам также необходимо учесть другие проблемы, в том числе систематическую ошибку выборки и систематическую ошибку временного периода.
Систематическая ошибка выборки — это смещение выборки, связанное с систематическим исключением некоторых элементов совокупности в соответствии с определенным признаком.
Одним из типов систематической ошибки выборки является систематическая ошибка выжившего. Например, если мы определим нашу выборку, как облигации взаимных фондов США, которые продолжают деятельность в настоящее время, и мы сделаем выборку доходности только по этим фондам, мы будем систематически исключать фонда, которые не выжили (прекратили деятельность) к настоящему моменту.
Прекратившие деятельность фонды, скорее всего, в среднем хуже оставшихся фондов. В результате, эффективность фондов, рассчитанная на основе этой выборки, может быть смещена вверх.
Систематическая ошибка временного периода связана с вероятностью того, что когда мы используем выборку из временных рядов, наш статистический вывод может быть чувствительным к начальным и конечным датам периода выборки.
В нашей гипотезе о премии за риск мы имеем дело с американскими акциями. Согласно Dimson, Marsh и Staunton (2018) за период с 1900 по 2017 год включительно (118 ежегодных наблюдений), среднеарифметическая премия за риск для американских акций по отношению к доходности облигаций (overline X_{RP}) составила 7.5% в год.
Выборочное стандартное отклонение годовой премии за риск составило 19.5%. Используя Формулу 3, найдем стандартную ошибку выборочного среднего:
( dst s_{overline X} = s big / sqrt n = 19.5% / sqrt {118} ) = 1.795%.
Тестовая статистика равна:
( dst z = overline X_{RP} big / s_{overline X}) = 7.5%/1.795% = 4.18.
6 этап. Принятие статистического решения.
Шестой этап проверки гипотезы означает принятие статистического решения.
В нашем примере, поскольку тестовая статистика (z = 4.18) больше критического значения 1.645, мы отвергаем нулевую гипотезу в пользу альтернативной гипотезы о том, что премия за риск для американских акций является положительной.
Первые шесть шагов являются статистическими шагами. Наше итоговое решение принимается с использованием статистического решения.
7 этап. Принятие экономического или инвестиционного решения.
Седьмой и заключительный шаг в проверке гипотез заключается в принятии экономического или инвестиционного решения. Экономическое или инвестиционное решение принимает во внимание не только статистические решения, но и все соответствующие экономические вопросы.
На шестом этапе, мы нашли убедительные статистические доказательства того, что премия за риск для американских акций является положительной. Величина расчетной премии за риск, 7.5% в год, является также очень значимой экономически.
Исходя из этих соображений, инвестор может принять решение инвестировать часть средств в американские акции. Ряд нестатистических соображений, таких как толерантность инвестора к риску и его финансовое положение, может также повлиять на процесс принятия решений.
Предшествующее обсуждение поднимает проблему, которая часто возникает на этом этапе принятия решений. Мы часто находим, что небольшие различия между переменной величиной и ее гипотетическим значением являются статистически значимыми, но не значимыми экономически.
Например, мы можем проверить инвестиционную стратегию и отклонить нулевую гипотезу о том, что средняя доходность стратегии равна нулю на основе большой выборки.
Формула 1 показывает, что чем меньше стандартная ошибка выборочной статистики (делитель в формуле), тем больше значение тестовой статистики и тем больше шанс на то, что нулевая гипотеза будет отклонена, при прочих равных условиях. Стандартная ошибка уменьшается по мере увеличения размера выборки (n), так что при очень больших выборках, мы можем отклонить нулевую гипотезу.
Мы можем обнаружить, что, хотя стратегия обеспечивает статистически значимую положительную среднюю доходность, результаты не являются экономически значимыми, если учесть транзакционные издержки, налоги и риски.
Даже если мы приходим к выводу, что результаты стратегии являются экономически значимыми, мы должны изучить логику того, почему стратегия могла бы работать в будущем, прежде чем реализовывать ее фактически. Такие соображения нельзя включить в проверку гипотезы.
Перед тем как завершить тему процесса проверки гипотез, мы должны обсудить важный альтернативный подход, называемый подходом проверке гипотез с. Аналитики и исследователи часто включают в отчеты о проверке гипотез p-значение (также называемое предельным уровнем значимости, англ. ‘marginal significance level’).
Определение p-значения.
P-значение (p-уровень значимости или p-критерий, англ. ‘p-value’) является наименьшим уровнем значимости, при котором может быть отвергнута нулевая гипотеза.
Для значения тестовой статистики 4.18 в проверке гипотезы о премии за риск, с помощью функции электронной таблицы для стандартного нормального распределения, мы вычисляем р-значение 0.000015. Мы можем отклонить нулевую гипотезу на этом уровне значимости.
Чем меньше р-значение, тем сильнее доказательства против нулевой гипотезы и в пользу альтернативной гипотезы. P-значение для двухсторонней проверки того, что параметр равен нулю, часто генерируется автоматически с помощью статистических и эконометрических программ.
Мы можем использовать электронные таблицы для расчета p-значения. В Microsoft Excel, например, мы можем использовать функции TTEST, NORMSDIST, CHIDIST и FDIST для расчета р-значений для f-тестов, z-тестов, хи-квадрат тестов, и F-тестов, соответственно.
Мы можем использовать р-значение в рамках процедуры проверки гипотез, представленной выше, в качестве альтернативы критическим значениям.
Если р-значение меньше нашего заданного уровня значимости, мы отвергаем нулевую гипотезу. В противном случае, мы не отвергаем нулевую гипотезу.
Используя p-значение таким образом, мы приходим к такому же выводу, что и при использовании критических значений. Например, поскольку 0.000015 меньше 0.05, мы отвергаем нулевую гипотезу в проверке гипотезы о премии за риск.
P-значение, тем не менее, обеспечивает более точную информацию о силе доказательств, чем подход с использованием критических значений. P-значение 0.000015 указывает на то, что нулевая гипотеза отвергается на гораздо меньшем уровне значимости, чем 0.05.
Если один исследователь рассматривает вопрос, используя уровень значимости 0.05, а другой исследователь использует уровень значимости 0.01, читатель может столкнуться с проблемой, сравнивая полученные результаты.
Эта проблема породила подход к представлению результатов проверки гипотез, при котором указываются p-значения и не указывается спецификация уровня значимости (этап 3). Интерпретация статистических результатов остается на усмотрение пользователя исследования. Этот подход к представлению результатов иногда называют подходом к проверке гипотез с использованием р-значения.
Davidson и MacKinnon (1993) оспорили достоинство этого подхода:
«Подход с использование p-значения по не обязательно заставит нас принять решение о нулевой гипотезе. Если мы получим p-значение равное, скажем, 0.000001, мы почти наверняка захотим отклонить нуль.
Но если мы получим p-значение равное, скажем, 0.04, или даже 0.004, мы не обязаны отклонять его. Мы можем просто отбросить результат прочь, как информацию, которая ставит под сомнение нулевую гипотезу, но сама по себе не убедительна.
Мы считаем, что это несколько агностическое отношение к статистическим проверкам, в которых p-значения рассматриваются просто как части информации, которую мы можем использовать, но можем и не использовать». (Стр. 80)
Вопрос 1. Модель множественной регрессии с тремя объясняющими переменными без свободного коэффициента имеет вид: y =
- Ответ: b1x1 + b2x2 + b3x3
Вопрос 2. При автокорреляции оценка коэффициентов регрессии становится:
- Ответ: неэффективной
Вопрос 3. Cитуация, при которой нулевая гипотеза была отвергнута, хотя была истинной, носит название:
- Ответ: ошибки I рода
Вопрос 4. При использовании уровня значимости, равного 5%, истинная гипотеза отвергается в __________________ случаев.
- Ответ: 5%
Вопрос 5. Для идентификации АР и СС моделей сначала делают оценки
- Ответ: автокорреляционной функции
Вопрос 6. Значение статистики Дарбина-Уотсона находится между значениями
- Ответ: 0 и 4
Вопрос 7. Пересмотр оценок в методе Кокрана-Оркатта выполняется до тех пор, пока не будет __________________ оценок.
- Ответ: получена требуемая точность
Вопрос 8. Способ оценивания (estimator) — общее правило для получения __________________ какого-либо параметра по данным выборки.
- Ответ: приближенного численного значения
Вопрос 9. Явление, когда строгая линейная зависимость между переменными приводит к невозможности применения МНК, называется:
- Ответ: полной коллинеарностью
Вопрос 10. Выборочная дисперсия зависимой переменной регрессии равна __________________ объясненной дисперсии зависимой переменной и необъясненной дисперсии зависимой переменной.
- Ответ: сумме
Вопрос 11. Четвертое условие Гаусса-Маркова состоит в том, что для любого k cov (uk, хk) равна:
- Ответ: 0
Вопрос 12. Эластичность y по x рассчитывается __________________ величины относительного изменения y на величину относительного изменения x.
- Ответ: делением
Вопрос 13. Если выборка достаточно полно отражает изучаемые параметры генеральной совокупности, то ее называют:
- Ответ: репрезентативной
Вопрос 14. Целью эконометрики является получение количественных выводов о свойствах экономических явлений и процессов по данным
- Ответ: выборки
Вопрос 15. Если все наблюдения лежат на линии регрессии, то коэффициент детерминации R2 для модели парной регрессии равен:
- Ответ: единице
Вопрос 16. Если две переменные независимы, то их теоретическая ковариация равна:
- Ответ: 0
Вопрос 17. Обычно прогнозы, получаемые с помощью моделей Бокса-Дженкинса, оказываются на практике __________________ прогнозов, построенных по макроэкономическим моделям.
- Ответ: не хуже
Вопрос 18. Весовые коэффициенты в методе скользящего среднего
- Ответ: всегда больше нуля
Вопрос 19. Если вычисленное значение статистики Спирмена превысит некое критическое значение, то принимается решение о:
- Ответ: наличии гетероскедастичности
Вопрос 20. Отклонение еi в i-м наблюдении yi от регрессии с двумя объясняющими переменными:
- Ответ: ei = yi — a — b1x1 — b2x2
Вопрос 21. Положительная автокорреляция — ситуация, когда случайный член регрессии в следующем наблюдении ожидается:
- Ответ: того же знака, что и в настоящем наблюдении
Вопрос 22. При построении отдельных уравнений регрессии для каждого из 4-х кварталов сумма сезонных отклонений должна равняться:
- Ответ: 0
Вопрос 23. Коэффициент Тейла лежит в пределах
- Ответ: от 0 до 1
Вопрос 24. Множественный регрессионный анализ является __________________ парного регрессионного анализа.
- Ответ: развитием
Вопрос 25. При положительной автокорреляции DW
- Ответ:
Вопрос 26. Процесс Юла описывается моделью
- Ответ: АР (2)
Вопрос 27. Эконометрический инструментарий базируется на методах и моделях
- Ответ: математической статистики
Вопрос 28. Если из экономических соображений известно, что b >= b0, то нулевая гипотеза отвергается только при:
- Ответ: t > tкрит
Вопрос 29. При вычислении t-статистики применяется распределение
- Ответ: Стьюдента
Вопрос 30. Аналитические методы выделения неслучайной составляющей основаны на допущении, что …
- Ответ: известен общий вид неслучайной составляющей
Вопрос 31. Наблюдение зависимой переменной регрессии в предшествующий момент, используемое как объясняющая переменная, называется __________________ переменной.
- Ответ: лаговой
Вопрос 32. Явление, когда нестрогая линейная зависимость между объясняющими переменными в модели множественной регрессии приводит к получению ненадежных оценок регрессии, называют:
- Ответ: мультиколлинеарностью
Вопрос 33. Для модели парной регрессии оценки, полученные по МНК, являются несмещенными, эффективными, состоятельными, если …
- Ответ: выполнены условия Гаусса-Маркова
Вопрос 34. Если элементы набора данных не являются статистически независимыми, то речь идет о:
- Ответ: временном ряде
Вопрос 35. Метод наименьших квадратов — метод нахождения оценок параметров регрессии, основанный на минимизации __________________ квадратов остатков всех наблюдений.
- Ответ: суммы
Вопрос 36. Тест Бокса-Кокса (решетчатый поиск) — прямой компьютерный метод выбора наилучших значений __________________ модели в заданных исследователем пределах с заданным шагом (решеткой).
- Ответ: параметров нелинейной
Вопрос 37. Уравнение y = a + bx, где a и b — оценки параметров a и b, полученные в результате оценивания модели y = a + bx + u по данным выборки, называется уравнением
- Ответ: линейной регрессии
Вопрос 38. Фиктивную переменную для коэффициента наклона вводят как __________________ фиктивной переменной, отвечающей за исследуемую категорию, и интересующей нефиктивной переменной.
- Ответ: произведение
Вопрос 39. Ситуация, когда не отвергнута ложная гипотеза, называется:
- Ответ: ошибкой II рода
Вопрос 40. Доверительный интервал в 99% __________________ интервал в 95%.
- Ответ: шире, чем
Вопрос 41. В множественном регрессионном анализе коэффициент детерминации определяет ____________________________________ регрессией.
- Ответ: долю дисперсии y, объясненную
Вопрос 42. Гетероскедастичность заключается в том, что дисперсия случайного члена регрессии __________________ наблюдений.
- Ответ: зависит от номера
Вопрос 43. Третье условие Гаусса-Маркова состоит в том, что cov (ui, uj) = 0, если …
- Ответ: i ¹ j
Вопрос 44. В модели множественной регрессии всегда желательно присутствие хотя бы одной __________________ переменной для того, чтобы обеспечить надлежащий уровень достоверности оценок.
- Ответ: нефиктивной
Вопрос 45. Зависимая переменная может быть представлена как фиктивная в случае, если она
- Ответ: является качественной по своему характеру
Вопрос 46. Множество наблюдений, составляющих часть генеральной совокупности, называется:
- Ответ: выборкой
Вопрос 47. Сглаживание временного ряда означает устранение
- Ответ: случайных остатков
Вопрос 48. Если автокорреляция отсутствует, то DW»:
- Ответ: 2
Вопрос 49. В методе скользящего среднего веса определяется с помощью:
- Ответ: МНК
Вопрос 50. Отличие одностороннего теста от двустороннего заключается в том, что он имеет только
- Ответ: одно критическое значение
Вопрос 51. Сумма квадратов остатков всех наблюдений — __________________ сумма квадратов отклонений.
- Ответ: остаточная
Вопрос 52. F-статистика для __________________ является в точности квадратом t-статистики для rx, y.
- Ответ: коэффициента детерминации
Вопрос 53. Для уравнения регрессии у=4+2х и наблюденных данных х=4, у=14 остаток в наблюдении равен:
- Ответ: 2
Вопрос 54. Фиктивная переменная для коэффициента наклона предназначена для установление влияния категории на:
- Ответ: коэффициент при нефиктивной переменной
Вопрос 55. Для линейного регрессионного анализа требуется линейность
- Ответ: только по параметрам
Вопрос 56. Второе условие Гаусса-Маркова заключается в том, что …
- Ответ: s2 (ui) — не зависит от i
Вопрос 57. Любой набор категорий можно описать некоторой совокупностью __________________ переменных.
- Ответ: фиктивных
Вопрос 58. В экономике отрицательная автокорреляция встречается __________________ положительная.
- Ответ: гораздо реже, чем
Вопрос 59. Итерационные методы — компьютерные __________________ методы поиска наилучших значений параметров нелинейной модели.
- Ответ: сходящиеся
Вопрос 60. Коэффициент Тейла основан на расчете
- Ответ: среднеквадратичного значения ошибки прогноза приростов
Вопрос 61. Процесс СС (2) имеет автокорреляционную функцию, которая:
- Ответ: обращается в ноль после некоторой точки
Вопрос 62. Набор категорий представляет собой конечный набор __________________ событий.
- Ответ: взаимоисключающих
Вопрос 63. Авторегрессионная схема называется схемой первого порядка, если описываемое __________________ равно 1.
- Ответ: максимальное запаздывание
Вопрос 64. В модели АР (1) частная автокорреляционная функция случайных остатков, разделенных двумя тактами времени, равна:
- Ответ: 0
Вопрос 65. Для выполнения теста Чоу используется распределение
- Ответ: Фишера
Вопрос 66. Коэффициент детерминации равен __________________ выборочной корреляции между y и a + bx.
- Ответ: квадрату
Вопрос 67. Если в регрессионную модель включена лишняя переменная, то оценки коэффициентов оказываются, как правило, …
- Ответ: неэффективными
Вопрос 68. Для производственного процесса, описываемого функцией Кобба-Дугласа, увеличение капитала (К) и труда (i) в 4 раза приводит к увеличению объема выпуска (у):
- Ответ: в 4 раза
Вопрос 69. Коэффициент ранговой корреляции имеет дисперсию
- Ответ: 1/ (n — 1)
Вопрос 70. Коэффициент Тейла служит критерием
- Ответ: успешности сделанного прогноза
Вопрос 71. Метод скользящего среднего относятся к __________________ методам выделения неслучайной составляющей.
- Ответ: алгоритмическим
Вопрос 72. На первом этапе применения теста Голдфелда-Квандта в выборке все наблюдения
- Ответ: Упорядочиваются по возрастанию х
Вопрос 73. Регрессором в уравнении парной линейной регрессии называется:
- Ответ: объясняющая переменная
Вопрос 74. Число степеней свободы (верхнее и нижнее) для отношения RSS2 / RSS1 в тесте Голдфелда-Квандта равно:
- Ответ: n’ — k — 1
Вопрос 75. Доля объясненной дисперсии зависимой переменной в общей выборочной дисперсии y выражается коэффициентом
- Ответ: детерминации
Вопрос 76. Значение оценки является:
- Ответ: случайной величиной
Вопрос 77. Для регрессии второго порядка y = 12+7x1-3x2 отклонение от регрессии наблюдения (х1=2, х2=1, y=20) равно:
- Ответ: е=3
Вопрос 78. Критерий восходящих и нисходящих серий позволяет:
- Ответ: выявить неслучайную составляющую
Вопрос 79. На больших временах процесс формирования значений временного ряда находится под воздействием __________________ факторов.
- Ответ: долговременных и циклических
Вопрос 80. Критерий серий, основанный на медиане, позволяет:
- Ответ: выявить неслучайную составляющую
Вопрос 81. Близко к линии регрессии находится наблюдение, для которого теоретическое распределение случайного члена имеет
- Ответ: малое стандартное отклонение
Вопрос 82. Марковский процесс описывается моделью
- Ответ: АР (1)
Вопрос 83. Метод Кокрана-Оркатта — компьютерный итерационный метод устранения
- Ответ: автокорреляции
Вопрос 84. Второе условие Гаусса-Маркова предполагает, что дисперсия случайного члена __________________ в каждом наблюдении.
- Ответ: постоянна
Вопрос 85. Как правило в эталонной категории
- Ответ: все фиктивные переменные равны 0
Вопрос 86. Коэффициент наклона в уравнении линейной регрессии показывает __________________ изменяется y при увеличении x на одну единицу.
- Ответ: на сколько единиц
Вопрос 87. Оценка параметров в лаговой структуре Койка делается:
- Ответ: решетчатым методом
Вопрос 88. Эффективная оценка — несмещенная оценка, имеющая __________________ среди всех несмещенных оценок.
- Ответ: наименьшую дисперсию
Вопрос 89. В критерии серий, основанном на медиане, протяженность самой длинной серии временного ряда 5, 1, 4, 2 равна:
- Ответ: 1
Вопрос 90. Выборочная дисперсия расчетных значений величины y называется __________________ дисперсией зависимой переменной.
- Ответ: объясненной
Вопрос 91. Свойства коэффициентов регрессии как случайных величин зависят от свойств __________________ уравнения.
- Ответ: остаточного члена
Вопрос 92. Модель Бокса-Дженкинса — это модель …
- Ответ: АРПСС
Вопрос 93. Исследование соотношения между спросом на реальные денежные остатки и ожидаемым изменением уровня цен описывается моделью
- Ответ: Кейгана
Вопрос 94. Оценка ρ, полученная МНК для авторегрессионной схемы первого порядка рассчитывается по формуле __________________, ek — остатки в наблюдениях.
- Ответ: cov (ek-1, ek) / var (ek-1)
Вопрос 95. Фиктивные переменные включаются в модель множественной регрессии, если необходимо установить влияние каких-либо __________________ факторов.
- Ответ: дискретных
Вопрос 96. Для проверки нулевой гипотезы H0: b= b0 применяется тест
- Ответ: Стьюдента
Вопрос 97. Дисперсии оценок а и b __________________ дисперсии остаточного члена s2 (u).
- Ответ: прямо пропорциональны
Вопрос 98. Категория — это событие, которое определенно __________________ в каждом наблюдении.
- Ответ: либо происходит, либо нет
Вопрос 99. Область принятия гипотезы — множество значений __________________, при попадании в которое нулевая гипотеза не отвергается.
- Ответ: оценок параметра
Вопрос 100. Ловушка dummy trap приводит к:
- Ответ: полной коллинеарности
Вопрос 101. Модель Линтнера основывается на предположении, что желаемый объем дивидендов
- Ответ: пропорционален прибыли
Вопрос 102. Детерминированная переменная может рассматриваться как предельный вариант случайной переменной, принимающей свое единственное значение с вероятностью
- Ответ: 1
Вопрос 103. Показатель выборочной ковариации позволяет выразить связь между двумя переменными
- Ответ: единым числом
Вопрос 104. Эконометрика — часть экономической науки, занимающаяся разработкой и применением __________________ методов анализа экономических процессов.
- Ответ: математических
Вопрос 105. Статистика Дарбина-Уотсона проверяет нулевую гипотезу Но:
- Ответ: отсутствие автокорреляции
Вопрос 106. Зависимость объемов введенных основных фондов от капитальных вложений описывается:
- Ответ: регрессионной моделью с распределенными лагами
Вопрос 107. Для того, чтобы установить влияние категории на коэффициент регрессии при нефиктивной переменной, в модель включают:
- Ответ: фиктивную переменную для коэффициента наклона
Вопрос 108. При отрицательной автокорреляции DW
- Ответ: >2
Вопрос 109. На экзамене в группе из 15 студентов 4 человека получили отличную оценку, 8 человек — оценку хорошо, 3 человека — оценку удовлетворительно. Средний бал по группе равен:
- Ответ: 4,06
Вопрос 110. При использования обычного МНК наблюдению высокого качества придается вес __________________ наблюдению низкого качества.
- Ответ: такой же как
Вопрос 111. Фиктивная переменная взаимодействия — это __________________ фиктивных переменных.
- Ответ: произведение
Вопрос 112. При попадании оценки в критическое значение:
- Ответ: сохраняется неопределенность в отношении гипотезы
Вопрос 113. Модель Кейгана — модель, описывающая гиперинфляцию с помощью модели
- Ответ: адаптивных ожиданий
Вопрос 114. При проведении теста Голдфелда-Квандта из рассмотрения исключаются __________________ наблюдений.
- Ответ: средние (n — 2n’)
Вопрос 115. Фиктивные переменные, предназначены для обозначения различных лет, кварталов, месяцев и т.п. — это __________________ фиктивные переменные.
- Ответ: сезонные
Вопрос 116. Теоретическая ковариация двух случайных величин определяется как математическое ожидание __________________ отклонений этих величин от их средних значений.
- Ответ: произведения
Вопрос 117. В модели парной регрессии у* = 4 + 2х изменение х на 2 единицы вызывает изменение у на __________________ единиц.
- Ответ: 4
Вопрос 118. Вероятности, с которыми случайная величина принимает свои значения, называют __________________ случайной величины.
- Ответ: законом распределения
Вопрос 119. Мерой разброса значений случайной величины служит:
- Ответ: дисперсия
Вопрос 120. При снижении уровня значимости риск совершить ошибку I рода
- Ответ: уменьшается
Вопрос 121. Фиктивная переменная — переменная, принимающая в каждом наблюдении значения:
- Ответ: 0 или 1
Вопрос 122. На больших временах __________________ факторы описываются монотонной функцией.
- Ответ: долговременные
Вопрос 123. Необходимость применения специальных статистических методов для обработки экономической информации вызвана __________________ данных.
- Ответ: стохастической природой
Вопрос 124. При использовании метода Монте-Карло результаты наблюдения генерируются с помощью
- Ответ: датчика случайных чисел
Вопрос 125. Для отношения RSS2/RSS1 в рамках теста Голдфелда-Квандта проводят тест
- Ответ: Фишера
Вопрос 126. В парном регрессионном анализе коэффициент детерминации R2 равен:
- Ответ: rх;у2
Вопрос 127. Подбор порядка аппроксимирующего полинома производится при помощи
- Ответ: метода последовательных разностей
Вопрос 128. Функция цены — функция, где аргументом является __________________, а значением функции — цена ошибки.
- Ответ: род ошибки
Вопрос 129. Если нулевая гипотеза Н0: β = β0, то альтернативная гипотеза Н1 — это:
- Ответ: β≠β0
Вопрос 130. Невыполнение 2 и 3 условий Гаусса-Маркова, приводит к потере свойства __________________ оценок.
- Ответ: эффективности
Вопрос 131. Эксперимент по методу Монте-Карло — искусственный, контролируемый эксперимент, проводимый для проверки и сравнения эффективности различных
- Ответ: статистических методов
Вопрос 132. Нижний индекс переменной (t-s) означает, что она является:
- Ответ: лаговой
Вопрос 133. Автокорреляция первого порядка — ситуация, когда случайный член uк коррелирует с:
- Ответ: Uк-1
Вопрос 134. Для применения теста Зарембки необходимо
- Ответ: преобразование масштаба наблюдений у
Вопрос 135. Если элементы набора данных не являются одинаково распределенными, то речь идет о:
- Ответ: временном ряде
Вопрос 136. Нелинейная модель у = f (x), в которой возможна замена переменной z = g (x), приводящая получившуюся модель y = F (z) — к линейной, называется моделью, нелинейной по:
- Ответ: переменным
Вопрос 137. Гетероскедастичность приводит к __________________ оценок параметров регрессии по МНК.
- Ответ: неэффективности
Вопрос 138. Число степеней свободы для уравнения множественной (m-мерной) регрессии при достаточном числе наблюдений n составляет:
- Ответ: n — m — 1
Вопрос 139. В критерии восходящих и нисходящих серий, общее число серий временного ряда 5, 7, 6, 4, 3, 1 равно:
- Ответ: 2
Вопрос 140. Ловушка dummy trap — выбор совокупности фиктивных переменных, сумма которых
- Ответ: константа
Вопрос 141. Оценка параметра находится __________________ доверительного интервала.
- Ответ: в центре
Вопрос 142. Данные по определенному показателю, полученные для разных однотипных объектов, называются:
- Ответ: перекрестными
Вопрос 143. При увеличении размера выборки оценка математического ожидания
- Ответ: становится более точной
Вопрос 144. При стремлении размера выборки к бесконечности стандартное отклонение математического ожидания стремится к:
- Ответ: 0
Вопрос 145. Доля числа исходов, благоприятствующих данному событию, в общем числе равновероятных исходов называется __________________ этого события.
- Ответ: вероятностью
Вопрос 146. Нижнее число степеней свободы F-cтатистики в случае парной регрессии равно:
- Ответ: n-2
Вопрос 147. Автокорреляционная функция принимает значения в пределах
- Ответ: от -1 до 1
Вопрос 148. Фиктивная переменная взаимодействия — фиктивная переменная, предназначенная для установления влияния на регрессию __________________ событий.
- Ответ: одновременного наступления нескольких независимых
Вопрос 149. Метод Зарембки процедура выбора между линейной и __________________ моделями:
- Ответ: логарифмической
Вопрос 150. Функция спектральной плотности позволяет установить:
- Ответ: частоты колебаний
Вопрос 151. При проведении теста Голдфелда-Квандта предполагается, что стандартное отклонение остаточного члена регрессии растет с __________________ переменной.
- Ответ: ростом объясняющей
Вопрос 152. Ранг наблюдения переменной — номер наблюдения переменной в упорядоченной __________________ последовательности.
- Ответ: по возрастанию значений наблюдаемой величины
Вопрос 153. Коэффициенты при сезонных фиктивных переменных показывают __________________ при смене сезона.
- Ответ: численную величину изменения, происходящего
Вопрос 154. При высоком уровне значимости проблема заключается в высоком риске допущения
- Ответ: ошибки II рода
Вопрос 155. Тест ранговой корреляции Спирмена — тест на:
- Ответ: гетероскедастичность
Вопрос 156. Статистика для теста ранговой корреляции Спирмена имеет __________________ распределение.
- Ответ: нормальное
Вопрос 157. МНК дает __________________ для данной выборки значение коэффициента детерминации R2.
- Ответ: максимальное
Вопрос 158. Функция Кобба-Дугласа имеет вид Y =
- Ответ: AKa L1-a
Вопрос 159. Процесс АР (2) имеет автокорреляционную функцию, которая:
- Ответ: имеет бесконечную протяженность
Вопрос 160. Утверждение о том, что неизвестный параметр модели принадлежит другому заданному множеству В, АÇВ = Æ, называется:
- Ответ: альтернативной гипотезой
Вопрос 161. Эконометрика получает количественные зависимости для экономических соотношений, основываясь в первую очередь на:
- Ответ: данных
Вопрос 162. Строгая линейная зависимость между переменными — ситуация, когда __________________ двух переменных равна 1 или -1.
- Ответ: выборочная корреляция
Вопрос 163. При рассмотрении спектральной плотности ограничиваются значениями ω, лежащими в пределах
- Ответ: от 0 до π
Вопрос 164. Функция Кобба-Дугласа называется:
- Ответ: производственной функцией
Вопрос 165. Утверждение о том, что неизвестный параметр модели принадлежит заданному множеству А, называется:
- Ответ: нулевой гипотезой
Вопрос 166. Проверка гипотезы Н0: R2 = 0 происходит с помощью теста
- Ответ: Фишера
Вопрос 167. Спектральная плотность может принимать __________________ значения.
- Ответ: только положительные
Вопрос 168. В модели множественной регрессии за изменение __________________ регрессии отвечает несколько объясняющих переменных.
- Ответ: одной зависимой переменной
Вопрос 169. Функция потерь, используемая при выборе между несмещенной и эффективной оценкой, определяет стоимость неточности как функцию
- Ответ: размера ошибки
Вопрос 170. Для уравнения регрессии у = 3х — 2 прогнозное значение зависимой переменной, если объясняющая переменная равна 4, — это:
- Ответ: 10
Вопрос 171. Тест Глейзера устанавливает наличие __________________ связи между стандартным отклонением остаточного члена регрессии и объясняющей переменной.
- Ответ: нелинейной
Вопрос 172. Чем больше число наблюдений, тем __________________ зона неопределенности для критерия Дарбина-Уотсона.
- Ответ: уже
Вопрос 173. Остаток в i-ом наблюдении по модели парной регрессии y=a+bx равен:
- Ответ: yi — (a + bxi)
Вопрос 174. Модель парной регрессии — __________________ модель зависимости между двумя переменными.
- Ответ: линейная
Вопрос 175. Граничное значение области принятия гипотезы с p%-ной вероятностью совершить ошибку I рода определяется __________________ при p-процентном уровне значимости.
- Ответ: критическим значением теста
Вопрос 176. Спецификация запаздываний применительно к переменным в модели называется:
- Ответ: лаговой структурой
Вопрос 177. Если независимые переменные имеют ярко выраженный временной тренд, то они оказываются:
- Ответ: тесно коррелированными
Вопрос 178. Первое условие Гаусса-Маркова заключается в том, что __________________ для любого i.
- Ответ: М (ui) = 0
Вопрос 179. В критерии восходящих и нисходящих серий, длина самой длинной серии временного ряда 1, 5, 4, 1, 6 равна:
- Ответ: 2
Вопрос 180. Идентификация модели СС (2) сводится к решению системы двух __________________ уравнений.
- Ответ: нелинейных
Вопрос 181. Выборочная дисперсия как оценка теоретической дисперсии имеет __________________ смещение.
- Ответ: отрицательное
Вопрос 182. Функция спроса y = a xb pg n может быть линеаризована посредством
- Ответ: логарифмирования
Вопрос 183. Оценка стандартного отклонения случайной величины, полученная по данным выборки, называется стандартной __________________ случайной величины.
- Ответ: ошибкой
Вопрос 184. Оценивание каждого параметра в уравнении регрессии поглощает __________________ свободы в выборке.
- Ответ: одну степень
Вопрос 185. Выборочная корреляция является __________________ теоретической корреляции.
- Ответ: оценкой
Вопрос 186. Точность оценок по МНК улучшается, если увеличивается:
- Ответ: количество наблюдений
Вопрос 187. При добавлении объясняющей переменной в уравнение регрессии коэффициент детерминации
- Ответ: не уменьшается
Вопрос 188. В критерии серий, основанном на медиане, общее число серий временного ряда 1, 3, 5, 4, 2 равно:
- Ответ: 3
Вопрос 189. Для функции Кобба-Дугласа у=100к1/3*i2/3 эластичность выпуска продукции по капиталу равна:
- Ответ: 1/3
Вопрос 190. В процессе формирования значений всякого временного ряда всегда участвуют __________________ факторы.
- Ответ: случайные
Вопрос 191. Первый шаг метода Зарембки заключается в вычислении __________________ y по выборке.
- Ответ: среднего геометрического
Вопрос 192. Плоскость регрессии y = a + b1x1 + b2x2 — двумерная плоскость в __________________ пространстве.
- Ответ: трехмерном
Вопрос 193. Для функции y = 4x0,2, эластичность равна:
- Ответ: 0,2
Вопрос 194. Поправка Прайса-Уинстена — метод спасения __________________ в автокорреляционной схеме первого порядка.
- Ответ: первого наблюдения
Вопрос 195. В лаговой структуре Койка надо оценить только:
- Ответ: три параметра
Вопрос 196. Наилучший способ устранения автокорреляции — установление ответственного за нее фактора и включение соответствующей __________________ переменной в регрессию.
- Ответ: объясняющей
Вопрос 197. Автокорреляция представляет тем большую проблему, чем
- Ответ: меньше интервал между наблюдениями
Вопрос 198. Проблема, связанная со смещением оценки коэффициентов регрессии, в одном случае, или с утратой эффективности этих оценок в другом случае неправильной спецификации переменных, перестает существовать, если коэффициент парной корреляции между переменными равен:
- Ответ: 0
Вопрос 199. Выборочная дисперсия остатков в наблюдениях Var (y — (a + bx)) называется __________________ дисперсией зависимой переменной.
- Ответ: необъясненной
Вопрос 200. Тест ранговой корреляции Спирмена — тест, устанавливающий, имеет ли стандартное отклонение остаточного члена регрессии нестрогую линейную зависимость с __________________ переменной.
- Ответ: объясняющей
Вопрос 201. Если совокупность значений случайной величины представляет собой конечный или счетный набор возможных чисел, то случайная величина называется:
- Ответ: дискретной
Вопрос 202. Стандартные ошибки, вычисленные при гетероскедастичности
- Ответ: занижены по сравнению с истинными значениями
Вопрос 203. Логарифмическое преобразование позволяет осуществить переход от нелинейной модели y = 5x2u к модели
- Ответ: ln y = ln 5 + 2 ln x + ln u
Вопрос 204. Для одностороннего критерия нулевой гипотезы Н0: β =β0 альтернативная гипотеза Н1:
- Ответ: β > β
Вопрос 205. Для функции Кобба-Дугласа у=80К3/4*i1/4 эластичность выпуска продукции по труду равна:
- Ответ: 1/4
Вопрос 206. Если опущена переменная, которая должна входить в регрессионную модель, то оценки коэффициентов регрессии оказываются:
- Ответ: смещенными
Вопрос 207. Если между двумя переменными существует строгая положительная линейная зависимость, то коэффициент корреляции между ними принимает значение, равное:
- Ответ: единице
Вопрос 208. Процесс выбора необходимых для регрессии переменных и отбрасывание лишних переменных называется:
- Ответ: спецификацией переменных
Вопрос 209. Результаты проверки гипотезы H0: b = b0 представляются на __________________ значимости.
- Ответ: двух уровнях
Вопрос 210. Всю совокупность реализаций случайной величины называют __________________ совокупностью.
- Ответ: генеральной
Вопрос 211. Остатки значений log y __________________ остатков значений y.
- Ответ: значительно меньше
Вопрос 212. Общая (ТSS), объясненная (ESS) и необъясненная (RSS) суммы квадратов отклонений находятся в следующих соотношениях
- Ответ: TSS = RSS + ESS
Вопрос 213. Если F-статистика Фишера превысит критическое значение Fкрит, то регрессия считается:
- Ответ: значимой
Вопрос 214. Число степеней свободы для t-статистики равно числу наблюдений в выборке __________________ количество оцениваемых коэффициентов.
- Ответ: минус
Вопрос 215. Если коэффициент Тейла равен нулю, то …
- Ответ: прогноз сделан успешно
Вопрос 216. Верхнее число степеней свободы F-cтатистики в случае парной регрессии равно:
- Ответ: одному
Вопрос 217. Автокорреляция — нарушение __________________ условия Гаусса-Маркова.
- Ответ: третьего
Вопрос 218. Совокупность фиктивных переменных — некоторое количество фиктивных переменных, предназначенное для описания
- Ответ: набора категорий
Вопрос 219. Стандартное отклонение случайной величины характеризует среднее ожидаемое расстояние между наблюдениями этой случайной величины и ее:
- Ответ: математическим ожиданием
Вопрос 220. В авторегрессионной схеме первого порядка uкн = рuк + ek предполагается, что значение ek в каждом наблюдении:
- Ответ: не зависит от его значений во всех других наблюдениях
Вопрос 221. Цель регрессионного анализа состоит в объяснении поведения
- Ответ: зависимой переменной
Вопрос 222. Разность между математическим ожиданием оценки и истинным значением оцениваемого параметра называют:
- Ответ: смещением
Вопрос 223. В авторегрессионной схеме первого порядка зависимость между последовательными случайными членами описывается формулой uk+1 = __________________, где ρ — константа, ek+1 — новый случайный член.
- Ответ: ρuk + e k+1
Вопрос 224. В функции Кобба-Дугласа вида log Y = a + b1 log k + b2 log l (k — индекс затрат капитала, l — индекс затрат труда) роль замещающей переменной для показателя технического прогресса играет:
- Ответ: log k
Вопрос 225. Наиболее частая причина положительной автокорреляции заключается в постоянной направленности воздействия __________________ переменных.
- Ответ: не включенных в уравнение
Вопрос 226. Для линеаризации функции Кобба-Дугласа необходимо предварительно обе части уравнения
- Ответ: разделить на L
Вопрос 227. О наличии данной частоты в спектре временного ряда свидетельствует __________________ спектральной плотности.
- Ответ: пик на графике
Вопрос 228. При добавлении еще одной переменной в уравнение регрессии коэффициент детерминации:
- Ответ: не уменьшается
Вопрос 229. Стандартные отклонения коэффициентов регрессии обратно пропорциональны величине _________, где n – число наблюдений:
- Ответ: n
Вопрос 230. Зависимая переменная может быть представлена как фиктивная в случае если она:
- Ответ: трудноизмерима
Вопрос 231. Тест Фишера является:
- Ответ: односторонним
Вопрос 232. Выборочная корреляция является __________оценкой теоретической корреляции:
- Ответ: состоятельной
Вопрос 233. Определение отдельного вклада каждой из независимых переменных в объясненную дисперсию в случае их коррелированности является ___________ задачей:
- Ответ: невыполнимой
Вопрос 234. Условие гомоскедастичности означает, что вероятность того, что случайный член примет какое-либо конкретное значение _________ наблюдений:
- Ответ: одинакова для всех
Вопрос 235. Значения t-статистики для фиктивных переменных незначимо отличается от:
- Ответ: 0
Вопрос 236. Из перечисленных факторов: 1) число объясняющих переменных, 2) количество наблюдений в выборке, 3)конкретные значения переменных, критические значения статистики Дарбина-Уотсона зависят от:
- Ответ: 1, 2
Вопрос 237. Значение статистики DW находится между значениями:
- Ответ: 0 и 4
Вопрос 238. Наблюдение зависимой переменной регрессии в предшествующий момент, используемое как объясняющая переменная, называется:
- Ответ: лаговой
Вопрос 239. Чем больше число наблюдений, тем __________ зона неопределенности для критерия Дарбина-Уотсона:
- Ответ: уже
Вопрос 240. МНК автоматически дает ___________ для данной выборки значение коэффициента детерминации R2:
- Ответ: максимальное
Вопрос 241. В авторегрессионной схеме первого порядка предполагается, что значение в каждом наблюдении:
- Ответ: не зависит от его значения во всех других наблюдениях
Вопрос 242. Линия регрессии _______ через точку ( , ) :
- Ответ: всегда проходит
Вопрос 243. Если предположение о природе гетероскедастичности верно, то дисперсия случайного члена для первых наблюдений в упорядоченном ряду будет ________ для последних:
- Ответ: ниже, чем
Вопрос 244. Стандартные ошибки, вычисленные при гетероскедастичности:
- Ответ: занижены по сравнению с истинными значениями
Вопрос 245. Критерий Дарбина-Уотсона –метод обнаружения _________ с помощью статистики Дарбина-Уотсона:
- Ответ: автокорреляции
Вопрос 246. Параметры множественной регрессии ?1 , ?2 ,… ?м показывают _________ соответствующих экономических факторов:
- Ответ: степень влияния
Вопрос 247. Во множественном регрессионном анализе коэффициент детерминации определяет _______регрессией:
- Ответ: долю дисперсии y, объясненную
Вопрос 248. Сумма квадратов отклонений величины y от своего выборочного значения _____ сумма квадратов отклонений:
- Ответ: общая
Вопрос 249. Фиктивная переменная взаимодействия – фиктивная переменная, предназначенная для
- Ответ: одновременного наступления нескольких независимых
Вопрос 250. Автокорреляция первого порядка – ситуация, когда коррелируют случайные члены регрессии в __________ наблюдениях:
- Ответ: последовательных
Вопрос 251. Фиктивная переменная – переменная, принимающая в каждом наблюдении:
- Ответ: только два значения 0 или 1
Вопрос 252. Для того, чтобы установить влияние какого-либо события на коэффициент линейной регрессии при нефиктивной переменной, в модель включают:
- Ответ: фиктивную переменную для коэффициента наклона
Вопрос 253. Оценка параметра для модели множественной регрессии в случае двух независимых переменных вычисляется по формуле: а =
- Ответ: 1 1 2 2 y ? b x ? b x
Вопрос 254. Процесс выбора необходимых переменных для регрессии переменных и отбрасывание лишних переменных называется:
- Ответ: спецификацией переменных
Вопрос 255. Из перечисленного: 1) число объясняющих переменных, 2) количество наблюдений в выборке, 3) конкретные значения переменных критические значения статистики Дарбина-Уотсона зависят от:
- Ответ: 1, 2
Вопрос 256. Число степеней свободы для уравнения m-мерной регрессии при достаточном числе наблюдений n составляет:
- Ответ: n-m-1
Вопрос 257. Наилучший способ устранения автокорреляции – установление ответственного за нее фактора и включение соответствующей ___________ переменной в регрессию:
- Ответ: объясняющей
Вопрос 258. Строгая линейная зависимость между переменными – ситуация, когда ________ двух переменных равна 1 или -1:
- Ответ: выборочная корреляция
Вопрос 259. Значение статистики Дарбина-Уотсона находится между значениями:
- Ответ: 0 и 4
В Учи.ру мы стараемся даже небольшие улучшения выкатывать A/B-тестом, только за этот учебный год их было больше 250. A/B-тест — мощнейший инструмент тестирования изменений, без которого сложно представить нормальное развитие интернет-продукта. В то же время, несмотря на кажущуюся простоту, при проведении A/B-теста можно допустить серьёзные ошибки как на этапе дизайна эксперимента, так и при подведении итогов. В этой статье я расскажу о некоторых технических моментах проведения теста: как мы определяем срок тестирования, подводим итоги и как избегаем ошибочных результатов при досрочном завершении тестов и при тестировании сразу нескольких гипотез.
Типичная схема A/B-тестирования у нас (да и у многих) выглядит так:
- Разрабатываем фичу, но перед раскаткой на всю аудиторию хотим убедиться, что она улучшает целевую метрику, например, вовлечённость.
- Определяем срок, на который запускается тест.
- Случайно разбиваем пользователей на две группы.
- Одной группе показываем версию продукта с фичей (экспериментальная группа), другой — старую (контрольная).
- В процессе мониторим метрику, чтобы вовремя прекратить особо неудачный тест.
- По истечении срока теста сравниваем метрику в экспериментальной и контрольной группах.
- Если метрика в экспериментальной группе статистически значимо лучше, чем в контрольной, раскатываем протестированную фичу на всех. Если же статистической значимости нет, завершаем тест с отрицательным результатом.
Всё выглядит логично и просто, дьявол, как всегда, в деталях.
Статистическая значимость, критерии и ошибки
В любом A/B-тесте присутствует элемент случайности: метрики групп зависят не только от их функционала, но и от того, какие пользователи в них попали и как они себя ведут. Чтобы достоверно сделать выводы о превосходстве какой-то группы, нужно набрать достаточно наблюдений в тесте, но даже тогда вы не застрахованы от ошибок. Их различают два типа:
- Ошибка первого рода происходит, если мы фиксируем разницу между группами, хотя на самом деле её нет. В тексте также будет встречаться эквивалентный термин — ложноположительный результат. Статья посвящена именно таким ошибкам.
- Ошибка второго рода происходит, если мы фиксируем отсутствие разницы, хотя на самом деле она есть.
При большом количестве экспериментов важно, чтобы вероятность ошибки первого рода была мала. Её можно контролировать с помощью статистических методов. Например, мы хотим, чтобы в каждом эксперименте вероятность ошибки первого рода не превышала 5% (это просто удобное значение, для собственных нужд можно брать другое). Тогда мы будем принимать эксперименты на уровне значимости 0.05:
- Есть A/B-тест с контрольной группой A и экспериментальной — B. Цель — проверить, что группа B отличается от группы A по какой-то метрике.
- Формулируем нулевую статистическую гипотезу: группы A и B не отличаются, а наблюдаемые различия объясняются шумом. По умолчанию всегда считаем, что разницы нет, пока не доказано обратное.
- Проверяем гипотезу строгим математическим правилом — статистическим критерием, например, критерием Стьюдента.
- В результате получаем величину p-value. Она лежит в диапазоне от 0 до 1 и означает вероятность увидеть текущую или более экстремальную разницу между группами при условии верности нулевой гипотезы, то есть при отсутствии разницы между группами.
- Значение p-value сравнивается с уровнем значимости 0.05. Если оно больше, принимаем нулевую гипотезу о том, что различий нет, иначе считаем, что между группами есть статистически значимая разница.
Проверить гипотезу можно параметрическим или непараметрическим критерием. Параметрические опираются на параметры выборочного распределения случайной величины и обладают большей мощностью (реже допускают ошибки второго рода), но предъявляют требования к распределению исследуемой случайной величины.
Самый распространенный параметрический тест — критерий Стьюдента. Для двух независимых выборок (случай A/B-теста) его иногда называют критерием Уэлча. Этот критерий работает корректно, если исследуемые величины распределены нормально. Может показаться, что на реальных данных это требование почти никогда не удовлетворяется, однако на самом деле тест требует нормального распределения выборочных средних, а не самих выборок. На практике это означает, что критерий можно применять, если у вас в тесте достаточно много наблюдений (десятки-сотни) и в распределениях нет совсем уж длинных хвостов. При этом характер распределения исходных наблюдений неважен. Читатель самостоятельно может убедиться, что критерий Стьюдента работает корректно даже на выборках, сгенерированных из распределений Бернулли или экспоненциального.
Из непараметрических критериев популярен критерий Манна — Уитни. Его стоит применять, если ваши выборки очень малого размера или есть большие выбросы (метод сравнивает медианы, поэтому устойчив к выбросам). Также для корректной работы критерия в выборках должно быть мало совпадающих значений. На практике нам ни разу не приходилось применять непараметрические критерии, в своих тестах всегда пользуемся критерием Стьюдента.
Проблема множественного тестирования гипотез
Самая очевидная и простая проблема: если в тесте кроме контрольной группы есть несколько экспериментальных, то подведение итогов с уровнем значимости 0.05 приведёт к кратному росту доли ошибок первого рода. Так происходит, потому что при каждом применении статистического критерия вероятность ошибки первого рода будет 5%. При количестве групп и уровне значимости
вероятность, что какая-то экспериментальная группа выиграет случайно, составляет:
Например, для трёх экспериментальных групп получим 14.3% вместо ожидаемых 5%. Решается проблема поправкой Бонферрони на множественную проверку гипотез: нужно просто поделить уровень значимости на количество сравнений (то есть групп) и работать с ним. Для примера выше уровень значимости с учётом поправки составит 0.05/3 = 0.0167 и вероятность хотя бы одной ошибки первого рода составит приемлемые 4.9%.
Метод Холма — Бонферрони
Искушенный читатель знает и о методе Холма — Бонферрони, который всегда обладает большей мощностью, чем поправка Бонферрони, то есть реже совершает ошибки второго рода. В этом методе мы сортируем гипотез по возрастанию значений p-value и начинаем их сравнивать по порядку с требуемым уровнем значимости, который увеличивается в зависимости от номера шага
по формуле:
P-value первой гипотезы сравнивается с уровнем статистический значимости . Если гипотеза принимается, то переходим ко второй и сравниваем её p-value с уровнем статистической значимости
, и так далее. Как только какая-то гипотеза отвергается, процесс останавливается и все оставшиеся гипотезы так же отвергаются. Самое жёсткое требование (и такое же, как в поправке Бонферрони) накладывается на гипотезу с наименьшим p-value, а большая мощность достигается за счёт менее жёстких условий для последующих гипотез. Цель A/B-теста — выбрать одного единственного победителя, поэтому методы Бонферрони и Холма — Бонферрони абсолютно идентичны в этом приложении.
Строго говоря, сравнения групп по разным метрикам или срезам аудитории тоже подвержены проблеме множественного тестирования. Формально учесть все проверки довольно сложно, потому что их количество сложно спрогнозировать заранее и подчас они не являются независимыми (особенно если речь идёт про разные метрики, а не срезы). Универсального рецепта нет, полагайтесь на здравый смысл и помните, что если проверить достаточно много срезов по разным метрикам, то в любом тесте можно увидеть якобы статистически значимый результат. А значит, надо с осторожностью относиться, например, к значимому приросту ретеншена пятого дня новых мобильных пользователей из крупных городов.
Проблема подглядывания
Частный случай множественного тестирования гипотез — проблема подглядывания (peeking problem). Смысл в том, что значение p-value по ходу теста может случайно опускаться ниже принятого уровня значимости. Если внимательно следить за экспериментом, то можно поймать такой момент и ошибочно сделать вывод о статистической значимости.
Предположим, что мы отошли от описанной в начале поста схемы проведения тестов и решили подводить итоги на уровне значимости 5% каждый день (или просто больше одного раза за время теста). Под подведением итогов я понимаю признание теста положительным, если p-value ниже 0.05, и его продолжение в противном случае. При такой стратегии доля ложноположительных результатов будет пропорциональна количеству проверок и уже за первый месяц достигнет 28%. Такая огромная разница кажется контринтуитивной, поэтому обратимся к методике A/A-тестов, незаменимой для разработки схем A/B-тестирования.
Идея A/A-теста проста: симулировать на исторических данных много A/B-тестов со случайным разбиением на группы. Разницы между группами заведомо нет, поэтому можно точно оценить долю ошибок первого рода в своей схеме A/B-тестирования. На гифке ниже показано, как изменяются значения p-value по дням для четырёх таких тестов. Равный 0.05 уровень значимости обозначен пунктирной линией. Когда p-value опускается ниже, мы окрашиваем график теста в красный. Если бы в этом время подводились итоги теста, он был бы признан успешным.
Рассчитаем аналогично 10 тысяч A/A-тестов продолжительностью в один месяц и сравним доли ложноположительных результатов в схеме с подведением итогов в конце срока и каждый день. Для наглядности приведём графики блуждания p-value по дням для первых 100 симуляций. Каждая линия — p-value одного теста, красным выделены траектории тестов, в итоге ошибочно признанных удачными (чем меньше, тем лучше), пунктирная линия — требуемое значение p-value для признания теста успешным.
На графике можно насчитать 7 ложноположительных тестов, а всего среди 10 тысяч их было 502, или 5%. Хочется отметить, что p-value многих тестов по ходу наблюдений опускались ниже 0.05, но к концу наблюдений выходили за пределы уровня значимости. Теперь оценим схему тестирования с подведением итогов каждый день:
Красных линий настолько много, что уже ничего не понятно. Перерисуем, обрывая линии тестов, как только их p-value достигнут критического значения:
Всего будет 2813 ложноположительных тестов из 10 тысяч, или 28%. Понятно, что такая схема нежизнеспособна.
Хоть проблема подглядывания — это частный случай множественного тестирования, применять стандартные поправки (Бонферрони и другие) здесь не стоит, потому что они окажутся излишне консервативными. На графике ниже — доля ложноположительных результатов в зависимости от количества тестируемых групп (красная линия) и количества подглядываний (зелёная линия).
Хотя на бесконечности и в подглядываниях мы вплотную приблизимся к 1, доля ошибок растёт гораздо медленнее. Это объясняется тем, что сравнения в этом случае независимыми уже не являются.
Байесовский подход и проблема подглядывания
Можно встретить мнение, что Байесовский подход к анализу A/B-тестов избавляет от проблемы подглядывания. Это не так, хотя и его можно настроить соответствующим образом. Отличную статью с дополнительными материалами можно почитать здесь.
Методы досрочного завершения теста
Есть варианты тестирования, позволяющие досрочно принять тест. Расскажу о двух из них: с постоянным уровнем значимости (поправка Pocock’a) и зависимым от номера подглядывания (поправка O’Brien-Fleming’a). Строго говоря, для обеих поправок нужно заранее знать максимальный срок теста и количество проверок между запуском и окончанием теста. Причём проверки должны происходить примерно через равные промежутки времени (или через равные количества наблюдений).
Pocock
Метод заключается в том, что мы подводим итоги тестов каждый день, но при сниженном (более строгом) уровне значимости. Например, если мы знаем, что сделаем не больше 30 проверок, то уровень значимости надо выставить равным 0.006 (подбирается в зависимости от количества подглядываний методом Монте-Карло, то есть эмпирически). На нашей симуляции получим 4% ложноположительных исходов — видимо, порог можно было увеличить.
Несмотря на кажущуюся наивность, некоторые крупные компании пользуются именно этим способом. Он очень прост и надёжен, если вы принимаете решения по чувствительным метрикам и на большом трафике. Например, в «Авито» по умолчанию уровень значимости принят за 0.005.
O’Brien-Fleming
В этом методе уровень значимости изменяется в зависимости от номера проверки. Надо заранее определить количество шагов (или подглядываний) в тесте и рассчитать уровень значимости для каждого из них. Чем раньше мы пытаемся завершить тест, тем более жёсткий критерий будет применён. Пороговые значения статистики Стьюдента (в том числе значение на последнем шаге
), соответствующие нужному уровню значимости, зависят от номера проверки
(принимает значения от 1 до общего количества проверок
включительно) и рассчитываются по эмпирически полученной формуле:
Код для воспроизведения коэффициентов
from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score
import matplotlib.pyplot as plt
# datapoints from https://www.aarondefazio.com/tangentially/?p=83
total_steps = [
2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60
]
last_z = [
1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081,
2.107, 2.123, 2.134, 2.143, 2.164, 2.17
]
features = [
[1/t, 1/t**0.5] for t in total_steps
]
lr = LinearRegression()
lr.fit(features, last_z)
print(lr.coef_) # [ 0.33729346, -0.63307934]
print(lr.intercept_) # 2.247105015502784
print(explained_variance_score(lr.predict(features), last_z)) # 0.999894
total_steps_extended = np.arange(2, 80)
features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ]
plt.plot(total_steps_extended, lr.predict(features_extended))
plt.scatter(total_steps, last_z, s=30, color='black')
plt.show()
Соответствующие уровни значимости вычисляются через перцентиль стандартного распределения, соответствующий значению статистики Стьюдента
:
perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2
На тех же симуляциях это выглядит так:
Ложноположительных результатов получилось 501 из 10 тысяч, или ожидаемые 5%. Обратите внимание, что уровень значимости не достигает значения в 5% даже в конце, так как эти 5% должны «размазаться» по всем проверкам. В компании мы пользуемся именно этой поправкой, если запускаем тест с возможностью ранней остановки. Прочитать про эти же и другие поправки можно по ссылке.
Метод Optimizely
Метод Optimizely хорош тем, что позволяет вообще не фиксировать дату окончания теста, а требуемый уровень значимости рассчитывается на каждый момент времени как функция от количества наблюдений в тесте. Интуитивно лично мне их метод нравится меньше, так как в нём жёсткость критерия увеличивается по ходу теста. То есть она минимальна в первые дни, когда случайный шум оказывает наибольшее влияние на метрики. В методе O’Brien-Fleming’a ситуация противоположная.
Калькулятор A/B-тестов
Специфика нашего продукта такова, что распределение любой метрики очень сильно меняется в зависимости от аудитории теста (например, номера класса) и времени года. Поэтому не получится принять за дату окончания теста правила в духе «тест закончится, когда в каждой группе наберётся 1 млн пользователей» или «тест закончится, когда количество решённых заданий достигнет 100 млн». То есть получится, но на практике для этого надо будет учесть слишком много факторов:
- какие классы попадают в тест;
- тест раздаётся на учителей или учеников;
- время учебного года;
- тест на всех пользователей или только на новых.
Тем не менее, в наших схемах A/B-тестирования всегда нужно заранее фиксировать дату окончания. Для прогноза продолжительности теста мы разработали внутреннее приложение — калькулятор A/B-тестов. Основываясь на активности пользователей из выбранного сегмента за прошлый год, приложение рассчитывает срок, на который надо запустить тест, чтобы значимо зафиксировать аплифт в X% по выбранной метрике. Также автоматически учитывается поправка на множественную проверку и рассчитываются пороговые уровни значимости для досрочной остановки теста.
Все метрики у нас рассчитываются на уровне объектов теста. Если метрика — количество решённых задач, то в тесте на уровне учителей это будет сумма решённых задач его учениками. Так как мы пользуемся критерием Стьюдента, можно заранее рассчитать нужные калькулятору агрегаты по всем возможным срезам. Для каждого дня со старта теста нужно знать количество людей в тесте , среднее значение метрики
и её дисперсию
. Зафиксировав доли контрольной группы
, экспериментальной группы
и ожидаемый прирост от теста
в процентах, можно рассчитать ожидаемые значения статистики Стьюдента
и соответствующее p-value на каждый день теста:
Далее легко получить значения p-value на каждый день:
pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2
Зная p-value и уровень значимости с учетом всех поправок на каждый день теста, для любой продолжительности теста можно рассчитать минимальный аплифт, который можно задетектировать (в англоязычной литературе — MDE, minimal detectable effect). После этого легко решить обратную задачу — определить количество дней, необходимое для выявления ожидаемого аплифта.
Заключение
В качестве заключения хочу напомнить основные посылы статьи:
- Если вы сравниваете средние значения метрики в группах, скорее всего, вам подойдёт критерий Стьюдента. Исключение — экстремально малые размеры выборки (десятки наблюдений) или аномальные распределения метрики (на практике я таких не встречал).
- Если в тесте несколько групп, пользуйтесь поправками на множественное тестирование гипотез. Подойдёт простейшая поправка Бонферрони.
- Сравнения по дополнительным метрикам или срезам групп тоже подвержены проблеме множественного тестирования.
- Выбирайте дату завершения теста заранее. Вместо даты также можно зафиксировать количество наблюдений в группе.
- Не подводите итоги теста раньше этой даты. Это можно делать, только если вы заранее решили пользоваться методами, подразумевающими досрочное завершение, например, методом O’Brien-Fleming.
- Когда вносите изменения в схему A/B-тестирования, всегда проверяйте её жизнеспособность A/A-тестами.
Несмотря на всё вышенаписанное, бизнес и здравый смысл не должны страдать в угоду математической строгости. Иногда можно выкатить на всех функционал, не показавший значимого прироста в тесте, какие-то изменения неизбежно происходят вообще без тестирования. Но если вы проводите сотни тестов в год, их аккуратный анализ особенно важен. Иначе есть риск, что количество ложноположительных тестов будет сравнимо с реально полезными.
5.3. Ошибки первого и второго рода
Ошибка первого рода состоит в том, что гипотеза будет отвергнута, хотя на самом деле она правильная. Вероятность
допустить такую ошибку называют уровнем значимости и обозначают буквой («альфа»).
Ошибка второго рода состоит в том, что гипотеза будет принята, но на самом деле она неправильная. Вероятность
совершить эту ошибку обозначают буквой («бета»). Значение
называют мощностью критерия – это вероятность отвержения неправильной
гипотезы.
В практических задачах, как правило, задают уровень значимости, наиболее часто выбирают значения .
И тут возникает мысль, что чем меньше «альфа», тем вроде бы лучше. Но это только вроде: при уменьшении
вероятности —
отвергнуть правильную гипотезу растёт вероятность — принять неверную гипотезу (при прочих равных условиях).
Поэтому перед исследователем стоит задача грамотно подобрать соотношение вероятностей и
, при этом учитывается тяжесть последствий, которые
повлекут за собой та и другая ошибки.
Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я приведу пару
нестатистических примеров.
Петя зарегистрировался в почтовике. По умолчанию, – он считается добропорядочным пользователем. Так считает антиспам
фильтр. И вот Петя отправляет письмо. В большинстве случаев всё произойдёт, как должно произойти – нормальное письмо дойдёт до
адресата (правильное принятие нулевой гипотезы), а спамное – попадёт в спам (правильное отвержение). Однако фильтр может
совершить ошибку двух типов:
1) с вероятностью ошибочно отклонить нулевую гипотезу (счесть нормальное письмо
за спам и Петю за спаммера) или
2) с вероятностью ошибочно принять нулевую гипотезу (хотя Петя редиска).
Какая ошибка более «тяжелая»? Петино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра
целесообразно уменьшить уровень значимости , «пожертвовав» вероятностью
(увеличив её). В результате в основной ящик будут попадать все
«подозрительные» письма, в том числе особо талантливых спаммеров. …Такое и почитать даже можно, ведь сделано с любовью 
Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность следует увеличить (в пользу уменьшения
вероятности ). Не хотел я
приводить подобные примеры, и даже отшутился на сайте, но по какой-то мистике через пару месяцев сам столкнулся с непростой
дилеммой. Видимо, таки, надо рассказать:
У человека появилась серьёзная болячка. В медицинской практике её принято лечить (основное «нулевое» решение). Лечение
достаточно эффективно, однако не гарантирует результата и более того опасно (иногда приводит к серьёзному пожизненному
увечью). С другой стороны, если не лечить, то возможны осложнения и долговременные функциональные нарушения.
Вопрос: что делать? И ответ не так-то прост – в разных ситуациях разные люди могут принять разные
решения (упаси вас).
Если болезнь не особо «мешает жить», то более тяжёлые последствия повлечёт ошибка 2-го рода – когда человек соглашается
на лечение, но получает фатальный результат (принимает, как оказалось, неверное «нулевое» решение). Если же…, нет, пожалуй,
достаточно, возвращаемся к теме:


| Оглавление |
Ошибки первого и второго рода. Понятие о статистических критериях
Проверить статистическую гипотезу – значит проверить, согласуются ли данные, полученные из выборки с этой гипотезой. При этом проверяемая гипотеза может подтвердиться, а может и не подтвердиться. Проверка статистических гипотез сопряжена с возможностью допустить ошибку.
Ошибка первого рода состоит в том, что будет отвергнута верная гипотеза.
Ошибка второго рода состоит в том, что будет принята ложная гипотеза.
Вероятность совершения ошибки первого рода обозначается 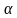
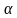
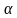
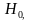
Вероятность не отклонить ложную гипотезу обозначается 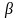
При проверке нулевой гипотезы могут возникнуть следующие ситуации (табл.):
|
|
верная |
ложная |
|
отклоняется |
Ошибка второго рода |
Решение верное |
|
не отклоняется |
Решение верное |
Ошибка второго рода |
Проверка любой статистической гипотезы осуществляется с помощью статистического критерия.
Статистический критерий – это случайная величина [статистика], которая используется с целью проверки нулевой гипотезы.
В дальнейшем статистический критерий непараметрических гипотез будем обозначать, как правило, буквой
Статистические критерии носят название соответственно распределению: 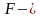
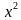
Наблюдаемое значение статистического критерия – это значение критерия, которое рассчитано по выборке с определенным законом распределения.
Множество всех возможных значений выбранного статистического критерия разделяется на два непересекающихся подмножества. Первое из этих подмножеств включает в себя значения критерия, при которых нулевая гипотеза отвергается, а второе – те значения критерия, при которых нулевая гипотеза принимается.
Критическая область – это множество возможных значений статистического критерия, при которых нулевая гипотеза отвергается.
Область принятия гипотезы [область допустимых значений] – это множество возможных значений статистического критерия, при которых нулевая гипотеза принимается.
В том случае, если наблюдаемое значение статистического критерия (рассчитанное по выборочной совокупности) принадлежит критической области, нулевую гипотезу отвергают. Если же наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то нулевая гипотеза принимается.
Критические точки [квантили] – это точки, которые разграничивают критическую область и область принятия гипотезы.
Выделяют одностороннюю и двустороннюю критические области. Дадим определения данных критических областей на примере условного статистического критерия 
Правосторонняя критическая область определяется неравенством 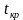
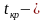
Левосторонняя критическая область определяется неравенством 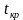
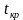
Двусторонняя критическая область определяется неравенствами 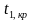
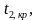
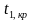
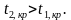
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Радиолокация
- 4.2 Компьютеры
- 4.2.1 Компьютерная безопасность
- 4.2.2 Фильтрация спама
- 4.2.3 Вредоносное программное обеспечение
- 4.2.4 Поиск в компьютерных базах данных
- 4.2.5 Оптическое распознавание текстов (OCR)
- 4.2.6 Досмотр пассажиров и багажа
- 4.2.7 Биометрия
- 4.3 Массовая медицинская диагностика (скрининг)
- 4.4 Медицинское тестирование
- 4.5 Исследования сверхъестественных явлений
- 5 См. также
- 6 Примечания
Определения
Пусть дана выборка 

где 

,
сопоставляющий каждой реализации выборки 
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
| Верная гипотеза | |||
|---|---|---|---|
 |
 |
||
| Результат применения критерия |
 |
 верно принята верно принята |
 неверно принята неверно принята (Ошибка второго рода) |
 |
 неверно отвергнута неверно отвергнута (Ошибка первого рода) |
 верно отвергнута верно отвергнута |
О смысле ошибок первого и второго рода
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы 



С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 


Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда нарушители классифицируются как авторизованные пользователи (ошибки первого рода)
- когда авторизованные пользователи классифицируются как нарушители (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[3]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[4]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.[5] Самый низкий уровень наблюдается в Нидерландах, 1%.[6]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[7]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.[8]
См. также
- Статистическая значимость
- Ложноположительный
- Атака второго рода
- Случаи ложного срабатывания систем предупреждения о ракетном нападении
- Receiver_operating_characteristic
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения.». Стр. 26
- ↑ Valerie J. Easton, John H. McColl. Statistics Glossary: Hypothesis Testing.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95% женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research).
Управление стратегическими рисками является одним из наиболее интересных и широких блоков в технологии риск-менеджмента. В основе стратегических рисков лежат ошибки, допущенные при принятии решений о стратегии развития организации.
Стратегические риски обладают тремя важными свойствами:
- Риски с очень высоким влиянием. Во многих случаях реализация стратегических рисков привела либо к уходу компаний с рынка, либо к значительной потере капитализации.
- Риски, которые имеют значительный временной лаг. Это событие реализуется «не завтра», оно может произойти через несколько лет. Однако его реализация окажет значительное влияние на бизнес. Управляя любыми рисками, мы управляем событиями, которые могут реализоваться в будущем, а не в настоящий момент. У стратегических рисков промежуток времени от момента, в котором мы находимся, до момента, когда они реализуются, значительно больше, чем у рисков других видов. Именно поэтому стратегическим рискам часто не уделяют необходимого внимания. Директору пейджинговой компании в конце 1990-х годов риск того, что ключевой сотрудник может уволиться в ближайшие дни, казался куда как более важным, чем риск потенциального изменения спроса на услуги через несколько лет. Хотя сейчас, по прошествии времени, совершенно очевидно, что если не будет спроса на услуги, то этот ключевой сотрудник будет не нужен вообще.
- Стратегические риски могут быть любыми: операционными, кредитными, рисками ликвидности и т.д. Риск, связанный с персоналом, может стать стратегическим для организации, если все технологии компании находятся в голове одного сотрудника, рыночная стоимость которого увеличивается. Сегодня причин для опасений вроде бы нет, но если через несколько лет этого сотрудника переманят конкуренты, то риск будет значительно влиять на бизнес. Точно так же IT-риск может быть стратегическим для бизнеса, если, к примеру, информационная система банка имеет емкость, значительно меньшую, чем та, которая понадобится через несколько лет.
Для того, чтобы управлять стратегическими рисками, необходимо научиться:
- видеть стратегические риски бизнеса;
- оценивать риски, связанные с выбором стратегии;
- оценивать риски, связанные с реализуемостью стратегии.
Управление стратегическими рисками является, пожалуй, наиболее сложно формализуемой частью технологии риск-менеджмента. Рассмотрим шаги этой технологии.
Как распознать стратегические риски
Научиться видеть стратегические риски можно с помощью методологий стратегического менеджмента. В них вы сможете найти способы оценки структуры отрасли и конкурентов, а этой информации будет уже достаточно для того, чтобы получить представление о существующих стратегических рисках. В качестве примера такой методологии можно взять логику Портера и проанализировать:
- существующих и потенциальных конкурентов;
- покупателей;
- существующие товары-заменители;
- наших поставщиков.
Анализ первых трех факторов даст нам возможность оценить стратегические бизнес-риски, потому что появление новых конкурентов, услуг-субститутов, а также поведение клиентов определяют потенциальный уровень спроса на наши услуги и, соответственно, доходы и прибыль бизнеса. Управление такими рисками необходимо для того, чтобы больше зарабатывать. Поставщики же (четвертая категория) могут влиять на наши издержки. Стратегическое управление рисками, связанными с поставщиками, необходимо для того, чтобы меньше терять. Рассмотрим каждую из этих категорий.
1. Конкуренты. Чтобы оценить вероятность и влияние рисков, связанных с появлением новых конкурентов, нужно в первую очередь определить, насколько велики барьеры вхождения в отрасль. Чем они выше, тем ниже риск того, что вашу рыночную нишу кто-то сможет занять. Для того, чтобы его оценить, нужно проанализировать следующие факторы.
- Насколько зависят издержки бизнеса от масштабов производства. Чем выше эта зависимость (чем больше бизнес — тем меньше издержки), тем сложнее потенциальным конкурентам будет нас догнать.
- Насколько дифференцированы наши услуги. Чем они уникальнее, тем сложнее с ними конкурировать.
- Какие минимальные инвестиции потребуются конкурентам для того, чтобы начать бизнес, конкурирующий с нашим.
- Каковы издержки покупателей, связанные с заменой ваших услуг на услуги конкурентов. Например, смена оператора связи: все, кто еще не успел узнать новый номер, не смогут до вас дозвониться. Соответственно, у вас возникают издержки переключения (для снижения их и была придумана переадресация звонков).
- Насколько открыт доступ к каналам закупок товаров и услуг, которые требуются для работы аналогичного бизнеса. Если в городе только у нас есть договор с поставщиками, которые имеют ограниченные ресурсы, то риски появления новых конкурентов незначительны — они просто не смогут купить эти товары.
- Есть ли у нас ноу-хау, которое защищено авторскими правами.
- Каковы «кривые обучения» у наших технологий. Для того, чтобы организовать работу, руководству нужно накопить определенный опыт. Хотя риск-менеджмент может ускорить этот процессу времени он все равно требует. В каком-то бизнесе меньше, в каком-то — больше. Естественно, что чем больше времени займет процесс обучения и приобретения опыта, тем меньше риски появления новых конкурентов.
Анализ этих факторов поможет вам оценить риски, связанные с появлением новых конкурентов и с соответствующим изменением спроса на ваши услуги.
2. Услуги-субституты (заменители). Именно такой риск реализовался в случае всех пейджинговых компаний, компаний Polaroid и Kodak.
3. Клиенты. Чтобы увидеть стратегические риски, необходимо проанализировать и спрогнозировать поведение наших клиентов. Важными здесь являются следующие факторы:
- структура «клиентского портфеля»: если бизнес зависит от одного или нескольких крупных клиентов, он более уязвим, чем в случае диверсифицированной клиентской базы;
- какую долю в общих издержках клиентов составляют услуги нашего бизнеса: чем они выше, тем более тщательно клиенты будут выбирать поставщика услуг, соответственно, тем выше вероятность их перехода к конкурентам;
- смогут ли наши клиенты найти аналогичный продукт (в случае, если услуги являются стандартными);
- насколько велики издержки клиента, связанные с переходом к конкуренту;
- насколько информированы наши клиенты о состоянии дел в отрасли (каковы реальные издержки, цены конкурентов и т.д.) Чем ниже степень их информированности, тем меньше вероятность изменения спроса на наши услуги.
4. Поставщики. Чтобы увидеть стратегические риски, связанные с увеличением издержек бизнеса, нужно оценить поставщиков, потому что любой бизнес в той или иной степени от них зависит. Для того чтобы оценить уровень этой зависимости и распознать соответствующие риски, необходимо проанализировать следующие аспекты.
- Число поставщиков, предоставляющих услуги, которые нам требуются. Риски, которые возникают в ситуации, когда бизнес зависим от поставщика-монополиста, очевидны. Если у нас в распоряжении есть только один поставщик аттракционов, мы полностью от него зависим, поскольку цены, которые он определяет — это наши издержки.
- Наличие поставщиков, предлагающих услуги-субституты. Чем их больше, тем меньше наша зависимость от них, соответственно, меньше наша уязвимость.
- Значимость сотрудничества для поставщика. Если поставщик одновременно с вашим заказом получит заказ из крупного предприятия на десятикратную партию товаров, то, скорее всего, распределение ресурсов поставщика будет не в нашу пользу.
- У бизнеса значительные издержки, связанные со сменой поставщика. Это полная аналогия издержкам переключения у клиентов, только в этом случае в качестве клиента выступаем мы.
Стратегические риски и стратегическое планирование
Управление стратегическими рисками тесно связано со стратегическим планированием. При определении стратегии развития организации стратегические риски могут возникнуть в следующих ситуациях.
- При выборе стратегии развития. Стратегия может быть «правильной» и «неправильной». Мы можем верно определить, куда идти, а можем ошибиться. Конечно, гарантии правильности стратегических решений никакая технология дать не сможет, но то, что при выборе стратегии необходимо управлять рисками, — сомнений не вызывает.
- При реализации выбранной стратегии развития. Стратегия может быть реализована и не реализована. Соответственно, стратегия может быть правильной, но не реализуемой. Риски, которые возникают при внедрении стратегии в жизнь, автоматически становятся стратегическими.
Рассмотрим технологию стратегического планирования в наиболее простом варианте.
- Во-первых, стратегия организации должна быть определена на некий конкретный период.
- Во-вторых, стратегию необходимо конкретизировать. Когда понятно, куда двигаться, нужно определить время и средства, которые потребуются, чтобы пройти этот путь и достичь четких, измеримых целей в первый год, потом во второй год и т. д. Таким образом, мы формулируем цели, которых необходимо достичь, чтобы стратегия была реализована. Достижение цели подразумевает какие-то действия. Например, если цель, направленная на реализацию стратегии «Выход на новый рынок», — «обеспечить объем продаж X в соседнем городе», то действий, направленных на достижение этой цели, может быть очень много. Например, может потребоваться модификация продукта, исследование нового рынка, открытие филиала и т. д. Именно такая «обычная» деятельность в рамках единого направления и называется реализацией стратегии.
- Определить эти действия — следующая задача. В итоге мы получим набор действий, которые необходимо выполнить, чтобы последовательно достичь поставленных целей и реализовать стратегию. Группа действий, направленная на достижение цели, называется проектом.
Таким образом, мы получили вполне конкретную цепочку: «стратегия — цели — проекты».
Цепочка, которую мы только что рассмотрели — это всего лишь одна итерация стратегического планирования. Чтобы стратегическое планирование на самом деле стало процессом, необходим систематический анализ достижения целей, возможностей их пересмотра, самой стратегии и т. д.

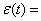

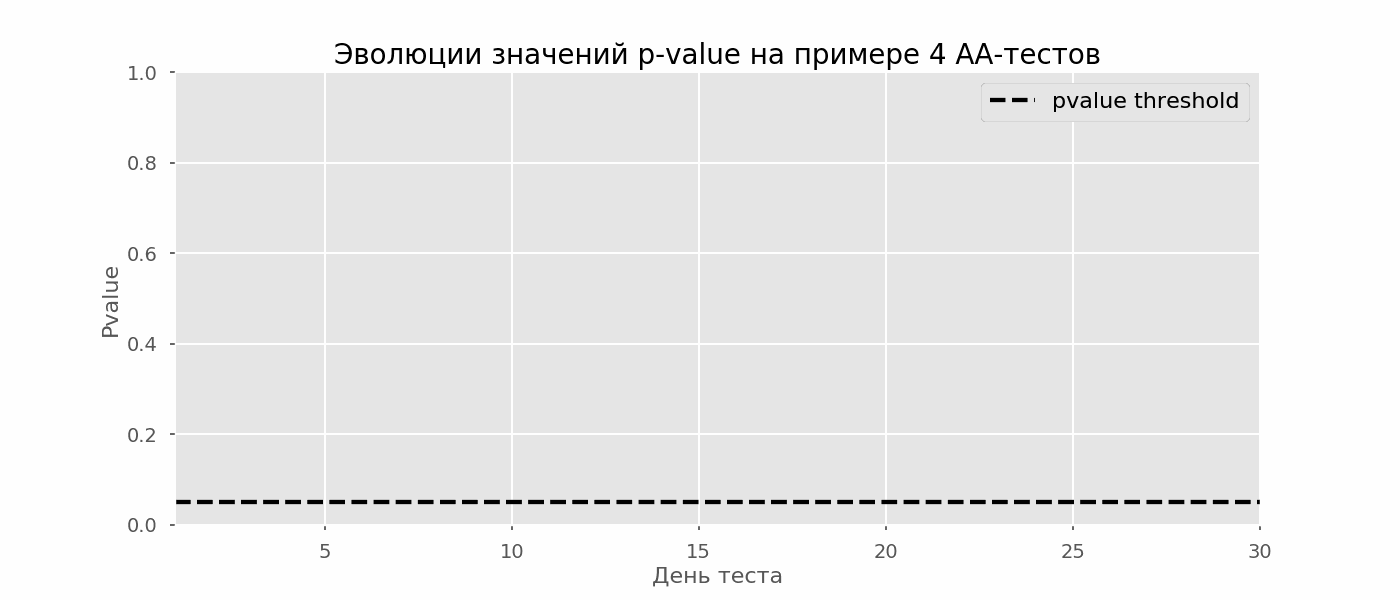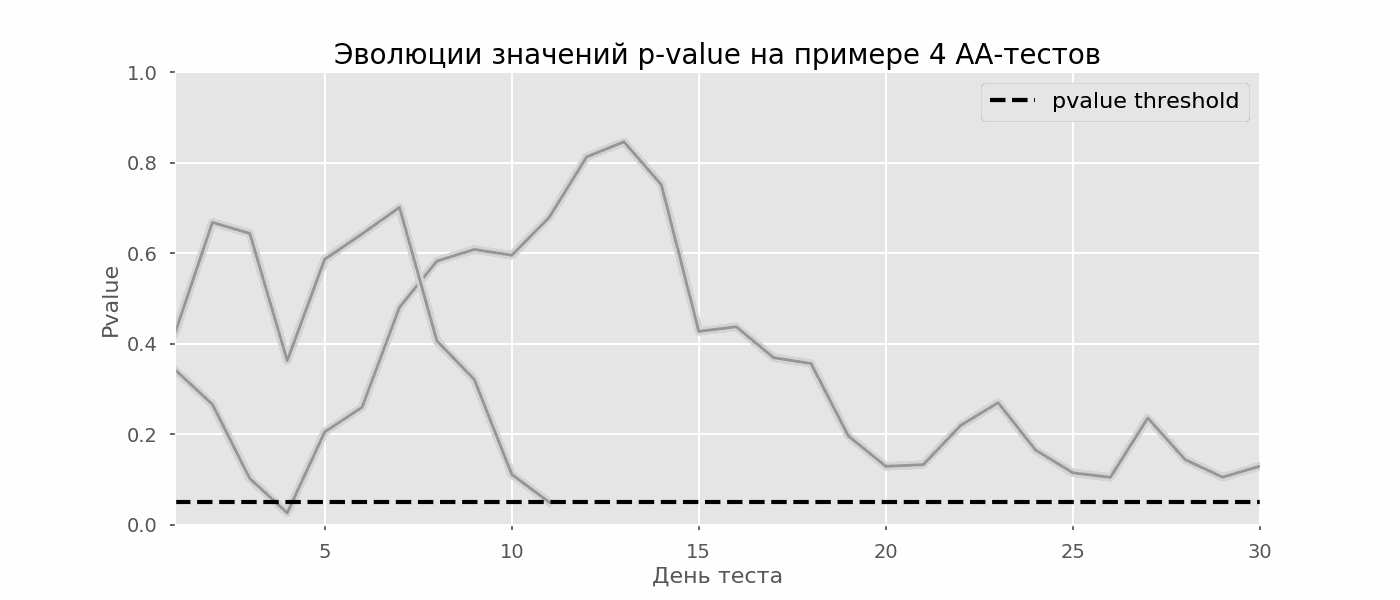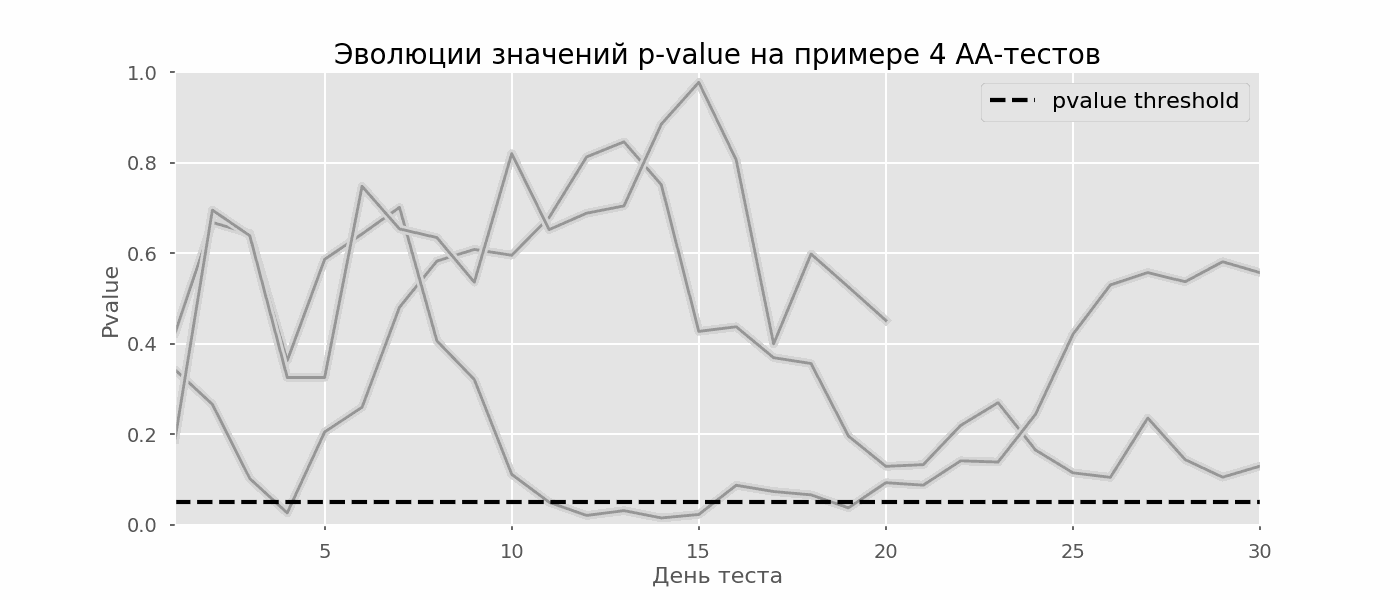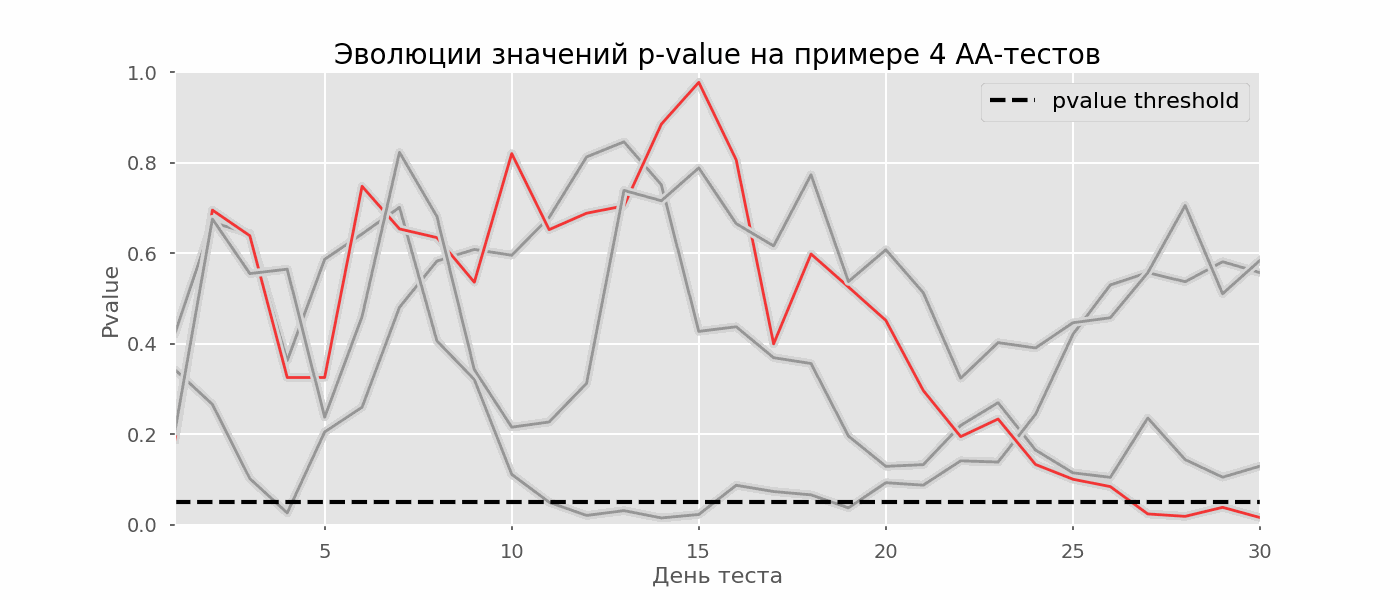
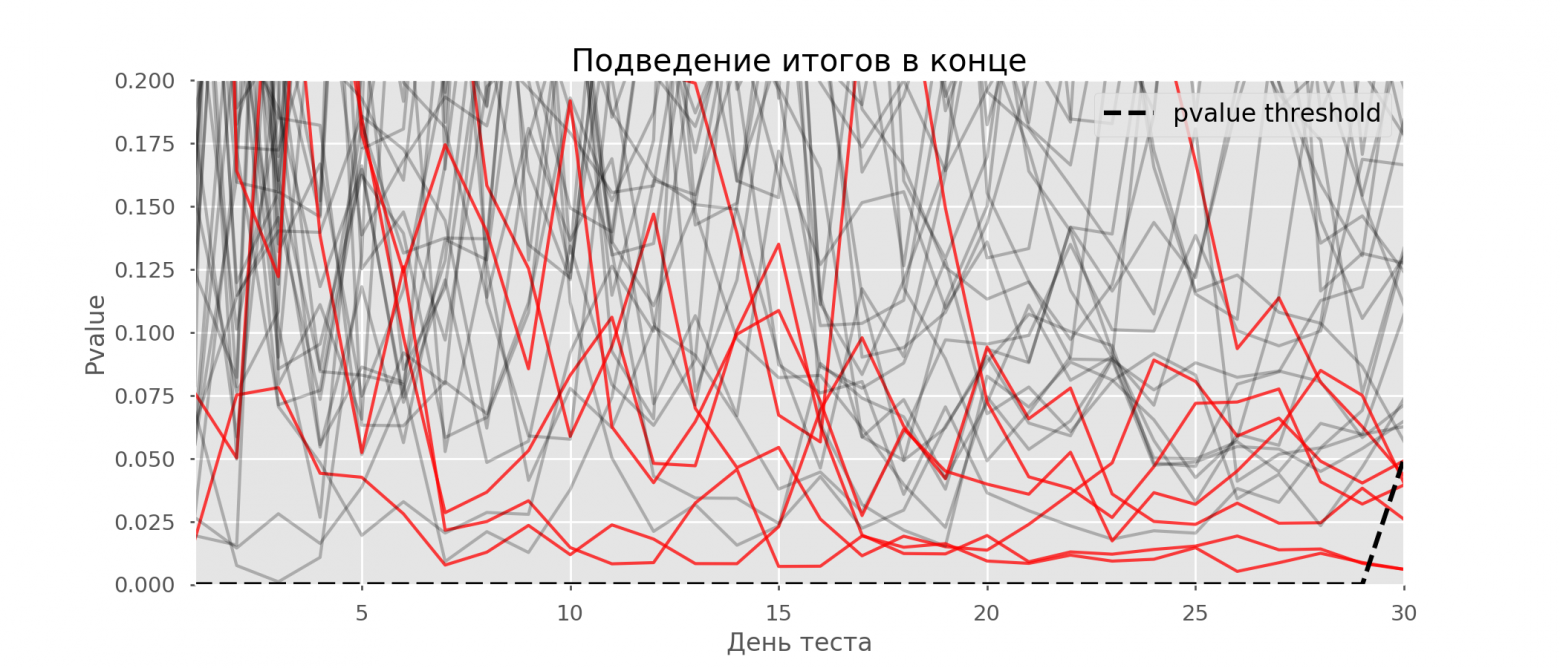
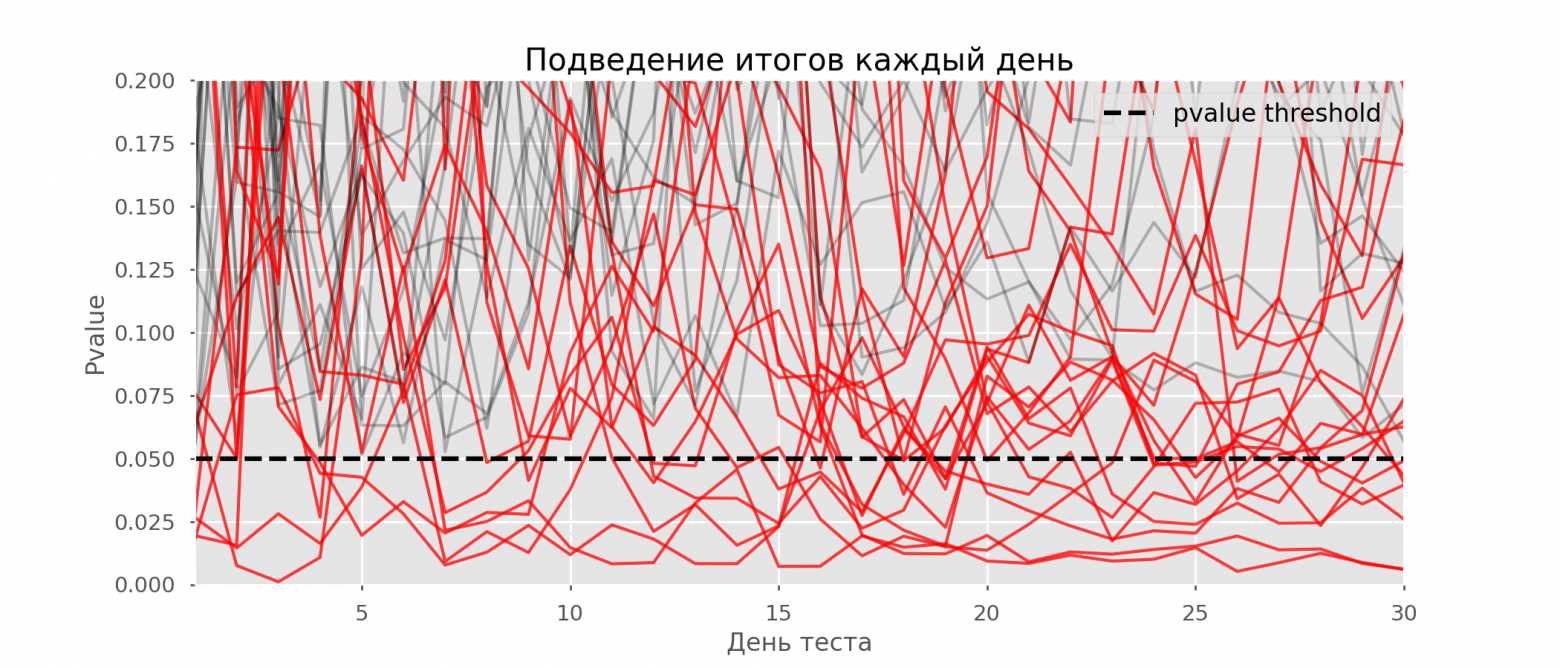

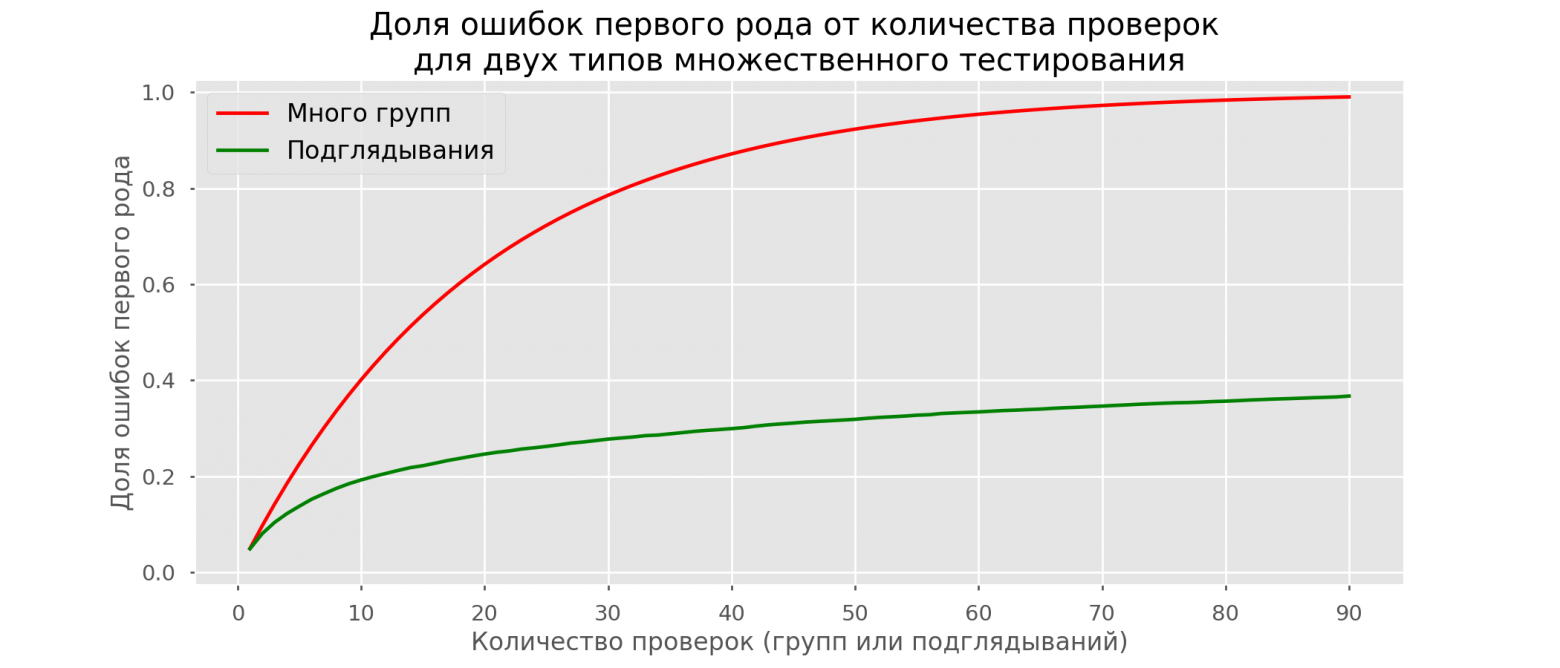



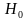

 ,
, соответствует гипотезе
соответствует гипотезе  .
. .
.