Значение ошибки при выполнении расчетов - Oshibku.top - решение и исправление самых разных ошибок

Исправление
распространенных ошибок в формулах

Для
проверки формул на наличие ошибок можно
применять определенные правила. Эти
правила действуют как средство проверки
орфографии, которое проверяет данные,
введенные в ячейки, на наличие ошибок.
Эти правила не гарантируют полного
отсутствия ошибок на листе, но помогают
избежать распространенных ошибок.
Каждое из этих правил можно включать и
выключать независимо от других.

Ошибки
можно отмечать и исправлять двумя
способами: по одной ошибке (как в средстве
проверки орфографии) или немедленно по
мере их возникновения на листе во время
ввода данных. В обоих случаях при
обнаружении ошибки в ячейке в ее левом
верхнем углу появляется треугольник.

Ячейка
с ошибкой в формуле

Ошибку
можно устранить, используя предлагаемые
MS
Excel варианты, или пропустить, нажав
кнопку Пропустить ошибку. Если пропустить
ошибку в определенной ячейке, то при
последующих проверках наличие ошибки
в этой ячейке определяться не будет.
Однако состояние всех пропущенных
ошибок можно сбросить, чтобы они
отображались снова.

Включение
и отключение правил проверки ошибок

На вкладке Файл
выберите команду Параметры,
а затем — категорию Формулы.
В области Правила
контроля ошибок
установите или снимите флажок для
любого из перечисленных далее правил.

Ячейки, которые
содержат формулы, приводящие к
ошибкам. В
данной формуле используется неправильный
синтаксис, аргументы или типы данных.
Значения таких ошибок: #ДЕЛ/0!, #Н/Д,
#ИМЯ?, #ПУСТО!, #ЧИСЛО!, #ССЫЛКА! и #ЗНАЧ!.
Каждое из этих значений ошибки вызывается
различными причинами, и такие ошибки
устраняются разными способами.

Примечание Если
значение ошибки ввести непосредственно
в ячейку, оно будет сохранено как значение
ошибки, но отмечаться как ошибка не
будет. Однако если на эту ячейку будет
ссылаться формула из другой ячейки, для
этой ячейки будет возвращено значение
ошибки.

Несогласованная
формула в вычисляемом столбце
таблицы. Вычисляемый
столбец может содержать формулы,
отличающиеся от формулы столбца, что
приводит к возникновению исключения.
Исключения вычисляемого столбца
возникают при указанных ниже действиях.
- Ввод в ячейку
  вычисляемого столбца данных, отличных
  от формулы.
- Ввод в ячейку
  вычисляемого столбца формулы с
  последующим нажатием кнопкиОтменитьна
  панели
  быстрого доступа.
- Ввод новой формулы
  в вычисляемый столбец, который уже
  содержит одно или несколько исключений.
- Копирование в
  вычисляемый столбец данных, которые
  не соответствуют формуле вычисляемого
  столбца.

Примечание Если
копируемые данные содержат формулу,
эта формула перезапишет данные в
вычисляемом столбце.

Перемещение или
удаление ячейки в другой области
листа, на которую ссылается одна из
строк вычисляемого столбца.

Ячейки, которые содержат
годы, представленные 2 цифрами. Ячейка
содержит дату в текстовом формате,
которая в случае использования в
формулах может быть отнесена к
неправильному веку. Например, дата в
формуле =ГОД(«1.1.31») может относиться
как к 1931-му, так и к 2031-му году. Это
правило служит для выявления неоднозначных
дат в текстовом формате.

Числа,
отформатированные как текст или с
предшествующим апострофом. Ячейка
содержит числа, хранящиеся в виде
текста. Обычно это является следствием
импорта данных из других источников.
Числа, хранящиеся в виде текста, могут
стать причиной неправильной сортировки,
поэтому лучше преобразовать их в
числовой формат.
Формулы,
несогласованные с остальными формулами
в области. Формула
не соответствует шаблону других смежных
формул. В большинстве случаев формулы,
расположенные в соседних ячейках,
отличаются только используемыми
ссылками. В приведенном, далее примере,
состоящем из четырех смежных формул,
приложение MicrosoftExcel
показывает ошибку в формуле =СУММ(A10:F10),
поскольку значения в смежных формулах
изменились на одну строку, а в формуле
=СУММ(A10:F10)
— на 8 строк. В данном случае, ожидаемой
формулой является =СУММ(A3:F3).

Если используемые в формуле
ссылки не соответствуют ссылкам в
смежных формулах, приложение
MicrosoftExcelвыводит
ошибку.

Формулы, не
охватывающие смежные ячейки. Формула
может не включать ссылки на данные,
вставленные между исходным диапазоном
и ячейкой с формулой. Это правило
позволяет сравнить ссылку в формуле
с фактическим диапазоном ячеек, смежных
с ячейкой формулы. Если смежные ячейки
содержат дополнительные значения и
не являются пустыми, MicrosoftExcelвыведет
рядом с формулой ошибку.

Например, в случае
применения этого правила приложение
MicrosoftExcel
выведет ошибку рядом с формулой
=СУММ(A2:A4),
поскольку между указанным в формуле
диапазоном ячеек и ячейкой с формулой
(A8) находятся заполненные ячейки A5, A6 и
A7, на которые также должна быть ссылка
в формуле.

Незаблокированные
ячейки, содержащие формулы. Формула
не заблокирована в целях ее защиты. По
умолчанию все ячейки блокируются, но
защита была снята для этой ячейки.
Когда формула защищена, ее нельзя
изменить, не сняв защиту. Убедитесь,
что защита этой ячейку действительно
не требуется. Блокирование ячеек,
содержащих формулы, позволяет защитить
их от изменений и избежать возникновения
ошибок в будущем.

Формулы, которые
ссылаются на пустые ячейки. Формула
содержит ссылку на пустую ячейку. Это
может привести к неверным результатам,
как показано в приведенном далее
примере.

Предположим, нужно
вычислить среднее значение для чисел
из указанного ниже столбца ячеек. Если
третья ячейка будет пустой, она не будет
учтена при выполнении вычисления, и
результатом будет 22,75. Если третья ячейка
будет содержать значение 0, результатом
будет 18,2.

В таблицу введены
недопустимые данные. В
таблице произошла ошибка проверки.
Чтобы просмотреть параметры проверки
для ячейки, на вкладке Данные
в группе Работа
с данными
нажмите кнопку Проверка
данных.

Последовательное
исправление распространенных ошибок
в формулах

Внимание! Если
на листе уже выполнялась проверка
ошибок, то ошибки, которые были пропущены,
не будут отображаться, пока их состояние
не будет сброшено.

Выберите лист, на
котором требуется проверить наличие
ошибок.
Если расчет листа
выполнен вручную, нажмите клавишу F9,
чтобы выполнить расчет повторно.
На вкладке Формулы
в группе Зависимости
формул
нажмите кнопку группы Проверка
наличия ошибок.

В случае обнаружения
ошибок открывается диалоговое окно
Контроль
ошибок.

Чтобы повторно
проверить пропущенные ранее ошибки,
выполните указанные ниже действия.
1. Нажмите кнопку
  Параметры.
2. В разделе Контроль
  ошибок
  нажмите кнопку Сброс
  пропущенных ошибок.
3. Нажмите кнопку
  ОК.
4. Нажмите
  кнопкуПродолжить.

Примечание Сброс
пропущенных ошибок применяется ко всем
ошибкам, которые были пропущены на всех
листах активной книги.

Расположите
диалоговое окно Контроль
ошибок
непосредственно под строкой
формул .

Нажмите одну из
управляющих кнопок в правой части
диалогового окна. Доступные действия
зависят от типа ошибки.

Примечание Если
нажать кнопку Пропустить
ошибку,
помеченная ошибка при последующих
проверках будет пропускаться.

Нажмите кнопкуДалее.
Выполняйте эти
действия, пока проверка ошибок не будет
завершена.

К
началу страницы

Пометка
и исправление распространенных ошибок
формул на листе

Откройте вкладку
Файл.
Нажмите кнопку
Параметры
и выберите категорию Формулы.
Убедитесь, что в
области Контроль
ошибок
установлен флажокВключить
фоновый поиск ошибок.
Чтобы изменить
цвет треугольника, которым помечаются
ошибки, выберите нужный цвет в поле
Цвет
индикаторов ошибок.
Нажмите кнопку «ОК», чтобы закрыть
диалоговое окно Параметры
Excel.
Чтобы исправить
ошибку на листе, выберите ячейку с
треугольником в левом верхнем углу.
Нажмите появившуюся
рядом с ячейкой кнопку Контроль
ошибоки
выберите нужный пункт. Доступные команды
зависят от типа ошибки. Первый пункт
содержит описание ошибки.

Если нажать
кнопкуПропустить
ошибку,
помеченная ошибка при последующих
проверках будет пропускаться.

Повторите два
предыдущих действия.

Исправление
значения ошибки

Если формула
содержит ошибку, которая не позволяет
правильно выполнить вычисления, будет
показано значение ошибки, например
#####, #ДЕЛ/0!, #Н/Д, #ИМЯ?, #ПУСТО!, #ЧИСЛО!,
#ССЫЛКА! и #ЗНАЧ!. Каждый тип ошибки
вызывается разными причинами, и такие
ошибки устраняются разными способами.

В таблице ниже
приведены ссылки на статьи с подробным
описанием ошибок и краткий вступительный
обзор каждой ошибки.

Ссылка на статью с подробным описанием	Описание
Исправление ошибки #####	Эта ошибка появляется в том случае, если ширины столбца недостаточно, чтобы показать все знаки в ячейке, или если ячейка содержит отрицательные значения даты или времени. Так, при вычислении формулы, которая вычитает более позднюю дату из более ранней, например =15.06.2008-01.07.2008 , получится отрицательное значение даты.
Исправление ошибки #ДЕЛ/0!	Эта ошибка появляется в том случае, если число делится на ноль (0) или на ячейку, в которой нет значения.
Исправление ошибки #ЗНАЧ!	Эта ошибка появляется в том случае, если формула содержит ячейки с разными типами данных. Если включена проверка ошибок в формулах, при наведении указателя мыши на смарт-тег появится всплывающая подсказка «Значение, используемое в формуле, имеет неправильный тип данных». Обычно для исправления этой ошибки достаточно внести в формулу небольшие изменения.
Исправление ошибки #ИМЯ?	Эта ошибка появляется в том случае, если текст в формуле не удается распознать. Например, имя диапазона или функции может иметь неверное написание.
Исправление ошибки #Н/Д	Эта ошибка появляется в том случае, если значение для функции или формулы недоступно.
Исправление ошибки #ПУСТО!	Эта ошибка появляется в том случае, если указано пересечение двух областей, которые на самом деле не пересекаются. Оператором пересечения служит пробел, который разделяет ссылки в формуле. Например, области A1:A2 и C3:C5 не пересекаются, и если ввести формулу =СУММ(A1:A2 C3:C5) , будет показана ошибка #ПУСТО!.
Исправление ошибки #ССЫЛКА!	Эта ошибка появляется в том случае, если ссылка на ячейку является неверной. Например, вы могли удалить ячейки, на которые ссылались другие формулы, или вставить перемещенные ячейки на место тех ячеек, на которые ссылались другие формулы.
Исправление ошибки #ЧИСЛО!	Эта ошибка появляется в том случае, если формула или функция содержит недопустимые числовые значения.

Вычисления
в таблицах

Ознакомление
с правилами ввода простых формул

Формулы представляют
собой выражения, по которым выполняются
вычисления значений на листе. Формула
начинается со знака равенства (=).Формула
может содержать некоторые или все из
следующих элементов: функции, ссылки,
операторы и константы.

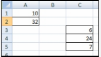
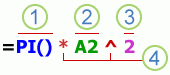
Части формулы

Функции.
Функция ПИ() возвращает значение числа
Пи: 3,142…

Ссылки.
A2 возвращает значение ячейки A2.

Константы.
Числа или текстовые значения, введенные
непосредственно в формулу, например 2.

Операторы.
Оператор ^ («крышка») возводит число
в степень, а оператор * («звездочка»)
перемножает два или более числа.

Исправление
распространенных ошибок во время ввода
формул

В приведенной ниже
таблице перечислены некоторые наиболее
распространенные ошибки, совершаемые
пользователями при вводе формул, и
способы их исправления.

Убедитесь, что…	Дополнительные сведения
Каждая формула начинается со знака равенства (=)	Если знак равенства опустить, введенные значения могут быть отображены как текст или дата. Например, если ввести СУММ(A1:A10), MicrosoftExcel отобразит текстовую строку СУММ(A1:A10) и не станет вычислять значение формулы. Если ввести 11/2, Excel отобразит дату (например, «2 ноября» или «02.11.2009») вместо того, чтобы разделить 11 на 2.
Все открывающие и закрывающие скобки согласованы	Убедитесь, что у каждой скобки имеется соответствующая ей пара. Чтобы функция в формуле работала правильно, важно, чтобы каждая скобка стояла на своем месте. Например, формула *=ЕСЛИ(B5<0);»Неверно»;B51,05) работать не будет, потому что в ней две закрывающие и только одна открывающая скобка. Правильная формула будет выглядеть так: =ЕСЛИ(B5<0;»Неверно»;B51,05)*.
Для указания диапазона используется двоеточие	При указании ссылки на диапазон ячеек используйте двоеточие (:) в качестве разделителя между первой и последней ячейками диапазона. Например: A1:A5.
Введены все необходимые аргументы	Некоторым функциям листа требуются аргументы (Аргумент. Значения, используемые функцией для выполнения операций или вычислений. Тип аргумента, используемого функцией, зависит от конкретной функции. Обычно аргументы, используемые функциями, являются числами, текстом, ссылками на ячейки и именами.), тогда как другие функции (например, ПИ) аргументов не принимают. Кроме того, убедитесь, что вы не ввели слишком много аргументов. Например, функция ПРОПИСН принимает в качестве аргумента только одну строку текста.
Введены аргументы правильного типа	Для некоторый функций листа, например СУММ, требуются числовые аргументы. Другие функции, напримерЗАМЕНИТЬ, требуют текстового значения по меньшей мере для одного из аргументов. Прииспользования в качестве аргумента данных неверного типа можно получить неправильные результаты или ошибку.
Количество вложенных функций не превышает 64	Внутри одной функции можно ввести (или вложить) не более 64 уровней функций. Например, формула =ЕСЛИ(КОРЕНЬ(ПИ())<2;»Меньше двух!»;»Больше двух!») содержит три функции: функция ПИ вложена в функцию КОРЕНЬ, которая, в свою очередь, вложена в функцию ЕСЛИ.
Имена других листов заключены в одинарные кавычки	Если в формуле имеются ссылки на значения или ячейки других листов или книг, имена которых содержат небуквенные знаки, такие имена необходимо заключить в одинарные кавычки ( ‘ ).
Ссылаясь на лист в формуле, следует поместить после его имени восклицательный знак (!).	Например, чтобы вернуть значение ячейки D3 листа с именем «Данные за квартал» в той же книге, воспользуйтесь формулой =’Данные за квартал’!D3.
Включен путь к внешним книгам	Убедитесь, что каждая внешняя ссылка (Внешняя ссылка. Ссылка на ячейку или диапазон ячеек в другой книге Microsoft Excel или ссылка на имя, определенное в другой книге.) содержит имя книги и путь к ней. Ссылка на книгу включает в себя имя этой книги и должна быть заключена в квадратные скобки ([]). Кроме того, в ссылке должно быть указано имя листа в книге. Например, формула со ссылкой на ячейки с A1 по A8 на листе с именем «Продажи» в книге (в настоящий момент открытой в Excel) с именем Кв2 Операции.xlsx, будет выглядеть примерно так: =[Кв2 Операции.xlsx]Продажи!A1:A8. Если книга, на которую требуется сослаться, не открыта в Excel, ссылку на нее все же можно включить в формулу. Нужно указать полный путь к файлу, как в следующем примере: =ЧСТРОК(‘C:\Мои документы\[Кв2 Операции.xlsx]Продажи’!A1:A8). Эта формула возвращает число строк в диапазоне, включающем ячейки с A1 по A8 в другой книге (а именно, 8). Примечание Если полный путь содержит пробелы, как в предыдущем примере, его необходимо заключить в одинарные кавычки (в начале пути и после имени листа, перед восклицательным знаком).
Числа введены без форматирования	Не форматируйте числа, которые вводите в формулах. Например, если вам нужно ввести значение $1,000, введите в формулу просто 1000. Если ввести запятую как часть числа, Excel будет трактовать ее как разделительный знак. Если требуется, чтобы числа отображались с разделителями тысяч и миллионов или с символами валюты, отформатируйте ячейки после ввода чисел. Например, если нужно добавить 3100 к значению в ячейке A3, и вы ввели формулу =СУММ(3,100;A3), приложение Excel сложит числа 3 и 100, а затем добавит результат к значению ячейки A3, вместо того чтобы добавить 3100 к значению A3. А если введена формула =ABS(-2,134), будет показана ошибка, поскольку функция ABS принимает только один аргумент.
Избегайте деления на ноль	При попытке разделить значение в ячейке на значение в другой ячейке, содержащей ноль или не содержащей никакого значения, будет показана ошибка #ДЕЛ/0!.

Формулы

Вычисления
в Excel
выполняются с помощью Формул. Формула
начинается со знака равно (=)
и состоит из элементов (операндов:
константы, ссылки на ячейки или диапазоны
ячеек, функции), соединенных операторами
(знаки операций).

Применение
операторов в формулах

Оператор. Знак или
символ, задающий тип вычисления в
выражении. Существуют математические,
логические операторы, операторы сравнения
и ссылок

Арифметические
операторы.

Арифметическийоператор	Значение	Пример
+ (знак плюс)	Сложение	23+3
– (знак минус)	Вычитание / Унарный минус	35–166 / –1
* (звездочка)	Умножение	23*(-321)
/ (косая черта)	Деление	3/3
% (знак процента)	Процент	20%
^ (крышка)	Возведение в степень	3^2 (аналогично 3*3)

Операторы
сравнения.

Используются для
сравнения двух значений. Результатом
сравнения является логическое значение:
либо ИСТИНА, либо ЛОЖЬ.

Операторсравнения	Значение	Пример
= (знак равенства)	Равно	A1=B1
> (знак больше)	Больше	A1>B1
< (знак меньше)	Меньше	A1<B1
>= (знак больше и знак равенства)	Больше или равно	A1>=B1
<= (знак меньше и знак равенства)	Меньше или равно	A1<=B1
<> (знак «не равно»)	Не равно	A1<>B1

Текстовый оператор
конкатенации.
Операция (&) используется для объединения
нескольких текстовых строк в одну
строку.

Текстовый
оператор

Значение

Пример

&
(амперсанд)

Объединение
последовательностей символов в одну
последовательность.

Выражение

«Северный
» & » ветер» эквивалентно
строке

«Северный
ветер».

Оператор
ссылки.
Для описания ссылок на диапазоны ячеек
используются следующие операторы.

Оператор ссылки	Значение	Пример
: (двоеточие)	Оператор диапазона используется для ссылки на все ячейки между крайними ячейками диапазона, включая эти ячейки.	B5:B15
, (запятая)	Оператор объединения объединяет несколько ссылок в одну ссылку.	СУММ(B5:B15,D5:D15)
(пробел)	Оператор пересечения задает пересечение двух диапазонов.	A6:D6

Порядок выполнения
действий в формулах

Если
в формуле содержится несколько операторов,
то порядок вычислений в MicrosoftExcel
определяется приоритетом операторов.
Раньше выполняются операции с более
высоким приоритетом, затем — с менее
высоким. Для изменения порядка выполнения
операций используются скобки. Вначале
вычисляются те части формулы, которые
заключены в скобки, затем — остальные
части.

	Оператор	Описание
	: (двоеточие) (пробел) , (запятая)	Операторы ссылок
	–	Унарный минус (например –1)
	%	Процент
	^	Возведение в степень
	* и /	Умножение и деление
	+ и –	Сложение и вычитание
	&	Объединение двух текстовых строк в одну
	= <><= >= <>	Сравнение

Адреса,
которые используются в формулах, получили
название ссылок.
Ссылки позволяют связывать между собой
любые ячейки
электронной
таблицы и проводить необходимую обработку
табличных
данных.

Ссылка
— это адрес объекта (ячейки, строки,
столбца, диапазона),
используемый при записи формулы.

Способы
ввода формул: набрать
ее

вручную

с
помощью указания

в
строке формул или непосредственно в
ячейке.

Строка
формул

— отмена
последнего действия,

—
для подтверждения ввода данных или
изменения содержимого ячеек,

—
активизировать Мастер функций для
работы с функциями.

В
этом случае с клавиатуры нужно вводить
только операторы, а адреса ячеек
указываются мышью.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
#
23.08.2019159.74 Кб26оп.doc

Источник

После ввода или корректировки формулы, а также при изменении любого значения функции иногда появляется ошибка формулы, а не требуемое значение. Всего табличный редактор распознает семь основных типов таких неправильных расчетов. Как выглядят ошибки в Excel и как их исправить — разберем ниже.

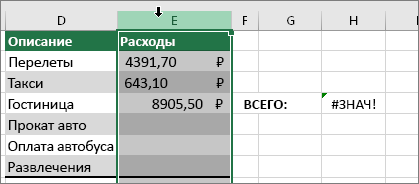
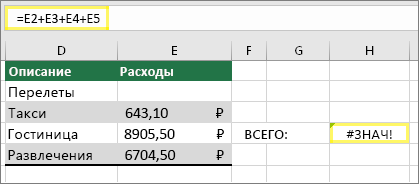
Сейчас мы опишем формулы, показанные на картинке с подробной информацией по каждой ошибке.

1. #ДЕЛ/О! – «деление на 0». Чаще всего возникает при попытке делить на ноль. То есть заложенная в ячейке формула, выполняя функцию деления, натыкается на ячейку с нулевым значением или где стоит «Пусто». Чтобы устранить проблему, проверьте все участвующие в вычислениях ячейки и исправьте все недопустимые значения. Второе действие, приводящее к #ДЕЛ/О! – это ввод неверных значений в некоторые функции. Такие как =СРЗНАЧ(), если при расчете в диапазоне значений стоит 0. Тот же результат спровоцируют незаполненные ячейки, к которым обращается формула, требующая их для расчета конкретных данных.
2. #Н/Д – «нет данных». Так Excel помечает значения, непонятные формуле (функции). Введя неподходящие цифры в функцию, вы обязательно вызовете эту ошибку. При ее появлении проследите, все ли входные ячейки заполнены правильно, а особенно те из них, где светится такая же надпись. Часто встречается при использовании =ВПР()
3. #ИМЯ? – «недопустимое имя». Показатель некорректного имени формулы или какой-то ее части. Проблема исчезает, если проверить и подправить все названия и имена, сопровождающие алгоритм вычислений.
4. #ПУСТО! – «в диапазоне пустое значение». Сигнал о том, что где-то в расчете прописаны непересекающиеся области или проставлен пробел между указанными диапазонами. Довольно редкая ошибка. Выглядеть ошибочная запись может так:

=СУММ(G10:G12 I8:J8)

Excel не распознает такие команды.
5. #ЧИСЛО! – ошибку вызывает формула, содержащая число, не соответствующее рамкам обозначенного диапазона.
6. #ССЫЛКА! – предупреждает о том, что исчезли ячейки, связанные с этой формулой. Проверьте, скорее всего были удалены ячейки, указанные в формуле.
7. #ЗНАЧ! – неверно выбран тип аргумента для работы функции.

8. Бонус, ошибка ##### — ширина ячейки недостаточна для отображения всего числа

Кроме того, Excel выдает предупреждение о неправильной формуле. Программа попытается подсказать вам, как именно следует сделать расстановку пунктуации (например скобок). Если предложенный вариант отвечает вашим требования, жмите «Да». Если подсказка требует ручной корректировки, тогда выберите «Нет» и переставьте скобки сами.

Содержание

Ошибки в Excel. Применение функции ЕОШИБКА() для Excel 2003
Ошибки в Excel. Применение ЕСЛИОШИБКА() для Excel 2007 и выше
Похожие статьи

Ошибки в Excel. Применение функции ЕОШИБКА() для Excel 2003

Хорошо помогает ликвидировать ошибки в Excel функция =ЕОШИБКА(). Действует она путем нахождения ошибок в ячейки, если находит ошибку в формуле возвращает значение ИСТИНА и наоборот. В комбинации с =ЕСЛИ() она позволят заменить значение, если найдена ошибка.

Рабочая формула: =ЕСЛИ(ОШИБКА(выражение);ошибка;выражение).

=ЕСЛИ(ЕОШИБКА(А1/А2);””;А1/А2)

Пояснение: если при выполнении А1/А2 найдена ошибка, будет возвращено пусто («»). Если все прошло корректно (т.е. ЕОШИБКА(А1/А2) = ЛОЖЬ), то рассчитывается А1/А2.

Ошибки в Excel. Применение ЕСЛИОШИБКА() для Excel 2007 и выше

Одна из причин, почему я быстро перешел на Excel 2007, была ЕСЛИОШИБКА() (самая главная причина — это СУММЕСЛИМН)

Функция еслиошибка содержит возможности обеих функций – ЕОШИБКА() и ЕСЛИ(). Доступна в более новых версиях Excel, что очень удобно

Инструмент активируется следующим образом: =ЕСЛИОШИБКА(значение; значение при ошибке). Вместо «значение» ставится расчетное выражение/ссылка на ячейку, а вместо «значение при ошибке» — то, что следует вернуть при появлении неточности. Например, если при расчете А1/А2 выдается #ДЕЛ/О!, то формула будет выглядеть следующим образом:

=ЕСЛИОШИБКА(А1/А2;””)

Пример файла «Ошибки в формулах» качайте здесь

А так же рекомендую почитать почему формула может не считаться или считаться неправильно — здесь.

Источник

Ошибка #ЗНАЧ! в Excel означает: «Формула вводится неправильно. Или что-то не так с ячейками, на которые указывают ссылки». Эта ошибка возникает в самых разных случаях, и найти ее точную причину может быть сложно. Сведения на этой странице включают распространенные проблемы и решения ошибки.

Используйте раскрывающийся список ниже или перейдите к одной из других областей:

Проблемы с вычитанием
Проблемы с пробелами и текстом
Другие решения

Исправление ошибок определенных функций

Ваша функция не отображается в этом списке? Попробуйте другие решения, перечисленные ниже.

Проблемы с вычитанием

Если вы раньше не работали в Excel, вероятно, вы неправильно вводите формулу вычитания. Это можно сделать двумя способами:

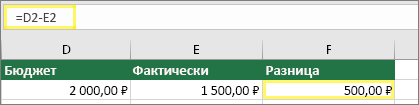
Вычтите одну ссылку на ячейку из другой

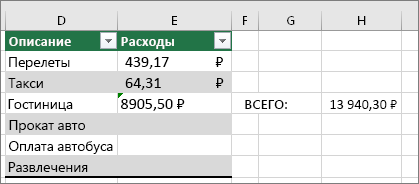
Введите два значения в двух отдельных ячейках. В третьей ячейке вычтите одну ссылку на ячейку из другой. В этом примере ячейка D2 содержит плановую сумму, а ячейка E2 — фактическую. F2 содержит формулу =D2-E2.

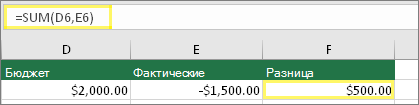
Или используйте функцию СУММ с положительными и отрицательными числами

Введите положительное значение в одной ячейке и отрицательное — в другой. В третьей ячейке используйте функцию СУММ, чтобы сложить две ячейки. В этом примере ячейка D6 содержит плановую сумму, а ячейка E6 — фактическую как негативное число. F6 содержит формулу =СУММ(D6;E6).

Если используется Windows, ошибка #ЗНАЧ! может возникнуть даже при вводе самой обычной формулы вычитания. Проблему можно решить следующим образом.

Для начала выполните быструю проверку. В новой книге введите 2 в ячейке A1. Введите 4 в ячейке B1. Затем введите формулу =B1-A1 в ячейке C1. Если возникнет ошибка #ЗНАЧ! перейдите к следующему шагу. Если сообщение об ошибке не появилось, попробуйте другие решения на этой странице.
В Windows откройте панель управления «Региональные стандарты».
- Windows 10: нажмите кнопку Пуск, введите Регион, а затем выберите панель управления Регион .
- Windows 8. На начальном экране введите Регион, выберите Параметры, а затем — Регион.
- Windows 7: выберите Пуск, введите Регион, а затем выберите Регион и язык.
На вкладке Форматы выберите Дополнительные параметры.
Найдите пункт Разделитель элементов списка. Если в поле разделителя элементов списка указан знак «минус», замените его на что-то другое. Например, разделителем нередко выступает запятая. Также часто используется точка с запятой. Однако для вашего конкретного региона может подходить другой разделитель элементов списка.
Нажмите кнопку ОК.
Откройте книгу. Если ячейка содержит ошибку #VALUE!, дважды щелкните ее для редактирования.
Если там, где для вычитания должны быть знаки «минус», стоят запятые, замените их на знаки «минус».
Нажмите клавишу ВВОД.
Повторите эти действия для других ячеек, в которых возникает ошибка.

Вычтите одну ссылку на ячейку из другой

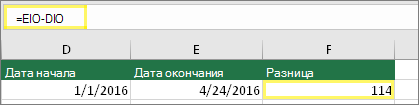
Введите две даты в двух отдельных ячейках. В третьей ячейке вычтите одну ссылку на ячейку из другой. В этом примере ячейка D10 содержит дату начала, а ячейка E10 — дату окончания. F10 содержит формулу =E10-D10.

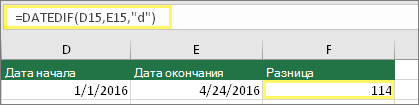
Или используйте функцию РАЗНДАТ

Введите две даты в двух отдельных ячейках. В третьей ячейке используйте функцию РАЗНДАТ, чтобы найти разницу дат. Дополнительные сведения о функции РАЗНДАТ см. в статье Вычисление разницы двух дат.

Растяните столбец по ширине. Если значение выравнивается по правому краю — это дата. Но если оно выравнивается по левому краю, это значит, что в ячейке на самом деле не дата. Это текст. И Excel не распознает текст как дату. Ниже приведены некоторые решения, которые помогут решить эту проблему.

Проверка наличия начальных пробелов

Дважды щелкните дату, которая используется в формуле вычитания.
Разместите курсор в начале и посмотрите, можно ли выбрать один или несколько пробелов. Вот как выглядит выбранный пробел в начале ячейки:

Если в ячейке обнаружена эта проблема, перейдите к следующему шагу. Если вы не видите один или несколько пробелов, перейдите к следующему разделу и проверьте параметры даты на компьютере.
Выберите столбец, содержащий дату, выбрав его заголовок столбца.
Выберите Data > Text to Columns (Текст > столбцы).
Дважды нажмите кнопку Далее .
На шаге 3 из 3 мастера в разделе Формат данных столбца выберите Дата.
Выберите формат даты и нажмите кнопку Готово.
Повторите эти действия для других столбцов, чтобы убедиться, что они не содержат пробелы перед датами.

Проверка параметров даты на компьютере

Excel полагается на систему дат вашего компьютера. Если дата ячейки не введена в той же системе дат, Excel не распознает ее как дату true.

Например, предположим, что компьютер отображает даты в формате мм.дд.гггг. Если ввести такую дату в ячейке, Excel распознает ее как дату, а вы сможете использовать ее в формуле вычитания. Однако если вы ввели такую дату, как дд/мм/гг, Excel не распознает ее как дату. Вместо этого дата будет рассматриваться как текст.

Существует два решения этой проблемы: Вы можете изменить систему дат, которая используется на компьютере, чтобы она соответствовала системе дат, которая нужна в Excel. Или в Excel можно создать новый столбец и использовать функцию ДАТА, чтобы создать настоящую дату на основе даты в текстовом формате. Вот как это сделать, если система дат вашего компьютера — дд.мм.гггг, а в ячейке A1 записан текст 12/31/2017.

Создайте такую формулу: =ДАТА(ПРАВСИМВ(A1;4);ЛЕВСИМВ(A1;2);ПСТР(A1;4;2))
Результат будет 31.12.2017.
Чтобы использовать формат дд.мм.гг, нажмите клавиши CTRL+1 (или + 1 на Mac).
Выберите другой языковой стандарт, в котором используется формат дд.мм.гг, например Немецкий (Германия). Когда вы закончите применять формат, результатом будет 31/12/2017 , и это настоящая дата, а не текстовая дата.

Примечание: Формула выше написана с использованием функций ДАТА, ПРАВСИМВ, ПСТР и ЛЕВСИМВ. Обратите внимание, что она написана с предположением, что текстовая дата содержит два символа для дней, два символа для месяцев и четыре символа года. Возможно, вам потребуется настроить формулу в соответствии с датой.

Проблемы с пробелами и текстом

Часто ошибка #ЗНАЧ! возникает, потому что формула ссылается на другие ячейки, содержащие пробелы или (что еще сложнее) скрытые пробелы. Из-за этих пробелов ячейка может выглядеть пустой, хотя на самом деле таковой не является.

1. Выберите ячейки, на которые указывают ссылки

Найдите ячейки, на которые ссылается формула, и выделите их. Во многих случаях рекомендуется удалить пробелы для всего столбца, так как можно заменить несколько пробелов одновременно. В этом примере при выборе E выделяется весь столбец.

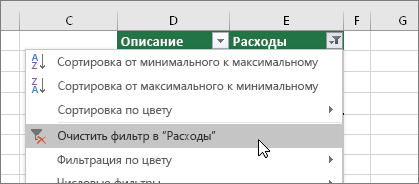
2. Найдите и замените

На вкладке Главная выберите Найти & Выберите > Заменить.

3. Удалите пробелы

В поле Найти введите один пробел. Затем в поле Заменить удалите все, что там может быть.

4. Замените одно или все вхождения

Если вы уверены, что все пробелы в столбце должны быть удалены, выберите Заменить все. Если вы хотите выполнить пошаговое выполнение и заменить пробелы ни на что не по отдельности, сначала можно нажать кнопку Найти далее , а затем нажать кнопку Заменить , если вы уверены, что пространство не требуется. После этого ошибка #ЗНАЧ! ошибка может быть устранена. Если нет — перейдите к следующему шагу.

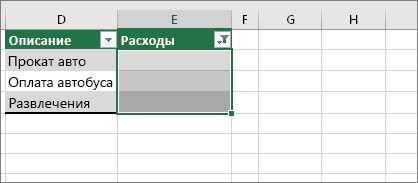
5. Включите фильтр

Иногда скрытые символы, отличные от пробелов, могут сделать ячейку пустой, если она на самом деле не пуста. Например, это может происходить из-за одинарных кавычек в ячейке. Чтобы убрать эти символы из столбца, включите фильтр, последовательно выбрав Главная > Сортировка и фильтр > Фильтр.

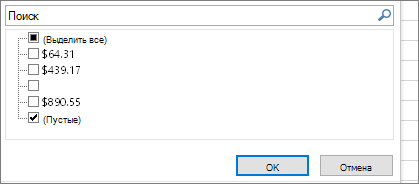
6. Установите фильтр

Щелкните стрелку фильтра и снимите флажок Выделить все. Затем установите флажок Пустые.

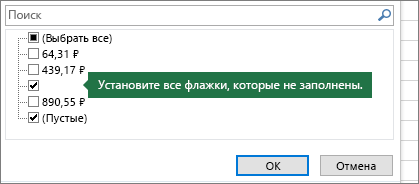
7. Установите все флажки без названия

Установите все флажки, напротив которых ничего не указано, как на этом рисунке.

8. Выделите пустые ячейки и удалите их

Если Excel вернет пустые ячейки, выделите их. Затем нажмите клавишу DELETE. Это очищает все скрытые символы в ячейках.

9. Очистите фильтр

Щелкните стрелку фильтра , а затем выберите Очистить фильтр из… , чтобы все ячейки были видны.

10. Результат

Если причиной появления ошибки #ЗНАЧ! были пробелы, вместо ошибки отобразится результат формулы, как показано в нашем примере. Если нет — повторите эти действия для других ячеек, на которые ссылается формула. Или попробуйте другие решения на этой странице.

Примечание: В этом примере обратите внимание, что ячейка E4 содержит зеленый треугольник, а число выравнивается по левому краю. Это значит, что число имеет текстовый формат. Позже это может привести к дополнительным проблемам. Если вы заметили эту проблему, рекомендуем преобразовать числа из текстового формата в числовой.

Ошибку #ЗНАЧ! могут вызвать текст и специальные знаки в ячейке. Но иногда сложно понять, в каких именно ячейках они присутствуют. Решение: Используйте функцию ISTEXT для проверки ячеек. Обратите внимание, что ISTEXT не устраняет ошибку, а просто находит ячейки, которые могут вызвать ошибку.

Пример с ошибкой #ЗНАЧ!

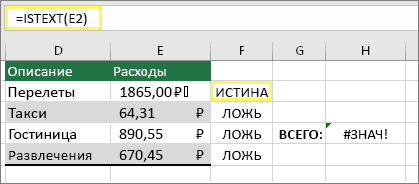
Вот пример формулы с ошибкой #ЗНАЧ! . Ошибка, скорее всего, возникает из-за ячейки E2. Специальный символ отображается в виде небольшого прямоугольника после «00». Или, как показано на следующем рисунке, можно использовать функцию ЕТЕКСТ в отдельном столбце для поиска текста.

Этот же пример с функцией ЕТЕКСТ

Здесь в столбец F добавлена функция ЕТЕКСТ. Все ячейки в порядке, кроме одной со значением ИСТИНА. Это значит, что ячейка E2 содержит текст. Чтобы решить эту проблему, можно просто удалить содержимое ячейки и еще раз ввести число 1865,00. Вы также можете использовать функцию ПЕЧСИМВ, чтобы убрать символы, или функцию ЗАМЕНИТЬ, чтобы заменить специальные знаки на другие значения.

Использовав функцию ПЕЧСИМВ или ЗАМЕНИТЬ, вы можете скопировать результат в буфер обмена, а затем выбрать Главная > Вставить > Специальная вставка > Значения. Кроме того, может потребоваться преобразовать числа из текстового формата в числовой.

Формулы с математическими операциями, такими как + и *, могут не вычислить ячейки, содержащие текст или пробелы. В таком случае попробуйте использовать вместо них функцию. Функции часто игнорируют текстовые значения и вычисляют все в виде чисел, устраняя #VALUE! . Например, вместо =A2+B2+C2 введите =СУММ(A2:C2). Или вместо =A2*B2 введите =ПРОИЗВЕД(A2,B2).

Другие решения

Выберите ошибку

Сначала выделите ячейку с ошибкой #ЗНАЧ! .

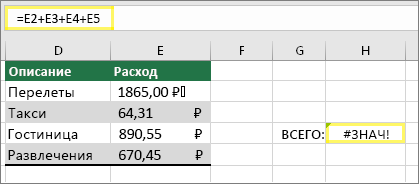
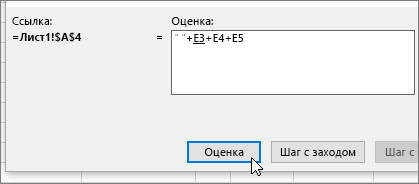
Щелкните «Формулы» > «Вычислить формулу»

Выберите Формулы > Оценка формулы > Оценка. Excel по отдельности проходит по частям формулы. В данном случае формула =E2+E3+E4+E5 выдает ошибку из-за скрытого пробела в ячейке E2. Пробела не видно, если смотреть на ячейку E2. Но его можно увидеть здесь. Он отображается как » «.

Иногда вам может быть нужно вместо ошибки #ЗНАЧ! выводить что-то свое, например собственный текст, ноль или пустую ячейку. В этом случае можно добавить в формулу функцию ЕСЛИОШИБКА. IFERROR проверяет наличие ошибки и, если да, заменяет ее другим значением по вашему выбору. Если ошибки нет, исходная формула вычисляется. IFERROR работает только в Excel 2007 и более поздних версиях. В предыдущих версиях можно использовать функцию ЕСЛИ(ЕОШИБКА()).

Предупреждение: IFERROR скрывает все ошибки, а не только #VALUE! . Ошибки не рекомендуется скрывать, так как они часто указывают на то, что какое-то значение нужно исправить, а не просто скрыть. Мы не рекомендуем использовать эту функцию, если вы не уверены, что формула работает так, как вам нужно.

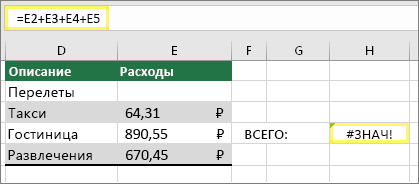
Ячейка с ошибкой #ЗНАЧ!

Вот пример формулы, в которой ошибка #ЗНАЧ! вызвана скрытым пробелом в ячейке E2.

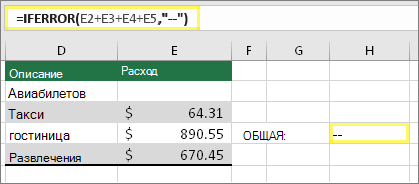
Ошибка, скрытая функцией ЕСЛИОШИБКА

А вот эта же формула с добавленной функцией ЕСЛИОШИБКА. Ее можно прочитать как «Вычислить формулу, но если возникнет какая-либо ошибка, заменить ее двумя дефисами.» Помните, что также можно использовать «», чтобы ничего не отображать вместо двух дефисов. Или вы можете подставить свой текст, например: «Ошибка суммирования».

К сожалению, как вы видите, функция ЕСЛИОШИБКА не устраняет ошибку, а только скрывает ее. Так что используйте ее, если точно уверены, что ошибку лучше скрыть, чем исправить.

В какой-то момент подключение к данным может стать недоступным. Чтобы исправить ошибку, восстановите подключение или, если это возможно, импортируйте данные. Если у вас нет доступа к подключению, попросите автора книги создать для вас новый файл. В идеале новый файл будет содержать только значения и не будет подключений. Это можно сделать, скопировав все ячейки и вставив только в качестве значений. Чтобы вставить только значения, можно выбрать Главная > Вставить > Вставить специальные значения >. При этом будут удалены все формулы и подключения, а ошибки #ЗНАЧ! исчезнут.

См. также

Полные сведения о формулах в Excel

Рекомендации, позволяющие избежать появления неработающих формул

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Введение
- 1.1 Постановка вопроса. Виды погрешностей
2 Виды мер точности
3 Предельные погрешности
4 Погрешности округлений при представлении чисел в компьютере
5 Погрешности арифметических операций
6 Погрешности вычисления функций
7 Числовые примеры
8 Список литературы
9 См. также

Введение

Постановка вопроса. Виды погрешностей

Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.

При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления.
При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации.
Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.

Итак, следует различать погрешности модели, дискретизации и округления. В вопросе преобладания какой-либо погрешности ответ неоднозначен. В общем случае нужно стремиться, чтобы все погрешности имели один и тот же порядок. Например, нецелесообразно пользоваться разностными схемами, имеющими точность 10⁻⁶, если коэффициенты исходных уравнений задаются с точностью 10⁻².

Виды мер точности

Мерой точности вычислений являются абсолютные и относительные погрешности. Абсолютная погрешность определяется формулой

$\Delta(\tilde a)=|\tilde a-a|,$

где $\tilde a$ – приближение к точному значению .
Относительная погрешность определяется формулой

$\delta(\tilde a)=\frac{|\tilde a-a|}{a}.$

Относительная погрешность часто выражается в процентах. Абсолютная и относительная погрешности тесно связаны с понятием верных значащих цифр. Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой цифры слева. Например, число 0,000129 имеет три значащих цифры. Значащая цифра называется верной, если абсолютная погрешность числа не превышает половины веса разряда, соответствующего этой цифре. Например, $\tilde a=9348$ , абсолютная погрешность $\Delta(\tilde a)=15$ . Записывая число в виде

$9348=9\cdot10^3+3\cdot10^2+4\cdot10^1+8\cdot10^0,$

имеем $0,5\cdot10^1<\Delta(\tilde a)<0,5\cdot10^2$ , следовательно, число имеет две верных значащих цифр (9 и 3).

В общем случае абсолютная погрешность должна удовлетворять следующему неравенству:

$\Delta(\tilde a)<0,5\cdot10^{m-n+1} ,$

где — порядок (вес) старшей цифры, — количество верных значащих цифр.
В рассматриваемом примере $\Delta(\tilde a)\le0,5\cdot10^{3-2+1}\le0,5\cdot10^2=50$ .

Относительная погрешность связана с количеством верных цифр приближенного числа соотношением:

$\delta(\tilde a)\le\frac{\Delta(\tilde a)}{\alpha_m}10^m\le\frac{10^{m-n+1}}{\alpha_m10^m}\le\frac{1}{\alpha_m10^{n-1}},$

где $\alpha_m$ — старшая значащая цифра числа.

Для двоичного представления чисел имеем $\delta(\tilde a)\le2^{-n}$ .

Тот факт, что число $\tilde a$ является приближенным значением числа с абсолютной погрешностью $\Delta(\tilde a)$ , записывают в виде

$a=\tilde a\pm\Delta(\tilde a),$

причем числа $\tilde a$ и $\Delta(\tilde a)$ записываются с одинаковым количеством знаков после запятой, например, $a=2,347\pm0,002$ или $a=2,347\pm2\cdot10^{-3}$ .

Запись вида

$a=\tilde a(1\pm\delta(\tilde a))$

означает, что число $\tilde a$ является приближенным значение числа с относительной погрешностью $\delta(\tilde a)$ .

Так как точное решение задачи как правило неизвестно, то погрешности приходится оценивать через исходные данные и особенности алгоритма. Если оценка может быть вычислена до решения задачи, то она называется априорной. Если оценка вычисляется после получения приближенного решения задачи, то она называется апостериорной.

Очень часто степень точности решения задачи характеризуется некоторыми косвенными вспомогательными величинами. Например точность решения системы алгебраических уравнений

AX=F

характеризуется невязкой

$R=F-A\tilde X,$

где $\tilde X$ — приближенное решение системы.
Причём невязка достаточно сложным образом связана с погрешностью решения $\Delta(X)=\tilde X-X$ , причём если невязка мала, то погрешность может быть значительной.

Предельные погрешности

Пусть искомая величина является функцией параметров $t_1, \ldots , t_n \in \Omega, \qquad a*$ — приближенное значение . Тогда предельной абсолютной погрешностью называется величина

$D(a^*) = \sup\limits_{(t_1, \ldots ,t_n) \in \Omega } \left|{a(t_1, \ldots ,t_n) - a^*}\right| ,$

Предельной относительной погрешностью называется величина .

Пусть $\left|{t_j - t_j^*}\right| \le \Delta (t_j^* ), \qquad j = 1 \div n$ — приближенное значение $a^* = a(t_1^*, \ldots ,t_n^* )$ . Предполагаем, что — непрерывно дифференцируемая функция своих аргументов. Тогда, по формуле Лагранжа,

$a(t_1, \ldots ,t_n) - a^* = \sum\limits_{j = 1}^n \gamma_j (\alpha )(t_j - t_j^*),$

где $\gamma_j (\alpha ) = a^{\prime}_{t_j}(t_1^* + \alpha (t_1 - t_1^*), \ldots ,t_n^* + \alpha (t_n - t_n^*)), \qquad 0 \le \alpha \le 1$ .

Отсюда

$\left|{a(t_1, \ldots ,t_n) - a^*}\right| \le D_1 (a^*) = \sum\limits_{j = 1}^n b_j \Delta (t_j^*),$

где $b_j = \sup\limits_\Omega \left|{a^{\prime}_{t_j}(t_1, \ldots ,t_n)}\right|$ .

Можно показать, что при малых $\rho = \sqrt{{(\Delta (t_1^* ))}^2 + \ldots + {(\Delta (t_n^* ))}^2 }$ эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой

$\left|{a(t_1, \ldots ,t_n) - a^*}\right| \le D_2 (a^*),$

где $D_2 (a^*) = \sum\limits_{j = 1} \left|{\gamma_j (0)}\right| \Delta (t^*)$ .

Несложно показать, что:

$\Delta ( \pm t_1^* \pm , \ldots , \pm t_n^*) = \Delta (t_1^* ) + \ldots + \Delta (t_n^* )$ — предельная погрешность суммы или разности равна сумме предельных погрешностей.
$\delta (t_1^* \cdots t_m^* \cdot d_1^{* - 1} \cdots d_m^{* - 1} ) = \delta (t_1^* ) + \ldots + \delta (t_m^*) + \delta (d_1^*) + \ldots + \delta (d_n^*)$ — предельная относительная погрешность произведения или частного приближенного равна сумме предельных относительных погрешностей.

Погрешности округлений при представлении чисел в компьютере

Одним из основных источников вычислительных погрешностей является приближенное представление чисел в компьютере, обусловленное конечностью разрядной сетки (см. Международный стандарт представления чисел с плавающей точкой в ЭВМ). Число , не представимое в компьютере, подвергается округлению, т. е. заменяется близким числом $\tilde a$ , представимым в компьютере точно.
Найдем границу относительной погрешности представления числа с плавающей точкой. Допустим, что применяется простейшее округление – отбрасывание всех разрядов числа, выходящих за пределы разрядной сетки. Система счисления – двоичная. Пусть надо записать число, представляющее бесконечную двоичную дробь

$a=\underbrace{\pm2^p}_{order}\underbrace{\left(\frac{a_1}{2}+\frac{a_2}{2^2}+\dots+\frac{a_t}{2^t}+\frac{a_{t+1}}{2^{t+1}}+\dots\right)}_{mantissa},$

где $a_j=\{0\\1$ , $\qquad (j=1,2,...)$ — цифры мантиссы.
Пусть под запись мантиссы отводится t двоичных разрядов. Отбрасывая лишние разряды, получим округлённое число

$\tilde a=\pm2^p\left(\frac{a_1}{2}+\frac{a_2}{2^2}+\dots+\frac{a_t}{2^t}\right).$

Абсолютная погрешность округления в этом случае равна

$a-\tilde a=\pm2^p\left(\frac{a_{t+1}}{2^{t+1}}+\frac{a_{t+2}}{2^{t+2}}+\dots\right).$

Наибольшая погрешность будет в случае $a_{t+1}=1, \qquad a_{t+2}=1,$ , тогда

$|a-\tilde a|\le\pm2^p\frac{1}{2^{t+1}}\underbrace{\left(1+\frac{1}{2}+\frac{1}{2^2}+\dots\right)}_{=2}=2^{p-t}.$

Т.к. $|M|\ge0,5$ , где — мантисса числа , то всегда a_1=1 . Тогда $|a|\ge2^p\cdot2^{-1}=2^{p-1}$ и относительная погрешность равна $\frac{|a-\tilde a|}{|a|}\le2^{-t+1}$ . Практически применяют более точные методы округления и погрешность представления чисел равна

( 1 )

$\frac{|a-\tilde a|}{|a|}\le2^{-t},$

т.е. точность представления чисел определяется разрядностью мантиссы .
Тогда приближенно представленное в компьютере число можно записать в виде $\tilde a=a(1\pm\epsilon)$ , где $|\epsilon|\le2^{-t}$ – «машинный эпсилон» – относительная погрешность представления чисел.

Погрешности арифметических операций

При вычислениях с плавающей точкой операция округления может потребоваться после выполнения любой из арифметических операций. Так умножение или деление двух чисел сводится к умножению или делению мантисс. Так как в общем случае количество разрядов мантисс произведений и частных больше допустимой разрядности мантиссы, то требуется округление мантиссы результатов. При сложении или вычитании чисел с плавающей точкой операнды должны быть предварительно приведены к одному порядку, что осуществляется сдвигом вправо мантиссы числа, имеющего меньший порядок, и увеличением в соответствующее число раз порядка этого числа. Сдвиг мантиссы вправо может привести к потере младших разрядов мантиссы, т.е. появляется погрешность округления.

Округленное в системе с плавающей точкой число, соответствующее точному числу , обозначается через fl(x) (от англ. floating – плавающий). Выполнение каждой арифметической операции вносит относительную погрешность, не большую, чем погрешность представления чисел с плавающей точкой (1). Верна следующая запись:

$fl(a\box b)=a\box b(1\pm\epsilon),$

где $\box$ — любая из арифметических операций, $|\epsilon|\le2^{-t}$ .

Рассмотрим трансформированные погрешности арифметических операций. Арифметические операции проводятся над приближенными числами, ошибка арифметических операций не учитывается (эту ошибку легко учесть, прибавив ошибку округления соответствующей операции к вычисленной ошибке).

Рассмотрим сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.

Если сумма точных чисел равна

$S=a_1+a_2+\dots+a_n,$

сумма приближенных чисел равна

$\tilde S=a_1+\Delta(a_1)+a_2+\Delta(a_2)+\dots+a_n+\Delta(a_n),$

где $\Delta(a_i), \qquad i=1,2,...,n$ — абсолютные погрешности представления чисел.

Тогда абсолютная погрешность суммы равна

$\Delta(S)=\Delta(a_1)+\Delta(a_2)+\dots+\Delta(a_n).$

Относительная погрешность суммы нескольких чисел равна

( 2 )

$\delta(S)=\frac{\Delta(S)}{S}=\frac{a_1}{S}\left(\frac{\Delta(a_1)}{a_1}\right)+\frac{a_2}{S}\left(\frac{\Delta(a_2)}{a_2}\right)+\dots=\frac{a_1\delta(a_1)+a_2\delta(a_2)+\dots}{S},$

где $\delta(a_i), \qquad i=1,2,...,n$ — относительные погрешности представления чисел.

Из (2) следует, что относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

$min \quad \delta(a_k)\le\delta(S)\le max \quad \delta(a_k), \qquad k=1,2,...,n, \quad a_k>0.$

При сложении чисел разного знака или вычитании чисел одного знака относительная погрешность может быть очень большой (если числа близки между собой). Так как даже при малых $\Delta(a_i)$ величина может быть очень малой. Поэтому вычислительные алгоритмы необходимо строить таким образом, чтобы избегать вычитания близких чисел.

Необходимо отметить, что погрешности вычислений зависят от порядка вычислений. Далее будет рассмотрен пример сложения трех чисел.

$\tilde S_1=(x_1+x_2)(1+\delta_1),$

( 3 )

$\tilde S=(\tilde S_1+x_3)(1+\delta_2)=(x_1+x_2)(1+\delta_1)(1+\delta_2)+x_3(1+\delta_2).$

При другой последовательности действий погрешность будет другой:

$\tilde S_1=(x_3+x_2)(1+\delta_1),$

$\tilde S=(x_3+x_2)(1+\delta_1)(1+\delta_2)+x_1(1+\delta_2).$

Из (3) видно, что результат выполнения некоторого алгоритма, искаженный погрешностями округлений, совпадает с результатом выполнения того же алгоритма, но с неточными исходными данными. Т.е. можно применять обратный анализ: свести влияние погрешностей округления к возмущению исходных данных. Тогда вместо (3) будет следующая запись:

$\tilde S=\tilde x_1+\tilde x_2+\tilde x_3,$

где $\tilde x_1=x_1(1+\delta_1)(1+\delta_2), \quad \tilde x_2=x_2(1+\delta_1)(1+\delta_2), \quad \tilde x_3=x_3(1+\delta_2).$

При умножении и делении приближенных чисел складываются и вычитаются их относительные погрешности.

$S=a_1\cdot a_2,$

$\tilde S=a_1\cdot a_2(1+\delta(a_1))(1+\delta(a_2))$

≅ $a_1\cdot a_2(1+\delta(a_1)+\delta(a_2)),$

с точностью величин второго порядка малости относительно $\delta$ .

Тогда $\delta(S)=\delta(a_1)+\delta(a_2)$ .

Если $S=\frac{a_1}{a_2}$ , то $\Delta(S)=\frac{a_1(1+\delta_1)}{a_2(1+\delta_2)}-\frac{a_1}{a_2}=\frac{a_1(\delta_1-\delta_2)}{a_2(1+\delta_2)}\approx \frac{a_1}{a_2}(\delta_1-\delta_2), \qquad \delta(S)$ ≅ $\delta_1-\delta_2.$

При большом числе n арифметических операций можно пользоваться приближенной статистической оценкой погрешности арифметических операций, учитывающей частичную компенсацию погрешностей разных знаков:

$\delta_\Sigma \approx \delta_{fl} \quad \sqrt{n},$

где $\delta_\Sigma$ – суммарная погрешность, $|\delta_{fl}|\le\epsilon$ – погрешность выполнения операций с плавающей точкой, $\epsilon$ – погрешность представления чисел с плавающей точкой.

Погрешности вычисления функций

Рассмотрим трансформированную погрешность вычисления значений функций.

Абсолютная трансформированная погрешность дифференцируемой функции y=f(x) , вызываемая достаточно малой погрешностью аргумента $\Delta(x)$ , оценивается величиной $\Delta(y)=\|f'(x)\|\Delta(x)$ .

Если f(x)>0 , то $\delta(y)=\frac{\|f'(x)\|}{f(x)}\Delta(x)=\left|(ln(f(x)))'\right|\cdot\Delta(x)$ .

Абсолютная погрешность дифференцируемой функции многих аргументов , вызываемая достаточно малыми погрешностями $\Delta(x_1), \Delta(x_2), ..., \Delta(x_n)$ аргументов оценивается величиной:

$\Delta(y)=\sum\limits_{i=1}^n\left|\frac{\partial f}{\partial x_i}\right|\Delta(x_i)$

Если , то $\delta(y)=\sum\limits_{i=1}^n\frac{1}{f}\cdot\left|\frac{\partial f}{\partial x_i}\right|\cdot\Delta(x_i)=\sum\limits_{i=1}^{n}\left|\frac{\partial l_n(f)}{\partial x_i}\right|\Delta(x_i)$ .

Практически важно определить допустимую погрешность аргументов и допустимую погрешность функции (обратная задача). Эта задача имеет однозначное решение только для функций одной переменной y=f(x) , если f(x) дифференцируема и $f'(x)\not=0$ :

$\Delta(x)=\frac{1}{\|f'(x)\|}\Delta(y)$

Для функций многих переменных задача не имеет однозначного решения, необходимо ввести дополнительные ограничения. Например, если функция наиболее критична к погрешности $\Delta(x_i)$ , то:

$\Delta(x_i)=\frac{\Delta(y)}{\left|\frac{\partial f}{\partial x_i}\right|}\qquad$

(погрешностью других аргументов пренебрегаем).

Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:

$\Delta(x_i)=\frac{\Delta(y)}{n\left|\frac{\partial f}{\partial x_i}\right|},\qquad i=\overline{1,n}.$

Числовые примеры

Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.

ПРИМЕР 1. Вычислить все корни уравнения

$x^4 - 4x^3 + 8x^2 - 16x + 15.\underbrace{99999999}_8 = {(x - 2)}^4 - 10^{- 8} = 0.$

Точное решение задачи легко найти:

$(x - 2)^2 = \pm 10^{- 4},$

$x_1= 2,01; x_2= 1,99; x_{3,4}= 2 \pm 0,01i.$

Если компьютер работает при $\delta _M > 10^{ - 8}$ , то свободный член в исходном уравнении будет округлен до 16,0 и, с точки зрения представления чисел с плавающей точкой, будет решаться уравнение , т.е. $x_{1,2,3,4} = 2$ , что, очевидно, неверно. В данном случае малые погрешности в задании свободного члена $\approx10^{-8}$ привели, независимо от метода решения, к погрешности в решении $\approx10^{-2}$ .

ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:

$u''(t) = u(t), \qquad u(0) = 1, \qquad u'(0) = - 1.$

Общее решение имеет вид:

$u(t) = 0,5[u(0) + u'(0)]e^t + 0,5[u(0) - u'(0)]e^{- t}.$

При заданных начальных данных точное решение задачи: $u(x) = e^{-t}$ , однако малая погрешность $\delta$ в их задании приведет к появлению члена $\delta e^t$ , который при больших значениях аргумента может существенно исказить решение.

ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:

$\stackrel{\cdot}{u} = 10u,\qquad u = u(t),\\ u(t_0) = u_0,\qquad t \in [0,1].$

Его решение: $u(t) = u_0e^{10(t - t_0 )}$ , однако значение u(t_0) известно лишь приближенно: $u(t_0) \approx u_0^*$ , и на самом деле $u^*(t) = u_0^*e^{10(t - t_0)}$ .

Соответственно, разность u* - u будет:

$u^* - u = (u_0^* - u_0)e^{10(t - t_0)}.$

Предположим, что необходимо гарантировать некоторую заданную точность вычислений $\epsilon > 0$ всюду на отрезке $t \in [0,1]$ . Тогда должно выполняться условие:

$|{u^*(t) - u(t)}| \le \varepsilon.$

Очевидно, что:

$\max\limits_{t \in [0,1]} |{u^*(t) - u(t)}| = |{u*(1) - u(1)}| = |{u_0^* - u_0}|e^{10(1 - t_0)}.$

Отсюда можно получить требования к точности задания начальных данных $\delta: \qquad|u_0^* - u_0| < \delta, \qquad \delta \le \varepsilon e^{ - 10}$ при t_0= 0 .

Таким образом, требование к заданию точности начальных данных оказываются в $e^{10}$ раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.

Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.

ПРИМЕР 4. Решением системы линейных алгебраических уравнений (СЛАУ):

$\left\{ \begin{array}{l} u + 10v = 11, \\ 100u + 1001v = 1101; \\ \end{array} \right.$

является пара чисел $\{1, \quad 1\}$ .

Изменив правую часть системы на 0,01 , получим возмущенную систему:

$\left\{ \begin{array}{l} u + 10v = 11.01, \\ 100u + 1001v = 1101; \\ \end{array} \right.$

с решением $\{11.01, \quad 0.00\}$ , сильно отличающимся от решения невозмущенной системы. Эта система также плохо обусловлена.

ПРИМЕР 5. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность $\delta_M = 0,0005$ . Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки $u = 1,001,\quad v = 1,002$ , разность которых составляет $\Delta = |v_M - u_M| = 0,001$ .

В памяти машины эти же числа представляются в виде:

$u_M = u(1 + \delta_M^u), \quad v_M = v(1 + \delta_M^v)$

, причем $\mid \delta_M^u\mid \le \delta_M$

и $\mid \delta_M^v\mid \le \delta_M.$

Тогда:

$u_M - u \approx u\delta_M^u, \quad v_M - v \approx v\delta_M^v.$

Относительная ошибка при вычислении разности будет равна:

$\delta = \frac{(u_M - v_M) - (u - v)}{(u - v)} = \frac{(u_M - u) - (v_M - v)}{(u - v)} = \frac{\delta_M^u - \delta_M^v}{(u - v)}.$

Очевидно, что $\delta = \left|{\frac{\delta_M^u - \delta_M^v}{\Delta }} \right| \le \frac{2\delta_M}{0,001} \approx 2000\delta_M = 1$ , т.е. все значащие цифры могут оказаться неверными.

ПРИМЕР 6. Рассмотрим рекуррентное соотношение $u_{i+1} = qu_i, \quad i \ge 0, \quad u_0 = a,\quad q > 0, \quad u_i > 0.$

Пусть при выполнении реальных вычислений с конечной длиной мантиссы на -м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением $u_i^M = u_i + \delta_i$ , тогда вместо $u_{i+1}$ получим $u_{i + 1}^M = q(u_i + \delta_i) = u_{i + 1} + q\delta_i$ , т.е. $\delta_{i + 1} = q\delta_i,\quad i = 0,1,\ldots$ .

Следовательно, если |q| > 1 , то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае $\mid q\mid \le 1$ погрешность не возрастает и численный алгоритм устойчив.

Список литературы

А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
http://www.mgopu.ru/PVU/2.1/nummethods/Chapter1.htm
http://www.intuit.ru/department/calculate/calcmathbase/1/4.html

См. также

Практикум ММП ВМК, 4й курс, осень 2008

Источник

Возможные ошибки при выполнении расчетов

После запуска расчета система может выдать ряд ошибок, ошибки бывают нескольких
типов:

ошибки по топологии сети;
ошибки по семантической информации;
ошибки по результатам расчета;
остальные ошибки.

При этом, пока не будут устранены ошибки первых двух типов, расчет не запустится.
Для того чтобы определить по какому объекту выдана ошибка, выполните двойной щелчок
левой кнопкой мыши по строке с ошибкой, после чего объект, по которому выдана
ошибка, замигает. Если ошибка связана с семантикой, то откроется окно семантической
информации и курсор встанет на строку, в которой необходимо внести или исправить
информацию.

Далее, для исправления ошибки, необходимо (в зависимости от ее типа) либо
исправить графическую информацию (отредактировать сеть), либо семантическую (внести
или исправить данные в базе).

Ошибки по топологии сети

Ошибка Z001: ID=ХХ Участок не имеет узла

Данная ошибка скорей является не ошибкой, а предупреждением, поэтому она
выводится синим цветом и не является причиной остановки расчета.

Такое предупреждение будет выведено при неправильном нанесении сети, когда
начальный или конечный узел участка не связан с каким-либо объектом, хотя при
этом визуально может казаться, что участок связан с точечным объектом.

Для проверки связности всей сети воспользуйтесь разделом « Поиск связанных и не связанных ». Для исправления
ошибки воспользуйтесь разделом «Редактирование элементов объекта».

ХХ — индивидуальный номер объекта (ID или Sys), автоматически присваиваемый
при изображении сети.
Ошибка Z013: ID=XX Узел содержит недопустимый набор
связей

Ошибка 141: сток ID=XX содержит более одного входящего
ребра.

Данная ошибка выводится при неправильном нанесении сети, в том случае, когда к
объекту присоединено недопустимое количество участков.
Ошибка Z003: ID=XX В конструкторском расчете из узла может выходить
только один участок

Конструкторский расчёт нельзя использовать, если из колодца выходит несколько
самотечных участков. Ограничение математической модели.
Ошибка Из узла один участок должен выходить

Следует проверить ориентацию участков. Также можно использовать опцию автоматического изменения
направлений участков.

Ошибки по семантической информации

Ошибка Z004: Неверное значение поля

Данная ошибка выводится при наличии некорректных данных или при отсутствии
исходной информации хотя бы в одной строке необходимой для расчетов. Для
устранения ошибки необходимо дважды щелкнуть левой кнопкой мыши по
сообщению, после чего откроется окно семантической информации по объекту с
неверными или отсутствующими данными, и курсор встанет на поле, где
необходимо ввести или исправить информацию.
Не найдено поле

В базе данных нет необходимого поля. Следует обновить структуру слоя сети
или подключить недостающее поле в настройке слоя. Возможно, что поле
потребуется добавить вручную.
Ошибка Z007: В базе по объекту ‘Название объекта’ не задано
поле исходных данных для значения ‘Название поля’

В ошибке указывается название типового объекта и поле, необходимые для
выполнения расчёта. Если в базе данных поле уже создано, то следует настроить поле для
выполнения расчётов.

Ошибки по результатам расчета

Предупреждение 08: перепад высот превышает длину канала
ID=XX

Следует проверить исходные данные по объекту с ошибкой. Длина участка не
должны быть меньше, чем перепад высот начального и конечного узла.
Ошибка Z012: ID=17 В сортаменте отсутствует минимально
необходимый диаметр (1.20 м)

Данная ошибка возникает при выполнении конструкторского расчета. Следует
проверить какие диаметры существуют в сортаменте, возможно необходимо добавить
недостающие. Также следует проверить расходы в сети. Обязательно проверить
сортаменты на всех участках, если используются различные материалы.
Ошибка Z010: ID=XX Отметка дна колодца больше отметки
поверхности земли (56.79 м > 54.30 м)

Следует проверить исходные данные узла XX, и внести необходимые
изменения.
Предупреждение Z603: ID=XX Излив на землю (05.00000037
л/с)

Ошибка возникает, если колодец открытого типа (поле
Тип: открытый\закрытый). В результате расчёта
уровень воды в колодце больше его глубины и происходить излив на
поверхность.
Предупреждение Z604: ID=270 Погрешность суммы расходов в узле
(1.62030890 л/с)

Погрешность связности (%) ….. -32.520 Данная
ошибка возникает при недостаточном времени анализа сети. Следует в настройках
расчёта увеличить время анализа сети.

	Примечание
Для сходимости расчета с кольцами, отрицательными уклонами, развилками и при динамическом режиме, требуется большой интервал времени анализа сети, до ее выхода на стабильный режим. В результате расчета определяется Погрешность связности (%) .Чем больше время анализа расчета, тем меньше становится погрешность (но увеличивается время расчета). Погрешность связанности должна быть менее единицы (должна стремиться к 0).

Примечание

Для сходимости расчета с кольцами, отрицательными уклонами, развилками и при
динамическом режиме, требуется большой интервал времени анализа сети, до ее выхода на
стабильный режим. В результате расчета определяется Погрешность связности (%) .Чем
больше время анализа расчета, тем меньше становится погрешность (но увеличивается время
расчета). Погрешность связанности должна быть менее единицы (должна стремиться к
0).

Источник

Ошибки в Excel. Применение функции ЕОШИБКА() для Excel 2003

Ошибки в Excel. Применение ЕСЛИОШИБКА() для Excel 2007 и выше

Исправление ошибок определенных функций

Проблемы с вычитанием

Вычтите одну ссылку на ячейку из другой

Или используйте функцию СУММ с положительными и отрицательными числами

Вычтите одну ссылку на ячейку из другой

Или используйте функцию РАЗНДАТ

Проблемы с пробелами и текстом

1. Выберите ячейки, на которые указывают ссылки

2. Найдите и замените

3. Удалите пробелы

4. Замените одно или все вхождения

5. Включите фильтр

6. Установите фильтр

7. Установите все флажки без названия

8. Выделите пустые ячейки и удалите их

9. Очистите фильтр

10. Результат

Пример с ошибкой #ЗНАЧ!

Этот же пример с функцией ЕТЕКСТ

Другие решения

Выберите ошибку

Щелкните «Формулы» > «Вычислить формулу»

Ячейка с ошибкой #ЗНАЧ!

Ошибка, скрытая функцией ЕСЛИОШИБКА

См. также

Материал из MachineLearning.

Содержание

Введение

Постановка вопроса. Виды погрешностей

Виды мер точности

Предельные погрешности

Погрешности округлений при представлении чисел в компьютере

Погрешности арифметических операций

Погрешности вычисления функций

Числовые примеры

Список литературы

См. также

Возможные ошибки при выполнении расчетов

Ошибки по топологии сети

Ошибки по семантической информации

Ошибки по результатам расчета

Интересное по теме: