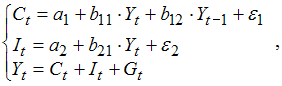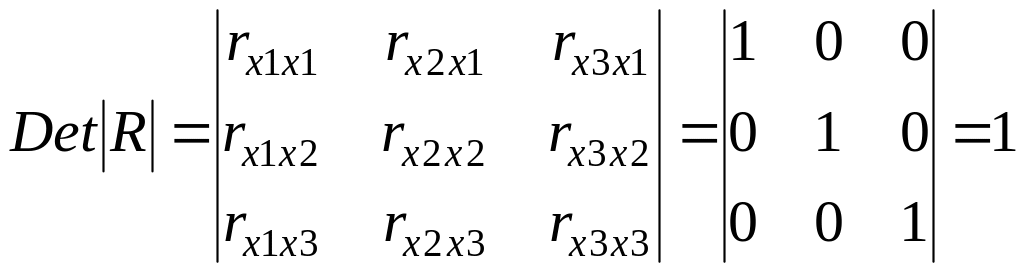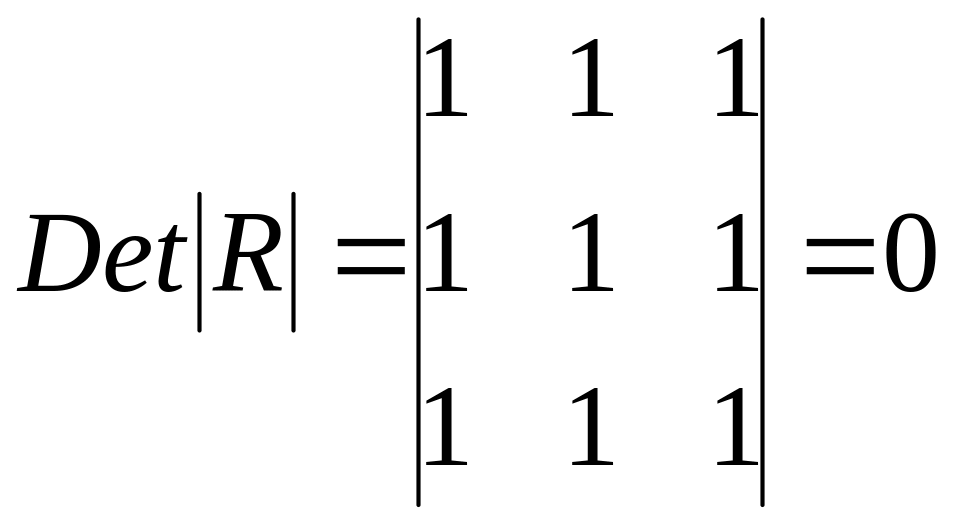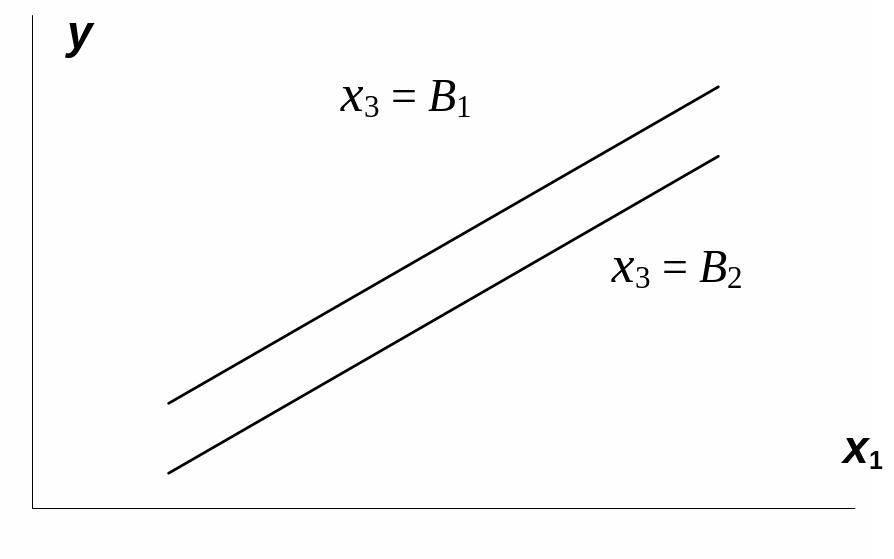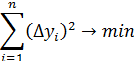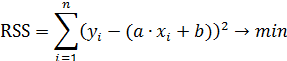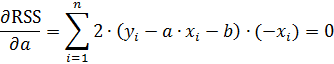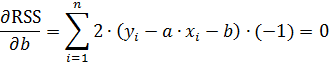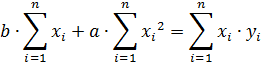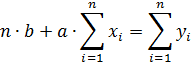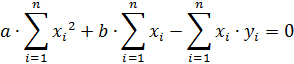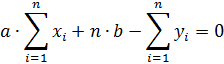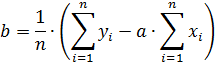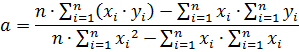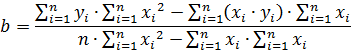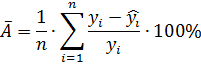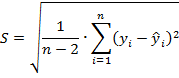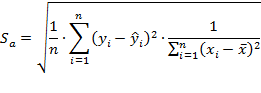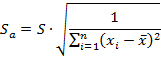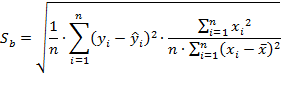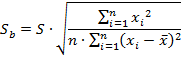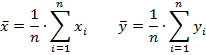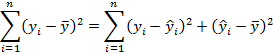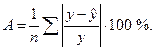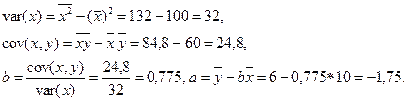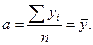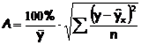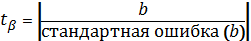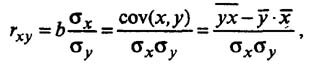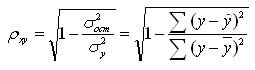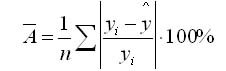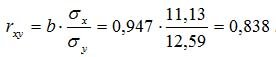Вопрос № 71829
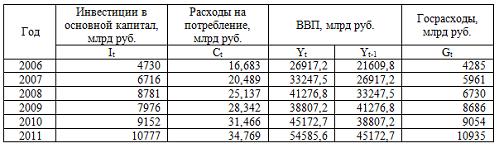
Имеются данные Росстата за период 2006 – 2011 гг. для построения одной из модификаций модели Кейнса
где Сt – расходы на потребление в текущем периоде, млрд руб.,
Yt – ВВП в текущем периоде, млрд руб.,
Yt-1 – ВВП в предыдущем периоде, млрд руб.,
Gt – государственные расходы, млрд руб.,
It – инвестиции в основные фонды, млрд руб.
Для решения систем одновременных уравнений не может быть использован ________ метод наименьших квадратов.
косвенный
двухшаговый
трехшаговый
обобщенный
Вопрос № 71881
Предпосылкой применения корреляционного анализа является утверждение:
совокупность значений факторных и результативных признаков имеет распределение Стьюдента
совокупность значений факторных признаков распределена по нормальному закону, а результативного – по произвольному
совокупность значений результативного признака распределена по нормальному закону, а закон распределения совокупности факторных признаков – произвольный
совокупность значений факторных и результативных признаков распределена по нормальному закону
Вопрос № 71922
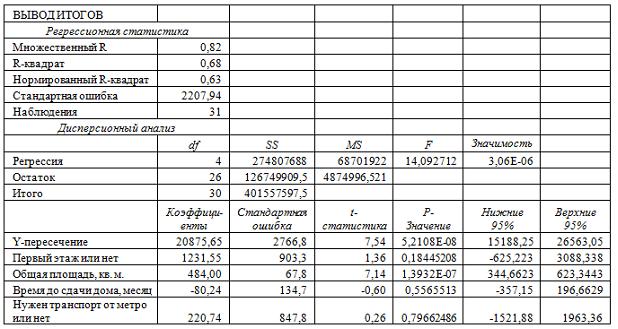
Имеются данные (31 наблюдений) о стоимости однокомнатных квартир, реализованных на первичном рынке в Выборгском районе Санкт-Петербурга. Цена квартиры измеряется в условных единицах. Фиктивная переменная «Первый этаж или нет» равна 1, если квартира расположена на первом этаже, или 0, если на любом другом этаже. Общая площадь измеряется в квадратных метрах. Время до сдачи дома измеряется в месяцах. Фиктивная переменная «Нужен транспорт до метро или нет» равна 0, если дом расположен в 15 минутах пешком от метро, и 1 в противном случае.
C помощью инструмента «Регрессия» анализа данных Excel рассчитаны приведенные в таблице показатели, характеризующую зависимость цены квартиры от факторов.
Параметр при соответствующем факторе считается значимым, если …
соответствующая величина Р-значения больше заданного уровня значимости
соответствующая величина t-статистики по модулю меньше критического значения
соответствующая величина t-статистики по модулю больше критического значения
соответствующая величина Р-значения меньше заданного уровня значимости
Вопрос № 72392
В таблице представлены результаты дисперсионного анализа. Значение остаточной суммы квадратов равно числу, определенному на пересечении …
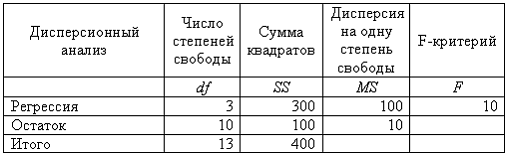
столбца «MS» и строки «Остаток»
столбца «df» и строки » Остаток»
столбца «SS» и строки «Регрессия»
столбца «SS» и строки «Остаток»
Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
(2.39)
Для
нашего примера эта величина составит:
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
;
S2
– остаточная сумма квадратов отклонений
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.
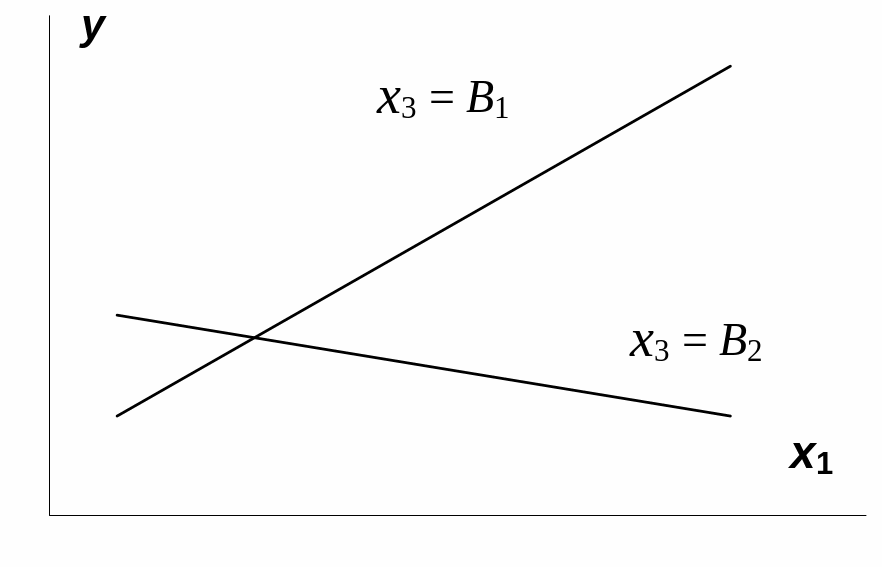
Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аппроксимация метод приближения, при котором некоторые величины (или объекты) выражаются через другие, более простые величины (или объекты). Таким образом, аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к более простым математическим моделям, которые более удобны к изучению.
В качестве исходных данных задан массив экспериментально полученных значений двух измеряемых величин: y1, y2, y3, … yn и x1, x2, x3, … xn , которые связаны некоторой функциональной зависимостью y=f(x), вид которой заранее не известен. Каждая пара совместно измеренных значений (xi, yi) определяет положение некоторой точки. Величины xi и yi не свободны от погрешностей, поэтому определяемые ими точки не лежат точно на какой-то кривой, а образуют некоторое облако с нечеткими границами. Необходимо определить регрессионную кривую y=f(x), проходящую через данную область точек.
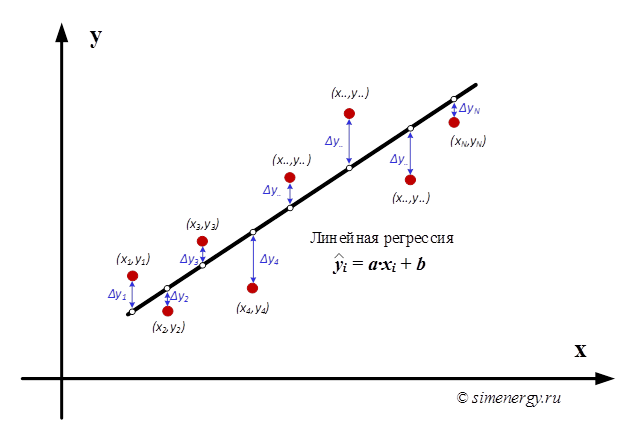
Линейная регрессия (англ. Linear regression) — модель зависимости одной переменной y от другой или нескольких других переменных x (факторов, регрессоров, независимых переменных) с линейной функцией зависимости:
где переменные «a» и «b» – параметры зависимости y=f(x).
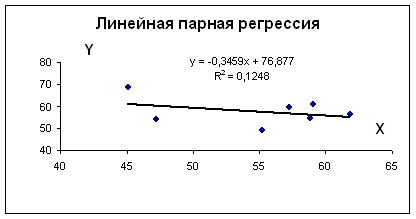
Рис.1. Линейная регрессия
Выбор параметров «a» и «b» должен быть выполнен таким образом, чтобы искомая теоретическая кривая y=f(x) наилучшим образом проходила через заданную область точек. Существуют различные критерии выбора наилучшего соответствия экспериментальных точек и регрессионной кривой. Одним из наиболее общих способов отыскания оценок истинных значений искомых параметров является разработанный Лежандром и Гауссом метод наименьших квадратов (МНК).
Примечание: Метод получения оценок параметров оптимальной прямой с помощью минимизации суммы квадратов отклонений называется Методом Наименьших Квадратов (сокращенно МНК) или Ordinary Least Squares (сокращенно OLS), а полученные оценки параметров называются МНК- или OLS-оценками.
Суть метода наименьших квадратов заключается в том, чтобы подобрать такие значения коэффициентов, при которых сумма квадратов отклонений измеренных в эксперименте значений (xi, yi) от искомой кривой y=f(x) была бы минимальна.
Обозначим функцию, которую требуется минимизировать через переменную RSS (Resudiual Sum of Squares) – остаточная сумма квадратов отклонений.
Сумма квадратов отклонений является функцией двух независимых переменных: «a» и «b». Для нахождения минимума суммы квадратов отклонений функции необходимо приравнять к нулю ее частные производные по «a» и «b».
Преобразуем полученную систему выражений
Перепишем систему уравнений в следующем виде
Из последнего выражения определяем параметр «b»
Далее подставляем полученное выражение в первое уравнение. Решая полученную систему уравнение, определим неизвестные параметры «a» и «b» (коэффициенты регрессионной кривой)
С учетом найденных коэффициентов «a» и «b» строится регрессионная кривая по следующему выражению:
где переменная — значения регрессионной кривой.
После того, как найдено уравнение линейной регрессии, проводится оценка, как уравнения в целом, так и отдельных его параметров.
П.1. Средняя ошибка аппроксимации
Общей характеристикой качества построенной регрессии (не только парной и линейной, но и любой другой) является средняя ошибка аппроксимации, которая показывает среднее отклонение расчетных значений от фактических. Средняя ошибка аппроксимации рассчитывается по формуле:
где переменная — значения регрессионной кривой
, переменная
– значения из массива исходных данных, а переменная 𝑛 — количество измерений.
Значение средней ошибки аппроксимации до 15% свидетельствует о хорошо подобранной модели уравнения.
П.2. Стандартная ошибка регрессии
Стандартная ошибка регрессии (Standard Error) — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии.
Стандартная ошибка регрессии определяется как корень квадратный из остаточной дисперсии
где переменная — значения регрессионной кривой
, переменная
– значения из массива исходных данных, а переменная 𝑛 — количество измерений.
В знаменателе формулы используется выражение , которое соответствует количеству степеней свободы: N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели y=a*x+b переменная k равна 1).
Значение стандартной ошибки позволяет увидеть степень отклонения значений, полученных с помощью регрессии, от фактически наблюдаемых, и таким образом оценить точность соответствующей модели.
Значение стандартной ошибки измеряет степень отличия реальных значений Y от уравнения линейной регрессии. Малая стандартная ошибка оценки, полученная при регрессионном анализе, свидетельствует, что все точки данных находятся очень близко к прямой регрессии. Если стандартная ошибка оценки велика, точки данных могут значительно удаляться от прямой.
П.3. Интервальные оценки параметров уравнения регрессии
Помимо определения качества уравнения регрессии в целом, также проводится оценка отдельных его параметров, а именно интервальные оценки параметров уравнения регрессии (Standard Error Coefficients).
Уравнение регрессии (y=ax+b) содержит коэффициенты «a» и «b», которые определяются теоретически по исходным данным. В результате полученное уравнение с определённой точностью описывает изменение экспериментальных данных. Поскольку уравнение регрессии может быть использовано при анализе и прогнозировании необходимо для данных коэффициентов уметь определять доверительные интервалы, в границах которых с определенной вероятностью находятся действительные значения параметров.
П.1. Доверительный интервал для коэффициента регрессии «a» определяется следующим соотношением
где переменная — стандартная ошибка оценки коэффициента регрессии «a»
Стандартная ошибка определяется по следующему выражению:
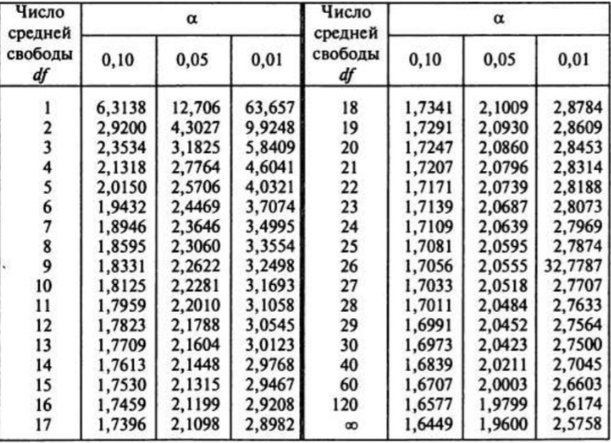
где переменная определяется из таблицы критических точек распределения Стьюдента в зависимости от уровня ошибки
, а
— среднее значение параметра.
П.2. Доверительный интервал для коэффициента регрессии «b» определяется следующим соотношением
где переменная – стандартная ошибка оценки свободного члена уравнения регрессии (коэффициента регрессии «b»)
Стандартная ошибка определяется по следующему выражению:
где переменная определяется из таблицы критических точек распределения Стьюдента в зависимости от уровня ошибки
, а
— среднее значение параметра.
Переменная определяется из таблицы критических точек распределения Стьюдента. Для этого в качестве исходных данных выбирается уровень ошибки (0,10 или 0,05 или 0,01 или другие значения в расширенной таблице), а далее выбирается значение переменной
в зависимости от количества степеней свободы: N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели y=a*x+b переменная k равна 1).
Рис.2. Таблица критических точек распределения Стьюдента в зависимости от уровня ошибки
Другой способ проверки статистической значимости параметров регрессии непосредственно не связан с построением доверительных интервалов. Проверка гипотезы осуществляется с помощью критерия Стьюдента (t-критерий Стьюдента). На основе полученных значений параметров регрессионной кривой, а также рассчитанных стандартных ошибок оценки коэффициента регрессии определяются эмпирические значения t-статистик:
где переменные «a» и «b» — значение параметра, а переменные и
— стандартная ошибка оценки коэффициента регрессии.
Далее полученные значения сравниваются со значениями , которые берутся из таблицы критических точек распределения Стьюдента при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы: N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели y=a*x+b переменная k равна 1). Если расчетное значение превышает по абсолютной величине табличное значение, то соответствующий коэффициент является статистически значимым с заданной доверительной вероятностью.
П.4. Линейный коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона характеризует существование линейной зависимости между двумя случайными величинами. Для случайных величин X и Y выборочный коэффициент корреляции определяется по формуле:
Параметры и
— стандартные отклонения, соответствующие случайным величинам X и Y, а cov(X,Y) – коэффициент ковариации переменных X и Y.
где 𝑥𝑖, 𝑦𝑖 – элементы выборки, n – размер выборки, а — среднее значение параметров.
Используя формулы средних перепишем выражение для определения линейного коэффициента корреляции Пирсона.
Все значения коэффициента корреляции находятся в интервале от -1 до +1. Близость к нулю абсолютного значения обычно означает слабую линейную взаимосвязь между переменными. В случае если абсолютное значение
близко к единице, то это говорит о сильной линейной взаимосвязи между ними. Коэффициент корреляции отражает тесноту именно линейной связи между переменными, т.е. близость его к нулю свидетельствует об отсутствии именно линейной зависимости. Однако при этом переменные могут иметь связь другого вида: нелинейную.
Также формула для определения коэффициента корреляции Пирсона может быть использована для анализа двух других случайных величин: значений из массива исходных данных и значений регрессионной кривой .
П.5. Коэффициент детерминации
Следующим критерием оценки качества точности уравнения регрессии является коэффициент детерминации (Coefficient of determination). Коэффициент детерминации определяется как отношение объясненной ошибки (SSR) к общей ошибки (SST).
Коэффициент детерминации представляет собой квадрат корреляционного отношения.
Коэффициент детерминации является удобной оценкой степени связи между регрессивной линией и фактическими данными. Коэффициент детерминации показывает, какая доля общей вариации исследуемого показателя определяется (детерминируется) совокупным влиянием функции регрессии (т. е. выбранными нами объясняющими показателями).
Данное выражение переписывают в другом виде в случае линейной регрессии, т.к. в случае линейной регрессии с константой справедливо следующее соотношение:
В результате для линейной регрессии с константой коэффициент детерминации определяется следующим образом:
где 𝑦𝑖 – элементы выборки, n – размер выборки, — среднее значение параметров, а
– значения функции линейной регрессии .
Примечание: Еще раз обращаем Ваше внимание, что данная запись справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.
Коэффициент детерминации измеряет долю изменчивости Y, которую можно объяснить с помощью информации об изменчивости (разнице значений) независимой переменной X. Коэффициент детерминации изменяется в диапазоне от −∞ до 1.
Если коэффициент детерминации равен 1, это соответствует идеальной модели, когда все точки наблюдений лежат точно на линии регрессии, т.е. сумма квадратов их отклонений равна 0.
Если коэффициент детерминации равен 0, это означает, что связь между переменными регрессионной модели отсутствует, и вместо нее для оценки значения выходной переменной можно использовать простое среднее ее наблюдаемых значений.
Так же следует обратить внимание, что в случае линейной регрессии коэффициент корреляции значений из массива исходных данных и значений регрессионной кривой равен квадратному корню из коэффициента детерминации
:
П.6. Критерий Фишера (F-тест)
Критерий Фишера (F-критерий Фишера) — статистический критерий для оценки значимости различия дисперсий двух случайных выборок, который позволяет оценивать значимость линейных регрессионных моделей. В частности, он используется для проверки целесообразности включения или исключения независимых переменных (признаков) в регрессионную модель.
Критерий Фишера позволяет подтвердить или опровергнуть нулевую гипотезу с помощью сравнения дисперсии двух независимых выборок. Нулевая гипотеза — принимаемое по умолчанию предположение о том, что не существует связи между двумя наблюдаемыми событиями.
Для определения статистической значимости в начале рассчитывается значение F-критерия Фишера. Фактическое значение статистики Фишера равно отношению удельных (рассчитанных на одну степень свободы) факторной и остаточной дисперсий:
где n – объём выборки, m – число параметров «Х» в уравнении регрессии.
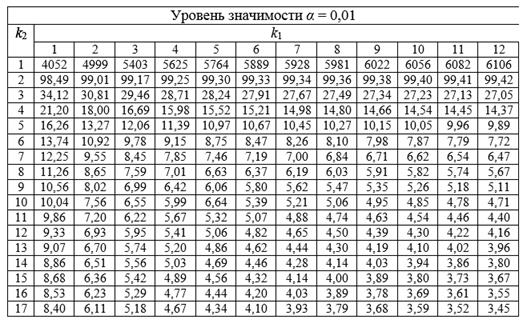
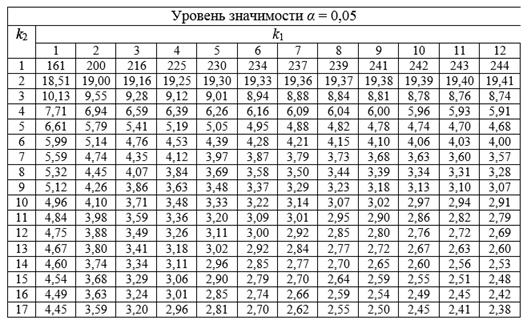
Затем значение F-критерия Фишера сравнивают с критическим (или табличным) значением. При этом табличное значение определяется на основе числа наблюдений, степеней свободы и заданного уровня значимости следующим образом: Fтабл (a; k1; k2), где k1 = m, где m – это количество факторов в построенной регрессионной модели (число степеней свободы большей дисперсии), а k2 = n – m – 1, где n – число наблюдений (число степеней свободы меньшей дисперсии).
Рис.3. Таблица критических точек распределения Фишера-Снедекора при допустимом уровне значимости a=0.01
Рис.4. Таблица критических точек распределения Фишера-Снедекора при допустимом уровне значимости a=0.05
В частности, для линейной регрессии (частный F-критерий) переменные k1 = 1, k2 = n – 2 (n – число наблюдений).
Вычисленное значение F – отношения признается достоверным, если оно больше табличного. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, то есть подтверждается статистическая значимость всего уравнения и показателя тесноты связи.
П.1. В случае если значение критерия Фишера больше критического
, то принимается нулевая гипотеза и делается вывод об отсутствии статистически значимых различий частоты исхода в зависимости от наличия фактора риска.
П.2. В случае если значение критерия Фишера меньше критического
, то принимается альтернативная гипотеза и делается вывод о наличии статистически значимых различий частоты исхода в зависимости от воздействия фактора риска. Соответственно уравнение регрессии считается статистически незначимым и тем самым признается ненадежность уравнения регрессии.
Интерпретация частного F — критерия Фишера следующая: в том случае, когда рассчитанная величина частного Fxi превышает критическое значение, то дополнительное включение фактора xi в регрессионную модель статистически оправданно и коэффициент регрессии bi при соответствующем факторе xi статистически значим. Но если рассчитанная величина Fxi меньше табличного, то дополнительное включение в модель фактора xi не оправдано, т.к. данный фактор, как и коэффициент регрессии при нём является статистически незначимым.
П.7.Использование нелинейных функций.
Аппроксимация опытных данных также может быть выполнена нелинейными функциями. При этом отдельные нелинейные функции могут быть приведены к линейным функциям путем замены переменных. Соответственно, для этих нелинейных функций, могут использоваться методы для анализа линейной функции. Рассмотрим данные нелинейные функций и методику преобразования данных функций к линейному виду.
П.7.1. Задана исходная нелинейная функция #1 (Степенная функция)
Преобразуем функцию с линейному виду с помощью логарифмирования. В результате получим функцию в следующем виде:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #1 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
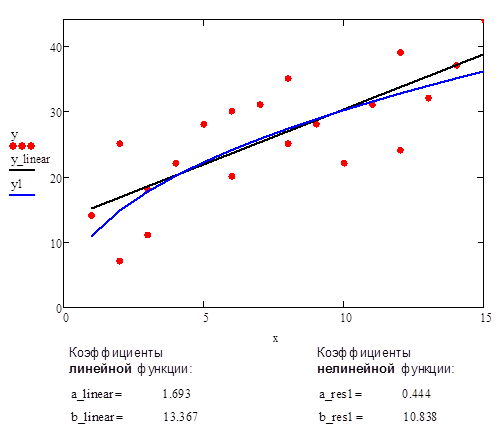
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #1.
Рис.5. Аппроксимации данных с помощью прямой линии и нелинейной функции #1 (Степенная функция)
П.7.2. Исходная нелинейная функция #2 (логарифмическая функция)
Делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #2 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
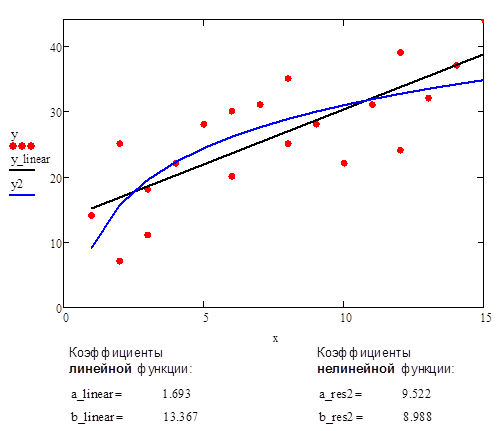
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #2.
Рис.6. Аппроксимации данных с помощью прямой линии и нелинейной функции #2 (логарифмическая функция)
П.7.3. Исходная нелинейная функция #3 (экспоненциальная функция)
Преобразуемая функция с помощью логарифмирования к следующему виду:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #3 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
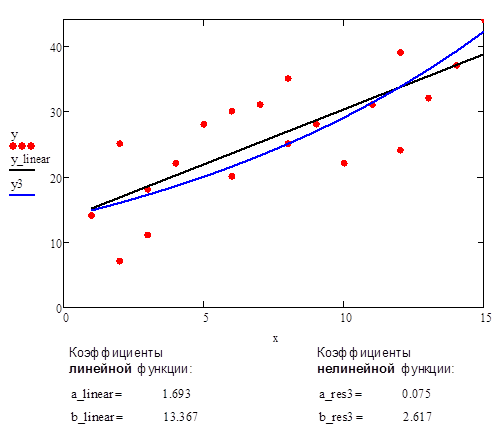
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #3.
Рис.7. Аппроксимации данных с помощью прямой линии и нелинейной функции #3 (экспоненциальная функция)
П.7.4. Исходная нелинейная функция #4 (экспоненциальная функция)
Преобразуемая функция с помощью логарифмирования к следующему виду:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #4 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
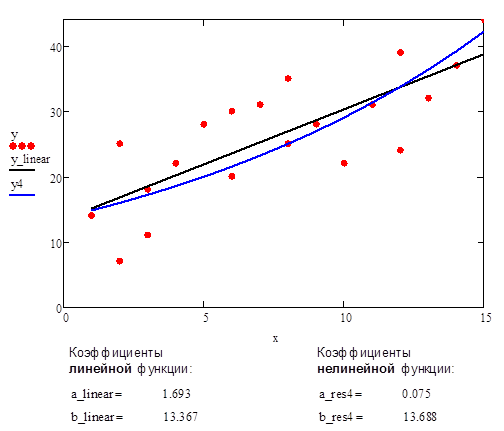
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #4.
Рис.8. Аппроксимации данных с помощью прямой линии и нелинейной функции #4 (экспоненциальная функция)
П.7.5. Исходная нелинейная функция #5 (гиперболическая функция, гипербола)
Делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #5 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
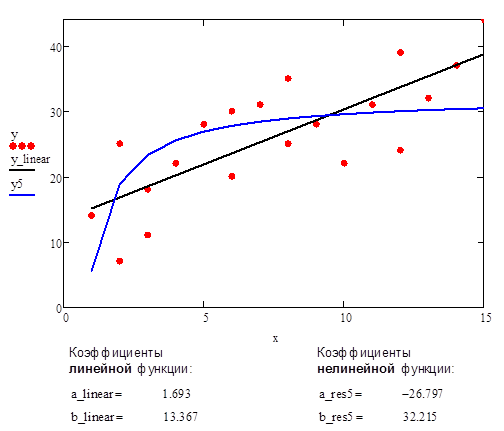
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #5.
Рис.9. Аппроксимация данных с помощью прямой линии и нелинейной функции #5 (гиперболическая функция, гипербола)
П.7.6. Исходная нелинейная функция #6 (дробно-линейная функция)
Преобразуемая функция к следующему виду:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #6 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
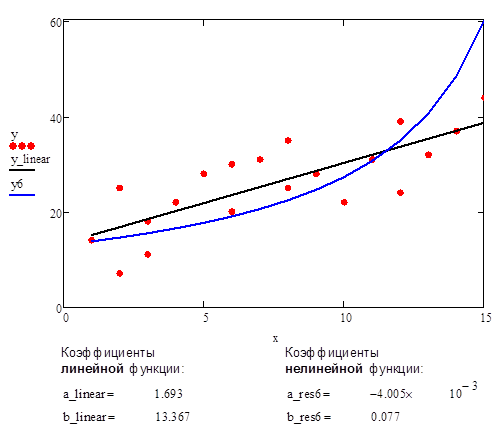
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #6.
Рис.10. Аппроксимация данных с помощью прямой линии и нелинейной функции #6 (дробно-линейная функция)
П.7.7. Исходная нелинейная функция #7 (Дробно-линейная функция)
Преобразуемая функция к следующему виду:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #7 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
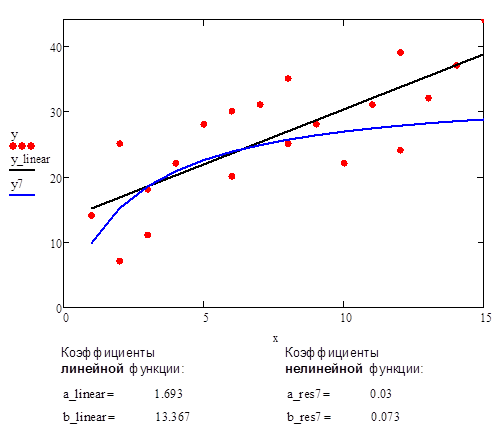
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #7.
Рис.11. Аппроксимация данных с помощью прямой линии и нелинейной функции #7 (дробно-линейная функция)
Выбор аппроксимирующей функции является важной задачей, так как от выбранной функции в существенной мере зависят количественные характеристики и качественные свойства описания объекта.
Средняя ошибка аппроксимации
По семи территориям Уральского района за 199Х г. известны значения двух признаков.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации Аср и F-критерий Фишера.
Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии.
а) линейное уравнение регрессии;
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = -0.35, a = 76.88
Уравнение регрессии: y = -0.35 x + 76.88
| x | y | x 2 | y 2 | x • y | y(x) | (y i -y cp ) 2 | (y-y(x)) 2 | |y — y x |:y |
| 45,1 | 68,8 | 2034,01 | 4733,44 | 3102,88 | 61,28 | 119,12 | 56,61 | 0,1094 |
| 59 | 61,2 | 3481 | 3745,44 | 3610,8 | 56,47 | 10,98 | 22,4 | 0,0773 |
| 57,2 | 59,9 | 3271,84 | 3588,01 | 3426,28 | 57,09 | 4,06 | 7,9 | 0,0469 |
| 61,8 | 56,7 | 3819,24 | 3214,89 | 3504,06 | 55,5 | 1,41 | 1,44 | 0,0212 |
| 58,8 | 55 | 3457,44 | 3025 | 3234 | 56,54 | 8,33 | 2,36 | 0,0279 |
| 47,2 | 54,3 | 2227,84 | 2948,49 | 2562,96 | 60,55 | 12,86 | 39,05 | 0,1151 |
| 55,2 | 49,3 | 3047,04 | 2430,49 | 2721,36 | 57,78 | 73,71 | 71,94 | 0,172 |
| 384,3 | 405,2 | 21338,41 | 23685,76 | 22162,34 | 405,2 | 230,47 | 201,71 | 0,5699 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(45.1) = -0.35*45.1 + 76.88 = 61.28
y(59) = -0.35*59 + 76.88 = 56.47
. . .
Ошибка аппроксимации
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:
F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Средняя ошибка аппроксимации
Оценку качества построенной модели дает коэффициент детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений зависимой переменной от фактических:
Допустимый предел значений A – не более 8-10 %.
Пример 2.5. Построим регрессионные зависимости: а) расходов на питание (y) и личным доходом (x); б) расходов на питание (y) и временем (t) по следующим данным (усл. ед.):
и оценим качество подгонки.
а) Пусть истинная модель описывается выражением y = a + b x + e.
По выборочным наблюдениям определяем оценки (a; b).
Исходные данные и расчетные показатели представим в виде следующей расчетной таблицы:
| Год | X | Y | X 2 | Xy | 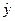 |
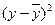 |
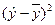 |
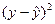 |
| -0,2 | 38,44 | 1,44 | ||||||
| 2,9 | 9,61 | 0,81 | ||||||
| 9,1 | 9,61 | 3,61 | ||||||
| 12,2 | 38,44 | 0,04 | ||||||
| Итого | 96,1 | 9,9 | ||||||
| Сред. | 84,8 | 21,2 | 19,22 | 1,98 | ||||
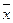 |
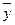 |
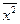 |
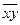 |
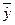 |
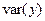 |
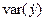 |
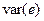 |
Cледовательно, 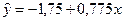
Коэффициент b = 0,775 показывает, что при увеличения дохода на 1 усл. ед расходы на питание увеличиваются в среднем на 0,775 усл. ед.
Замечание.В Excel оценки (a, b) можно также определить с помощью функций:
Условие 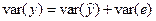
Качество подгонки оцениваем коэффициентом детерминации:
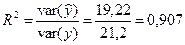
Значимость коэффициента R 2 проверяем по F-тесту
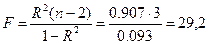
Произведем проверку значимости R 2 двумя способами.
1. При α = 0,05, n1= 1 и n2 = 3 по таблице или с помощью функции FРАСПОБР(α; n1; n2) находим Fкр = 10,13. Поскольку F = 29,2 > Fкр = 10,13, то R 2 = 0,952 значим при 5 % уровне.
2. Наблюдаемому (расчетному) значению критерия F = 29,2 соответствует значимость F =0,0124, которую можно определить в Excel с помощью функции FРАСП(F; n1; n2).
Поскольку значимостьF = 0,0124 2 значим при уровне 5 %.
б) Пусть истинная модель y = a + b t + e, (модель временного ряда). Выборочная регрессия 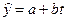
Представим исходные и расчетные показатели в виде расчетной таблицы:
| Год | t | Y | t 2 | ty | 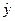 |
| –0,2 | |||||
| 2,9 | |||||
| 9,1 | |||||
| 12,2 | |||||
| Итого | |||||
| Среднее | 24,2 | ||||
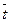 |
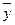 |
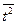 |
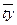 |
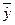 |
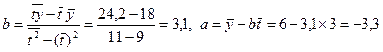
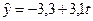
Коэффициент b = 3,1 показывает, что за год расходы на питание в среднем возрастают на 3,1 единиц.
Пример 2.6. Покажем, что в модели регрессии без свободного члена
Y = b X + e оценка МНК дляbесть:
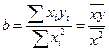
Выборочная регрессия для этой модели есть 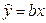
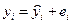
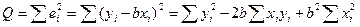
Запишем необходимые условия экстремума:
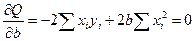
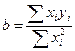
Вычисление R 2 при отсутствии свободного члена некорректно; при этом не выполняется условие 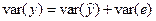
Пример 2.7. Покажем, что в модели регрессии Y = a + e оценка МНК для a есть: 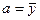
Выборочная регрессия для заданной модели есть 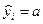
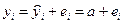
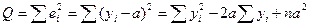
Запишем необходимые условия экстремума:
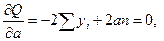
Выборочная регрессия 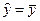
Расчет средней ошибки аппроксимации. Практическое применение
СОА показывает среднее отклонение расчетных данных результативного признака от фактических. Допустимый предел 8-10%.
Величина отклонений фактических и расчетных значений результативного признака 
Поскольку 
Отклонения 

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации:
Возможно и иное определение средней ошибки аппроксимации:
Если А =10-12%, то можно говорить о хорошем качестве модели.
Смысл средней ошибки аппроксимации в том, что это один из многих способов оценить разницу между аппроксимированнм и реальным значениями изучаемой величины. То есть это «квантификатор» потерь (в экономическом смысле) или риска.
27) Эластичность в социально-экономических моделях. Частные коэффициенты эластичности. Практическое применение.
Эластичность — мера чувствительности одной переменной (например: спроса или предложения) к изменению другой (например: цены, дохода), показывающая, на сколько процентов изменится первый показатель при изменении второго на 1 %.
Внимание отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае двухфакторной модели вычисляются по формулам:

В экономических исследованиях широкое применение находит такой показатель, как коэффициент эластичности. Если зависимость между переменными x и y имеет вид y=f(x) , то коэффициент эластичности Э вычисляется по формуле
Коэффициент эластичности Э показывает, на сколько процентов в среднем изменится результативный признак у при изменении фактора х на 1 % от своего номинального значения. Для линейной регрессии коэффициент эластичности равен
28. t-критерий Стьюдента. Алгоритм выполнения. Практическое применение.
t – критерий Стьюдента проводится с целью проверки значимости каждого параметра в отдельности.
Если проверяется значимость каждого параметра, то выбирают t – критерий Стьюдента и гипотеза строится 
Алгоритм t – критерия:
1) Выдвигается H0 и H1 гипотезы, рассчитываются значения статистики, лежащей в основе критерия и дающей ему название – t-статистика.
Сконфигурировав линейнуб ф-ию (вызвав «линейн») и вызвав предварительно выбранный диапазон ячеек (2×5) статистику (в поле «статистика» = 1), стандартная ошибка соответствующего коэф-та находится под ним:
2) Из таблицы t-распределения с заданным уровнем значимости, кот задает № столбца и числом степеней свободы, рассчитанному на основе числа наблюдений № — кол-во оцениваемых параметров задает № строки, выбирается t-табличное.
| Число степеней свободы Уровни значимости | 1% | 5% | 10% |
| … | |||
| t 1% | t 5% |
N=10; Число степеней свободы = 8. Уровень значимости всегда берется по двустороннему критерию.
3) Сравниваем 
Следовательно, делается вывод о статистической значимости.
28. F-критерий Фишера. Алгоритм выполнения. Практическое применение.
F-критерий Фишера проводится с целью проверки значимости всей модели в целом.
Алгоритм F– критерия:
1) При выдвижении Н0 сравниваются (строятся отношения) дисперсий (Дфак – факторной и Дост – остаточной). И на основе их соотношения рассчитывается F-статистика:
F-статистика – величина, лежащая в основе критерия и дающая ему название.
Дисперсия рассчитывается в рамках дисперсионного анализа (см далее).
| B | A |
| СО (b) | СО (a) |
| R 2 | СО (y) |
| F-статистика | ЧСС |
 |
СО – стандартная ошибка
В нулевой гипотезе (Н0) делается предположение о равенстве дисперсии факторной и дисперсии остаточной.
H1 : Дф 
В случае, если удастся принять альтернативную гипотезу дополнительно делается сравнение дисперсии через неравенства: Дф 
2) Из таблиц F-распределения выбираются критические (табличные) значения F -статистики. Таблица сформирована с учетом:
1. Уровня значимости (в заголовке таблицы);
2. Числа степеней свободы – ЧСС (равно номеру строки, номер строки в таблице F-критерий, t-критерий), для парной модели ЧСС = n -2 (n – число наблюдений);
3. Кол-во независимых переменных – НП (номер столбца).
Число степеней свободы рассчитывается в общем виде по формуле:
ЧСС = n-k-1, k – кол-во независимых переменных
3) Выполняется сравнение F-статистики из п. 1 с F-критическими из п. 2 (2 при 1%, и 5%).
Для отклонения нулевой гипотезы требуется выполнение неравенства:
В противном случае делается вывод о статистической значимости уравнения регрессии в целом.
Дисперсионный анализ
В дисперсионном анализе и в F-критерии Фишера рассматривают условно сконструированные дисперсии на основе соответствующих сумм квадратов. В основе лежит равенство (**) – разложение общей суммы квадратов отклонений СВ от среднего на факторную и остаточную сумму квадратов.
Для перехода к дисперсиям соответствующая сумма квадрата делится на ЧСС (свое для каждой суммы).
Определить ЧСС для расчета среднего значения СВ y, имеющей 5 значений.
| yi | Y1 | y2 | y3 | y4 | y5 |
 |
|||||
 |
-2 | -1 |
а — СО (а)* t табл 1%
Для линейной парной модели выполняется след связь между F и t критериями:
Таким образом, говорят о равносильности в данном частном случае этих двух критериев на практике.
В ряде прикладных программ и задач требуется оценить значимость коэффициента корреляции. Для этого строится гипотеза:
Н0: r генерал = 0
H1: r генерал не равно 0
Проверка осуществляется на основе расчета t – статистики через выборочный коэф-т корреляции, а затем на основе таблиц t – распределения выполняется сравнение рассчитанного значения с табличным.
Для линейной парной модели r 2 – это формула для расчета коэф-та детерминации: R 2 = r 2 .
Чем ближе R 2 к единице, тем лучше регрессия аппроксимирует эмпирические данные (приближает наблюдаемые данные).
Если R 2 = 1, то эмпирические точки лежат на линии регрессии, и между экзогенной и эндогенной переменными сущ-ет лин функциональная зависимость.
Если R 2 = 0, то изменение эндогенной переменной у всецело опр-ся изменением всех неучтенных в модели факторов (от изменения x не зависит).
| yi = |  |
+ |  |
 |
 R 2 = 0,3 R 2 = 0,3 |
 1 – R 2 = 0,7 1 – R 2 = 0,7 |
В прикладных задачах всегда начинают исследование с линейной функции, затем берут либо степенную, либо показательную. Затем полином второй степени и в редком случае третьей.
источники:
http://helpiks.org/7-5944.html
http://lektsii.org/6-58481.html
Коэффициент корреляции
Тесноту (силу) связи изучаемых показателей в предмете эконометрика оценивают с помощью коэффициента корреляции Rxy, который может принимать значения от -1 до +1.
Если Rxy > 0,7 — связь между изучаемыми показателями сильная, можно проводить анализ линейной модели
Если 0,3 < Rxy < 0,7 — связь между показателями умеренная, можно использовать нелинейную модель при отсутствии Rxy > 0,7
Если Rxy < 0,3 — связь слабая, модель строить нельзя
Для нелинейной регрессии используют индекс корреляции (0 < Рху < 1):
Средняя ошибка аппроксимации
Для оценки качества однофакторной модели в эконометрике используют коэффициент детерминации и среднюю ошибку аппроксимации.
Средняя ошибка аппроксимации определяется как среднее отклонение полученных значений от фактических
Допустимая ошибка аппроксимации не должна превышать 10%.
В эконометрике существует понятие среднего коэффициента эластичности Э – который говорит о том, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины.
Пример нахождения коэффициента корреляции
Исходные данные:
|
Номер региона |
Среднедушевой прожиточный минимум в день одного трудоспособного, руб., |
Среднедневная заработная плата, руб., |
|
1 |
81 |
124 |
|
2 |
77 |
131 |
|
3 |
85 |
146 |
|
4 |
79 |
139 |
|
5 |
93 |
143 |
|
6 |
100 |
159 |
|
7 |
72 |
135 |
|
8 |
90 |
152 |
|
9 |
71 |
127 |
|
10 |
89 |
154 |
|
11 |
82 |
127 |
|
12 |
111 |
162 |
Рассчитаем параметры парной линейной регрессии, составив таблицу
| x |
x2 |
y |
xy |
y2 |
|
|
1 |
81 |
6561 |
124 |
10044 |
15376 |
|
2 |
77 |
5929 |
131 |
10087 |
17161 |
|
3 |
85 |
7225 |
146 |
12410 |
21316 |
|
4 |
79 |
6241 |
139 |
10981 |
19321 |
|
5 |
93 |
8649 |
143 |
13299 |
20449 |
|
6 |
100 |
10000 |
159 |
15900 |
25281 |
|
7 |
72 |
5184 |
135 |
9720 |
18225 |
|
8 |
90 |
8100 |
152 |
13680 |
23104 |
|
9 |
71 |
5041 |
127 |
9017 |
16129 |
|
10 |
89 |
7921 |
154 |
13706 |
23716 |
|
11 |
82 |
6724 |
127 |
10414 |
16129 |
|
12 |
111 |
12321 |
162 |
17982 |
26244 |
|
Среднее |
85,8 |
7491 |
141,6 |
12270,0 |
20204,3 |
|
Сумма |
1030,0 |
89896 |
1699 |
147240 |
242451 |
| σ |
11,13 |
12,59 |
|||
| σ2 |
123,97 |
158,41 |
формула расчета дисперсии σ2 приведена здесь.
Коэффициенты уравнения y = a + bx определяются по формуле
Получаем уравнение регрессии: y = 0,947x + 60,279.
Коэффициент уравнения b = 0,947 показывает, что при увеличении среднедушевого прожиточного минимума в день одного трудоспособного на 1 руб. среднедневная заработная плата увеличивается на 0,947 руб.
Коэффициент корреляции рассчитывается по формуле:
Значение коэффициента корреляции более — 0,7, это означает, что связь между среднедушевым прожиточным минимумом в день одного трудоспособного и среднедневной заработной платой сильная.
Коэффициент детерминации равен R2 = 0.838^2 = 0.702
т.е. 70,2% результата объясняется вариацией объясняющей переменной x.